- 1CEMSE Division, King Abdullah University of Science and Technology (KAUST), Thuwal, Saudi Arabia
- 2Institute for Communication Systems (ICS), University of Surrey, Guildford, United Kingdom
The fifth-generation cellular network requires dense installation of radio base stations (BS) to support the ever-increasing demands of high throughput and coverage. The ongoing deployment has triggered some health concerns among the community. To address this uncertainty, we propose an EMF-aware probabilistic shaping design for hardware-distorted communication systems. The proposed scheme aims to minimize human exposure to radio frequency (RF) radiations while achieving the target throughput using probabilistic shaping. The joint optimization of the transmit power and nonuniform symbol probabilities is a non–convex optimization problem. Therefore, we employ alternate optimization and successive convex approximation to solve the subsequent problems. Our findings reveal a significant reduction in the users’ exposure to EMF while achieving the requisite quality of service with the help of probabilistic shaping in a hardware-distorted communication system.
1 Introduction
The next-generation wireless communication networks are expected to fulfill the ever-increasing demands of higher data rates, ultra-reliability, minimal latency, high energy efficiency, and massive connectivity for many users/devices (Latva-aho et al., 2020). The fifth-generation (5G) wireless technology is envisioned to support numerous diverse services, such as enhanced mobile broadband (eMBB), ultra-reliable low latency communication (URLLC), and massive machine-type communication (mMTC) (Wan et al., 2018). Some of the new spectra allocated for 5G deployments, for example, millimeter waves, suffer from relatively high path loss, limiting the coverage area. Thus, network densification becomes essential for achieving the promised data rate, which can be realized over space [e.g., dense deployment of base stations (BSs) in small cells] and frequency (large segments of the RF spectrum in diverse bands) (Bhushan et al., 2014).
Installation of 5G cellular technology with extreme node and network densification (with BSs being closer to users) is raising health concerns about the impact of electric and magnetic fields (EMFs) exposure on the population. These worries have sparked several protests against 5G technology and led to some attacks on the 5G BSs (Elzanaty et al., 2021). Recently, anti-5G protests have been held in 30 countries around the world against the threat of 5G wireless technology to public health, the environment, and privacy.
Indeed, the thermal effect is the only proven health impact from RF nonionizing short-term exposure. Therefore, it is necessary to keep the radiation intensity below specific values defined by the exposure regulations and guidelines, such as those of the Federal Communications Commission (FCC) and the International Commission on Non-Ionizing Radiation Protection (ICNIRP) (Buchner and Rivasi, 2020). Nevertheless, there is a debate about severe health impacts due to long-term exposure to EMF (National Toxicology Program, 2018a,b; Vornoli et al., 2019). Hence, the International Agency for Research on Cancer (IARC) classified RF radiation as “possibly carcinogenic to humans” (Vornoli et al., 2019; Group, 2013; Wilbourn et al., 1986).
Recently, a comprehensive study revealed that exposure due to the uplink (UL) from user equipment (UE) is higher than from the BS due to the proximity of the UE to the user (Lou et al., 2021). Another work has proposed an architectural solution to minimize the EMF exposure using reconfigurable intelligent surfaces (Ibraiwish et al., 2022). Another study focused on meticulous cellular network planning to limit exposure from the BSs exploiting MIMO while ensuring coverage and capacity constraints (Matalatala et al., 2018). From the regulatory aspects, some possible risk mitigation strategies are dismission of legacy 2G/3G/4G technologies and reduction of emissions from noncellular sources (Chiaraviglio et al., 2021).
Nevertheless, as mentioned earlier, the EMF exposure–based research does not consider any hardware impairments, which can drastically affect the system performance, such as raising the noise floor. For instance, in order to reach the target data rates in eMBB, hardware distortion (HWD) should be mitigated. Generally, users send a much higher power, escalating their RF exposure to achieve the target rate. The users may still not reach the required throughput due to the saturation for the data rate at a higher SNR as the distortion noise increases with the transmit power.
HWD requires some meticulously designed systems to compensate for its effect and mitigate performance loss. Improper Gaussian signaling (IGS) is an effective compensation signaling scheme that can alleviate the impact of several interference and imperfection sources (Javed et al., 2019). However, realizing the IGS comes with inherent problems of the unbounded peak-to-average power ratio and high detection complexity (Santamaria et al., 2018; Javed et al., 2020). As a consequence, researchers employ finite discrete asymmetric signaling (AS) schemes that can be achieved by geometric shaping (GS), probabilistic shaping (PS), or hybrid shaping (HS) (Elzanaty and Alouini, 2022; Javed et al., 2021). In this work, we propose asymmetric signaling by adopting PS to tackle improper HWD and minimize EMF exposure to the users while maintaining throughput quality of service (QoS). The contributions of this study are summarized as follows:
• We model HWD and EMF exposure in the next-generation wireless cellular network. We present an appropriate receiver and rigorous error probability analysis considering the improper distortion noise.
• We propose probability shaping as a form of asymmetric signaling to effectively mitigate improper HWDs and reduce EMF exposure while maintaining QoS in terms of user throughput.
• We employ alternate optimization to jointly design the transmit power of users and nonuniform symbol probabilities. We further use successive convex approximation and the Newton–Raphson method to solve subsequent problems.
The rest of the article is organized such that Section 2 illustrates the system description and adopted models to characterize the radiation exposure and HWD. The error probability analysis is carried out in Section 3, while Section 4 covers the problem formulation and optimization framework. Numerical results are presented in Section 5, followed by the conclusion in Section 6.
2 System Description
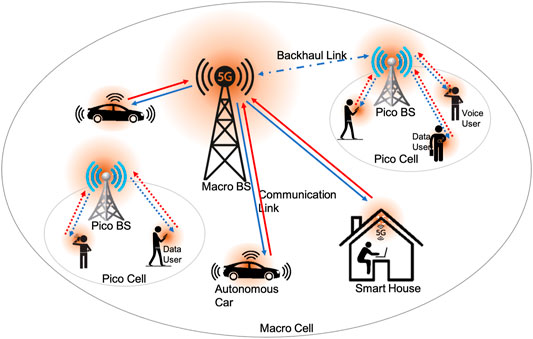
In this section, we quantify the EMF exposure of the human population in a next-generation wireless cellular communication system. The network comprises a macro-cell with a macro BS and multiple pico-cells with their serving pico BSs. Apart from the transmitting radiations from the BSs in the downlink (DL), we are interested in the EMF exposure caused by handheld devices. For instance, the RF radiations emitting from cell phones and smartwatches are stronger nearer the users, resulting in near-field exposure, whereas the EMF transmission density from BS towers situated far from the users render far-field exposure. Likewise, increasing applications and use cases including but not limited to autonomous vehicles and smart homes/offices, etc., are extending their radiation footprint near humans. Figure 1 demonstrates a strong radiation pattern near users in the case of voice users when compared with data users. In addition, we account for the performance degradation caused by the additive HWDs accumulating from the various blocks in nonideal RF transceivers. We propose a generalized digital communication system capable of transmitting nonuniformly distributed symbols (from a uniform bitstream using distribution matching) while using an appropriate receiver for optimal detection.
2.1 Radiation Exposure
The modeling and quantification of human exposure in a wireless cellular network are critical to facilitate the reduction efforts. Numerous studies have identified the essential parameters influencing this end exposure (Kuehn et al., 2019; Lou et al., 2021; Vermeeren et al., 2015a). The EMF exposure, quantified as the exposure index (EI), is primarily dictated by the network topology, environment, radio access technology, user scenarios, and service types (Kuehn et al., 2019). The EI can be written as the weighted sum of all branches in the chain of exposure (Lou et al., 2021).
where the specific absorption rate (SAR), measured in W/kg, is the power absorbed per mass of the exposed tissue for a given period, with SARUL and SARDL indicating the normalized values of the UL- and DL-induced SARs when the mean transmit power α = 1W and the mean received power density ϱ = 1W/m2, respectively. The EI is integrated over different age groups g (e.g., children, young people, adults, and seniors), user posture p (e.g., standing and sitting), environments e (e.g., indoor, outdoor, and commuting), radio access technology r (e.g., GSM, UMTS, Wi-Fi, 5G), layers l (macro, micro, pico, and femto), and service/usage types s (e.g., voice and data) (Tesanovic et al., 2014). We consider an exposure scenario of the next-generation cellular network in an indoor environment where the reference SAR is averaged over different population ages and postures, accommodating both data and voice usage types. The EI for both the UL and DL can be given by EI = EIUL + EIDL, combining the DL exposure induced all day long by base stations/access points and the UL exposure incurred by individual wireless communication devices.
Contrary to the general perception, the SAR from the UL renders the dominant part instead of the one from DL with low ϱ (generally
2.2 Hardware-Impaired Signal Model
The nonlinear transfer functions of various transmitter RF stages, such as the digital-to-analog converter, band-pass filter, and high-power amplifier, result in additive distortion noise ηt, which is distributed as a zero-mean complex Gaussian random variable
The Gaussian model for the aggregate residual RF distortions is based on various theoretical investigations, including the central limit theorem and measurement results after applying existing compensation schemes (Wenk, 2010; Zetterberg, 2011; Boulogeorgos et al., 2016; Xia et al., 2015; Suzuki et al., 2008; Studer et al., 2010; Duy et al., 2015; Björnson et al., 2014; and references therein). This can also be motivated analytically by the central limit theorem. The accumulative distortions raise the noise floor of the transmitted signal as xtx = xm + ηt, where xm is the single-carrier band-pass–modulated signal taken from M-ary QAM, M-ary PSK, or M-ary PAM constellation with a probability mass function pm ≜ pX (xm), rendering the transmission probability of symbol xm, and p ≜ [p1, p2, … , pM]. Let us define the set that includes all the possible symbol distributions as
The information-bearing signal is transmitted with an average power α and received under an additive white Gaussian noise (AWGN) condition and receiver distortions
where
2.3 Noise Distribution and Optimal Receiver
Considering the aggregate noise
These individual variances are obtained by simultaneously solving the equations of variance, that is,
Unequal power distribution among the quadrature noise components and nontrivial correlation coefficient marks the improper nature of aggregate additive distortions. Given the nonuniform symbol probabilities and improper noise, we propose a maximum a posterior (MAP) detector for the optimal detection as opposed to the conventional minimum Euclidean or maximum likelihood (ML) detectors (Javed et al., 2021). Thus, the detection criterion is given by
where
3 Error Probability Analysis
In this section, we derive the symbol error probability Ps for a system transmitting M-ary–modulated symbols with prior probabilities pm and subjected to HWD using the union-bound and pairwise error probability as follows:
The pairwise error probability, for receiving an erroneous symbol xm given xn was transmitted, can be derived using the following MAP rule:
Using (7) and few simplifications, we get the following bit error probability as
where βmn is defined as
with
4 Problem Formulation and Optimization
We propose a PS scheme, as a possible form of AS schemes, to effectively mitigate the drastic effects of additive distortions while transmitting with minimum power to minimize the EMF exposure. To this end, we employ a higher-order Mnu probabilistically shaped quadrature amplitude modulation (QAM) offering more degrees of freedom and adaptive rates. The optimization problem targets the joint design of the transmit power and symbol probabilities which minimize the exposure index while maintaining a throughput quality constraint. Assuming that the set includes all possible values of α as
where
The joint optimization problem is challenging due to the non-convex constraints. Therefore, we adopt an alternate optimization approach to iteratively solve the transmit power and symbol probabilities using the subproblems (14) and (21), respectively. The alternate optimization Algorithm 1 begins with some initial feasible points p(j) and α(j) and evaluates
Algorithm 1. Alternate Optimization
The problem P1(a) is a non–convex optimization problem due to the constraint (14c). Interestingly, 1/H(p) is convex, as the second derivative is always positive (see Appendix). However, the bit error probability is a non–convex function in p. Therefore, we tackle this challenge using the successive convex approximation approach based on the Taylor series approximation of the bit error probability. The first-order Taylor series approximation of a function
Thus, we need to compute
In order to compute
where Ωmn is defined as
Applying the Leibniz integral rule on (17) yields the following partial derivative:
Now,
Conclusively, we can solve P1 (a) by replacing
Intuitively, the throughput of probabilistically shaped Mnu-ary QAM is an increasing function of α because
The root of the nonlinear equation
It is worthy to note that ϒ′(α(j)) ≠ 0 and is computed from (17) as
where
with
5 Numerical Results
In this section, we present some numerical results to quantify the EMF exposure caused by the proposed PS scheme instead of conventional no-shaping (NS). We consider an indoor active user in the next-generation cellular network suffering from improper HWDs. We assume κ ∈ {0, 1}, ρ = 0.9,
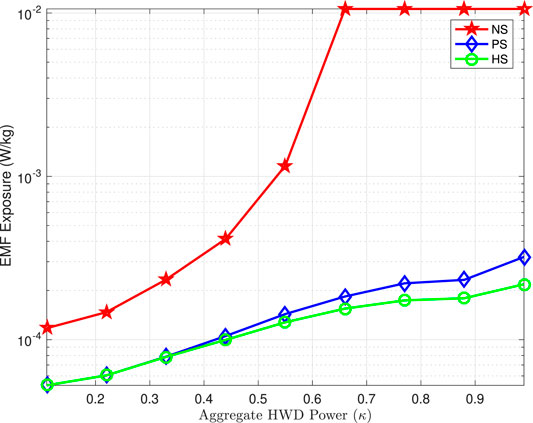
At first, we investigate the EMF exposure of a single active user for a range of HWD levels. We present the comparison between the traditional NS scheme employing Mu − QAM and the proposed PS scheme employing Mnu − QAM. For a fair comparison, we minimize the exposure index of Mu − QAM with uniform distribution pu (NS) scheme to ensure a throughput threshold of
The simulation results provide insights into the exposure index of non-shaping versus probabilistic shaping for a range of HWDs to achieve a target throughput, as shown in Figure 2. Evidently, they reveal the superiority of employing PS to successfully limit the EMF exposure while maintaining the QoS in terms of throughput. The advantage of PS over NS is particularly prominent for higher distortion levels. Moreover, we move a step further to investigate the performance of the HS scheme with Mnu − QAM employing an aggregate of GS and PS as detailed in the study by Javed et al. (2021). Interestingly, HS reduces the EMF exposure for higher distortion levels, but the gain is insignificant given the added complexity in designing GS and PS parameters. Conclusively, PS is the preferred choice as it can reduce EMF exposure up to 98% with affordable complexity.
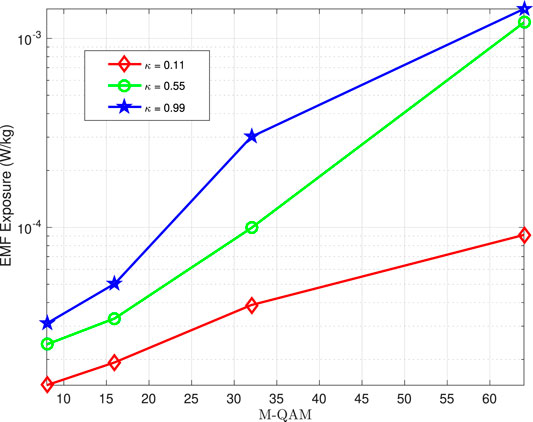
Next, we study the impact of varying the modulation order for three different distortion levels on the EMF exposure as shown in Figure 3. We assumed a modulation order Mnu ranging from 8-QAM to 64-QAM for the proposed PS. Noticeably, the increasing modulation order increases the EMF exposure for all HWD levels, that is, least, medium, and high distortion levels, however, at different paces. Intuitively, more transmit power is required to meet the QoS constraint in a highly distorted system instead of the least distorted system, which advocates a considerable EMF exposure of higher distortion levels.
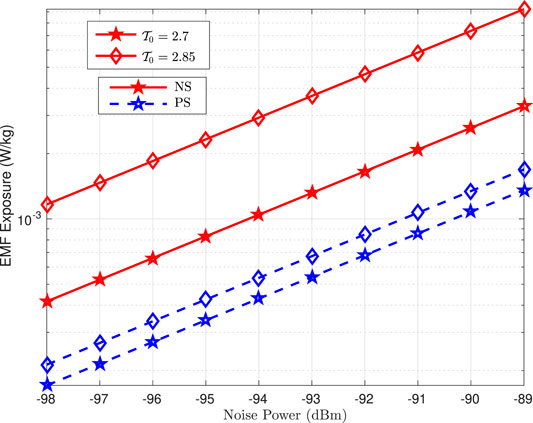
Similarly, we analyzed the benefits of PS over NS for a range of noise variance (−98dBm to −89dBm) for two different target throughputs, that is,
6 Conclusion
Throughout this study, we highlight the significance of employing probabilistic shaping (PS) to mitigate the drastic effects of improper hardware distortions and effectively reduce the user’s EMF exposure while maintaining a target threshold. The numerical results reveal up to a 98% reduction in the exposure index with the help of PS as compared to the conventional NS. Further investigation demonstrates a minor gain with HS over PS with significant added complexity. Thus, we conclude that mere PS is the preferred choice to reduce the exposure index, given a trade-off between lowering the EI and increasing computational complexity.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The study was conducted as a collaboration among all authors. AE conceived the work. The manuscript was mainly drafted by SJ and was revised and approved by all co-authors.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bhushan, N., Junyi Li, J., Malladi, D., Gilmore, R., Brenner, D., Damnjanovic, A., et al. (2014). Network Densification: the Dominant Theme for Wireless Evolution into 5G. IEEE Commun. Mag. 52, 82–89. doi:10.1109/mcom.2014.6736747
Björnson, E., Hoydis, J., Kountouris, M., and Debbah, M. (2014). Massive MIMO Systems with Non-ideal Hardware: Energy Efficiency, Estimation, and Capacity Limits. IEEE Trans. Inf. Theor. 60, 7112. doi:10.1109/TIT.2014.2354403
Björnson, E., Matthaiou, M., and Debbah, M. (2013). A New Look at Dual-Hop Relaying: Performance Limits with Hardware Impairments. IEEE Trans. Commun. 61, 4512. doi:10.1109/TCOMM.2013.100913.13
Boulogeorgos, A.-A. A., Chatzidiamantis, N. D., and Karagiannidis, G. K. (2016). Energy Detection Spectrum Sensing under RF Imperfections. IEEE Trans. Commun. 64, 2754–2766. doi:10.1109/tcomm.2016.2561294
Buchner, K., and Rivasi, M. (2020). The International Commission on Non-ionizing Radiation protection: Conflicts of Interest, Corporate Capture and the Push for 5G. Brussels: European Parliament – Michèle Rivasi (Europe Écologie) and Klaus Buchner (Ökologisch-Demokratische Partei).
Chiaraviglio, L., Elzanaty, A., and Alouini, M.-S. (2021). Health Risks Associated with 5G Exposure: A View from the Communications Engineering Perspective. IEEE Open J. Commun. Soc. 2, 2131–2179. doi:10.1109/OJCOMS.2021.3106052
Duy, T. T., Duong, T. Q., da Costa, D. B., Bao, V. N. Q., and Elkashlan, M. (2015). Proactive Relay Selection with Joint Impact of Hardware Impairment and Co-channel Interference. IEEE Trans. Commun. 63, 1594–1606. doi:10.1109/tcomm.2015.2396517
Elzanaty, A., Chiaraviglio, L., and Alouini, M.-S. (2021). 5G and EMF Exposure: Misinformation, Open Questions, and Potential Solutions. Front. Comms. Net. 2, 5. doi:10.3389/frcmn.2021.635716
Elzanaty, A. M., and Alouini, M.-S. (2022). Communicating over a Free-Space Optical Channel Using Distribution Matching. US Patent App 17/357, 450.
Group, I. W. (2013). Non-ionizing Radiation, Part 2: Radiofrequency Electromagnetic fields. IARC Monogr. Eval. Carcinog Risks Hum. 102, 1.
Ibraiwish, H., Elzanaty, A., Al-Badarneh, Y. H., and Alouini, M.-S. (2022). EMF-aware Cellular Networks in RIS-Assisted Environments. IEEE Commun. Lett. 26, 123–127. doi:10.1109/LCOMM.2021.3120688
Javed, S., Amin, O., Ikki, S. S., and Alouini, M.-S. (2017). Asymmetric Hardware Distortions in Receive Diversity Systems: Outage Performance Analysis. IEEE Access 5, 4492–4504. doi:10.1109/access.2017.2672543
Javed, S., Amin, O., Shihada, B., and Alouini, M.-S. (2020). A Journey from Improper Gaussian Signaling to Asymmetric Signaling. IEEE Commun. Surv. Tutorials 22, 1539–1591. doi:10.1109/COMST.2020.2989626
Javed, S., Amin, O., Shihada, B., and Alouini, M.-S. (2019). Improper Gaussian Signaling for Hardware Impaired Multihop Full-Duplex Relaying Systems. IEEE Trans. Commun. 67, 1858–1871. doi:10.1109/tcomm.2018.2884986
Javed, S., Elzanaty, A., Amin, O., Shihada, B., and Alouini, M.-S. (2021). When Probabilistic Shaping Realizes Improper Signaling for Hardware Distortion Mitigation. IEEE Trans. Commun. 69, 5028–5042. doi:10.1109/tcomm.2021.3074978
Kelley, C. T. (2003). Solving Nonlinear Equations with Newton’s Method. Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM), University City Science Center.
Kuehn, S., Pfeifer, S., Kochali, B., Kuster, N., and Bern, C. (2019). Modelling of Total Exposure in Hypothetical 5G mobile Networks for Varied Topologies and User Scenarios. Final Rep. Project CRR 816.
Latva-aho, M., Leppänen, K., Clazzer, F., and Munari, A. (2020). Key Drivers and Research Challenges for 6G Ubiquitous Wireless Intelligence. Oulu: 6G Flagship, University of Oulu.
Liu, A., Lau, V. K. N., and Kananian, B. (2019). Stochastic Successive Convex Approximation for Non-convex Constrained Stochastic Optimization. IEEE Trans. Signal. Process. 67, 4189–4203. doi:10.1109/tsp.2019.2925601
Lou, Z., Elzanaty, A., and Alouini, M.-S. (2021). Green Tethered UAVs for EMF-Aware Cellular Networks. IEEE Trans. Green. Commun. Netw. 5, 1697–1711. doi:10.1109/TGCN.2021.3102086
Matalatala, M., Deruyck, M., Tanghe, E., Martens, L., and Joseph, W. (2018). “Optimal Low-Power Design of a Multicell Multiuser Massive MIMO System at 3.7 GHz for 5G Wireless Networks,” in Wireless Communications and Mobile Computing 2018. doi:10.1155/2018/9796784
National Toxicology Program (2018a). Toxicology and Carcinogenesis Studies in Hsd: Sprague Dawley SD Rats Exposed to Whole-Body Radio Frequency Radiation at a Frequency (900 MHz) and Modulations (GSM and CDMA) Used by Cell Phones. Tech. rep., NTO 595, 1–446. doi:10.22427/NTP-TR-595
National Toxicology Program (2018b). Toxicology and Carcinogenesis Studies in B6C3F1/N Mice Exposed to Whole-Body Radio Frequency Radiation at a Frequency (1,900 MHz) and Modulations (GSM and CDMA) Used by Cell Phones. Tech. rep., NTO 596, 1–305. doi:10.22427/NTP-TR-596
Santamaria, I., Crespo, P., Lameiro, C., and Schreier, P. (2018). Information-theoretic Analysis of a Family of Improper Discrete Constellations. Entropy 20, 45. doi:10.3390/e20010045
Schenk, T. (2008). RF Imperfections in High-Rate Wireless Systems: Impact and Digital Compensation. Springer Dordrecht.
Studer, C., Wenk, M., and Burg, A. (2010). “MIMO Transmission with Residual Transmit-RF Impairments,” in Proc. Int. ITG Workshop on Smart Antennas (WSA) (Bremen, Germany: IEEE), 189. doi:10.1109/wsa.2010.5456453
Suzuki, H., Thi Van Anh Tran, T. V. A., Collings, I. B., Daniels, G., and Hedley, M. (2008). Transmitter Noise Effect on the Performance of a MIMO-OFDM Hardware Implementation Achieving Improved Coverage. IEEE J. Select. Areas Commun. 26, 867–876. doi:10.1109/jsac.2008.080804
Tesanovic, M., Conil, E., De Domenico, A., Aguero, R., Freudenstein, F., Correia, L. M., et al. (2014). The LEXNET Project: Wireless Networks and EMF: Paving the Way for Low-EMF Networks of the Future. IEEE Vehicular Techn. Mag. 9, 20. doi:10.1109/MVT.2014.2312272
Vermeeren, G., Plets, D., Joseph, W., Martens, L., Oliveira, C., Sebastião, D., et al. (2015a). Low EMF Exposure Future Networks D2. 8 Global Wireless Exposure Metric Definition. Tech. Rep.
Vermeeren, G., Plets, D., Joseph, W., Martens, L., Oliveira, C., Sebastião, D., et al. (2015b). Low EMF Exposure Future Networks D2. 8 Global Wireless Exposure Metric Definition. Tech. rep., LEXNET Project Deliverable 2, 1–66.
Vornoli, A., Falcioni, L., Mandrioli, D., Bua, L., and Belpoggi, F. (2019). The Contribution of In Vivo Mammalian Studies to the Knowledge of Adverse Effects of Radiofrequency Radiation on Human Health. Ijerph 16, 3379. doi:10.3390/ijerph16183379
Wan, L., Guo, Z., Wu, Y., Bi, W., Yuan, J., Elkashlan, M., et al. (2018). 4G\/5G Spectrum Sharing: Efficient 5G Deployment to Serve Enhanced Mobile Broadband and Internet of Things Applications. IEEE Veh. Technol. Mag. 13, 28–39. doi:10.1109/MVT.2018.2865830
Wenk, M. (2010). MIMO-OFDM-testbed: Challenges, Implementations, and Measurement Results. Zurich: ETH Zurich.
Wilbourn, J., Haroun, L., Heseltine, E., Kaldor, J., Partensky, C., and Vainio, H. (1986). Response of Experimental Animals to Human Carcinogens: an Analysis Based upon the IARC Monographs Programme. Carcinogenesis 7, 1853–1863. doi:10.1093/carcin/7.11.1853
Xia, X., Zhang, D., Xu, K., Ma, W., and Xu, Y. (2015). Hardware Impairments Aware Transceiver for Full-Duplex Massive MIMO Relaying. IEEE Trans. Signal. Process. 63, 6565–6580. doi:10.1109/tsp.2015.2469635
Zetterberg, P. (2011). Experimental Investigation of TDD Reciprocity-Based Zero-Forcing Transmit Precoding. EURASIP J. Adv. Signal. Process. 2011, 5. doi:10.1155/2011/137541
Appendix
Appendix A: Proof of Convexity
The first- and second-order derivatives of 1/H(p) are given as
The second-order derivative is always positive given the nonnegative and concave nature of information entropy. Hence, we can safely conclude that 1/H(p) is a convex function in p.
Keywords: asymmetric signaling, error probability analysis, hardware impairments, improper noise, non-uniform probabilities, radiation exposure
Citation: Javed S, Elzanaty A, Amin O, Alouini M-S and Shihada B (2022) EMF-Aware Probabilistic Shaping Design for Hardware-Distorted Communication Systems. Front. Comms. Net 3:859809. doi: 10.3389/frcmn.2022.859809
Received: 21 January 2022; Accepted: 04 April 2022;
Published: 30 May 2022.
Edited by:
Mohamed Saad, University of Sharjah, United Arab EmiratesReviewed by:
Gabriella Tognola, National Research Council (CNR—EIIT), ItalySaeed Abdallah, University of Sharjah, United Arab Emirates
Copyright © 2022 Javed, Elzanaty, Amin, Alouini and Shihada. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sidrah Javed, c2lkcmFoLmphdmVkQGthdXN0LmVkdS5zYQ==
 Sidrah Javed
Sidrah Javed Ahmed Elzanaty
Ahmed Elzanaty Osama Amin
Osama Amin Mohamed-Slim Alouini
Mohamed-Slim Alouini Basem Shihada
Basem Shihada