A beam-tracking framework for THz networks

Introduction

The utilization of millimeter wave (mmWave) and terahertz (THz) bands can offer larger bandwidth and increased data rates with respect to lower frequency communications Boulogeorgos et al. (2019a, 2018); Basar et al. (2019); Francesco Foglia et al. (2020); MacCartney et al. (2016). With increasing frequency, however, pathloss increases Kokkoniemi et al. (2021) and blockage becomes stronger Jacob et al. (2012), potentially degrading the communication quality. A straightforward way to mitigate pathloss is by using directional antennas, which must be properly aligned on the transmitter and the receiver, as misalignment may greatly reduce the received power, unintentionally leading to the opposite outcome Boulogeorgos et al. (2019b); Papasotiriou et al. (2020); Priebe et al. (2012). To make the alignment of the antennas possible, the direction of each antenna in relation to the other must be known. This can be achieved through localization, beam-training and beam-tracking. Localization by itself may not be accurate enough for the pencil-beams that are required in THz communications and may require additional equipment which is not always available. Beam-training requires high pilot overhead and guarantees high reliability. Beam-tracking aims to reduce the training overhead, most commonly through a location or angular-based prediction, and Kalman filters, while keeping the high reliability of the beam-training Ning et al. (2022). The use of mmWave and THz frequencies, makes the links extremely susceptible to blockage, as the received power can be reduced by 20− 40 dB MacCartney et al. (2016); Jacob et al. (2012); Stratidakis et al. (2020b) when an object or human blocks the line-of-sight (LoS). This greatly affects beam-tracking, as the UE in a completely blocked link is impossible to find, making the accuracy of the predictions less accurate.

There are several works about beam-tracking Liu F. et al. (2020); Zhang et al. (2020); Liu X. et al. (2020); Stratidakis et al. (2020a); Chen et al. (2022); Stratidakis et al. (2019); Neema et al. (2021); Gao et al. (2014). In Liu F. et al. (2020), a radar-assisted predictive beam-tracking for vehicle-to-infrastructure systems is presented. The authors use the radar functionality of road side units (RSUs) to estimate the motion parameters of the vehicles, along with the reflectivity of the vehicle bodies to track the vehicles with low overhead. In Zhang et al. (2020), the authors propose two beam-tracking methods for an unmanned aerial vehicle (UAV)-assisted system, one for random and one for inertial user mobility, both with an angular bound-dependent prediction for the vehicle motion. In Liu X. et al. (2020), an experiment is performed, in order to track the user mobility using a deep neural network and achieve an 80% accuracy. In Stratidakis et al. (2020a), the authors utilize multiple levels of a hierarchical codebook with mobility prediction, in order to scan a wide area using low pilot overhead. In Chen et al. (2022), the authors propose two tracking methods, on based on a hubrid dynamic array-of-subarrays with multiple signal classification and one based on a deep convolutional neural network, with the purpose of achieving millidegree level accuracy. The authors in Stratidakis et al. (2019), use several APs to track the user from different locations. All APs estimate the location of the UE separately and then they combine their estimations to form a common prediction for the next location of the UE. This way the APs can continue tracking the UE even when their link to the UE is blocked. The common prediction however, assumes highly accurate localization, which, at the time of writing, is not possible for APs to perform. In Neema et al. (2021), a vision-aided beam-tracking method was proposed. The beam-tracking is performed with the use of visual data from a video source with the help of image processing techniques that can estimate the location of the UE, predict blockage and handover, and estimate the required power of a link. Although, the vision-aided approach seems very promising, it raises privacy concerns. The authors in Gao et al. (2014) propose a double-link beam-tracking method, where the devices are tracked through two different paths, the main and a reflected one. This way, when the main link is blocked, the switch to the second link reduces the outage probability significantly. In higher frequencies, however, the reflected path is not a realistic approach, due to the higher path loss. Furthermore, the total pilot overhead for tracking is doubled due to the two paths without increasing the efficiency of the tracking method in non-blockage situations.

Contribution

In high frequency communications, blockage is expected to be a serious problem with losses up to 40 dB at 73 GHz from the human body MacCartney et al. (2016) and up to $\sim 15$ dB at 28 GHz from the human hand, depending on the hand grip ? In higher frequencies, these numbers are expected to be higher. In order to deal with this problem, the use of multiple APs and RISs has been considered to increase the LoS paths as the path reflected by a wall will be affected by severe signal power attenuation due to the high frequencies. However, each additional AP and RIS, increases the beam-tracking pilot overhead with the only benefit being the increased number of LoS paths to the UE. The main contributions of this paper are the classification of the main parameters that affect the tracking reliability into two main categories and the development of a beam-tracking framework that works with multiple cooperating APs to a) increase the tracking reliability, and (b) keep the pilot overhead low at all times for all APs even when most of the links are blocked.

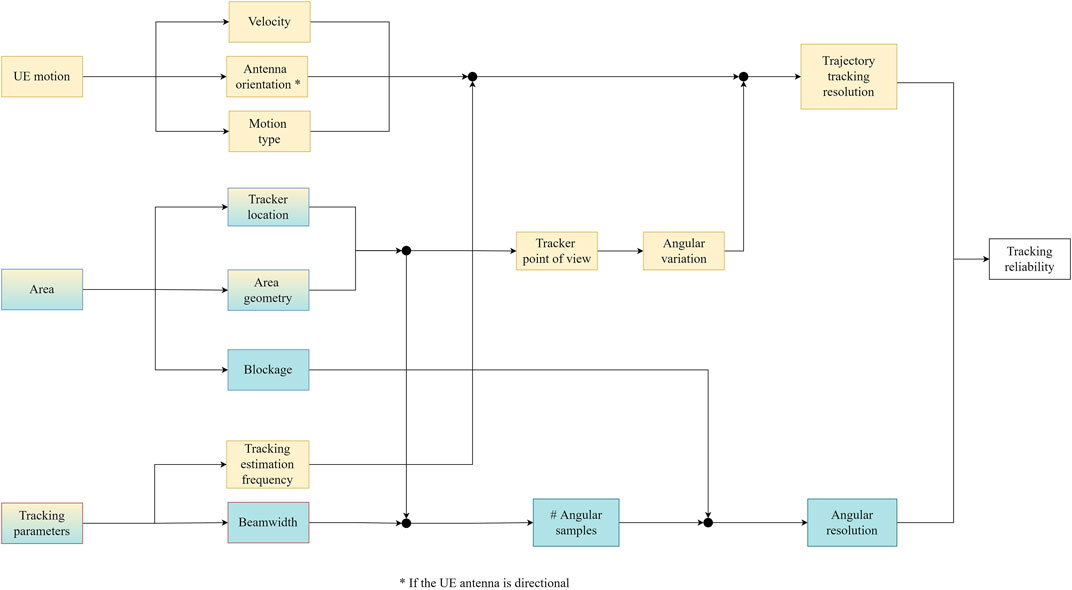
The parameters that affect the reliability of tracking algorithms can be organized in two major categories, those that affect the trajectory tracking resolution and those that affect the angular resolution. The trajectory tracking resolution refers to the successful tracking estimations over time, while the angular resolution refers to the number of scanning directions and the successful tracking in one timeslot. The trajectory tracking resolution is mainly affected by the motion of the UE, while the angular resolution by blockage as it blocks at least one beam direction, depending on the size of the obstacle and the beamwidth of the tracking antenna. Furthermore, depending on the location of tracker and the shape of the area, the maximum number of scanning directions can be reduced. For example, a tracker placed at a corner of a rectangular room can scan up to a range of 90^o horizontally instead of 180^o which would be the case if it was placed on a wall. More importantly, the location of the AP affects its point of view regarding the motion of the UE, which makes the use of multiple beam-tracking AP especially attractive.

In this paper, a beam-tracking method that focuses on both categories is proposed. The proposed method makes use of multiple APs to track the UE from different locations and ensure that at least one AP will track the UE. Each AP uses an hierarchical codebook to reduce the pilot overhead. The APs predict the next UE location and scan a small area around the prediction with low pilot overhead. Furthermore, the APs that estimated the location of the UE send their estimations to a common node, in order to combine them and send the new estimated location to the APs that failed to find the UE. This way, they can continue performing their predictions and keep the pilot overhead low. The performance of the proposed tracking method is measured through Monte-Carlo simulations, with the probability of success in estimating the UE direction relative to the AP, the average number of pilots per timeslot that is required for tracking and the MSE as metrics. The simulations are performed for different tracking estimation frequencies and for different number of blocked AP-UE links. The proposed algorithm is compared to Stratidakis et al. (2019), that was designed for operation under low ranging errors. The results show that the proposed algorithm is more robust to ranging errors, which translates to increased probability of successful estimation and reduction of the required number of pilots.

Notations

Unless otherwise stated, a lower and upper case bold letter denotes a vector and a matrix, respectively; A^H the conjugate transpose, card(A) denotes the cardinality of set A, supp(A) denotes the support of set A and ${\mathrm{mod}}_N(\left(\cdot \right))$ denotes the modulo operation with respect to N.

System model

A typical THz massive multiple-input multiple-output (MIMO) system is considered as shown in Figure 1, with multiple APs and one UE. The APs are equipped with uniform linear arrays (ULAs) of N antenna elements, while the UE with an omnidirectional antenna. In the downlink, the baseband equivalent received signal vector for the UE can be obtained as Gao et al. (2017).

$\mathbf{y}={\mathbf{h}}^H\mathbf{P}\mathbf{s}+\mathbf{z},(1)$

where h ∈ N × 1 and P ∈ N ×1 denote the MIMO channel vector and the digital precoding vector, s, stands for the transmitted signal vector with normalized power, i.e. $\mathbb{E}\left[\mathbf{s}{\mathbf{s}}^H\right]=\mathbf{I}$, and $\mathbf{z}\sim \mathcal{C}\mathcal{N}(0,{\sigma }^2\mathbf{I})$ stands for the additive Gaussian noise (AWGN) vector with variance σ². The precoding matrix satisfies the total transmit power constraint, i.e. $\mathrm{t}\mathrm{r}\left(\mathbf{P}{\mathbf{P}}^H\right)\le P$, with P being the total transmit power.

FIGURE 1

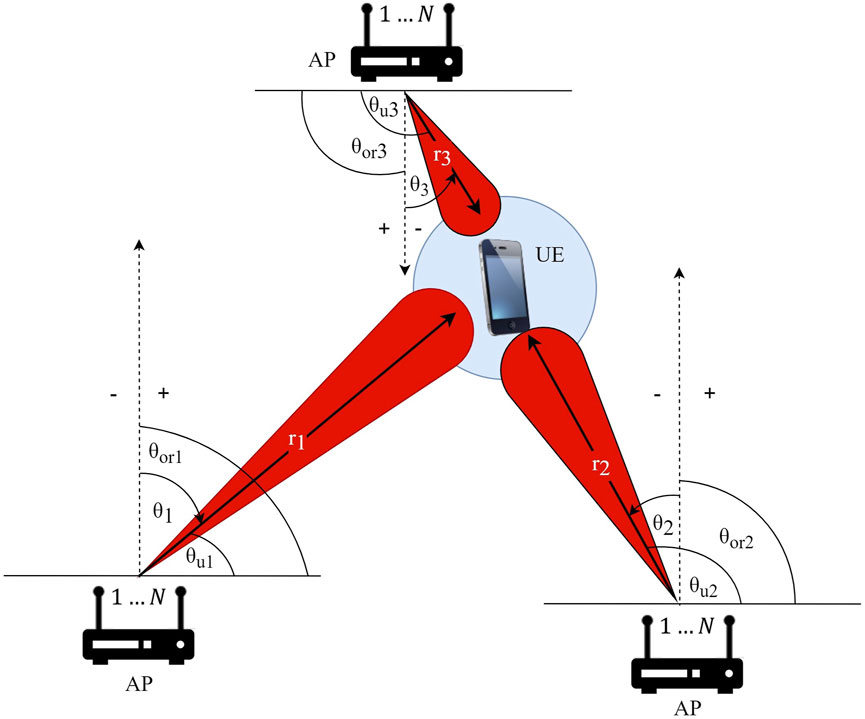
FIGURE 1. System model. The dashed lines depict the orientation of the AP antennas and the positive and negative signs affect only the angle θ_i.

Adopting the Saleh-Valenzuela model for the THz channel, h can be obtained as Saleh and Valenzuela (1987).

$\mathbf{h}={\beta }^{\left(0\right)}\mathbf{a}\left({\psi }^{\left(0\right)}\right)+\sum _{i=1}^L{\beta }^{\left(i\right)}\mathbf{a}\left({\psi }^{\left(i\right)}\right),(2)$

where β⁽⁰⁾ and β⁽ⁱ⁾ denote the complex gains of the LoS and non-LoS components, respectively, $\mathbf{a}\left(\psi \right)$ stands for the steering vector in the spatial direction ψ, while ψ⁽⁰⁾ and ψ⁽ⁱ⁾ respectively represent the spatial directions of the LoS and non-LoS components. In the nLoS components of the THz band, scattering induces more than 20 dB attenuation Papasotiriou et al. (2018); Boulogeorgos et al. (2019a); Boulogeorgos et al. (2019b). Therefore, the LoS component is sufficient to describe the link. As a result, (2) can be simplified as h ≈ βa(ψ). The array steering vector can be written as

$\mathbf{a}\left(\psi \right)=\frac{1}{\sqrt{N}}{\left[e^{-j2\pi \psi m}\right]}_{m\in \mathcal{I}\left(N\right)},(3)$

where $\mathcal{I}(N)=l-(N-1)/2$, with l = 0, 1, … , N − 1 stands for a symmetric set of indices centered around zero. The spatial direction is connected with the wavelength λ and the inter-element antenna spacing d through $\psi \triangleq \frac{d}{\lambda }\sin \left(\theta \right)$, with θ being the actual direction of the UE. It is assumed that d = λ/2. Without loss of generality, the hierarchical codebook in (Xiao et al., 2016, Sec.III.C.3) has been considered, with K = log₂(N) codebook levels. The beamspace channel can be obtained through Eq. 2 as

$\mathbf{y}={\mathbf{h}}^H{\mathbf{W}}_{\mathbf{k}}^H\mathbf{P}\mathbf{s}+\mathbf{z},(4)$

where W_k ∈ N × N denotes the codebook matrix, with k = 1, … K being the current codebook level.

Tracking reliability parameters

The parameters that affect the reliability of tracking can be divided into two categories, the ones that affect the trajectory tracking resolution (Liu F. et al. (2020); Zhang et al. (2020); Liu X. et al. (2020); Stratidakis et al. (2020a); Chen et al. (2022)) and the ones that affect the angular resolution (Stratidakis et al. (2019); Neema et al. (2021); Gao et al. (2014)), as shown in Figure 2. More specifically, the trajectory tracking resolution refers to the successful trajectory mapping. It is affected by the motion type (e.g. linear or irregular/random), velocity and antenna orientation (if the antenna is directional) of the UE and the tracking estimation frequency $(\frac{estimations}{\sec })$ and determines the prediction accuracy of the direction/location of the UE relative the tracker. On the other hand, angular resolution refers to the number of directions that can be successfully scanned and it is mainly affected by the number of angular samples and blockage as it impedes the scanning of specific directions. The number of angular sample refers to the number of directions that can be scanned and while it is directly affected by the antenna beamwidth, it also depends on area parameters, such as the location of the AP and the area geometry. For example, the walls of a room can make the scanning of some directions meaningless. Assuming that the tracker is static, if it is placed in the middle of a room, it can scan up to a range of 360^o, if it is placed on a wall up to 180^o, and if it is placed at the corner of a rectangular room, up 90^o. This mainly affects the initialization phase of beam-tracking algorithms that require some kind of exhaustive search. More importantly, the location of the tracker affects the point of view of the tracker regarding the motion of the UE, and can decrease the angular changes as shown in Figure 3, where the angular changes are shown for two different UE motions by two APs in a long rectangular room. AP one is placed at the center of the bottom wall and AP2 is placed at the center of the right wall which is much smaller than the bottom wall. The motion of UE one in (a) is sinusoidal with the angular changes presented in 3(b), while the motion of UE two in (c) is linear with the angular changes presented in (d). The general direction of both motions is depicted with the black arrow and the colored arrows denote the AP antenna orientation. Due to the difference in the size of the walls, the angular changes of the UEs in relation to AP two are smaller than in relation to AP 1 as shown in Figures 3B,D. Moreover, small angular changes mean small prediction errors, which are easy to compensate for. Finally, as blockage can obstruct the RIS-User link some direction become unscannable.

FIGURE 2

FIGURE 2. Tracking reliability parameters.

FIGURE 3

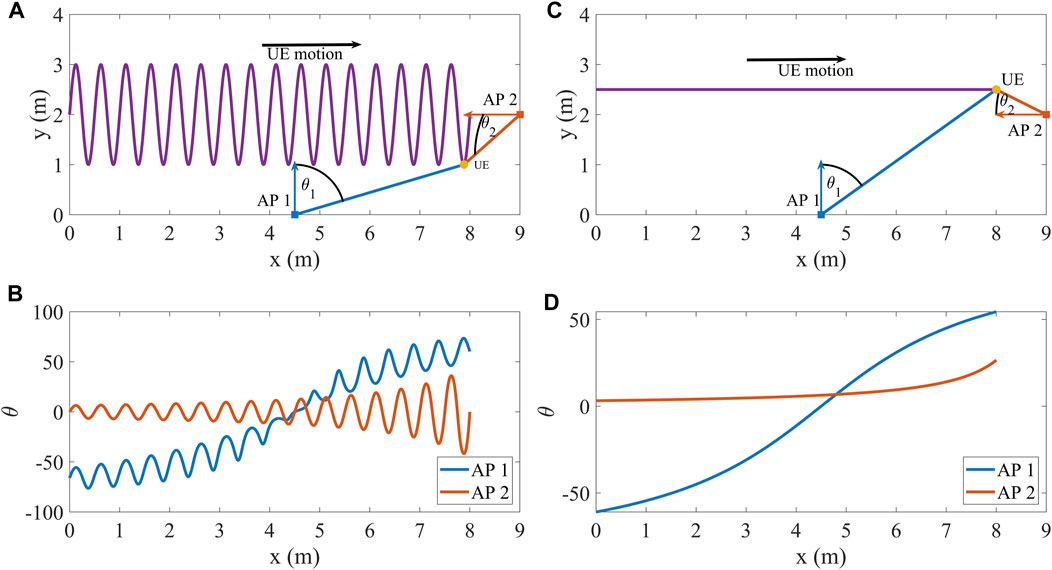
FIGURE 3. AP location point of view regarding the motion of (A,B): UE one and (C,D) UE 2, where the colored arrows denote the antenna orientation of each AP and the black color denotes the general direction of the UE motions.

Proposed method

In this section, a beam-tracking algorithm, that is based on Stratidakis et al. (2019, 2020b), is presented, that makes use of the location estimation performed by multiple cooperating APs, each equipped with an antenna array of N elements and an hierarchical codebook. The increased number of APs placed at different locations takes advantage of each AP’s point of view on the same UE as shown in Figure 3. The hierarchical codebook helps reduce the pilot overhead and the cooperation between the APs helps keep the overhead low, while increasing the probability of successful tracking even when some links are blocked. In the first three timeslots, the algorithm performs an hierarchical search to find the direction of the UE with low power overhead, and then uses a ranging method to find the AP-UE distance in order to estimate the UE location. In the next timeslots, each AP predicts the next UE location based on the estimations of the three previous timeslots and uses a small number of codebook levels each with a small number of codewords to track the UE with low pilot overhead. Furthermore, in each timeslot the APs send their location estimations to a common node that combines the location estimations of all the APs to make a common prediction of the next UE location. The common prediction is only used by an AP that failed to find the UE, so it can continue tracking with low pilot overhead. The algorithm can be divided into two phases, the initialization and the beam-tracking phase.

Initialization

The initialization takes place in the first three timeslots. Note that in order for the algorithm to “break out” of the initialization phase, the estimations in all three timeslots must be successful.

1. Hierarchical search: The AP performs an hierarchical search by alternating between two codewords of each codebook level. As the codebook follows a binary-tree structure, the first codebook level can be skipped in favor of the entire second level that offers higher gain without increasing the pilot overhead. The AP finds the general direction of the UE using the 4 codewords of the second level. Then it refines the estimation with the 1-level higher codebook level and alternating between the two codewords that correspond to the “branch” of the selected lower level codeword. The AP continues to refine the estimation with higher level codewords until the last codebook level. More specifically, with the second codebook level, the ith AP estimates the beamspace channel ${\tilde{\mathbf{h}}}_i$ with all 4 codewords and find the strongest element n_k, where k = 1, … , K is the current codebook level. With the higher levels, the strongest element n_k can be assumed to be 2n_k−1–1. The AP must then detect the $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}({\tilde{\mathbf{h}}}_i)$ as Gao et al. (2017).

$\begin{array}{c}\hfill \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\tilde{\mathbf{h}}}_i\right)={\mathrm{mod}}_N\left\{n_k-\frac{N_P}{2},\dots ,n_k+\frac{N_P-2}{2}\right\},\end{array}(5)$

assuming that the number of pilots, N_P, is even, where

$N_P=\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}\left(\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\tilde{\mathbf{h}}}_{i,k}\right)\right).(6)$

Then the AP must estimate the non-zero elements of ${\tilde{\mathbf{h}}}_i$. As the higher level codewords generate narrower beams, the estimation becomes more accurate with each level.

2. Ranging: The AP estimates the AP-UE distance using a two-way ranging method (e.g. Guo et al. (2019)) as

$\widetilde{r_i}=r_i+e_i,(7)$

where i = 1, … , M denotes the ith AP, r_i is the actual AP-UE distance between the ith AP and the UE, and e_i is a normally distributed random variable with zero mean and standard deviation σ_e Kim and Kim (2010).

3. Location estimation: With the knowledge of both the direction and distance of the UE in relation to the AP, the location of the UE can be easily estimated as

${\mathbf{p}}_i\left(x,y\right)={\tilde{r}}_i\left(\cos {\theta }_{u_i},\sin {\theta }_{u_i}\right),(8)$

where x and y stand for the coordinates of the UE location and

${\theta }_{u_i}={\theta }_{o{r}_i}-{\theta }_i,(9)$

where θ_i is the main lobe direction of the highest level codeword of the ith AP with which the direction of the UE was estimated and θ_or is the angle between the x-axis and the ith AP antenna orientation.

4. Cooperation: After obtaining the location of the UE, all the APs send the information to a common node in order to make a common estimation using the center of gravity of all the estimations.

Beam-tracking

The beam-tracking takes place after three consecutive successful estimations of the angle UE location.

5. Location prediction: The APs predict the location of the UE in the next timeslot assuming a linear motion.

6. Direction estimation: Then, the AP uses the second highest codebook level to track the UE by alternating between 4 codewords that generate beams around and towards the direction of the prediction. In order to find the suitable codeword, the AP must detect the support of ${\tilde{h}}_i$ with the use of n_k as in Eq. 5.

7. Refinement: The estimation is then refined by alternating between the 2 codewords of the last codebook level that belong to the branch of the codeword of the second highest level as in the Hierarchical search of the initialization. The use of multiple codebook levels in this step increases the robustness of the algorithm, in cases of non-linear motions and non-constant speed, while keeping the pilot overhead low.

8. Ranging, location estimation and cooperation: After obtaining the angle θ_i, the AP performs the ranging, location estimation and cooperation as in the initialization.

Algorithm 1. Proposed Algorithm.

Simulation results

In this section, the effectiveness of the proposed approach is evaluated in terms of probability of success and average number of pilots. Probability of success is the probability of at least one AP successfully tracking the UE in all motions, timeslots and number of APs. The average number of pilots is estimated over all motions, timeslots and number of APs. The results are derived by means of Monte-Carlo simulations in 3,000 different motions generated by the random motion generation used in Stratidakis et al. (2020a). Specifically, the random motion consists of random walk with a step of 2 m and interpolation with frequency Q_I, that simulates the tracking estimation frequency $(\frac{estimations}{\sec })$.A 9 × 9 m² area is considered, with 1, two or three tracker APs placed at different locations depending on their numbers. In the case of one AP, it is placed at [4.5,0], in the case of two APs, one is placed at [3,0] and one at [6,0] and in the case of three APs, one is placed at [1,0], one at [4.5, nine] and one at [9,0]. The central frequency is 150 GHz, the AP is equipped with an antenna array of 256 elements and the UE is equipped with an omnidirectional antenna. In the initialization phase of the algorithm, the total number of pilots is 16. In the beam-tracking phase, the two highest codebook levels are used, with the second highest level requiring four pilots and the highest level requiring 2, for a total of six pilots. This means that the total minimum average number of pilots in each timeslot (including the initialization phase) is $\sim 6$ and the maximum is 16, which is the case only when the algorithm fails to make three consecutive successful estimations. The standard deviation of the ranging part of the algorithm is assumed to be σ_e = 30 cm.

Tracking estimation frequency

The tracking estimation frequency, $Q_I(\frac{estimations}{\sec })$, is a significant parameter in tracking as it can determine the accuracy of the predictions. With low Q_I the estimated locations of the user resemble random points and they cannot be predicted. With high Q_I, the random points begin to be connected and the prediction becomes more accurate. The tracking estimation frequency can be simulated by changing the interpolation frequency of a random-walk method as in Stratidakis et al. (2020a). An example of the effect of Q_I in tracking is presented in Figure 4, where the proposed algorithm is compared with the algorithm in Stratidakis et al. (2019). Specifically, in (a) the probability of success in tracking the UE and in (b) the average number of pilots are presented as a function of Q_I for different numbers of AP trackers. The algorithm in Stratidakis et al. (2019) uses multiple APs to find the direction of the UE relative to each AP using essentially a single-level codebook. After an AP successfully tracks the UE, it estimates the AP-UE range and then calculates the location of the UE. The locations are sent to a common node that calculates the location of the UE based on the center of gravity of the location estimations of each AP. The common node then sends the new location estimation to the APs, which use it to track the UE more accurate and to predict the next location of the UE. The algorithm in Stratidakis et al. (2019) uses 128 pilots in the initialization phase which lasts for three timeslots and six pilots thereafter. Both algorithms restart when they fail to estimate the direction UE, i.e. the UE is outside of the beams. For both algorithms, with increasing Q_I, the probability of success increases and the average number of pilots per timeslot decreases regardless of the number of APs. For example, with the proposed algorithm, when one AP is used, the probability of success increases from 75.3% with Q_I = 1–99.7% with Q_I = 20 and the average number of pilots with the proposed approach decreases from 13.5 with Q_I = 1 to 6.1 with Q_I = 20. While the prediction may be inaccurate for one tracker, it can be accurate for another tracker. The accuracy of the prediction depends on the location of the tracker and the motion direction and velocity of the user relative to the tracker. Both algorithms take advantage of this with the use of multiple APs and the common location estimation. For instance, with two APs, the probability of success with the proposed algorithm increases from 76.4% with Q_I = 1–99.9% with Q_I = 20 and the average number of pilots decreases from 13.4 to 6. With three APs, the probability of success with the proposed algorithm increases from 78.1 to 100% and the average number of pilots decreases from 13.3 to 6. The difference between using one AP and multiple APs is best shown with Q_I = 6, where with the proposed approach it reaches a maximum of 4.6% between using one and two APs and 7% between using two and three APs. It can be observed that with multiple trackers that cooperate when required to predict the user’s next location, the probability of success increases and the average number of pilots decreases substantially. On the other hand, the algorithm in Stratidakis et al. (2019) that is designed for operation under low ranging error is here outperformed by our proposed algorithm. Specifically, the common location estimation is highly inaccurate in relation to the antenna beamwidth of the APs due to the high value of σ_e, and using it to estimate the direction fo the UE is counterproductive. In this case, increasing the number of APs is detrimental for the probability of success. For example with one AP, the probability of success increased from 74.6 to 99.5%. With two APs it increases from 43.6 to 82% and with three APs it increases from 53 to 77.7%. Furthermore, the average number of pilots with two and three APs is misleading as the common location estimation, which is inaccurate, is used in both the prediction (that reduces the required number of pilots) and the direction estimation. In other words, the common location estimation in Stratidakis et al. (2019) makes the prediction of the next UE location possible, reducing the required number of pilots, and makes the direction estimation inaccurate as the center of gravity of the independent location estimations is far (in relation to the narrow beamwidth) from the actual location of the UE due to the high ranging error.

FIGURE 4

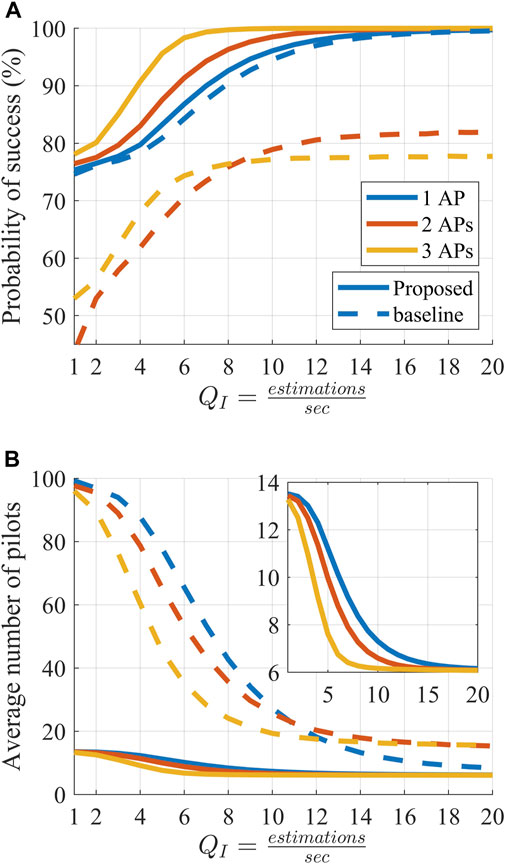
FIGURE 4. Performance of the proposed beam-tracking method under different estimation frequencies, Q_I. (A): Probability of successful tracking per number of tracker APs. (B): Average number of pilots per timeslot for different number of tracker APs.

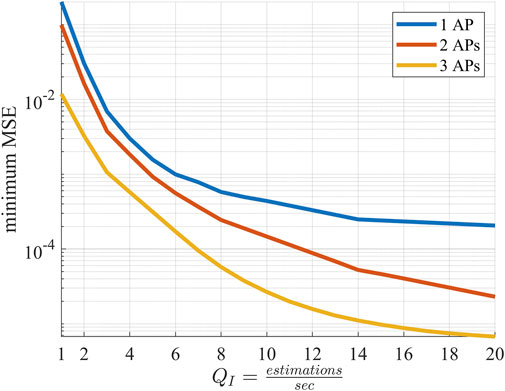
In Figure 5, the minimum MSE, is presented as a function of the tracking estimation frequency, Q_I. The minimum MSE is calculated as $MSE=\frac{1}{N}{\sum }_{i=1}^N{({\tilde{\theta }}_i-{\theta }_i)}^2$, where ${\tilde{\theta }}_i$ is the estimated direction and θ_i is the actual direction of the UE in relation to the AP that offers the lowest misalignment between all the APs. Using the error of the AP with the lowest misalignment the advantage of using multiple APs to track the UE with the proposed algorithm is shown. It can be observed that by increasing the number of tracking APs the minimum MSE is decreased. Furthermore, increasing Q_I decreases the minimum MSE and increases the difference between using 1, two and three APs. For example, the minimum MSE with one AP starts at 0.2 with Q_I = 1 and ends at 2 × 10^–4 with Q_I = 20. With two APs it starts at 0.1 with Q_I = 1 and ends at 2.3 × 10^–5 with Q_I = 20. With three APs the minimum MSE starts at 0.01 with Q_I = 1 and ends at 6.7 × 10^–6 with Q_I = 20.

FIGURE 5

FIGURE 5. Minimum MSE under different estimation frequencies, Q_I.

Blockage

Blockage is another significant parameter that can make a tracking attempt fail as it can reduce the received power to zero. Note that, only the case of total blockage is studied in this paper. With only one AP if the link is blocked the tracking either cannot continue and the algorithm has to restart, or continue with reduced prediction accuracy. With multiple APs, and a common location estimation, even when a link is blocked the algorithm on than AP does not need to restart. Therefore, it can keep using the prediction and continue tracking the UE with low pilot overhead. The basic requirement is for at least one AP to be able to track the UE in every timeslot, even if it is not the same everytime. As an example, in Table 1, the probability of success and average number of pilots are presented for 4 cases of blockage probability, Pb. The 4 cases are 0% in all AP-UE links, 50% in one AP-UE link, 50% in two AP-UE links and 50% in three AP-UE links. The tracking estimation frequency Q_I is 15 and the blocked link is random in every timeslot. In Table 1 the probability of success in tracking the UE is shown, while in Table 1 the average number of pilots per timeslot is presented. With one AP, when Pb = 0%, the probability of success is 99.2%, while when Pb = 50%, it is 74%. The corresponding average number of pilots is 6.3 with Pb = 0% and 12.5 with Pb = 50%. With two APs, when Pb = 0%, the probability of success is 99.8%, when Pb = 50% on one AP-UE link it is 98% and when Pb = 50% on two AP-UE links it is 80.8% with average number of pilots 6.14, 6.7 and 11.5 respectively. With three APs, the probability of success without blockage is 100%, when Pb = 50% on one AP-UE link it is 99.8%, when Pb = 50% on two AP-UE links it is 98% and when Pb = 50% on three AP-UE links it is 90%. The respective average number of pilots is 6.1, 6.14, 6.7 and 8.9. It can be observed that with Pb = 50% on all APs, the higher the number of APs, the higher the probability of success and the lower the pilot overhead. In this case, the difference in probability of success between using one and three APs to track the UE is 16% and the difference in average number of pilots is 3.6.

TABLE 1

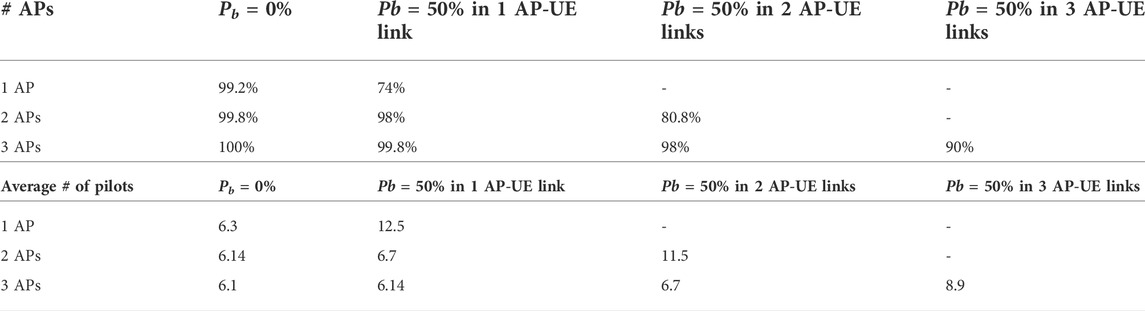
TABLE 1. A: Probability of success and B: Average number of pilots in links with fixed probability of blockage in each timeslot. The blocked link is random in every timeslot.

Discussion

The results can be further improved with additional APs, but at the expense of increasing cost. One promising solution to the cost of multiple APs is the use of reconfigurable intelligent surfaces (RISs). RISs require less energy to operate as they simply redirect the signal transmitted by the AP towards the UE instead of re-transmitting it. Furthermore, RISs do not amplify the existing AWGN like the amplify-and-forward relays, and lack the delay of decode-and-forward relays Boulogeorgos and Alexiou (2020); Bjornson et al. (2020). As with the APs, the RISs would offer different points of view and increase the probability of success, especially in the presence of blockage. However, an RIS is not autonomous and requires a transmitter to function, which means that the AP must track the UE once directly and once through the RIS. Localization can help reduce or even avoid this unnecessary tracking overhead, depending on its accuracy.

Conclusion

In this paper, the parameters that affect the reliability of tracking are presented and divided into two categories, the trajectory tracking resolution and the angular resolution. The trajectory tracking resolution contains the parameters that affect the prediction of the tracking algorithms and the angular resolution contains the parameters that affect successful estimation in each timeslot. Furthermore, a beam-tracking method is proposed to address the challenges of the two categories. The proposed method makes use of multiple APs and an hierarchical codebook to track the user from different locations with low pilot overhead even when most links are blocked. The performance of this beam-tracking method is measured through Monte-Carlo simulations with the probability of success in tracking the UE, the average number of pilots that was required per timeslot and the MSE as metrics. The simulations are performed for different tracking estimation frequencies and for different number of blocked links. The simulations show a big difference between using a one AP and using two or three APs, especially with low tracking estimation frequency or blockage. In relation to the authors’ previous beam-tracking algorithms, the proposed algorithm is more robust to ranging errors, offers increased probability of successful estimation and reduced required number of pilots under realistic ranging errors especially with multiple APs.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization and Methodology, GS, SD, and AA. Formal Analysis and validations, GS and SD. Simulations and Visualization, GS. Writing—Review and Editing, GS, SD, and AA.

Funding

This work was supported by the European Commission’s Horizon 2020 Research and Innovation Programme under Agreement 871464 (ARIADNE).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Basar, E., Renzo, M. D., Rosny, J. D., Debbah, M., Alouini, M.-S., and Zhang, R. (2019). Wireless communications through reconfigurable intelligent surfaces. IEEE Access 7, 116753–116773. doi:10.1109/access.2019.2935192

CrossRef Full Text | Google Scholar

Bjornson, E., Ozdogan, O., and Larsson, E. G. (2020). Intelligent reflecting surface versus decode-and-forward: How large surfaces are needed to beat relaying? IEEE Wirel. Commun. Lett. 9, 244–248. doi:10.1109/lwc.2019.2950624

CrossRef Full Text | Google Scholar

Boulogeorgos, A.-A. A., Alexiou, A., Merkle, T., Schubert, C., Elschner, R., Katsiotis, A., et al. (2018). Terahertz technologies to deliver optical network quality of experience in wireless systems beyond 5G. IEEE Commun. Mag. 56, 144–151. doi:10.1109/mcom.2018.1700890

CrossRef Full Text | Google Scholar

Boulogeorgos, A.-A. A., and Alexiou, A. (2020). Performance analysis of reconfigurable intelligent surface-assisted wireless systems and comparison with relaying. IEEE Access 8, 94463–94483. doi:10.1109/ACCESS.2020.2995435

CrossRef Full Text | Google Scholar

Boulogeorgos, A.-A. A., Papasotiriou, E. N., and Alexiou, A. (2019a). Analytical performance assessment of THz wireless systems. IEEE Access 7, 11436–11453. doi:10.1109/ACCESS.2019.2892198

CrossRef Full Text | Google Scholar

Boulogeorgos, A.-A. A., Papasotiriou, E. N., and Alexiou, A. (2019b). “Analytical performance evaluation of thz wireless fiber extenders,” in IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), 1–6. doi:10.1109/PIMRC.2019.8904434

CrossRef Full Text | Google Scholar

Chen, Y., Yan, L., Han, C., and Tao, M. (2022). Millidegree-level direction-of-arrival estimation and tracking for terahertz ultra-massive mimo systems. IEEE Trans. Wirel. Commun. 21, 869–883. doi:10.1109/TWC.2021.3100073

CrossRef Full Text | Google Scholar

Francesco Foglia, M., Clemente, A., and Gonzalez-Jimenez, J. L. (2020). High-gain $D$ -band transmitarrays in standard PCB Technology for beyond-5G communications. IEEE Trans. Antennas Propag. 68, 587–592. doi:10.1109/tap.2019.2938630

CrossRef Full Text | Google Scholar

Gao, B., Xiao, Z., Zhang, C., Su, L., Jin, D., and Zeng, L. (2014). “Double-link beam tracking against human blockage and device mobility for 60-ghz wlan,” in 2014 IEEE Wireless Communications and Networking Conference (WCNC), 323–328. doi:10.1109/WCNC.2014.6951988

CrossRef Full Text | Google Scholar

Gao, X., Dai, L., Zhang, Y., Xie, T., Dai, X., and Wang, Z. (2017). Fast channel tracking for terahertz beamspace massive MIMO systems. IEEE Trans. Veh. Technol. 66, 5689–5696. doi:10.1109/tvt.2016.2614994

CrossRef Full Text | Google Scholar

Guo, G., Chen, R., Ye, F., Peng, X., Liu, Z., and Pan, Y. (2019). Indoor smartphone localization: A hybrid wifi rtt-rss ranging approach. IEEE Access 7, 176767–176781. doi:10.1109/ACCESS.2019.2957753

CrossRef Full Text | Google Scholar

Jacob, M., Priebe, S., Dickhoff, R., Kleine-Ostmann, T., Schrader, T., and Kurner, T. (2012). Diffraction in mm and sub-mm wave indoor propagation channels. IEEE Trans. Microw. Theory Tech. 60, 833–844. doi:10.1109/tmtt.2011.2178859

CrossRef Full Text | Google Scholar

Kim, E., and Kim, K. (2010). Distance estimation with weighted least squares for mobile beacon-based localization in wireless sensor networks. IEEE Signal Process. Lett. 17, 559–562. doi:10.1109/lsp.2010.2047169

CrossRef Full Text | Google Scholar

Kokkoniemi, J., Lehtomäki, J., and Juntti, M. (2021). A line-of-sight channel model for the 100–450 gigahertz frequency band. EURASIP J. Wirel. Commun. Netw. 88, 2021. doi:10.1186/s13638-021-01974-8

CrossRef Full Text | Google Scholar

Liu, F., Yuan, W., Masouros, C., and Yuan, J. (2020a). Radar-assisted predictive beamforming for vehicular links: Communication served by sensing. IEEE Trans. Wirel. Commun. 19, 7704–7719. doi:10.1109/TWC.2020.3015735

CrossRef Full Text | Google Scholar

Liu, X., Yu, J., Qi, H., Yang, J., Rong, W., Zhang, X., et al. (2020b). Learning to predict the mobility of users in mobile mmwave networks. IEEE Wirel. Commun. 27, 124–131. doi:10.1109/MWC.001.1900241

CrossRef Full Text | Google Scholar

MacCartney, G. R., Deng, S., Sun, S., and Rappaport, T. S. (2016). “Millimeter-wave human blockage at 73 GHz with a simple double knife-edge diffraction model and extension for directional antennas,” in IEEE 84th Vehicular Technology Conference (VTC-Fall) (Montreal, QC, Canada: IEEE). doi:10.1109/vtcfall.2016.7881087

CrossRef Full Text | Google Scholar

Neema, M., Gopi, E. S., and Katoj, P. K. (2021). “User spatial localization for vision aided beam tracking based millimeter wave systems using convolutional neural networks,” in 2021 10th International Conference on Information and Automation for Sustainability (ICIAfS), 7–12. doi:10.1109/ICIAfS52090.2021.9605960

CrossRef Full Text | Google Scholar

Ning, B., Chen, Z., Tian, Z., Han, C., and Li, S. (2022). A unified 3d beam training and tracking procedure for terahertz communication. IEEE Trans. Wirel. Commun. 21, 2445–2461. doi:10.1109/TWC.2021.3112493

CrossRef Full Text | Google Scholar

Papasotiriou, E. N., Boulogeorgos, A.-A. A., and Alexiou, A. (2020). Performance analysis of THz wireless systems in the presence of antenna misalignment and phase noise. IEEE Commun. Lett. 1, 1211–1215. doi:10.1109/lcomm.2020.2981336

CrossRef Full Text | Google Scholar

Papasotiriou, E. N., Kokkoniemi, J., Boulogeorgos, A.-A. A., Lehtomaki, J., Alexiou, A., and Juntti, M. (2018). “A new look to 275 to 400 GHz band: Channel model and performance evaluation,” in IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC) (Bologna, Italy: IEEE). doi:10.1109/pimrc.2018.8580934

CrossRef Full Text | Google Scholar

Priebe, S., Jacob, M., and Kürner, T. (2012). “The impact of antenna directivities on thz indoor channel characteristics,” in 2012 6th European Conference on Antennas and Propagation (EUCAP), 478–482. doi:10.1109/EuCAP.2012.6205849

CrossRef Full Text | Google Scholar

Saleh, A., and Valenzuela, R. (1987). A statistical model for indoor multipath propagation. IEEE J. Sel. Areas Commun. 5, 128–137. doi:10.1109/JSAC.1987.1146527

CrossRef Full Text | Google Scholar

Stratidakis, G., Boulogeorgos, A.-A. A., and Alexiou, A. (2019). “A cooperative localization-aided tracking algorithm for THz wireless systems,” in IEEE Wireless Communications and Networking Conference (WCNC), Marrakech, Morocco.

CrossRef Full Text | Google Scholar

Stratidakis, G., Ntouni, G. D., Boulogeorgos, A. A., Kritharidis, D., and Alexiou, A. (2020a). “A low-overhead hierarchical beam-tracking algorithm for thz wireless systems,” in 2020 European Conference on Networks and Communications (EuCNC), 74–78. doi:10.1109/EuCNC48522.2020.9200946

CrossRef Full Text | Google Scholar

Stratidakis, G., Papasotiriou, E. N., Konstantinis, H., Boulogeorgos, A.-A. A., and Alexiou, A. (2020b). “Relay-based blockage and antenna misalignment mitigation in THz wireless communications,” in 2020 2nd 6G Wireless Summit (6G SUMMIT) (Levi, Finland: IEEE). doi:10.1109/6gsummit49458.2020.9083750

CrossRef Full Text | Google Scholar

Xiao, Z., He, T., Xia, P., and Xia, X. (2016). Hierarchical codebook design for beamforming training in millimeter-wave communication. IEEE Trans. Wirel. Commun. 15, 3380–3392. doi:10.1109/TWC.2016.2520930

CrossRef Full Text | Google Scholar

Zhang, W., Zhang, W., and Wu, J. (2020). UAV beam alignment for highly mobile millimeter wave communications. IEEE Trans. Veh. Technol. 69, 8577–8585. doi:10.1109/TVT.2020.2997740

CrossRef Full Text | Google Scholar