Empowering 6G maritime communications with distributed intelligence and over-the-air model sharing

Introduction: Shipping and maritime transportation have gradually gained a key role in worldwide economical strategies and modern business models. The realization of Smart Shipping (SMS) powered by advanced 6G communication networks, as well as innovative Machine Learning (ML) solutions, has recently become the focal point in the maritime sector. However, conventional centralized learning schemes are unsuitable in the maritime domain, due to considerable data communication overhead, stringent energy constraints, increased transmission failures in the harsh propagation environment, as well as data privacy concerns.

Methods: To overcome these challenges, we propose the joint adoption of Federated Learning (FL) principles and the utilization of the Over-the-Air computation (AirComp) wireless transmission framework. Thus, this paper initially describes the mathematical considerations of a 6G maritime communication system, focusing on the heterogeneity of the relevant nodes and the channel models, including an Unmanned Aerial Vehicle (UAV)-aided relaying model that is usually required in maritime communications. The communication network, enhanced with the AirComp technique for efficiency purposes, forms the technical basis for the collaborative learning across multiple Internet of Maritime Things (IoMT) nodes in FL tasks. The workflow of the FL/AirComp scheme is illustrated and proposed as a communication-efficient and privacy-aware SMS framework, considering spectrum and energy efficiency aspects under a sum transmitting power constraint.

Results: Then, the performance of the proposed methodology is assessed in an important ML task, related to intelligent maritime transportation systems, namely, the prediction of the Cargo Ship Propulsion Power using real data originating from six cargo ships and utilizing long-short-term-memory (LSTM) neural networks. Upon extensive experimentation, FL showed higher prediction accuracy relative to the typical Ensemble Learning technique by a factor of 3.04. The AirComp system performance was evaluated under varying noise conditions and number of IoMT nodes, using simulation data for the channel state information by regulating the power of the transmitting IoMT entities and the scaling factor at the shore base station.

Discussion: The results clearly indicate the efficiency of the proposed FL/AirComp scheme in achieving low computation error, collaborative learning, spectrum efficiency and privacy protection in wireless maritime communications, while providing adequate accuracy levels with respect to the optimization objective.

1 Introduction

The maritime domain is currently experiencing significant transformational shifts, boosted by the digitization of the related infrastructure, communication networks, as well as the modernization of the relevant marine services. The concept of Smart Shipping (SMS) has recently emerged, including smart services and applications that can be provided on-demand to smart vessels, smart ports and indirectly to all the involved stakeholders (for instance, trading and transportation companies and public authorities, transportation passengers, etc.) (Schaefer and Barale, 2011; Wang et al., 2020). These applications, however, are based on a rather complex interconnected mesh between marine entities, such as ports, ships, vessels and maritime IoT (IoMT) nodes that are becoming omnipresent (Trakadas et al., 2022; Nomikos et al., 2023). To this end, more efficient implementation of the smart applications can be achieved by leveraging Machine Learning (ML) approaches, since they are virtually the sole methods that base their performance on considerable amounts of historical data, while they can also provide corrective suggestions and make decisions in such complicated environments, revealing complex interdependencies between parameters that seem uncorrelated and cannot be modeled by conventional techniques (Akyuz et al., 2019; Alop, 2019). Critical parameters associated with the intelligent maritime transportation systems that are subjected to optimization from the ML algorithms include, amongst others, vessel fuel consumption, vessel speed, ship routing, predictive maintenance of vessel equipment and port resources (Giannopoulos et al., 2023b).

Noteworthy, all the aforementioned variables that are targeted for optimization are linked to increased energy consumption, since the marine domain is characterized by a significant environmental footprint (Jahanbakht et al., 2021). In addition, the recent gradual population of the marine environment with IoMT nodes is expected to further escalate its environmental impact (Foretich et al., 2021). Although the imminent requirement of finding energy-efficient solutions is partially addressed by the introduction of ML methods, the support of the asymmetrical scaling of the number of devices that need to participate in the marine environment as active nodes is unsustainable in the long-term. More specifically, all these heterogeneous IoMT devices (fishing vessels, underwater devices, ferries, etc.) that are present in a marine network need not only to periodically provide their collected data to a cloud server, but they need to actively communicate with each other, participating in learning frameworks (Xia et al., 2020). For this reason, it is typically required that the IoMT nodes have a minimal computational power and an energy surplus to execute simple ML tasks. In this context, state-of-the-art ML methods that are currently being developed for the maritime sector need to adhere to three basic requirements: (i) high-performant in terms of accuracy, since they base their predictions on considerable amounts of historical data and aim at regulating configuration parameters of vessels; (ii) energy-efficient, targeting to optimize parameters that influence directly the energy consumption. This consideration also includes the transmitting power of the IoMT nodes, which is one of the main reasons related to battery depletion. Even though communication protocols for wireless sensor networks can be modified and utilized, the energy related to task execution needs to be further reduced; (ii) privacy-preserving, since the data that are shared among the IoMT nodes or between the nodes and a centralized cloud server are, in most cases, sensitive and owned by multiple stakeholders (for instance private companies, public authorities, etc.). Therefore, the technical solutions must take into account data privacy issues, without degrading the performance of the IoMT nodes, as well as the accuracy of the ML algorithms.

1.1 Federated learning and over-the-air computation

Each individual IoMT node in the maritime network possesses a certain amount of computational capacity, in order to be able to execute simple tasks during the training and inference phases of the included ML logic, as well as perform fundamental computations, linked to the communication operation with other nodes or a cloud server. It is critical that these processes are conducted in a coherent manner, in terms of energy efficiency and resource optimization (for instance spectrum efficiency maximization and cpu utilization minimization), without deteriorating the performance of the ML predictions. Current ML schemes are based on centralized learning, where data from all the IoMT devices are transmitted to a cloud (centralized) server through the mobile or the satellite network (Xia et al., 2020; Giannopoulos et al., 2021; Wang et al., 2021). The ML model that resides in the cloud server is hence trained with the data encountered by all the nodes that participate in the learning framework, providing wider observability and leading to enhanced performance. However, the centralized approach involves data transmission and data gathering to the centralized server and is therefore energy inefficient. In addition, this approach exhibits high latency during the inference phase of the algorithm, since data queries are transmitted to the cloud to be used as input for ML model inference, and the output (model estimation) needs to be also transmitted back to the respective IoMT node (Niknam et al., 2020). Finally, the data generated at the IoMT devices do not remain at their origin, potentially jeopardizing privacy preservation and violating data ownership.

On the other hand, completely decentralized approaches involve tailored ML models that have been trained with local data experienced by each individual vessel. Although the ML models are hosted directly at the IoMT devices (data transfer is not required in decentralized methods) and data ownership is guaranteed, they suffer from the generalizability principle, since they have been over-fitted to the local data (Wahab et al., 2021). For instance, the ML model of a vessel that targets to predict the fuel consumption and has only encountered in its local environment specific conditions (e.g., low winds), is expected to perform rather poorly when it is in the presence of generic environmental conditions (e.g., medium or high winds). To overcome this challenge, federated learning (FL) methods have been introduced, leveraging the collective intelligence based on the data encountered by a swarm of IoMT devices (Victor et al., 2022; Giannopoulos et al., 2023a). Instead of using centralized schemes, where the performance of the ML model is preferable due to full visibility of the data from all the participating nodes, FL methods enable the indirect aggregation of the local model parameters that have been constructed via the locally observed data to transfer intelligence that has been extracted from the IoMT nodes (McMahan et al., 2017; Aledhari et al., 2020).

In this context, the nodes that participate in the FL scheme might be individual vessels (e.g., a fishing boat), but also clusters of IoMT nodes owned by a single stakeholder. The optimization variables typically include parameters such as optimized trajectory according to external weather conditions and optimized speed and power for minimum fuel consumption (Wahab et al., 2021; Zhang et al., 2021). In the FL framework, the cloud server is used to aggregate the parameters of the device models, which have been trained with the locally observed data. The individual ML model parameters of the edge IoMT nodes are then fused into a collaborative global model, which is then periodically acknowledged back to the local devices to update their models during the training process (Niknam et al., 2020; Giannopoulos et al., 2023b). The FL model therefore exhibits collective intelligence, since it uses knowledge extracted from various local data originating from multiple IoMT nodes, while also retaining high accuracy in the performance of the ML tasks. Moreover, the FL methods involve reduction of the transmission-related energy and minimization of inference-related latency, compared to the centralized methods. Finally, the FL process provides data privacy preservation, since data remain at the edge nodes while the local and global model parameters that are transferred through the wireless medium can be encrypted.

The FL framework can be further enhanced and complemented by the use of spectrum-efficient methods for optimization of the wireless resources. Typical multiple access techniques for higher spectrum utilization include, amongst others, frequency division multiple access and non-orthogonal multiple access (NOMA) schemes. Furthermore, the Over-the-Air computation (AirComp) method has been recently introduced to encompass multiple signals originating from heterogeneous sources (Zang et al., 2020). In an AirComp system, all nodes transmit simultaneously their pre-processed signals, using the same bandwidth over a mobile network. The AirComp method leverages the superposition property of the transmitted signals, which are temporally combined together and received by a fusion center. The latter entity applies a nomographic scaling function to the combined received signal, directly obtaining an estimation of the desired signals originating from the IoMT sensors (Liu et al., 2020). AirComp is considerably efficient in terms of spectrum utilization and effectively fits to the FL distributed scheme, since the pre-processed signals sent to the receiver/fusion center represent the ML model parameters of each IoMT node (e.g., neural network weights) (Yang et al., 2020). The goal is to identify the power allocation of the involved IoMT nodes, as well as the scaling function in the fusion center in order to enhance the energy-efficiency, albeit without degrading the performance of the AirComp system (Cao et al., 2020).

The integration of AirComp with FL addresses several limitations in distributed ML-aided systems by improving computational efficiency and resource utilization. FL enables collaborative model training on decentralized devices while preserving data privacy, but resource- and energy-constrained edge nodes might not be able to cope with excessive computation requirements. In greater detail, running complex ML models on resource-constrained edge devices will quickly deplete their batteries. By integrating AirComp with FL, computation tasks can be offloaded to more powerful devices, thus reducing the burden on the edge devices, improving energy efficiency and the lifetime of battery-dependent network nodes, and guaranteeing scalability in IoT deployments, comprising a massive number of devices.

1.2 6G maritime communication networks

A Maritime Communications Network (MCN) is formed in a localized geographical area and contains multiple nodes that need to access the network. This can be achieved through a shore Base Station (shore BS) that is located on the land, in close proximity to the sea level, and has backhaul connectivity to the mobile network and the internet (Nomikos et al., 2022). Alternatively, the connectivity of the MCN nodes can be achieved through satellite communications, in cases that they are not located in the vicinity of a shore BS (Wang et al., 2021). Considering the former cellular communication scheme, it is worth noting that the propagation characteristics of the maritime wireless channels often involve severe channel losses, resulting in signal re-transmission, poor spectrum utilization and increased energy consumption (Wang et al., 2018). Furthermore, the satellite communications are not in principle preferred as the primary communication solution, due to their increased cost and inferior spectral efficiency (Huo et al., 2020). The nodes constituting the MCN can be fishing boats, vessels for search and rescue (SAR) or ocean exploration operations, IoMT sensors that monitor the water quality or quantify the pollution levels, etc. (Wang et al., 2018).

Recently, Unmanned Aerial Vehicles (UAVs), Unmanned Surface Vehicles (USVs) and Unmanned Underwater Vehicles (UUVs) have been also introduced as active nodes in the MCNs (Wang et al., 2021). Although these nodes can assume the typical role of a participating node, their mobility also enables their utilization for dynamic resource provisioning, extending the performance and the range of the cellular networks (Bithas et al., 2020). For instance, UAVs are expected to generally support mission critical services and disaster relief operations in remote locations (Li et al., 2020). Regarding the maritime requirements in modern 6G networks, UAVs, USVs and UUVs will act as relaying nodes in the MCNs, enabling multi-hop communication between shore BSs and the maritime nodes (Nomikos et al., 2022). In this manner, the MCN can guarantee high-capacity links and an adequately broadband quality of service to the IoMT devices, permitting the transmission of real-time video and control (Luo et al., 2022).

1.3 Paper contributions

In principle, the present paper proposes the joint adoption of FL and AirComp in the 6G-enabled maritime networks. Both FL and AirComp are well-established methodologies that are used in the frame of the future highly-demanding networks. FL emerges as a privacy-preserving technique for enabling distributed and collaborative intelligence across multiple local learning agents, while AirComp is a physical-layer spectrum-efficient technique that allows multiple agents to transmit data over a common multi-access channel, instead of using multiple transmitting channels. Note that, in the AirComp concept, all agents contribute to the computation of a nomographic function (e.g., mean, sum). Given that FL is proposed as the dominant ML method in the future 6G networks (massive maritime IoT nodes are served by the MCNs) for purposes of privacy protection and knowledge sharing, a major obstacle is faced by the strict requirements for excessive transmissions (frequent transmissions between nodes and base stations) and high spectrum availability (massive links are used). To mitigate the need for high spectrum usage and high energy consumption, AirComp is coupled with the FL towards improving energy (all AirComp agents respect a predefined transmission power budget) and spectrum (all AirComp agents transmit over a single multi-access channel) efficiency.

To this end, we present a coalescence of FL and AirComp solutions for communication-efficient and privacy-aware smart shipping. The present framework is primarily motivated from the need for data communication load reduction, along with the optimization of the wireless resources (transmitter power and spectrum utilization), the privacy preservation that the FL and AirComp methods foster, as well as the enhanced model sharing abilities and energy efficiency aspects. More specifically, our work focuses on intelligent maritime transportation systems where communication among geographically dispersed network nodes (ships) and a shore-based BS at a data fusion center is established by UAVs. This setup requires the efficient integration of privacy-preserving ML techniques with energy- and spectral-efficient wireless communication. Thus, our FL-based solution promotes the participation of stakeholders in the data sharing process due to data gravity, overcoming limitations of centralized learning approaches where data are transferred to central locations for processing. Meanwhile, lifetime maximization and communication reliability for the battery-dependent maritime and aerial nodes that support critical maritime services is ensured through AirComp. In summary:

1) We couple FL methods with AirComp in the frame of the future 6G MCNs, so as to promote over-the-air model sharing between the local agents and beneficial spectrum utilization towards communication efficiency, while boosting the privacy preservation and promoting data ownership.

2) A heterogeneous system model is proposed for the representation of the MCN, including a plethora of maritime entities that take part in the learning process, such as UAV, USV, UUV, buoys, vessels and cargo ships. In addition, to allow fast model aggregation, we consider the shore BS being equipped with Data Fusion functionality such that local model parameters are combined via MAC.

3) In contrast to the majority of current AirComp studies that consider peak-power constraint at each FL agent, we optimize the system parameter configuration to provide low computation error, flexibility in power allocation and adjustable energy efficiency for the whole MCN. Towards this end, a sum power budget among the participating IoMT nodes is considered, meaning that power control of the existing maritime entities ensures that total power consumption limits are not exceeded.

4) Experimental results regarding both the FL performance and the AirComp-based error minimization are demonstrated. For the former, we built LSTM models and an FL model based on real data, towards predicting the fuel consumption of large cargo ships. For the latter, we simulated realistic channel conditions (considering both small- and large-scale fading) and measured the AirComp error for different MCN densities and environmental noise conditions.

1.4 Paper structure

The rest of the paper is organized as follows: Section 2 describes in detail the system and communication model of the heterogeneous MCN, introducing the relevant parameters and mathematically formulating the channel models and the relaying links using UAV nodes. Moreover, Section 3 provides considerations related to the AirComp system, illustrating the key parameters that affect its performance, namely, the power allocation of the IoMT nodes and the scaling factor of the fusion center. Section 4 presents the workflow of the proposed FL method in conjunction with the AirComp system, while performance evaluation based on the experimental data is provided in Section 5. Finally, Section 6 concludes the paper, describing extensions of the current work.

2 System and communication model

This section describes the system model associated with a heterogeneous MCN. To this end, diverse types of IoMT entities are considered to be located across the three layers of the MCN, namely, the Underwater IoMT (UWI) layer, the Sea-Surface IoMT (SSI) layer and the Aerial-Relay IoMt (ARI) layer. For purposes of providing collaborative intelligence, MCN allows the interaction between the three-tier IoMT Area and a Land Area, where the shore BS-Data Fusion (SBS-DF) is able to fuse multiple signals received through a MAC. AirComp is also supported to enable communication efficiency, with an MCN Agent exploiting the Channel State Information (CSI) from all IoMT entities to propose power control and Data Fusion scaling policies. In this manner, this section also presents the channel modelling associated with the uplink communication, which in turn is crucial for the AirComp performance.

2.1 Heterogeneous MCN model

A general-purpose MCN is assumed, as depicted in Figure 1. The MCN includes three layers of heterogeneous IoMT entities (UWI, SSI and ARI) intercommunicating with each other for exchanging data, sharing alarms or forwarding local models. The lower UWI layer contains the UUVs which are capable of collecting underwater data (e.g., images, sensing, temperature, sea currents, pollution levels) and either send them horizontally to another UUV, or forward them vertically to their managing entity, which is one or multiple USV(s). The middle SSI and the upper ARI layers include intelligent IoMT entities that are able to train their own local models based on locally collected data. In line with the foreseen 6G communications, the considered MCN can also deploy an on-demand aerial relay network in the ARI layer, so as to allow distant communication between SSI entities and the shore BS. UAVs can also act as relays when an SSI entity intents to transmit data under harsh propagation conditions. The final communication links directed towards the shore BS as the destination of information are combined though a MAC. Under this system model, MCN can enable all the learning IoMT agents to locally built AI models and, then, to collaboratively construct FL models by performing the model averaging over-the-air (through the MAC). Finally, the computation error associated with the difference between the desired and the achieved model average can be minimized by properly regulating: (i) the transmitting uplink power of the learning IoMT agents and (ii) the data fusion scaling factor. To that end, an MCN Agent directly linked with the SBS-DF (via a backhaul link) is responsible for running a computation error minimization algorithm, so as to proactively suggest an optimal configuration of the uplink power levels and the Rx-scaling factor.

FIGURE 1

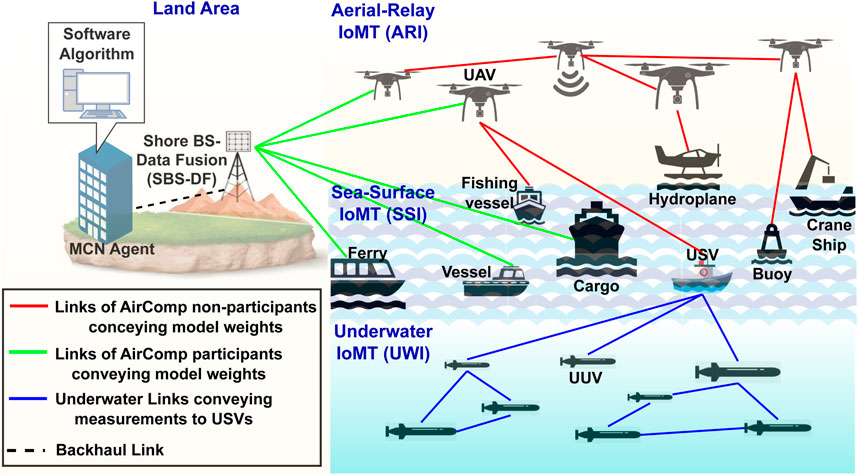
FIGURE 1. A heterogeneous 6G Maritime Communication Network (MCN) which is comprised of a Land Area and a three-tier Internet of Maritime Things (IoMT) Area. At the IoMT Area, there are three layers including a set of Underwater, Sea-Surface and Aerial Things, which are capable of training their own models and send them (in)directly towards the shore BS for averaging. At the Land Area, there is a shore BS, which is able to fuse multiple signals transmitted over a multi-access channel, and the corresponding MCN Agent, which implements all the algorithmic, intelligence and management operations related to the MCN.

Formally, we let $\mathcal{N}=\{\mathrm{1,2},\dots ,N\}$ denote the set of the SSI/ARI entities participating in the learning process. This means that $\mathcal{N}$ contains the IDs of all FL agents that aims to send their locally trained models directly or indirectly (via the relay network) towards the SBS-DF for averaging. The set of the locally pre-trained models is denoted as $\mathcal{M}=\{M_1,M_2,\dots ,M_N\}$, where M_n is the local model of FL agent n $(n\in \mathcal{N})$. Note that, M_n can be considered as a pre-processed function in the form of an array that contains the adjusted model weights/parameters upon local training rounds. The dimensions of the array exclusively depends on the dimensionality of the local AI model. Also, we let the set of the aerial relay nodes to be notated as $\mathcal{R}=\{R_1,R_2,\dots ,R_L\}$, where L is the total number of the relay nodes.

Since the AirComp system only concerns the IoMT entities that transmit towards the SBS-DF, we separate the set of the learning agents $\mathcal{N}$ from the set of the AirComp participants, which is denoted as $\mathcal{A}=\{a_1,a_2,\dots ,a_K\}$, where K is the total number of AirComp participants (see green links in Figure 1). Also, since a given relay node R_l (l ∈ {1, 2, … , L}) can serve multiple learning agents, this means that the total number of AirComp participants is at most equal to N, i.e., K ≤ N. In the extreme cases in which either: (i) all learning agents transmit directly to the SBS-DF or (ii) each learning agent has its own relay node for forwarding the model weights to the SBS-DF, then K = N. Note that, each element $a_k\in \mathcal{A}$ is the ID of the kth AirComp participant and is drawn from the union set $\mathcal{N}\cup \mathcal{R}$. This means that each AirComp participant is either: (i) a learning agent directly transmitting to the SBS-DF or (ii) a relay node transmitting to the SBS-DF the model parameters of another learning agent.

Each AirComp participant $a_k\in \mathcal{A}$ transmits at the power level of p_k, whereas the sum power of all AirComp participants P_total cannot exceed a maximum power threshold P_thres. This means that the total power allocation should satisfy the following equation:

$P_{\mathit{total}}={\displaystyle \sum _{k=1}^K}{p}_k\le P_{\mathit{thres}}(1)$

We also denote as $\mathcal{P}=\{p_1,p_2,\dots ,p_K\}$ the set of the power levels of the AirComp participants. At the Land Area level, we assume that the superposed signal $\widehat{Y}$ received by the SBS-DF is scaled by applying a scaling function G(⋅) at the Data Fusion. Given known channel quality indicators related to the links of the AirComp participants, a software algorithm (running at the MCN Agent) calculates the proper configuration of the scaling function G(⋅) and the power allocation set $\mathcal{P}$ that ensures low computation error (see Section 3) and respects the maximum power budget. Finally, the algorithmic results are acknowledged to the AirComp participants before they start to upload their local pre-trained models (see Section 2.2 for the uplink channel modelling). More details about how the relaying process is achieved are presented in Section 2.3, whereas details on how the learning cycle unfolds are provided in Section 4.

2.2 Channel models

In this subsection, the channel models related to all IoMT-to-IoMT and IoMT-to-SBS interfacing are described. Note that, the channel models engaging UWI entities are not modelled, since underwater communications are beyond the scope of this article and do not result in loss of generality. Thus, below, we formally present all the uplink channel models that are engaged in the paths connecting local models (i.e., the learning agents) to the Data Fusion for averaging. For ease of exposure, Figure 2 shows the geometrical considerations associated with the channel models described below.

FIGURE 2

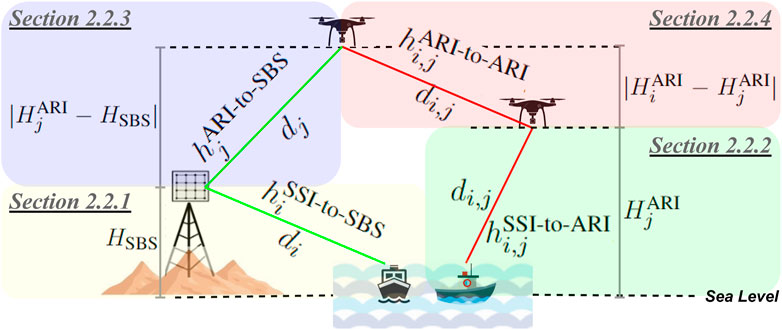
FIGURE 2. Geometrical considerations and mathematical notations underlying the channel modelling of all communication links.

2.2.1 From sea things to shore BS

Here, the direct (without relaying) communication link between SSI entities and the SBS-DF is analyzed. Given that the propagation conditions of a maritime environment are characterized, in general, by the mixing of both a large-scale fading (LSF) and a small-scale fading (SSF) component, the SSI-to-SBS channel model includes both LSF and SSF components. The LSF component is slowly-varying and is composed by a Line-of-Sight (LoS) term reflecting the signal attenuation due to path loss, as well as a Non-Line-of-Sight (NLoS) term representing the signal attenuation due to the presence of scatterers (e.g., scattering, shadowing, diffraction). The SSF component is rapidly-varying and reflects the signal loss due to multi-path propagation (Tang et al., 2021). In addition, the LoS component is affected by the density, the maximum dimensions, the height of scatterers that are located in the MCN area, and the elevation angle between the SSI entity and the SBS-DF. Based on the aforementioned and according to previous studies (Nasir et al., 2019; Nomikos et al., 2023), the SSI-to-SBS channel coefficient can be expressed as:

$h_i^{\text{SSI}-\text{to}-\text{SBS}}=C_i^{\text{SSF}}\cdot \sqrt{C_i^{\text{LSF}}},(2)$

where $C_i^{\text{LSF}}$ is the LSF coefficient of the link between the ith SSI entity and the SBS, and $C_i^{\text{SSF}}$ is the SSF coefficient of the SSI-to-SBS link that follows the complex Gaussian distribution $\mathcal{C}\mathcal{N}(\mathrm{0,1})$. The LSF coefficient can be expressed in dB as:

$C_i^{\text{LSF}}\left[dB\right]=\frac{\eta \text{LoS}-\eta \text{NLoS}}{1+\alpha e^{-b\left({\rho }_i-\alpha \right)}}+20{\log }_{10}\left(d_i\right)+20{\log }_{10}\left(\frac{4\pi f}{c}\right)+\eta \text{NLoS},(3)$

where d_i is the distance between the ith SSI entity and the SBS, f is the carrier frequency, c is the speed of light, ηLoS, ηNLoS are coefficients related to the LoS and NLoS terms, respectively, and α, b are constant propagation parameters. The parameter ρ_i quantifies the elevation angle between the ith SSI entity and the SBS:

${\rho }_i=\frac{180}{\pi }\arcsin \left(\frac{H_{\text{SBS}}}{d_i}\right),(4)$

where H_SBS is the height of the shore BS (above the sea level).

The channel coefficient reflects the quality of a given link under specific propagation conditions. We assume that CSI of all the involved communication links is accurately estimated at the moment of the communication link establishment, or it can be estimated on-demand by the SBS (Du et al., 2022). Noteworthy, although the channel coefficients are in general time-varying due to the dynamic environmental conditions, here we assume static channels without loss of generality, since CSI estimation is done rarely in time (when an AirComp participant needs to upload the local model parameters), thus giving instantaneous CSI estimations with high precision. Finally, the variance of thermal noise at a given receiver r is denoted by ${\sigma }_r^2$ (where $r\in \mathcal{R}$ refers to an ARI entity or r = SBS refers to the SBS), which corresponds to an Additive White Gaussian Noise (AWGN) distribution with zero mean and variance equal to ${\sigma }_r^2$.

2.2.2 From sea things to aerial things

Following similar concepts as in the SSI-to-SBS case, the channel coefficient between the ith SSI and the jth ARI entity, $h_{i,j}^{\text{SSI}-\text{to}-\text{ARI}}$, is given by Eq. 2. To compute the LSF coefficient, we use Eqs. 3, 4 by replacing d_i with d_i,j, which denotes the distance between the ith SSI and the jth ARI entity, and H_SBS with $H_j^{\text{ARI}}$, which is the height of the jth ARI entity above sea level.

2.2.3 From Aerial Things to shore BS

In the same manner, the channel coefficient between the jth ARI entity and the SBS, $h_j^{\text{ARI}-\text{to}-\text{SBS}}$, is given by Eq. 2. The LSF coefficient is calculated via Eqs. 3, 4 by replacing d_i with d_j, which denotes the distance between the jth ARI entity and the SBS, and H_SBS with $|H_j^{\text{ARI}}-H_{\text{SBS}}|$, which is the relative height between the jth ARI entity and the SBS.

2.2.4 From aerial things to aerial things

Similarly, the channel coefficient between the ith and the jth ARI entities, $h_{i,j}^{\text{ARI}-\text{to}-\text{ARI}}$, is given by Eq. 2. The LSF coefficient is computed by Eqs. 3, 4 by replacing d_i with d_i,j, which denotes the distance between the ith and the jth ARI entities, and H_SBS with $|H_i^{\text{ARI}}-H_j^{\text{ARI}}|$, which is the relative height between the ith and jth ARI entities.

2.3 Relaying model

In this subsection, we describe the principles underlying the UAV-based relay network that is considered in this paper. Without loss of generality, we only describe the single-hop relaying (one hop from learning agents to the destination relay node), whereas the described modelling can be easily extended for the multi-hop relaying case. Considering a time slot based counting, at a given time slot, the relay network is formed by a subset of active ARI entities drawn from the set $\mathcal{R}$ for purposes of forwarding the local model weights of the SSI entities, which experience poor channel conditions. To allow optimum placement of relay nodes, we assume that the UAV positioning is achieved by applying a known algorithm (Chen et al., 2018). We also assume buffer-aided UAVs, meaning that each ARI entity is able to store the models to be forwarded in a buffer. Let $\mathcal{B}=\{B_1,B_2,\dots ,B_L\}$ be the set of buffers’ occupation level, which means that element B_l denotes the number of pre-trained model arrays (drawn from the set $\mathcal{M}$) that are stored in the buffer of relay node $R_l\in \mathcal{R}$.

The relaying model includes all the algorithmic logic that is followed to empty all the buffers when an aggregation step is requested. In other words, emptying the buffers means that all the stored models are successfully forwarded to the MAC for over-the-air computation. Local training steps of all learning agents are performed in every time slot, whereas aggregation steps are performed every T_FL time slots. Assuming that an aggregation step is to be performed at time slot t, there is a delay for emptying all the buffers before aggregation starts, so as to ensure that all local models participate in the averaging. Given that each AirComp participant can transmit only one pre-trained model over MAC at a time slot, the total delay required for emptying all the buffers is defined by the worst-case buffer (i.e., the mostly-occupied buffer), which requires B_worst time slots to be emptied. To this end, the delay (in time slots) required for emptying all the buffers is equal to the highest occupation level B_worst at the moment of aggregation step request, and is given as:

$B_{\mathit{worst}}=\underset{R_l\in \mathcal{R}}{\max }{B}_l(5)$

From the aforementioned and Eq. 5, it is implied that the pre-trained models stored in the buffers are sequentially offloaded to the SBS-DF over MAC, with the latest pre-trained model being offloaded at time slot t + B_worst (where t is the time slot of aggregation step request).

For clarity, Figure 3 depicts an example of how the relaying process unfolds, given that an aggregation step is to be performed at time slot t. The example considers N = 8 learning agents, L = 3 relay nodes and K = 5 AirComp participants. The pre-trained models of the learning agents 1, 2, … , 8 are denoted as M₁, M₂, … , M₈, respectively. The temporal sequence from time slot t to the time slot of the aggregation completion t + B_worst is the following:

• Time slot t: All the buffers are empty, all the links are inactive, all local models are kept at the learning agents.

• Time slot t + 1: Learning agents 1 and 2 directly transmit their models over MAC, relay node R₁ transmits the model M₃, relay node R₂ transmits the model M₄ and stores models M₅ and M₆, relay node R₃ transmits the model M₇ and stores model M₈.

• Time slot t + 2: Relay node R₂ transmit the model M₅ and keeps stored model M₆, relay node R₃ transmits the model M₈.

• Time slot t + 3: Relay node R₂ transmits the model M₆. At the end of this time slot, all models are averaged and ready to be scaled by the SBS-DF by applying G (⋅).

FIGURE 3

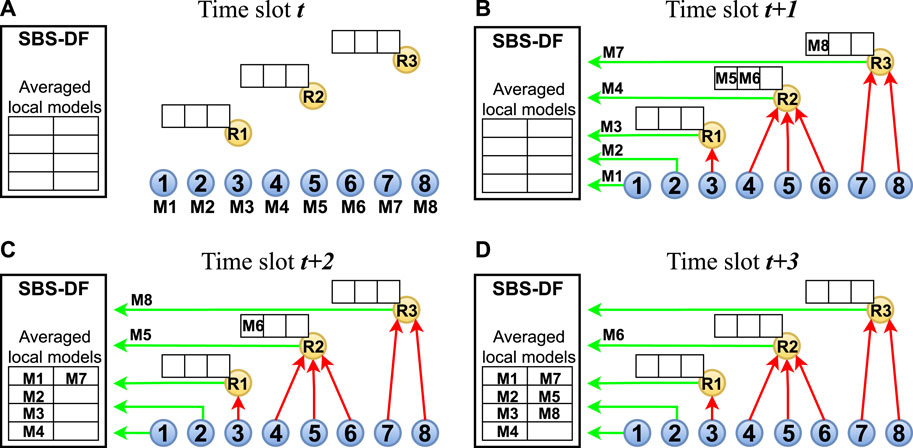
FIGURE 3. An example of relaying temporal sequence starting from the aggregation step request at time slot t. (A) The initial state where all the buffers are empty, all the links are inactive, and all local models are kept at the learning agents. (B) Learning agents 1 and 2 directly transmit their models over MAC, whereas each of the relay nodes transmits one model and stores the remaining models. (C) One model is again transmitted by each of the non-empty relay nodes. (D) The mostly occupied relay node transmits the last model and all the local models are now uploaded for aggregation.

Notably, delays introduced by buffer emptying prerequisites are met only during the training process of the FL and do not produce significant waiting times (usually a few time slots). Also, these delays have zero impact on the final inference phase of the FL operation, since the final FL models can be directly inferred without aggregation and relaying steps.

3 Over-the-air model sharing

This section formulates the AirComp error minimization problem, which enables: (i) all the AirComp participants to properly regulate their power levels and (ii) the SBS-DF to properly define the Rx-scaling, targeting at the error minimization between the desired and the received signal. The AirComp algorithm is executed in the MCN Agent, which, upon performing some calculations (see equations of Section 3.2), sends the proposed Tx/Rx-scaling factors to the actors (Data Fusion and AirComp participants) immediately before the beginning of each aggregation step.

3.1 Problem formulation

AirComp is an emerging technology and has been proposed as a mathematical tool for function representation in a plethora of 5G and beyond use cases. Recently, AirComp has been coupled with FL techniques, so as to leverage effective collection and computation across multiple local agents via signal superposition. This section mathematically describes the AirComp problem formulation, expressed in terms of the maritime system model. Contrary to the majority of the existing AirComp studies that consider peak-power constraint at each FL agent (e.g., IoMT entity), here we present an optimal system parameter configuration (i.e., Tx/Rx scaling policy) to minimize the computation Mean Squared Error (MSE) of an AirComp-aided MCN under a sum-power of all AirComp participants.

In brief, a wireless distributed ML paradigm is considered, in which each IoMT entity inside the MCN adopts distributed Stochastic Gradient Descent (SGD) algorithms for ML model training. Each IoMT entity computes the gradient of its local cost function (based on its own dataset) in terms of the model weights. Concurrently, forwards the model weight array to the SBS-DF or to a relay node. AirComp participants send all the parameters to the SBS-DF over MAC, which then applies an Rx-scaling function to produce an accurate computation of the average of the gradients. Finally, SBS-DF broadcasts the FL model to the involved parties for further iteration until convergence (Liu et al., 2020).

An AirComp-aided MCN sytem with K single-antenna AirComp participants is assumed. When an aggregation step is requested at time t, each AirComp participant $a_k\in \mathcal{A}$ has to transmit (over MAC) the pre-processed signal $M_k\in \mathcal{M}$. Pre-processed signals have zero mean and normalized variance (Liu et al., 2020). Each AirComp participant’s antenna linearly scales the signal M_k by the factor $\sqrt{p_k}$, whereas the wireless channel further scales the transmitted signal by the coefficient h_k, where $h_k=h_k^{\text{SSI}-\text{to}-\text{SBS}}$ or $h_k=h_k^{\text{ARI}-\text{to}-\text{SBS}}$. The receiver SBS-DF applies the Rx-scaling factor G targeting at minimizing the computation distortion between the received signal $\widehat{Y}$ and the wanted signal Y. The wanted signal is given by Eq. 6 as:

$Y={\displaystyle \sum _{k=1}^K}{M}_k(6)$

Due to Tx-scaling, channel losses and Rx-scaling, the received signal is computed by the following formula:

$\widehat{Y}=G\left({\displaystyle \sum _{k=1}^K}\sqrt{p_k}{h}_k{M}_k+n\right)(7)$

where n is the reception noise at the SBS-DF with zero mean and variance σ². Considering a linear Rx-scaling G(x) = G ⋅ x, the computation distortion is literally the MSE between Y and $\widehat{Y}$ and can be computed as (Zang et al., 2020):

$\text{MSE}=\mathbb{E}\left[|Y-\widehat{Y}{|}^2\right]={\displaystyle \sum _{k=1}^K}|G{h}_k\sqrt{p_k}{|}^2+{\sigma }^2|G{|}^2(8)$

Using the definition of MSE from Eq. 8 and the total power bugdet from Eq. 1, an optimization problem regarding the computation distortion minimization under the total power limitation can be formulated by Eqs. 9a, 9b as:

$\left({\mathbf{P}}_{\mathbf{1}}\right):\underset{\left\{p_k\right\},G}{\min }{\displaystyle \sum _{k=1}^K}|G{h}_k\sqrt{p_k}{|}^2+{\sigma }^2|G{|}^2(\mathrm{9a})$

$\text{subject\hspace{0.17em}to}{\displaystyle \sum _{k=1}^K}{p}_k\le P_{\mathit{thres}}(\mathrm{9b})$

3.2 Controlling transmitters and receiver

Problem (P₁) is non-convex and can be converted into a convex one (Zang et al., 2020). Then, the solution of the convex problem is derived as the global minima of the target function, according to which the minimization of MSE is solely achieved by handling G and {p_k}. The optimal Rx-scaling factor G_opt is given by:

$G_{\mathit{opt}}={\left(\frac{1}{P_{\mathit{thres}}}{\displaystyle \sum _{k=1}^K}{\left(\frac{P_{\mathit{thres}}{h}_k}{{\sigma }^2+P_{\mathit{thres}}{h}_k^2}\right)}^2\right)}^{1/2}(10)$

Finally, the optimal power level of the k^thAirComp participants is written as:

$p_k^{\mathit{opt}}=\frac{P_{\mathit{thres}}^3{h}_k^2}{{\left({\sigma }^2+P_{\mathit{thres}}{h}_k^2\right)}^2{\sum }_{k=1}^K{\left(\frac{P_{\mathit{thres}}{h}_k}{{\sigma }^2+P_{\mathit{thres}}{h}_k^2}\right)}^2},\forall k=\mathrm{1,2},\dots ,K(11)$

Eqs 10, 11 define the Tx- and Rx-scaling regulation policy applied by the MCN Agent before AirComp transmission takes place. To this end, assuming that the aggregation step is periodically requested, a channel estimation round is performed one slot prior the aggregation step, so as to provide the channel coefficient measurements {h_k} for the calculation of $\{p_k^{\mathit{opt}}\}$ and G_opt.

In summary, the AirComp system aims to jointly regulate the transmitting power levels {p_k} of the AirComp participants and the Rx-scaling factor η of the SBS-DF, ensuring: (i) minimization of the computation distortion (MSE) and (ii) no excess of the total power budget.

4 Distributed learning workflow

This section outlines the complete learning workflow across the distributed FL agents. We considered that the nomographic target function is the extraction of the mean weight matrix across the local weights, an approach known as FedAvg (McMahan et al., 2017). The proposed pipeline can be easily adopted for any other nomographic target function, such as FedSGD (McMahan et al., 2017) or other mean-based method (Skianis et al., 2023).

The workflow sequence of the proposed distributed AirComp-aided learning method for MCNs can be summarized in the following steps:

1) Local data collection: The learning process is initiated when the distributed learning agents have sufficient data samples to be trained on. To this end, proper sensing equipment has been installed to each IoMT entity. For the case of USVs, data can be collected though multiple UUVs.

2) Parameter initialization: Random weights are assigned to all local models before the beginning of the training phase. Also, the SGD optimizers are set for the upcoming batch learning rounds.

3) Hyper-parameter tuning for local training: Local experimentation with regards to the impact of the crucial hyper-parameters (e.g., learning rate, model density) takes place to ensure optimal performance convergence. Model evaluation is based on testing the model performance by inferring it with samples that are not encountered during the training.

4) Local training rounds: When the optimal tuning is obtained, multiple training epochs are performed to compute the matrix of local model parameters. Note that, the training is based on feed-forwarding batch of training samples, whereas an epoch is completed when the whole training set has been fed to the model.

5) Relay network placement: Periodically (let T_FL be the aggregation period), the local models should be averaged via AirComp. To achieve this, it is firstly essential to optimally place all the UAVs, such that the maximum reliability is achieved. We assume that the placement policy is implemented as in (Chen et al., 2018), guaranteeing that the placement of both static and mobile UAVs is aware of the total power loss, the overall outage, and the overall bit error rate.

6) Estimation of channel state: All channel coefficients are acknowledged to the SBS-DF, which in turn sends the CSI indices to the MCN Agent though a backhaul link. Notably, under highly dynamic conditions, channel estimation is quite challenging, since successive channel estimation steps are required for accurate outcomes. However, in the considered case, AirComp transmission takes place every T_FL time slots, thus the channel estimation is performed rarely in time, and not in every time slot, without incurring high overheads.

7) Calculation of AirComp scaling policy: With known channel coefficients, MCN Agent is able to compute the optimal G_opt and $\{p_k^{\mathit{opt}}\}$ according to Eqs 10, 11, respectively, for the upcoming AirComp transmission. The suggestions are sent back to the SBS-DF and AirComp participants.

8) Relay network emptying: By applying the relaying model presented in Section 2.3, the UAVs carrying models from local learning agents are sequentially offloaded.

9) AirComp transmission: The AirComp participants transmit over MAC the local model weights. Before transmission, each AirComp participant scales the signals according to the power levels suggested by the MCN Agent.

10) Target function calculation: When the superposed signal is arrived at SBS-DF, the suggested Rx-scaling factor is applied to ensure optimal computation distortion.

11) Local model update: The FL model is returned back to all the learning agents via the path used for uploading the local models.

12) Learning termination: Steps 4–11 are repeated until a high-performance FL model is derived. The learning termination condition can be convergence-based, threshold-based or timeout-based.

13) Learning restart: A restarting operation can be also supported when further training is requested based on more recently-collected datasets upon observing performance degradation.

14) FL model re-usability: Finally, there is also a possibility for new IoMT learning agents entering the MCN to exploit the pre-trained FL model. This transfer learning approach enabled by FL can ensure that no time-consuming training process are required for new-comers, as the transferred models have global MCN-wide observability. Note that, different transferring policies could be also adopted driven by specific needs or observations (e.g., a type-specific IoMT inherits the model of the same type IoMT entities).

To concretely describe the sequence of the training steps, Figure 4 depicts a simplified workflow for the offline FL training of multiple AirComp participants. Note that, we have merged some of the analytical steps presented above for the ease of readability.

FIGURE 4

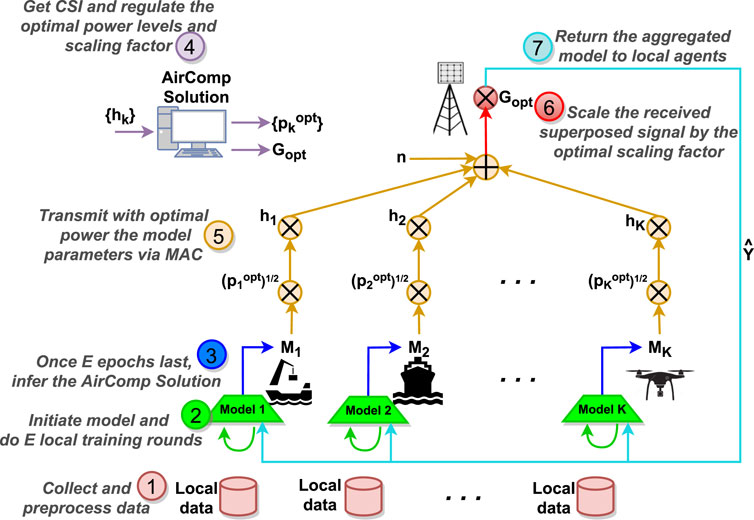
FIGURE 4. Simplified algorithmic workflow of the offline FL training procedure. Steps 2–7 are repeated for R aggregation rounds.

5 Numerical results

In this section, a numerical scenario related to the presented MCN architecture is demonstrated. Using a real dataset, the key goal is to quantitatively show how UAV-aided MCNs can leverage FL and AirComp technologies to provide data privacy, communication efficiency and collaborative learning. We conducted: (i) experiments to fine-tune the local hyper-parameters of multiple FL agents, (ii) experiments about the FL performance among multiple FL agents considering real data and (iii) simulations (due to the lack of real maritime-related channel data) about the AirComp errors achieved by a heterogeneous MCN, considering multiple AirComp participants and aerial relay nodes.

All algorithmic materials ran on Python 3.11 using Sci-kit learn and Tensorflow v2.12 libraries. The training was carried out on a personal desktop (AMD Ryzen 7 1800X Processor CPU, 8 Cores, 3.60 GHz, RAM 32 GB).

5.1 Experimental scenario

Based on a real dataset containing Automatic Identification System (AIS) data, we designed a multivariate regression problem to predict the temporal patterns of the Cargo Ship Propulsion Power (CSPP) and solved it via FL. Specifically, the dataset included AIS data for six twin cargo ships, with the following available timeseries data:

1) Ground Speed (GS): The speed (in knots) of the cargo ship relative to the static observer at the land.

2) Water Speed (WS): The speed (in knots) of cargo ship relative to water currents.

3) Wind Intensity (WI): The wind strength (in Beaufort or bft) ranging from integer values between 0–12.

4) Wind Angle (WA): The wind direction (in degrees) with respect to the instantaneous heading of the cargo ship.

5) Ship Trim (ST): This is the mid-line depth (in meters) of the ship which is calculated as the difference between the depth at the bow’s perpendicular and the stern’s perpendicular. It is measured relative to the waterline at the middle of the ship and indexes the minimum depth to sail without risks.

6) Cargo Ship Propulsion Power (CSPP): The primary propulsive power (in kilo-Watts or kW) of the cargo ship, expressed in kW. It is linearly related with the electrical requirements of the diesel engine, thus presenting positive correlation with fuel oil consumption.

The sampling period of all timeseries was 15 min, whereas the recordings refer to several pathways of the cargo ships. The dataset size exceeded the 20,000 samples per variable.

The experimental scenario considers an wide MCN area that monitors the six cargo ships through a connected pair of SBS and MCN Agent. The MCN supports UAV-based relaying to facilitate the distant communication between the ships and the MCN Agent. We consider an aerial relay network with fixed size, including 12 UAVs to enable single or two-hop relaying for each ship. The channel models for the UAV-to-UAV, UAV-to-SBS and Ship-to-UAV links are derived by the equations of Section 2.2. Each cargo ship is able to locally store the collected AIS data, as well as to periodically perform local training rounds based on local data. The common goal of the cargo ships is to build a distributed FL model, that will be generalized with respect to the knowledge of all individual ships. The intelligent maritime transportation system target in this scenario is the prediction of future CSPP values based on the current and previous values of the AIS data. Thus, each ship trains a Long Short-Term Memory Memory Network (LSTM) using a 5-variable input, namely, GS, WS, WI, WA and ST, as predictor and the future values of CSPP as forecasting output. LSTMs exhibit the ability to estimate (non-)linear complex relationships between input(s) and desired output, while also handling temporal dependencies of timeseries, so their utilization was preferred in this scenario.

In intelligent maritime transportation systems, accurate prediction of the fuel consumption can enable prognostics, proactive strategies and timely adjustments that, in turn, can reduce both the operational costs and the environmental footprint of the ship. In addition, FL can facilitate ships to estimate their upcoming fuel consumption in unknown conditions, i.e., they can grasp the knowledge of the other ships through the federation. To concretely describe the aspects of the proposed system, the structure of the experimental scenario is as follows:

• The impact of the critical hyper-parameter of the local ship models was initially investigated towards learning optimality and stability.

• Comparison of the FL-based LSTM model against a baseline distributed learning algorithm, which is based on the Ensemble Learning (EL) technique across the six local ship model.

• Validation of the AirComp-based model sharing under varying power constraints and noise conditions. Simulations regarding this task aim to quantify the computation error depending on the number of the AirComp participants.

5.2 Impact of local learning parameters

Before testing the performance of the collaborative FL scheme, a local parameter tuning was conducted. In this subsection, several parameter configurations of the local LSTM models are tested to ensure optimum setup. The construction of a single LSTM model, constructed by stacking several LSTM cell and a Multi-Layer Perceptron (MLP) layer, requires careful selection of hyper-parameters, especially those presenting high impact on the model convergence. The most critical parameter is the learning rate α, which controls how abruptly or smoothly the LSTM weights are set during backpropagation iterations. Another crucial learning factor is the LSTM depth D, which determines the model size and, subsequently, the overall model complexity. Both parameters have a potential influence on the model performance, so they are both selected for fine-tuning. In general, the configuration of a deep and dense neural network is not a priori known. Hence, all the hyperparameters (learning rate α, number of hidden layers D, etc.) are adjusted upon extensive simulations. The goal is to optimally set the values of the hyperparameters, so as to ensure low error convergence. Based on this ground-truth, the selection of α and D is totally driven by experimental simulations.

The following LSTM setups were considered: (i) activation function of all LSTM units: Rectified Linear Unit (ReLU), (ii) optimizer to implement SGD during backpropagation iterations: Adaptive Moment estimation (Adam), (iii) Past-values window length: 5, (iv) Forecast moment: 15 min, (v) Number of neurons in each hidden layer were {128, 64, 32, 16} for D = 4, {128, 64, 32} for D = 3, {128, 64} for D = 2, and {128} for D = 1.

We also trained each cargo ship model using 90% of the data samples, while keeping the residual 10% for testing the model performance on unseen samples. By setting diverse values for both α and D, we extract a trained model, for each local LSTM model. Figure 5 shows the learning curves (i.e., MSE as a function of training epochs) for different values of the learning rate α = 0.0001, 0.001, 0.01, exhibiting optimum performance for α = 0.001 in all single models. Similarly, Figure 6 shows the learning curves for different values of the LSTM depth D = 1, 2, 3, 4, showing the lowest error for D = 1 hidden layer with 128 neurons. The aforementioned values are selected to obtain a reasonable trade-off between neural network density and performance. In this sense, almost all ship-specific models exhibited the best accuracy for D = 1, whereas negligible performance gain was obtained for D = 2 in two ships. Note also that, all ship models are required to finally have the same dimensions and architecture for successfully train the FL scheme, since FL uses edge-by-edge averaging and aligned dimensionality across local models is essential.

FIGURE 5

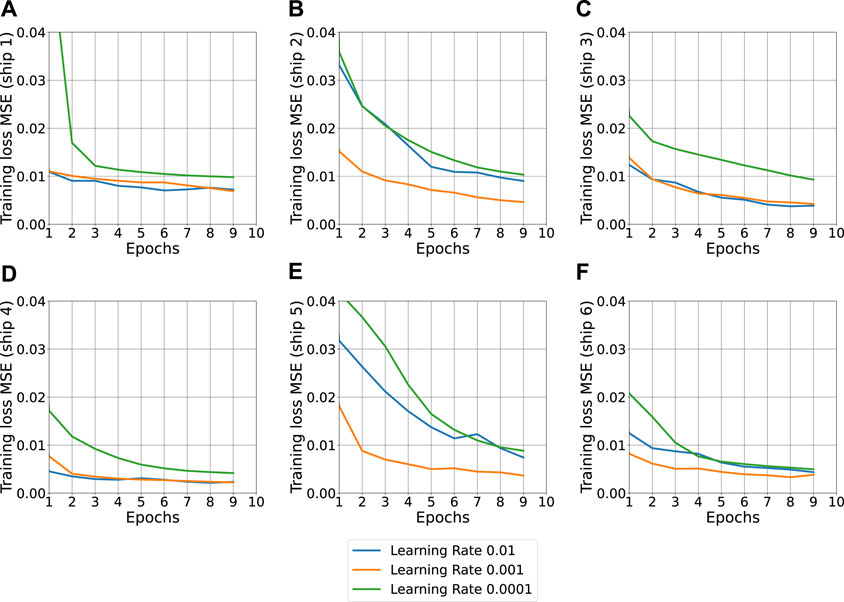
FIGURE 5. Training Loss curves for the six training ships. Each subplot depicts the training MSE as a function of the training epochs for varying values of the learning rate a = [10^–4,10^–3,10^–2,10^–1]. Panels (A–F) correspond to the ships 1–6, respectively.

FIGURE 6

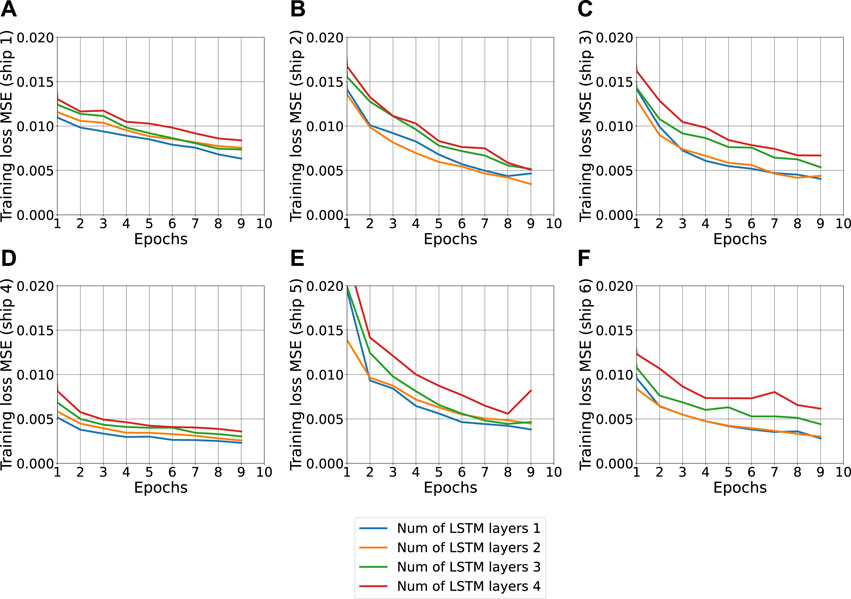
FIGURE 6. Training Loss curves for the six training ships. Each subplot depicts the training MSE as a function of the training epochs for varying values of the number of LSTM layers N_LSTM = [1,2,3,4]. Panels (A–F) correspond to the ships 1–6, respectively.

5.3 Comparative performance

A straightforward solution to combine different local models and achieve collaborative predictive capabilities would be that given a new data sample that requires model inference, the collaborative prediction for that sample can be the average prediction across the local predictions of each ship model. This prediction policy is similar to the concept of Ensemble Learning (EL) and does not require any federation process except for the training of the local models. Such an EL approach is less complex than the FL and it was unknown whether it could be more effective than FL. Thus, this section compares the following two schemes, as an attempt to test the FL efficiency against the baseline:

• Federated Learning (FL): This scheme is implemented according to the FedAvg method (McMahan et al., 2017). Following this approach, each AirComp participant uploaded the local model weights and the SBS-DF extract the weight average across the local parameters. The weighting is based on the sample size of each AirComp participant’s model, so as to make the large (or small) sample sized contribute the largest (or lowest) to the FL model.

• Ensemble Learning (EL): This scheme basically trains all local models based on local ship data. Then, the inference data are passed through each local model and, then, to get the final prediction, all prediction outputs are averaged. In this way, the average “opinion” across all ship models is derived.

The performance of the two methods is validated against a subset of samples from the testing set that have not been encountered during the training process. In specific, the testing data consists of the final 50 testing samples from all six ships integrated into a single dataset in order to quantify the output performance of the two methods in heterogeneous inputs and verify the collaborative learning framework. To that end, the predicted values of the CSPP variable are illustrated in Figure 7 for the FedAvg and ES methods and compared to the ground-truth values of the testing set. To quantify the performance of both methods, we computed the goodness of fit (GoF) between the model-predicted and actual curves, with FedAvg presenting a GoF of 90.3%, whereas EL showed a GoF of 29.7%. Note that, both methods were able to capture the trends of the CSPP curves, with FL being also accurate in predicting the absolute CSPP values, as opposed to EL. Evidently, the FedAvg method outperforms the EL collaborative scheme, approximating the variations of the testing samples and achieving a higher goodness of fit by a factor of 3.04.

FIGURE 7

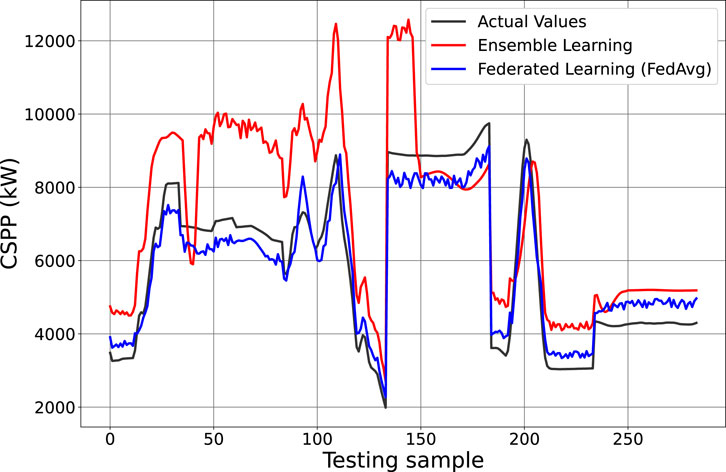
FIGURE 7. Estimated values generated by the FedAvg and EL collaborative models vs. ground-truth CSPP values. To assess the overall federated performance across all ships, the testing curves were comprised of testing samples from all six ships (50 samples per ship).

5.4 Forecast moment versus past-values window

The main goal of this section is to investigate the impact of the look-back window and the forecast moment, given that it is not feasible to know the exact relationship between them towards achieving optimal performance. Thus, we experimented with nine combinations of Past-Values Window and Forecast Moment pairs (3-by-3 pairs) in order to select the optimum configuration, offering the highest accuracy (or the lowest error). In practice, we conducted nine different FL model training sessions. Each FL model was derived by multiple aggregation rounds across six local LSTM models. Finally, we measured the FL algorithms’ performance as the inverse error function (i.e., accuracy).

To this end, we quantify the impact of these two variables related to the input timeseries in the prediction accuracy of the CSPP. The forecast moment represents the temporal prediction ability of the presented framework, i.e., the particular point in the upcoming future time instances where prediction of CSPP is required. In this context, large values of forecast moment are in principle preferred in the maritime domain, since timely predictions allow significant time windows for prognostics, predictive maintenance and in general, proactive strategies. Furthermore, the past-values window variable denotes the temporal window before the current time instance that the model requires for prediction. Specifically, small values of past-values window variable signify that the CSPP estimation is based on recent environmental conditions and cargo ship parameters (latest values of the 5-variable input are taken into account in the CSPP forecast), whereas larger values of the parameter target to additionally consider long-range dependencies that may be present in the input variables (e.g., biased ship trim, independence of CSPP from long-term WA values, etc.).

We therefore investigate a balance between the configuration of the two aforementioned parameters and the accuracy in the CSPP prediction. It is worth mentioning that increased past-values windows result in significant augmentation of the computational overhead. Although this increase may have negligible impact in the training process of centralized schemes in terms of latency requirements, it should in general be avoided during the training and inference phases of collaborative learning frameworks that aim at incorporating lightweight ML models. In addition, it is expected that large values of forecast moment will result in gradual degradation of the prediction accuracy, since intuition dictates that future CSPP values cannot be estimated only by long-range dependencies, but also exhibit short-term relationships.

Figure 8 demonstrates the resulting accuracy for various values of the past-values window and forecast moment parameters. The results are shown for forecast moment values of {15, 45, 75} min, whereas the past-values window length took the values 5, 10 and 15 (equal to the number of previous data samples). Moreover, the prediction accuracy is expressed as the Mean Absolute Error (MAE) between model-predicted and actual curves. To highlight the relative performance across the various learning configurations and scale the performance in the range 0–1, the final MAE values were transformed in normalized accuracy values based on the minimum MAE (i.e., the normalized MAE was equal to the minimum MAE divided by the measured MAE. This means that the optimal normalized accuracy was unity for the minimum-MAE configuration. We observed that a forecast moment of 15 min and a past-values window of equal to 5 was the best configuration.

FIGURE 8

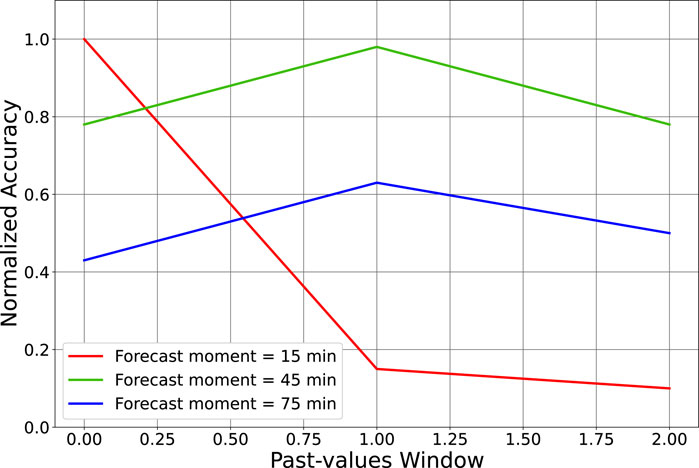
FIGURE 8. Impact of Forecast moment and Past-values Window parameters on the accuracy of the CSPP prediction. The normalized accuracy was computed as the ratio between the minimum and the measured MAE and ranges between 0–1.

As readily observed in Figure 8, for the minimum past-values window, the relative normalized accuracy deteriorates as the forecast moment increases (normalized accuracy of 0.78 and 0.43 respectively). On the other hand, the best normalized accuracy is observed for the minimum past-values window length of 5 and the shortest forecast moment of 15 min. For the case of 45-min forecast moment and 10-point long past-values window, we obtain a close-to-unity performance. Finally, it is evident that the prediction accuracy degrades for a past-values window of 15, regardless of the value of the forecast moment parameter, which can be attributed to the complexity escalation of the LSTM network (larger input layer size). Towards this direction, a reasonable trade-off between computational complexity, proactive strategies, timely adjustments and accuracy in the CSPP estimation indicates the use of forecast moment and past-values window of 15 min and five points, respectively, as optimal fine-tuned parameters.

5.5 Impact of power budget and noise on the AirComp error

Following the workflow described in Section 4, the AirComp solution is used to transmit all the local neural network weights that were derived by local training rounds in the FL framework. The transmitting power levels are obtained by the AirComp solution to ensure low computation error. This means that, once each ship-specific model completes a predefined number of local training epochs (thus updating locally its model weights), the resulting model parameters are transmitted through the MAC towards the shore BS. Finally, the shore BS computes the mean across all local model parameters (nomographic function), scales the mean signal to ensure optimal computation distortion (the difference between the actual and the transmitted superposed signals) and returns the averaged model to the local nodes.

In this context, this subsection aims to show the outcomes of the AirComp solution (see Section 3.2) applied in a maritime setting, especially when the critical factors for the AirComp performance are varying. Those crucial factors are the power budget P_thres and the noise variance at the AirComp receiver σ². We assume an MCN area with a shore BS that superposes the signals from many MIoT nodes. These nodes send their data to the shore BS for FL purposes within the area. Due to the absence of real data regarding the channel coefficients of all links, we use the equations presented in Section 2.2 to calculate the uplink channel coefficients. The IoMT entities are randomly spread in the area at a random distance from the SBS between [D_min, D_max]. Table 1 summarizes the network and environmental characteristics considered in this subsection.

TABLE 1

TABLE 1. Environment and maritime network characteristics.

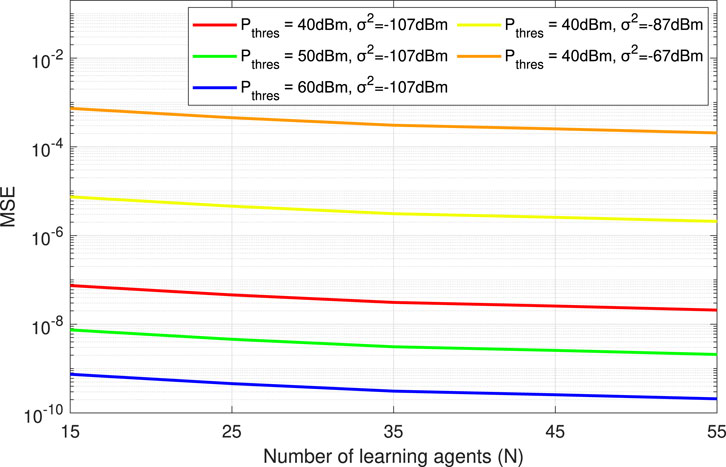
Figure 9 shows the AirComp error as a function of N for different values of P_thres and σ². In general, MSE decreases with increasing N regardless of P_thres and σ², suggesting that dense MCN areas with multiple learning agents can show enhanced AirComp performance than sparse MCN areas. In turn, given that the 6G era envisions all sectors, including maritime, to be extremely densified, coupling FL with AirComp can be the optimal choice for the provision of communication efficiency and privacy preservation. As expected, MSE is inversely proportional to the P_thres given that large power budget improves the propagation conditions and, thus, the AirComp performance. More importantly, this positive relation between MSE and P_thres defines a trade-off between the AirComp efficiency and the power consumption/energy efficiency of the whole MCN, since larger P_thres will improve the MSE at the expense of degrading the energy efficiency. Thus, given specific power consumption and MSE limitations, the optimal selection of P_thres should ensure an equilibrium between sufficient MSE and conservative power consumption. Finally, MSE increases with increasing σ² due to the presence of noise at the receiver input. This fact adds another factor in the P_thres selection in the sense that, depending on the application or use case, σ² may impose further increment in P_thres to guarantee the target MSE.

FIGURE 9

FIGURE 9. AirComp error as a function of N for different values of P_thres and σ².

Key observations from the scaling policy presented here and in Section 3.2 are summarized as follows:

• The optimal Rx-scaling factor G_opt monotonically decreases as a function of the total power budget P_thres.

• The optimal transmitting power levels $\{p_k^{\mathit{opt}}\}$ monotonically increase as a function of the total power budget P_thres.

• The links showing low or high quality channel conditions use lower power level than those showing medium quality channel conditions.

• The optimal MSE monotonically decreases as a function of the Signal-to-Noise Ratio (SNR = P_thres/σ²) and the channel-power gains.

6 Conclusion and work extensions

In summary, this paper presented a general architecture of 6G heterogeneous maritime communication networks (MCNs), including underwater, sea-surface and aerial nodes. To support decentralized learning framework across multiple Internet of Maritime Things (IoMT), the Federated Learning (FL) technique is adopted. Contrary to the conventional centralized learning schemes, FL enables collaborative, privacy-preserving and communication-efficient learning. To allow further communication efficiency, model sharing operations required by FL are implemented over-the-air following the principles of Over-the-Air Computation (AirComp) system. According to AirComp, all local model parameters are transmitted in a common access channel towards the data fusion, which in turn scales the superposed signal to derive the average model. System optimization design included the selection of the power levels of IoMT entities and the scaling factor of the data fusion to guarantee efficient computation of the average model, while respecting the total power budget. Based on a numerical scenario regarding the fuel consumption prediction of the six cargo ships, the performance and the influential aspects of the FL/AirComp system were outlined. Overall, combining FL with AirComp in the future 6G maritime networks can address the challenging collaborative learning and communication-related needs expected in the upcoming intelligent maritime systems.

Some of the work extensions that could be implemented on the basis of the presented framework are summarized as:

• The proposed scheme could be adopted to support multi-hop relaying of the local models. In this direction, total hopping delay and/or power consumption could be considered for minimization.

• The objective function of the optimization problem could be reformed to focus on jointly minimizing the computation distortion and the energy-efficiency of the MCN (Spantideas et al., 2021).

• The impact of the AirComp-induced error in the FL performance should be evaluated. In specific, the effect of the computation error of the fused signal expressed by Eq. 7 due to the transmitter power-scaling and the receiver denoising-scaling in the accuracy of the FL training needs to be quantified, taking into account real CSI data.

• The MCN could be also be partitioned into multiple AirComp subsystems for further improving the spectral and energy efficiency of the system. For instance, this means that a given UAV collecting data from multiple SSI entities can be considered as data fusion that receives the diverse signal over a MAC, so as to optimize its own computation error.

• Another possible extension could the consideration of intelligent reflecting surfaces attached on the UAVs, enabling fast yet reliable model aggregation under unfavorable wireless propagation maritime environments.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Data from Private Maritime Company. Requests to access these datasets should be directed to Zy5udHJvdWxpYXNAaHlkcnVzLWVuZy5jb20=.

Author contributions

MZ: Conceptualization, Formal Analysis, Methodology, Software, Writing–original draft. SS: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft. AG: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Writing–original draft. NN: Conceptualization, Formal Analysis, Supervision, Writing–review and editing. PT: Conceptualization, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was partly supported by the “Trustworthy And Resilient Decentralised Intelligence For Edge Systems (TaRDIS)” Project, funded by EU HORIZON EUROPE program, under grant agreement No 101093006.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akyuz, E., Cicek, K., and Celik, M. (2019). A comparative research of machine learning impact to future of maritime transportation. Procedia Comput. Sci. 158, 275–280. doi:10.1016/j.procs.2019.09.052

CrossRef Full Text | Google Scholar

Aledhari, M., Razzak, R., Parizi, R. M., and Saeed, F. (2020). Federated learning: a survey on enabling technologies, protocols, and applications. IEEE Access 8, 140699–140725. doi:10.1109/access.2020.3013541

PubMed Abstract | CrossRef Full Text | Google Scholar

Alop, A. (2019). The main challenges and barriers to the successful “smart shipping”. TransNav Int. J. Mar. Navigation Saf. Sea Transp. 13, 521–528. doi:10.12716/1001.13.03.05

CrossRef Full Text | Google Scholar

Bithas, P. S., Nikolaidis, V., Kanatas, A. G., and Karagiannidis, G. K. (2020). Uav-to-ground communications: channel modeling and uav selection. IEEE Trans. Commun. 68, 5135–5144. doi:10.1109/TCOMM.2020.2992040

CrossRef Full Text | Google Scholar

Cao, X., Zhu, G., Xu, J., and Huang, K. (2020). Optimized power control for over-the-air computation in fading channels. IEEE Trans. Wirel. Commun. 19, 7498–7513. doi:10.1109/twc.2020.3012287

CrossRef Full Text | Google Scholar

Chen, Y., Feng, W., and Zheng, G. (2018). Optimum placement of uav as relays. IEEE Commun. Lett. 22, 248–251. doi:10.1109/LCOMM.2017.2776215

CrossRef Full Text | Google Scholar

Du, H., Deng, Y., Xue, J., Meng, D., Zhao, Q., and Xu, Z. (2022). Robust online csi estimation in a complex environment. IEEE Trans. Wirel. Commun. 21, 8322–8336. doi:10.1109/TWC.2022.3165588

CrossRef Full Text | Google Scholar

Foretich, A., Zaimes, G. G., Hawkins, T. R., and Newes, E. (2021). Challenges and opportunities for alternative fuels in the maritime sector. Marit. Transp. Res. 2, 100033. doi:10.1016/j.martra.2021.100033

CrossRef Full Text | Google Scholar

Giannopoulos, A., Gkonis, P., Bithas, P., Nomikos, N., Ntroulias, G., and Trakadas, P. (2023a). Federated learning for maritime environments: use cases, experimental results, and open issues. Techrxiv. Available at: https://www.techrxiv.org/doi/full/10.36227/techrxiv.22133549.v1.

Google Scholar

Giannopoulos, A., Nomikos, N., Ntroulias, G., Syriopoulos, T., and Trakadas, P. (2023b). “Maritime federated learning for decentralized on-ship intelligence,” in Artificial intelligence applications and innovations (Cham: Springer), 195–206.

CrossRef Full Text | Google Scholar

Giannopoulos, A., Spantideas, S., Capsalis, N., Gkonis, P., Karkazis, P., Sarakis, L., et al. (2021). “Wip: demand-driven power allocation in wireless networks with deep q-learning,” in 2021 IEEE 22nd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM) (IEEE), Pisa, Italy, 07-11 June 2021, 248–251.

CrossRef Full Text | Google Scholar

Huo, Y., Dong, X., and Beatty, S. (2020). Cellular communications in ocean waves for maritime internet of things. IEEE Internet Things J. 7, 9965–9979. doi:10.1109/JIOT.2020.2988634

CrossRef Full Text | Google Scholar

Jahanbakht, M., Xiang, W., Hanzo, L., and Azghadi, M. R. (2021). Internet of underwater things and big marine data analytics—a comprehensive survey. IEEE Commun. Surv. Tutorials 23, 904–956. doi:10.1109/comst.2021.3053118

CrossRef Full Text | Google Scholar

Li, X., Feng, W., Wang, J., Chen, Y., Ge, N., and Wang, C.-X. (2020). Enabling 5G on the ocean: a hybrid satellite-UAV-terrestrial network solution. IEEE Wirel. Commun. 27, 116–121. doi:10.1109/MWC.001.2000076

CrossRef Full Text | Google Scholar

Liu, W., Zang, X., Li, Y., and Vucetic, B. (2020). Over-the-air computation systems: optimization, analysis and scaling laws. IEEE Trans. Wirel. Commun. 19, 5488–5502. doi:10.1109/twc.2020.2993703

CrossRef Full Text | Google Scholar

Luo, H., Wang, J., Bu, F., Ruby, R., Wu, K., and Guo, Z. (2022). Recent progress of air/water cross-boundary communications for underwater sensor networks: a review. IEEE Sensors J. 22, 8360–8382. doi:10.1109/JSEN.2022.3162600

CrossRef Full Text | Google Scholar

McMahan, B., Moore, E., Ramage, D., Hampson, S., and y Arcas, B. A. (2017). Communication-efficient learning of deep networks from decentralized data. Artif. Intell. Statistics (PMLR) 54, 1273–1282.

Google Scholar

Nasir, A. A., Tuan, H. D., Duong, T. Q., and Poor, H. V. (2019). Uav-enabled communication using noma. IEEE Trans. Commun. 67, 5126–5138. doi:10.1109/TCOMM.2019.2906622

CrossRef Full Text | Google Scholar

Niknam, S., Dhillon, H. S., and Reed, J. H. (2020). Federated learning for wireless communications: motivation, opportunities, and challenges. IEEE Commun. Mag. 58, 46–51. doi:10.1109/mcom.001.1900461

CrossRef Full Text | Google Scholar

Nomikos, N., Giannopoulos, A., Trakadas, P., and Karagiannidis, G. K. (2023). “Uplink noma for uav-aided maritime internet-of-things,” in 2023 19th International Conference on the Design of Reliable Communication Networks (DRCN), Vilanova i la Geltru, Spain, 17-20 April 2023, 1–6. doi:10.1109/DRCN57075.2023.10108290

CrossRef Full Text | Google Scholar

Nomikos, N., Gkonis, P. K., Bithas, P. S., and Trakadas, P. (2022). A survey on uav-aided maritime communications: deployment considerations, applications, and future challenges. IEEE Open J. Commun. Soc. 4, 56–78. doi:10.1109/OJCOMS.2022.3225590

CrossRef Full Text | Google Scholar

Schaefer, N., and Barale, V. (2011). Maritime spatial planning: opportunities and challenges in the framework of the eu integrated maritime policy. J. Coast. Conservation 15, 237–245. doi:10.1007/s11852-011-0154-3

CrossRef Full Text | Google Scholar

Skianis, K., Giannopoulos, A., Gkonis, P., and Trakadas, P. (2023). Data aging matters: federated learning-based consumption prediction in smart homes via age-based model weighting. Electronics 12, 3054. doi:10.3390/electronics12143054

CrossRef Full Text | Google Scholar

Spantideas, S. T., Giannopoulos, A. E., Kapsalis, N. C., Kalafatelis, A., Capsalis, C. N., and Trakadas, P. (2021). “Joint energy-efficient and throughput-sufficient transmissions in 5g cells with deep q-learning,” in 2021 IEEE International Mediterranean Conference on Communications and Networking (MeditCom) (IEEE), Athens, Greece, 07-10 September 2021, 265–270.

CrossRef Full Text | Google Scholar

Tang, R., Feng, W., Chen, Y., and Ge, N. (2021). NOMA-based UAV communications for maritime coverage enhancement. China Commun. 18, 230–243. doi:10.23919/JCC.2021.04.017

CrossRef Full Text | Google Scholar

Trakadas, P., Masip-Bruin, X., Facca, F. M., Spantideas, S. T., Giannopoulos, A. E., Kapsalis, N. C., et al. (2022). A reference architecture for cloud–edge meta-operating systems enabling cross-domain, data-intensive, ml-assisted applications: architectural overview and key concepts. Sensors 22, 9003. doi:10.3390/s22229003

PubMed Abstract | CrossRef Full Text | Google Scholar

Victor, N., Alazab, M., Bhattacharya, S., Magnusson, S., Maddikunta, P. K. R., Ramana, K., et al. (2022). Federated learning for iout: concepts, applications, challenges and opportunities. arXiv preprint arXiv:2207.13976. Available at: https://doi.org/10.48550/arXiv.2207.13976.

Google Scholar

Wahab, O. A., Mourad, A., Otrok, H., and Taleb, T. (2021). Federated machine learning: survey, multi-level classification, desirable criteria and future directions in communication and networking systems. IEEE Commun. Surv. Tutorials 23, 1342–1397. doi:10.1109/comst.2021.3058573

CrossRef Full Text | Google Scholar

Wang, J., Zhou, H., Li, Y., Sun, Q., Wu, Y., Jin, S., et al. (2018). Wireless channel models for maritime communications. IEEE Access 6, 68070–68088. doi:10.1109/ACCESS.2018.2879902

CrossRef Full Text | Google Scholar

Wang, M. M., Zhang, J., and You, X. (2020). Machine-type communication for maritime internet of things: a design. IEEE Commun. Surv. Tutorials 22, 2550–2585. doi:10.1109/COMST.2020.3015694

CrossRef Full Text | Google Scholar

Wang, Y., Feng, W., Wang, J., and Quek, T. Q. S. (2021). Hybrid satellite-UAV-terrestrial networks for 6G ubiquitous coverage: a maritime communications perspective. IEEE J. Sel. Areas Commun. 39, 3475–3490. doi:10.1109/JSAC.2021.3088692

CrossRef Full Text | Google Scholar

Xia, T., Wang, M. M., Zhang, J., and Wang, L. (2020). Maritime internet of things: challenges and solutions. IEEE Wirel. Commun. 27, 188–196. doi:10.1109/MWC.001.1900322

CrossRef Full Text | Google Scholar

Yang, K., Jiang, T., Shi, Y., and Ding, Z. (2020). Federated learning via over-the-air computation. IEEE Trans. Wirel. Commun. 19, 2022–2035. doi:10.1109/twc.2019.2961673

CrossRef Full Text | Google Scholar

Zang, X., Liu, W., Li, Y., and Vucetic, B. (2020). Over-the-air computation systems: optimal design with sum-power constraint. IEEE Wirel. Commun. Lett. 9, 1524–1528. doi:10.1109/lwc.2020.2996194

CrossRef Full Text | Google Scholar

Zhang, Z., Guan, C., Chen, H., Yang, X., Gong, W., and Yang, A. (2021). Adaptive privacy-preserving federated learning for fault diagnosis in internet of ships. IEEE Internet Things J. 9, 6844–6854. doi:10.1109/jiot.2021.3115817

PubMed Abstract | CrossRef Full Text | Google Scholar