- 1Department of Digital Systems, University of Piraeus, Piraeus, Greece
- 2Department of Information and Communication Systems Engineering, School of Engineering, University of the Aegean, Samos, Greece
- 3Department of Digital Industry Technologies, National and Kapodistrian University of Athens, Athens, Greece
The exploitation of unmanned aerial vehicles (UAVs) in enhancing network performance in the context of beyond-fifth-generation (5G) communications has shown a variety of benefits compared to terrestrial counterparts. In addition, they have been largely conceived to play a central role in data dissemination to Internet of Things (IoT) devices. In the proposed work, a novel stochastic geometry unified framework is proposed to study the downlink performance in a UAV-assisted IoT network that integrates both UAV-base stations (UAV-BSs) and terrestrial IoT receiving devices. The framework builds upon the concept of the aerial UAV corridor, which is modeled as a finite line above the IoT network, and the one-dimensional (1D) binomial point process (BPP) is employed for modeling the spatial locations of the UAV-BSs in the aerial corridor. Subsequently, a comprehensive SNR-based performance analysis in terms of coverage probability, average rate, and energy efficiency is conducted under three association strategies, namely, the nth nearest-selection scheme, the random selection scheme, and the joint transmission coordinated multi-point (JT-CoMP) scheme. The numerical results reveal valuable system-level insights and trade-offs and provide a firm foundation for the design of UAV-assisted IoT networks.
1 Introduction
With the ever-increasing number of unmanned aerial vehicles (UAVs), UAV-based wireless communications are expected to play a pivotal role in the establishment of upcoming future networking infrastructures. Due to their inherent mobility and flexibility, they can act as aerial base stations (BSs) by supporting wireless connectivity for existing terrestrial BSs and providing reliable and cost-effective on-the-fly communications (Lin et al., 2021; Lin et al., 2022). In addition, they can offer additional throughput and coverage in some hotspots or assist in emergencies, disasters, and critical situations (Matracia et al., 2023) for ground users. In such scenarios, the deployment of UAVs is crucial for providing maximum coverage (Shakoor et al., 2021).
As we step toward the sixth-generation (6G) communication networks, the UAVs are envisioned to constitute a core pillar of the Internet of Things (IoT) networks (Lin et al., 2022), aiming to realize massive connections among several devices. The UAVs can now be quickly deployed and configured for numerous special scenarios to support IoT devices on the ground. As such, the UAVs are envisioned to cooperate to serve IoT either for communication purposes or for energy transfer and power harvesting (Yao et al., 2020). An IoT network that integrates UAVs for supporting IoT device communications will be called a UAV-assisted IoT network. Due to the UAVs’ ability to hover at high altitudes, an increased probability of establishing line-of-sight (LOS) links with the IoT devices can be achieved. Nevertheless, in this case, the UAVs’ power consumption is a limiting factor for several 6G-related application scenarios, which may require high energy efficiency. To tackle such an issue, there has been research work focusing on energy efficiency enhancement for UAV-assisted networks (Huq et al., 2023; Yu et al., 2023). Recently, there has also been growing research interest in studying secure and reliable UAV-assisted IoT networks. Some works have already focused on the performance analysis of such networks (Zhang et al., 2019; Lei et al., 2020). This is because stochastic geometry shows potential of modeling extremely complicated next-generation UAV-assisted IoT networks and enabling tractable performance analysis.
Going beyond beyond-LoS (BLOS) UAV mobility, UAV traffic congestion is expected to occur due to the rapidly increasing number of UAVs and the limited airspace, especially in low-altitude territories. However, the first concern of using UAVs is the security. The role of the UAVs in 6G networks is expected to be significantly upgraded, with swarms operating in the airspace of the modern city skies. However, any accident or misbehavior may cause social unrest and delay the establishment of UAV-enabled/supported applications and services. Therefore, the requirement for organized and well-behaved aerial platforms is a prerequisite for the general approval of drone utilization. To this aim, UAV corridors may be conceptualized as virtual air corridors with flight paths designated for the safe and legal operation of multiple drones. However, in these corridors, congestion of UAV swarms is expected, whose consequences can be alleviated by using lanes and rules for the autonomous mobility and movement of the UAVs, similar to the highway and traffic code regulating the coexistence of vehicles on the roads (Xu et al., 2020). Nevertheless, the introduction of multiple UAV corridors to reduce and control the UAV swarms is expected to lead to a UAV corridor-based aerial network. In order for the UAVs inside the corridor to execute a task successfully, either for communication or harvesting purposes, coordination among the UAVs can be applied (Dang-Ngoc et al., 2022).
1.1 Related work and motivation
Due to the continuous motion of the UAVs for various reasons, including the influence of the wind or the existence of obstacles within the line-of-sight, it is rather optimistic to assume that the locations of the aerial BSs do not modify. Therefore, in order to improve the network design, various stochastic geometry models have been adopted in wireless communication networks, in which swarms of UAVs are used for communication purposes (Enayati et al., 2019; Boschiero et al., 2020; Shi and Deng, 2022; Wang et al., 2023). For example, in Enayati et al. (2019), a new network of ABSs has been proposed, in which the binomial point process (BPP) was exploited to model a snapshot of the UAVs’ positions. In Boschiero et al. (2020), a stochastic geometry has been employed for investigating the coverage probability of UAV stations that operate in mmWaves. In the same frequency band, in Shi and Deng (2022), BPP has been applied to model the location of a swarm of UAVs, and the coverage probability was also investigated under the assumption of the closest distance criterion. Finally, in Wang et al. (2023), an inhomogeneous Poisson point process (PPP) was used to model the locations of the UAVs, and analytical expressions were employed for the total coverage probability. The performance of aerial networks can be further enhanced if cooperative UAV transmission policies are employed (Bithas and Moustakas, 2023).
One of the most efficient approaches for enabling cooperative transmissions is the coordinated multipoint (CoMP) (Irmer et al., 2011), which eliminates the intra-cell interference with a small cost on the additional signaling that is required. The undoubted advantages of this technology are the reason why it has also been employed in UAV-assisted communication networks, in which tools of stochastic geometry have also been used (Li et al., 2020; Wang et al., 2022; Fan et al., 2023; Sun et al., 2023). In Li et al. (2020), a CoMP transmission scheme has been proposed in a 3D model consisting of aerial BSs and aerial user equipment. Based on a binomial-Delaunay tetrahedralization analysis, achievable data rates and coverage probability were studied. In Wang et al. (2022), a 3D multi-layer UAV-terrestrial heterogeneous network was investigated, where CoMP technology was applied and the coverage probability was studied with the aid of the tool of stochastic geometry. In Sun et al. (2023), an uplink CoMP transmission scheme was studied in a cellular UAV network using a stochastic geometry-based analytical framework. For this scheme, among other performance metrics, analytical expressions for the coverage probability and area spectral efficiency were obtained. Very recently, in Fan et al. (2023), a 3D UAV-assisted communication network has been assumed, in which CoMP transmission has been integrated. Based on the theory of stochastic geometry, a UAV formation control strategy was proposed that shaped the required geometric pattern of the CoMP strategy. Although the path loss can significantly reduce the signal reception quality at the receiving devices and given that the UAV-BSs within swarms or groups usually coordinate to execute a task, the exploitation of CoMP at the UAVs can significantly enhance the received signal power at the IoT devices and, at the same time, reduce the UAVs’ energy consumption.
As the density of the UAVs increases, it is mandatory that rules similar to the ones used by the air traffic authorities will be proposed. The idea of organized and connected routes in the sky has been proposed in relation to this, denoted as aerial highways or UAV corridors (Cherif et al., 2021b; Bhuyan et al., 2021). This simple idea has also been adopted in the area of UAV-assisted communications, where recently, several investigations have been presented (Singh et al., 2021; Bernabè et al., 2022; Fu et al., 2023; Karimi-Bidhendi et al., 2023; Singh et al., 2023). In Singh et al. (2021), the placement of BSs that serve UAV corridors has been studied and the minimum set of BS that satisfies a predefined quality of service constraint is selected. In Bernabè et al. (2022), an algorithm has been proposed to optimize the electronic tilt of BSs in order to improve the quality of service in UAV-assisted communication scenarios where aerial corridors have been assumed. In Karimi-Bidhendi et al. (2023), based on the results of quantization theory, an iterative algorithm that optimized the antenna tilts at the BS was proposed for maximizing the received signal strength in UAV flying corridors. In Singh et al. (2023), a drone corridor is defined to be a set of 3D lanes where the UAVs may take flight. In this context, a design of each lane trajectory is proposed that minimizes the total ground risk across all lanes while simultaneously satisfying the received signal strength constraints. Finally, in Fu et al. (2023), a multi-UAV corridor is proposed for avoiding unnecessary flight exploration by UAVs, which offers improved performance in terms of user rates.
In summary, even though the concept of an aerial corridor has appeared in the open technical bibliography, its manifestation in the performance analysis at system levels under a realistic stochastic geometry framework has not been studied, which is the main objective of this paper. Triggered by all the aforementioned details, this work proposes, for the first time, a stochastic geometry framework to study a UAV corridor-assisted IoT network, where the spatial locations of the UAV-BSs are modeled as a one-dimensional (1D) binomial point process (BPP) in a corridor, modeled as a finite 1D line above the ground. Please note that the BPP can ensure that a swarm of a finite number of UAV-BSs will be uniformly and independently distributed in the UAV corridor, and therefore, no congestion in a particular region of the corridor is expected, while at the same time, it also yields tractable analysis. Subsequently, an SNR-based performance analysis in terms of coverage probability, average rate, and energy efficiency is conducted under three association strategies.
1.2 Contributions
The main contributions of this paper are the following:
1) Modeling of a UAV aerial corridor with a finite number of UAV-BSs in a UAV-assisted IoT network: By employing the 1D uniform BPP for modeling the spatial locations of the UAV-BSs in an aerial UAV corridor, a fixed and finite number of N UAVs-BSs is uniformly and independently distributed in a line above the ground. To the best of the authors’ knowledge, this is the first time that a stochastic geometry framework has been proposed for modeling the spatial locations of UAV-BSs in aerial corridors.
2) Performance analysis: Three association schemes are proposed, namely, a nth nearest UAV-BS association policy, a random selection policy, and the JT-CoMP scheme. Subsequently, an SNR-based performance analysis1, in terms of coverage probability, average achievable rate, and energy efficiency, is conducted for the three schemes, and analytical expressions for all performance metrics are obtained. As key intermediate results, the joint PDF of the distances between the receiver and the nth nearest UAV-BSs to the receiver, as well as the Laplace transform of the aggregate received power distribution from the cooperation set
3) System-level insights: Several fruitful insights can be gained by investigating the behavior of the coverage probability in response to the energy efficiency of the IoT-based UAV network. The obtained results show that although the coverage performance under the JT-CoMP scheme is far superior compared to the one under the nearest-selection scheme, the JT-CoMP scheme is more energy-consuming when only a few UAV-BSs are deployed in the corridor. Moreover, the nearest-selection scheme seems to be more energy-efficient for higher UAV deployment heights compared to the JT-CoMP scheme.
2 System model
2.1 Network model
Consider a downlink finite UAV-assisted IoT network, which integrates both terrestrial IoT receiving devices and UAV-BSs. Without loss of generality, the IoT devices are assumed to be uniformly and independently distributed according to an independent stationary point process in a finite area
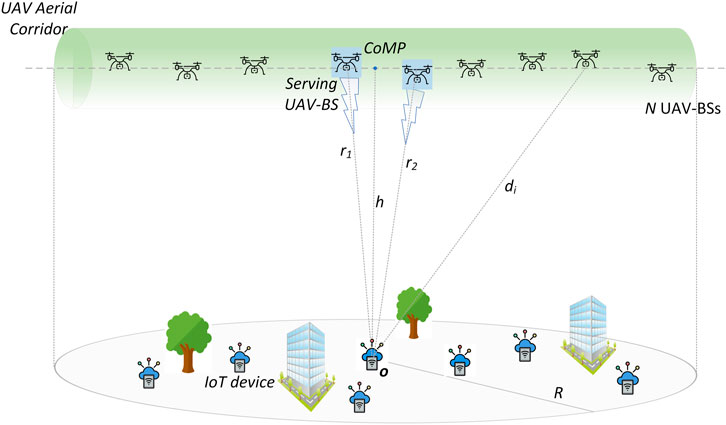
FIGURE 1. Illustration of the finite UAV-assisted IoT network, which integrates terrestrial IoT receiving devices and UAV-BSs.
2.2 Association strategies
2.2.1 nth nearest-selection scheme
In this scheme, the receiver is assumed to be served successively by its nth nearest UAV-BS. The special case of the closest selection strategy is of particular interest, which provides the maximum average received power, i.e.,
where yc denotes the location of the closest UAV-BS and ‖ ⋅‖ denotes the Euclidean norm. For notational simplicity, we also define r1 = ‖yc‖.
2.2.2 Random selection scheme
In this scheme, the receiver is selected randomly with uniform distribution among all UAV-BSs. This leads to the following:
where n (⋅) denotes the number of elements in a set and Unif{⋅} denotes the uniform-selection operation. The main merit of this scheme is that the receiver performs a fast response due to not acquiring other UAV-BSs’ channel state information (CSI), and therefore, each of the UAV-BS has the same opportunity to be selected as the serving BS.
2.2.3 JT-CoMP scheme
In this scheme, the receiver is simultaneously served by its nth, n > 1, and nearest UAV-BSs. In this case, the n nearest UAV-BSs are assumed to use the same system resources, and their spatial locations form the cooperation set
2.3 Path loss and channel models
2.3.1 Path loss
The channel conditions are characterized by different path-loss exponents, which are denoted by α. Then, following the standard power-law path-loss model for the path between the receiver and a UAV-BS located at yi ∈ Ψ, the random path-loss function is defined as the following:
where
2.3.2 Large-scale fading
Due to the presence of obstacles between a UAV-BS and the receiver, e.g., buildings and trees, it is assumed that shadowing exists. Therefore, in the considered wireless channel model, large-scale fading (or shadowing) co-exists with small-scale fading. Subsequently, the shadowing random fluctuations are modeled by the inverse-gamma distribution, which has been recently used in UAV-assisted communication scenarios (Bithas et al., 2020). Notably, the inverse-gamma distribution can not only adequately capture the shadowing conditions in UAV communications but also maintain analytical tractability. The probability density function (PDF) of the inverse-gamma distribution is given by the following equation:
for i = 1, … N, where q > 1 is the shaping parameter of the distribution related to the severity of the shadowing, i.e., lower values of q result in lighter shadowing conditions, γ denotes the scaling parameter, and Γ(⋅) is the gamma function (Gradshteyn and Ryzhik, 2007, eq. (8.310.1)). Note that the inverse-gamma distribution is suitable and has been exploited for real-world UAV communication scenarios, and at the same time, it allows for a tractable performance analysis (Bithas and Moustakas, 2023).
2.3.3 Small-scale fading
The channels are assumed to experience Nakagami-m fading with a different fading parameter, m. Therefore, the channel power gains {hi}, following a gamma distribution, hi ∼gamma
Note that
2.4 SNR definition and performance metrics
2.4.1 SNR definition
Under the nth nearest UAV-BS association policy, the SNR at the receiver is given by the following equation:
where σ2 is the additive white Gaussian noise power. For the special case of the nearest selection association scheme, i.e., n = 1, the SNR at the receiver can be rewritten as follows:
Under the random selection scheme, the SNR at the receiver is given by the following equation:
Under the JT-CoMP scheme, the SNR at the receiver is given by the following equation:
Remark 1. Similarly to Hou et al. (2022), this work argues that based on low-complexity channel estimation algorithms (Jiang et al., 2020), the global CSI is assumed to be perfectly known at the UAV-BSs, if required. In addition, the assumption of perfect global CSI knowledge is common in stochastic geometry-based scientific papers related to UAV-assisted communication networks (Hou et al., 2019; Hou et al., 2020), where extensive signaling overhead is assumed for CSI acquisition at the UAVs. Nevertheless, performance analysis of UAV-assisted communications under imperfect CSI is a very common optimization problem, which requires a new analytical framework to be developed that is beyond the scope of the paper.
2.4.2 Performance metrics
The coverage probability is defined as the probability that the SNR at the receiver exceeds a predefined threshold γth,
and the average achievable rate of the receiver is given by Armeniakos and Kanatas (2022) as the following:
where (a) follows through the change in the variable γth + 1 = et and Bw is the bandwidth available to the link of interest. The average energy efficiency is defined as the ratio of the average rate and the total power consumption, i.e.,
where Ptot is the total power consumption given by Bithas and Moustakas (2023) as the following:
where PcRx and PcTx denote the UAVs’ transmitter and receiver circuit powers required for signaling purposes, respectively. Note that Eq. 13 indicates that all UAV-BSs collect signaling information required for communication purposes, whereas only n UAV-BSs transmit information at a given time. Moreover, in Eq. 13, ω denotes the amplifier power efficiency given by
3 Performance analysis
In this section, the SNR-based performance analysis, in terms of coverage probability, the average achievable rate, and energy efficiency, is presented for the three association schemes.
3.1 Coverage probability analysis
In this subsection, the coverage probability analysis under the three association schemes is presented.
3.1.1 n-th nearest-selection scheme
Lemma 1. The PDF of the distance rn is given by the following equation:
Proof. Let ui denote the horizontal distance between the receiver and the projection of a UAV on the ground. Then, the unordered set of distances {ui} comprises independent and identically distributed (i.i.d.) random variables, with the cumulative distribution function (CDF) of each element given by
By order statistics (Ahsanullah et al., 2013), the PDF of rn can be obtained as the following:
After applying some simplifications, Lemma 1 yields.
Lemma 2. The PDF of the path-loss term l (rn) is given by the following equation:
for
Proof. The PDF of
After applying the binomial expansion to
Therefore,
Through the change of variables n + k = i and with the aid of the definition of the Gauss hypergeometric function 2F1 (⋅, ⋅, ⋅, x), as defined by Gradshteyn and Ryzhik (2007); (Eqs 9, 10) through power series, the following formula is exploited: 2F1
Theorem 1. The coverage probability of the receiver under the nth nearest UAV-BS association policy is given by the following equation:
where
Proof. First, let W = Si l (rn). PDF fW(w) can directly be obtained through the well-known formula for the product of two independent random variables as
Next, let Z = hiW. The PDF fZ(z) is similarly given by
Finally, the CDF of SNR FSNR (γth) can be obtained through fZ(z) as
Finally, by applying Gradshteyn and Ryzhik (2007) (eq. (3.351.1) for calculating FSNR (γth), and after some manipulations,
3.1.2 Random selection scheme
Lemma 3. The PDF of the path-loss term l (di) is given by the following equation:
for
Proof. The PDF of
where
Theorem 2. The coverage probability of the receiver under the random selection scheme is given by the following equation:
Proof. The proof follows similar lines as the proof presented for theorem 2, and thus, it is omitted here.
3.1.3 JT-CoMP scheme
Lemma 4. The joint PDF
Proof. By order statistics, the joint PDF of all order distances
Lemma 5. The Laplace transform of the SNR at the receiver under the JT-CoMP scheme assuming the n nearest UAV-BSs in
Proof. The Laplace transform of the SNR can be obtained as follows:
where (a) follows from independence between xi, hi, and ri, and after applying the moment generating function (MGF) of the gamma random variable hi, (b) follows after deconditioning over the i.i.d. random variable xi with the PDF
Theorem 3. The coverage probability of the receiver under the JT-CoMP scheme assuming the n nearest UAV-BSs in
Proof. Having obtained
3.2 Average rate and energy efficiency analysis
Based on the expressions for the coverage probability derived in theorems 1, 2 and 3, the average achievable rate of the receiver under the three association schemes can now be obtained as follows:
where (a) follows from the Gauss–Chebysev quadrature approximation and can be exploited to reduce the computational complexity due to nested integrals and has been applied in previous studies (Cherif et al., 2021a; Armeniakos and Kanatas, 2022). Under the adopted approximation, one more integration with an infinite upper limit is avoided. The parameter M is to be adjusted for high accuracy and
after substituting Eqs 13, 32 in Eq. 33.
4 Results and discussion
In this section, the simulation and numerical results are presented to evaluate and compare the performance achieved in the IoT-based UAV network under the two different association schemes. The accuracy of the analytical results is verified by comparing them with the simulated results obtained from Monte Carlo simulations. For all the numerical results, the following parameters have been used, unless stated otherwise: N = 5 UAV-BSs, R = 200 m, h = 100 m, p = 20 dBm, m = 2, q = 3, α = 2, σ2 = −74 dBm, γth = 3 dB, and fc = 3500 MHz. Under the JT-CoMP scheme, the cooperation set consists of the locations of the nearest two UAV-BSs from the receiver, and therefore, Cn=2, unless otherwise stated. Moreover, PcRx = 0.15 W, PcTx = 0.1 W, and η = 0.35. In order to focus on the average spectral efficiency, we will normalize the average achievable rate by Bw, which is equivalent to considering Bw = 1 in Eq. 32.
Figure 2 compares the coverage probability versus γth under the three schemes for different values of n. It is observed that JT-CoMP significantly enhances the coverage performance of the network, and the curves become the steepest. Moreover, the coverage performance under the random selection scheme is clearly degraded compared to the case where the receiver is served by the UAV-BS providing the maximum average power. Nevertheless, the random selection scheme yields undoubtedly low overhead for the IoT receiver’s signaling because no CSI information is acquired. Furthermore, the performance of the network under the random selection scheme corresponds to that under selecting the serving UAV-BS as the average UAV-BS when the UAVs are ordered in the ascending order according to their Euclidean distance. As such, the performance of the network under the nth nearest selection scheme for n = 3 is close to that under the random selection scheme.
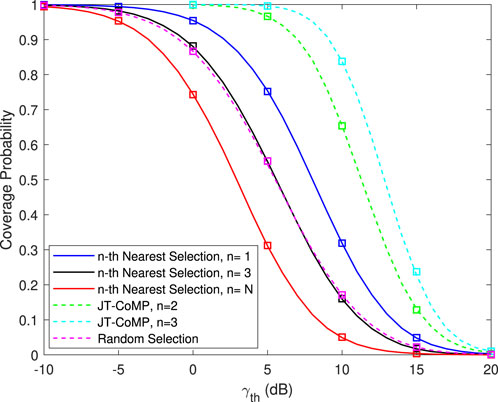
FIGURE 2. Coverage probability versus γth under the three schemes for different values of n, with N =5, R =200 m, and h =100 m. Markers denote analytical results.
Figure 3 presents the coverage probability versus h under the three schemes for different values of R. A first observation is that the coverage probability for all the schemes deteriorates as the height h of the UAV-BSs increases for all values of the deployment radius R. Moreover, the differences among the curves are larger for smaller values of the deployment height h, that is, the enhancement in the coverage performance between different values of R tends to be smaller as h increases. The JT-CoMP scheme significantly improves the coverage performance of the network, especially for smaller values of the UAVs’ deployment height h.
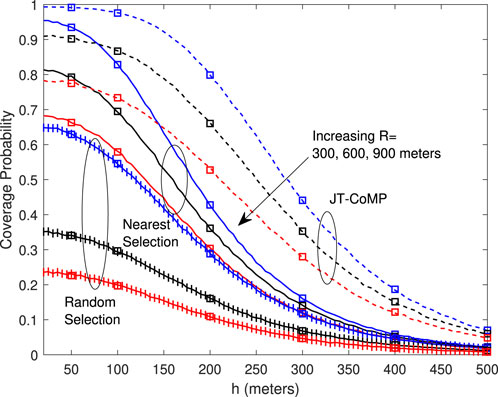
FIGURE 3. Coverage probability versus h under the three schemes for different values of R, with N =5, γth =6 dB, and Cn=2. Markers denote analytical results.
Figure 4 shows the coverage probability versus R under the three schemes for different values of N. As can be observed, in all the cases, the performance of the network improves as the number of UAV-BSs increases. This is because with an increase of N, the probability that the UAV-BSs get closer to the receiver increases. As expected, the coverage performance of the network under the JT-CoMP scheme significantly outperforms the corresponding one under the nearest selection one, especially for smaller values of R. Finally, the coverage performance of the network under the random selection scheme is significantly degraded.
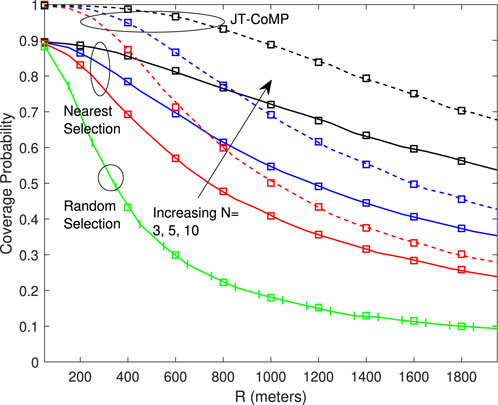
FIGURE 4. Coverage probability versus R under the three schemes for different values of N, with γth =6 dB and Cn=2. Markers denote analytical results.
Figure 5 compares the average spectral efficiency versus h under the three schemes for different shadowing conditions. In particular, Figure 5A compares the average spectral efficiency versus h under the nearest selection and JT-CoMP schemes. Moreover, for completeness, an alternative approach of the JT-CoMP scheme is presented, denoted as JT-CoMPfp, with fixed power
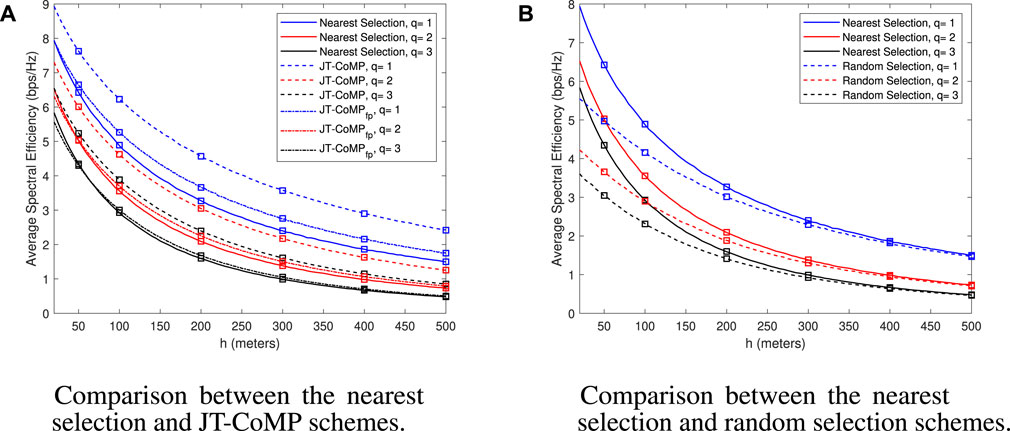
FIGURE 5. Average spectral efficiency versus h under the three schemes for different shadowing conditions, with N = 5, R = 200 m, and Cn = 2. Markers denote analytical results: (A) Comparison between the nearest selection and JT-CoMP schemes; (B) Comparison between the nearest selection and random selection schemes.
Figure 6 compares the coverage probability and the energy efficiency versus N for the three schemes under investigation. The power consumption model given by Eq. 13 considers both UAVs’ transmitter and receiver circuit powers required for signaling purposes and the amplifier power efficiency. A first observation is that the coverage performance under JT-CoMPfp is much better compared to that under the nearest selection scheme, with a cost of lower energy efficiency. However, the energy efficiency of both the schemes tends to be the same for higher values of N. This is because with the increase in N, the serving BSs get closer to the receiver, and hence, the received power increases. This, in turn, increases the probability that the rate threshold is achieved with lower power consumption, which increases the energy efficiency. Moreover, the term PcRx in Eq. 13 becomes dominant, facilitating the convergence in the performance of the techniques. Notably, under both the nearest selection and the JT-CoMPfp schemes, there exists a value of N that yields the best trade-off between the coverage performance and energy efficiency. For N = 5 under both the schemes, an increase in N slightly increases the coverage probability but significantly degrades the energy efficiency. Finally, the performance in terms of both coverage probability and energy efficiency under the random selection scheme is the worst, as expected.
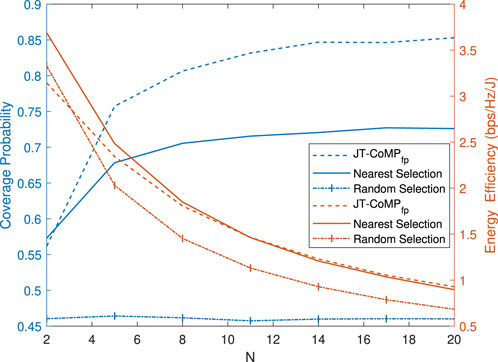
FIGURE 6. Coverage probability and energy efficiency versus N under the three schemes for γth =6 dB, R =200 m, h =100 m, and Cn=2.
Finally, Figure 7 compares the achievable energy efficiency versus p under the three schemes for different values of h. In particular, Figure 7A compares the energy efficiency versus p under the nearest selection and the JT-CoMPfp schemes. A first observation is that the performance of the network, in terms of energy efficiency under the nearest selection scheme, clearly outperforms the corresponding performance under the JT-CoMPfp scheme only for lower values of h. This is because JT-COMPfp simultaneously uses n transmitters, which means that the effect of PcTx in Eq. 13 is also multiplicative. However, as h increases, the serving UAV-BS under the nearest selection scheme must transmit at higher power to achieve the target rate threshold, which results in increased power consumption. Moreover, by increasing h under the nearest selection scheme, the optimal transmit power also increases. As h increases, the received signal power decreases, thereby degrading the achievable spectral efficiency. Thus, the UAV-BS must transmit at higher power to combat this degradation, which reduces its energy efficiency. On the other hand, under the JT-CoMPfp scheme, the target rates are achieved at the receiver for both values of h as a result of higher received power. Therefore, the optimal transmit power is retained at the same value for both UAVs’ deployment height. Figure 7B compares the energy efficiency versus p under the random selection and JT-CoMPfp schemes. As expected, the energy efficiency under the random selection scheme has the worst performance, especially for the low value of h.
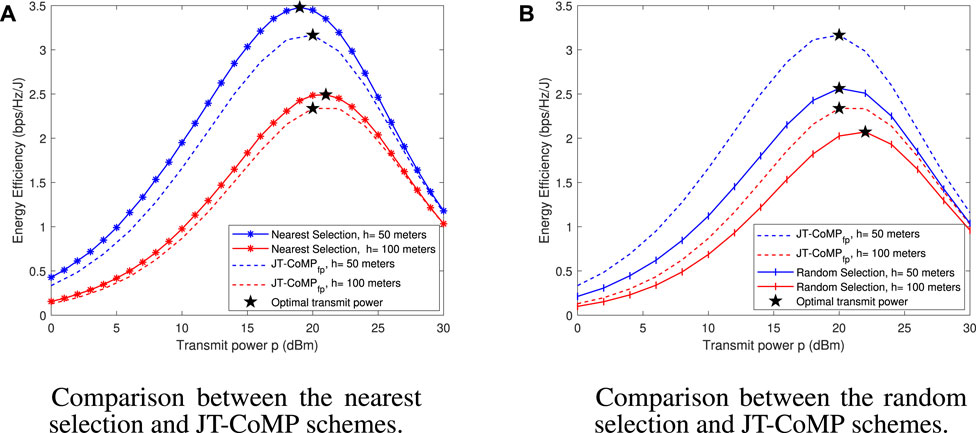
FIGURE 7. Energy efficiency versus p under the three schemes for different values of h, with N = 5, R = 200 m, and Cn = 2: (A) Comparison between the nearest selection and JT-CoMP schemes; (B) Comparison between the random selection and JT-CoMP schemes.
5 Conclusion
In this work, a novel stochastic geometry framework was proposed for UAV-assisted IoT networks to address the performance of a ground IoT device. Building on the concept of an aerial UAV corridor, a performance analysis, in terms of coverage probability, average rate, and energy efficiency, was conducted by modeling the spatial locations of UAV-BSs as a 1D BPP, which is a key novelty of this paper. As system level insights, it was revealed that i) the coverage performance under the JT-CoMP scheme significantly outperforms the corresponding performance under the nearest-selection scheme for the smaller UAV deployment radius R and height h; ii) as the shadowing conditions become severer, the achievable spectral efficiency under the JT-CoMP scheme with fixed total transmission power approaches the corresponding one under the nearest-selection scheme, and the achievable spectral efficiency under the random selection scheme approaches the corresponding one under the nearest selection scheme for the higher deployment heights of the UAV-BSs; iii) N = 5 yields the best trade-off between the coverage performance and energy efficiency both under the JT-CoMPfp and the nearest selection schemes; and iv) the energy efficiency under the nearest-selection scheme outperforms the corresponding efficiency under the JT-CoMP scheme only for lower UAV deployment heights h.
Based on the derived insights, a promising future research direction is to extend the current stochastic geometry framework to a multi-corridor-assisted UAV IoT network, where the lanes will be deployed in the three-dimensional space at different heights. Finally, performance analysis of the proposed framework under imperfect CSI is a challenge to be met.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
HA: conceptualization, methodology, investigation, software, validation, visualization, and writing–original draft. KM: methodology, supervision, writing–review and editing. PB: methodology, supervision, writing–review and editing, investigation. AK: methodology, supervision, writing–review and editing, conceptualization.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the European Commission’s Horizon Programme under Agreement 101139291 (iSEE-6G).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1SNR-based performance analysis has been widely studied in the open literature, especially for next-generation UAV-assisted IoT networks (Mahmoud et al., 2021; Qin et al., 2023). A common assumption is that the interference from other UAVs’ transmitters is negligible at the receiver, thanks to interference management techniques such as frequency reuse and extreme beamforming capabilities. Along similar conceptual lines, such an approach has also been followed in this work, where the frequency reuse factor (q) is assumed to be equal to N.
References
Ahsanullah, M., Nevzorov, V. B., and Shakil, M. (2013). An introduction to order statistics, 8. Berlin, Germany: Springer.
Armeniakos, C. K., and Kanatas, A. G. (2022). Performance comparison of wireless aerial 3D cellular network models. IEEE Commun. Lett. 26, 1779–1783. doi:10.1109/LCOMM.2022.3181332
Bernabè, M., Lopez-Perez, D., Gesbert, D., and Bao, H. (2022). “On the optimization of cellular networks for UAV aerial corridor support,” in GLOBECOM 2022-2022 IEEE Global Communications Conference (IEEE), Rio de Janeiro, 4 Dec 2022 – 8 Dec 2022, 2969. –2974.
Bhuyan, A., Güvenç, I., Dai, H., Sichitiu, M. L., Singh, S., Rahmati, A., et al. (2021). “Secure 5G network for a nationwide drone corridor,” in 2021 IEEE Aerospace Conference, Big Sky, Montana, USA, 6-13 March 2021, 1–10. doi:10.1109/AERO50100.2021.9438162
Bithas, P. S., and Moustakas, A. L. (2023). Generalized UAV selection with distributed transmission policies. IEEE Trans. Commun. 71, 741–756. doi:10.1109/TCOMM.2022.3229665
Bithas, P. S., Nikolaidis, V., Kanatas, A. G., and Karagiannidis, G. K. (2020). UAV-to-ground communications: channel modeling and UAV selection. IEEE Trans. Commun. 68, 5135–5144. doi:10.1109/tcomm.2020.2992040
Boschiero, M., Giordani, M., Polese, M., and Zorzi, M. (2020). “Coverage analysis of UAVs in millimeter wave networks: a stochastic geometry approach,” in 2020 International Wireless Communications and Mobile Computing (IWCMC) (IEEE), Limassol, Cyprus, June 15-19, 2020, 351–357.
Cherif, N., Alzenad, M., Yanikomeroglu, H., and Yongacoglu, A. (2021a). Downlink coverage and rate analysis of an aerial user in vertical heterogeneous networks (vhetnets). IEEE Trans. Wirel. Commun. 20, 1501–1516. doi:10.1109/TWC.2020.3033940
Cherif, N., Jaafar, W., Yanikomeroglu, H., and Yongacoglu, A. (2021b). 3D aerial highway: the key enabler of the retail industry transformation. IEEE Commun. Mag. 59, 65–71. doi:10.1109/MCOM.010.2100072
Dang-Ngoc, H., Nguyen, D. N., Ho-Van, K., Hoang, D. T., Dutkiewicz, E., Pham, Q.-V., et al. (2022). Secure swarm UAV-assisted communications with cooperative friendly jamming. IEEE Internet Things J. 9, 25596–25611. doi:10.1109/jiot.2022.3197975
Enayati, S., Saeedi, H., Pishro-Nik, H., and Yanikomeroglu, H. (2019). Moving aerial base station networks: a stochastic geometry analysis and design perspective. IEEE Trans. Wirel. Commun. 18, 2977–2988. doi:10.1109/twc.2019.2907849
Fan, X., Wu, P., and Xia, M. (2023). “Air-to-ground communications beyond 5G: the formation control of UAV swarm,” in 2023 IEEE International Conference on Acoustics, Speech, and Signal Processing Workshops (ICASSPW), Rhodes Island, Greece, 4-10 June 2023. 1–5. doi:10.1109/ICASSPW59220.2023.10193143
Fu, C.-W., Ku, M.-L., Chen, Y.-J., and Quek, T. Q. (2023). UAV trajectory, user association and power control for multi-UAV enabled energy harvesting communications: offline design and online reinforcement learning. IEEE Internet Things J., 1. doi:10.1109/jiot.2023.3325841
Hou, T., Liu, Y., Song, Z., Sun, X., and Chen, Y. (2019). Multiple antenna aided noma in uav networks: a stochastic geometry approach. IEEE Trans. Commun. 67, 1031–1044. doi:10.1109/TCOMM.2018.2875081
Hou, T., Liu, Y., Song, Z., Sun, X., and Chen, Y. (2020). Uav-to-everything (u2x) networks relying on noma: a stochastic geometry model. IEEE Trans. Veh. Technol. 69, 7558–7568. doi:10.1109/TVT.2020.2994167
Hou, T., Liu, Y., Song, Z., Sun, X., Chen, Y., and Hanzo, L. (2022). Mimo assisted networks relying on intelligent reflective surfaces: a stochastic geometry based analysis. IEEE Trans. Veh. Technol. 71, 571–582. doi:10.1109/TVT.2021.3129308
Huq, K. M. S., Otung, I. E., and Rodriguez, J. (2023). A study of coverage probability-based energy-efficiency analysis for UAV-aided THz-enabled 6G networks. IEEE Trans. Intelligent Transp. Syst. 24, 7404–7411. doi:10.1109/TITS.2022.3188653
Irmer, R., Droste, H., Marsch, P., Grieger, M., Fettweis, G., Brueck, S., et al. (2011). Coordinated multipoint: concepts, performance, and field trial results. IEEE Commun. Mag. 49, 102–111. doi:10.1109/mcom.2011.5706317
Jiang, H., Zhang, Z., Wang, C.-X., Zhang, J., Dang, J., Wu, L., et al. (2020). A novel 3d uav channel model for a2g communication environments using aod and aoa estimation algorithms. IEEE Trans. Commun. 68, 7232–7246. doi:10.1109/TCOMM.2020.3011716
Karimi-Bidhendi, S., Geraci, G., and Jafarkhani, H. (2023). Optimizing cellular networks for UAV corridors via quantization theory. arXiv preprint arXiv:2308.01440.
Lei, H., Wang, D., Park, K.-H., Ansari, I. S., Jiang, J., Pan, G., et al. (2020). Safeguarding uav iot communication systems against randomly located eavesdroppers. IEEE Internet Things J. 7, 1230–1244. doi:10.1109/JIOT.2019.2953903
Li, Y., Miridakis, N. I., Tsiftsis, T. A., Yang, G., and Xia, M. (2020). Air-to-air communications beyond 5G: a novel 3D CoMP transmission scheme. IEEE Trans. Wirel. Commun. 19, 7324–7338. doi:10.1109/TWC.2020.3010569
Lin, Z., Lin, M., Champagne, B., Zhu, W.-P., and Al-Dhahir, N. (2021). Secrecy-energy efficient hybrid beamforming for satellite-terrestrial integrated networks. IEEE Trans. Commun. 69, 6345–6360. doi:10.1109/TCOMM.2021.3088898
Lin, Z., Niu, H., An, K., Wang, Y., Zheng, G., Chatzinotas, S., et al. (2022). Refracting ris-aided hybrid satellite-terrestrial relay networks: joint beamforming design and optimization. IEEE Trans. Aerosp. Electron. Syst. 58, 3717–3724. doi:10.1109/TAES.2022.3155711
Mahmoud, A., Muhaidat, S., Sofotasios, P. C., Abualhaol, I., Dobre, O. A., and Yanikomeroglu, H. (2021). Intelligent reflecting surfaces assisted uav communications for iot networks: performance analysis. IEEE Trans. Green Commun. Netw. 5, 1029–1040. doi:10.1109/TGCN.2021.3068739
Matracia, M., Kishk, M. A., and Alouini, M.-S. (2023). UAV-aided post-disaster cellular networks: a novel stochastic geometry approach. IEEE Trans. Veh. Technol. 72, 9406–9418. doi:10.1109/TVT.2023.3247920
Qin, Y., Kishk, M. A., and Alouini, M.-S. (2023). Stochastic geometry-based trajectory design for multi-purpose uavs: package and data delivery. IEEE Trans. Veh. Technol., 1–16. doi:10.1109/TVT.2023.3323682
Shakoor, S., Kaleem, Z., Do, D.-T., Dobre, O. A., and Jamalipour, A. (2021). Joint optimization of uav 3-d placement and path-loss factor for energy-efficient maximal coverage. IEEE Internet Things J. 8, 9776–9786. doi:10.1109/JIOT.2020.3019065
Shi, X., and Deng, N. (2022). Modeling and analysis of mmwave UAV swarm networks: a stochastic geometry approach. IEEE Trans. Wirel. Commun. 21, 9447–9459. doi:10.1109/twc.2022.3176906
Singh, S., Bhattacherjee, U., Ozturk, E., Güvenç, İ., Dai, H., Sichitiu, M., et al. (2021). “Placement of mmwave base stations for serving urban drone corridors,” in 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring) (IEEE), Helsinki, Finland, April 25-28, 2021. 1–6.
Singh, S., Sichitiu, M. L., Güvenç, İ., and Bhuyan, A. (2023). Minimizing ground risk in cellular-connected drone corridors with mmwave links. IEEE Trans. Aerosp. Electron. Syst. 59, 7923–7937. doi:10.1109/taes.2023.3301824
Sun, H., Nan, Y., Li, Y., Wang, X., Li, S., and Quek, T. Q. (2023). Uplink CoMP transmission for cellular-connected UAV networks. IEEE Wirel. Commun. Lett. 12, 1513–1517. doi:10.1109/lwc.2023.3281198
Wang, R., Kishk, M. A., and Alouini, M.-S. (2023). Resident population density-inspired deployment of k-tier aerial cellular network. IEEE Trans. Wirel. Commun. 22, 7989–8002. doi:10.1109/twc.2023.3257222
Wang, W., Jiang, Y., Fei, Z., and Guo, J. (2022). Coverage performance of the multilayer UAV-terrestrial hetnet with CoMP transmission scheme. Front. Inf. Technol. Electron. Eng. 23, 61–72. doi:10.1631/fitee.2100310
Xu, C., Liao, X., Tan, J., Ye, H., and Lu, H. (2020). Recent research progress of unmanned aerial vehicle regulation policies and technologies in urban low altitude. IEEE Access 8, 74175–74194. doi:10.1109/access.2020.2987622
Yao, Y., Zhu, Z., Huang, S., Yue, X., Pan, C., and Li, X. (2020). Energy efficiency characterization in heterogeneous IoT system with UAV swarms based on wireless power transfer. IEEE Access 8, 967–979. doi:10.1109/ACCESS.2019.2961977
Yu, P., Ding, Y., Li, Z., Tian, J., Zhang, J., Liu, Y., et al. (2023). Energy-efficient coverage and capacity enhancement with intelligent UAV-BSs deployment in 6G edge networks. IEEE Trans. Intelligent Transp. Syst. 24, 7664–7675. doi:10.1109/TITS.2022.3198834
Keywords: energy efficiency, internet of things, joint transmission coordinated multi-point, performance analysis, stochastic geometry, unmanned aerial vehicle, UAV corridors
Citation: Armeniakos HK, Maliatsos K, Bithas PS and Kanatas AG (2024) A stochastic geometry-based performance analysis of a UAV corridor-assisted IoT network. Front. Comms. Net 5:1337697. doi: 10.3389/frcmn.2024.1337697
Received: 13 November 2023; Accepted: 07 February 2024;
Published: 26 February 2024.
Edited by:
Sofie Pollin, KULeuven, BelgiumReviewed by:
Kang An, National University of Defense Technology, ChinaZeeshan Kaleem, COMSATS University Islamabad, Pakistan
Zhuangzhuang Cui, KULeuven, Belgium
Copyright © 2024 Armeniakos, Maliatsos, Bithas and Kanatas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Harris K. Armeniakos, aGFybWVuQHVuaXBpLmdy
 Harris K. Armeniakos
Harris K. Armeniakos Konstantinos Maliatsos
Konstantinos Maliatsos Petros S. Bithas
Petros S. Bithas Athanasios G. Kanatas
Athanasios G. Kanatas