Corrective Filter Based on Kinematics of Human Hand for Pose Estimation

1 Introduction

Depth based 3D hand tracking (or hand pose estimation) is the problem of predicting the 3D hand pose given a single depth image of the hand at any angle. The major challenges of this problem are: 1) Self-occlusion where the hand occludes itself, 2) Object interaction where the hand interacts with other objects, and 3) Movements that require additional hands interacting together. It is used in many applications in fields such as Human-Computer Interaction (HCI) (Yeo et al., 2015; Lyubanenko et al., 2017), Virtual Reality (VR) (Cameron et al., 2011; Lee et al., 2015; Ferche et al., 2016), and gaming. These applications require accurate tracking as any error will affect the immersiveness and, ultimately, the end-user experience. Important applications such as surgical simulations (Chan et al., 2013) rely on accurate tracking of the hand to ensure the user’s proper procedural knowledge for real-life surgeries. Entertainment based applications such as racing simulators and sports games require accurate poses of the hand poses for truly immersive gaming experiences. Hence, 3D hand tracking has become a leading problem in Computer Vision with commercial and academic interests.

One of the critical problems in hand tracking is the realism of the output. This problem of hand pose realism has been studied in a partial aspect as “highly accurate tracking” in earlier work as increasing the tracker’s accuracy and reducing the poses’ overall position-based error. Many studies overlooked this problem by focusing solely on the accuracy of the hand tracking models. Such models have low errors in benchmark tests such as the NYU (Tompson et al., 2014), ICVL (Tang et al., 2016), HANDS 2017 (Yuan et al., 2017) and BigHand2.2M (Yuan et al., 2017). However, high accuracy does not always translate to realistic hand output. Such an example is a simple case of a hand pose that matches all joint positions of the actual hand pose except one joint, which is at an anatomically implausible angle from the previous joint (such as a finger bent backward). This error can disrupt the immersiveness of the individual during the game or simulation. Moreover, from a human perspective (Pelphrey et al., 2005), the error can affect the internal human system leading to false information and mismatch in the motor cortex and the visual system. Other solutions to this problem include inverse kinematics based solutions such as Wang and Popović (2009) and using kinematic priors such as Thayananthan et al. (2003). However, these solutions are tailor-made for their hand trackers and not built for generic use. Hence, this problem is the focus and motivation of our paper.

This paper proposes a filter that functions on the human hand’s biomechanical principles and kinematics. This filter’s novelty is the use of bounds and rules derived from the human hand’s biomechanical aspects to produce a more realistic rendering of the hand pose. The hand is an articulated body with joints, and corresponding bounds (Gustus et al., 2012), and the filter is created using these rules and bounds. The input is the pose of the human hand in the form of joint locations and angles from the hand tracker and outputs the closest possible hand as per the real human hand’s bounds. The filter can be plugged into any hand tracker and enhance its performance. Later in Anatomical Anomaly Test, we show that the proposed filter improves the realism of the hand poses predicted by the state-of-the-art trackers as compared to the poses without using the filter. We also elaborate on the filter rules and bounds in Anatomical Filter.

2 Related Work

In this section, we discuss a few state-of-the-art methods for 3D hand tracking. Joo et al. (2014) proposed a real-time hand tracker using the Depth Adaptive Mean Shift algorithm, a variant of the classic computer vision method known as CAM—Shift (Bradski, 1998). It tracks the hand in real-time, however, only in two dimensions due to the limitations of traditional computer vision techniques. Other similar 2D based trackers include works such as Held et al. (2016); El Sibai et al. (2017). Taylor et al. (2016) proposed an efficient and fast 3D hand tracker algorithm that utilizes only the CPU to track the hand using iterative methods. This method’s drawback is that the hand is treated as a smooth body, and the joints and bones are not distinguished in the model, frequently resulting in anatomically implausible hand structures when tracking.

Recent state-of-the-art models utilize deep learning to achieve highly accurate 3D trackers with low errors in the order of millimeters. Deep learning provides new perspectives to computer vision problems with 3D Convolutional Neural Networks (CNNs) (Ge et al., 2017; Simon et al., 2019) and other such models. There are many survey works and literature available in the field of hand tracking, concerning appearance and model-based hand tracker using depth images (Sagayam and Hemanth, 2017; Deng et al., 2018; Dang et al., 2019; Li et al., 2019). Model-based tracking (Stenger et al., 2001; de La Gorce et al., 2008; Hamer et al., 2009; Oikonomidis et al., 2010) creates a 3D model of the hand and aligns it according to the visual data provided. Tagliasacchi et al. (2015) made a fast 3D model-based tracking using gradient-based optimization to track the hand position and pose. The drawback of this method is that a wristband must be worn on the hand to be tracked, and the model does not incorporate the angular velocity bounds of the human hand. Although the angle bounds are incorporated in the model, during certain conditions, the hand pose derived from the algorithm results in hand poses, which are impossible for a natural hand. Other models still suffer from heavy computational requirements such as 3D CNNs, which require voxelization (Ge et al., 2017) of the image for pose estimation. Works such as Sharp et al. (2015), Malik et al. (2018), Wan et al. (2018), Xiong et al. (2019), Kha Gia Quach et al., 2016 proposed fast 3D hand trackers with high accuracy, but at the expense of heavy computational algorithms and can track only a single hand. Works such as Misra and Laskar (2017), Roy et al. (2017), Deng et al. (2018) utilize deep learning for hand tracking but in 2D.

Focusing on realism and multi-hand interaction, Mueller et al. (2019) proposed a model that uses a single depth camera to track hands while they move and interact with each other. It can also take the fingers’ collision to the other hand into account to a certain degree. It was trained using available and synthetically created data as well. This method’s drawback is that it is computationally expensive and cannot predict poses when the hand moves very fast. There are also discrepancies in some interactions when the calibration is imperfect.

To the best of our knowledge, none of the existing hand tracking approaches have explicitly corrected the predicted pose by using a filter based on the biomechanics principle as is being proposed in this work. The main contributions of this work are:

1. A filter based on the human hand’s biomechanics, ensuring that the output of the hand tracker conforms to the rules of true human hand kinematics and enhances the immersiveness of the end application.

2. An approach of adding a modular filter that can be easily plugged into an existing hand tracker with little or no modifications.

3. A smooth trade-off between realism and the hand pose accuracy

3 Anatomical Filter

The anatomical filter takes the pose from the tracker as input and then adjusts the individual joint angles according to their biomechanical limits. The overview of the filter is shown in Figure 1. Filter Construction describes the construction and working of the anatomical filter. Biomechanics of the Hand describes the anatomical bounds and rules used to create the anatomical filter.

FIGURE 1

FIGURE 1. Overview of the anatomical filter. The depth image first passes through the hand tracker, and then a pose is retrieved (the unaltered pose). This pose then passes through the anatomical filter, and then the filtered pose is given as the output.

3.1 Filter Construction

The filter utilizes the bounds explained in Biomechanics of the Hand and corrects the hand pose according to the bounds. The first step is to calculate the joint angles since most hand trackers’ output is the joint’s location in 3D space and not the joint’s angle of rotation. Each joint’s angles are computed separately using 3D transformations such that the joint with its dependent joints are aligned on the XY plane. Then, using the vectors computed from each pair of joints, the Euler angles of each joint are calculated.

The second step is to calculate the deviation of each joint from its limit. Considering the current joint angle of a particular joint as ${\theta }_{\text{c}}=[{\theta }_x,{\theta }_y,{\theta }_z]$, where ${\theta }_x$, ${\theta }_y$, and ${\theta }_z$ are the individual angles to each axis, the anatomical error of the particular joint is derived in Eq. 1

${\epsilon }_{\text{d}}^{\theta }=\{\begin{array}{l}{\theta }_{\text{d}}-{\theta }_{\text{upper}}\text{if }{\theta }_{\text{d}}>{\theta }_{\text{upper}}\\ {\theta }_{\text{lower}}-{\theta }_{\text{d}}\text{if }{\theta }_{\text{d}}<{\theta }_{\text{lower}}\\ 0\text{otherwise}\end{array}\text{where }d=x,y,z(1)$

The third step is to correct the joint’s angle using the error derived from Eq. 1. The correction’s strength is adjusted using a factor α and is shown in Eq. 2.

${\theta }_{\text{d}\left(\text{new}\right)}=\{\begin{array}{l}{\theta }_{\text{d}}-{\alpha }^{\ast }{\epsilon }_{\text{d}}^{\theta }\text{if }{\theta }_{\text{d}}>{\theta }_{\text{upper}}\\ {\theta }_{\text{d}}+{\alpha }^{\ast }{\epsilon }_{\text{d}}^{\theta }\text{if }{\theta }_{\text{d}}<{\theta }_{\text{lower}}\\ {\theta }_{\text{d}}\text{otherwise}\end{array}(2)$

where $d=x,y,z$ and $\alpha \in \left[\mathrm{0,1}\right]$. If $\alpha =0$, then there is no correction and the resultant angle is the original angle. If $\alpha =1$, then the angle is 100% corrected based on the hand’s biomechanical rules.

3.2 Biomechanics of the Hand

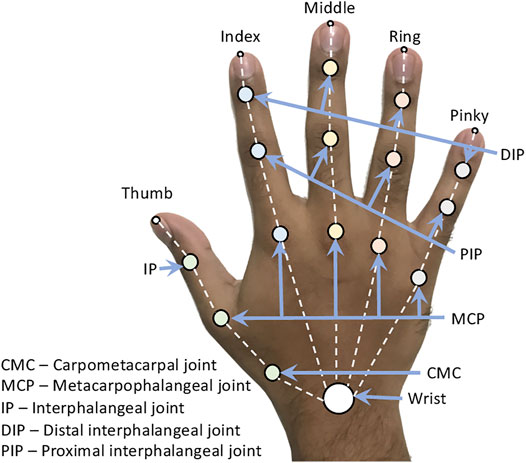
In the human hand, there are 27 bones with 36 articulations and 39 active muscles (Ross and Lamperti, 2006), as shown in Figure 2. According to Kehr et al., 2017, the lower arm’s distal area consists of the distal radio-ulnar joint, the thumb and finger carpometacarpal (CMC) joints, the palm, and the fingers. These muscles map up to 19 degrees of freedom with complex functions such as grasping and object manipulation. The key joints for the movements of the hand are:

1. Metacarpophalangeal (MCP) joint

2. Distal interphalangeal (DIP) joint

3. Proximal interphalangeal (PIP) joint

4. Carpometacarpal (CMC) joint

FIGURE 2

FIGURE 2. Structure of the human hand.

The wrist is simplified to six-degrees-of-freedom (DoF), consisting of three DoFs for movement and three DoFs for rotation across the three axes. The thumb’s CMC joint is integrated into the wrist and is an important joint since it enables a wide range of hand movements by performing the thumb’s opposition. According to Chim (2017), the CMC joint has three DoFs: 45° abduction and 0° adduction, 20° flexion and 45° extension, and 10° of rotation in the CMC joint.

There are five MCP joints in which the first MCP joint is connected to the thumb’s CMC joint. The remaining four MCP joints are attached to the wrist of the hand. The MCP joint of the thumb is a two DoF joint that provides flexion 80° and extension 0°, abduction 12° and adduction 7°. The remaining MCP joints are also two DoF joints and provide flexion 90° and extension 40°, as well as abduction 15° and adduction 15°. Clear illustrations and details regarding these bounds can be found in works such as Hochschild (2015) and Ross and Lamperti (2006).

There are two types of interphalangeal (IP) joints: the distal and proximal (DIP and PIP) joints. The thumb only has a single IP joint, while the other fingers have both DIP and PIP joints. The PIP joints provide flexion 130° and extension 0°. The DIP joints, including the thumb IP joint, provide flexion 90° and extension 30°.

These rules and bounds are all incorporated in the construction of the filter and shown in Table 1. When the filter activates, each joint of the hand-pose is compared with these rules and then corrected to output a hand-pose that conforms to the hand’s biomechanics.

TABLE 1

TABLE 1. Angular bounds for each joint of the hand derived from Hochschild (2015) and Ross and Lamperti (2006).

4 Baseline Hand Tracking Model

To compare the state-of-the-art trackers with the anatomical filter, we made a simple hand tracker to serve as a baseline model. The baseline model is trained with the filter attached to compare with the other state-of-the-art models that were not trained with such filters.

4.1 Architecture

We created our hand tracker using the ResNet-50 (He et al., 2016) as a backbone with transfer learning (Torrey and Shavlik, 2010) to utilize the powerful model for 3D hand pose detection. The architecture is shown in Figure 3, and the process diagram is shown in Figure 1. Since the ResNet originally performs classification using a softmax layer, we use the model without the top classification layer which results in a an output of size 6 $\times$ 6 $\times$ 2048. The size of the input image after pre-processing is 176 $\times$ 176 $\times$ 1 which is then replicated for the three channels as the input to the backbone model should be a 3-channel image. The output features from the backbone model is then compressed by passing it through a single convolutional layer of size 512 $\times$ 6 $\times$ 6. The resultant features is flattened (to size 512 $\times$ 1) and then passes through two fully connected dense layers of sizes 258 and 63, respectively. The first dense layer uses a ReLU activation function whereas the last layer uses a linear activation function. This output is filtered using our anatomical filter and then the estimated pose is retrieved. The code was built using Keras and used the Adam optimizer (Kingma and Ba, 2014) with the learning rate set to 0.00035. The model trained on the full training data with 20% of the data for validation until there was no improvement in validation error for five epochs.

FIGURE 3

FIGURE 3. Architecture of the model used for the hand tracker with the anatomical filter.

4.2 Dataset Used

The dataset used for the evaluation is the HANDS 2017 (Yuan et al., 2017), which consists of more than 900,000 images for training and 99 video segments of depth images for testing pose estimators. The images consist of various poses that are complex and challenging for estimating the correct pose. Our model is first used without any filter to evaluate it on the dataset, and then the anatomical filter is used to correct the hand pose. Then the whole system is re-evaluated with a grid search to incorporate all possible α values. To use the filter on the current state-of-the-art A2J model (Xiong et al., 2019) and V2V-Posenet (Moon et al., 2018), the “frames” subset of the HANDS2017 dataset is used, which contains 295510 independent hand images that covers a wide variety of challenging hand poses.

5 Results and Analysis

The focus of this work is improving the realism of the predicted hand poses. To demonstrate that our proposed method can work with any pose prediction model, we designed the following experiments.

1. We study the effect of the filter on the output of various state-of-the-art trackers. We chose a simple baseline model, the A2J model, and the V2V-Posenet model as the trackers. We show that the outputs are more realistic when corrected by the anatomical filter.

2. We quantify the anatomical error and show how the filter reduces this error with various configurations.

3. We study the effect of α on the baseline model using the filter.

4. We show the best-case and worst-case scenarios of the filter correction.

5. We test the error of the state-of-the-art models using the filter with various configurations.

5.1 Filter Function on the State-of-The-Art Trackers

To understand the filter’s function, Figure 4 shows the working of the filter for a single frame of the dataset. Figure 4A shows the A2J model prediction of a simple pose in the dataset and our filter’s correction of the pose. The figure shows that the thumb is bent in an anatomically implausible manner, shown in detail (selected by a dotted circle). The highlighted angle in yellow is known as the anatomical error (shown in Figure 4A), and the anatomical filter corrects this error. The corrected angle is shown in green, and the process is repeated for all joints. The resulting pose is shown in Figure 4A as the corrected pose. A similar scenario is shown in Figure 4B for the V2V-Posenet model. These discrepancies in the poses disrupt the user experience if used in an immersive application such as gaming or simulation-based training programs. Our filter corrects these errors at the minor expense of overall 3D error, resulting in a smoother application experience.

FIGURE 4

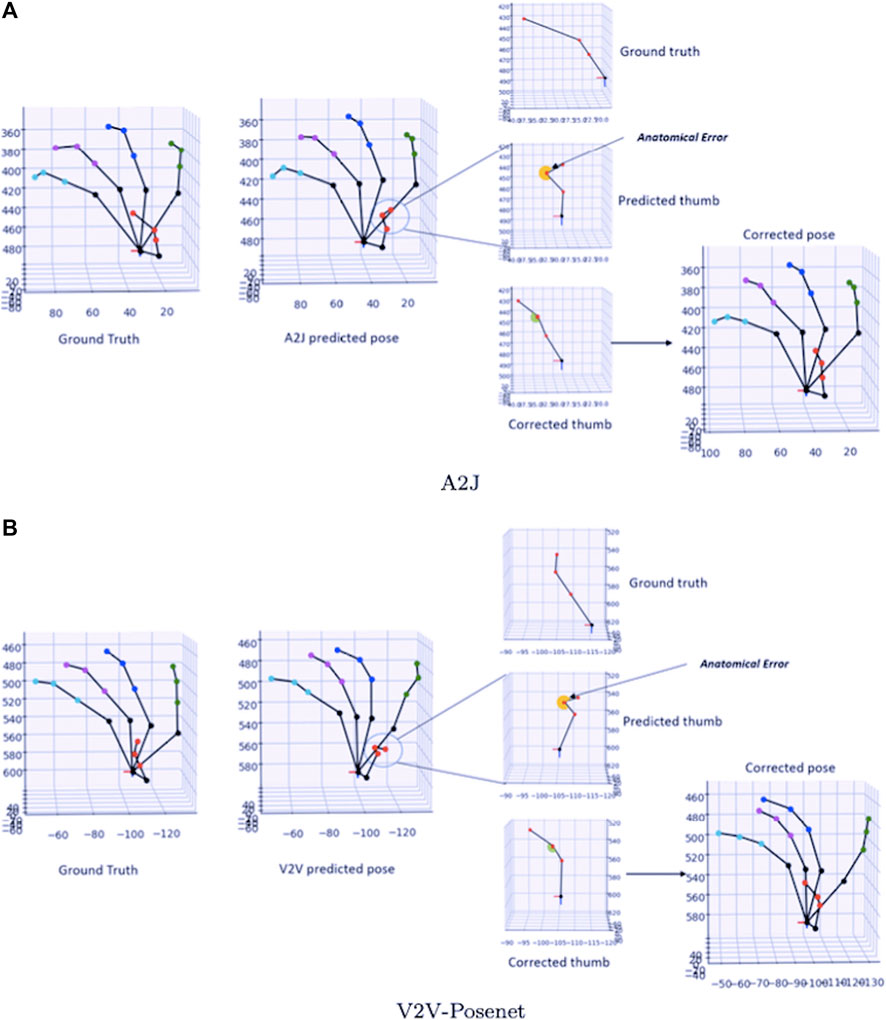
FIGURE 4. The type of corrections performed by the anatomical filter. (A) shows the correction by the A2J model and (B) shows the correction of the V2V-Posenet model. The dotted circles indicate an anomaly in the joint. In the zoomed graph, the yellow semi-circle denotes the joint which has an error, and the green semi-circle denotes the corrected joint.

5.2 Anatomical Anomaly Test

To quantify the direct factor relating to the anatomical structure based realism of the human hand pose, we derive a quantity that we refer to as the anatomical error. This error is derived for the three models and shown in Figure 5, which is the mean joint degree that overshoots or undershoots the anatomical bounds of the corresponding joint of the hand. The higher the error, the more “unreal” the given hand pose is according to the hand’s anatomical structure. The error is high for both the A2J and V2V-Posenet models, which reduces smoothly as α increases. This reduction is because α directly controls these errors in the filter. Figure 5B shows the percentage of frames in which the hand pose has an anatomical error above 100 degrees. The quantified results for these tests are shown in Table 2. From the graph and table, we infer that our model predicts more realistic poses with lower anatomical errors with a small trade-off with 3D Joint Position Error.

FIGURE 5

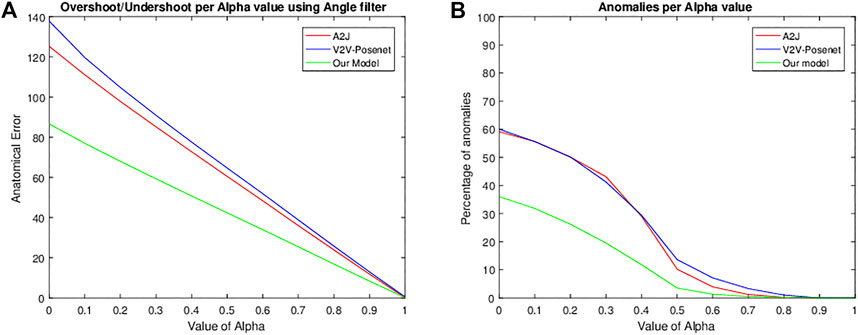
FIGURE 5. Graphical visualization of the anatomical errors of two state-of-the-art models, namely A2J (Xiong et al., 2019) in (A) and V2V-Posenet (Moon et al., 2018) in (B) compared to our model using the angle filter attached to the end of the model for every value of α. The x-axis corresponds to the value of α used for the filter. The y-axis in (A) corresponds to the model’s anatomical error, which is the mean joint degree that overshoots or undershoots the anatomical bounds of the corresponding joint of the hand. In (B), the y-axis corresponds to the percentage of frames in which the anatomical error exceeded 100 degrees.

TABLE 2

TABLE 2. Percentage of poses with anatomical anomalies at the specified ranges, comparing the baseline model with the state-of-the-art models. The test was performed on a subset of 20000 test images of the HANDS2017 dataset.

5.3 Effect of α on our Model Using the Anatomical Filter

The mean 3D joint position error is usually computed for 3D hand tracking models, which is computed by calculating the individual 21 joint distances from the estimated model to the ground truth pose and deriving the mean of that sum. The mean is then computed for each video segment. To measure the hand pose’s error, we introduce a metric known as 3D joint angle error. The 3D joint angle error is similar to the position error; however, this error measures the difference between the 26-DoF vector derived from the joint locations as per Biomechanics of the Hand. Together, these two errors represent the 3D joint pose error. First, the 3D joint position and angle errors of our model are calculated for different α values. A graphical representation of the results is shown in Figure 6. The x-axis is the α set for the filter as per Eq. 2. The y-axis represents a different measure for each sub-figure in Figure 6. In Figure 6A, the y-axis corresponds to the mean 3D joint position error. In Figure 6B, the y-axis corresponds to the mean degree error of the model. Finally, in Figure 6C, the y-axis corresponds to the deviation factor, which is the value the error deviates from the point where the filter was not used (unfiltered error). Since there are two error metrics computed, each error’s deviation is computed separately and then combined using the arithmetic mean. This method is possible since the deviation factor has no unit. For example, a deviation factor of one means that the error did not change from the unfiltered model, and the filter is of no use. However, if the deviation factor is lower than one, then the new model performs better than the unfiltered model and vice versa if the factor is above one. Figure 6C shows that the deviation factor is lowest at $\alpha =0.3$. Hence the model shows the best results when the filter is set at 30% strength. Beyond that value, the deviation factor steadily increases to a point beyond one. This decrease is shown quantitatively in Table 3, where the error of the filter is lower than that of the other configurations when $\alpha =0.3$.

FIGURE 6

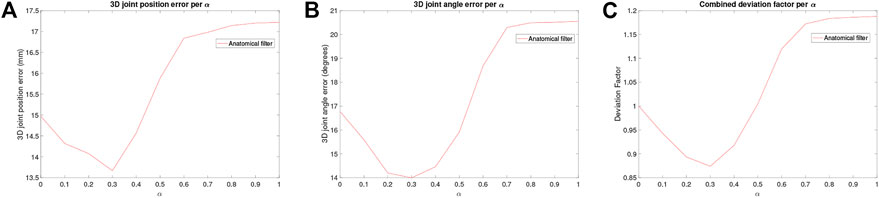
FIGURE 6. Graphical visualization of the results computed for every value of α used in the filter on our custom model. The x-axis corresponds to the value of α used for the filter. In Panel 6A, the y-axis corresponds to the mean 3D joint position error of the model, which is the mean distance of each joint of the estimated pose to the joint of the corresponding ground truth pose. In Panel 6B, the y-axis corresponds to the 3D joint angle error of the model, which is the mean error between the 27 DoF vector of the estimated pose to the corresponding vector of the ground truth pose. Finally, in Panel 6C, the y-axis corresponds to the deviation factor, which is the value the error (both joint position and angle errors together) deviates from the point where the filter was not used (unfiltered error).

TABLE 3

TABLE 3. 3D Joint Errors (3DJE) and 3D Angle Errors (3DAE) derived from the HANDS2017 dataset with all the models. Bold values represent the lowest error in each column.

5.4 Effect of α on State-of-The-Art Models Using the Anatomical Filter

In order to study the effect of the filter on the overall 3D joint position error, the filter was tested on the current state-of-the-art A2J model (Xiong et al., 2019) and V2V-Posenet (Moon et al., 2018) using the “frames” subset of the HANDS2017 dataset. Figure 7 shows the results of the test using various configurations of the angle filter described in Eq. 2. The position errors at $\alpha =0$ are the reported errors of 8.570 and 9.95 mm, respectively, as reported by Xiong et al. (2019) and Moon et al. (2018). When increasing the filter’s strength, the error slightly reduces (8.530 and 9.94 mm) and then increases monotonically beyond that value. To visualize the minor changes that occur when α ranges from 0 to 0.4, a smaller test was also performed with alpha ranging from 0 to 0.4 with a step size of 0.02. This test is done for both the A2J model and the V2V-Posenet model, and the individual graphs are also shown in Figure 7. From the figure, we derive that at $\alpha =0.08$, the filter improves the A2J model and $\alpha =0.075$ for V2V Posenet since the error reduces at the filter strength, seen from both the main graph and the zoomed graphs. The 3D joint error at $\alpha =0.1$ is 17.24 for the baseline model and 9.62 for the A2J model with $\alpha =0.08$ and 11.21 for the V2V Posenet model with $\alpha =0.075$. This shows that the simple baseline model has comparable performance to the state-of-the-art models in terms of anatomical correctness, and using the filter in the model improves the overall performance of the model significantly.

FIGURE 7

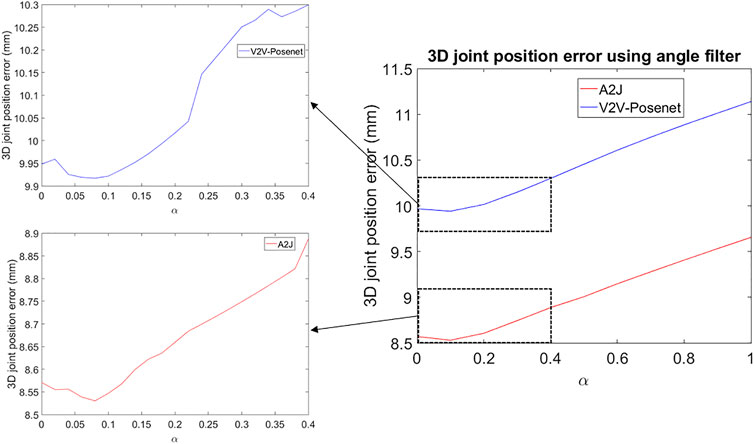
FIGURE 7. Graphical visualization of the results of two state-of-the-art models, namely A2J (Xiong et al., 2019) and V2V-Posenet (Moon et al., 2018) using the angle filter attached to the end of the model for every value of α. The x-axis corresponds to the value of α used for the filter. The y-axis is the mean 3D joint position error of the model, which is the mean distance of each joint of the estimated pose to the corresponding ground truth pose. Since the improvement is minor, a zoomed version of the selected regions is also shown for the respective models.

5.5 Best-Case and Worst-Case Scenarios

When the filter corrects the hand’s pose based on the hand biomechanics, inevitably, the hand pose drifts from the original pose. This drift can either make the pose closer to the ground truth or defer from it. The former is the best-case scenario, while the latter is the worst-case scenario. The scenarios are shown in Figure 8. The yellow dots correspond to the predicted joints’ position, and the blue dots correspond to the ground truth joints’ position. The yellow dots must be as close to the corresponding blue dots as possible, ideally overlapping them. The first case is the positive scenario where one joint error occurred in the pose. When the anatomical filter corrected this pose, the error was reduced. The second case is the non-ideal scenario where the error resides in the bottom joint. When this error is corrected, the secondary joints above the corrected joint all shift their positions, hence drifting from the ground truth. The final correction shifts the distance even more, hence, increasing the total error. This shift results in a hand pose that conforms to the rules. However, the overall pose is now further from the ground truth.

FIGURE 8

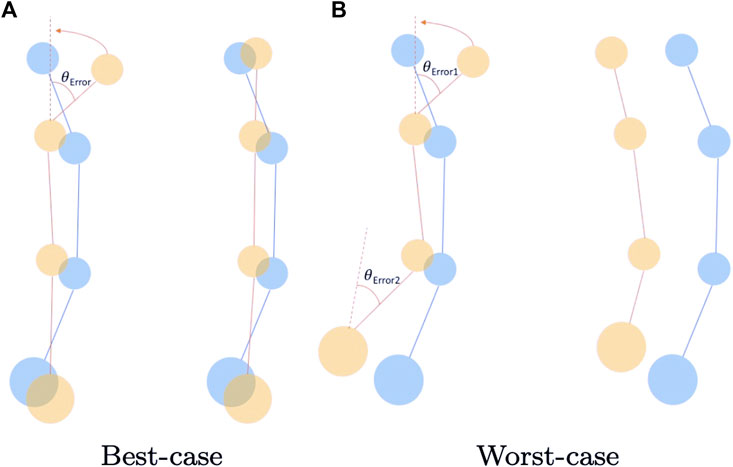
FIGURE 8. Simple 2D illustration for the best-case and worst-case corrections performed by the anatomical filter. (A) shows the best-case scenario and (B) shows the worst-case scenario. The blue circles indicate joint locations of a single index finger from the ground truth. The yellow circles indicate the position of the estimated joints from the hand tracker.

6 Summary, Limitations and Future Work

This paper proposed the anatomical filter, which functions on the human hand’s biomechanical principles. The filter is modular and can be easily plugged into existing hand trackers with little or no modifications. The results showed that the filter does improve the current state-of-the-art trackers when used in 10% strength, and it was also shown that the state-of-the-art trackers have high errors in terms of anatomical rules and bounds.

The filter’s computational requirements are high since the angles and bounds are calculated and compared for each joint in the hand. This process increases the time taken to estimate output for each input frame and runs at lower speeds when running real-time tracking. Our future work is to optimize the filter to compute angles and bounds in fewer functions and reduce the time taken to estimate the filtered pose. Optimized methods such as inverse kinematics based modeling (Aristidou, 2018) methods can effectively correct the joints in real-time. Future works also include utilizing the law of mobility as per Manivannan et al. (2009), which states that the two-point discrimination improves from proximal to distal body parts. Hence, the filter’s strength can be changed from the hand’s proximal parts towards the hands’ distal part. Other future works include enhanced optimizations such as implementing the filter function into the model architecture itself instead of attaching the filter at the end of the model. The baseline model used in this paper highlights the importance of using anatomical rules during training and can improve the model’s accuracy, not only in anatomical correctness but also in pose error. Using the filter inside the model may also reduce training and testing time and also reduce excessive computations.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found in the following links: http://icvl.ee.ic.ac.uk/hands17/, https://imperialcollegelondon.app.box.com/v/hands2017.

Author Contributions

JI is the primary author who designed and performed the experiments. He also analyzed the data and wrote the paper. MM and BR supervised the entire research process from concept creation to paper writing and guidance during the experiments.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aristidou, A. (2018). Hand Tracking with Physiological Constraints. Vis. Comput. 34, 213–228. doi:10.1007/s00371-016-1327-8

CrossRef Full Text | Google Scholar

Bradski, G. R. (1998). Computer Vision Face Tracking for Use in a Perceptual User Interface. Santa Clara, CA: Intel Technology.

Cameron, C. R., DiValentin, L. W., Manaktala, R., McElhaney, A. C., Nostrand, C. H., Quinlan, O. J., et al. (2011). “Hand Tracking and Visualization in a Virtual Reality Simulation,” in 2011 IEEE Systems and Information Engineering Design Symposium, Charlottesville, VA (IEEE), 127–132.

Google Scholar

Chan, S., Conti, F., Salisbury, K., and Blevins, N. H. (2013). Virtual Reality Simulation in Neurosurgery. Neurosurgery 72, A154–A164. doi:10.1227/neu.0b013e3182750d26

CrossRef Full Text | Google Scholar

Chim, H. (2017). Hand and Wrist Anatomy and Biomechanics. Plast. Reconstr. Surg. 140, 865. doi:10.1097/prs.0000000000003745

PubMed Abstract | CrossRef Full Text | Google Scholar

Dang, Q., Yin, J., Wang, B., and Zheng, W. (2019). Deep Learning Based 2D Human Pose Estimation: A Survey. Tinshhua Sci. Technol. 24, 663–676. doi:10.26599/TST.2018.9010100

CrossRef Full Text | Google Scholar

de La Gorce, M., Paragios, N., and Fleet, D. J. (2008). “Model-based Hand Tracking with Texture, Shading and Self-Occlusions,” In 2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, Alaska: IEEE, 1–8.

Google Scholar

Deng, X., Zhang, Y., Yang, S., Tan, P., Chang, L., Yuan, Y., et al. (2018). Joint Hand Detection and Rotation Estimation Using CNN. IEEE Trans. Image Process. 27, 1888–1900. doi:10.1109/TIP.2017.2779600

PubMed Abstract | CrossRef Full Text | Google Scholar

El Sibai, R., Abou Jaoude, C., and Demerjian, J. (2017). “A New Robust Approach for Real-Time Hand Detection and Gesture Recognition,” In 2017 International Conference on Computer and Applications (ICCA). Dubai: Springer, 18–25. doi:10.1109/COMAPP.2017.8079780

CrossRef Full Text | Google Scholar

Ferche, O., Moldoveanu, A., and Moldoveanu, F. (2016). Evaluating Lightweight Optical Hand Tracking for Virtual Reality Rehabilitation. Rom. J. Human-Computer Interaction 9, 85.

Google Scholar

Ge, L., Liang, H., Yuan, J., and Thalmann, D. (2017). “3d Convolutional Neural Networks for Efficient and Robust Hand Pose Estimation from Single Depth Images,” In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE: Honolulu, Hawaii, 5679–5688. doi:10.1109/CVPR.2017.602

CrossRef Full Text | Google Scholar

Gia Quach, K., Nhan Duong, C., Luu, K., and Bui, T. D. (2016). “Depth-based 3d Hand Pose Tracking,” In 2016 23rd International Conference on Pattern Recognition (ICPR). Cancún, México: IEEE, 2746–2751.

Google Scholar

Gustus, A., Stillfried, G., Visser, J., Jörntell, H., and van der Smagt, P. (2012). Human Hand Modelling: Kinematics, Dynamics, Applications. Biol. cybernetics 106, 741–755. doi:10.1007/s00422-012-0532-4

CrossRef Full Text | Google Scholar

Hamer, H., Schindler, K., Koller-Meier, E., and Gool, L. V. (2009). “Tracking a Hand Manipulating an Object,” In 2009 IEEE 12th International Conference on Computer Vision. Kyoto, Japan: IEEE, 1475–1482.

Google Scholar

He, K., Zhang, X., and Ren, S., and S un, J. (2016). “Deep Residual Learning for Image Recognition,” In Proceedings of the IEEE conference on computer vision and pattern recognition. Las Vegas, Nevada: IEEE, 770–778.

Google Scholar

Held, D., Thrun, S., and Savarese, S. (2016). “Learning to Track at 100 FPS with Deep Regression Networks,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics (Cham: Springer), 9905, 749–765. doi:10.1007/978-3-319-46448-0_45

CrossRef Full Text | Google Scholar

Hochschild, J. (2015). Functional Anatomy For Physical Therapists (New York: Thieme).

Joo, S. I., Weon, S. H., and Choi, H. I. (2014). Real-time Depth-Based Hand Detection and Tracking. Scientific World J. 2014, 284827. doi:10.1155/2014/284827

CrossRef Full Text | Google Scholar

Kehr, P., Graftiaux, A. G., hirt, B., seyhan, h., and wagner, m. (2017). R. Zumhasch: Hand and Wrist Anatomy and Biomechanics: a Comprehensive Guide. Eur. J. Orthopaedic Surg. Traumatol. 27, 1029. doi:10.1007/s00590-017-1991-z

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: A Method for Stochastic Optimization. arXiv preprint arXiv, 1412, 6980.

Google Scholar

Lee, P.-W., Wang, H.-Y., Tung, Y.-C., Lin, J.-W., and Valstar, A. (2015). “Transection: Hand-Based Interaction for Playing a Game within a Virtual Reality Game,” In Proceedings of the 33rd Annual ACM Conference Extended Abstracts on Human Factors in Computing Systems New York, NY: Association for Computing Machinery, 73–76.

Google Scholar

Li, R., Liu, Z., and Tan, J. (2019). A Survey on 3d Hand Pose Estimation: Cameras, Methods, and Datasets. Pattern Recognition 93, 251–272. doi:10.1016/j.patcog.2019.04.026

CrossRef Full Text | Google Scholar

Lyubanenko, V., Kuronen, T., Eerola, T., Lensu, L., Kälviäinen, H., and Häkkinen, J. (2017). “Multi-camera finger Tracking and 3d Trajectory Reconstruction for Hci Studies,” In International Conference on Advanced Concepts for Intelligent Vision Systems, Antwerp, Belgium. Cham: Springer, 63–74.

CrossRef Full Text | Google Scholar

Malik, J., Elhayek, A., and Stricker, D. (2018). Structure-Aware 3D Hand Pose Regression from a Single Depth Image, Vol. 2. Cham: Springer. doi:10.1007/978-3-030-01790-3

CrossRef Full Text

Manivannan, M., Periyasamy, R., and Narayanamurthy, V. (2009). Vibration Perception Threshold and the Law of Mobility in Diabetic Mellitus Patients. Prim. Care Diabetes 3, 17–21. doi:10.1016/j.pcd.2008.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Misra, S., and Laskar, R. H. (2017). “Multi-factor Analysis of Texture and Color-Texture Features for Robust Hand Detection in Non-ideal Conditions,” In Proc. of the 2017 IEEE Region 10 Conference (TENCON). Penang, Malaysia: IEEE, 1165–1170.

Google Scholar

Moon, G., Yong Chang, J., and Mu Lee, K. (2018). “V2v-posenet: Voxel-To-Voxel Prediction Network for Accurate 3d Hand and Human Pose Estimation from a Single Depth Map,” In Proceedings of the IEEE conference on computer vision and pattern Recognition. Salt Lake City, Utah: IEEE, 5079–5088.

Google Scholar

Mueller, F., Davis, M., Bernard, F., Sotnychenko, O., Verschoor, M., Otaduy, M. A., et al. (2019). Real-time Pose and Shape Reconstruction of Two Interacting Hands with a Single Depth Camera. ACM Trans. Graphics (Tog) 38, 1–13. doi:10.1145/3306346.3322958

CrossRef Full Text | Google Scholar

Oikonomidis, I., Kyriazis, N., and Argyros, A. A. (2010). “Markerless and Efficient 26-dof Hand Pose Recovery,” In Asian Conference on Computer Vision, Queenstown, New Zealand. Berlin, Heidelberg: Springer, 744–757.

Google Scholar

Pelphrey, K. A., Morris, J. P., Michelich, C. R., Allison, T., and McCarthy, G. (2005). Functional Anatomy of Biological Motion Perception in Posterior Temporal Cortex: an Fmri Study of Eye, Mouth and Hand Movements. Cereb. Cortex 15, 1866–1876. doi:10.1093/cercor/bhi064

PubMed Abstract | CrossRef Full Text | Google Scholar

Ross, L. M., and Lamperti, E. D. (2006). Thieme Atlas of Anatomy: General Anatomy and Musculoskeletal System (Thieme). NY: Thieme Medical Publishers.

Roy, K., Mohanty, A., and Sahay, R. R. (2017). “Deep Learning Based Hand Detection in Cluttered Environment Using Skin Segmentation.” In IEEE International Conference on Computer Vision Workshops. Venice, Italy: IEEE, 640–649. doi:10.1109/ICCVW.2017.81

CrossRef Full Text | Google Scholar

Sagayam, K. M., and Hemanth, D. J. (2017). Hand Posture and Gesture Recognition Techniques for Virtual Reality Applications: a Survey. Virtual Reality 21, 91–107. doi:10.1007/s10055-016-0301-0

CrossRef Full Text | Google Scholar

Sharp, T., Keskin, C., Robertson, D., Taylor, J., Shotton, J., Kim, D., et al. (2015). “Accurate, Robust, and Flexible Real-Time Hand Tracking,” In Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems. Seoul, Korea: ACM, 3633–3642.

Google Scholar

Simon, M., Amende, K., Kraus, A., Honer, J., Samann, T., Kaulbersch, H., et al. (2019). “Complexer-yolo: Real-Time 3d Object Detection and Tracking on Semantic point Clouds,” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops.

Google Scholar

Stenger, B., Mendonca, P. R. S., and Cipolla, R. (2001). “Model-based 3d Tracking of an Articulated Hand,” in Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI. CVPR 2001, 2, II.

Google Scholar

Tagliasacchi, A., Schröder, M., Tkach, A., Bouaziz, S., Botsch, M., and Pauly, M. (2015). “Robust Articulated-Icp for Real-Time Hand Tracking,” in Computer Graphics Forum (Hoboken, New Jersey: Wiley Online Library), 34, 101–114. doi:10.1111/cgf.12700

CrossRef Full Text | Google Scholar

Tang, D., Chang, H. J., Tejani, A., and Kim, T.-K. (2016). Latent Regression forest: Structured Estimation of 3d Hand Poses. IEEE Trans. Pattern Anal. Machine Intelligence 39, 1374–1387. doi:10.1109/TPAMI.2016.2599170

Google Scholar

Taylor, J., Bordeaux, L., Cashman, T., Corish, B., Keskin, C., Sharp, T., et al. (2016). Efficient and Precise Interactive Hand Tracking through Joint, Continuous Optimization of Pose and Correspondences. ACM Trans. Graphics (Tog) 35, 1–12. doi:10.1145/2897824.2925965

CrossRef Full Text | Google Scholar

Thayananthan, A., Stenger, B., Torr, P. H., and Cipolla, R. (2003). Learning a Kinematic Prior for Tree-Based Filtering. BMVC (Citeseer) 2, 589–598. doi:10.5244/C.17.60

Google Scholar

Tompson, J., Stein, M., Lecun, Y., and Perlin, K. (2014). Real-time Continuous Pose Recovery of Human Hands Using Convolutional Networks. ACM Trans. Graphics 33, 1–5. doi:10.1145/2629500

CrossRef Full Text | Google Scholar

Torrey, L., and Shavlik, J. (2010). “Transfer Learning,” in Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques (Hershey, Pennsylvania: IGI global), 242–264.

Google Scholar

Wan, C., Probst, T., Gool, L. V., and Yao, A. (2018). Dense 3D Regression for Hand Pose Estimation. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Salt Lake City, Utah: IEEE, 5147–5156. doi:10.1109/CVPR.2018.00540

CrossRef Full Text | Google Scholar

Wang, R. Y., and Popović, J. (2009). Real-time Hand-Tracking with a Color Glove. ACM Trans. graphics (Tog) 28, 1–8. doi:10.1145/1531326.1531369

CrossRef Full Text | Google Scholar

Xiong, F., Zhang, B., Xiao, Y., Cao, Z., Yu, T., Zhou, J. T., et al. (2019). “A2J: Anchor-To-Joint Regression Network for 3D Articulated Pose Estimation from a Single Depth Image,” in Proceedings of the IEEE International Conference on Computer Vision 2019-October Seoul, Korea: IEEE, 793–802. doi:10.1109/ICCV.2019.00088

CrossRef Full Text | Google Scholar

Yeo, H.-S., Lee, B.-G., and Lim, H. (2015). Hand Tracking and Gesture Recognition System for Human-Computer Interaction Using Low-Cost Hardware. Multimedia Tools Appl. 74, 2687–2715.

CrossRef Full Text | Google Scholar

Yuan, S., Ye, Q., Stenger, B., Jain, S., and Kim, T.-K. (2017). “Bighand2. 2m Benchmark: Hand Pose Dataset and State of the Art Analysis,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2605–2613.

Google Scholar