- 1NASA Goddard Space Flight Center, Greenbelt, MD, United States
- 2Department of Space Studies, Southwest Research Institute, Boulder, CO, United States
Structures in the solar wind result from two basic mechanisms: structures injected or imposed directly by the Sun, and structures formed through processing en route as the solar wind advects outward and fills the heliosphere. On the largest scales, solar structures directly impose heliospheric structures, such as coronal holes imposing high speed streams of solar wind. Transient solar processes can inject large-scale structure directly into the heliosphere as well, such as coronal mass ejections. At the smallest, kinetic scales, the solar wind plasma continually evolves, converting energy into heat, and all structure at these scales is formed en route. “Mesoscale” structures, with scales at 1 AU in the approximate spatial range of 5–10,000 Mm and temporal range of 10 s–7 h, lie in the orders of magnitude gap between the two size-scale extremes. Structures of this size regime are created through both mechanisms. Competition between the imposed and injected structures with turbulent and other evolution leads to complex structuring and dynamics. The goal is to understand this interplay and to determine which type of mesoscale structures dominate the solar wind under which conditions. However, the mesoscale regime is also the region of observation space that is grossly under-sampled. The sparse in situ measurements that currently exist are only able to measure individual instances of discrete structures, and are not capable of following their evolution or spatial extent. Remote imaging has captured global and large scale features and their evolution, but does not yet have the sensitivity to measure most mesoscale structures and their evolution. Similarly, simulations cannot model the global system while simultaneously resolving kinetic effects. It is important to understand the source and evolution of solar wind mesoscale structures because they contain information on how the Sun forms the solar wind, and constrains the physics of turbulent processes. Mesoscale structures also comprise the ground state of space weather, continually buffeting planetary magnetospheres. In this paper we describe the current understanding of the formation and evolution mechanisms of mesoscale structures in the solar wind, their characteristics, implications, and future steps for research progress on this topic.
1 Introduction
The solar corona is comprised of a hot, ≥1 MK plasma that expands outward into the solar system, carrying magnetic field with it, and reaching flow speeds greater than the Alfvén speed. This flow is the solar wind, and defines the heliosphere. The solar wind is not laminar, but is dynamic and filled with structures on many spatial and temporal scales, from the large down through kinetic dissipation scales. The largest scales are directly imposed onto or injected into the solar wind, and include the timescale of solar rotation, the spatial scales associated with the global coronal magnetic field, and phenomena such as coronal mass ejections (CMEs). At the other end of the size spectrum are the smallest scales, those where electron- and ion-scale kinetic physics and dissipation occur, which are all formed through evolution en route. There is a many-orders-of magnitude spread in scale sizes between the large-scale structure and the kinetic dissipation scales of the solar wind (Verscharen et al., 2019). Neither observations nor simulations are currently capable of spanning the mesoscales. We define mesoscales to include this multiple-decade size range that is larger than the dissipation scale and similar plasma scales, and smaller than the largest-scale structures. Unlike the large scale structures, which are always imposed/injected, and the small scale structures, which evolve en route, mesoscale structures can be created through either mechanism. At 1 AU, mesoscales occur between approximately 5–10,000 Mm, or 10 s to 7 h under the assumption that the structures are strictly advecting. For in situ measurements, which measure the solar wind at a single point, the spatial scale is related to the measured temporal scale by L = Vsw ∗ duration, while in images both spatial and temporal scales can be directly measured.
In Figure 1 we show a conceptual view of the full range of scales in the solar wind, and highlight representative examples of solar wind phenomena observed at the different scales. The y-axis shows the range of scale sizes from large-scale to kinetic. From left to right, we provide representative cartoon examples of each scale, example spectral slopes of the measured plasma variations, the corresponding turbulence regime, whether the scales’ creation is dominated by injected/imposed versus evolution, the ability of current observations to measure them, and the ability of current simulations to model them.
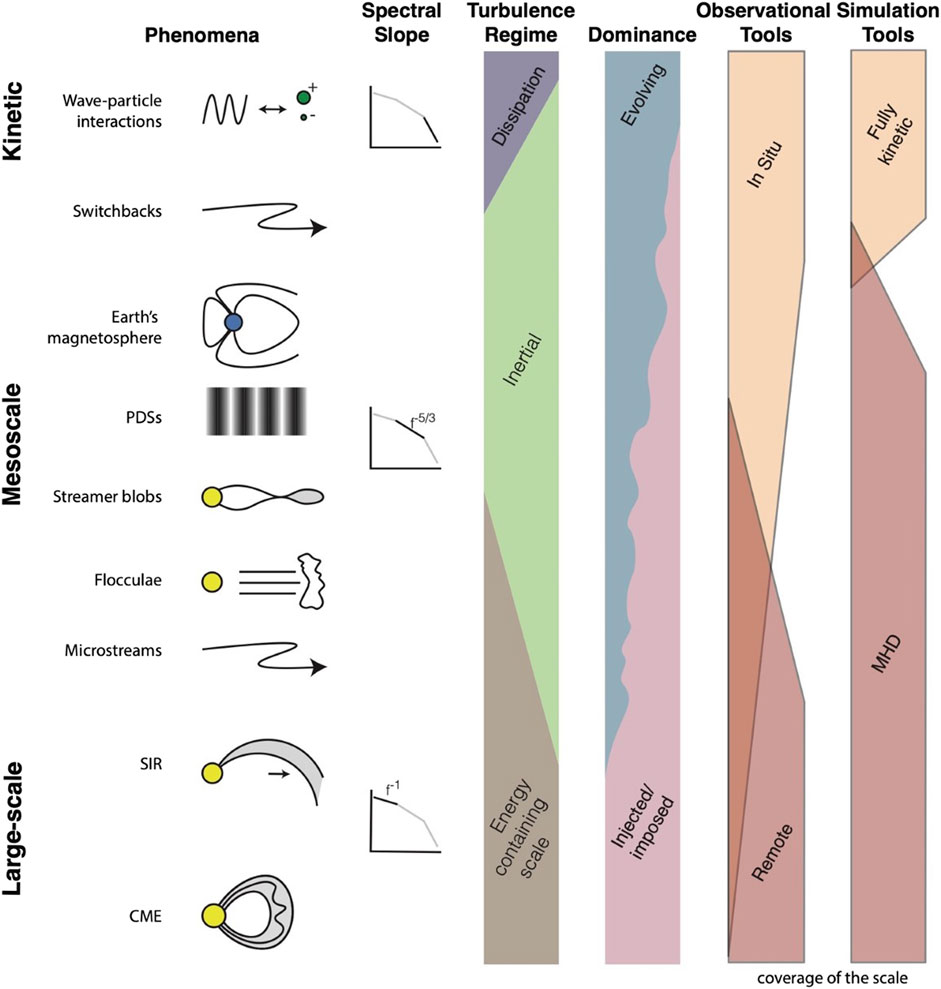
FIGURE 1. The spatial scales of solar wind phenomena span from the kinetic (<the ion inertial length) to a large fraction of the Heliosphere. The three spatial regimes, kinetic, mesoscale, and large-scale roughly parallel the three turbulence regimes, dissipation, inertial, and energy containing. Structure at the large-scale is clearly injected and imposed by the Sun; structure at the smallest scales has evolved en route. Mesoscale structures are created through evolution and injected/imposed, and which mechanism dominates is ambiguous due to insufficient observations (both in situ and remote) and the inability of current numerical simulations to span from kinetic through mesoscales to large-scale.
At the smallest scale lies the kinetic scale, where plasma dynamics and structure are dictated by the motion of individual particles. The transition between the kinetic and the mesoscale is generally considered to be related to the ion inertial length, di, or the ion gyroradius. At 1 AU, the observed break in the spectra of magnetic field fluctuations from the inertial range to the dissipation scales typically is observed to occur at advected time scales of several seconds (Leamon et al., 1999), or equivalently on spatial scales on the order of hundreds of km through a few Mm via the Taylor hypothesis (that spatial crossing time dominates temporal behavior of the solar wind as measured in situ). This scale is close to the proton cyclotron frequency (Verscharen et al., 2019) though multiple mechanisms have been suggested to explain this spectral break (Leamon et al., 1999). Note also that the Taylor hypothesis has limitations in the context of turbulence (Treumann et al., 2019; Bourouaine and Perez, 2020; Perez et al., 2021). At these small scales, all of the structure and dynamics are created as a result of processing and evolution en route to 1 AU. Any injected or imposed structure from the corona begins to evolve on timescales as rapid as the wave-particle interaction time scale (Bruno and Carbone, 2013); structural evolution on small scales has been observed both in-situ (Elliott et al., 2016) and (on larger scales) remotely (DeForest et al., 2015).
The largest scale solar wind structures are all imposed/injected from the Sun. For example, the traditional solar wind separation by speed into “fast” and “slow” wind (Neugebauer and Snyder, 1962; Neugebauer and Snyder, 1966; McComas et al., 1998), are empirically associated with and imposed by the large scale solar structures coronal holes and coronal streamers, respectively. Co-rotating interaction regions (CIR) and stream interaction regions (SIR) form due to adjacent faster and slower wind regions in combination with solar rotation, producing compression regions where the fast wind catches up with the slow, and rarefaction regions behind (Gosling and Pizzo, 1999). This is an example of directly imposed structures that have been observed in white light and tracked to 1 AU using combined STEREO SECCHI Heliospheric imager data and L1 in situ observations (Rouillard et al., 2009; Rouillard et al., 2010a; Rouillard et al., 2010b), and evidence of them survives out to 10 AU (Richardson, 2018).
The transition from the large scale to the mesoscale range is more ambiguous than the transition from small scale to mesoscales. For the purposes of this paper, we define the mesoscales to be the scales at 1 AU at which structures can be both imposed/injected from the Sun as well as generated en route. The upper end is roughly 10,000 Mm (or 7 h), based on observational and theoretical evidence for mesoscale structures that were created in both ways. These sources of mesoscale structure are not mutually exclusive, as structures from the solar atmosphere will also evolve as they advect. Thus, the complexity in this mesoscale regime is a result of the presence of both imposed/injected and evolved structures, and the interplay between them. Determining the fractional amount of mesoscale structures formed through imposed/injected versus evolved is important for understanding both solar wind formation and turbulent evolution, and the answer is likely dependent on solar wind type and radial distance (evolution time) from the Sun.
Mesoscale solar wind structures are important to study for at least three reasons. First, like the solar wind, the Sun is also dynamic and filled with structures of many scales. Many of the spatial structures are imposed directly onto the heliosphere, and many of the transient dynamics are injected directly into the solar wind as it is formed. Thus, the solar wind and its structures contain imprints of the physical processes that heat the corona and that release and accelerate the solar wind (Viall and Borovsky, 2020). In particular, the traditional bimodal solar wind classification by speed overly simplifies the inherent nature and mesoscale structure of the solar wind. Furthermore, the bimodal classification does not account for solar wind observed to be of other “types” with distinct properties (Roberts et al., 2020a), e.g., slow wind that is highly Alfvénic (Roberts et al., 1987; D’Amicis and Bruno, 2015). Rather than only two types of solar wind, solar wind formation can occur via many different pathways, or combinations of physical mechanisms and source locations (Viall and Borovsky, 2020), each of which injects and imposes different structures with unique properties into the solar wind. Some pathways to solar wind formation result in solar wind plasma with properties and mesoscale structures that cannot be interpreted with the simple bimodal classification.
A key aspect of the new framework that allows for many pathways to solar wind formation is that it considers the time history of the solar plasma as it becomes the solar wind. This oft-ignored time history of solar wind formation imparts unique, observable imprints of the physical regime and processes that dominate each step; mesoscale structures can be one of the results. Observations of collisionality (Kasper et al., 2008; Kasper et al., 2017) and composition (Zurbuchen et al., 2002) are also examples where the solar wind exhibits a continuum of states rather than bimodality, and are examples where the time history of the plasma likely influences the resulting solar wind characteristics. The three steps of solar wind formation time history are source, release, and acceleration. The first step is the source of the plasma–i.e., whether it originates from a coronal hole (CH), which are tenuous and cooler, an active region (AR), which are dense and hot, or from the quiet sun (QS), which are of medium temperatures and densities. Separating the solar wind source into these three types of locations in the corona, which themselves are associated with different solar magnetic field configurations and plasma conditions, is essentially an empirical proxy for coronal heating (Viall et al., 2021). The second step is the release of plasma–whether the plasma is on open magnetic field lines, with one footpoint rooted in the Sun and the other already open to the heliosphere, or whether the plasma is on closed magnetic field lines, with both magnetic footpoints rooted in the Sun, requiring reconnection for the plasma to be released into solar wind. The third step is plasma acceleration, a process that continues through the high corona. All three steps can occur through a single physical process, such as turbulence; in such cases, the coronal heating mechanism, solar wind release, and solar wind acceleration all result from the same process (Cranmer et al., 2017). However, whenever the second step is reconnection, then steps one and three are necessarily separate processes because they occur in different physical regimes, thus leaving distinct plasma observables and structures in that parcel of solar wind. This time history of solar wind formation provides the seeding for eventual turbulence, and can also lead to the direct creation of mesoscale structures.
The second reason for studying mesoscales is that as the solar wind advects outward, these structures evolve, decay, and generate new mesoscale structures through turbulence, and thus represent a “laboratory” for studying this fundamental process (Bruno and Carbone, 2013).
The third reason for studying mesoscales is that dynamic solar wind and embedded mesoscale structures continually buffet all of the planets in our solar system, and are the medium through which larger structures and energetic particles propagate. Mesoscale structures and dynamics provide a fundamental transfer of energy from the Sun to Geospace, and constitute the ground-state of space weather–the every-day driving of Geospace that happens even during ambient conditions.
In the next three sections we delve into further detail on structures in the solar wind, represented in Figure 1, and elaborate on the three above-mentioned reasons that understanding mesoscale structures in the solar wind is critical for advancing our understanding of solar wind formation and evolution. In Section 2, we describe evidence of imposed and injected structures that leave imprints of coronal heating, and of the solar wind release and acceleration mechanisms. In Section 3 we describe evidence of turbulent evolution destroying and creating structures. In Section 4 we describe how these different types of mesoscale structures drive dynamics in the magnetosphere. Finally, in Section 5 we discuss the interplay and ambiguity between evolution vs. injection/imposing of these structures, when and under what conditions each mechanism may dominate, and outline potential paths forward for scientific understanding of this complex interconnection.
2 Imposed and Injected Structure in the Solar Wind
Much of the mesoscale structure and variability in the solar wind, especially observed within 1 AU, is imposed and injected from the Sun. For decades, researchers have speculated that many in-situ detected solar wind structures have a solar origin (Crooker et al., 1993; Crooker et al., 1996b), predating observations that were capable of conclusively and routinely differentiating between possible sources. Some fraction of the injected or imposed structures provide the energy for the turbulent cascade, or otherwise evolve as they advect, which we will describe in Section 3. In this section we focus on identifiable structures that are unambiguously of solar origin.
There exist two main observational methods for unambiguously identifying structures that were injected/imposed from the Sun. The first and most direct method is through remote imaging. This is typically done in white light, which is sensitive to electron density and location relative to the Thomson Surface (Vourlidas and Howard, 2006; Howard and DeForest, 2012), or extreme ultraviolet (EUV) emission, which is sensitive to electron density squared and is a function of temperature. When remote images exist with sufficient cadence and coverage, structures can be tracked in time from the solar corona as they accelerate outward into the solar wind (Sheeley et al., 1999; Viall et al., 2010; Viall and Vourlidas, 2015-07; DeForest et al., 2016; Alzate and Morgan, 2017; Rouillard et al., 2020; Alzate et al., 2021).
The second method is to use in situ observations of ionic and charge state composition. These quantities are frozen into the plasma at heights in the corona at which the collisional ionization and recombination rates are small. Therefore, above these heights these properties do not evolve, thus compositional changes observed in situ indicate that the structure was formed in the chromosphere and/or corona. The ionic charge states are generally frozen in by 1.5–3 solar radii, but some elements are not frozen in until as high as four or five solar radii (Landi et al., 2012). The relative abundance of elements with low first ionization potential (FIP) are set lower down in the chromosphere and a relative enhancement of the abundance of low FIP elements is an indicator of plasma release from the closed field corona (Peter, 1998; Laming, 2015). Recent theoretical work argues that the relative abundance of the element sulfur may be a unique indicator of the release of plasma from previously closed-magnetic field lines (Laming et al., 2019). The relative amount of ions as a function of mass can also change in the corona through gravitational effects (Raymond et al., 1997; Weberg et al., 2012-11). This could be the result of closed magnetic field lines with flows that are small enough such that gravitational settling occurs (Feldman et al., 1998). The relative amount of He 2++, or alpha/proton (AHe) ratio is also set in the solar atmosphere, but it is currently unknown which physical mechanism(s) determines the final ratio observed in the solar wind. AHe could be the result of mass dependent processes, particularly when closed field lines open to the solar wind, and lighter protons escape faster than alpha particles (Endeve et al., 2005-05). Currently, observations indicate that AHe is largely the result of FIP fractionation through the chromosphere (Rakowski and Laming, 2012), with an AHe “shutoff” (a rapid depletion in AHe) occurring prior to solar cycle onset that is likely the result of a mechanism near or below the photosphere (Alterman et al., 2021). In summary, the nature of the compositional change are linked to the physical processes involved in creating the solar wind and mesoscale structures that are injected/imposed from the Sun. Thus, such mesoscale structures contain imprints of the physical mechanisms that heat the solar corona and release and accelerate the solar wind.
Related, although specific entropy (T/nγ) is not a conserved quantity, as it evolves with distance from the Sun, it is anticorrelated with the conserved quantity of charge state and therefore it can also be used as a proxy indicator of imposed or injected structures (Pagel et al., 2004). Likewise, temperature changes, which are not conserved, can be used when observed close to the Sun as a tracer of solar-created structures by the release of hotter plasma from closed-magnetic field lines on the sun through reconnection (Stansby and Horbury, 2018; DiMatteo et al., 2019). For example, in recent work on mesoscale-sized patches of switchbacks using data from Parker Solar Probe, (Woodham et al., 2020) argued that, based on enhanced T‖ in the patches relative to their surroundings, the patches themselves could be structure injected from reconnection in the solar corona.
In a few isolated cases, which we describe in the examples below, it has been possible to directly link remote observations with in situ measurements of injected and imposed mesoscale structures and follow them from their creation at the Sun out into the Heliosphere. However, in most cases it is unknown how far out into the heliosphere the remotely observed structures survive. Likewise, even when compositional changes observed in situ indicate a solar creation mechanism, it is usually not known precisely which solar structures created the in situ-determined structures. When mesoscale structures are observed without compositional variations, their source is ambiguous, and could have been due to evolution en route, or imposed/injected structure. Thus, most connections between specific in situ phenomena and remote phenomena are qualitative.
The largest structure that the Sun imposes on the Heliosphere is that of its magnetic field, in which the global magnetic polarity inversion line in the corona results in the structure of the Heliospheric Current Sheet (HCS). As the solar cycle progresses, the Sun’s magnetic field becomes more complex, and can even form multiple HCSs. The HCS as a structure imposed from the Sun was confirmed through predictions using the magnetic field extrapolated from the photospheric measurements (Hoeksema et al., 1983) as well as with the AHe changes associated with the HCS (Gosling et al., 1981). There is evidence that the Sun also imposes spatial structures on mesoscales that survive at least through the inner heliosphere, and possibly out as far as Ulysses measurements (1–5 AU). The complexity of the photospheric magnetic field produces a web of separatrices, the S-web, (Antiochos et al., 2011; Linker et al., 2011; Titov et al., 2011; Pontin and Wyper, 2015) in the solar corona on mesoscales. Separatrices in the corona are regions where reconnection-released solar wind is most likely to occur. Thus, the imprint of the spatial structure of the S-web is predicted to impose boundaries between reconnection-released wind and open-field wind in the heliosphere on mesoscales (Crooker et al., 2004; Crooker and McPherron, 2012; Aslanyan et al., 2021). Recent simulations of interchange reconnection, which is induced at the lanes between cells of magnetic footpoint driving, predict that remnants of the scale size and pattern of photospheric driving by supergranular flows should be imposed along S-web corridors and into the solar wind (Aslanyan et al., 2021).
Another example of imposed mesoscale structure may be a type of pressure balance structure (PBS) observed by Ulysses, in which the changes in plasma pressure are approximately balanced by the changes in magnetic pressure and have a timescale of less than a day (McComas et al., 1995). There is evidence that polar plumes observed in polar coronal holes may be imposing these heliospheric counterparts as imprints in the polar solar wind (Poletto, 2015). Even in the ecliptic, fast speed streams observed by Helios also showed evidence of PBSs that were correlated with those expected from a superradial expansion of plumes into the heliosphere (Thieme et al., 1989; Thieme et al., 1990). Though PBSs can also be created through mechanisms en route such as slow mode waves (Yao et al., 2013a; Yao et al., 2013b), the high beta portion of the type of PBSs observed by Ulysses were highly correlated with AHe, and therefore likely of solar origin (Reisenfeld et al., 1999). Given the association of the observations with high latitudes during solar minimum (and therefore likely polar coronal holes), and the association with the high beta portion of the structures, (Reisenfeld et al., 1999) suggested that the structures were polar plume extensions. However, the structures’ observed frequency did not follow the expected frequency vs. latitude distribution for co-rotating features, and PBS signatures may also be susceptible to instability and mixing (Parhi et al., 1999).
Towards the middle range of the mesoscales, (Borovsky, 2008) studied the scale size of flux tubes observed at 1 AU and found a median scale size of ∼440 Mm, and suggested that they were fossilized structures imposed by structures from the Sun. (Borovsky, 2016) examined what they classified as “unperturbed coronal hole plasma” between 0.3 and 2.3 AU and found the plasma to be structured in many of its components, including in AHe and proton specific entropy variations, confirming a solar source to much of the coronal hole wind variability. They argued the radial size scales measured at the spacecraft correspond to longitudinal scales at the Sun as a result of solar rotation. Assuming this geometry, they concluded that the longitudinal scales of the corresponding structures at the Sun would be a significant fraction of a supergranule (which are 30–35 Mm diameter in the photosphere). Thus, they could be due to open magnetic field funnels imposing structure on the solar wind. Examining the boundaries between these mesoscale structures, (Borovsky, 2020b) showed that discontinuous changes in AHe are correlated with discontinuities in the magnetic field direction, i.e., current sheets. They showed that this correlation applies to all types of solar wind, and that the discontinuities are weaker away from the changes in AHe. Lastly, they showed that sharp changes in electron strahl intensity also corresponded to larger discontinuities in the magnetic field direction. Together, these observations support the interpretation that much of the mesoscale structure in the solar wind is likely imposed flux-tube structure from the solar corona.
There are also time-dynamic processes in the solar atmosphere that inject structure into the solar wind and heliosphere. The largest injected transient structures are CMEs. These are explosive events that can have speeds of up to thousands of km/s. They involve the buildup and release of magnetic energy at a magnetic polarity inversion line. Though large CMEs are generally considered to be created by different phenomena than the ambient solar wind, the same mechanism of magnetic energy build up at a polarity inversion line and subsequent release that creates CMEs is likely also responsible for a spectrum of mesoscale structures in the solar corona from pseudostreamer jets (Kumar et al., 2021) down to small X-ray and EUV jets (Sterling et al., 2015; Wyper et al., 2017). It is predicted that such jets in polar coronal holes could inject mesoscale structures into the solar wind that could be observed in the near-Sun environment with Parker Solar Probe (Roberts et al., 2018). However, based on empirically-determined jet rates and filling factors (Savcheva et al., 2007; Sako et al., 2013), (Roberts et al., 2018) estimated that Parker Solar Probe would only encounter an average coronal hole jet about once in 50–100 days of observations. While it is currently unknown how far out into the heliosphere distinguishable jet signatures survive, it has long been thought that microstreams observed in Ulysses could be remnants of x-ray or EUV jets. Microstreams have velocities ± 35 km/s relative to background, last 6 h or longer, and occur in conjunction with large angle magnetic discontinuities. They have higher kinetic temperatures, proton flux, and a slight enhancement of low FIP elements compared to the average fast solar wind. The compositional changes associated with microstreams indicate a solar origin (Neugebauer et al., 1995; Neugebauer et al., 1997). (Neugebauer, 2012) argued specifically for coronal x-ray jets as the solar source, but polar plumes are also a possibility due to their association with x-ray jets (Neugebauer et al., 1997; Poletto, 2015). Using simulations of jets, (Karpen et al., 2016) demonstrated that the associated Alfvén wave and density and velocity enhancements produced by jets are sustained through the outer corona, and are consistent with in situ observations of microstreams. Similarly, (Velli et al., 2011) simulated polar plumes and demonstrated that the observed velocity increase in microstreams could be explained by different heat deposition in plumes. Evidence suggests that plumes are driven by jetting activity at their base (Raouafi et al., 2016), thus for progress it is likely necessary to treat x-ray jets and plumes as different observable manifestations of a common process.
At the large scales, but at slower speeds, are slow helmet streamer blowout CMEs, a subset of which are the so-called “stealth” CMEs, that do not have an obvious signature in the low corona (Howard and Tappin, 2008; Robbrecht et al., 2009). Stealth CMEs originate higher up in the corona, are slow (about 300 km/s) (Ma et al., 2010; Howard and Harrison, 2013), and, though “stealthy,” their connection through the global-scale coronal magnetic field to the low corona can be identified through advanced image processing (Alzate and Morgan, 2017). (Lynch et al., 2016) modeled a stealth CME by imposing a large scale global shear meant to represent the effects of differential rotation on the global coronal magnetic field. They showed that the footpoint energization in such driving takes place across the polarity inversion line associated with the HCS and helmet streamers, as opposed to a polarity inversion line in an active region.
As with explosive CMEs, streamer blowout CMEs likely also represent the large end of a continuum of structures created through a common physical mechanism. There is an abundance of mesoscale structures that are also associated with the HCS. (Crooker et al., 1993; Crooker et al., 1996a) identified mesoscale structures within the HCS in situ at L1, which they demonstrated could not be due to a wavy HCS traversed by the spacecraft. Instead, they suggested a solar source to the structures because the observed structures were consistent with tangled flux ropes, and flux ropes are generally considered a signature of reconnection. (Suess et al., 2009) expanded on prior in situ studies of the AHe depletions occurring at the HCS, and showed that the AHe changes are not centered on the HCS. The offset AHe changes are consistent with solar reconnection-injected structure near the HCS, rather than a static HCS. Thus, the imposed large scale structure of the HCS is also comprised of injected structures at mesoscales; this picture is most recently confirmed by Parker Solar Probe in situ observations close to the Sun (Lavraud et al., 2020). Also consistent with this picture, mesoscale plasma blobs are observed in remote white light imaging to be released from the tips of helmet streamers on scales of many hours (Sheeley et al., 1997; Wang et al., 1998; Wang et al., 2000; Harrison et al., 2009; Rouillard et al., 2009; Sheeley and Rouillard, 2010). Their continued acceleration is observed out to 30 solar radii, where they reach typical speeds of around 300 km/s. In some cases, streamer blobs have been tracked from their helmet streamer release out to their observation in situ at 1 AU (Rouillard et al., 2010a; Rouillard et al., 2010b), and Parker Solar Probe in situ data taken around 30 solar radii (Rouillard et al., 2020). Reconnection at the helmet streamer seems to be fundamental to the release of blobs. Observations in white light of raining inflows (Sheeley et al., 1997; Wang et al., 2000) and the dipolarizations associated with blobs (Sanchez-Diaz et al., 2017), suggests that the reconnection often occurs around four to five solar radii. MHD models (Higginson and Lynch, 2018; Lynch, 2020) and 2D thermal models (Allred and MacNeice, 2015; Endeve et al., 2005-05) also show that helmet streamer tips are dynamic and prone to reconnection. This general picture of streamer reconnection led (Lynch et al., 2016) to argue that stealth CMEs represents the middle of the continuum between fast CMEs and mesoscale helmet streamer blobs, wherein the same universal process of shear across a polarity inversion line leads to reconnection-released plasma into the heliosphere.
On mesoscales of tens of minutes to a couple of hours are puffs and periodic density structures. Some of these have been observed in white light images to originate at the Sun as low as 2.5 solar radii, and can be followed out to about 50 solar radii (Sheeley et al., 1997; Viall et al., 2010; Viall and Vourlidas, 2015-07; DeForest et al., 2016; DeForest et al., 2018). As with helmet streamer blobs, periodic density structures occur preferentially near the HCS (Viall and Vourlidas, 2015-07). They occur at several characteristic scales, including 90 min (Viall and Vourlidas, 2015-07) and shorter (DeForest et al., 2018). In a simulation of reconnection at the helmet streamer, (Réville et al., 2020) demonstrated that periodic density structures at the HCS could be the result of the tearing mode. On the other hand, (Allred and MacNeice, 2015) and (Schlenker et al., 2021) argued that the periodicity was determined by the interplay between heating and expansion of the last closed field lines, and the retraction of field lines after reconnection. (Pylaev et al., 2017) argued for a third mechanism, wherein a standing shock at the 90 min acoustic cutoff frequency of the corona drives reconnection. Regardless of the precise mechanism, the timescale of the resulting density structures is a constraint on how magnetic reconnection occurs at the helmet streamers. With limitations of current remote white light instruments in terms of sensitivity, and temporal and spatial resolution, periodic density structures are too small and faint to see in more tenuous wind outside of streamers, or beyond about 50 Rsun where the density and associated signal is too weak. However, (DiMatteo et al., 2019) identified several instances of 90 min periodic density structures at the HCS close to the Sun in Helios data. They were associated with temperature changes, and thus determined to be of solar origin. At 1 AU, (Kepko et al., 2016) showed an example of 90 min periodic density structures associated with compositional changes, and (Viall et al., 2009b) showed an example of 30 min periodic density structures associated with AHe changes. Thus, at least some periodic density structures survive through the inner heliosphere. Both (Kepko et al., 2016) and (DiMatteo et al., 2019) showed evidence that at least one of the structures in the periodic density train was a flux rope, and so consistent with reconnection as their formation mechanism.
More generally, mesoscale structures in the heliosphere away from the HCS are expected as a result of interchange reconnection at the boundaries between open and closed fields or S-web arcs (Higginson et al., 2017a; Higginson et al., 2017b). Indeed, (Mason et al., 2019) observed evidence of interchange reconnection at a null-point topology (i.e., a distinct closed magnetic field structure from the helmet streamer) in the corona. With current sensitivity limitations in EUV data, it was not possible to see the solar wind outflows associated with the reconnection. In one event of periodic density structures observed close to the Sun by Helios, the solar coronal source was confirmed via concurrent temperature changes, and the location was determined to be far from the HCS, an important test of the S-web theory of reconnection-released solar wind (DiMatteo et al., 2019). Analyzing 25 years of Wind solar wind density data, (Kepko et al., 2020) identified periodic density structures in all types of solar wind, including fast, ecliptic wind. They occurred at particular timescales, or equivalent radial length scales, that were associated with the solar cycle, and the terminator (McIntosh et al., 2019). Since the 25 years Wind study used all periodic density structures that were identified, without testing for associated compositional changes, it is possible that not all of those were created at the Sun. Even for those that are, further investigation is required to determine if their properties are a function of different types of solar wind sources, e.g. reconnection at the HCS versus other S-web arcs.
3 Turbulent Structuring in the Solar Wind
Structuring and/or destruction of mesoscale solar wind structures can also occur through turbulence. As Figure 1 shows, the scales of observed solar wind mesoscales also correspond to the energy containing and inertial range scales expected from turbulence. Both fluid and MHD turbulence are driven by nonlinearities represented by the underlying equations of motion. These nonlinearities lead to cross-scale cascades of energy first described by Kolmogorov (1941) and Kraichnan (1967) and treated by many authors (Frisch, 1995; Bruno and Carbone, 2013). The turbulent cascade carries energy and structure from the large energy-containing scale through a very broad inertial range of scales (roughly encompassing the mesoscales defined above) that are dominated by the turbulent cascade, to a dissipation scale where the energy becomes a source of heat (Leamon et al., 1998). In the case of the solar wind, the energy containing scales are determined by dynamics and structure of the corona itself (Tu and Marsch, 1995; Chae et al., 1998; Cranmer et al., 1999). A large variety of mechanisms including hydrodynamics, MHD modes, and magnetic reconnection, can give rise to turbulent cascades; once the system develops a cross-scale energy cascade and characteristic spectral power-law signature, it is considered “turbulent” regardless of the specific mechanism. The importance of a cross-scale cascade is that it gives rise to perturbations in all major measurable parameters of the flow, including density, velocity and magnetic fields, and other structural identifiers. The specific relationship between different types of perturbation depends on the mechanism itself.
There are many lines of evidence indicating that the solar wind is processed by turbulence as it moves through the solar system, e.g., see review by (Matthaeus and Velli, 2011). To measure the turbulence properties using in situ data requires the inclusion of the Taylor approximation that the dominant source of variability is spatial structures sweeping over the spacecraft. Therefore, time spectra yield equivalent spatial spectra of perturbations in all major wind parameters (Matthaeus and Velli, 2011); the validity of the Taylor approximation is also corroborated by multi-spacecraft measurements of at least some coherence parameters (e.g., Matthaeus et al. (2005)). That corroboration is important, because the Taylor approximation is known to be limited in the context of turbulence (Klein et al., 2014; Bandyopadhyay et al., 2020).
The presence of a turbulent cascade at 1 AU has long been inferred from time spectra of in situ measurements (Coleman, 1966; Horbury et al., 2005). Comparisons of the magnetic field spectra measurements show that the break point between the energy containing scales and the inertial range evolves with distance from the Sun. In the fast wind, this break point occurs near 10 mHz at 0.3 AU and steadily evolves to lower frequencies at larger distances of less than 0.1 mHz at 4.8 AU (Bruno et al., 2009; Bruno and Carbone, 2013). Those results also showed that the slow wind is not observed to have a corresponding break between the inertial and energy containing scales, but more recent results with Parker Solar Probe show that the slow wind has a break to energy containing scales, but at a lower frequency than the fast wind (Chen et al., 2021).
The correlation length is often used to define the large end of the inertial range of scale, under the assumption that it represents the largest scale of turbulent eddies. Multi-spacecraft measurements have yielded 1,000–2000 Mm as the correlation scale at 1 AU (Matthaeus et al., 2005), corresponding to 1–2 h crossing time, although the measurement itself is sensitive to analysis technique (Isaacs et al., 2015) and may be longer. While in-situ measurements are limited to statistical analyses of the overall character of the solar wind, imaging measurements afford direct detection of individual features. The coherence length result is corroborated by test particle analysis using features in comet Encke’s tail (DeForest et al., 2015), which also identified an eddy size scale of approximately 1,000–2000 Mm (i.e., with roughly 90 min crossing time) at 1AU. However, the comet tail result may be affected by a turbulent “vortex street” from interaction between the solar wind and the comet (Nisticò et al., 2018), and therefore may differ from the turbulent field of the bulk solar wind itself. This uncertainty associated with the characteristic coherence length is reflective of the difficulty of measuring the “native” solar wind flow. While ample spectral signatures indicate the presence of a turbulent cascade, definitively measuring the spectral limits of the cascade - and therefore the dominant processes affecting solar wind variability at different scales - remains an open problem, in part because different solar wind parameters yield different spectral characteristics (Bruno and Carbone, 2013).
In addition to direct spectral measurements and correlation lengths, several other key results demonstrate that the statistical characteristics of the solar wind evolve with propagation, approaching a state consistent with turbulent processing. Tracing of the cross-helicity evolution with distance from the Sun provided one of the first clear lines of evidence that nonlinear dynamical evolution occurs in the solar wind (Roberts et al., 1987). More recently (Telloni et al., 2021) measured a stream of solar wind at 0.1 and 1.0 AU and showed that the magnetic spectral density, flatness, and higher order moment scaling laws were consistent with Alfvénic fluctuations near the Sun evolving into fully developed turbulence. Similarly, (Chen et al., 2020) showed that turbulence evolves between 0.17 and 1 AU: at 0.17 AU the data showed increased energy spectral density, a slope of −3/2, lower magnetic compressibility, and increased relative amount of outward propagating Alfvénic fluctuations compared to inward. Close to the Sun, both the magnetic field and velocity spectra have a slope of −3/2, but only the magnetic spectra is observed to steepen with distance, and the outward dominance of the Alfvénic fluctuations is observed to decrease with distance (Chen et al., 2021; Shi et al., 2021). The evolution of the outward wave dominance as well as the evolution of the spectral break point with distance is supported by MHD simulations of turbulence (Roberts et al., 1991). As physics-based models of turbulence become more complex, they are able to reproduce many of the observed characteristics of the solar wind (Roberts and Ofman, 2019; Adhikari et al., 2021).
The dissipation scale, which defines the small-scale end of the turbulent inertial range of scales, varies with plasma condition and with distance from the Sun; a useful benchmark at 1 AU is 2 s (Leamon et al., 1998), or approximately 600 km. At scales much smaller than this, the spectrum steepens as kinetic phenomena convert the perturbations to fully randomized heat. More recent work has demonstrated that the relationship between temperature and velocity evolves with distance in a way that is consistent with turbulent processing (Elliott et al., 2012; Lionello et al., 2014). Entropy also increases and has less variability with distance, indicating heating and turbulent processing (Roberts et al., 2005). The so-called switchbacks observed by Parker Solar Probe exhibit different break scales between inertial and dissipation scales and increased level of intermittency than the surrounding wind, perhaps contributing to the turbulent heating in the inner heliosphere (Martinović et al., 2021).
Importantly for the purposes of this paper, active turbulence would process any injected or imposed mesoscale structures from the Sun. A general trend of processing and statistical modification is observed to continue to over 30 AU as solar wind features are “worn down” by dynamic interaction with other parcels of wind (Elliott et al., 2016). The solar wind at 0.33 AU was observed with the Helios spacecraft to contain more and sharper spikes in velocity (Horbury et al., 2018) than further away from the Sun, and the trend continues inward to the corona itself in the form of switchbacks observed by Parker Solar Probe (Bale et al., 2019; Kasper et al., 2019). Indeed, the microstreams observed by Ulysses - likely related to the larger of the switchbacks that do survive - are themselves observed to evolve in distance from the Sun (Reisenfeld et al., 1999). This corroborates the picture of a solar wind whose structure evolves from the “young” state with spatial and temporal structure injected by coronal processes, to a more processed state that reflects the observed turbulent spectrum further from the Sun.
There is also evidence that turbulence generates new structures in the solar wind on mesoscales. As one example, there is an active debate as to whether the switchbacks observed by Parker Solar Probe (and described above) are created through turbulence or not, with many arguing that their observed characteristics are consistent with turbulent formation (Squire et al., 2020; Tenerani et al., 2020; Shoda et al., 2021). In another example, work by (DeForest et al., 2016) showed that at least some compact bright features in the images form in the solar wind as it propagates. They identified “flocculae” that are observed to “fade in” to the overall flow between 20 and 80 solar radii from the Sun (see Figure 1). Typical flocculae are oblong: about the same size as streamer puffs (∼1 solar radius at 30 solar radii altitude) but 3x–10x wider. These have been interpreted as signs of the isotropization of shear-driven turbulence (Chhiber et al., 2019), which may arise locally or be excited as anisotropic magnetically-guided turbulence carried from the outer corona itself (Cranmer, 2012; Cranmer and Woolsey, 2015; Oughton et al., 2015). Similarly, analysis of Helios data showed that the heliospheric current sheet becomes more complex with distance, as indicated by more current-sheet crossings (Roberts et al., 2005). In contrast, a statistical analysis of Helios, IMP8, Wind, ACE and Ulysses data also showed that the occurrence rate of flux ropes in the HCS decreases in frequency and and flux ropes are larger in size with distance from the Sun (Cartwright and Moldwin, 2008; Cartwright and Moldwin, 2010), indicating that they likely merge.
Taken as a whole, these results indicate that solar wind is turbulent. Structure at or below 1,000 Mm observed at 1 AU are well within the turbulent cascade, in a sequence that begins with both spatial and temporal driving in the corona and processes the imprinted structure through turbulent evolution of shear flows and eddies. Large-scale turbulent eddies appear to form and be isotropized at or shortly above the transition from the low-β corona to moderate-β solar wind, likely about 0.3 AU from the Sun (DeForest et al., 2016), and the cascade appears to fully develop between this distance and 1 AU although the turbulence may remain anisotropic toward the smaller-scale end of the inertial range (Bruno and Carbone, 2013). However, many injected and imposed structures observed on scales of tens of minutes and scales of hundreds to several thousand Mm have been observed to survive to at least 1 AU. We return to the inherent ambiguity of these results and its interpretation in the context of mesoscale structures in Section 5.
4 Magnetospheric Impact of Structures
The structured solar wind impacts the magnetosphere in several ways. The solar wind dynamic pressure,
Large scale solar wind structures, such as CIRs or SIRs that form when a faster wind overtakes a slower wind, are important drivers of magnetospheric activity (Gosling and Pizzo, 1999; Tsurutani et al., 2006; Kilpua et al., 2017). In particular, for Earth’s radiation belts it has been recognized for decades that there is a strong correlation between solar wind speed and the flux of relativistic electrons, particularly in the outer zone and for Vsw > 500 km/s (Paulikas and Blake, 1979; Miyoshi and Kataoka, 2005; Borovsky and Denton, 2006; Bortnik et al., 2006; Yuan and Zong, 2012). While CMEs are often considered to be large drivers of space weather, SIR-driven geomagnetic storms often exhibit higher fluxes of radiation belt electrons compared to CME-driven storms (Borovsky and Denton, 2006; Kataoka and Miyoshi, 2006; Kilpua et al., 2015; Turner et al., 2019), especially at larger radial distances (>4.5 RE) and during the declining phase of the solar cycle. The general process of radiation belt enhancements is energization via local chorus waves combined with radial diffusion (see review by Li and Hudson (2019)). While the comparatively long overall SIR scale is important for radiation belt flux enhancements, the mesoscale structures embedded within that large scale structure appear to be an important contributor as well. The compression region between the fast and slow wind is filled with dynamic pressure fluctuations that provide a source of broadband compressional power that drives magnetospheric ultra low frequency (ULF) waves (Kilpua et al., 2013; Kepko and Viall, 2019). ULF waves are known to be an important magnetospheric process that can lead to enhanced radial diffusion, energization, or even loss to atmospheric precipitation. When combined with high solar wind dynamic pressure, this externally driven ULF wave activity can scatter electrons to large radial distances where they can fill a broad region of the radiation belts, or can be lost due to magnetopause shadowing (Turner et al., 2012; Hietala et al., 2014). The entire SIR driving of the magnetosphere can take several days, with the loss of outer zone electrons apparently more dominant during the early part of the SIR, and a net increase in the flux of energetic electrons over the course of the entire SIR event. This highlights the importance of understanding all of the mesoscale aspects of solar wind driving within large scale events.
The subset of mesoscale structure that manifest as periodic density structures are of particular interest for magnetospheric dynamics, because they can drive magnetospheric ULF pulsations at discrete periodicities for extended intervals. There is now a substantial body of research demonstrating magnetospheric pulsations that are directly-driven by solar wind periodic density structures (Kepko et al., 2002; Stephenson and Walker, 2002; Kepko and Spence, 2003; Viall et al., 2009a; Villante et al., 2013; DiMatteo and Villante, 2017). This includes observations of solar wind-driven pulsations in ground magnetometer data (Villante and Tiberi, 2016), high latitude ionospheric radar observations (Fenrich and Waters, 2008), polar UV imaging data (Liou et al., 2008), and even the equatorial ionosphere (Dyrud et al., 2008). MHD simulations have confirmed that cyclic solar wind dynamic pressure structures directly drive magnetospheric oscillations, and locations of field line resonance will even amplify the waves (Claudepierre et al., 2010; Hartinger et al., 2014). The apparent frequencies of periodic density structures in the frame of the magnetosphere is often between 0.5 and 4 mHz (Viall et al., 2009a; Kepko et al., 2020), which is similar to the drift period of radiation belt particles. Kepko and Viall (2019) showed an event where radiation belt particles were precipitating to the atmosphere with a periodicity determined by the solar wind periodic density driver. Recent work utilizing Balloon Array for Radiation-belt Relativistic Electron Losses (BARREL) measurements of particle precipitation suggests an association between solar wind periodic density structures and electromagnetic ion cyclotron (EMIC) wave power enhancements, which scatters energetic electrons into the loss cone where they are then lost to Earth’s atmosphere (Breneman et al., 2020).
An additional mesoscale solar wind structure-magnetosphere interaction that needs to be considered are intervals of large interplanetary magnetic field (IMF) that could lead to enhanced reconnection at the dayside magnetopause. Earth’s magnetic field points northward at the magnetopause, and therefore when the IMF has a large southward component (Bsouth), magnetic reconnection is likely to occur. Dayside magnetic reconnection is the primary mechanism by which solar wind energy enters the magnetosphere, and is the ultimate source of much of the dynamics that occur, including geomagnetic storms and substorms. High speed solar wind (>750 km/s) is known to be dominated by large amplitude Alfvén waves (Tsurutani et al., 1994). Within SIRs, these Alfvén waves are compressed and increase in amplitude as the high speed flow impinges upon the slower flow ahead, leading to a pile-up of large amplitude fluctuations in solar wind IMF Bsouth. The combination of high solar wind speed, density, and Bsouth often leads to intense geomagnetic activity. The auroral activity driven by this solar wind interaction has been termed High Intensity Long Duration Continuous AE Activity (HILDCAA) (Tsurutani and Gonzalez, 1987). The relationship between these large amplitude Alfvén waves and the mesocale density structures that are also inherent to SIRs is an area ripe for study.
In some ways, the magnetospheric impact of solar wind structures is independent of whether the solar wind structures are injected/imposed versus formed en route through turbulence. On the other hand, while turbulence and coronal processes can both produce mesoscale structures in the geoeffective size scale range of 100 Mm and greater, coronal processes may produce mesoscale structures with different properties. For example, it seems that unique processes in the corona make them periodic (Kepko et al., 2016; Viall et al., 2009b; Viall and Vourlidas, 2015-07). In another example, (Kepko and Viall, 2019) demonstrated that SIRs compress and amplify existing periodic density structures in the slow wind, thereby increasing their impact on Earth’s magnetosphere. This is a clear example of where both the injection mechanisms and evolution impacted Earth’s response. In summary, for full predictability of space weather at Earth and the nature of the magnetospheric driving, it is important to understand how much and which types of mesoscale structures are formed through turbulence, or injected/imposed from the solar corona.
5 Discussion
Figure 1 describes the phenomenological structure in the solar wind, from kinetic through mesoscale to large-scale. The turbulence regimes discussed in Section 3, and the injected and imposed structures from the Sun discussed in Section 2, both produce solar wind structures at mesoscales. There is a clear interplay between imposed and injected structure, the evolution of such structure en route to 1 AU, and turbulence creating new structures, all of which comprise the zoo of mesoscale structures at 1 AU. The goal is to understand this interplay and to determine which type of structures dominate the solar wind under which conditions.
5.1 Differentiating Injected/Imposed vs. Turbulent Structure
There exist many solar wind phenomena on mesoscales for which we cannot determine with certainty whether the associated structures are injected/imposed or are generated en route. As Figure 1 shows, this is due to lack of both in situ and remote observations as well as a lack of applicable models with simultaneous coverage and resolution. Many observations are non-unique to either formation process. When structures are observed in situ without compositional changes or a direct link to tracked structures in images, their source is ambiguous, and could have been created via either mechanism (Owens et al., 2011).
Correlation lengths and power law spectra are commonly interpreted in terms of turbulence. However, many physical processes, e.g., any autoregressive process, can result in power law spectra and correlation lengths. Time series of discontinuities can produce a power law with a slope of −5/3 (Borovsky, 2010). There is strong evidence (Borovsky and Burkholder, 2020) that the high frequency end of the magnetic power spectra corresponds to the break point associated with the thickness of the current sheets at strong tangential discontinuities, and the amplitude is associated with the time between current sheets. Likewise, turbulence or other nonlinear processes are likely involved in heating the solar corona (Rappazzo et al., 2008; Cranmer et al., 2017; Klimchuk and Antiochos, 2021). If such mechanisms also affect the creation of the structures in the solar wind, then the spectra and correlation lengths could reflect the remnants of that process, rather than actively evolving turbulence (Viall and Borovsky, 2020). Related, the spectra of velocity, magnetic field, and density each have different spectral slopes, which flatten differently, and different break points (Roberts, 2010; Šafránková et al., 2015). Caution should be taken when inferring the properties of variability in one plasma parameter from the properties of variability in the others. These considerations, together with the evidence of continued wind processing with distance (Elliott et al., 2016), yield an ambiguous picture: there is no clear indicator that either turbulence or solar structuring is the primary driver of solar wind mesoscale structure far from the Sun itself.
There do exist indications that both solar and turbulent processes are important to shaping the solar wind. For example, as described in Section 2, there is a population of in-situ detected magnetic flux ropes that have been observed simultaneously in white light that are unambiguously formed at the helmet streamer tip through reconnection and advect along the HCS. But the population of all flux ropes in the solar wind, including those at the HCS, could also be due to turbulence (Cartwright and Moldwin, 2008; Cartwright and Moldwin, 2010; Zheng and Hu, 2018; Zhou et al., 2021), and there is evidence that both populations of flux ropes exist in the inner heliosphere (Murphy et al., 2020). Active reconnection is observed to be taking place far out into the solar wind (Gosling and Szabo, 2008), and reconnection across the HCS is very prevalent close to the Sun (Phan et al., 2021), as well as at the boundaries of switchbacks (Froment et al., 2021). This determination is itself subject to discussion: flux rope identification in situ is a difficult problem, and different criteria can result in very different event lists (Feng et al., 2007). Torsional Alfvén waves injected from the Sun, for example, can share properties with flux ropes (Higginson and Lynch, 2018), and flux ropes, plasmoids and magnetic islands can exhibit similar features in the data (Khabarova et al., 2021). Furthermore, turbulent processing is nearly certain to shred and/or merge existing flux tubes or flux ropes in a process analogous to the “magnetochemistry” observed in the photospheric magnetic field (Schrijver et al., 1997), further emphasizing the need for cross-scale measurements to identify those processes.
Switchbacks are another example of mesoscale structures that could be remnants of reconnection at the Sun, or shear flows from structure at the Sun, or turbulence. (Martinović et al., 2021) presented evidence of their formation via turbulence, while (Larosa et al., 2021) argue for the firehose instability to play a role, since only 73% of switchbacks are Alfvénic. (Drake et al., 2021) argue that switchbacks are the result of flux ropes created through interchange reconnection in the corona, and (Tenerani et al., 2020) modeled switchbacks and showed that they persist for up to hundreds of Alfvén crossing times, and thus could be formed in the corona. To date, no single model has been able to explain all the observed features of switchbacks, and the struggle has been to identify unique distinguishing observations that could differentiate the generation mechanisms. It is possible that multiple mechanisms are acting. Whatever their creation, switchbacks are an important mesoscale feature of the solar wind, with many of their signatures persisting further out into the solar wind (where the larger ones were often called microstreams), in observations made by Helios (Horbury et al., 2018), ACE (Gosling et al., 2009) and Ulysses (Neugebauer et al., 1995).
5.2 Injected and Imposed Structures and the Turbulent Cascade
A natural question is how mesoscale structures injected and imposed into the solar wind survive to 1 AU, rather than being wiped out by the turbulent cascade, since they populate the same range of spatial scales. In an analysis of Helios, ACE, Wind and Ulysses observations of AHe and flux tube boundaries, (Borovsky, 2012) showed that there is no evidence of mixing across flux tube boundaries or of stretching and folding of boundaries. As described in Section 2, PBSs measured by Ulysses showed a correlation with AHe, suggesting that those PBSs survived through the inner heliosphere (Reisenfeld et al., 1999). This correlation decreased with distance from the Sun, consistent with the eventual evolution and mixing of the polar plume plasma with other plasma (Parhi et al., 1999). This indicates that turbulence is acting, but suggests that 1 AU is still early in the processing of mesoscale structures. The turbulent processing of mesoscale structures may even be a function of latitude, because the effects of solar rotation increases dynamical interactions between streams in the ecliptic. In fact, microstreams and pressure balance structures are easier to detect in Ulysses high-latitude data than ecliptic data (Suess, 2001), and this is thought to be because enhanced dynamic interactions in the ecliptic make it more difficult to detect them.
One possibility is that in the inner heliosphere, some imposed and injected mesoscale structures persist, and turbulence grows within and is bounded by those structures. For example, (Roberts and Goldstein, 1987) showed the magnetic field spectra have a slope of −2 due to sharp jumps in the data, but the spectra follow −5/3 after removal of the jumps. (Borovsky, 2008) argues for fossil, or imposed, flux tubes wherein the turbulence evolves within the flux tubes. Different solar wind streams have different turbulence characteristics (Roberts et al., 2005), and speed is not as important as solar wind source in determining those properties (Shi et al., 2021), indicating that the initial conditions of turbulence on individual flux tubes plays a role. As a final example, if the injected and imposed structures result in large shear flows as implied by the flows measure in (DeForest et al., 2018), turbulence could occur and grow preferentially at such boundaries.
5.3 Importance of Mesoscale Structures as Propagation Medium
CIRs, SIRs and CMEs were mentioned in Section 1 and shown in Figure 1 as examples of injected and imposed large-scale structures that persist far into the Heliosphere. Their nature is affected by the solar wind into which they propagate, and there is evidence that these large-scale phenomena may have sub structures that evolve en route. Recent work showed several examples of injected density structures that are compressed and swept up by a higher speed stream behind (Kepko and Viall, 2019). These structures existed in the solar wind, injected at the time of solar wind formation, and were simply swept up with little evolution other than compression. Along these same lines, (Borovsky and Denton, 2010; Borovsky, 2020a) provided evidence that CIRs and interplanetary shocks are not regions of enhanced turbulence. Rather, turbulence measures changed steadily across CIRs, in correlation with source region changes from fast coronal hole wind to slower streamer belt wind. Similarly, the planar magnetic structures upstream of CMEs are thought to be the result of the alignment and compression of preexisting mesoscale structures in the solar wind (Neugebauer et al., 1993) and this resulting structuring is important for geomagnetic impact (Palmerio et al., 2016).
Energetic particle propagation is also highly dependent on the solar wind structure, as the magnetic field can funnel particles, while fluctuations of the magnetic field and density (Reid and Kontar, 2010; Klein and Dalla, 2017) can scatter particles. Many observations of energetic particles have been shown to be consistent with the random walk of field lines from turbulence (Jokipii, 1966; Chhiber et al., 2020). Dropouts in energetic particles and electron strahl also indicate changes in the magnetic topology such as HCS crossings or local kinks in the magnetic field (Crooker et al., 1982; Borovsky, 2008). Strahl intensity and width is correlated with magnetic discontinuities (Borovsky, 2021); more generally, energetic particle changes during ambient solar wind conditions are correlated with changes in magnetic field and plasma at tangential discontinuities (Neugebauer and Giacalone, 2015; Tessein et al., 2015). (Rosenvinge et al., 2009) showed that STEREO energetic particle data exhibit intensity variations that suggested a linkage to flux tubes with diameters ∼ 6,000 Mm, with additional variations suggesting flux tube-funneling on scales down to 500 Mm. On smaller scales are dropouts, where the intensity (particle counts per energy bin) in energetic particles decreased, which was also attributed to trapping along flux tubes (Mazur et al., 2000; Chollet and Giacalone, 2008). The dropouts were attributed to flux tubes on the scales of 10–100 Mm (Giacalone et al., 2000; Chollet and Giacalone, 2011). Interestingly, strahl particles respond to switchback structure observed in Parker Solar Probe, but higher energy particles energies do not, possibly because their larger gyroradius may not be able to respond to steep rotational discontinuities (Bandyopadhyay et al., 2021).
6 Future Progress
As shown in the right part of Figure 1, sparse observations have been a limiting factor in understanding the nature and evolution of mesoscale structure in the solar wind. Capturing the imposed and injected structure from the Sun, as well as the subsequent evolution and creation of new structures, requires continuous imaging from the low, through the middle, to the high corona, e.g., from the photosphere through at least five solar radii. This is where the closed magnetic field lines, and non-radial corona transitions to a radial, flow-dominated wind. Higher still, the wind undergoes additional physical transitions up through, for example, near 30 Rsun, where the solar wind exceeds the Alfvén speed and many mesoscale structures are “frozen” into the solar wind flow. The highly structured nature of the solar wind implies that there is not likely a single radius that this transition occurs at, but rather a zone over which the Alfvénic transition occurs (DeForest et al., 2018). This requires observations that are continuously sampled in time and have spatial coverage such that structures in the solar wind can be followed from their source in the solar atmosphere to the solar wind. Simultaneously, the observations must have the spatial and temporal resolution and sensitivity to capture the size scales of interest. Remote observations such as from SDO, STEREO, SOHO, shown in Figure 1, currently covers a large fraction of this transition. However, coverage is still not global, as it is limited in latitude, and has gaps in coverage in distance from the Sun. Furthermore, the sensitivity and resolution achieved is just able to sample the largest of the mesoscale range. WISPR has the potential to make measurements at the small mesoscale range, and could help fill this gap. In the future, the Polarimeter to UNify the Corona and Heliosphere (PUNCH) mission will have the combined global spatial coverage with temporal and spatial resolution and sensitivity to address the source of mesoscale structures, their propagation through the inner heliosphere, and interplay between injected and imposed structures with turbulence. The COronal Diagnostic EXperiment (CODEX) mission will measure temperature and velocity simultaneously with density and will be able to image changes in temperature and flow injected and imposed from the Sun. Finally, all images of the solar corona and solar wind have been taken from the ecliptic, limiting the ability to measure the azimuthal extent of structures. The solar polar viewpoint is uniquely able to sample the effects of rotation on the solar wind. Solar Orbiter (Müller et al., 2020) will reach an orbital inclination of approximately 30° during the extended phase of the mission, which will provide azimuthal measurements of mesoscale structures and some constraints on rotational effects. A solar-polar mission that images with a sustained view from above 70° could determine the role of co-rotation with the corona on the creation of mesoscale structures, and the azimuthal structuring and scale sizes of such structures.
At the other end of the spectrum, in situ measurements of the small scale kinetics have been well studied with magnetospheric missions like MMS (Burch et al., 2016; Bandyopadhyay et al., 2018; Roberts et al., 2020b; Chasapis et al., 2020) and Cluster (Escoubet et al., 1997; Osman and Horbury, 2006; Sahraoui et al., 2009; Roberts et al., 2013) when they are in the solar wind, and the radial dimension of mesoscale structures are captured well with the 1AU assets Wind, ACE, SOHO, STEREO. With the limited in situ sampling currently available, these measurements are sparse, so require long averages to build statistics and a global picture. The connection between the global scales and mesoscales can not be done without constellations of in situ measurements. Even with ideal separation of the STEREO spacecraft with each other and L1, connecting mesoscales to global scales, and disentangling time dynamics from spatial structure is not possible (Jian et al., 2009; Simunac et al., 2009) using these data alone.
Current computational ability is also limited. Computations that span the global scales down to kinetic scales of the solar wind are not currently possible. As with observations, it is at the mesoscales that simulations are incapable of placing constraints on theories. The highest resolution MHD models of the heliosphere can only resolve scales of >150 Mm (Merkin et al., 2016; Gombosi et al., 2018), capturing the global-mesoscale transition, but not the full cascade through the mesoscales. On the other hand, it is too computationally expensive to expand kinetic simulations up beyond dissipation scales to capture the mesoscales. Hybrid simulations, even if they resolve the same spatial range as MHD, still need to resolve a finer temporal range (gyromotion) and more degrees of freedom (velocity space), with a resultant sacrifice in the simulation size. As we enter the age of exascale supercomputing (1018 computations per second), better resolved hybrid simulations will become possible, including 6-days Vlasov codes, as well as new approaches for mesocale simulations, such as spectral and implicit kinetic solvers, which would enable simulation of the full mesoscale range.
7 Conclusion
The solar wind contains structures that are injected and imposed directly by the Sun and structures that are generated and evolve en route due to turbulence. At the extremes of the spatial scales, it is simple to differentiate these creation mechanisms. Yet there exists a several orders of magnitude gap between these two scales, the mesoscale. In this regime, with a size scale at 1 AU of ∼5–10,000 Mm and time scales of 10 s–7 h, both injected/imposed and structures generated en route co-exist, and it is often difficult to disentangle the two. Competition between the imposed and injected structures with turbulent and other evolution leads to complex structuring and dynamics. Injected mesoscales carry imprints of the processes that release solar plasma and heats and accelerates the solar wind, and therefore studying them can provide insight into the generation of the solar wind. The mesoscale regime is also the region of observation space that is grossly under-sampled. Sparse in situ measurements are limited to radial profiles of the solar wind as the wind advects past the spacecraft, and remote imaging currently cannot resolve many mesoscales. There is very limited azimuthal coverage, and even less out of the ecliptic coverage. Understanding mesoscale structures is important as they are drivers of Earth’s magnetosphere, and important upstream conditions for the structuring of CMEs, CIRs, and the propagation of energetic particles.
Author Contributions
NMV led the development of the overall structure of the manuscript and the section on imposed and injected structures. CED took the lead on the turbulence section. LK took the lead on magnetospheric impacts and created the figure. All authors contributed to the discussion.
Funding
NMV and LK were supported by the NASA competed Internal Scientist Funding Model (ISFM). CED was supported by NASA’s Heliophysics Explorers program (PUNCH mission).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors acknowledge Simone Di Matteo, Aaron Roberts, and the ISFM team “Connecting the corona to solar wind structure and magnetospheric impact using modeling and remote and in situ observations” for their helpful discussion on this topic.
References
Adhikari, L., Zank, G. P., Zhao, L. L., Telloni, D., Horbury, T. S., O’Brien, H., et al. (2021). Evolution of Anisotropic Turbulence in the Fast and Slow Solar Wind: Theory and Solar Orbiter Measurements. Astron. Astrophysics [Epub ahead of print]. doi:10.1051/0004-6361/202140672
Allred, J. C., and MacNeice, P. J. (2015). An MHD Code for the Study of Magnetic Structures in the Solar Wind. Comput. Sci. Discov. 8, 015002. doi:10.1088/1749-4680/8/1/015002
Alterman, B. L., Kasper, J. C., Leamon, R. J., and McIntosh, S. W. (2021). Solar Wind Helium Abundance Heralds Solar Cycle Onset. Solar Phys. 296, 67. doi:10.1007/s11207-021-01801-9
Alzate, N., and Morgan, H. (2017). Identification of Low Coronal Sources of “Stealth” Coronal Mass Ejections Using New Image Processing Techniques. Astrophysical J. 840, 103. doi:10.3847/1538-4357/aa6caa
Alzate, N., Morgan, H., Viall, N., and Vourlidas, A. (2021). Connecting the Low to High Corona: A Method to Isolate Transients in STEREO/COR1 Images. ApJ accepted in press
Antiochos, S. K., Mikić, Z., Titov, V. S., Lionello, R., and Linker, J. A. (2011). A Model for the Sources of the Slow Solar Wind. Astrophysical J. 731, 112. doi:10.1088/0004-637x/731/2/112
Aslanyan, V., Pontin, D. I., Wyper, P. F., Scott, R. B., Antiochos, S. K., and DeVore, C. R. (2021). Effects of Pseudostreamer Boundary Dynamics on Heliospheric Field and Wind. Astrophysical J. 909, 10. doi:10.3847/1538-4357/abd6e6
Bale, S. D., Badman, S. T., Bonnell, J. W., Bowen, T. A., Burgess, D., Case, A. W., et al. (2019). Highly Structured Slow Solar Wind Emerging from an Equatorial Coronal Hole. Nature 576, 237–242. doi:10.1038/s41586-019-1818-7
Bandyopadhyay, R., Chasapis, A., Chhiber, R., Parashar, T. N., Maruca, B. A., Matthaeus, W. H., et al. (2018). Solar Wind Turbulence Studies Using MMS Fast Plasma Investigation Data. Astrophysical J. 866, 81. doi:10.3847/1538-4357/aade93
Bandyopadhyay, R., Matthaeus, W. H., Chasapis, A., Russell, C. T., Strangeway, R. J., Torbert, R. B., et al. (2020). Direct Measurement of the Solar-Wind taylor Microscale Using MMS Turbulence Campaign Data. Astrophysical J. 899, 63. doi:10.3847/1538-4357/ab9ebe
Bandyopadhyay, R., Matthaeus, W. H., McComas, D. J., Joyce, C. J., Szalay, J. R., Christian, E. R., et al. (2021). Energetic Particle Behavior in Near-Sun Magnetic Field Switchbacks from PSP. Astron. Astrophysics 650, L4. doi:10.1051/0004-6361/202039800
Borovsky, J. E., and Burkholder, B. L. (2020). On the Fourier Contribution of Strong Current Sheets to the High-Frequency Magnetic Power SpectralDensity of the Solar Wind. J. Geophys. Res. Space Phys. 125, e2019JA027307. doi:10.1029/2019ja027307
Borovsky, J. E. (2010). Contribution of Strong Discontinuities to the Power Spectrum of the Solar Wind. Phys. Rev. Lett. 105, 111102. doi:10.1103/physrevlett.105.111102
Borovsky, J. E., and Denton, M. H. (2006). Differences between CME-Driven Storms and CIR-Driven Storms. J. Geophys. Res. Space Phys. 111, A07S08. (c) 2006: American Geophysical Union. doi:10.1029/2005ja011447
Borovsky, J. E., and Denton, M. H. (2010). Solar Wind Turbulence and Shear: A Superposed-Epoch Analysis of Corotating Interaction Regions at 1 AU. J. Geophys. Res. Space Phys. 115, n/a. doi:10.1029/2009ja014966
Borovsky, J. E. (2021). Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection between the Earth and the Sun. Front. Astron. Space Sci. 8, 646443. doi:10.3389/fspas.2021.646443
Borovsky, J. E. (2008). Flux Tube Texture of the Solar Wind: Strands of the Magnetic Carpet at 1 AU?. J. Geophys. Res. Space Phys. 113, n/a. doi:10.1029/2007ja012684
Borovsky, J. E. (2012). Looking for Evidence of Mixing in the Solar Wind from 0.31 to 0.98 AU. J. Geophys. Res. Space Phys. 117, n/a. doi:10.1029/2012ja017525
Borovsky, J. E. (2020a). The Compression of the Heliospheric Magnetic Structure by Interplanetary Shocks: Is the Structure at 1AU a Manifestation of Solar-Wind Turbulence or Is it Fossil Structure from the Sun?. Front. Astron. Space Sci. 7, 582564. doi:10.3389/fspas.2020.582564
Borovsky, J. E. (2020b). The Magnetic Structure of the Solar Wind: Ionic Composition and the Electron Strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019gl084586
Borovsky, J. E. (2016). The Plasma Structure of Coronal Hole Solar Wind: Origins and Evolution. J. Geophys. Res. Space Phys. 121, 5055–5087. doi:10.1002/2016ja022686
Bortnik, J., Thorne, R. M., O’Brien, T. P., Green, J. C., Strangeway, R. J., Shprits, Y. Y., et al. (2006). Observation of Two Distinct, Rapid Loss Mechanisms during the 20 November 2003 Radiation belt Dropout Event. J. Geophys. Res. Space Phys. 111, A12216. doi:10.1029/2006ja011802
Bourouaine, S., and Perez, J. C. (2020). Interpreting Solar Wind Turbulent Spectra beyond Taylor’s Hypothesis. Astrophysical J. 893, L32. doi:10.3847/2041-8213/ab7fb1
Breneman, A. W., Halford, A. J., Millan, R. M., Woodger, L. A., Zhang, X., Sandhu, J. K., et al. (2020). Driving of Outer Belt Electron Loss by Solar Wind Dynamic Pressure Structures: Analysis of Balloon and Satellite Data. J. Geophys. Res. Space Phys. 125. doi:10.1029/2020ja028097
Bruno, R., and Carbone, V. (2013). The Solar Wind as a Turbulence Laboratory. Living Rev. Solar Phys. 10, 2. doi:10.12942/lrsp-2013-2
Bruno, R., Carbone, V., Vörös, Z., D’Amicis, R., Bavassano, B., Cattaneo, M. B., et al. (2009). Coordinated Study on Solar Wind Turbulence during the Venus-Express, ACE and Ulysses Alignment of August 2007. Earth, Moon, and Planets 104, 101–104. doi:10.1007/s11038-008-9272-9
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Cartwright, M. L., and Moldwin, M. B. (2008). Comparison of Small-Scale Flux Rope Magnetic Properties to Large-Scale Magnetic Clouds: Evidence for Reconnection across the HCS?. J. Geophys. Res. Space Phys. 113, n/a. doi:10.1029/2008ja013389
Cartwright, M. L., and Moldwin, M. B. (2010). Heliospheric Evolution of Solar Wind Small-Scale Magnetic Flux Ropes. J. Geophys. Res. Space Phys. 115, A08102. doi:10.1029/2009JA014271
Chae, J., Schuhle, U., and Lemaire, P. (1998). SUMER Measurements of Nonthermal Motions: Constraints on Coronal Heating Mechanisms. Astrophysical J. 505, 957–973. doi:10.1086/306179
Chasapis, A., Matthaeus, W. H., Bandyopadhyay, R., Chhiber, R., Ahmadi, N., Ergun, R. E., et al. (2020). Scaling and Anisotropy of Solar Wind Turbulence at Kinetic Scales during the MMS Turbulence Campaign. Astrophysical J. 903, 127. doi:10.3847/1538-4357/abb948
Chen, C. H. K., Bale, S. D., Bonnell, J. W., Borovikov, D., Bowen, T. A., Burgess, D., et al. (2020). The Evolution and Role of Solar Wind Turbulence in the Inner Heliosphere. Astrophysical J. Suppl. Ser. 246, 53. doi:10.3847/1538-4365/ab60a3
Chen, C. H. K., Chandran, B. D. G., Woodham, L. D., Jones, S. I., Perez, J. C., Bourouaine, S., et al. (2021). The Near-Sun Streamer belt Solar Wind: Turbulence and Solar Wind Acceleration. Astron. Astrophysics 650, L3. doi:10.1051/0004-6361/202039872
Chhiber, R., Goldstein, M. L., Maruca, B. A., Chasapis, A., Matthaeus, W. H., Ruffolo, D., et al. (2020). Clustering of Intermittent Magnetic and Flow Structures Near Parker Solar Probe ’s First Perihelion—A Partial-Variance-Of-Increments Analysis. Astrophysical J. Suppl. Ser. 246, 31. doi:10.3847/1538-4365/ab53d2
Chhiber, R., Usmanov, A. V., Matthaeus, W. H., and Goldstein, M. L. (2019). Contextual Predictions for the Parker Solar Probe . I. Critical Surfaces and Regions. Astrophysical J. Suppl. Ser. 241, 11. doi:10.3847/1538-4365/ab0652
Chollet, E. E., and Giacalone, J. (2011). Evidence of Confinement of Solar-Energetic Particles to Interplanetary Magnetic Field Lines. Astrophysical J. 728, 64. doi:10.1088/0004-637x/728/1/64
Chollet, E. E., and Giacalone, J. (2008). Multispacecraft Analysis of Energetic Ion Flux Dropouts. Astrophysical J. 688, 1368–1373. doi:10.1086/592378
Claudepierre, J. S. G., Hudson, M. K., Lotko, W., Lyon, J. G., and Denton, R. E. (2010). Solar Wind Driving of Magnetospheric ULF Waves: Field Line Resonances Driven by Dynamic Pressure Fluctuations. J. Geophys. Res. 115, A11202. doi:10.1029/2010JA015399
Coleman, P. J. (1966). Variations in the Interplanetary Magnetic Field: Mariner 2: 1. Observed Properties. J. Geophys. Res. 71, 5509–5531. doi:10.1029/jz071i023p05509
C. P. Escoubet, C. T. Russell, and R. Schmidt (1997). Cluster - Science and Mission Overview (Dordrecht: Springer Netherlands). doi:10.1007/978-94-011-5666-0/_/1
Cranmer, S. R., Field, G. B., and Kohl, J. L. (1999). Spectroscopic Constraints on Models of Ion Cyclotron Resonance Heating in the Polar Solar Corona and High-Speed Solar Wind. Astrophysical J. 518, 937–947. doi:10.1086/307330
Cranmer, S. R., Gibson, S. E., and Riley, P. (2017). Origins of the Ambient Solar Wind: Implications for Space Weather. Space Sci. Rev. 212, 1345–1384. doi:10.1007/s11214-017-0416-y
Cranmer, S. R. (2012). Self-Consistent Models of the Solar Wind. Space Sci. Rev. 172, 145–156. doi:10.1007/s11214-010-9674-7
Cranmer, S. R., and Woolsey, L. N. (2015). Driving Solar Spicules and Jets with Magnetohydrodynamic Turbulence: Testing a Persistent Idea. Astrophysical J. 812, 71. doi:10.1088/0004-637x/812/1/71
Crooker, N. U., Burton, M. E., Phillips, J. L., Smith, E. J., and Balogh, A. (1996). Heliospheric Plasma Sheets as Small-Scale Transients. J. Geophys. Res. 101, 2467–2474. doi:10.1029/95ja03148
Crooker, N. U., Burton, M. E., Siscoe, G. L., Kahler, S. W., Gosling, J. T., and Smith, E. J. (1996). Solar Wind Streamer belt Structure. J. Geophys. Res. Space Phys. 101, 24331–24341. doi:10.1029/96ja02412
Crooker, N. U., Huang, C. L., Lamassa, S. M., Larson, D. E., Kahler, S. W., and Spence, H. E. (2004). Heliospheric Plasma Sheets. J. Geophys. Res. - Space Phys. 109, A03107. doi:10.1029/2003ja010170
Crooker, N. U., and McPherron, R. L. (2012). Coincidence of Composition and Speed Boundaries of the Slow Solar Wind. J. Geophys. Res. Space Phys. 117, A09104. doi:10.1029/2012ja017837
Crooker, N. U., Siscoe, G. L., Russell, C. T., and Smith, E. J. (1982). Factors Controlling Degree of Correlation between ISEE 1 and ISEE 3 Interplanetary Magnetic Field Measurements. J. Geophys. Res. Space Phys. 87, 2224–2230. doi:10.1029/ja087ia04p02224
Crooker, N. U., Siscoe, G. L., Shodhan, S., Webb, D. F., Gosling, J. T., and Smith, E. J. (1993). Multiple Heliospheric Current Sheets and Coronal Streamer belt Dynamics. J. Geophys. Res. Space Phys. 98, 9371–9381. doi:10.1029/93ja00636
D’Amicis, R., and Bruno, R. (2015). On the Origin of the Highly Alfvénic Slow Solar Wind. Astrophysical J. 805, 84. doi:10.1088/0004-637x/805/1/84
DeForest, C. E., Howard, R. A., Velli, M., Viall, N., and Vourlidas, A. (2018). The Highly Structured Outer Solar Corona. Astrophysical J. 862, 18. doi:10.3847/1538-4357/aac8e3
DeForest, C. E., Matthaeus, W. H., Howard, T. A., and Rice, D. R. (2015). Turbulence in the Solar Wind Measured with Comet Tail Test Particles. Astrophysical J. 812, 108. doi:10.1088/0004-637x/812/2/108
DeForest, C. E., Matthaeus, W. H., Viall, N. M., and Cranmer, S. R. (2016). Fading Coronal Structure and the Onset of Turbulence in the Young Solar Wind. Astrophysical J. 828, 66. doi:10.3847/0004-637x/828/2/66
DiMatteo, S., Viall, N. M., Kepko, L., Wallace, S., Arge, C. N., and MacNeice, P. (2019). Helios Observations of Quasiperiodic Density Structures in the Slow Solar Wind at 0.3, 0.4, and 0.6 AU. J. Geophys. Res. Space Phys. 124, 837–860. doi:10.1029/2018ja026182
DiMatteo, S., and Villante, U. (2017). The Identification of Solar Wind Waves at Discrete Frequencies and the Role of the Spectral Analysis Techniques. J. Geophys. Res. Space Phys. 122, 4905–4920. doi:10.1002/2017ja023936
Drake, J. F., Agapitov, O., Swisdak, M., Badman, S. T., Bale, S. D., Horbury, T. S., et al. (2021). Switchbacks as Signatures of Magnetic Flux Ropes Generated by Interchange Reconnection in the corona. Astron. Astrophysics 650, A2. doi:10.1051/0004-6361/202039432
Dyrud, L. P., Behnke, R., Kepko, E. L., Sulzer, M., and Zafke, S. (2008). Ionospheric ULF Oscillations Driven from above Arecibo. Geophys. Res. Lett. 35, L14101. doi:10.1029/2008gl034073
Elliott, H. A., Henney, C. J., McComas, D. J., Smith, C. W., and Vasquez, B. J. (2012). Temporal and Radial Variation of the Solar Wind Temperature-Speed Relationship. J. Geophys. Res. Space Phys. 117, n/a. doi:10.1029/2011ja017125
Elliott, H. A., McComas, D. J., and DeForest, C. E. (2016). Long-term Trends in the Solar Wind Proton Measurements. Astrophysical J. 832, 66. doi:10.3847/0004-637x/832/1/66
Endeve, E., Lie-Svendsen, O., Hansteen, V. H., and Leer, E. (2005). Release of Helium from Closed-Field Regions of the Sun. Astrophysical J. 624, 402–413. doi:10.1086/428938
Feldman, U., Schühle, U., Widing, K. G., and Laming, J. M. (1998). Coronal Composition above the Solar Equator and the North Pole as Determined from Spectra Acquired by the SUMER Instrument on SOHO. Astrophysical J. 505, 999–1006. doi:10.1086/306195
Feng, H. Q., Wu, D. J., and Chao, J. K. (2007). Size and Energy Distributions of Interplanetary Magnetic Flux Ropes. J. Geophys. Res. Space Phys. 112, n/a. doi:10.1029/2006ja011962
Fenrich, F. R., and Waters, C. L. (2008). Phase Coherence Analysis of a Field Line Resonance and Solar Wind Oscillation. Geophys. Res. Lett. 35, 4. (c) 2008: American Geophysical Union. doi:10.1029/2008gl035430
Froment, C., Krasnoselskikh, V., Wit, T. D. d., Agapitov, O., Fargette, N., Lavraud, B., et al. (2021). Direct Evidence for Magnetic Reconnection at the Boundaries of Magnetic Switchbacks with Parker Solar Probe. Astron. Astrophysics 650, A5. doi:10.1051/0004-6361/202039806
Giacalone, J., Jokipii, J. R., and Mazur, J. E. (2000). Small-scale Gradients and Large-Scale Diffusion of Charged Particles in the Heliospheric Magnetic Field. Astrophysical J. 532, L75–L78. doi:10.1086/312564
Gombosi, T. I., Holst, B. v. d., Manchester, W. B., and Sokolov, I. V. (2018). Extended MHD Modeling of the Steady Solar corona and the Solar Wind. Living Rev. Solar Phys. 15, 4. doi:10.1007/s41116-018-0014-4
Gosling, J., and Pizzo, V. (1999). Formation and Evolution of Corotating Interaction Regions and Their Three Dimensional Structure. Space Sci. Rev. 89, 21–52. doi:10.1023/a:1005291711900
Gosling, J. T., Borrini, G., Asbridge, J. R., Bame, S. J., Feldman, W. C., and Hansen, R. T. (1981). Coronal Streamers in the Solar Wind at 1 AU. J. Geophys. Res. Space Phys. 86, 5438–5448. doi:10.1029/ja086ia07p05438
Gosling, J. T., McComas, D. J., Roberts, D. A., and Skoug, R. M. (2009). A One-Sided Aspect of Alfvenic Fluctuations in the Solar Wind. Astrophysical J. 695, L213–L216. doi:10.1088/0004-637x/695/2/l213
Gosling, J. T., and Szabo, A. (2008). Bifurcated Current Sheets Produced by Magnetic Reconnection in the Solar Wind. J. Geophys. Res. Space Phys. 113, 8. doi:10.1029/2008ja013473
Harrison, R. A., Davies, J. A., Rouillard, A. P., Davis, C. J., Eyles, C. J., Bewsher, D., et al. (2009). Two Years of the STEREO Heliospheric Imagers. Solar Phys. 256, 219–237. doi:10.1007/s11207-009-9352-7
Hartinger, M. D., Welling, D., Viall, N. M., Moldwin, M. B., and Ridley, A. (2014). The Effect of Magnetopause Motion on Fast Mode Resonance. J. Geophys. Res. Space Phys. 119, 8212–8227. doi:10.1002/2014ja020401
Hietala, H., Kilpua, E. K. J., Turner, D. L., and Angelopoulos, V. (2014). Depleting Effects of ICME-Driven Sheath Regions on the Outer Electron Radiation belt. Geophys. Res. Lett. 41, 2258–2265. doi:10.1002/2014gl059551
Higginson, A. K., Antiochos, S. K., DeVore, C. R., Wyper, P. F., and Zurbuchen, T. H. (2017). Dynamics of Coronal Hole Boundaries. Astrophysical J. 837, 113. doi:10.3847/1538-4357/837/2/113
Higginson, A. K., Antiochos, S. K., DeVore, C. R., Wyper, P. F., and Zurbuchen, T. H. (2017). Formation of Heliospheric Arcs of Slow Solar Wind. Astrophysical J. 840, L10. doi:10.3847/2041-8213/aa6d72
Higginson, A. K., and Lynch, B. J. (2018). Structured Slow Solar Wind Variability: Streamer-Blob Flux Ropes and Torsional Alfvén Waves. Astrophysical J. 859, 6. doi:10.3847/1538-4357/aabc08
Hoeksema, J. T., Wilcox, J. M., and Scherrer, P. H. (1983). The Structure of the Heliospheric Current Sheet: 1978–1982. J. Geophys. Res. Space Phys. 88, 9910–9918. doi:10.1029/ja088ia12p09910
Horbury, T. S., Forman, M. A., and Oughton, S. (2005). Spacecraft Observations of Solar Wind Turbulence: an Overview. Plasma Phys. Controlled Fusion 47, B703. doi:10.1088/0741-3335/47/12b/s52
Horbury, T. S., Matteini, L., and Stansby, D. (2018). Short, Large-Amplitude Speed Enhancements in the Near-Sunfast Solar Wind. Monthly Notices R. Astronomical Soc. 478, 1980–1986. doi:10.1093/mnras/sty953
Howard, T. A., and DeForest, C. E. (2012). The Thomson Surface. I. Reality and Myth. Astrophysical J. 752, 130. doi:10.1088/0004-637x/752/2/130
Howard, T. A., and Harrison, R. A. (2013). Stealth Coronal Mass Ejections: A Perspective. Solar Phys. 285, 269–280. doi:10.1007/s11207-012-0217-0
Howard, T. A., and Tappin, S. J. (2008). Three-Dimensional Reconstruction of Two Solar Coronal Mass Ejections Using the STEREO Spacecraft. Solar Phys. 252, 373–383. doi:10.1007/s11207-008-9262-0
Isaacs, J. J., Tessein, J. A., and Matthaeus, W. H. (2015). Systematic Averaging Interval Effects on Solar Wind Statistics. J. Geophys. Res. Space Phys. 120, 868–879. doi:10.1002/2014ja020661
Jian, L. K., Russell, C. T., Luhmann, J. G., Galvin, A. B., and MacNeice, P. J. (2009). Multi-Spacecraft Observations: Stream Interactions and Associated Structures. Solar Phys. 259, 345. doi:10.1007/s11207-009-9445-3
Jokipii, J. R. (1966). Cosmic-Ray Propagation. I. Charged Particles in a Random Magnetic Field. Astrophysical J. 146, 480. doi:10.1086/148912
Karpen, J. T., DeVore, C. R., Antiochos, S. K., and Pariat, E. (2016). Reconnection-driven Coronal-Hole Jets with Gravity and Solar Wind. Astrophysical J. 834, 62. doi:10.3847/1538-4357/834/1/62
Kasper, J. C., Bale, S. D., Belcher, J. W., Berthomier, M., Case, A. W., Chandran, B. D. G., et al. (2019). Alfvénic Velocity Spikes and Rotational Flows in the Near-Sun Solar Wind. Nature 576, 228–231. doi:10.1038/s41586-019-1813-z
Kasper, J. C., Klein, K. G., Weber, T., Maksimovic, M., Zaslavsky, A., Bale, S. D., et al. (2017). A Zone of Preferential Ion Heating Extends Tens of Solar Radii from the Sun. Astrophysical J. 849, 126. doi:10.3847/1538-4357/aa84b1
Kasper, J. C., Lazarus, A. J., and Gary, S. P. (2008). Hot Solar-Wind Helium: Direct Evidence for Local Heating by Alfvén-Cyclotron Dissipation. Phys. Rev. Lett. 101, 261103. doi:10.1103/physrevlett.101.261103
Kataoka, R., and Miyoshi, Y. (2006). Flux Enhancement of Radiation belt Electrons during Geomagnetic Storms Driven by Coronal Mass Ejections and Corotating Interaction Regions. Space Weather 4, n/a. doi:10.1029/2005sw000211
Kepko, L., and Spence, H. E. (2003). Observations of Discrete, Global Magnetospheric Oscillations Directly Driven by Solar Wind Density Variations. J. Geophys. Res. Space Phys. 108, 1257. (c) 2003: American Geophysical Union. doi:10.1029/2002ja009676
Kepko, L., Spence, H. E., and Singer, H. J. (2002). ULF Waves in the Solar Wind as Direct Drivers of Magnetospheric Pulsations. Geophys. Res. Lett. 29, 39-1–39-4. doi:10.1029/2001gl014405
Kepko, L., Viall, N. M., Antiochos, S. K., Lepri, S. T., Kasper, J. C., and Weberg, M. (2016). Implications of L1 Observations for Slow Solar Wind Formation by Solar Reconnection. Geophys. Res. Lett. 43, 4089–4097. doi:10.1002/2016gl068607
Kepko, L., and Viall, N. M. (2019). The Source, Significance, and Magnetospheric Impact of Periodic Density Structures within Stream Interaction Regions. J. Geophys. Res. Space Phys. 124, 7722– 7743. doi:10.1029/2019ja026962
Kepko, L., Viall, N. M., and Wolfinger, K. (2020). Inherent Length Scales of Periodic Mesoscale Density Structures in the Solar Wind over Two Solar Cycles. J. Geophys. Res. Space Phys. 125, e2020JA028037. doi:10.1029/2020ja028037
Khabarova, O., Malandraki, O., Malova, H., Kislov, R., Greco, A., Bruno, R., et al. (2021). Current Sheets, Plasmoids and Flux Ropes in the Heliosphere. Space Sci. Rev. 217, 38. doi:10.1007/s11214-021-00814-x
Kilpua, E. K. J., Balogh, A., Steiger, R. v., and Liu, Y. D. (2017). Geoeffective Properties of Solar Transients and Stream Interaction Regions. Space Sci. Rev. 212, 1271–1314. doi:10.1007/s11214-017-0411-3
Kilpua, E. K. J., Hietala, H., Koskinen, H. E. J., Fontaine, D., and Turc, L. (2013). Magnetic Field and Dynamic Pressure ULF Fluctuations in Coronal-Mass-Ejection-Driven Sheath Regions. Ann. Geophysicae 31, 1559–1567. doi:10.5194/angeo-31-1559-2013
Kilpua, E. K. J., Hietala, H., Turner, D. L., Koskinen, H. E. J., Pulkkinen, T. I., Rodriguez, J. V., et al. (2015). Unraveling the Drivers of the Storm Time Radiation belt Response. Geophys. Res. Lett. 42, 3076–3084. doi:10.1002/2015gl063542
Klein, K.-L., and Dalla, S. (2017). Acceleration and Propagation of Solar Energetic Particles. Space Sci. Rev. 212, 1107–1136. doi:10.1007/s11214-017-0382-4
Klein, K. G., Howes, G. G., and TenBarge, J. M. (2014). The Violation of the Taylor Hypothesis in Measurements of Solar Wind Turbulence. Astrophysical J. 790, L20. doi:10.1088/2041-8205/790/2/l20
Klimchuk, J. A., and Antiochos, S. K. (2021). How Turbulent Is the Magnetically Closed Corona?. Front. Astron. Space Sci. 8, 662861. doi:10.3389/fspas.2021.662861
Kolmogorov, A. (1941). The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akademiia Nauk SSSR Doklady 30, 301–305.
Kraichnan, R. H. (1967). Inertial Ranges in Two-Dimensional Turbulence. Phys. Fluids 10, 1417. doi:10.1063/1.1762301
Kumar, P., Karpen, J. T., Antiochos, S. K., Wyper, P. F., DeVore, C. R., and Lynch, B. J. (2021). From Pseudostreamer Jets to Coronal Mass Ejections: Observations of the Breakout Continuum. Astrophysical J. 907, 41. doi:10.3847/1538-4357/abca8b
Laming, J. M. (2015). The FIP and Inverse FIP Effects in Solar and Stellar Coronae. Living Rev. Solar Phys. 12, 2. doi:10.1007/lrsp-2015-2
Laming, J. M., Vourlidas, A., Korendyke, C., Chua, D., Cranmer, S. R., Ko, Y.-K., et al. (2019). Element Abundances: A New Diagnostic for the Solar Wind. Astrophysical J. 879, 124. doi:10.3847/1538-4357/ab23f1
Landi, E., Gruesbeck, J. R., Lepri, S. T., Zurbuchen, T. H., and Fisk, L. A. (2012). Charge State Evolution in the Solar Wind. II. Plasma Charge State Composition in the Inner corona and Accelerating Fast Solar Wind. Astrophysical J. 761, 48. doi:10.1088/0004-637x/761/1/48
Larosa, A., Krasnoselskikh, V., Wit, T. D. d., Agapitov, O., Froment, C., Jagarlamudi, V. K., et al. (2021). Switchbacks: Statistical Properties and Deviations from Alfvénicity. Astron. Astrophysics 650, A3. doi:10.1051/0004-6361/202039442
Lavraud, B., Fargette, N., Réville, V., Szabo, A., Huang, J., Rouillard, A. P., et al. (2020). The Heliospheric Current Sheet and Plasma Sheet during Parker Solar Probe’s First Orbit. Astrophysical J. 894, L19. doi:10.3847/2041-8213/ab8d2d
Leamon, R. J., Smith, C. W., Ness, N. F., Matthaeus, W. H., and Wong, H. K. (1998). Observational Constraints on the Dynamics of the Interplanetary Magnetic Field Dissipation Range. J. Geophys. Res. Space Phys. 103, 4775–4787. doi:10.1029/97ja03394
Leamon, R. J., Smith, C. W., Ness, N. F., and Wong, H. K. (1999). Dissipation Range Dynamics: Kinetic Alfvén Waves and the Importance of βe. J. Geophys. Res. Space Phys. 104, 22331–22344. doi:10.1029/1999ja900158
Li, W., and Hudson, M. (2019). Earth’s Van Allen Radiation Belts: From Discovery to the Van Allen Probes Era. J. Geophys. Res. Space Phys. 124, 8319–8351. doi:10.1029/2018ja025940
Linker, J. A., Lionello, R., Mikić, Z., Titov, V. S., and Antiochos, S. K. (2011). The Evolution of Open Magnetic Flux Driven by Photospheric Dynamics. Astrophysical J. 731, 110. doi:10.1088/0004-637x/731/2/110
Lionello, R., Velli, M., Downs, C., Linker, J. A., and Mikić, Z. (2014). Application of a Solar Wind Model Driven by Turbulence Dissipation to a 2D Magnetic Field Configuration. Astrophysical J. 796, 111. doi:10.1088/0004-637x/796/2/111
Liou, K., Takahashi, K., Newell, P. T., and Yumoto, K. (2008). Polar Ultraviolet Imager Observations of Solar Wind-Driven ULF Auroral Pulsations. Geophys. Res. Lett. 35, 16101. doi:10.1029/2008gl034953
Lynch, B. J. (2020). A Model for Coronal Inflows and In/Out Pairs. Astrophysical J. 905, 139. doi:10.3847/1538-4357/abc5b3
Lynch, B. J., Masson, S., Li, Y., DeVore, C. R., Luhmann, J. G., Antiochos, S. K., et al. (2016). A Model for Stealth Coronal Mass Ejections. J. Geophys. Res. Space Phys. 121 (10677–10), 697. doi:10.1002/2016ja023432
Ma, S., Attrill, G. D. R., Golub, L., and Lin, J. (2010). Statistical Study of Coronal Mass Ejections with and without Distinct Low Signatures. Astrophysical J. 722, 289–301. doi:10.1088/0004-637x/722/1/289
Martinović, M. M., Klein, K. G., Huang, J., Chandran, B. D. G., Kasper, J. C., Lichko, E., et al. (2021). Multiscale Solar Wind Turbulence Properties inside and Near Switchbacks Measured by the Parker Solar Probe. Astrophysical J. 912, 28. doi:10.3847/1538-4357/abebe5
Mason, E. I., Antiochos, S. K., and Viall, N. M. (2019). Observations of Solar Coronal Rain in Null Point Topologies. Astrophysical J. 874, L33. doi:10.3847/2041-8213/ab0c5d
Matthaeus, W. H., Dasso, S., Weygand, J. M., Milano, L. J., Smith, C. W., and Kivelson, M. G. (2005). Spatial Correlation of Solar-Wind Turbulence from Two-Point Measurements. Phys. Rev. Lett. 95, 231101. doi:10.1103/physrevlett.95.231101
Matthaeus, W. H., and Velli, M. (2011). Who Needs Turbulence?. A Review of Turbulence Effects in the Heliosphere and on the Fundamental Process of Reconnection. Space Sci. Rev. 160, 145–168. doi:10.1007/s11214-011-9793-9
Mazur, J. E., Mason, G. M., Dwyer, J. R., Giacalone, J., Jokipii, J. R., and Stone, E. C. (2000). Interplanetary Magnetic Field Line Mixing Deduced from Impulsive Solar Flare Particles. Astrophysical J. 532, L79–L82. doi:10.1086/312561
McComas, D. J., Bame, S. J., Barraclough, B. L., Feldman, W. C., Funsten, H. O., Gosling, J. T., et al. (1998). Ulysses’ Return to the Slow Solar Wind. Geophys. Res. Lett. 25, 1–4. doi:10.1029/97gl03444
McComas, D. J., Barraclough, B. L., Gosling, J. T., Hammond, C. M., Phillips, J. L., Neugebauer, M., et al. (1995). Structures in the Polar Solar Wind: Plasma and Field Observations from Ulysses. J. Geophys. Res. Space Phys. 100, 19893–19902. doi:10.1029/95ja01634
McIntosh, S. W., Leamon, R. J., Egeland, R., Dikpati, M., Fan, Y., and Rempel, M. (2019). What the Sudden Death of Solar Cycles Can Tell Us about the Nature of the Solar Interior. Solar Phys. 294, 88. doi:10.1007/s11207-019-1474-y
Merkin, V. G., Lyon, J. G., Lario, D., Arge, C. N., and Henney, C. J. (2016). Time-dependent Magnetohydrodynamic Simulations of the Inner Heliosphere. J. Geophys. Res. Space Phys. 121, 2866–2890. doi:10.1002/2015ja022200
Miyoshi, Y., and Kataoka, R. (2005). Ring Current Ions and Radiation belt Electrons during Geomagnetic Storms Driven by Coronal Mass Ejections and Corotating Interaction Regions. Geophys. Res. Lett. 32,L21105. doi:10.1029/2005gl024590
Müller, D., Cyr, O. C. S., Zouganelis, I., Gilbert, H. R., Marsden, R., Nieves-Chinchilla, T., et al. (2020). The Solar Orbiter mission. Astron. Astrophysics 642, A1. doi:10.1051/0004-6361/202038467
Murphy, A. K., Winslow, R. M., Schwadron, N. A., Lugaz, N., Yu, W., Farrugia, C. J., et al. (2020). A Survey of Interplanetary Small Flux Ropes at Mercury. Astrophysical J. 894, 120. doi:10.3847/1538-4357/ab8821
Neugebauer, M., Clay, D. R., and Gosling, J. T. (1993). The Origins of Planar Magnetic Structures in the Solar Wind. J. Geophys. Res. Space Phys. 98, 9383–9389. doi:10.1029/93ja00216
Neugebauer, M. (2012). Evidence for Polar X-ray Jets as Sources of Microstream Peaks in the Solar Wind. Astrophysical J. 750, 50. doi:10.1088/0004-637x/750/1/50
Neugebauer, M., and Giacalone, J. (2015). Energetic Particles, Tangential Discontinuities, and Solar Flux Tubes. J. Geophys. Res. Space Phys. 120, 8281–8287. doi:10.1002/2015ja021632
Neugebauer, M., Goldstein, B. E., McComas, D. J., Suess, S. T., and Balogh, A. (1995). Ulysses Observations of Microstreams in the Solar Wind from Coronal Holes. J. Geophys. Res. Space Phys. 100, 23389–23395. doi:10.1029/95ja02723
Neugebauer, M., Ruzmaikin, A., and McComas, D. J. (1997). Wavelet Analysis of the Structure of Microstreams in the Polar Solar Wind. AIP Conf. Proc. 385, 41–46. doi:10.1063/1.51765
Neugebauer, M., and Snyder, C. W. (1966). Mariner 2 Observations of the Solar Wind: 1. Average Properties. J. Geophys. Res. 71, 4469–4484. doi:10.1029/jz071i019p04469
Neugebauer, M., and Snyder, C. W. (1962). Solar Plasma Experiment. Science 138, 1095–1097. doi:10.1126/science.138.3545.1095-a
Nisticò, G., Vladimirov, V., Nakariakov, V. M., Battams, K., and Bothmer, V. (2018). Oscillations of Cometary Tails: a Vortex Shedding Phenomenon?. Astron. Astrophysics 615, A143. doi:10.1051/0004-6361/201732474
Osman, K. T., and Horbury, T. S. (2006). Multispacecraft Measurement of Anisotropic Correlation Functions in Solar Wind Turbulence. Astrophysical J. 654, L103–L106. doi:10.1086/510906
Oughton, S., Matthaeus, W. H., Wan, M., and Osman, K. T. (2015). Anisotropy in Solar Wind Plasma Turbulence. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 373, 20140152. doi:10.1098/rsta.2014.0152
Owens, M. J., Wicks, R. T., and Horbury, T. S. (2011). Magnetic Discontinuities in the Near-Earth Solar Wind: Evidence of In-Transit Turbulence or Remnants of Coronal Structure?. Solar Phys. 269, 411–420. doi:10.1007/s11207-010-9695-0
Pagel, A. C., Crooker, N. U., Zurbuchen, T. H., and Gosling, J. T. (2004). Correlation of Solar Wind Entropy and Oxygen Ion Charge State Ratio. J. Geophys. Res. Space Phys. 109. doi:10.1029/2003ja010010
Palmerio, E., Kilpua, E. K. J., and Savani, N. P. (2016). Planar Magnetic Structures in Coronal Mass Ejection-Driven Sheath Regions. Ann. Geophysicae 34, 313–322. doi:10.5194/angeo-34-313-2016
Parhi, S., Suess, S. T., and Sulkanen, M. (1999). Can Kelvin-Helmholtz Instabilities of Jet-like Structures and Plumes Cause Solar Wind Fluctuations at 1 AU?. J. Geophys. Res. Space Phys. 104, 14781–14787. doi:10.1029/1999ja900041
Paulikas, G. A., and Blake, J. B. (1979). Effects of the Solar Wind on Magnetospheric Dynamics: Energetic Electrons at the Synchronous Orbit. Quantitative Model. magnetospheric Process. Geophys. Monogr. Ser. 21, 180–202. doi:10.1029/gm021p0180
Perez, J. C., Bourouaine, S., Chen, C. H. K., and Raouafi, N. E. (2021). Applicability of Taylor’s Hypothesis during Parker Solar Probe Perihelia. Astron. Astrophysics 650, A22. doi:10.1051/0004-6361/202039879
Peter, H. (1998). Element Separation in the Chromosphere Ionization-Diffusion Models for the FIP-Effect. Space Sci. Rev. 85, 253–260. doi:10.1023/a:1005150500590
Phan, T. D., Lavraud, B., Halekas, J. S., Øieroset, M., Drake, J. F., Eastwood, J. P., et al. (2021). Prevalence of Magnetic Reconnection in the Near-Sun Heliospheric Current Sheet. Astron. Astrophysics 650, A13. doi:10.1051/0004-6361/202039863
Pontin, D. I., and Wyper, P. F. (2015). The Effect of Reconnection on the Structure of the Sun’s Open-Closed Boundary. Astrophysical J. 805, 39. doi:10.1088/0004-637x/805/1/39
Pylaev, O. S., Zaqarashvili, T. V., Brazhenko, A. I., Melnik, V. N., Hanslmeier, A., and Panchenko, M. (2017). Oscillation of Solar Radio Emission at Coronal Acoustic Cut-Off Frequency. Astron. Astrophysics 601, A42. doi:10.1051/0004-6361/201629218
Rakowski, C. E., and Laming, J. M. (2012). On the Origin of the Slow Speed Solar Wind: Helium Abundance Variations. Astrophysical J. 754, 65. doi:10.1088/0004-637x/754/1/65
Raouafi, N. E., Patsourakos, S., Pariat, E., Young, P. R., Sterling, A. C., Savcheva, A., et al. (2016). Solar Coronal Jets: Observations, Theory, and Modeling. Space Sci. Rev. 201, 1–53. doi:10.1007/s11214-016-0260-5
Rappazzo, A. F., Velli, M., Einaudi, G., and Dahlburg, R. B. (2008). Nonlinear Dynamics of the Parker Scenario for Coronal Heating. Astrophysical J. 677, 1348–1366. doi:10.1086/528786
Raymond, J. C., Kohl, J. L., Noci, G., Antonucci, E., Tondello, G., Huber, M. C. E., et al. (1997). Composition of Coronal Streamers from the SOHO Ultraviolet Coronagraph Spectrometer. Solar Phys. 175, 645–665. doi:10.1023/a:1004948423169
Reid, H. A. S., and Kontar, E. P. (2010). Solar Wind Density Turbulence and Solar Flare Electron Transport from the Sun to the Earth. Astrophysical J. 721, 864. doi:10.1088/0004-637x/721/1/864
Reisenfeld, D. B., McComas, D. J., and Steinberg, J. T. (1999). Evidence of a Solar Origin for Pressure Balance Structures in the High-Latitude Solar Wind. Geophys. Res. Lett. 26, 1805. doi:10.1029/1999gl900368
Réville, V., Velli, M., Rouillard, A. P., Lavraud, B., Tenerani, A., Shi, C., et al. (2020). Tearing Instability and Periodic Density Perturbations in the Slow Solar Wind. Astrophysical J. 895, L20. doi:10.3847/2041-8213/ab911d
Richardson, I. G. (2018). Solar Wind Stream Interaction Regions throughout the Heliosphere. Living Rev. Solar Phys. 15, 1. doi:10.1007/s41116-017-0011-z
Robbrecht, E., Berghmans, D., and Linden, R. A. M. V. d. (2009). Automated LASCO CME Catalog for Solar Cycle 23: Are CMEs Scale Invariant?. Astrophysical J. 691, 1222–1234. doi:10.1088/0004-637x/691/2/1222
Roberts, D. A. (2010). Demonstrations that the Solar Wind Is Not Accelerated by Waves or Turbulence. Astrophysical J. 711, 1044–1050. doi:10.1088/0004-637x/711/2/1044
Roberts, D. A., Ghosh, S., Goldstein, M. L., and Mattheaus, W. H. (1991). Magnetohydrodynamic Simulation of the Radial Evolution and Stream Structure of Solar-Wind Turbulence. Phys. Rev. Lett. 67, 3741–3744. doi:10.1103/physrevlett.67.3741
Roberts, D. A., Goldstein, M. L., Klein, L. W., and Matthaeus, W. H. (1987). Origin and Evolution of Fluctuations in the Solar Wind: Helios Observations and Helios-Voyager Comparisons. J. Geophys. Res. Space Phys. 92, 12023–12035. doi:10.1029/ja092ia11p12023
Roberts, D. A., and Goldstein, M. L. (1987). Spectral Signatures of Jumps and Turbulence in Interplanetary Speed and Magnetic Field Data. J. Geophys. Res. Space Phys. 92, 10105–10110. doi:10.1029/ja092ia09p10105
Roberts, D. A., Karimabadi, H., Sipes, T., Ko, Y.-K., and Lepri, S. (2020). Objectively Determining States of the Solar Wind Using Machine Learning. Astrophysical J. 889, 153. doi:10.3847/1538-4357/ab5a7a
Roberts, D. A., Keiter, P. A., and Goldstein, M. L. (2005). Origin and Dynamics of the Heliospheric Streamer belt and Current Sheet. J. Geophys. Res. Space Phys. 110,A06102. doi:10.1029/2004ja010541
Roberts, D. A., and Ofman, L. (2019). Hybrid Simulation of Solar-wind-like Turbulence. Solar Phys. 294, 153. doi:10.1007/s11207-019-1548-x
Roberts, M. A., Uritsky, V. M., DeVore, C. R., and Karpen, J. T. (2018). Simulated Encounters of the Parker Solar Probe with a Coronal-Hole Jet. Astrophysical J. 866, 14. doi:10.3847/1538-4357/aadb41
Roberts, O. W., Li, X., and Li, B. (2013). Kinetic Plasma Turbulence in the Fast Solar Wind Measured by Cluster. Astrophysical J. 769, 58. doi:10.1088/0004-637x/769/1/58
Roberts, O. W., Nakamura, R., Torkar, K., Narita, Y., Holmes, J. C., Vörös, Z., et al. (2020). Sub-ion Scale Compressive Turbulence in the Solar Wind: MMS Spacecraft Potential Observations. Astrophysical J. Suppl. Ser. 250, 35. doi:10.3847/1538-4365/abb45d
Rosenvinge, T. T. v., Richardson, I. G., Reames, D. V., Cohen, C. M. S., Cummings, A. C., Leske, R. A., et al. (2009). The Solar Energetic Particle Event of 14 December 2006. Solar Phys. 256, 443–462. doi:10.1007/s11207-009-9353-6
Rouillard, A. P., Davies, J. A., Lavraud, B., Forsyth, R. J., Savani, N. P., Bewsher, D., et al. (2010). Intermittent Release of Transients in the Slow Solar Wind: 1. Remote Sensing Observations. J. Geophys. Res. Space Phys. 115, n/a. doi:10.1029/2009ja014471
Rouillard, A. P., Kouloumvakos, A., Vourlidas, A., Kasper, J., Bale, S., Raouafi, N.-E., et al. (2020). Relating Streamer Flows to Density and Magnetic Structures at the Parker Solar Probe. Astrophysical J. Suppl. Ser. 246, 37. doi:10.3847/1538-4365/ab579a
Rouillard, A. P., Lavraud, B., Davies, J. A., Savani, N. P., Burlaga, L. F., Forsyth, R. J., et al. (2010). Intermittent Release of Transients in the Slow Solar Wind: 2. In Situ Evidence. J. Geophys. Res. Space Phys. 115, n/a. doi:10.1029/2009ja014472
Rouillard, A. P., Savani, N. P., Davies, J. A., Lavraud, B., Forsyth, R. J., Morley, S. K., et al. (2009). A Multispacecraft Analysis of a Small-Scale Transient Entrained by Solar Wind Streams. Solar Phys. 256, 307–326. doi:10.1007/s11207-009-9329-6
Šafránková, J., Němeček, Z., Němec, F., Přech, L., Pitňa, A., Chen, C. H. K., et al. (2015). Solar Wind Density Spectra Around the Ion Spectral Break. Astrophysical J. 803, 107. doi:10.1088/0004-637x/803/2/107
Sahraoui, F., Goldstein, M. L., Robert, P., and Khotyaintsev, Y. V. (2009). Evidence of a Cascade and Dissipation of Solar-Wind Turbulence at the Electron Gyroscale. Phys. Rev. Lett. 102, 231102. doi:10.1103/physrevlett.102.231102
Sako, N., Shimojo, M., Watanabe, T., and Sekii, T. (2013). A Statistical Study of Coronal Active Events in the north Polar Region. Astrophysical J. 775, 22. doi:10.1088/0004-637x/775/1/22
Sanchez-Diaz, E., Rouillard, A. P., Davies, J. A., Lavraud, B., Pinto, R. F., and Kilpua, E. (2017). The Temporal and Spatial Scales of Density Structures Released in the Slow Solar Wind during Solar Activity Maximum. Astrophysical J. 851, 32. doi:10.3847/1538-4357/aa98e2
Savcheva, A., Cirtain, J., DeLuca, E. E., Lundquist, L. L., Golub, L., Weber, M., et al. (2007). A Study of Polar Jet Parameters Based on Hinode XRT Observations. Publications Astronomical Soc. Jpn. 59, S771–S778. doi:10.1093/pasj/59.sp3.s771
Schlenker, M., Antiochos, S., MacNeice, P., and Mason, E. (2021). The Effect of Thermal Non-ewuilibrium on Helmet Streamers. Astrophysical J. 916 (2), 115. doi:10.3847/1538-4357/ac069d
Schrijver, C. J., Title, A. M., van Ballegooijen, A. A., Hagenaar, H. J., and Shine, R. A. (1997). Sustaining the Quiet Photospheric Network: The Balance of Flux Emergence, Fragmentation, Merging, and Cancellation. Astrophysical J. 487, 424–436. doi:10.1086/304581
Sheeley, N. R., and Rouillard, A. P. (2010). Tracking Streamer Blobs into the Heliosphere. Astrophysical J. 715, 300. doi:10.1088/0004-637x/715/1/300
Sheeley, N. R., Walters, J. H., Wang, Y., and Howard, R. A. (1999). Continuous Tracking of Coronal Outflows: Two Kinds of Coronal Mass Ejections. J. Geophys. Res. Space Phys. 104, 24739–24767. doi:10.1029/1999ja900308
Sheeley, N. R., Wang, Y.-M., Hawley, S. H., Brueckner, G. E., Dere, K. P., Howard, R. A., et al. (1997). Measurements of Flow Speeds in the corona between 2 and 30 R⋅. Astrophysical J. 484, 472–478. doi:10.1086/304338
Shi, C., Velli, M., Panasenco, O., Tenerani, A., Réville, V., Bale, S. D., et al. (2021). Alfvénic versus Non-alfvénic Turbulence in the Inner Heliosphere as Observed by Parker Solar Probe. Astron. Astrophysics 650, A21. doi:10.1051/0004-6361/202039818
Shoda, M., Chandran, B. D. G., and Cranmer, S. R. (2021). Turbulent Generation of Magnetic Switchbacks in the Alfvénic Solar Wind. Astrophysical J. 915, 52. doi:10.3847/1538-4357/abfdbc
Simunac, K. D. C., Kistler, L. M., Galvin, A. B., Lee, M. A., Popecki, M. A., Farrugia, C., et al. (2009). In Situ Observations of Solar Wind Stream Interface Evolution. Solar Phys. 259, 323. doi:10.1007/s11207-009-9393-y
Squire, J., Chandran, B. D. G., and Meyrand, R. (2020). In-situ Switchback Formation in the Expanding Solar Wind. Astrophysical J. 891, L2. doi:10.3847/2041-8213/ab74e1
Stansby, D., and Horbury, T. S. (2018). Number Density Structures in the Inner Heliosphere. Astron. Astrophysics 613, A62. doi:10.1051/0004-6361/201732567
Stephenson, J. A. E., and Walker, A. D. M. (2002). HF Radar Observations of Pc5 ULF Pulsations Driven by the Solar Wind. Geophys. Res. Lett. 29, 8–1–8–4. doi:10.1029/2001gl014291
Sterling, A. C., Moore, R. L., Falconer, D. A., and Adams, M. (2015). Small-scale Filament Eruptions as the Driver of X-ray Jets in Solar Coronal Holes. Nature 523, 437–440. doi:10.1038/nature14556
Suess, S. (2001). “Fine Structure in the Corona and Solar Wind at High Heliographic Latitudes at Solar Maximum,” in The 3-D Heliosphere at Solar Maximum, Proceedings of the 34th ESLAB Symposium (Netherlands: Noordwijk), 55–58. doi:10.1007/978-94-017-3230-7_10
Suess, S. T., Ko, Y., Steiger, R. v., and Moore, R. L. (2009). Quiescent Current Sheets in the Solar Wind and Origins of Slow Wind. J. Geophys. Res. Space Phys. 114, n/a. doi:10.1029/2008ja013704
Telloni, D., Sorriso-Valvo, L., Woodham, L. D., Panasenco, O., Velli, M., Carbone, F., et al. (2021). Evolution of Solar Wind Turbulence from 0.1 to 1 au during the First Parker Solar Probe–Solar Orbiter Radial Alignment. Astrophysical J. Lett. 912, L21. doi:10.3847/2041-8213/abf7d1
Tenerani, A., Velli, M., Matteini, L., Réville, V., Shi, C., Bale, S. D., et al. (2020). Magnetic Field Kinks and Folds in the Solar Wind. Astrophysical J. Suppl. Ser. 246, 32. doi:10.3847/1538-4365/ab53e1
Tessein, J. A., Ruffolo, D., Matthaeus, W. H., Wan, M., Giacalone, J., and Neugebauer, M. (2015). Effect of Coherent Structures on Energetic Particle Intensity in the Solar Wind at 1 AU. Astrophysical J. 812, 68. doi:10.1088/0004-637x/812/1/68
Thieme, K., Marsch, E., and Schwenn, R. (1990). Spatial Structures in High-Speed Streams as Signatures of fine Structures in Coronal Holes. Ann. Geophysicae 8, 713–723.
Thieme, K., Schwenn, R., and Marsch, E. (1989). Are Structures in High-Speed Streams Signatures of Coronal fine Structures?. Adv. Space Res. 9, 127–130. doi:10.1016/0273-1177(89)90105-1
Titov, V. S., Mikić, Z., Linker, J. A., Lionello, R., and Antiochos, S. K. (2011). Magnetic Topology of Coronal Hole Linkages. Astrophysical J. 731, 111. doi:10.1088/0004-637x/731/2/111
Treumann, R. A., Baumjohann, W., and Narita, Y. (2019). On the Applicability of Taylor’s Hypothesis in Streaming Magnetohydrodynamic Turbulence. Earth, Planets and Space 71, 41. doi:10.1186/s40623-019-1021-y
Tsurutani, B. T., Gonzalez, W. D., Gonzalez, A. L. C., Guarnieri, F. L., Gopalswamy, N., Grande, M., et al. (2006). Corotating Solar Wind Streams and Recurrent Geomagnetic Activity: A Review. J. Geophys. Res. Space Phys. 111, A07S01. doi:10.1029/2005ja011273
Tsurutani, B. T., and Gonzalez, W. D. (1987). The Cause of High-Intensity Long-Duration Continuous AE Activity (HILDCAAS) - Interplanetary Alfven Wave Trains. Planet. Space Sci. 35, 405. doi:10.1016/0032-0633(87)90097-3
Tsurutani, B. T., Ho, C. M., Smith, E. J., Neugebauer, M., Goldstein, B. E., Mok, J. S., et al. (1994). The Relationship between Interplanetary Discontinuities and Alfvén Waves: Ulysses Observations. Geophys. Res. Lett. 21, 2267–2270. doi:10.1029/94gl02194
Tu, C. Y., and Marsch, E. (1995). MHD Structures, Waves and Turbulence in the Solar Wind: Observations and Theories. Space Sci. Rev. 73, 1–210. doi:10.1007/bf00748891
Turner, D. L., Kilpua, E. K. J., Hietala, H., Claudepierre, S. G., O’Brien, T. P., Fennell, J. F., et al. (2019). The Response of Earth’s Electron Radiation Belts to Geomagnetic Storms: Statistics from the Van Allen Probes Era Including Effects from Different Storm Drivers. J. Geophys. Res. Space Phys. 124, 1013–1034. doi:10.1029/2018ja026066
Turner, D. L., Shprits, Y., Hartinger, M., and Angelopoulos, V. (2012). Explaining Sudden Losses of Outer Radiation belt Electrons during Geomagnetic Storms. Nat. Phys. 8, 208. doi:10.1038/nphys2185
Velli, M., Lionello, R., Linker, J. A., and Mikić, Z. (2011). Coronal Plumes in the Fast Solar Wind. Astrophysical J. 736, 32. doi:10.1088/0004-637x/736/1/32
Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The Multi-Scale Nature of the Solar Wind. Living Rev. Solar Phys. 16, 5. doi:10.1007/s41116-019-0021-0
Viall, N. M., and Borovsky, J. E. (2020). Nine Outstanding Questions of Solar Wind Physics. J. Geophys. Res. Space Phys. 125, e2018JA026005. doi:10.1029/2018ja026005
Viall, N. M., Kepko, L., and Spence, H. E. (2009). Relative Occurrence Rates and Connection of Discrete Frequency Oscillations in the Solar Wind Density and Dayside Magnetosphere. J. Geophys. Res. Space Phys. 114, n/a. (c) 2009: American Geophysical Union. doi:10.1029/2008ja013334
Viall, N., De Moortel, I., Downs, C., Klimchuk, J. A., Parenti, S., and Reale, F. (2021). “The Heating of the Solar Corona,” in Solar Physics and Solar Wind. Editors N. E. Raouafi, A. Vourlidas, Y. Zhang, and L. J. Paxton, 35–82. doi:10.1002/9781119815600.ch2
Viall, N. M., Spence, H. E., and Kasper, J. (2009). Are Periodic Solar Wind Number Density Structures Formed in the Solar corona?. Geophys. Res. Lett. 36, 23102. doi:10.1029/2009gl041191
Viall, N. M., Spence, H. E., Vourlidas, A., and Howard, R. (2010). Examining Periodic Solar-Wind Density Structures Observed in the SECCHI Heliospheric Imagers. Solar Phys. 267, 175–202. (c) 2010: Springer Science+Business Media B.V. doi:10.1007/s11207-010-9633-1
Viall, N. M., and Vourlidas, A. (2015). Periodic Density Structures and the Origin of the Slow Solar Wind. Astrophysical J. 807, 176. doi:10.1088/0004-637x/807/2/176
Villante, U., Corpo, A. D., and Francia, P. (2013). Geomagnetic and Solar Wind Fluctuations at Discrete Frequencies: A Case Study. J. Geophys. Res. Space Phys. 118, 218–231. doi:10.1029/2012ja017971
Villante, U., and Tiberi, P. (2016). Occurrence and Characteristics of Nighttime ULF Waves at Low Latitude: The Results of a Comprehensive Analysis. J. Geophys. Res. Space Phys. 121, 4300–4315. doi:10.1002/2015ja022137
Vourlidas, A., and Howard, R. A. (2006). The Proper Treatment of Coronal Mass Ejection Brightness: A New Methodology and Implications for Observations. Astrophysical J. 642, 1216–1221. doi:10.1086/501122
Wang, Y.-M., Sheeley, N. R., Socker, D. G., Howard, R. A., and Rich, N. B. (2000). The Dynamical Nature of Coronal Streamers. J. Geophys. Res. Space Phys. 105, 25133. doi:10.1029/2000ja000149
Wang, Y. M., Sheeley, N. R., Walters, J. H., Brueckner, G. E., Howard, R. A., Michels, D. J., et al. (1998). Origin of Streamer Material in the Outer Corona. Astrophysical J. 498, L165–L168. doi:10.1086/311321
Weberg, M. J., Zurbuchen, T. H., and Lepri, S. T. (2012). ACE/SWICES Observations of Heavy Ion Dropouts within the Solar Wind. Astrophysical J. 760, 30. doi:10.1088/0004-637x/760/1/30
Woodham, L. D., Horbury, T. S., Matteini, L., Woolley, T., Laker, R., Bale, S. D., et al. (2020). Enhanced Proton Parallel Temperature inside Patches of Switchbacks in the Inner Heliosphere. A&A 650, L1. doi:10.1051/0004-6361/202039415
Wyper, P. F., Antiochos, S. K., and DeVore, C. R. (2017). A Universal Model for Solar Eruptions. Nature 544, 452–455. doi:10.1038/nature22050
Yao, S., He, J. S., Tu, C. Y., Wang, L. H., and Marsch, E. (2013). Small-scale Pressure-Balanced Structures Driven by Mirror-Mode Waves in the Solar Wind. Astrophysical J. 776, 94. doi:10.1088/0004-637X/776/2/94
Yao, S., He, J. S., Tu, C. Y., Wang, L. H., and Marsch, E. (2013). Small-scale Pressure-Balanced Structures Driven by Oblique Slow Mode Waves Measured in the Solar Wind. Astrophysical J. 774, 59. doi:10.1088/0004-637X/774/1/59
Yuan, C. J., and Zong, Q. (2012). Quantitative Aspects of Variations of 1.5–6.0 MeV Electrons in the Outer Radiation belt during Magnetic Storms. J. Geophys. Res. Space Phys. 117, n/a. doi:10.1029/2011ja017346
Zheng, J., and Hu, Q. (2018). Observational Evidence for Self-Generation of Small-Scale Magnetic Flux Ropes from Intermittent Solar Wind Turbulence. Astrophysical J. 852, L23. doi:10.3847/2041-8213/aaa3d7
Zhou, M., Man, H. Y., Deng, X. H., Pang, Y., Khotyaintsev, Y., Lapenta, G., et al. (2021). Observations of Secondary Magnetic Reconnection in the Turbulent Reconnection Outflow. Geophys. Res. Lett. 48, e2020GL091215. doi:10.1029/2020gl091215
Keywords: sun, heliosphere, solar wind, geospace, space weather, turbulence, solar variability, mesoscales
Citation: Viall NM, DeForest CE and Kepko L (2021) Mesoscale Structure in the Solar Wind. Front. Astron. Space Sci. 8:735034. doi: 10.3389/fspas.2021.735034
Received: 02 July 2021; Accepted: 10 August 2021;
Published: 25 August 2021.
Edited by:
Marina Stepanova, University of Santiago, ChileReviewed by:
Roberto Elías Navarro, University of Concepcion, ChileDaniel Verscharen, University College London, United Kingdom
Copyright © 2021 Viall, DeForest and Kepko. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: N. M. Viall, nicholeen.m.viall@nasa.gov
 N. M. Viall
N. M. Viall C. E. DeForest
C. E. DeForest L. Kepko
L. Kepko