1
Department of Brain and Cognitive Sciences, University of Rochester, Rochester, NY, USA
2
Department of Neurobiology, Yale University School of Medicine, New Haven, CT, USA
Humans and animals are more likely to take an action leading to an immediate reward than actions with delayed rewards of similar magnitudes. Although such devaluation of delayed rewards has been almost universally described by hyperbolic discount functions, the rate of this temporal discounting varies substantially among different animal species. This might be in part due to the differences in how the information about reward is presented to decision makers. In previous animal studies, reward delays or magnitudes were gradually adjusted across trials, so the animals learned the properties of future rewards from the rewards they waited for and consumed previously. In contrast, verbal cues have been used commonly in human studies. In the present study, rhesus monkeys were trained in a novel inter-temporal choice task in which the magnitude and delay of reward were indicated symbolically using visual cues and varied randomly across trials. We found that monkeys could extract the information about reward delays from visual symbols regardless of the number of symbols used to indicate the delay. The rate of temporal discounting observed in the present study was comparable to the previous estimates in other mammals, and the animal�s choice behavior was largely consistent with hyperbolic discounting. Our results also suggest that the rate of temporal discounting might be infl uenced by contextual factors, such as the novelty of the task. The fl exibility furnished by this new inter-temporal choice task might be useful for future neurobiological investigations on inter-temporal choice in non-human primates.
The rewards that humans and animals seek to obtain are often not delivered immediately after the required actions are completed. In such cases, the subjective desirability or utility of the expected reward decreases with its delay, and this is referred to as temporal discounting. Consequently, during inter-temporal choice in which the decision makers choose between rewards delivered after unequal delays, they might in some cases prefer a small but immediate reward to a larger but more delayed reward. Such impulsive choices can be often parsimoniously accounted for by a discount function, which is defined as the fraction of the subjective value of a delayed reward relative to that of the same reward delivered immediately. The value of a delayed reward multiplied by the discount function is referred to as the temporally discounted value. In addition, denoting the discount function as F(D), in which D refers to the delay of a reward, the ratio F′(D)/F(D) is referred to as the discount rate and indicates how rapidly the discount function decreases with delay. Abnormally high discount rate underlies a number of psychiatric disorders, including substance abuse and pathological gambling (see Reynolds, 2006
).
Regardless of the absolute value of discount rate, if the discount rate is constant and does not change with the reward delay, the discount function is exponential (Samuelson, 1937
). This implies that the relative preference for two different rewards available at time t1 and t2 would not be affected when their delays are altered by the same amount and become available at time t1 + Δt and t2 + Δt, respectively. The fact that the preference between the two delayed rewards does not change with the elapse of time is referred to as time-consistency, but this assumption is commonly violated (Ainslie and Herrnstein, 1981
; Green et al., 1981
, 1994
; Rachlin and Green, 1972
; Strotz, 1955–1956
). In addition, a large number of empirical studies have found that behaviors of humans and animals during inter-temporal choice are better described by hyperbolic discount functions that violate time consistency (Frederick et al., 2002
; Green and Myerson, 2004
; Kalenscher and Pennartz, 2008
). A decision maker with a hyperbolic discount function might prefer a larger and more delayed reward when both rewards have relatively large delays, but his or her preference might change when their delays are reduced by the same amount.
Although hyperbolic discount functions have successfully described behaviors for many different animal species, including humans, the overall rate of temporal discounting varied tremendously between humans and other animals. The reasons for this discrepancy are not fully understood, but might be related to the differences in the methods to measure the discount functions for humans and animals. In human studies, choices are typically presented using verbal cues, and the subjects are often allowed to engage in other activities while waiting for the delivery of rewards. In contrast, animals are tested in a more controlled environment and consume their chosen rewards after experiencing the corresponding delays. Moreover, in previous animal studies, reward delays and magnitudes are either fixed or adjusted gradually across successive trials so that they must be estimated from the animal’s experience. In the present study, we trained rhesus monkeys in a new inter-temporal choice task in which the information about the magnitude and delay of each reward is delivered symbolically and as a result could be manipulated independently across trials. We found that the animal’s behaviors were largely better accounted for by hyperbolic discount functions, whereas the form and rate of temporal discounting might be influenced by the novelty of the task.
Animal Preparation and Apparatus
Two male rhesus monkeys (monkeys D and J; body weight = 9.5 and 9.0 kg) were tested. During an aseptic surgery, a set of four titanium head posts were attached to the animal’s skull for the purpose of fixing the animal’s head during the experiment. The animals were seated in a primate chair and faced a 17-inch computer monitor located 57 cm away. A custom-designed software was used to control the task and coordinate data acquisition. Eye movements were monitored using a video eye tracking system with 225 Hz sampling rate (ET-49, Thomas Recording, Germany). All the procedures used in the present study were in accordance with the guidelines of the National Institutes of Health and were approved by the University of Rochester Committee on Animal Research.
Inter-Temporal Choice Task
General
Each trial began when the animal fixated a white square (0.9° × 0.9°) presented at the center of the monitor (Figure 1
). After a 1-s fore-period during which the animal was required to maintain its fixation of the central square within a 2°-radius window, two targets (1° disk in diameter) were presented 8° to the left and right of fixation. The animal was required to continue its central fixation until the white square was extinguished 1 s later. At the end of this cue period, the animal was then required to shift its gaze towards one of the two targets. One of the targets (TS) was green and delivered a small reward when it was chosen by the animal, whereas the other target (TL) was red and delivered a large reward. The delay between the fixation of the chosen target and the reward delivery was indicated by a variable number of small disks (0.9° in diameter) presented around each target. When the target was presented without any disks, the animal was rewarded after a 0.5 delay (Experiment I) or immediately (Experiments II and III) upon fixation of its chosen target. Otherwise, disks were extinguished one at a time according to a specific schedule described below, and the animal was rewarded after all the disks were extinguished. Yellow disks were extinguished at the rate of 0.5 s/disk (Experiment I) or 1.0 s/disk (Experiments II and III). In Experiment III, a mixture of yellow (1.0 s/disk) and cyan (4.0 s/disk) disks were used in some trials. The brightness of a yellow disk was fixed until it was extinguished, whereas a cyan disk dimmed gradually during the 4-s period before it was extinguished. The target that was not chosen by the animal and its clock were extinguished immediately after the animal fixated its chosen target. If the animal chose the large reward, the central white square for the next trial was presented following a 2-s inter-trial interval after the reward delivery. If the animal chose the small reward, the inter-trial interval was increased by the difference in the reward delays for the small and large reward targets. Therefore, the onset of the next trial was not affected by the animal’s choice.
Figure 1. Spatiotemporal sequences of the inter-temporal choice task. Three different types of clocks are referred to as ordered, random, and mixed. For both ordered and random clocks, the reward delay was indicated by the number of yellow disks that disappeared in a fixed or random order, respectively. Each yellow and cyan disk in mixed clocks corresponds to 1 and 4 s added to the reward delay, respectively.
The animal was required to maintain its fixation of the chosen target during the reward delay, but was allowed to re-fixate the target without any penalty if the target was re-fixated within 0.3 s after breaking the fixation. This also allowed the animals to blink without any penalty during the fixation on its chosen target. Throughout the experiment, the proportion of the trials that were aborted due to the animal’s failure to maintain its fixation during the reward delay was relatively low and never exceeded 2% of the trials. This always corresponded to a relatively small proportion fixation breaks during the entire trials, never exceeding 17% of all fixation breaks (mean = 1.6% and 6.9% for monkeys D and J, respectively). Moreover, extensive training was not necessary for fixation during the reward delays, and the animals frequently made saccades among the small disks. Although we could not quantify the additional efforts necessary for the fixation of the chosen target during the reward delays, these observations indicate that such efforts are likely to be relatively minor.
Reward delays and clocks
All the disks in the clock for a given target were presented on the circumference of an imaginary circle (4.0° in diameter) concentric with the target. In the following, the position of a disk in a given clock is described by its clockwise angular deviation from the position directly above the target. Disks were presented only at multiples of 45° (Figure 1
). In the present study, three different types of clocks were used, and referred to as ordered, random, and mixed, respectively. For ordered and random clocks, only yellow disks were used, whereas mixed clocks included both yellow and cyan disks. In an ordered clock with n yellow disks, disks were presented at the positions corresponding to 0°, 45°,…, (n − 1) × 45°, and were extinguished counter-clockwise during the reward delay so that the disk at 0° position was always extinguished at the end of the reward delay (Figure 1
, top). In random and mixed clocks, the positions of disks were determined randomly, and they were extinguished in a random order during the delay period (Figure 1
middle and bottom).
Preliminary training
Each animal was initially trained to fixate the central white square. Next, it was trained to choose between the green small-reward target and the red large-reward target, while the delay for the small reward was always 0.5 s. Within a few days, both animals were gradually exposed to various reward delays and started to choose the large-reward target less frequently as its reward delay increased. No rewards were omitted during this training period, as long as the animal performed the task correctly. Before the data collection began for Experiment I, monkeys D and J were trained for this inter-temporal choice task for 9 and 12 days, respectively.
Experiment I
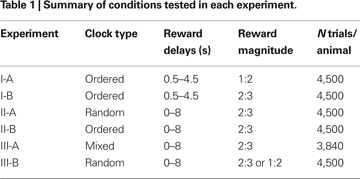
During the trials of Experiment I, only the ordered clocks were used and all disks in the clocks were yellow. The reward delay for the clock with n yellow disks was (n + 1)/2 s, where n = 0, 1,…8, corresponding to the delays ranging from 0.5 to 4.5 s. Among the 64 possible combinations of reward delays for the two targets, only those in which the reward delay for the large-reward target was equal to or longer than the delay for the small-reward target were used. This resulted in 45 different combinations of the reward delays. The positions of the large-reward and small-reward targets were counter-balanced across trials, resulting in 90 trials in a block. In Experiment I-A, the animal received 0.2 and 0.4 ml of apple juice for small and large rewards, respectively. The size of the small reward was increased to 0.27 ml in Experiment I-B, in order to encourage the animals to choose the small-reward target more frequently. Each animal performed 10 blocks (900 trials) each day (Table 1
). Monkey D was tested in Experiment I-A for 5 days and then in Experiment I-B for 5 days, whereas the order of these two experiments was reversed for Monkey J.
Experiment II
In Experiment II, the clock with n yellow disks indicated that the reward delay was n seconds (n = 0, 1,…, 8). Thus, reward delays ranged between 0 and 8 s. During Experiment II, the small and large rewards were 0.27 and 0.4 ml of juice. As in Experiment I, all possible combinations of reward delays were used as long as the delay for the large reward was equal to or larger than the delay for the small reward. Each animal performed 10 blocks (900 trials) daily. Only the random clocks were used in Experiment II-A, whereas for Experiment II-B, only the ordered clocks were used (Table 1
). After Experiment I, both animals were tested in neurophysiological experiments in which a subset of conditions included in Experiment II-A was used (Kim et al., 2008
). Accordingly, Experiment II was conducted approximately 6 and 8 months after Experiment I for monkeys D and J, respectively. Both animals were tested for 5 days in Experiment II-A, and then for 5 days in Experiment II-B.
Experiment III
In Experiment III-A, mixed clocks were introduced to test whether the animals could extract the information about the reward delays independently of the number of disks in the clock. During Experiment III, a clock that includes nY yellow disks and nC cyan disks indicated the reward delay of (nY + 4 nC) s. Therefore, clocks did not include any cyan disks (nC = 0) if the reward delay was less than 4 s. In addition, when the reward delay was 4, 5, 6, or 7 s, a given delay was indicated by one of two different types of clocks (nC = 0 or 1). For example, the delay of 4 s could be indicated by (nY, nC) = (4, 0) or (0,1), and the delay of 5 s by (5, 0) or (1, 1). Finally, three different types of clocks were used to indicate the 8-s reward delay, namely, (nY, nC) = (8, 0), (4, 1), or (0, 2). Accordingly, 15 different types of clocks were available to indicate the reward delay ranging from 0 to 8 s. To limit the number of different combinations of clocks, the reward delays for the small-reward target were restricted to 0, 2, 4, and 6 s. Excluding the cases in which the delay for the small reward is longer than the delay for the large reward, therefore, a total of 64 different combinations of clocks were used in Experiment III-A. The positions of the large-reward and small-reward targets were counter-balanced, and this resulted in 128 trials in a given block. Both monkeys were tested for 5 days in Experiment III-A and completed six blocks (768 trials) each day. In Experiment III-A, the animal was rewarded by 0.27 and 0.4 ml of juice for choosing the small-reward and large-reward target, respectively.
Prior to Experiment III-A, both animals were trained with mixed clocks for several weeks. This preliminary training began approximately 5 and 3 months after Experiment II for monkeys D and J, respectively. During this preliminary training, each animal was trained for 17 days (monkey D) or 13 days (monkey J) with a subset of reward delays used in Experiment III-A in which the delay for the small reward was either 0 or 2 s. Each animal was then trained for another day (day 18 and day 14 for monkeys D and J, respectively) with all the conditions described above for Experiment III-A before collecting the data described in the Results. After Experiment III-A, one of the monkeys (monkey J) was tested using the mixed clocks in a neurophysiological experiment (Kim et al., 2008
). During this period, only a subset of reward delays in Experiment III-A was used (0 and 2 s for small reward and 0, 2, 5, and 8 s for large reward). Both animals were then tested in Experiment III-B in order to investigate whether exposure to mixed clocks influenced the animal’s discount function. Experiment III-B was identical to Experiment II-A, except that the magnitude of small reward was reduced to 0.2 ml for monkey J.
Data Analysis
In the following, the symbol Ω is used to denote a set of variables corresponding to the magnitudes and delays of small and large rewards. Namely, Ω = {ATS, ATL, DTS, DTL}, in which ATS (ATL) and DTS (DTL) refer to the magnitude and delay of small (large) reward, respectively. To estimate the animal’s discount function from its choices, we assumed that the probability of choosing TS given Ω, P(TS|Ω), was determined by the difference in the temporally discounted values for the two targets. In other words, denoting the temporally discounted value of a given target x as DV(Ax, Dx),
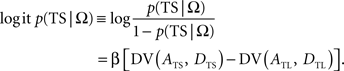
This is also known as softmax transformation, and is equivalent to the Boltzmann distribution given by the following:
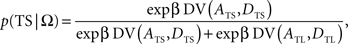
where β denotes the inverse temperature controlling the randomness of the animal’s choices. In addition, p(TL|Ω) = 1 − p(TS|Ω). Therefore, p(TS|Ω) = p(TL|Ω) = 0.5, if the temporally discounted values are equal for both targets, and p(TS) approaches 1, as the temporally discounted value of TS increases. The temporally discounted value of the reward with the magnitude A and delay D is determined by the following:
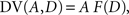
where F(D) refers to a discount function. An exponential discount function corresponds to the following:
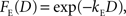
where kE denotes the discount rate (s−1). A hyperbolic discount function can be given by the following:
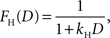
where the parameter kH controls the steepness of discounting. We have also tested three additional discount functions. One of them is a variant of hyperbolic discount function in which the more immediate reward is not discounted and the more delayed reward is discounted according to the hyperbolic discount function based on the difference in the delays of the two rewards (Green et al., 2005
). In addition, the general hyperbolic discount function (Green and Myerson, 2004
; Takahashi et al., 2008
), FG, and the β-δ discount function (Phelps and Pollak, 1968
), Fβ-δ, are given by the following:
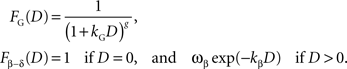
It should be noted that the general hyperbolic discount function shown above is mathematically equivalent to the so-called q-exponential discount function (Cajueiro, 2006
; Takahashi et al., 2008
), which is given by the following:
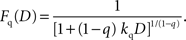
The parameters of the general hyperbolic discount function and q-exponential discount function are related by the following;
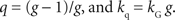
Denoting the animal’s choice in trial t as ct (=TS or TL), the likelihood of the animal’s choices was given by,
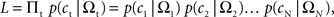
where Ωt denotes the magnitudes and delays for the rewards in trial t, and N the number of trials. For each discount function, model parameters were chosen to maximize the log likelihood (Pawitan, 2001
), using a function minimization procedure in Matlab (Mathworks, Natick, MA, USA). Since the models with exponential and hyperbolic discount functions both include two parameters (β and k), these two models were compared using their log likelihood. This was carried out for the entire data from a given experiment as well as separately for each daily session. The general hyperbolic and β-δ discount functions included an additional parameter. Therefore, the Bayesian information criterion (BIC) was used to compare the performance of models with different numbers of parameters. BIC was computed as follows:
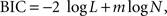
where N is the number of trials and m the number of model parameters (e.g., 2 for the model with exponential or hyperbolic discount function). For the results obtained from monkey D in Experiments I-B and III-A, the process of parameter search failed to converge for the general hyperbolic discount function. In these two cases, the values of the parameters in the general hyperbolic discount functions were computed by estimating the parameters of the q-exponential discount function instead and converting them as described above. Since the general hyperbolic discount function and q-exponential discount function are mathematically equivalent, the log likelihood for the best parameters of these two models should be the same.
During Experiment III-A, the physical reward delay was given by (nY + 4 nC) s, in which nY and nC indicate the numbers of yellow and cyan disks, respectively. Temporally discounted values of rewards associated with mixed clocks were computed without assuming that the animal accurately estimated the value of nC. This was done by using the subjective delays for cyan disks, which were estimated as a free parameter in the maximum likelihood procedure described above. In other words, the subjective reward delays used to compute temporally discounted values were given by (nY + DC nC) s, in which DC refers to the subjective delay for one cyan disk.
Experiment I
In Experiment I, the reward delays ranged from 0.5 to 4.5 s, and the disks were always removed in a counter-clock direction (referred to as “ordered” clocks; Figure 1
). In Experiment I-A, the ratio for the small and large reward was 1:2, whereas this ratio was 2:3 in Experiment I-B (Table 1
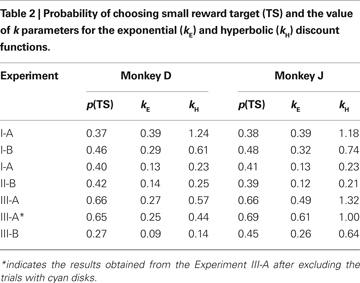
). In both Experiments I-A and I-B, the animals almost always chose the large reward when the reward delays were 0.5 s for both targets. Monkey D never chose the small-reward target, whereas monkey J chose the small-reward target in 1% and 3% of the trials when the reward delays were both 0.5 s during Experiments I-A and I-B, respectively. Therefore, both animals displayed a clear preference for the large reward when both large and small rewards were immediately available. In contrast, collapsed across all possible reward delays, the probability that the animal chose the small-reward target through the entire Experiment I-A was 0.37 and 0.38 for monkeys D and J (Table 2
). Therefore, both animals chose the small-reward target much more frequently, when the large reward was delayed. The corresponding values for Experiment I-B were 0.46 and 0.48, indicating that the animals were more likely to choose the small reward when its magnitude was more similar to that of the large reward. This difference is unlikely to reflect the difference in the animal’s experience with the task, since the two animals were tested for Experiments I-A and I-B in different orders. Most importantly, both animals were increasingly more likely to choose the small-reward target as the delay for the small reward decreased and the delay for the large reward increased (Figure 2
), and this was true for both Experiments I-A and I-B (data not shown). Therefore, the animal’s choice between two different rewards was systematically affected by both the magnitudes and delays of rewards. This suggests that the animal’s preference for a given reward might be parsimoniously described by its temporally discounted value.
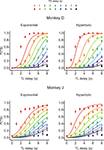
Figure 2. Choice behaviors in Experiment I-A. Plots show the probability that the animal would choose the small-reward target as a function of the delays for the large-reward (TL) and small-reward (TS) targets, which are indicated in the abscissa and by different colored symbols, respectively. Lines indicate the predictions from the exponential (left) or hyperbolic (right) discount functions. Error bars, SEM.
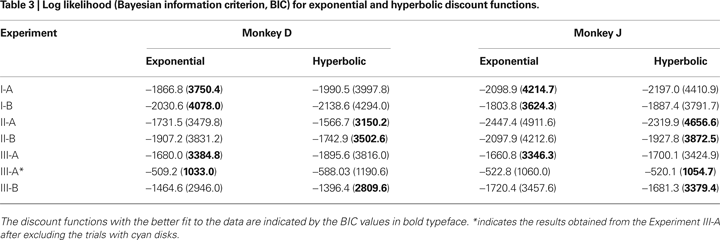
To test whether the animal’s behavior during the inter-temporal choice task was better accounted for by an exponential or hyperbolic discount function, we compared the log likelihood of the choice models based on these two discount functions (see Data Analysis). When the analysis was applied to the entire data set, the exponential discount function provided a better fit to the data for both animals (Figure 2
; Table 3
). This was true for both Experiments I-A and I-B. The results were similar, even when the same analysis was applied separately to the data from each daily session (Figure 3
). The data from both animals were fit better by an exponential discount function, except for the 2 days in Experiment I-B in monkey J (Figure 3
). When the model with the exponential discount function was fit to the entire data set from Experiment I-A, the maximum likelihood estimates of the discount rate were 0.39 s−1 for both animals. This value decreased to 0.29 and 0.32 for monkeys D and J in Experiment I-B (Table 2
), although the results from individual daily sessions were somewhat more variable (Figure 4
). For an exponential discount function, the temporally discounted value would be reduced by 50% for the delay equal to −(1/kE) log 0.5. Therefore, the approximate half-life for the subjective value of a reward was 2.2–2.4 s.
Figure 3. Daily changes in the log likelihood ratio between the exponential and hyperbolic discount function. Positive (negative) values indicate that the exponential (hyperbolic) discount function accounted for the behavioral data better.
Figure 4. Daily changes in the parameter k for the exponential (top) and hyperbolic (bottom) discount function. For Experiment III-A, squares indicate the values obtained from the trials in which the clocks did not include any cyan disks. For some sessions during Experiment III-A (monkey J), the model parameters did not converge for the hyperbolic discount function and therefore omitted.
Experiment II
In Experiment II-A, the maximum reward delay was increased to 8 s. In addition, the positions of yellow disks in the clocks were randomized in Experiment II-A (referred to as “random” clocks; Figure 1
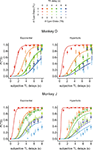
). In Experiment II-B, only the ordered clocks were used to test whether the animal’s behavior was affected by the manner in which the clocks represent the reward delays. As in Experiment I, the percentage of trials in which the animal chose the small-reward target was relatively small (<6%) when the reward delays were 0 s for both targets. In contrast, the overall probability that the animal would choose the small reward across all the reward delays used in Experiment II-A was 0.40 and 0.41 for monkeys D and J, respectively. The corresponding values for Experiment II-B were 0.42 and 0.39. Therefore, both animals chose the small reward targets much more frequently when the large reward was not available immediately. In addition, similar to the results in Experiment I, the animals chose the small reward increasingly more often as the delay for the large reward increased and as the delay for the small reward decreased in both Experiment II-A (Figure 5
) and II-B (not shown).
Figure 5. Choice behaviors in Experiment II-A. Same format as in Figure 2
.
In contrast to the results in Experiment I, the data from Experiment II were fit better by a hyperbolic discount function than by an exponential discount function. This was true for both Experiments II-A and II-B (Table 3
). The slope and discount rate of a hyperbolic discount function decrease with delay. Consistent with this feature of hyperbolic discounting, the comparison between the data and the predictions from the best-fitting exponential discount function shows that the animals were particularly more likely to choose the small reward available without any delays than predicted by the exponential discount function (Figure 5
, left). For Experiment II-A, the value of parameter kH in the hyperbolic discount function was 0.23 for both animals. The corresponding values for Experiment II-B were 0.25 and 0.21. For hyperbolic discount function, the temporally discounted value is reduced by half when the reward delay is 1/kH. This implies that the half-life for the subjective value of reward was approximately 4.0 to 4.8 s. Moreover, the overall results from Experiments II-A and II-B were relatively similar (Figure 4
). Therefore, the animals reliably extracted the information about reward delays from the visual displays regardless of the manner in which the disks were arranged and removed in the clocks.
Experiment III
To test whether the animals can reliably estimate reward delays from the clocks without relying entirely on the number of disks, clocks used in Experiment III-A sometimes included a combination of yellow and cyan disks. Yellow and cyan disks increased the reward delay for a given target by 1 and 4 s/disk, respectively. Not surprisingly, when the animals were first exposed to mixed clocks, their choices were largely determined by the number of disks in each clock, regardless of their colors. For example, when the animals chose between a small reward with a 2-s delay and a large reward with a 5-s delay, they were at first more likely to choose the small reward if the 5-s delay was indicated by five yellow disks compared to when the same delay was indicated by a mixed clock with one yellow disk and one cyan disk (Figure 6
A). This difference was gradually diminished during the preliminary training, especially for monkey D, whereas it was not completely eliminated for monkey J. We have also estimated the subjective delay associated with each cyan disk using a maximum likelihood procedure (see Data Analysis) for the data obtained during the preliminary training. Consistent with the changes in the choice probabilities, the subjective delays for cyan disks were initially relatively close to the delay for yellow disks (1 s) and gradually increased towards the correct value (4 s; Figure 6
B). This was true regardless of whether the subjective delays were estimated using exponential or hyperbolic discount functions.
Figure 6. Time course for the learning of delay information from the mixed clocks. (A) The plot shows daily changes in the probability that the animal would choose the small-reward target with a 2-s delay instead of the large-reward target with a 5-s delay. The delay for the large reward was indicated by either five yellow disks (filled circles) or by a combination of a yellow disk and a cyan disk (empty circles). (B) Daily changes in the subjective delay attributed to a single cyan disk. This was determined separately for exponential and hyperbolic discount functions. The actual delays corresponding to the yellow (1 s) and cyan (4 s) disks are indicated by the dotted lines. Large symbols show the results from the last 5 days that were included in the main analysis. Gray background indicates the period in which only a subset of conditions tested in Experiment III-A were used for the purpose of training. The results for monkey J during the first several days are missing, because cyan dots were introduced more gradually for this animal.
During Experiment III-A, the probability of choosing the small reward was 0.66 for both monkeys. To examine how the animal’s choice was influenced by the delays for small and large rewards, we assumed that the subjective delay for a mixed clock was given by (nY + DC nC) s, in which nY and nC refer to the numbers of yellow and cyan disks and DC was the subjective delay for a cyan disk. For exponential discount functions, the maximum likelihood estimate of DC was 3.82 and 2.34 s for monkeys D and J, whereas corresponding values for hyperbolic discount functions were 4.17 and 2.46 s, respectively. This analysis showed that the animals tended to choose the small-reward target more frequently as the subjective delays for the large reward increased, and that this was relatively unaffected by the number of cyan disks used to indicate the delay for the large reward (Figure 7
). In contrast to the results from Experiment II-A, however, the results from Experiment III-A were better fit by an exponential discount function. This was true, even when physical delays were used instead of subjective delays (not shown). Moreover, the exponential discount functions fit the results from monkey D better, even when the analysis was applied after excluding the trials with mixed clocks (Table 3
). For monkey J, the hyperbolic discount function provided the better fit to the data when the trials with mixed clocks were excluded, but the difference in the log likelihood for the two discount functions was relatively small. For Experiment III-A, the discount rate estimated for the best-fitting exponential discount function was 0.27 and 0.49 s−1 for moneys D and J, respectively (Table 2
).
Figure 7. Choice behaviors in Experiment III-A. The delays for large reward were calculated using the subjective delay for the cyan disk, whereas the physical reward delays and the number of cyan disks used for the small-reward and large-reward targets are indicated by the colors and sizes of the symbols. Lines indicate the predictions from the exponential (left) or hyperbolic (right) discount functions. Error bars, SEM.
After Experiment III-A, monkey J was tested for several months in a neurophysiological experiment using a subset of conditions included in Experiment III-A. The choice behavior of this animal during this period was better accounted for by a hyperbolic discount function than by an exponential discount function (61 of 69 sessions, 88.4%). To test whether the animal’s discount function was irreversibly modified by the exposure to the mixed clocks, we have also re-tested both animals using only the clocks with yellow disks. During this experiment (III-B), the choice behaviors of both animals were better accounted for by hyperbolic discount functions (Table 3
; Figure 3
). These results suggest that the exponential discounting found in Experiment III-A was specifically related to the introduction of mixed clocks. Finally, we have fit the exponential and hyperbolic discount functions to the entire dataset collected from all the experiments described above. The results showed that the hyperbolic discount function provided a better fit to the data. The log likelihood ratio between the hyperbolic and exponential discount functions was 419.2 and 574.4 for monkeys D and J, respectively.
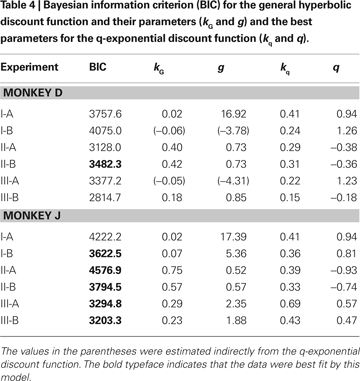
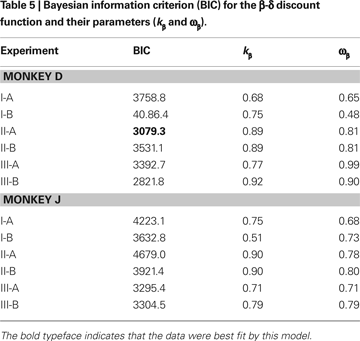
Other Discount Functions
Both exponential and hyperbolic discount functions include only one free parameter, making it possible to compare their performance using the log likelihood directly (Table 2
). When the number of parameters differs for different models, the likelihood tends to improve with the use of additional parameters. Therefore, we used the Bayesian information criterion to compare the performance of two additional discount functions, referred to as a general hyperbolic discount function (Mazur, 1987
) and a β-δ discount function (Laibson, 1997
). For the results obtained in Experiment I-A, an exponential discount function remained as the best model even when these additional discount functions were considered (Table 4
). Exponential discount functions also best accounted for the behaviors of monkey D in Experiment I-B and Experiment III-A, whereas the results from monkey J in these two experiments were best accounted for by a general hyperbolic discount function. The data from monkey D in Experiments II-A was also most consistent with a β-δ discount function (Table 5
), whereas a hyperbolic discount function still accounted for the data from monkey D in Experiment III-B. In all the remaining cases, the results were best accounted for by the general hyperbolic discount functions (Table 4
), including four out of six cases in which the data were better accounted for by hyperbolic discount functions than by exponential discount functions. We have also tested a variant of hyperbolic discount function in which only the more delayed reward is discounted according to the difference in the delays for the two alternative rewards (Green et al., 2005
), but found that this model did not account for the data better than the exponential or hyperbolic discount functions in any of the experiments.
Models of Temporal Discounting
Reward resulting from a particular action is often delayed in real life. In addition, a large number of laboratory studies have demonstrated that decision makers tend to choose an action leading to a more immediate reward delivery, when the difference in the reward magnitude is relatively small. This pattern of choice behavior can be parsimoniously accounted for by the concept of temporal discounting. Despite the methodological differences that often existed in various studies, the results from previous studies have been quite consistent and largely favored a hyperbolic discount function over an exponential discount function (Kalenscher and Pennartz, 2008
; Kirby, 1997
; Kirby and Maraković, 1995
; Madden et al., 2003
; Mazur, 1987
; Murphy et al., 2001
; Myerson and Green, 1995
; Rachlin et al., 1991
; Simpson and Vuchinich, 2000
; Woolverton et al., 2007
).
For exponential discount function, the discount rate is constant, whereas for hyperbolic discount functions, discount rate decreases with reward delay. This hyperbolic discount function might arise due to the uncertainty in hazard rates (Luhmann et al., 2008
; Sozou, 1998
) or in the discount rate itself (Azfar, 1999
). Alternatively, hyperbolic discounting may result from logarithmic time perception (Takahashi, 2005
), since it has been shown that the individual variability in delay discounting might be related to time perception (Barkley et al., 2001
; Reynolds and Schiffbauer, 2004
; Wittmann et al., 2007
). The logarithmic time perception implies that the subjective delay, τ, is given by the following function of physical delay, D.
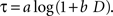
When a constant discount rate is applied to this subjective duration, then the resulting discount function for the physical delay for a particular reward would be a general hyperbolic discount function of the following form.
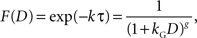
where k is the discount rate in the exponential discount function and g = k a. It has been shown that the general hyperbolic discount function tends to account for the behaviors of human decision makers better than the original hyperbolic discount function (Green and Myerson, 2004
; Myerson and Green, 1995
; Takahashi et al., 2008
). Therefore, logarithmic time perception might provide a parsimonious explanation for the shape of discount function commonly observed in human decision makers.
In the present study, we have examined the choice behaviors of two rhesus monkeys during a novel inter-temporal choice task, and found that the results were consistent with exponential discount functions only in a minority of cases. First, the animals showed exponential discounting when the range of reward delays was relatively small and did not include rewards without any delays, as in Experiment I. The range of reward delays during Experiment I was between 0.5 and 4.5 s, which was smaller than those used in the remaining experiments, and might not have been sufficient to observe a detectable change in the discount rate. Second, although both animals devalued delayed rewards hyperbolically during Experiment II, they returned to exponential discounting when the mixed clocks were introduced in Experiment III-A. For one animal (monkey D), the results from Experiment III-A still strongly favored an exponential discount functions even when the analysis was restricted to the trials including the clocks that were already familiar to the animals, namely, the clocks that included only yellow disks. For the other animal (monkey J), the results for the same subset of trials could not clearly distinguish between these two discount functions, although the hyperbolic discount function was slightly favored. Therefore, these results suggest that the exposure to a novel context might bias the animal to devaluate delayed rewards according to an exponential discount function. Indeed, when one of the animals was further tested using the mixed clocks during the subsequent neurophysiological experiment, its behavior was largely consistent with hyperbolic discounting (Kim et al., 2008
). Therefore, it is also possible that the animals showed exponential discounting during Experiment I due to the lack of sufficient experience with the task used in the present study. Although the neural mechanisms involved in switching between exponential and hyperbolic discount function are unknown, it is possible that extensive experience with a particular type of inter-temporal choice makes the process of decision making more habitual. Therefore, it would be important for future research to test whether the contributions of the prefrontal cortex and basal ganglia during inter-temporal choice change with experience.
Temporal Discounting in Humans and Animals
Although temporal discounting in both humans and other animals are well accounted for by hyperbolic discount functions, the value of the parameter k that controls the rate of discounting varies substantially across different animal species. For example, pigeons tend to discount the value of a delayed reward more steeply than rats and monkeys. The values of the parameter kH in the hyperbolic discount function ranged from 0.3 to 2.24 s−1 for pigeons (Green et al., 2004
, 2007
; Mazur, 2000
). If the subjective value of a delayed reward is given by a hyperbolic discount function, its half-life would be 1/kH. In other words, the value of a particular reward would be halved after the interval of 1/kH. Accordingly, pigeons would be roughly indifferent between an immediate reward and another reward which is twice as large but delayed by 0.4–3.3 s. The value of kH parameter for rats ranged from 0.07 to 0.36 s−1 (Green et al., 2004
; Richards et al., 1997
), corresponding to the half-life of 2.8–14.3 s. In the present study, although the exact value of kH varied according to the range of reward delays and the type of clocks used to signal reward delays, it was relatively stable and remained close to 0.2 s−1 during the course of Experiment II. This is comparable to the results obtained for the rats in previous studies. Similar results have been found in new world monkeys. For example, tamarins and marmosets are willing to wait on average for 7.9 and 14.4 s to choose the reward three times as large as the immediately available reward (Stevens et al., 2005
). Assuming that they discount the value of delayed rewards hyperbolically, these results correspond to the kH-values of 0.25 and 0.14 s, respectively. However, other studies have found substantially less steep discounting in rhesus monkeys. For example, when rhesus monkeys were trained to choose between different doses of cocaine injections, the value of kH parameter was 0.008 s−1, corresponding to the half-life of 125 s (Woolverton et al., 2007
). In addition, rhesus monkeys become less risk-seeking as inter-trial intervals increase, when they choose between a small but certain reward and a large but uncertain reward (Hayden and Platt, 2007
). It has been suggested that the animal’s choice during this task might be determined by the temporally discounted value of a delayed reward expected in subsequent trials (Hayden and Platt, 2007
). Under this assumption, the value of kH parameter in the hyperbolic discount function that best fit the animal’s choice behaviors was 0.033 s−1. Thus, although the value of kH parameter estimated in the present study was comparable to the previous estimates of other non-human primates, it was smaller than the values from the previous studies on rhesus monkeys.
Compared to the values of kH obtained for non-human animals, the values of kH estimated for the hyperbolic discount function in humans is substantially smaller, ranging from 4.0 × 10−4 to 0.027 days−1 (Johnson and Bickel, 2002
; Madden et al., 1997
, 2003
; Murphy et al., 2001
; Takahashi et al., 2008
), corresponding to the half-life of 37 to 2,500 days. Therefore, the half-life for the subjective value of delayed reward is many orders of magnitude larger in humans than in other animals. The difference in the rate of discounting between humans and animals may arise from a number of factors. For example, animal studies have always used the primary rewards, such as food or water, whereas human studies have largely relied on conditioned reinforcements, such as money. Indeed, human subjects show steeper discounting when tested with primary rewards compared to when they are tested with money (Estle et al., 2007
; McClure et al., 2004
, 2007
). In addition, children and adolescents tend to show steeper discounting than in adults (Green et al., 1994
; Olson et al., 2007
; Scheres et al., 2006
). This might be mediated at least in part by the gradual maturation of the prefrontal cortex (Kim et al., 2008
; McClure et al., 2004
, 2007
). Indeed, apes and humans show similar rate of temporal discounting when tested under similar conditions (Rosati et al., 2007
).
Neural Correlates of Temporal Discounting
An essential feature of inter-temporal choice is that the decision makers combine the information about the magnitude and delay of reward. Single-neuron recording studies in monkeys have found that the information about the magnitude of expected reward is distributed in a large number of cortical and subcortical areas, including the prefrontal cortex (Leon and Shadlen, 1999
), posterior parietal cortex (Dorris and Glimcher, 2004
; Platt and Glimcher, 1999
; Sugrue et al., 2004
), and basal ganglia (Hollerman et al., 1998
; Kawagoe et al., 1998
). In addition, the information about the immediacy of reward is also found in the prefrontal cortex (Sohn and Lee, 2007
; Tsujimoto and Sawaguchi, 2005
). Some neurons in the dorsolateral and orbitofrontal cortex encode the information about both the magnitude and delay of expected reward (Roesch and Olson, 2005a,b
; Roesch et al., 2006
). In most previous studies, however, the effects of reward magnitude and delay on neural activity were examined separately. In addition, many of these studies have examined the changes in neural activity related to the magnitude and delay of reward during the task in which the animals were instructed to produce a particular behavioral response in each trial. Accordingly, it was not necessary for the animals to compute the temporally discounted values of alternative rewards. In contrast, single-neuron recordings during the same inter-temporal choice used in the present study showed that the individual neurons in the dorsolateral prefrontal cortex encode the temporally discounted value of the reward expected from a particular target by combining the information about its magnitude and delay (Kim et al., 2008
). Similarly, neuroimaging studies in human subjects have suggested that the dorsolateral prefrontal cortex might play an important role in evaluating the value of delayed reward (Luhmann et al., 2008
; McClure et al., 2004
, 2007
; Tanaka et al., 2004
). Whereas comparing the values of immediate and delayed rewards is likely to engage multiple brain areas, including the basal ganglia, amygdala, orbitofrontal cortex, insula, and posterior cingulate cortex (Cardinal et al., 2001
; Kable and Glimcher, 2007
; Luhmann et al., 2008
; Roesch et al., 2006
; Winstanley et al., 2004
; Wittmann et al., 2007
), how each of these multiple areas contributes to inter-temporal choice remains poorly understood. For example, whether the information about the magnitude and delay of reward is processed separately before these two different types of information are integrated in such areas as the prefrontal cortex is currently known. The behavioral task used in the present study provides means to manipulate the delays of different rewards independently across trials, and therefore might be useful in elucidating the neural basis of temporal discounting and inter-temporal choice in animals.
Authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We are grateful to Lindsay Carr and Bradley Davis for their help with the experiments. This research was supported by the grants from the NIH (RL1 DA024855, P01 NS048328, and P30 EY000785).