Department of Mathematics, University of Sussex, Brighton, UK
Violence is widespread throughout the natural world, prominent examples being predatory violence between species, seasonal violent competition for mating rights and territories within species and food competition both within and between species. These interactions are generally between unrelated individuals with no social connection. There are, however, examples of violent behaviour which occurs within groups of individuals who otherwise cooperate to live, have significant social bonds and may also be related, and that is the primary focus of this paper. Examples are in the establishment and maintenance of dominance hierarchies, or in infanticide, where (usually) incoming males attempt to kill existing infants in a group. Such violence can seem paradoxical, but in fact is often perfectly logical for the individual perpetrating the violence, as distinct from the group as a whole. We discuss such situations from the perspective of evolutionary game theory, and also consider wider questions of interspecific violence.
Violent interactions between individuals of myriad species occur throughout nature. The most obvious and common acts of violence occur in predation, when individuals consume those (usually) of another species, for example cheetahs hunting antelopes such as Thompson’s gazelles. Violence, or the threat of violence, also occurs when stronger carnivores such as lions and hyenas steal prey items from cheetahs. In this paper we will concentrate rather on intraspecific interactions, where the reasons for violence are sometimes less obvious.
The central theme of this paper is that in most (but not all, see e.g. Barr et al., 2008
) circumstances in non-humans, resort to violence is logical, based upon the interests of the animals concerned. We consider violent interactions in terms of the strategic choices of the participants using game theory, and consider some examples. Typically violence may occur in encounters between a subset of individuals in a group, and we are interested in the effect of the chosen behaviour on the larger group. For games a single measure of success, a reward, is needed and Darwinian fitness fits this requirement well. Animals do not behave rationally but if strategies are faithfully reproduced in offspring, successful strategies will propagate, and evolutionary stability is thus a good substitute for rationality. A key feature is that the fitnesses of different phenotypes/strategies depend upon their frequencies so that an individual’s reward depends upon its opponent’s strategy as well as its own. Note that although a strategy is chosen by an individual to optimise its own performance given the behaviour of others, this does not usually produce optimal results for any group of individuals as a whole.
We outline the ideas of game theory with the classic example of balancing risk and reward, the Hawk–Dove game (see Maynard Smith, 1982
). This models a pair of individuals of a single species contesting a valuable resource, for example a territory. In real populations contestants often engage in ritualistic contests, which we shall refer to as displays, to decide the winner. Only if neither backs down do violent interactions occur, and thus injuries are kept to a minimum. An interesting question is, why does one individual not cheat, and resort to violence sooner? This is one example of a strategy of restraint, where individuals do not use maximum force, even to achieve a valuable prize.
In the model there are two individuals contesting a reward of value V (so increasing the Darwinian fitness by V of an individual who gains it). An individual playing the strategy Hawk will escalate the contest until its opponent withdraws, or it is injured and so must withdraw itself. An individual playing Dove will display, but will withdraw if the other individual escalates, thus avoiding injury. A Hawk versus Hawk contest will result in injury to the loser, which is a cost C in Darwinian fitness. Hence there is both a greater potential reward, and a greater risk, associated with the Hawk strategy.
The game can be summarised by the following payoff matrix:
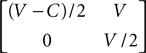
When there are few Hawks in the population, Hawks do well and thus increase in number. Provided that the cost C is sufficiently large, when there are many Hawks in the population, Hawks do badly and thus decrease in number. The population settles on a mixture of the two types, which can be shown to be an evolutionarily stable strategy (ESS), at p = V/C, provided that V < C. If V > C, then Hawk is always the best strategy irrespective of the population mixture, and the population evolves to only contain Hawks. The proportion of violent contests that result in injury is simply the proportion of contests that involve two Hawks and is thus (V/C)2, and so if V is much less than C, few violent contests happen, as is often the case in reality.
We now proceed to consider three different natural scenarios, each of which features the central question of whether to be aggressive or not, where the aggressive option contains both the prospect of greater rewards, but also a greater risk. Each of the three situations has its own specific features, and the nature of the risks and rewards in each case are rather different. All have been modelled mathematically using game theory, and in each case the major (often only) strategic choice is the level of violence to employ.
Kleptoparasitism and the Model of Broom and Ruxton (1998)
Kleptoparasitism is the stealing by one animal of food that has been caught by another. Interspecific and intraspecific kleptoparasitism are widespread among vertebrates, and commonly observed amongst birds, especially seabirds. Examples of intraspecific kleptoparasitism amongst seabirds include gulls (Steele and Hockey, 1995
) and oystercatchers feeding on cockles (Triplet et al., 1999
), whereas skuas are common interspecific kleptoparasites (Spear et al., 1999
). A good review paper is Iyengar (2008)
, which emphasises the wide range of species that employ this behaviour. Kleptoparasitism has been modelled using game theory in a number of papers, in particular a series of papers starting with Broom and Ruxton (1998)
. In this paper individuals move between searching for food and handling food items, and when a searching individual discovers one handling food, it can mount a challenge or not, which is the strategic element of the model. Note that the model is more appropriate for fast moving individuals, and the classical seabird interactions were the inspiration behind it.
Contests between individuals take time; if a pair fight this prevents them from engaging in searching or handling activity for the duration of the contest, and contest time is one of the key parameters of the model. In fact contest time acts as a surrogate for a number of costs associated with a real contest. For example contests could involve high energetic costs, and so require a subsequent (possibly substantial) period of rest, and is additional time when the protagonists cannot be engaging in the other two main behaviours of searching and handling. Similarly minor injuries might require a recovery time before foraging can recommence (note that the risk of major injury, e.g. resulting from Hawk versus Hawk contests in the previous section, requires a different framework since the resultant cost cannot be adequately described by lost time). Contests thus have an effect on the distribution of behaviours within the population, so that decisions taken within a contest can affect all individuals, not just the two involved.
The other model parameters are listed in Table 1
; values for a typical example are given in Holmgren (1995)
(see also Luther and Broom, 2004
). In this simple version of the model it is either best to challenge all the time or never. The key factor that relates to whether kleptoparasitism is advantageous or not is the value of the product νffta, with stealing optimal if and only if this value is less than 1, meaning that challenging should occur if and only if the expected contest length is sufficiently short, the rate at which food can be searched for is sufficiently low or the food density is sufficiently low.
In general kleptoparasitism reduces the overall amount of food consumed, as time that could be spent foraging is spent fighting instead. Allowing the food density of the population to vary, there is a critical point where it is always best to challenge if food density is below a certain level, and never best above that level, and there is a step change in the rate of food consumption at the critical point. Thus at low food densities it is optimal for each individual to challenge, but all do worse as a result. In this sense the game is very much like the classical prisoners’ dilemma model, described by the payoff matrix below.
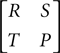
The prisoners’ dilemma is characterized by two strategies Cooperate and Defect, where the payoff for Defect against Cooperate (T) is the largest, decreasing through Cooperate against Cooperate (R), Defect against Defect (P) and Cooperate against Defect (S) i.e. T > R > P > S. The classic dilemma occurs because it is best to play Defect conditional on the opponent’s strategy (whichever strategy that is, since T > R and P > S), but every individual following its own best strategy leads to the worse collective result of all playing Defect and receiving P, as opposed to playing Cooperate and receiving R.
Further Modelling Developments
The work of Broom and Ruxton (1998)
has been developed in a number of ways since. For example, when individuals are allowed to not resist challenges in Broom et al. (2004b)
, there are three possibilities for an ESS, Hawk (challenge and resist), Retaliator (do not challenge but resist) and Marauder (challenge but do not resist) and two ESSs can occur for the same parameter values. In the later paper of Broom et al. (2008)
different strategies were allowed to have different foraging rates depending upon whether the individuals involved were prepared to challenge others, and so presumably have to look out for the possibility of making such a challenge (the original paper of Broom and Ruxton, 1998
did also consider this possibility). In this paper all three of the above strategies can be ESSs simultaneously, the strategy Dove (neither challenge nor resist) can be an ESS, and a number of other possibilities occur.
The Marauder strategy seems at first paradoxical, since all individuals are prepared to challenge for food, but none are willing to defend food items. Given fights take no time, as food is immediately conceded, this means that the feeding rate in the population is not reduced by this behaviour. Marauder is associated with both higher feeding rates and higher fight times, when it is important not to waste time in contests, either because rewards without fighting are high as in the former case, or because the cost of fighting is high as in the latter one. There is a significant overlap in the regions where Marauder and Retaliator are ESSs, so that either all challenges and nobody resists, or nobody challenges and all are prepared to resist, and it does not matter which occurs. Note that a similar scenario is observed in the owner intruder game of Maynard Smith and Parker (1976)
, where individuals challenges others for their territories based upon the Hawk Dove game (a strategy consists of the choice of Hawk or Dove for each position of owner and intruder). It does not matter whether all choose Hawk as owner and Dove as intruder (the Bourgeois strategy), as is common in nature, or the reverse strategy of Hawk as intruder and Dove as owner, which is much rarer but observed, and resembles Marauder. In real scenarios Marauder behaviour would be characterized by frequent short contests, and one example of where this is observed is in oystercatchers (Stillman et al., 1997
).
Broom and Rychtar (in press)
allow individuals not just to challenge a lone handler, but to join fighting groups of any size. This is typical behaviour in seagulls, especially when feeding in relatively dense populations when such possibilities occur frequently, as in Steele and Hockey (1995)
. It is clear that as food becomes scarcer, individuals should be prepared to tackle larger groups, with a corresponding smaller chance of success, and indeed this occurs in the model. An interesting feature is that this extra willingness to fight depresses the feeding rate of the population further, as individuals are often engaged in time-consuming contests, which makes it even more worthwhile for any individual to want to make challenges. ESSs are of the form of challenging groups of below size K for some constant K, and it is possible to have many simultaneous ESSs if the population is dense.
Introduction to Infanticide
The killing of infants by conspecific males has been reported for many, mostly mammalian, species. There are several plausible hypotheses for an act of infanticide, for instance the elimination of a competitor for a limited food supply or utilisation of the infant for food. The most common explanation is the sexual selection hypothesis of male–male competition for reproduction. The killing of infants results in an advantage for the male killer under the following conditions: only unrelated infants are killed, premature loss of an infant enables the mother to conceive the next infant sooner and the chances of the killer siring the next infant are high. There is a lot of data supporting this hypothesis from carnivores, particularly lions, and rodents, for example.
The most investigated group where this behaviour has been observed is primates, for example langurs and howlers. Infanticide is relatively common in groups which only contain one breeding male, which from time to time is replaced by a different male. When infanticide is attempted mothers and other group members often defend the infant, but due to sexual dimorphism in most primates, male defence is more effective, and infanticide is both more difficult and riskier when a defending male is present.
Early models of infanticide treated it as a simple genetic trait, and used the benefit of infanticide as a strategy to show how it would spread through the population. Breden and Hausfater (1990)
showed that these effects are unlikely to override within group costs of infanticide, since infanticidal males are more likely to be group-mates with other infanticidal males, and infanticide whilst benefiting the killer, is harmful to the group. More plausibly, infanticide is part of a conditional strategy, where most males will practice infanticide in some conditions, but not others. Most previous theoretical work considers a single male group scenario, which is common in the well-studied Hanuman langur.
Recent data show that infanticide also occurs in groups with more than one male, for example in chacma baboons, Japanese macaques, long-tailed macaques and also Hanuman langurs. Reported cases accord with the sexual selection hypothesis in that only unrelated infants are killed, the subsequent inter-birth interval is shortened, and the presumed killers are likely to father the next infant e.g. in red howlers and Hanuman langurs. There is however, much variation in the prevalence of infanticide within and between different primate populations and species. Important factors include the number of males per group, male replacement rates and age at weaning. Low rates of infanticide are common when males enter at the bottom of the male hierarchy, higher rates occurring when new males are immediately dominant.
A Model of Infanticide in Multi-Male Groups
Broom et al. (2004a)
considers a two-male group with an infant that is a potential target for infanticide. One of the males is the presumed father, the other is a new male who has recently joined the group. The new male may attempt infanticide or not, and the father may defend the infant or not if an attempt is made (an attempt here will be a potentially long campaign, so there is only one such “attempt”).
The model gives predictions for the type of circumstances when infanticide should be prevelant. For example, the new male should attack the infant if his chances of fathering the next infant are large, the chances of killing the infant are large or the average number of extra births following infanticide is large. The father should defend the infant if the target infant has a high chance of survival to maturity, the probability that the infant will be killed is significantly decreased if the father defends or his residual reproductive value is low e.g. he is old. The third of these occurs because with little residual reproductive value he can be more reckless about his own safety, whereas a young male with many further breeding opportunities cannot afford to jeopardize these through injury.
These factors are directly influenced by the infant’s age and the dominance relationship between the males. As the infant gets older, the benefit of killing it declines, and it may also become of greater value to its father, as the probability of it surviving to adulthood increases. Thus in general there are two thresholds where younger infants should be attacked despite defence, older infants should not be attacked irrespective of defence but defence should deter attack in intermediately aged infants (although these thresholds can be outside of the standard infant range, so that in a given scenario only one or two of these three situations may occur as the infant grows older). Infanticide should be more common in populations where the incoming male is dominant, as in chacma baboons or Hanuman langurs, since such a dominant has a higher chance of success, a lower chance of injury during the attempt, and a greater chance of benefiting through fathering the next infant.
These examples suggest that the observed variation of infanticide in primate multi-male groups may be explained by differences in male migration patterns and the resulting differences in age and dominance rank of competing males. The model might even be able to explain differences across time in a given group or population.
Stability and Maintenance of Dominance Hierarchies
Many individuals spend a large proportion of their lives in groups. When such groups are formed, social relationships occur which form common patterns and dominance relationships are often highly structured. A common occurrence is the linear dominance hierarchy: A dominates all, B dominates all but A, C dominates all but A and B, down to a bottom individual dominated by all. There are advantages to the group to be structured in this way; for example, food can be allocated within the group with minimal costly infighting. It may, however, be beneficial to the individuals who occupy low places in the hierarchy to disrupt the hierarchy if they can.
There has been significant work on the stability and maintenance of these structures over time. Such hierarchies conceal a range of possible contests that could occur between their members. If a potential contest occurs, each individual must balance the potential benefits (e.g. increase in rank) against costs (e.g. injury). Stability, and low levels of violence, will occur when lower ranked individuals are rarely willing to challenge for higher positions. Experiments in fowl show that linear hierarchies are often stable, and that if an individual is removed, and subsequently put back later, it often automatically returns to its previous position without conflict. Important theoretical work has considered reproductive skew, starting with Vehrencamp (1983)
, where the higher the reproductive skew, the greater the advantage of occupying the top position(s) in the hierarchy. It is also important that subordinate individuals prefer to remain part of the group. A model where subordinates are given limited mating rights (stay and peace incentives) in order not to leave the group or challenge dominants was developed in Keller and Reeve (1994)
. Such situations are observed in different species of ant with colonies involving multiple queens, and the predicted relationships between levels of skew and relatedness that come out of the models (the higher the relatedness, the higher skew) is observed in reality (Fournier and Keller, 2001
).
Broom et al. (2009)
introduce a model which considers a variety of factors. In addition to resource holding potential (RHP), reproductive skew and demography often suggested previously, they stress the importance of (i) the variance in relatedness; (ii) the costs and likelihood of interventions; and (iii) the value of resources and rank in different life stages, which might be tightly linked to the life history of a species. For example, in arboreal primate groups the costs associated with fighting might be higher, e.g. falling from trees. Coalitions are also less likely since in such groups it is more difficult for a third party to influence fights, the energetic/time cost of trying to interfere would be higher and losing will be more costly as already mentioned. This might explain the fact that arboreal groups are characterized by lower rates of agonism and generally less despotic hierarchies. The model here is perhaps better suited to some primate contests, for example the spontaneous aggression of bonnet macaques (Silk, 1992
), rather than others involving more elaborate coalitioniary behaviour, where individuals have the chance to continually update their strategy during a contest.
Dominance Hierarchy Formation
A new individual will often join an existing group following simple rules, such as a daughter slotting in below its mother. What happens if a group of individuals are all meeting for the first time? When modelling this situation, it is useful to consider three elements: the nature/rules of an individual conflict, the pattern of pairing of individuals to fight and the effect of a given outcome of a fight between two particular individuals (on their dominance, but also on which conflicts occur subsequently). The level of violence in individual contests, and so in the formation of the hierarchy as a whole, is closely linked to the eventual benefits of attaining high position and the costs of engaging in such violence. It is useful to consider sub-groups of a larger hierarchy, in particular triads, sub-groups of three. Linear hierarchies require all triads to be transitive (A beats B, C; B beats C) and the number of non-transitive triads is a measure of the distance from linearity of a hierarchy.
Important experimental work has been carried out by Chase and co-workers on hierarchy formation, for example by Chase and Rohwer (1987)
. Considering triads within flocks of Harris’ sparrows, more triads (95%) were transitive than would be expected by completely random pairwise dominance relations (75%). Initial relationships from the first two interactions were more likely than average to be those certain to lead to transitivity (A beats B, C or A, B beat C, not A beats B beats C) and reversals, swaps of dominance between two birds, were more common in initially intransitive triads. The combination of these two effects, when part of a larger group of animals, helps explain the significant linearity. Note that observations of other species, e.g. chickens and rhesus monkeys, have shown much higher rates of linearity.
In recent (as yet unpublished) work on the classic dominance subject, the chicken, W.B. Lindquist and I.D. Chase looked at groups of four Leghorn hens, their interactions and the hierarchies that emerged. Dominant individuals generally emerged early on, and there was a relative lack of “pair-flips” where A attacks B, and B attacks A. The phenomenon of “bursting” was observed, where one individual repeatedly attacked another, with the likely aim of establishing dominance over it, and it appears that dominance emerges from a concentrated and purposeful sequence of interactions.
Winner and Loser Models
An important type of model of dominance hierarchy formation is the winner-loser model, for example Dugatkin (1997) and Bonabeau et al. (1999)
. These models are based upon a sequence of pairwise interactions. The winner effect occurs if winning a contest increases an individual’s chances of winning a subsequent contest. The loser effect occurs if losing a contest increases an individual’s chances of losing a subsequent contest.
These effects have been shown experimentally, for instance in blue-footed boobies (e.g. Drummond and Canales, 1998
). Strong winner and loser effects among chicks were observed, when previous winners and previous losers were paired with inexperienced individuals who had not participated in contests. Interestingly, the winner effects decreased with the passage of time, but the loser effects remained intact throughout the 10 days of the experiment. This pattern, with loser effects more significant than winner effects, is a common one in animals.
In general, models of dominance hierarchy formation involving winner and loser effects assume the following. Individuals have dominance scores depending upon their history. These individuals are paired following a set of rules, e.g. at random or in a sequence leading to every pair of individuals meeting (all-play-all), and an interaction between paired individuals happens with a probability based upon the dominance level of the two individuals. If an interaction occurs, the winner is determined by a function of their two dominance scores. The dominance levels of players are updated based upon the result of the contest; the winner’s dominance is increased, and the loser’s decreased. Individual interactions reinforce the dominance of winners over losers, and over time can tend to hierarchies that are linear, for instance from the original models of this type of Landau (1951a
,b
). It should be noted that the current models do not as yet incorporate some of the behaviour observed by W.B. Lindquist and I.D. Chase.
The effects can be different if models contain winner and loser effects, just winner effects or just loser effects. Clear hierarchies tend to result from winner effects alone, whereas for loser effects alone the hierarchy below the α individual tends to be indistinct (Dugatkin, 1997
). Loser effects often dominate winner effects, especially if, as indicated above, they endure for a longer time. A third effect, the bystander effect, has been introduced, where the behaviour of individuals observing, but not participating in, a contest is affected by the result of the contest, when meeting one of the contestants that its observations have provided information about. For example in green swordtail fish (Earley and Dugatkin, 2002
) bystanders often avoid aggression against winners and even losers that have been aggressive.
Population Structures
Mesterton-Gibbons and Dugatkin (1995)
introduced an all play all contest where individuals’ RHP varied, considering the probability of a linear hierarchy emerging. They consider the cases where the individuals can accurately assess the RHPs of opponents, and when they make no assessment. With assessment, weaker individuals can give up without a fight and avoid costs, and the outcome of some contests is thus predictable. If RHP is assessed prior to the contest a linear hierarchy can be formed with high probability for a group of moderate size, e.g. 7 or 8. Without assessment, there are more real fights, and linear hierarchies only form with high probability for very small groups, e.g. 4.
Broom et al. (2000)
modelled dominance hierarchy formation as a knockout contest. In this paper, individuals are paired at random, initially with 2n identical individuals. They play a Hawk–Dove contest, where there is a cost for a Hawk versus Hawk loss, and the reward V is replaced by progress to the next round; in any given round, the losers of individual contests are eliminated and the winners go through to the next round and are then repaired. Individuals receive a reward depending on the round they are eliminated, so an individual eliminated in round k receives reward Vk. The important top two positions, occupied by the overall winner and losing finalist, are thus established quickly with relatively little conflict, the total number of contests being one less than the group size. Real populations do not play these games exactly, of course, but they could be a reasonable approximation for large groups, e.g. black grouse and other species come together in leks (Hoglund and Alatalo, 1995
). As individuals compete, winners may move to the more advantageous centre ground, so that winners will tend to face other winners. Broom and Cannings (2002)
developed this model further to use a Swiss tournament, the key difference being that this involves all players in a continuing sequence of contests, until they have sorted themselves into an order with a unique individual that has won all its contests, whereas in Broom et al. (2000)
losers are eliminated, so that the number of active players decreases as the contest progresses. The eventual position of an individual is decided by the number of contests that it has won. In the model contests between dominants tend to be violent, those between subordinates less so, with early stage contests intermediate. As differences in rewards increases, the overall level of violence increases on a sliding scale. Defeat leads an individual to be more passive, whereas victory does not necessarily make it more aggressive. Thus loser effects are emergent from the model, but winner effects are not, which is consistent with real behaviour as in Earley and Dugatkin (2002)
.
Violence is prevalent in the animal world, and takes place for logical reasons, from the point of view of the individuals involved, and game theoretical modelling is a valuable method for analysing the interactions between these individuals. Intra-group violence, although propagated by individual needs, can serve a useful purpose for the group, but benefits some more than others, e.g. in dominance hierarchy formation. In other situations violence is beneficial to the individual concerned, but detrimental to the health of the group e.g. in infanticide. It is also possible to have situations where violence is beneficial to the individual conditional on the behaviour of others, but that for the group as a whole, no violence would be preferable to all players being violent. Every individual can be worse off, even though their violence is “logical” e.g. in kleptoparasitism, so that even some behaviours that look illogical, can have a logical basis. A second example of this scenario is the prisoners’ dilemma, where defection is the optimal strategy even though it eventually leads to a result that is worse for both players.
The population structure and the consequences of the results of individual contests differ markedly for the various games that we consider. The infanticide model is effectively a single event, where the new male may or may not try to kill the infant, and the father then may or may not defend, with no subsequent contests and so no structure of multiple linked contests. The Hawk–Dove game involves a series of independent contests, where the result of an interaction has no bearing on future interactions, so although there are many contests, there is no dependence structure between them. The kleptoparasitism models involve simple pairwise games which are not independent, since there is an indirect effect on the frequency of subsequent interactions, so that an individual contest affects the whole population, and not just the contestants. For the maintenance of dominance hierarchies, there is a variety of possible interactions, involving the co-location of the various members of the hierarchy. As long as groups are small, all such interactions can be assumed to occur eventually, and consequently the hierarchy must be stable under all possible interactions. If the hierarchy is stable under all interactions, individual contests do not affect each other, since nothing ever changes, but any result which changes the hierarchy could have a significant effect on the whole group. In the two varieties of model affecting dominance hierarchy formation, the winner–loser models and the structured games, there is a sequence of games where earlier games either affect the results of later contests, for example by increasing the chance of a previous winner of winning again, or which opponents are involved in such contests, for example by winners being repaired with winners, or both.
Game theory arguably works better in the biological world than the economic one, as Darwinian fitness and evolutionary stability make a good substitute for the rationality assumed in human games, whilst humans often do not behave rationally. This lack of rationality applies even more to the concept of violence between humans. Thus the concept of violence in the animal world can also perhaps be approached in a more straightforward manner. Vast complications remain, but animal researchers and modellers do not usually need to worry about the rationality of their subjects.
To what extent is there scope for the application of these methods to human violent behaviour? For the vast majority of human history, people have been subject to evolutionary forces in the same way as animals as described above, where the choice of taking violent actions has an effect on the subsequent number of surviving offspring. Such choices are less directly relevant in modern society for a variety of reasons. Firstly, at least in much of the world, there is not the strong evolutionary competition where the strongest survive and the weakest perish. Secondly, the way modern societies measure success is different to in the past, so that violent behaviour is perhaps less likely to attain a high status position (although it is not always true that those we consider successful are successful in evolutionary terms i.e. the number of surviving offspring). Thirdly, violence amongst people is often regarded as an aberration, due to poor upbringing, mental health etc. so that it is questionable how much of human violent behaviour can be classed as strategic. However, it is also the case that violence may have an evolutionary cause, due to the long history of when it was effective, even in the modern world where it is no longer so effective. Thus evolutionary modelling may have something to offer, but great care needs to be taken that its application is appropriate where it is used, and this will be more problematic than in the animal world.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
I am grateful to my collaborators on my co-authored work which is mentioned here Carola Borries, Chris Cannings, Andreas Koenig, Roger Luther, Graeme Ruxton, Jan Rychtar and Glenn Vickers and also to the following grants which supported this work: BBSRC grant GR/J31520, Nuffield grant SCI/180/97/125/G, EPSRC grant EP/E043402/1 and NSF grant 0634182.
