1
Department of Physiology, Centre for Neuroscience Studies and Canadian Institutes of Health Research Group in Sensory-Motor Systems, Queen’s University, Kingston, ON, Canada
2
Department of Economics, Queen’s University, Kingston, ON, Canada
In learning models of strategic game play, an agent constructs a valuation (action value) over possible future choices as a function of past actions and rewards. Choices are then stochastic functions of these action values. Our goal is to uncover a neural signal that correlates with the action value posited by behavioral learning models. We measured activity from neurons in the superior colliculus (SC), a midbrain region involved in planning saccadic eye movements, while monkeys performed two saccade tasks. In the strategic task, monkeys competed against a computer in a saccade version of the mixed-strategy game “matching-pennies”. In the instructed task, saccades were elicited through explicit instruction rather than free choices. In both tasks neuronal activity and behavior were shaped by past actions and rewards with more recent events exerting a larger influence. Further, SC activity predicted upcoming choices during the strategic task and upcoming reaction times during the instructed task. Finally, we found that neuronal activity in both tasks correlated with an established learning model, the Experience Weighted Attraction model of action valuation (Camerer and Ho, 1999
). Collectively, our results provide evidence that action values hypothesized by learning models are represented in the motor planning regions of the brain in a manner that could be used to select strategic actions.
In reinforcement learning models, an individual’s choice is a probabilistic function of the current values of possible actions, which in turn are functions of past choices and past rewards (Sutton and Barto, 1998
). These learning models are based on the concept of choice reinforcement, traced back to the Law of Effect (Thorndike, 1898
; Erev and Roth, 1998
).
Empirical studies have supported such learning models in a variety of strategic environments with mixed strategy equilibria (Mookherjee and Sopher, 1994
, 1997
; Erev and Roth, 1998
; Camerer and Ho, 1999
; Ho et al., 2007
, 2008
). However, because learning models predict serial dependence in sequential choices, they conflict with independent (uncorrelated) choice predicted by repetition of the stage game Nash Equilibrium in a repeated game. For example, while laboratory studies of the matching pennies game in humans confirm the equilibrium prediction of a 50/50 ratio of choices, sequential dependencies in individual choices remain (Mookherjee and Sopher, 1994
; Ochs, 1995
). Similar results have been observed against a computer opponent in studies of both humans (Spiliopoulos, 2008
) and monkeys (Lee et al., 2004
; Thevarajah et al., 2009
). Studies of a broader class of mixed strategy games also exhibit similar choice dependencies though not all the authors address learning models directly (O’Neill, 1987
; Brown and Rosenthal, 1990
; Rapoport and Boebel, 1992
; Rapoport and Budescu, 1992
; McCabe et al., 2000
).
The goal of this study is to look for evidence of neuronal signals that correlate with the action values predicted by the Experience Weighted Attraction (EWA) learning model (Camerer and Ho, 1999
). We use EWA because it is both empirically established and a general formulation. It incorporates simple reinforcement learning (Win/Stay-Lose/Shift), both cumulative reinforcement learning and average reinforcement learning (or Q-Learning) (Watkins, 1989
; Erev and Roth, 1998
), and belief-based models (Fudenberg and Levine, 1998
), as special cases of its parameterization. In fact, it is entirely reasonable for behaviour to lie in some middle ground of the above model restrictions of EWA, and empirical evidence suggests it does (Camerer and Ho, 1999
; Ho et al., 2008
).
Evidence that learning models are instantiated by the brain has been found from measuring neural signals while humans and animals decide. Evaluative signals are encoded, in part, via dopaminergic structures which represent the difference between realized and expected reward following an action (Schultz, 2004
; Caplin et al., 2010
). In addition, neural signals have been found that encode the combination of actions and their associated outcomes during adaptive decision-making (Barraclough et al., 2004
; Lau and Glimcher, 2007
; Seo et al., 2007
; Luk and Wallis, 2009
). Finally, some neural signals reflect the value of potential actions. Thus they may play an important role in driving the choice process (Platt and Glimcher, 1999
; Dorris and Glimcher, 2004
; Rushworth et al., 2004
; Sugrue et al., 2004
; Samejima et al., 2005
; Padoa-Schioppa and Assad, 2006
; Kennerley et al., 2006
; Lau and Glimcher, 2008
; Jocham et al., 2009
).
We build on this previous work by looking for action value signals within a brain region quite close to the motor output, the intermediate layers of the superior colliculus (SCi). The SCi has a number features that suggest it may encode action value. The SCi is topographically organized as a map of potential saccadic eye movements (Robinson, 1972
; Schiller and Stryker, 1972
) and determines when and where a saccade will be directed (Glimcher and Sparks, 1992
; Dorris et al., 1997
). The SCi receives input signals from upstream brain regions involved in choosing saccades in both strategic environments (Barraclough et al., 2004
; Dorris and Glimcher, 2004
; Seo et al., 2007
; Seo and Lee, 2008
) and non-strategic environments (Schultz, 1998
; Sugrue et al., 2004
; Samejima et al., 2005
; Lau and Glimcher, 2007
, 2008
). The topographic organization of the SCi ensures that any value-related signals we observe are closely associated with specific actions. Moreover, strong lateral inhibition between distant SCi locations could play an important role in selecting between action values associated with competing saccades (Munoz and Istvan, 1998
; Dorris et al., 2007
). Finally, the SCi sends commands to premotor neurons in the brainstem (Moschovakis and Highstein, 1994
), as well as providing feedback to dopaminergic neurons in the ventral tegmental area and substantia nigra (Comoli et al., 2003
; Dommett et al., 2005
).
We measured preparatory activity in the SCi while a monkey played a simultaneous move game of matching pennies against a computer algorithm designed to exploit serial dependence in the monkey’s choices. To control for any serial dependence outside of strategic competition, we also measured activity during a sequential move game with random payoffs. First, we hypothesize that SCi activity displays serial dependence based on both previous saccades and their outcomes, and that more recent events will exert a stronger influence. Second, we hypothesize that SCi activity predicts upcoming strategic choices. Finally, we hypothesize that activity in the SCi provides a signal that is correlated with the current value of actions in the EWA learning model. Collectively, our results support the conclusion that action value signals are represented in the motor planning regions of the brain in a manner suitable for selecting strategic actions.
Electrophysiological experiments were conducted on two male rhesus monkeys (Macaca mulatta), weighing between 9–13.5 kg each, while they performed saccadic eye movement tasks. All procedures were approved by the Queen’s University Animal Care Committee and complied with the guidelines of the Canadian Council on Animal Care. Animals were under the close supervision of the university veterinarian. Physiological recording techniques as well as the surgical procedures have been described previously (Munoz and Istvan, 1998
; Thevarajah et al., 2009
).
General Methodology
Behavioral paradigms, visual displays, delivery of liquid reward, and storage of both neuronal discharge and eye position data were under the control of a PC computer running a real-time data acquisition system (Gramalkn, Ryklin Software). Red visual stimuli (11 cd/m2) were produced with a digital projector (Duocom InFocus SP4805, refresh rate 100 Hz) and back-projected onto a translucent screen that spanned 50° horizontal and 40° vertical of the visual space. Right eye position was recorded at 500 Hz with resolution of 0.1° using an infra-red eye tracker system (Eyelink II, SR Research). Trials were aborted online if eye position was not maintained within ±3° of the appropriate spatial location or if saccades were initiated outside the 70–300 ms temporal window following target presentation. We have further discussion of aborted trials in Section “Results”.
The activity of single neurons was recorded with tungsten microelectrodes (Frederick Haer, 1–2 MΩ at 1 kHz) and sampled at 1 kHz. Data analysis was performed offline using Matlab, version 7.6.0 (Mathworks Inc.) on an Intel Core 2 Duo processor. To quantify neuronal activity, each spike train was convolved with a post-synaptic activation function with a rise time of 1 ms and a decay time of 20 ms (Thompson et al., 1996
).
Neuronal Classification
We recorded the activity from saccade-related neurons located between 1.0 and 3.0 mm below the surface of the SC. The center of each neuron’s response field was defined as the location, relative to central fixation, associated with the most vigorous activity during target-directed saccades. One target was always placed at this location (referred to hereafter as in) and the other at the mirror-image location in the opposite hemi-field (out) except ten experiments where two neurons located in opposite colliculi were recorded simultaneously. For these dual neuron experiments, the two targets were located in opposite hemifields corresponding to the response fields of the two neurons under study. To be included in our analysis, neurons had to meet two requirements: (1) motor burst, a transient burst of activity that was time-locked to onset of the saccade into the response field that surpassed 100 spikes/s and (2) preparatory activity, neural activity during the 50 ms that followed presentation of the mixed-strategy targets that exceeded 30 spikes/s and was significantly greater than the mean activity 100 ms before fixation point offset (paired t-test, p < 0.01). Note that in the modelling Section “Value, SCi Activity and Actions”, this preparatory activity will be designated 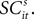
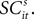
Behavioral Tasks
Monkeys performed two behavioral tasks. In the strategic task, monkeys were free to choose between two saccade targets while they competed against an adaptive computer opponent playing the matching pennies game. In the instructed task, monkeys were instructed which saccade to make with the presentation of a single saccade target on each trial. The purpose of the instructed task is to characterize how SCi activity is shaped by previous choices and outcomes. The strategic task is used to emphasize this relationship between SCi activity and the history of the game, and determine whether SCi activity is predictive of choice in a strategic decision making environment.
Strategic task
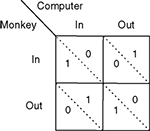
Monkeys competed in a saccadic version of the repeated mixed-strategy game matching-pennies against an adaptive computer opponent (Figure 1
). Each trial, both the subject and computer reveal a strategy in or out. The monkey, pre-designated the “matcher”, wins if their strategies match, and the computer, pre-designated the “non-matcher”, wins if their strategies differ. The unique Minimax/Nash Equilibrium in mixed strategies is for each player to play in and out with equal probability (von Neumann and Morgenstern, 1947
; Nash, 1951
), though our analysis does not require that equilibrium play is achieved. Because our experimental setup limits the ability for the monkey to suffer a loss we replaced a loss with a withholding of reward, though the equilibrium remains unchanged. The payoff matrix is given in Figure 2 and has been previously studied experimentally in humans (Mookherjee and Sopher, 1994
) and monkeys (Lee et al., 2004
; Thevarajah et al., 2009
).
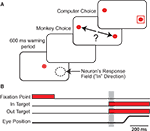
Figure 1. Strategic Task. (A) Each panel represents successive visual displays presented to the monkey. Red circles represent the central fixation point and choice targets respectively. In the third panel, arrows indicate the monkeys possible saccadic choices. One of the saccade targets was always placed in the center of the neuron’s response field (i.e., in target) as indicted with the dashed circle. The out target was placed in the opposite hemifield. The red square indicates the choice of the computer opponent. (B) Time-line of strategic task. Grey shaded region indicates the 50 ms epoch during which SCi preparetory activity was sampled for neuronal analyses. The stimuli setup and time-line were identical for the instructed task (not shown) except that only one target was presented per trial and the red square surrounded the target only on rewarded trials.
Figure 2. Payoff matrix for strategic task.
Subjects were required to maintain central gaze fixation throughout the 800 ms presentation of the fixation point, and after its removal during a fixed 600 ms warning period. Subjects were free to saccade towards either of two simultaneously presented targets, i.e. in and out of the response field. The fixed warning period and known target locations facilitated advanced selection and preparation of saccades (Thevarajah et al., 2009
). After fixating on the target stimulus for 300 ms, a red square, which indicated the computer opponent’s choice, appeared around one of the targets for 500 ms. The monkey received a 0.3 mL liquid reward if both players chose the same target and nothing otherwise. The computer opponent performed statistical analyses on the subject’s history of previous choices and payoffs and exploited systematic biases in their choice strategy (see algorithm 2 from Lee et al., 2004
for specific details).
Instructed task
The instructed task was identical to the strategic task with two exceptions. First, only a single saccade target was presented on each trial. This target was equally likely to be presented in or out. Second, reward was equally likely to be received or withheld for successful completion of each trial. Therefore, the expected value of the instructed task is equal to the equilibrium payoff of the strategic task, but saccadic choice was under sensory instruction in the former and under voluntary control in the latter.
Dependence on Previous Choices and Rewards
To examine any biases exerted by previous saccades and rewards, we segregated SCi activity and saccadic responses on the current trial t based on past (t − n, where 1 ≤ n ≤ 7) and future (t + n, where 1 ≤ n ≤ 3) events (Maljkovic and Nakayama, 1994
). Future events were examined for control purposes as these should not exert any influence on the current trial. This sequential analysis is illustrated in Figures 5 and 6
which shows neuronal activity on the current trial segregated into four categories based on four possible events that occurred on the previous trial. (1) a rewarded saccade into the response field (in/R), (2) an unrewarded saccade into the response field (in/U), (3) a rewarded saccade out of the response field (out/R), and (4) an unrewarded saccade out of the response field (out/U).
We estimated preparatory activity from the postsynaptic spike activation function during the 50 ms following target presentation (Figure 5
, grey bar). This represented the neuronal firing rate just before saccadic responses were made yet still uncontaminated by visual inputs related to target presentation (Dorris et al., 2000
).
The same sequential analysis was performed on choice selection during the strategic task. Response biases were quantified by determining the probability of the monkey selecting the in target on the current trial based on past or future events.
Comparatively, for the instructed task, sequential analysis was performed on SRTs rather than saccade choice since saccade location was instructed. SRTs were defined as the time to initiate a saccade following target presentation. Computer software determined the beginning and end of each saccade using a velocity and acceleration threshold. These events were verified by an experimenter to ensure accuracy. Response biases were quantified by examining the influence of an event n trials in the past or future on trials only where saccades were instructed to in.
Sequences of trials were constructed from the raw data based on the following criteria. First only sequences of 5 or more consecutive non-aborted trials in length were analyzed. Second, single aborted trials were removed and the sequence was treated as continuous. Third, sequences were started anew if two or more aborted trials occurred in succession. We felt these criteria struck a balance between providing sufficient sequential data for the analysis in this section while removing those sequences with poor continuity.
EWA Learning
The behavior of the subject in trial t of experiment i is coded as

Let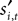 denote the computer opponent’s choice. Whether reward is received depends on both choices and the experiment being conducted. Let indicate that a reward was received in trial t of experiment i and 0 otherwise.
denote the computer opponent’s choice. Whether reward is received depends on both choices and the experiment being conducted. Let indicate that a reward was received in trial t of experiment i and 0 otherwise.
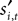 denote the computer opponent’s choice. Whether reward is received depends on both choices and the experiment being conducted. Let indicate that a reward was received in trial t of experiment i and 0 otherwise.
denote the computer opponent’s choice. Whether reward is received depends on both choices and the experiment being conducted. Let indicate that a reward was received in trial t of experiment i and 0 otherwise.
In both tasks, a reward is only received when the choices match, 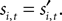 During the strategic task the computer opponent makes its choice simultaneously, and if the choices match the subject is rewarded with R = 1. During the instructed task,
During the strategic task the computer opponent makes its choice simultaneously, and if the choices match the subject is rewarded with R = 1. During the instructed task, 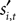 is chosen before si,t, but even if the choices agree the monkey is only rewarded half the time:
is chosen before si,t, but even if the choices agree the monkey is only rewarded half the time:
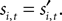 During the strategic task the computer opponent makes its choice simultaneously, and if the choices match the subject is rewarded with R = 1. During the instructed task,
During the strategic task the computer opponent makes its choice simultaneously, and if the choices match the subject is rewarded with R = 1. During the instructed task, 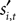 is chosen before si,t, but even if the choices agree the monkey is only rewarded half the time:
is chosen before si,t, but even if the choices agree the monkey is only rewarded half the time:
Therefore the expected payoff during the instructed task equals the equilibrium expected payoff in the strategic task.
An EWA learning model posits an action value 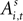 for each strategy s in trial t in experiment i, and includes free parameters which control how action value evolves. On a given trial, it yields a continuous propensity to choose each action, si,t+1, as a monotonic function of current action values
for each strategy s in trial t in experiment i, and includes free parameters which control how action value evolves. On a given trial, it yields a continuous propensity to choose each action, si,t+1, as a monotonic function of current action values 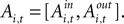
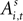 for each strategy s in trial t in experiment i, and includes free parameters which control how action value evolves. On a given trial, it yields a continuous propensity to choose each action, si,t+1, as a monotonic function of current action values
for each strategy s in trial t in experiment i, and includes free parameters which control how action value evolves. On a given trial, it yields a continuous propensity to choose each action, si,t+1, as a monotonic function of current action values 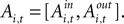
At the start of the experiment 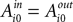 for each strategy so that values are equal in the first trial. In general, after trial t the current value of strategy s is updated according to a formula that depends on whether s was chosen or not. If strategy s was chosen then its updated value can be written as a combination of past value (with weight ϕ) and current reward:
for each strategy so that values are equal in the first trial. In general, after trial t the current value of strategy s is updated according to a formula that depends on whether s was chosen or not. If strategy s was chosen then its updated value can be written as a combination of past value (with weight ϕ) and current reward:
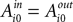 for each strategy so that values are equal in the first trial. In general, after trial t the current value of strategy s is updated according to a formula that depends on whether s was chosen or not. If strategy s was chosen then its updated value can be written as a combination of past value (with weight ϕ) and current reward:
for each strategy so that values are equal in the first trial. In general, after trial t the current value of strategy s is updated according to a formula that depends on whether s was chosen or not. If strategy s was chosen then its updated value can be written as a combination of past value (with weight ϕ) and current reward: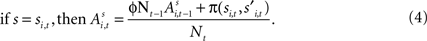
Alternatively, if strategy s was not chosen then its updated value depends on past value (with weight ϕ) and foregone payoffs:
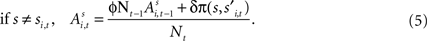
The weight δ is the foregone payoff the subject would have received had it counterfactually chosen s. In both equations, Nt is a trial weight which evolves according to

On a given trial, the probability of choosing si,t = in is defined as

and the parameters λ,ϕ,δ,ρ, and N0 are estimated via maximum likelihood. The estimated parameters (except λ) are then used to generate a sequence of fitted action values which we use in our analysis. Importantly, Ai,t is computed using only choices and rewards (both actual and fictitious) through trial t, which implies that it can directly enter a model of choice for the next trial, t+1. For a complete definition of the EWA model and estimation procedure, see the APPENDIX.
Win-Stay/Lose-Switch Learning
Since EWA is based on a reinforcement premise, it includes a Win-Stay, Lose-Switch choice dependency as a special case. Relative to trial t + 1, a Win-Stay outcome for strategy s is coded with an indicator for s = si,t and πi,t = 1. A Lose-Switch outcome is s ≠ si,t and πi,t = 0. This behavior can be captured by a different value, 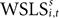 with its own updating formula,
with its own updating formula,
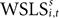 with its own updating formula,
with its own updating formula,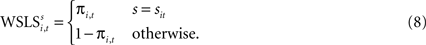
As in the EWA model, current reward affects the evolution of action value (here represented by 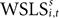 ). Similarly, the strength of the connection between WSLSi,t and si,t+1 can be modulated with additional parameters (see Eq. 7). But unlike Eqs. 4 and 5, the WSLS model of value in Eq. 8 does not account for past events before period t nor does it account for a fictitious assessment of actions not chosen (foregone payoffs).
). Similarly, the strength of the connection between WSLSi,t and si,t+1 can be modulated with additional parameters (see Eq. 7). But unlike Eqs. 4 and 5, the WSLS model of value in Eq. 8 does not account for past events before period t nor does it account for a fictitious assessment of actions not chosen (foregone payoffs).
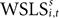 ). Similarly, the strength of the connection between WSLSi,t and si,t+1 can be modulated with additional parameters (see Eq. 7). But unlike Eqs. 4 and 5, the WSLS model of value in Eq. 8 does not account for past events before period t nor does it account for a fictitious assessment of actions not chosen (foregone payoffs).
). Similarly, the strength of the connection between WSLSi,t and si,t+1 can be modulated with additional parameters (see Eq. 7). But unlike Eqs. 4 and 5, the WSLS model of value in Eq. 8 does not account for past events before period t nor does it account for a fictitious assessment of actions not chosen (foregone payoffs).Both Win-Stay/Lose-Switch and the more general EWA models of value predict dependence in the sequence of actions si,t across adjacent trials. One method for exploring this dependence is to use the updating equations to generate predictors for actions in the following trial. First, we can rewrite Eq. 8 as the sum of two terms,
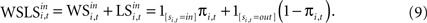
This formulation motivates a probit model for choice of the form:
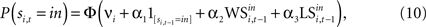
for t = 1,…,Ti and ϕ() denotes the standard normal distribution function (see Wooldridge, 2001
for a discussion of the probit and tobit model introduced below). The term νi is a fixed effect for experiment i. is the indicator function which yields 1 if si,t = in and 0 otherwise. A simple Win-Stay/Lose-Switch hypothesis would predict α1 = 0 since the WS and LS variables would capture all the dependence in the sequence of decisions. Further, it would predict that α2 = α3, since the effects of winning and losing are symmetric.
Value, SCi Activity and Actions
To address how value is encoded in neural signals, we introduce our measurement of 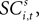 defined as the SCi activity associated with saccade target s in trial t of experiment i. In 10 experiments we observe
defined as the SCi activity associated with saccade target s in trial t of experiment i. In 10 experiments we observe 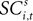 for both choices; for the other 58 we observe it only for one choice, s = in. To test whether SCi activity encodes the value of actions, in the form of a choice, we estimate the probit
for both choices; for the other 58 we observe it only for one choice, s = in. To test whether SCi activity encodes the value of actions, in the form of a choice, we estimate the probit
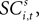 defined as the SCi activity associated with saccade target s in trial t of experiment i. In 10 experiments we observe
defined as the SCi activity associated with saccade target s in trial t of experiment i. In 10 experiments we observe 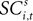 for both choices; for the other 58 we observe it only for one choice, s = in. To test whether SCi activity encodes the value of actions, in the form of a choice, we estimate the probit
for both choices; for the other 58 we observe it only for one choice, s = in. To test whether SCi activity encodes the value of actions, in the form of a choice, we estimate the probit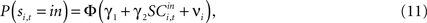
for t = 1,…,Ti. Associating 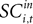 with the value of s = in is the hypothesis that γ2 > 0. Rejecting the hypothesis γ2 = 0 in favour of γ2 > 0 is a necessary condition for SC_{i,t} to encode value, but is not sufficient proof that it does.
with the value of s = in is the hypothesis that γ2 > 0. Rejecting the hypothesis γ2 = 0 in favour of γ2 > 0 is a necessary condition for SC_{i,t} to encode value, but is not sufficient proof that it does.
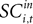 with the value of s = in is the hypothesis that γ2 > 0. Rejecting the hypothesis γ2 = 0 in favour of γ2 > 0 is a necessary condition for SC_{i,t} to encode value, but is not sufficient proof that it does.
with the value of s = in is the hypothesis that γ2 > 0. Rejecting the hypothesis γ2 = 0 in favour of γ2 > 0 is a necessary condition for SC_{i,t} to encode value, but is not sufficient proof that it does.For the 10 experiments in which we measure SCi activity associated with both choices, we can also estimate a probit of the form
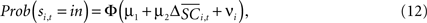
where 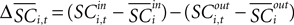 is the difference in SCi activity across actions relative to their within-experiment means,
is the difference in SCi activity across actions relative to their within-experiment means, 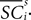 A positive value for Δ
A positive value for Δ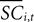 indicates the de-meaned activity associated with the in target was larger than for out. If choice depends on the comparative value of actions, and value is encoded in SCi activity, then choice probabilities should depend on differences in SCi activity. Thus we hypothesize that μ2 > 0.
indicates the de-meaned activity associated with the in target was larger than for out. If choice depends on the comparative value of actions, and value is encoded in SCi activity, then choice probabilities should depend on differences in SCi activity. Thus we hypothesize that μ2 > 0.
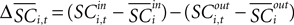 is the difference in SCi activity across actions relative to their within-experiment means,
is the difference in SCi activity across actions relative to their within-experiment means, 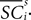 A positive value for Δ
A positive value for Δ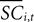 indicates the de-meaned activity associated with the in target was larger than for out. If choice depends on the comparative value of actions, and value is encoded in SCi activity, then choice probabilities should depend on differences in SCi activity. Thus we hypothesize that μ2 > 0.
indicates the de-meaned activity associated with the in target was larger than for out. If choice depends on the comparative value of actions, and value is encoded in SCi activity, then choice probabilities should depend on differences in SCi activity. Thus we hypothesize that μ2 > 0.Our final hypothesis is that SCi activity reflects the action valuation in the EWA model. To test it, we consider a random-effects regression of the form:
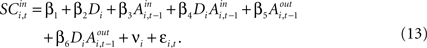
For experiments involving the strategic task, we define Di = 1, with Di = 0 for the instructed task. The constant term, β1, records the conditional mean activity for the sample of neurons examined, while β2 measures the effect of the strategic task on this baseline activity. The coefficient β3 captures the relationship between SCi activity (in the response field) and the EWA action value of choosing in. The strength of association between SCi activity and action value in the strategic task is determined by the value of the interaction parameter β4. To capture any relationship between SCi activity (for in) and the valuations of alternative actions we include 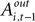 as a regressor with parameter β5. Again, this relationship in the strategic task is reflected by the interaction parameter β6. Our hypothesis is that only EWA action value for in positively influences SC activity: β3 > 0, β3 + β4 > 0, β5 ≤ 0, β5 + β6 ≤ 0.
as a regressor with parameter β5. Again, this relationship in the strategic task is reflected by the interaction parameter β6. Our hypothesis is that only EWA action value for in positively influences SC activity: β3 > 0, β3 + β4 > 0, β5 ≤ 0, β5 + β6 ≤ 0.
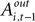 as a regressor with parameter β5. Again, this relationship in the strategic task is reflected by the interaction parameter β6. Our hypothesis is that only EWA action value for in positively influences SC activity: β3 > 0, β3 + β4 > 0, β5 ≤ 0, β5 + β6 ≤ 0.
as a regressor with parameter β5. Again, this relationship in the strategic task is reflected by the interaction parameter β6. Our hypothesis is that only EWA action value for in positively influences SC activity: β3 > 0, β3 + β4 > 0, β5 ≤ 0, β5 + β6 ≤ 0.Since SCi activity varies continuously, we can estimate equation 13 as a regression. However, on some trials there is no SCi activity measured during our 50 ms preparatory epoch, thus there is left- censoring at zero of the endogenous variable 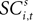 for a small but sizeable portion of trials. We account for this censoring by estimating equation 13 as a tobit model.
for a small but sizeable portion of trials. We account for this censoring by estimating equation 13 as a tobit model.
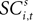 for a small but sizeable portion of trials. We account for this censoring by estimating equation 13 as a tobit model.
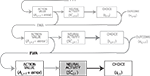
for a small but sizeable portion of trials. We account for this censoring by estimating equation 13 as a tobit model.We should emphasize the timing of our regression equations 12 and 13, presented graphically in Figure 3
. The EWA valuation 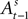 is a function of all observed choices and rewards through trial t − 1 (see Appendix). SCi activity in trial t,
is a function of all observed choices and rewards through trial t − 1 (see Appendix). SCi activity in trial t, 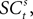 is a function of
is a function of 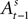 therefore is a function of all choices and rewards through trial t − 1. Finally, the chosen action st is a function of the SCi activity in trial t. Importantly,
therefore is a function of all choices and rewards through trial t − 1. Finally, the chosen action st is a function of the SCi activity in trial t. Importantly, 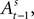 does not include any information from the trial t choice. Thus the maintained hypothesis is that past action predicts current SCi activity which predicts upcoming choice in the current trial.
does not include any information from the trial t choice. Thus the maintained hypothesis is that past action predicts current SCi activity which predicts upcoming choice in the current trial.
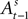 is a function of all observed choices and rewards through trial t − 1 (see Appendix). SCi activity in trial t,
is a function of all observed choices and rewards through trial t − 1 (see Appendix). SCi activity in trial t, 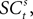 is a function of
is a function of 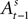 therefore is a function of all choices and rewards through trial t − 1. Finally, the chosen action st is a function of the SCi activity in trial t. Importantly,
therefore is a function of all choices and rewards through trial t − 1. Finally, the chosen action st is a function of the SCi activity in trial t. Importantly, 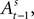 does not include any information from the trial t choice. Thus the maintained hypothesis is that past action predicts current SCi activity which predicts upcoming choice in the current trial.
does not include any information from the trial t choice. Thus the maintained hypothesis is that past action predicts current SCi activity which predicts upcoming choice in the current trial.Figure 3. Schematic illustrating the recursive EWA computation and its hypothesized influence on SCi activity. In our experiments, we record and analyze current neural activity (SCi,t, gray box). SCi,t lies at the nexus between action value, calculated from past events, and choice on a trial t. Action value (Ai,t−1) is recursively updated based on an EWA learning model whose main inputs are past choices (si,t−1) and their realized or forgone outcomes (πi,t−1). Action value also includes an error term to highlight that the calculated Ai,t−1 only approximates and does not fully capture underlying valuation, in addition to any error arising from noisy neural signals. As such, the relationship between hypothesized Ai,t–1 and neural activity is likely weaker (thin arrows) than between neural activity and the observable si,t (thick arrows).
Algorithm for Computer Opponent
The computer algorithm which the monkey competes against is primarily designed to elicit equilibrium behavior from the monkey, that is, a 50/50 randomization of choices. In doing so, the algorithm does not play the Nash strategy itself. This somewhat paradoxical setup is a result of the unstable nature of mixed strategies highlighted by Harsanyi (1973)
. When the computer is not adaptive, but simply randomizes its choices, the monkey is indifferent between his strategies (any strategy the monkey chooses will be rewarded on half of the trials) and the monkey’s choices become strongly biased in one direction (Lee et al., 2004
). For this reason, the algorithm was designed to exploit the monkey’s choice biases, perhaps more in line with what constitutes (approximate) equilibrium in such games. Refer to algorithm 2 from Lee et al. (2004)
for additional details on the computer opponent.
We begin by characterizing the effects of current and previous trials on both behavior and SCi activity in Sections “Analysis of Current Trial”, “Dependence of Choice on Previous Trial” and “Sequential Dependence of Choice”. In section “Dependence of Choice on Previous Trial”, we formally test for a Win-Stay/Lose-Switch strategy. The ability of SCi neurons to predict choice is examined in section “Neuronal Choice Prediction”. In section “Behavioural EWA Estimates”, we fit the EWA model to choice data and generate sequences of action values for each monkey. Finally, having established that choice is dependent on previous trials, and SCi activity predicts choice on a given trial, in Section “Encoding EWA Action Value” we test our hypothesis that SCi neurons represent the action-specific valuations posited by EWA.
We have data from 68 experiments where neurons satisfied our criteria for inclusion (See Section “Materials and Methods”). In 10 of these experiments, we were able to measure SCi activity associated with both saccades simultaneously, 20 neurons total. In the remaining 58 experiments, we were able to measure SCi activity associated with only one of the potential saccades.
The data consists of a choice, preparatory SCi activity, and a saccadic response time (SRT) for a set of i = 1…78 neurons respectively with Ti ordered trials. In 38 of these experiments, data were collected for both the strategic task and the instructed task control. This sub-sample of 38 neurons is used in Sections “Analysis of Current Trial”, and “Dependence of choice on previous trial”, and “Sequential dependence of choice”. In this sub-sample, a mean of 246 ± 11 SEM trials per neuron were analyzed during the strategic task and a mean of 146 ± 8 SEM trials per neuron were analyzed during the instructed task. The full sample is used in Section “Neuronal Choice Prediction”, while Sections “Behavioural EWA Estimates” and “Encoding EWA Action Value” drop experiments in which greater than 30% of the trials were aborted. These experiments were dropped since many aborted trials within an experiment may interrupt the sequence of valuation posited by EWA learning. The cut-off 30% was set to balance choice sequence consistency and sample size.
Analysis of Current Trial
We will briefly characterize saccade behaviors and SCi preparatory activity on the current trial before examining the effects of events on previous trials. A more detailed current trial analysis can be found in Thevarajah et al. (2009)
. All reported statistics are (mean ± se).
The allocation of saccade choices did not differ between the two targets during the strategic task [p(in) = 49.8 ± 0.6%; paired t-test p > 0.05]. Moreover, SRTs did not differ between the two targets during the instructed task (in: 192.9 ± 4.2 ms, out: 186.1 ± 3.7 ms, p > 0.05). These behavioral measures suggest that, on average, saccade preparation processes were not biased towards any one particular target location during either task. However, in the strategic task the monkey was rewarded on only 42.2% of the trials, whereas in the instructed task the monkey was rewarded half the time (Table 1
).
Table 1. Frequencies of choice dependencies in strategic game.
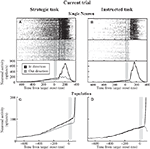
In both tasks, neuronal activity steadily increased during the warning period in advance of choosing either target (Figure 4
). Overall preparatory activity was greater regardless of saccade direction during the strategic task compared to the instructed task (in: p < 0.05, out: p < 0.05). Moreover, in the strategic task activity was segregated for saccades in (99.9 ± 8.8 spikes/s) and out (80.2 ± 7.2 spikes/s, paired t-test, p < 0.001), whereas activity was not segregated between in (63.5 ± 6.5 spikes/s) and out (64.5 ± 6.5 spikes/s) saccades during the instructed task (paired t-test, p > 0.05). This greater overall activation and neuronal selectivity during the strategic task may occur because saccades are under voluntary control and can be planned in advance. In the instructed task the monkey must wait for the presentation of the target.
Figure 4. SCi activity during the current trial. (A, B) Activity of a representative SCi neuron during the strategic (A) and instructed (B) tasks. Rasters (top panels) and post-synaptic activation functions (bottom panel) are sorted based on saccades directed in (black) and out (gray) of the neuron’s response field. The shaded gray bar denotes the epoch during which preparatory activity was analyzed. (C, D) Mean activity of neuron sample in which both strategic (C) and instructed (D) tasks were recorded (38 neurons).
Dependence of Choice on Previous Trial
We examine sequential choice dependencies by segregating behavior and neuronal activity on the events of the previous trial (i.e., previous choice and its reward outcome). Particularly, we test for the prevalence of a WS/LS strategy.
The influence of previous trials on subsequent saccadic responses
We begin by summarizing the frequencies of WS/LS choice patterns in the strategic task over all experiments (Table 1
). Choices were repeated in a WS/LS pattern in 55.5% of the trials. A WS was observed in 62.1% of post-win trials vs. LS observed in 50.6% of post-loss trials, which suggests a WS/LS strategy is solely due to a Win-Stay rather than Lose-Shift bias. The larger percentage of losing trials suggests the computer opponent was able to exploit this tendency in choice patterns.
To further assess the influence of previous trial events, we estimate Eq. 10 which models choice as a function of lagged choice and the Win-Stay and Lose-Switch variables. Estimates of the fixed-effects probit are presented in Table 2
. The explicit prediction of the simple WS/LS strategy is rejected because the estimated coefficients α2 and α3 are significantly different from each other: the tendency to repeat rewarded actions is greater than the tendency to switch from unrewarded actions. We can also note that the tendency to repeat choices is largely due to the Win-Stay bias since α1 is not significantly different from zero.
Table 2. Probit estimates of si,t+1 on lagged choice and Win-Stay/Lose-Switch outcomes.
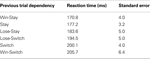
To measure any biases in the instructed task, saccadic reaction times (SRTs) were examined in Table 3
. Considering that target location and outcome were stochastic, therefore unpredictable, these previous events had a surprisingly large influence on SRTs. Repeating an action resulted in faster SRTs than switching actions (Stay vs. Switch, binomial test p < 10−11). SRTs were particularly biased if a saccade direction was previously rewarded (Win-Stay vs. Lose-Stay, binomial test p < 10−5; Win-Switch vs. Lose-Switch, binomial test p < 10−3). This suggests preparation biases were a function of both previous choices and their outcomes.
Table 3. Reaction time dependencies in instructed task.
The Influence of previous trials on Sci preparatory activity
Figure 5
illustrates how SCi activity was also influenced by the previous trial. The black dashed line shows mean activity over all experiments. Each of the coloured lines depicts how current trial activity was influenced by choices and outcomes on the previous trial. This influence is most prevalent at the end of the warning period (gray-shaded area). Therefore we will use SCi activity in this epoch for the sequential analysis that follows.
Figure 5. Mean activity of neuronal sample (38 neurons) segregated on previous trials during the strategic (A) and instructed (B) tasks respectively. The black dashed line represents the mean activity for all trials. The colored lines also represent current trial activity, but this activity is segregated into four categories based on the combination of target choice (in or out) and their outcomes (R or U). Note that the mean activity is a sum of each of the four colored lines weighted by the proportion of trials in each category. Line widths represent the SEM. The shaded gray bar denotes the epoch during which preparatory activity was sampled during subsequent analyses.
Sequential Dependence of Choice
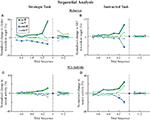
Having observed a dependency in choices and outcomes in the previous trial, we will now characterize this dependency over multiple trials. Two sequential patterns were evident in both tasks (Figure 6
). First, more recent events had the greatest influence. Second, actions that were rewarded generally had a more pronounced effect, both in terms of magnitude and duration, than unrewarded actions (Figure 6
, dark colored lines vs. light colored lines). Whether a previous trial was rewarded or not, did not, by itself, affect SC activity or saccade behaviors. Instead, the effects of reward influenced a particular saccade location rather than providing a general motivating or alerting effect for both actions.
Figure 6. Saccade behavior and SCi activity segregated on previous and future trials. The data for each trial sequence is presented as the percentage change from the mean data for all trials at trial t (black dots). Note that each data point in the trial sequence represents the influence of an earlier or later trial on the current trial. Therefore, the four colored data points at each time sequence always sum to the mean data point at time t when weighted by the proportion of trials in each category. (A) Changes in in target choices during the strategic task. (B) Changes in in target SRTs during the instructed task. Note that the the ordinate axis has been flipped because SRTs are negatively correlated with SCi activity. (C) Changes in SCi activity during the strategic task. (D) Changes in SCi activity during the instructed task. Filled squares indicate significant differences from the mean activity. Representative standard errors are shown for in/R data points.
The strategic and instructed tasks also differed in two ways during this sequential analysis. First, future events were correlated with choice selection in the strategic but not the instructed task (Figure 6
A). This seemingly paradoxical finding is a consequence of the computer exploiting the monkey’s Win-Stay bias. That is, monkeys were more likely to lose following a rewarded trial as they tended to repeat actions. This phenomena is evident in the Lose-Stay bias observed in future choices in Figure 6
A. Second, modulation of SCi activity by past events was greater for the instructed task than for the strategic task. For example, the change in activity imposed by the previous trial was approximately three times as large during the instructed task compared to the strategic task (compare the spread in data along the vertical axis in Figures 6
C vs. D).
Neuronal Choice Prediction
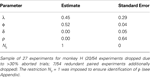
Having characterized serial dependency in choices, the second step in determining whether neurons in the SCi encode action value is to determine if activity predicts choice. The ten experiments where we measured two neurons simultaneously, one for each target, allows us to specify how opposing SCi activity is compared in Eq. 12. Results for the fixed-effects probit estimation are given in Table 4
.
Table 4. Probit estimates of si,t based on difference in activity from neurona1 pairs.
The parameter μ2 measures the impact of SCi activity on the probability of an in saccade and is both positive and highly significant. To interpret the magnitude of the coefficient μ2, we take the predicted probabilities from the regression and compare them to the observed choices by two methods. The first rounds the probabilities to the nearest integer and compares them to the choices, resulting in a prediction rate of 65%. The second simulates choices from the binomial distribution using the predicted probabilities, and compares the simulated choices to the actual choices, resulting in a prediction rate of 56% for 1000 simulations. Comparatively, 1000 independent draws from a 50/50 binomial distribution would predict 56% of the trials (560 matches of the monkey’s choice) with probability 6.3 × 10−5. Results did not change significantly when we estimated on half the sample and predicted out of sample.
For the entire 78 neuron sample, we can also assess how well single neurons predict choice from Eq. 11. Results are reported in Table 5
. Again, we observe that the estimate of SCi activity, γ2, is both positive and highly significant. As before, our assessment of the magnitude of the parameter γ2 relies on in-sample prediction. Rounding the fitted probabilities results in a 60% prediction rate for the 78 individual neurons, while simulating the choices results in a 53% prediction rate. As expected, the single neuron is a worse predictor compared to the the paired neuron analysis, presumably because choice is based on a comparison of valuation between the two targets. Again, 1000 independent 50/50 draws would still only predict 53% with probability 0.03.
Table 5. Probit estimates of si,t based on activity from individual neurons.
Behavioural EWA Estimates
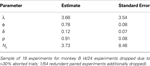
To generate a sequence of action values which reflect each monkey’s valuation on a given trial, we estimated the EWA model on choice data (see Section “EWA Learning” and APPENDIX). Estimates are reported in Tables 6 and 7
. We observe significant heterogeneity in the fitted EWA parameters, similar to Ho et al. (2008)
. Estimates suggest Monkey H (54/78 experiments) is a cumulative reinforcement learner (δ = 0, ρ = 0), while Monkey B (24/78 experiments) has a fictive learning component and averages rewards as in Q-Learning (δ > 0, ρ = ϕ). For each monkey, the estimates for ϕ, δ, ρ, and N0 are used to generate the sequence 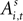 which we use in section “Encoding EWA Action Value”.
which we use in section “Encoding EWA Action Value”.
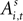 which we use in section “Encoding EWA Action Value”.
which we use in section “Encoding EWA Action Value”.Table 6. EWA Estimates for Monkey B.
Table 7. EWA Estimates for Monkey H.
Encoding EWA Action Value
The EWA action value is a function of the observed choices and reward structure of the game. Our final hypothesis is that SCi activity reflects the fitted action values from Section “Behavioural EWA Estimates”. To test this hypothesis, we estimate Eq. 13 separately for each monkey and its appropriate action value 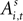 . Results are reported in Tables 8 and 9
.
. Results are reported in Tables 8 and 9
.
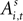 . Results are reported in Tables 8 and 9
.
. Results are reported in Tables 8 and 9
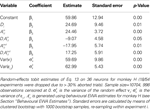
.Table 8. Estimates of 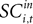 , on EWA action values and task type for monkey H.
, on EWA action values and task type for monkey H.
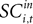 , on EWA action values and task type for monkey H.
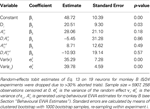
, on EWA action values and task type for monkey H.Table 9. Estimates of SCi,t on EWA action values and task type for monkey B.
For monkey H (Table 8
), the instructed task relationship between EWA action value and SCi activity for target in is positive, significant and large in magnitude Over the observed range of the EWA action value (0.00 < Ai,t < 1.96), this represents an 81% change in SCi activity relative to baseline activity of 59.86 spikes/s. Notably, this relationship is partially offset by the out EWA action value (H0: β3 + β5 = 0, p = 0.36). If the action values of the two targets were equal 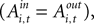 the estimates predict there would still be an increase in SCi activity for the in target. This suggests that a given SC neuron encodes the action value for the target it is associated with on the topographic map, but other neurons (valuable targets) can partially inhibit this valuation.
the estimates predict there would still be an increase in SCi activity for the in target. This suggests that a given SC neuron encodes the action value for the target it is associated with on the topographic map, but other neurons (valuable targets) can partially inhibit this valuation.
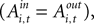 the estimates predict there would still be an increase in SCi activity for the in target. This suggests that a given SC neuron encodes the action value for the target it is associated with on the topographic map, but other neurons (valuable targets) can partially inhibit this valuation.
the estimates predict there would still be an increase in SCi activity for the in target. This suggests that a given SC neuron encodes the action value for the target it is associated with on the topographic map, but other neurons (valuable targets) can partially inhibit this valuation.As expected from our sequential analysis, the relationship between SC activity and action value is attenuated in the strategic task though it is still positive and significant (H0: β3 + β4 = 0, p = 0.00). The estimates yield a 36% increase in SC activity relative to baseline (β1 + β2 = 84.5 spikes/s) over the range of 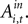 However the out EWA action value now has no impact (H0: β5 + β6 = 0, p = 0.82) suggesting no inhibition from out target neurons during this measurement epoch of the strategic task.
However the out EWA action value now has no impact (H0: β5 + β6 = 0, p = 0.82) suggesting no inhibition from out target neurons during this measurement epoch of the strategic task.
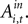 However the out EWA action value now has no impact (H0: β5 + β6 = 0, p = 0.82) suggesting no inhibition from out target neurons during this measurement epoch of the strategic task.
However the out EWA action value now has no impact (H0: β5 + β6 = 0, p = 0.82) suggesting no inhibition from out target neurons during this measurement epoch of the strategic task.Estimation results for monkey B have considerably more variance (Table 9
). In the instructed task, we still observe a positive coefficient for 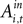
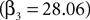 but with a larger p-value (p = 0.18) and a smaller magnitude relative to baseline (33%) over the observed range of action values (0.00 < Ai,t < 0.58). While the estimate for attenuation in the strategic sample is of the correct sign (β4 < 0), it is not significantly different from zero (p = 0.86). The estimates for the out action value are also highly variable and not significantly different from zero in either task. We should note that the sub-sample for monkey B contains half as many observations and neurons as the sub-sample for monkey H, though this efficiency loss likely does not account for all of the increased variability of the estimates.
but with a larger p-value (p = 0.18) and a smaller magnitude relative to baseline (33%) over the observed range of action values (0.00 < Ai,t < 0.58). While the estimate for attenuation in the strategic sample is of the correct sign (β4 < 0), it is not significantly different from zero (p = 0.86). The estimates for the out action value are also highly variable and not significantly different from zero in either task. We should note that the sub-sample for monkey B contains half as many observations and neurons as the sub-sample for monkey H, though this efficiency loss likely does not account for all of the increased variability of the estimates.
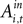
 but with a larger p-value (p = 0.18) and a smaller magnitude relative to baseline (33%) over the observed range of action values (0.00 < Ai,t < 0.58). While the estimate for attenuation in the strategic sample is of the correct sign (β4 < 0), it is not significantly different from zero (p = 0.86). The estimates for the out action value are also highly variable and not significantly different from zero in either task. We should note that the sub-sample for monkey B contains half as many observations and neurons as the sub-sample for monkey H, though this efficiency loss likely does not account for all of the increased variability of the estimates.
but with a larger p-value (p = 0.18) and a smaller magnitude relative to baseline (33%) over the observed range of action values (0.00 < Ai,t < 0.58). While the estimate for attenuation in the strategic sample is of the correct sign (β4 < 0), it is not significantly different from zero (p = 0.86). The estimates for the out action value are also highly variable and not significantly different from zero in either task. We should note that the sub-sample for monkey B contains half as many observations and neurons as the sub-sample for monkey H, though this efficiency loss likely does not account for all of the increased variability of the estimates.Summary of Findings
This study examined whether a valuation of future actions, constructed as a function of previous choices and rewards, is represented by the superior colliculus in a strategic environment. Our results show that SCi preparatory activity was shaped by both previous saccades and their outcomes, particularly a Win-Stay bias, and more recent events had a more pronounced effect. These sequential biases were reflected in upcoming choices during the strategic task and upcoming saccadic reaction times during the instructed task.
SCi activity was also predictive of upcoming strategic saccades on a trial-by-trial basis (Tables 4 and 5
); at a rate of 60% for single neurons and 65% for opposing neuron pairs. Although our pool of neuron pairs was small (10 pairs), this improvement in prediction suggests that it is not the absolute level of activity, but the relative level of activity between potential actions, that is best correlated to choice.
The fact that SCi activity was both shaped by previous choices and rewards and predicted future choices suggest it as a candidate neural correlated of action values posited by behavioural learning model. Our analysis demonstrated that SCi activity was correlated on a trial-by-trial basis with the EWA learning valuation. Specifically, SCi activity was positively correlated with the action value for its response field, with some evidence that it is negatively correlated with the action value of the alternative target. Collectively, our empirical and modelling results suggest that hypothesized action value signals are represented in the motor planning regions of the brain in a manner that could be used to select strategic actions.
Effects of Previous Actions and Rewards
Serial dependence of choices has previously been observed in strategic and non-strategic environments. Consistent with previous studies, more recent events had a greater influence on both choices (Juttner and Wolf, 1992
; Maljkovic and Nakayama, 1994
; Dorris et al., 2000
; Barraclough et al., 2004
; Lee et al., 2004
; Lau and Glimcher, 2005
) and neuronal activity (Dorris et al., 2000
; Bayer and Glimcher, 2005
; Seo and Lee, 2007
), and these influences decayed with time (Figure 6
). Unlike the computer opponent which weighed all past events equally, monkeys gave more weight to recent events when selecting actions. This policy may be an efficient solution for using past events to predict future rewarded actions given organisms have a limited memory store (Anderson et al., 1996
; Callicott et al., 1999
), and it allows organisms to more readily adapt to a changing environment.
Sequential effects have been characterized previously in the SCi during a task similar to our instructed task (Dorris et al., 2000
). Although target location was unpredictable in this previous study, all saccades were rewarded; therefore the contribution from repeating a motor action, or repeating a rewarded location, remained unclear. By allocating rewards unpredictably, we were able to isolate the contribution of these factors. Previously unrewarded actions had a biasing effect, but to a lesser extent than previously rewarded actions. We found no effect of previously rewarded trials when analyzed independently of actions, which suggested that reward, at least our task, did not have a generalized alerting or motivating effect. Instead, SCi activity was found to be influenced by a combination of both previous actions and rewards. These biases, in turn, were reflected in saccade behaviors (Figure 6
).
Finally, we observed differences in how SC activity was influenced by previous events during the two tasks. First, the overall level of SC activity was greater preceding strategic than instructed saccades (i.e., compare black dashed lines in Figures 5
A vs. B). Strategic saccades may have been more fully prepared because the locations of the two targets were known in advance whereas the location of the single target had to be identified before the saccade preparation processes could be completed in the instructed task. Second, previous events exerted less influence on SCi activity during the strategic task (i.e., compare Figures 6
C vs. D). This was observed in the magnitude of the sequential dependencies and the number of previous trials which exerted an influence. Although having sequential biases was seemingly unnecessary in the instructed task, as the monkey could neither control nor predict saccade direction or reward, having such biases were relatively inconsequential. In the strategic task however, sequential biases led to exploitation by the computer opponent as evidenced by a reduced reward rate (Table 1 and Barraclough et al., 2004
). Our results suggest the influence of previous events, borne out in sequential dependencies, can be attenuated in strategic situations.
Win-Stay Bias
Though the analysis in Sections “Dependence of Choice on Previous Trial” and “Sequential Dependence of Choice” revealed notable choice tendencies in the strategic sample, many of which are incorporated in the EWA learning model, there is one in particular we wish to highlight. Although both effects were significant, subjects repeated winning choices more often than switching from losing choices controlling for repeated choices (α2 > α3), or a Win-Stay bias. This observation is a rejection of a strict Win-Stay/Lose-Switch model of choice in repeated games.
However, a stronger Win-Stay bias is compatible with our candidate model of action value (EWA). If unchosen winning actions are updated by a fraction δ < 1 relative to chosen winning actions, the difference in the action value after a rewarded trial is larger than after an unrewarded trial:
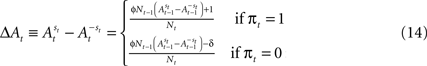
Therefore
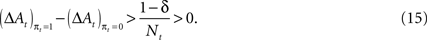
This result holds generally for all models nested by EWA, as long as δ < 1. A Win-Stay bias may be exacerbated in our experiment because our payoff matrix is not zero-sum (Figure 2
); not matching the opponent constituted a withholding of reward rather than a loss of reward. This asymmetry in payoffs may bias the subject’s responses in favour of rewarded trials.
Predicting Choice
Our results indicate that the activity of individual SCi neurons can predict upcoming choices with 60% reliability. Although significantly better than chance, the SCi may not appear to be a particularly impressive predictor. However, a number of issues must be taken under consideration to make this judgment.
The predictive capability of SCi neurons depends on the number of neurons in the population, the correlation in their firing patterns, and the manner in which downstream structures read-out these predictive signals. Although we only had a sample of 10 neuronal pairs, our results demonstrate that simply comparing the relative firing of two opposing neurons increases prediction from 60% to 65%. Moreover, while the predictive capability of any one (or two) neuron(s) may be weak, this is a very consistent prediction across the neuronal population (see Figure 5
D from Thevarajah et al., 2009
). Therefore, these small individual biases can be amplified to provide a strong signal for selecting strategic actions.
Although the SCi is required for generating saccades (Hanes and Wurtz, 2001
) and manipulating SCi activity alters saccadic choices (Carello and Krauzlis, 2004
; McPeek and Keller, 2004
; Dorris et al., 2007
; Thevarajah et al., 2009
), the robust activity for out direction saccades (Figure 4
) demonstrates that the reverse is not true; executing a saccade is not a pre-requisite for preparatory SCi activity. This evidence strongly suggests that a causal arrow passes from SCi to choice uni-directionally (Figure 3
). Similarly, if action value is indeed a function of past choices, then it must be action value that influences SCi activity. If these arrows were not uni-directional then current activity or choices would paradoxically cause past choices.
Neuronal Correlates of Experience Weighted Attraction
Our preliminary analysis has shown that both behaviour and SCi activity are correlated with previous choices and rewards, particularly through a reinforcement of rewarded choices (Win-Stay). To formalize this result, we found a neural correlate of a general learning model based upon this reinforcement premise. This model calculates an action value on each trial as a function of the history of observed choices and payoff structure of the game. Therefore, our results in Section “Encoding EWA Action Value” are consistent with the hypothesis that neurons in the SCi encode the history of the two tasks in the form of learned action values for each potential action. A given neuron in the SCi is correlated with the action value of its target in both tasks, though the magnitude of this relationship is attenuated in the strategic task. Further, SCi activity is negatively correlated with the action values of competing targets in the instructed task, but not in the strategic task during the period we measure. This suggests that both the attenuation of the value/SCi relationship, and the lack of inhibition from competing neurons within the preparatory period we measure, may serve a strategic purpose.
The EWA model we use in this study (Camerer and Ho, 1999
) is a general learning model that has proven successful in predicting play both in and out of sample in a wide variety of games. The role EWA plays in our analysis is akin to an objective valuation. It is a function of past choices and rewards which reflects a component of the relative value of each strategy. As such, there remain unaddressed components of value. Learning models do not assess the forward-looking value of an action. That is, there is no consideration of repeated game strategies such as “leading” an opponent in order to exploit him in later periods (though we should emphasize the only unique repeated game equilibrium in matching pennies is the stage game equilibrium). Our analysis also does not address satiation in the experiment nor learning between experiments. However, the relative success of EWA in predicting choice in a strategic environment suggests that its historical, objective component is important in the ultimate valuation of an action.
As a theoretical construct of valuation, both the simplifying assumptions mentioned above and additional neural and/or behavioural factors will combine to limit the explanatory power of EWA (referred to in Figure 3
). But even if the SC is not coding action value as specified by EWA, the fact that EWA action value significantly predicts SC activity suggests that the correct model will share many features of the EWA formulation. Whether a complete model actually nests EWA as a special case remains an open question that is beyond the scope of this paper.
There has been some progress in identifying the neural correlates of the functional elements of EWA. It has been previously observed that the striatum encodes the difference between realized and expected reward, suggesting the striatum may form part of a learning system in the brain (Schultz, 1998
; Caplin et al., 2010
). Rewriting Eq. 18 for only the chosen strategy sit highlights the role the striatum may play in a general EWA formulation:

where

and Δit is the dopaminergenic response system analyzed in Caplin et al. (2010)
. Left unspecified here is the means by which all action values for unchosen actions, s ≠ sit, are updated (see Lohrenz et al., 2007
).
Other important components associated with reinforcement learning models are also encoded in a network of cortical structures that send projections to the SCi. In contrast to the SCi, the signals carried by these cortical structures are much more heterogeneous across individual neurons. A proportion of neurons in the dorsolateral prefrontal cortex (Barraclough et al., 2004
), dorsal anterior cingulated cortex (Seo and Lee, 2008
) and lateral intraparietal cortex (Platt and Glimcher, 1999
; Dorris and Glimcher, 2004
; Seo et al., 2009
) encode relevant information necessary to construct action value such as past choices, opponent’s choices, the animal’s reward history, as well as functions of action value. Like the SCi, some cortical signals display serial dependencies over trials (Seo and Lee, 2007
).
Role of the SCi Within the Saccade Decision Circuit
We propose that the SCi is involved in three important aspects of selecting strategic saccades:
1. integrating value related inputs and tagging action values to particular saccade vectors;
2. selecting a saccade in a process where action value representations are compared;
3. providing feedback of choices to dopaminergic centres.
First, as outlined in Section “Neuronal Correlates of Experience Weighted Attraction”, the SCi receives inputs from regions that encode functional elements of action value learning models. Because the SCi integrates many inputs, and outputs to pre-motor neurons, its representations of action value may be particularly suited for choosing final actions. Moreover, the topographic organization of the SCi allows value representations to be tagged to particular saccade vectors.
Second, the SCi provides a platform where multiple action value representations can compete and ultimately be resolved to choose a particular action. The topographic map within the SCi is organized based on the principle of local excitation and distant inhibition (Munoz and Istvan, 1998
; Trappenberg et al., 2001
; Dorris et al., 2007
). Once activity reaches a certain threshold level on this map, a saccade command is sent to pre-motor neurons in the brainstem (see Moschovakis and Highstein, 1994
for review). Therefore, the SCi is perhaps the last site within the visuosaccadic circuit where action value can be represented to influence saccade selection without directly triggering (or necessarily resulting in) saccades.
Third, the SCi sends direct mono-synaptic projections to dopaminergic neurons in the substantia nigra and ventral tegmental area (Comoli et al., 2003
; Dommett et al., 2005
). Therefore, the SCi may provide feedback on selected actions, thus providing a critical component for the reinforcement learning circuitry of the striatum.
Our results suggest that the evolutionarily old SCi does not simply execute sensory-driven reflexive saccades but also encodes action value signals that can be used to select voluntary, strategic saccades. As would be expected from a brain region involved in the decision process, SCi activity simultaneously reflects past choices and their outcomes, and predicts future choice. Similarly, learning models, such as EWA, recursively compute action values from past events to probabilistically choose future actions. We demonstrate that these small trial-to-trial fluctuations in SCi activity are not entirely random but have serial dependencies which can be captured, in part, by the EWA learning model.
The goal of EWA learning is to construct a model that predicts play across a wide variety of games yet retains a framework that is psychologically sound. In an EWA learning model, each strategy has an attraction (which we re-labelled action value) that is updated based on observed choices and the payoff structure.
We introduce EWA in the context of a player who faces a single opponent. Each period the player chooses s from one of two alternatives, s ∈ {in, out}. For each trial t, the subject makes a choice st, the opponent chooses 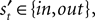 and the subject receives a payoff
and the subject receives a payoff 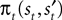 as defined in Section “EWA Learning”. We drop the experiment subscript i here for illustration.
as defined in Section “EWA Learning”. We drop the experiment subscript i here for illustration.
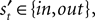 and the subject receives a payoff
and the subject receives a payoff 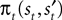 as defined in Section “EWA Learning”. We drop the experiment subscript i here for illustration.
as defined in Section “EWA Learning”. We drop the experiment subscript i here for illustration.Once a choice is made and payoff received in trial t, the attraction of strategy s in trial t is defined as a recursive function of past attractions, choices, and rewards by means of
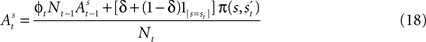
where 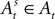 and
and 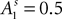 at the beginning of each experiment.
at the beginning of each experiment.
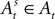 and
and 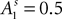 at the beginning of each experiment.
at the beginning of each experiment.The first component of Eq. 18, 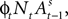 is a depreciation of the previous period’s action value. The second component,
is a depreciation of the previous period’s action value. The second component, 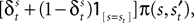 is determined by the choice and reward of the current trial. The experience weight Nt is given by
is determined by the choice and reward of the current trial. The experience weight Nt is given by
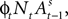 is a depreciation of the previous period’s action value. The second component,
is a depreciation of the previous period’s action value. The second component, 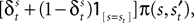 is determined by the choice and reward of the current trial. The experience weight Nt is given by
is determined by the choice and reward of the current trial. The experience weight Nt is given by 
with N0 = 0. Assuming 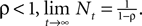
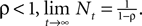
Finally, after a choice is made and a reward is determined in trial t, 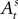 is updated to reflect the valuation of every candidate choice in trial t. On a given trial, the probability of choosing si,t = in is defined as
is updated to reflect the valuation of every candidate choice in trial t. On a given trial, the probability of choosing si,t = in is defined as
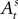 is updated to reflect the valuation of every candidate choice in trial t. On a given trial, the probability of choosing si,t = in is defined as
is updated to reflect the valuation of every candidate choice in trial t. On a given trial, the probability of choosing si,t = in is defined as
which yields a likelihood function for our observed choices

which is estimated via maximum likelihood using the log- likelihood function
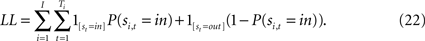
In addition to the identification restrictions detailed in Ho et al. (2008)
, we had to make an additional identification assumption for monkey H. We found that the restriction 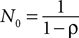 was always binding, so we restricted N0 = 1 for this monkey to ensure identification of ρ, although the estimates are robust to N0 ≤ 1.
was always binding, so we restricted N0 = 1 for this monkey to ensure identification of ρ, although the estimates are robust to N0 ≤ 1.
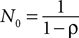 was always binding, so we restricted N0 = 1 for this monkey to ensure identification of ρ, although the estimates are robust to N0 ≤ 1.
was always binding, so we restricted N0 = 1 for this monkey to ensure identification of ρ, although the estimates are robust to N0 ≤ 1.The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by a Career Development Award from the Human Frontier Science Program (HFSP), a Discovery Grant from the National Science and Engineering Research Council (NSERC) of Canada and a group grant from the Canadian Institutes of Health Research (CIHR) awarded to MCD. We thank J. Green, S. Hickman, M. Lewis, F. Paquin and R. Pengelly for technical assistance. J. Turner provided programming expertise and E. Ryklin customized the data acquisition program. D. Byrne and D. Standage provided constructive feedback regarding the manuscript.