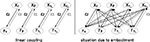1
ERATO Synergistic Project, JST, Laboratory for Intelligent Systems and Informatics, Department of Mechano-Informatics, Graduate School of Information Science and Technology, University of Tokyo, Bunkyo-ku, Tokyo, Japan
2
Artificial Intelligence Laboratory, University of Zurich, Zurich, Switzerland
Pattern generators found in the spinal cord are no more seen as simple rhythmic oscillators for motion control. Indeed, they achieve flexible and dynamical coordination in interaction with the body and the environment dynamics giving to rise motor synergies. Discovering the mechanisms underlying the control of motor synergies constitutes an important research question not only for neuroscience but also for robotics: the motors coordination of high dimensional robotic systems is still a drawback and new control methods based on biological solutions may reduce their overall complexity. We propose to model the flexible combination of motor synergies in embodied systems via partial phase synchronization of distributed chaotic systems; for specific coupling strength, chaotic systems are able to phase synchronize their dynamics to the resonant frequencies of one external force. We take advantage of this property to explore and exploit the intrinsic dynamics of one specified embodied system. In two experiments with bipedal walkers, we show how motor synergies emerge when the controllers phase synchronize to the body’s dynamics, entraining it to its intrinsic behavioral patterns. This stage is characterized by directed information flow from the sensors to the motors exhibiting the optimal situation when the body dynamics drive the controllers (mutual entrainment). Based on our results, we discuss the relevance of our findings for modeling the modular control of distributed pattern generators exhibited in the spinal cord, and for exploring the motor synergies in robots.
During the 1960s and 1970s, central pattern generators (CPGs) were considered to be neural circuits capable of producing single patterned motor output in the absence of sensory feedback. However, more recent investigations have demonstrated that they can adapt to a large variety of tasks scenarios and environmental conditions (Bizzi and Clarac, 1999
; Ivanenko et al., 2005
; Ting and MacPherson, 2005
). Such adaptability and continuous adjustment of behavior is made possible by specific activations of muscles groups, also known as muscle synergies (Bernstein, 1967
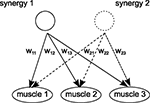
). Given that each muscle can be also activated by several synergies, it reflects the considerable flexibility and complexity in the motor systems’ dynamics (see Figure 1
). Hence, the rhythmical patterns found in CPGs are more likely to be created dynamically by interacting with other signals rather than stored. As the motor system combines modularity, plasticity (Bizzi et al., 1995
; Rabinovich et al., 2006
; Choi and Bastian, 2007
; Miall, 2007
), but also robustness to perturbations (Torres-Oviedo et al., 2006
), one might ask how this complexity could be organized? Despite all the progresses done, little is known about the mechanisms regulating the flexible coordination of the motor synergies (Ting, 2007
), how they integrate the body dynamics, and how animals acquire them (if so). Understanding these mechanisms is important for neuroscience since it underlines the so-called Bernstein’s problem (Bernstein, 1967
) – how do we face the enormous dimensionality to control our body – but also for robotics to control high dimensional systems.
Figure 1. Concept of motor synergies. One motor synergy constitutes particular grouping of muscles for certain weights configurations (Bizzi and Clarac, 1999
). In the same time, one muscle can be activated by several synergies (Ting, 2007
); this demonstrates how modular and flexible the motor system is.
Motor synergy, the muscles grouping by few order parameters, has been an answer for Bernstein to explain how infants, during their early development, face the enormous dimensionality problem of linking sensors and motors activities for producing coordinated movements. Although CPGs can autonomously establish some regular rhythmic firing patterns, they are under the constant supervision of descending chemical substances known as neuromodulators (Selverston et al., 2000
; Rabinovich et al., 2006
). As neuromodulators control the activity of CPGs, they are in a sense the meta-controllers that realize the CPGs’ coordination or separation (Doya, 2002
). We hypothesize that they do not only regulate the partial synchronization of CPGs to each other, but also to the body dynamics to create one specific rhythm dynamically. Hence, a better image is perhaps to view the neuromodulators governing the global coordination (or synergy) between the body dynamics and the pattern generators to the generation of the ongoing motion (Wolf and Pearson, 1988
; Calabrese, 1995
; Marder and Calabrese, 1996
).
We propose to model this mechanism of dynamical phase synchronization (PS) between the body dynamics and its nonlinear controllers for the discovery and the control of its motor synergies. It is known that chaotic systems are capable to phase synchronize their dynamics to the resonant frequencies of any weak external force coupled to them. Within an embodied system, we exploit this property to transiently match the resonant frequencies of the body’s limbs and to coordinate their dynamics with each other (Lungarella and Berthouze, 2002
, 2004
; Kuniyoshi and Suzuki, 2004
; Pitti et al., 2005
, 2006
; Kuniyoshi and Sangawa, 2006
). Such scenario permits to incorporate the body dynamics within the control loop, reproducing the modular and bottom-up aspects of the biological motor synergies (Schoner et al., 1988
; Kelso and Haken, 1995
; Taga, 1995
; Seo and Slotine, 2007
) whereas other methods account more on the role of internal dynamics over the body for motion generation (cf. Nakanishi et al., 2004
; Buchli et al., 2006
). In two experiments with bipedal walkers, we show that at PS, the body and the controllers mutually and dynamically entrain themselves to each other yielding emergent behavioral patterns (e.g., walking patterns). In other words, the motion self-assembles in real-time as the coupled systems interact flexibly. From an information-theoretical viewpoint, this stage is characterized by a directed information flow from the sensors to the motors which corresponds to an efficient control in the sense given by (Touchette and Lloyd, 2000
): i.e., exploitation of the external information (body dynamics) by the controllers with compact information sent (optimum motor command).
The paper is organized as follows. In Section ‘Materials and Methods’ we present the mechanism of PS in coupled dynamical systems and the necessary conditions required for its realization. We explain then how this phenomenon can be exploited to explore and control the intrinsic modes of coordination of one embodied system. In Section ‘Results’, we present two experiments done with a simple knee-less compass-like biped and a more complex walker with knees. For both systems, we explore their parameter space and focus on the particular values corresponding to the motor synergies. In these stages the neural controller and the body mutually entrain themselves to each other to induce flexible coordinations. Based on our results, we discuss then the relevance of our findings for modeling the modular control of distributed pattern generators in the spinal cord.
In this section, we present the phenomenon of PS for chaotic systems and our framework for the control and the discovery of the motor synergies in embodied systems. We then expose its information theoretical implications and the methods we use to quantify the causal dependencies in sensorimotor information flows.
Phase Synchronization in Coupled Chaotic Systems
To explain the principle of PS, let us consider the discrete nonlinear dynamical system F(x) where x = x(t)∈Rd is the system’s d dimensional vector sampled at the discrete time step t. The system is perturbed with a weak external periodic force P such that:

where P(t) = [A1cos(ωt + δ1), A2cos(ωt + δ2),…,Adcos(ωt + δd)]. The applied periodic force has the frequency ω and is weighted by the coefficients Aj = 1,2,…,d. Under these conditions, it is possible to observe PS (see Rosenblum et al., 1996
; Pikovsky et al., 1997
). This means that although the system’s amplitude remains chaotic, its dynamics change in such a way that the phase ψ of the chaotic attractor meets the one of the external force ϕ.

with m and n as integer and Ω the frequency of the oscillator such that:

Therefore, PS means that the phase of the oscillator always stays close enough to the phase of the force (m = n = 1), or to the one of its harmonics (m > n); or, alternatively, the frequency of the oscillator, Ω, is close to a harmonic of the force’s frequency (m < n). Whether we obtain PS or not, depends on the properties of the force applied (i.e. its coupling strength vector A) which drives the system’s dynamics into the neighborhood of ω (Gonzalez-Miranda, 2004
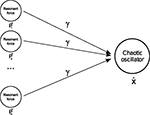
). Moreover, P in our example is a compound force constituted of multiple resonant frequencies; we can interpret it, however, as the linear combination of many resonant forces p (see Figure 2
).
Figure 2. Phase synchronization. For specific coupling values γ, a chaotic system is able to match and combine the natural resonance frequencies of two or more forces.

It means that one oscillator can phase synchronize not exclusively to one system but also to many. This expresses the important point that nonlinear oscillators are capable of synchronizing themselves to any other systems or group of systems and to adapt to their intrinsic modes (i.e., their resonant frequencies). As a result, a nonlinear oscillator can be viewed as a model-free system requiring no a priori knowledge about the governing equations of the dissipative system to synchronize to it. Therefore, as long as PS is satisfied, we can produce flexible coordination and plastic grouping among different systems (e.g., the musculo-skeleton system).
Applied to biological systems, PS is associated to specific muscles coordinations (synergistic states) arising from particular couplings (Kelso, 1995
). The spanning of the coupling parameters values in their interval range can reveal therefore when such stage occurs among the limbs and to which motor synergies they are associated to.
Feedback Resonance and Emergence of Coordination in Coupled Systems
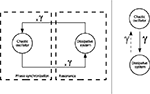
Resonance should not be mistaken with synchronization. The former phenomenon describes the situation in a passive system when a signal is amplified at its resonant frequencies even by tiny external forces (e.g., a pendulum, a mass-spring-damper system). The latter expresses the state of precise time locking in an active system (e.g., a chaotic system). Here, we combine the actions of both mechanisms in order to coordinate the dynamics of an active system (the controller) to a passive one (the body) with weak coupling between the two. The first one synchronizes to the resonant frequencies of the second which in return re-amplifies them at each loop cycle (see Figure 3
).
Figure 3. Joint mechanism of phase synchronization and feedback resonance between an active system and a dissipative system. Depending on the values of the coupling parameter {γ}, the chaotic oscillator synchronizes or not to the phase of the dissipative system.The occurrence of this stage produces a resonance regime in the device. In our framework, we conceive motor synergies as the mutual entrainment between the internal controller and the dissipative system.
Within such conditions, the chaotic oscillator coupled to a dissipative system forms a compound system capable of mutually entraining its sub-parts as the chaotic controller meets the resonant frequencies of the dissipative system, and the later weakly perturbs at precise timing the phase of the chaotic system. This situation, occurring at PS, depends however on the coupling strength between the two systems. Hence, by modulating their coupling values, the oscillators will phase synchronize more or less strongly.
Let us consider the case of two coupled systems A and B, with A being a chaotic oscillator similar to F, and B a passive system having a resonant term similar to P (Eq. 4) with a dissipative term D. Then, the coupling between the two systems can be formulated with the symmetric equations,

where γ is a coupling parameter which allows the two systems to mutually entrain with each other (see Figure 3
). PS occurs when the phase 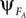 of system A matches the one of
of system A matches the one of 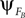 of B. Such mutual entrainment is typically accompanied by resonant modes generated by the two systems depending on γ. In biomechanical models of muscles for instance, such modes are characterized by synergistic states and nonlinear stiffness yielding a hardening or softening of their compliance (Miller, 2004
).
of B. Such mutual entrainment is typically accompanied by resonant modes generated by the two systems depending on γ. In biomechanical models of muscles for instance, such modes are characterized by synergistic states and nonlinear stiffness yielding a hardening or softening of their compliance (Miller, 2004
).
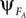 of system A matches the one of
of system A matches the one of 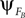 of B. Such mutual entrainment is typically accompanied by resonant modes generated by the two systems depending on γ. In biomechanical models of muscles for instance, such modes are characterized by synergistic states and nonlinear stiffness yielding a hardening or softening of their compliance (Miller, 2004
).
of B. Such mutual entrainment is typically accompanied by resonant modes generated by the two systems depending on γ. In biomechanical models of muscles for instance, such modes are characterized by synergistic states and nonlinear stiffness yielding a hardening or softening of their compliance (Miller, 2004
).In many points, our strategy stays close to existing motor system models: i.e., the modeling via PS (1) the coordination of group muscles and (2) the dynamical coupling of one muscle to many synergies (see Figures 1 and 3
). But in comparison with others, it differs by putting more emphasis on the sensory information to create one rhythm dynamically, not learnt in advance or parametrically defined (Kurz and Stergiou, 2005
; Aoi and Tsuchiya, 2007
; Manoonpong et al., 2007
). Our assumption finds justification in the fact that sensory feedback contributes together with the CPGs activity to the generation of the ongoing motion via neuromodulators (Wolf and Pearson, 1988
; Calabrese, 1995
; Levi et al., 2005
; Rabinovich et al., 2006
). We exploit this control mechanism in the following experiments. But before, let’s explain its implications from information theory and the method used to quantify the causal dependencies in sensorimotor information flows.
Information Theoretical Considerations
In an information theoretical viewpoint, the phase synchronized chaotic controller works as a pass-band filter selecting the resonant terms of the dissipative system connected with. Its properties (e.g., efficiency, robustness) depends however of the level of PS between the two systems. Hence, PS can be described as a communication channel between the active controller and the mechanical system (Touchette and Lloyd, 2000
; Baptista and Lopez, 2002
; Baptista and Kurths, 2005
). One advantage to describe the information theoretic aspect of controllability is to quantify the efficiency of the control and to measure how information is exchanged between the two systems. The information of a system B (e.g., the same as described in the previous section) can then be estimated by the chaotic system A depending on the signal per noise ratio in its chaotic dynamics and its apparent information production rate – the Shannon source entropy of the chaotic set. The quantity of information produced and exchanged between the two systems is then directly dependent on the capacity of system A to phase synchronize and to the overall level of PS between the two systems which depends to the coupling parameter γ; its values modulate the ‘tuning’ to the resonant frequencies of system B. The amount of information in the chaotic channel is then:

with IC(A, B) the mutual information in the channel between the transmitter B and the receiver A. The term 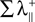 is the sum of the positive Lyapunov exponents associated to the synchronization manifold between A and B, and the term
is the sum of the positive Lyapunov exponents associated to the synchronization manifold between A and B, and the term 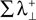 is the sum of the positive Lyapunov exponents associated to the transversal manifold between A and B. The term
is the sum of the positive Lyapunov exponents associated to the transversal manifold between A and B. The term 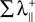 represents the information produced by the synchronization trajectories, and it corresponds to the amount of information transmitted. The term
represents the information produced by the synchronization trajectories, and it corresponds to the amount of information transmitted. The term 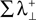 represents the information produced by the nonsynchronous trajectories, and it corresponds to the information lost in the transmission, the information that is erroneously retrieved in the receiver.
represents the information produced by the nonsynchronous trajectories, and it corresponds to the information lost in the transmission, the information that is erroneously retrieved in the receiver.
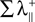 is the sum of the positive Lyapunov exponents associated to the synchronization manifold between A and B, and the term
is the sum of the positive Lyapunov exponents associated to the synchronization manifold between A and B, and the term 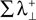 is the sum of the positive Lyapunov exponents associated to the transversal manifold between A and B. The term
is the sum of the positive Lyapunov exponents associated to the transversal manifold between A and B. The term 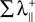 represents the information produced by the synchronization trajectories, and it corresponds to the amount of information transmitted. The term
represents the information produced by the synchronization trajectories, and it corresponds to the amount of information transmitted. The term 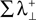 represents the information produced by the nonsynchronous trajectories, and it corresponds to the information lost in the transmission, the information that is erroneously retrieved in the receiver.
represents the information produced by the nonsynchronous trajectories, and it corresponds to the information lost in the transmission, the information that is erroneously retrieved in the receiver.The control of one system by discovering its resonant frequencies requires the joint mechanisms of PS and feedback resonance which demands:

the condition to have IC(A, B) > 0 and IC(B, A) > 0. Moreover, these conditions for asymptotic stability depend to the coupling strength γ.
In our experiments, we measure the information transfer between time series to detect directionality during this stage using transfer entropy (Schreiber, 2000
).
Given two time series xA,t and yB,t, transfer entropy essentially quantifies the deviation from the generalized Markov property: p(xA,t + 1|xA,t) = p(xA,t + 1|xA,t, yB,t), where p denotes the transition probability:
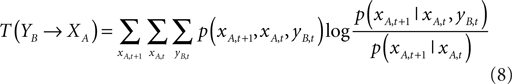
where the sums are over all amplitudes states, and the index T(YB→XA) indicates the influence of YB on XA. The transfer entropy is explicitly non-symmetric under the exchange of XA and YB – a similar expression exists for T(XA→YB) – and can thus be used to detect the directed exchange of information (e.g., information flow, or causal influence) between two systems A and B.
In this section, we describe and discuss the two experiments done with the simple compass-like biped model (1 degree of freedom) and the more complex biped walker with knees (5 degrees of freedom).
Compass-Like Biped Model
The compass-like biped walker is a two-legged mechanical system linked at the hip and controlled by a torque command. It is typically studied for its qualitative properties to exploit its passive dynamics for locomotion having a very stable limit cycle given a small energy supply (McGeer, 1990
; Goswami et al., 1997
, 1998
). Our numerical experiments, simulated in Matlab, are done in the sagittal plane with no slope (at horizontal ground level).
Our aim is to understand how the chaotic controller synchronizes with the biped walker’s dynamics to produce emergent coordinations and how do they entrain with each other. Depending on the coupling strength between the two systems and in regard to the level of PS, we study which types of interactions arise between the body and the controller and which ones permit a stable behavior: a motor synergy. In such stage, we measure the causal information flow between the two systems and characterize their synergistic state.
The equations of motion describing the compass walker are reproduced in Appendix ‘Compass-Gait Biped Model’. The biped has only 1 degree of freedom in the hip and is actuated by a torque command. The hip angle A(t) formed between the two legs (measured in radians) is the input signal sent to the controller. We select the logistic map function fμ(z) to control the walker’s torque command defined as follows:

The parameter μ ∈ [0; 2.0] controls the dynamics of the discrete chaotic map limited to the interval [−1, 1]. Although simple, this chaotic map can be used to generate PS in coupled map lattice (Fujisaka and Yamada, 1983
; Kaneko and Tsuda, 2000
). We coupled its dynamics to the walker’s hip torque command as done in Eq. 5:
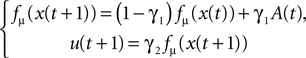
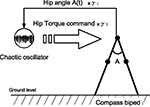
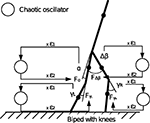
with γ1 and γ2 the coupling strength between the controller and the mechanical system (see Figure 4
). Moreover, since the swinging legs balance, dissipate and recover potential energy, the biped can be assimilated to a spring-damper-like or a pendulum-like system; a passive and dissipative system with resonant and damping forces. Hence, we can theoretically achieve PS for particular couplings. The nonlinear oscillator may thus synchronize or not to the phase of the hip angle signal A(t) (i.e., the walker’s pace) for certain coupling values only.
Figure 4. Control architecture for the compass biped walker coupled to one chaotic system. We hypothetize that for specific coupling values γ1 and γ2, we will have the chaotic system matching the phase of the walker dynamics.
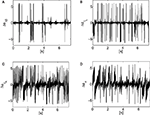
In this experiment, we fix the chaotic map’s control parameter μ to its near maximum chaotic regime 1.95. We set the time step iteration of the simulation to 5 ms. Then, we define the body-controller linkage with a symmetric coupling γ1 = γ2 = 0.1. These values correspond to the stage when the controller phase synchronizes to the biped dynamics. We display the time series of the hip angle and of the torque command in Figures 5
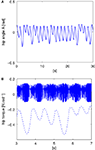
A,B. We observe that for these couplings, the biped is capable to walk: the envelope of the chaotic controller dynamically matches the slow pace of the walker’s stride. The notwithstanding result is that it is emergent: this stable and flexible coordination results neither from the internal dynamics only nor from the biped but ‘from scratch’ from their dynamical interaction.
Figure 5. The pace of the compass walker is described by the amplitude of its hip angle A(t) plotted in (A) and the controller dynamics plotted in plain lines in (B). Its stride is not fixed but dynamic as the amplitude of the hip angle varies from small ranges to higher ones. The chaotic map’s fast dynamics match and entrain its envelope to the biped’s dynamics (dashed line plotted below). The coupling between the two systems is set symmetrically with γ1 = γ2 = 0.1, and μ = 1.95.
As the state of synchronization is realized, the oscillator (Figure 5
B) matches dynamically the phase of the input signal (Figure 5
A) without any a priori knowledge about the mechanical system properties. In this stage, the behavior self-assembles in an apparent self-organizing process (Kelso and Haken, 1995
; Thelen and Smith, 1995
; Pfeifer and Iida, 2004
). Both systems dynamically entrain themselves and mutually constrain their dynamics to each other in order to sustain their coordination: the walker maintains a stable regime around its unique basin of attraction (see the phase plot of the hip angle in Figures 6
A,B) with a relatively small gain between [−0.1, 0.1] (see Figure 5
B). However, these results do not inform about the underlying coordination mechanism and the directionality of the causal flow between the controller and the biped: How control is distributed between the internal and the external dynamics? And how they interact from each other and exchange information? We propose to study it thereinafter.
Figure 6. Phase plot of the biped hip angle’s amplitude variation during locomotion (A) and its evolution over time (B); the time delay is set to 50 ms with a sampling time of 5 ms. The hip torques trajectory follows the intrinsic attractor in which the biped belongs. Its dynamics converge sometimes to it and sometimes slightly diverge from it.
Measuring the causal information flow in the sensorimotor loop
The sensorimotor information flow between the nonlinear oscillator and the compass walker constitutes the relative amount of information transferred that is needed to achieve a stable locomotion. Our hypothesis is that the controller achieves an adequate control only if its dynamics fit perfectly the complexity of those of the body. This corresponds to the situation when a minimum level of information is exchanged between the two systems.
We measure the causal influence of the oscillator on the body dynamics using the transfer entropy method defined in the ‘Materials and Methods’ section. We analyze the bidirectional relations for the coupling strengths in the interval γ1 = γ2 = γ ∈ [0; 0.25] averaged over 50 trials for each coupling. Figure 7
plots the averaged walking duration against γ (Figure 7
A), the corresponding causal influence values from the body to the controller TeS→M (Figure 7
B), and reversely from the controller to the body TeM→S (Figure 7
C).
Figure 7. Sensorimotor information flow for γ1 = γ2 = γ ∈ [0; 0.25] over 50 trials for each values. (A) Plot of the average walking duration stability (in seconds) dependent to the coupling strength γ. Transfer entropy measure of resp. TeS→M in (B) corresponding to the causal influence of the body on the controller dynamics, and TeM→S in (C) corresponding to the causal influence induced by the controller on the body dynamics. The stable walking area γ ∈ [0.05, 0.015] corresponds to inverted and asymmetric information flow from the body dynamics over the controller for which TeS→M >> TeM→S: the body controls the controller (!). Phase synchronization permits the controller to fully exploit the body dynamics in order to control it in return.
In these plots, the area of stable locomotion corresponds to the interval γ ∈ [0.05; 0.15]. This area, although narrow, concentrates the permissible range of stable coordinations between the controller and the walker. Conversely for γ < 0.05, the walker is unable to preserve a stable gait pattern without any compensation from an external energy source. There, TeM→S value is therefore zero which means that the controller has no effect on the biped dynamics. For γ > 0.15, the action of the controller to the body dynamics imposes a too high gain on the torque motion and lacks the necessary loose coupling to let the biped to recover freely its own balance. The system’s dynamics are thus unstable.
In comparison, in the interval of solutions for γ ∈ [0.05; 0.15], we observe a complete state transition of the global system for which the biped’s walking is stable over 30 s suggesting a perfect coordination between the oscillator and the body dynamics. There, the corresponding causal relationships between the biped and the controller reveals some characteristics about the systems’ interactions not possible to observe from the time series; for instance, (i) that the two systems do not interact identically since the information flow between the two systems is strongly asymmetric (i.e., TeS→M >> TeM→S) even though their coupling strength is symmetric (i.e., γ1 = γ2) and (ii) that the information flow is strongly biased in favor of the sensor to motor direction as TeS→M >> TeM→S. It follows that the controller strongly exploits the body dynamics information in order to achieve the control. Or differently said, the body controls the controller which is an antagonistic view on how we normally consider the controller-body coupled system. A first insight would have been to have the controller affecting the body and not the reverse. As a result from an energetic and informational viewpoint, this mechanism is efficient because a relatively small amount of information only is needed for the chaotic controller to actually control the dynamics of the walker (TeM→S < 0.05 bits). This means that the code sent by the chaotic oscillator to the biped is compact and structured. Hence, the action of the controller, despite its chaotic dynamics, can be considered to be energy efficient from an information theoretical viewpoint (Touchette and Lloyd, 2000
).
Aside to current CPG models which exhibit mostly monotonic and cyclic patterns, chaotic control through PS relies advantageously on the body ongoing motion dynamics for which the weight γ represents the global parameter that controls the overall synergistic state (Bizzi and Clarac, 1999
; Ting, 2007
). We adapt in the following this control mechanism to the discovery of the motor synergies in a kneed bipedal walker.
Five-Link Biped Model
In the previous section, we presented the mechanism of PS that governs the coordination between controller and body dynamics for the case of the compass-like biped walker. Although simple, the experiment demonstrates that a dynamical phase and frequency locking can be achieved between a chaotic controller and a mechanical system with passive dynamics for only particular sensory-motor couplings, at PS. In this situation, the motion is ‘assembled’ in real-time without predefining the internal dynamics of the controller: the real-time exploitation of the body dynamics by the nonlinear oscillator achieves the emergence of a weak and partial control. The stability of the coordination then, is directly related to the level of synchronization.
We hypothetize that the same idea can be applied to a higher dimensional system. We expect that its controllability will be nevertheless preserved thanks to the control of global synchronization within the system. The discovery of the specific coupling values permitting the global and local PS between its sub-components may guarantee the overall stable dynamical coordination of the ensemble in a self-organized fashion.
To this end, we use a more complex model with a simulation of the bipedal walker version with knees. The ensemble forms a 5 degrees of freedom system detailed in Appendix ‘Five-linked Biped Model’. This system is composed of two legs linked at the hip, each leg consisting of two segments jointed at the knees. The upper part (torso) consists of a vertical bar in unstable equilibrium like the pole of a cart. When the legs are in movement, the upper part of the body has to recover its stable vertical equilibrium in order to ensure the overall balance of the ensemble (Lockhart and Ting, 2007
). The biped state vector q can be summarized as follow:
q = [α, Δβ, γL, γR]T
with α the angle formed by the torso with the vertical axis, Δβ = βL − βR the angle between the two legs, and γ(L,R) the angle of the two knees between the two segments. The applied momentum vector Fq corresponding to the coordinates q is:
Fq = [Fα, FΔβ, FγL, FγR]T.
Similar with the compass-like walker, each oscillator is coupled to one specific joint with no internal connection to the other units. Each one receives as input the normalized joint angle information (in radians) and controls the corresponding torque (in N/rad). We adopt once more the logistic map fμ(z) (Eq. 9) with slightly modified coupling equations:
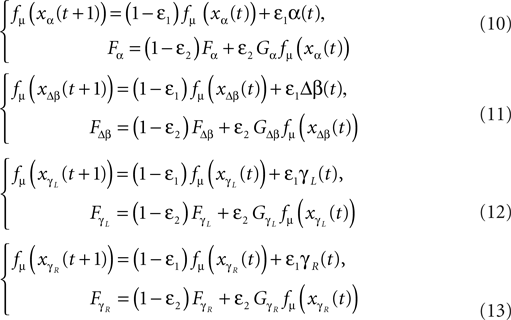
with ε1 and ε2 in the interval [0, 1], the respective sensor and motor coupling parameters common for all the joints and the set Gα, GΔβ, 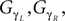 the respective torque gains specific to the joint motors defined to G ∈ [0, 20]. Here, the pair {ε1, ε2} and the gain G control the sensory-motor coupling linearly over the whole system (see Figure 8
) however the phase relations between the oscillators are not linear because any postural changes in one limb perturb in return some other parts; the graphs in Figure 9
describe this situation. Therefore, in order to produce stable rhythms, the oscillators have to coordinate themselves externally through the body dynamics. This stage occurs when the controllers merge the incoming information about the body’s dynamics at PS by matching the biped’s morphology, the intrinsic phase relations between its limbs.
the respective torque gains specific to the joint motors defined to G ∈ [0, 20]. Here, the pair {ε1, ε2} and the gain G control the sensory-motor coupling linearly over the whole system (see Figure 8
) however the phase relations between the oscillators are not linear because any postural changes in one limb perturb in return some other parts; the graphs in Figure 9
describe this situation. Therefore, in order to produce stable rhythms, the oscillators have to coordinate themselves externally through the body dynamics. This stage occurs when the controllers merge the incoming information about the body’s dynamics at PS by matching the biped’s morphology, the intrinsic phase relations between its limbs.
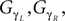 the respective torque gains specific to the joint motors defined to G ∈ [0, 20]. Here, the pair {ε1, ε2} and the gain G control the sensory-motor coupling linearly over the whole system (see Figure 8
) however the phase relations between the oscillators are not linear because any postural changes in one limb perturb in return some other parts; the graphs in Figure 9
describe this situation. Therefore, in order to produce stable rhythms, the oscillators have to coordinate themselves externally through the body dynamics. This stage occurs when the controllers merge the incoming information about the body’s dynamics at PS by matching the biped’s morphology, the intrinsic phase relations between its limbs.
the respective torque gains specific to the joint motors defined to G ∈ [0, 20]. Here, the pair {ε1, ε2} and the gain G control the sensory-motor coupling linearly over the whole system (see Figure 8
) however the phase relations between the oscillators are not linear because any postural changes in one limb perturb in return some other parts; the graphs in Figure 9
describe this situation. Therefore, in order to produce stable rhythms, the oscillators have to coordinate themselves externally through the body dynamics. This stage occurs when the controllers merge the incoming information about the body’s dynamics at PS by matching the biped’s morphology, the intrinsic phase relations between its limbs.Figure 8. Control scheme of the kneed biped. Each joint is linearly coupled to a chaotic unit receiving in return its joint angle. The sensory inputs are pondered by the coupling parameter ε1, and the motor outputs are weighted by ε2. Hence, the pair {ε1, ε2} controls the whole biped’s dynamics. The limbs coordination arise when the isolated chaotic units globally phase synchronize to each other through the body.
Figure 9. Control scheme of the kneed biped from Figure 8
. The variables {ε1, ε2} linearly couple the chaotic oscillators to their respective limbs (left). However, due to their embodiment, the isolated controllers receive dynamically the phase information from the different body parts: the situation is comparable to the schema in the right side where the pair {ε1, ε2} controls the global level of synchronization. In this parameter space, particular values will correspond to characteristic limbs coordinations (i.e., its motor synergies).
A better view of the control scheme is to see the weights {ε1, ε2} as the true global controllers modulaZ the level of coordination between the limbs and for which specific values may produce proper coupling between the musculo-skeleton system and the chaotic controllers (see Figure 9
). Thus, these weights are responsible for activating particular motor synergies; e.g., muscles grouping and behavioral patterns. To observe these synergies, we span the parameters space of the three variables {ε1, ε2, G} ∈ [0, 1] × [0, 1] × [0, 20] on which we annotate the standing duration of the biped (averaged over 15 trials for each values). We plot the two maps for the pairs {ε1, ε2} and {G, ε2} in Figures 10
A,B). These maps reveal specific patterns for stable sensory-motor coordination in the parameters space. As they appear only for certain intervals, these regions indicate where coupling is efficient for which the controllers match the body’s structural regularities; for instance, its morphology as well as the stiffness of the joints.
Figure 10. Walking duration performance map for the kneed biped for the control parameters pair {G, ε2} ∈ [0; 1] × [0; 20] in (A) and {ε1, ε2} ∈ [0; 1] × [0; 1] in (B). They reveal hidden information structure and correlations for particular coupling strengths. These relations correspond to the stable coordinations occurring between the internal controllers and the biped dynamics, its intrinsic behavioral patterns.
For small durations below 3 s, the gain is either too weak to entrain a positive feedback (G < 7 in Figure 10
A) or too strong to keep balance and coordination (G > 12 in Figure 10
A and ε2 > 0.20 in Figures 10
A,B). In between, when the biped stands longer than 4 s, the state corresponds to specific constraints for which the ensemble is able to coordinate its limbs dynamically and to walk for a duration of up to 8 s (see Figure 11
). Such state results from a global phase transition for which the body and the neural controllers match their dynamics. We draw the corresponding time series in Figure 12
.
Figure 11. Motion sequence of the kneed biped walker for the parameters ε1 = 0.10, ε2 = 0.10, output Gain G = 10. The body and the controllers mutually entrain themselves with each other in an emergent manner. The body dynamics feeded back to the controllers contribute to regulate its own motion.
Figure 12. Time series of the sensors and motor dynamics for the parameters {ε1, ε2, G} ∈ [0; 1] × [0; 1] × [10]. (A) time series of the joint angles of the hip Δβ, of the knees γ{L,R}, of the torso alpha, and their respective torque command activation in (B) resp. FΔβ, Fγ{L,R},and Fα. Regular sensorimotor patterns are discovered and stabilized dynamically in the whole system, i.e., partial and dynamic phase synchronization (see the dashed and plain lines in (A)) – till one perturbation destroys the coordination.
One can remark from the graph that the whole system generates regular and dynamically stable sensory-motor patterns in the temporal range from the millisecond to the second order. That is, each chaotic unit maintains a specific rhythm along with its associated limb but also with others. These oscillators combine indirectly specific local action and global integration, a flexible synchronization to several rhythms. The plots of the phase difference between the sensor and the motor signals displayed in Figure 13
illustrate this status. Statistically, the overall phase differences are mainly null showing PS and global integration. However, the phase slips occurring from time to time correspond to saccades in the motion that are recovered dynamically. PS causes the balance of plasticity and stability of the global sensory-motor coordination. As for the previous case, it shows the kind of motor synergies rised from the controllers and the biped interactions but neither how the parts exchange information nor how they are causally integrated, what we investigate in the next section.
Figure 13. Phase difference Δϕ evolution between the biped sensors and motor dynamics during locomotion. The coordination in each joint is dynamic with lot of variance, however stable since centered in 0.
Measuring the causal sensory-motor information flow
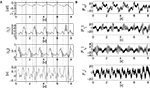
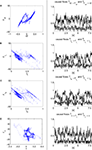
In the previous section, we found that particular sensory-motor coupling values rise the global synergistic state in the biped’s phase space responsible for locomotion. We want to characterize this state and understand how energy and information are exchanged within the biped limbs and the controllers. We analyze the sensory-motor information flow measured between the controllers and the body dynamics during motion as we did for the compass biped. To this end, we display the phase plots of the joints with their respective causality measure of the sensory-motor information flow in Figure 14
.
Figure 14. Phase plots and causality measure of the sensorimotor information flow in all the joints during walking; resp. left and right column. In the right, the causal flows from the body dynamics X to its controller FX, 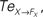 are drawn in plain lines. The causal flows from the controller FX to its sensory variable X,
are drawn in plain lines. The causal flows from the controller FX to its sensory variable X, 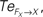 are drawn in dashed lines. During walking, the body and the controllers flexibly entrain themselves dynamically. This coordination depends bothly on the current posture of the body and on the ongoing internal dynamics. However, the causal flows between the two systems reveals that the body drives most of the time the internal dynamics
are drawn in dashed lines. During walking, the body and the controllers flexibly entrain themselves dynamically. This coordination depends bothly on the current posture of the body and on the ongoing internal dynamics. However, the causal flows between the two systems reveals that the body drives most of the time the internal dynamics 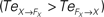 which means that the controllers exploit efficiently the body passive dynamics. Nevertheless, for short periods, the causal flow in the embodied system is inverted (when we have
which means that the controllers exploit efficiently the body passive dynamics. Nevertheless, for short periods, the causal flow in the embodied system is inverted (when we have 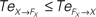 ) exhibiting the situation when the controllers actively drive the biped.
) exhibiting the situation when the controllers actively drive the biped.
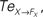 are drawn in plain lines. The causal flows from the controller FX to its sensory variable X,
are drawn in plain lines. The causal flows from the controller FX to its sensory variable X, 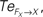 are drawn in dashed lines. During walking, the body and the controllers flexibly entrain themselves dynamically. This coordination depends bothly on the current posture of the body and on the ongoing internal dynamics. However, the causal flows between the two systems reveals that the body drives most of the time the internal dynamics
are drawn in dashed lines. During walking, the body and the controllers flexibly entrain themselves dynamically. This coordination depends bothly on the current posture of the body and on the ongoing internal dynamics. However, the causal flows between the two systems reveals that the body drives most of the time the internal dynamics 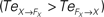 which means that the controllers exploit efficiently the body passive dynamics. Nevertheless, for short periods, the causal flow in the embodied system is inverted (when we have
which means that the controllers exploit efficiently the body passive dynamics. Nevertheless, for short periods, the causal flow in the embodied system is inverted (when we have 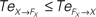 ) exhibiting the situation when the controllers actively drive the biped.
) exhibiting the situation when the controllers actively drive the biped.Similar to the compass biped, the causal flow in the kneed biped is asymmetric in the direction from the body to controller for all the joints: TSensor→Motor ≈ 3 × TMotor→Sensor. The controllers and the body mutually synchronize; the body’s dynamics constrain the controllers’ ones continuously whereas the latters conduct a weak and almost indirect guidance on the body motion. It follows that the controllers regulate the body limbs motion intermittently only at critical moment when TSensor→Motor ≈ TMotor→Sensor. The internal controllers phase synchronize to the biped’s limbs most of the time but their linkage and influence are flexible and can vary over time. In the swing phase of the left leg for instance, the passive dynamical motion of the knee γL in Figure 14
B dominates its controller 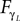 and drive its behavior since we have
and drive its behavior since we have 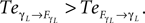 Conversely, ground contact’s perturbation during stance phase (when the tip of the leg is in contact with the ground) disrupts synchronization and the internal dynamics regulate the body dynamics. We observe this situation when
Conversely, ground contact’s perturbation during stance phase (when the tip of the leg is in contact with the ground) disrupts synchronization and the internal dynamics regulate the body dynamics. We observe this situation when 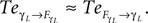 In the whole system, the coordination transits from the free passive exploitation of the body parts to a collective and active control of the ensemble at specific moments and for precise temporal durations at ground contact. Coordination is brittle but stable, the failing of the coordination in one single joint may entrain therefore the breaking of the global coordination as of the global synergistic state in a bottom-up manner.
In the whole system, the coordination transits from the free passive exploitation of the body parts to a collective and active control of the ensemble at specific moments and for precise temporal durations at ground contact. Coordination is brittle but stable, the failing of the coordination in one single joint may entrain therefore the breaking of the global coordination as of the global synergistic state in a bottom-up manner.
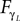 and drive its behavior since we have
and drive its behavior since we have 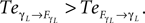 Conversely, ground contact’s perturbation during stance phase (when the tip of the leg is in contact with the ground) disrupts synchronization and the internal dynamics regulate the body dynamics. We observe this situation when
Conversely, ground contact’s perturbation during stance phase (when the tip of the leg is in contact with the ground) disrupts synchronization and the internal dynamics regulate the body dynamics. We observe this situation when 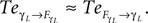 In the whole system, the coordination transits from the free passive exploitation of the body parts to a collective and active control of the ensemble at specific moments and for precise temporal durations at ground contact. Coordination is brittle but stable, the failing of the coordination in one single joint may entrain therefore the breaking of the global coordination as of the global synergistic state in a bottom-up manner.
In the whole system, the coordination transits from the free passive exploitation of the body parts to a collective and active control of the ensemble at specific moments and for precise temporal durations at ground contact. Coordination is brittle but stable, the failing of the coordination in one single joint may entrain therefore the breaking of the global coordination as of the global synergistic state in a bottom-up manner.We propose in this paper a framework based on the mechanisms of PS and resonance to model the motor synergies arising dynamically from the coupling between internal controllers and its embodied system. We exploit the property of chaotic systems to synchronize their phase to any resonant frequencies and explore the natural synergies of one embodied system. At PS, chaotic controllers lock transiently their phase to the body dynamics and generate a global entrainment. One of the results is that the controllability problem is then transferred from a problem of high dimension in the body parameter space (e.g., for the kneed biped q = [x0, y0, α, βL, βR, γL, γR]T ∈ ℜT) to a problem of lower dimension in the coupling parameters space (e.g., the pair {ε1, ε2} ∈ ℜ2) by searching the areas of stability corresponding to PS, a scenario in line with synergistic viewpoint of humans’ motion control where the neuromodulators regulate the CPGs’ dynamics (Bernstein, 1967
; Kelso and Haken, 1995
; Bizzi and Clarac, 1999
).
Consequently, the internal controllers entrain themselves along with the body dynamics for specific coupling. In this stage, the embodied system transits to a global coordination corresponding to efficient control in an information theoretical viewpoint: i.e., characteristic asymmetric information flow between the internal and external dynamics (cf. Fradkov, 1999
; Touchette and Lloyd, 2000
) and exploitation of the sensory information. Here, the body dynamics dominate the activity over the control command which exploits in return the sensory information to act weakly and intermittently on the motion. It follows that the controllers stabilize the overall global dynamics with a compact code: the body plays an active part in the control by constraining and conducting its pace for most of the time (cf. Thelen and Smith, 1995
; Miall, 2007
). From a developmental perspective, the exploration stage of the parameters space in our experiments could correspond to the period when babies, in their first 2 months, systematically experience various sensory-motor coordinations in a random fashion till the finding of the most optimum ones; that is, the synchronized motions; an early period found for the exploration and acquisition of the general movements (Rochat, 1998
; Taga et al., 1999
).
Details of the Bipedal Models
Compass-gait biped model
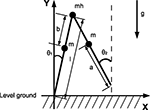
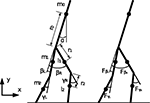
We consider a knee-less compass-like two link three-mass biped model with analog characteristics to the McGeer’s model (McGeer, 1990
) (see Figure 15
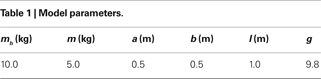
). The biped is modeled in the sagittal plane in an horizontal ground level (no slope), the transition is assumed inelastic and without slipping, and the viscosity in the joints are ignored. We summarize the simulation’s variables and parameters in Table 1
. The posture of the walking model is determined from the global position of the tip of one leg and from the angles of the legs. The vector of the Lagrangian coordinate q is chosen as:
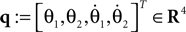
Figure 15. Model of the compass-gait biped.
where θ1 and θ2 are the corresponding swing and stance legs angle, 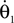 and
and 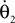 are the respective derivatives. The motion kinematics are given by:
are the respective derivatives. The motion kinematics are given by:
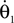 and
and 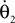 are the respective derivatives. The motion kinematics are given by:
are the respective derivatives. The motion kinematics are given by:
with θ = [θ1, θ2]T, the system’s angle vector and
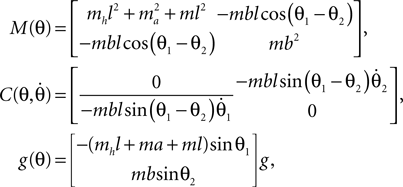
and the torque control vector,
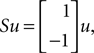
Here M, C, g and S are the inertia matrix, a centrifugal-Coriolis matrix, a gravitational term and a conversion matrix from an input torque u to the generalized force respectively. The double-support phase is the moment when both legs touch the ground. In this period, the angles of the swing leg and the stance leg are exchanged as 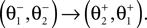 This state with α the angle formed between the two legs is when we have:
This state with α the angle formed between the two legs is when we have:
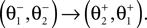 This state with α the angle formed between the two legs is when we have:
This state with α the angle formed between the two legs is when we have:
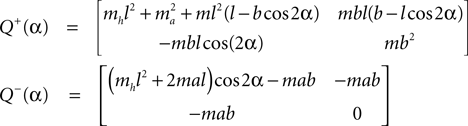
and α always positive

We define the kth step is one step from the double-support phase to just before the end of the next single-support phase.
The step duration is the duration time of one step. The kth step duration is denoted Tk, k = 1, 2,…,. The walking speed is calculated from the kth step length divided by the kth step duration and is valid only when walking motion continues. This value is given by:

Five-Linked Biped Model
Generalized coordinates of the kneed biped walker (see Figure 16
):
Figure 16. Model of the biped walker with knees.
q = [x0, y0, α, βL, βR, γL, γR]T
Generalized forces corresponding to the coordinates:
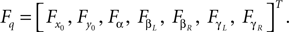
Positions of the thigh center of mass in Cartesian coordinates: 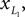
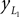 and
and 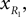
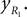 Positions of the shin center of mass in Cartesian coordinates:
Positions of the shin center of mass in Cartesian coordinates: 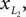
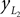 and
and 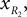
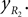
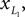
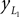 and
and 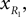
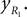 Positions of the shin center of mass in Cartesian coordinates:
Positions of the shin center of mass in Cartesian coordinates: 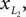
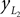 and
and 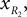
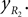
Leg tip positions in Cartesian coordinates: xLG, yLG and xRG, yRG. These coordinates can be stated using the generalized coordinates (correspondingly for the right leg):
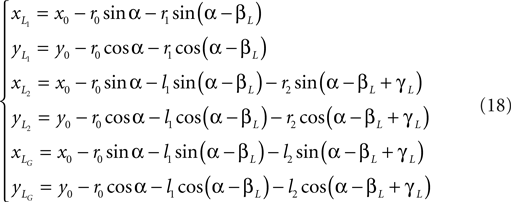
Translational energy of the system:
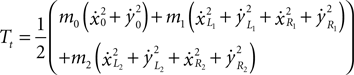
Rotational energy of the system (missing from the original model):
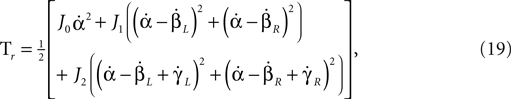
where J0, J1 and J2 are the inertia of the torso, thigh and shin, respectively.
Total kinetic energy:
T = Tt + Tr.
Formulas of the generalized forces (left leg):
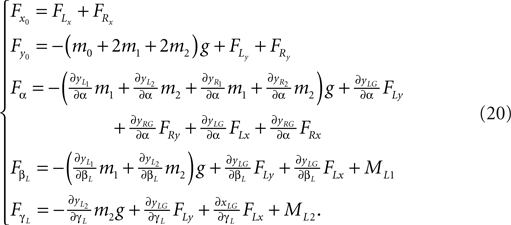
Lagrangian equations:
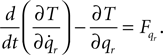
Now for each element qr in q and 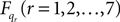 calculate the Lagrangian equation, and collect the coefficients of the second time derivates of the generalized coordinates to A. This gives the seven rows in the final dynamic equation:
calculate the Lagrangian equation, and collect the coefficients of the second time derivates of the generalized coordinates to A. This gives the seven rows in the final dynamic equation:
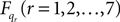 calculate the Lagrangian equation, and collect the coefficients of the second time derivates of the generalized coordinates to A. This gives the seven rows in the final dynamic equation:
calculate the Lagrangian equation, and collect the coefficients of the second time derivates of the generalized coordinates to A. This gives the seven rows in the final dynamic equation: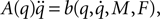
where
M = [ML1, MR1, ML2, MR2]T
and
F = [FLx, FLy, FRx, FRy]T.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors would like to thank the reviewers for their helpful comments and to acknowledge the ERATO Synergistic project which provided the grant for this research.
Buchli, J., Righetti, L., and Ijspeert, A. (2006). Engineering entrainment and adaptation in limit cycle systems – from biological inspiration to applications in robotics. Biol. Cybern. 95, 645–664. Available at: http://dx.doi.org/10.1007/s00422-006-0128-y
.
Nakanishi, J., Morimoto, J., Endo, G., Cheng, G., Schaal, S., and Kawato, M. (2004). An Empirical Exploration of Phase Resetting for Robust Biped Locomotion with Dynamical Movement Primitives. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, pp. 919–924.
Pitti, A., Lungarella, M., and Kuniyoshi, Y. (2005). Quantification of emergent behaviors induced by feedback resonance of chaos. In Recent Advances in Artificial Life: Advances in Natural Computation, Vol. 3, H. A. Abbass, T. Bossomaier, and J. Wiles, eds (Singapore, World Scientific), pp. 199–213.