1
Sony Computer Science Laboratory Paris, Paris, France
2
INRIA Bordeaux-Sud-Ouest, France
3
Ecole Polytechnique Federale de Lausanne, EPFL – CRAFT, Lausanne, Switzerland
Intrinsic motivation, centrally involved in spontaneous exploration and curiosity, is a crucial concept in developmental psychology. It has been argued to be a crucial mechanism for open-ended cognitive development in humans, and as such has gathered a growing interest from developmental roboticists in the recent years. The goal of this paper is threefold. First, it provides a synthesis of the different approaches of intrinsic motivation in psychology. Second, by interpreting these approaches in a computational reinforcement learning framework, we argue that they are not operational and even sometimes inconsistent. Third, we set the ground for a systematic operational study of intrinsic motivation by presenting a formal typology of possible computational approaches. This typology is partly based on existing computational models, but also presents new ways of conceptualizing intrinsic motivation. We argue that this kind of computational typology might be useful for opening new avenues for research both in psychology and developmental robotics.
There exists a wide diversity of motivation systems in living organisms, and humans in particular. For example, there are systems that push the organism to maintain certain levels of chemical energy, involving the ingestion of food, or systems that push the organism to maintain its temperature or its physical integrity in a zone of viability. Inspired by these kinds of motivation and their understanding by (neuro-) ethologists, roboticists have built machines endowed with similar systems with the aim of providing them with autonomy and properties of life-like intelligence (Arkin, 2005
). For example sowbug-inspired robots (Endo and Arkin, 2001
), praying mantis robots (Arkin et al., 1998
) dog-like robots (Fujita et al., 2001
) have been constructed.
Some animals, and this is most prominent in humans, also have more general motivations that push them to explore, manipulate or probe their environment, fostering curiosity and engagement in playful and new activities. This kind of motivation, which is called intrinsic motivation by psychologists (Ryan and Deci, 2000
), is paramount for sensorimotor and cognitive development throughout lifespan. There is a vast literature in psychology that explains why it is essential for cognitive growth and organization, and investigates the actual potential cognitive processes underlying intrinsic motivation (Berlyne, 1960
; Csikszentmihalyi, 1991
; Deci and Ryan, 1985
; Ryan and Deci, 2000
; White, 1959
). This has gathered the interest of a growing number of researchers in developmental robotics in the recent years, and several computational models have been developed (see Barto et al., 2004
; Oudeyer et al., 2007
for reviews).
However, the very concept of intrinsic motivation has never really been consistently and critically discussed from a computational point of view. It has been used intuitively by many authors without asking for what it really means. Thus, the first objective and contribution of this paper is to present an overview of this concept in psychology followed by a critical reinterpretation in computational terms. We show that the definitions provided in psychology are actually unsatisfying. As a consequence, we will set the ground for a systematic operational study of intrinsic motivation by presenting a typology of possible computational approaches, and discuss whether it is possible or useful to give a single general computational definition of intrinsic motivation. The typology that we will present is partly based on existing computational models, but also presents new ways of conceptualizing intrinsic motivation. We will try to focus on how these models relate to each other and propose a classification into broad but distinct categories.
Intrinsic Motivation and Instrumentalization
According to Ryan and Deci (2000)
(pp. 56),
Intrinsic motivation is defined as the doing of an activity for its inherent satisfaction rather than for some separable consequence. When intrinsically motivated, a person is moved to act for the fun or challenge entailed rather than because of external products, pressures, or rewards.
Intrinsic motivation is clearly visible in young infants, that consistently try to grasp, throw, bite, squash or shout at new objects they encounter. Even if less important as they grow, human adults are still often intrinsically motivated while they play crosswords, make paintings, do gardening or just read novels or watch movies. Yet, to get a clearer picture of intrinsic motivation, one needs to understand that it has been defined by contrast to extrinsic motivation:
Extrinsic motivation is a construct that pertains whenever an activity is done in order to attain some separable outcome. Extrinsic motivation thus contrasts with intrinsic motivation, which refers to doing an activity simply for the enjoyment of the activity itself, rather than its instrumental value. (Ryan and Deci, 2000
)
We see that a central feature that differentiates intrinsic and extrinsic motivation is instrumentalization. We also see that the concepts of intrinsic and extrinsic motivations form a different distinction than the one between internal and external motivations. In the computational literature, “intrinsic” is sometimes used as a synonym to “internal”, and “extrinsic” as a synonym to “external”. Yet, it is in fact a confusion. Indeed, there are extrinsic motivations that can be internal and vice versa. In fact, there are different kinds of instrumentalizations that can be classified as more or less self-determined (Ryan and Deci, 2000
). Let us give examples to be more clear.
For example, a child that does thoroughly his homework might be motivated by avoiding the sanctions of his parents if he would not do it. The cause for action is here clearly external, and the homework is not done for its own sake but for the separate outcome of not getting sanctions. Here the child is extrinsically and externally motivated.
On the other hand, it is possible that a child could do thoroughly his homework because he is persuaded that it will help him get the job he dreams of, later when he will be an adult. In this case, the cause for action is internally generated, and the homework is again not achieved for its own sake but because the child thinks it will lead to the separate outcome of getting a good job.
Finally, it is also possible that a child does thoroughly its homework for the fun of it, and because he experiences pleasure in the discovery of new knowledge or considers for example its math problem just as fun as playing a video game. In this case, its behavior is intrinsically (and internally) motivated.
These different kinds of motivations can also sometimes be superposed or interleaved in the same global activity. For example, it is quite possible that a child doing his homework is partly extrinsically motivated by getting a high grade at the exam and partly intrinsically motivated by learning new interesting things. Also, for example, imagine a child that is intrinsically motivated by playing tennis but has to ride its bicycle to get to the tennis court (and does not like particularly riding bicycles). In this case, the riding of the bicycle is an internal and extrinsically motivated behavior that spins out of the intrinsically motivated behavior of playing tennis.
What Makes an Activity Intrinsically Motivating?
Given this broad distinction between intrinsic and extrinsic motivation, psychologists have tried to build theories about which features of activities make them intrinsically motivating for some people (and not all) at some times (the same activity might be intrinsically motivating for a person at a given time, but no more later on). They have studied how these motivations could be functionally implemented in an organism, humans in particular, and several theoretical directions have been presented.
Drives to manipulate, drives to explore. In the 1950s, psychologists started by trying to give an account of intrinsic motivation and exploratory activities on the basis of the theory of drives (Hull, 1943
), which are specific tissue deficits like hunger or pain that the organisms try to reduce. For example, (Montgomery, 1954
) proposed a drive for exploration and (Harlow, 1950
) a drive to manipulate. This drive naming approach had many short-comings which were criticized in detail by White (1959)
: intrinsically motivated exploratory activities have a fundamentally different dynamics. Indeed, they are not homeostatic: the general tendency to explore is not a consummatory response to a stressful perturbation of the organism’s body.
Reduction of cognitive dissonance. Some researchers then proposed another conceptualization. Festinger’s theory of cognitive dissonance (Festinger, 1957
) asserted that organisms are motivated to reduce dissonance, which is the incompatibility between internal cognitive structures and the situations currently perceived. Fifteen years later a related view was articulated by Kagan stating that a primary motivation for humans is the reduction of uncertainty in the sense of the “incompatibility between (two or more) cognitive structures, between cognitive structure and experience, or between structures and behavior” (Kagan, 1972
). However, these theories were criticized on the basis that much human behavior is also intended to increase uncertainty, and not only to reduce it. Human seem to look for some forms of optimality between completely uncertain and completely certain situations.
Optimal incongruity. In 1965, Hunt developed the idea that children and adult look for optimal incongruity (Hunt, 1965
). He regarded children as information-processing systems and stated that interesting stimuli were those where there was a discrepancy between the perceived and standard levels of the stimuli. For, Dember and Earl, the incongruity or discrepancy in intrinsically-motivated behaviors was between a person’s expectations and the properties of the stimulus (Dember and Earl, 1957
). Berlyne developed similar notions as he observed that the most rewarding situations were those with an intermediate level of novelty, between already familiar and completely new situations (Berlyne, 1960
).
Motivation for effectance, personal causation, competence and self-determination. Eventually, a last group of researchers preferred the concept of challenge to the notion of optimal incongruity. These researchers stated that what was driving human behavior was a motivation for effectance (White, 1959
), personal causation (De Charms, 1968
), competence and self-determination (Deci and Ryan, 1985
). Basically, these approaches argue that what motivates people is the degree of control they can have on other people, external objects and themselves, or in other words, the amount of effective interaction. In an analogous manner, the concept of optimal challenge has been put forward, such as for example in the theory of “Flow” (Csikszentmihalyi, 1991
).
After having made a broad review of intrinsic motivation in psychology, we will here start to take a computational viewpoint. To begin with, we will describe how motivations in general are conceived and used in computer and robotic architectures. We will then present a set of important distinctive dimensions, among which the intrinsic-extrinsic distinction, that are useful to organize the space of possible motivation systems.
Motivational variables and drives. While motivation is sometimes implemented in an implicit manner in simple robot architectures, such as phototaxis in Braitenberg vehicles (Braitenberg, 1984
), it is now rather common to implement it directly and explicitly in the form of a module that tracks the value of a number of internal “motivational” variables and sends signals to the rest of the architecture (Arkin, 2005
; Breazeal, 2002
; Huang and Weng, 2004
; Konidaris and Barto, 2006
). For example, one often encounters an energy level variable, associated with a zone of comfort (i.e., a range of values), and when this variable gets out of this zone, the system sends signals to the rest of the architecture, and to the action selection module in particular, so that the robot finds a charging station as soon as possible. This homeostatic system can also be implemented as a Hullian drive (Hull, 1943
; Konidaris and Barto, 2006
), energy level being a variable ranging from 0 (totally unsatisfied) to 1 (satiated), and constantly sending its value to the action selection system in order to maintain it as close to 1 as possible.
Computational Reinforcement Learning and rewards. It is often the case in robotic systems that the action strategy that allows to keep motivational variables as satiated as possible is neither fixed nor initially hand-coded, but rather should be learnt. The standard framework in which this happens is “computational reinforcement learning (CRL)” (Sutton and Barto, 1998
). This framework has introduced many algorithms targeted at finding strategies to maximize “rewards”, which is the pivotal concept of CRL. Very importantly, the meaning of the term “reward” is used in a specific technical manner in CRL and is different from the meaning of the term “reward” in psychology, and in particular in the theory of operant conditioning (Skinner, 1953
). Nevertheless, these two meanings overlap and this has produced a number of confusions in the literature. In CRL, a “reward” is technically only a numerical quantity that is measured continuously and used to drive the action selection mechanism so that the cumulated value of this quantity in the future is maximized. CRL theory is completely agnostic about what/how/where this value is generated. Coming back to robots implementing ethologically inspired motivation system, this value could be for example the value of the robot’s internal level of energy. But, and this is how CRL is often used in the computational literature, this value could also be set directly by a human engineer or by an external program built by a human engineer. For example, a number of experiments in which engineers try to build robots that can walk forward have used CRL algorithms with a reward being a value coming from an external system (e.g., camera on the ceiling) observing how fast (or not) the robot moves (the value being the speed). It is in these experiments that the term “reward” overlaps with the term “reward” used in the operant conditioning literature, and where it denotes the getting of an external object/event/property such as money, food or a high grade at school. But one has to keep in mind that in a robot using CRL, a reward can be completely internally defined and be analogous to the very release of a neurotransmitter.
Rewards as a common currency for multiple motivations. One of the nice features of the reward concept in CRL is that, being a numerical quantity, it can act as a “common currency” among several coexisting motivations in a single architecture (McFarland and Bosser, 1994
). Indeed, in a typical organism, natural or artificial, different and possibly conflicting motives can try to push actions in certain directions: for example, one may have a drive for energy level maintenance co-existing with a drive for physical integrity maintenance, a drive for sleeping, and a drive pushing towards the search for social partners. In order to arbitrate between the possibly conflicting actions entailed by all these motivations, one uses the possibility to numerically compare the expected rewards associated with each of them. Moreover, one often sees architectures in which a (possibly adaptive) numerical weight is associated to each of these rewards (Konidaris and Barto, 2006
).
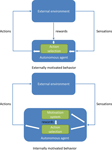
Internal vs. external motivations. Given this architectural framework for implementing motivations in a robot, one can investigate a first kind of distinction between internal and external motivations. This difference relates to autonomy and lies in the functional location of the mechanism that computes/generates the reward. If the reward, i.e., the numerical quantity that the system has to maximize, comes from the outside of the autonomous system, then it is called external. This is the above mentioned example of the walking robot driven by a reward coming from a human or a system with a camera mounted on the ceiling. If the reward is computed and generated internally by the autonomous system, then it is called internal. This is the above mentioned example of the reward associated to the satiation of an energy maintenance drive. This difference is summarized on Figure 1
. Yet, this difference can be sometimes subtle in the case of robots. Computers allow us to do manipulations that are impossible with humans. For example, an engineer could very well build an autonomous machine that is capable of monitoring by itself whether it is walking forward or not and at what speed, and could incorporate in the robot’s internal architecture a motivation to go forward as fast as possible. In practice, this will produce more or less the same behavior that with the walking detection system mounted on the ceiling, but technically we have here an internal reward (which is nevertheless extrinsic as we will see). Of course, this kind of manipulation is not possible with humans, and it is much more difficult to find this kind of “limit” example in humans.
Figure 1. The difference between external and internal motivations in the CRL framework: in externally motivated behavior, rewards are computed outside the agent and imposed to it, whereas in internally motivated behavior, rewards are computed inside the agent and self-determined. This figure is inspired from Barto et al. (2004)
.
Intrinsic vs. extrinsic motivations. Now we come to how we can conceptualize the difference between intrinsic and extrinsic motivation in this computational framework. We saw earlier that intrinsic motivation was defined in psychology as characterizing activities that were “fun” or “challenging” for their own sake, whereas extrinsic motivation characterized activities achieved in order to reach a specific goal defined separately. To a computer scientist, these definitions are actually rather vague and could be computationally interpreted in a variety of incompatible manners. First, it seems that the properties that make an activity intrinsically motivating (the “fun”, the “challenge”, the “novelty”, the “cognitive dissonance” or the “optimal incongruity”) are crucial to the very definition of intrinsic motivation, but there is no unified approach or consensus on what they actually are in the psychology literature. Second, the concept of goal or instrumentalization that differentiates intrinsic from extrinsic is in fact ambiguous. Indeed, one could for example imagine the existence of a motivation such that a positive reward is generated each time a novel situation is encountered. In a CRL framework, the system tries to maximize rewards, and so getting rewards is a goal! Thus, the search for novel situations, which is typically presented as intrinsically motivated behavior in the psychology literature, is directed by the goal of getting internal rewards, and so is technically extrinsically motivated. We thus see that the concept of “separate goal” used to define extrinsic motivation is too vague and should probably be amended with a number of specific properties. But what properties shall characterize a goal involved in extrinsic, and not intrinsic, motivation? The problem of defining precisely a distinction is made even harder by the fact that, as we have seen above, intrinsic and extrinsic motivations are not exclusive concepts: a given activity can be at the same time intrinsically and extrinsically motivated. Nevertheless, this discussion shows again that the distinction between intrinsic and extrinsic is different than the distinction between internal and external (which, as we saw, is much simpler). It can be said safely that all external motivations, as defined in the previous paragraph, are not intrinsic, whatever the interpretation of “activities that are fun or challenging for their own sake” is. It can also be said safely that internal motivations can be intrinsic or extrinsic or both.
Given this confusion due to science’s low level of understanding of motivations in humans, the most pragmatic approach to intrinsic motivation from a computational point of view is maybe to avoid trying to establish a single general definition and rather try to make a map based on a series of existing or possible operational approaches. This is what we will do in the next section, as well as identify examples of computationally defined motivations that shall not be considered as intrinsic. Nevertheless, as we will see, this enumeration of examples will lead us to a proposal for such a general computational definition of intrinsic motivation. This definition will be described in the discussion, and we will argue that in spite of being non-intuitive from a psychological theory point of view, it might be fruitful for the organization of research.
Homeostatic vs. heterostatic motivations. To make the landscape of motivation features more complete, one has also to present the distinction between two important classes of motivations: homeostatic and heterostatic. The most frequent type of motivation found in robots, which is also probably the most frequent in the animal kingdom, are homeostatic systems that consist in pushing organisms to maintain some of their properties in a “viable” or “comfort” zone. This is the example of the motivation for maintaining battery energy above a certain threshold (and necessarily below a maximum which cannot be over passed), or a motivation for maintaining an intermediate level of social stimulation (Breazeal, 2002
). In a Hullian perspective, homeostatic motivations correspond to drives that can be satiated (for example, a food drive is satiated after eating enough food). On the opposite side, there exists heterostatic motivation systems that continuously push an organism away from its habitual state. Homeostatic motivations are systems which try to compensate the effect of perturbations (external or internal) on the organism, while heterostatic motivations are systems that try to (self-) perturbate the organism out of its equilibrium. In Hullian terms, heterostatic motivations are drives that cannot be satiated. For example, as will see below, there can be a motivation pushing explicitly an organism to search for novel situations: in the CRL framework, rewards are provided every time a novel situation is encountered. In this case, there is no equilibrium state that the motivation is trying to maintain, but rather the organism would permanently obtain reward if it would experience novelty over and over again (but note that it is possible to imagine a motivation system that provides rewards only when novelty is experienced at an intermediate level of frequency, in which case this becomes a homeostatic motivation).
Fixed vs. adaptive motivations. Finally, a last but equally important distinction is the fixed vs. adaptive property of motivation systems. In psychology terms, a fixed motivation system is one that will always value the same sensorimotor situation in the same manner during the entire individual’s life time. In a CRL framework, a fixed motivation system is one that will always provide the same reward for the same sensorimotor situation during the individual’s life time
[1
. On the contrary, an adaptive motivation system is one that will value the same situation differently as time passes (or, in a CRL framework, it will not necessarily provide the same reward for the same situation as time passes). For example, the energy maintenance motivation may be fixed if the zone of energy comfort always remains the same, or may be adaptive if for example the individual’s body grows with time and the motivation is implemented in such a way that the comfort zone shifts its boundaries accordingly. If an individual is able to remember the situation it has already experienced, then a drive for novelty is adaptive: a situation that was novel and thus attractive at some point, will not be anymore after having experienced it.
A significant number of cognitive architectures including particular models of intrinsic motivation have already been developed in the literature (e.g., Barto and Simsek, 2005
; Bonarini et al., 2006
; Huang and Weng, 2002
; Kaplan and Oudeyer, 2003
; Marshall et al., 2004
; Merrick and Maher, 2008
; Oudeyer et al., 2005
, 2007
;Schmidhuber, 1991
; Thrun, 1995
). Yet, they are most often ad hoc and it is not clear to understand how they relate to each other and to the general concepts of the psychology literature. As we will show, it also appears that a large set of potentially interesting computational approaches have not yet been implemented and studied.
The goal of this section is to present a typological and formal framework that may allow researchers to understand better and map the space of possible models. This typology is the result of several years of theoretical development and actual practice of computational models of intrinsic motivation systems (Kaplan and Oudeyer, 2003
, 2007a
,b
; Oudeyer and Kaplan, 2006
;Oudeyer et al., 2005
, 2007
). It is grounded in the knowledge of the psychology literature and of the existing computational models, but tries both to go further the vagueness of the former and to generalize the particular robotic implementations. An underlying assumption in this typology is that we position ourselves in the computational reinforcement learning framework (CRL). Thus, the typology relies on the formal description of the different types of reward computations that may be considered as defining an intrinsic motivation system. The typology is focused on the definition of rewards, and voluntarily leaves unspecified the particular CRL algorithms (e.g., Q-learning or Sarsa, see Sutton and Barto, 1998
for a presentation of possible algorithms) in which it can be plugged into because we think it is an orthogonal research issue.
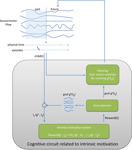
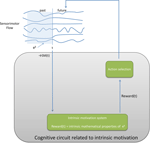
Furthermore, while we focus here on the definition of rewards related to intrinsic motivation, it is implicit that, on a particular robot, these intrinsic rewards might be integrated together with other types of reward systems (e.g., hunger, social presence,…). It should also be noted that when we will present figures summarizing each of the broad types that we present, we only show the cognitive circuits that are directly relevant to the intrinsic motivation system, but it is implicit that there might be many other modules running concurrently in the complete cognitive architecture of a particular robot.
In this typology, some kinds of models of intrinsic rewards have already been implemented and tested in the literature. From these models, a number of variants are proposed. Some of these variants are necessary improvements of the basic models that came as a result of actual experiments with robots. Some other variants come as natural formal variants and are thus extremely similar in terms of implementation, but interestingly correspond intuitively to some of human motivation that are not classically considered as intrinsic in psychology. The consequence of this in terms of how intrinsic motivation shall be conceptualized is elaborated in the discussion section. Finally, we also propose new formal models of intrinsic motivation, that correspond to important approaches in psychology but that seem to have never been investigated operationally in a computational framework.
To our knowledge, this is the first time that such a typology is presented, and we hope it will help to structure future research. Yet, it is also important to understand what this typology is not meant to be:
- we do not claim that this list is exhaustive or that there would be no other way to organize approaches into types.
- the list of formal approaches that we present is not intended to include methods for programming particular equations in particular robots. For the computation of some types of rewards, it has already been done elsewhere in the literature, and for some other, it is the subject of future research. Yet, where it is relevant, we provide references to papers that describe practical methods and architectures that allow to implement a particular approach in a particular robot.
- this typology is not a review of existing computational models of intrinsic motivation, which is available in Oudeyer et al. (2007) , but rather a presentation of a large formal framework in which existing and future models may be positioned.
- this typology does not say anything concerning what kind of behaviour might appear when one of the presented formal models is implemented in a robot and how far it could be used as a basis for open-ended development: in fact, several of the presented models are explicitly behaviouraly contradictory, but they are included both because they have already been used as such in the literature or because of their formal similarity. As a consequence, it should also be noted that this typology, and thus the general conceptualization of intrinsic motivation that we propose, is based on the mechanisms at play rather than on the actual results that they produce.
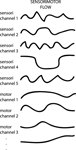
In the following, we organize the space of computational models of intrinsic motivation into three broad classes that all share the same formal notion of a sensorimotor flow experienced by a robot. We assume that the typical robot is characterized by a number of sensory channels, denoted si , and motor channels denoted mi, whose values continuously flow with time, hence the notations si(t) and mi(t) (see Figure 2
). The vector of all sensorimotor values at time t is denoted SM(t). Three features are important for the following computational models:
Figure 2. A robot is characterized by the continuous flow of values of its sensory and motor channels, denoted SM(t).
- these channels may correspond to any kind of physical or internal variable of a robot (for example coming from infra-red sensors, microphone sensors, virtual internal sensors like a face presence detector, low-level joint values of an arm, global direction of movement of the body,…);
- what these sensory channels actually are, i.e., their “meaning”, is NOT taken into account;
- the set of sensorimotor channels taken into account in intrinsic motivation measures of a situation may be smaller than the set of all sensorimotor channels available to the robot.
Knowledge-Based Models of Intrinsic Motivation
A first computational approach to intrinsic motivation is based on measures of dissonances (or resonances) between the situations experienced by a robot and the knowledge and expectations that the robot has about these situations. Here the word “situation” might refer as well to a passive observation activity in which a robot does nothing but focus its attention on a particular aspect of the environment, as to an active activity in which the robot performs actions and compares the actual outcome of its actions to its knowledge and expectations about these actions.
Within this approach, there are two sub-approaches related to the way knowledge and expectations are represented: information theoretic/distributional and predictive.
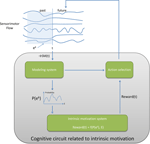
Information theoretic and distributional models. This approach is based on the use of representations, built by the robot, that estimate the distributions of probabilities of observing certain events ek in particular contexts, defined as mathematical configurations in the sensorimotor flow. There are several types of such events, but the probabilities that are measured are typically either the probability of observing a certain state SMk in the sensorimotor flow, denoted P(SMk), or the probability of observing particular transitions between states, such as P(SMk(t), SMl(t + 1)), or the probability of observing a particular state after having observed a given state P(SMk(t + 1)|SMl(t)). Here, the states SMk can be either be direct numerical prototypes or complete regions within the sensorimotor space (and it may involve a mechanism for discretizing the space). In the following, we will consider all these eventualities possible and just use the general notation P(ek). We will assume that the robot possesses a mechanism that allows it to build internally, and as it experiences the world, an estimation of the probability distribution of events across the whole space E of possible events (but the space of possible events is not predefined and should also be discovered by the robot, so typically this is an initially empty space that grows with experience). Finally, we use the concept of entropy, which characterizes the shape of the distribution function, for discretized spaces:

and for continuous spaces:

Figure 3
summarizes the general architecture of information theoretic approaches to intrinsic motivation.
Uncertainty motivation (UM). The tendency to be intrinsically attracted by novelty has often been used as an example in the literature on intrinsic motivation. A straightforward manner to computationally implement it is to build a system that, for every event e k that is actually observed, will generate a reward r (e k ) inversely proportional to its probability of observation:
Figure 3. The general architecture of information theoretic/distributional knowledge-based computational approaches to intrinsic motivation.

where C is a constant. This reward computation mechanism can then be integrated within a CRL architecture, which is going to select actions so that the expected cumulated sum of these rewards in the future will be maximized. Actually, this will be implicit in all following definitions, that concentrate on the explicit mechanism for defining and computing rewards. Various models based on UM-like mechanisms were implemented in the computational literature (e.g., Huang and Weng, 2004
).
Information gain motivation (IGM). It has also often been proposed in psychology and education that humans have a natural propensity to learn and assimilate (Ryan and Deci, 2000
). In information theoretic terms, this notion of assimilation or of “pleasure of learning” can be modeled by the decrease of uncertainty in the knowledge that the robot has of the world after an event ek has happened:
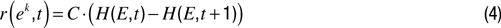
Examples of implementation of this information gain motivation can be found for instance in Fedorov (1972) and Roy and McCallum (2001)
(but note that in these paper the term “motivation system” is not used). It should be noted that, in practice, it is not necessarily tractable in continuous spaces. Actually, this is potentially a common problem to all distributional approaches.
Distributional surprise motivation (DSM). The pleasure of experiencing surprise is also sometimes presented. Surprise is typically understood as the observation of an event that violates strongly expectations, i.e., an event that occurs and was strongly expected not to occur. Mathematically, one can model it as:

where C is a constant. Note that this is somewhat different from UM in that there is a non-linear increase of reward as novelty increases. An event can be highly novel and rewarding for UM, but not very surprising if one did not expect more another event to take place instead of it (e.g., any random event in a flat uniform distribution is novel and rewarding for UM but not surprising and very little rewarding for DSM).
Distributional familiarity motivation (DFM). In the psychology literature, intrinsic motivations refer generally to mechanisms that push organisms to explore their environment. Yet, there are direct variants of previous possible systems that are both simple and correspond intuitively to existing forms of human motivation. For example, modifying the sign of UM would model a motivation to search situation which are very frequently observed, and thus familiar:

We will discuss below whether we should consider this as an intrinsic motivation.
Predictive models. Often, knowledge and expectations in robots are not represented by complete probability distributions, but rather based on the use of predictors such as neural networks or support vector machines that make direct predictions about future events (see Figure 4
). In this kind of architecture, it is also possible to define computationally various forms of intrinsic motivations. These predictors, denoted Π, are typically used to predict some properties Prk or sensorimotor states SMk that will happen in the future (close or far) given the current sensorimotor context SM(t) and possibly the past sensorimotor context. Similarly to above, we will denote all properties and states under the generic notation ek. We will also use the notation SM(→t) to denote a structure which encodes the current sensorimotor context and possibly the past contexts. Thus, a general prediction of a system will be denoted:
Figure 4. The general architecture of predictive knowledge-based computational approaches to intrinsic motivation.

We then define Er(t) as the error of this prediction, being the distance between the predicted event ẽk(t + 1) and the event that actually happens ek(t + 1):

Figure 4
summarizes the general architecture of predictive knowledge-based computational approaches to intrinsic motivation.
Predictive novelty motivation (NM). It then comes naturally to propose a first manner to model a motivation for novelty in this framework. Interesting situations are those for which the prediction errors are highest:

where C is a constant. Examples of implementation of this kind of motivation system can be found for example in Barto et al. (2004) and Thrun (1995)
.
Intermediate level of novelty motivation (ILNM). According to psychologists that proposed that humans are attracted by situations of intermediate/optimal incongruity, one can update the previous mechanism by introducing a threshold Eσs that defines this intermediate level of novelty:

where C1 and C2 are constants. Yet, this definition has the drawback of leaving the tuning of the threshold to the intuition of the human engineer. As a matter of fact, having a single threshold for the whole sensorimotor space might even be quite problematic in practice, since notions of novelty and similarities might vary a lot in different parts of that space, and developing mechanisms for automatic adaptive thresholding is a difficult problem.
Learning progress motivation (LPM). Several researchers have proposed another manner to model optimal incongruity which avoids the problem of setting a threshold, and is related to the information gain measurement described in the information theoretic section above. It consists in modeling intrinsic motivation with a system that generates rewards when predictions improve over time. Thus, the system will try to maximize prediction progress, i.e., the decrease of prediction errors. Prediction progress has also been referred as “learning progress” in Oudeyer et al. (2007)
. To get a formal model, one needs to be precise and subtle in how the decrease is computed. Indeed, as argued in Oudeyer et al. (2007)
, the possible naive implementation comparing prediction errors between a window around time t and a window around time t – θ is in fact nonsense: this may for example attribute a high reward to the transition between a situation in which a robot is trying to predict the movement of a leaf in the wind (very unpredictable) to a situation in which it just stares at a white wall trying to predict whether its color will change (very predictable). The system should not try to compare very different sensorimotor situations and qualitatively different predictions. This is why a possibility is to use a mechanism that will allow the robot to group similar situations into regions ℛn within which comparison is meaningful. The number and boundaries of these regions are typically adaptively updated. Then, for each of these regions, the robot monitors the evolution of prediction errors, and makes a model of their global derivative in the past, which defines learning progress, and thus reward, in these regions. Mathematically:
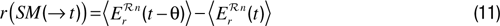
with SM(t) belonging to region ℛn and where 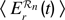 is the mean of predictions errors made by the predictor in the last τ predictions made about sensorimotor situations SM(t) belonging to region ℛn. A detailed study about how to implement such a system is provided in Oudeyer et al. (2007)
.
is the mean of predictions errors made by the predictor in the last τ predictions made about sensorimotor situations SM(t) belonging to region ℛn. A detailed study about how to implement such a system is provided in Oudeyer et al. (2007)
.
A different manner to compute learning progress has also been proposed in Schmidhuber (1991)
. It consists in measuring the difference in prediction error of the predictor Π, about the same sensorimotor context SM(→t), between the first prediction and a second prediction made just after the predictor has been updated with a learning rule:

where

with Π being the updated predictor after the learning update due to the prediction Π(SM(→ t)) and the perception of the actual consequence ek(t + 1).
Predictive surprise motivation (SM). In analogy to DSM, it is also possible to use the predictive knowledge-based framework to model a motivation for surprise. As explained above, surprise can be understood as the occurrence of an event that was strongly not expected or as the nonoccurrence of an event that was strongly expected. Here, as opposed to the previous paragraphs, and because surprise is related to a particular event with a short time span, there is a necessity to have a mechanism that models explicitly, at each time step, the strength of predictions, i.e., of expectations. Thus, we need to introduce a meta-predictor MetaΠ that tries to predict at time t what will be the error Er(t) of Π at time t:

where 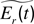 is the predicted absolute error of Π. Technically, MetaΠ is a machine of the same kind as Π, and can be a neural network or a support vector machine for example. It is updated at each time step after the actual Er(t) has been measured. Alternatively, MetaΠ could be implemented simply as computing the mean of recent errors for the same prediction in the recent past. We can then define a system that provides high rewards for highly surprising situations, based on the ratio between the actual error in prediction and the expected level of error in prediction (surprising situations are those for which there is an actually high error in prediction but a low level of error was expected):
is the predicted absolute error of Π. Technically, MetaΠ is a machine of the same kind as Π, and can be a neural network or a support vector machine for example. It is updated at each time step after the actual Er(t) has been measured. Alternatively, MetaΠ could be implemented simply as computing the mean of recent errors for the same prediction in the recent past. We can then define a system that provides high rewards for highly surprising situations, based on the ratio between the actual error in prediction and the expected level of error in prediction (surprising situations are those for which there is an actually high error in prediction but a low level of error was expected):
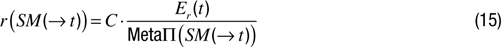
where C is a constant.
Predictive familiarity motivation (FM). As in information theoretic models, the structure of above mentioned predictive models can be used to implement a motivation to experience familiar situations:

where C is a constant. This implementation might nevertheless be prone to noise and reveal not so useful in the real world, since it is only based on predictions local in time and space. To get a more robust system for familiarity, a possibility is to compute a smoothed error of past predictions in the vicinity of the current sensorimotor context. One can use the concept of regions introduced in the LPM paragraph:

where SM(→t) falls in the sensorimotor regions ℛn. As in LPM, this architecture assumes a mechanism that allows to build incrementally the ℛn regions. This mechanism can be based on iterative region splitting as in Oudeyer et al. (2007)
, or simply be based on a (possibly adaptive) threshold Tf on the distance from SM(→t):
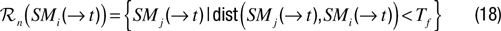
where dist (·,·) is a distance measure.
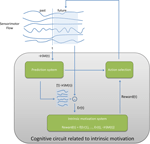
Competence-Based Models of Intrinsic Motivation
A second major computational approach to intrinsic motivation is based on measures of competence that an agent has for achieving self-determined results or goals. Interestingly, this approach has not yet been studied in the computational literature, but we think that it contains a high potential for future research. Indeed, it is directly inspired from important psychological theories of effectance (White, 1959
), personal causation (De Charms, 1968
), competence and self-determination (Deci and Ryan, 1985
), and “Flow” (Csikszentmihalyi, 1991
). Central here is the concept of “challenge”, with associated measures of difficulty as well as measures of actual performance. A challenge here will be any sensorimotor configuration SMk, or any set {Pk } of properties of a sensorimotor configuration, that the individual sets by itself and that it tries to achieve through action. Thus, a challenge is here a self-determined goal, denoted gk. It is the properties of the achievement process, rather than the “meaning” of the particular goal being achieved, that will determine the level of interestingness of the associated activity. While prediction mechanisms or probability models, as used in previous sections, can be used in the goal-reaching architecture, they are not mandatory (for example, one can implement systems that try to achieve self-generated goals through Q-learning and never explicitly make predictions of future sensorimotor contexts). Furthermore, while in some cases, certain competence-based and knowledge-based models of intrinsic motivation might be somewhat equivalent, they may often produce very different behaviors. Indeed, the capacity to predict what happens in a situation is only loosely coupled to the capacity to modify a situation in order to achieve a given self-determined goal.
More technically, we will assume here a cognitive architecture in which there is a “know-how” module KH(tg) that is responsible for planning actions in order to reach self-determined goals gk and that learns through experience. There is also a motivation module, which will attribute rewards based on the performance of KH(tg). There are two time scales in this architecture: the traditional physical time scale corresponding to atomic actions, denoted t, and an abstract time scale related to the sequence of goal-reaching episodes, denoted tg. A goal-reaching episode is defined by the setting of a goal gk(tg) at time tg, followed by a sequence of actions determined by KH(tg) in order to try to reach gk(tg), and with a duration bounded by a timeout threshold Tg. After the goal has been reached or the timeout has stopped KH(tg), a new goal-reaching episode can begin, at abstract time tg + 1. At the end of each episode, the sensorimotor configuration that has been reached, denoted gk(tg), is compared to the initial goal gk(tg), in order to compute the level of (mis )achievement la(gk, tg) of gk:

This level of achievement will then be the basis of the computation of an internal reward, and thus be the basis for evaluating the level of interestingness of the associated goal. Finally, there is a module responsible for choosing appropriately goals that will provide maximal rewards, and that can typically be implemented by algorithms developed in the CRL framework. Figure 5
summarizes the general architecture of competence-based approaches to intrinsic motivation.
Figure 5. The general architecture of competence-based computational approaches to intrinsic motivation.
Episodes are related to temporally extended actions in option theory (Sutton et al., 1999
). However, to our knowledge, this paper presents the first description of competence-based models of intrinsic motivation.
We will now present several example systems differentiated by the way rewards are computed.
Maximizing incompetence motivation (IM). A first competence-based approach to intrinsic motivation can be a system which pushes the robot to set challenges/goals for which its performance is lowest. This is a motivation for maximally difficult challenges. This can be implemented as:

Note that here and everywhere in the competence based approaches, rewards are generated only at the end of episodes. The previous equation measures incompetence, and thus interestingness, in trying to reach a given goal only in a single trial/episode. It might be useful to build a reward system taking into account the performance of the robot about the same goal in previous episodes, especially for goals for which there is a high variance in performance. The equation would be:
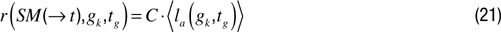
where 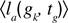 denotes the mean of performances in trying to reach gk in the last τ episodes in which this goal was set up. This reward system could still be updated in order to allow for generalization in the computation of the interestingness of a goal. In the two previous equations, the interestingness of a given goal gk did not depend on the performance of the robot in similar goals. Yet, this could be a useful feature: think for example of a robot playing with its arm, and discovering that it is interesting to try to grasp an object that is 30 cm away on the table in front of it. It would be potentially useful that the robot would infer that trying to grasp an object that is 35 cm away is also interesting without having to recompute the level of interestingness from scratch. To achieve this, a possible solution is to use an equation of the type:
denotes the mean of performances in trying to reach gk in the last τ episodes in which this goal was set up. This reward system could still be updated in order to allow for generalization in the computation of the interestingness of a goal. In the two previous equations, the interestingness of a given goal gk did not depend on the performance of the robot in similar goals. Yet, this could be a useful feature: think for example of a robot playing with its arm, and discovering that it is interesting to try to grasp an object that is 30 cm away on the table in front of it. It would be potentially useful that the robot would infer that trying to grasp an object that is 35 cm away is also interesting without having to recompute the level of interestingness from scratch. To achieve this, a possible solution is to use an equation of the type:
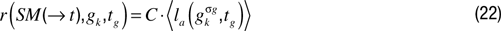
where 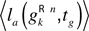 denotes the mean performances in trying to reach goals gkσg such that dist(gk, gkσg) < σg, with dist (·,·) being a distance function and σg a numerical threshold. Thus, with this formula, one considers all goals that are closer than a given threshold as equivalent to the current goal for the computation of its interestingness.
denotes the mean performances in trying to reach goals gkσg such that dist(gk, gkσg) < σg, with dist (·,·) being a distance function and σg a numerical threshold. Thus, with this formula, one considers all goals that are closer than a given threshold as equivalent to the current goal for the computation of its interestingness.
Maximizing competence progress – aka Flow motivation (CPM). Maximizing incompetence does not model very well the psychological models of optimal challenge and “flow” proposed by (Csikszentmihalyi, 1991
). Flow refers to the state of pleasure related to activities for which difficulty is optimal: neither too easy nor too difficult. As difficulty of a goal can be modeled by the (mean) performance in achieving this goal, a possible manner to model flow would be to introduce two thresholds defining the zone of optimal difficulty. Yet, the use of thresholds can be rather fragile, require hand tuning and possibly complex adaptive mechanism to update these thresholds during the robot’s lifetime. Another approach can be taken, which avoids the use of thresholds. It consists in defining the interestingness of a challenge as the competence progress that is experienced as the robot repeatedly tries to achieve it. So, a challenge for which a robot is bad initially but for which it is rapidly becoming good will be highly rewarding. Thus, a first manner to implement CPM would be:
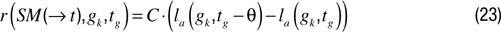
corresponding to the difference between the current performance for task gk and the performance corresponding to the last time gk was tried, at a time denoted tg – θ. Again, because of possible high variance in goal achievement, one could use smoothed differences:
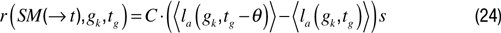
with 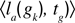 being the mean performance in trying to reach gk in the last τ corresponding episodes, and
being the mean performance in trying to reach gk in the last τ corresponding episodes, and 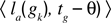 being the mean performance in trying to reach gk between episodes tg – θ – τ and tg – θ. Again, this formula does not include generalization mechanisms, and might reveal inefficient in continuous sensorimotor spaces. One can update it using the same mechanism as in IM:
being the mean performance in trying to reach gk between episodes tg – θ – τ and tg – θ. Again, this formula does not include generalization mechanisms, and might reveal inefficient in continuous sensorimotor spaces. One can update it using the same mechanism as in IM:
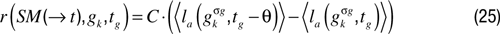
with the same notations as for IM. The concept of regions (see LPM) could as well be used here.
Maximizing competence (CM). It is also possible to implement a motivation that pushes a robot to experience well-mastered activities in this formal competence-based framework. One can use the following formula:
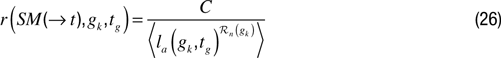
where gk falls in the region ℛn of the goal space. This architecture assumes a mechanism that allows to build incrementally the ℛn regions. This mechanism can be based on iterative region splitting as in Oudeyer et al. (2007)
, or simply be based on a (possibly adaptive) threshold σg on the distance from gk :

where dist (·,·) is a distance measure.
Morphological Models of Intrinsic Motivation
The two previous computational approaches to motivation were based on measures characterizing the relation of a cognitive learning system and the flow of sensorimotor values. A third approach that can be taken is only based on mathematical/morphological properties of the flow of sensori-motor values, irrespective of what the internal cognitive system might predict or master. Figure 6
summarizes the general architecture of morphological computational approaches to intrinsic motivation. We will now present two examples of possible morphological computational models of intrinsic motivation.
Figure 6. The general architecture of morphological computational approaches to intrinsic motivation.
Synchronicity motivation (SyncM). The synchronicity motivation presented here is based on an information theoretic measure of short-term correlation (or reduced information distance) between a number of sensorimotor channels. With such a motivation, situations for which there is a high short-term correlation between a maximally large number of sensorimotor channels are very interesting. This can be formalized in the following manner.
Let us consider that the sensorimotor space SM is a set of n information sources {SMi} and that possible values for these information sources typically correspond to elements belonging to an arbitrary number of bins. At each time t, a element SMi corresponds to the information source SMiand the following notation can be used: SMi(t) = smi
The conditional entropy for two information sources SMi and SMj can be calculated as
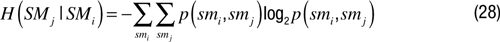
where p(smj|smi ) = p(smj, smi )/p(smi ).
H (SMj|SMi ) is traditionally interpreted as the uncertainty associated with SMj if the valueof SMi is known.
We can measure synchronicity s(SMj, SMi ) between two information sources in various manners.
Crutchfield’s normalized information distance (which is a metric) between two information sources is defined as (Crutchfield, 1990
):
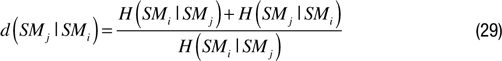
Based on this definition we can define synchronicity as

Alternatively we can assimilate synchronicity to mutual information
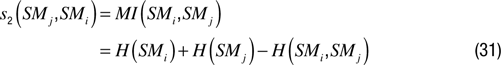
We can also measure the correlation between the two time series
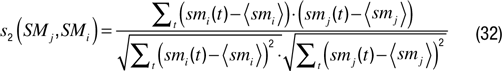
Whatever, the type of measure used we can define the reward associated with a given recent time window as
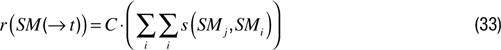
Synchrony detection between two (or more) information sources is thought to be a critical mechanism for infant learning and cognitive development (e.g., object interaction skills Watson, 1972
, self-modeling Rochat and Striano, 2000
, word-learning Gogate and Bahrick, 1998
). Although generally not as a motivational variable, synchrony measures have been used in several recent formal models (e.g., Hershey and Movellan, 2000
; Prince et al., 2003
).
Stability motivation (StabM) and Variance motivation (VarM). The stability motivation pushes to act in order to keep the sensorimotor flow close from its average value.

where 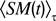 is the average of the sensorimotor vector over the last τ time steps.
is the average of the sensorimotor vector over the last τ time steps.
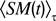 is the average of the sensorimotor vector over the last τ time steps.
is the average of the sensorimotor vector over the last τ time steps.Opposite of the stability motivation, the variance motivation reward situations for which values have high variance in sensorimotor channels.
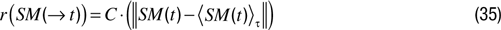
where 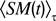 is the average of the sensorimotor vector over the last τ time steps.
is the average of the sensorimotor vector over the last τ time steps.
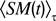 is the average of the sensorimotor vector over the last τ time steps.
is the average of the sensorimotor vector over the last τ time steps.Both could be viewed as rationale strategies in certain contexts. Stability permits to act in order to decrease the inherent instability of perception and could lead for instance to tracking behavior (Kaplan and Oudeyer, 2003
). On the contrary, variance motivation could lead to explore unknown sensorimotor contingencies far from equilibrium.
For clarity sake, we will shortly present in this section some computational models of non-intrinsic motivation systems which are nevertheless internal.
Let’s imagine for instance that one wants to build a robot with a social presence motivation and that this robot can recognize faces in its environment. If the robot does not see enough faces, it should act as if it is lonely and look for social interaction. if it sees too many, it should be overwhelmed and try to avoid new social interactions. If we define Fτ (t) the average number of faces seen during the last τ timeframes and 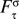 the optimal average number faces, the reward for socially balanced interaction (SocM) could be defined as (C 1 and C 2 being some constants to be defined):
the optimal average number faces, the reward for socially balanced interaction (SocM) could be defined as (C 1 and C 2 being some constants to be defined):

If the same manner, we can program a reward for energy maintenance that pushes the robot to maintain energy at an intermediary level (EnerM) (between starvation and indigestion) by defining E(t) the energy at time t and Eσ the optimal energy level and the following reward formula:

Motivation systems of these kinds have been investigated by many researchers (e.g., see Breazeal, 2002
for a series of relevant examples). They are very good for simulating natural complex balanced behavior. However, they should not be considered as intrinsic motivation systems as they are defined based on measures related to specific sensori channels (energy level, number of faces seen).
In spite of the diversity of the computational approaches of intrinsic motivation that we presented, there is a point of convergence for all of them. Each of the described models defines a certain interpretation of intrinsic motivation in terms of properties of the flow of sensorimotor values and of its relation to the knowledge and know-how of the system independently of the meaning of the sensorichannels that are involved. This definition contrasts greatly with definitions based on behavioral observation (activities with no apparent goal except the activity itself) and may at first seem non-intuitive as its behavioral consequences can only be explored through computational modeling and robotic experiments. Moreover, simple variants of these intrinsic motivation systems will not push a system towards exploration (e.g., FM, CM or StabM will push a robot to stand still), but we believe it is formally more coherent to conceptualize them also as intrinsic motivations, even if some psychologists would not do so. In fact, we believe that this kind of systematic computational approach to intrinsic motivation can play a crucial role in organizing the debate around their very definition, as well as their role in behavior, learning and development, in particular because it permits to discuss hypothesis on a clearly defined common ground.
The table on Figure 7
presents all the models discussed in this paper and the families to which they belong (Intrinsic vs. Extrinsic, Adaptive vs. Fixed, Knowledge-based, Competence-based or Morphological, Information theoretic or Predictive, Homeostatic vs. Heterostatic). For each model we give a rough estimation of its exploration potential (how likely such a motivation can lead to exploratory and investigation behaviours) and of its organization potential (how likely such a motivation can lead to a structured and organized behaviour). We also estimate the computational cost and number of computational models existing so far for each of the categories. This table permits to clarify the landscape of intrinsic motivation models, show the potential of certain families and the underinvestigated areas. Indeed, we believe that most of the challenges are ahead of us.
Figure 7. This table presents all the models discussed in this paper and the families to which they belong. For each model we give a rough estimation of its exploration potential (how likely such a motivation can lead to exploratory and investigation behaviours) and of its organization potential (how likely such a motivation can lead to a structured and organized behaviour). We also estimate the computational cost and number of computational models existing so far for each of the categories.
First, it is now crucially important to understand how such kind of “agnostic” disembodied computer architecture can lead to specific behavioral organization when associated with specific embodiment and placed in particular environment. The same intrinsic motivation system can lead to very different outcomes depending on the type of physical or virtual system it is linked to. What is particularly interesting is that this type of architecture permits to consider embodiment as a controllable variable clearly separated from the control system.
Second, this typology can act as an invitation to investigate in a systematic manner which kinds of intrinsic motivation system among the ones we have reviewed can lead to open-ended developmental trajectories in some ways similar to the one observed during children’s development. Our past research and experiments provided a number of hints showing that models of intrinsic heterostatic adaptive motivations are the one which hold the greatest promises because they can combine both high exploration and organization potentials (e.g., information gain motivation - IGM-, maximizing learning progress motivation -LPM-, maximizing competence progress (Flow) motivation -CPM-). Such types of motivation systems push robots to explore their world in a progressive and organized manner, avoiding situations or goals which are too easy or too difficult at a given stage of their development. For example, in Oudeyer et al. (2007)
, we present the Playground Experiment, in which an implementation of the LPM model is shown to allow the self-organization of a complex developmental trajectory. In this experiment, the robot knows very few things about its body and its environment: it basically only knows the unlabelled list of its sensors and motors (but for example does not know that some of them are related to vision and some other are related to touch). We have shown that the Learning Progress Motivation, coupled with an adequate region splitting mechanism, allows the robot to bootstrap broad sensorimotor categories and associated behaviours. Typically, the robot begins with a phase of random body babbling, which is then followed by a phase in which it plays in a focused manner with individual parts of its body, which is then followed by a phase in which the robot tries different kind of actions towards objects, which is then followed by a phase in which the robot discovers particular affordances between actions and objects (for example, the robot tries repeatedly to bite a bitable object, or to vocalize to a distant “adult” robot).
Such existing implementations were focused only on a particular kind of motivation integrated in a particular robot and environment. A great challenge is now to understand which kind of behavioral trajectories are linked with each system and to progress in our understanding of their role for cognitive open-ended development. In addition, there are good chances that the other types of intrinsic motivation systems we identify in this paper are also interesting in certain contexts, leading to relevant behavior or new learning opportunities.
Third, robotic or simulated experiments with intrinsic motivation systems should permit to shed new lights on both psychological and neurophysiological data. We have already discussed the relevance of these models, and in particular of the LPM model, for certain research debates in developmental psychology [e.g., language acquisition (Oudeyer and Kaplan, 2006
), development of imitation (Kaplan and Oudeyer, 2007b
)] and proposed some hypotheses for putative underlying neural circuits (Kaplan and Oudeyer, 2007a
). However, as in these domains very few experimental work actually deal with intrinsic motivation, in most of the cases, these new models are an invitation to perform new experiments.
Finally, we must investigate the practical applicative aspects of these systems. Intrinsically motivated machines are fascinating. However, in certain application contexts, their intrinsic openness is a weakness. Learning how to design these machines of a new kind so that their huge potential can be unveiled in practice is one of the major challenge we still have to tackle.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors wish to thank the reviewers for their helpful comments.
Footnote
- ^ Here, and as everywhere is the text, the term “sensorimotor situation” is used in its most general sense and for example includes internal physiological variables.
Huang, X., and Weng, J. (2002). Novelty and reinforcement learning in the value system of developmental robots. In Proceedings of the 2nd International Workshop on Epigenetic Robotics: Modeling Cognitive Development in Robotic Systems, Lund University Cognitive Studies, Vol. 94, C. Prince, Y. Demiris, Y. Marom, H. Kozima and C. Balkenius, eds (Edinburgh, Scotland, Lund University), pp. 47–55.
Kaplan, F., and Oudeyer, P.-Y. (2003). Motivational principles for visual know-how development. In Proceedings of the 3rd International Workshop on Epigenetic Robotics: Modeling Cognitive Development in Robotic Systems, Lund University Cognitive Studies, Vol. 101, C. Prince, L. Berthouze, H. Kozima, D. Bullock, G. Stojanov and C. Balkenius, eds (Boston, USA, Lund University), pp. 73–80.
Kaplan, F., and Oudeyer, P.-Y. (2007b). The progress-drive hypothesis: an interpretation of early imitation. In Models and Mechanisms of Imitation and Social Learning: Behavioural, Social and Communication Dimensions, C. Nehaniv and K. Dautenhahn, eds (New York, Cambridge University Press), pp. 361–377.
Prince, C., Hollich, G., Helder, N., Mislivec, E., Reddy, A., Salunke, S., and Memon, N. (2003). Taking synchrony seriously: a perceptual-level model of infant synchrony detection. In Proceedings of the Fourth International Workshop on Epigenetic Robotics: Modeling Cognitive Development in Robotic Systems, Lund University Cognitive Studies, Vol. 117, L. Berthouze, H. Kozima, C. Prince, G. Sandini, G. Stojanov, G. Metta and C. Balkenius, eds (Edinburgh, Scotland, Lund University).