- 1Ningbo Cigarette Factory, China Tobacco Zhejiang Industrial Co., Ltd., Ningbo, China
- 2Department of Engineering Mechanics, Zhejiang University, Hangzhou, China
- 3Technology Center, China Tobacco Zhejiang Industrial Co. Ltd., Hangzhou, China
- 4Zhejiang Provincial Engineering Research Center for the Safety of Pressure Vessel and Pipeline, Ningbo University, Ningbo, China
A numerical study is performed using the Discrete Element Method (DEM) to investigate flow and mixing of elongated particles in rotating drums. Spherical particles and their mixtures have been extensively explored in the previous work, while the present study focuses on the elongated rod-like particles and binary mixtures of the elongated particles with two different aspect ratios. Different drum sizes are used to examine scale-up behaviors in such dynamic processes. For both monodisperse and binary particle systems, dynamic angle of repose is determined mainly by a Froude number Fr, measuring the ratio of centrifugal force to gravitational force on a particle, while it is insensitive to scale-up ratio α, defined as the ratio of cross-sectional areas of the current drum to the reference one. Average particle velocity and contact force generally increase with both Froude number and scale-up ratio. Mixing rate of the particles is significantly promoted by increasing Fr, and it maintains constant at small Fr and decreases slowly with increasing α at large Fr. Some differences are observed between the monodisperse and binary systems: i) The mixing index eventually achieves the same high level for all the monodisperse systems, while the final mixing indices are smaller with smaller Fr for the binary systems; ii) The mixing rate of the binary mixtures has a stronger dependence on the scale-up ratio
1 Introduction
In many industries such as pharmaceutical, food processing, materials engineering, and so on, mixing of solid particles, which may have different sizes, shapes and densities, is a critical process. In order to achieve efficient and reliable mixing, rotating drums are frequently used because of excellent capacity for bulk solids handling (Jiang et al., 2023; Xu et al., 2023; Dong et al., 2024). Combined with their ability of heat transfer efficiency (Figueroa et al., 2010; Gui et al., 2013), the rotating drums are applied in a broad range of industrial processes involving drying, reactions, segregation, coating, grinding, heating, and cooling operations (Trojosky, 2019; Orozco et al., 2020; Liu et al., 2024). Six different regimes (from slipping to centrifuging) have been recognized based upon a Froude number, defined as the ratio of centrifugal to gravitational forces (Beaulieu et al., 2021; Chen et al., 2024). To obtain homogenous mixtures, the rolling and cascading regimes should be adopted (Norouzi et al., 2015). In these flow regimes, active and passive regions of particle motion are observed. In the passive region, the particles move as a rigid body, and their velocity is lower than that of the particles in the active layer. An active layer of the flowing particles is formed, when the particles reach the highest point along the wall, and then they fall like an avalanche under gravitational forces. The active layer is much thinner than the passive region, due to the existence of a yield stress for the particle flow. The mixing, segregation and heat transfer mainly happen in the active layer where the shearing rate is high (Alizadeh et al., 2013).
The outcomes of the particle mixing depend upon the size of the mixer. Many studies on the particle mixing are typically conducted at the laboratory scale, instead of industrial level. The relevance of the results obtained from the small scales to those at the large scales remains unclear (Portillo et al., 2008). A lot of studies have been done previously on various scaling conditions to determine the scale-up laws (Ding et al., 2001) that ensure similarities in dynamic behaviors of granular materials across the drums of different sizes (Govender, 2016). Various dimensionless numbers have been proposed in the scale-up studies. Recently, He et al. (2024) studied the segregation of bi-dispersed spherical particles caused by particle size difference inside different cylindrical drums, and they found that the contact forces and power consumption strongly depended on the Froude number. Herman et al. (2021) found that the similar mixing quality was achieved in a scale up process by keeping the same kinematic and dynamic similarities in bladed mixers. In their study, they used monodispersed spherical particles and proposed scaling correlations for average particle velocity
in which
Experimental scale-up studies of the granular flows are usually expensive and labor intensive. Also, it’s very difficult to obtain the particle-scale information in the experiments for a deeper, microscopic understanding of the physical processes. To address these deficiencies, numerical approach, such as the Discrete Element Method (DEM), was used to simulate the drum rotating processes (Li et al., 2022), and the scale-up of the particulate systems in the drums was studied (Li et al., 2020). In the DEM simulations of the polyhedral particle flows (Vu et al., 2024), it was found that the active layer depth and curvature and particle velocity could be expressed as functions of the Froude number. In the DEM studies of heat transfer in a rotary drum (Ardalani et al., 2023), it was found that a larger number of baffles installed inside the drum led to a higher rate of heat transfer, while the temperature distributions of the particles and bed uniformity were unaffected by the changes in the baffle number.
Most grains and particles in the industries have non-spherical shapes (Ma et al., 2022). Flow patterns of the particles with anisotropic shapes are more complex at various rotational speeds of the drums (Yang et al., 2008). The non-spherical particle shapes give rise to segregation (Yang et al., 2017; Kumar et al., 2024; Miao et al., 2024), and thus influence the mixing performance (He et al., 2020). In the studies of the rotating drums, elongated, rod-like particles gained interests of many researchers (Yu et al., 2018; Yu et al., 2020), because of their important applications in fibrous materials (Rudge et al., 2008) and pharmaceutics (Kodam et al., 2012). As the motion of the rod-like particles is more restrained inside the drum due to interlocking particle-particle contacts (Li et al., 2021), their dynamics and mixing behaviors are different from the spherical particles. Some open questions are still remaining in the rotating drums of the rod-like particles. For instance, how are the particle flow and mixing patterns and quantities influenced when the drum size is changed? Do the rod-like particles have different scale-up behaviors from the spherical particles?
This work aims to address these questions by performing the DEM simulations. The flow and mixing of monodisperse and binary elongated, rod-like particles in the rotating drums of different sizes are simulated. The scale-up behaviors are discussed for angle of repose, particle mixing rate, average particle velocity, and contact forces.
2 Computational set-up
2.1 Discrete element method
In the Discrete Element Method (DEM), an elongated particle is represented by a sphero-cylinder. Each particle is considered as a discrete entity and its translational and rotational motion in Equations 4, 5 is described by Newton’s second law of motion,
where translational and angular velocities of the particle
The resultant contact force between a particle and another particle or a wall boundary can be decomposed into a normal contact force and a tangential one. In this work, the normal contact force
in which the normal contact stiffness
and
Linear spring-dashpot Coulomb limit model (Zhu et al., 2007) is employed to calculate tangential contact force at time
in which,
and
2.2 Numerical model
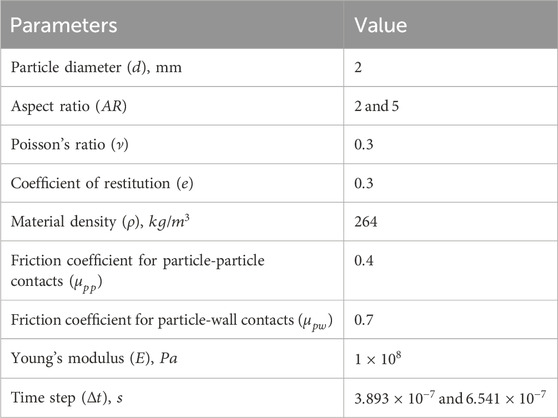
The dynamics of elongated sphero-cylinder particles in a rotating drum is simulated. As shown in Figure 1, the particles have a diameter of
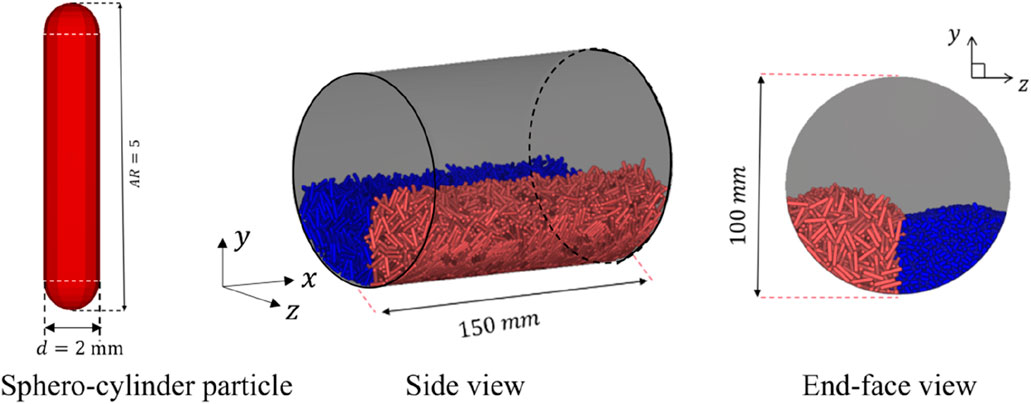
Figure 1. Numerical models of an elongated sphero-cylinder particle and a rotating drum. Before the rotation of the drum, the elongated particles are colored differently side-by-side in the drum to track the mixing behavior in the flow process.
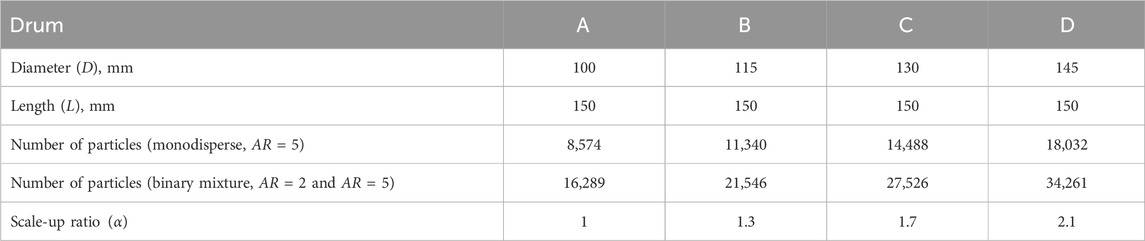
To examine scale-up rules for the present drum systems, four drums of different diameters, i.e. Drum A to D, are used in the simulations, as shown in Table 2. As the flow patterns and mixing behaviors show no dependences on it, the length of the drum L remains the same for the four drums. To achieve the similarity of the system, the same fill ratio, defined as the total volume of the particles to the volume of the drum, is specified to the four drums, for which the number of particles increases linearly with the volume of the drum. The monodisperse particles have particle aspect ratio of AR = 5. The binary mixtures are composed of two components with AR = 2 and AR = 5, respectively, and both components have volume concentrations of 50% in the mixtures. For the drum systems, a scale-up ratio
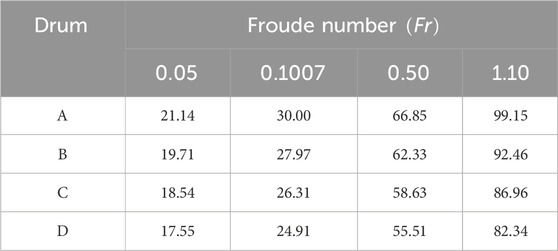
A Froude number
in which
2.3 Lacey mixing index
Various mixing indices exist and it is critical to choose a proper one to describe the degree of particle mixing for a specific process (Bhalode and Ierapetritou, 2020). The Lacey mixing index (Lacey, 1954)
in which,
In the calculation, the whole particle system is partitioned into many subdomains, namely boxes. The variances of an initial mixing state and a completely mixed state are represented by
3 Monodisperse system of elongated particles
3.1 Dynamic angle of repose
A slope of particles with a wavy surface is formed in the rotating drum, as shown in Figure 2. Larger curvature of the granular surface is obtained for the elongated particles compared to the spherical particles (Cui et al., 2023). To describe the particle flow patterns, the profile of the granular surface is fitted using a straight line. The inclination angle of the straight line
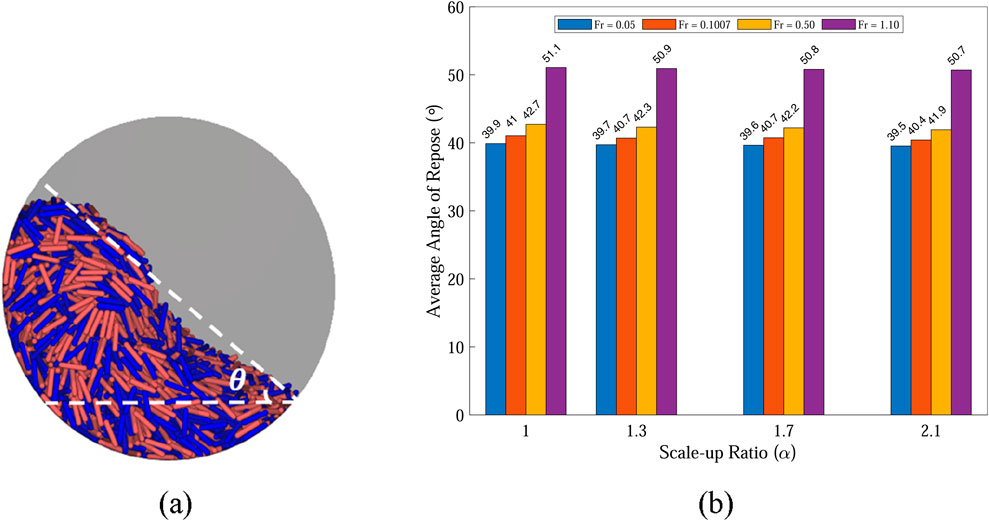
Figure 2. (a) Illustration of dynamic angle of repose
3.2 Particle velocities
Different particle flow regimes can be observed in the drums, as shown in Figure 3. The particles have higher velocities as they cascade down on the curved surface. The particles contacting the inner surface of the drum generally have the same velocities to the surface (like non-slip boundary), and thus their velocities increase with increasing Froude number Fr for a given drum. Low-velocity regimes are formed in the centers of the circulating particle assemblies.
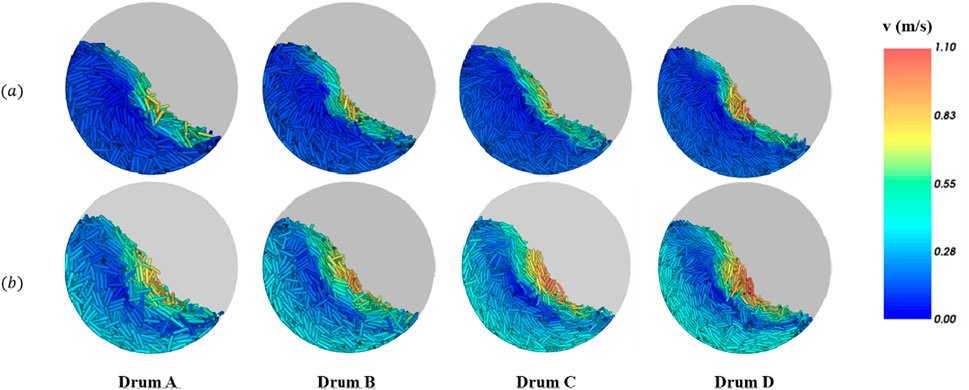
Figure 3. Velocity distribution of the sphero-cylinder particles in the different drums at the steady state with (a) Fr = 0.1007 (top row) and (b) Fr = 0.50 (bottom).
The probability distributions of the particle velocities are shown in Figure 4. Low particle velocities correspond to the central region. Intermediate velocities correspond to the boundary layer of the particles contacting the rotating wall, and thus the peak probability occurs at a higher particle velocity in a larger drum. The long tail in a probability distribution curve at the higher particle velocities (particle velocities are greater than 0.2 m/s in Figure 4a and greater than 0.4 m/s in Figure 4b) is associated with the rapid flowing particle surface region, in which shear rates are higher and velocity distribution is wider.
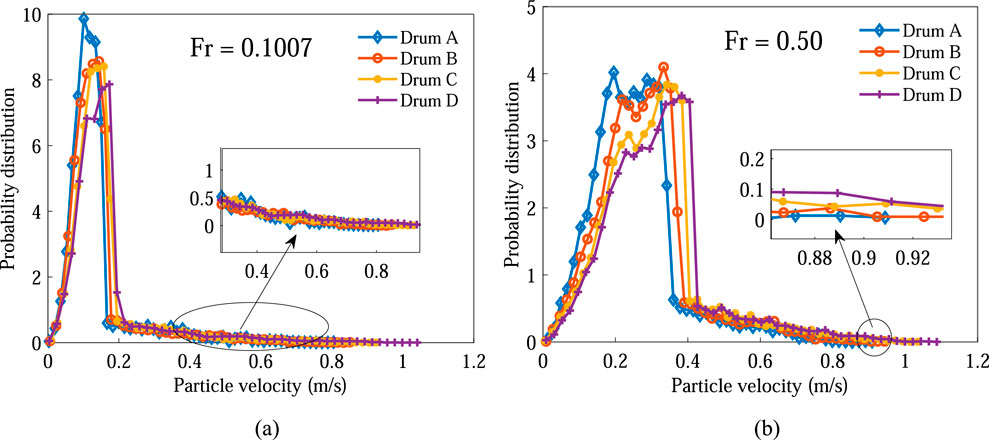
Figure 4. Probability distributions of particle velocities in different drums for (a) Fr = 0.1007 and (b) Fr = 0.50. The inserts show the zoom-in views of a part of the long tail of the distribution curve.
For a given Froude number Fr, the average particle velocity increases with the scale-up ratio
in which
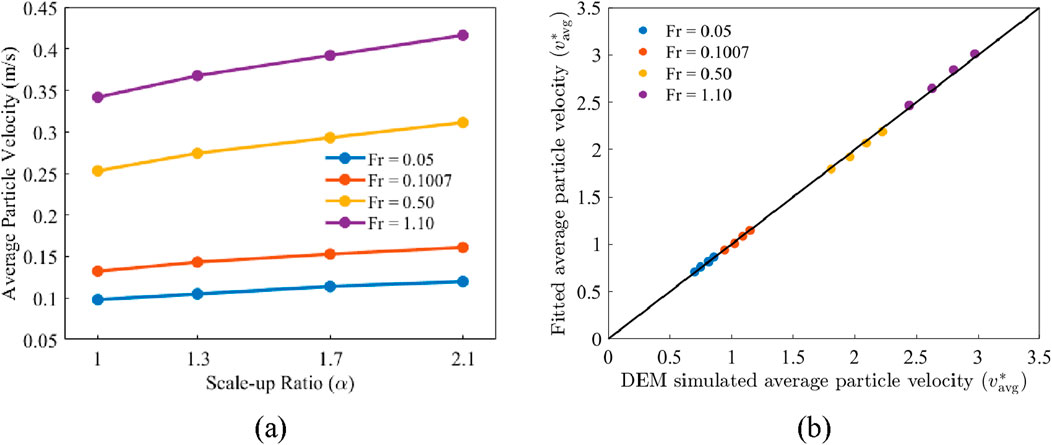
Figure 5. (a) Average particle velocity versus scale-up ratio
3.3 Contact forces on the particles
The contact forces exerted on the particles due to particle-particle and particle-wall contacts determine attrition and breakage of the particles and erosion on the drum walls. The average contact force exhibits significant increase as both scale-up ratio
in which
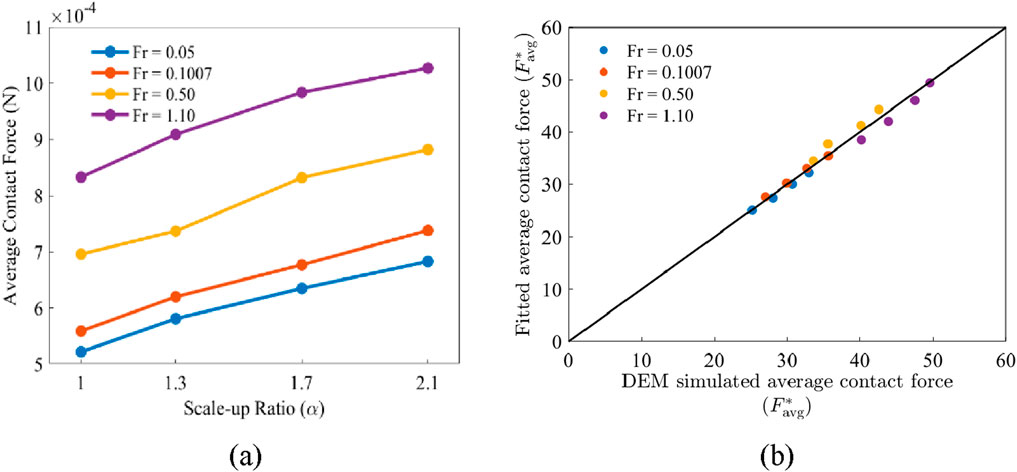
Figure 6. (a) Average contact force versus scale-up ratio
3.4 Mixing performance
To observe and quantify the mixing behavior, the monodisperse particles are partitioned equally in number and colored differently in blue (left-hand side) and red (right-hand side), as shown in Figure 7. To ensure the consistent particle loading, two rectangular inlet regions with the fixed dimensions were used in all drum. However, as the drum cross-sectional area increases, the relative inlet area becomes smaller, leading to slight variations in the initial packing profile at
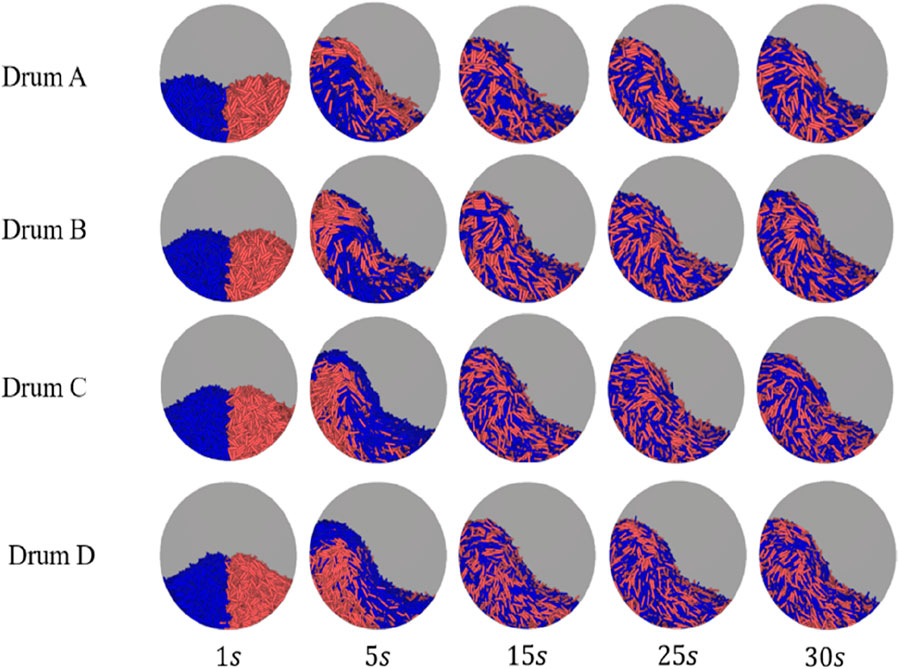
Figure 7. Snapshots of temporal evolution of mixing patterns of monodisperse particles in different drums at Fr = 0.1007.
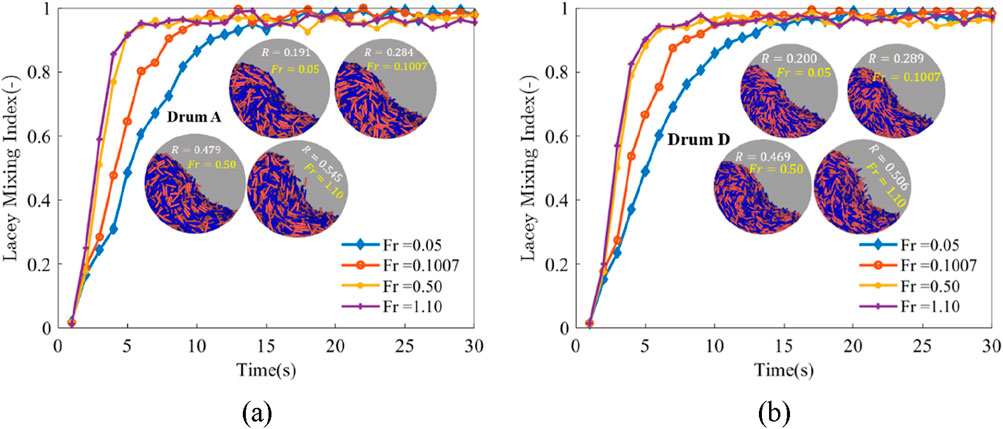
Figure 8. Time evolution of Lacey mixing index L at various Froude numbers Fr in (a) Drum A and (b) Drum D. The inset images show the mixed particle patterns at t = 30 s and the mixing rates R for the four Froude numbers.
According to Figure 8, the Lacey mixing index L and elapsed time t follow an error function (Herman et al., 2022a; He et al., 2024) in the form,
in which exp (−) represents the exponential function,
Fitting to the Lacey index L-t curves (Figure 8) using Equation 17, the mixing rate R can be determined for each mixing process. As shown in Figure 9a, the mixing rate R is almost independent on the scale-up ratio
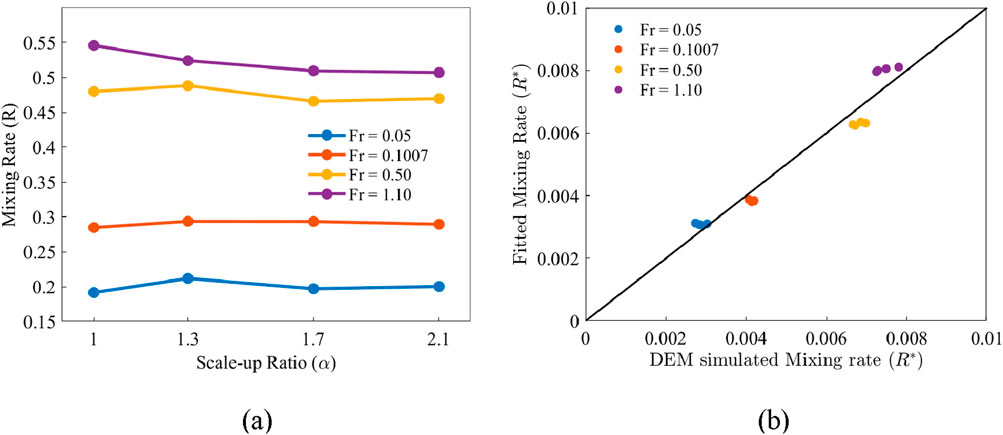
Figure 9. (a) Mixing rate versus scale-up ratio
By fitting to the data in Figure 9a, a power law is determined to correlate the mixing rate R, Froude number Fr, and scale-up ratio
which indicates that
For the spherical particles, the average particle velocity
4 Binary mixtures of elongated particles
The scale-up behaviors of monodisperse systems of the elongated particles with AR = 5 in the drums of different sizes are investigated in the previous section (Section 3). In this section, we aim to examine the scale-up behaviors of binary mixtures in rotating drums, and we will explore the links and differences between the monodisperse and binary systems. In the present simulation studies, the binary mixtures are composed of two particle components with AR = 2 and AR = 5, respectively, and each component occupies a volume concentration of 50% in the mixtures. The particle properties and drum parameters are listed in Tables 1, 2.
4.1 Dynamic angle of repose
For the binary mixtures of the elongated particles, the average dynamic angle of repose
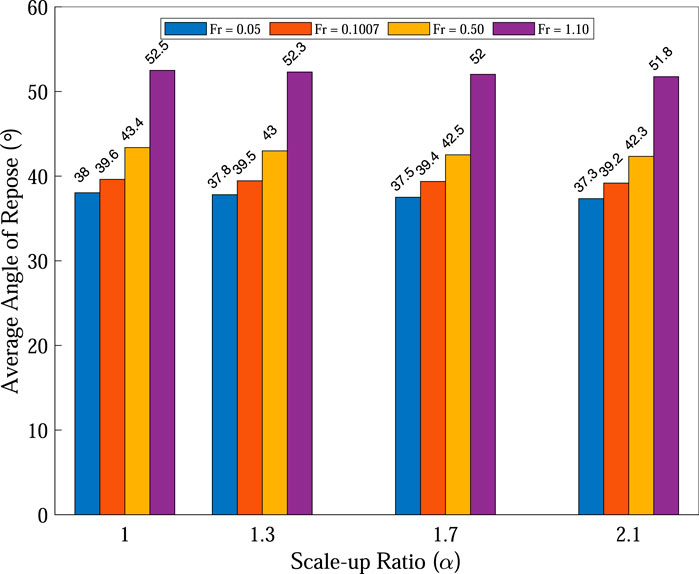
Figure 10. Average dynamic angle of repose of the binary mixtures at different scale-up ratios
4.2 Particle velocities
Figure 8a shows the relationship between average particle velocity, scale-up ratio, and Froude number for different drums. It can be observed that the particle velocities improve with the increase in Froude number at a constant drum scale-up ratio. It’s due to the larger speed of the drum because the dominancy of centrifugal forces becomes higher than the inertial forces, and particles are pushed to the drum’s wall easily which enhances the particle’s velocity inside the drum. Furthermore, the average velocity of particles increases with the scale-up ratio, it’s because of drum diameter. Figure 8b shows the comparison plot between DEM simulated velocities and the Fitted velocities of the particles inside the different drums at different Froude number using the following power function:
For the binary mixtures, the average particle velocity
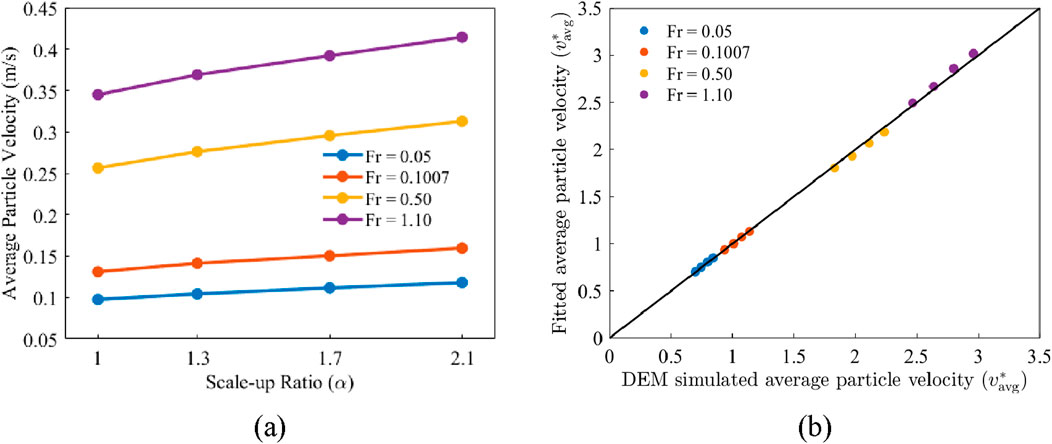
Figure 11. (a) Average particle velocity versus scale-up ratio
The parameters in Equation 19 are close to those in Equation 15, indicating that the monodisperse and binary systems have the similar scale-up behaviors of the average particle velocities. A very agreement is obtained between the predictions by Equation 19 and the DEM results, as shown in Figure 11b.
4.3 Contact forces on the particles
As shown in Figure 12a, the average contact force increases with increasing scale-up ratio
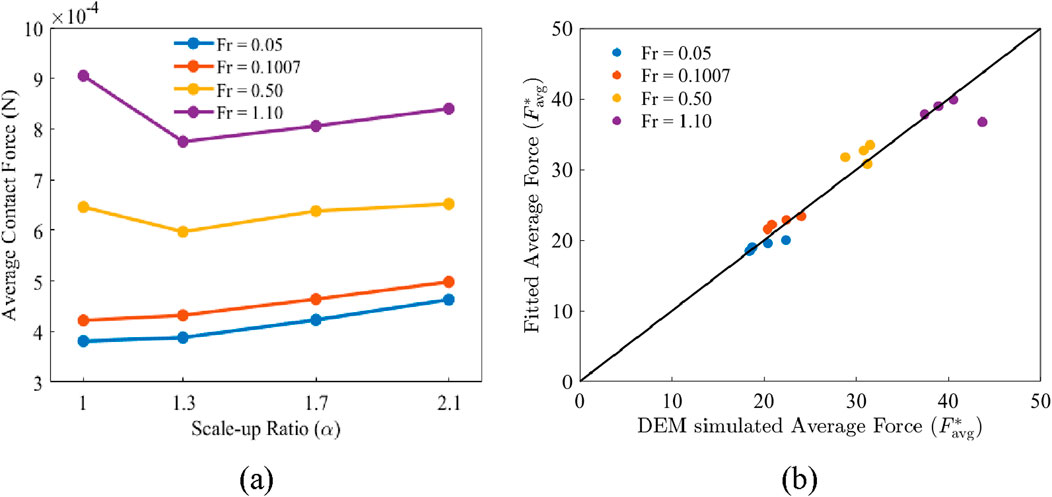
Figure 12. (a) Average contact force versus scale-up ratio
Some predictions of the average contact forces by Equation 20 show significant deviations from the DEM results (Figure 12b), as the deviations originate from the non-monotonic changes of the contact force with increasing scale-up ratio at the high Froude numbers.
4.4 Mixing performance
In the binary mixtures, the longer particles with AR = 5 are colored in red and the shorter particles with AR = 2 in blue. The flow and mixing processes of the binary mixtures in the four different drums are shown in Figure 13. From the perspective of the radial view (the view direction parallel to the axis of the cylindrical drum), similar piling and mixture patterns are observed in the four drums. From the axial view (the view direction perpendicular to the axis of the cylindrical drum), the mixing is uniform in the axial direction of the Drum B, and such uniform mixing in the axial direction is observed in all the four drums. The radial and angular mixing is dominant in the present rotating drums.
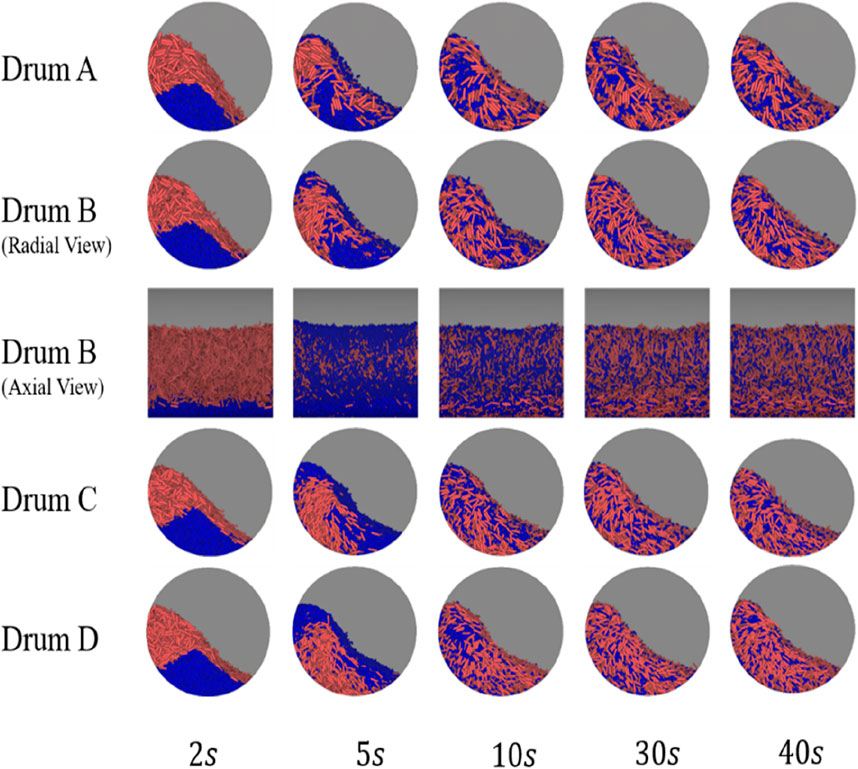
Figure 13. Snapshots of temporal evolution of mixing patterns of binary mixtures in different drums at Fr = 0.05.
In the circulating flows of the binary mixtures, the Lacey mixing index L increases over time before it reaches and fluctuates around an upper limit, as shown in Figure 14. The time duration required to achieve the upper limit decreases with increasing Froude number Fr. It is also observed that the upper limit of L increases with Fr for the binary mixtures (Figure 14), which is different from the monodisperse systems for which the upper limit of L is independent on Fr (Figure 8). The eventual mixing index L of the monodisperse particles is very close to 1, while the eventual L of the binary mixtures at Fr = 0.05 is only about 0.8. Thus, the particle size difference in the binary mixtures prevents the mixing of the two particle components, and the mixing can be improved by increasing Fr (i.e. rotational speed for a given drum).
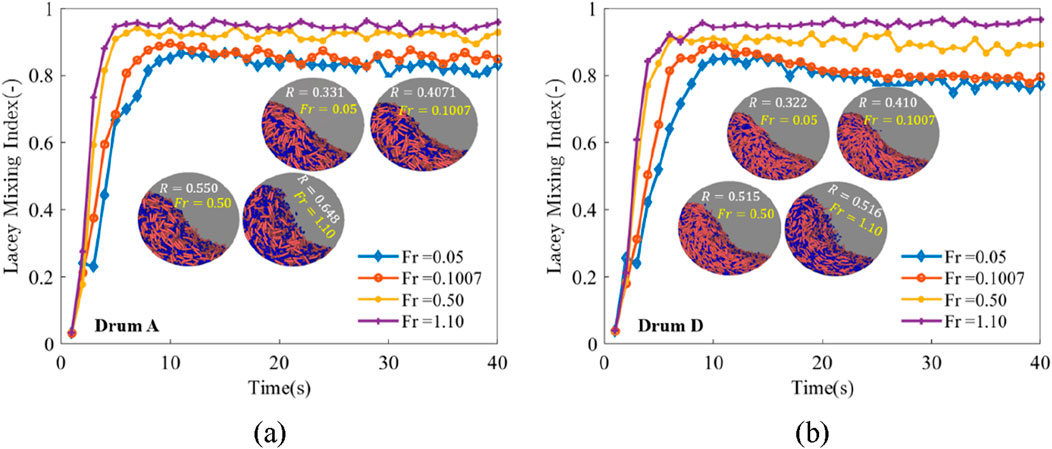
Figure 14. Time evolution of Lacey mixing index L at various Froude numbers Fr for the binary mixtures in (a) Drum A and (b) Drum D. The inset images show the mixed particle patterns at t = 40 s and the mixing rates R for the four Froude numbers.
Like the monodisperse particles (Figure 9a), for the binary mixtures (Figure 15a), the mixing rate R is nearly independent on the scale-up ratio
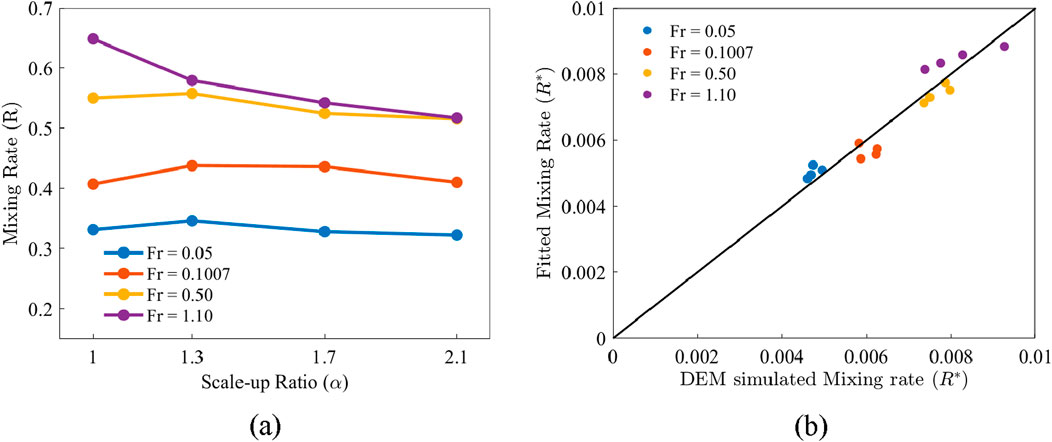
Figure 15. (a) Mixing rate versus scale-up ratio
Compared to the correlation of the monodisperse system (Equation 18), the magnitude of the exponent above
5 Conclusion
In this work, flow and mixing of elongated particles in rotating drums is numerically investigated using the Discrete Element Method (DEM). The scale-up behaviors of dynamic angle of repose, particle velocity, contact force, and mixing ratio have been examined by adopting four drums of different sizes. Similarities and differences in the dynamics, mixing, and scale-up rules between monodisperse and binary particle systems are discussed. Some conclusions are drawn as follows.
• The dynamic angle of repose is determined mainly by Froude number Fr while it is insensitive to scale-up ratio α for both the monodisperse and binary systems of elongated particles.
• The scaling correlations based on Fr and α are significantly different between the spherical particles and elongated rod-like particles, indicating that particle shape has an impact on the scaling behavior.
• Average particle velocity increases as Froude number Fr and/or scale-up ratio α increase for both the monodisperse and binary systems, due to the increase in the boundary velocity of the drum.
• With increasing scale-up ratio α, the average contact force increases for the monodisperse systems while it changes non-monotonically at large Froude numbers for the binary systems.
• The mixing rate of the particles is significantly promoted by increasing Fr. The mixing rate maintains constant at small Fr and it decreases slowly with increasing α at large Fr, as it takes longer time for the particles to travel a longer distance to mix well globally in larger drums.
• The mixing index eventually achieves the same high level at various Froude numbers Fr for the monodisperse systems, while the final mixing indices are smaller at smaller Fr for the binary systems. In addition, it found that the mixing rate of the binary mixtures has a stronger dependence on the scale-up ratio α than the monodisperse systems.
This work provides some new results and primary insights on scale-up behaviors of flow and mixing of elongated particles. It is expected to be useful in the design of handling of non-spherical particles in rotating drums. In order to achieve a more comprehensive understanding of the scale-up rules, much larger scale-up ratios should be considered in the future work.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
JS: Visualization, Methodology, Formal Analysis, Writing – review and editing, Writing – original draft, Software, Investigation. NN: Methodology, Visualization, Investigation, Validation, Software, Formal Analysis, Writing – original draft, Writing – review and editing. HF: Investigation, Visualization, Writing – review and editing, Formal Analysis. GL: Writing – review and editing, Formal Analysis, Investigation. ML: Writing – review and editing, Investigation, Formal Analysis. YG: Writing – review and editing, Methodology, Supervision, Formal Analysis. JL: Project administration, Supervision, Formal Analysis, Writing – review and editing. JT: Formal Analysis, Project administration, Methodology, Writing – review and editing, Supervision, Investigation.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
Authors JS, GL, and JT were employed by China Tobacco Zhejiang Industrial Co., Ltd. Authors HF and ML were employed by China Tobacco Zhejiang Industrial Co. Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alizadeh, E., Dubé, O., Bertrand, F., and Chaouki, J. (2013). Characterization of mixing and size segregation in a rotating drum by a particle tracking method. AIChE J. 59, 1894–1905. doi:10.1002/aic.13982
Ardalani, E., Borghard, W. G., Glasser, B. J., and Cuitiño, A. M. (2023). Scale-up of heat transfer in a rotary drum equipped with baffles. Powder Technol. 429, 118879. doi:10.1016/j.powtec.2023.118879
Beaulieu, C., Vidal, D., Niyonkuru, C., Wachs, A., Chaouki, J., and Bertrand, F. (2021). Effect of particle angularity on flow regime transitions and segregation of bidisperse blends in a rotating drum. Comput. Part. Mech. 9, 443–463. doi:10.1007/s40571-021-00421-1
Bhalode, P., and Ierapetritou, M. (2020). A review of existing mixing indices in solid-based continuous blending operations. Powder Technol. 373, 195–209. doi:10.1016/j.powtec.2020.06.043
Chen, G., Mei, Y., Zhang, Y., and Jin, B. (2024). DEM investigation on flow regime transition of cylindrical particle in a rotating drum. 22, 893, 912. doi:10.1515/ijcre-2024-0029
Cui, X., Dai, J., Xu, H., and Gao, X. (2023). SuperDEM simulation and experiment validation of nonspherical particles flows in a rotating drum. Ind. Eng. Chem. Res. 62, 6525–6535. doi:10.1021/acs.iecr.3c00919
Ding, Y. L., Forster, R. N., Seville, J. P. K., and Parker, D. J. (2001). Scaling relationships for rotating drums. Chem. Eng. Sci. 56, 3737–3750. doi:10.1016/S0009-2509(01)00092-6
Dong, T., Yang, S., and Wang, S. (2024). Super-quadric DEM study of cylindrical particle behaviours in a rotating drum. Powder Technol. 437, 119511. doi:10.1016/j.powtec.2024.119511
Figueroa, I., Vargas, W. L., and McCarthy, J. J. (2010). Mixing and heat conduction in rotating tumblers. Chem. Eng. Sci. 65, 1045–1054. doi:10.1016/j.ces.2009.09.058
Govender, I. (2016). Granular flows in rotating drums: a rheological perspective. Miner. Eng. 92, 168–175. doi:10.1016/j.mineng.2016.03.021
Gui, N., Yan, J., Xu, W., Ge, L., Wu, D., Ji, Z., et al. (2013). DEM simulation and analysis of particle mixing and heat conduction in a rotating drum. Chem. Eng. Sci. 97, 225–234. doi:10.1016/j.ces.2013.04.005
Han, J., Shen, K., Guo, Y., Xiong, H., and Lin, J. (2023). Discrete element simulations of flexible ribbon-like particles. Powder Technol. 429, 118950. doi:10.1016/j.powtec.2023.118950
He, J., Wang, Y., Yang, L., Zheng, Q., Xu, J., Liu, S., et al. (2024). Similarity analysis of size-induced segregation and flow behavior during the scaling up process of rotating drums. Powder Technol. 448, 120252. doi:10.1016/j.powtec.2024.120252
He, S., Gan, J., Pinson, D., Yu, A., and Zhou, Z. (2020). A discrete element method study of monodisperse mixing of ellipsoidal particles in a rotating drum. Ind. Eng. Chem. Res. 59, 12458–12470. doi:10.1021/acs.iecr.9b06623
Herman, A. P., Gan, J., and Yu, A. (2021). GPU-based DEM simulation for scale-up of bladed mixers. Powder Technol. 382, 300–317. doi:10.1016/j.powtec.2020.12.045
Herman, A. P., Gan, J., Zhou, Z., and Yu, A. (2022a). Discrete particle simulation for mixing of granular materials in ribbon mixers: a scale-up study. Powder Technol. 400, 117222. doi:10.1016/j.powtec.2022.117222
Herman, A. P., Zhou, Z., Gan, J., and Yu, A. (2022b). Scaling up studies for mixing of granular materials in rotating drums. Powder Technol. 403, 117408. doi:10.1016/j.powtec.2022.117408
Jiang, C., An, X., Li, M., Wu, Y., Gou, D., and Wu, Y. (2023). DEM modelling and analysis of the mixing characteristics of sphere-cylinder granular mixture in a rotating drum. Powder Technol. 426, 118653. doi:10.1016/j.powtec.2023.118653
Kodam, M., Curtis, J., Hancock, B., and Wassgren, C. (2012). Discrete element method modeling of bi-convex pharmaceutical tablets: contact detection algorithms and validation. Chem. Eng. Sci. 69, 587–601. doi:10.1016/j.ces.2011.11.011
Kumar, S., Khatoon, S., Dubey, P., Yogi, J., and Anand, A. (2024). Shape-dependent radial segregation in rotating drum: insights from DEM simulations. Powder Technol. 432, 119134. doi:10.1016/j.powtec.2023.119134
Lacey, P. M. C. (1954). Developments in the theory of particle mixing. J. Appl. Chem. 4, 257–268. doi:10.1002/jctb.5010040504
Li, L., Kemp, I., and Palmer, M. (2020). A DEM-based mechanistic model for scale-up of industrial tablet coating processes. Powder Technol. 364, 698–707. doi:10.1016/j.powtec.2020.01.087
Li, M., Wu, Y., Qian, Y., An, X., and Li, H. (2021). DEM simulation on mixing characteristics and macroscopic/microscopic flow behaviors of different-shaped sphero-cylinders in a rotating drum. Ind. Eng. Chem. Res. 60, 8874–8887. doi:10.1021/acs.iecr.1c00962
Li, Y., You, Y., Gou, D., Yu, A., and Yang, R. (2022). A DEM based scale-up model for tumbling ball mills. Powder Technol. 409, 117854. doi:10.1016/j.powtec.2022.117854
Liu, Z., Ma, H., Zhou, L., Xu, C., Zhang, X., and Zhao, Y. (2024). DEM-DDM investigation of the intra-tablet coating uniformity for tablets with different shapes. Powder Technol. 438, 119666. doi:10.1016/j.powtec.2024.119666
Ma, H., Zhou, L., Liu, Z., Chen, M., Xia, X., and Zhao, Y. (2022). A review of recent development for the CFD-DEM investigations of non-spherical particles. Powder Technol. 412, 117972. doi:10.1016/j.powtec.2022.117972
Miao, Q., Cao, Y., Zhu, W., Huang, P., Huang, L., Yu, A., et al. (2024). Segregation flow behavior of polydisperse particle mixture with skewed distribution in a rotating drum. Powder Technol. 444, 120041. doi:10.1016/j.powtec.2024.120041
Norouzi, H. R., Zarghami, R., and Mostoufi, N. (2015). Insights into the granular flow in rotating drums. Chem. Eng. Res. Des. 102, 12–25. doi:10.1016/j.cherd.2015.06.010
Orozco, L. F., Nguyen, D.-H., Delenne, J.-Y., Sornay, P., and Radjai, F. (2020). Discrete-element simulations of comminution in rotating drums: effects of grinding media. Powder Technol. 362, 157–167. doi:10.1016/j.powtec.2019.12.014
Portillo, P. M., Ierapetritou, M., Tomassone, S., Mc Dade, C., Clancy, D., Avontuur, P. P. C., et al. (2008). Quality by design methodology for development and scale-up of batch mixing processes. J. Pharm. Innovation 3, 258–270. doi:10.1007/s12247-008-9048-9
Rudge, J. F., Holness, M. B., and Smith, G. C. (2008). Quantitative textural analysis of packings of elongate crystals. Contrib. Mineral. Petrol 156, 413–429. doi:10.1007/s00410-008-0293-1
Trojosky, M. (2019). Rotary drums for efficient drying and cooling. Dry. Technol. 37, 632–651. doi:10.1080/07373937.2018.1552597
Vu, D. C., Amarsid, L., Delenne, J.-Y., Richefeu, V., and Radjai, F. (2024). Rheology and scaling behavior of polyhedral particle flows in rotating drums. Powder Technol. 434, 119338. doi:10.1016/j.powtec.2023.119338
Xu, G., Zhang, Y., Yang, X., Chen, G., and Jin, B. (2023). Effect of drum structure on particle mixing behavior based on DEM method. Particuology 74, 74–91. doi:10.1016/j.partic.2022.05.008
Yang, R. Y., Yu, A. B., McElroy, L., and Bao, J. (2008). Numerical simulation of particle dynamics in different flow regimes in a rotating drum. Powder Technol. 188, 170–177. doi:10.1016/j.powtec.2008.04.081
Yang, S., Zhang, L., Luo, K., and Chew, J. W. (2017). DEM study of the size-induced segregation dynamics of a ternary-size granular mixture in the rolling-regime rotating drum. Phys. Fluids 29, 123301. doi:10.1063/1.5008297
Yu, F., Zhang, S., Zhou, G., Zhang, Y., and Ge, W. (2018). Geometrically exact discrete-element-method (DEM) simulation on the flow and mixing of sphero-cylinders in horizontal drums. Powder Technol. 336, 415–425. doi:10.1016/j.powtec.2018.05.040
Yu, F., Zhang, Y., Zheng, Y., Han, M., Chen, G., and Yao, Z. (2020). Comparison of different effective diameter calculating methods for sphero-cylinders by geometrically exact DEM simulations. Powder Technol. 360, 1092–1101. doi:10.1016/j.powtec.2019.10.097
Keywords: elongated particle, flow, mixing, scale-up, DEM
Citation: Song J, Naeem N, Fan H, Li G, Li M, Guo Y, Lin J and Tie J (2025) Flow and mixing of elongated particles in rotating drums of different sizes. Front. Chem. Eng. 7:1636010. doi: 10.3389/fceng.2025.1636010
Received: 27 May 2025; Accepted: 20 June 2025;
Published: 04 July 2025.
Edited by:
Shiliang Yang, Kunming University of Science and Technology, ChinaReviewed by:
Yanjie Li, Beijing Forestry University, ChinaYuanhe Yue, Hebi University of Technology, China
Copyright © 2025 Song, Naeem, Fan, Li, Li, Guo, Lin and Tie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Numan Naeem, bnVtYW4ubmFlZW1Aemp1LmVkdS5jbg==; Jinxin Tie, dGllamlueGluQHpqdG9iYWNjby5jb20=; Yu Guo, eWd1b0B6anUuZWR1LmNu
 Jinhua Song1
Jinhua Song1 Numan Naeem
Numan Naeem Yu Guo
Yu Guo Jianzhong Lin
Jianzhong Lin