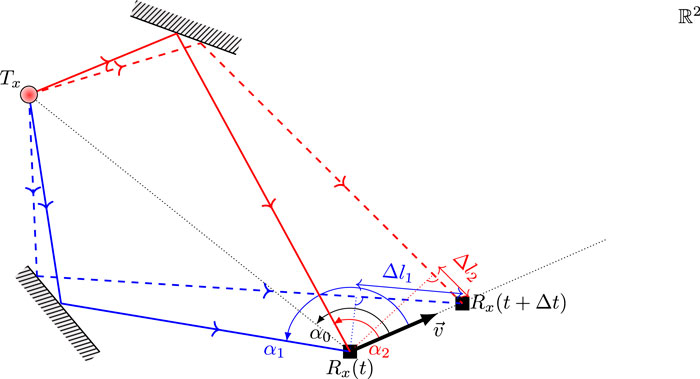
- Department of Telecommunications, Faculty of Electrical Engineering, University of Sarajevo, Sarajevo, Bosnia and Herzegovina
This paper introduces a novel statistical simulator designed to model propagation in two-way diffuse power (TWDP) fading channels. The simulator employs two zero-mean stochastic sinusoids to simulate specular components, while a sum of sinusoids is used to model the diffuse one. Using the developed simulator, the autocorrelation and cross-correlation functions of the quadrature components, as well as the autocorrelation of the complex and squared envelope, are derived for the first time in literature for channels experiencing TWDP fading. The statistical properties of the proposed simulator are thoroughly validated through extensive simulations, which closely align with the theoretical results.
1 Introduction
Mobile radio channel simulators are widely used as cost-effective alternatives to field trials, providing reproducible solutions for rapid performance evaluation by accurately replicating the statistical properties of real-world communication channels Xiao et al. (2006). Consequently, numerous small-scale fading simulators have been proposed to date for modeling various channel conditions, typically relying on filtering or sum-of-sinusoids (SoS) approaches, which are designed to capture both the first- and second-order statistics of signals following specific characteristics.
Among these, the earliest SoS simulators were designed for frequency non-selective Rayleigh channels Jakes and Cox (1994); Pop and Beaulieu (2001); Zheng and Xiao (2002); Xiao et al. (2006); Alimohammad et al. (2009); Wang et al. (2012). They are commonly used to model non-line-of-sight (NLOS) propagation conditions, where no strong specular components exist between the transmitter and the receiver. As a result, such signals consist solely of a diffuse component composed of many low-power scattered waves. Consequentially, corresponding small-scale fading simulators are created by representing the received signal as a superposition of a finite number of sinusoids, mostly with random amplitudes, frequencies, and/or phases. Thereby, to capture the statistical properties of signals received under the described conditions, Clark introduced a mathematical model assuming that the receiver receives
The simulators mentioned above are also employed to model low-power scattered waves within Rician simulators, which are designed to simulate channels where the received signal consists of one strong specular component (typically line-of-sight, LoS) alongside a diffuse component. As a result, many Rician SoS simulators have been proposed to date, each exhibiting more or less desired statistical properties and specific computational efficiencies Xiao et al. (2006); Alimohammad et al. (2009); Wang et al. (2012).
However, to date, little attention has been given to the development of small-scale fading simulators that account for more than one dominant specular component, such as those required for two-wave with diffuse power (TWDP) fading channels. In these channels, the received signal contains two strong specular components in addition to numerous low-power scattered waves, which can lead to unique propagation characteristics including a bimodal distributed envelope (Maric et al., 2021; Figure 4) and phase (Maric and Njemcevic, 2025; Figure 4) characteristics and, under the certain conditions, performance worse than those observed in Rayleigh channels (Maric et al., 2021; Figure 5), which cannot be modeled using the existing simulators.
These, propagation conditions have been empirically validated in a variety of emerging wireless communication scenarios. For instance, TWDP fading has been observed in mmWave 5G networks utilizing directional antennas or antenna arrays Rappaport et al. (2015), as well as in wireless sensor networks operating in cavity environments Frolik (2007). Furthermore, ray-tracing simulations have confirmed the suitability of the TWDP model for characterizing outdoor mmWave propagation in train-to-infrastructure Zöchmann et al. (2019a) and vehicle-to-vehicle Zöchmann et al. (2019b) communication scenarios, particularly at 60 GHz in urban environments. Indoor mmWave measurement campaigns Zöchmann et al. (2019) have also demonstrated that the TWDP model accurately captures indoor propagation behavior. Additionally, TWDP fading has been shown to provide the best fit for near-body mmWave communication channels, both in the front and back body regions Mavridis et al. (2015). Moreover, similar fading conditions have been reported in static sensor networks placed within cavity environments, including buses, aircrafts Frolik (2007), and even inside large transport helicopters Frolik (2008). Accordingly, it is desirable to create a flexible and accurate channel simulator that can be effectively used for performance evaluation and validation of analytical expressions, derived for various designs of digital communication systems operating over the channels with TWDP fading.
Consequently, in this paper, the SoS-based simulator for modeling propagation in TWDP channels is proposed, being primary focused on generating correlated signal samples of TWDP multipath fading process. In the proposed simulator, the specular components are modeled as zero-mean stochastic sinusoids with pre-determined angles of arrival and random initial phases, while the diffuse component is simulated using the NLOS model proposed in Xiao et al. (2006). The simulator is used to derive the autocorrelation and cross-correlation functions of the quadrature components, as well as the autocorrelation of the complex envelope and its square, for signals propagating in TWDP channels. The statistical properties of the proposed simulator are compared with those calculated for the reference model, demonstrating excellent agreement between them.
Accordingly, we developed a SoS simulator capable of generating realistic TWDP fading waveforms, enabling the accurate evaluation of second-order statistics such as the level crossing rate (LCR) and average fade duration (AFD), which can be utilized for the design and optimization of channel coding schemes, interleaving strategies, and diversity techniques in channels exhibiting TWDP fading.
2 The reference TWDP channel model
TWDP model assumes that the normalized envelope of the received signal consists of two specular and diffuse components, so the normalized TWDP signal can be expressed as Durgin et al. (2002):
where
In order to simulate the above defined TWDP fading process, let’s assume communication scenario in which the receiver moves with constant velocity vector
Due to the motion of the receiver, the instantaneous phase of each specular component’s phase,
where the angle of arrival
where
where the uniformity of the specular components’ phases
Considering the aforementioned and the fact that the specular and scattered components are all zero-mean with mutually independent initial phases, the autocorrelation of the TWDP complex envelope’s in-phase component,
where
where
where
So, in case when ideal Clark’s model is used to model diffuse component, when
where
Note that the derived expressions represent the statistical correlation properties of non-realizable stochastic reference model for the TWDP channel (since they are derived for
3 The TWDP channel simulator
Based on the described reference model, the TWDP channel simulator is constructed following previously derived assumptions about the characteristics of the specular components. However, to simulate diffuse component using finite number of sinusoids, a detailed literature overview is performed, reveling the existence of many different models Jakes and Cox (1994); Pop and Beaulieu (2001); Zheng and Xiao (2002); Xiao et al. (2006); Alimohammad et al. (2009); Wang et al. (2012), etc. Among these, the model proposed by (Xiao et al., 2006, Equations 6a-6c, 7) (where
where
Obviously, the autocorrelation and cross-correlation functions given by Equation 10a; Equation 10b; Equation 10c do not depend on the number of sinusoids
It is important to note that the proposed simulator exhibits several key characteristics. First and foremost, it is wide-sense stationary (WSS), as its mean value remains constant and its autocorrelation function depends solely on the time difference
In addition, the proposed simulation model can be directly applied to generate uncorrelated fading waveforms for scenarios involving frequency-selective TWDP fading channels, MIMO systems, and diversity combining techniques, since
where
4 Numerical results
Verification of the proposed TWDP fading simulator is performed by comparing simulation results for finite
Accordingly, the simulations are conducted for many different combinations of TWDP fading parameters
4.1 Evaluation of correlation properties
Although extensive simulations are performed to evaluate TWDP correlation statistics, due to the space limitations, only simulation results obtained for the real and imaginary part of the autocorrelation of the complex envelope, together with the autocorrelation function of the envelope square, are shown in Figures 2a–c.
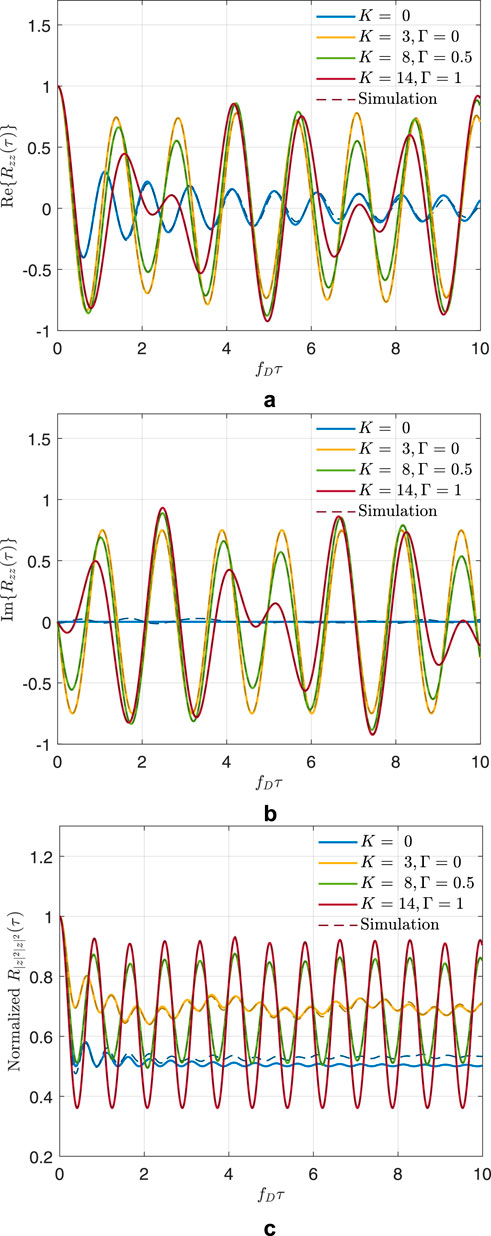
Figure 2. Correlation properties of TWDP complex envelope process. (α1=π/4, α2=2π/3). (a) The real part of the autocorrelation function of TWDP complex envelope. (b) The imaginary part of the autocorrelation function of TWDP complex envelope. (c) The autocorrelation function of TWDP squared envelope.
The corresponding statistics of the TWDP reference model given by Equations 9c, 9d are also included in the figures for comparison purpose, showing perfect match between simulated and theoretically obtained results in all cases except for the autocorrelation of the squared envelope in channel undergoing Rayleigh fading, as expected. Namely, in case when the strength of the diffuse component is large within the overall signal strength (i.e., when
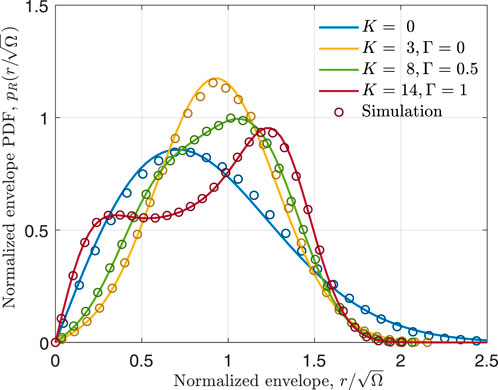
4.2 Evaluation of envelope PDF
Figure 3 shows the fading envelope PDF obtained using the proposed TWDP simulator with the specified set of simulation parameters, along with the results from the analytical expression for the TWDP envelope PDF given in Maric et al. (2021). Although better agreement between the simulated and theoretical results can be achieved by increasing
4.3 Evaluation of LCR
The simulation results of the normalized level crossing rate (LCR) for the proposed TWDP simulator are shown in Figures 4a,b. In Figure 4a, the results obtained using the proposed simulator are presented alongside those calculated using the analytical expression (Rao et al., 2014, Equation 36) derived for specific combination of AoAs in TWDP channels (i.e., when
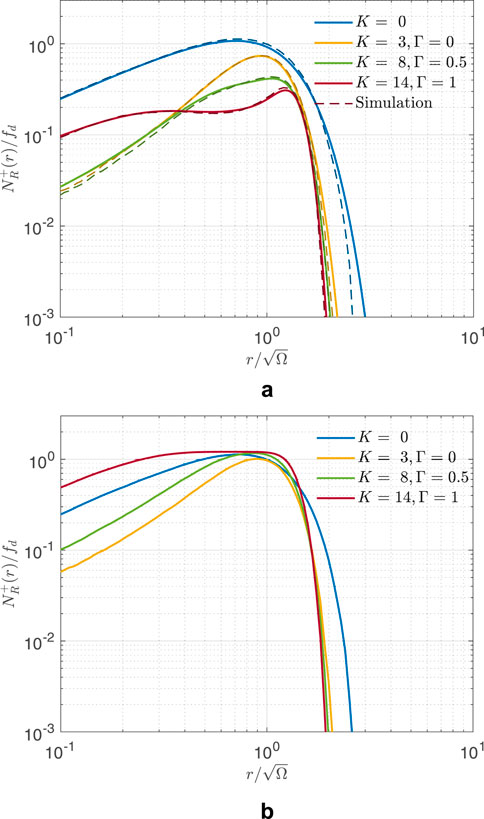
Figure 4. TWDP envelope LCR for different channel setups. (a) TWDP LCR (α1=π/2, α2=-π/2). (b) Simulated TWDP LCR (α1=π/4, α2=2π/3).
For demonstration purpose, LCRs obtained using proposed simulator are plotted in Figure 4b, for different TWDP parameters and arbitrary AoAs, showing substantially different behaviors compared to the perpendicular cases presented in Figure 4a.
5 Conclusion
In this paper, the SoS-based TWDP channel simulator is proposed, enabling us to simulate Rayleigh, better-than-Rayleigh and worse-than-Rayleigh fading conditions. The simulator is constructed by using two zero-mean stochastic sinusoid with pre-selected Doppler frequencies and random initial phases, while the diffuse component is modeled using one of the existing Rayleigh channel simulators. For the described channel, analytical expressions for the autocorrelation and cross-correlation functions of quadrature components, as well as the autocorrelation of the complex envelope and its square, are first derived for the reference TWDP model. These expressions are then compared with those obtained using the proposed simulator for various combinations of channel and environmental parameters, demonstrating excellent agreement between them. Additionally, the proposed simulator is used to obtain diagrams of the envelope PDF and the LCR, which closely match those calculated using the existing analytical expressions. Since Rayleigh and Rician models are spatial cases of TWDP model itself, the results obtained using the proposed simulator (for specific sets of TWDP parameters) are finally compared to those from the literature obtained using the existing Rician/Rayleigh simulators, also showing the perfect match between them.
Accordingly, for the first time in the literature, a simulator is provided for accurate evaluation of first- and second-order statistics of signals propagating in channels with TWDP fading. As such, it can serve as a valuable tool for optimizing the design of interleaver/deinterleaver and channel coding/decoding units in these channels, thereby contributing to the overall enhancement of wireless communication system performance in such environments.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
AM: Conceptualization, Formal Analysis, Software, Writing – original draft, Writing – review and editing. PN: Formal analysis, Software, Conceptualization, Writing – original draft, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was founded by Ministry of Science, Higher Education, and Youth of Canton Sarajevo, Bosnia and Herzegovina, under the grant 27-02-35-33087-23/24 (ASPK5GMM).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alimohammad, A., Fard, S., Cockburn, B., and Schlegel, C. (2009). Compact Rayleigh and Rician fading simulator based on random walk processes. Commun. IET 3, 1333–1342. doi:10.1049/iet-com.2008.0297
Clarke, R. H. (1968). A statistical theory of mobile-radio reception. Bell Syst. Tech. J. 47, 957–1000. doi:10.1002/j.1538-7305.1968.tb00069.x
Wolfram Research (2025). Wolfram function site. Available online at: https://functions.wolfram.com.
Durgin, G., Rappaport, T., and de Wolf, D. (2002). New analytical models and probability density functions for fading in wireless communications. IEEE Trans. Commun. 50, 1005–1015. doi:10.1109/TCOMM.2002.1010620
Frolik, J. (2007). A case for considering hyper-Rayleigh fading channels. IEEE Trans. Wirel. Commun. 6, 1235–1239. doi:10.1109/twc.2007.348319
Frolik, J. (2008). On appropriate models for characterizing hyper-Rayleigh fading. IEEE Trans. Wirel. Commun. 7, 5202–5207. doi:10.1109/t-wc.2008.070968
Maric, A., Kaljic, E., and Njemcevic, P. (2021). An alternative statistical characterization of TWDP fading model. Sensors 21, 7513. doi:10.3390/s21227513
Maric, A., and Njemcevic, P. (2025). On the conditional phase distribution of the TWDP multipath fading process. arXiv. doi:10.48550/arXiv.2502.03385
Mavridis, T., Petrillo, L., Sarrazin, J., Benlarbi-Delaï, A., and De Doncker, P. (2015). Near-body shadowing analysis at 60 GHz. IEEE Trans. Antennas Propag. 63, 4505–4511. doi:10.1109/tap.2015.2456984
Patel, C., Stuber, G., and Pratt, T. (2005). Comparative analysis of statistical models for the simulation of Rayleigh faded cellular channels. IEEE Trans. Commun. 53, 1017–1026. doi:10.1109/TCOMM.2005.849735
Pätzold, M., and Hogstad, B. (2006). Classes of sum-of-sinusoids Rayleigh fading channel simulators and their stationary and ergodic properties-Part I. WSEAS Trans. Math. 5, 222–230.
Pätzold, M., and Laue, F. (1998). Statistical properties of Jakes’ fading channel simulator. VTC ’98. 48th IEEE Vehicular Technology Conference 2, 712–718. doi:10.1109/VETEC.1998.683675
Pop, M., and Beaulieu, N. (2001). Limitations of sum-of-sinusoids fading channel simulators. IEEE Trans. Commun. 49, 699–708. doi:10.1109/26.917776
Rao, M., Lopez-Martinez, F. J., and Goldsmith, A. (2014). “Statistics and system performance metrics for the two wave with diffuse power fading model,” in 2014 48th annual conference on information sciences and systems (CISS), 1–6. doi:10.1109/CISS.2014.6814106
Rappaport, T., Heath, R., Daniels, R., and Murdock, J. (2015). Millimeter wave wireless communications. Upper Saddle River, NJ, USA: Prentice Hall.
Skima, M. A., Ghariani, H., and Lahiani, M. (2014). A multi-criteria comparative analysis of different Rayleigh fading channel simulators. AEU - Int. J. Electron. Commun. 68, 550–560. doi:10.1016/j.aeue.2014.01.001
Wang, J., Ma, X., Teng, J., and Cui, Y. (2012). Efficient and accurate simulator for Rayleigh and Rician fading, Transactions of Tianjin University, 18, 243–247. doi:10.1007/s12209-012-1888-1
Xiao, C., Zheng, Y. R., and Beaulieu, N. C. (2006). Novel sum-of-sinusoids simulation models for Rayleigh and Rician fading channels. IEEE Trans. Wirel. Commun. 5, 3667–3679. doi:10.1109/TWC.2006.256990
Zheng, Y., and Xiao, C. (2002). Improved models for the generation of multiple uncorrelated Rayleigh fading waveforms. IEEE Commun. Lett. 6, 256–258. doi:10.1109/LCOMM.2002.1010873
Zöchmann, E., Blumenstein, J., Marsalek, R., Rupp, M., and Guan, K. (2019a). “Parsimonious channel models for millimeter wave railway communications,” in 2019 IEEE Wireless Communications and Networking Conference (WCNC), 1–6. doi:10.1109/WCNC.2019.8885923
Zöchmann, E., Caban, S., Mecklenbräuker, C. F., Pratschner, S., Lerch, M., Schwarz, S., et al. (2019). Better than Rician: modelling millimetre wave channels as two-wave with diffuse power. EURASIP J. Wirel. Commun. Netw., 2019. doi:10.1186/s13638-018-1336-6
Keywords: TWDP fading, sum-of-sinusoids (SOS), channel simulation, level crossing rate (LCR), wireless channel
Citation: Maric A and Njemcevic P (2025) On the simulation and correlation properties of TWDP fading process. Front. Commun. Netw. 6:1587497. doi: 10.3389/frcmn.2025.1587497
Received: 04 March 2025; Accepted: 30 April 2025;
Published: 02 July 2025.
Edited by:
Jules M. Moualeu, University of the Witwatersrand, South AfricaReviewed by:
Seong Ki Yoo, Coventry University, United KingdomAhmad Bazzi, New York University Abu Dhabi, United Arab Emirates
Copyright © 2025 Maric and Njemcevic. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Almir Maric, YWxtaXIubWFyaWNAZXRmLnVuc2EuYmE=
 Almir Maric
Almir Maric Pamela Njemcevic
Pamela Njemcevic