Graph-theoretic approach to mobility-aware frequency assignment via deep Q-learning

Due to the increasing demand for frequency resources in wireless networks, efficient frequency assignment has become a critical challenge. Unlike conventional cellular systems, where frequency allocation is centrally managed by a base station, device-to-device (D2D) communication, especially in mission-critical scenarios, introduces additional complexity due to its decentralized nature. In this study, we model a D2D communication network as a graph and formulate the frequency assignment task as a graph coloring problem. While previous research has primarily relied on heuristic or artificial intelligence (AI)-based methods to determine node ordering, we propose a novel framework that integrates deep Q-learning (DQN) with graph neural networks (GNNs) to enhance assignment efficiency. To ensure interference-free operation, we explicitly incorporate net filter discrimination (NFD), which captures realistic interference constraints. Unlike previous AI-based approaches that focus solely on minimizing the number of assigned frequency blocks, our method jointly optimizes both the total frequency span and the ordering cost. Extensive simulations show that the proposed approach significantly outperforms greedy baselines, particularly in complex and dynamic environments. Furthermore, by incorporating device mobility into the simulations, we validate the robustness and adaptability of the proposed framework. These results underscore the potential of DQN-based methods to enable scalable and reliable frequency assignment in mission-critical wireless networks.

1 Introduction

1.1 Motivation of the frequency assignment in wireless networks

Modern communication systems rely heavily on the radio-frequency (RF) spectrum, which is a fundamentally limited resource. The rapid growth of users and applications continues to intensify the competition for available bands, underscoring the need for more efficient and equitable spectrum assignment strategies. Spectrum management operates within a hierarchical framework: the International Telecommunication Union (ITU) oversees the harmonization and coordination of frequency usage across nations. At the national level, governments allocate spectrum primarily through auctions or direct administrative licensing. At the user level, certain unlicensed bands—such as those supporting Wi-Fi and Bluetooth—are designated for open public use without the need for a license, as recognized by the Cellular Telecommunications Industry Association (CTIA).

When considering sixth-generation (6G) communication systems, the demand for efficient frequency and adaptive frequency assignment strategies becomes even more critical as these systems aim to support unprecedented levels of connectivity, data throughput, and reliability. In particular, the upper mid-band spectrum—ranging from 7 to 24 GHz—has emerged as a key target due to its potential to support both a wide bandwidth and favorable propagation conditions. However, many bands in this range are already occupied by incumbent services such as fixed satellite and radar systems, which complicate coexistence and spectrum sharing. Therefore, developing efficient and interference-aware spectrum assignment mechanisms is not merely desirable but essential—particularly in mission-critical or time-sensitive applications where coexistence with incumbent users must be ensured without compromising system performance. To reflect real-world spectrum challenges, our study models the frequency assignment within the 7 GHz band, where coexistence with existing users is becoming a greater concern.

In this context, numerous studies have aimed to enhance the efficiency of frequency assignment (Yaipairoj and Harmantzis, 2006; Hale, 1980; Yilmaz et al., 2017; Kumar and Milleth, 2018). For example, Yaipairoj and Harmantzis (2006) demonstrated that auction-based congestion pricing can enable more efficient spectrum assignment in commercial networks facing increasing wireless data demand. Even within licensed bands, maximizing efficiency remains essential: operators must minimize interference while ensuring reliable service. Although licensing helps reduce the risk of congestion and passive interception, it does not eliminate interference entirely. In certain domains—most notably, military operations—frequency resources must be allocated with a dual emphasis on service reliability and interference minimization. Mission-critical systems, therefore, implement robust protective measures such as strong encryption, frequency hopping, and spectrum scrambling to safeguard links against eavesdropping and jamming. However, these protective schemes often require non-trivial setup delays, rendering conventional resource assignment methods inadequate for scenarios that require rapid frequency reassignment in response to sudden environmental changes. As a result, recent research has increasingly focused on developing adaptive assignment strategies that maintain spectral efficiency and security under dynamic conditions.

1.2 Frequency assignment problem formulated as a graph coloring problem

Numerous studies have adopted graph-theoretic approaches to optimize frequency assignment because the problem—defined by numerous devices and stringent interference constraints—can be effectively represented using a graph model. This formulation is commonly referred to as the frequency assignment problem (FAP), with the objective of minimizing a particular metric, such as the frequency span or interference. FAP is closely related to the classical graph coloring problem and can be generalized by modeling communication links as nodes in a graph, where frequencies are assigned in a way that minimizes interference. The graph coloring problem is defined as follows: given a graph $G=(V,E)$, as illustrated in Figure 1, colors are assigned to the nodes such that no two adjacent nodes share the same color. This constraints can be mathematically expressed as Equation 1:

$\text{Find\hspace{0.17em}}f:V\to \mathcal{C},\text{s.t.}\forall \left\{V_i,V_j\right\}\in E,f\left(V_i\right)\ne f\left(V_j\right),(1)$

where $\{V_0,\dots ,V_5\}\in V$ denotes the set of nodes illustrated in Figure 1 and $\mathcal{C}$ represents the set of possible colors.

Figure 1

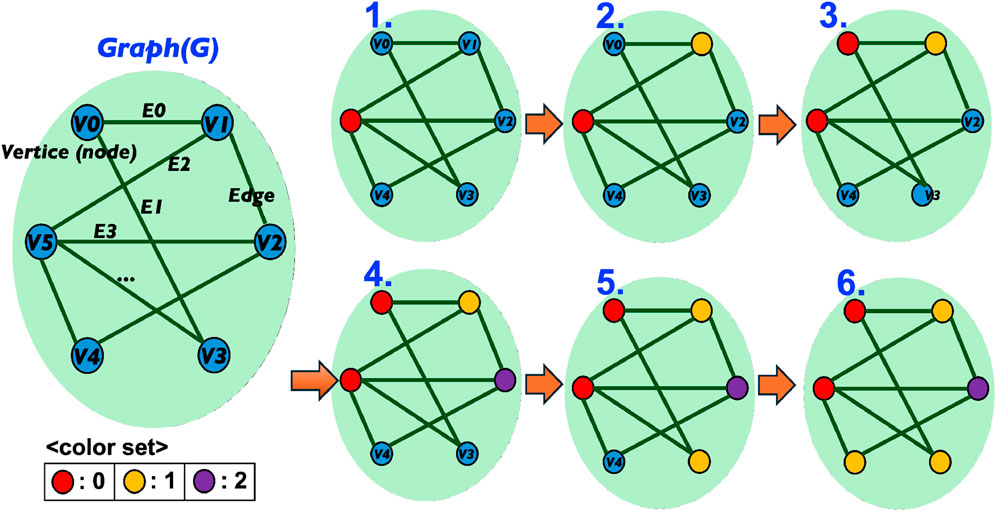
Figure 1. Graph $G$ consists of six nodes for graph coloring assignment. The color set comprises integer-labeled colors $\{\mathrm{0,1,2}\}$, each representing a distinct frequency block. The six steps on the right illustrate the sequential coloring process, where each node is assigned a color such that no two adjacent nodes share the same color. This process reflects frequency assignment in communication networks.

As an illustrative example, Figure 1 shows a valid coloring of graph $G$. The vertices (nodes) are processed in order of $V_5$, $V_1$, $V_0$, $V_2$, $V_3$, and $V_4$. The color set is $C=\mathrm{0,1,2}$, where the indices 0, 1, and 2 correspond to the colors “red,” “yellow,” and “purple,” respectively. For each node, we greedily assign the lowest-indexed color in $C$ that does not violate the interference constraint imposed by the colors already assigned to its neighbors. Following this rule, node $V_5$ is first assigned color 0. Next, node $V_1$ is assigned color 1, which is the smallest admissible color given the current partial assignment. Applying the same greedy rule to each subsequent node yields the complete coloring, as shown in the sixth step on the right-hand side of Figure 1.

Since the graph coloring problem is known to be nondeterministic polynomial-time hard (NP-hard) (Zoellner, 1973), finding an optimal solution is computationally intractable in most cases. As a result, researchers have commonly relied on heuristic methods to obtain feasible solutions. While many earlier studies applied graph coloring to unweighted graphs satisfying the constraint in 1, more recent work has incorporated net filter discrimination (NFD) to account for frequency guard bands. NFD is a metric that quantifies the extent to which a receiver can reject interference from adjacent frequency channels, enabling a more realistic representation of communication systems (Yilmaz et al., 2017; Jeon et al., 2021; Jeon et al., 2019). By guiding the minimum required separation between assigned frequencies, NFD introduces additional constraints into the coloring process. This results in a constrained version of the graph coloring problem, which can be formally expressed as follows:

$\text{Find\hspace{0.17em}}f:V\to \mathcal{C},\text{s.t.}\forall \left\{V_i,V_j\right\}\in E,|f\left(V_i\right)-f\left(V_j\right)|>W_{V_i{V}_j},(2)$

where $W_{V_i{V}_j}$ is the weight of the edge $\{V_i,V_j\}\in E$, reflecting the NFD value. The required frequency is encoded in the edge weight (see Section 2.1.1 for details), where $W_{V_i{V}_j}$ represents the minimum frequency offset needed to ensure acceptable communication quality between the two interfering links. Although several heuristic methods have considered edge weight to enforce frequency separation constraints, most artificial intelligence (AI)-based approaches still neglect this aspect. In this work, we explicitly incorporate NFD into the proposed AI-assisted frequency assignment framework to better reflect realistic communication conditions.

1.3 Objective metrics in FAP: minimum order vs. minimum span

The possible objective metrics include the order and span of frequency bands. The order refers to the number of distinct frequency blocks used in an assignment and corresponds to the $minimumorderfrequencyassignmentproblem$ (MO-FAP) (Aardal et al., 2007). This objective aligns with the classical graph coloring goal of minimizing the number of assigned colors. In traditional graph-theoretic terms, the $chromaticnumber$ of a graph is defined as the minimum number of colors required to color the nodes such that no two adjacent nodes share the same color. Accordingly, substantial research has focused on determining the chromatic number or approximating it through heuristic coloring methods (Brown, 1972; Welsh and Powell, 1967). Scheduling problems have also been modeled as graph coloring tasks, where minimizing the chromatic number corresponds to achieving optimal resource allocation.

However, since computing the chromatic number is NP-hard, many studies instead focus on heuristically minimizing the number of colors used. A similar principle applies to frequency assignment, where minimizing the number of frequency blocks improves spectral efficiency. This objective becomes even more valuable in multi-cell wireless systems, where minimizing the number of frequencies assigned within a cell can facilitate frequency reuse across spatially separated regions. By reusing frequencies in non-interfering areas, network operators can reduce the total spectrum demand while maintaining service quality, especially in large-scale and high-density deployments. The MO-FAP is particularly effective when frequency resources are independent as the total spectrum usage is approximately proportional to the order. Additionally, reducing the number of assigned frequencies enhances adaptability by increasing the likelihood of identifying alternative solutions within a constrained frequency range.

Another important objective is to minimize the span, which is defined as the range between the minimum and maximum frequency values used in a given assignment. This problem is referred to as the minimum span frequency assignment problem (MS-FAP) (Aardal et al., 2007). Unlike MO-FAP, which focuses on minimizing the number of frequencies used, MS-FAP aims to compress the frequency allocation into a narrow contiguous block. This is particularly useful in scenarios where preserving contiguous, unused portions of the spectrum is desirable as it enables more flexible accommodation of the potential applications within the remaining bandwidth. Minimizing the span enhances the overall robustness as it enables the assigned frequencies to be more readily shifted to an alternative frequency region in the event of interference or malicious attacks. A compact frequency assignment also facilitates more efficient frequency reuse, particularly within confined environments or adjacent cells, by minimizing spectral leakage and limiting the footprint of active channels. To address this objective, prior studies have explored various heuristic methods. Just as the chromatic number provides a theoretical lower bound for MO-FAP, meta-heuristic approaches have been employed to estimate lower bounds for MS-FAP (Costa et al., 2002), thereby guiding the search for near-optimal solutions.

Notably, technical reports in the field of network and telecommunications engineering—including studies conducted by NASA (Heyward, 1992)—have applied heuristic methods and parallel scheduling models to minimize the frequency span. These approaches have demonstrated practical effectiveness in real-world satellite communication experiments, highlighting the applicability of MS-FAP to mission-critical systems. In this study, we propose two complementary approaches: MO-FAP and MS-FAP, each targeting a different objective—minimizing the number of frequency blocks and minimizing the overall frequency span, respectively.

1.4 Heuristic strategies in FAP

Given the NP-hard nature of the graph coloring problem, previous studies have explored various heuristic approaches, such as the greedy algorithm, genetic algorithm, and tabu search (Yilmaz et al., 2017; Kumar and Milleth, 2018; Colombo, 2006). Among these, DSATUR (Brélaz, 1979), an advanced greedy algorithm that dynamically decides the next node to color based on the saturation degree, has demonstrated strong performance in addressing the minimum order. However, certain heuristics, particularly local search methods such as greedy algorithms and tabu search, are often susceptible to becoming trapped in the local optima, limiting their ability to identify globally optimal solutions. To overcome this issue, some studies have employed genetic algorithms, which, as global search methods, can explore a broader solution space and help escape the local optima. Despite this advantage, genetic algorithms also face challenges in terms of scalability and computational efficiency, particularly in large-scale or real-time frequency assignment scenarios.

1.5 AI-driven approaches in FAP

To enhance performance in frequency assignment, neural networks and reinforcement learning have recently emerged as promising alternatives to traditional heuristics. Previous studies have applied AI-based approaches to graph coloring problems across various domains, including computer science. For instance, a deep learning-based approximate graph coloring algorithm was proposed for designing the register allocation (Das et al., 2020). Other studies have explored AI-driven methods for minimizing the number of assigned frequency blocks, demonstrating performance comparable to or exceeding that of conventional heuristics (Watkins et al., 2023; Langedal and Manne, 2024). Huang et al. (2019) demonstrated that reinforcement learning significantly enhances heuristic performance. However, the training process in that work required approximately 300 GPUs and became increasingly time-consuming as the graph size increased. Although these studies primarily focused on minimizing the number of frequency blocks and demonstrated improved results, they often suffer from scalability issues due to the high computational costs and extensive GPU resources required for training. To address these limitations, we propose a learning-based frequency assignment framework that reduces computational complexity while maintaining or surpassing the performance of existing AI-based methods. Building on the recent advances in AI-based frequency assignment methods, we summarize the key contributions of the proposed approach in the following section.

1.6 Comparison of FAP approaches

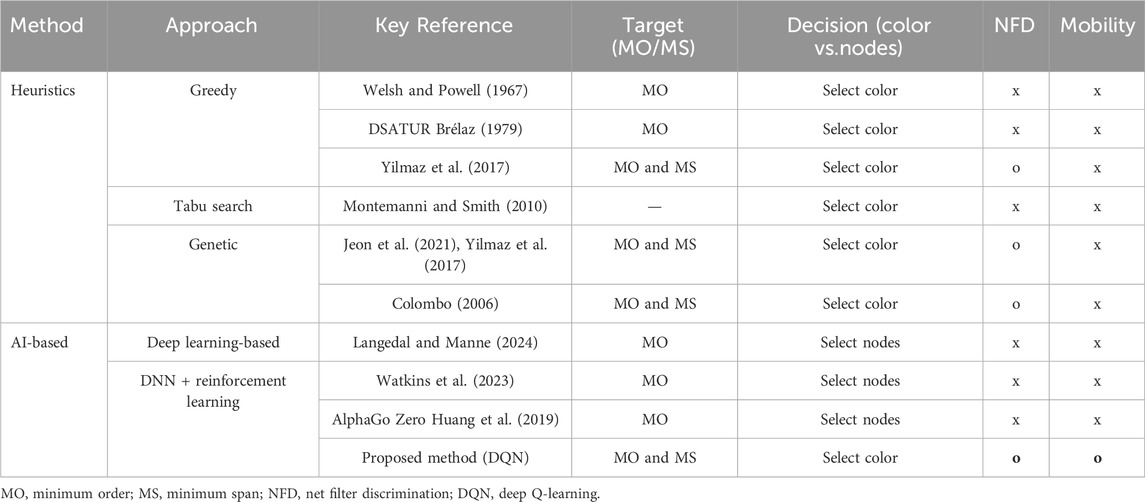
Table 1 summarizes prior research that employs various methods to address the graph coloring problem, encompassing both heuristic and AI-based approaches. The table categorizes each study based on its objective, the primary decision-making strategy employed, and whether the method accounts for NFD—i.e., graph coloring on edge-weighted graphs—or device mobility. Among heuristic techniques, greedy algorithms are the most widely used, with numerous variations reported in the literature. Notable extensions of the basic greedy approach include DSATUR and its derivatives (Welsh and Powell, 1967; Brélaz, 1979; Yilmaz et al., 2017), which dynamically select nodes based on the saturation degree. Additionally, broader search strategies such as tabu search (Montemanni and Smith, 2010) and genetic algorithms (Colombo, 2006; Jeon et al., 2021) have been extensively studied to improve solution quality and avoid local optima. A typical greedy method involves two main steps: determining the node sequence and assigning colors. Although both steps rely on heuristic decisions, the color assignment step is typically considered the core decision-making component and is labeled accordingly in Table 1. Some studies are further enhanced by introducing novel strategies for determining the node sequence, which can significantly impact the quality of the final solution. These heuristic approaches have been widely applied to both MO-FAP and MS-FAP, aiming to minimize either the number of frequency blocks or the overall frequency span required.

Table 1

Table 1. Classifications of frequency assignment methods and their characteristics.

In recent years, artificial intelligence has emerged as a promising alternative to classical heuristics for frequency resource assignment. Several studies have demonstrated the effectiveness of learning-based approaches in addressing the limitations of traditional methods. Most existing research has applied learning models to determine the node sequence—primarily to support color (frequency) assignment—and has largely been restricted to unweighted graph settings. As illustrated in Figure 2, real-world scenarios such as emergency response require efficient and adaptive frequency management, which existing methods often struggle to provide. The proposed approach is designed to address these challenges more effectively.

Figure 2

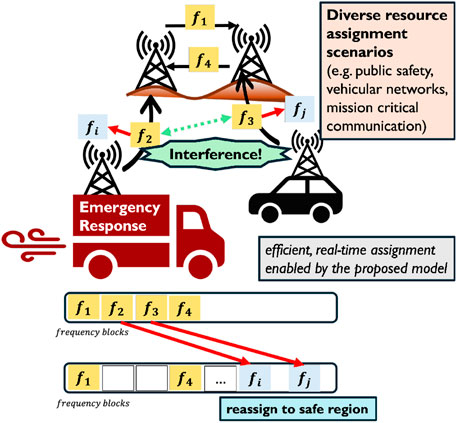
Figure 2. Illustration of the proposed frequency assignment framework applied to a real-world, mission-critical scenario. The top panel shows interference caused by spectrum congestion in a dynamic environment. To prevent communication failure, frequencies $f_2$ and $f_3$ are reassigned to safer bands $f_i$ and $f_j$, respectively. The proposed model enables real-time reassignment to safer frequency regions while maintaining efficient spectrum utilization.

1.7 Contributions

In this study, we propose a novel DQN-based framework that integrates graph-based representations with reinforcement learning to enable efficient and adaptive frequency assignment. To improve the applicability of the solution in real-world environments, the proposed model explicitly accounts for device mobility. The primary contributions of this work are as follows:

• We propose an AI-based framework that enhances the performance of heuristic methods while improving learning efficiency by simplifying the training process used in prior studies.

• We incorporate device mobility into the simulation environment to demonstrate the superior adaptability and performance of the proposed AI-based method compared to conventional algorithms.

2 Methodology

2.1 System model and baseline heuristic approaches

2.1.1 Graph representation of the communication system

In the context of the FAP, the communication system information is typically represented as a graph to enable the application of graph coloring techniques. Each communication link between a pair of transmitters is modeled as a node in the graph, and an edge is established between two nodes if the corresponding links are subject to interference.

For clarity, an example of graph representation is provided below. In Figure 3, a communication system consisting of four devices is illustrated. In this example, all device pairs form communication links, resulting in a total of six links (for the convenience of explaining, we do not consider the direction of the communication). The red dotted line in Figure 3 represents the communication links, which are mapped to six corresponding graph nodes. The blue arrow in Figure 3 indicates ${\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{k}}_0\to V_0$, and for all the links, they are converted into nodes $\{V_0,\dots ,V_5\}$. The edges of the $GraphG$ are formed when interference exists between the communication links (nodes). The edge weight $W_{i,j}$ quantifies the interference between links $i$ and $j$. $W_{i,j}$ is defined as the signal power, measured in decibels, received at the target node from the transmitter of link $i\in V$, as calculated by Yilmaz et al. (2017) and Jeon et al. (2021):

$W_{i,j}={\left[P_{t\left(i_t\right)}\right]}_{\text{dBm}}+{\left[G_{i_t{j}_r}\right]}_{\text{dBm}}-{\left[P{L}_{i_t{j}_r}\right]}_{\text{dBm}}-T_s,(3)$

where $i_t,j_r$ are the transmitter and receiver of the link $i,j$, respectively, and $P_{t(i_t)}$ is the transmitting power of the transmitter of the link $i$, $G_{i_t{j}_r}$ is the product of the antenna gains at both the transmitter of link $i$ and the receiver of link $j$, $P{L}_{i_t{j}_r}$ is the free-space path loss from the transmitter of link $i$ to the receiver of link $j$ based on ITU-R P.525 (ITU-R, 1994), and $T_s$ is the receiver sensitivity threshold. We consider the frequency separation only when the computed $W_{i,j}$ value in dBm exceeds 0. In other words, an edge is generated between nodes $i$ and $j$ when $W_{i,j}>0$. After computing the interference between the communication links (the nodes), the edge of $GraphG$ is formed (the graph at the center in Figure 3), which signifies the presence of interference between the links.

Figure 3

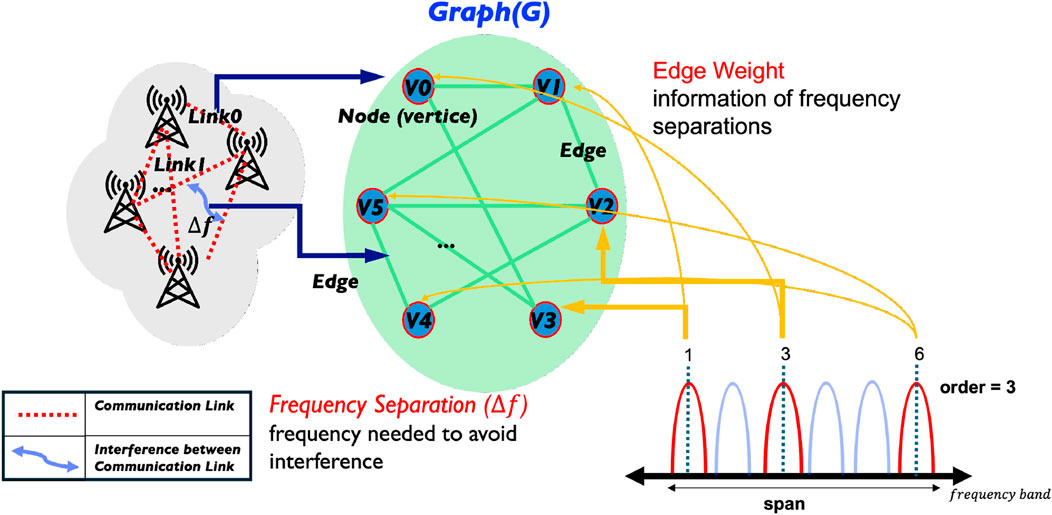
Figure 3. Illustration of a frequency assignment map. A wireless communication system is transformed into a graph $G$, where each node represents a communication link and each edge weight denotes the required frequency separation $(\mathrm{\Delta }f)$ between interfering links. The objective is to assign frequencies that satisfy these constraints while minimizing either the number of frequency blocks (MO-FAP) or the total frequency span (MS-FAP). This graph-based formulation visually illustrates how frequency assignment problems are modeled and addressed.

As discussed earlier, effective frequency assignment must account for interference constraints to ensure reliable, interference-free operation. These constraints are modeled using NFD, which quantifies the minimum required frequency separation between communication links. This separation requirement is encoded as edge weights in the interference graph, as demonstrated in prior studies (Yilmaz et al., 2017; Mannino and Sassano, 2003). NFD depends on both the transmitter’s spectrum emission mask and the receiver’s filter characteristics, and it determines the minimum frequency offset necessary to protect the desired signal at the receiver from adjacent-channel interference. The NFD function $F_{\text{NFD}}$ is defined in Equation 4.

$F_{\text{NFD}}\left(\mathrm{\Delta }f\right)=W_0,(4)$

where $W_0(\mathrm{d}\mathrm{B})$ represents the attenuation level when the frequency separation between two signals is $\mathrm{\Delta }f(\mathrm{H}\mathrm{z})$. The variable $\mathrm{\Delta }f$ indicates the minimum frequency separation required between two links to prevent mutual interference. This implies that, when combined with the edge weight definition in Equation 3, the center frequencies of links $i$ and $j$ must be separated by at least $F_{\text{NFD}}^{-1}(\max (0,W_{i,j},W_{j,i}))$ to avoid signal degradation.

We define the set of assignable center frequencies as $F=\{f_0,\dots ,f_m\}$, where $m$ denotes the number of available frequency channels. A frequency assignment is defined as a mapping $F:V\to \{\mathrm{1,2},\dots ,m\}$, where $F(V_i)=k$ indicates that the frequency $f_k\in F$ is assigned to link $V_i\in V$. The goal is to assign frequencies such that the separation constraint derived from the NFD model is satisfied, as expressed by

$U\cdot |F\left(V_i\right)-F\left(V_j\right)|\ge F_{\text{NFD}}^{-1}\left(\max \left(0,W_{V_i{V}_j},W_{V_i{V}_j}\right)\right).(5)$

Here, $U$ is the unit frequency interval (i.e., the frequency spacing between consecutive channels). Inequality (Equation 5) ensures that the resulting frequency assignment maintains sufficient separation between interfering links, thereby enhancing communication robustness and preserving signal quality. Once the communication system is represented as a weighted interference graph, various algorithms can be applied to perform the frequency assignment. The following section presents the proposed methodology for efficient frequency resource assignment, building upon this graph-based formulation.

2.1.2 Heuristic algorithms for FAP

As discussed in Section 2.1.1, graph coloring is an NP-hard problem, which means that the computational complexity required to find an optimal solution increases exponentially with the number of nodes. This makes the exact solution impractical for real-time applications, constituting a significant challenge for their deployment in communication systems—especially in mission-critical scenarios. In this study, we adopt the greedy algorithm as a representative heuristic approach. The greedy algorithm makes locally optimal choices at each step to approximate a globally optimal solution, thereby balancing computational efficiency and solution quality.

The greedy algorithm is widely used for its linear-time complexity and computational efficiency. Its implementation may vary by incorporating techniques such as backtracking and approximation to suit different problem settings. Among these variants, DSATUR has been suggested (Brélaz, 1979; Watkins et al., 2023) as an effective greedy method. It dynamically determines the node coloring sequence based on the saturation degree. In this study, we modify the DSATUR algorithm to enhance its compatibility with reinforcement learning. For benchmarking purposes, we implement two versions of the greedy algorithm: the minimum order greedy algorithm (MO-greedy) and the minimum span greedy algorithm (MS-greedy). Both variants begin by determining a node coloring sequence and then assigning the minimum admissible color to each node. The objective of MO-greedy is to minimize the number of distinct frequency blocks (ordering cost), while MS-greedy focuses on minimizing the overall frequency span. The node sequence in the greedy algorithm is determined based on the degree, which is defined using two criteria: first, the number of neighboring nodes and, second, the sum of edge weights. Due to its greedy nature, the resulting frequency assignment may not be globally optimal. However, the algorithm operates in linear time, making it suitable for time-sensitive applications. The following section provides a detailed explanation of the specific greedy methodologies applied in this study.

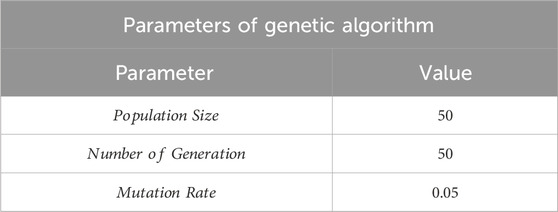
To extend the search space and mitigate the local limitations of greedy algorithms, we also incorporate a genetic algorithm. By introducing evolutionary mechanisms such as selection, crossover, and mutation, the genetic algorithm enhances the ability to explore the global optima. Prior studies (Colombo, 2006) have shown that the genetic algorithm achieves results that are comparable to or better than those of other well-known heuristics in various benchmark problems. Comparing the outcomes of the genetic algorithm with those of the proposed AI-based approach enables us to evaluate the relative effectiveness and adaptability of the proposed method.

Algorithm 1

Algorithm 1. Minimum span greedy algorithm (MS-greedy).

Algorithm 2

Algorithm 2. Minimum order greedy algorithm (MO-greedy).

2.1.2.1 MS-greedy

The MS-greedy algorithm is a heuristic method derived from the greedy algorithm, specifically adopted to minimize the span of assigned frequency blocks. Since minimizing the span is generally more challenging than minimizing the order (Aardal et al., 2007), it is essential to assign frequency blocks in a manner that effectively reflects the graph structure. The degree of a node captures key structural information and implicitly encodes node priority, making it a valuable heuristic for guiding the assignment process. To reduce the overall frequency span, the algorithm prioritizes the reuse of recently assigned frequency blocks whenever feasible. The detailed procedure of MS-greedy is outlined in Algorithm 1. At each step, the algorithm selects the node with the highest degree and assigns it a frequency from the set of feasible candidates—i.e., frequencies that satisfy the interference constraints—while attempting to minimize the span.

2.1.2.2 MO-greedy

The MO-greedy algorithm is designed to minimize the total number of frequency blocks used, which is also known as the order. Prior to the actual frequency assignment, each node in the graph is preliminarily evaluated based on the weights of its connecting edges, which are simplified to binary values: an edge weight of 1 indicates interference (i.e., connectivity), while 0 indicates no interference. These preprocessing steps, detailed in Algorithm 2, are intended to reflect the essential structure of the graph and inform the assignment sequence. By encoding connectivity in this manner, the algorithm derives a node order that prioritizes nodes with higher degrees—those more likely to cause interference—thus reducing the chance of conflicts during assignment. Once the sequence is determined, frequencies are assigned greedily to each node using the lowest feasible frequency block, with the objective of minimizing the total number of distinct frequencies.

Algorithm 3

Algorithm 3. Genetic algorithm.

2.1.2.3 Genetic algorithm

The genetic algorithm introduces controlled randomness into the solution process, enabling exploration of a broader solution space beyond what greedy algorithms can achieve. For both the MO-greedy and MS-greedy algorithms, randomness is incorporated through standard genetic operations, including crossover, mutation, and selection. These operations enhance the algorithm’s ability to escape the local optima and increase the likelihood of discovering globally optimal solutions. The detailed procedure of the genetic algorithm is outlined in Algorithm 3. The initial population is seeded using solutions generated by the greedy coloring algorithm, providing a strong starting point. One-point crossover is applied to recombine segments from parent solutions, while mutation introduces random variations to maintain diversity and prevent premature convergence. Tournament selection is used to retain fitter individuals based on a predefined fitness function, which is evaluated separately for the MO and MS objectives. To ensure that offspring solutions remain feasible with respect to the interference constraints, a repair function is applied after crossover and mutation. This function enforces NFD constraints, which require that the frequency difference between any two adjacent nodes must be greater than or equal to the corresponding edge weight. During the repair process, if any pair of connected nodes violates this condition, the assigned frequencies are adjusted to satisfy the minimum separation required by the edge weight. In cases where no valid adjustment can be made due to conflicts with other neighboring nodes, the entire assignment for the conflicting node may be regenerated. This ensures that all individuals in the population remain feasible throughout the evolutionary process.

2.2 Proposed approach: Artificial intelligence-based method

In this study, we propose a DQN framework integrated with a graph neural network (GNN) architecture to obtain pseudo-optimal solutions for the FAP, demonstrating superior performance compared to conventional heuristic approaches. DQN, a reinforcement learning technique, enables more effective exploration of the solution space than traditional greedy algorithms, which inherently operate as local search methods with limited exploration capability. Reinforcement learning offers a principled framework for balancing exploration and exploitation, making it particularly suitable for sequential decision-making tasks such as graph coloring, where each frequency assignment influences subsequent decisions. Within our framework, the GNN serves as a feature to extract the meaningful structural properties of the graph, providing rich embeddings for effective policy learning. The Q-learning agent then interacts with the environment iteratively, optimizing a long-term reward signal to guide the frequency assignment process toward globally effective and interference-aware solutions. We denote the two variants of our DQN-GNN model as MO-DQN and MS-DQN, corresponding to the objectives of minimizing the order and span, respectively.

We adopt the GNN architecture to process the graph-structured inputs and effectively encode topological information. GNNs are designed to learn from the node, edge, and graph-level structures, making them particularly well-suited for pattern-based prediction tasks such as frequency assignment. Their ability to generalize across varying graph topologies has been demonstrated in a wide range of applications (Wu et al., 2021; Langedal and Manne, 2024). However, conventional GNNs may face limitations when generalizing to unseen graphs or scaling to deeper architectures, often due to issues such as over-smoothing and vanishing gradients. To address these challenges, we integrate GNN with DQN. In this framework, the GNN component serves as a structural encoder that embeds the input graph by capturing node relations via edge connectivity—an essential feature for learning effective frequency assignments under interference constraints.

DQN integrates classical Q-learning with deep neural networks to approximate the action-value function $Q(s,a)$, which estimates the expected cumulative reward of taking action $a$ in state $s$. The learning process follows the Bellman update policy (Waqar et al., 2024):

$Q\left(s,a\right)\leftarrow Q\left(s,a\right)+\alpha \left[r+\gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right],(6)$

where $r$ is the immediate reward, $s^{\prime }$ is the next state, $\gamma \in \left.\left[\mathrm{0,1}\right.\right)$ is the discount factor, and $\alpha$ is the learning rate. A higher $\gamma$ biases the agent toward future rewards, potentially increasing learning time while promoting long-term optimization. In traditional Q-learning, the function $Q(s,a)$ is stored in a lookup table. However, for large and high-dimensional state spaces, DQN approximates $Q(a,s)$ using deep neural networks. In our environment, actions correspond to assigning frequencies to nodes, a task that is discrete and high-dimensional. To manage this complexity, we employ a GNN as the Q-network. The GNN encodes structural information from the graph, producing meaningful embeddings over which Q-learning is performed. An $ϵ-$ greedy policy is adopted to balance exploration and exploitation: with probability $ϵ$, a random action is selected to encourage exploration; otherwise, the action with the highest predicted Q-value is chosen. This integration of DQN with GNN enables scalable and adaptive frequency assignment by effectively learning from graph-structured input while optimizing long-term performance.

2.2.1 Network architecture of the proposed model

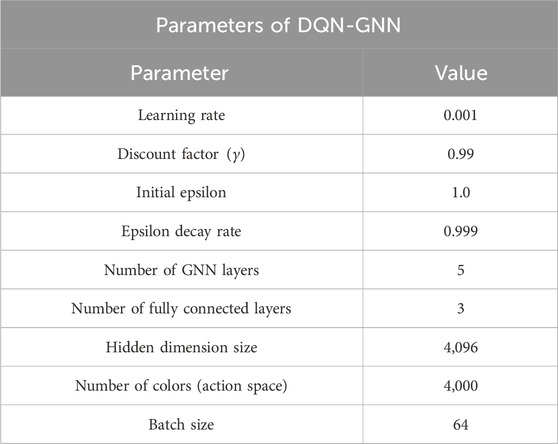
The overall network architecture of the proposed model is illustrated in Figure 4. It consists of multiple interconnected layers that collectively compute the Q-values. The model employs a deep neural network composed of five graph convolutional network (GCN) layers, implemented using the PyTorch Geometric library, followed by three fully connected layers. The GCN layers capture topological information and aggregate features across neighboring nodes, while the fully connected layers transform the learned node embeddings into Q-values corresponding to possible actions. The depth of the GCN (five layers) was empirically chosen due to the balance between representational expressiveness and training stability. The input to the model is a node feature vector whose length corresponds to the number of nodes in the graph. The hidden and output layers consist of 4,096 and 4,000 units, respectively. The output dimensionality is fixed at 4,000 to align with the number of available frequency blocks. All model weights are randomly assigned at the initialization stage. Given that GNN structures are known for their ability to learn from graph-structured data, this architecture is designed to generalize well across diverse graph topologies, thus providing a robust foundation for adaptive and scalable frequency assignment.

Figure 4

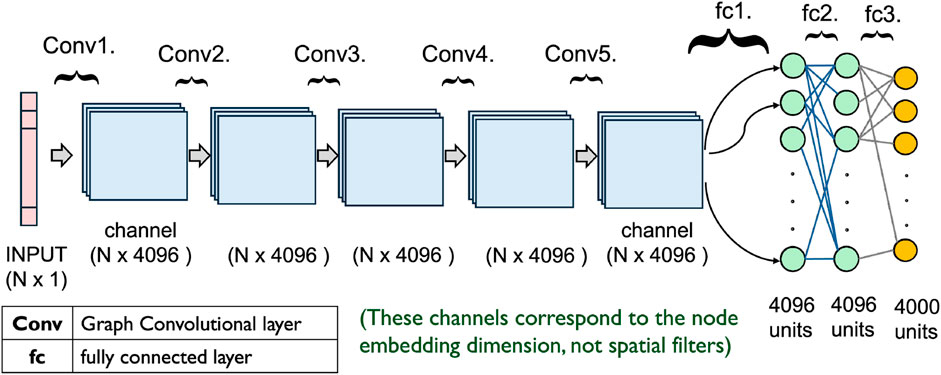
Figure 4. Network architecture of the proposed DQN-GNN model. The input node features are first processed through five graph convolutional network (GCN) layers and passed through three fully connected layers to generate Q-values over 4,000 possible frequency blocks.

2.2.2 Reinforcement learning design: state, action, and reward

To implement reinforcement learning effectively, it is essential to define the key components of the model: the state, action, and reward.

In conventional DQN models, the state is typically represented by a single vector or image that encodes the current environment. In our framework, the state is composed of the communication graph structure and the current frequency assignment vector. The GNN processes the graph to extract structural embeddings that capture node connectivity and interference relationships. The frequency assignment vector is denoted as $v={[f_0,\dots ,f_n]}^{\text{T}}$, where $f_i$ represents the frequency assigned to node $i$ in a graph with $n$ nodes. This combined state representation captures both the topological and assignment-specific information, enabling the model to make context-aware decisions that consider the structure of the network and the current state of frequency usage.

At each decision step, the agent selects a frequency block to assign to a node—this corresponds to the action in the reinforcement learning framework. Nodes are processed sequentially in a fixed order determined by their degree. This predefined sequence simplifies the training process and helps the Q-network converge more efficiently, particularly when dealing with large-scale graphs. During exploitation, the agent chooses the frequency corresponding to the highest predicted Q-value. For exploration, a greedy search strategy is employed to reduce computational overhead as it increases the likelihood of selecting feasible frequencies based on prior heuristic knowledge. To ensure compliance with the interference constraints defined by the NFD in (5), a list of candidate frequencies is precomputed for each node. The agent then selects an action from this filtered set, thereby ensuring that all actions maintain communication quality by preventing harmful interference.

The reward is computed after each frequency assignment and reflects the efficiency of the current solution. In the MO-DQN model, the reward is based on the increase in the number of distinct frequency blocks used. Specifically, the agent receives a fixed negative reward whenever the number of distinct blocks increases. Since at most one new negative block can be added per step, the reward is inherently binary—either a penalty is applied for introducing a new block, or no penalty is given if the current order is maintained. This design encourages the agent to avoid unnecessary expansion of the frequency set and aligns well with the MO-FAP objective. In the MS-DQN model, the reward is determined by the change in the total frequency span after each assignment. A negative reward is applied whenever the span increases, penalizing inefficient spectrum usage. Similar to the MO case, we adopt a binary reward scheme to enhance training stability—assigning a small penalty for span increases and 0 otherwise. This binary reward structure improves learning dynamics by providing clearer signals at critical decision points while avoiding noisy gradients caused by minor fluctuations. As shown by Bellemare et al. (2016), sparse and binary rewards can enhance the stability of policy learning and promote efficient exploration, particularly in high-dimensional or combinatorial state spaces. In our setting, this approach enables the agent to focus on impactful decisions, delay unnecessary spectrum expansion, and achieve more stable and consistent policy improvement.

Furthermore, to ensure that Q-values reflect the effectiveness of the full assignment, updates are performed only after the entire graph has been colored. The Bellman equation (Equation 6 is used to update Q-values, and the network is trained by minimizing the mean-squared-error (MSE) between the predicted and target Q-values. The DQN parameters are optimized via backpropagation using the Adam optimizer, with all layers updated jointly to progressively refine the agent’s policy.

3 Simulation results

3.1 Simulation setup

The efficiency of the proposed resource assignment model is evaluated within a virtual communication system. We generate a virtual communication system by randomly placing the devices and their corresponding communication links. The simulation area is defined as a square region of $100\times 100[\mathrm{k}{\mathrm{m}}^{\mathrm{2}}]$, and it consists of a total of 200 devices. An example of a randomly generated topology is illustrated in Figure 5, where 200 communication links are formed between randomly selected pairs of 200 devices. These links are then mapped to graph nodes, representing the structure used for frequency assignment. Interference between communication links is modeled based on free space attenuation, using the standard ITU P.525 (ITU-R, 1994). All devices are assumed to operate with identical transmission power, antenna characteristics, and receiver sensitivity. The receiver sensitivity—the minimum received power that is detectable by a receiver—is set to −79.12 dBm in this study. The frequency spectrum is divided into blocks, each with a bandwidth of 15 MHz, within a total band of 600 MHz. The key simulation parameters are summarized in Table 2. The detailed parameters of genetic algorithm and DQN-GNN model is provided in Tables 3, 4.

Figure 5

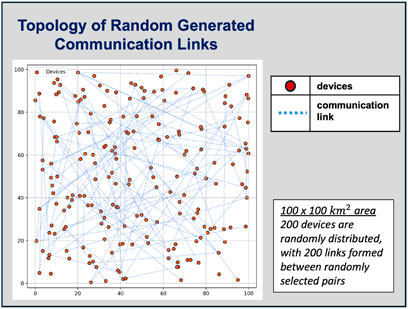
Figure 5. Topology of a randomly generated simulation scenario is shown. A total of 200 devices are randomly distributed in the $100\times 100[\mathrm{k}{\mathrm{m}}^{\mathrm{2}}]$ area, forming 200 communication links.

Table 2

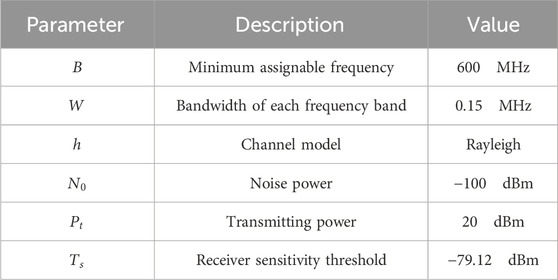
Table 2. The key simulation parameters used to model the wireless communication environment in our experiments.

Table 3

Table 3. Parameter settings of the genetic algorithm for 200 communication links.

Table 4

Table 4. Parameter settings of the DQN-GNN model for 200 communication links.

In the simulation, the performance of both the greedy algorithm and the proposed DQN-GNN learning method is evaluated using randomly generated communication links. The fundamental objectives of the FAP are twofold: first, to eliminate all perceivable interference between communication links and, second, to prevent the detectability of intended signals by potential attacks. To meet these objectives, the proposed method ensures successful frequency assignment for all devices in the network. Specifically, it guarantees stable communication across all transmitter–receiver pairs. This validates the feasibility and reliability of the method in scenarios requiring interference-free and secure communication.

3.2 Results and discussion

To enable a fair comparison, we evaluate the performance of the greedy algorithm, the genetic algorithm, and the proposed DQN-based learning model, each targeting both the minimum span and minimum order objectives. The evaluation is conducted on randomly generated communication link instances. For each method, the average frequency span and ordering cost are recorded as the primary performance metrics. All the resulting frequency assignments satisfy the interference constraints, ensuring interference-free communication. Specifically, each node meets the requirement that each node is assigned a frequency greater than the corresponding edge weight, as defined in (Equation 2).

3.2.1 Comparison when the number of nodes increases

To evaluate the scalability of the proposed DQN-GNN approach, we increased the number of D2D communication links and compared the resulting frequency assignments with those obtained by a greedy heuristic and a stochastic variant based on a genetic algorithm. For each link set size $\{\mathrm{10,20,50,100,200}\}$, we generated 100 random network topologies and computed the average frequency span and ordering cost. The result is summarized in Figure 6, where the left plot depicts the average span, and the right plot presents the average ordering cost as the number of links increases. Since both metrics are minimization objectives, lower values indicate better performance.

Figure 6

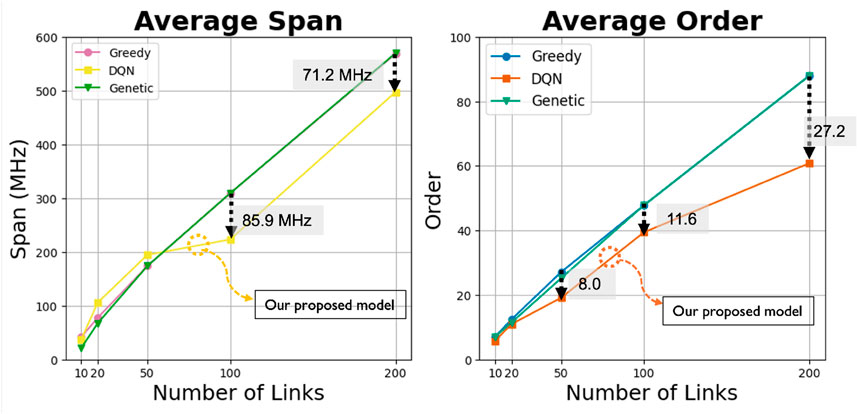
Figure 6. Performance variation in the average span (left) and average order (right) as the number of communication links increases from 10 to 200. Greedy heuristics exhibit a linear trend, while the proposed model consistently enhances both the span and order.

An analysis of the results reveals that the greedy algorithm exhibits a near-linear relationship in both frequency span and ordering cost as the number of communication links increases. The genetic algorithm provides marginal improvements over the greedy approach in smaller instances but similarly shows a near-linear performance trend as the network scales. In contrast, the DQN-GNN model consistently outperforms both heuristic methods, with its advantage becoming more pronounced in larger-scale scenarios. As the number of links increases, both the average span and ordering cost increase more slowly under the DQN model, demonstrating its superior scalability and effectiveness in managing complex frequency assignment tasks.

Since the graph coloring problem is NP-hard, its computational complexity increases exponentially with the number of communication links. Consequently, the performance of the three methods—greedy, genetic, and DQN—appears nearly indistinguishable for small-scale instances. However, as the link count increases, the superiority of the DQN-based approach becomes increasingly evident. As earlier studies have noted, minimizing the span is generally more challenging than reducing the ordering cost. This is reflected in our results, where the average span decreased less significantly than the average order. Notably, the performance gap between the greedy algorithm and the DQN model is more pronounced in the average-order metric. Although the genetic algorithm demonstrates a marginal advantage in minimizing the span for smaller graphs, the DQN-GNN model consistently outperforms it once the number of links exceeds 100—clearly surpassing both the genetic and greedy methods. Although the genetic algorithm explores a broader solution space than the greedy heuristic, its reliance on random variation leads to increased computational cost. Consequently, its performance tends to regress toward that of the greedy algorithm as the graph size increases. In contrast, the DQN strategy effectively learns to minimize both the span and order, surpassing both greedy and genetic approaches as it receives appropriate rewards during training. Its ability to generalize and expand the effective search space without incurring prohibitive computational overhead enables the DQN-GNN model to achieve superior performance, particularly in large-scale scenarios. These results confirm that the proposed model preserves its effectiveness in large-scale scenarios. Despite the growing complexity of the input graphs, the performance gains scale favorably, and the decision quality does not degrade.

3.2.2 Scenario of a 200-node graph

Figure 7 presents the mean span and mean order obtained from 100 randomly generated graphs, each containing 200 communication links (nodes). As mentioned in Section 2.1, the total span of the given frequency band is 600 MHz, consisting of 4,000 frequency blocks (each block is 0.15 MHz wide). To evaluate the effectiveness of the proposed approach, we compared four algorithms—MS-greedy, MO-greedy, MS-DQN, and MO-DQN—on large graphs.

Figure 7

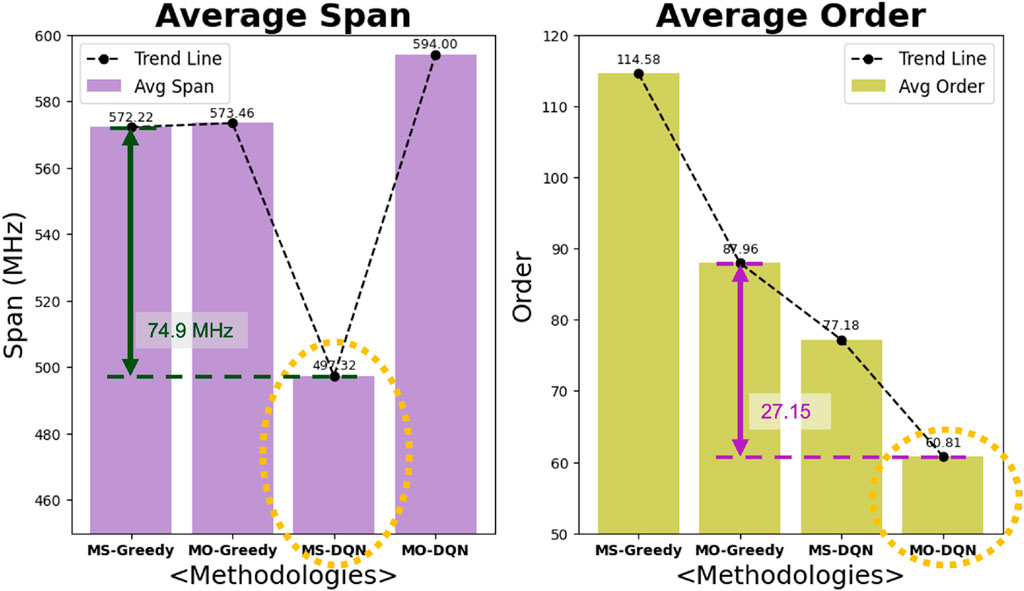
Figure 7. Average span and order achieved by four methods—MS-greedy, MO-greedy, MS-DQN, and MO-DQN—for the case of 200 communication links. MS-DQN and MO-DQN achieve the best performance in their respective objectives.

Among the evaluated methods, MO-DQN leverages the full frequency band to produce highly efficient frequency assignments. Specifically, MO-DQN reduces the number of required frequency blocks by approximately 60 and 30 frequency blocks compared to MS-greedy and MO-greedy, respectively, as shown in the right-hand plot of Figure 7. This corresponds to an improvement of 30% over MO-greedy in terms of ordering cost, demonstrating the model’s ability to effectively minimize frequency block usage while satisfying interference constraints. Moreover, MS-DQN demonstrates improved performance in terms of reducing the ordering cost compared to MO-greedy. It achieved an average order of 77.18 across 100 test graphs—12% lower than MO-greedy—demonstrating improved performance in reducing the frequency blocks.

With respect to the frequency span, MS-greedy holds only a marginal advantage over MO-greedy—their average spans differ by an almost negligible amount. In contrast, when considering the ordering cost, MO-greedy surpasses MS-greedy by approximately 30 frequency blocks. It underscores the difficulty of compressing the frequency range in graph coloring formulations, as demonstrated by prior studies (Aardal et al., 2007). When the DQN framework is trained with the objective of minimizing the span, performance improves across all algorithmic variants. In particular, MS-DQN achieves the best result, achieving a 13% reduction compared to the best-performing heuristic baseline. These findings suggest that the reinforcement learning model equipped with a neural-network Q-function learns to explore the solution space far more effectively than heuristic approaches. On large-scale graphs, MS-DQN achieves a significant reduction in the frequency span, while both MS-DQN and MO-DQN also demonstrate superior performance in minimizing the ordering cost compared to their greedy counterparts. These results underscore the advantage of using deep reinforcement learning in addressing multi-objective frequency assignment problems.

3.2.3 Scenario with device mobility

In D2D networks, device mobility is an important factor to consider for seamless communication. As users move, the network must maintain reliable communication links by dynamically assigning appropriate frequency resources. To emulate realistic operating conditions, we introduced random mobility into our simulation without relying on predefined motions. Specifically, we began with 200 devices forming 100 communication links, represented as a graph with 100 nodes. Then, 10 devices were randomly selected and randomly relocated within a 4 km radius, independently of any movement pattern. Their original communication links were kept identical. Consequently, the edges of the graph largely unchanged, yet the edge weights—expressed as NFD values—are recomputed to capture the new inter-device interference introduced by mobility. We compare the frequency assignment results produced by a heuristic model with those obtained from our reinforcement learning model to quantify their performance gap.

Overall, the experimental results demonstrate a clear advantage of our learning-based approach. The DQN-GNN framework consistently demonstrated significant improvements in reducing both the order and span of the frequency assignment. Specifically, MO-DQN achieves the lowest ordering cost, while MS-DQN attains the minimum span among the four methods. MO-DQN reduced the ordering cost by 14.6 frequency blocks, corresponding to a 32% improvement over MO-greedy. The two greedy baselines produce nearly identical spans, and although MO-greedy offers a slight ordering improvement over MS-greedy, these results indicate that heuristic methods lose effectiveness once mobility is introduced into the environment. In contrast, our learning-based model consistently outperforms the greedy methods. As illustrated in Figure 8, MS-DQN reduced the frequency span by 39.5 MHz, representing a reduction of approximately 12.6% relative to the best greedy method, while simultaneously achieving a lower ordering cost. These findings suggest that reinforcement learning offers a distinct advantage when the underlying graphs exhibit similar structural patterns.

Figure 8

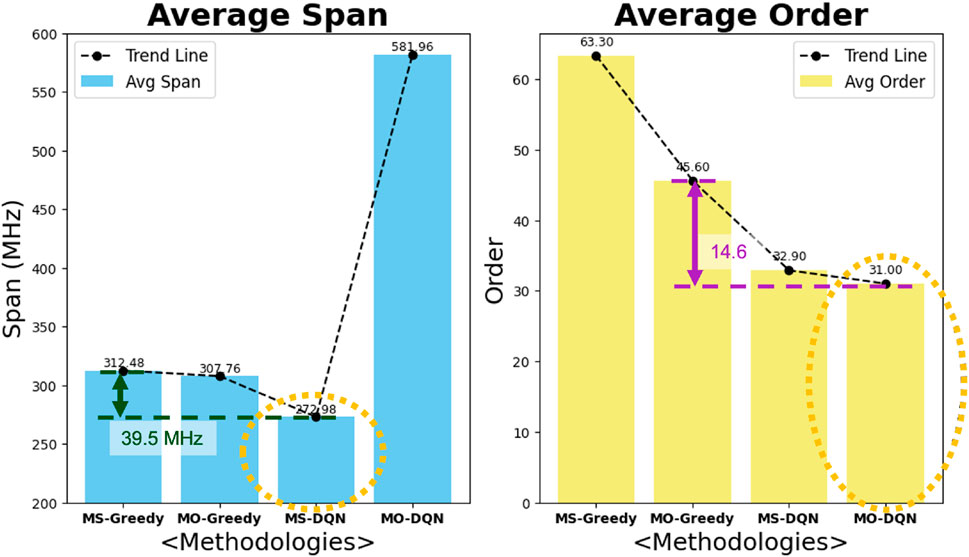
Figure 8. Average span and order results over 10 randomly generated graphs, each with 100 communication links and 10 mobile devices. MS-DQN and MO-DQN exhibit the best performance in minimizing the span and order, respectively.

3.3 Comparison of computational complexity

In real-world deployments, especially in mission-critical communication, frequency assignments must be applied with minimal latency. While traditional heuristic methods run in roughly linear time with respect to the number of nodes, learning-based approaches raise concerns regarding their substantial training complexity. As the network size increases, the state–action space expands exponentially, resulting in a corresponding increase in the required training time. To verify that the proposed model is practically deployable, we measured the execution time of each method. Table 5 summarizes the mean runtime per graph, which was averaged over 100 randomly generated instances with 200 nodes each. It shows the average time required for training or to obtain a result for a single graph for each method. All algorithms were executed on the same hardware (a single NVIDIA GeForce RTX 4090 GPU) to ensure a fair comparison of their computational footprints. We report the average running times of the greedy algorithm, the genetic algorithm, and the proposed DQN-GNN approach. In Table 5, train-DQN denotes the time required to train the model on a single graph instance, whereas execute-DQN denotes the inference time needed to produce a solution with the pre-trained model.

Table 5

Table 5. Average time consumption for a single graph of 200 nodes. The time refers to the time required to obtain a frequency assignment solution, whereas train-DQN denotes the time spent for training the model.

As shown in Table 5, the genetic algorithm exhibits the longest runtime among all methods, even surpassing the training time of the DQN-GNN model. This excessive runtime stems from the genetic algorithm’s dependence on random mutation, which frequently generates infeasible solutions that violate interference constraints. Consequently, a time-consuming repair process is required for each offspring to ensure NFD-compliant frequency assignments, which significantly increases the overall execution time.

In contrast, although the DQN-GNN model incurs an initial training cost—approximately 20 times longer than that of the greedy algorithm—the runtime during inference is nearly identical to that of the greedy approach. This parity highlights a key advantage of our framework: once trained, the DQN-GNN model can deliver fast, near-instantaneous decisions, making it suitable for mission-critical communication systems with stringent latency constraints. The scalability and consistency of its inference performance make the DQN approach highly practical, especially when trained over a sufficiently diverse set of environmental scenarios. Thus, although the initial training phase requires substantial computational effort, once trained, the model can be deployed repeatedly at minimal cost, thus ensuring compatibility with real-time operational requirements.

4 Conclusion

In this study, we proposed a reinforcement learning-based frequency assignment framework that integrates DQN with GNN to efficiently allocate spectrum resources under interference constraints, incorporating both the NFD metric and device mobility. The model architecture employs multiple graph convolutional layers to extract structural features of the communication network, such as node connectivity and interference levels. These encoded representations are then processed by a fully connected Q-network, which sequentially assigns frequencies by estimating long-term cumulative rewards. This decoupled design enables the model to learn interference-aware assignment strategies that generalize effectively across diverse network topologies and densities.

Extensive evaluations demonstrate that the proposed DQN-GNN model consistently outperforms conventional heuristics in both frequency span and ordering cost. In high-density or mobility-intensive scenarios, the model maintains spectrum efficiency and exhibits sub-linear scaling behavior, reflecting its robustness and ability to capture structural patterns.

Future work will focus on extending this framework to support real-time mobility and dynamic environmental conditions, thereby broadening its applicability to mission-critical scenarios such as emergency communications, public safety systems, and robust wireless network deployments. In addition, a promising research direction is to adapt the proposed model for full-duplex (FD) communication environments, which allow simultaneous transmission and reception over the same frequency band. We plan to extend our model to handle FD scenarios by incorporating recent advances in digital self-interference cancellation (SIC) (Kim et al., 2025; Lee et al., 2025). Integrating SIC techniques into the frequency assignment process may enable interference-aware scheduling under stronger co-channel constraints, thereby further improving spectrum efficiency in FD-capable networks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

HK: Methodology, Validation, Writing – original draft, Software, Writing – review and editing, Formal analysis, Investigation. H-BJ: Validation, Writing – review and editing, Investigation. YJ: Investigation, Writing – review and editing, Funding acquisition. JP: Investigation, Writing – review and editing, Funding acquisition. C-BC: Funding acquisition, Investigation, Validation, Conceptualization, Writing – review and editing, Supervision.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Korea Research Institute for Defense Technology (KRIT)- Grant funded by Defense Acquisition Program Administration (DAPA) (KRIT-CT-24-004).

Conflict of interest

Athors YJ and JP were employed by Hanwha System.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aardal, K. I., van Hoesel, S. P. M., Koster, A. M. C. A., Mannino, C., and Sassano, A. (2007). Models and solution techniques for frequency assignment problems. Ann. Oper. Res. 153, 79–129. doi:10.1007/s10479-007-0178-0

CrossRef Full Text | Google Scholar

Bellemare, M. G., Srinivasan, S., Ostrovski, G., Schaul, T., Saxton, D., and Munos, R. (2016). Unifying count-based exploration and intrinsic motivation. Red Hook, NY, United States: Curran Associates, Inc. NeurIPS.

Google Scholar

Brélaz, D. (1979). New methods to color the vertices of a graph. Commun. ACM 22, 251–256. doi:10.1145/359094.359101

CrossRef Full Text | Google Scholar

Brown, J. R. (1972). Chromatic scheduling and the chromatic number problem. Manag. Scir. 19, 456–463. doi:10.1287/mnsc.19.4.456

CrossRef Full Text | Google Scholar

Colombo, G. (2006). A genetic algorithm for frequency assignment with problem decomposition. Int. J. Mob. Netw. Des. Innov. 1, 102–112. doi:10.1504/ijmndi.2006.010812

CrossRef Full Text | Google Scholar

Costa, A., Smith, J. C., and Nitkin, L. K. (2002). Generation of lower bounds for the minimum-span frequency-assignment problem. Discrete Appl. Math. 118, 73–85.

Google Scholar

Das, D., Ahmad, S. A., and Kumar, V. (2020). “Deep learning-based approximate graph-coloring algorithm for register allocation,” in Proc. LLVM-HPC and HiPar, 23–32.

Google Scholar

Hale, W. (1980). Frequency assignment: theory and applications. Proc. IEEE 68, 1497–1514. doi:10.1109/proc.1980.11899

CrossRef Full Text | Google Scholar

Heyward, A. O. (1992). Achieving spectrum conservation for the minimum-span and minimum-order frequency assignment problems. NASA Lewis Research Center.

Google Scholar

Huang, J., Patwary, M., and Diamos, G. (2019). Coloring big graphs with alphagozero. arXiv Prepr. doi:10.48550/arXiv.1902.10162

CrossRef Full Text | Google Scholar

ITU-R (1994). Recommendation ITU-R P.525-2: calculation of free-space attenuation. Int. Telecommun. Union. Ser. P–Radiowave Propag. Available online at: https://www.itu.int/rec/R-REC-P.525/en.

Google Scholar

Jeon, H.-B., Koo, B.-H., Chae, C.-B., Park, S.-H., and Lee, H. (2019). Game theory based hybrid frequency assignment with net filter discrimination constraints. ICT Express 5, 89–93. doi:10.1016/j.icte.2018.05.004

CrossRef Full Text | Google Scholar

Jeon, H.-B., Koo, B.-H., Park, S.-H., Park, J., and Chae, C.-B. (2021). Graph-theory-based resource allocation and mode selection in D2D communication systems: the role of full-duplex. IEEE Wirel. Commun. Lett. 10, 236–240. doi:10.1109/lwc.2020.3025312

CrossRef Full Text | Google Scholar

Kim, Y., Wong, K.-K., Zhang, J., and Chae, C.-B. (2025). Low complexity frequency domain nonlinear self-interference cancellation for flexible duplex. IEEE Trans. Wirel. Commun. 24, 6627–6642. doi:10.1109/twc.2025.3554988

CrossRef Full Text | Google Scholar

Kumar, A. R., and Milleth, J. K. (2018). “A frequency assignment technique for effective sinr and throughput management in a battlefield,” in Proc. Nat. Conf. Commun. (NCC), 1–6.

Google Scholar

Langedal, K., and Manne, F. (2024). Graph neural networks as ordering heuristics for parallel graph coloring. arXiv Prepr. doi:10.48550/arXiv.2408.05054

CrossRef Full Text | Google Scholar

Lee, H., Kim, J., Choi, G., Roberts, I. P., Choi, J., and Lee, N. (2025). Nonlinear self-interference cancellation with adaptive orthonormal polynomials for full-duplex wireless systems. IEEE Trans. Wirel. Commun. 24, 5796–5810. doi:10.1109/twc.2025.3549429

CrossRef Full Text | Google Scholar

Mannino, C., and Sassano, A. (2003). An enumerative algorithm for the frequency assignment problem. Discrete Appl. Math. 129, 155–169. doi:10.1016/s0166-218x(02)00239-1

CrossRef Full Text | Google Scholar

Montemanni, R., and Smith, D. H. (2010). Heuristic manipulation, tabu search and frequency assignment. Comput. Oper. Res. 37, 543–551. Hybrid Metaheuristics. doi:10.1016/j.cor.2008.08.006

CrossRef Full Text | Google Scholar

Waqar, N., Wong, K.-K., Chae, C.-B., Murch, R., Jin, S., and Sharples, A. (2024). Opportunistic fluid antenna multiple access via team-inspired reinforcement learning. IEEE Trans. Wirel. Commun. 23, 12068–12083. doi:10.1109/twc.2024.3387855

CrossRef Full Text | Google Scholar

Watkins, G., Montana, G., and Branke, J. (2023). “Generating a graph colouring heuristic with deep q-learning and graph neural networks,” in Proc. LION 17 (Springer), 553–569. 14286 of Lecture Notes in Computer Science.

Google Scholar

Welsh, D. J. A., and Powell, M. B. (1967). An upper bound for the chromatic number of a graph and its application to timetabling problems. Fomput. J. 10, 85–86. doi:10.1093/comjnl/10.1.85

CrossRef Full Text | Google Scholar

Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Yu, P. S. (2021). A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 32, 4–24. doi:10.1109/tnnls.2020.2978386

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaipairoj, S., and Harmantzis, F. C. (2006). Auction-based congestion pricing for wireless data services. Proc. IEEE Int. Conf. Comm. (ICC). 3, 1059–1064. doi:10.1109/icc.2006.254887

CrossRef Full Text | Google Scholar

Yilmaz, H. B., Koo, B.-H., Park, S.-H., Park, H.-S., Ham, J.-H., and Chae, C.-B. (2017). Frequency assignment problem with net filter discrimination constraints. IEEE/KICS J. Commun. Netw. 19, 329–340. doi:10.1109/jcn.2017.000057

CrossRef Full Text | Google Scholar

Zoellner, J. A. (1973). Frequency assignment games and strategies. IEEE Trans. Electromagn. Compat. EMC-15, 191–196. doi:10.1109/temc.1973.303294

CrossRef Full Text | Google Scholar