Abstract
Reinforcement learning (RL) has shown superior performance in solving sequential decision problems. In recent years, RL is gradually being used to solve unmanned driving collision avoidance decision-making problems in complex scenarios. However, ships encounter many scenarios, and the differences in scenarios will seriously hinder the application of RL in collision avoidance at sea. Moreover, the iterative speed of trial-and-error learning for RL in multi-ship encounter scenarios is slow. To solve this problem, this study develops a novel intelligent collision avoidance algorithm based on approximate representation reinforcement learning (AR-RL) to realize the collision avoidance of maritime autonomous surface ships (MASS) in a continuous state space environment involving interactive learning capability like a crew in navigation situation. The new algorithm uses an approximate representation model to deal with the optimization of collision avoidance strategies in a dynamic target encounter situation. The model is combined with prior knowledge and International Regulations for Preventing Collisions at Sea (COLREGs) for optimal performance. This is followed by a design of an online solution to a value function approximation model based on gradient descent. This approach can solve the problem of large-scale collision avoidance policy learning in static-dynamic obstacles mixed environment. Finally, algorithm tests were constructed though two scenarios (i.e., the coastal static obstacle environment and the static-dynamic obstacles mixed environment) using Tianjin Port as an example and compared with multiple groups of algorithms. The results show that the algorithm can improve the large-scale learning efficiency of continuous state space of dynamic obstacle environment by approximate representation. At the same time, the MASS can efficiently and safely avoid obstacles enroute to reaching its target destination. It therefore makes significant contributions to ensuring safety at sea in a mixed traffic involving both manned and MASS in near future.
1 Introduction
Maritime transportation is often deemed as the foundation of international trade and economy. For decades, research on ship navigation safety has therefore been growing with regards to both classical hazards and emerging risks brought by new technologies such as maritime surface autonomous ships (MASS). Although the occurrence frequency of marine accidents has decreased with the development of an integrated bridge system, navigation-related marine accidents still result in catastrophic consequences today including those arising from human factors (Zhang et al., 2021). It is particularly worrisome when fast powered vessels approach to or pass through inland waterways and/or busy waters (e.g. ports), there are new collision risks of different degrees involving the give ways by a ship (Mou et al., 2010). Furthermore, it becomes more complicated when fishing vessels are concerned as they sometimes overlook the International Regulation for the preventing Collision at Sea (COLREGs) (Yi, 2015). To address such concerns, it is necessary and beneficial to develop an intelligent collision avoidance decision-making system to enhance safety during navigation.
Within this context, most academic research efforts are put forward to develop intelligent collision avoidance decision methods by using various algorithms. The approaches are generally divided into rule-based, soft computing, and learning-based categories. The most representative rule-based algorithms are finite state machines and rule bases. Wang et al. (2021) proposed a local collision avoidance algorithm for unmanned surface vehicles (USVs), which is composed of collision risk assessment, steering occasion determination, and navigation waypoint update. These three parts are solved by finite state machines. Yu et al. (2021) incorporated key dynamic risk factors into a rule-based Bayesian Network approach to model ship and offshore installations collision risk. The dynamic collision avoidance knowledgebase including procedural knowledge, the knowledge of the facts based on a database technology, and the knowledge of the cause and effect analysis of ship collision, has been consolidated into the effects of Personifying Intelligent Decision-making for Vessel Collision Avoidance (Li et al., 2010). Although the rule-based algorithm has clear logic, strong visibility, and stability, it leads to inconsistent vessel behavior due to the condition of state cutting. It is easy to have the overlaps between the triggering conditions of a behavior, resulting in system failures. Further, there are bottlenecks in the processing of complex working conditions and the improvement of algorithm performance (Tam et al., 2009; Wang et al., 2022). To solve these problems, many scholars have proposed soft computing methods, such as genetic algorithm (Tsou et al., 2010), velocity Obstacle (Wang et al., 2020), fuzzy logic (Fiskin et al., 2021), geometric calculation (Ding et al., 2021), and model predictive control (Yuan and Gao, 2022). However, these soft computing methods have exposed their limitations in the MASS collision avoidance applications, among which is the difficulty of tackling new collision avoidance risks due to lack of scene adaptability after a MASS attempt to avoids multiple ships successively (Burmeister and Constapel, 2021).
In recent years, with the rapid development of artificial intelligence technology, the learning-based algorithms attract increasing attention in autonomous navigation and decision-making systems (Huang et al., 2020; Ferreira et al., 2022; Rødseth et al., 2022). According to different principles, such systems are divided into decision-making methods related to deep learning (Chen et al., 2020; Grigorescu et al., 2020) and the interactive learning theory or reward mechanism (Gao et al., 2018; Gao et al., 2021). Within the context of MASS, some scholars used deep learning for autonomous ship collision avoidance parameter training (Chen et al., 2021), ship behavior prediction (Murray and Perera, 2021) and trajectory prediction (Liu et al., 2022). Meanwhile, the others have begun to construct anthropomorphic and human-like intelligent collision avoidance decisions based on reinforcement learning (RL). By considering scene dimension reduction and segmentation, an intelligent collision avoidance decision model for autonomous ships is constructed based on deep reinforcement learning (DRL) to realize safe navigation and obstacle avoidance in an uncertain environment (Zhang et al., 2019). Xu et al. proposed a path planning and dynamic collision avoidance algorithm based on deep reinforcement learning for unmanned surface vehicles (USVs), subject to COLREGs (Xu et al., 2022). Xie et al. (2020) combined the long short-term memory neural network (LSTM) inverse model-based controller and the model-free A3C policy, to achieve ship collision avoidance under unknown environments. An automatic collision avoidance algorithm was proposed by combining the LSTM and RL in continuous action spaces (Sawada et al., 2021). However, deep learning has, upon the authors’ best knowledge, yet been applied for end-to-end adaptive navigation, largely due to the difficulty by the complex and changeable marine environment. The use of the RL algorithm to learn the anti-collision of autonomous ships, is at large presented in a discrete space.
In addition, other problems such as poor initial performance and slow convergence speed on DRL-based autonomous planning and decision-making are also revealed in the related research. Zhao et al. (2020) propose a novel DRL model which is composed of an actor, an adaptive critic, and a routing simulator. The adaptive critic is mainly to accelerate the convergence rate and improve the solution quality for autonomous vehicle. For unmanned aerial vehicles (UAVs) trajectory planning, a navigation reward and a navigation effort are fusion for a novel reward function, to improve DRL convergence speed (Li et al., 2022). In addition to changing the network structure similar to the above two literatures, another popular approach is to introduce transfer learning, domain transfer and knowledge transfer included, which improves the DRL network training effect by reducing the random probability of state transition and increasing the sampling speed (Shi et al., 2021; Li et al., 2021). However, in the maritime sailing environment, the change of a scene domain is extremely inconspicuous. Existing work dedicated to cross-task transfer in autonomous systems is only designed for homogeneous scenario or similar scene domains. To address them, this paper aims to develop an approximate representation reinforcement learning collision avoidance (AR-RLCA) method for collision avoidance of MASS at a continuous state space. The research adopts the solution method of function approximation with parametric value given by prior knowledge.
The main contributions of this work are summarized as follows.
-
(1) We discuss continuous state space collision avoidance, pointing out mainly challenges in the development of the DRL based collision avoidance decision-making method.
-
(2) Aiming at the discussed problem, a novel DRL method with prior knowledge based approximate representation is proposed. This method provides DRL collision avoidance decision-making with a workable direction.
-
(3) We design a novel online solution method to the parametric approximation model based on gradient descent. Moreover, the coastal static obstacle environment and the static-dynamic obstacles environment experiments are conducted to validate the AR-RLCA.
The rest of this paper is organized as follows. Section 2 describes the definitions and theories of multi-ship collision avoidance and reinforcement learning. Section 3 presents the framework of the algorithm development that constitutes the main contributions of this paper, including approximate representation, a reward function, and a value function approximation solution method. The simulation and result, including analysis, obtained using the algorithms are presented in Section 4. In this section, we set up simulation experiments from two environments, the coastal static obstacle environment and the static-dynamic obstacles mixed environment, respectively, to verify the algorithm. Finally, the conclusion and future work are presented in Section 5.
2 Definitions and theories
This section outlines all the definitions and the theories relating to collision avoidance in Section 2.1 and reinforcement learning in Section 2.2.
2.1 Continuous state space collision avoidance problem
Ships sailing collision risk increases along with the growing complexity of maritime traffic in the water. When multiple ships are encountered, in the whole process of sequential collision avoidance, the navigation situation of MASS presents a continuous state space. According to the COLREGs, there are three kinds of encounter scenarios, including head-on, overtaking, and crossing, which are shown in Figure 1. In addition, this paper adopts a way of avoiding collision mainly by turning according to the requirements of a good seamanship.
Figure 1
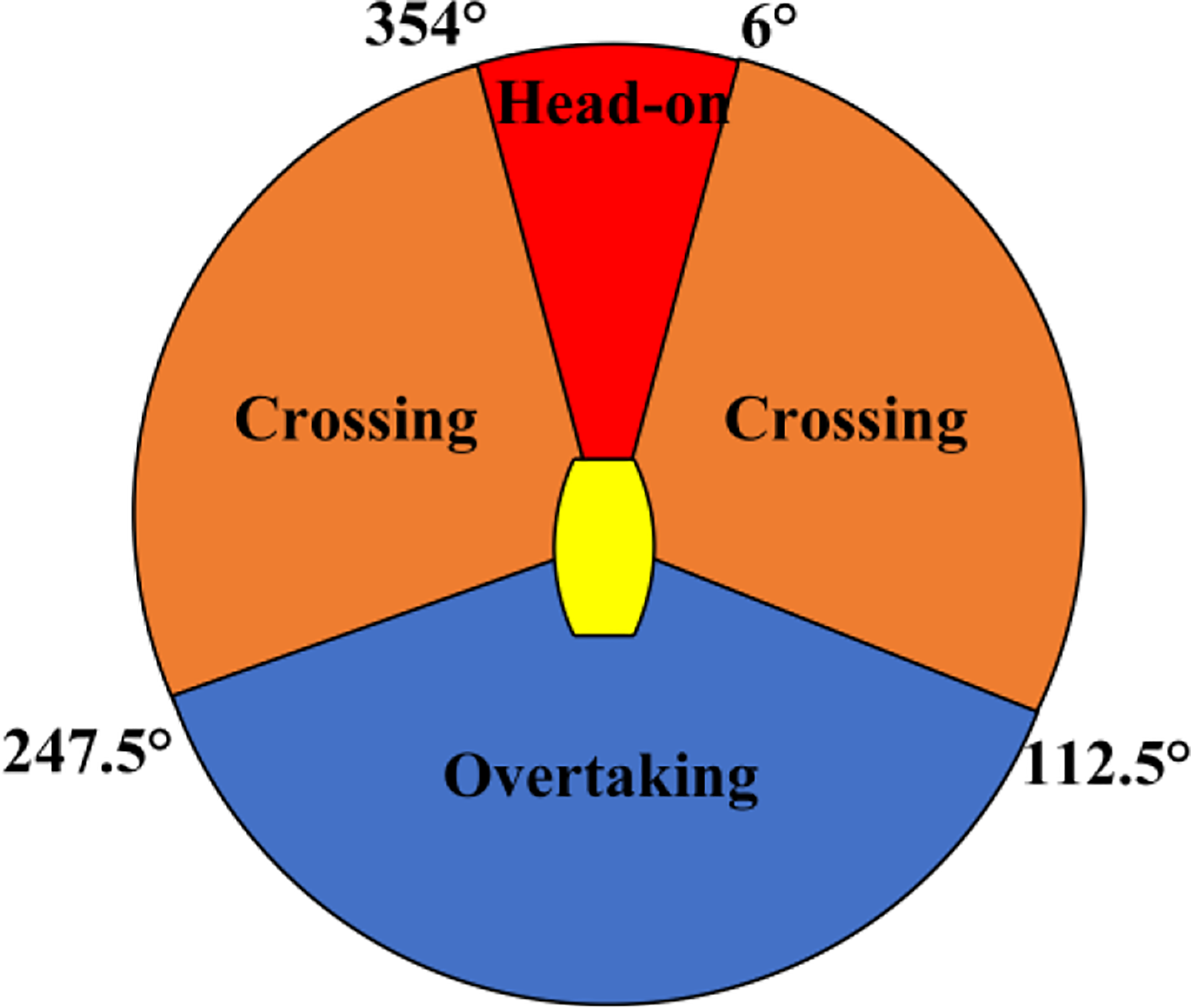
Encounter scenarios division diagram.
Continuous state space collision avoidance problem can be regarded as a Markov decision process. When there are some risks of collision with multiple ships, any MASS will avoid collision according to the degree of danger posed by the target ships. MASS will adopt various motion behaviors. Until all obstacles are avoided, including both static and dynamic obstacles. After each anti-collision action, the status of operating environment will change. In such scenarios, the autonomous ship will get the evaluation feedback of this behavior. As shown in Figure 2, this situation leads to the sequential collision avoidance of autonomous ships in a continuous state space scenario.
Figure 2
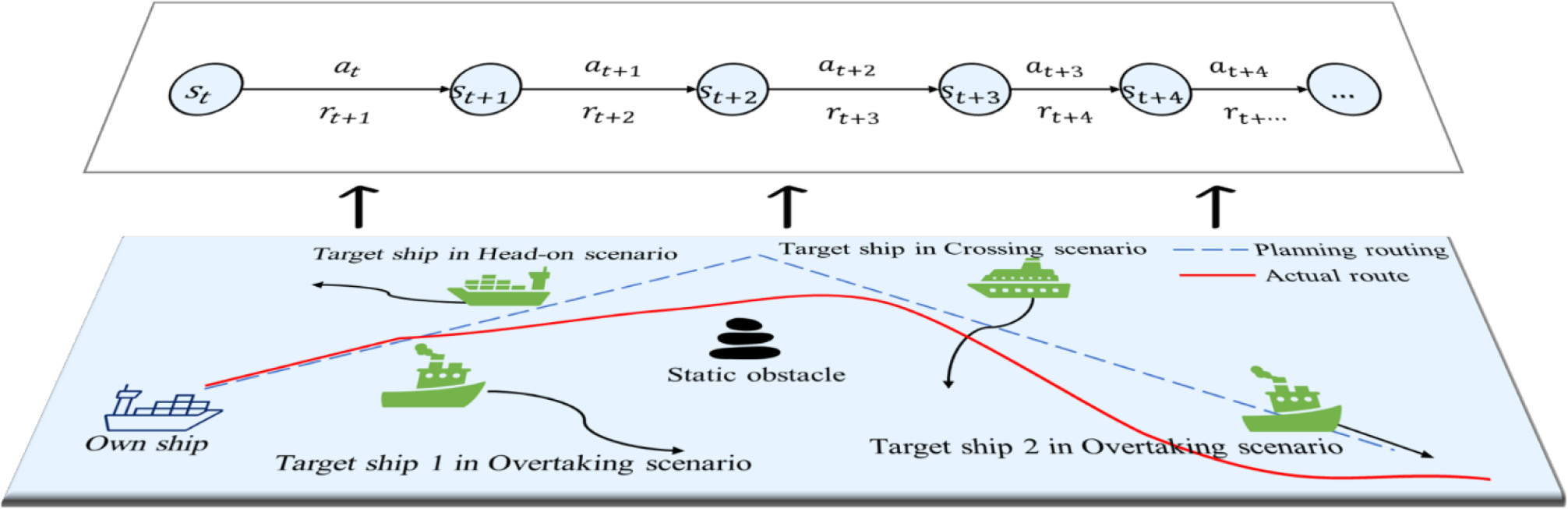
Collision avoidance of autonomous ships in a continuous state space scenario. Graph flow of upper and lower layers: the lower layer is the schematic diagram of the physical scene. In the scene, there is a static obstacle and four target ships (dynamic obstacles). Four target ships form the head-on, crossing, and overtaking scenarios with the own ships. In the upper layer, st represents the state at time t, at represents the anti-collision action at time t, rt+1 represents the reward from st to st+1 by action at at time t.
2.2 Reinforcement learning
Learning by interaction with a sailing environment is the primary method for crew members to acquire good seamanship. One of the main characteristics of this learning process is the ability to adapt to uncertain environments and gradually enhance its own ability. In the field of artificial intelligence, this learning method usually has two characteristics: one is to actively test the environment. Second, the feedback from the environment to the tentative action must be evaluative. This learning method is named the RL (Sutton and Barto, 2018). RL is an interactive learning method, which mainly includes two stages: trial-and-error search and delay return. RL problems can be described using a Markov decision process (MDP) framework. MDP contains 4 parts: state space X, action space U, environment’s migration function f, and reward function R, i.e., X, U, f, R.
The task of autonomous ships is to learn an anti-collision strategy π: X →U, in the process of interacting with the environment. This strategy maximizes the cumulative reward (1).
where t is the time step. γ< 1 is a constant, which determines the relative proportions of delay versus immediate reward.
In RL, a value function is employed to link the optimal objective and policy of the MDP, including the Q-value and V-value functions. Under a certain policy π (x) and a state x, taking a given action u, the Q-value function Qπ: X × U → ℝ is:
Thus, we can calculate the optimal policy π*.
3 Methods
To solve an autonomous ship collision avoidance problem in a continuous state space, first, we use the approximate representation based on prior knowledge to reduce the effect of difference between the various states and scenarios. Secondly, a new safety reward function is designed. Lastly and most importantly, we proposed a method of value function approximation to solve the RL collision avoidance problem in a continuous state space.
3.1 Approximate representation
In solving a collision avoidance problem, it has been acknowledged that it is notoriously difficult to store and learn every state. Therefore, in the continuous state space, we use an approximate representation to learn approximate storage for an anti-collision policy. On one hand, using approximate representation can improve the sampling efficiency and iteration speed. On the other hand, approximate representation offers a better performance in scenarios generalization. This makes it an attractive candidate for its application in this study.
In the Q-value iterative algorithm in a random environment, the uncertainty of the random problem itself needs to be considered in addition to sampling evaluation.
where the E is expected function. l represents the number of state basis function (BF).
According to the COLREGs, there are three BF of MASS encounter scenarios, which are mentioned in Figure 1. Thus, the prior knowledge of the BF as shown in Table 1.
Table 1
| Feature | Definition | |
|---|---|---|
| Overtaking |
vos > vTS |
hasFrontScenario = Overtaking Scenario |
| Head-on |
|
hasFrontScenario = Head-on Scenario |
| Crossing |
|
hasFrontScenario = Crossing Scenario |
The prior knowledge about the BF.
is the Euclidean distance of Target ship (TS) and Own ship (OS). n mile is the nautical mile, a unit used to measure a distance at sea (1 n mile ≈ 1852 m). It is noteworthy that, the ships concerned in this study should have a length of greater than 50M (Wu, 2014).
Consequently, we adopt the method of parameterized state function mapping, from a parameter state space to a target state space. The method takes into account the state approximator whose state is parameterized into an n-dimensional vector ω. Each parameter state vector corresponds to an approximate state basis function.
In this paper, the linear state function approximator with parameters consists of three BF ϕ1, ϕ2, ϕ3: X × U → ℝ and three-dimensional parameter vectors. Therefore, the linear calculation formula of the approximate Q value corresponding to the state action pair (x,u) is given as:
where ϕ (x,u) is a n-dimensional vector composed of BF.
For a two-dimensional situation, this paper uses a rough coding technology as a continuous state space set. This technology completely covers the state space in the navigation environment of autonomous ships with N circles. Each circle represents a feature. For different state characteristics of overtaking, head-on, and crossing encounter scenarios, we have adopted different generalization methods as shown in Figure 3. In an overtaking scenario, the encounter situation changes slowly, leading to the choice of the wide generalization. Conversely, because the encounter situation changes quickly in the head-on scenario, we use a narrow generalization. Comparatively, the scenario change of crossing encounter is more complex, which does not reflect a symmetrical mapping in the vertical and horizontal directions. Thus, asymmetric generalization is proposed for this scenario because of its strong generalization ability in the direction of its elongation. According to good seamanship, the ellipse whose major axis is 1.5 times the ship length is the generalization unit area for crossing scenario. A circle with a diameter of 1.5 times the length of the ship is used as the generalized unit area of the overtaking scenario. A circle with a diameter of the length of the ship serves as the generalized unit area for head-on scenario. In the same generalized unit area, generally only one state transfer is made, except when there is an emergency risk.
Figure 3
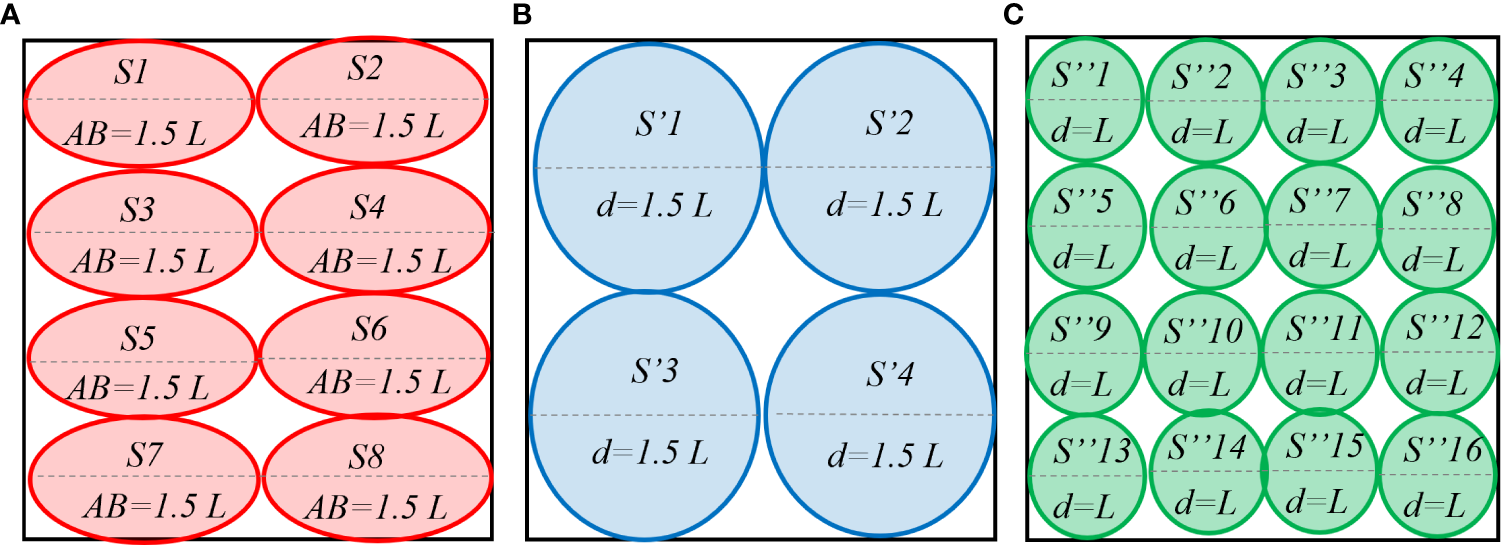
Schematic diagram of the influence of (A) crossing, (B) overtaking, and (C) head-on scenarios features on generalization. S represents the state of the environment. AB is major axis of ellipse. d is the circle diameter. L indicates the length of the ship.
During online sampling, the three encounter scenarios identified for the first time are used as the reference scenario, and an index table is built. The status action of BF can be expressed as:
where [i,j] represents a scalar index of the state space and the action space. i,j represents the number of state space and action space, respectively.
3.2 Reward function
For continuous learning and training of continuous state space events, the reward function should be phased, and goal constrained. Initially, we apply a dense reward function as implemented in Wang et al. (2021). Equation (9) specifies the collision aspects and goal aspects construction in the reward function. In the continuous space searching model, a MASS sailing situation is divided into N state spaces, which includes the safety state and the obstacle areas.
where (x,y)os is the position of OS. (x,y)obstacle is the position of obstacles, and (x,y)goal is the goal position. dsafezone is the radius of a MASS safe zone. In this paper, we take this value as the length of 5 pixels.
The MASS should select the action search strategy that meets “early, large, wide and clear” requirements from the COLREGs. Therefore, in the design of a reward function, the behavior of approaching obstacles will be given a penalty value, and vice versa. Therefore, we set different safety zones and risk zones for obstacles and ship.
As shown in Figure 4, if the TS enters the safe area of the OS, a collision will occur, but there is still a risk of collision when sailing within the risk zones. Therefore, it is necessary to promote waypoint selected by the OS to be outside the risk zones through the interaction of the risk reward function. CR is for assessing the risk value in encounter scenario (Chun et al., 2021).
Figure 4
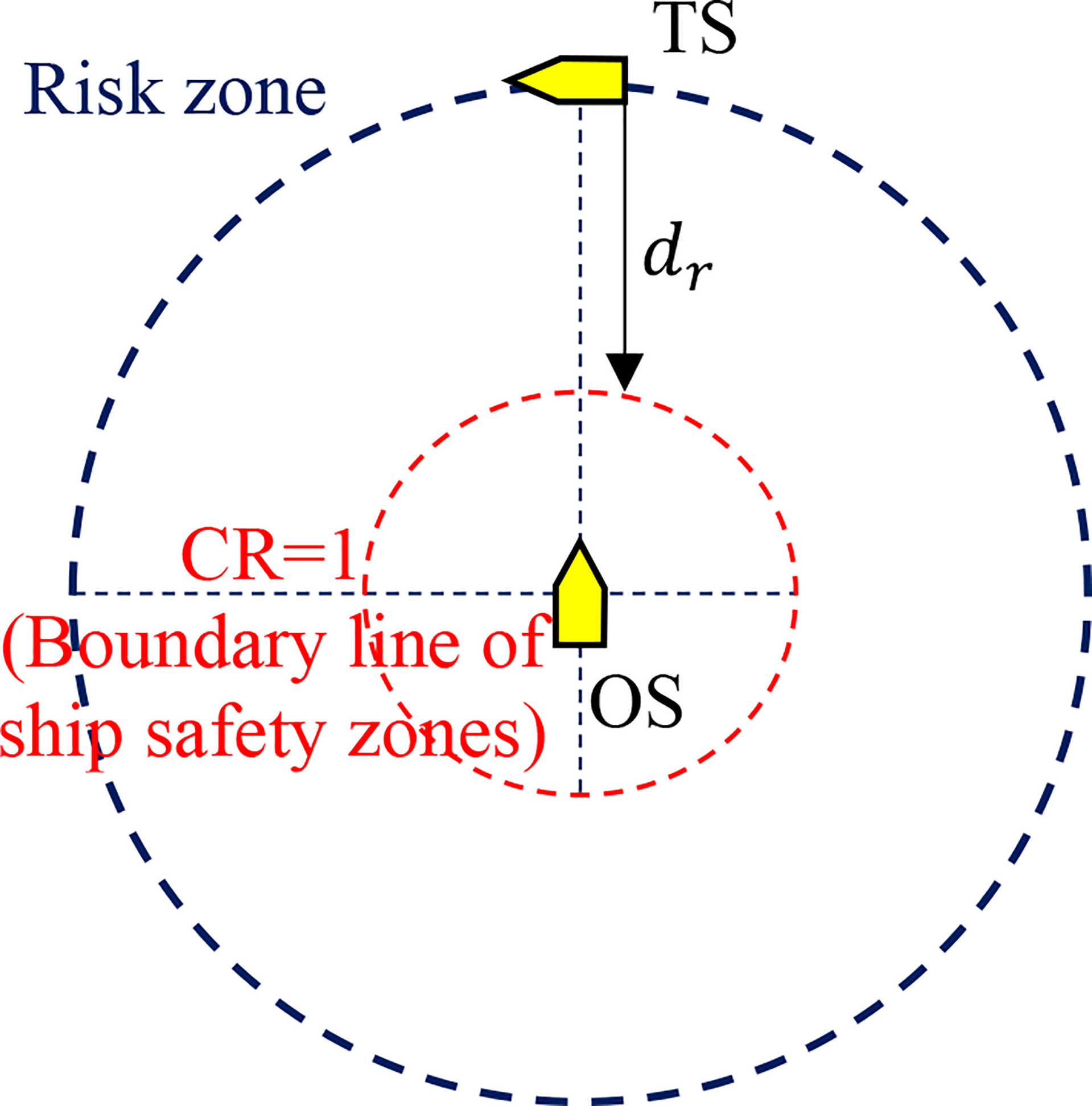
The schematic diagram of safety zones and risk zones for obstacles and own ship.
where, DCPA is the distance to the closest point of approach, and TCPA is defined as the time to the closest point of approach. V is speed of TS. CR0 is a criterion risk to determine that the OS earliest anti-collision. dr is the radius of risk zone.
Therefore, the risk reward function is as follows.
At the same time, to improve the stability of the ship’s steering motion, we added a reward function for the steering angular constraint, as shown in equation (12).
where ω is a single steering angular variation.
In summary, the cumulative reward is calculated as follows.
3.3 Value function approximation solution
In this paper, we design an online solution method to the parametric approximation model based on gradient descent. Using Equation (6), the optimal value function is approximated by minimizing the mean square error (MSE) (Mitchell, 1997).
where ωt is the parameter vector. Qπ (x,u) and are the real value and estimated value at time t, respectively. is the weight distribution of the state-action (x,u). expresses the error of temporal difference (TD), indicated by symbol δ.
Further, the parameter vector is solved as follows:
To sum up, we combine the approximate representation of a state value function and RL to achieve the collision avoidance solution for MASS in a continuous state space. Three groups of state BF are set for the continuous state space. Then, the MSE is solved by the state value function approximation learning model and continuous renewing of MSE by interacting with the environment. Finally, the state value function is solved using the gradient descent to approximate the model. The pseudo code of Algorithm 1 is shown below, while the algorithm framework is shown in Figure 5.
Figure 5
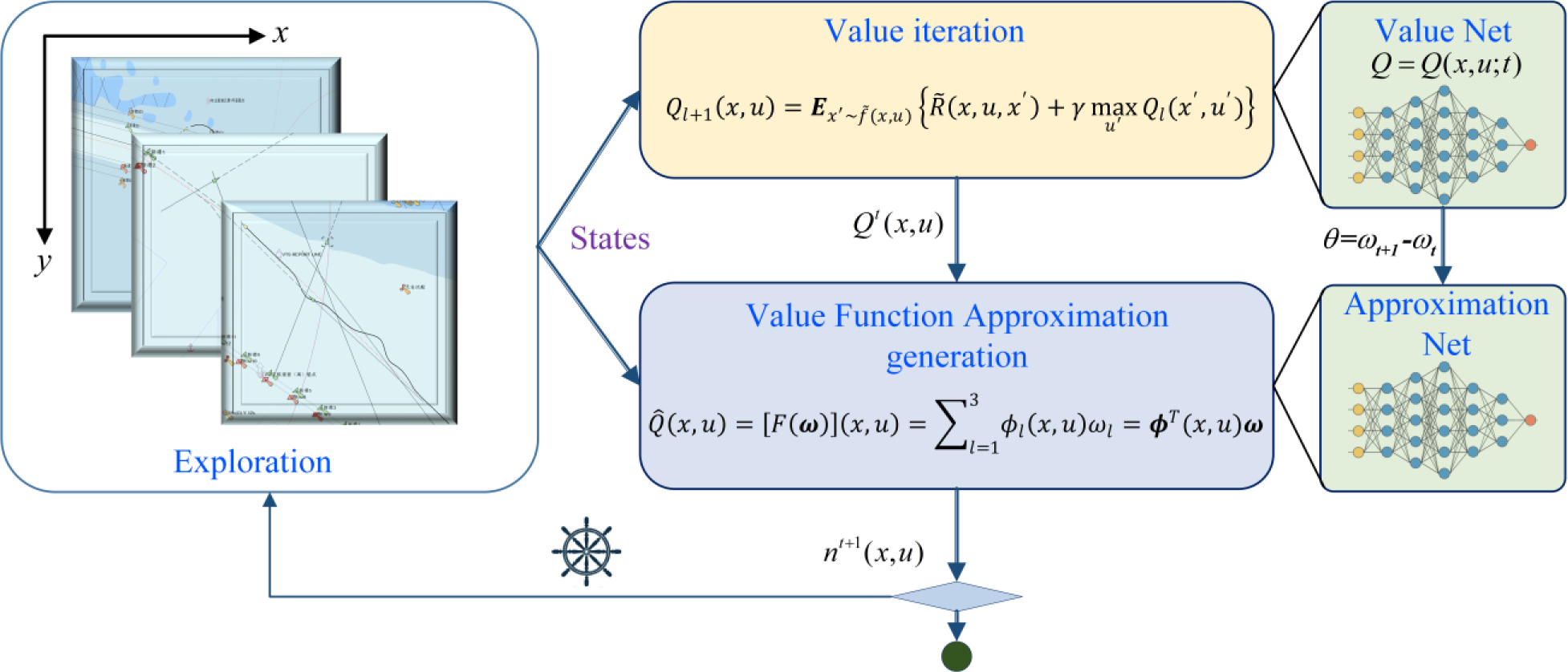
Q-valued function approximation learning algorithm framework.
Algorithm 1. Q-valued function approximation learning algorithm based on gradient descent
1. Input BF ϕ1, ϕ2, ϕ3: X × U → ℝ, state transfer function T, Reward function R, Discount factor γ.2. Initialize parameter vector, ω0 ←03. Initialize MASS state x04. repeat (for each time step t = 0,1,2·;·;·;)① ut← ε greedy (for exploration and exploitation)② action ut, caculate xt+1 and rt+1③ ωt+1←ωt+α[rt+1+γmaxu′(ϕT(xt+1,u′)ωt)−ϕT(xt,ut)ωt]ϕ(xt,ut)④ until ωt+1-ωt< θ⑤output ω* = ωt+1
4 Simulation and result
In this section, the validity and suitability of our method on the MASS collision avoidance in the two scenarios are evaluated: the coastal static obstacle environment and the static-dynamic obstacle mixed environment. The first scenario (the coastal static obstacle environment) aims to test the exploration and exploitation ability of AR-RLCA. Tianjin Port is taken as an illustrative example for the simulation using Python 3 and Pygame platform. Referring to (Lillicrap et al., 2015; Henderson et al., 2018), the hyperparameters of our method are shown in Table 2. In this study, we set up the initial epsilon as 0.5, and the final epsilon as 0.01.
Table 2
| Parameter | Value |
|---|---|
| γ | 0.9 |
| α | 0.99 |
| t | 2500 |
| Num. Nodes | 10000 |
| ε | 1~0.01 |
| θ | 0.001 |
The hyperparameters of AR-RLCA.
γ is the discount factor. α is the learning rate. t is total epoch of training. Num. Nodes represents the data storage nodes from exploration to exploitation. ε is the epsilon. θ is the termination condition parameter.
4.1 Scenario 1: The coastal static obstacle environment
In this scenario, the MASS anti-collision planning in the coastal static obstacle environment, including seaboard and static obstacle ships of different sizes is simulated. The projection of the chosen harbors in Tianjin port is designated as a simulation environment of 684*806 pixels. As shown in Figure 6, the gray circle represents the static obstacle ship, and the brown polygon represents the seaboard. As shown in Figure 6A, the start point is set as (631, 503) with a blue circle, and the goal point is set as (190, 348) with a red circle.
Figure 6
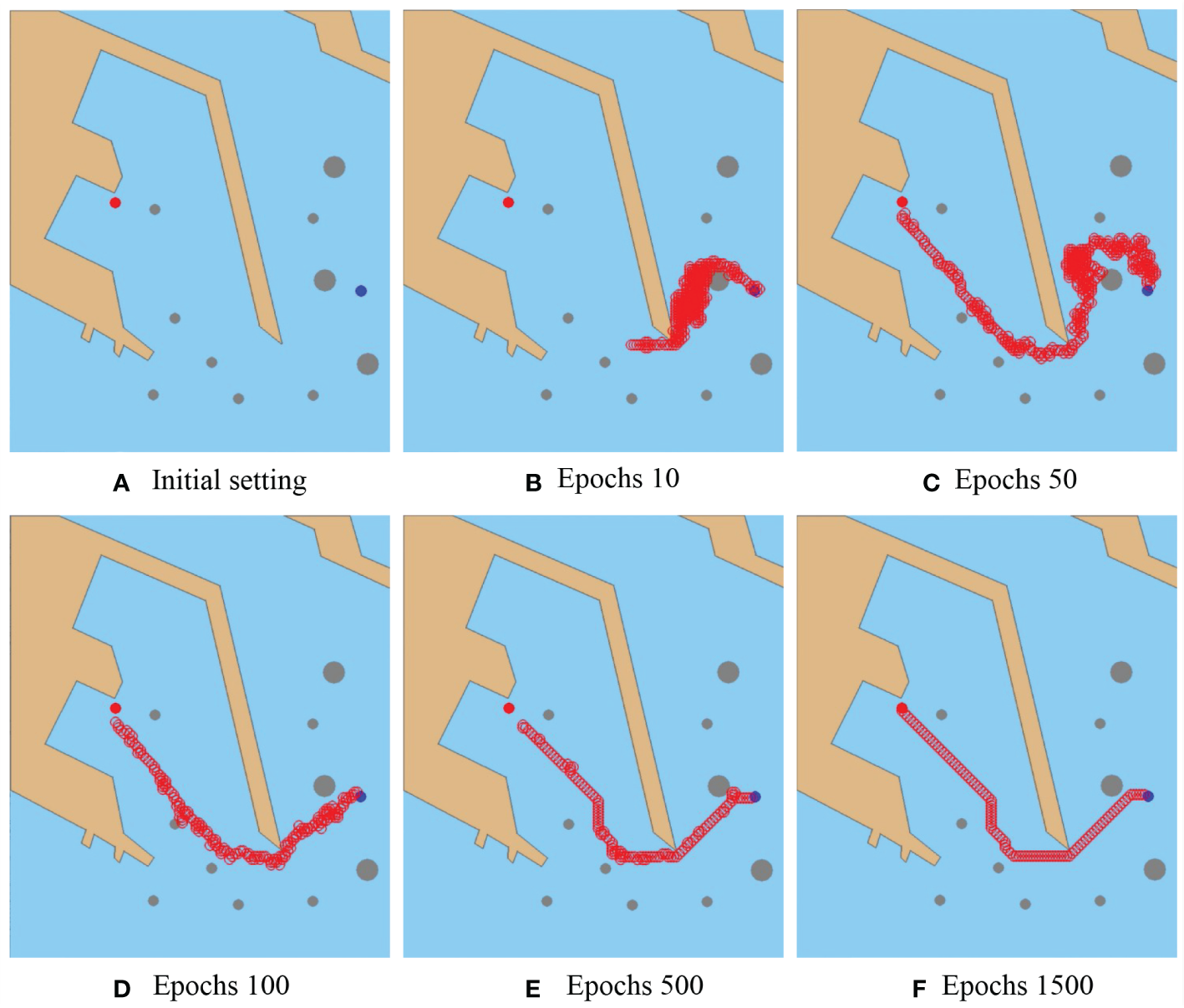
Result of collision avoidance in the coastal static environment. Snapshots of the six epochs in simulation: (A) initial setting, (B) epochs 10, (C) epochs 50, (D) epochs 100, (E) epochs 500, and (F) epochs 1500. The red hollow circle is the collision avoidance path of the MASS. A safety area of 5 pixels is set for the MASS to be away from all the obstacles. In the training scenario, the MASS’s goal is to sail from the start point to the goal point safe.
As shown in Figure 6B, the condition represents the initial exploration stage in which the algorithm is searching for samples and storing the learning experience in the memory pool. In this stage, the algorithm’s first search takes many steps and can get stuck in local iterations. Through the interactive training of the reward function, the target point is found for the first time at the 50th epochs, as shown in Figure 6C, and continued with the search as there was still random search and trial and error. Gradually, the MASS improves learning experience utilization. As shown in Figures 6D, E the MASS has an approximate target direction. Following these steps, the random search for probability of avoidance trajectories gradually decreases. The avoidance path planned by the algorithm tends to be stable and optimized at the 1500th epochs. In the end, MASS successfully avoided all static obstacles and achieved safe sailing from the initial point to the target point.
In order to analyze the learning convergence performance of the algorithm, the training step variation in each iteration was counted. As shown in Figure 7, there are three-part visualization about step-epoch. The first is a whole line chart from epoch 0 to epoch 2500. From this part, we can see the AR-RLCA algorithm is convergent and has a good interactive learning ability. At the initial epoch, the algorithm needs to explore and sample obstacle environments to search for the obstacles and goal points. So, 17,405 steps are taken in the initial epoch. In addition, to better present the algorithm performance, we zoom in the convergence trend graph of two key nodes (see Figures 7A, B). The part A is a step-epoch area chart. It can be seen from the 100th epochs that the integral area of step line is getting smaller and smaller. It can be demonstrated that the utilization of learning experience accumulated on the exploration is improved. The part B can present another critical node, the 1500th epoch. At this point, the algorithm reaches the condition for terminating the iteration, and finds the avoidance path with the largest cumulative reward.
Figure 7
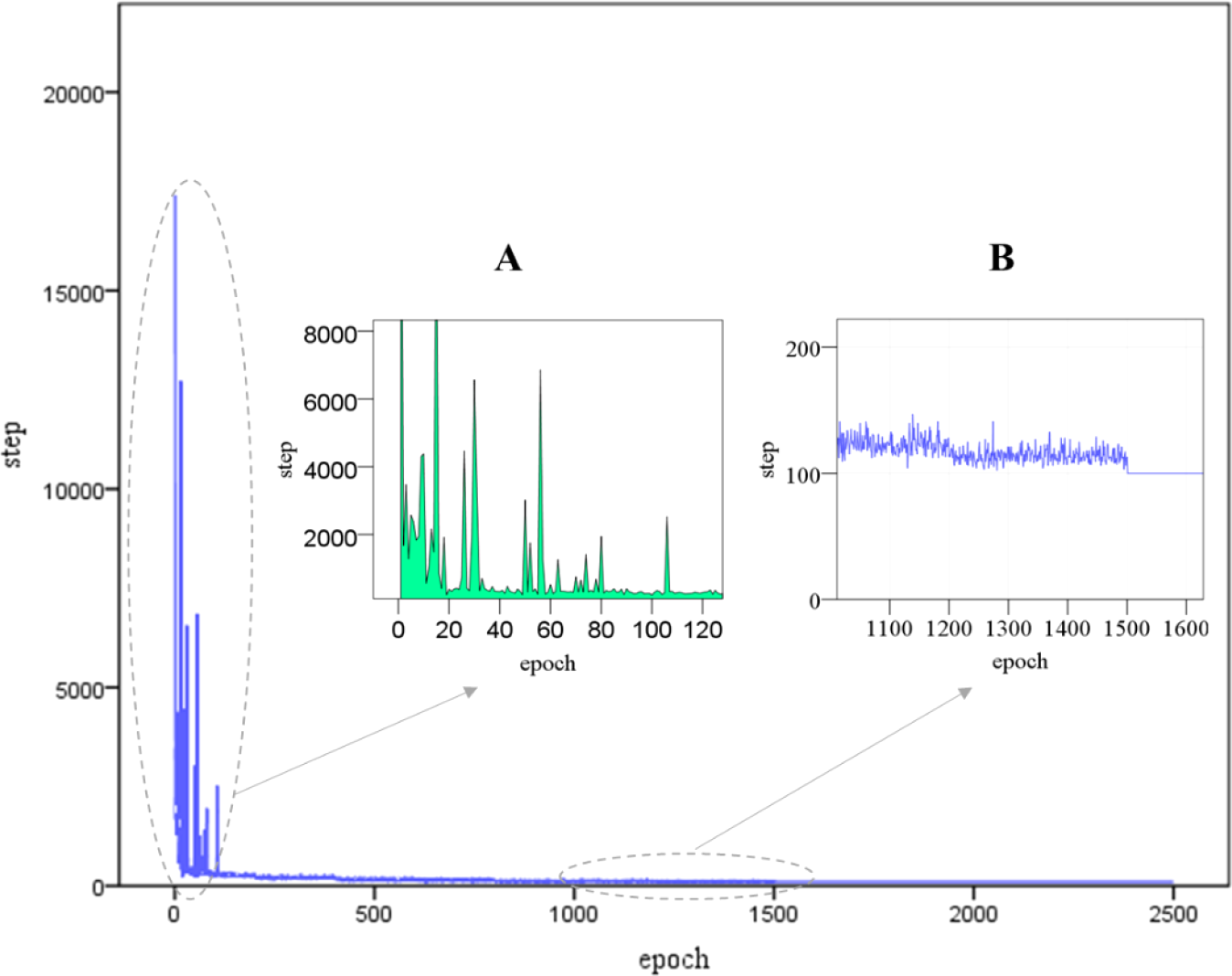
Training step variation with each epoch from the start point to the goal in simulation scenario 1, including And enlarged (A) 0-120 epochs and (B) 1100-1600 epochs two parts.
4.2 Scenario 2: The static-dynamic obstacles mixed environment
In the actual coastal environment, there are often static and dynamic obstacles. This requires a MASS to avoid the target ships (TS), static obstacles (SO), and seaboard. In this section, we simulate a static-dynamic mixed environment, to verify the collision avoidance performance in a continue state space. The environment state settings are shown in Table 3.
Table 3
| Obstacles | Initial point | Goal point | Speed | Safe Zone |
|---|---|---|---|---|
| TS1 | (406,600) | (340,490) | (5,5) | 15 |
| TS2 | (630,448) | (495,313) | (3,5) | 10 |
| TS3 | (325,562) | (493,625) | (8,3) | 15 |
| SO1 | (583,281) | — | (0,0) | 20 |
| SO2 | (357,398) | — | (0,0) | 10 |
| SO3 | (192,415) | — | (0,0) | 20 |
| SO4 | (223,323) | — | (0,0) | 10 |
| SO5 | (220,640 | — | (0,0) | 15 |
| SO6 | (576,710) | — | (0,0) | 10 |
| SO7 | (638,574) | — | (0,0) | 10 |
| SO8 | (498,515) | — | (0,0) | 20 |
| SO9 | (455,213) | — | (0,0) | 15 |
| Seaboard | Brown Polygon | — | — | — |
The initial environment state settings parameters of the static-dynamic obstacles mixed environment.
The data units in the table are described by pixels.
As shown in Figure 8, the start point is set as (211,190) with a blue circle, and the goal point is set as (619,183) with a red circle. In the simulation experiment, the target ship is set as a dynamic obstacle sailing at a constant speed. Through offline sampling and online value function approximation training, the ship sails from the start point to the goal safe. The anti-collision trajectory is shown in Figure 8. As shown in Figure 8A, the MASS is sampling the sailing environment and trying anti-collision. Ship attempts multiple random actions at almost the same location. Therefore, the trajectory direction looks very unstable. In the early stage of training, MASS cannot find a better obstacle avoidance trajectory in a multi-obstacle environment. As shown in Figure 8B, the MASS successfully avoids TS1 and TS3, when it forms a head-on encounter situation and a crossing encounter situation. The taken right turn motion also complies with the COLREGs to avoid these two target ships. However, the trajectory of avoidance is still very volatile. As shown in Figure 8C, MASS forms a crossing encounter situation with TS2, and there are some static obstacles in front of TS2. Therefore, the MASS makes a large right turn as soon as possible, not only to avoid passing through the bow of TS2, but also to successfully avoid static obstacles. Finally, the algorithm iteration is completed in 1500 epochs, avoiding three target ships and static obstacles successfully.
Figure 8
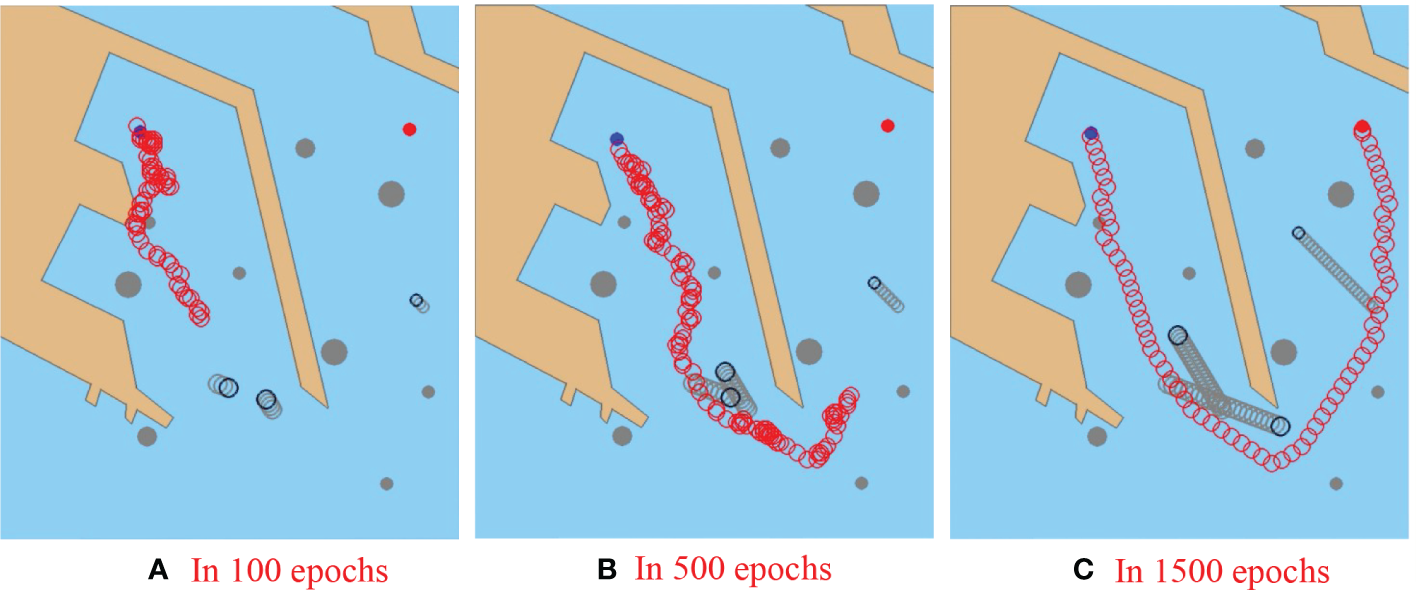
Result of collision avoidance in the static-dynamic obstacles mixed environment. Snapshots of three time-steps in simulation: (A) 100 epochs, (B) 500 epochs, and (C) 1500 epochs. The red hollow circle is the collision avoidance path of a MASS. A safety area of 5 pixels is set for the MASS to keep a safe distance from obstacles. In the training scenario, the MASS’s goal is to sail from the start point to the goal point safe.
In order to analyze the learning convergence performance, the training step variation in each iteration is counted. As shown in Figure 9, there are a whole line chart and two partial magnifications chart. As the whole line chart from epoch 0 to epoch 2500, it is observed that the AR-RLCA algorithm is convergent. At the initial training, the algorithm takes many steps to interact with the environment through a reward function. However, after the offline training and online approximate representation, the algorithm has shown a good convergence performance in the dynamic obstacle environment. In addition, to better present the algorithm performance, we also zoom the convergence trend graph of two key nodes (see Figure 9). The part A is a step-epoch area chart. It can well represent the exploratory properties of the algorithm. The part B includes the 1500th iteration, where the optimal avoidance path output after the algorithm satisfies the convergence conditions is clearly seen.
Figure 9
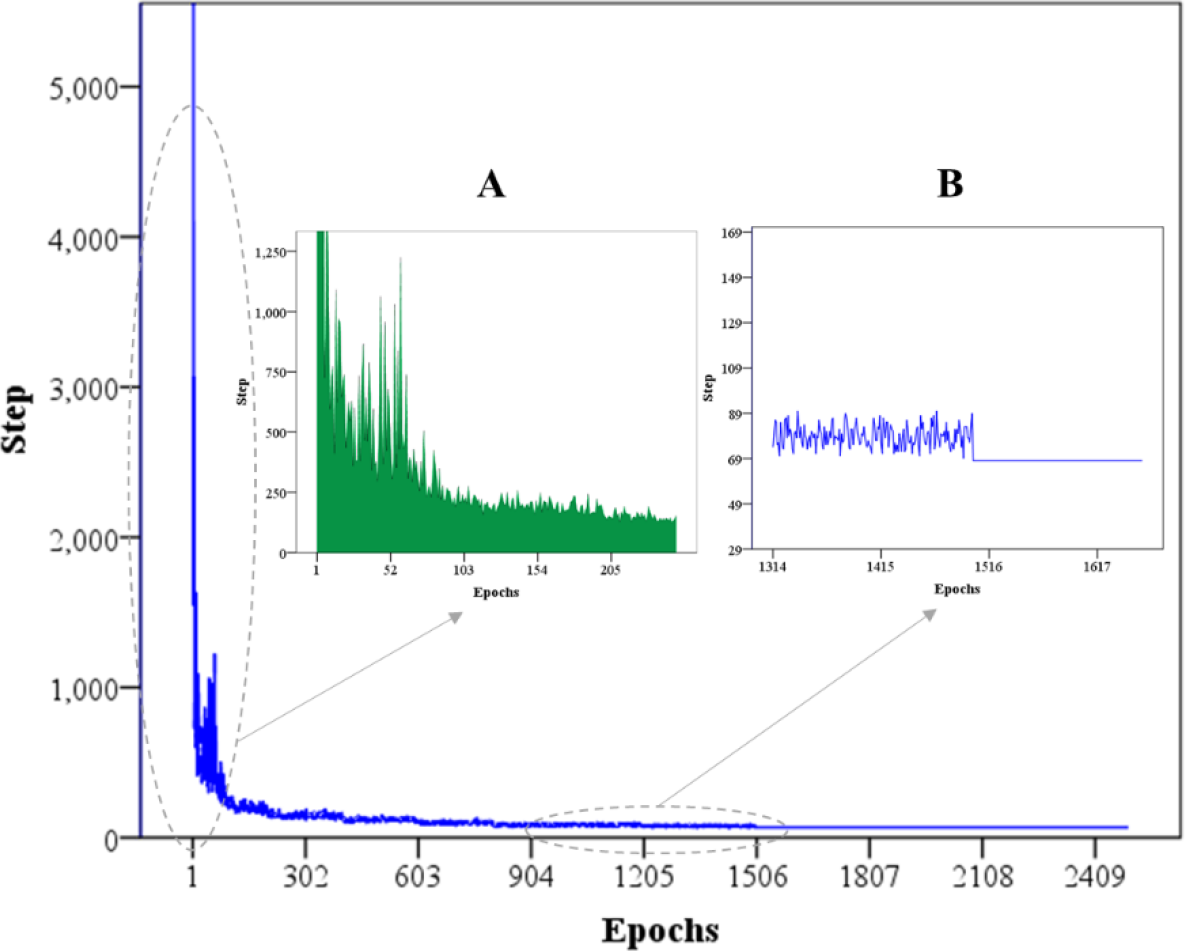
Training step variation with each epoch from the start point to the goal in simulation scenario 2, including And enlarged (A) 1-205 epochs and (B) 1314-1617 epochs two parts.
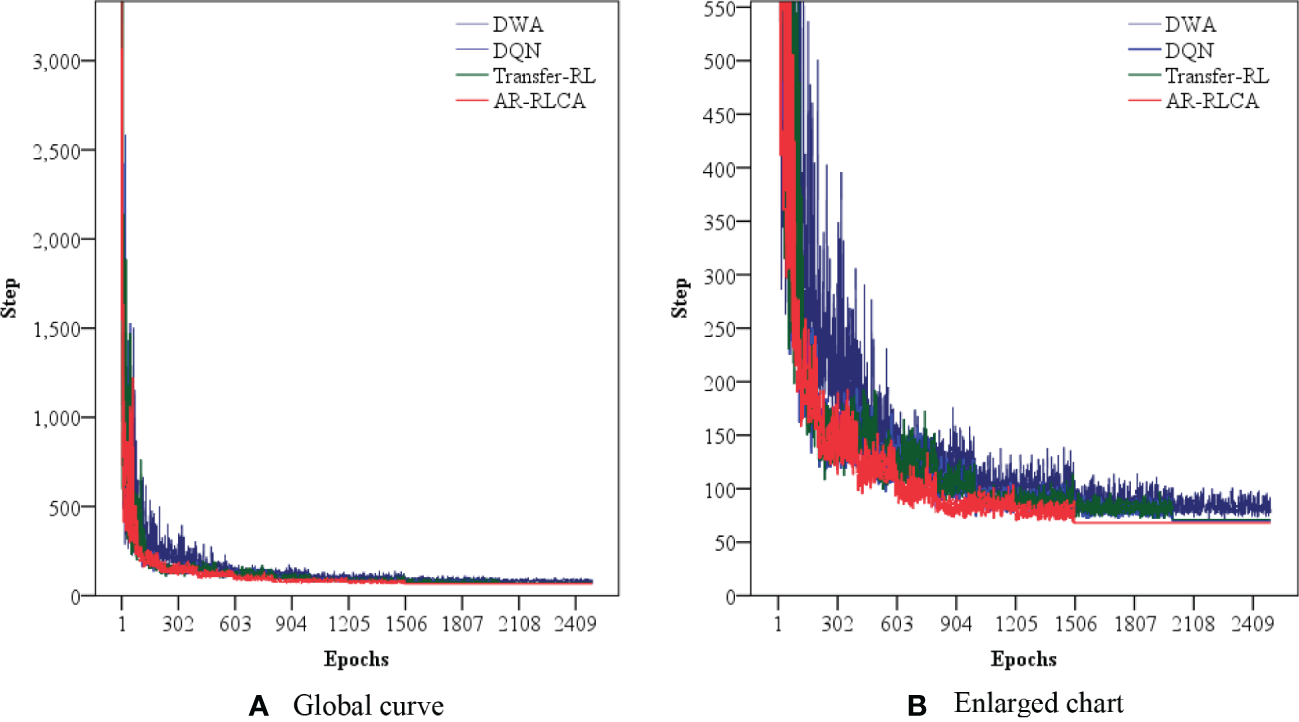
In order to verify the convergence performance and iteration effect of this algorithm, we compare the training steps and result data of the Dynamic Window Approach (DWA), Deep Q-Network (DQN), Transfer RL, and our algorithm. Figure 10 shows the training step - epochs curve chart, where the X-axis is the epochs of training, and the Y-axis is the cumulative step in each epoch.
Figure 10
The training Step-Epochs chart, including (A) Global curve and (B) Enlarged chart.
Figure 10A is the global curve of training step – epochs chart. It can be seen from the Figure 10A that DWA, DQN, Transfer-RL, and AR-RLCA algorithm converges. It shows that basically all of them can solve complex collision avoidance problems in continuous state environment. However, we enlarge the curve chat, as shown in Figure 10B. DWA, DQN, Transfer-RL, and AR-RLCA algorithm have different convergence performance. Compared with learning-based algorithms (DQN, Transfer-RL, and AR-RLCA), DWA have the largest step size fluctuations, and they don’t even stop iterating in the 2500th epochs. The performance of DQN and Transfer-RL is similar. The optimal obstacle avoidance path is planned at about the 2000th epochs. But in terms of trajectory volatility, Transfer-RL is slightly better than DQN. The algorithm proposed in this paper, AR-RLCA, is undoubtedly better than the other three groups of algorithms in solving the problem of continuous state space collision avoidance. Convergence is the earliest, and the trajectory is more stable.
In addition, we count the reward interactions of the DWA, DQN, Transfer-RL, and AR-RLCA algorithms. As shown in Figure 11, the proposed algorithm, AR-RLCA has less reward interaction in the later stage of iteration, and most of them are distributed in the early stage of exploration. Basically, the AR-RLCA algorithm gets the maximum expectation at 1200 epochs. It highlights that the algorithm proposed in this paper can efficiently balance exploration and utilization, achieving rapid convergence. From the perspective of the number and density of bubbles, AR-RLCA is also the best in decision-making and planning results.
Figure 11
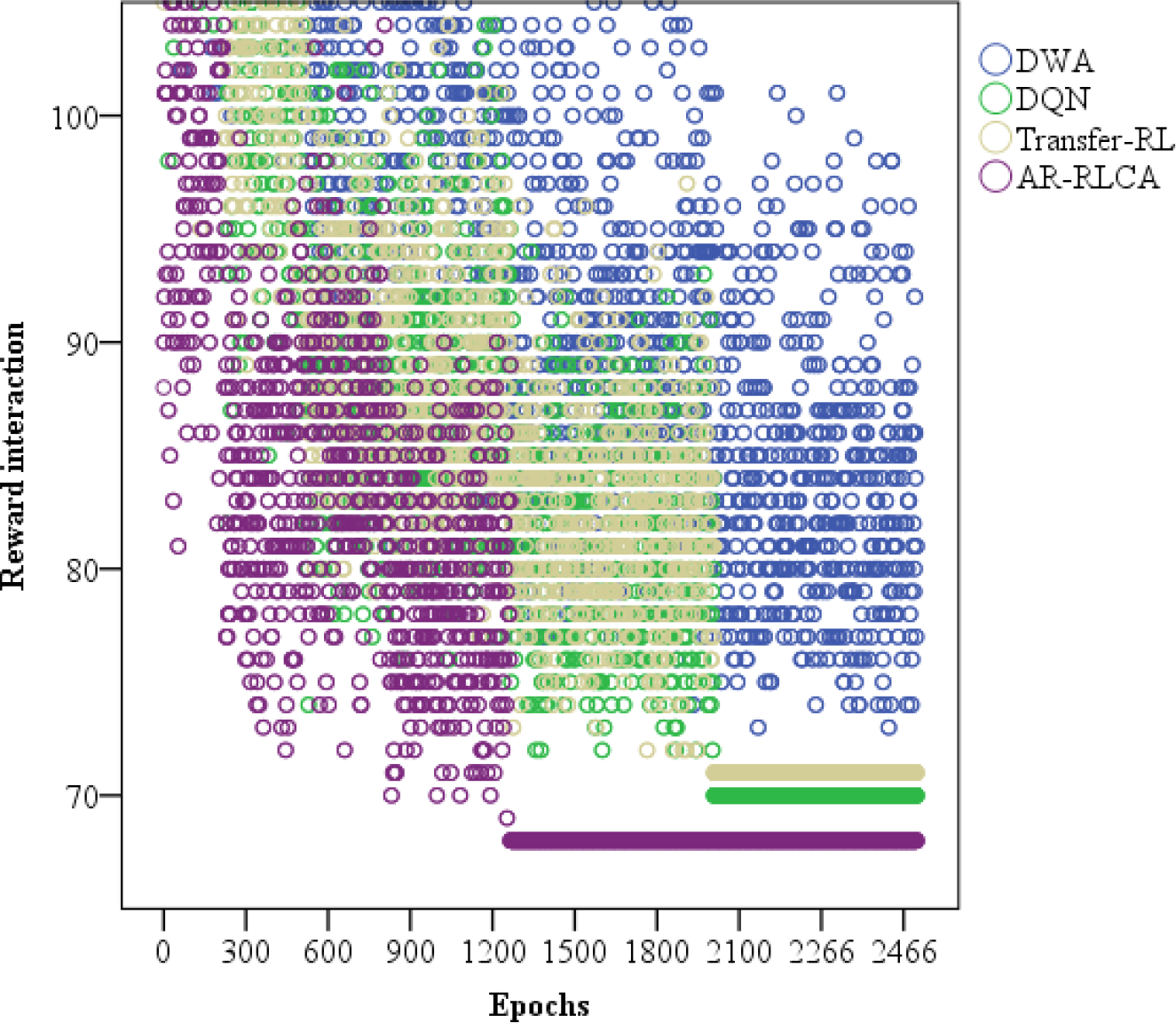
The reward interaction bubble chart.
After conducting multiple experiments, statistical analysis is performed on the reward interaction of multiple experiments separately. According to the reward function design in Section 3.2, the reward interaction in this paper is mainly divided into collision reward, risk TS1 reward, risk TS2 reward, risk TS3 reward, and stability reward. As shown in Figure 12, it is the statistics of the reward interaction of algorithms. For each algorithm, multiple sets of experiments are carried out to take the average value for analysis. From the count situation, the number of reward interactions for DQN, Transfer-RL, and AR-RLCA is reduced at once. This further illustrates that the AR-RLCA algorithm does not cause too much risk during exploration and training. Especially in the face of dynamic obstacles TS1, TS2, and TS3, AR-RLCA will highlight the excellent performance of low risk. Because TS3, like TS2, forms a crossing encounter scenario with OS, no risks emerge after completing the approximate representation for TS3. From the density-histogram of reward interaction, AR-RLCA has a good performance in collision avoidance decision-making in dynamic-static obstacles environments.
Figure 12
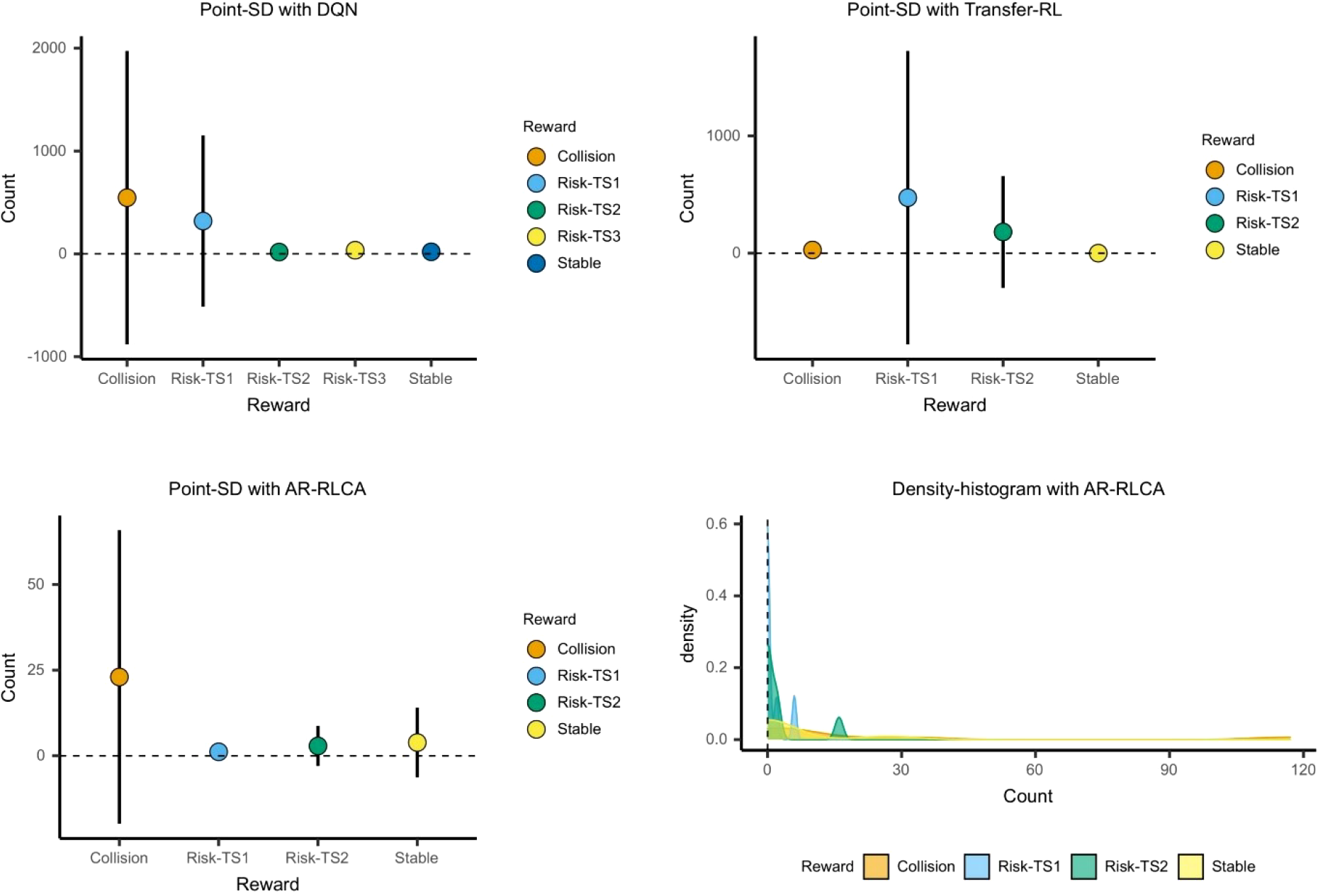
The point-SD and density chart of reward interaction.
Finally, we record and analyze the anti-collision rate and final step under each algorithm. The result is shown in Table 4. AR-RLCA has the highest obstacle avoidance success rate, and step size for planning is the smallest. In addition, the convergence trend spectral radius of the four groups of algorithms is all less than 1, which just shows that the algorithms have converged. However, the spectral radius of the convergence matrix of AR-RLCA is the smallest, that is, the convergence of AR-RLCA is the fastest.
Table 4
| Algorithm | DWA | DQN | Transfer-RL | AR-RLCA |
|---|---|---|---|---|
| Anti-collision success rate | 97.5% | 97.7% | 98.4% | 98.5% |
| Step of final epochs | 81 | 70 | 71 | 68 |
| Convergence trend spectral radius | 0.20000 | 0.00230 | 0.00217 | 0.00064 |
The result data of different algorithms.
5 Conclusion and future work
This paper presents an approximate representation reinforcement learning algorithm applied to a continuous state space collision to solve a MASS collision avoidance problem. It is critical to strike a balancing balance between two independent tasks of initial feature offline exploration and online collision avoidance for achieving good performance. In the final simulation experiment, the results show that the approximate representation can effectively solve the problem of slow initial iteration of large-scale continuous states in dynamic obstacle environments. Through trial-and-error training, it is demonstrated that the algorithm can successfully plan a safe avoidance path under the constraints of the COLREGs. The results of comparative experiments show that integrating approximate representation into RL network is a new idea to solve the problem of collision avoidance in continuous state space and improve the convergence speed.
In the future work, an improvement to the excitation function based on the actual trajectory data to match the actual sailing situation, to build a data-driven human-like reinforcement learning model should be further addressed. The model would be pre-trained using real data such as Automatic Identification System (AIS) data and radar image data. The reward function obtained by pre-training would be used to support online decision-making. The resulting decisions are bound to be more accurate and have robust performance in an uncertain environment.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization and Methodology, CW and XZ; Software, CW; Validation, CW; Writing-Original Draft Preparation, CW, XZ, ZY, and MB; Writing-Review and Editing, CW, ZY, and MB; Visualization, CW and KL; Funding Acquisition, XZ. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by Dalian Science and Technology Innovation Fund (2022JJ12GX015); the Central Guidance on Local Science and Technology Development Found of Shenzhen, China (2021Szvup014), and China Scholarship Council (No. 202106570022); This work is also financially supported by the European Research Council project (TRUST CoG 2019 864724).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Burmeister H. C. Constapel M. (2021). Autonomous collision avoidance at Sea: A survey. Front. Robotics AI8, 739013. doi: 10.3389/frobt.2021.739013
2
Chen S. Leng Y. Labi S. (2020). A deep learning algorithm for simulating autonomous driving considering prior knowledge and temporal information. Computer-Aided Civil Infrastructure Eng.35 (4), 305–321. doi: 10.1111/mice.12495
3
Chen X. Liu Y. Achuthan K. Zhang X. Chen J. (2021). A semi-supervised deep learning model for ship encounter situation classification. Ocean Eng.239, 109824. doi: 10.1016/j.oceaneng.2021.109824
4
Chun D. H. Roh M. I. Lee H. W. Ha J. Yu D. (2021). Deep reinforcement learning-based collision avoidance for an autonomous ship. Ocean Eng.234, 109216. doi: 10.1016/j.oceaneng.2021.109216
5
Ding Z. Zhang X. Wang C. Li Q. An L. Ding Z. et al . (2021). Intelligent collision avoidance decision-making method for unmanned ships based on driving practice. Chin. J. OF SHIP Res.16 (1), 31. doi: 10.19693/j.issn.1673-3185.01781
6
Ferreira F. Quattrini Li A. Rødseth ØJ. (2022). Navigation and perception for autonomous surface vessels. Front. Robotics AI, 9. doi: 10.3389/frobt.2022.918464
7
Fiskin R. Atik O. Kisi H. Nasibov E. Johansen T. A. (2021). Fuzzy domain and meta-heuristic algorithm-based collision avoidance control for ships: Experimental validation in virtual and real environment. Ocean Eng.220, 108502. doi: 10.1016/j.oceaneng.2020.108502
8
Gao H. Qin Y. Hu C. Liu Y. Li K. (2021). An interacting multiple model for trajectory prediction of intelligent vehicles in typical road traffic scenario. IEEE Trans. Neural Networks Learn. Syst.34971543, 1–12. doi: 10.1109/TNNLS.2021.3136866
9
Gao H. Shi G. Xie G. Cheng B. (2018). Car-following method based on inverse reinforcement learning for autonomous vehicle decision-making. Int. J. Advanced Robotic Syst.15 (6), 1729881418817162. doi: 10.1177/1729881418817162
10
Grigorescu S. Trasnea B. Cocias T. Macesanu G. (2020). A survey of deep learning techniques for autonomous driving. J. Field Robotics37 (3), 362–386. doi: 10.1002/rob.21918
11
Henderson P. Islam R. Bachman P. Pineau J. Precup D. Meger D. (2018). “Deep reinforcement learning that matters,” in Proceedings of the AAAI Conference on Artificial Intelligence (New Orleans, Lousiana, USA), 32 (1), 3207–3214. doi: 10.1609/aaai.v32i1.11694
12
Huang Y. Chen L. Chen P. Negenborn R. R. Van Gelder P. H. A. J. M. (2020). Ship collision avoidance methods: State-of-the-art. Saf. Sci.121, 451–473. doi: 10.1016/j.ssci.2019.09.018
13
Li Y. Fang H. Li M. Ma Y. Qiu Q. (2022). “Neural network pruning and fast training for DRL-based UAV trajectory planning,” in 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC). (Taipei, Taiwan), 574–579. doi: 10.1109/ASP-DAC52403.2022.9712561
14
Li L. Yang S. Zhou W. Chen G. (2010). “Mechanism for constructing the dynamic collision avoidance knowledge-base by machine learning,” in 2010 International Conference on Manufacturing Automation. (Hong Kong, China), 279–285. doi: 10.1109/ICMA.2010.4
15
Li S. Snaiki R. Wu T. (2021). A knowledge-enhanced deep reinforcement learning-based shape optimizer for aerodynamic mitigation of wind-sensitive structures. Computer-Aided Civil Infrastructure Eng.36 (6), 733–746. doi: 10.1111/mice.12655
16
Lillicrap T. P. Hunt J. J. Pritzel A. Heess N. Erez T. Tassa Y. et al . (2015). Continuous control with deep reinforcement learning. arXiv preprint arXiv1509, 2971. doi: 10.48550/arXiv.1509.02971
17
Liu R. W. Liang M. Nie J. Yuan Y. Xiong Z. Yu H. et al . (2022). STMGCN: Mobile edge computing-empowered vessel trajectory prediction using spatio-temporal multi-graph convolutional network. IEEE Trans. Ind. Inf18 (11), 7977–7987. doi: 10.1109/TII.2022.3165886
18
Mitchell T. M. (1997). Machine learning Vol. 1 (New York: McGraw-hill).
19
Mou J. M. van der Tak C. Ligteringen H. (2010). Study on collision avoidance in busy waterways by using AIS data. Ocean Eng.37 (5-6), 483–490. doi: 10.1016/j.oceaneng.2010.01.012
20
Murray B. Perera L. P. (2021). An AIS-based deep learning framework for regional ship behavior prediction. Reliability Eng. System Saf.215, 107819. doi: 10.1016/j.ress.2021.107819
21
Rødseth Ø.J. Lien Wennersberg L. A. Nordahl H. (2022). Towards approval of autonomous ship systems by their operational envelope. J. Mar. Sci. Technol.27 (1), 67–76. doi: 10.1007/s00773-021-00815-z
22
Sawada R. Sato K. Majima T. (2021). Automatic ship collision avoidance using deep reinforcement learning with LSTM in continuous action spaces. J. Mar. Sci. Technol.26 (2), 509–524. doi: 10.1007/s00773-020-00755-0
23
Shi H. Li J. Mao J. Hwang K. S. (2021). Lateral transfer learning for multiagent reinforcement learning. IEEE Trans. Cybernetics, 1–13. doi: 10.1109/TCYB.2021.3108237
24
Sutton R. S. Barto A. G. (2018). Reinforcement learning: An introduction. (Cambridge: MIT press).
25
Tam C. Bucknall R. Greig A. (2009). Review of collision avoidance and path planning methods for ships in close range encounters. J. Navigation62 (3), 455–476. doi: 10.1017/S0373463308005134
26
Tsou M. C. Kao S. L. Su C. M. (2010). Decision support from genetic algorithms for ship collision avoidance route planning and alerts. J. Navigation63 (1), 167–182. doi: 10.1017/S037346330999021X
27
Wang C. Wang N. Xie G. Su S. F. (2022). “Survey on collision-avoidance navigation of maritime autonomous surface ships,” in Offshore robotics (Singapore: Springer), 1–33. doi: 10.1007/978-981-16-2078-2_1
28
Wang D. Zhang J. Jin J. Mao X. (2021). Local collision avoidance algorithm for a unmanned surface vehicle based on steering maneuver considering colregs. IEEE Access9, 49233–49248. doi: 10.1109/ACCESS.2021.3058288
29
Wang S. Zhang Y. Li L. (2020). A collision avoidance decision-making system for autonomous ship based on modified velocity obstacle method. Ocean Eng.215, 107910. doi: 10.1016/j.oceaneng.2020.107910
30
Wang C. Zhang X. Wang L. (2021). “Navigation situation adaptive learning-based path planning of maritime autonomous surface ships,” in 2021 6th International Conference on Transportation Information and Safety (ICTIS). (Wuhan, China), 342–347. doi: 10.1109/ICTIS54573.2021.9798502
31
Wu Z. (2014). Ship collision avoidance and watch keeping. (Dalian: Dalian Maritime University Press).
32
Xie S. Chu X. Zheng M. Liu C. (2020). A composite learning method for multi-ship collision avoidance based on reinforcement learning and inverse control. Neurocomputing411, 375–392. doi: 10.1016/j.neucom.2020.05.089
33
Xu X. Cai P. Ahmed Z. Yellapu V. S. Zhang W. (2022). Path planning and dynamic collision avoidance algorithm under COLREGs via deep reinforcement learning. Neurocomputing468, 181–197. doi: 10.1016/j.neucom.2021.09.071
34
Yi Z. (2015). Study on collision between fishing vessels and merchant ships within the China coastal waters. [master’s thesis]. Malmo: WORLD MARITIME UNIVERSITY.
35
Yuan W. Gao P. (2022). Model predictive control-based collision avoidance for autonomous surface vehicles in congested inland waters. Math. Problems Eng.2022, 7584489. doi: 10.1155/2022/7584489
36
Yu Q. Liu K. Yang Z. Wang H. Yang Z. (2021). Geometrical risk evaluation of the collisions between ships and offshore installations using rule-based Bayesian reasoning. Reliability Eng. System Saf.210, 107474. doi: 10.1016/j.ress.2021.107474
37
Zhang X. Wang C. Jiang L. An L. Yang R. (2021). Collision-avoidance navigation systems for maritime autonomous surface ships: A state of the art survey. Ocean Eng.235, 109380. doi: 10.1016/j.oceaneng.2021.109380
38
Zhang X. Wang C. Liu Y. Chen X. (2019). Decision-making for the autonomous navigation of maritime autonomous surface ships based on scene division and deep reinforcement learning. Sensors19 (18), 4055. doi: 10.3390/s19184055
39
Zhao J. Mao M. Zhao X. Zou J. (2020). A hybrid of deep reinforcement learning and local search for the vehicle routing problems. IEEE Trans. Intelligent Transportation Syst.22 (11), 7208–7218. doi: 10.1109/TITS.2020.3003163
Summary
Keywords
autonomous ship, collision avoidance, deep reinforcement learning, approximate representation, continuous state space
Citation
Wang C, Zhang X, Yang Z, Bashir M and Lee K (2023) Collision avoidance for autonomous ship using deep reinforcement learning and prior-knowledge-based approximate representation. Front. Mar. Sci. 9:1084763. doi: 10.3389/fmars.2022.1084763
Received
30 October 2022
Accepted
22 December 2022
Published
19 January 2023
Volume
9 - 2022
Edited by
Yamin Huang, Wuhan University of Technology, China
Reviewed by
Yuanqiao Wen, Wuhan Institute of Technology, China; Ruobin Gao, Nanyang Technological University, Singapore; Osiris A. Valdez Banda, Aalto University, Finland
Updates
Copyright
© 2023 Wang, Zhang, Yang, Bashir and Lee.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xinyu Zhang, zhang.xinyu@sohu.com
This article was submitted to Ocean Observation, a section of the journal Frontiers in Marine Science
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.