Determination of Long-Term (1993–2019) Sea Level Rise Trends Around the Korean Peninsula Using Ocean Tide-Corrected, Multi-Mission Satellite Altimetry Data

It is vital to improve estimations of long-term trends in global and regional sea level rise to help mitigate and adapt to climate change. Satellite altimetry data have been widely used for this purpose; however, data collected in regions with strong tidalmotions often suffer from significant aliasing effects unless they are sufficiently corrected using accurate ocean tide models.Long-term trends estimated from altimetry data are often also considerably affected by regional circulation changes, and by artificial effects arising from inconsistencies between different satellite missions. Here, we focused on two regions with high (>5 mm⋅yr^–1) rates of long-term linear trend in sea level rise (LTSLR) around the Korean Peninsula (KP). We addressed the impacts of tidal correction and mission inconsistency in satellite altimetry data, and discussed the potential impacts of circulation changes on LTSLR. Because the LTSLR estimation is affected by the aliasing effects of altimetry data when the tidal motions are not corrected sufficiently, yet the correction depends on the performance of ocean tide models, we employed eight ocean tide models to correct altimetry data for comparison and validated the results against observations from 13 tide gauge (TG) stations around the KP. We also estimated LTSLR from 1993 to 2019 using annual mean sea level anomalies (SLAs) from two satellite (two-sat) and all 21 satellite (all-sat) missions, with corrections for ocean tides. The TPXO9 model showed the most reasonable spatial LTSLR rate pattern (∼3 mm⋅yr^–1), with the smallest difference from TG observations. It performed best near the west coast where the tidal range was the largest and when using two-sat data, because of inconsistencies in all-sat altimetry data. In contrast, off the east coast, where the impact of tidal correction is negligible, the high (∼7 mm⋅yr^–1) LTSLR rates were robust regardless of ocean tide models and altimetry missions, potentially driven by long-term changes in regional circulation. Our results highlight the importance of tidal correction and mission inconsistency for improving LTSLR estimations around the KP. They also have significant implications for determining regional sea level rise under changing circulation patterns, within and beyond the region.

Introduction

Global mean sea level rise is currently accelerating (IPCC, 2019); therefore, the ability to accurately evaluate long-term trends in regional sea level rise, which often deviate from the global trend, is becoming increasingly important (Cazenave and Llovel, 2010; Nicholls and Cazenave, 2010; Church and White, 2011; Stammer et al., 2013). As high-precision satellite altimetry data have been collected since 1992, multi-decadal trends in sea-level rise have been reported, thereby providing evidence of significant regional-scale spatial variations (Fasullo and Nerem, 2018; IPCC, 2019). However, the estimation of regional-scale long-term linear trends in sea level rise (LTSLR) is often hampered by strong tidal motions, when not sufficiently corrected in the altimetry data, and by inconsistencies between different satellite missions (Vinogradov and Ponte, 2011). On the other hand, the LTSLR may modify the tidal motions (Devlin et al., 2017; Idier et al., 2017), further complicating regional patterns of LTSLR estimated from the altimetry data by correcting the tidal motions. Regional LTSLR is also affected by sea level changes driven by other processes beyond the tides, such as mesoscale eddy variability (Qiu et al., 2015)

LTSLR around the KP has been reported to exhibit a prominent spatial pattern from September 1992 to May 2019, based on satellite altimetry data (Watson, 2019; Watson and Lim, 2020). High LTSLR rates (>5 mm⋅yr^–1) above the global average trend(without glacial isostatic adjustment of 3.7 ± 0.4 mm⋅yr^–1) have been reported for two regions around the KP (Watson and Lim, 2020): (1) within Gyeonggi Bay, near the west coast of the KP (gray box in Figure 1), and (2) in the vicinity of Ulleung Island [tide gauge (TG) station number 13 in Figure 1], off the east coast of the KP. In addition to long-term sea level rise, the sea level around the KP significantly changes at interannual and decadal timescales in relation to large-scale patterns of climatic variability, such as the Pacific Decadal Oscillation (Cheng et al., 2015; Kim et al., 2018) and Arctic Oscillation, via changes in sea surface temperature and air-sea heat exchange (Park et al., 2015). These changes are also driven by regional circulation and the upper ocean heat content (Choi et al., 2004, 2009; Kang et al., 2005; Yoon et al., 2016; Pak et al., 2019). Interannual variations in sea level, averaged over the East Asian marginal seas in summer and winter, have been suggested to be caused by changes in regional sea surface wind patterns (Han et al., 2020a,b). However, despite these previous studies on the processes underlying interannual and decadal variations in sea level around the KP, the physical drivers and data issues influencing the high LTSLR rates near the west coast and off the east coast remain poorly understood.

FIGURE 1

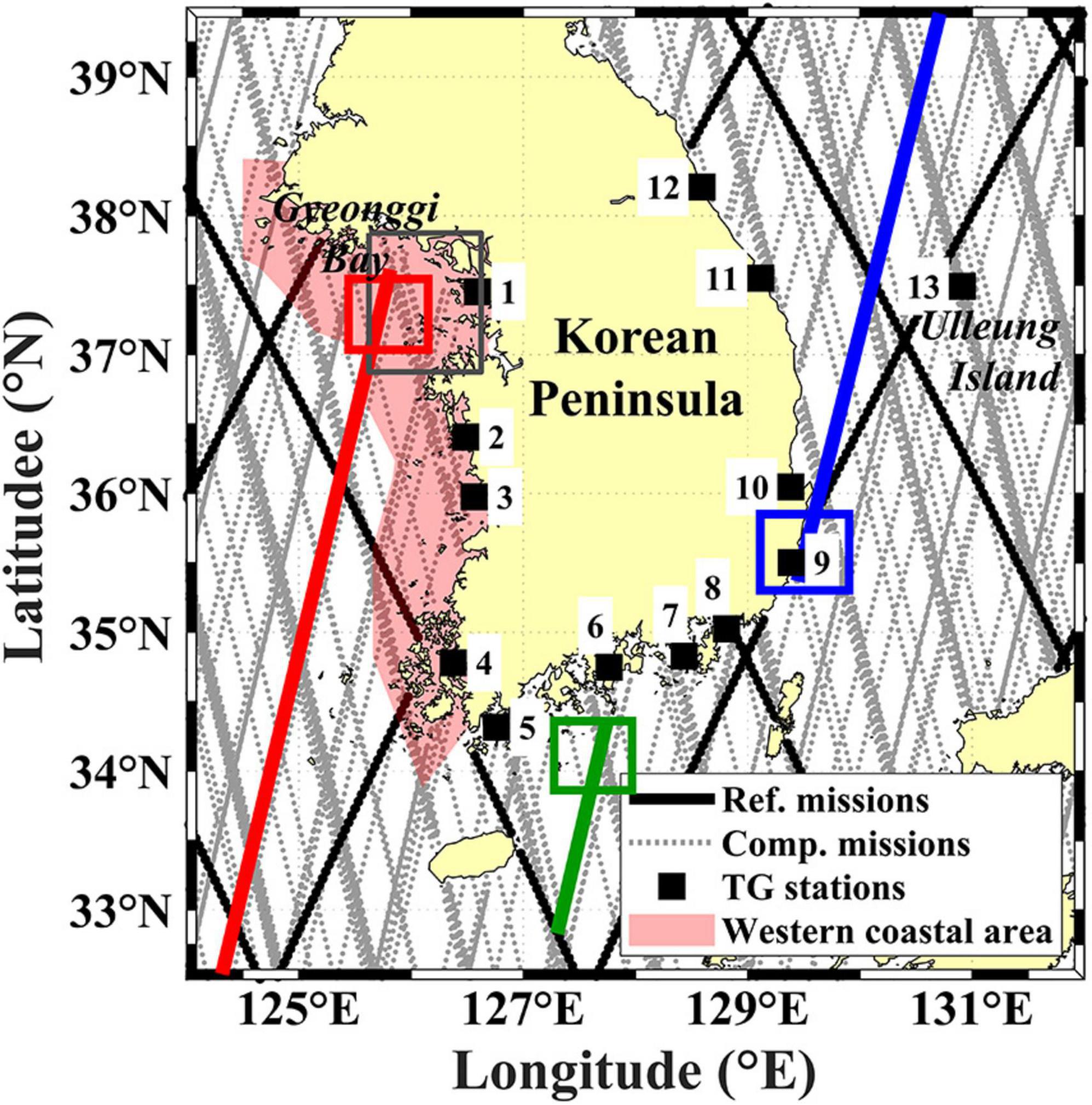
Figure 1. Tracks of reference (black) and selected complementary (gray) satellite altimetry missions, and locations of tide gauge (TG) stations around Korean Peninsula (KP) labeled with numbers (black squares). Sea level anomalies (SLAs) along three descending tracks crossing the west (thick red line), south (thick green line), and east (thick blue line) coasts of KP are shown for comparative purposes. Areas near the coast (<50 km) in these selected tracks are highlighted by colored boxes. The western coastal area and Gyeonggi Bay area near the TG station IC (number 13), where the tidal ranges were relatively high, are shown by red shading and a 1^° × 1^° gray box, respectively.

Tidal characteristics are distinctly different between the west and east coasts around the KP primarily owing to contrasting bathymetric conditions—west coast of the KP bordered by shallow shelf sea (Yellow Sea) vs. east coast of the KP bordered by deep, semi-enclosed marginal sea (East Sea). Tidal motions are strong and the tidal range of dominant semi-diurnal tides reaches up to 10 m near the west coast, whereas very small tidal motions are reported with a typical tidal range of a few cm off the east coast (Nishida, 1980; Kang et al., 1991). The tidal range of most dominant tidal constituent M₂ is double that of the second-dominant semi-diurnal component S₂ in both coastal regions, whereas the tidal charts for both tidal constituents are very similar (An, 1977; Kang et al., 1991, 1995). Tidal motions are dominant among the high-frequency (frequency higher than the sampling frequency of satellite altimeter) sea level fluctuations near the west coast.

In this study, to address the causes of the high LTSLR rates in these two regions around the Korean Peninsula (KP), we aimed to elucidate the impacts of (1) correcting altimetry data for ocean tides using different ocean tide models, (2) inconsistencies between different satellite altimetry missions, and (3) changes in regional circulation on LTSLR.

Data and Methods

Data

Sea level data recorded every minute and averaged every hour at 13 tide gauge (TG) stations around the KP were used in this study (Figure 1 and Table 1). Hourly TG sea level data (SLA_TG) at four TG stations on each coast were selected to represent sea levels near the west (IC, BR, GS, and MP), south (WD, YS, TY, and GDD), and east coasts (US, PH, MH, and SC), whereas the Ulleung Island TG station (ULD) was selected to represent sea level far off the east coast. The duration of SLA_TG used for tidal harmonic analysis varied from 34 to 60 year, depending on the start dates of the TG sea level records (Table 1), while the SLA_TG data collected at all 13 TG stations from 1993 to 2019 were used to estimate LTSLR. To correct the SLA_TG for the glacial isostatic adjustment (GIA), the rate of sea level change derived from the GIA global model (ICE-5G v1.3) with a spatial resolution of 1° was used (Peltier, 2004).

TABLE 1

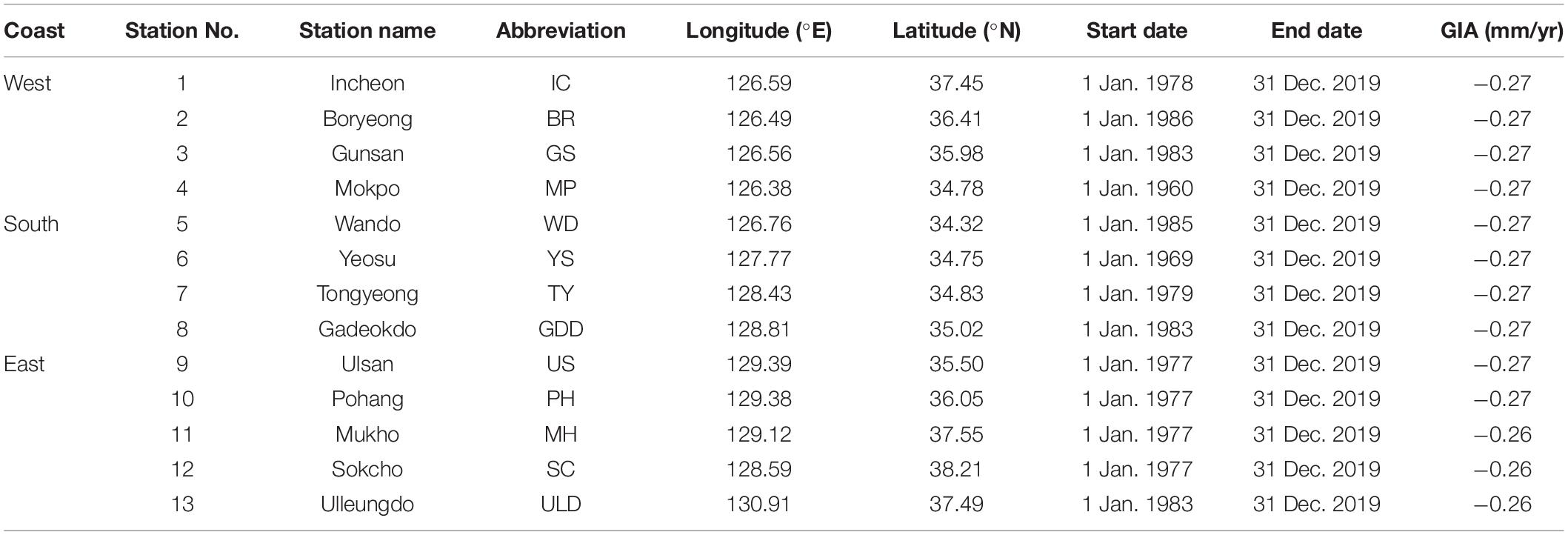
Table 1. Locations, names, start and end dates, and relative sea level changing rates due to glacial isostatic adjustment (GIA) of TG sea level stations/records used in this study.

Sea level anomalies (SLAs) from along-track satellite altimetry data (L3) and gridded products (both two-sat and all-sat) merged from 21 satellite missions were obtained from the Copernicus Marine Environment Monitoring Service (CMEMS). The SLAs from along-track satellite altimetry data (L3) are the difference from the mean profiles of each satellite mission or the gridded mean sea surface (CNES_CLS_2015) (Pujol et al., 2016). These data were used to estimate the spatial LTSLR pattern around the KP (Figure 1). The tidal correction component of the along-track altimetry data was estimated by the Finite Element Solution 2014 (FES2014) ocean tide model (Taburet et al., 2019). The repetitive orbits of reference missions (TOPEX/POSEIDON; T/P, 1993–2002; Jason-1: J1, 2002–2008; Jason-2: J2, 2008–2016; Jason-3: J3, 2016–2021), each with a cycle of 10 days, had relatively wide inter-track distances (Figure 2A). The complementary missions (ERS-1: E1, 1992–1996; ERS-2: E2, 1995–2003; Envisat; EN, 2002–2010; Envisat new orbit; ENN, 2010–2012; Saral/Altika; AL, 2013–2016; Sentinel-3A: S3A, 2016–2019) for the two-satellite (two-sat) merged gridded product had a cycle of 35 days and exhibited narrow inter-track distances (Pujol et al., 2016). Other complementary (Cryosat-2: C2, 2011–2019; HaiYang-2A: H2, 2014–2016; Geosat Follow On: G2, 2000–2008) and opportunity missions (T/P-interleaved; TPN, 2002–2005; J1-interleaved: J1N, 2009–2012; J2-interleaved: J2N, 2016–2017; J1 in the geodetic phase: J1G, 2012–2013; E1 in the geodetic phase: E1G, 1994–1995; H2 in the geodetic phase: H2G, 2016–2019; J2 long repeat orbit: J2G, 2017; Saral-DP/Altika; ALG, 2015–2019) with cycles ranging from 9 to 168 days were used for the all-satellite (all-sat) merged gridded product; these missions had intermediate inter-track distances. All along-track altimetry data were subsampled every second and every 6.6 km following each track; they were low-pass filtered with a cut-off wavelength of 65 km (Pujol et al., 2016).

FIGURE 2

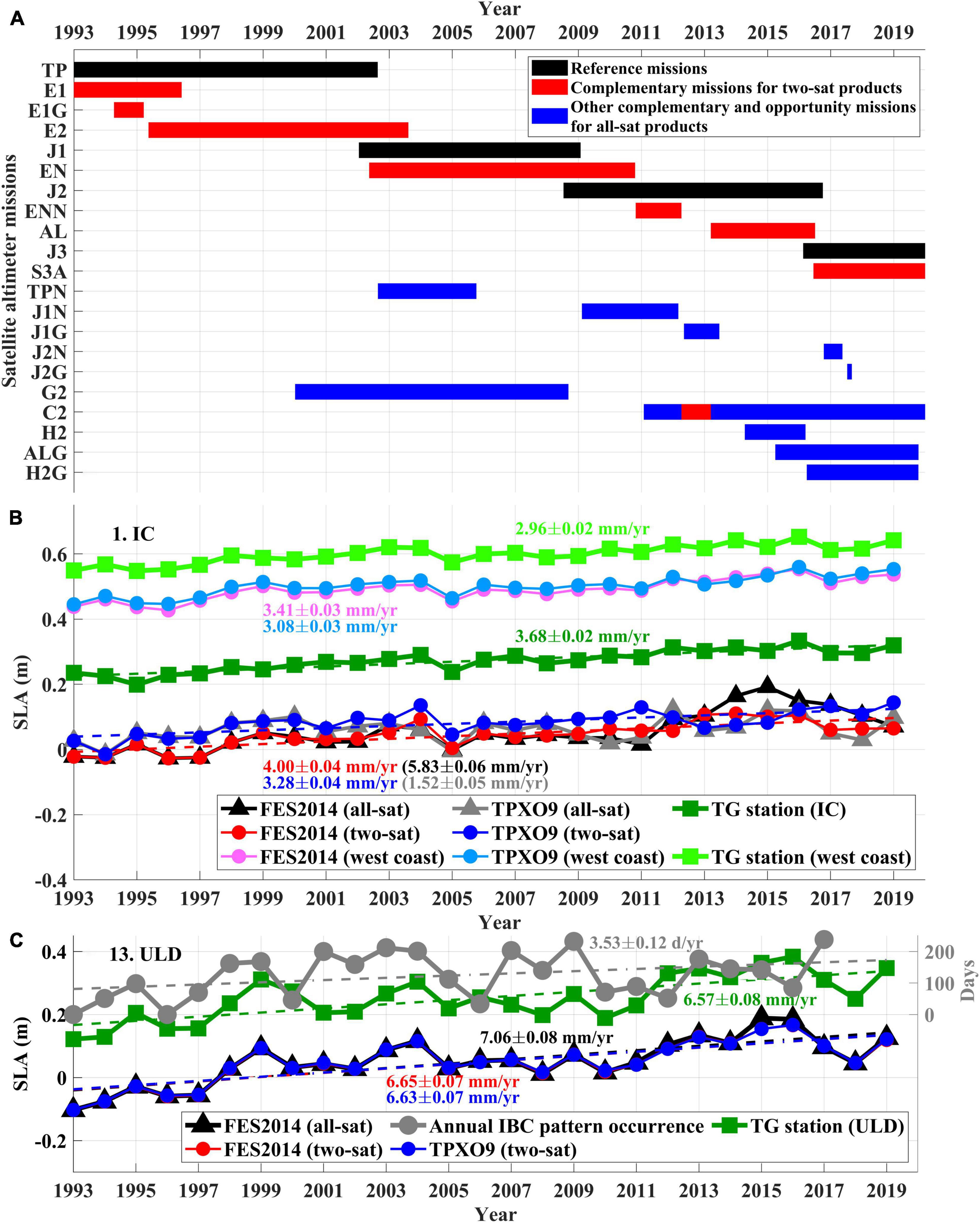
Figure 2. (A) Timeline of operational satellite altimetry missions for two-sat (black and red) and all-sat (black, red, and blue) merged gridded sea level products. Time series are shown for annual mean SLA_TG (green), SLA_FES2014 (black and red), and SLA_TPXO9 (gray and blue) nearby TG stations of (B) IC and (C) ULD, for two-sat (red and blue) and all-sat (black and gray) missions. For two-sat missions, Annual mean SLA_TG averaged over four TG stations (IC, BR, GS, MP) on the west coast (light green) and SLA_FES2014 (pink) and SLA_TPXO9 (sky blue) averaged over the western coastal area (marked with red shading in Figure 1) are superimposed in (B). In (C), red lines are not visible as they are identical to blue lines; annual occurrence days of Inertial Boundary Current (IBC) pattern are also shown (gray line, right y-axis). Numbers in colors corresponding to dashed lines denote LTSLR.

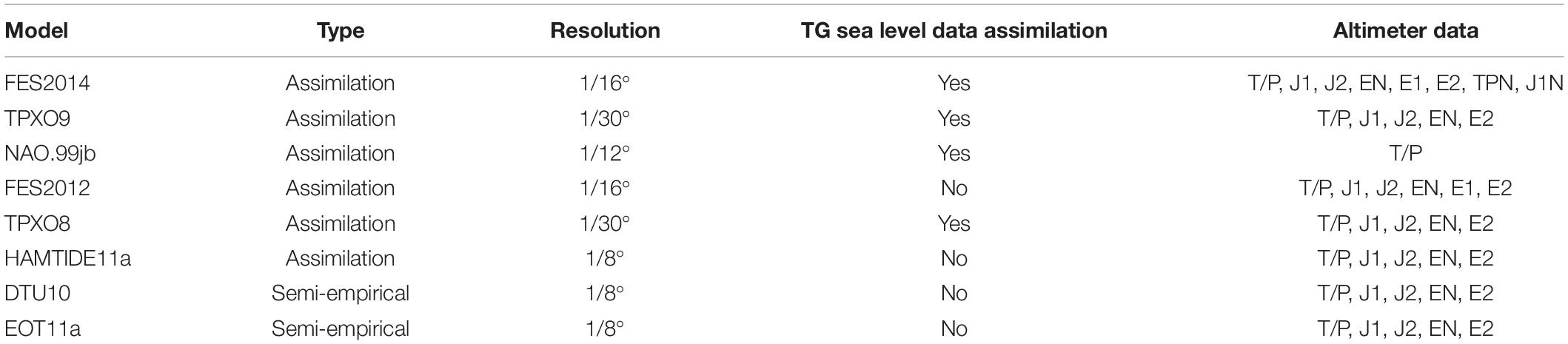
Tidal harmonic constants (amplitude and phase) for eight major tidal constituents (M₂, S₂, K₁, O₁, P₁, Q₁, N₂, and K₂) from barotropic ocean tide models were used to correct the along-track altimetry data (Table 2). The eight ocean tide models used here can be divided into two categories: semi-empirical models (DTU10: developed at Technical University of Denmark, and EOT11a: Empirical Ocean Tide model from multi-mission satellite altimetry) and assimilation models (FES2012, FES2014, TPXO8: TOPEX/Poseidon global ocean tide model ver. 8.0, TPXO9, HAMTIDE11a: Hamburg direct data Assimilation Methods for TIDEs, and NAO.99jb: National Astronomical Observatory of Japan). The latter were obtained by assimilating altimeter data into the barotropic hydrodynamic model (Seifi et al., 2019). The horizontal resolutions of these models range from 1/8^° to 1/30^° (Table 2). All of these models except for EOT11a (Savcenko and Bosch, 2012) use their own bathymetry data based on ETOPO1, ETOPO5, the General Bathymetric Chart of the Oceans (GEBCO), Shuttle Radar Topography Mission 15 (SRTM15), and Danish National Space Centre 2008 (DNSC08) data (Matsumoto et al., 2000; Egbert and Erofeeva, 2002, 2018; Cheng and Andersen, 2011; Carrère et al., 2013; Taguchi et al., 2014; Seifi et al., 2019).

TABLE 2

Table 2. Descriptions of eight ocean tide models used in this study.

Methods

The original along-track SLA data, prior to correction for ocean tides (SLA_raw), were obtained by adding the tidal prediction component ($h_{tide}^{FES2014}$) to the CMEMS L3 SLA data (SLA_corrected), using the output products of the present version of the operational ocean tide model, FES2014, that is, $SL{A}_{raw}=SL{A}_{corrected}+h_{tide}^{FES2014}$. Then, the original SLA data were corrected for ocean tides using the eight ocean tide models discussed in section “Data,” including FES2014, by subtracting the tidal prediction component of each ocean tide model (M) as a function of longitude (x), latitude (y), and time (t), that is, $h_{tide}^M(x,y,t$), from the reconstructed original SLA data (SLA_raw). Note that $h_{tide}^M(x,y,t$) was computed based on the tidal harmonic constants derived from each model, using Equation (1) (Byun and Cho, 2009):

$h_{tide}^M(x,y,t)=\sum _j{f}_j\left(t\right)A_j^M\text{cos}\{{\mathrm{\omega }}_j\mathrm{\tau }+V{o}_j\left(t_0\right)+u_j\left(t\right)-G_j^M\}(1)$

Here, A and G are the tidal amplitude and Greenwich phase of each ocean tide model at a given location, respectively; ω is the tidal frequency of the jth tidal constituent (M₂, S₂, K₁, O₁, P₁, Q₁, N₂, and K₂), t₀ is the arbitrary reference time, which was set to January 1, 1993; τ is the elapsed time; f and u are the nodal amplitude factor and the nodal angle used to consider the lunar node modulations over a period of 18.61 year; and Vo is an astronomical argument that is used to determine the phase to the reference time of an arbitrary time series (Byun and Cho, 2009). Here, we compared the tidal corrections of the satellite altimetry only by the eight major tidal constituents from each tidal model, because 98% of the tidal fluctuations are explained by the eight tidal constituents in this region. For the tidal corrections by other minor tidal constituents, the results of the FES2014 were identically applied, that is, $h_{\text{minor}}^{FES2014}=h_{tide}^{FES2014}-h_{8major}^{FES2014}$. Thus, $SL{A}_{corrected}=SL{A}_{raw}-h_{minor}^{FES2014}-h_{8major}^M$. The tidal harmonic constants from the SLA_TG were estimated using the Unified Tidal Analysis and Prediction (UTide) package, which was developed for MATLAB software (Codiga, 2011). Hereafter, the ocean tide models to estimate SLA_corrected are denoted as a subscript, for example, SLA_FES2014 refers to the SLA_corrected obtained using the FES2014 model.

Tidal harmonic constants were also obtained from SLA_TG for a whole period in each TG station (Table 1) after correcting the atmospheric pressure loading (Lyu et al., 2002; Nam et al., 2004), while the difference between the observed and modeled constants was quantified using the root-mean-squared (RMS) values. UTide was used to yield tidal harmonic constants from observations and models. UTide can treat long time series data, e.g., longer than 18.6 y, and can deal with data having irregular temporal intervals. The tidal constants obtained using the ocean tide models were spatially interpolated to estimate those at the TG stations to allow for comparisons with TG observations; RMS was used for this purpose (Foreman et al., 1993):

$RM{S}_j=\sqrt{\frac{1}{2}[{\left(A_j^{m}cos\left(G_j^m\right)-A_j^{v}cos\left(G_j^v\right)\right)}^2+{\left(A_j^{m}sin\left(G_j^m\right)-A_j^{v}sin\left(G_j^v\right)\right)}^2]}(2)$

The superscripts m and v denote the tidal constants for the j^th tidal constituent derived from the model and observation, respectively. Here, the results from only M₂ constituent that is dominant in the region (An, 1977; Kang et al., 1995) were considered.

The SLA_corrected data along the irregular tracks of a few satellite missions were linearly interpolated to yield values at a grid of 0.25 × 0.25°and a temporal interval of 14 days, considering the generation scheme of the gridded satellite altimetry data (Pujol et al., 2016). The along-track data from the reference missions and five complementary missions (ERS-1/2, Envisat, Saral/Altika, and Sentinel-3A) were merged to create the “two-sat” merged data. This combination is similar to the two-satellite merged gridded products provided by CMEMS. Data from the other complementary and opportunity missions were included in the “all-sat” merged data. LTSLRs were estimated using linear regression (Thomson and Emery, 2014) from the annual mean time series of SLA_TG of 28 y (1993–2021) at each TG station and SLA_corrected at each grid, for both “all-sat” and “two-sat” missions. These estimations are denoted herein as R_TG, R_allsat, and R_twosat, respectively. The relative sea level change rates due to the GIA at each TG station (Tamisiea and Mitrovica, 2011) were subtracted from the R_TG for a GIA correction (Table 1). In addition, the name of the ocean tide model is appended to the subscript. For example, R_{twosat–FES2014} represents LTSLR estimated from the “two-sat” mission SLA data, corrected using the FES2014 model. Finally, the spatial patterns of R_allsat and R_twosat corrected by the eight ocean tide models around the KP were compared.

Results

Assessment of Ocean Tide Model

The differences in SLA_corrected among the ocean tide models were large near the coasts (within 50 km of the coastline) of KP. Differences were particularly large near the west coast, often exceeding 1 m along the altimetry tracks (colored boxes in Figures 1, 3). The TPXO9, FES2014, and NAO.99jb models exhibited relatively low RMS differences between observations and models regarding the M₂ tidal constant (and other tidal constituents). There were a few exceptions, however, such in as the case of TG station MP (number 4); the bathymetry nearby this station is complex (Figure 4). As the tidal range decreased, the RMS difference generally decreased from the west to south coasts, and from the south to east coasts, for most models (Figure 4). High RMS differences were found for TPXO8, HAMTIDE, EOT11a, and DTU10 at TG stations along the west and south coasts. For example, there was a 137 cm difference between the TPXO8 model and observations at TG station IC. This indicates that these models struggled to simulate the tidal prediction component (h^M_tide) to effectively correct for ocean tides and estimate LTSLR from satellite altimetry data in these regions. It is noteworthy that the FES2014 model, which is used in the operational production of CMEMS L3 SLA, was outperformed by the TPXO9, where the latter yielded overall minimum RMS difference as the ocean tides in the region are best simulated by the TPXO9 model (Figure 4).

FIGURE 3

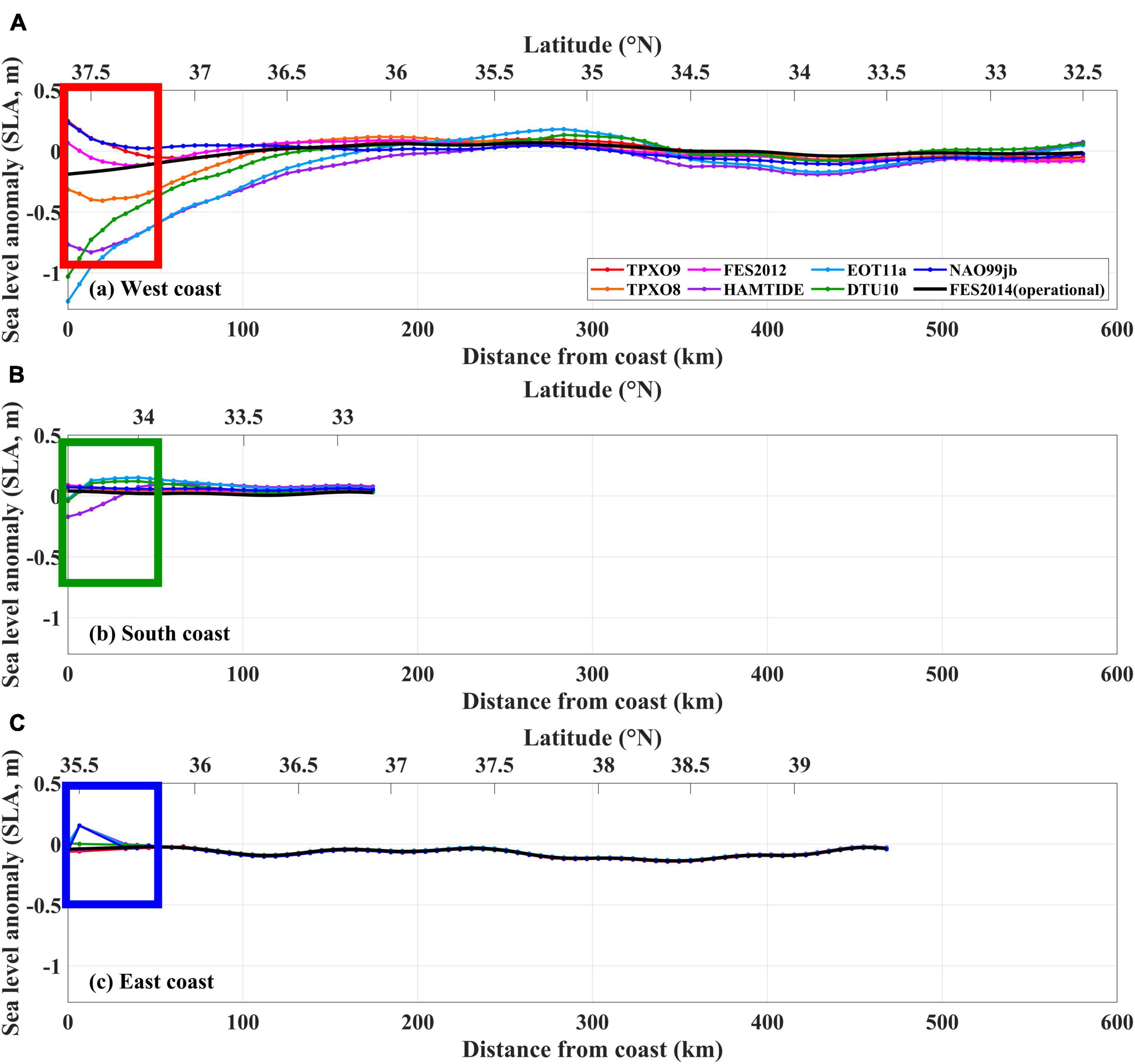
Figure 3. Snapshot of SLA (m) along selected descending tracks as a function of distance (km) off the (A) west (from 02:03 to 02:04 UTC 11 January 2009), (B) south (from 01:52 to 01:53 13 May 2018), and (C) east (from 01:45 to 01:46 17 February 2006) coasts of KP (marked with thick colored lines in Figure 1). Data were corrected by eight ocean tide models (colored lines; see legend in upper-right corner). Areas near the coast (<50 km) are highlighted by colored boxes (as in Figure 1).

FIGURE 4

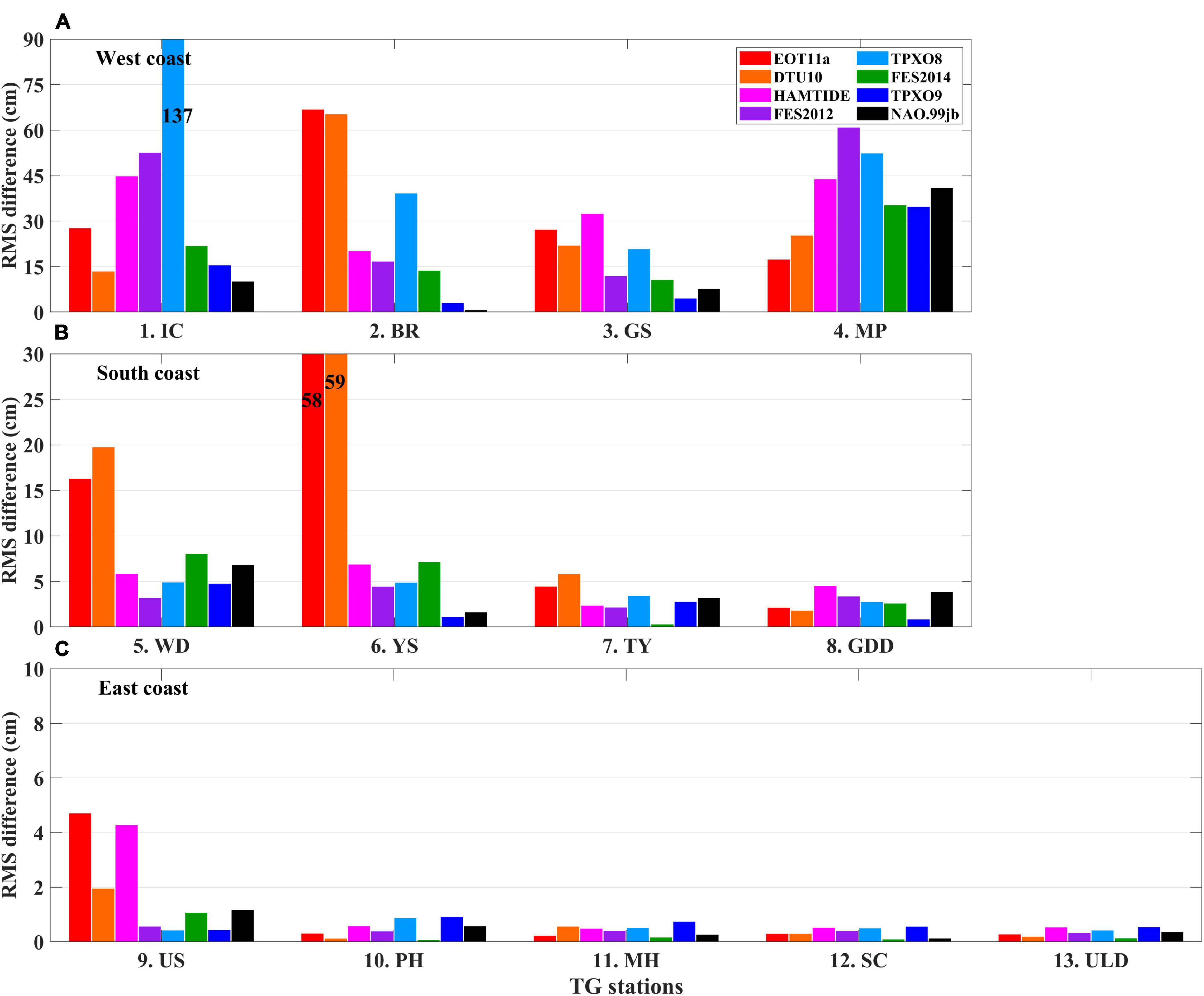
Figure 4. Column chart of root-mean-squared (RMS) difference (cm) between observed and modeled M₂ tidal constants (see texts for details) for TG stations along (A) west, (B) south, and (C) east coasts of KP (locations are remarked in Figure 1). Observed and modeled M₂ tidal constants obtained by harmonic analysis of observed SLA and eight ocean tide models, respectively, are also shown (colors correspond to legend in upper-right corner). Numbers on columns for IC (TG station number 1) and YS (TG station number 6) denote RMS differences exceeding y-axis range.

The M₂ tidal charts obtained from the tidal prediction components of the TPXO9 and NAO.99jb models were more reasonable than those of the other models, in the sense that they predicted westward- and poleward-propagating barotropic Kelvin waves along the south and west coasts (Figure 5). By definition, co-range lines that are orthogonal to co-tidal lines should run parallel to coastlines at scales longer than a few hundreds of kilometers, corresponding to the barotropic Rossby radius of deformation at a given latitude and water depth (tens of meters). However, other models exhibited small curvatures with localized features and inconsistent non-orthogonal lines between co-range and co-tidal lines. In particular, both of the models that did not show small curvatures predicted two co-tidal lines with phases of 210° and 240° and co-range lines that were nearly orthogonal to these co-tidal lines (aligned NNW-SSE, corresponding to the large-scale coastline direction). These models commonly yielded a tidal range of ∼6 m at the TG station IC, matching the reported mean tidal range (5.74 m). In contrast, the other models, which exhibited small curvatures in the two co-tidal lines and non-parallel co-range lines within Gyeonggi Bay, significantly underestimated or overestimated the tidal range at IC (Figure 5).

FIGURE 5

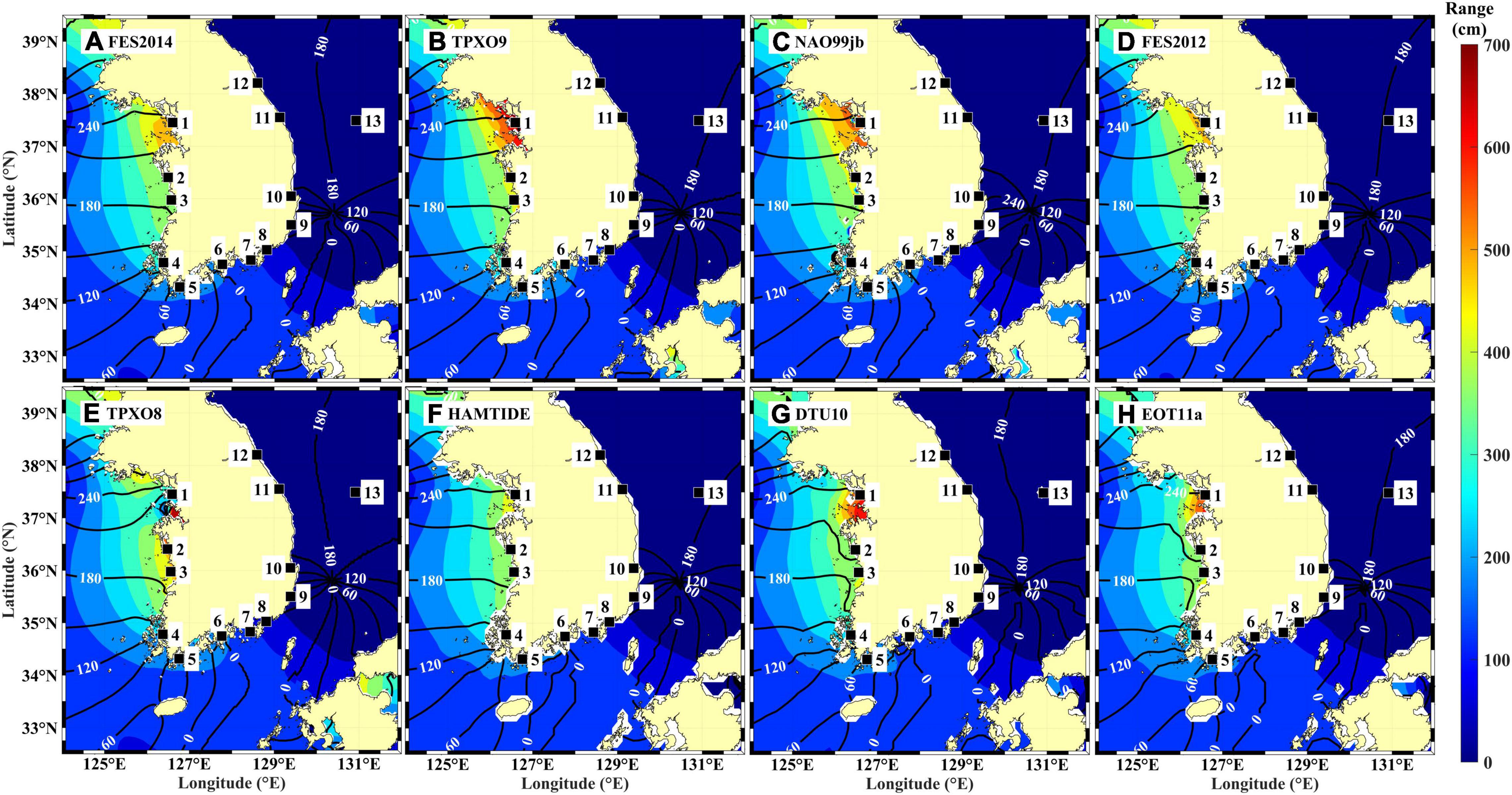
Figure 5. M₂ tidal charts for eight ocean tide models (A: FES2014, B: TPXO9, C: NAO.99jb, D: FES2012, E: TPXO8, F: HAMTIDE11a, G: DTU10, and H: EOT11a) with co-phase lines (black solid contours; phases in degrees are denoted with white labels) and co-range lines (colors correspond to scale bar shown at right of figure). Contour intervals for tidal phase (black) and amplitude (colors) are 30^° and 60 cm, respectively. Black squares denote TG stations.

Spatial Pattern of Linear Trend in Sea Level Rise

The spatial LTSLR patterns derived using the SLA from two-sat missions and corrected by each ocean tide model (R_twosat) demonstrated two regions of high (>5 mm⋅yr^–1) rates: within the Gyeonggi Bay, near the west coast, and in the vicinity of Ulleung Island, off the east coast. The former was not consistently predicted among the models, whereas the latter was consistently simulated, regardless of the model used to correct ocean tides (Figure 6). Near the west coast, for example, the LTSLR rates from the all-sat and two-sat missions were higher when corrected by the FES2014 model (R_{allsat–FES2014} and R_{twosat–FES2014}) than when corrected by the TPXO9 model (R_{allsat–TPXO9} and R_{twosat–TPXO9}). This yielded non-negligible differences in LTSLR, particularly within the Gyeonggi Bay in the vicinity of TG station IC (number 1) off the west coast (Figures 6A–I). Similar or worse inconsistencies in LTSLR were also observed among the other models; for example, R_{twosat–HAMTIDE}, R_{twosat–DTU10}, and R_{twosat–EOT11a} near the west coast (Figures 6J–L). In contrast to the inconsistencies in LTSLR among the missions and tide models, differences were not pronounced (typically < 1 mm⋅yr^–1) near TG station ULD (number 13) off the east coast. Here, high LTSLR rates were robustly predicted across missions and models (Figure 6).

FIGURE 6

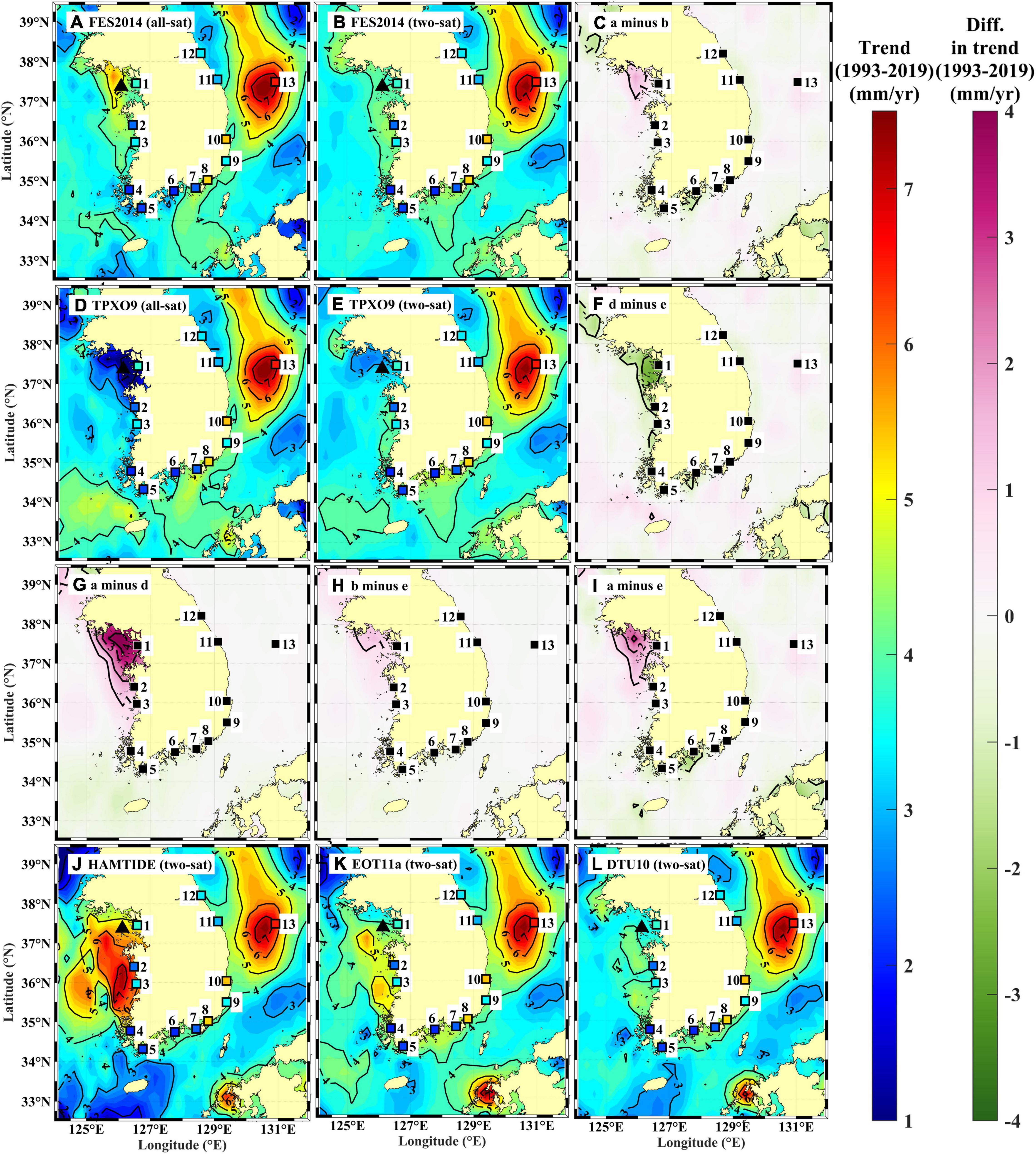
Figure 6. Spatial patterns of linear long-term (1993–2019) trends of sea level rise (LTSLR) derived using SLA data from (A,D) all-sat and (B,E,J,K,L) two-sat satellite altimetry missions, with corrections for ocean tides by (A,B) FES2014,(D,E) TPXO9, (J) HAMTIDE11a, (K) EOT11a, and (L) DTU10. LTSLR differences are shown (C,F) between all-sat and two-sat missions (C: R_{allsat−FES2014}−R_{twosat−FES2014}, f: R_{allsat−TPXO9}−R_{twosat−TPXO9}), (G,H) between FES2014 and TPXO9 model corrections (g: R_{allsat−FES2014}−R_{allsat−TPXO9}, h: R_{twosat−FES2014}−R_{twosat−TPXO9}), and (I) between all-sat mission with FES2014 and two-sat mission with TPXO9 (R_{allsat−FES2014}−R_{twosat−TPXO9}). Two scale bars for LTSLR and its difference in mm⋅yr^–1 are shown at right of figure. LTSLR derived using SLA data from TG observations (R_TG) are shown in (A,B,D,E,J,K,L), with colored squares using same color scale as LTSLR. In (A,B,D,E,J,K,L), location of selected point near TG station IC (number 1), within Gyeonggi Bay, is shown by black triangles.

The inconsistencies in LTSLR between the FES2014(R_{allsat–FES2014} and R_{twosat–FES2014}) and TPXO9 models(R_{allsat–TPXO9} and R_{twosat–TPXO9}) in the area within Gyeonggi Bay were visible in the spatial patterns of the difference between all-sat and two-sat missions (R_{allsat–FES2014} minus Rallsat−TPXO9 and R_{twosat–FES2014} minus R_{twosat–TPXO9}). This indicates that higher LTSLR rates were predicted forSLA_FES2014 than for SLA_TPXO9(Figures 6G,H). The time series of annual mean SLA_FES2014 and SLA_TPXO9 for two-sat missions at a selected location within the Gyeonggi Bay (126.125^°E, 37.375^°N; black triangles in Figure 6) were not well correlated. This yielded higher (4.00 ± 0.04 mm⋅yr^–1) and lower (3.28 ± 0.04 mm⋅yr^–1) LTSLR rates, respectively (red and blue in Figure 2B), than that observed at the TG station IC (R_TG 3.95 ± 0.02 mm⋅yr^–1, green in Figure 2B). The LTSLR averaged over the western coastal area (marked with red shading in Figure 1) for the two-sat mission TPXO9 (3.08 ± 0.03 mm⋅yr^–1) was slightly closer to R_TG averaged over the area (3.23 ± 0.02 mm⋅yr^–1) than that obtained using the two-sat mission with model FES2014 (3.41 ± 0.03 mm⋅yr^–1). This further supports the abovementioned interpretation that TPXO9 outperformed FES2014 (Figure 2B).

In the area within Gyeonggi Bay, LTSLR was inconsistent even when the same model was used for ocean tide corrections; significant differences were obtained when using all-sat compared to two-sat missions for FES2014 (R_{allsat–FES2014} minus R_{twosat–FES2014}) and TPXO9 (R_{allsat–TPXO9} minus R_{twosat–TPXO9}). This indicates that significantly higher (for SLA_FES2014) and lower (for SLA_TPXO9) LTSLR rates were obtained for the all-sat missions than for the two-sat missions (Figures 6C,F). The LTSLR rates derived from annual mean SLA_FES2014 and SLA_TPXO9 for the all-sat missions at the selected location within the Gyeonggi Bay (black triangles in Figure 6) were markedly higher (5.83 ± 0.06 mm⋅yr^–1) and lower (1.52 ± 0.05 mm⋅yr^–1; black and gray in Figure 2B) than those for the two-sat missions (red and blue in Figure 2B), and compared to the R_TG observed at the TG station IC (green in Figure 2B).

In contrast, the high LTSLR rates modeled in the vicinity of TG station ULD (number 13) off the east coast were robust across missions and models (Figure 6). Only small (<0.5 mm⋅yr^–1) differences were observed between R_{twosat–FES2014} (6.65 ± 0.07 mm⋅yr^–1) and R_{twosat–TPXO9} (6.63 ± 0.07 mm⋅yr^–1) at a nearby selected location (130.914^°E, 37.491^°N) and R_TG (6.83 ± 0.08 mm/yr) at the ULD (red, blue, and green in Figure 2C). The spatial pattern of LTSLR derived from SLA_corrected showed significantly higher rates in the vicinity of the ULD, regardless of the satellite missions or ocean tide models used (Figure 6). This pattern revealed a high correlation (correlation coefficient=0.95) between SLA_corrected and SLA_TG at the ULD (Figure 2C).

Discussion

Impact of Tidal Correction of Satellite Altimetry Data on Linear Trend in Sea Level Rise Near the West Coast

Two regions of high (>5 mm⋅yr^–1) LTSLR rates were previously reported around the KP between late 1992 and mid-2019. These regions exceeded the global average trend without GIA (3.7 ± 0.4 mm⋅yr^–1); they were derived using CMEMS global gridded L4 satellite altimetry data, for which ocean tides are corrected by FES2014 (Watson, 2019; Watson and Lim, 2020). The high LTSLR rates identified in this study in the vicinity of Ulleung Island (TG station ULD) off the east coast among the two regions, with a peak value exceeding 7 mm⋅yr^–1 using annual mean L3 altimetry data from 1993 to 2019 (Figure 6), are robust to different altimetry missions and ocean tide models. This trend is thus consistent with previously reported findings (Watson, 2019; Watson and Lim, 2020). However, the previously reported high LTSLR rates within Gyeonggi Bay were significantly different from those observed at the TG station IC. This area was shown to be very sensitive to whether the altimetry data were derived from all-sat or two-sat products, and to which ocean tide model was used to correct the data, as found in this study. Although the operational FES2014 model was shown here to provide better estimates of tidal motion than a few models, such as HAMTIDE, EOT11a, and DTU10, other models, such as TPXO9, could better correct satellite altimetry data for ocean tides, thereby yielding better tidal predictions and better LTSLR estimates in the region. In particular, TPXO9 yielded the minimum RMS difference from TG observations in tidal constants, providing a more realistic pattern of LTSLR around the KP (Figure 6E).

FES2014 uses relatively complicated bathymetry data, as do FES2012, TPXO8, and HAMTIDE11. In detail, along the iso-depth of 30 m, its bathymetry is more complex than those of TPXO9 and NAO.99jb (Figures 7A,D,F vs. Figures 7B,C), which results in an underestimation of the tidal range near the coast within Gyeonggi Bay (Figure 5). In spite of TPXO8 and TPXO9 having the same horizontal resolution (1/30^°), the complicated (TPXO8) vs. smooth (TPXO9) bathymetric representation results of these two models resulted in markedly different (low vs. high, respectively) performance in reproducing the tidal prediction component, compared to TG observations (Figure 4). This resulted in (less vs. more, respectively) reasonable M₂ tidal charts (Figure 5), indicating the importance of model bathymetry, rather than resolution. The bottom drag of complex bathymetry affects the barotropic tidal energy, meaning that tidal energy dissipation is modeled more effectively for complicated bathymetry; this results in decreased tidal amplitudes and increased uncertainty in estimating reasonable tidal constants (Song et al., 2013; Taguchi et al., 2014). Complex model bathymetry was identified as being responsible for underestimated tidal amplitudes for FES2014 and HAMTIDE11a, in comparison to TPXO9 (Figures 5A,B,F, 7A,B,F,H). FES2014 assumes a deeper bottom depth than in TPXO9 in Gyeonggi Bay. This could also explain the reduced tidal amplitude (Figures 5A,B, 7A,B,H) as tidal waves, which are shallow-water waves, propagate more slowly in shallower bottom depths, thus exhibiting increased amplitudes (e.g., TPXO9 provides higher tidal amplitudes for slower propagating tidal waves in shallower bottom depths than FES2014).

FIGURE 7

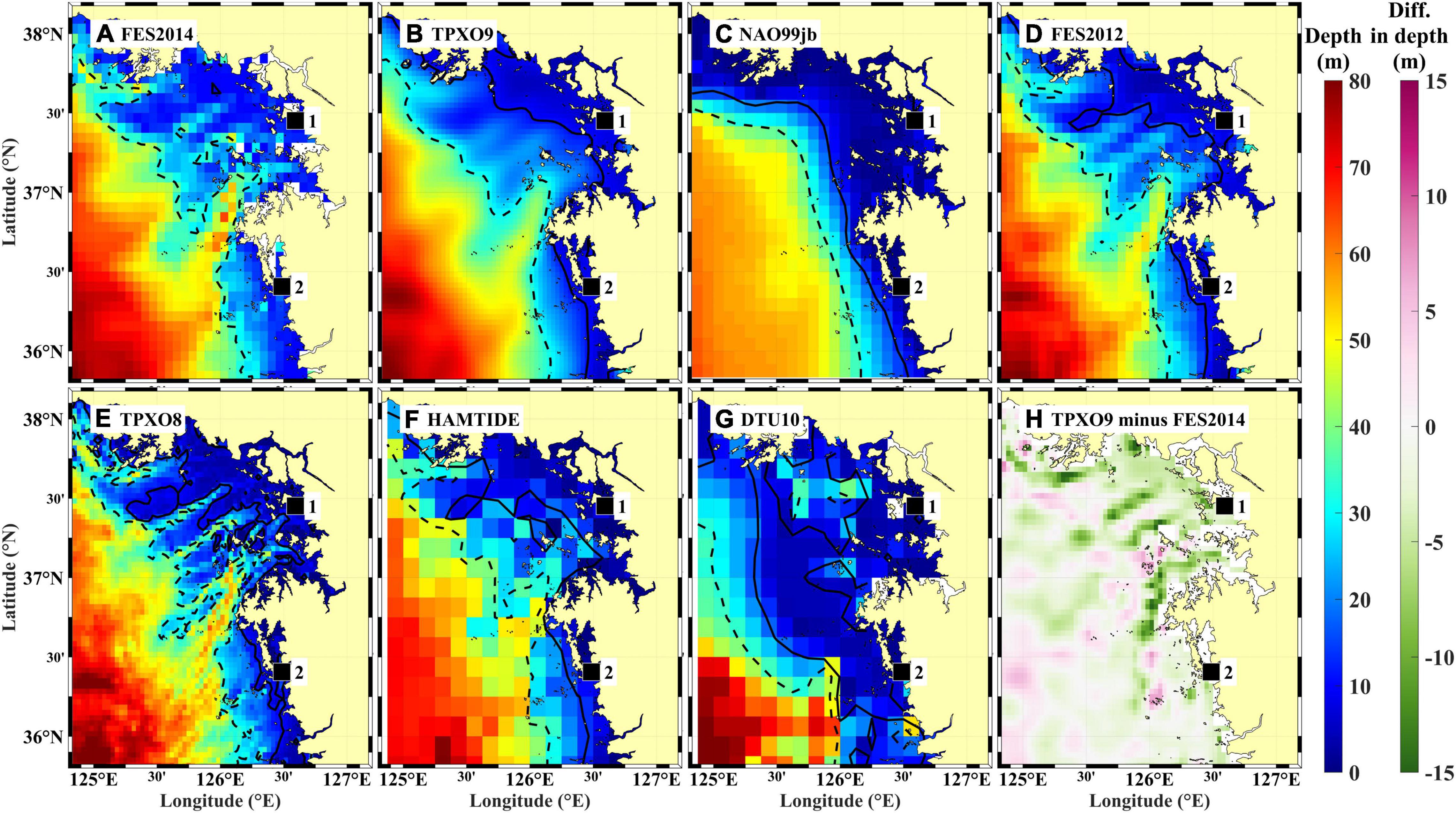
Figure 7. Bathymetries in and around Gyeonggi Bay applied in seven ocean tide models (A: FES2014, B: TPXO9, C: NAO.99jb, D: FES2012, E: TPXO8, F: HAMTIDE11a, and G: DTU10). Color scale for each panel is shown at right of figure (water depth in m), alongside horizontal resolution corresponding to each model. Black solid and dashed lines in (A–G) denote iso-depths of 10 and 30 m, respectively. In (H), difference in bathymetric representation between TPXO9 and FES2014 models is shown with 1/30^° horizontal resolution. Locations of two TG stations (IC and BR) are denoted by black squares.

The reduced tidal amplitude of FES2014 yielded higher SLA_FES2014at high tide and lower SLA_FES2014 at low tide than the SLA_TPXO9, as $h_{tide}^{FES2014}<h_{tide}^{TPXO9}$ and $SL{A}_{raw}-h_{tide}^{FES2014}>SL{A}_{raw}-h_{tide}^{TPXO9}$ for positive (high tide) and $h_{tide}^{FES2014}>h_{tide}^{TPXO9}$ and $SL{A}_{raw}-h_{tide}^{FES2014}<SL{A}_{raw}-h_{tide}^{TPXO9}$ for negative (low tide) SLA. The aliasing effects of altimetry data sampled across a selected 1^° × 1^° area in the vicinity of TG station IC (125.5–126.5^°E, 36.9–37.9^°N; marked with gray box in Figure 1) occurred more frequently at low tides in the early 1990s, whereas they occurred more frequently at high tides in 2013–2017 (Figure 8A). The tidal ranges reach up to several meters and are sampled by satellite altimetry at random timings—more often low tides earlier and high tides later—increasing the LTSLR rates up to 26.6 ± 0.6 and 34.3 ± 0.4 mm⋅yr^–1 for two-sat and all-sat missions, respectively when not corrected by the ocean tide model (Figures 8A,B). Even though the ocean tides are corrected from the altimetry data, the tidal correction would not completely remove the tidal signals and cause the aliasing effects depending on the model performance, and the differences in SLA_corrected among the ocean tide models often exceed 1 m in the vicinity of TG station IC (Figure 3), yielding the LTSLR rates highly sensitive to the model used for the correction. Thus, slightly but significantly higher LTSLR rates were obtained using two-sat and all-sat missions when the ocean tides were corrected by FES2014 (R_{twosat–FES2014} and R_{allsat–FES2014}), compared to TPXO9 simulations (R_{twosat–TPXO9} and R_{allsat–TPXO9}) or TG observations (R_TG) at the IC, and compared to those averaged over the western coastal area (Figures 2, 6). Stronger over-estimations of LTSLR were confirmed from the case corrected by the HAMTIDE model (R_{twosat–HAMTIDE}). This model significantly underestimated the tidal amplitude near TG station IC (Figures 5F, 6J).

FIGURE 8

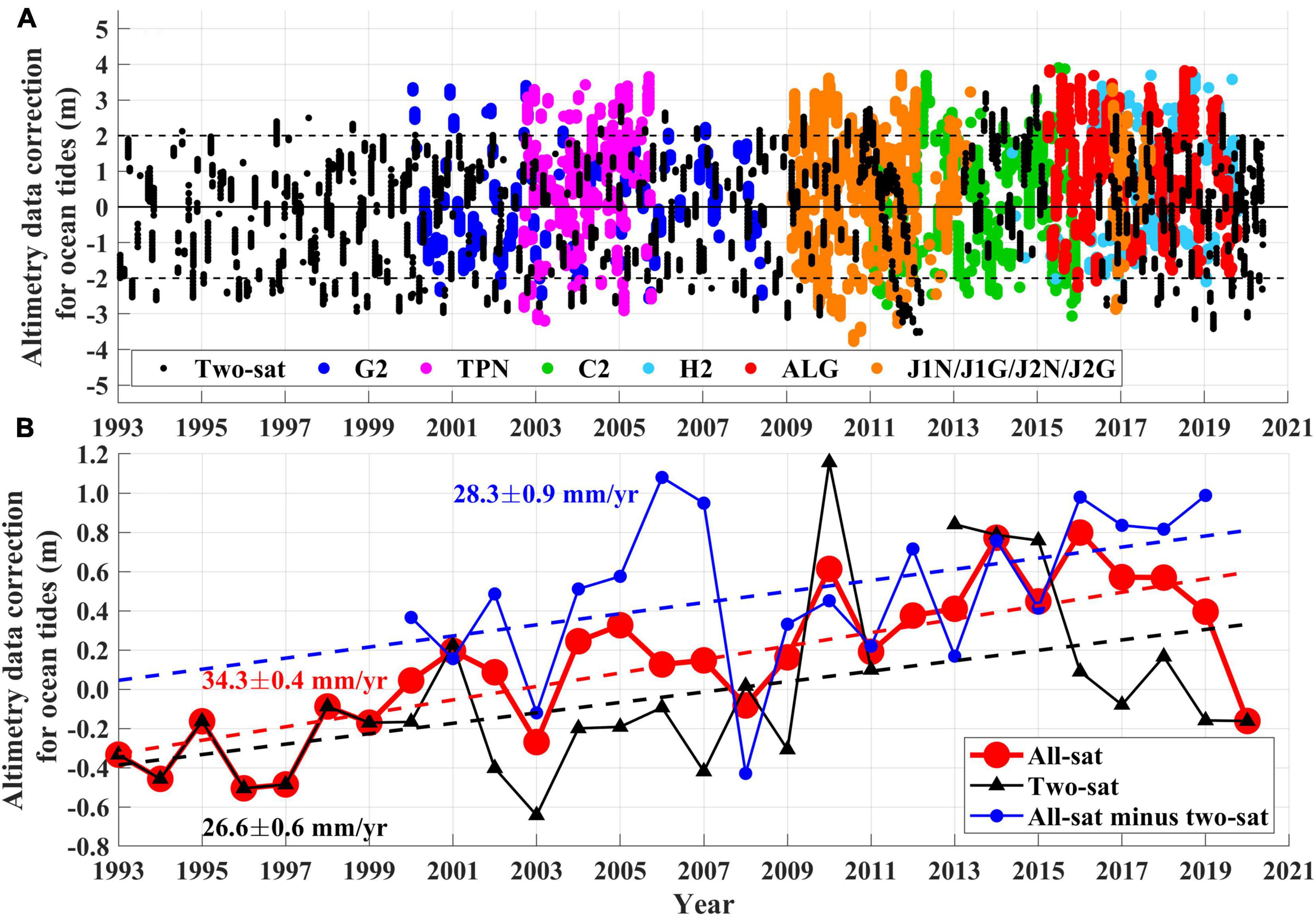
Figure 8. (A) Time series of ocean tide prediction component ($h_{tide}^{FES2014}$) used to correct satellite altimetry data by FES2014 model along the tracks for two-sat reference and complementary satellites (black dots) and for other missions for all-sat products (G2; blue, TPN; pink, C2; green, H2; sky-blue, ALG; red, J1N/J1G/J2N/J2G; orange circles). All information is shown for 1 × 1^° grid near TG station IC within Gyeonggi Bay (gray box in Figure 1 and black triangles in Figure 6). Horizontal grid lines are denoted at 0 and ± 2 m. (B) As for (A) but showing annual mean values for all-sat (large red circles) and two-sat (black triangles) products, alongside their difference (small blue circles Numbers in colors corresponding to dashed lines denote LTSLR.

The performances of the semi-empirical ocean tide models (DTU10 and EOT11a) were very low; they yielded large RMS differences in their M₂ tidal constants at a few TG stations (BR, WD, YS, TY, and US) compared to other models (Figure 4). These models also generated unreasonable M₂ tidal charts with distorted co-phase lines (Figures 5G,H), as they did not assimilate the TG observational data, instead only using satellite altimetry data. This was an issue, as the satellite altimetry data suffered from strong aliasing effects in regions with strong tidal motions such as Gyeonggi Bay, particularly near the coast. Altimetry data, when sampled along-track, have a relatively long cycle period compared to the timescales of SLA fluctuations (such as tidal motions). Furthermore, these data are corrected by global models (which are often not as accurate as regional models). Therefore, they do not provide reliable SLAs 25–50 km away from the coast, due to the measurement gap (Saraceno et al., 2008; Seifi et al., 2019). High LTSLR rates with complex patterns were simulated along the west coast by the DTU10 and EOT11a models. These estimations may be as unrealistic (Figures 6K,L), similarly to the cases corrected by the HAMTIDE and FES 2014 models (Figures 6A,B,D,E), due to the imperfect removal of tidal motions from the satellite altimetry data.

Impact of Inconsistent Satellite Altimetry Missions on Linear Trend in Sea Level Rise Near the West Coast

The LTSLR estimated from the altimetry data is not only dependent onthe tidal correction but also other high-frequency (frequency higher than sampling rate of altimeter) motions to cause the aliasing effects and other factors affecting sea level changes, which may cause inconsistency, as a whole, among the LTSLRs derived fromdifferent combinations of altimetry missions. However, sea level fluctuations are dominated by the tidal motions in the area near the west coast of KP, raising a possibility of mission inconsistency primarily derived from the tidal corrections for different periods of altimetry missions. Significantly distinct spatial LTSLR patterns were modeled within the Gyeonggi Bay between two-sat and all-sat missions, with differences exceeding 1 mm⋅yr^–1 being obtained when using the same model to correct ocean tides. FES2014 and TPXO9 (Figures 6A–F), for example, demonstrated that inconsistency among the satellite missions represented an additional source of error for the estimation of LTSLR. Over the selected 1 × 1^° area in the vicinity of TG station IC (marked with gray box in Figure 1) altimetry SLA data were sampled more frequently at low tides in the early 1990s and at high tides in 2013–2017 by two-sat missions. Furthermore, data were also sampled by all-sat missions more frequently at low tides in the early 1990s (G2) and at high tides in the mid-to-late 2000s and 2010s (TPN, J1N/J1G/J2N/J2G, C2, ALG, and H2) (Figure 8A). As the SLA data were provided for complementary and opportunity satellite missions for the all-sat mission products (but not for two-sat), these data were sampled more frequently at high tides in recent years. The resulting aliasing effects would therefore cause even higher LTSLR rates for all-sat than two-sat missions, unless ocean tides were accurately corrected. This increase in LTSLR resulting from the addition of missions was corrected by FES2014. FES2014 underestimated the tidal amplitude but successfully accounted for the higher annual mean SLA_FES2014 near the TG stations IC in 2014–2018 for all-sat, more so than for two-sat (black vs. red in Figure 2B). The spatial patterns in LTSLR (positive within Gyeonggi Bay) also differed between the all-sat and two-sat missions (Figure 6C). In contrast, the tidal ranges were slightly over-estimated by TPXO9, so LTSLR may have decreased due to the newly added missions. This could explain the lower annual mean SLA_TPXO9 observed near the TG station IC in 2004–2005, 2009–2011, 2015, and 2017–2019 for all-sat missions, compared to for two-sat missions (gray vs. blue in Figure 2B). Furthermore, the spatial LTSLR patterns differed between all-sat and two-sat missions (negative within Gyeonggi Bay, Figure 6F).

Another issue regarding inconsistency among satellite missions is that different platforms use different mean sea surface (MSS) sources; MSS is a temporal mean value of sea surface height, or the sum of the reference ellipsoid, geoid, and mean dynamic topography; it is generally estimated as a mean profile by averaging the sea surface height at the same along-track location over a period of 20 years from 1993 to 2012 (Pujol et al., 2016). However, non-repeating or recent satellite missions (i.e., J1G, J2G, C2, AL, and H2, which have only been operating since 2011) cannot be used to directly estimate MP. Rather, the gridded MSS (CNES_CLS_2015) or the MP estimated based on other altimetry missions are used (TP/J1/J2 measurements for 1993–2012; Pujol et al., 2016; Taburet et al., 2019). Thus, the SLA data referencing this relatively inaccurate MSS for these non-repeating or recent altimetry missions would have generated an additional source of error that might have increased near the coast. This could be particularly influential in areas with strong tidal motions, such as Gyeonggi Bay.

The GIA components might affect the comparison between altimeter and TG data, and spatial pattern of LTSLR around the KP. Although our understanding of the GIA components around the KP is only at a primitive stage, the GIA model suggests marginally significant spatial variations in sea level changes in the order of 0.01 mm⋅yr^–1 within the study area (Table 1). The high (>5 mm/yr) LTSLRs in the two regions near the west coast and off the east coast cannot be explained by the GIA effects, but future study on the spatial pattern of LTSLR should consider these effects. Also, extra care is needed to consider the TG sea level data as it is occasionally affected by significant vertical land motion. The LTSLR estimated from TG station PH data for a period of 1985–2014 was 7.2 mm⋅yr^–1, which was markedly higher than that (1.8 mm⋅yr^–1) estimated from the neighboring TG station US data for the same period (Yoon, 2016). Because of this discrepancy, these cannot be considered likely changes in relative sea levels. Previous reports suggest the effects of vertical land motion on the estimation of LTSLR based on the TG station data may be responsible for such a large difference in the LTSLR at neighboring TG stations (Palanisamy Vadivel et al., 2021). Although the high LTSLR at the TG station IC may not be included in the cases of significant vertical land motion (Palanisamy Vadivel et al., 2021), future study on spatial patterns of LTSLR at the TG stations around the KP needs to consider the effects of vertical land motion. Finally, this study focused on the LTSLR around the KP for the specific period (from 1993 to 2019) to best use the satellite altimetry data, yet it significantly varies over the period of estimation. For example, the LTSLR at the TG station IC estimated for a period from 1985 to 2014 (3.7 mm⋅yr^–1) is more than double that estimated for the period from 1960 to 2014 (0.9 mm⋅yr^–1), raising the possibility of accelerating regional sea level rise as well as spatially different LTSLRs (Yoon, 2016). The factors affecting sea level changes around the KP, as sampled for different periods in different ways for different missions and corrected/processed in different ways, may only enhance the inconsistency between the altimetry missions.

High Linear Trend in Sea Level Rise Rate in the Vicinity of Ulleung Island off the East Coast

High (∼7 mm⋅yr^–1) LTSLR rates were reported in the vicinity of Ulleung Island, both here and in previous studies (Watson, 2019; Watson and Lim, 2020). These high LTSLR rates could not be explained by aliasing effects arising from incomplete correction for ocean tides, or by inconsistencies between altimetry missions, as the region is far (hundreds of km) off the east coast and the tidal range is relatively small. Consequently, the high LTSLR was robust to missions and tide models (Figure 6). Near the TG station ULD, R_{twosat–FES2014} (6.65 ± 0.07 mm⋅yr^–1) and R_{twosat–TPXO9} (6.63 ± 0.07 mm⋅yr^–1) yielded small differences from R_TG (6.83 ± 0.08 mm⋅yr^–1) at the mentioned station (red, blue, and green in Figure 2C, respectively). As the tide off the east coast of the KP is very small (Kang et al., 1991), the RMS of all tidal models (<1 cm) and the corrected LTSLR (<0.1 mm⋅yr^–1) demonstrate very small differences. Interannual and decadal variations in upper ocean heat content linked to regional circulation may have acted as controlling drivers for the SLA variability observed at the ULD (Choi et al., 2004, 2009; Kang et al., 2005; Yoon et al., 2016). This implies that the high LTSLR rates in the region derived from long-term changes in regional circulation with strong mesoscale variability. The pathway of the Tsushima Warm Current (TWC) varies remarkably over time, so the SLA at the TG station ULD increases when it lies to the south of the subpolar front (leading to warmer water, a higher heat content, and thus a higher steric sea level and SLA). This occurs under a regional circulation pattern named the Inertial Boundary Current (IBC) and previous works suggest more frequent occurrence of the IBC pattern in the 2010s compared to the early 1990s (Pak et al., 2019). Comparing a time series of the annual occurrence days of the IBC from 1993 to 2017 with SLA_FES2014, SLA_TPXO9, and SLA_TG (Figures 2C; Pak et al., 2019) revealed a positive trend with a rate of 3.53 ± 0.12 d⋅yr^–1, which was consistent with higher SLA. This was indicative of circulation changes from non-IBC to IBC patterns, though it could not fully explain the long-term changes in regional circulation. Furthermore, long-term variability of the mesoscale eddies in the vicinity of the island may be related to the high LTSLR rates as it is reported that the warm (anticyclonic) eddies have more frequently occupied the island in recent years (Shin et al., 2005; Lee et al., 2019), increasing the LTSLR rates. This raises the possibility that the changes in regional ocean circulation patterns could explain the high LTSLR rates observed in and around the ULD, although a thorough investigation of the circulation processes and their consequences on regional sea level rise remains to be conducted.

Conclusion

This study revealed that corrections for ocean tides and mission inconsistencies in satellite altimetry data can both significantly impact the estimation of LTSLR in regions with strong tidal motions near the west coast of the KP (within Gyeonggi Bay). In contrast, estimations of high (∼7 mm⋅yr^–1) LTSLR rates off the east coast (in the vicinity of Ulleung Island) were found tobe more robust. The FES 2014 model is currently used globally to correct ocean tides when providing merged altimetry products. Here, however, it was found to significantly underestimate tidal amplitudes near the west coast of the KP, owing to the model’s deeper and more complex representation of bathymetry. These characteristics resulted in higher predicted LTSLR rates owing to the aliasing effects of miscorrected tidal oscillations sampled in a different phase in the 1990s (low tides) and 2010s (high tides). This disparity was particularly evident compared to the best performing model (TPXO9). Similarly, LTSLR rates near the west coast derived from SLA corrected by semi-empirical ocean tide models (DTU10 and EOT11a) provided unreasonable co-tidal and co-range lines in tidal charts and large RMS differences in tidal constants, compared to TG observations. Furthermore, the high LTSLR rates reported near the west coast by previous studies were shown to be artificially produced, partly due to inconsistencies between satellite altimetry missions. These inconsistencies yielded different degrees of aliasing effects owing to inconsistent MSS usage. In contrast to the highly variable LTSLR rates observed near the west coast, which were influenced by satellite missions and ocean tide models, the high (∼7 mm⋅y^–1) LTSLR rates off the east coast (both reported previously and derived here from altimetry data) were found to be robust and consistent between missions and models. They were consistent with TG observations (ULD), and may be explained by the changing regional ocean circulation patterns, which require further studies.

The results presented here suggest that previously reported high LTSLR rates near the west coast are not realistic features, but instead are artificial impacts arising from the miscorrection of ocean tides, and from inconsistencies among satellite altimetry missions. In contrast, the realistically high LTSLR rates observed off the east coast are potentially linked to changes in regional circulation. These results highlight the better performance of the two-sat altimetry data corrected by TPXO9 for estimation of LTSLR on the large tidal regions as well as changes in regional circulation for better understanding the LTSLR around the KP, e.g., most realistic pattern is shown in Figure 6E. These findings are also applicable to other coastal regions, where the tidal motions are often strong.

Data Availability Statement

The TG data were provided by KHOA and are available at https://www.khoa.go.kr/koofs. Along-track satellite altimetry data were produced and distributed by the CMEMS (https://marine.copernicus.eu/). The tidal constants and bathymetries used in ocean tide models were acquired via the web links for FES2012 and FES2014 (https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/global-tide-fes.html), TPXO8 and TPXO9 (https://www.tpxo.net/global), NAO.99jb (https://www.miz.nao.ac.jp/staffs/nao99/index_En.html), HAMTIDE11a (https://icdc.cen.uni-hamburg.de/en/hamtide.html), DTU10 (https://www.space.dtu.dk/english/research/scientific_data_and_models/global_ocean_tide_model), and EOT11a (https://openadb.dgfi.tum.de/en/products/empirical-ocean-tide-model/).

Author Contributions

KL and SN: conceptualization. KL, D-SB, and SN: methodology. KL and D-SB: data acquisition. KL: formal analysis, writing–original draft preparation, visualization, and data curation. KL, SN, Y-KC, D-SB, and K-YJ: investigation and writing–review and editing. SN: supervision. K-YJ and SN: project administration. All authors have read and agreed to the published version of the manuscript.

Funding

This research formed a part of the project titled “Deep Water Circulation and Material Cycling in the East Sea (20160040)” funded by the Ministry of Oceans and Fisheries (MOF), Republic of Korea. This research was funded by the Korea Hydrographic and Oceanographic Agency (KHOA), MOF, through the “Analysis and Prediction of Sea Level Change in Response to Climate Change around the Korean Peninsula” program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank two reviewers for constructive comments, and G.D. Pak and D. Stammer for providing the annual occurrence days of IBC pattern data and the bathymetry data of the HAMTIDE11a model, respectively.

References

An, H. S. (1977). A numerical experiment of the M2 tide in the Yellow Sea. J. Oceanogr. Soc. Jpn. 33, 103–110. doi: 10.1007/bf02110016

CrossRef Full Text | Google Scholar

Byun, D. S., and Cho, C. W. (2009). Exploring conventional tidal prediction schemes for improved coastal numerical forecast modeling. Ocean Model. 28, 193–202. doi: 10.1016/j.ocemod.2009.02.001

CrossRef Full Text | Google Scholar

Carrère, L., Lyard, F., Cancet, M., Guillot, A., and Roblou, L. (2013). FES 2012: a new global tidal model taking advantage of nearly 20 years of altimetry. 20 years of prog. Radar Altimetry 710:13.

Google Scholar

Cazenave, A., and Llovel, W. (2010). Contemporary sea level rise. Ann. Rev. Mar. Sci. 2, 145–173.

Google Scholar

Cheng, Y., and Andersen, O. B. (2011). Multimission empirical ocean tide modeling for shallow waters and polar seas. J. Geophys. Res. 116:C11001.

Google Scholar

Cheng, Y., Plag, H. P., Hamlington, B. D., Xu, Q., and He, Y. (2015). Regional sea level variability in the Bohai Sea, Yellow Sea, and East China Sea. Contin. Shelf Res. 111, 95–107. doi: 10.1016/j.csr.2015.11.005

CrossRef Full Text | Google Scholar

Choi, B. J., Haidvogel, D. B., and Cho, Y. K. (2004). Nonseasonal sea level variations in the Japan/East Sea from satellite altimeter data. J. Geophys. Res. 109:C12028.

Google Scholar

Choi, B. J., Haidvogel, D. B., and Cho, Y. K. (2009). Interannual variation of the polar front in the Japan/East Sea from summertime hydrography and sea level data. J. Mar. Syst. 78, 351–362. doi: 10.1016/j.jmarsys.2008.11.021

CrossRef Full Text | Google Scholar

Church, J. A., and White, N. J. (2011). Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 32, 585–602. doi: 10.1007/978-94-007-2063-3_17

CrossRef Full Text | Google Scholar

Codiga, D. L. (2011). Unified Tidal Analysis and Prediction Using the UTide MATLAB Functions. Technical Report. 2011-01. Narragansett, RI: Graduate School of Oceanography, 59.

Google Scholar

Devlin, A. T., Jay, D. A., Talke, S. A., Zaron, E. D., Pan, J., and Lin, H. (2017). Coupling of sea level and tidal range changes, with implications for future water levels. Sci. Rep. 7:17021. doi: 10.1038/s41598-017-17056-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Egbert, G. D., and Erofeeva, S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmos. Oceanic Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:eimobo>2.0.co;2

CrossRef Full Text | Google Scholar

Egbert, G. D., and Erofeeva, S. Y. (2018). “TPXO9, a new global tidal model in TPXO series,” in Proceedings of the Ocean Science Meeting, Portland, OR, 11–16. doi: 10.29252/joc.10.38.11

CrossRef Full Text | Google Scholar

Fasullo, J. T., and Nerem, R. S. (2018). Altimeter-era emergence of the patterns of forced sea-level rise in climate models and implications for the future. Proc. Natl. Acad. Sci. U.S.A. 115, 12944–12949. doi: 10.1073/pnas.1813233115

PubMed Abstract | CrossRef Full Text | Google Scholar

Foreman, M. G. G., Henry, R. F., Walters, R. A., and Ballantyne, V. A. (1993). A finite element model for tides and resonance along the north coast of British Columbia. J. Geophys. Res. 98, 2509–2531. doi: 10.1029/92jc02470

CrossRef Full Text | Google Scholar

Han, M., Cho, Y.-K., Kang, H.-W., Nam, S., Byun, D.-S., Jeong, K.-Y., et al. (2020a). Impacts of atmospheric pressure on the annual maximum of monthly sea-levels in the northeast Asian marginal seas. J. Mar. Sci. Eng. 8:425.

Google Scholar

Han, M., Nam, S., Cho, Y.-K., Kang, H.-W., Jeong, K.-Y., and Lee, E. (2020b). Interannual variability of winter sea levels induced by local wind stress in the northeast Asian marginal seas: 1993–2017. J. Mar. Sci. Eng. 8:774. doi: 10.3390/jmse8100774

CrossRef Full Text | Google Scholar

Idier, D., Paris, F., Le Cozannet, G. L., Boulahya, F., and Dumas, F. (2017). Sea-level rise impacts on the tides of the European Shelf. Continent. Shelf Res. 137, 56–71.

Google Scholar

IPCC (2019). IPCC Special Report on the Ocean and Cryosphere in a Changing Climate [Pörtner, H. -O., D. C. 18 Roberts, Masson, V., -Delmotte, P. Z., Tignor, M., Poloczanska, E. S., Mintenbeck, K., Nicolai, M. (in press). 19 Petzold, eds B. Rama, and N. Weyer]. Geneva: IPCC.

Google Scholar

Kang, S. K., Cherniawsky, J., Foreman, M., Min, H. S., Kim, C. H., and Kang, H. W. (2005). Patterns of recent sea level rise in the East/Japan Sea from satellite altimetry and in situ data. J. Geophys. Res. 110:C07002. doi: 10.1029/2004JC002565

CrossRef Full Text | Google Scholar

Kang, S. K., Chung, J. Y., Lee, S. R., and Yum, K. D. (1995). Seasonal variability of the M2 tide in the seas adjacent to Korea. Continent. Shelf Res. 15, 1087–1113. doi: 10.1016/0278-4343(94)00066-v

CrossRef Full Text | Google Scholar

Kang, S. K., Lee, S. R., and Yum, K. (1991). Tidal computation of the East China Sea. The Yellow Sea and the East Sea. Elsevier Oceanogr. Ser. 54, 25–48.

Google Scholar

Kim, Y. S., Jang, C. J., and Yeh, S.-W. (2018). Recent surface cooling in the Yellow and East China Seas and the associated North Pacific climate regime shift. Continent. Shelf Res. 156, 43–54.

Google Scholar

Lee, K., Nam, S., and Kim, Y. G. (2019). Statistical characteristics of East Sea mesoscale eddies detected, tracked, and grouped using satellite altimeter data from 1993 to 2017. Sea 24, 267–281.

Google Scholar

Lyu, S. J., Kim, K., and Perkins, H. T. (2002). Atmospheric pressure-forced subinertial variations in the transport through the Korea Strait. Geophys. Res. Lett. 29, 8-1–8-4.

Google Scholar

Matsumoto, K., Takanezawa, T., and Ooe, M. (2000). Ocean tide models developed by assimilating TOPEX/POSEIDON altimeter data into hydrodynamical model: a global model and a regional model around Japan. J. Oceanogr. 56, 567–581.

Google Scholar

Nam, S. H., Lyu, S. J., Kim, Y. H., Kim, K., Park, J. H., and Watts, D. R. (2004). Correction of TOPEX/POSEIDON altimeter data for nonisostatic sea level response to atmospheric pressure in the Japan/East Sea. Geophys. Res. Lett. 31:L02304.

Google Scholar

Nicholls, R. J., and Cazenave, A. (2010). Sea-level rise and its impact on coastal zones. Science 328, 1517–1520. doi: 10.1126/science.1185782

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishida, H. (1980). Improved tidal charts for the western part of the north Pacific Ocean. Rep. Hydrogr. Res. 15, 55–70.

Google Scholar

Pak, G., Kim, Y. H., and Park, Y.-G. (2019). Lagrangian approach for a new separation index of the East Korea warm current. Ocean Sci. J. 54, 29–38. doi: 10.1007/s12601-018-0059-2

CrossRef Full Text | Google Scholar

Palanisamy Vadivel, S. K., Kim, D., Jung, J., Cho, Y.-K., and Han, K.-J. (2021). Monitoring the vertical land motion of tide gauges and its impact on relative sea level changes in Korean Peninsula using sequential SBAS-InSAR time-series analysis. Remote Sens. 13, 1–22.

Google Scholar

Park, K. A., Lee, E. Y., Chang, E., and Hong, S. (2015). Spatial and temporal variability of sea surface temperature and warming trends in the Yellow Sea. J. Mar. Syst. 143, 24–38.

Google Scholar

Peltier, W. R. (2004). Global glacial isostasy and the surface of the ice-age Earth: the ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet Sci. 32, 111–149.

Google Scholar

Pujol, M.-I., Faugère, Y., Taburet, G., Dupuy, S., Pelloquin, C., Ablain, M., et al. (2016). DUACS DT2014: the new multi-mission altimeter data set reprocessed over 20 years. Ocean Sci. 12, 1067–1090.

Google Scholar

Qiu, B., Chen, S., Wu, L., and Kida, S. (2015). Wind-versus eddy-forced regional sea level trends and variability in the North Pacific Ocean. J. Clim. 28, 1561–1577. doi: 10.1175/jcli-d-14-00479.1

CrossRef Full Text | Google Scholar

Saraceno, M., Strub, P. T., and Kosro, P. M. (2008). Estimates of sea surface height and near-surface alongshore coastal currents from combinations of altimeters and tide gauges. J. Geophys. Res. 113:C11013.

Google Scholar

Savcenko, R., and Bosch, W. (2012). EOT11a-Empirical Ocean Tide Model from Multi-Mission Satellite Altimetry. DGFI Report No. 89. München: Deutsches Geodätisches Forschungsinstitut.

Google Scholar

Seifi, F., Deng, X., and Baltazar Andersen, O. (2019). Assessment of the accuracy of recent empirical and assimilated tidal models for the Great Barrier Reef, Australia, using satellite and coastal data. Remote Sens. 11:1211.

Google Scholar

Song, D., Wang, X. H., Zhu, X., and Bao, X. (2013). Modeling studies of the far-field effects of tidal flat reclamation on tidal dynamics in the East China Seas. Estuar. Coast. Shelf Sci. 133, 147–160.

Google Scholar

Stammer, D., Cazenave, A., Ponte, R. M., and Tamisiea, M. E. (2013). Causes for contemporary regional sea level changes. Ann. Rev. Mar. Sci. 5, 21–46. doi: 10.1146/annurev-marine-121211-172406

PubMed Abstract | CrossRef Full Text | Google Scholar

Taburet, G., Sanchez-Roman, A., Ballarotta, M., Pujol, M.-I., Legeais, J.-F., Fournier, F., et al. (2019). DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean Sci. 15, 1207–1224.

Google Scholar

Taguchi, E., Stammer, D., and Zahel, W. (2014). Inferring deep ocean tidal energy dissipation from the global high-resolution data-assimilative HAMTIDE model. J. Geophys. Res. Oceans 119, 4573–4592.

Google Scholar

Tamisiea, M. E., and Mitrovica, J. X. (2011). The moving boundaries of sea level change: understanding the origins of geographic variability. Oceanography 24, 24–39.

Google Scholar

Thomson, R. E., and Emery, W. J. (2014). Data Analysis Methods in Physical Oceanography, 3rd Edn. Amsterdam: Elsevier, 250–254.

Google Scholar

Vinogradov, S. V., and Ponte, R. M. (2011). Low-frequency variability in coastal sea level from tide gauges and altimetry. J. Geophys. Res. 116:C07006.

Google Scholar

Watson, P. J. (2019). Updated mean sea-level analysis: South Korea. J. Coast. Res. 35, 241–250.

Google Scholar

Watson, P. J., and Lim, H.-S. (2020). An update on the status of mean sea level rise around the Korean Peninsula. Atmosphere 11:1153.

Google Scholar

Yoon, J. J. (2016). Analysis of long-period sea-level variation around the Korean Peninsula. J. Coast. Res. 75, 1432–1436.

Google Scholar

Yoon, S. T., Chang, K. I., Na, H., and Minobe, S. (2016). An east-west contrast of upper ocean heat content variation south of the subpolar front in the East/Japan Sea. J. Geophys. Res. Oceans 121, 6418–6443.

Google Scholar