Precision-tailored ocean wave modeling: enhancing efficiency in the MASNUM wave model through mixed-precision techniques

Introduction: To enhance the simulation performance of wave numerical models, high-precision ocean models are widely utilized. However, the low efficiency of high-precision numerical computation remains one of the key bottlenecks hindering the advancement of wave forecasting.

Methods: To address this issue, this study introduces a mixed-precision framework based on variable-specific precision allocation, applied to the MArine Science and Numerical Modeling (MASNUM) ocean wave model, considering physical sensitivities.

Results: The results demonstrate that by strategically reducing the precision of non-critical variables to single-precision (float32) or half-precision (float16), the mixed-precision scheme significantly improves computational efficiency while maintaining the accuracy of the simulation results. Specifically, compared to the double-precision baseline, the mixed-precision approach results in minimal accuracy loss, with SMAPE values for significant wave height ranging between 0.12% and 0.43%, and RMSE ranging from 0.01 m to 0.02 m.

Discussion: In terms of computational performance, combined structural and precision optimizations yield a 2.97–3.39× speedup over double-precision. The findings robustly demonstrate the potential of mixed-precision computing for high-resolution, real-time ocean forecasting applications, providing valuable insights for balancing computational efficiency and simulation accuracy.

1 Introduction

Ocean Waves have a wide and profound impact on the marine environment, involving multiple fields such as marine ecosystems, climate, maritime transportation, and marine pollution control. Therefore, the accuracy of wave forecasting has garnered widespread attention. The core of wave forecasting lies in wave numerical models, which provide efficient and cost-effective methods to address these complex issues. Wave numerical models predict wave dynamics by solving the wave dynamics equations, incorporating external forcing factors such as wind fields and atmospheric pressure fields (Liang et al., 2019; Shchepetkin and McWilliams, 2005; Booij et al., 1999). However, the development of numerical simulation capabilities is constrained by the progress in high-performance computing. In recent years, scientists have focused on achieving more accurate, detailed, and comprehensive simulation results by continuously improving physical parameterizations, enhancing spatiotemporal resolution, and coupling different system models (Zhuang et al., 2018; Palmer, 2012; Matsueda and Palmer, 2011). These efforts aim to enhance the predictive power of models. Nevertheless, such improvements often come at the cost of significant computational demands, leading to challenges such as insufficient computing resources and excessive energy consumption in traditional simulations.

To address these challenges, mixed-precision computing has emerged as a cutting-edge technology in numerical simulations (Düben and Palmer, 2014; Thornes, 2016; Sun et al., 2023; Göddeke et al., 2007). Mixed-precision involves using different levels of numerical precision within the same computational task, namely incorporating double-precision floating-point numbers (double64), single-precision floating-point numbers (float32), and half-precision floating-point numbers (float16). The goal is to strike a balance between computational performance and numerical precision. In this context, the advantages of each precision level are leveraged based on the specific needs of the computation. Double-precision offers high accuracy but incurs higher computational and memory costs. Single-precision provides a good compromise between precision and performance, while half-precision is less precise but offers significant improvements in computational and memory efficiency (Baboulin et al., 2009). This approach is particularly crucial for large-scale or real-time numerical simulations, such as hurricane forecasts, weather predictions and fluid dynamic simulations.

Previous research results indicate that, in the weather and climate prediction models, simulations using appropriately reduced precision in high-resolution models tend to yield better results at lower computational costs, compared to traditional high-precision low-resolution numerical simulations (Thornes et al., 2017; Düben et al., 2015, 2017; Hatfield et al., 2019; Vána et al., 2017). Additionally, conducting inexact calculations at a small scale, rather than relying solely on parameterization, is more effective in reducing computational and energy consumption, without negatively impacting the quality of simulation results (Düben et al., 2014; Chantry et al., 2019). Maynard and Walters (2019) suggested that atmospheric model developers continued exploring the reduction of computational precision to enhance simulation efficiency, particularly in mixed-precision arithmetic in the ENDGame dynamical core of the Unified Model. In ocean simulations, Yamagishi and Matsumura (2016) achieved a 4.7-fold increase in the execution speed of the non-hydrostatic ocean model “kinaco” on GPU compared to CPU by applying mixed-precision in the P/H solver and other techniques. Prims et al. (2019) applied mixed-precision methods to the Nucleus for European Modelling of the Ocean (NEMO), utilizing the reduced-precision emulator (RPE) for precision reduction. Their results revealed that in the NEMO model, 652 variables (69.2%) could be represented using single-precision. Lai et al. (2021) reduced numerical precision in both the shallow water wave equation (SWE) and Princeton Ocean Model (POM) models, and the simulation results validated the feasibility of the mixed-precision approach. Therefore, mixed-precision methods in the field of numerical simulations hold potential advantages for enhancing performance, conserving computational resources, and advancing scientific research.

The MArine Science and Numerical Modeling (MASNUM) ocean wave model is the third-generation global ocean wave model developed by the Laboratory of Marine Environmental Science and Numerical Modeling at the First Institute of Oceanography, Ministry of Natural Resources, China (Sun et al., 2021, 2014; Yang et al., 2005; Sun et al., 2018; Teng et al., 2016). Based on LAGFD-WAM wave model, the numerical wave model is established in spherical coordinate system, and the balance equation of wave energy spectrum and its complex characteristic line equation are derived. This model possesses the capability to simulate and predict global, regional, and nearshore wave environments and is widely applied in marine scientific research and numerical forecasting (Zhuang et al., 2021). This study focuses on the MASNUM model, classifying variables within the model based on their mathematical properties and physical attributes. The sensitivity of various physical processes in the MASNUM model to mixed-precision results is analyzed. Precision formats for different variables are determined, enabling the application of mixed-precision in the MASNUM model. The structure of this paper is structured as follows: Section 2 presents the methodology, while Section 3 provides a detailed analysis and discussion of the simulation experiments conducted using the mixed-precision scheme, along with its application on a 20,000-core system. Finally, Section 4 summarizes the study and explores directions for future research.

2 Methods

2.1 MASNUM wave model

The MASNUM wave model is a numerical simulation approach based on the energy balance equation in wavenumber space, where the wave spectrum is the primary simulation target. The wavenumber spectrum calculation in the MASNUM wave model mainly includes the propagation function and source function. The source function accounts for the following physical mechanisms: wind input, nonlinear wave-wave interactions, bottom friction, wave breaking dissipation, and wave-current interactions. The governing equations of the model use the conservation equation of the wave energy spectrum in the spherical coordinate system:

$\begin{array}{ll}SS=S_{in}+S_{ds}+S_{bo}+S_{nl}+S_{cu}& (1)\end{array}$

where $S_{in}$, $S_{ds}$, $S_{bo}$, $S_{nl}$, $S_{cu}$ are the wind input source function, breaking dissipation source function, bottom friction dissipation source function, nonlinear wave-wave interaction source function, wave-current interaction source function, respectively.

The MASNUM model is a wave numerical simulation program developed using the Fortran programming language. This program primarily consists of modules for inputting model data, performing numerical computations for waves, solving wave characteristic vectors, and outputting results. The wave numerical computation section includes the propagate and implsch functions. The parallel computing processes of the MASNUM model are as follows: First, a source code image is created and run on each computing node. Then, the parallel environment is initialized, and the topographic data is read. Next, the main computation and communication sections are executed, followed by the output of model files. Finally, the parallel environment is terminated.

2.2 Experimental configuration

In the initialization section, the MASNUM model offers two versions for all variables: single-precision and double-precision. The double precision options yield more accurate simulation results but come with increased computational cost. Conversely, the single-precision version significantly reduces computational and communication overhead, although it may not yield the desired simulation accuracy. In addition to double-precision and single-precision, a half-precision option is also available to further accelerate computation. This study employs a mixed-precision method using different combinations of double-precision, single-precision, and half-precision to enhance the computational speed and efficiency of the MASNUM model while ensuring simulation accuracy. Therefore, due to the limitations of CPU in half-precision computation, we have ported the MASNUM program to a GPU, utilizing the GPU-optimized half-precision operations for mixed-precision testing.

The server node configuration for the CPU machine used in this experiment is a high-performance computing cluster with dual Intel Gold 6258R processors (56 cores), x86_64 architecture, and 192GB of memory. The GPU machine uses A100 GPU cards, based on NVIDIA’s Ampere architecture, featuring 6,912 CUDA cores, double-precision computing capability of 9.7 TFLOPS, single-precision computing capability of 19.5 TFLOPS, and support for half-precision computation. The software environment consists of the NVIDIA HPC SDK suite (version 22.2) with the NVIDIA compiler, CUDA version 11.6, and OpenMPI version 3.1.5. The system runs on CentOS 8.5 with a kernel version of 4.18.0-348.7.1. In terms of hardware communication bandwidth, the data transfer rate between the CPU and GPU reaches 32 GB/s, the interconnect bandwidth between GPU cards can achieve 600 GB/s. For performance optimization, the code is compiled with the -O2 optimization level.

The MASNUM software uses the CUDA interface for GPU porting. The main processes are as follows:

1. Search for GPU device environment: Match the GPU card with MPI processes.

2. Allocate GPU memory: Request memory for variables and computational data space in the device’s VRAM.

3. Copy data to the GPU: Transfer the necessary information from the host memory to the device’s VRAM.

4. Execute GPU kernel functions: Perform parallel computations on the device.

5. Copy data from the GPU: Transfer results from the device’s VRAM back to the host.

The ported program executes the main source functions on the GPU and returns the results to the CPU. The main functions are developed using the CUDA FORTRAN language interface, while the half-precision components are written using the CUDA C language interface. The C interface encapsulates relevant functions for use by the source FORTRAN program. In steps (3) and (4) above, when data is copied and transferred between the host and device, data type conversion is required for half-precision data types. The specific implementation details are provided in the Appendix A.

In this study, all experiments are conducted using global-scale simulations with a spatial resolution of 0.25°and a time step of 1 hour. The forcing wind field is derived from NCEP reanalysis data (https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html, Kalnay et al., 1996), which has a coarser spatial resolution of 2.5° and a time step of 6 hours. The simulations cover January 2021. Significant wave height, a key indicator of wave characteristics, effectively represents the energy and intensity of ocean waves. Therefore, significant wave height is chosen as the primary diagnostic variable for MASNUM model output analysis.

2.3 Hotspot analysis

To identify the module with the highest simulation computation time in the MASNUM model and improve the computation speed using mixed-precision, we performed a hotspot analysis. The hotspot analysis was conducted using the profiling feature provided by the INTEL compiler, which collects statistics on the time spent in functions and loops, iteration counts, and average, minimum, and maximum call frequencies. The results showed that the majority of the runtime in the MASNUM model is spent in the readwi function, accounting for 88% of the total runtime (see Figure 1). We used the MPI_WTIME() function to measure the time spent in the readwi function, and the results indicated that its subfunction implsch function in the model’s computational section accounts for the largest portion of the runtime, reaching 77.5%. The governing equation of the model (as shown in Equation 1) is included in the implsch module. Therefore, this study aims to implement mixed-precision calculations for the implsch function’s source code to enhance the computational speed of MASNUM.

Figure 1

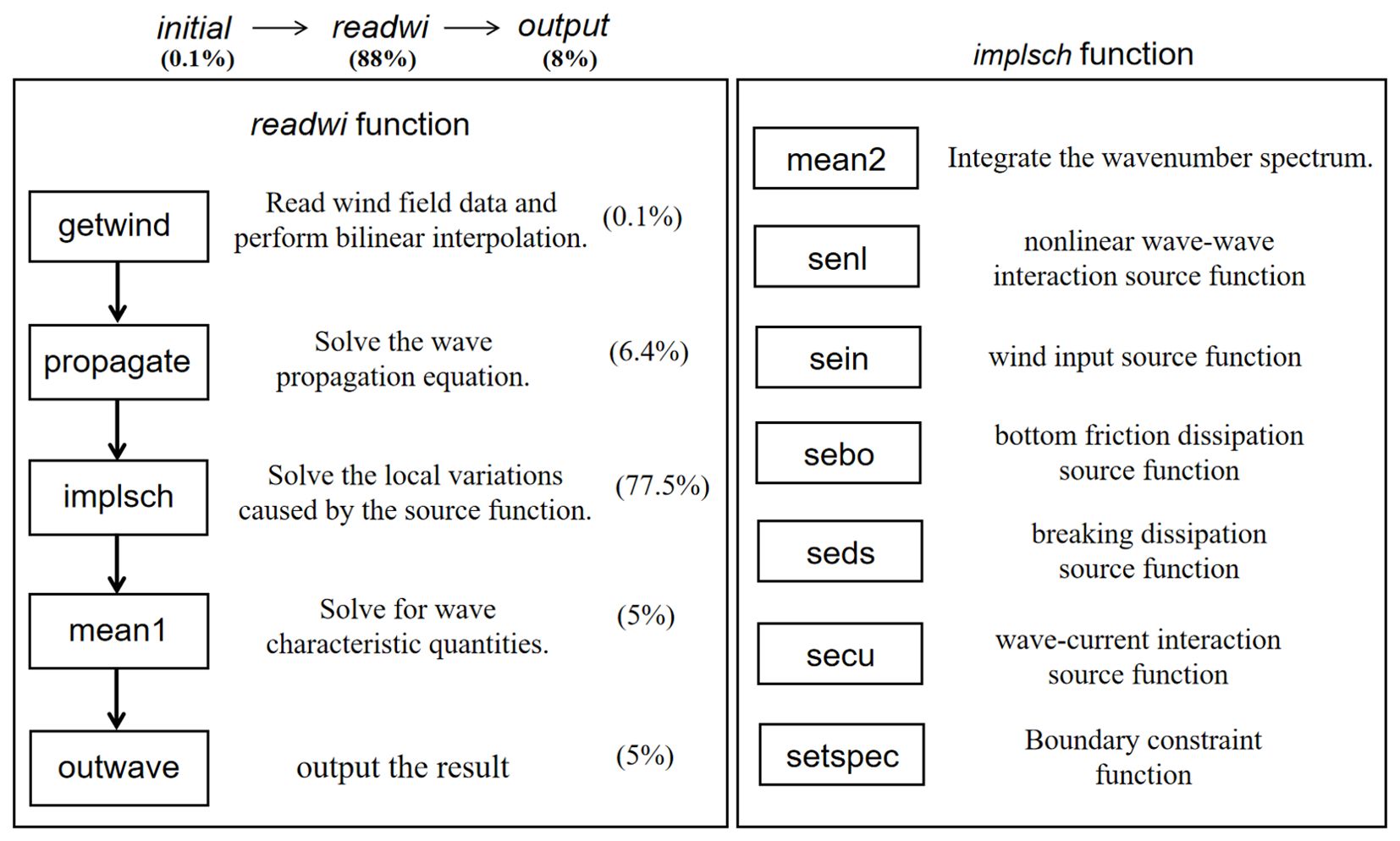
Figure 1. Percentage of runtime for each section in the MASNUM model and for each source function within the implsch function.

In summary, this study defines the precision formats of variables in different source functions within the implsch module based on the conservation equation (as shown in Equation (1)) of the ocean wave energy spectrum to implement mixed-precision. Then, numerical simulations are conducted according to the mixed-precision settings, and the accuracy of the simulation results is evaluated to improve simulation speed and efficiency while ensuring the accuracy of the results.

3 Results and discussion

3.1 Benchmark experiments

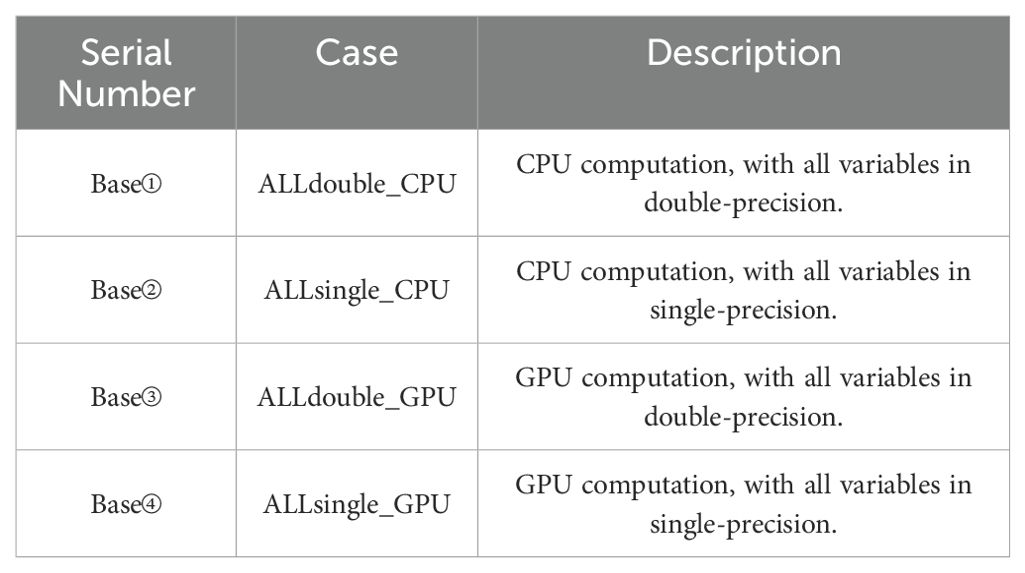
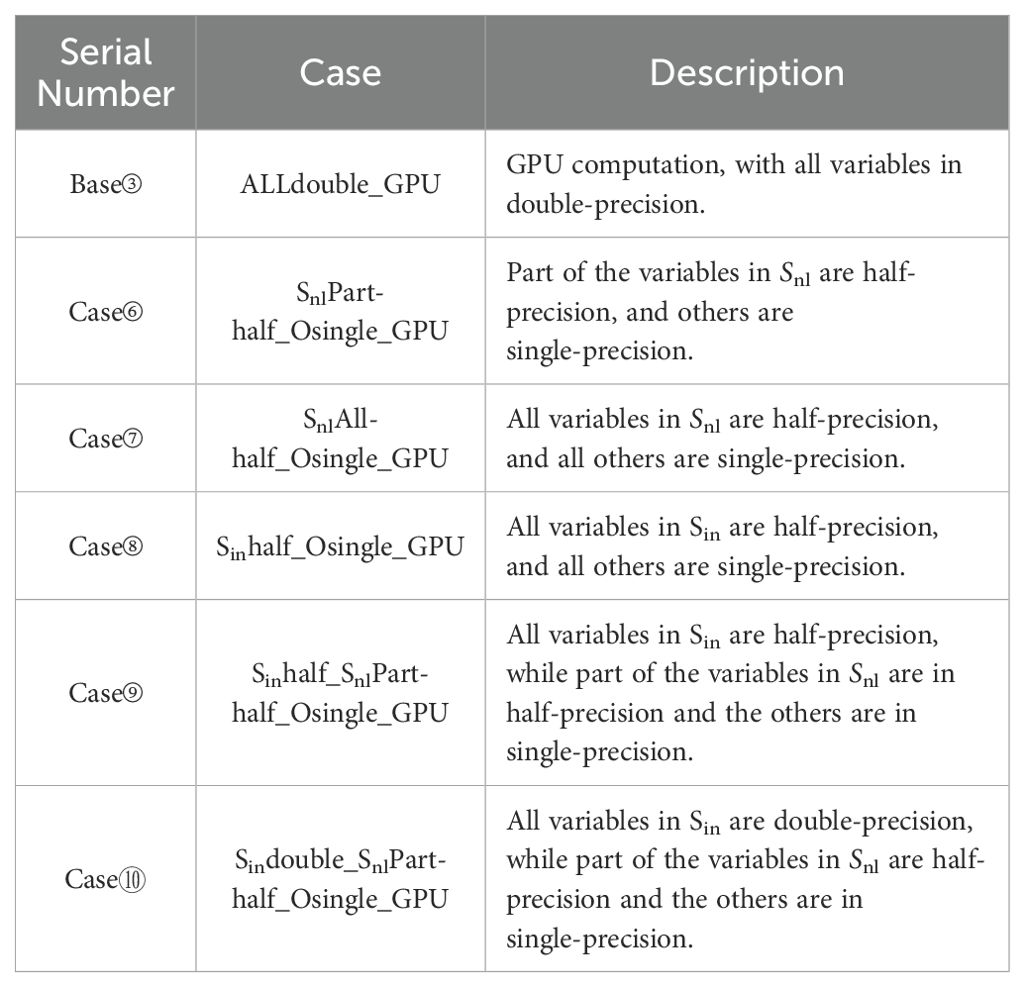
Due to the constraints of half-precision arithmetic in CPU architectures, five critical source functions from the implsch module (governed by Equation 1) are ported to a GPU environment for mixed-precision evaluation. The specific porting and optimization methods are detailed in Section 2.2. Baseline experiments utilized double-precision and single-precision configurations, executed on both CPU (2 cores) and hybrid CPU-GPU (2 CPU cores + 2 NVIDIA A100 GPUs). Key experimental descriptions are summarized in Table 1.

Table 1

Table 1. Baseline experimental descriptions.

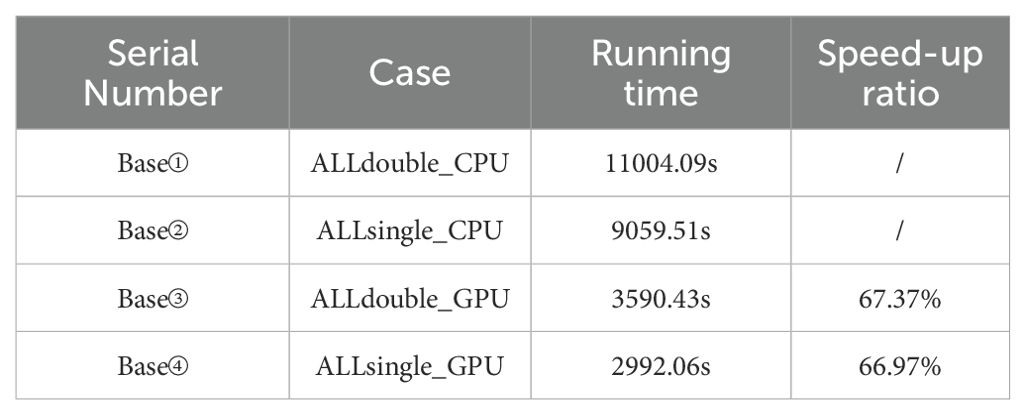
As shown in Table 2, the ALLdouble_CPU (Base①) and ALLsingle_CPU (Base②) required 11004.09 seconds and 9059.51 seconds, respectively, to complete one model month for the implsch module using 2 CPU cores. In contrast, their GPU-accelerated counterparts, ALLdouble_GPU (Base③) and ALLsingle_GPU (Base④), required 3590.43 seconds and 2992.06 seconds, corresponding to computational speedups of 67.37% and 66.97% relative to CPU execution, respectively. This improvement is attributable to the use of a CUDA-based development approach during the porting process, which leverages CUDA acceleration.

Table 2

Table 2. Time required to run one model month of the implsch module using 2 CPU cores.

3.2 Sensitivity experiments in CPU environments

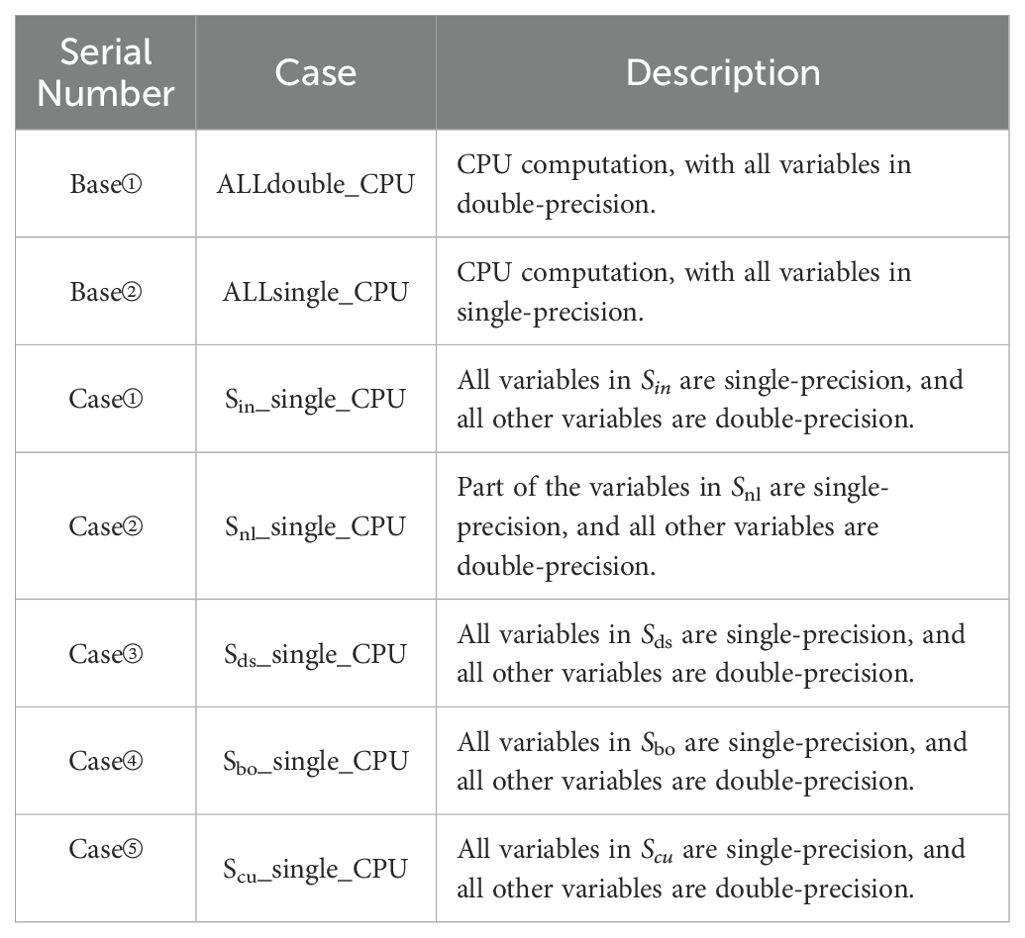
A systematic sensitivity analysis was conducted to assess the trade-offs between computational efficiency and numerical accuracy when transitioning from double-precision to single-precision arithmetic. Starting with the double-precision MASNUM configuration, variables within five source terms (Equation 1) were selectively reduced to single-precision. Notably, the nonlinear wave-wave interaction source function, which dominates computational cost due to its complexity (Komen et al., 1994), exhibited significant error amplification when fully converted to single-precision. Therefore, to balance increased computational efficiency with the accuracy of simulation results, only a subset of variables in the nonlinear wave-wave interaction source function were precision-reduced. The settings for the sensitivity experiments are shown in Table 3.

Table 3

Table 3. Sensitivity experiments in a CPU computing environment.

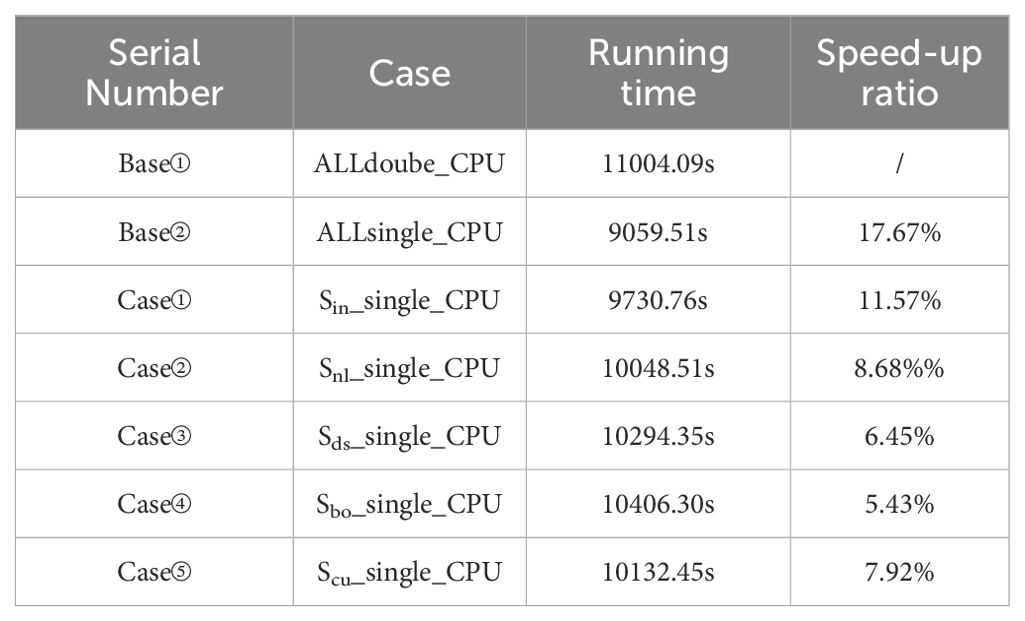
The computational performance of the implsch module was rigorously evaluated using the MPI_WTIME function, with simulations conducted on a dual-core CPU configuration. Table 4 shows the total runtime for simulating January 2021 using 2 CPU cores. As summarized in Table 4, aside from the highest speed-up of 17.67% achieved by converting all variables to single-precision, the most significant improvements in speed were observed for the wind input source function (Case①, S_in_single_CPU) and the nonlinear wave-wave interaction source function (Case②, S_nl_single_CPU), with speedups of 11.57% and 8.68%, respectively. These were followed by the wave-current interaction source function (Case⑤, S_cu_single_CPU) and the breaking dissipation source function (Case③, S_ds_single_CPU), with speed-ups of 7.92% and 6.45%, respectively. The smallest improvement was seen for the bottom friction dissipation source function (Case④, S_bo_single_CPU), with a speed-up of 5.43%. The relative speedup ratios for all sensitivity experiments, normalized to the ALLdouble_CPU baseline, are visually contrasted in Figure 2.

Table 4

Table 4. Runtime of the “implsch” module for one model month using 2 CPU cores.

Figure 2

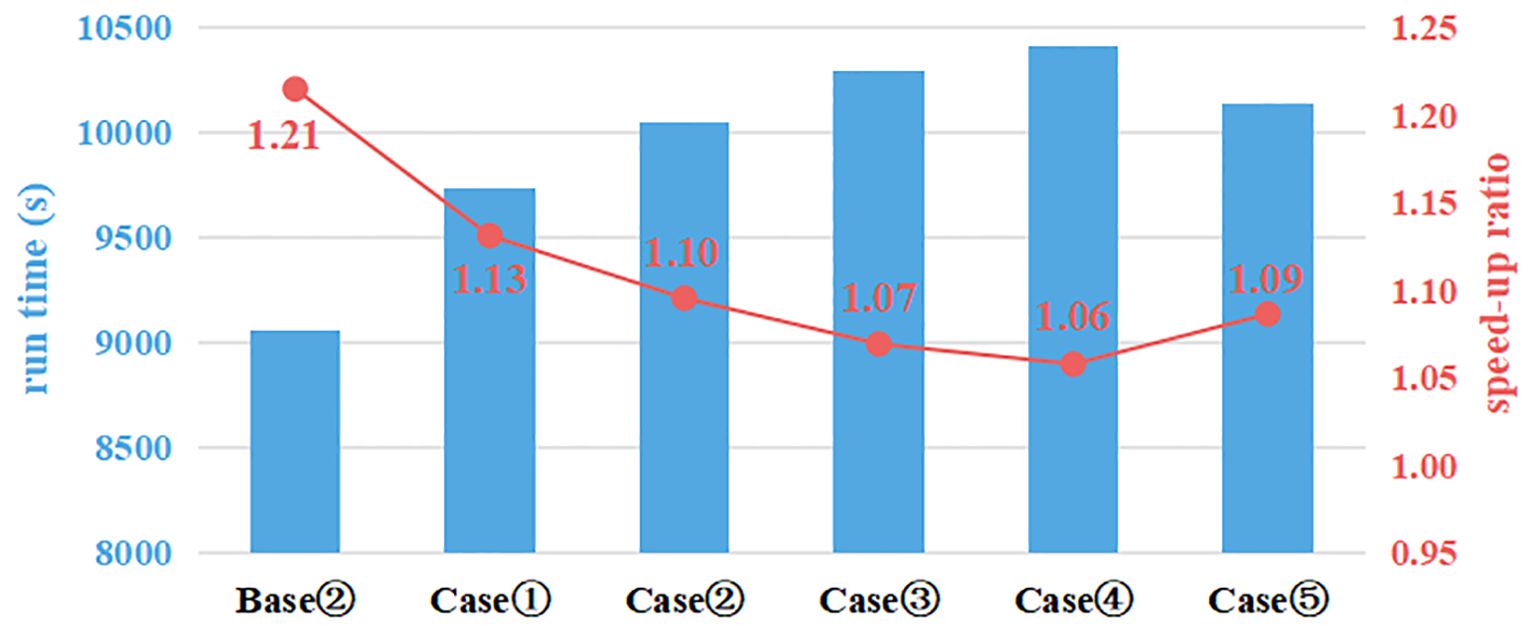
Figure 2. Run time (blue) and speed-up ratios (red) of each sensitivity experiment relative to ALLdouble_CPU.

While computational gains are evident, the impact of precision reduction on simulation fidelity was quantified through error analysis of significant wave height. Figure 3 shows the spatial distribution of error analysis for significant wave height across experimental cases. As shown in the figure, converting the wind input source function (Case①, S_in_single_CPU) and the nonlinear wave-wave interaction source function (Case②, S_nl_single_CPU) to single-precision results in the largest errors, followed by the breaking dissipation source function (Case③, S_ds_single_CPU). The error for the bottom friction dissipation source function (Case④, S_bo_single_CPU) is almost zero. The wave-current interaction source function (Case⑤, S_cu_single_CPU) is not discussed further in this experiment since the circulation was set to zero, resulting in no impact on the outcome.

Figure 3

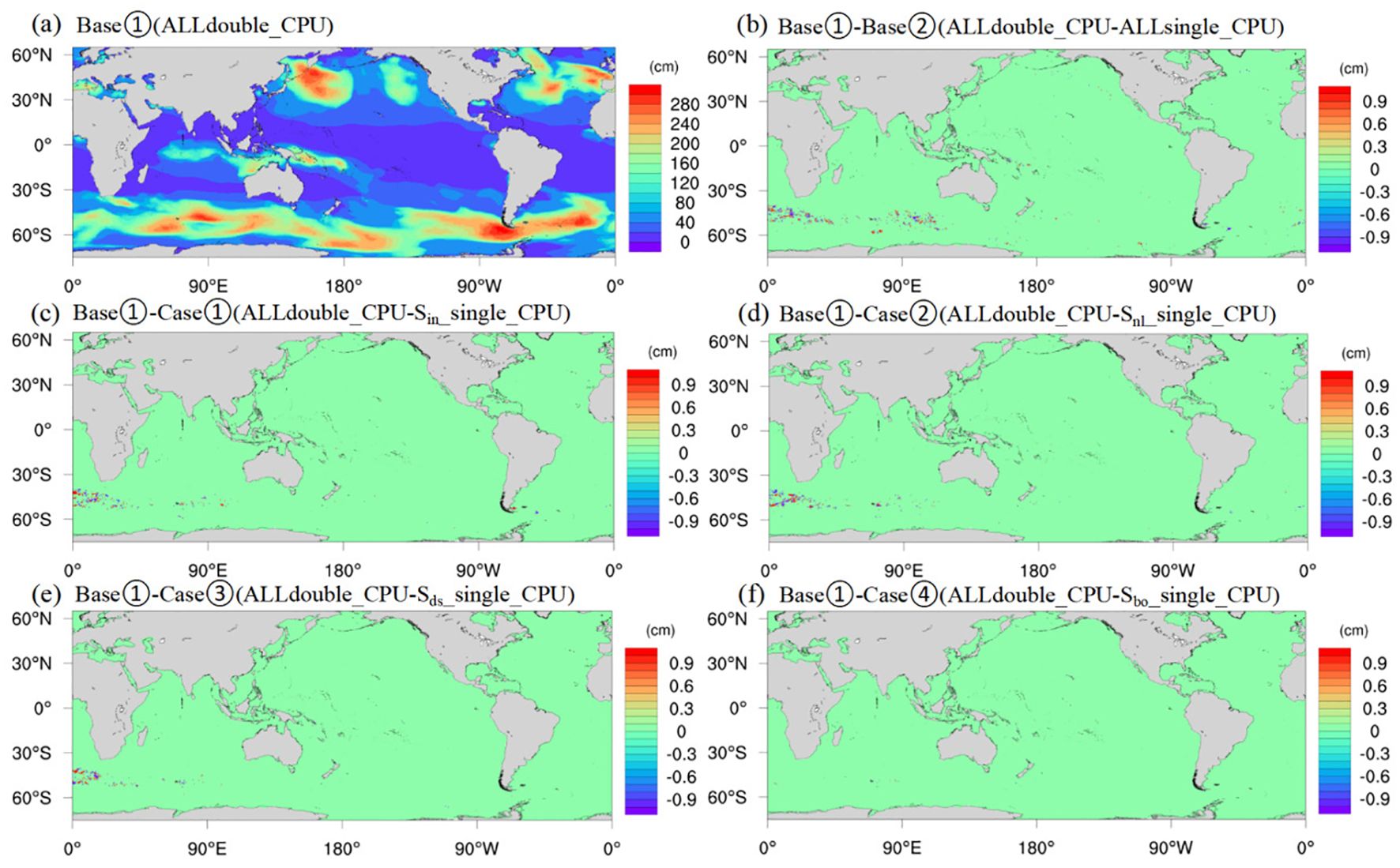
Figure 3. Spatial distribution of significant wave height for Base ① (a) on January 31, 2021, and the Spatial distribution of error in significant wave height for Base ② (b) and Case ① to ④ (c–f) relative to Base ①.

3.3 Sensitivity experiments in GPU environments

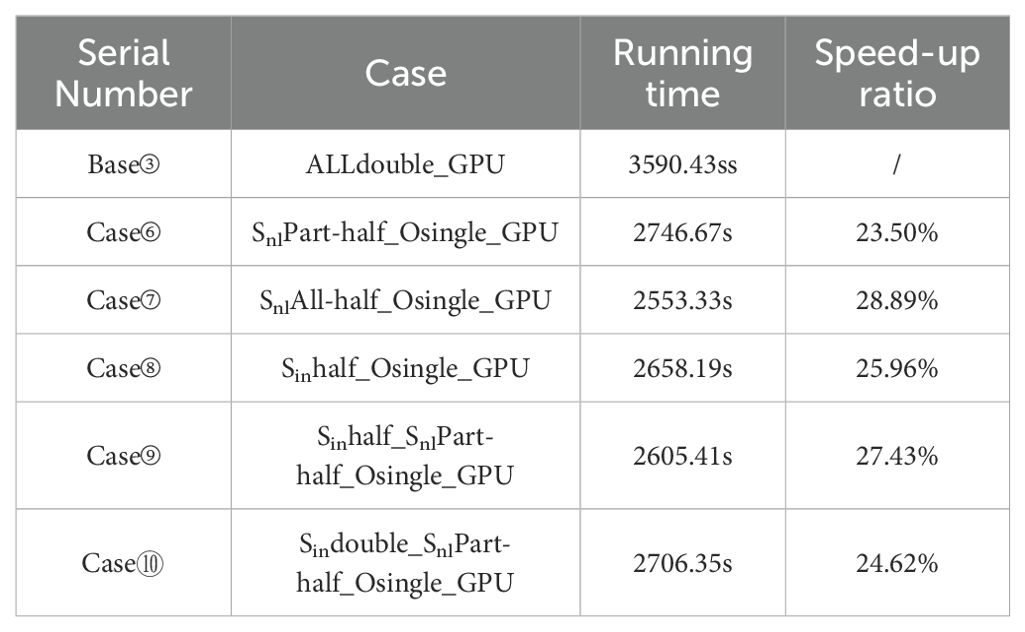
Building on the CPU-based sensitivity experiments, this study extends the analysis to a GPU-accelerated framework, focusing on the wind input and nonlinear wave-wave interaction source functions due to their dominant computational cost. The GPU implementation, leveraging CUDA-based optimization, revealed that CPU-GPU communication and data precision conversion introduce significant overhead, rendering precision adjustments for smaller computational components inefficient. Consequently, precision reduction was selectively applied to wind input and nonlinear wave-wave interaction source functions, with ALLdouble_GPU serving as the baseline. The simulations were conducted on a hybrid CPU-GPU system (2 CPU cores + 2 NVIDIA A100 GPUs), as detailed in Table 5.

Table 5

Table 5. Sensitivity experiments in a GPU computing environment.

Table 6 summarizes the runtime for the implsch module across precision configurations. Figure 4 provides an analysis of the error in wave height with ALLdouble_GPU (Base③) as the baseline, where Figure 4a shows the spatial distribution of the wave height for ALLdouble_GPU. It can be seen that the North Atlantic (NA), Northwestern Pacific (NWP), and Antarctic Circumpolar Current (ACC) regions are high-wave areas of wave height. Additional spatial distributions of relative errors for all cases are provided in Appendix B; Supplementary Figure S1, which offers a more intuitive visualization of the primary areas where error hotspots are concentrated. As shown in the figures, the distribution pattern of the relative error maps is generally consistent with that of the error maps, with higher errors primarily concentrated in regions of strong current velocities, such as the western boundary currents and the Antarctic Circumpolar Current, where flow velocities are larger. These areas also exhibit larger significant wave heights, as seen in Figure 4a for Northwestern Pacific (NWP), North Atlantic (NA), and Antarctic Circumpolar Current (ACC). The potential reasons for higher errors in these regions may be related to strong currents and larger wave heights. Strong current areas typically have more complex dynamic characteristics, which may lead to greater variations and inaccuracies in model predictions. Combining Table 6; Figure 4, it can be seen that using half-precision for all variables in the nonlinear wave-wave interaction source function and single-precision for all others (Case⑦, S_nlAll-half_Osingle_GPU, Figure 4c; Supplementary Figure S1c) achieves the best speed-up effect, reaching 28.89%. However, this configuration also results in the largest error in significant wave height. Next, configurations where variables in the wind input source function are all in half-precision and some variables in the nonlinear wave-wave interaction source function are in half-precision while others are in single-precision (Case⑨, S_inhalf_S_nlPart-half_Osingle_GPU, Figure 4e; Supplementary Figure S1c) and where variables in the wind input source function are all in half-precision and all others are in single-precision (Case⑧, S_inhalf_Osingle_GPU, Figure 4d; Supplementary Figure S1d) achieve speed-ups of 27.43% and 25.96%, respectively, with relatively smaller errors in significant wave height. When the variables in the wind input source function are all in double-precision, and some variables in the nonlinear wave-wave interaction source function are in half-precision while others are in single-precision (Case⑩, S_indouble_S_nlPart-half_Osingle_GPU, Figure 4f; Supplementary Figure S1f), or when some variables in the nonlinear wave-wave interaction source function are in half-precision while others are in single-precision (Case⑥, S_nlPart-half_Osingle_GPU, Figure 4b; Supplementary Figure S1b), the speed-up effects are the smallest, achieving 24.62% and 23.50%, respectively, while the errors are also the smallest.

Table 6

Table 6. Time required for the implsch module to run one model month using 2 GPU cores.

Figure 4

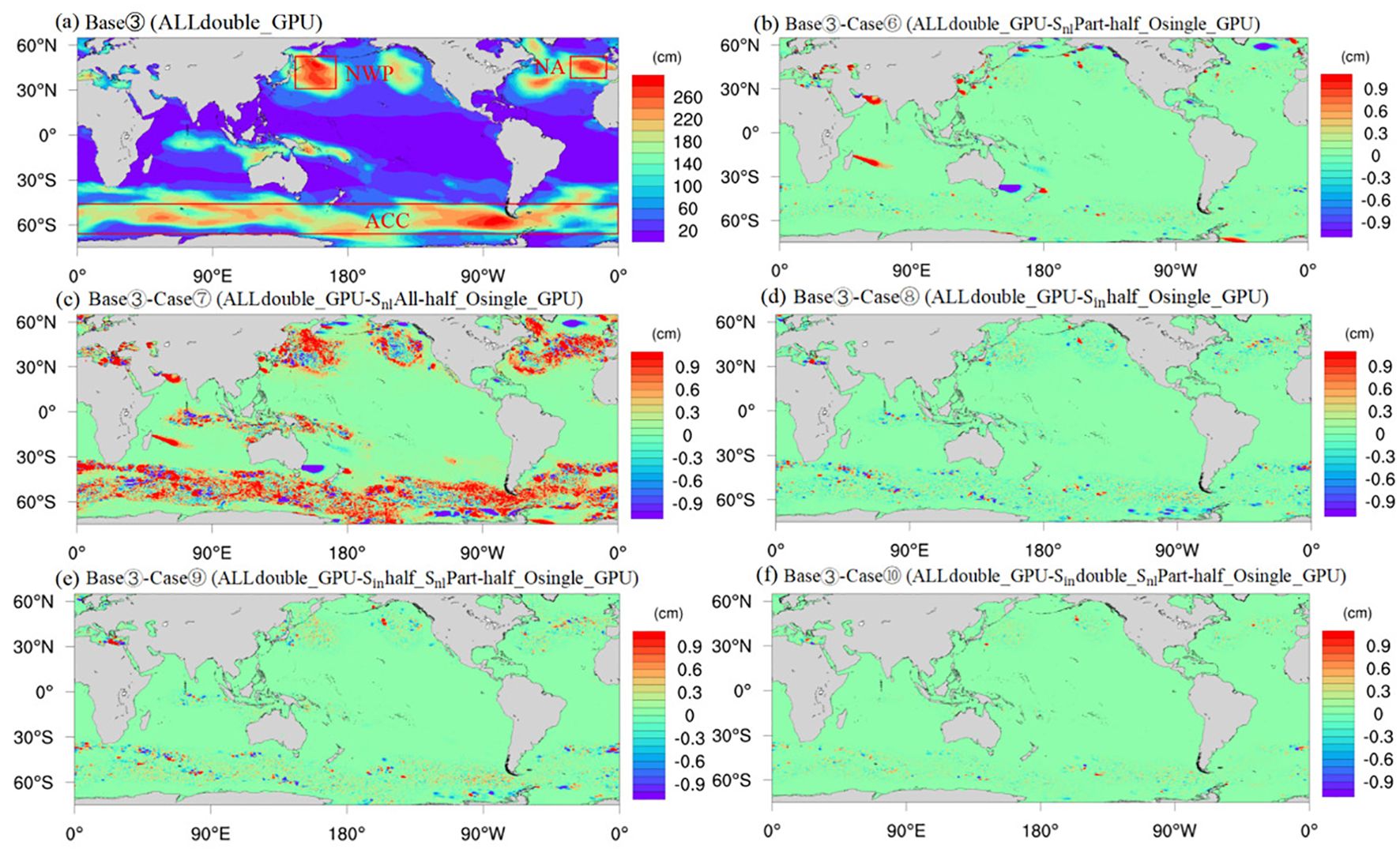
Figure 4. (a) Spatial distribution of significant wave height for Base ③ on January 31, 2021, and (b-f) the spatial distribution of error for Case ⑥ to ⑩ relative to Base ③ (The red boxed area in (a) represents the selected evaluation region: North Atlantic (NA); Northwestern Pacific (NWP); Antarctic Circumpolar Current (ACC)).

In addition, this study uses scatter plots and evaluation metrics such as Symmetric Mean Absolute Percentage Error (SMAPE), Root Mean Squared Error (RMSE), and Correlation Coefficient (R) to assess the performance of the mixed-precision model (see Appendix C for formula). We selected the high-value area of wave height (NA, NWP and ACC, the red boxed area in Figure 4a) to evaluate the simulation results of significant wave height, as shown in Figure 5. In these three regions, the SMAPE values for Case ⑥, ⑧, ⑨ and ⑩ range from 0.12% to 0.43%, indicating small errors, and the simulation results are more accurate compared to Case ⑦ (with SMAPE values ranging from 1.38% to 1.69%). This is mainly because half-precision is stored in 16 bits, with only 3–4 significant digits. During calculation, half-precision may result in rounding errors due to the small number of significant digits, and as the number of calculation steps increases, errors accumulate. In MASNUM mode, the non-linear source function (Case ⑦) has a large amount of code and more complex calculations, leading to larger errors. The R shows that the simulation results of Case ⑥ to ⑩ are highly consistent with Base ③, demonstrating a strong correlation. RMSE is very sensitive to larger errors (outliers), and higher RMSE values typically indicate larger prediction biases for certain extreme values. For Case ⑦, the RMSE values in the NWP, ACC and NA regions are 0.06m, 0.04m, and 0.06m, respectively, which are larger compared to Case ⑥, ⑧, ⑨ and ⑩ (with RMSE ranging from 0.01m to 0.02m), indicating that the simulation results for Case ⑦ have larger errors at high-value points, as can also be seen in the scatter plots. The similarity between subplots in Figures 5a, B is mainly due to the fact that Case⑥ applies half-precision to the variables in the innermost loop variables of S_nl, while Case⑦ applies half-precision to the entire S_nl. Since both Case⑥ and Case⑦ involve changes only in the precision of the S_nl, with all other source term settings remaining the same, the resulting outputs are expected to exhibit a high degree of similarity.

Figure 5

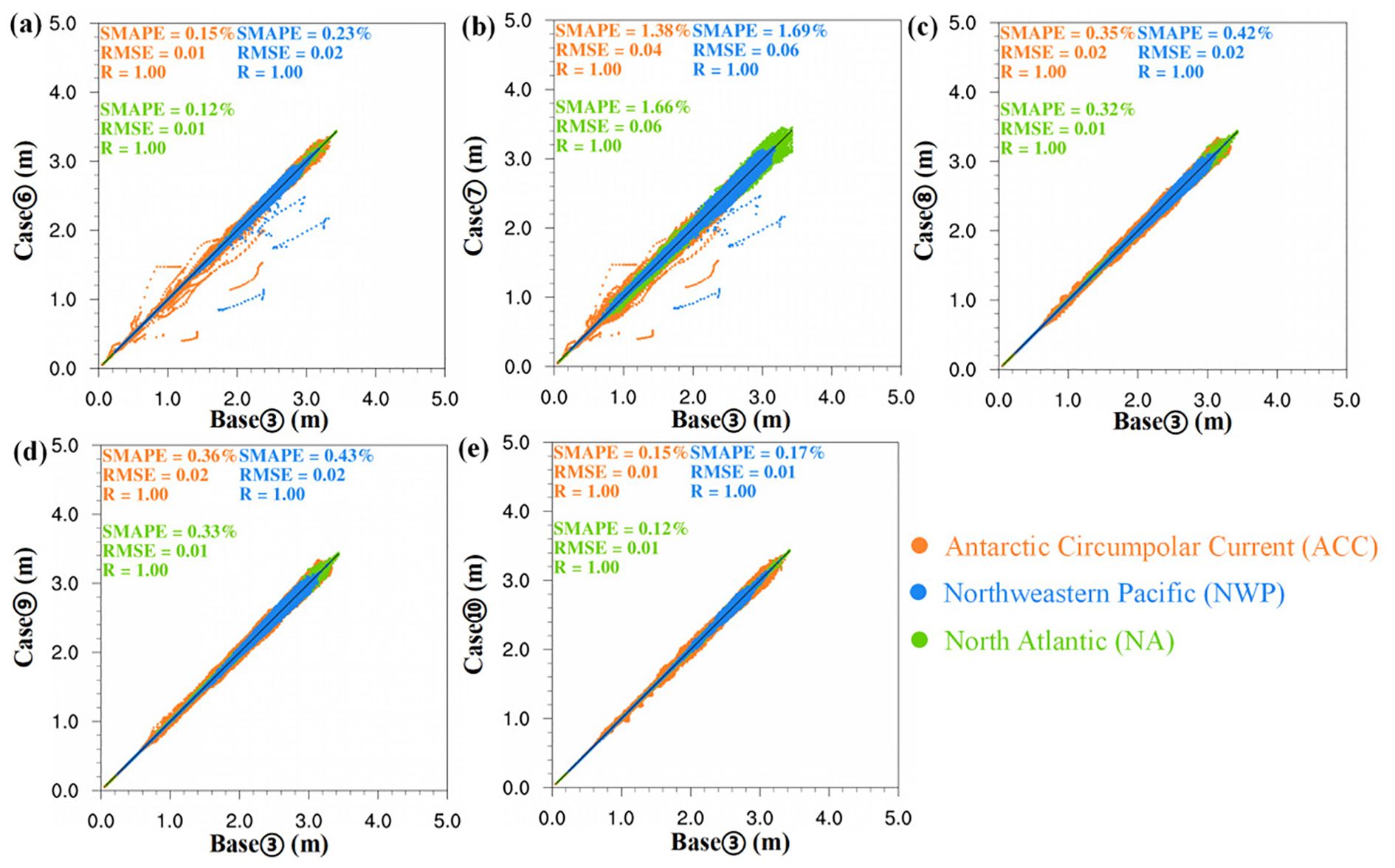
Figure 5. Scatter plot of Case ⑥ to ⑩ (a–e) relative to Base ③ on January 31, 2021 (Blue: Northwestern Pacific (NWP); Yellow: Antarctic Circumpolar Current (ACC); Green: North Atlantic (NA)). The linear regression line (black solid line) is provided. Also shown are the statistical parameters: SMAPE, RMSE and R.

3.4 Scalability analysis on a 20,000-core system

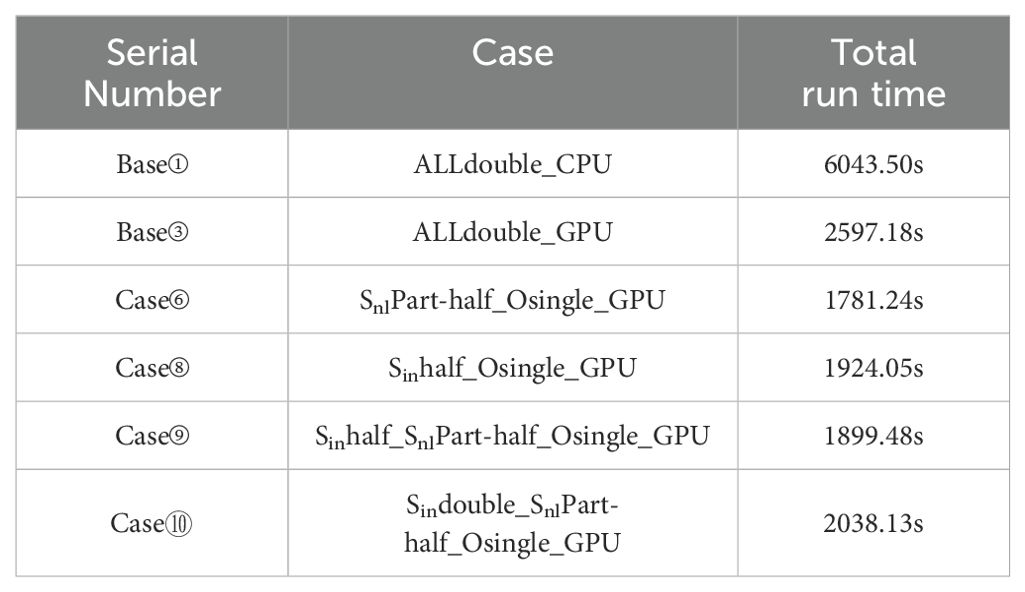
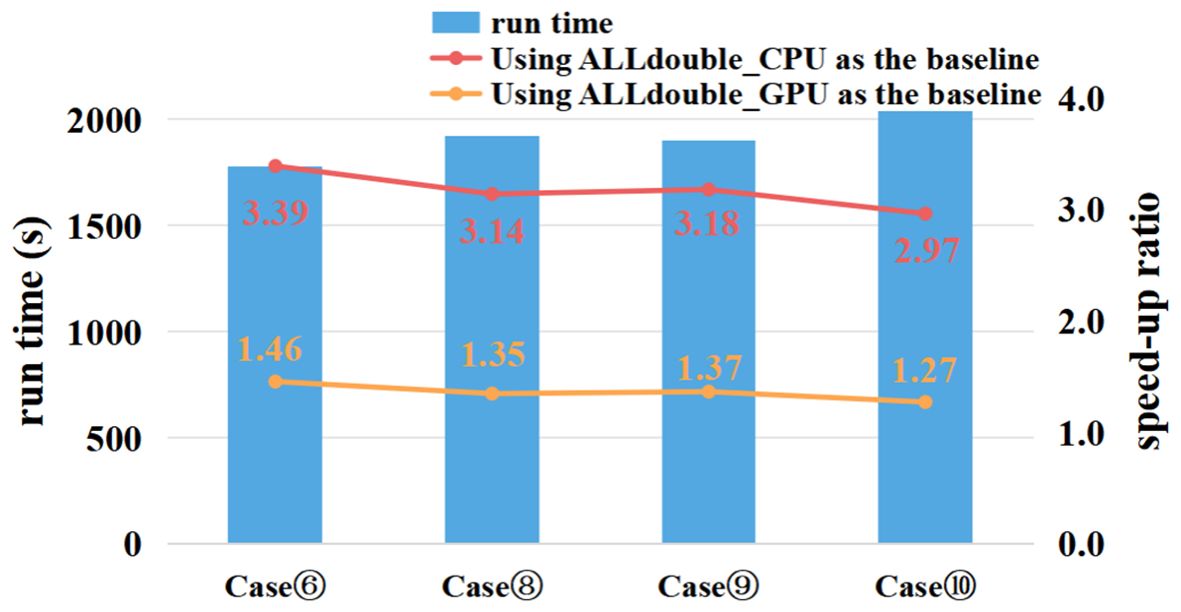
To evaluate the scalability of mixed-precision optimizations, the simulations were conducted on a 20,000-core hybrid CPU-GPU (4 CPU cores + 4 NVIDIA A100 GPUs). Relative to the ALLdouble_GPU baseline, mixed-precision configurations achieved speedups of 1.27–1.46 times, while comparisons to ALLdouble_CPU demonstrated combined structural and precision optimization gains of 2.97–3.39 times (Table 7; Figure 6). These results underscore the potential of mixed-precision to enhance computational efficiency in large-scale ocean modeling applications.

Table 7

Table 7. Time required for the MASNUM model to run one model month using 4 CPU cores.

Figure 6

Figure 6. Speed-up ratios of each experiment for running one model month.

4 Conclusions

High-precision numerical simulations are traditionally employed to minimize numerical errors and enhance the credibility of model outputs. However, as demonstrated by prior studies, such approaches are not universally optimal, often resulting in excessive computational costs and resource inefficiencies. This study addresses this challenge by introducing a mixed-precision framework for the MASNUM wave model, strategically balancing numerical accuracy with computational efficiency.

By applying tailored combinations of double, single, and half-precision to the model’s source terms, we achieved significant computational gains without compromising simulation fidelity. The results showed that the evaluation metrics of the mixed-precision schemes had SMAPE (Symmetric Mean Absolute Percentage Error) values of 0.12% - 0.43% and RMSE (Root Mean Square Error) values of 0.01m - 0.02m, ensuring robust accuracy in the MASNUM model’s simulation results. On a 20,000-core system, these optimizations delivered speedups of 1.27–1.46× relative to the double-precision baseline. Furthermore, during the process of porting the MASNUM model to GPU systems, structural optimizations were performed, resulting in speedups of 2.97 to 3.39 times for the mixed-precision versions compared to the double-precision version.

This study demonstrates the feasibility and advantages of applying mixed-precision methods in high-resolution wave modeling. By selectively reducing the precision for less sensitive variables, significant improvements in simulation efficiency and reductions in computational costs can be achieved. The value of mixed-precision methods is not limited to the MASNUM model but can be effectively extended to other mainstream ocean wave models, such as WaveWatch III (WW3) (Tolman et al., 2016). WW3 features a modular architecture in which physical source terms are implemented as independent components, facilitating targeted precision control. From a physical process perspective, different source terms exhibit varying sensitivity to numerical precision. For instance, nonlinear wave–wave interactions (S_nl) are particularly precision-sensitive, and computations involving DIA or GMD approximations should be maintained at FP32 or even FP64 precision (Tolman, 2013; van Vledder, 2006). In terms of performance optimization, WW3 natively supports CUDA Fortran, making it suitable for deploying FP16 matrix operations accelerated by tensor cores on GPU platforms.

The benefits of this approach are particularly evident in large-scale, high-resolution numerical simulations, offering a new technological pathway for efficient and accurate ocean wave forecasting. However, the current implementation is limited by the overhead associated with data transfer between the CPU and GPU, which accounts for a significant portion of the GPU runtime. Future work will focus on minimizing these bottlenecks through unified memory architectures and expanding the mixed-precision framework to other ocean models, further validating its potential for large-scale, real-time simulations.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XL: Methodology, Formal analysis, Investigation, Writing – original draft, Writing – review and editing, Funding acquisition. SG: Methodology, Investigation, Data Analysis, Writing – original draft, Writing – review and editing. QH: Data Processing, Visualization, Validation, Writing – original draft, Writing – review and editing. JZ: Data Processing, Visualization, Validation, Writing – original draft, Writing – review and editing. ZZ: Investigation, Validation, Writing – original draft, Writing – review and editing. FX: Investigation, Validation, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by Key R&D Program of Laoshan Laboratory (No.LSKJ202202203), the Open Fund Project of the Key Laboratory of Marine Environmental Science and Numerical Modeling, Ministry of Natural Resources. (No.2021-YB-02).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2025.1586015/full#supplementary-material

References

Baboulin M., Buttari A., Dongarra J., Kurzak J., Langou J., Langou J., et al. (2009). Accelerating scientific computations with mixed precision algorithms. Comput. Phys. Commun. 180, 2526–2533. doi: 10.1016/j.cpc.2008.11.005

Crossref Full Text | Google Scholar

Booij N., Ris R. C., and Holthuijsen L. H. (1999). A third-generation wave model for coastal regions - 1. Model description and validation. J. Geophys. Res. Oceans 104, 7649–7666. doi: 10.1029/98jc02622

Crossref Full Text | Google Scholar

Chantry M., Thornes T., Palmer T., and Düben P. (2019). Scale-selective precision for weather and climate forecasting. Monthly Weather Rev. 147, 645–655. doi: 10.1175/mwr-d-18-0308.1

Crossref Full Text | Google Scholar

Düben P. D., McNamara H., and Palmer T. N. (2014). The use of imprecise processing to improve accuracy in weather & climate prediction. J. Comput. Phys. 271, 2–18. doi: 10.1016/j.jcp.2013.10.042

Crossref Full Text | Google Scholar

Düben P. D. and Palmer T. N. (2014). Benchmark tests for numerical weather forecasts on inexact hardware. Monthly Weather Rev. 142, 3809–3829. doi: 10.1175/mwr-d-14-00110.1

Crossref Full Text | Google Scholar

Düben P. D., Russell F. P., Niu X. Y., Luk W., and Palmer T. N. (2015). On the use of programmable hardware and reduced numerical precision in earth-system modeling. J. Adv. Mode. Earth Syst. 7, 1393–1408. doi: 10.1002/2015ms000494

PubMed Abstract | Crossref Full Text | Google Scholar

Düben P. D., Subramanian A., Dawson A., and Palmer T. N. (2017). A study of reduced numerical precision to make superparameterization more competitive using a hardware emulator in the OpenIFS model. J. Adv. Mode. Earth Syst. 9, 566–584. doi: 10.1002/2016ms000862

Crossref Full Text | Google Scholar

Göddeke D., Strzodka R., and Turek S. (2007). Performance and accuracy of hardware-oriented native-, emulated- and mixed-precision solvers in FEM simulations. Int. J. Parallel Emergent Distrib. Syst. 22, 221–256. doi: 10.1080/17445760601122076

Crossref Full Text | Google Scholar

Hatfield S., Chantry M., Düben P., Palmer T., and Acm (2019). “Accelerating high-resolution weather models with deep-learning hardware,” in 6th Platform for Advanced Scientific Computing Conference (PASC) (Zurich, Switzerland: ACM, New York, NY, USA). Jun 12-14, WOS:000769995100001. doi: 10.1145/3324989.3325711

Crossref Full Text | Google Scholar

Kalnay E., Kanamitsu M., Kistler R., Collins W., Deaven D., Gandin L., et al. (1996). The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–472. doi: 10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2

Crossref Full Text | Google Scholar

Lai J. Y., Gan L., Wang L. N., and Ieee (2021). “Mixed-precision methods to reconstruct numerical ocean simulations,” in 19th IEEE International Symposium on Parallel and Distributed Processing with Applications (IEEE ISPA) (New York, NY: IEEE), 681–688. Sep 30-Oct 03, WOS:000766837400084. doi: 10.1109/ISPA-BDCloud-SocialCom-SustainCom52081.2021.00099

Crossref Full Text | Google Scholar

Liang B. C., Gao H. J., and Shao Z. X. (2019). Characteristics of global waves based on the third-generation wave model SWAN. Mar. Struct. 64, 35–53. doi: 10.1016/j.marstruc.2018.10.011

Crossref Full Text | Google Scholar

Matsueda M. and Palmer T. N. (2011). Accuracy of climate change predictions using high resolution simulations as surrogates of truth. Geophys. Res. Lett. 38. doi: 10.1029/2010gl046618

Crossref Full Text | Google Scholar

Maynard C. M. and Walters D. N. (2019). Mixed-precision arithmetic in the ENDGame dynamical core of the Unified Model, a numerical weather prediction and climate model code. Comput. Phys. Commun. 244, 69–75. doi: 10.1016/j.cpc.2019.07.002

Crossref Full Text | Google Scholar

Palmer T. N. (2012). Towards the probabilistic Earth-system simulator: a vision for the future of climate and weather prediction. Q. J. R. Meteorol. Soc. 138, 841–861. doi: 10.1002/qj.1923

Crossref Full Text | Google Scholar

Prims O. T., Acosta M. C., Moore A. M., Castrillo M., Serradell K., Cortés A., et al. (2019). How to use mixed precision in ocean models: exploring a potential reduction of numerical precision in NEMO 4.0 and ROMS 3.6. Geosci. Model Dev. 12, 3135–3148. doi: 10.5194/gmd-12-3135-2019

Crossref Full Text | Google Scholar

Shchepetkin A. F. and McWilliams J. C. (2005). The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 9, 347–404. doi: 10.1016/j.ocemod.2004.08.002

Crossref Full Text | Google Scholar

Sun M., Du J. T., Yang Y. Z., and Yin X. Q. (2021). Evaluation of assimilation in the MASNUM wave model based on Jason-3 and CFOSAT. Remote Sens. 13. doi: 10.3390/rs13193833

Crossref Full Text | Google Scholar

Sun J., Li X. G., Yang Q. Y., Tian Y., Wang S. B., and Yang M. Q. (2023). Hydrodynamic numerical simulations based on residual cooperative neural network. Adv. Water Resour. 180. doi: 10.1016/j.advwatres.2023.104523

Crossref Full Text | Google Scholar

Sun M., Yang Y. Z., Yin X. Q., and Du J. T. (2018). Data assimilation of ocean surface waves using Sentinel-1 SAR during typhoon Malakas. Int. J. Appl. Earth Observ. Geoinform. 70, 35–42. doi: 10.1016/j.jag.2018.04.004

Crossref Full Text | Google Scholar

Sun M., Yin X., and Yang Y. (2014). Construction and application in global wave data assimilation of static sample set. Oceanol. Limnol. Sin. 45, 918–927. doi: 10.11693/hyhz20131000149

Crossref Full Text | Google Scholar

Teng Y., Han L., Yang Y., Qiao F., Sun B., and Lu J. (2016). Numerical experiments on wavenumber directional discretization in the MASNUM Wave Model. J. Trop. Oceanogr. 35, 82–95. doi: 10.11978/2014019

Crossref Full Text | Google Scholar

Thornes T. (2016). Can reducing precision improve accuracy in weather and climate models? Weather 71, 147–150. doi: 10.1002/wea.2732

Crossref Full Text | Google Scholar

Thornes T., Düben P., and Palmer T. (2017). On the use of scale-dependent precision in Earth System modelling. Q. J. R. Meteorol. Soc. 143, 897–908. doi: 10.1002/qj.2974

PubMed Abstract | Crossref Full Text | Google Scholar

Tolman H. (2013). A Generalized Multiple Discrete Interaction Approximation for resonant four-wave interactions in wind wave models. Ocean Model. 70, 11–24. doi: 10.1016/j.ocemod.2013.02.005

Crossref Full Text | Google Scholar

Tolman H., Accensi M., Alves J.-H., Ardhuin F., Barbariol F., Benetazzo A., et al. (2016). User manual and system documentation of WAVEWATCH III (R) version 5.16. NOAA / NWS / NCEP / MMAB Technical Note 329, 326.

Google Scholar

Vána F., Düben P., Lang S., Palmer T., Leutbecher M., Salmond D., et al. (2017). Single precision in weather forecasting models: an evaluation with the IFS. Monthly Weather Rev. 145, 495–502. doi: 10.1175/mwr-d-16-0228.1

Crossref Full Text | Google Scholar

van Vledder G. (2006). The WRT method for the computation of non-linear four-wave interactions in discrete spectral wave models. Coastal Eng. 53, 223–242. doi: 10.1016/j.coastaleng.2005.10.011

Crossref Full Text | Google Scholar

Yamagishi T. and Matsumura Y. (2016). “GPU acceleration of a non-hydrostatic ocean model with a multigrid Poisson/Helmholtz solver,” in 16th Annual International Conference on Computational Science (ICCS) (Univ Calif, San Diego Supercomputer Ctr, San Diego, CA), 1658–1669. Jun 06-08, WOS:000579452200155. doi: 10.1016/j.procs.2016.05.502

Crossref Full Text | Google Scholar

Yang Y., Qiao F., Zhao W., Teng Y., and Yuan Y. (2005). MASNUM ocean wave numerical model in spherical coordinates and its application. Acta Oceanol. Sin. 27, 1–7. doi: 10.3321/j.issn:0253-4193.2005.02.001

Crossref Full Text | Google Scholar

Zhuang Z. P., Yuan Y. L., Zheng Q. A., Zhou C. J., Zhao X. H., and Zhang T. (2021). Effects of buoyancy flux on upper-ocean turbulent mixing generated by non-breaking surface waves observed in the South China Sea. J. Geophys. Res. Oceans 126. doi: 10.1029/2020jc016816

Crossref Full Text | Google Scholar

Zhuang Z., Yuan Y., and Yang G. (2018). An ocean circulation model in σS-z-σB hybrid coordinate and its validation. Ocean Dyn. 68, 159–175. doi: 10.1007/s10236-017-1124-6

Crossref Full Text | Google Scholar

Appendix A: half-precision computation pipeline

Half-Precision Computation Pipeline.

Appendix B: supplementary data

Supplementary Figure 1 | (a) Spatial distribution of significant wave height for Base ③ on January 31, 2021, and (b-f) the spatial distribution of relative errors for Case ⑥ to ⑩ relative to Base ③ on January 31, 2021. (The red boxed area in panel (a) represents the selected evaluation region: North Atlantic (NA); Northwestern Pacific (NWP); Antarctic Circumpolar Current (ACC)).

Appendix C: statistical metrics for evaluating model performance

The model performance evaluation criteria used in this study are Symmetric Mean Absolute Percentage Error (SMAPE), Root Mean Squared Error (RMSE), and Correlation Coefficient (R), and the formulas are shown below.

$$SMAPE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{|\stackrel{\wedge }{y_i}-y_i|}{(|\stackrel{\wedge }{y_i}|+|y_i|)/2}}\times 100\%$$

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(\stackrel{\wedge }{y_i}-y_i)}^2}}$$

$$R=\frac{{\displaystyle \sum _{i=1}^n(y_i-\stackrel{\wedge }{y})(x_i-\stackrel{\wedge }{x})}}{\sqrt{{\displaystyle \sum _{i=1}^n{(y_i-\stackrel{\wedge }{y})}^2{\displaystyle \sum _{i=1}^n{(x_i-\stackrel{\wedge }{x})}^2}}}}$$

$$Relative Error= \frac{\widehat{y_i}- y_i}{y_i}\times 100\%$$