Improving short-term forecasts of sea ice edge and marginal ice zone around Svalbard

Sea ice is a major threat to marine operations around Svalbard, and accurate short-term (1–5 days) forecasts of sea ice edge (SIE) and marginal ice zone (MIZ) are crucial for safe marine operations. In this paper, we investigate the effects of assimilating the AMSR2 sea ice concentration (SIC), the Norwegian sea ice chart, and the OSTIA sea surface temperature (SST) on the short-term forecasts of SIE and MIZ around Svalbard. The used model, Barents-LAON, is based on the coupled ROMS-CICE model with the Local Analytical Optimal Nudging (LAON) for data assimilation. The assimilation effects are evaluated through seven model experiments, from Free run to the full assimilation of OSTIA SST, AMSR2 SIC, and ice chart. The results show that the Free run of Barents-LAON contains a large cold bias, which significantly overestimates the sea ice extent and underestimates the SST. Assimilation of SST mildly improves the analyses of SIE and MIZ, and additional assimilations of AMSR2 SIC and ice chart considerably improve the analyses and forecasts. We show that 1–3 days of forecasts of SIE and MIZ with assimilations of both SIC and SST outperform the CMEMS operational forecasts TOPAZ5 and neXtSIM, the US Navy GOFS3.1 system, and the Norwegian Meteorological Institute’s Barents-EPS. The assimilation of both ice chart and OSTIA SST is shown to have the largest improvement for MIZ analysis and forecasts. All the Barents-LAON short-term SIE forecasts with assimilations of SIC and SST outperform the sea ice chart persistence forecasts after the first day. However, all the MIZ forecasts, regardless of using the operational models or the current model experiments, are shown to have lower skills than the sea ice chart persistence. This suggests two possible defects: 1) the present AMSR2 SIC is not sufficiently accurate for separating MIZ from dense pack ice, and 2) some important physical processes may be lacking for the transformation between dense pack ice and MIZ in the present coupled ocean and sea ice models.

1 Introduction

Svalbard is the northernmost territory of Norway, composed of an archipelago in the Arctic Ocean about midway between mainland Norway and the North Pole. Compared to other areas at similar latitudes, the climate on Svalbard and the surrounding seas is considerably milder, wetter, and cloudier, due mainly to the atmospheric heat and moisture transport associated with the warm West Spitsbergen Current (AMAP, 2017). As a result, Svalbard waters have long been an area of high-level maritime activities from a pan-Arctic perspective (Olsen et al., 2020). Along with the reducing Arctic sea ice, there is a continuous growth in marine activities such as shipping, fisheries, tourism, and oil and gas exploration around Svalbard (AMAP, 2017; Olsen et al., 2020), with remarkable increases in the operational seasons and navigational areas (Stocker et al., 2020).

Sea ice is a major threat to ships and offshore operations around Svalbard. In general, operations in sea ice would require ice-strengthened vessels or icebreakers with a sufficient ice class. Off-shore platforms, harbors, and coastal loading terminals would also require much stronger construction than those in ice-free waters. However, most ships and fishing vessels are not well ice-strengthened; therefore, they must be run in a confined area for safety purposes. In such a case, it is critically important to frequently monitor and accurately predict the sea ice conditions to assist safe marine operations. Accurate short-term (1–5 days) forecasts of sea ice edge (SIE) and marginal ice zone (MIZ) are of particular importance for supporting such marine operations around Svalbard.

SIE is the demarcation between open sea and sea ice of any kind (WMO, 2014). It can generally be separated into two types: compacted and diffuse. The compacted SIE refers to the close and clear-cut SIE, which is compacted commonly by winds/currents and occasionally by waves. The diffuse SIE refers to the poorly defined SIE, which has an area of dispersed ice. In practical usages, SIE is often defined as the demarcation where sea ice concentration (SIC) equals 0.15 in the passive microwave radiometer (PMR) sea ice mapping and climate modeling communities. By contrast, it is often defined as the demarcation where SIC = 0.1 in the operational ice charting community, such as the Norwegian Meteorological Institute ice chart (https://cryo.met.no) and US National Ice Center (NIC) ice chart (https://usicecenter.gov/Products). To our knowledge, there have been no intercomparison studies for these two SIE definitions. Basically, the ice chart combines a large number of satellite observations, so it generally provides a more accurate description of the SIE. By contrast, the PMR tends to underestimate the SIC in low SIC areas (Cavalieri, 1994; Breivik et al., 2009; Kern et al., 2019; Wang et al., 2024). As a result, the SIE in the ice chart generally defines a larger sea ice extent than in the PMR observations, when they use the same SIC of 0.1 for demarcation. Using a higher SIC (0.15) in the PMR observations tends to provide a SIE even more inside into the sea ice area compared with using SIC = 0.1. Therefore, except for compacted SIE, the SIE in the sea ice chart generally defines a larger sea ice extent than that in the PMR observations. In the current study, we have used SIC = 0.1 as the demarcation for model SIE, which agrees with the ice charting practice. Wang et al. (2023) argue that choosing SIC = 0.1 as the demarcation for SIE has several benefits. Most importantly, it has a clear physical representation that distinguishes open water (SIC < 1/10) and very open drift ice (SIC in 1–3/10), as defined in WMO (2014). In addition, it provides a consistent definition for the joint sea ice modeling and charting community. Here, we also use SIC = 0.1 as the demarcation for SIE.

According to WMO (2014), MIZ is defined as the region of an ice cover affected by waves and swell penetrating into the ice from the open ocean. Typical MIZ conditions are found along the southern edges of the ice pack in the Bering Sea, Greenland Sea, and Barents Sea, in the Baffin Bay, and along the complete northern edge of the Antarctic ice cover (Røed and O’Brien, 1983). MIZ is a dynamic zone under strong interactions between the atmosphere, ocean, sea ice, and waves, frequently with strong atmosphere-ice-ocean activities such as rapid sea ice freezing/melting (Josberger, 1983; Tucker et al., 1991), mesoscale ocean and atmosphere eddies (Johannessen et al., 1987; Inoue and Hori, 2011), turbulence (Padman and Dillon, 1991; Sunfjord et al., 2007), and ocean upwelling and downwelling (Røed and O’Brien, 1983; Häkkinen, 1986), therefore playing a critical role in the polar climate system. Due to the relatively low SIC and SIT, the MIZ is also an area much more navigable than the inner dense pack ice (Stephenson et al., 2011). Ocean waves and swell are the primary source of energy for ice breakup in the MIZ and are, therefore, the main driver determining its properties and extent (Squire et al., 1995; Squire, 2007; Dumont et al., 2011). The relatively small ice floes in the MIZ influence the mechanical properties of the ice and, thus, its response to winds and ocean waves and currents (Shen et al., 1987; Feltham, 2005). These small ice floes have a significant effect on the summer sea ice melting due to the increased lateral perimeters compared to large ice floes over the same area (Steele, 1992).

Due to the complicated interactions between atmosphere, ocean, sea ice, and waves, accurate modeling of MIZ is still one of the most challenging tasks in the sea ice research, particularly the MIZ dynamics (Bennetts et al., 2022; Dumont, 2022). In order to quantify the MIZ, Wang et al. (2024) separate the MIZ as traditional MIZ and dynamical MIZ. The traditional MIZ is defined solely on the basis of the SIC, commonly being [0.1–0.8]. By contrast, the dynamical MIZ can be parameterized through a combination of SIC and SIT. Although not adequate for describing the MIZ dynamics, the traditional MIZ has been applied in a large number of MIZ-related problems, such as sea ice charting (e.g., the NIC ice chart), satellite observations (e.g., Strong, 2012; Liu et al., 2019), primary productions (e.g., Barber et al., 2015), marine ecosystems (e.g., Wassmann, 2011; Arrigo, 2014), and ship navigation (e.g., Palma et al., 2019). Because the dynamical MIZ has not been systematically observed and its theory is still under development, in this study, we only consider the modeling of the traditional MIZ, which has been available in operational ice services for decades.

Sea ice around Svalbard, particularly in the Fram Strait and Barents Sea, is strongly affected by the atmosphere circulation (Vinje, 2001; Maslanik et al., 2012), and the northward Atlantic warm water (Sandø et al., 2010; Smedsrud et al., 2013). Consequently, the sea ice conditions in this area are often under rapid and complex changes, resulting in extra challenges in accurate predictions of SIE and MIZ. Several operational sea ice forecast models have been monitored in the Norwegian Meteorological Institute with a focus on the evaluation of the forecast skills. These model systems include TOPAZ4 (Sakov et al., 2012) and its successor TOPAZ5 (now operational) and neXtSIM (Williams et al., 2021) at the EU Copernicus Marine Environmental Monitoring Service (CMEMS), the Global Ocean Forecasting System (GOFS 3.1) at the US Naval Research Lab (Posey et al., 2015), and the Barents-2.5km Ensemble Prediction System (Barents-EPS) at the Norwegian Meteorological Institute (Röhrs et al., 2023). It is often seen that the first 2 days of forecasts of these operational models have larger integrated ice edge error (IIEE) than persistence forecast.

The discrepancy between the modeled and observed SIE and MIZ has long been noticed in the operational sea ice forecasts and climate simulations. It is suspected that the insufficient representation of the MIZ processes, particularly the wave-ice interaction, may be the main reason for the low prediction capabilities of the sea ice models (Kohout et al., 2014; Dumont, 2022). In this study, we show that lack of accurate sea ice observations may be another important reason, since the widely used PMR generally has a poor capability in capturing low SIC (Cavalieri, 1994; Breivik et al., 2009; Kern et al., 2019; Wang et al., 2024). Assimilation of such biased observations would, therefore, also induce similar biases. In fact, a close inspection of the operational forecasts indicates that the IIEE is already large in the first day forecast, whereas the increase in the IIEE remains relatively small in the later days. This suggests that the main IIEE of the operational forecasts is in the initial condition, resulting from the data assimilation of PMR observations.

The main purpose of this study is to investigate whether and to what extent the assimilation of AMSR2 SIC and ice chart can improve the short-term forecasts of SIE and MIZ. Using the Local Analytical Optimal Nudging (LAON) method, Wang et al. (2023) assimilated the high-resolution AMSR2 SIC in a pan-Arctic coupled ocean and sea ice model (HYCOM-CICE). It is found that the LAON assimilation can significantly improve the simulated SIC and produce significantly more accurate SIE and MIZ than the CMEMS analyses TOPAZ4 and neXtSIM, as well as the PMR satellite observations AMSR2 SIC. In this study, we apply the LAON method in a regional coupled ocean and sea ice model (Barents-LAON) for the assimilation of AMSR2 SIC and sea ice chart. Due to the large systematic bias of the model system, we here also assimilate SST to avoid large bias of the simulated sea ice cover.

The present study is organized as follows. In section 2, we describe the regional coupled ocean and sea ice model system Barents-LAON. Section 3 introduces the observed SIC for assimilation and evaluation, as well as four SIC products from operational forecast models. Section 4 describes the evaluation metrics. In Section 5, we perform 5-day forecast experiments to evaluate the effects of assimilating AMSR2 SIC, sea ice chart, and OSTIA SST on the forecasts of SIE and MIZ. The results are compared with TOPAZ5, neXtSIM, GOFS 3.1, and Barents-EPS. The discussion and conclusions are given in Section 6.

2 Model and data assimilation

Barents-LAON is based on the METROMS COIN model (Wang, 2025), which is an independent branch of the METROMS model system (Kristensen et al., 2017). LAON is the optimal version of the Combined Optimal Interpolation and Nudging (COIN; Wang et al., 2013) method for data assimilation (Wang et al., 2023). METROMS is a coupled ocean and sea ice model based on the coupled Regional Ocean Modeling System (ROMS, version 3.7) and the Los Alamos sea ice model (CICE, version 5.1.2). The Barents-LAON model domain is the same as the Barents-2.5km, being a horizontal grid with a resolution of 2.5 km for the Barents Sea and Svalbard areas (Röhrs et al., 2023; also see Figure 1). The METROMS model physics has been well described in the previous studies (Duarte et al., 2022; Röhrs et al., 2023), and the LAON sea ice data assimilation system has been presented in the coupled HYCOM-CICE model (Wang et al., 2023). In this study, we extend the LAON method also for SST assimilation and implemented in the Barents-LAON system. The model components and data assimilation are briefly described below.

Figure 1

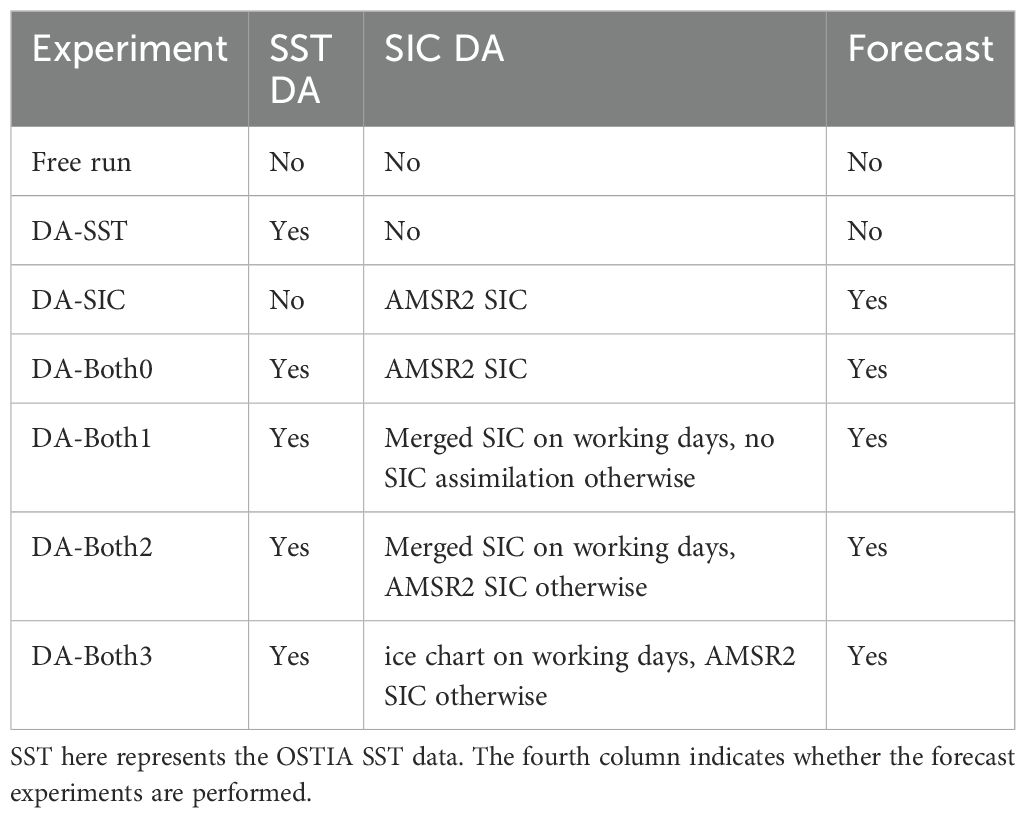
Figure 1. Barents-2.5km model domain shown by the thick rectangle. The red dots show the annual mean fluxes of the rivers (in total, 318), with the maximum of about 292.5 m³ s⁻¹.

2.1 Ocean model

ROMS is a free-surface, terrain-following, primitive equations ocean model (Shchepetkin and McWilliams, 2005). It solves the Boussinesq primitive equations, with the basic state variables being temperature, salinity, surface elevation, and horizontal current velocities. The model setup includes a second order turbulence closure scheme with turbulent kinetic energy and a generic length scale as state variables (Warner et al., 2005). In the vertical, 42 layers are used with an increasing vertical resolution from 1.2 m to 0.2 m in the top 100 m. It uses split explicit time stepping for solving slow baroclinic modes separately from fast barotropic modes, with the time steps being 90 and 3 s, respectively. Momentum and tracers are advected using a third-order upwind scheme in the horizontal and a fourth-order centered scheme in the vertical. Turbulent kinetic energy and length scale are advected vertically and horizontally using a fourth-order centered scheme. Tracers are mixed along surfaces of constant geopotential, whereas momentum is mixed along the bottom topography following coordinate surfaces. The model uses the same configuration as in the work of Röhrs et al. (2023).

2.2 Sea ice model

CICE is a dynamic and thermodynamic, multiple ice-thickness category sea ice model (Hunke et al., 2015). In each computational cell, sea ice conditions, such as ice concentration and thickness, are described by the sub-grid scale distributions on the basis of the ice thickness distribution (ITD) theory (Thorndike et al., 1975). Evolution of the ice conditions is solved by splitting it into three pieces, namely, a horizontal two-dimensional (2D) transport, a vertical one-dimensional (1D) transport in the thickness space, and a redistribution of the ice in the thickness space through a ridging model. In our simulations, the original five category ITD (kcatbound = 0) is selected to describe the ice conditions, and the vertical snow and ice are resolved with seven ice layers and one snow layer for each ice thickness category.

The ice velocity is calculated from the sea ice momentum equation that account for air and water drags, Coriolis force, sea surface tilt, and the divergence of internal ice stress. In this study, the internal stress is calculated on the basis of the elastic-viscous-plastic (EVP) rheology (Hunke et al., 2015), using the revised EVP approach (Bouillon et al., 2013). The ice strength is reformulated according to Rothrock (1975). The sea ice advection is calculated using the incremental remapping scheme (Lipscomb and Hunke, 2004). The subgrid sea ice deformation and the redistribution of various ice categories follow Rothrock (1975), with a modified expression for the participation function (Lipscomb et al., 2007).

The sea ice thermodynamic growth rate is determined by solving the 1D vertical heat balance equations for each ice thickness category and snow, using the mushy-layer scheme that also accounts for the evolution of sea ice salinity (Turner et al., 2013). The upper snow/ice boundary (i.e., ice or snow surface) is assumed to be balanced under shortwave and longwave radiations and sensible, latent, and conductive heat fluxes when the surface temperature is below freezing. When the surface is warmed up to the melting temperature, it is held at the melting temperature and the extra heat is used to melt the snow/ice surface. The bottom sea ice boundary is assumed to be at dynamic balance, growing or melting due to the heat budget between ice conductive heat flux and the under-ice oceanic heat flux. The lateral melting is calculated using the default parameterization in CICE with a constant effective ice floe diameter of 300 m (Maykut and Perovich, 1987). The melt pond is assumed to occur only on level ice, following the LEVEL-ICE melt pond parameterization (Hunke et al., 2013).

2.3 Ocean-sea ice coupling

The ROMS-CICE coupling utilizes the Model Coupling Toolkit (MCT; Larson et al., 2005) for intermodel exchange of state variables and fluxes (Duarte et al., 2022; Röhrs et al., 2023). The surface fluxes of heat, mass, and momentum are designed to be calculated in the component with most information about the surface using required information from the other components. The coupling employs the principle of “levitated” ice, so there is no actual exchange of mass between the ocean and the ice. Freshwater and salt fluxes from the ice model are converted to a virtual salt flux before they are used in the ocean model. In this “massless” state, the ice does not displace water (e.g., water flows do not see under-ice morphology such as keels), and it is only seen by the ocean as a source of surface fluxes responding to the present ocean state. The ice and ocean models are run concurrently, with exchange of information every baroclinic ocean time step (90s). The information used by each model is, therefore, of little time lag compared with its own state.

2.4 Atmospheric forcing and model boundary conditions

The atmospheric forcing is the surface fields from the operational analysis of the Integrated Forecast System (IFS) at European Centre for Medium Weather Forecasts (ECMWF), including wind speed, air temperature, humidity, rain fall, and cloud cover. These forcing fields have a horizontal resolution of 0.1° and temporal resolution of 6 h. They are used to calculate surface fluxes as the ocean upper boundary conditions in ROMS and to calculate surface stress, heat fluxes, and snow aggregation on the ice cover in CICE.

The model boundary conditions are provided by the newly operationalized TOPAZ5 (CMEMS, 2024a). It provides daily averages of temperature, salinity, sea surface elevation, and ocean current velocities for the ocean component, and daily averages of sea ice fraction, sea ice thickness, first year ice age, snow depth, and ice velocity for the sea ice component. In ROMS, a sponge zone with up to 10-fold increased horizontal tracer diffusivity and viscosity is implemented within 30 grid points from the boundary. Nudging of passive tracers toward the boundary fields from TOPAZ5 is imposed within the sponge zone. 2D momentum anomalies are radiated out of the model domain using the tangential phase speed of the barotropic signal.

Point sources for river influx are specified along the coasts in the model domain which include locations, daily values for temperature, salinity, and flux. The red dots show the annual mean fluxes of the 318 rivers (Figure 1), with a maximum of about 292.5 m³ s⁻¹. Climatological values for rivers on the Svalbard archipelago are used, whereas river data on mainland Norway originates from daily estimates provided by the Norwegian Water Resources and Energy Directorate. Tidal forcing is provided as amplitudes and phases of the 10 major tidal constituents in the model domain, obtained from the TPXO global inverse barotropic model (Egbert and Erofeeva, 2002) and imposed on velocities and free surface elevation. The tidal signal is also added to velocities and surface elevation during the processing of boundary data.

2.5 LAON data assimilation

The LOAN data assimilation system is designed to nudge the model results to the optimal estimate such that (Wang et al., 2023)

$\begin{array}{ll}\frac{\partial X}{\partial t}=F(X,t)+\frac{K}{\text{Δ}T}[X_{obs}-X]& (1)\end{array}$

where X denotes any concerned variables to be assimilated, X_obs is the corresponding observations, ΔT is the observation time step, F(X, t) denotes the processes related to the model free run, and K is the Kalman gain, which, in the local situation, becomes

$\begin{array}{ll}K=\frac{{\sigma }_{mod}^2}{{\sigma }_{mod}^2+{\sigma }_{obs}^2}& (2)\end{array}$

where σ_obsis the observation standard deviation (SD), and σ_mod is the model SD approximated by the absolute difference between model and observation values (Wang et al., 2013, 2023; Fritzner et al., 2018)

$\begin{array}{ll}{\sigma }_{mod}=|X_{mod}-X_{obs}|& (3)\end{array}$

From Equations 1–3, the LAON assimilation of SST can be simply implemented following Wang et al. (2023)

$\begin{array}{ll}SS{T}_j=SS{T}_{j-1}+\frac{\text{Δ}t}{\text{Δ}T}K(SS{T}_{obs}-SS{T}_{j-1})& (4)\end{array}$

where SST and SST_obs are the model SST and observed SST, and subscript j = 1, 2, 3,…, N, in which N = ΔT/Δt is ratio of observation time step ΔT to the model time step Δt (Wang et al., 2023). For the multi-category CICE model, we apply a same formulation as in Wang et al. (2023). When the total model SIC a_ice is greater than 0, a proportional formulation is applied to update all the ice categories such that

$\begin{array}{ll}{a}_{n,j}=a_{n,j-1}(1+\gamma )& (5)\end{array}$

$\begin{array}{ll}{v}_{n,j}=v_{n,j-1}(1+\gamma )& (6)\end{array}$

$\begin{array}{ll}{v}_{sn,j}=v_{sn,j-1}(1+\gamma )& (7)\end{array}$

where v_n and v_sn are ice and snow volumes for the nth ice category, and the rate of incremental innovation γ is (Wang et al., 2023)

$\begin{array}{ll}\gamma =K\frac{\text{Δ}t}{\text{Δ}T}[\frac{a_{obs}}{max(a_{ice},0.1)}-1]& (8)\end{array}$

where a_obs and a_ice are the observed and model total SIC. The function max in Equation 8 is used to avoid huge values when a_obs/a_ice≫ 1. When a_ice= 0 and a_obs > 0, we assume that new model sea ice will form with the sea ice thickness as follows (Fritzner et al., 2018; Wang et al., 2023, 2024)

$\begin{array}{ll}{h}_{new}=0.02e^{2.8767a_{obs}}& (9)\end{array}$

In addition to the new model ice thickness (Equation 9), we set the new snow volume as 0.1 of the ice volume, sea ice salinity as 5 psu, and sea ice temperature at the freezing temperature with the corresponding entropy.

2.6 Model experiments

We performed seven experiments to investigate the effects of data assimilation on the analyses and forecasts of SIE and MIZ. Table 1 shows the experiments with varying assimilations of SST and SIC for the period from 1 January to 30 April 2024. Free run assimilates no data, DA-SST assimilates the OSTIA SST only, DA-SIC assimilates the AMSR2 SIC only, and DA-Both0 assimilates the AMSR2 SIC and OSTIA SST. DA-Both1 and DA-Both2 are both designed to assimilate the merged SIC and OSTIA SST, but with different treatments when sea ice charts are not available. In DA-Both1, no SIC assimilation is performed when ice chart is unavailable, whereas DA-Both2 assimilates the AMSR2 SIC instead when no ice chart is available. DA-Both3 also assimilates both SST and SIC but assimilates the ice chart only when it is available and assimilate AMSR2 SIC when the ice chart is unavailable. The reason for the experiments DA-Both1, DA-Both2, and DA-Both3 is that the ice chart is unavailable during weekends and holidays. By performing these experiments, we hope to identify a best approach to predicting the SIE and MIZ in such an imperfect conditions.

Table 1

Table 1. Data assimilation (DA) experiments together with the applied observations.

We note here that only five experiments were performed to investigate the effects of assimilation on the short-term forecasts (Table 1), with daily 5-day forecasts for the period from 2 January to 24 April 2024. The Free run and DA-SST contain very large biases. Their forecasts are generally of very limited values to real sea ice predictions, so are not performed.

The model initial fields, boundary conditions, and atmosphere forcing are the same for all the seven experiments. The initial fields are interpolated from the operational analyses of TOPAZ5 at 0 o’clock on 1 January 2024. The boundary conditions are daily mean fields interpolated from the TOPAZ5 analyses, and the atmosphere forcing fields are the 6-h operational analyses from the ECMWF, both from 1 January to 30 April 2024. Both SIC and SST observations are daily fields. For model analysis, each observation is considered as unchanged [see (Equations 4-7)] on the day and continuously assimilated into the model using the LAON method, from 0 o’clock to the last time step before the next day. After a full-day assimilation each day, a new restart file is generated for model forecasts at 0 o’clock of the next day. The forecast starts from 0 o’clock on the next day, and no observations are assimilated during the 120 h forecast period.

3 Data

We use three observed SIC products and four modeled SIC products in this study. The observations include AMSR2 SIC from the University of Bremen, sea ice chart from the Ice Service of the Norwegian Meteorological Institute (NIS) and the merged SIC from an optimal combination of the AMSR2 SIC and NIS ice chart. The modeled SIC products are from TOPAZ5, NeXtSIM, GOFS3.1, and Barents-EPS. All the data were interpolated to the model grid using the nearest neighbor interpolation.

3.1 Observed SIC

3.1.1 AMSR2 SIC

The AMSR2 microwave radiometer onboard the GCOM-W1 satellite measures the microwave emission from the Earth, at a nominal incident angle of 55° and a swath width of 1,450 km. The AMSR2 SIC dataset that we used here is the version 5.4 with a grid resolution of 3.125 km, which utilizes the highest spatially resolving AMSR2 channels at 89 GHz (Melsheimer, 2019). It uses the same ARTIST sea ice (ASI) algorithm as it was developed for the AMSR-E 89-GHz channel (Spreen et al., 2008). It has a higher spatial resolution than most other AMSR2 SIC datasets although the atmospheric influence can be higher. The uncertainty is calculated following the same procedure in Spreen et al. (2008), where the overall error sums from three sources: the radiometric error from the bright temperature, the variability of the tie points, and the atmospheric opacity. The uncertainty is expressed in terms of standard deviation (SD).

3.1.2 NIS ice chart

The ice chart is produced on the basis of manual interpretation of satellite data and other observations such as coastal station and ship reports (Copeland et al., 2024). The ice charting employs a variety of satellite observations to obtain a more realistic SIE and MIZ, and these have evolved since ice charting began in 1967 to include higher spatial resolution and all-weather capable sensors over the years. The main satellite data used are the weather independent Synthetic Aperture Radar (SAR) data from Sentinel-1, RADARSAT-2, and RADARSAT Constellation Mission (RCM). The analyst also uses visual and infrared data from METOP and NOAA Advanced Very High Resolution Radiometer (AVHRR), NOAA Visible Infrared Imaging Radiometer Suite (VIIRS), and Sentinel-3 Ocean and Land Colour Instrument (OLCI) and Sea and Land Surface Temperature Radiometer (SLSTR) in cloud-free conditions. These satellites provide coverage of the charting area several times a day and allow the ice chart to be produced in a scale-free vectorized format, with a nominal resolution of less than 400 m. A rasterized NetCDF-format is produced for Copernicus Marine Service with a resampling to 1-km grid spacing (Dinessen and Hackett, 2018). The NIS ice chart includes seven ice concentration categories following the WMO sea ice nomenclature (WMO, 2014): fast ice (SIC = 10/10), very close drift ice (9–10/10), close drift ice (7–8/10), open drift ice (4–6/10), very open drift ice (1–3/10), open water (<1/10), and ice free (0). For practical use, a mean value is applied to denote the different ice categories in the ice chart. The uncertainty is approximated as the half of the range of the corresponding ice category, except being 0.01 for the fast ice.

3.1.3 Merged SIC

According to Wang et al. (2020), assimilating merged multisensor observations is equivalent to assimilating all the observations concurrently. Therefore, the effect of assimilating both AMSR2 SIC and sea ice chart can be investigated using the merged AMSR2-ice chart data. In this study, we use the merged SIC from multisensor optimal merging of AMSR2 SIC and NIS ice chart (Wang et al., 2024). The AMSR2 SIC is the same as in 3.1.1, and the NIS ice chart the same as 3.1.2. The merged SIC effectively mitigated the original shortcomings in both the AMSR2 SIC and the NIS ice chart (Wang et al., 2024). Because the NIS ice chart is only available during the working days, the merged SIC on weekends and holidays is the same as the AMSR2 SIC.

3.2 Modeled SIC

3.2.1 TOPAZ5 SIC

The TOPAZ5 SIC is obtained from the CMEMS operational product (CMEMS, 2024a, accessed in April 2024), which is a nominal product of the CMEMS Arctic Monitoring and Forecasting Center (MFC) for ocean physics (Hackett et al., 2023). It is produced by the newly operationalized TOPAZ5 Arctic Ocean and sea ice prediction system, using the version 2.2.98 of HYCOM ocean model (Bleck, 2002) coupled to the CICE 5.1.2 (Hunke et al., 2015), with the deterministic ensemble Kalman filter (DEnKF; Sakov and Oke, 2008) for data assimilation. The model domain covers the North Atlantic and Arctic basins with a grid spacing of approximately 6–8 km. The model is run daily to provide 10 days of forecast (average of 10 members) of the three-dimensional (3D) physical ocean and sea ice variables. The data assimilation is performed weekly to provide 7 days analysis (ensemble average), in which a 100-member DEnKF is used to assimilate SIC, SIT, sea ice drift, SST, sea level anomaly and in situ temperature/salinity (T/S) profiles (Hackett et al., 2023). TOPAZ5 runs once a day at the Norwegian Meteorological Institute. The forecast and analysis are then interpolated and disseminated to a 6-km grid using the polar stereographic projection. The disseminated product is available as hourly surface fields, daily and 6-h averaged 3D fields.

3.2.2 neXtSIM SIC

The neXtSIM SIC is from the CMEMS operational product (CMEMS, 2024b, accessed in May 2024). It is an hourly product produced by the Arctic MFC through the neXtSIM sea ice prediction system (Hackett et al., 2023). The neXtSIM is a stand-alone sea ice model using the Brittle-Bingham-Maxwell sea ice rheology (Rampal et al., 2019; Williams et al., 2021), on an adaptive triangular mesh of 10-km average cell length. The model is forced with surface atmosphere fields from the ECMWF and ocean fields from TOPAZ5. It runs daily, assimilating manual ice charts, SIT from CS2SMOS in winter and providing 9-day forecasts (CMEMS, 2024b). The output variables are SIC, SIT, ice drift velocity, snow depths, sea ice type, sea ice age, ridge volume fraction, and albedo, provided at hourly frequency. The adaptive Lagrangian mesh is interpolated for convenience on a 3-km resolution regular grid in a polar stereographic projection.

3.2.3 GOFS 3.1 SIC

The GOFS3.1 SIC is from https://www.hycom.org/dataserver, with the forecasts downloaded once they became available. The GOFS 3.1 is based on the HYCOM version 2.2.99 (Metzger et al., 2017), coupled to the CICE version 4.0 (Hunke and Lipscomb, 2008). The model uses a tripole global grid (grid resolution about 9 km at equator, 7 km at mid-latitude, and 3.5 km at the North Pole). The atmospheric forcing is from the Navy Global Environmental Model (NAVGEM) at Fleet Numerical Meteorology and Oceanography Center (Hogan et al., 2014). The system uses the Navy Coupled Ocean Data Assimilation (NCODA) system (Cummings and Smedstad, 2013) for data assimilation, which is based on a 3D variational scheme and assimilates available satellite and in situ observations. The assimilated ocean variables are SST, SSH anomaly, and T/S profiles. For sea ice assimilation, the AMSR2 SIC is firstly merged with the semi-automated analysis from Interactive Multisensor Snow and Ice Mapping System (IMS) produced by the U.S. National Ice Center, which is then assimilated into CICE for operational forecast (Posey et al., 2015). The output variables include 3D ocean temperature; salinity and velocity; surface mixed layer and location of mesoscale features; and ice concentration, thickness, and drift.

3.2.4 Barents-EPS SIC

The Barents-EPS SIC is obtained from https://thredds.met.no/thredds/fou-hi/barents_eps.html (accessed in May 2024). It is produced in the Norwegian Meteorological Institute using the operational coupled ocean and sea ice ensemble prediction model Barents-2.5km v.20 (Röhrs et al., 2023). The model uses the same coupled ROMS-CICE model and configuration as in this study, but using the DEnKF (Sakov and Oke, 2008; Fritzner et al., 2019; Röhrs et al., 2023) for data assimilation. The assimilated variables include SIC, SST, and in situ T/S profiles. The model runs four times per day to provide 96 h of hourly ensemble mean and SD for SIC, SIT, ice velocity, SST, SSS, surface current velocity, and elevation.

4 Evaluation metrics

We use IIEE (Goessling et al., 2016) to evaluate the modeling skill for SIE and use integrated MIZ error (IME; Wang et al., 2023) to evaluate the modeling skill for MIZ. To be consistent with the NIS ice chart, we here use SIC = 0.1 as the demarcation for SIE and 0.85 as the demarcation between MIZ and dense pack ice. The prediction skills for SIE and MIZ are evaluated against the sea ice chart persistence. These metrics are briefly described below.

4.1 IIEE and IME

The IIEE is determined following Goessling et al. (2016)

$\begin{array}{ll}IIEE={\int }_A\text{max}(c_f-c_t,0)dA+{\int }_A\text{max}(c_t-c_f,0)dA,& (10)\end{array}$

where A denotes the whole model domain, the subscripts f and t denote the forecast and the truth (here, we use the NIS ice chart as an approximate). The variable c = 1 where SIC a ≥ 0.1 and c = 0 elsewhere. The first term on the right side of (Equation 10) denotes the overestimate, and the second term denotes the underestimate.

Similar to the formulation for the IIEE, the IME is defined as follows (Wang et al., 2023)

$\begin{array}{ll}IME={\int }_A\text{max}(c_f-c_t,0)dA+{\int }_A\text{max}(c_t-c_f,0)dA.& (11)\end{array}$

The only difference between Equations 10, 11 is the definition of the variable c. For the IME, c = 1 where SIC ∈ [0.1, 0.85], and c = 0 elsewhere.

4.2 Prediction skill of SIE and MIZ

We define the following metrics to evaluate the prediction skill for SIE,

$\begin{array}{ll}{S}_{SIE}=1-\frac{IIE{E}_m}{IIE{E}_r},& (12)\end{array}$

where the subscripts m and r denote the concerned model and reference, respectively. Similarly, we define the prediction skill for MIZ

$\begin{array}{ll}{S}_{MIZ}=1-\frac{IM{E}_m}{IM{E}_r}.& (13)\end{array}$

Equations 12, 13 provide a simple description of the prediction skills for the concerned model against the reference. It is seen that the skills would be positive when the modeled IIEE or IME is smaller than the reference, and vice versa. When the model predicts the same IIEE or IME as the reference, the skill would be 0. When the model perfectly predicts the SIE or MIZ, the modeled IIEE or IME would be 0, and the skill would be 1.

5 Results

5.1 Effects of assimilation on the analyses of SIE and MIZ

5.1.1 Daily SIC spatial distribution

Figure 2 compares the observed and modeled SIC on 19 February 2024. For the purpose of evaluating the analyses of SIE and MIZ, we have separated the whole ice cover into dense pack ice (SIC > 0.85) and MIZ (SIC ∈ [0.1,0.85]), with the rest as open water (SIC < 0.1). As pointed out in previous studies (Cavalieri, 1994; Kern et al., 2019; Wang et al., 2024), the PMR tends to underestimate low SIC area. This can also be seen when compared to the ice chart Figure 2a vs. Figure 2b), particularly where the AMSR2 MIZs are narrower.

Figure 2

Figure 2. SIC observations (a, b) and analyses (c–m) on 19 February 2024, with the ice cover separated into dense pack ice (red), MIZ (yellow), and open water (light blue). The blue lines show the SIE of the ice chart, and the green lines show the demarcation between MIZ and dense pack ice of the ice chart. Here, DA denotes data assimilation. The experiments are referred to Table 1.

The Free run indicates that the model system without data assimilation tends to significantly overestimate the sea ice cover (Figures 2c vs. 2b). This is particularly pronounced in the Greenland Sea. Assimilation of the OSTIA SST slightly reduces the large bias in the Greenland and Barents seas (Figures 2d vs. Figure 2b), but the overestimated sea ice cover in the Greenland Sea is still remarkable. By contrast, assimilation of SIC is able to substantially improve the simulation of the ice field. Even the assimilation of AMSR2 SIC alone can considerably improve the sea ice cover, although the MIZ is considerably overestimated in the northeastern Barents Sea (Figure 2e vs. Figure 2b). Additional assimilation of the OSTIA SST further improves the analyses of the SIE and MIZ (cf. Panels e and f with b in Figure 2). It is seen that the assimilation of AMSR2 SIC and OSTIA SST (Figure 2f) produces closer sea ice coverage to the ice chart (Figure 2b) than the AMSR2 observation (Figure 2a).

Figures 2g, h show the sea ice distribution using the assimilation of both merged SIC and OSTIA SST. Although both DA-Both1 and DA-Both2 assimilate the same merged SIC on 19 February 2024 (working day), there are still some noticeable differences in these two analyses, e.g., the MIZs in the Greenland Sea and west coast of Novaya Zemlya. When comparing these two experiments with DA-Both0 (Figure 2f), there are marked differences in the MIZs, e.g., in the Greenland Sea and west coast of Novaya Zemlya (cf. Panels f, g, d with b in Figure 2). In this case, DA-Both1 tends to be noticeably closer to the NIS ice chart (Figure 2g vs. Figure 2b). DA-Both3 also assimilates both OSTIA SST and SIC, using pure ice chart for the working days and AMSR2 SIC for the rest days. It provides a SIC analysis very close to DA-Both1 and DA-Both2 (cf. Figures 2g–i).

As a comparison, we also present the SIC analyses from the four operational products, namely, Barents-EPS, TOPAZ5, neXtSIM, and GOFS 3.1 (Figures 2j–m). In general, Barents-EPS overestimates the ice extent in the Greenland Sea, particularly overestimating the area of dense pack ice. TOPAZ5 generally has a much closer agreement with the ice chart, although it tends to overestimate the SIC in the northeastern Barents Sea. NeXtSIM tends to overestimate the SIC in the Greenland Sea and underestimate the MIZ there. GOFS3.1 generally gives an good analysis of the SIC, particularly in the Greenland Sea, although some underestimates occurs in the MIZ in the Barents Sea. This is partly due to the fact that GOFS3.1 assimilates the National Ice Center ice chart (Posey et al., 2015), whereas TOPAZ5 and Barents-EPS do not.

This daily distribution only provides one-case results. Further assessment of the model analyses is performed in Section 5.1.3, using IIEE and IME for the whole 4-month period—1 January to 30 April 2024.

5.1.2 Daily SST

Daily SST biases from the different experiments are shown in Figure 3, together with the daily ensemble mean SST bias from Barents-EPS (Figure 3a). These SST biases are evaluated against the daily OSTIA SST (CMEMS, 2024c). Except for the SST near the southern boundary and west of Svalbard, the Barents-EPS provides an analysis very close to the observation, with the mean bias of −0.01°C and SD of 0.40°C.

Figure 3

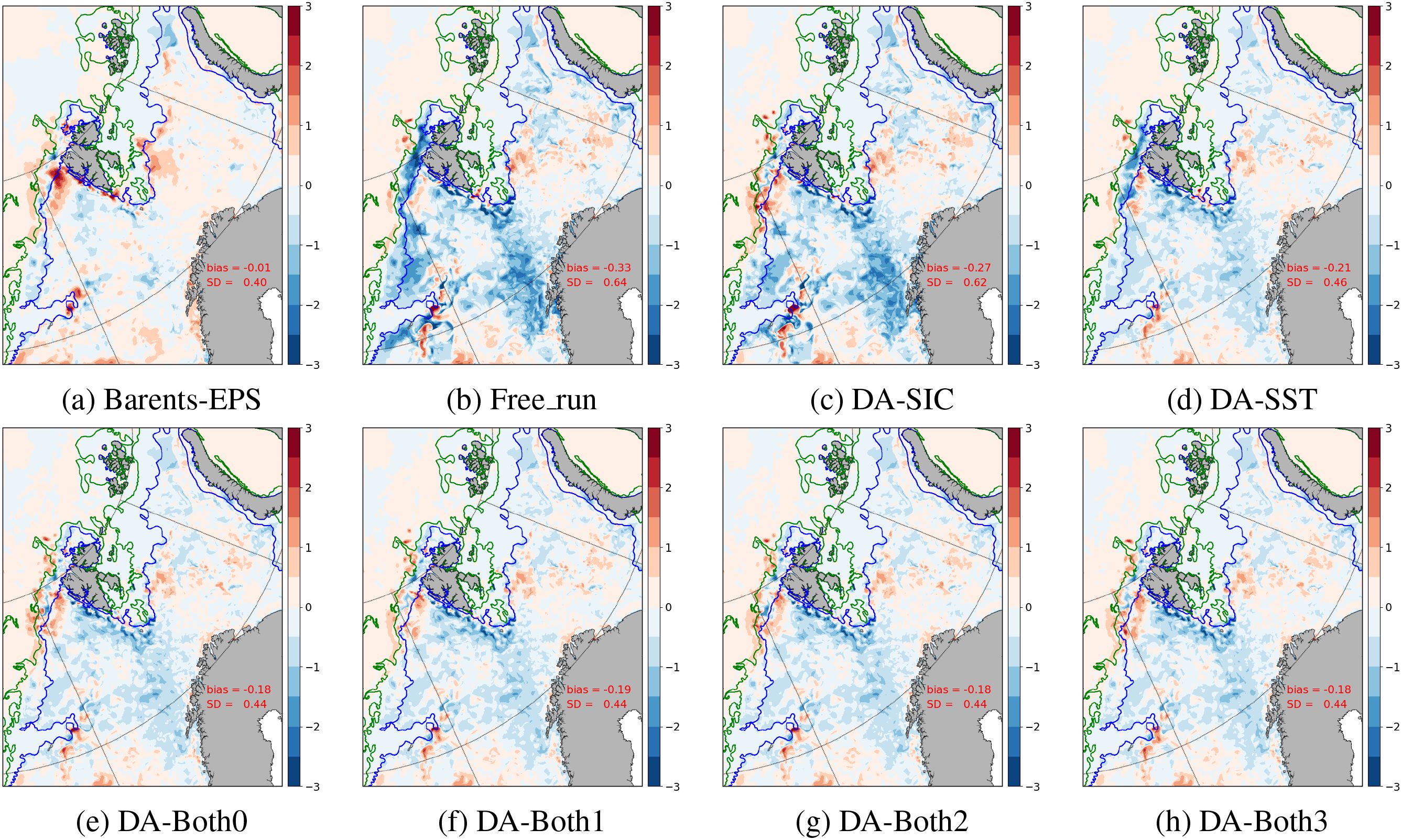
Figure 3. SST biases (°C) on 19 February 2024 from Barents-EPS (a) and the experiments (b–h). The blue lines show the SIE of the ice chart, and the green lines show the demarcation between MIZ and dense pack ice of the ice chart. Here DA denotes data assimilation. The experiments are referred to Table 1.

The Free run has a considerable cold bias in much of the Norwegian Sea and Greenland Sea (Figure 3b). The underestimate of the SST in the Greenland Sea is mainly due to the overestimated sea ice cover, under which the SST is maintained close to the freezing point. The underestimate of the SST in the Norwegian Sea is most likely due to the underestimate of the warm current from the south, as seen from the overall spatial pattern of the underestimated SST. Assimilation of the AMSR2 SIC significantly mitigates the underestimated SST in the Greenland Sea (Figure 3b vs. Figure 3c). However, there is almost no improvement in the ice-free Norwegian Sea. Both Free run and DA-SIC have large mean bias, being −0.33°C and −0.27°C, respectively.

Assimilation of SST significantly improves the simulated SST (Figure 3d). Over much of the Norwegian Sea and Greenland Sea, the large underestimation of the SST has been remarkably mitigated. However, there is still a mean bias of −0.22°C over the whole Barents region. In particular, the large cold SST bias remains north of Svalbard, due to the overestimated sea ice cover.

There is little difference in the SST when both SIC and SST are assimilated (Figures 3e–h). Compared with the assimilations of SIC alone (Figure 3c) and SST alone (Figure 3d), most of the large biases have been mitigated, except for the small areas along the west coast of Svalbard. It is noteworthy that the mean biases in these experiments are still about −0.18°C (Figures 3e–h). This indicates that the SST assimilation is still not optimal. Further investigations are needed to improve the SST analysis.

5.1.3 IIEE and IME

Figure 4 shows the IIEE and IME from 1 January to 30 April 2024 for all the model runs, the AMSR2 observations, and the four operational analyses (Barents-EPS, TOPAZ5, neXtSIM, and GOF3.1). All the IIEE and IME are calculated against the sea ice charts. The discontinuities in the IIEE and IME are due to the missing sea ice charts on weekends and holidays. It is seen that, in the whole simulation period, the Free run has very large IIEE (Figure 4a), largely over 4 × 10⁵ km² after 1 February, indicating a large bias in the model system. Compared with the Free run, the assimilation of the OSTIA SST (DA-SST) has a mild correction in the SIE, with the IIEE generally about 2 × 10⁵ km² after 1 February. Compared with the other model analyses, these two runs are significantly larger, being about three and two times of the other IIEEs (see the legend in Figure 4a). The relatively large IIEE of DA-SST is mainly due to the characteristics of the LAON assimilation, which only nudges the SST to the optimal estimate but without direct modification of the sea ice cover during the assimilation. Due to the systematic cold biases in both of the sea ice and ocean model components, the sea ice coverage would still be notably overestimated when only SST is assimilated, resulting in large IIEE. At the same time, the updated SST near the SIE would also be modified by the overestimated sea ice cover, resulting in underestimated SST and improved sea ice extent through sea ice melting. Such a change in the SST can be seen in the northern coast of Svalbard in Figure 3d.

Figure 4

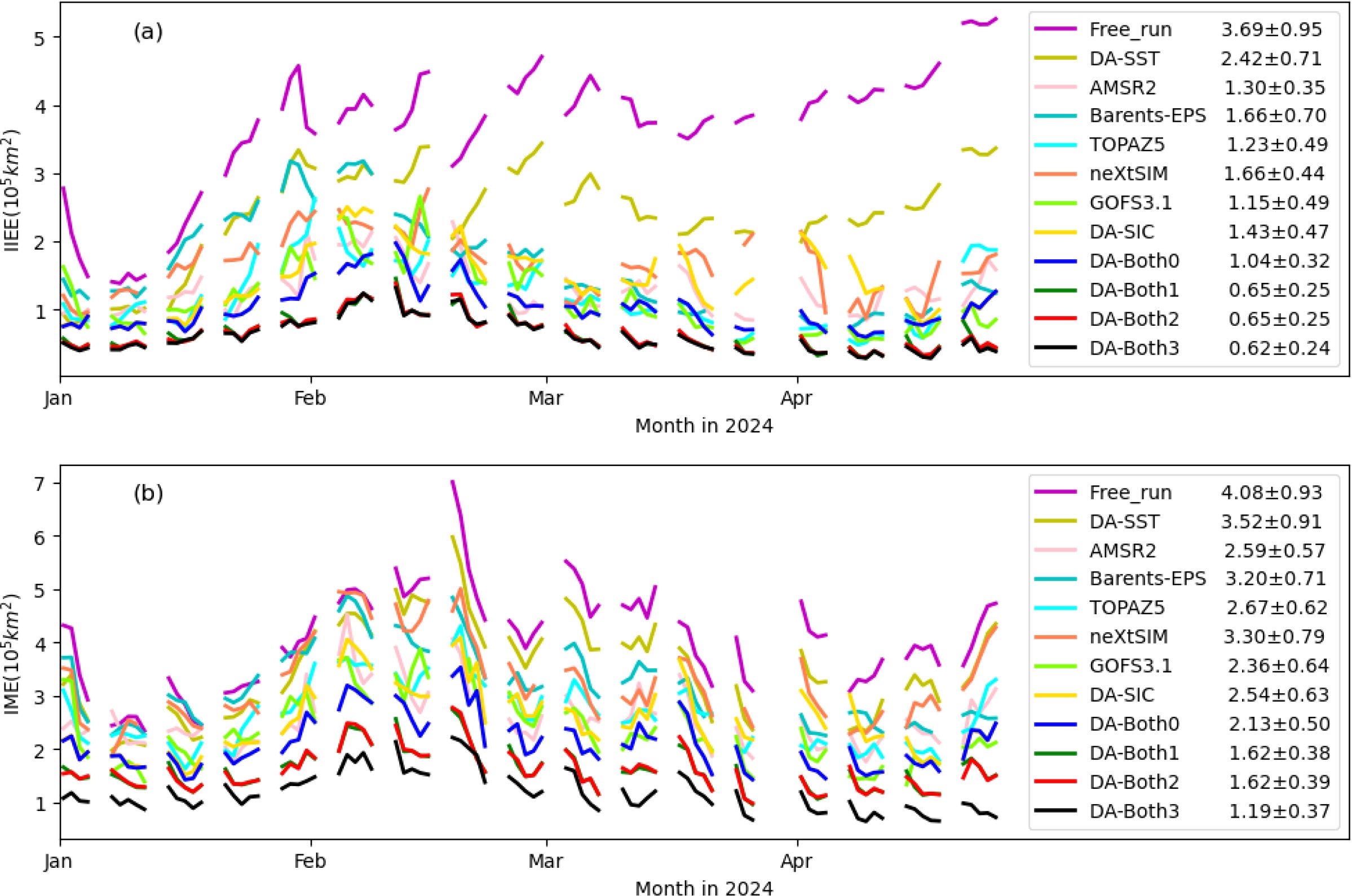
Figure 4. Time series of the integrated ice edge error (IIEE) and integrated marginal ice zone error (IME) for different products from 1 January to 30 April 2024: (a) IIEE and (b) IME. The numbers in the legends show the mean ± standard deviation of the corresponding IIEE and IME. The experiments are described in Table 1.

The AMSR2 observation provides a consistent reference for the present study to the earlier study in Wang et al. (2023), although for different sea areas. It is seen that TOPAZ5 IIEE has a smaller mean than the AMSR2 IIEE (see legend in Figure 4a). This is different from the TOPAZ4 IIEE, which is considerably larger than the AMSR2 IIEE (Wang et al., 2023), indicating a significant improvement in the model development of the TOPAZ system. Barents-EPS and neXtSIM generally produce similar large IIEE. GOFS3.1 produces a similar IIEE to TOPAZ5, both smaller than Barents-EPS and neXtSIM.

Due to the large bias in the model system, the assimilation of AMSR2 SIC alone (DA-SIC) tends to have large IIEE in the analysis (Figure 4a). Contrast to the results in the NorHAPS (Wang et al., 2023), DA-SIC IIEE is larger than the AMSR2 IIEE. It is also larger than those of TOPAZ5 and GOFS3.1 but still smaller than those of Barents-EPS and neXtSIM (Figure 4a). With the additional assimilation of the OSTIA SST (DA-Both0), the model produces smaller IIEE than all the other operational analyses. Further assimilation of the merged SIC provides further improvements, with the mean IIEE down to about 0.65 × 10⁵ km² (DA-Both1 and DA-Both2). There remains of little difference in the modeled IIEEs between DA-Both1 and DA-Both2, partly due to the fact that the evaluations are only based on the days when sea ice charts are available. DA-Both3 produces slightly lower IIEE than DA-Both1 and DA-Both2, indicating a slight advantage for SIE analysis.

Similar to the results in Wang et al. (2023), the IME is about twice of the IIEE for most analyses, suggesting about half of the IME is due to the misclassifications between MIZ and dense pack ice. In the present case, the Free run IME is very close to its IIEE (Figure 4), particularly after 1 February. This exceptional result can be well explained by Figure 2, where the Free run significantly overestimated the sea ice cover. In such a case, the open water and MIZ (Figure 2b) is largely modeled as dense pack ice in the Free run, thereby generating similar values of IME and IIEE (Figure 4). For the four operational analyses, only GOFS3.1 has lower IME than the AMSR2 observation. The assimilation of AMSR2 SIC alone produces slightly smaller IME than the AMSR2 observation but larger than that of GOFS3.1. The assimilations of both SIC and SST (DA-Both0, DA-Both1, DA-Both2, and DA-Both3) all produce lower IME than GOFS3.1. Both DA-Both1 and DA-Both2 produce considerably lower IME than DA-Both0 (Figure 4b), but there is generally little difference in the simulated SIE and MIZ between DA-Both1 and DA-Both2. It is noteworthy that DA-Both3 produces a considerably better MIZ analysis than DA-Both1 and DA-Both2, appearing to be the best option for the MIZ analysis. This tends to suggest that the present AMSR2 SIC is not very accurate for separating MIZ from dense pack ice.

5.2 Effects of assimilation on the forecasts of SIE and MIZ

5.2.1 Effect on SIE forecast

Figure 5 shows the prediction skills of the five experiments (DA-SIC, DA-Both0, DA-Both1, DA-Both2, and DA-Both3) and the four operational forecasts (Barents-EPS, TOPAZ5, neXtSIM, and GOFS3.1), evaluated against the persistence forecast of the sea ice chart using (Equations 12, 13). As noted in Section 4.2, positive skill indicates that the model prediction skill is higher than the referenced sea ice chart persistence, and vice versa. It is seen that all the mean prediction skills for the 1-day SIE forecast are low than 0 (see legend in Figure 5a), indicating these models are still less skillful in predicting the SIE than the sea ice chart produced one day before. For longer days of forecast, all the experiments using both SIC and SST assimilations have higher skills than the sea ice chart persistence (panels b–e in Figure 5). By contrast, the assimilation of SIC alone (DA-SIC) always shows notably negative skills. This indicates that a noticeable portion of the prediction skill is from the improved initial fields due to the addition of SST assimilation (see DA-SIC vs. DA-Both0 in Figure 4a). The initial fields without SST assimilation have a cold bias in the SST field, which enhances the freezing of open water near the SIE. The additional assimilation of SST significantly suppresses the SST underestimate and therefore mitigates the overestimate of the sea ice cover from excessive freezing.

Figure 5

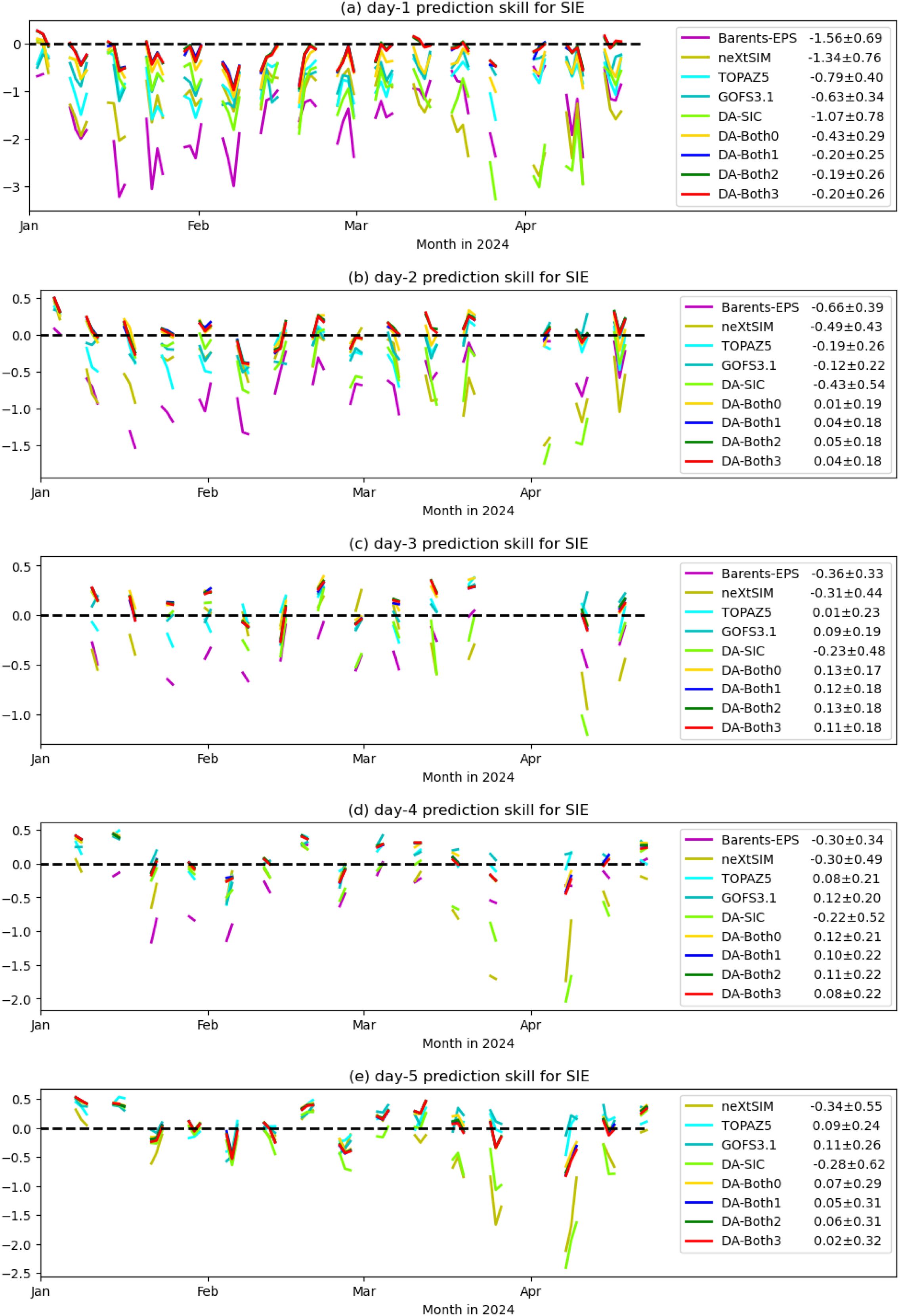
Figure 5. Prediction skills of the forecast SIE evaluated against the persistence forecast of sea ice chart, from 1 day to 5 days (a–e). The experiments are referred to Table 1. It is noted that Barents-EPS only provides 4 days of forecast.

It is noted that the seasonal simulation with only SST assimilation has quite high errors in the IIEE (DA-SST in Figure 4a). This is partly due to the characteristics of the LAON assimilation. In the situation of assimilating the SST alone, it only modifies the SST field but does not directly modify the sea ice cover. In such a case, the overestimated sea ice cover is only adjusted through the model physics. When the cold bias in the sea ice model component is large, the overestimate of the simulated sea ice cover tends to substantially remain, thereby resulting in a large bias in the simulated SIE. On the whole, the large IIEE in DA-SST is due to the model bias in the sea ice model component, whereas the improvement in the simulated SIE with additional SST assimilation is due to the overall improved initial ocean and sea ice conditions.

The experiments performed here assimilate SIC and SST using the LAON method. These two assimilated data are generally less than those used in the operational products that commonly include SIT, sea ice velocity, and SSS. Similar to the assimilation results in Wang et al. (2023), the LAON assimilation exhibits higher SIE prediction skills compared with the assimilations using EnKF (TOPAZ5 and BarentEPS), 3D variational (GOFS 3.1), and nudging (neXtSIM). There are generally little differences in the forecast IIEEs between DA-Both1, DA-Both2, and DA-Both3 (Figure 5). Due to the large systematic bias in the METROMS Barents-2.5km model (see the Free run in Figure 4), the effect of LAON data assimilation starts to diminish from 5-day forecast, and the prediction skills start to decrease accordingly (Figure 5). While still positive, the prediction skills of these experiments are surpassed by the operational forecasts of TOPAZ5 and GOFS3.1. TOPAZ5 and GOFS 3.1 become more skillful than the sea ice chart persistence after 3-day forecast (panels c–e in Figure 5), whereas Barents-EPS and neXtSIM remain to be negative prediction skills for all the 5 days (Figure 5).

5.2.2 Effects on MIZ forecast

Figure 6 illustrates the prediction skills for MIZ from 1 to 5 days of forecasts. On the whole, the LAON assimilations of both ice chart and SST (DA-Both1, DA-Both2, and DA-Both3) show remarkably higher skills than the other products, particularly for the 1–3 days of forecasts (see the mean skills in the legends). It is of negligible difference whether to assimilate the AMSR2 SIC during the weekends or holidays, as shown by the prediction skills between DA-Both1 and DA-Both2. DA-Both2 is slightly better in SIE forecast (Figure 5), whereas DA-Both1 is slightly better in MIZ forecast (Figure 6). DA-Both3 has the highest prediction skills for MIZ in the first two days (Figure 6). This suggests that the AMSR2 SIC is not as accurate as the ice chart for separating the MIZ from dense pack ice.

Figure 6

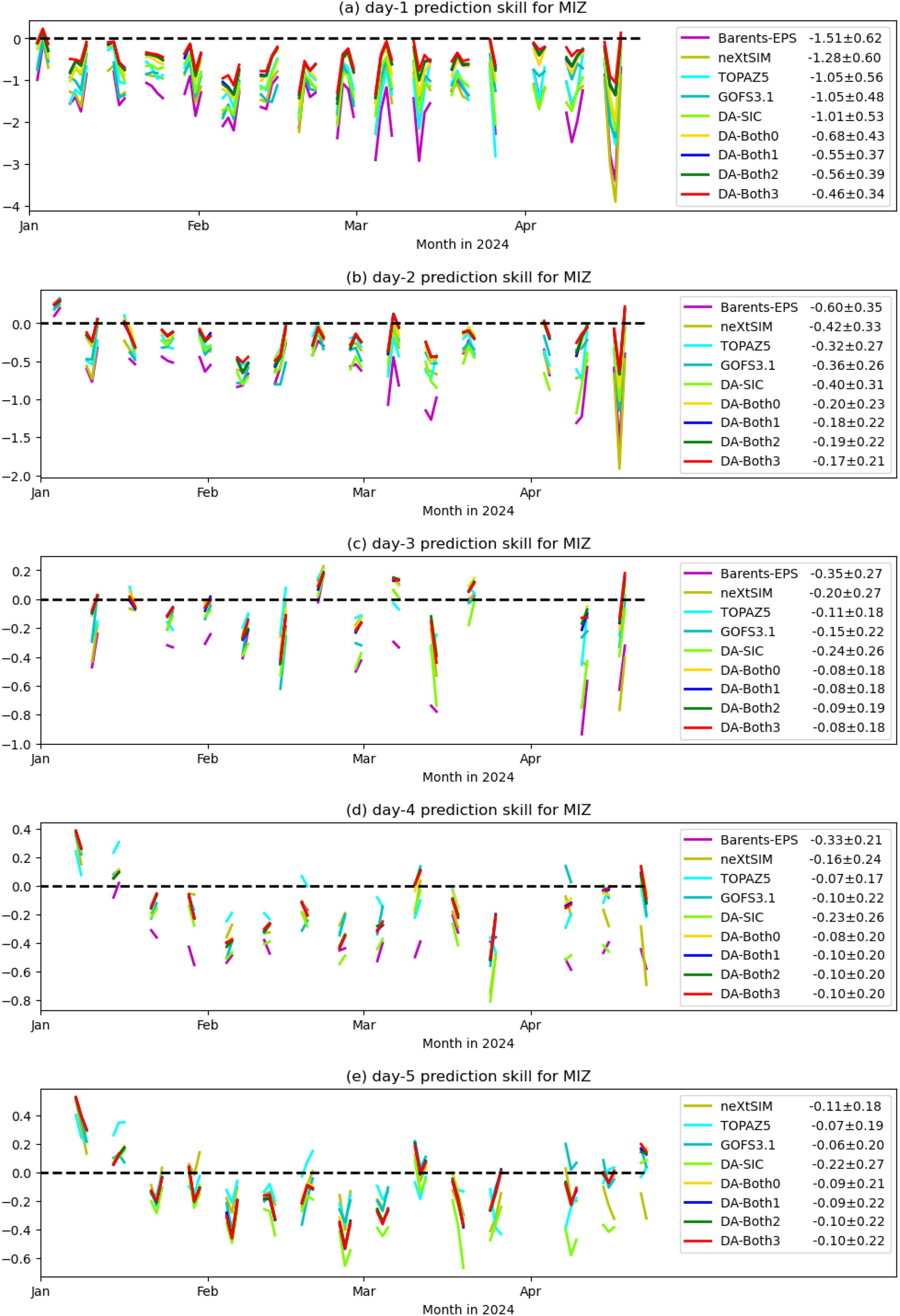
Figure 6. Prediction skills of the forecast MIZ evaluated against the persistence forecast of sea ice chart, from 1 to 5 days (a–e). The experiments are referred to Table 1. It is noted that Barents-EPS only provides 4 days of forecast.

DA-Both0 does not assimilate the sea ice chart, but it also shows comparable prediction skills to those assimilating the ice chart, except for the first day. This is partly due to the biases in the AMSR2 SIC observation and the model system. The AMSR2 SIC generally provides an underestimated sea ice extent, whereas the model system tends to provide an overestimate of the sea ice extent during the winter season. On the whole, the excessive growth of the model sea ice counteracts the initially underestimated sea ice cover with AMSR2 SIC assimilation, thus improving the prediction skill in the later days. This can be clearly seen in both Figures 5 and 6, where DA-Both0 has lower prediction skills than DA-Both1, DA-Both2 and DA-Both3 in the first 2 or 3 days but becomes to have higher or comparable prediction skills in the later days. Assimilation of SIC alone (DA-SIC) generally produces low prediction skills for MIZ forecasts. This indicates that additional assimilation of SST can significantly improve the forecast of MIZ when the model is highly biased, similar to the SIE forecasts (Section 5.2.1).

It is noteworthy that the mean prediction skills for MIZ are all negative for all the models and experiments from 1 to 5 days (Figure 6). This indicates that the model predictions are not yet sufficiently mature for skillful MIZ forecasts. Nevertheless, the LAON assimilation of the SIC and SST illustrates close prediction skills to the sea ice chart persistence forecasts, particularly for 3–5 days (Figure 6c–e). Considering the bias in the SST field (Section 5.1.2), improving the data assimilation may still be a feasible way to further improve the MIZ forecast.

6 Concluding remarks

Sea ice is a major threat to the marine operations around Svalbard. Accurate forecasts of SIE and MIZ are crucial but remain extremely challenging. A large number of efforts have been made in recent years to improve the mechanisms on the interactions among the atmosphere, ocean, sea ice, and waves (see overviews in Bennetts et al., 2022; Dumont, 2022). How these new understandings and developments can improve the forecasts of SIE and MIZ remains to be further verified, particularly for short-term operational forecasts.

In this study, by using a coupled ocean and sea ice model (METROMS) with the LAON data assimilation in a regional configuration (Barents-LAON), we demonstrate that the LAON is an effective method for data assimilation. Despite the large biases in the model system, the Barents-LAON with both SIC and SST assimilations can provide better analyses and better 1–3 days of forecasts of SIE and MIZ (Figures 4–6) than all the operational products (TOPAZ5, neXtSIM, GOFS3.1, and Barents-EPS). Although the assimilation of SST alone generally has a limited contribution to the improvements of SIE and MIZ analyses (Figure 4), the SST assimilation does have a notable contribution to the improvements of SIE and MIZ forecasts when it is performed together with the SIC assimilation (DA-SIC vs. DA-Both0 in Figures 5, 6). This change is due to the overall improvements in the initial ocean and sea ice conditions with SIC and SST assimilations.

The model experiments show that the differences in the prediction skills for SIE and MIZ are generally small between DA-Both1 and DA-Both2. This suggests that it is not very critical whether or not to assimilate the AMSR2 SIC on weekends and holidays, when the sea ice chart has been assimilated on working days. Additional assimilation of the AMSR2 SIC on weekend and holidays (DA-Both2) has slightly higher prediction skill for SIE forecasts (Figure 5), whereas no such assimilation (DA-Both1) appears to have slightly higher prediction skill for MIZ forecasts (Figure 6). However, more studies are needed to truly confirm this conclusion.

Assimilation of sea ice chart can significantly improve the analysis and short-term forecasts of SIE and MIZ. Compared with the assimilation of AMSR2 SIC and SST (DA-Both0), all the experiments with the assimilation of sea ice chart (DA-Both1, DA-Both2, and DA-Both3) show significantly lower IIEE and IME (Figure 4). In particular, DA-Both3 emerges to produce significantly better analyses (Figure 4) and 1–2 days of forecasts for MIZ compared with DA-Both1 and DA-Both2 (Figure 6), although they tend to provide similar analyses and forecasts for SIE (Figures 4, 5). This indicates that the additional assimilation of the AMSR2 SIC tends to degrade the analyses and forecasts of MIZ when the ice chart has already been assimilated. This implies that the present AMSR2 SIC is not sufficiently accurate for distinguishing the MIZ from dense pack ice.

The present prediction skills for SIE and MIZ differ considerably. The Barents-LAON with assimilations of both SIC and SST (DA-Both0, DA-Both1, DA-Both2, and DA-Both3) all outperform the sea ice chart persistence for SIE forecasts except for the first day (Figure 5). However, the mean prediction skills for MIZ are still lower than the sea ice chart persistence (Figure 6), in all the experiments and all the operational forecasts. This suggests that some important physical processes connected with the MIZ evolution may be not adequately described in the present coupled ocean and sea ice models, such as those related to waves. Such missing processes are particularly important for the regions of large transformation between MIZ and dense pack ice, as the Barents-LAON model does provide rather high prediction skills for SIE forecasts. The large model bias may be another factor leading to the unsatisfactory MIZ forecasts. Further improvements are needed for the present Barents-LAON to fully outperform the sea ice chart persistence for short-term SIE and MIZ forecasts.

The prediction skills for SIE and MIZ can be further improved, which is planned to be done in the near future. Firstly, the model system needs to be optimized. This is essential and actually a notable portion of the deterioration of the prediction skill is from the systematic model bias. As shown in Section 5, both of the ocean and sea ice model components have cold biases. Such model biases are highly likely related to the overestimated sea ice drift (Röhrs et al., 2023) and to the underestimated warm North Atlantic Current in the Norwegian Sea as seen in this study. These biases can be greatly mitigated through optimization of model parameters, for example using Green’s functions (Menemenlis et al., 2005) or machine learning (Kutz, 2023). Secondly, the assimilation of the SST may be refined. The present configuration for the assimilations of both SIC and SST still has a noticeable mean bias in the SST field, for example, about −0.18°C on 19 February 2024 (Figure 3). This bias tends to increase with time, which can deteriorate the analyses and forecasts of SIE and MIZ. A better assimilation can mitigate the overall SST bias, thus improving the forecasts of SIE and MIZ. Thirdly, using instantaneous SIC observations instead of the daily mean observations for data assimilation may also improve the analyses and forecasts, as shown using the EnKF (Durán Moro et al., 2024). Finally, coupling the model system with a wave model may further improve the MIZ, particularly for the demarcation between the MIZ and dense pack ice, as the wave-ice interactions influence both physical/dynamical and thermodynamical processes in the MIZ.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KW: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. CW: Formal analysis, Investigation, Validation, Writing – review & editing. NH: Data curation, Investigation, Validation, Writing – review & editing. AA: Data curation, Investigation, Validation, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by the Nordic Council of Ministers through project NOCOS DT (grant no. 102642), the Norwegian Research Council through project 4SICE (grant no. 328886), and the Norwegian FRAM Flagship program through project SUDARCO (grant no. 551323).

Acknowledgments

The authors are grateful to Gunnar Spreen in the University of Bremen for the discussion about the AMSR2 SIC. The constructive comments from the two reviewers are gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

AMAP (2017). Adaptation actions for a changing arctic (AACA) - barents area overview report, arctic monitoring and assessment programme (AMAP) (Oslo, Norway: AMAP).

Google Scholar

Arrigo K. R. (2014). Sea ice ecosystems. Annu. Rev. Mar. Sci. 6, 439–467. doi: 10.1146/annurev-marine-010213-135103

PubMed Abstract | Crossref Full Text | Google Scholar

Barber D., Hop H., Mundy C., B. E., Dmitrenko I., Tremblay J., et al. (2015). Selected physical, biological and biogeochemical implications of a rapidly changing arctic marginal ice zone. Prog. Oceanogr. 139, 122–150. doi: 10.1016/j.pocean.2015.09.003

Crossref Full Text | Google Scholar

Bennetts L., Bitz C., Feltham D. L., Kohout A. L., and Meylan M. H. (2022). Theory, modelling and observations ofmarginal ice zone dynamics: multidisciplinaryperspectives and outlooks. Phil.Trans.R.Soc. 380, 20210265. doi: 10.1098/rsta.2021.0265

PubMed Abstract | Crossref Full Text | Google Scholar

Bleck R. (2002). An oceanic general circulation model framed in hybrid isopycnic-cartesian coordinates. Ocean Model. 37, 55–88. doi: 10.1016/S1463-5003(01)00012-9

Crossref Full Text | Google Scholar

Bouillon S., Fichefet T., Legat V., and Madec G. (2013). The elastic-viscous-plastic method revisited. Ocean Model. 71, 1–12. doi: 10.1016/j.ocemod.2013.05.013

Crossref Full Text | Google Scholar

Breivik L., Carrieres T., and Eastwood S. (2009). Remote sensing of sea ice (Venice, Italy: ESA Publication WPP-306). doi: 10.5270/OceanObs09.cwp.11

Crossref Full Text | Google Scholar

Cavalieri D. J. (1994). A microwave technique for mapping thin sea ice. J. Geophys. Res. 99, 12561–12572. doi: 10.1029/94JC00707

Crossref Full Text | Google Scholar

CMEMS (2024a). Arctic ocean physics analysis and forecast, marine data store (mds). doi: 10.48670/moi-00001

Crossref Full Text | Google Scholar

CMEMS (2024b). Arctic ocean sea ice analysis and forecast, marine data store (mds). doi: 10.48670/moi-00004

Crossref Full Text | Google Scholar

CMEMS (2024c). Global ocean ostia sea surface temperature and sea ice analysis, marine data store (mds). doi: 10.48670/moi-00165

Crossref Full Text | Google Scholar

Copeland W., Wagner P., Hughes N., Everett A., and Robertsen T. (2024). The met Norway ice service: a comprehensive review of the historical and future evolution, ice chart creation, and end user interaction within metarea xix. Front. Mar. Sci. 11. doi: 10.3389/fmars.2024.1400479

Crossref Full Text | Google Scholar

Cummings J. and Smedstad O. (2013). “Variational data assimilation for the global ocean,” in Data assimilation for atmospheric, oceanic and hydrologic applications (Vol. II). Eds. Park S. and Xu L. (Springer-Verlag, Berlin, Heidelberg). doi: 10.1007/978-3-642-35088-713

Crossref Full Text | Google Scholar

Dinessen F. and Hackett B. (2018). Product user manual for regional high resolution sea ice charts Svalbard region (Toulouse, France: Copernicus Marine Service).

Google Scholar

Duarte P., Brændshøi J., Shcherbin D., Barras P., Albretsen J., Gusdal Y., et al. (2022). Implementation and evaluation of open boundary conditions for sea ice in a regional coupled ocean (roms) and sea ice (cice) modeling system. Geosci. Model. Dev. 15, 4373–4392. doi: 10.5194/gmd-15-4373-2022

Crossref Full Text | Google Scholar

Dumont D. (2022). Marginal ice zone dynamics: history, definitions and research perspectives. Phil. Trans. R. Soc A 380. doi: 10.1098/rsta.2021.0253

PubMed Abstract | Crossref Full Text | Google Scholar

Dumont D., Kohout A., and Bertino L. (2011). A wave-based model for the marginal ice zone including a floe breaking parameterization. J. Geophys. Res.-Oceans 116. doi: 10.1029/2010JC006682

Crossref Full Text | Google Scholar

Durán Moro M., Sperrevik A. K., Lavergne T., Bertino L., Gusdal Y., Iversen S. C., et al. (2024). Assimilation of satellite swaths versus daily means of sea ice concentration in a regional coupled ocean–sea ice model. Cryoshpere 18, 1597–1619. doi: 10.5194/tc-18-1597-2024

Crossref Full Text | Google Scholar

Egbert G. D. and Erofeeva S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. Atmos. Ocean. Tech. 19, 183-204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2

Crossref Full Text | Google Scholar

Feltham D. L. (2005). Granular flow in the marginal ice zone. Phil. Trans. R. Soc A 363, 1677–1700. doi: 10.1098/rsta.2005.1601

PubMed Abstract | Crossref Full Text | Google Scholar

Fritzner S., Graversen R., Christensen K. H., Rostosky P., and Wang K. (2019). Impact of assimilating sea ice concentration, sea ice thickness and snow depth in a coupled ocean-sea ice modelling system. Cryosphere 13, 491–509. doi: 10.5194/tc-13-491-2019

Crossref Full Text | Google Scholar

Fritzner S., Graversen R., Wang K., and Christensen K. (2018). Comparison between a multi-variate nudging method and the ensemble kalman filter for sea-ice data assimilation. J. Glaciol. 64, 387–396. doi: 10.1017/jog.2018.33

Crossref Full Text | Google Scholar

Goessling H. F., Tietsche S., Day J. J., Hawkins E., and Jung T. (2016). Predictability of the arctic sea ice edge. Geophys. Res. Lett. 43, 1642–1650. doi: 10.1002/2015GL067232

Crossref Full Text | Google Scholar

Hackett B., Bertino L., Ali A., Burud A., Williams T., Xie J., et al. (2023). PRODUCT USER MANUAL for arctic ocean physical and BGC analysis and forecasting products, issue: 5.17 (Toulouse, France: Copernicus Marine Service).

Google Scholar

Häkkinen S. (1986). Coupled ice-ocean dynamics in the marginal ice zones: Upwelling/downwelling and eddy generation. J. Geophys. Res. 91, 819–832. doi: 10.1029/JC091iC01p00819

Crossref Full Text | Google Scholar

Hogan T. F., Liu M., Ridout J. A., Peng M. S., Whitcomb T. R., Ruston B. C., et al. (2014). The navy glabal environmental model. Oceanography 27, 116–125. doi: 10.5670/oceanog.2014.66

Crossref Full Text | Google Scholar

Hunke E., Hebert D., and Lecomte O. (2013). Level-ice melt ponds in the los alamos sea ice model, cice. Ocean Mod. 71, 26–42. doi: 10.1016/j.ocemod.2012.11.008

Crossref Full Text | Google Scholar

Hunke E. and Lipscomb W. (2008). CICE: The Los Alamos sea ice model, documentation and software user’s manual, version 4.0. Tech. Rep. LA-CC-06-012 (Los Alamos, NM: LA-CC-06–012 Los Alamos National Laboratory).

Google Scholar

Hunke E., Lipscomb W., Turner A., Jeffery N., and Elliott S. (2015). CICE: the los alamos sea ice model documentation and software user’s manual, version 5.1 (LA-CC-06-012). Los Alamos, US.

Google Scholar

Inoue J. and Hori M. E. (2011). Arctic cyclogenesis at the marginal ice zone: A contributory mechanism for the temperature amplification? Geophys. Res. Lett. 38. doi: 10.1029/2011GL047696

Crossref Full Text | Google Scholar

Johannessen J. A., Johannessen O. M., Svendsen E., Shuchman R., Manley T., Campbell W. J., et al. (1987). Mesoscale eddies in the fram strait marginal ice zone during the 1983 and 1984 marginal ice zone experiments. J. Geophys. Res.-Oceans 92, 6754–6772. doi: 10.1029/JC092iC07p06754

Crossref Full Text | Google Scholar

Josberger E. G. (1983). Sea ice melting in the marginal ice zone. J. Geophys. Res.-Oceans 88, 2841–2844. doi: 10.1029/JC088iC05p02841

Crossref Full Text | Google Scholar

Kern S., Lavergne T., Notz D., Pedersen L., Tonboe R., Saldo R., et al. (2019). Satellite passive microwave sea-ice concentration data set intercomparison: closed ice and ship-based observations. Cryosphere 13, 3261–3307. doi: 10.5194/tc-13-3261-2019

Crossref Full Text | Google Scholar

Kohout A. L., Williams M. J. M., Dean S. M., and Meylan M. H. (2014). Storm-induced sea-ice breakup and the implications for ice extent. Nature 509, 604–607. doi: 10.1038/nature13262

PubMed Abstract | Crossref Full Text | Google Scholar

Kristensen N., Debernard J., Maartensson K., Wang S., and Hedstrom K. (2017). metno/metroms: Version 0.3 - before merge (v0.3). Geneva, Switzerland. doi: 10.5281/zenodo.1046114

Crossref Full Text | Google Scholar

Kutz J. N. (2023). Machine learning for parameter estimation. PNAS 120. doi: 10.1073/pnas.2300990120

PubMed Abstract | Crossref Full Text | Google Scholar

Larson J., Jacob R., and Ong E. (2005). The model coupling toolkit: A new fortran90 toolkit for building multiphysics parallel coupled models. he Int. J. High Perform. C. 19, 277–292. doi: 10.1177/1094342005056115

Crossref Full Text | Google Scholar

Lipscomb W. and Hunke E. (2004). Modeling sea ice transport using incremental remapping. Mon. Wea. Rev. 132, 1341–1354. doi: 10.1175/1520-0493(2004)132<1341:MSITUI>2.0.CO;2

Crossref Full Text | Google Scholar

Lipscomb W., Hunke E., Maslowski W., and Jakacki J. (2007). Improving ridging schemes for high-resolution sea ice models. J. Geophy. Res.-Ocean 112, C03S91. doi: 10.1029/2005JC003355

Crossref Full Text | Google Scholar

Liu J., Scott K. A., and Fieguth P. W. (2019). Detection of marginal ice zone in synthetic aperture radar imagery using curvelet-based features: a case study on the canadian east coast. J. Appl. Remote Sens. 13, 1–14. doi: 10.1117/1.JRS.13.014505

Crossref Full Text | Google Scholar

Maslanik J., Drobot S., Fowler C., Emery W., and Barry R. (2012). On the arctic climate paradox and the continuing role of atmospheric circulation in affecting sea ice conditions. Geophys. Res. Lett. 34, 1501–1515. doi: 10.1029/2006GL028269

Crossref Full Text | Google Scholar

Maykut G. A. and Perovich D. K. (1987). The role of shortwave radiation in the summer decay of a sea ice cover. J. Geophy. Res. 92, 7032–7044. doi: 10.1029/JC092iC07p07032

Crossref Full Text | Google Scholar

Melsheimer C. (2019). ASI version 5 sea ice concentration user guide, version V0.92 (Bremen, Germany: Unversity of Bremen).

Google Scholar

Menemenlis D., Fukumori I., and Lee T. (2005). Using green’s functions to calibrate an ocean general circulation model. Monthly Weather Reviewer 133, 1224–1240. doi: 10.1175/MWR2912.1

Crossref Full Text | Google Scholar

Metzger E. J., Helber R. W., Hogan P. J., Posey P., Thoppil P., Townsend T., et al. (2017). Global ocean forecast system 3.1 validation testing, NRL/MR/7320-17-9722 (Stennis Space Center, MS: Naval Research Laboratory).

Google Scholar

Olsen J., Hovelsrud G., and Kaltenborn (2020). Increasing shipping in the arctic and local communities’ Engagement: A case from longyearbyen on svalbard (New York, US: Springer). doi: 10.1007/978-3-030-28404-614

Crossref Full Text | Google Scholar

Padman L. and Dillon T. M. (1991). Turbulent mixing near the yermak plateau during the coordinated eastern arctic experiment. J. Geophys. Res. 96, 4769–4782. doi: 10.1029/90JC02260

Crossref Full Text | Google Scholar

Palma D., Varnajot A., Dalen K., Basaran I. K., Brunette C., Bystrowska M., et al. (2019). Cruising the marginal ice zone: climate change and arctic tourism. Polar Geogr. doi: 10.1080/1088937X.2019.1648585

Crossref Full Text | Google Scholar

Posey P. G., Metzger E. J., Wallcraft A. J., Hebert D. A., Allard R. A., Smedstad O. M., et al. (2015). Improving arctic sea ice edge forecasts by assimilating high horizontal resolution sea ice concentration data into the us navy’s ice forecast systems. Cryosphere 9, 1735–1745. doi: 10.5194/tc-9-1735-2015

Crossref Full Text | Google Scholar

Rampal P., Dansereau V., Olason E., Bouillon S., Williams T., Korosov A., et al. (2019). On the multi-fractal scaling properties of sea ice deformation. Cryosphere 13, 2457—2474. doi: 10.5194/tc-13-2457-2019

Crossref Full Text | Google Scholar

Røed L. P. and O’Brien (1983). A coupled ice-ocean model of upwelling in the marginal ice zone. J. Geophys. Res. 88, 2863–2872. doi: 10.1029/JC088iC05p02863

Crossref Full Text | Google Scholar

Röhrs J., Gusdal Y., Rikardsen E., Duran Moro M., Brændshøi J., Kristensen N. M., et al. (2023). Barents-2.5km v2.0: An operational data-assimilative coupled ocean and sea ice ensemble prediction model for the barents sea and svalbard. Geosci. Model. Dev. 16, 5401–5426. doi: 10.5194/gmd-16-5401-2023

Crossref Full Text | Google Scholar

Rothrock D. (1975). The energetics of the plastic deformation of pack ice by ridging. J. Geophys. Res. Oceans 80, 4514–4519. doi: 10.1029/JC080i033p04514

Crossref Full Text | Google Scholar

Sakov P., Counillon F., Bertino L., Lisæter K. A., Oke P. R., and Korablev A. (2012). Topaz4: an ocean-sea ice data assimilation system for the north atlantic and arctic. Ocean Sci. 8, 633-656. doi: 10.5194/os-8-633-2012

Crossref Full Text | Google Scholar

Sakov P. and Oke P. (2008). A deterministic formulation of the ensemble kalman filter: an alternative to ensemble square root filters. Tellus 60A, 361–371. doi: 10.1111/j.1600-0870.2007.00299.x

Crossref Full Text | Google Scholar

Sandø A., Nilsen J., Gao Y., and Lohmann K. (2010). Importance of heat transport and local air-sea heat fluxes for barents sea climate variability. J. Geophys. Res. - Oceans 115, C07013. doi: 10.1029/2009JC005884

Crossref Full Text | Google Scholar

Shchepetkin A. F. and McWilliams J. C. (2005). The regional ocean modeling system: A split-explicit, free-surface, topography following coordinates ocean model. Ocean Model. 9, 347–404. doi: 10.1016/j.ocemod.2004.08.002

Crossref Full Text | Google Scholar

Shen H. H., Hiber W. D., and Lepparanta M. (1987). The role of floe collisions in sea ice rheology. J. Geophys. Res.-Oceans 92, 7085–7096. doi: 10.1029/JC092iC07p07085

Crossref Full Text | Google Scholar

Smedsrud L., Esau I., Ingvaldsen R., Eldevik T., Haugan P., Li C., et al. (2013). The role of the barents sea in the arctic climate system. Rev. Geophys. 51, 415–449. doi: 10.1002/rog.20017

Crossref Full Text | Google Scholar

Spreen G., Kaleschke L., and Heygster G. (2008). Sea ice remote sensing using amsr-e 89-ghz channels. J. Geophys. Res. Oceans 113, C02S03. doi: 10.1029/2005jc003384

Crossref Full Text | Google Scholar

Squire V. A. (2007). Of ocean waves and sea-ice revisited. Cold Regions Sci. Tech. 49, 110–133. doi: 10.1016/j.coldregions.2007.04.007

Crossref Full Text | Google Scholar

Squire V. A., Dugan J. P., Wadhams P., RotTier P. J., and Liu A. K. (1995). Of ocean waves and sea-ice. Annu. Rev. Fluid Mechanics 27, 115–168. doi: 10.1146/annurev.fl.27.010195.000555

Crossref Full Text | Google Scholar

Steele M. (1992). Sea ice melting and floe geometry in a simple ice-ocean model. J. Geophys. Res.-Oceans 97, 17729–17738. doi: 10.1029/92JC01755

Crossref Full Text | Google Scholar

Stephenson S. R., Smith L. C., and Agnew J. A. (2011). Divergent long-term trajectories of human access to the arctic. Nat. Climate Change 1, 156–160. doi: 10.1038/nclimate1120

Crossref Full Text | Google Scholar

Stocker A., Renner A., and Knol-Kauffman M. (2020). Sea ice variability and maritime activity around svalbard in the period 2012–2019. Sci. Rep. 10, 17043. doi: 10.1038/s41598-020-74064-2

PubMed Abstract | Crossref Full Text | Google Scholar

Strong C. (2012). Atmospheric influence on arctic marginal ice zone position and width in the atlantic sector, february–april 1979–2010. Clim. Dyn. 39, 3091–3102. doi: 10.1007/s00382-012-1356-6

Crossref Full Text | Google Scholar

Sunfjord A., Fer Y., Kasajima I., and Svendsen H. (2007). Observations of turbulent mixing and hydrography in the marginal ice zone of the barents sea. J. Geophys. Res.-Oceans 112. doi: 10.1029/2006JC003524

Crossref Full Text | Google Scholar

Thorndike A., Rothrock D., Maykut G., and Colony R. (1975). The thickness distribution of sea ice. J. Geophys. Res. 80, 4501—4513. doi: 10.1029/JC080i033p04501

Crossref Full Text | Google Scholar

Tucker W. B., Grenfell T. C., Onstott R. G., Perovich D. K., Gow A. J., Shuchman R. A., et al. (1991). Microwave and physical properties of sea ice in the winter marginal ice zone. J. Geophys. Res. 96, 4573–4587. doi: 10.1002/jgrc.20171

Crossref Full Text | Google Scholar

Turner A. K., Hunke E. C., and Bitz C. M. (2013). Two modes of sea-ice gravity drainage: A parameterization for large-scale modeling. J. Geophys. Res. Oceans 118, 2279–2294. doi: 10.1002/jgrc.20171

Crossref Full Text | Google Scholar

Vinje T. (2001). Fram strait ice flux and atmospheric circulation: 1950-2000. J. Clim. 14, 3508–3517. doi: 10.1175/1520-0442(2001)014<3508:FSIFAA>2.0.CO;2

Crossref Full Text | Google Scholar

Wang K. (2025). metroms coin v2.0: Coupled ROMS-CICE with COIN/LAON data assimilation for SIC and SST. Geneva, Switzerland. doi: 10.5281/zenodo.15433887

Crossref Full Text | Google Scholar

Wang K., Ali A., and Wang C. (2023). Local analytical optimal nudging for assimilating amsr2 sea ice concentration in a high-resolution pan-arctic coupled ocean (hycom 2.2.98) and sea ice (cice 5.1.2) model. Cryosphere. 17, 4487–4510. doi: 10.5194/tc-17-4487-2023

Crossref Full Text | Google Scholar

Wang K., Debernard J., Sperrevik A. K., Isachsen P. E., and Lavergne T. (2013). A combined optimal interpolation and nudging scheme to assimilate osisaf sea-ice concentration into roms. Ann. Glaciology 64, 8–12. doi: 10.3189/2013aog62a138

Crossref Full Text | Google Scholar

Wang K., Lavergne T., and Dinessen F. (2020). Multisensor data merging of sea ice concentration and thickness. Adv. Polar Sci. 31, 1–13. doi: 10.3189/2013aog62a138

Crossref Full Text | Google Scholar

Wang K., Wang C., Dinessen F., Spreen G., Ricker R., and Tian-Kunze X. (2024). Multisensor data fusion of operational sea ice observations. Front. Mar. Sci. 11. doi: 10.3389/fmars.2024.1366002

Crossref Full Text | Google Scholar

Warner J. C., Sherwood C. R., Arango H. G., and Signell R. P. (2005). Performance of four turbulence closure models implemented using a generic length scale method. Ocean Model. 8, 81–113. doi: 10.1016/j.ocemod.2003.12.003

Crossref Full Text | Google Scholar

Wassmann P. (2011). Arctic marine ecosystems in an era of rapid climate change. Prog. Oceanography 90, 1–17. doi: 10.1016/j.pocean.2011.02.002

Crossref Full Text | Google Scholar

Williams T., Korosov A., Rampal P., and Ólason E. (2021). Presentation and evaluation of the arctic sea ice forecasting system nextsim-f. Cryosphere 15, 3207–3227. doi: 10.5194/tc-15-3207-2021

Crossref Full Text | Google Scholar

WMO (2014). SEA ICE NOMENCLATURE. No. 259 (Geneva, Switzerland: WMO).

Google Scholar