Advancing ship automatic navigation strategy with prior knowledge and hierarchical penalty in irregular obstacles: a reinforcement learning approach to enhanced efficiency and safety

With the global wave of intelligence and automation, ship autopilot technology has become the key to improving the efficiency of marine transportation, reducing operating costs, and ensuring navigation safety. However, existing reinforcement learning (RL)–based autopilot methods still face challenges such as low learning efficiency, redundant invalid exploration, and limited obstacle avoidance capability. To this end, this research proposes a GEPA model that integrates prior knowledge and hierarchical reward and punishment mechanisms to optimize the autopilot strategy for unmanned vessels based on deep Q-network (DQN). The GEPA model introduces a priori knowledge to guide the decision-making of the intelligent agent, reduces invalid explorations, and accelerates the learning convergence, and combines with hierarchical composite reward and punishment mechanisms to improve the rationality and safety of autopilot by means of end-point incentives, path-guided rewards, and irregular obstacle avoidance penalties. The experimental results show that the GEPA model outperforms the existing methods in terms of navigating efficiency, training convergence speed, path smoothness, obstacle avoidance ability and safety, with the number of training rounds to complete the task reduced by 24.85%, the path length reduced by up to about 70 pixels, the safety distance improved by 70.6%, and the number of collisions decreased significantly. The research in this paper provides an effective reinforcement learning optimization strategy for efficient and safe autonomous navigating of unmanned ships in complex marine environments, and can provide important theoretical support and practical guidance for the development of future intelligent ship technology.

1 Introduction

With the rapid development of the global intelligent shipping industry, the safety, operational efficiency and economic cost of maritime transportation are facing serious challenges and automation technology (Wang et al., 2023b), especially ship autopilot technology, is becoming one of the key technologies to enhance shipping efficiency, ensure navigation safety (Wang et al., 2019). At present, ship navigating mainly relies on manual operation, which is easily affected by human factors such as inexperience and fatigue of crew members, leading to inefficient navigation and even safety accidents (Wang et al., 2021a). According to the research in 2023 (Transportation security), in the collection of recent years, Zhejiang, Fujian and other domestic marine accident investigation centers in recent years 306, the United Kingdom, the United States, Japan and other offshore marine accident investigation reports 198, in 504 marine accident investigation report, which triggered the cause of accidents existed in the human factor 466, accounting for as high as 92%. In order to reduce the development of ship accidents worldwide and cater to the global shipping market’s demand for efficient, safe, and low-cost navigation, the application of ship autopilot technology has become particularly urgent.

Reinforcement learning (RL), as a class of intelligent decision-making methods with autonomous learning capability, shows great potential in the field of autopilot. Its core advantage lies in the ability of bits of intelligence to autonomously explore and optimize decision-making strategies through dynamic interaction with the environment. In the framework of RL, an intelligent agent continuously obtains feedback from its interaction with the environment, selects the optimal action and adjusts its behavioral strategy based on the feedback signals (reward or punishment). The process is trial-and-error interactive, and by evaluating the current state, the intelligent agent chooses an optimal action at each decision-making moment to maximize the long-term cumulative reward. This trial-feedback-adjustment learning mechanism enables reinforcement learning to adapt to complex dynamic environments and gradually improve autonomous decision-making capabilities. Especially in the unmanned ship autopilot task, the RL method does not need to rely on preset rules, but rather learns the optimal obstacle avoidance and navigation strategies through a large number of interactions, thus improving the adaptability of the ship in uncertain environments to realize the autopilot task.

Therefore, ship autopilot technology, especially the ship autopilot technology based on RL, is gradually becoming one of the core technologies to realize this goal. RL -based ship autopilot technology enables ship intelligent agent to learn and navigate autonomously in complex environments. Through reinforcement learning, the unmanned ship’s intelligent agent can choose the optimal action (such as steering, acceleration or deceleration, etc.) according to the current state (such as the ship’s position, speed, heading angle and surrounding obstacles, etc.). However, the unmanned ship intelligent agent is not able to make the optimal decision at the beginning, but gradually optimizes the decision-making process through continuous interaction and feedback. Every time the unmanned ship intelligent agent makes an action, the marine environment provides a reward signal that reflects the effectiveness of the action. By maximizing this feedback reward, the unmanned ship intelligent agent will eventually learn decision-making strategies that can efficiently and safely complete the autopilot task in the complex marine environment. However, despite the theoretically powerful decision-making ability of the RL -based unmanned ship piloting technology, the practical application still faces many challenges, which restricts its further development in the field of ship autopilot.

Currently, the unmanned ship autopilot technology based on RL faces three core challenges: low learning efficiency and too much ineffective exploration, a single reward and punishment mechanism, which makes it difficult to effectively integrate multiple reward and punishment information, and the traditional way of modeling the marine environment is too regular and lacks effective modeling of irregular obstacles.

RL-based unmanned ship learning is inefficient with too much ineffective exploration. Since reinforcement learning relies on a large number of trial-and-error processes, unmanned ship intelligent agent needs to optimize its decision-making strategies through constant interaction with the environment. However, at the beginning of training, unmanned ship intelligent agent cannot directly determine which actions are optimal, and need to obtain rewarding or punishing feedback after many attempts, and then adjust their decisions based on this feedback. This process consumes large computational resources and converges slowly, especially in the absence of a clear environment model, the intelligent agent often experiences a lot of ineffective exploration, leading to inefficient learning.

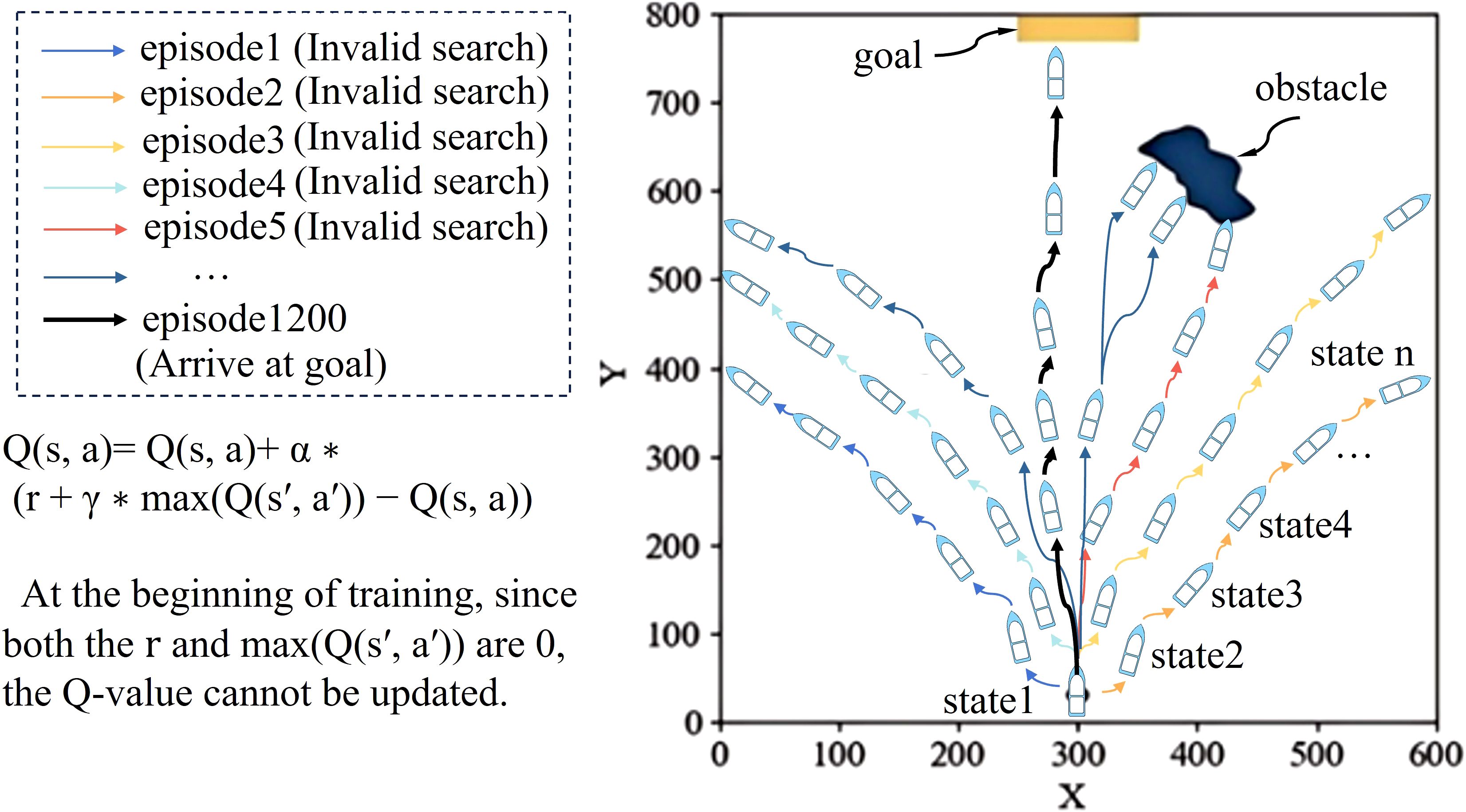
In the reinforcement learning framework, the Q-table (state-action value function table) is a crucial part of the learning process of an intelligent agent, which stores the expected rewards for performing various actions in different states and is constantly updated by the rewards or punishments from the environmental feedbacks in order to optimize the decision-making strategy. Under the reinforcement learning model of Online Learning, the update of the Q-table usually relies on the completion of the target state or the completion of the task, which means that at the beginning of the training period, the unmanned ship intelligent agents are unable to efficiently assess the quality of the actions during the exploration process, leading to a large number of ineffective explorations. Especially in complex marine environments, since the unmanned ship intelligent agent cannot obtain effective reward signals in a timely manner, the Q-table update is limited, which further prolongs the training time and makes the process computationally more costly and less efficient. Just as in Figure 1, the virtual channel environment is simulated in the figure, the x-axis and y-axis are the lateral position and vertical position of the channel, and the irregular objects in the figure simulate the irregular obstacles in the virtual channel environment. The formula in Figure 1 is the updating formula for Q-value, Q(s, a) is the Q-value of the executed action in the current state, r is the reward, γ is the discount factor, and max Q(s’, a’) is the maximum Q-value of the unmanned ship at the optimal action chosen in the next state.

Figure 1

Figure 1. Training convergence delay: Example of early-stage invalid trajectories.

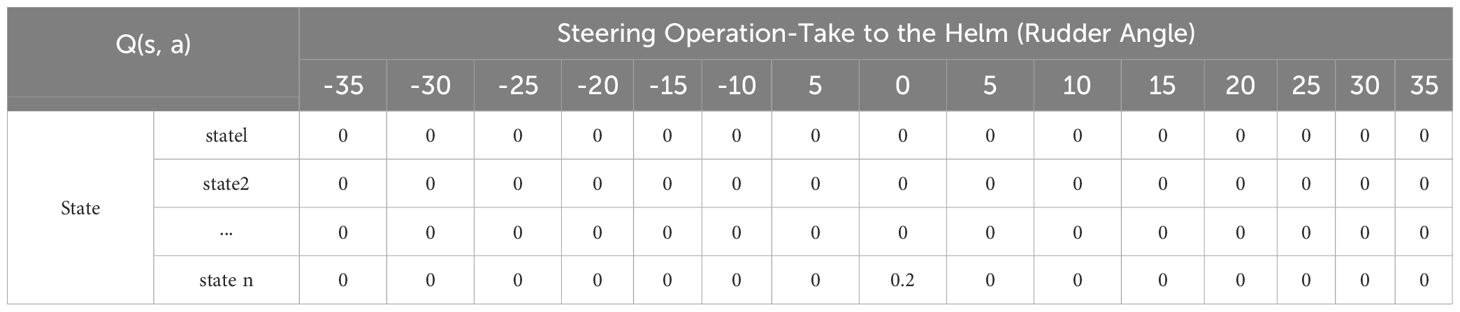
Table 1 briefly exemplifies the changes in the Q-value of the unmanned vessel during the training process, where Action is the rudder angle δ chosen by the unmanned vessel and State is the current position (horizontal and vertical coordinates) of the unmanned vessel in the channel environment. Figure 1 provides a simplified illustration showing that, during the early stages of training, the unmanned ship fails to update the Q-table effectively due to repeated episodes of unsuccessful exploration. It is not until a much later episode (e.g., Episode 1200) that the agent successfully reaches the goal for the first time, thereby triggering the initial Q-value update. The experimental results shown in Figure 1 and Table 1 indicate that the Q-value of the intelligent agent did not change in multiple rounds at the beginning of the training period (episode 1 to episode 1199), all of which were 0, indicating that it failed to obtain effective feedback from the environment. This is because the reward value r and max(Q(s’, a’) are both 0 and other values are equal, so the Q-value cannot be updated. And even in episode 5, where the intelligent agent received a penalty for colliding with an obstacle, it still failed to have a positive effect on the task optimization, and instead made the strategy adjustment more difficult. It was not until episode 1200, when the intelligent agent chose a rudder angle of 0, and the intelligent agent successfully reached the end point for the first time, that the Q-value could be updated.

Table 1

Table 1. Q-Table State-Action value mapping.

This lag in updating the Q-value significantly increases the training cost and reduces the learning efficiency. It should be noted that the values in the table are only examples to illustrate the phenomenon of Q-table update lag, and do not represent the actual values in the experiments.

To address this problem, we propose an optimization strategy that incorporates a priori knowledge to reduce ineffective exploration and speed up the training process. In the traditional manual piloting process, the crew usually relies on navigational experience to judge the environment and formulate navigation strategies, which can be regarded as a priori knowledge. In our experimental findings, the paths planned based on paths are highly similar to the optimal paths obtained from autonomous learning of unmanned vessels and thus can be used for path guidance in reinforcement learning training. For this reason, we propose to introduce a priori knowledge in reinforcement learning training so that the unmanned ship intelligent agents are equipped with preliminary navigation experience and guided by a priori paths during exploration, thus reducing the inefficient behaviors caused by random exploration. In addition, since the a priori path provides additional reward signals, the intelligent agent is able to update the Q-table before it reaches the end point, thus accelerating the strategy optimization and improving the convergence efficiency.

Although path planning algorithms can quickly generate feasible routes, it is difficult to directly use them for real navigation because their paths usually have large corners and lack of smoothness. Therefore, in this study, the a priori knowledge paths are mainly used as preliminary guidance paths for the intelligent agent, while the final optimal navigation paths still need to be generated by the unmanned intelligent agent ship to adapt to the complex marine environment.

However, the introduction of a priori knowledge alone does not sufficiently improve the adaptive ability of the unmanned vessel. The reward function design of traditional reinforcement learning methods is usually simple, relying only on end point rewards or basic obstacle avoidance penalties, failing to fully consider factors such as path optimization, local obstacle avoidance, and task execution efficiency. The limitation of this single reward and punishment mechanism not only affects the training effect of the intelligence, but also may cause the model to converge to a suboptimal solution in complex environments, which reduces navigation stability and safety. For this reason, this study further proposes a hierarchical composite reward and punishment mechanism, which integrates the end-point reward, the a priori knowledge path-guiding reward, and the hierarchical punishment of irregular obstacles, in order to optimize the navigating strategy of the unmanned ship intelligent agent. This mechanism enables the intelligent agent to obtain positive rewards when it is close to the a priori path during the training process, encouraging it to follow the efficient path; meanwhile, it imposes penalties when it is far away from the a priori path or close to the obstacles, ensuring that it can actively optimize the navigation strategy and improve the obstacle avoidance ability.

In addition, most of the traditional autopilot strategy methods are based on regularized raster modeling, which simplifies obstacles to circles or rectangles, but this is difficult to accurately simulate the irregularities of the real marine environment. For example, ships often need to cope with complex situations such as floating obstacles, dynamic target vessels, and ocean current interference in real navigation. To overcome this problem, this study introduces irregular obstacle modeling into the training environment of autopilot, so that the unmanned ship intelligent agent can adapt to the complex marine environment and improve the autonomous obstacle avoidance ability and decision-making stability. By combining the hierarchical composite reward and punishment mechanism, the modeling method not only optimizes the reasonableness of path planning but also ensures that the unmanned vessel takes into account the navigation efficiency and safety in the complex environment.

Compared to the reinforcement learning-based unmanned ship navigating method with completely random exploration, the GEPA (Guided Exploration with Prior knowledge and Adaptive Penalty) model proposed in this study, by combining prior knowledge, hierarchical composite reward and punishment (HCRP) and irregular obstacle modeling, reduces the number of invalid explorations and accelerates the speed of the Q-axis while reducing the number of obstacles. Ineffective exploration while accelerating the update speed of Q-tables, which significantly improves the efficiency of unmanned ship training based on reinforcement learning. In addition, the Hierarchical Composite Reward and Punishment (HCRP) mechanism combines end-point incentives, a priori knowledge rewards and irregular obstacle penalties, which not only optimizes the path planning and obstacle avoidance strategies but also strengthens the environmental adaptive capability of the unmanned ship intelligent agent, enabling it to achieve efficient, smooth and safe autonomous navigation in the face of the complex and uncertain marine environment. At the same time, irregular obstacle modeling further simulates the real marine environment, so that the intelligent agent has more accurate obstacle avoidance decision-making ability, and strengthens its robustness and autonomous navigation ability in the marine environment, which comprehensively improves the decision-making efficiency and adaptability of the autopilot system.

In this study, an autopilot strategy for irregular obstacle ships based on prior knowledge and hierarchical penalization is proposed, and the main contributions are as follows:

● This work incorporates prior trajectory information as a guiding signal in the reinforcement learning process, effectively improving training efficiency and reducing redundant exploration in the early stages of learning.

● We propose a novel hierarchical reward and penalty design that integrates goal-oriented incentives with obstacle-aware punishment, fostering safer and more stable decision-making under complex navigation constraints.

● The model integrates an irregular obstacle avoidance strategy, significantly improving its adaptability and enabling unmanned ships to operate reliably in complex and uncertain maritime environments.

The remainder of this paper is structured as follows. Section 2 reviews recent advancements in reinforcement learning–based autonomous navigation, classical path planning techniques, and irregular obstacle avoidance strategies, highlighting the existing challenges and motivating the proposed approach. Section 3 details the architecture of the proposed GEPA framework, including the agent structure, virtual channel environment, formal definition of prior knowledge, and the formulation of a hierarchical composite reward and penalty mechanism. The section also presents the reinforcement learning pipeline for training the unmanned ship. Section 4 presents comprehensive experimental evaluations encompassing the experimental configuration, virtual scenario design, and quantitative analysis of navigation performance, including training efficiency, path smoothness, trajectory length, safety margin, and collision frequency. Finally, Section 5 concludes the paper by summarizing the key contributions and outlining future research directions, particularly focusing on the extension of GEPA to dynamic maritime environments.

2 Related works

The global maritime industry is facing increasing demands for safety, operational efficiency, and cost control (Wang et al., 2020). Unmanned ship autonomous navigating technology is regarded as a key solution to these challenges, as it optimizes decision-making processes and reduces human errors, thereby enhancing operational safety and efficiency (Mnih et al., 2015). This section reviews the research progress of reinforcement learning (RL) in the field of autonomous ship navigating.

Deep Q-Network (DQN) have emerged as a powerful tool for autonomous navigating, including applications in unmanned ship autonomous control. DQN integrates Q-learning with deep neural networks, enabling intelligent agents to make decisions in high-dimensional state spaces, which is particularly beneficial in complex maritime environments (Mnih et al., 2015). first introduced DQN and achieved significant success in solving Atari game control tasks, demonstrating the potential of deep reinforcement learning in handling decision-making problems involving large-scale state spaces (Wen et al., 2022). proposed a multi-agent deep reinforcement learning (MADRL) approach to optimize dynamic obstacle avoidance and task execution strategies for unmanned surface vehicles (USVs) (Wang et al., 2022). applied artificial neural networks (ANNs) to improve trajectory planning, enabling USVs to autonomously adjust course in complex environments and achieve efficient collision avoidance (Gao et al., 2023). further improved the deep Q-learning algorithm, constructing an adaptive decision-making model and validating the adaptability and effectiveness of DQN under various marine conditions.

In the field of autonomous ship navigating, DQN has been widely applied to trajectory optimization and obstacle avoidance. For instance (Guo et al., 2020), proposed a DQN-based autonomous decision-making approach, allowing unmanned ships to dynamically adjust course and achieve real-time obstacle avoidance. Compared to traditional trajectory planning algorithms, DQN-based methods leverage reinforcement learning mechanisms, enabling autonomous ships to dynamically adjust movements, improving their ability to adapt to unpredictable environments. Furthermore, DQN-based approaches have been extended to more complex operational scenarios, such as crowded waters and irregular obstacles. The study by (Guo et al., 2020) demonstrated that DQN can derive navigating strategies directly from sensor data without relying on predefined environmental models, making it highly suitable for dynamic and uncertain marine environments (Yang and Han, 2023). further extended DQN’s application to collision avoidance in dynamic environments, introducing optimized parameter tuning methods to enhance the system’s capability to handle both static and moving obstacles.

The design of reward and penalty functions plays a crucial role in reinforcement learning (RL), particularly in unmanned ship autonomous navigating. Traditional reinforcement learning models often rely on simplistic reward structures, which may be insufficient for operating in complex marine environments. To address this challenge, researchers have introduced hierarchical and soft-constraint reward mechanisms to enhance learning efficiency and decision-making capabilities (Singh et al., 2020). proposed a multiagent reinforcement learning (MARL) framework incorporating a multi-level reward structure, guiding autonomous ships to optimize long-term decision-making objectives while ensuring collision avoidance safety. Similarly (Wang et al., 2023a), integrated prior knowledge-based approximation representations into deep reinforcement learning (DRL), improving decision-making capabilities in collision avoidance. To better tackle real-world maritime challenges, several studies have introduced hierarchical reward mechanisms for collision avoidance and trajectory optimization (Yang and Han, 2023). enhanced DQN by incorporating a multi-stage reward system, which assigns different penalty levels based on proximity to obstacles and deviation from the optimal trajectory (Guo et al., 2021). further refined the DQN reward function to better suit coastal waters, ensuring smoother autonomous navigating (Jiang et al., 2024). explores the effect of the reward function on ship (Li et al., 2025)introduces the Multi-Joint Adaptive Control Enhanced Reinforcement Learning System that enhances the autonomous stability of unmanned ship navigation in maritime settings.

Another key innovation involves integrating dynamic risk assessment into reward mechanisms (Zhang et al., 2019). proposed a scenario-based DRL model, classifying environments into different risk levels and adjusting the reward system accordingly (Shen et al., 2017). extended this approach by designing a DQN-based autonomous collision avoidance strategy, which dynamically adjusts penalties to ensure safe maneuvering in congested waters (Chen et al., 2025). proposed a bi-directional GRU-based reconstruction approach to recover missing AIS trajectory data. This method demonstrated robust performance and substantially increased the reliability of training datasets used for autonomous navigation models (Wang et al., 2021b). introduced a data-driven reinforcement learning control strategy tailored to complex marine environments. This method transformed constrained tracking errors into an unconstrained error stability problem under unknown dynamic conditions, thereby improving system adaptability (Liang et al., 2024). proposed a method combining a Wasserstein GAN with gradient penalty (WGAN-GP) and a trajectory encoder to detect abnormal vessel behaviors without manual annotation (Zhang et al., 2020). developed a model reference reinforcement learning approach incorporating classical control methods, allowing USVs to flexibly adjust control strategies based on strategic requirements in uncertain environments (Sun et al., 2020). proposed a deep deterministic policy gradient (DDPG)-based reinforcement learning algorithm for autonomous underwater vehicles (AUVs), integrating six-degree-of-freedom error accumulation to introduce soft penalty constraints, ensuring stability and precision in intelligent control systems (Du et al., 2022). designed a safe deep reinforcement learning adaptive control scheme, incorporating soft tracking rewards and interception reward constraints to optimize USV decision-making in interception tasks.

Hierarchical reward functions also enhance the generalization capability of reinforcement learning strategies. Rejaili and (Figueiredo and Abou Rejaili, 2018) explored how deep reinforcement learning algorithms can adapt to restricted waters by modifying reward structures (Lin et al., 2023). introduced distributed reinforcement learning to improve the robustness of USV autonomous decision-making, where a hierarchical reward mechanism helps the intelligent agent differentiate between short-term and long-term objectives. Researchers have also applied hierarchical reward mechanisms to energy efficiency optimization (Etemad et al., 2020). used reward shaping techniques to optimize fuel consumption while ensuring a smooth trajectory. Similarly (Alam et al., 2023), proposed a DRL model that balances speed control and trajectory efficiency, assigning different reward levels based on operational priorities.

In unmanned ship trajectory optimization, Rapidly-Exploring Random Tree (RRT) algorithms have been widely employed due to their efficient path-searching capabilities. RRT is particularly useful for operating in environments containing obstacles. For instance (Hu et al., 2025), proposed a heuristic RRT algorithm to enhance trajectory optimization in dynamic obstacle environments. Similarly (Shen et al., 2017), developed an RRT-based adaptive collision avoidance system, integrating deep reinforcement learning to optimize trajectory-following strategies, demonstrating how prior environmental knowledge can be utilized to avoid unexpected obstacles (Liang et al., 2021). proposed an unsupervised learning approach using a convolutional autoencoder (CAE) to extract low-dimensional features from AIS trajectory images, enabling fast and accurate similarity computation (Wang et al., 2021c). brought up the importance of guidance information for ships This method improves trajectory clustering performance and offers valuable support for trajectory learning and decision-making in RL-based autonomous ship navigation.

The collision avoidance strategy for irregular obstacles remains one of the core challenges in autonomous ship navigating, as real-world maritime environments often feature unpredictable and dynamically evolving obstacles. Due to variations in the shape, size, and movement patterns of obstacles, traditional reinforcement learning (RL) methods encounter significant difficulties in achieving effective obstacle avoidance.In recent years, researchers have concentrated on enhancing Deep Q-Network (DQN) algorithms and related RL models to improve the safety and maneuverability of autonomous ships operating in complex marine conditions (Ly et al., 2024). introduced Elastic Step DQN, a novel multi-step algorithm designed to mitigate DQN’s overestimation problem while enhancing its responsiveness to irregular obstacles. Similarly (Sivaraj et al., 2022), applied a DQN-based ship heading control method in both calm and turbulent waters, demonstrating that an optimized reward structure significantly improved the vessel’s obstacle avoidance capabilities in highly irregular maritime conditions.Another critical approach focuses on modifying the reward function to enhance adaptability in irregular obstacle environments (Guo et al., 2021). introduced an optimized DQN-based path-planning model with a customized reward function, enabling the reinforcement learning agent to prioritize avoidance strategies for obstacles of varying shapes.

Additionally, integrating reinforcement learning with prior knowledge has proven to be an effective method for improving obstacle avoidance capabilities in autonomous ships. For instance (Gu et al., 2023), proposed an improved RRT algorithm that leverages AIS prior information and DP compression, allowing the system to more accurately predict and avoid irregular obstacles. Likewise (Cao et al., 2022), developed an enhanced RRT-based path-planning model for inland vessels, significantly improving efficiency in ship identification and unexpected obstacle avoidance.Furthermore, hybrid methodologies have been explored to optimize autonomous ship trajectory planning (Xie and Li, 2020). combined RRT with a genetic algorithm (GA) to generate an optimal path that effectively accounts for irregular obstacles, offering a more adaptive approach to autonomous navigating (Li et al., 2022). further investigated RRT-based unmanned ship trajectory planning, ensuring enhanced adaptability in complex real-world marine environments.

In recent years, reinforcement learning has made significant advancements in autonomous ship navigating. Algorithms such as DQN have enabled intelligent agents to learn optimal decision-making strategies within high-dimensional state spaces, thereby enhancing environmental adaptability. However, current research still faces limitations in training efficiency, reward function design, and obstacle avoidance capabilities. Traditional reinforcement learning approaches rely on random exploration, leading to slow convergence and difficulties in meeting real-time operational requirements. Additionally, existing reward mechanisms are often simplistic, typically relying on terminal rewards or basic obstacle avoidance penalties, failing to balance trajectory optimization, local obstacle avoidance, and global task execution efficiency. Furthermore, current reinforcement learning models lack effective frameworks for modeling irregular obstacles, limiting collision avoidance performance in real-world maritime environments.

To address these challenges, this study proposes the GEPA (Guided Exploration with Prior Knowledge and Adaptive Penalty) model, incorporating innovations in prior knowledge guidance, hierarchical composite reward mechanisms, and irregular obstacle modeling. By integrating RRT-generated trajectories as prior knowledge, the GEPA model guides intelligent agents to reduce ineffective exploration, accelerate reinforcement learning convergence, and improve training efficiency. Compared to existing approaches, the GEPA model achieves notable improvements in reinforcement learning training efficiency, trajectory optimization, and obstacle avoidance accuracy, providing a more efficient and reliable solution for autonomous ship navigating in complex environments.

3 Model architecture

3.1 GEPA model architecture

The GEPA model proposed in this study, an unmanned ship autonomous navigating training framework based on deep Q-network (DQN) reinforcement learning, combines a first-order Nomoto motion model, a hierarchical composite rewards and penalties mechanism, and a virtual ocean environment, to optimize the navigating strategy of an unmanned ship intelligent agent, and to improve the efficiency of the training and the safety of navigation. The model includes an Agent Module, Virtual Channel Environment, and Hierarchical Composite Rewards and Penalties, which work together to ensure that the unmanned ship intelligent agent is able to the dules work together to ensure that the unmanned ship intelligent agent can gradually learn the optimal decision-making strategy in the complex environment, and the model diagram is shown in Figure 2.

Figure 2

Figure 2. The GEPA model architecture.

During the training process, the unmanned ship intelligent agent (Agent Module) first initializes its state in the virtual channel environment, obtaining its own position (x,y), heading angle ψ, speed v, and information about the surrounding obstacles. Subsequently, the intelligent agent selects the current action and updates the state under the constraints of the first-order Nomoto motion model to simulate the real navigation process of the ship. When the intelligent agent executes the action, the environment feeds back the new state and calculates immediate rewards based on the Hierarchical Composite Rewards and Penalties (Hierarchical Composite Rewards and Penalties) mechanism. Among them, the Hierarchical

Goal Convergence Incentive Reward encourages the unmanned vessel to approach the goal point step by step to accelerate the training convergence; the Prior Trajectory Guidance Reward utilizes the a priori knowledge of the path and provides additional rewards when the intelligent agent approaches the path, thus reducing ineffective exploration and accelerating the Q-table update speed; Hierarchical Irregular Obstacle Avoidance Penalty (HIOAP) makes the unmanned ship approach the curvature boundary of the irregular obstacle and applies progressive penalties to motivate the intelligent agent to actively avoid obstacles.

During the iterative optimization process of reinforcement learning, the intelligent agent stores historical decision trajectories through the experience playback mechanism and updates the Q-table using the DQN neural network to improve policy stability and generalization ability. After several rounds of training, the intelligent agent gradually learns to efficiently plan navigation paths in dynamic environments and has the ability to autonomous obstacle avoidance against complex irregular obstacles. Ultimately, the training framework enables the unmanned vessel to drive autonomously in complex marine environments, taking into account navigation efficiency, path smoothness and safety.

3.2 Agent module

In this study, we build upon the research methodology of (Chen et al., 2019) and utilize the firstorder Nomoto model to simulate the dynamic characteristics of unmanned ship, providing support for the reinforcement learning-based intelligent ship agent system. The Nomoto model, known for its simplicity and effectiveness, has been widely applied in maritime research, as it accurately characterizes the maneuverability and dynamic behavior of ships, offering a theoretical foundation for the development of autonomous ship navigating systems.

Through this motion model, the intelligent agent can obtain real-time dynamic information, such as position, heading, and velocity, within a simulation environment and make optimized control decisions based on this data. The model incorporates key parameters, including spatial coordinates, velocity, heading angle, rudder angle, yaw rate, turning ability, and lag factor, to replicate the dynamic behavior of ships. By integrating these factors, the first-order Nomoto model provides a simplified yet effective framework for simulating ship dynamics in autonomous navigating applications.

To facilitate the description of the position of the unmanned ship, an XOY coordinate system is established, where the X-axis coordinates denote the transverse position of the unmanned ship, the Y-axis coordinates denote the longitudinal position of the unmanned ship, and the heading angle is denoted by ψ. In addition, the rudder angle δ denotes the steering rudder angle, as shown in Figure 3.

Figure 3

Figure 3. The first order Nomoto ship model.

According to the first-order NOMOTO model, the position and heading of the unmanned vessel are updated using Equations 1, 2, which are given as follows:

$\begin{array}{ll}\{\begin{array}{l}{x}_{k+1}=x_k+v·\text{sin }\psi ·\text{Δ}t\hfill \\ y_{k+1}=y_k+v·\text{cos }\psi ·\text{Δ}t\hfill \end{array}& (1)\end{array}$

$\begin{array}{ll}\text{Δ}\phi =K{\delta }_k(t-T·e^{-t/T})& (2)\end{array}$

where the position variables x_k and y_k denote the lateral and vertical positions of the unmanned vessel at time k, respectively.

During the update process, the ship’s transverse position $x_k$ and longitudinal position $y_k$ are used to compute the transverse position $x_{k+1}$ and longitudinal position $y_{k+1}$ at the next moment based on the current heading angle $\psi$, velocity $v$, and time step $\text{Δ}t$. Meanwhile, the rate of change of heading angle $\text{Δ}\phi$ is computed by the NOMOTO equation, which combines the rudder angle ${\delta }_k$ with the steering lag coefficient $T$ and steering capacity coefficient $K$, describing the effect of rudder angle change on yaw rate and its response lag. By multiplying the yaw rate with the time step $\text{Δ}t$, it is possible to estimate the ship’s displacement in both the transverse and longitudinal directions, thus updating the ship’s position.

3.3 Virtual channel environment

In order to realize effective ship autopilot simulation, several virtual channel environments are constructed, in which several irregular obstacles are randomly distributed to simulate the obstacles in real navigation such as islands and reefs. The virtual environments developed using Tkinter can dynamically display the interaction between the ship and the obstacles to further enhance the decision-making ability of the intelligent agent in complex environments. The real and virtual environments are shown in Figure 4.

Figure 4

Figure 4. Real and virtual environment.

3.4 Definition of prior knowledge

Prior knowledge refers to pre-acquired environmental information and expert experience (Du et al., 2005). During the training process of unmanned ship, we utilize pre-generated paths from path planning algorithms as prior knowledge for the unmanned ship. This pre-established experience serves as guidance in the early stages of training and as a reference, thereby reducing ineffective exploration and accelerating the convergence of reinforcement learning.

In this study, we utilize trajectories generated by the Rapidly-Exploring Random Tree (RRT) algorithm as the source of prior knowledge. RRT is particularly well-suited for this purpose due to its ability to efficiently generate feasible and collision-free paths in complex, constrained environments, making it an ideal choice for generating initial reference paths in maritime scenarios. However, it is important to clarify that the core objective of introducing prior trajectories is not to emphasize the superiority of any specific path planning algorithm. Rather, the primary role of the prior trajectory is to serve as a form of experiential guidance, allowing the RL agent to navigate more efficiently during the early stages of learning. This guidance reduces random exploration, ultimately accelerating the learning convergence process.

While we have chosen RRT for this study, it is worth noting that other classical path planning algorithms—such as A* or Dijkstra—can equally be used as sources of prior knowledge. As long as these algorithms can generate reasonable and feasible trajectories, they can effectively guide the early exploration phase of the RL agent, providing the same benefits in terms of training efficiency.

It should also be noted that since RRT is inherently designed to work with regular, well-defined obstacle geometries, we adopted a rectangular simplification method to approximate irregular obstacles during the RRT path generation process. Specifically, the outermost points of each irregular obstacle were used to enclose it within a bounding rectangle to facilitate compatibility with RRT and ensure efficient path planning. However, this simplification was applied only during the prior path generation phase. In the actual training and navigation process governed by reinforcement learning, the agent interacts with and avoids the true, irregular obstacle boundaries, thereby preserving the realism and complexity of the simulated maritime environment.

3.5 Hierarchical composite rewards and penalties

3.5.1 Hierarchical goal convergence incentive and prior trajectory guidance reward

In autonomous ship navigating systems, efficiency is reflected not only in the vessel’s ability to successfully complete tasks but also in achieving them within the shortest time and with minimal energy consumption.

Inspired by (Yu et al., 2023), this study designs the Hierarchical Goal Convergence Incentive (HGCI) and Prior Trajectory Guidance Reward (PTGR) to guide Unmanned ship intelligent agent along optimal paths efficiently through well-structured rewards. The reward function incorporates prior knowledge paths, those generated by the RRT algorithm, enabling the intelligent agent to rapidly identify and select the most reasonable navigating trajectory. The reward function is designed as in Equations 3–8, which are given as follows:

$\begin{array}{ll}n=\{\begin{array}{ll}a,\hfill & L<\frac{H}{3}\hfill \\ b,\hfill & \frac{H}{3}\le L\le \frac{2H}{3}\hfill \\ c,\hfill & \frac{2H}{3}\le L\le H\hfill \\ d,\hfill & L\ge H\hfill \end{array}& (3)\end{array}$

$\begin{array}{ll}path=\text{min }\left[\sqrt{{(x-x_{{\text{path}}_j})}^2+{(y-y_{{\text{path}}_j})}^2},j\in \left\{1,\dots ,J\right\}\right]& (4)\end{array}$

$\begin{array}{ll}\text{Δ}{h}_t=\sqrt{{(x-x_{\text{path}})}^2+{(y-y_{\text{path}})}^2}& (5)\end{array}$

$\begin{array}{ll}L=\sqrt{{(x-x_{\text{star}})}^2+{(y-y_{\text{star}})}^2}& (6)\end{array}$

$\begin{array}{ll}H=y_{\text{goal}}-y_{\text{star}}& (7)\end{array}$

$\begin{array}{ll}{R}_t=\frac{n}{{(\Delta h_t)}^2}& (8)\end{array}$

In the reward function, x and y are the horizontal and vertical positions of the ship, L is the Euclidean distance of the ship from the end point, and H is the vertical distance from the end point to the starting point of the ship. The path of prior knowledge is generated by points, so there are many paths. $x_{\text{path}}$ and $y_{\text{path}}$ are the horizontal and vertical coordinates of the points on the RRT path closest to the ship. The reward function R_t is the Hierarchical Goal Convergence Incentive and Prior Trajectory Guidance Reward that we propose.

In the reward function, x and y are the horizontal and vertical positions of the ship, L is the Euclidean distance of the ship from the end point, and H is the vertical distance from the end point to the starting point of the ship, the path of prior knowledge is generated by points, so there are many paths and are the horizontal and vertical coordinates of the points on the RRT path closest to the ship, and that is the ship is the Hierarchical Goal Convergence Incentive and Prior Trajectory Guidance Reward that we propose. Hierarchical Goal Convergence Incentive and Prior Trajectory Guidance Reward.

3.5.2 Hierarchical irregular obstacle avoidance penalty

Safety is a critical factor in autonomous ship navigating, as ensuring collision avoidance with obstacles and channel boundaries is paramount to achieving a safe and efficient voyage. To address this fundamental safety requirement, we propose the Hierarchical Irregular Obstacle Avoidance Penalty (HIOAP), a reinforcement learning-based penalty mechanism designed to guide Unmanned ship intelligent agent in making effective obstacle avoidance decisions in irregular environments. By incorporating a refined hierarchical penalty structure, this mechanism enables autonomous vessels to navigate complex maritime conditions more safely and reliably. The penalty function is formulated as in Equations 9, 10, which are given as follows:

$\begin{array}{ll}{d}_i=\text{min }\left(\sqrt{{(x-x_{iϵ})}^2+{(y-y_{iϵ})}^2}\right),i\in \left\{1,\dots ,i\right\}& (9)\end{array}$

$\begin{array}{ll}{r}_{tc}=-\frac{N}{{(d_i)}^2}& (10)\end{array}$

where d_irepresents the Euclidean distance between the vessel and the center of the nearest obstacle, N is a hyperparameter used to adjust the penalty intensity, and i depends on the number of obstacles.

Different from traditional collision avoidance methods based on regular boundaries, this study adjusts the asymmetry and complex boundary shape of irregular obstacles. When calculating collision avoidance path, the unmanned ship agent not only considers the center point distance of the nearest obstacle, but also senses the curvature and shape of the boundary of irregular obstacles in real time, and avoids obstacles by combining the curvature boundary characteristics of irregular obstacles.

The hierarchical collision avoidance strategy introduced in this study employs a progressive penalty mechanism, in which the penalty value increases non-linearly as the autonomous vessel approaches an irregular obstacle. This mechanism allows the Unmanned ship intelligent agent to autonomously adjust its heading to prevent entering high-risk zones. Experimental results demonstrate that this approach significantly improves the accuracy of collision avoidance decision-making, thereby enhancing the ability of unmanned vessels to avoid obstacles in complex marine environments. Furthermore, in comparison to traditional methods that assume regularized boundary conditions, this approach demonstrates greater adaptability to irregular obstacles with asymmetric and intricate morphologies, leading to improved stability and maneuverability in autonomous ship navigating.

By integrating the Hierarchical Goal Convergence Incentive (HGCI), Prior Trajectory Guidance Reward (PTGR), and the Hierarchical Penalty Function for Irregular Obstacle Avoidance (HIOAP), this study proposes a comprehensive hierarchical reward and penalty mechanism aimed at optimizing reinforcement learning-based autonomous ship navigating. This mechanism establishes a balance between safety and efficiency, ensuring that unmanned vessels are encouraged to follow optimal paths efficiently while simultaneously being penalized for approaching obstacles. Ultimately, this hierarchical composite reward and penalty mechanism enables autonomous ships to make smarter decisions, effectively adapt to varied complex environments, and enhance their operational performance in real-world maritime applications.

3.6 Training of unmanned ship intelligent agent based on reinforcement learning

The GEPA model proposed in this study, an unmanned training framework based on deep Q-network (DQN) reinforcement learning, combines a first-order Nomoto motion model, a hierarchical composite rewards and penalties mechanism and a virtual ocean environment to optimize the path planning and obstacle avoidance strategies of the intelligent agent, and to improve the efficiency of the training and navigation safety. The model includes an Agent Module, a Virtual Channel Environment Module and a Hierarchical Composite Rewards and Penalties Module, which work together to enable the intelligent agent to gradually learn the optimal decision-making strategy in a complex marine environment. The modules work together to enable the intelligent agent to gradually learn the optimal decision-making strategy in the complex marine environment and realize efficient and stable autonomous navigating.

Prior to training, a path planning algorithm is used to plan a priori knowledge paths and a reward and penalty function is used to assign rewards to a priori knowledge paths. Then, during training, the unmanned ship intelligent agent (Agent Module) first initializes its state in a virtual channel environment, obtaining information about its own position (x, y), heading angle (ψ), velocity (v), and surrounding obstacles. The state of the surface boat is passed as input information to the Deep Q Network (DQN). The DQN network outputs a Q-value for each possible action based on the current state, which reflects the expected cumulative reward for selecting a particular action in that state. The intelligent agent selects the action with the highest Q-value and chooses the optimal rudder angle δ as the execution action based on ∈-greedy. Subsequently, the intelligent agent updates the position and heading angle based on the first-order Nomoto motion model to simulate the actual ship dynamic response and performs the sailing operation in the virtual marine environment, thus realizing autopilot.

The training core of reinforcement learning lies in dynamic optimization based on environmental feedback. After the intelligent agent executes an action, the environment calculates an immediate reward based on a hierarchical composite reward and punishment mechanism, which includes an endpoint proximity reward, an a priori path guidance reward, and an irregular obstacle avoidance penalty. The end-point proximity reward guides the intelligent agent to navigate efficiently toward the target point and is enhanced as the distance to the target is shortened; the a priori path-guided reward is based on the path generated by the rapid exploration random tree (RRT), which enables the intelligent agent to optimize its travel along the existing paths, reduces the ineffective exploration, and speeds up the update of the Q-table; and the irregular obstacle avoidance penalty not only performs obstacle avoidance based on the distance of the intelligent agent from the center of the obstacles but also combines The irregular obstacle avoidance penalty is not only based on the distance between the intelligent agent and the center of the obstacle but also combines with the curvature information of the obstacle boundary to adjust the obstacle avoidance strategy and impose progressive penalties, so as to optimize the autonomous obstacle avoidance capability and ensure navigation safety.

The strategy of the intelligent agent can be expressed as a function π(s), where s is the current state of the environment. The intelligent agent updates the strategy at each time step by interacting with the environment, using the time difference (TD) error and the Bellman equation to optimize the decision-making process. The Bellman equation is Equation 11.

$\begin{array}{ll}Q(s,a)=Q(s,a)+\alpha [r+\gamma \text{max }Q(s^{\prime },a^{\prime })-Q(s,a)]& (11)\end{array}$

where Q(s,a) represents the Q-value for state-action pair (s,a), r is the immediate reward, γ is the discount factor, $s^{\prime }$ is the next state, $a^{\prime }$ is the next action, α is the learning rate.

During the training process, the DQN intelligent agent collect state-action-reward-next-state experiences by interacting with the virtual channel environment. These experiences are stored in the experience playback buffer M, which facilitates the intelligentsia to sample batches of experiences to update the network parameters. The intelligent agent samples experience batches from the playback buffer and use these experiences to update the network weights and minimize the difference between the predicted Q-value and the target value derived from the Bellman equation. During training, the target Q network is updated every C rounds to improve the learning stability, while the exploration rate decay strategy (ϵ-decay) is used to gradually reduce the random exploration behaviors so that the intelligent agent is more inclined to select high-return actions in the later stages of training and accelerate the convergence.

Through this training framework, the unmanned ship intelligent agent of the GEPA model gradually learns the optimal unmanned ship piloting strategy, which enables it to perform autopilot efficiently in the virtual marine environment. The unmanned ship intelligent agent can not only avoid collision with obstacles, but also realize rapid navigation route planning and path adjustment, improve task completion efficiency, and adapt to different marine scenarios.

The GEPA model constructs an optimized training framework for autonomous navigating of unmanned vessels for autopilot control of unmanned vessels by integrating DQN reinforcement learning, first-order Nomoto motion model, hierarchical composite reward and punishment mechanism, and irregular obstacle modeling. The method combines the powerful adaptability of deep reinforcement learning with the high-precision simulation of the ship dynamic model, which can provide solid theoretical support and technical guarantee for the autonomous ship navigating technology in practical applications. Eventually, the unmanned ship will be able to navigate efficiently and safely in real marine environments, which provides an important reference and reference significance for the development and application of future unmanned vessels. The pseudo-code is as follows during the training process, the DQN intelligent agents collect state-action-reward-next-state experiences by interacting with the virtual airway environment. These experiences are stored in the experience playback buffer M, which facilitates the intelligentsia to sample batches of experiences to update the network parameters. The intelligent agent samples experience batches from the playback buffer and use these experiences to update the network weights and minimize the difference between the predicted Q-value and the target value derived from the Bellman equation. During training, the target Q network is updated every C rounds to improve the learning stability, while the exploration rate decay strategy (ϵ-decay) is used to gradually reduce the random exploration behaviors so that the intelligent agent is more inclined to select high-return actions in the later stages of training and accelerate the convergence.

Through this training framework, the unmanned ship intelligent agent of the GEPA model gradually learns the optimal unmanned ship piloting strategy, which enables it to perform autopilot efficiently in the virtual marine environment. The unmanned ship intelligent agent can not only avoid collision with obstacles, but also realize rapid navigation route planning and path adjustment, improve task completion efficiency, and adapt to different marine scenarios.

The GEPA model constructs an optimized training framework for autonomous navigating of unmanned vessels for autopilot control of unmanned vessels by integrating DQN reinforcement learning, first-order Nomoto motion model, hierarchical composite reward and punishment mechanism, and irregular obstacle modeling. The method combines the powerful adaptability of deep reinforcement learning with the highprecision simulation of the ship dynamic model, which can provide solid theoretical support and technical guarantee for the autopilot surface boat system in practical applications. Eventually, the system will be able to navigate efficiently and safely in real marine environments, which provides an important reference and reference significance for the development and application of future unmanned vessels. The pseudo-code of the proposed GEPA model is illustrated in Algorithm 1.

Algorithm 1. RL-based GEPA model for autonomous ship navigation.

4 Experimental analysis

4.1 Basic parameters of the experiment

In this section, we experimentally evaluate a ship irregular obstacle autopilot model based on prior knowledge and hierarchical punishment. We develop three models by combining hierarchical composite reward and punishment functions with deep Q-network: the primary model (GEPA) and the secondary models (GEPA-HG, GEPA-HVG). As a comparative benchmark, we replicated the ADF model proposed by (Chen et al., 2019), which only considers collision penalties and rewards for reaching the end point. In addition, to further validate the modeling capability, we also replicated the CurrenT-Nav model by (Du et al., 2022). Through comparative analysis, we provide insights into the performance of each model in different environments, especially the navigating ability and safety in complex and irregular obstacle courses.

ADF (Baseline Model): As the most basic reinforcement learning model for unmanned boats, this baseline model only contains simple endpoint rewards and obstacle penalties, the reward mechanism is relatively basic, and does not have a priori knowledge or hierarchical reward structure.

CurrenT-Nav (Baseline Model): Compared with the ADF model, CurrenT-Nav further introduces a dynamic composite reward mechanism and optimizes the reward structure to enhance the model’s adaptability in complex environments, and serves as a baseline model for comparison experiments. However, the dynamic reward value of this model is large and not in the same order of magnitude as the rewards of the other models, so this study only uses it for navigation ability assessment.

GEPA: (Our Model), this model carries a comprehensive set of hierarchical composite reward and punishment mechanisms, including Hierarchical Goal Convergence Incentive (HGCI), Prior Trajectory Guidance Reward (PTGR), and Irregular Obstacle Avoidance Hierarchical Punishment Function (HIOAP), in order to optimize the autopilot and obstacle avoidance strategies, and to improve the training efficiency and navigational safety of unmanned vessels.

GEPA-HG (Our Model - Variant 1): Horizontal Hierarchical Reward Model for Piloting Strategies with A Priori Knowledge, this variant uses a priori trajectory-inspired rewards, whose reward value is based on the horizontal distance of the unmanned vessel from the path of the a priori knowledge, which is different from the hierarchical goal-convergent incentives based on the Euclidean distance computation of the GEPA model (HGCI) and the a priori trajectory-guided rewards (PTGR). The reward function is designed as in Equations 12–14.

GEPA-HVG (Our Model - Variant 2): Horizontal Vertical Hierarchical Reward Model for Navigating Strategies with Prior Knowledge This variant carries both hierarchical goal incentive rewards and a priori trajectory incentive rewards. In this variant, the hierarchical target incentive is based on the vertical distance between the target point and the starting point, instead of the Euclidean distance calculation in the GEPA model. Meanwhile, the a priori trajectory incentive reward is still calculated based on the horizontal distance between the unmanned ship and the a priori knowledge path. The incentive function is designed as in Equations 15–19. The GEPA-HG incentive function formula is as follows:

$\begin{array}{ll}path=\text{min }\left(\left(x-x_{{\text{path}}_j}\right),j\in \left\{1,\dots ,J\right\}\right)& (12)\end{array}$

$\begin{array}{ll}\text{Δ}{h}_t=x-x_{\text{path}}& (13)\end{array}$

$\begin{array}{ll}{R}_t=\frac{\beta }{{(\Delta h_t)}^2}& (14)\end{array}$

where x is the horizontal position of the ship, $x_{{\text{path}}_j}$is the horizontal position of the point of the j-th path, the path is the point with the closest prior knowledge to the horizontal position of the ship, $x_{\text{path}}$ is the horizontal distance between the ship and the point of the path. The GEPA-HVG reward function is formulated as follows:

$\begin{array}{ll}\mu =\{\begin{array}{ll}e,\hfill & y<\frac{H}{3}\hfill \\ f,\hfill & \frac{H}{3}\le y\le \frac{2H}{3}\hfill \\ g,\hfill & \frac{2H}{3}\le y\le H\hfill \\ h,\hfill & y\ge H\hfill \end{array}& (15)\end{array}$

$\begin{array}{ll}path=\text{min }\left(\left(x-x_{{\text{path}}_j}\right),j\in \left\{1,\dots ,J\right\}\right)& (16)\end{array}$

$\begin{array}{ll}\text{Δ}{h}_t=x-x_{\text{path}}& (17)\end{array}$

$\begin{array}{ll}H=y_{\text{goal}}-y_{\text{star}}& (18)\end{array}$

$\begin{array}{ll}{R}_t=\frac{\mu }{{(\text{Δ}{h}_t)}^2}& (19)\end{array}$

where x is the horizontal position of the ship, x_pathjis the horizontal position of the point of the j-th path, the path is the point with the closest prior knowledge to the horizontal position of the ship, x_path is the horizontal distance between the ship and the point of the path, and H is denoted as the vertical distance from the end point to the start point of the ship.

Table 2 demonstrates the parameter configurations used in all model experiments, ensuring consistency and fairness across models. In particular, the first-order NOMOTO model was used for the ship model parameters, taking into account the maneuverability and motion response of the ship.

Table 2

Table 2. Parameter settings for RL -Based ship models.

Furthermore, all models were trained using identical reinforcement learning parameter settings, including the learning rate, discount factor, and batch size, to eliminate potential bias introduced by parameter discrepancies and to ensure the objectivity and comparability of the experimental results.

Table 3 shows the hyperparameters of the different models in the experiment, the following hyperparameters are only taken for this experiment, showing the hyperparameter settings of the different models in the experiment, including the key parameters of the Hierarchical Composite Reward and Punishment Mechanism and their variants’ specific values. It should be noted that the hyperparameters listed in the table are only the values taken for the settings of this experiment, which are used to verify the effectiveness of the GEPA model in reinforcement learning training, and do not represent its optimal choice in all application scenarios.

Table 3

Table 3. Hyperparameter configurations for GEPA model and its variants.

4.2 Design of virtual channel environments

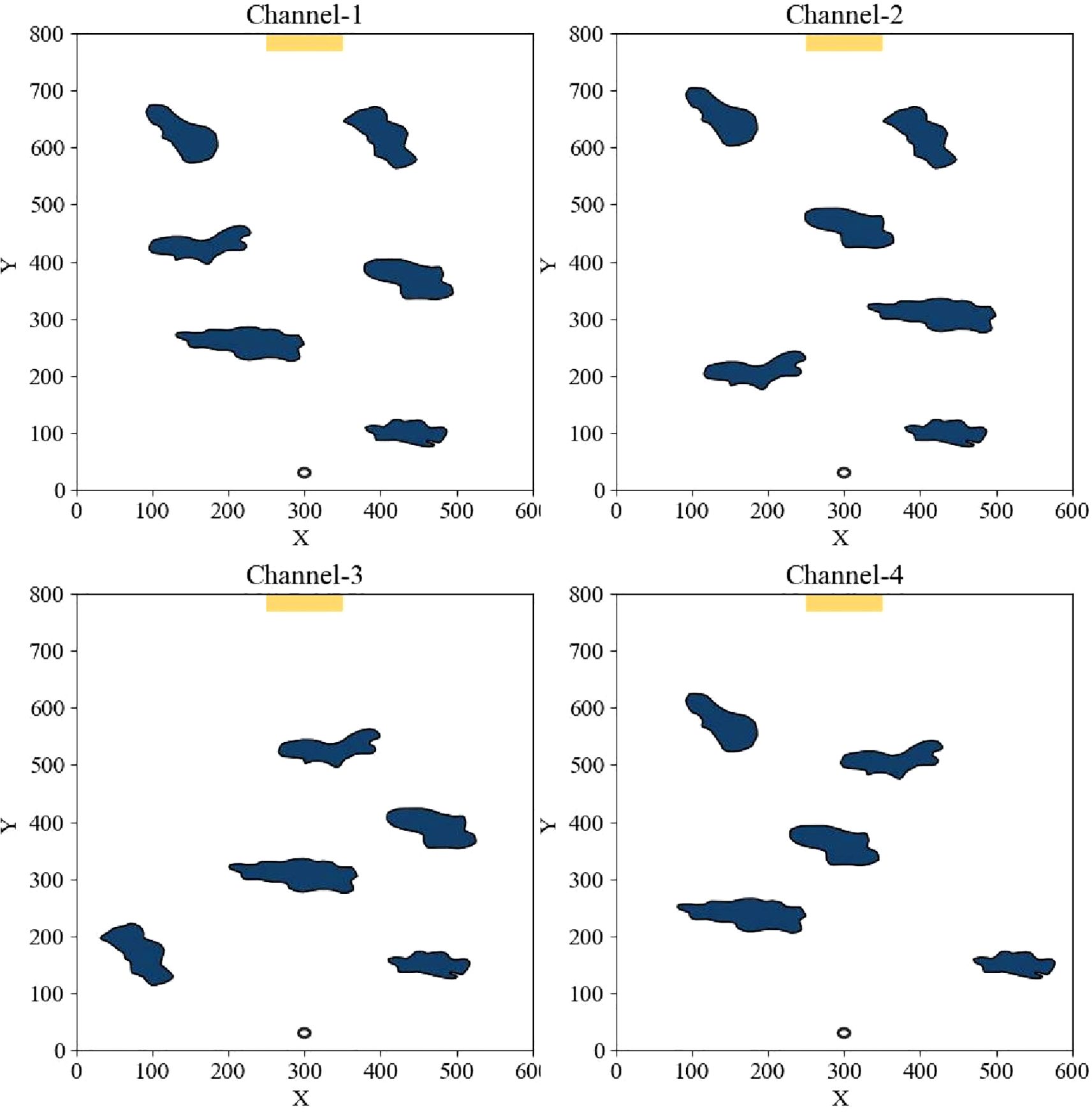
As shown in Figure 5, for the complex and irregular natural and man-made obstacle environments in the navigation area of the ship, we comprehensively consider the many situations that may be encountered in reality, as well as the avoidance measures that should be taken by the ship in different situations, and carefully plan four irregular obstacle channels with significant features, aiming to comprehensively test the autonomous navigation and obstacle avoidance capabilities of unmanned ships in response to irregular obstacles, namely Six-obstacle navigation channel (Channel-1), the zigzag sharp turn six-obstacle channel (Channel-2), the starboard restricted channel (Channel-3), and the port restricted channel (Channel-4).

Figure 5

Figure 5. Four types of irregular obstacle channel environments.

They have distinctive features: Channel-1, this channel is specially designed with six obstacles of irregular shapes, sizes and distributions to simulate the complex and changeable obstacle environments in the real world, mainly for the unmanned ship to be able to make simple twisting avoidance when encountering the obstacles, and pass straight through after dodging an irregular obstacle; Channel-2, this channel not only contains tightly arranged irregular obstacles, but also sets up several large arc curves and sharp turns at the end, to test the unmanned ship’s ability of path planning, sharp turn avoidance, and dynamic adjustment in emergency situations under extreme conditions. Channel-3 and Channel-4, by concentrating the obstacles on one side, the unmanned ship is tested to see if it will yaw and avoid the obstacles.

4.3 Assessment of smart ship navigation capabilities

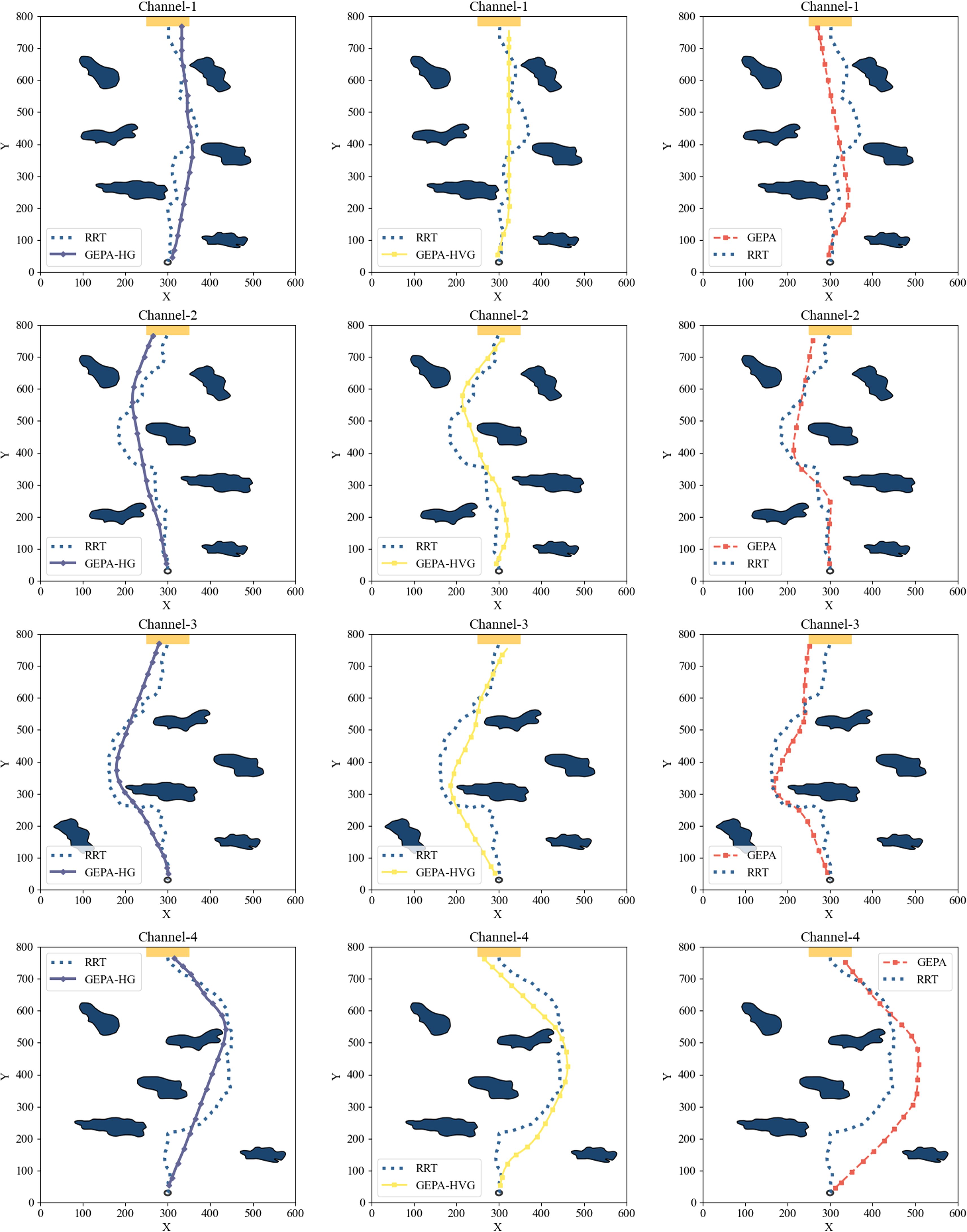
This experiment evaluates the autonomous navigation performance of the GEPA model compared to the traditional model (ADF) and the comparison model (CurrenT-Nav), while also referencing the path generated by the traditional path planning algorithm (RRT). The experimental data is derived from the autonomous navigation paths after 2000 training iterations, as shown in Figure 6.

Figure 6

Figure 6. Ship navigating capability.

In Channel-2, the ADF model exhibited two sharp turns, which pose significant risks in real-world ship navigation, potentially causing severe oscillations or loss of directional stability. In Channel-3, the ADF model selected a more winding path with dense obstacles, increasing the risk of collision. In contrast, the GEPA model demonstrated smoother rudder adjustments, actively choosing safer routes away from obstacles, thereby enhancing stability and navigational safety. However, due to the impact of the hierarchical composite reward and penalty mechanism, the intelligent agent might sometimes over-avoid obstacles, leading to slight deviations from the optimal path. The introduction of prior knowledge mitigates this issue, allowing the intelligent agent to optimize the navigation route while ensuring safety and maintaining accurate positioning.

A comparison between the GEPA model and the RRT-generated path reveals that GEPA produces smoother and more stable routes, whereas RRT paths exhibit a higher degree of randomness, often resulting in excessively winding trajectories, thereby increasing navigation risks. Particularly in complex environments, the GEPA model demonstrates superior path stability and operability compared to traditional pathfinding algorithms.

In Channel-1, the ADF model navigates dangerously close to obstacles, maintaining a shorter and less secure clearance distance. The CurrenT-Nav model, compared to ADF, maintains a greater safety margin, while the GEPA model actively selects safer routes, further enhancing navigation stability. In Channel-2, where the path involves dense obstacles and sharp turns, the GEPA model successfully plans ahead for obstacle avoidance, ensuring shorter and safer navigation routes, thereby exhibiting strong robustness. In Channel-3 and Channel-4, where ships are required to make significant rudder adjustments early on to avoid obstacles, the GEPA model effectively anticipates the need for avoidance maneuvers, selecting safe and efficient routes for navigation.

In Channel-1, the GEPA model demonstrates superior navigating performance and a more optimized fitted path, maintaining a greater clearance from obstacles. It also proactively avoids the first encountered obstacle, ensuring higher safety levels. In Channel-2, which features dense obstacles and requires sharp turns near the end, the GEPA model maintains its robustness, preemptively avoiding obstacles while keeping a safe distance and selecting shorter, efficient routes. In Channel-3 and Channel-4, where early-stage large rudder angle adjustments are necessary to avoid obstacles, the GEPA model successfully executes preemptive avoidance strategies and selects secure navigation routes, further enhancing its autonomous navigation capability.

4.4 Evaluation of autonomous ship navigating paths

To evaluate the impact of the hierarchical composite reward and penalty mechanism on the path fitting performance of the autonomous ship navigating model, this experiment tested three different hierarchical composite reward models on various channels and compared their generated paths with the prior knowledge path (RRT path).

To further validate the impact of the hierarchical composite reward and penalty mechanism on the effectiveness of path planning, we applied three hierarchical composite reward and penalty models in different waterways and compared their performance against a priori knowledge-based paths (RRTgenerated paths). As illustrated in Figure 7, the experimental results indicate that the paths generated by all three models closely resemble the a priori knowledge paths. Moreover, they exhibit greater smoothness and reduced path lengths compared to the original a priori paths. By manually adjusting the safety distance of the a priori paths, we ensured that the planned trajectories maintained a reasonable separation from obstacles, thereby enhancing both the safety and maneuverability of the generated paths.

Figure 7

Figure 7. Ship navigation path results.

4.5 Analysis of the first episode to reach the destination for intelligent ships

After conducting exhaustive data analysis and comparative evaluation, we performed a systematic experimental assessment of the GEPA model, its two variants, and the ADF model. The experimental results, presented in Figure 8, visualize the number of training rounds required to reach the endpoint for the first time and the corresponding variance across different fairways.

Figure 8

Figure 8. The first episode to reach the destination for intelligent ship.

The experimental findings indicate that the GEPA model and its variants, which incorporate prior knowledge guidance, required fewer training rounds to reach the endpoint compared to the ADF model. This result suggests that these models achieved faster convergence toward the target point, with the GEPA model demonstrating superior performance over the other models. Specifically, in Channel 1, the GEPA model required only 36.3 rounds to reach the endpoint, representing a 27.8% reduction in training rounds compared to the ADF model. This finding highlights the ability of GEPA-trained agents to converge more efficiently toward the optimal path. Similarly, in Channel 3, the GEPA model exhibited a substantial efficiency improvement, reducing the number of training rounds by 87.4% compared to the ADF model, thereby significantly accelerating task completion speed. These results validate the effectiveness of integrating prior knowledge with reinforcement learning and demonstrate that the introduction of a hierarchical composite reward and penalty mechanism can further enhance training efficiency in unmanned vessel autonomous navigating.

As illustrated in Figure 9, the average number of training rounds required to reach the endpoint for the GEPA model was 36.3, 233.2, 143.7, and 95.0 across different fairways. The results confirm that the GEPA model and its variants, when guided by prior knowledge, required fewer training rounds than the ADF model, with improvements of 14%, 35.5%, and 27.2%, respectively. On average, the efficiency gains reached 22.7%, demonstrating that, compared to traditional autonomous navigating strategies, ships employing the GEPA model exhibited greater efficiency in target point localization and significantly outperformed the traditional ADF method in path planning performance. Furthermore, vessels driven by the GEPA model achieved faster convergence to the target point, enhancing overall autonomous navigating efficiency, while the GEPA model outperformed its variant models.

Figure 9

Figure 9. Ship navigating path length results.

Taken together, the experimental results confirm that all models incorporating prior knowledge outperformed the original ADF model in terms of efficiency. However, under the influence of a more refined reward and penalty function, the GEPA model demonstrated superior performance compared to its variants, highlighting its enhanced effectiveness in optimizing.

4.6 Intelligent ship navigating path length analysis

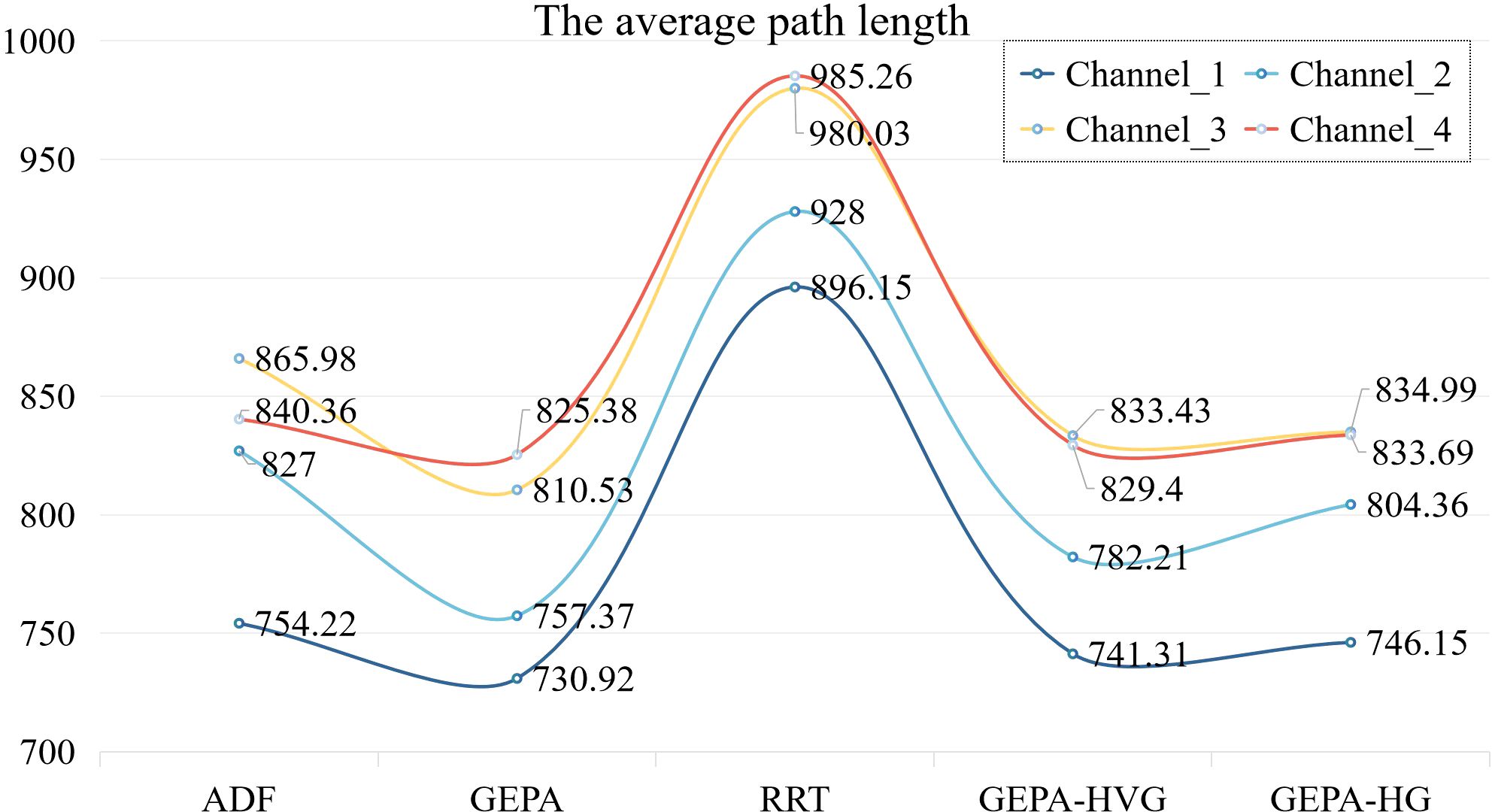
After conducting extensive experiments and performing statistical analysis of the data, a line graph (Figure 9) was generated, illustrating the average path lengths of different pathfinding models across various waterways, thereby providing a comparative analysis of efficiency performance.

The path optimization capability of the GEPA model was found to be significantly superior to that of the other models across all test channels. Its average path length remained the shortest in every scenario, highlighting its high efficiency. Compared to the ADF model, the GEPA model achieved path length reductions of 23.3, 69.63, 55.4, and 14.98 pixels across the four shipping lanes. This outcome indicates that the GEPA model was able to plan autonomous navigating paths more efficiently, thereby minimizing unnecessary detours. Moreover, in comparison with GEPA-HG and GEPA-HVG, the GEPA model demonstrated superior path lengths in most cases, underscoring the effectiveness of its improved reward and punishment functions in optimizing autonomous path planning.

This outstanding performance can be primarily attributed to the GEPA model’s adoption of an advanced hierarchical composite reward and penalty mechanism. This mechanism reinforces the influence of prior knowledge paths, allowing the reinforcement learning agent to converge toward efficient routes more rapidly, while the progressive penalty mechanism effectively mitigates unwanted path deviations. Furthermore, the traditional RRT model, due to its high degree of randomness, frequently exhibits significant distortions and irregularities in its generated paths, leading to substantially longer path lengths than those produced by other methods. These limitations make RRT-generated paths less suitable for direct application in autonomous navigating tasks. By contrast, the GEPA model successfully integrates prior knowledge with reinforcement learning, optimizing path planning to not only improve training efficiency but also enhance trajectory smoothness and energy efficiency in unmanned ship autonomous navigating.

4.7 Safety performance evaluation of autonomous ships in obstacle avoidance

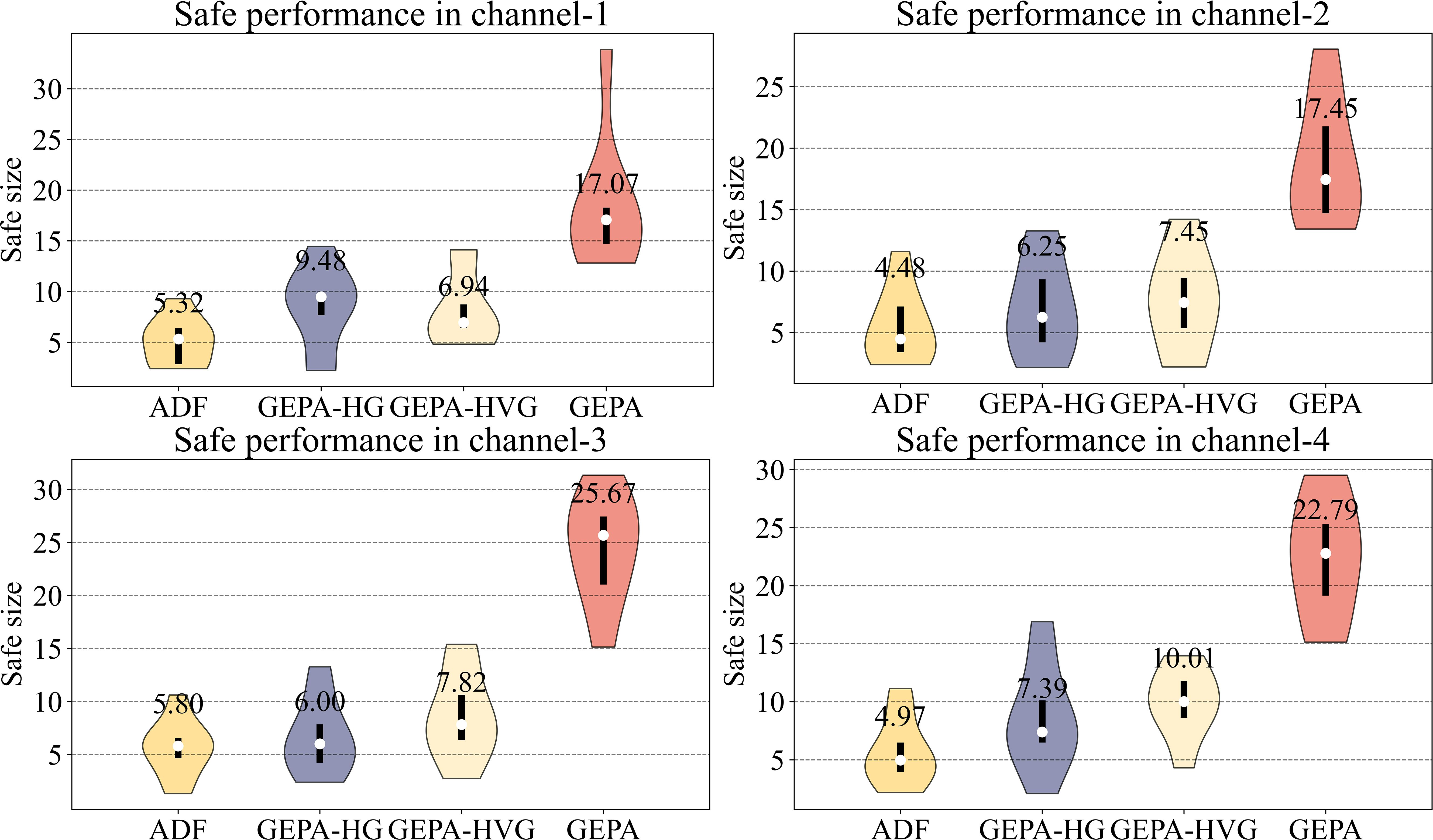
In the safety performance analysis, the data presented in violin plot (Figure 10) illustrates that the GEPA model consistently maintains a significant safety margin from irregular obstacles across various waterways, reflecting its exceptional safety performance. Under the influence of the hierarchical obstacle penalty function, the GEPA model successfully sustained a minimum safe distance of 15 pixels. This result outperformed all other models, particularly the ADF model, which maintained a safe distance of only 11 pixels. This finding indicates that the ADF model’s navigating frequently brings it dangerously close to obstacles, posing a substantial collision risk. The outstanding performance of the GEPA model underscores its superior safety in complex environments, as it effectively mitigates close encounters with obstacles, thereby providing a reliable safety guarantee for unmanned ship navigating.

Figure 10

Figure 10. Ship safety distance evaluation.

The core objective of this analysis was to assess whether reinforcement learning-based unmanned ship intelligent agent could effectively achieve collision-free autonomous navigating after implementing the hierarchical penalty mechanism, thereby ensuring higher safety standards. The data presented in Figure 10 further reinforces this conclusion, showing that the GEPA model maintained a safe distance of at least 17 pixels, whereas the ADF model’s minimum safety distance was only 5 pixels. The GEPA model outperformed the ADF model by 70.6% in maintaining a safe distance, further highlighting its superior collision avoidance capabilities.

The results of the ADF model indicate that its autonomous navigating strategy frequently led to paths in close proximity to obstacles, increasing the likelihood of collision risk. In contrast, the GEPA model consistently maintained a significant safety distance from irregular obstacles across various navigating scenarios, demonstrating its robust safety performance. These findings further confirm that the GEPA model enhances safety in complex environments by effectively avoiding close encounters with obstacles, ultimately providing a more reliable and secure autonomous navigating solution.

4.8 Collision frequency assessment within intelligent ship safety performance analysis

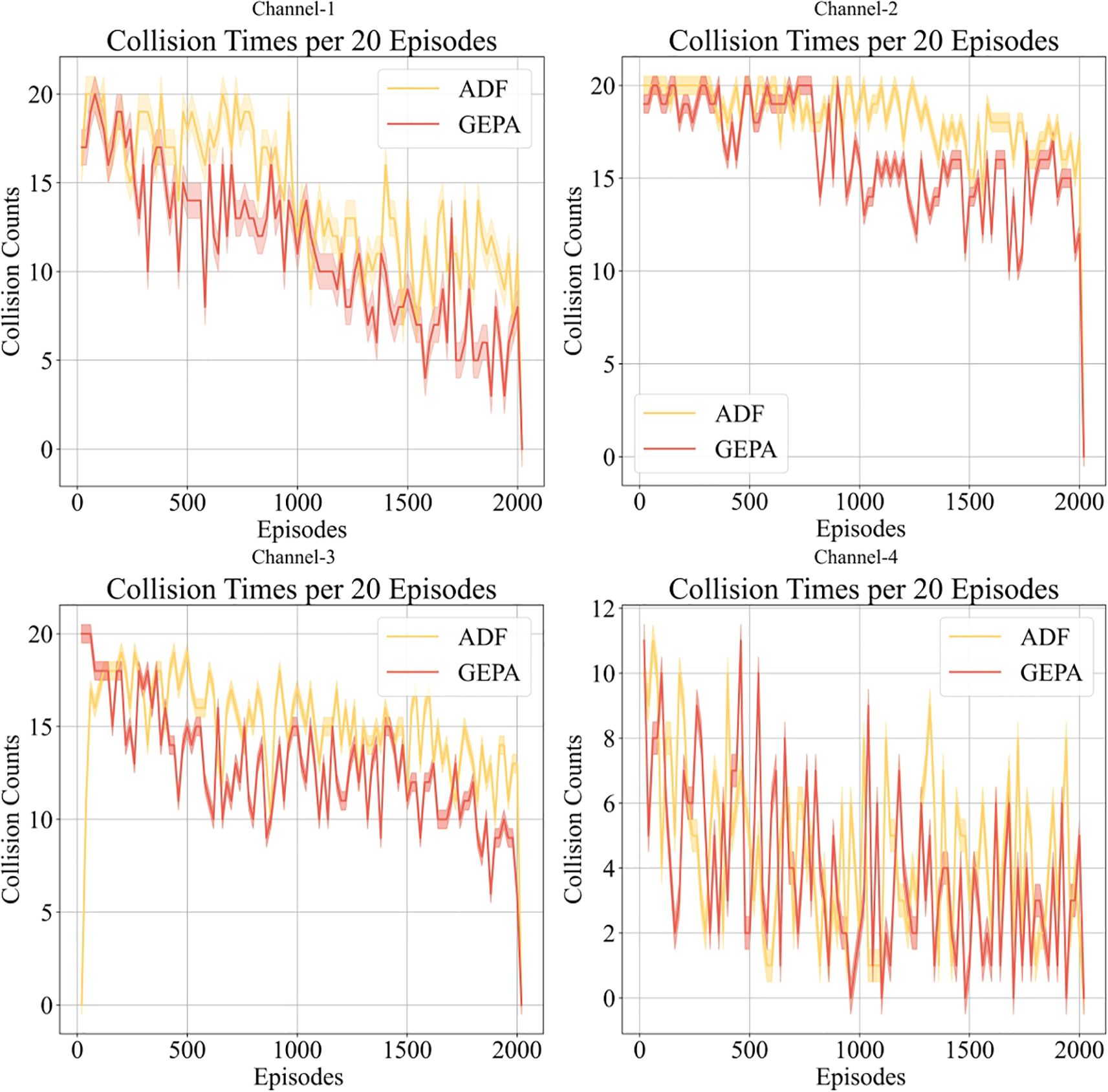
In Figure 11, we compare the number of obstacle collisions per 20 rounds over 2000 training iterations between the ADF and GEPA models to evaluate their obstacle avoidance capabilities and overall safety performance in a complex marine environment. The statistical results indicate that the ADF model exhibited a significantly higher number of collisions than the GEPA model, highlighting inherent limitations in its obstacle avoidance strategy, which failed to effectively mitigate collisions in challenging maritime conditions. Moreover, although both models exhibited a certain degree of fluctuation in collision frequency, the GEPA model consistently maintained a lower collision rate, demonstrating its superior robustness and adaptability in response to varied environmental challenges.

Figure 11

Figure 11. Evaluation of ship collision frequency.

Notably, the GEPA model fully integrates dynamic obstacle avoidance considerations into its reinforcement learning strategy through the implementation of a hierarchical composite reward and penalty mechanism. This mechanism enables the intelligent agent to anticipate and react to obstacles at an earlier stage, thereby significantly reducing unnecessary collisions. In contrast, the ADF model fails to effectively leverage environmental information, resulting in a higher risk of collision under more complex waterway conditions. The experimental findings further validate that a well-designed reward and penalty mechanism not only substantially reduces the collision probability of autonomous agents but also optimizes path planning and enhances the safety and stability of autonomous ship navigating. This research provides critical theoretical insights and practical contributions to the safety optimization of reinforcement learning applications in the field of unmanned ship autonomous navigating.

5 Summary and future prospects

In this study, a reinforcement learning-based autonomous ship navigating strategy that integrates prior knowledge with a hierarchical reward and penalty mechanism is proposed to enhance the maneuverability and obstacle avoidance performance of unmanned ships operating in complex marine environments. This approach directly addresses the safety and efficiency challenges currently faced by the global smart shipping industry. Experimental results demonstrate that the proposed GEPA model exhibits remarkable training efficiency and superior autonomous navigating stability across multiple test environments. By incorporating prior knowledge, reinforcement learning agents are able to minimize ineffective explorations and accelerate Q-value updates in the early training phase, thereby significantly enhancing the convergence efficiency of the learning process. Comparative experiments reveal that, relative to traditional methods, the GEPA model reduces the number of training rounds required for task completion by 24.85%, improves path planning efficiency, and enhances trajectory smoothness by mitigating unnecessary heading fluctuations, ultimately leading to improved autonomous navigating stability.

Furthermore, the hierarchical reward and penalty mechanism embedded in the GEPA model effectively optimizes the reinforcement learning-based obstacle avoidance strategy, enabling unmanned ship intelligent agent to make more precise navigational decisions in complex maritime environments. Experimental data indicate that this mechanism improves the safety distance of the unmanned vessel by 70.6% and significantly reduces collision occurrences, validating the robustness and reliability of the model in complex maritime settings. Additionally, this study incorporates irregular obstacle modeling, which more accurately simulates real-world maritime conditions and enhances the autonomous decision-making capabilities of unmanned vessels. This advancement enables ships to adjust their navigating strategies, thereby enhancing autonomous obstacle avoidance capabilities when confronted with obstacles of complex morphology.

Despite these notable achievements, it is important to acknowledge that the present study primarily addresses static environmental conditions and does not yet account for dynamic maritime challenges such as mobile obstacles, ocean currents, or stochastic environmental disturbances. To improve the model’s real-world applicability, future work should aim to extend the GEPA framework to dynamic scenarios. Structurally, the framework is amenable to such extensions. For example, real-time path replanning algorithms—such as Time-Variant RRT (TV-RRT), D*-Lite, or Model Predictive Control (MPC)—could be integrated to allow continuous adaptation to changing environmental stimuli. Moreover, dynamic reward shaping mechanisms can be introduced to account for predicted obstacle trajectories, velocity fields, and evolving goal positions, thereby enhancing the agent’s temporal responsiveness.

Additionally, the incorporation of real-time environmental data—such as wind speed, ocean current vectors, and marine traffic density—would enhance the situational awareness and generalization capacity of the learning agent. This could be further supported by online reinforcement learning techniques, which would enable continual policy adaptation under dynamic conditions. Future research may also consider incorporating dynamic environmental modeling components, including current fields, vessel interactions, and multi-agent cooperation strategies. These developments will collectively enable the GEPA framework to transition from simulation-based scenarios to real-world maritime applications, ultimately providing a robust, intelligent, and safety-assured navigation solution in highly uncertain oceanic environments (Alam et al., 2023).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HZ: Investigation, Visualization, Formal Analysis, Writing – original draft. JL: Visualization, Formal Analysis, Writing – original draft, Investigation. LC: Conceptualization, Methodology, Software, Writing – review & editing, Funding acquisition. SW: Writing – review & editing. RL: Conceptualization, Methodology, Software, Resources, Data curation, Funding acquisition, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the National Natural Science Foundation of China (Grant No. 52171346), the Ocean Young Talent Innovation Programme of Zhanjiang City (Grant No. 2022E05002), the Young Innovative Talents Grants Programme of Guangdong Province (Grant No. 2022KQNCX024), the Special Projects of Key Fields of Universities in Guangdong Province (Grant No. 2023ZDZX3003), the China Institute of Navigation Young Elite Scientist Sponsorship Program by CIN (Grant No. YESSCIN2023008), the College Student Innovation Team of Guangdong Ocean University (Grant No. CXTD2024018), the Natural Science Foundation of Guangdong Province (Grant No. 2021A1515012618), the Program for Scientific Research Start-up Funds of Guangdong Ocean University, the China Transportation Education Research Association (Grant No. JTYB20-28), the Guangdong Provincial Education Teaching Reform Research Project (Grant No. 010202132201), the Zhanjiang Federation of Social Science Circles (Grant No. ZJ20YB0), the Guangdong Provincial Education Science Planning Leading Group Office (Grant No. 2023GXJK313), Guangdong Ocean University (Grant No. C22809), the Hainan Province Teaching Reform Project (Grant No. Hnjg2024ZC-144), and the School of Port and Shipping Industry Technology Project (Grant No. GHCY2024014)..

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. During the preparation of this work, AI was used exclusively for English language editing to improve readability and grammar. The AI tool was NOT employed for any of the following purposes: Generating or interpreting research data, figures, or technical content. Formulating research hypotheses, methodologies, or conclusions. Conducting literature reviews or theoretical analysis. All intellectual contributions—including study design, algorithm development, experimental execution, and result interpretation—originate solely from the human authors. The final manuscript was rigorously reviewed and approved by all co-authors, who take full responsibility for its academic integrity and scholarly content.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alam M. S., Sudha S. K. R., and Somayajula A. (2023). Ai on the water: applying drl to autonomous vessel navigation. arXiv preprint arXiv 2310, 14938. doi: 10.48550/arXiv.2310.14938

Crossref Full Text | Google Scholar

Cao S., Fan P., Yan T., Xie C., Deng J., Xu F., et al. (2022). Inland waterway ship path planning based on improved rrt algorithm. J. Marine Sci. Eng. 10, 1460 doi: 10.3390/jmse10101460

Crossref Full Text | Google Scholar

Chen C., Chen X.-Q., Ma F., Zeng X.-J., and Wang J. (2019). A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean Eng. 189, 106299. doi: 10.1016/j.oceaneng.2019.106299

Crossref Full Text | Google Scholar

Chen J., Liang M., Peng C., Zhang J., and Huo S. (2025). “Improving maritime data: A machine learning-based model for missing vessel trajectories reconstruction,” in IEEE Transactions on Vehicular Technology. (Piscataway, NJ, United States: IEEE).

Google Scholar

Du C., Gao Y., and Zhang W. (2005). Q-learning with prior knowledge in multi-agent systems. J. Tsinghua University(Science Technology) 45, 981–984. doi: 10.16511/j.cnki.qhdxxb.2005.07.031

Crossref Full Text | Google Scholar

Du B., Lin B., Zhang C., Dong B., and Zhang W. (2022). Safe deep reinforcement learning-based adaptive control for usv interception mission. Ocean Eng. 246, 110477. doi: 10.1016/j.oceaneng.2021.110477

Crossref Full Text | Google Scholar

Etemad M., Zare N., Sarvmaili M., Soares A., Brandoli MaChado B., and Matwin S. (2020). Using deep reinforcement learning methods for autonomous vessels in 2d environments", in Advances in Artificial Intelligence: 33rd Canadian Conference on Artificial Intelligence, Canadian AI 2020, Ottawa, ON, Canada, May 13--15, 2020, Proceedings 33. 220–231. doi: 10.48550/arXiv.2003.10249

Crossref Full Text | Google Scholar

Figueiredo J. M. P. and Abou Rejaili R. P. (2018). Deep reinforcement learning algorithms for ship navigation in restricted waters. Mecatrone 3. doi: 10.11606/issn.2526-8260.mecatrone.2018.151953

Crossref Full Text | Google Scholar

Gao X., Dong Y., and Han Y. (2023). An optimized path planning method for container ships in bohai bay based on improved deep q-learning. IEEE Access 11, 91275–91292. doi: 10.1109/ACCESS.2023.3307480

Crossref Full Text | Google Scholar

Gu Q., Zhen R., Liu J., and Li C. (2023). An improved rrt algorithm based on prior ais information and dp compression for ship path planning. Ocean Eng. 279, 114595. doi: 10.1016/j.oceaneng.2023.114595

Crossref Full Text | Google Scholar

Guo S., Zhang X., Du Y., Zheng Y., and Cao Z. (2021). Path planning of coastal ships based on optimized dqn reward function. J. Marine Sci. Eng. 9, 210. doi: 10.3390/jmse9020210

Crossref Full Text | Google Scholar

Guo S., Zhang X., Zheng Y., and Du Y. (2020). An autonomous path planning model for unmanned ships based on deep reinforcement learning. Sensors 20, 426. doi: 10.3390/s20020426

PubMed Abstract | Crossref Full Text | Google Scholar

Hu W., Chen S., Liu Z., Luo X., and Xu J. (2025). Ha-rrt: A heuristic and adaptive rrt algorithm for ship path planning. Ocean Eng. 316, 119906. doi: 10.1016/j.oceaneng.2024.119906

Crossref Full Text | Google Scholar

Jiang X., Li J., Huang Z., Huang J., and Li R. (2024). Exploring the performance impact of soft constraint integration on reinforcement learning-based autonomous vessel navigation: Experimental insights. Int. J. Naval Architecture Ocean Eng. 16, 100609. doi: 10.1016/j.ijnaoe.2024.100609

Crossref Full Text | Google Scholar

Li J., Jiang X., Zhang H., Wu L., Cao L., and Li R. (2025). Multi-joint adaptive control enhanced reinforcement learning for unmanned ship. Ocean Eng. 318, 120121. doi: 10.1016/j.oceaneng.2024.120121

Crossref Full Text | Google Scholar

Li Z., Li L., Zhang W., Wu W., and Zhu Z. (2022). Research on unmanned ship path planning based on rrt algorithm. J. Phys.: Conf. Ser. 2281, 012004. doi: 10.1088/1742-6596/2281/1/012004

Crossref Full Text | Google Scholar

Liang M., Liu R. W., Li S., Xiao Z., Liu X., and Lu F. (2021). An unsupervised learning method with convolutional auto-encoder for vessel trajectory similarity computation. Ocean Eng. 225, 108803. doi: 10.1016/j.oceaneng.2021.108803

Crossref Full Text | Google Scholar

Liang M., Weng L., Gao R., Li Y., and Du L. (2024). Unsupervised maritime anomaly detection for intelligent situational awareness using ais data. Knowledge-Based Syst. 284, 111313. doi: 10.1016/j.knosys.2023.111313

Crossref Full Text | Google Scholar

Lin X., McConnell J., and Englot B. (2023). "Robust unmanned surface vehicle navigation with distributional reinforcement learning", in 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). 6185–6191. doi: 10.1109/IROS55552.2023.10342389

Crossref Full Text | Google Scholar

Ly A., Dazeley R., Vamplew P., Cruz F., and Aryal S. (2024). Elastic step dqn: A novel multi-step algorithm to alleviate overestimation in deep q-networks. Neurocomputing 576, 127170. doi: 10.1016/j.neucom.2023.127170

Crossref Full Text | Google Scholar

Mnih V., Kavukcuoglu K., Silver D., Rusu A. A., Veness J., Bellemare M. G., et al. (2015). Human-level control through deep reinforcement learning. nature 518, 529–533. doi: 10.1038/nature14236

PubMed Abstract | Crossref Full Text | Google Scholar

Shen H., Hashimoto H., Matsuda A., Taniguchi Y., and Terada D. (2017). "2017s-gs16–7 automatic collision avoidance of ships in congested area based on deep reinforcement learning", in Conference Proceedings The Japan Society of Naval Architects and Ocean Engineers 24, 651–656. doi: 10.14856/conf.24.0_651

Crossref Full Text | Google Scholar

Singh A. J., Kumar A., and Lau H. C. (2020). "Hierarchical multiagent reinforcement learning for maritime traffic management", in Proceedings of the 19th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2020), 1278-1286. doi: 10.5555/3398761.3398909

Crossref Full Text | Google Scholar

Sivaraj S., Rajendran S., and Prasad L. P. (2022). Data driven control based on deep q-network algorithm for heading control and path following of a ship in calm water and waves. Ocean Eng. 259, 111802. doi: 10.1016/j.oceaneng.2022.111802

Crossref Full Text | Google Scholar

Sun Y., Ran X., Zhang G., Wang X., and Xu H. (2020). Auv path following controlled by modified deep deterministic policy gradient. Ocean Eng. 210, 107360. doi: 10.1016/j.oceaneng.2020.107360

Crossref Full Text | Google Scholar

Wang N., Gao Y., and Zhang X. (2021b). Data-driven performance-prescribed reinforcement learning control of an unmanned surface vehicle. IEEE Trans. Neural Networks Learn. Syst. 32, 5456–5467. doi: 10.1109/TNNLS.2021.3056444

PubMed Abstract | Crossref Full Text | Google Scholar

Wang K., Liang M., Li Y., Liu J., and Liu R. W. (2019). “Maritime traffic data visualization: A brief review,” in 2019 IEEE 4th international conference on big data analytics (ICBDA) (Piscataway, NJ, United States: IEEE), 67–72.

Google Scholar

Wang H., Liu Z., Wang X., Graham T., and Wang J. (2021a). An analysis of factors affecting the severity of marine accidents. Reliability Eng. System Saf. 210, 107513. doi: 10.1016/j.ress.2021.107513

Crossref Full Text | Google Scholar

Wang X., Liu Z., Wang J., Loughney S., Zhao Z., and Cao L. (2021c). Passengers’ safety awareness and perception of wayfinding tools in a ro-ro passenger ship during an emergency evacuation. Saf. Sci. 137, 105189. doi: 10.1016/j.ssci.2021.105189

Crossref Full Text | Google Scholar

Wang X., Liu Z., Zhao Z., Wang J., Loughney S., and Wang H. (2020). Passengers’ likely behaviour based on demographic difference during an emergency evacuation in a ro-ro passenger ship. Saf. Sci. 129, 104803. doi: 10.1016/j.ssci.2020.104803

Crossref Full Text | Google Scholar

Wang R., Miao K., Li Q., Sun J., and Deng H. (2022). The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network. Nonlinear Eng. 11, 680–692. doi: 10.1515/nleng-2022-0260

Crossref Full Text | Google Scholar

Wang X., Xia G., Zhao J., Wang J., Yang Z., Loughney S., et al. (2023b). A novel method for the risk assessment of human evacuation from cruise ships in maritime transportation. Reliability Eng. System Saf. 230, 108887. doi: 10.1016/j.ress.2022.108887

Crossref Full Text | Google Scholar

Wang C., Zhang X., Yang Z., Bashir M., and Lee K. (2023a). Collision avoidance for autonomous ship using deep reinforcement learning and prior-knowledge-based approximate representation. Front. Marine Sci. 9, 1084763. doi: 10.3389/fmars.2022.1084763

Crossref Full Text | Google Scholar

Wen J., Liu S., and Lin Y. (2022). Dynamic navigation and area assignment of multiple usvs based on multi-agent deep reinforcement learning. Sensors 22, 6942 doi: 10.3390/s22186942

PubMed Abstract | Crossref Full Text | Google Scholar

Xie P. and Li W. (2020). Automatic pilot ship route planning based on a rrt guided genetic algorithm. J. Phys.: Conf. Ser. 1550, 032085. doi: 10.1088/1742-6596/1550/3/032085

Crossref Full Text | Google Scholar

Yang X. and Han Q. (2023). Improved dqn for dynamic obstacle avoidance and ship path planning. Algorithms 16, 220. doi: 10.3390/a16050220

Crossref Full Text | Google Scholar

Yu K., Lin F., Song Z., and Yu L. (2023). Path planning of mobile robot with deep reinforcement learning based on gradient reward. Mach. Tool Hydraulics 51, 32–38.

Google Scholar

Zhang Q., Pan W., and Reppa V. (2020). Model-reference reinforcement learning control of autonomous surface vehicles. (Piscataway, NJ, United States: IEEE), 5291–5296.

Google Scholar

Zhang X., Wang C., Liu Y., and Chen X. (2019). Decision-making for the autonomous navigation of maritime autonomous surface ships based on scene division and deep reinforcement learning. Sensors 19, 4055. doi: 10.3390/s19184055

PubMed Abstract | Crossref Full Text | Google Scholar