Cumulative confidence-driven task offloading for object detection in maritime Internet of Things

Maritime mobile edge computing (MMEC) technology facilitates the deployment of computationally intensive object detection tasks on Maritime Internet of Things (MIoT) devices with limited computing resources. However, the dynamic marine network and environmental interference in feature extraction adversely affect detection accuracy and cause delay. In this paper, we propose a cumulative confidence-driven joint scheduling strategy for image detection tasks in MMEC scenarios. The strategy employs lightweight and full models as the detection framework. Through an adaptive decision-making scheme for marine device image recognition, the proposed strategy accumulates results from different models within the framework to ensure quality of service (QoS). To obtain a dynamic offloading strategy that minimizes the total system cost of latency and energy consumption, the problem is divided into two subproblems, and a chemical reaction optimization algorithm is used to reduce the computational complexity. Then, a state normalization action project deep deterministic policy gradient (SNAP-DDPG) algorithm is proposed to handle environmental dynamics, achieving minimized system cost with satisfied QoS. The simulation results indicate that, compared to existing algorithms, the proposed SNAP-DDPG algorithm keeps object detection confidence, with latency reduced by 34.78%.

1 Introduction

High-precision object detection methods based on neural networks have been used in the fields of equipment maintenance, marine life monitoring, and security in Maritime Internet of Things (MIoT) (Liu et al., 2023a; Zhao et al., 2025; Lu et al., 2021; Liu et al., 2023b). These applications generate large amounts of real-time data that require low-latency processing to facilitate time-sensitive decision-making. Consequently, stringent requirements are imposed on both maritime communication infrastructure and edge device computational capabilities (Munusamy et al., 2023). To address this challenge, the development of an optimized detection framework coupled with an intelligent model offloading strategy presents a viable solution to mitigate computational constraints on resource-limited mobile devices.

However, as the parameters of NN networks are increasing, unstable network conditions and limited resources increase the local computation burden. Thus, selecting a suitable network architecture and efficient resource allocation strategy is crucial. Take the convolutional neural network (CNN)-based You Only Look Once (YOLO) algorithm as an example. In MIoT scenarios, it is necessary to balance detection accuracy with latency and energy consumption when making decisions between target detection network structures and MIoT networks. Generally, deeper and more complex models achieve higher accuracy at the cost of higher computational resource consumption (Jiang et al., 2025). A segmented YOLO architecture can be employed, where an optimal cut layer is selected, partitioning the model between local and edge devices, thereby balancing task loads across different nodes (Du et al., 2022; Xiao et al., 2022)—for example, regarding the model partitioning problem of edge offloading for heterogeneous devices, a partitioning and offloading strategy for heterogeneous task server systems is proposed to reduce the overall latency and energy consumption in model inference (Liao et al., 2023). Through joint optimization of model partitioning, the optimal partitioning and scheduling methods are analyzed (Duan and Wu, 2023). Reinforcement learning is used for adaptive offloading decisions in dynamic maritime environments. It assists partitioned CNN models by offering offloading strategies (Qu et al., 2023).

Although significant progress has been made in NN-based task offloading strategies, in the practical task collection of MIoT, object detection accuracy is affected by shooting angles over consecutive time intervals and the marine environment (Heller et al., 2022; Chen et al., 2024). We can infer multiple correlated results by reasoning over multiple different models and consecutive-frame images. Thus, this paper designs an adaptive decision-making scheme for device image recognition. Through a reinforcement learning algorithm, it generates offloading decisions in the detection model based on accumulated object detection results, thereby enhancing the role of lightweight models in detection results.

Specifically, this paper proposes a cumulative confidence-driven joint scheduling strategy for image detection tasks in MMEC scenarios. The strategy establishes a detection framework that integrates lightweight detection models on local devices with partially full models on local devices and the remaining full models on edge devices. The pressure on marine hardware can be eased by adjusting the offloading points. Given the impact of object locations and the marine environment on accuracy, we propose an adaptive decision-making scheme for marine-device image recognition. It uses accumulated detection results to identify final targets. We break the NP-hard problem into two subproblems and use chemical reaction optimization (CRO) to reduce computational complexity. Then, the optimized problem is transformed into a Markov decision process (MDP). We introduce the state normalization action project deep deterministic policy gradient (SNAP-DDPG) algorithm based on the DDPG algorithm. It incorporates normalization and action discretization mechanisms and uses accumulated confidence as a constraint. This addresses the dimension differences of environmental variables and increases the convergence rate of algorithms in marine dynamic environments. The main contributions are summarized as follows.

1. Aiming at the dynamic MIoT scenario with limited marine resources and easily changed detection target features, this paper proposes a cumulative confidence-driven joint scheduling strategy for image detection tasks in MMEC scenarios. This scheme can be tailored to customer demands and marine resources. By switching between lightweight and full models and aggregating detection results, it accomplishes object detection tasks.

2. We divide the NP-hard problem into two separate subproblems. The subproblem of device bandwidth and allocated computing resources is solved by the CRO algorithm. This minimizes total costs and reduces the computational complexity of our offloading decisions.

3. To address how dynamic marine environments and different environments affect image features, we proposed the SNAP-DDPG solution. It is based on accumulated confidence as a constraint condition. By state normalization and action discretization, the solution improves decision-making effectiveness and convergence speed.

The structure of this paper is as follows: Section 2 provides a comprehensive literature review. Section 3 presents the system scenario addressed in this paper and establishes a problem model. Section 4 introduces a DRL-based solution to the adaptive offloading problem. Section 5 presents simulations and discussions, and finally, Section 6 is the conclusion.

2 Related works

2.1 Object detection model

The advancement of artificial intelligence has fueled the rapid development of the Internet of Things. The detection models for maritime object detection have undergone a significant transition from traditional image-based methods to deep learning algorithms. The limited robustness of traditional algorithms in complex and dynamic marine environments makes them inadequate for comprehensive detection (Chen et al., 2023). With the improvement of computing power, deep learning algorithms, especially CNNs, have been widely used in maritime object detection.

One-stage CNN algorithms like YOLO provide a simpler classification process that can be directly applied to images (Zhen et al., 2023). The YOLO series, from YOLOv1 to YOLOv5, has progressively achieved a better balance between object detection accuracy and real-time processing (Gai et al., 2023; Wang et al., 2022; Olorunshola et al., 2023). The YOLO series has also led to various improved models that are adapted to specific marine environments—for example, Vignesh et al. applied YOLOv5 and used the lightweight characteristics of MobileNet to detect sea cucumbers underwater efficiently (Vignesh and Dhamodaran, 2024). Yang et al. enhanced the excellent stability of the YOLOv5 model in foggy conditions through class balance and data augmentation techniques (Yang et al., 2024). Zhu et al. improved the YOLOv5 algorithm by integrating multiple attention mechanisms and combining it with the DeepSort tracking algorithm, achieving real-time monitoring and tracking of marine objects (Zhu and Zhang, 2024).

This paper proposes a universal cumulative confidence-driven joint scheduling strategy for image detection tasks in MMEC scenarios based on the ideas above. The strategy can select appropriate lightweight and full models for different scenarios. Given that object locations and the marine environment affect accuracy, we propose an adaptive decision-making scheme for image recognition of marine devices. It uses accumulated detection results to identify the final detection targets.

2.2 Task offloading in MMEC system

As a key technology for next-generation networks, MMEC is crucial in various marine applications. It eases the pressure of limited computational resources on mobile marine devices, which struggle to meet the demands of complex CNN models. Conventional and intelligent offloading decision methods optimize offloading performance in MMEC environments.

Considering the growing marine activities, Wang et al. proposed a hybrid Stackelberg-bargaining game approach. It uses satellite assistance to maximize the utility of marine devices (Wang et al., 2025). Given the complexity of maritime image processing tasks, Li et al. examined the influence of video resolution on task scale and accuracy and decoupled and established an energy consumption optimization model, offloading tasks to marine edge servers (Li et al., 2023). Qi et al. proposed a joint optimization problem, which involves collaboratively making computation offloading decisions, deploying R-UAVs, and associating S-UAVs with rescue targets. Additionally, they designed an efficient iterative algorithm that breaks down the problem into three subproblems for resolution (Qi et al., 2024).

Traditional offloading methods lack long-term planning and ignore long-term decision-making impacts. In dynamic and time-varying MMEC scenarios, real-time offloading is challenging. Conversely, intelligent offloading decision-making methods can dynamically adjust strategies and consider task optimization globally. Reinforcement learning, iteratively interacting with the environment, enhances the system’s adaptability and enables optimal decisions (Shakya et al., 2023; Yan et al., 2022). Xu et al. proposed an enhanced version of the double-delay deep deterministic policy gradient algorithm, which aims to improve QoS in time-varying maritime scenarios (Xu et al., 2024). Cheng et al. proposed a multi-agent approximate strategy optimization solution that addresses low-latency challenges in multi-UAV-assisted mobile edge computing systems (Cheng et al., 2024). Liu et al. proposed a Deep Q-Network and Deep Deterministic Policy Gradient algorithm to optimize UAV trajectories and virtual machine configurations (Liu et al., 2022).

Inspired by existing studies, we propose the SNAP-DDPG solution, constrained by cumulative confidence. It can dynamically adapt to the maritime environment in real time, links customer demands to detection accuracy via accumulated confidence evaluation, and thus enhances QoS (Table 1).

Table 1

Table 1. List of important notations.

3 System model

3.1 Edge-assisted intelligent MIoT scenario

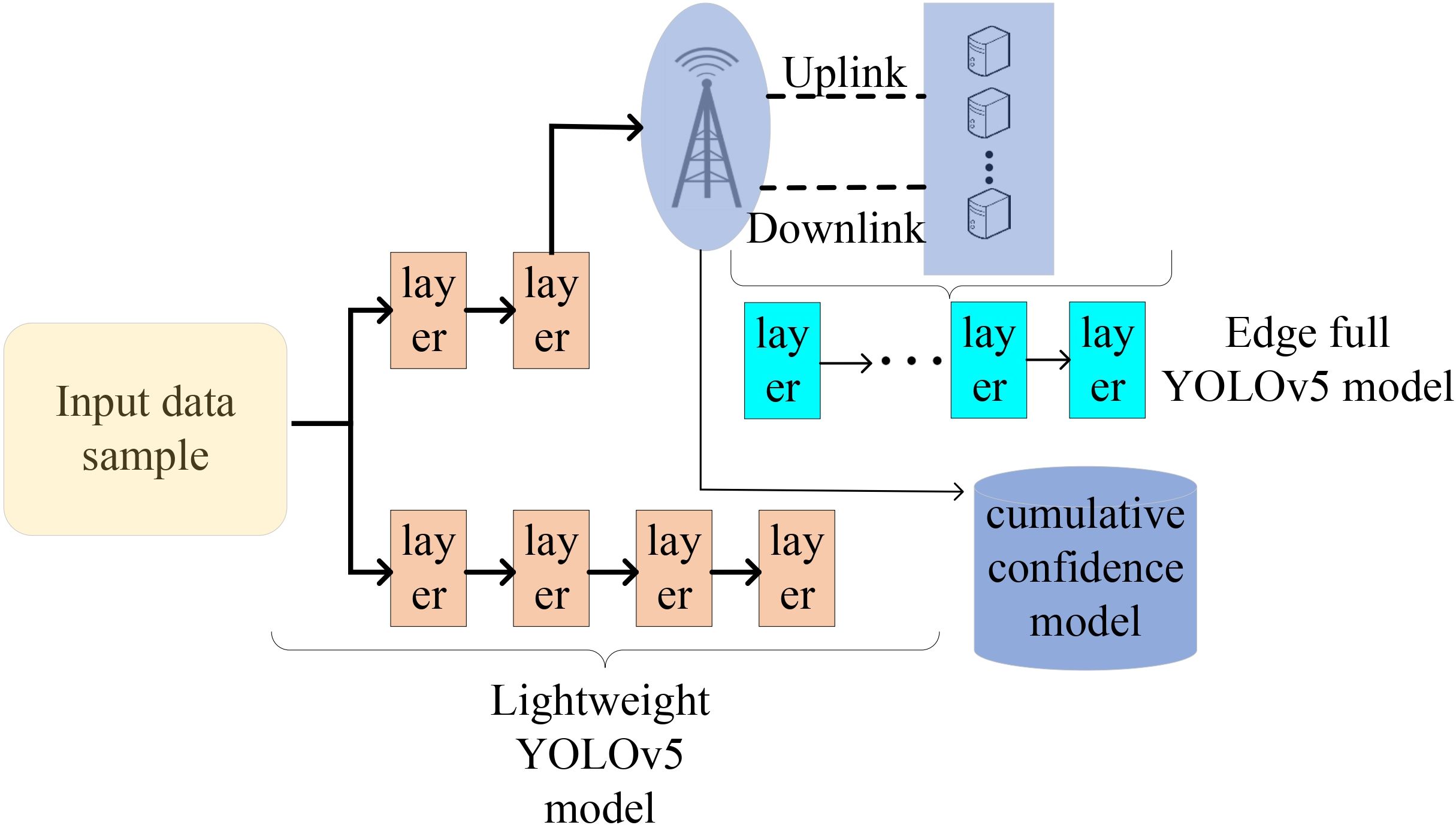
We consider using multiple maritime surveillance devices to collect video data of sea areas to ensure the security of sea areas. In particular, the available bandwidth B varies with the maritime environment, being affected by the resource occupation of other maritime devices and the marine weather (Liu et al., 2023c). As illustrated in Figure 1, the detection system comprises several marine monitoring devices $I=\left\{1,2,\cdots ,i,\cdots ,\left|I\right|\right\}$ deployed in the MMEC environment, a remote edge server, a user terminal, and a data center. An improved YOLOv5 algorithm framework with a lightweight objective detection model and a full objective detection model is developed on the local devices and the edge server (shown in Figure 1).

Figure 1

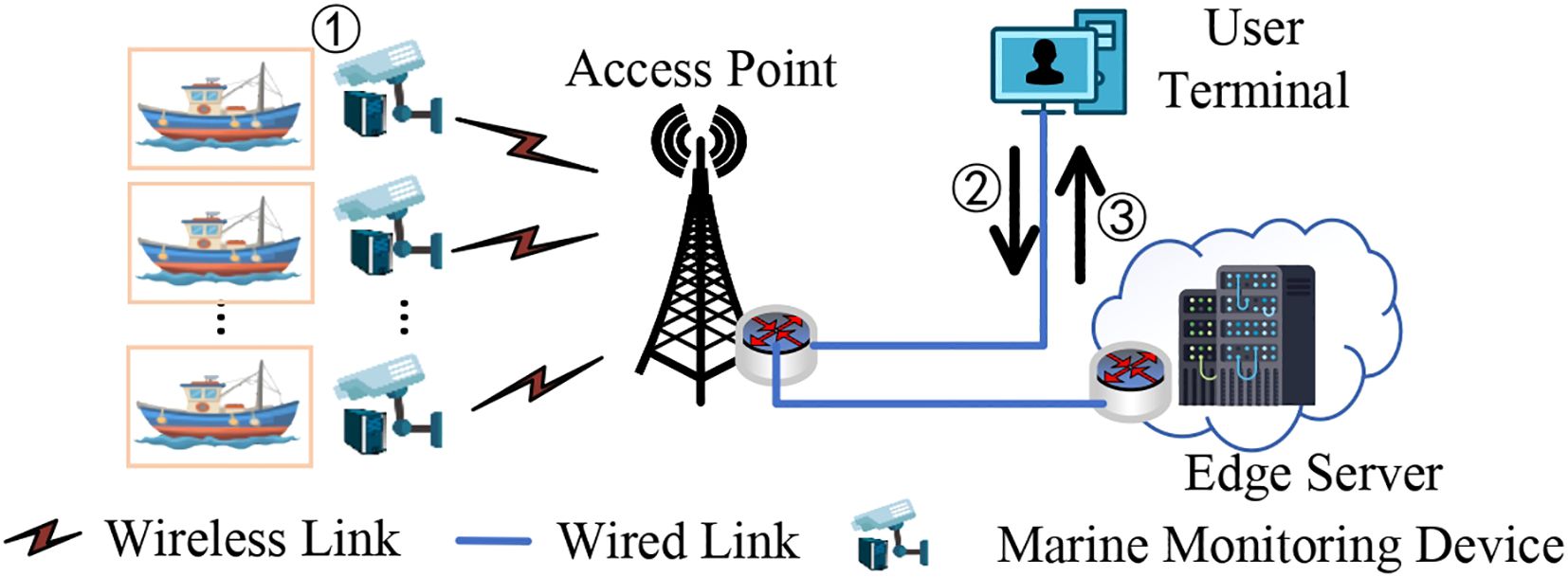
Figure 1. Edge-assisted image-based object detection system. ① Marine monitoring devices taking pictures. ② Transmission offloading decision. ③ Transmission detection results.

Marine monitoring devices: Each monitoring device generates an independent task and each task can be offloaded to the server. Each task has different data samples. The devices have the capability to collect real-time data from a predefined perspective within the MMEC environment and subsequently extract the captured videos into consecutive frames.

Local devices: Each local device carries a lightweight model and a part of the full model to execute object detection tasks for the images transmitted from the marine monitoring device.

Edge device: Collaborating with local devices, the edge server hosts another part of the full model to process the intermediate data from the local devices.

User terminal: The user terminal collects the system status data and has enough resources to train offloading strategies.

3.2 Business processing model

We consider both the deployment of a lightweight model of YOLOv5 locally and the offloading of a full YOLOv5 model for computation between the device and the edge server. The full YOLOv5 model is partitioned to obtain intermediate data samples locally on the device. These samples are then transmitted to the edge server for computation offloading. For the lightweight YOLOv5 model, all object detection modules L^a are executed locally, while for the full YOLOv5 model, different groups of modules L^c are offloaded to the edge server for computation, with the remaining modules L^b being executed locally based on decision-making (illustrated in Figure 2).

Figure 2

Figure 2. YOLOv5 object detection framework.

For the sake of simplicity, we assume device i generates an object detection task at slot k = 1, and the task completion time is denoted as T_i. The number of time slots is represented as K_i= ⌈T_i/τ⌉. Multiple detections may be generated within a single time slot. τ is the duration of a time slot of the system and k(k ≥ 1) as the integer index of the time slot.

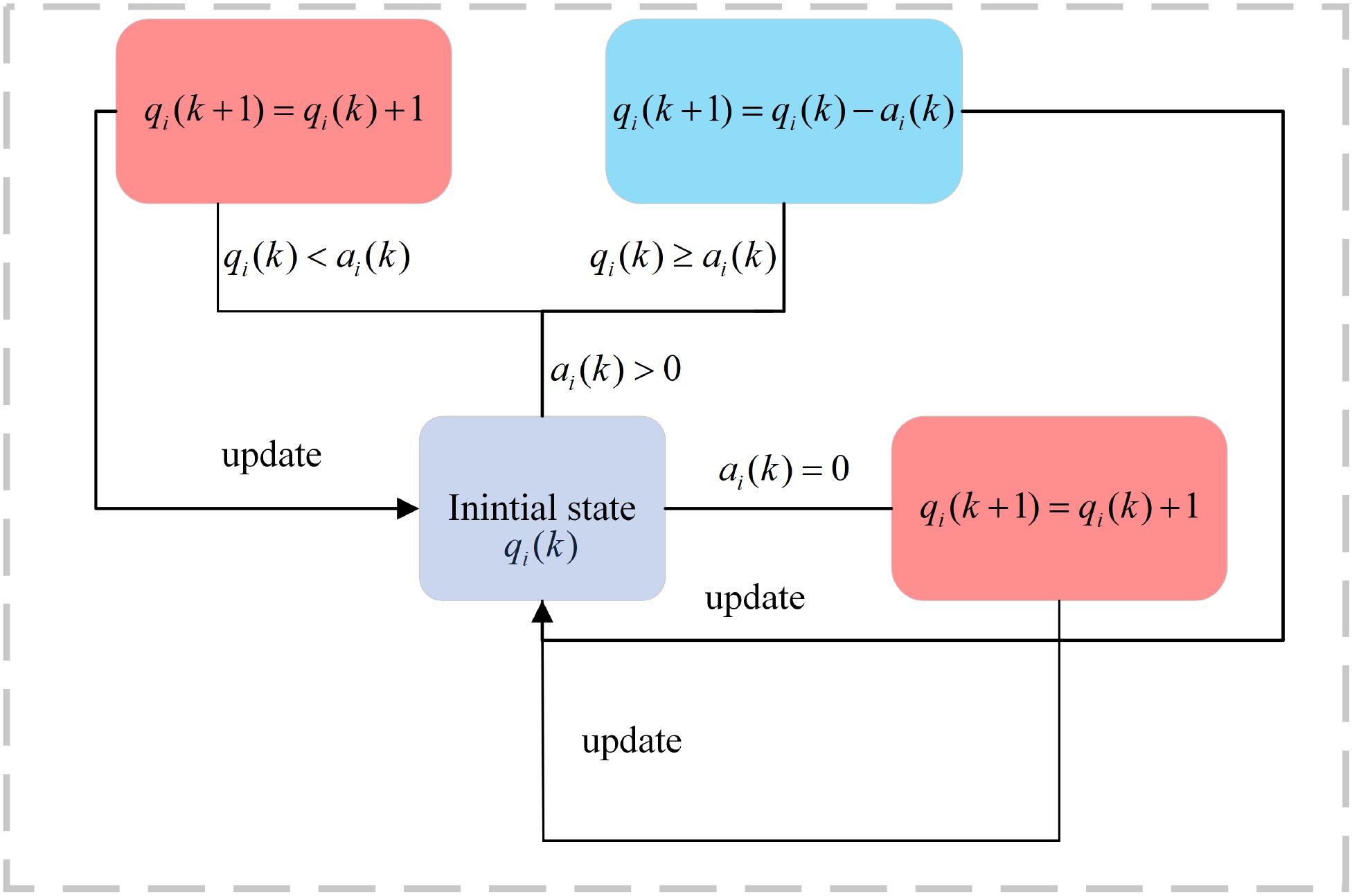
Given the limited resources of maritime edge devices, this scheme prioritizes local computing, with edge computing as an auxiliary tool to enhance the QoS. Let q_k represent the execution status of the lightweight object detection task at the beginning of time slot k, where q_i(k) denotes the number of datasets processed for object detection by device i during time slot k, with initial state q_i(1) = 0. Furthermore, $a_k\in {ℝ}^{\left|I\right|}$ represents the offloading decision vector for time slot k, which comprises a collection of action states among devices. The element a_i(k) corresponds to the action state of device i ∈ I and represents the offloading decision variable. a_i(k) = 0 indicates that the lightweight model is executed locally, updating its execution status as $q_i(k+1)=q_i(k)+1$. Conversely, when a_i(k) > 0 and the number of targets identified following the execution of the lightweight model exceeds the offloading decision variable a_i(k), the device will offload a_i(k) intermediate data samples to the edge server. In this case, the execution status is updated as $q_i(k+1)=q_i(k)-a_i(k)$. If the condition is not satisfied, the device defaults to executing the local lightweight model, resulting in $q_i(k+1)=q_i(k)+1$ (updated in Figure 3).

Figure 3

Figure 3. q_i(k) update process.

3.3 Computing model

Let FLOPs_lrepresent floating point operations (FLOPs) in the layer l. Let FLOPS_i denote floating point operations per second (FLOPS) of device i. Let $t_i^A$ denote the computational latency of the local computation of the lightweight detection model at device i, given by

$\begin{array}{ll}{t}_i^A=\frac{{\sum }_{l\in L^a}{\text{FLOPs}}_l}{{\text{FLOPS}}_i}\forall i\in I.& (1)\end{array}$

Let $t_i^B$ denote the local computational delay of the full detection model for the device i, which is given by

$\begin{array}{ll}{t}_i^B=\frac{{\sum }_{l\in L^b}{\text{FLOPs}}_l}{{\text{FLOPS}}_i}\forall i\in I,& (2)\end{array}$

where $l\in L^a$, $l\in L^c$ denotes the sum of all layers of $L^a$, $L^c$, respectively.

For the full model, each device is allocated fixed computational resources on the edge server; the resources are a constant FLOPS₀. $t_i^E(k)$ is denoted as the computational delay for full for device i during time slot k, given by

$\begin{array}{ll}{t}_i^E(k)=\frac{{\sum }_{l\in L^c}{\text{FLOPs}}_l}{{\text{FLOPS}}_0}\forall i\in I,& (3)\end{array}$

where $l\in L^b$ denotes the sum of all layers of $L^b$.

In practice, the computation time of the device must also take into account the memory and structure of the device itself and the data transfer between results. The computation time presented in this paper is an approximate estimation based on model simplification. However, it does not affect the subsequent performance analysis and results.

3.4 Communication model

Assuming a constant transmission delay for the wired network and considering the negligible impact of detection result data on transmission delay compared to sample data, this paper solely focuses on the wireless uplink transmission process from marine monitoring device to APs.

Let $W=\phi v_l$ denote the size (in bits) of the output data in the middle layer l, where φ is the size in bits of one floating point number and output data in layer l has v_lfloating point numbers.

Assume that $z^T(k)\in {ℝ}^{\left|I\right|}$ denotes the decision vector for the allocation of bandwidth during time slot k, and the element $z_i^T(k)$ denotes the proportion of bandwidth assigned to device i and ${\displaystyle {\sum }_i^I{z}_i^T(k)\le 1}$.

The electromagnetic interference over the sea surface that causes the transmission delay of device i in time slot k via the AP can be expressed as (Liu et al., 2022):

$\begin{array}{ll}{t}_i^T(k)=\frac{W}{[z_i^T(k)+ϵ]B{\log }_2(1+\frac{p_i{g}_i}{{\sigma }^2})}\forall i\in I,& (4)\end{array}$

where p_i is the transmit power of device i, g_i is the constant transmit power gain of the up link between device i and the AP, σ² is the waveguide channel noise, and the bandwidth used is B, where ϵ is a very small constant parameter with $0<ϵ\ll 1$, assuming the $t_i^{(1)}=(W/B[lo{g}_2(1+p_i{g}_i/{\sigma }^2)])$.

3.5 Energy model

The local computational energy consumption of the lightweight model at device i denoted by $e_i^A$ is given by

$\begin{array}{ll}{e}_i^A={\kappa }_i{(f_i)}^3{t}_i^A={\kappa }_i{(f_i)}^2{\displaystyle {\sum }_{l\in L^a}{u}_l\forall i\in I.}& (5)\end{array}$

The local computational energy consumption of a partially full model at device i can be demoted by $e_i^B$, which is given by

$\begin{array}{ll}{e}_i^B={\kappa }_i{(f_i)}^3{t}_i^B={\kappa }_i{(f_i)}^2{\displaystyle {\sum }_{l\in L^b}{u}_l\forall i\in I,}& (6)\end{array}$

where κ_i is the energy efficiency factor of device i (Lin et al., 2021).

The transmission energy loss of offloading an intermediate data sample from device i to the AP during time slot k is denoted by $e_i^T(k)$, which is given by

$\begin{array}{ll}{e}_i^T(k)=p_i{t}_i^T(k)\forall i\in I.& (7)\end{array}$

3.6 Cumulative confidence model for object detection

Consider an object detection task with categories M = {1,…,|M|}. YOLOv5 object detection framework detects a sequence of video frames and obtains a vector C of object detection results, C = (c₁,c₂,…,c_j). j is the total number of video frames extracted. c_i is the result of a video frame detection, i ∈ [1,j], where c_i= c{i,m}. Accumulate the detection results from 1 to j frames to get the cumulative target detection results for category m expressed as o_j,m, written as Qu et al. (2023)

$\begin{array}{ll}{o}_{j,m}=\frac{Pr(Y=m){\prod }_{j^{\prime }=1}^{j}Pr(c_{j^{\prime }}|Y=m)}{{\sum }_{m=1}^M[Pr(Y=m){\prod }_{j^{\prime }=1}^{j}Pr(c_{j^{\prime }}|Y=m)]}& (8)\end{array}$

In order to better quantify the value of the resulting o_j,m, we use a measure of the confidence level of the cumulative target detection results in the form of normalized entropy. The confidence level o is:

$\begin{array}{ll}\eta (o_{j,m})=1+{\displaystyle {\sum }_{m=1}^M\frac{o_{j,m}lo{g}_2(o_{j,m})}{lo{g}_{2}M},}& (9)\end{array}$

where η(z) has a value between 0 and 1 (Teerapittayanon et al., 2016, 2017).

The lightweight model and the full model are accumulated for the obtained target detection results according to (Equation 9).

Let ${\eta }_k\in {ℛ}^{\left|L\right|}$ denote the cumulative confidence level of each device in time slot k, where the element η_i(k) denotes the cumulative confidence level of device i at time slot k and ${\eta }_i(1)=0.\eta i(k)$ is obtained from (Equations 8, 9). For each device i, the object detection results need to be accumulated over multiple time slots until the device task requirements are satisfied. η_T represents the task requirements on the device, where ${\eta }_T=({\eta }_T(1),{\eta }_T(2),\dots ,{\eta }_T(i),\dots ,{\eta }_T(I))$ is the task threshold vector. η_T(i) is the task threshold for device i. P_i(k) denotes the delay penalty suffered by device i in time slot k. K_i is the task time limit for device i. P_i(k) is computed by the following rule: the P_i(k) is 0 when 1 ≤ k ≤ K_i, when k ≥ K_i, P_i(k) = (k − K_i+ 1)P, if η_i(k)< η_T, P is the delay penalty factor; thus, it can be obtained as

$\begin{array}{ll}{P}_i(k)=\{\begin{array}{ll}{(k-K_i+1)}^{+}P,\hfill & \text{if} {\eta }_i(k)<{\eta }_T\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}& (10)\end{array}$

4 Problem formulation and algorithm design

4.1 Joint offloading and resource allocation for multi-device cumulative object detection computation

In object detection tasks, the full model has higher accuracy than the lightweight model. More data can be offloaded via additional communication resources to quickly improve the detection confidence. In this paper, we are concerned with expressing the network resource consumption as a percentage of the bandwidth used within the region. ζ(k) is defined as the consumption ratio of system network resource in time slot k, where ζ(k) ∈ [0,1]. Thus, by refer to Subsection 3.4, we have:

$\begin{array}{ll}{\displaystyle {\sum }_{\forall i\in I}{z}_i^T(k)\le \zeta (k).}& (11)\end{array}$

According to Equations 1–4, for local computation edge computation and the total delay of transmission does not exceed the length of the designated time slot τ, which can be expressed as follows

$\begin{array}{ll}\{\begin{array}{l}{a}_i(k)[t_i^T(k)+t_i^E(k)+t_i^B]\le \tau ,\forall i\in I\\ t_i^A\le \tau ,\forall i\in I,\end{array}& (12)\end{array}$

to ensure each device’s task is completed within a single time slot (Bai et al., 2024).

Let $\psi (k)=\left\{\psi i(k),\forall i \in I\right\}$ be an auxiliary set of binary decision variables in the corresponding time slot k, where ψ_i(k) = 1 indicates that device i offloads data to the edge server and ψ_i(k) = 0 indicates that the task is completed on device i.

Let e_i(k) denote the total energy consumption of device i in time slot k, including transmission energy and local computation energy, calculated by (Equations 5–7)

$\begin{array}{ll}\begin{array}{l}{e}_i(k)={\psi }_i(k)a_i(k)(e_i^T(k)+e_i^B(k))+\\ [1-{\psi }_i(k)]e_i^A\forall i\in I.\end{array}& (13)\end{array}$

We consider differences in the focus on network and local resources in different scenarios. We denote the linear weighting factor of network and local resources by ω₁ ∈ (0,1). The total cost of time slot k is defined as c(k) which can be calculated by Equation 13

$\begin{array}{ll}c(k)={\omega }_1{\displaystyle {\sum }_{\forall i\in I}{e}_i(k)+(1-{\omega }_1)\zeta (k),}& (14)\end{array}$

When ω₁ is greater, the system is more inclined to prioritize local resources. In contrast, when ω₁ is smaller, the system is more inclined to prioritize network resources. Thus, our objective is to minimize (Equation 14) across all devices i in the system, as indicated by

$\begin{array}{ll}\underset{z^T(k),\zeta (k),a_i(k)}{\min }{\displaystyle {\sum }_k^{K}c(k)}& (15)\end{array}$

$\begin{array}{ll}s.t.z_i^T(k),\zeta (k)\in [0,1]\forall i\in I& (16)\end{array}$

$\begin{array}{ll}{\eta }_i(K)\ge {\eta }_T(i)\forall i\in I& (17)\end{array}$

$\begin{array}{ll}K=\underset{k}{\text{arg min}}({\eta }_i(k)\ge {\eta }_T(i))\forall i\in I.& (18)\end{array}$

Combining the equations above, it can be deduced that the target problem is a typical MINLP problem, which is also an NP-Hard problem. (Equation 16) denotes the value ranges of variables z_i^T(k) and ζ(k). (Equation 16) indicates that the device i completes the task in slot k in time τ. (Equation 11) indicates that the sum of network resources allocated to all devices must be less than ζ(k). (Equation 17) shows that the final task confidence must meet the threshold. (Equation 18) represents the need to minimize K.

In this paper, the action space is limited. In order to solve the computational complexity caused by multiple variables, we split the system completion process into each time slot. Considered as a subproblem within a certain time slot, we first determine the integer unloading decision variable a_kto find the corresponding minimum energy consumption c(k) and the corresponding ζ(k) and z^T(k) of the action, which we define as c^∗(k), ζ^∗(k), and z^T∗(k) (shown by Subsection 4.2). For the long-term adaptive offloading problem, the offloading decision of each device is determined based on the change of network state by transforming the adaptive offloading problem into MDP, as shown by Subsection 4.3.

4.2 Subproblem of resource allocation

Given the offloading decision vector a_k for time slot k, the optimization problem regarding total cost c(k) is as follows:

$\begin{array}{ll}\underset{z^T(k),\zeta (k)}{\min }c(k)& (19)\end{array}$

(Equations 11, 12, 16) (20) where Equation 20 is a conditional constrain.

The multi-objective combinatorial convex optimization issue discussed above is solved in this study using heuristic techniques (Zhou and Hua, 2022; Du et al., 2023). CRO is an effective heuristic method with fast convergence and a strong global search capability. It can be readily parallelized, is resilient to changes in parameters, and is not constrained by the initial solution. Consequently, the global optimal solution can be found efficiently for difficult optimization problems by employing CRO (Taylor et al., 2023).

We define the molecular group as X = {X₁,X₂,…,X_i} and define an action in the action space as a^∗. The corresponding molecular solution form for the two variables ζ(k) and z^T(k) can be denoted as X_i= {x₁,x₂,…x_i}, where x_i is an atom in the solution space, x_i= {0,1}.

We define P_E as the potential energy of the molecule, representing the fitness function c(k), where a lower fitness function represents less energy spent by the system. K_E is defined as the kinetic energy of the molecule, representing the degree of activity of the molecule during the chemical reaction algorithm, i.e., the ability of ζ(k) and z^T(k) to continue participating in the reaction. We define N_m as the minimum number of collisions of the system, representing the number of times a molecule reaches the minimum P_E to participate in the reaction.

We initialize the maximum number of iterations $U.X_i^u$ is the numerator solution for the u-th iteration and initialize K_E and P_E. At each iteration, the next generation of molecules is generated from the current generation of molecules. There are four basic operational operators in which the generation takes place, namely, single molecule collision, single molecule decomposition, intermolecular collision, and molecule synthesis, as shown in Figure 4. Each operation operator consumes a certain amount of K_E. P_m is defined as the intermolecular reaction probability. Each iteration initializes p. If the molecular probability p ≤ p_m, a unimolecular reaction is performed and if p > p_m, a multimolecular reaction is performed.

Figure 4

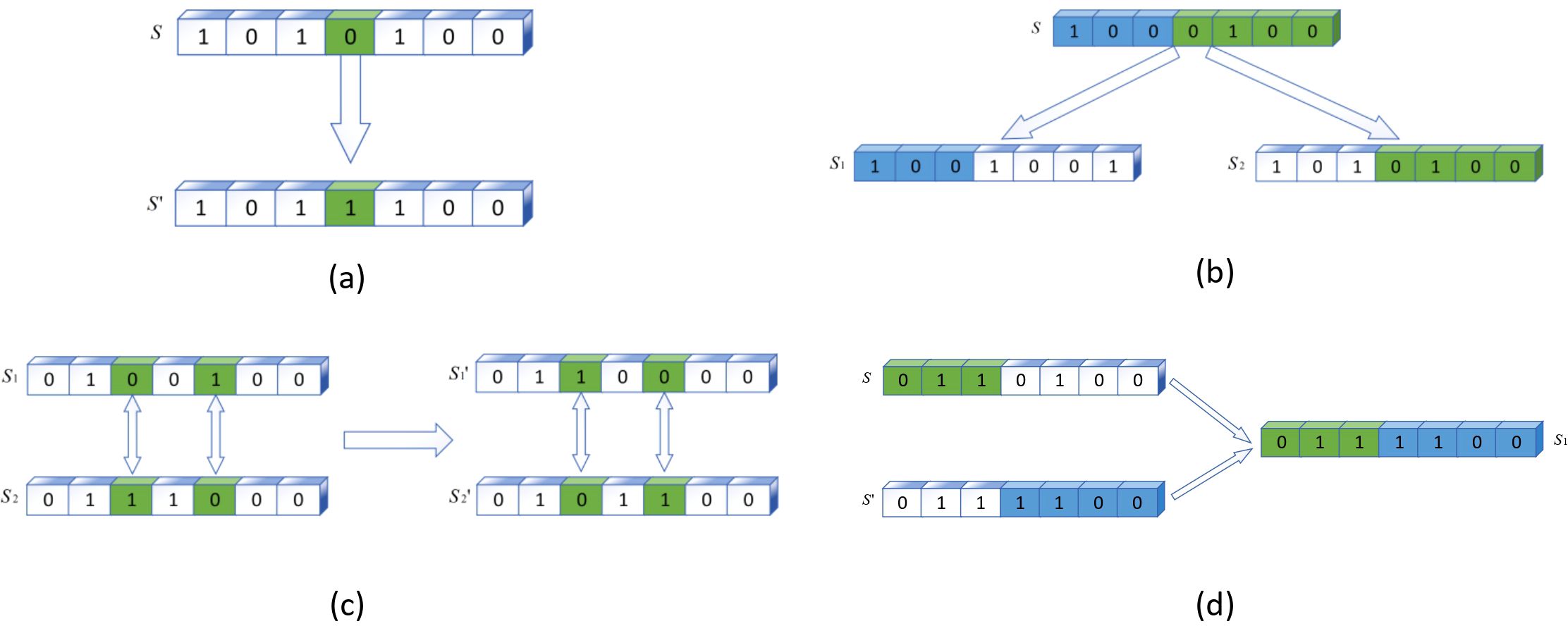
Figure 4. Schematic of the chemical reaction algorithm. (a) Single-molecule collisions. (b) Unimolecular decomposition. (c) Molecular collision. (d) Molecular synthesis.

In a multimolecular reaction, each molecular solution has a number of collisions $N^{\prime }$. When $N^{\prime }>N_m$, unimolecular decomposition takes place, $N^{\prime }\le N_m$, single molecule collision take place. In a multimolecular reaction, K_E > β_m, performs molecular synthesis. K_E≤ β_m, performs molecular collision. β_mis the threshold for performing molecular synthesis and is a constant. When there exists P_E≤ P_m, the reaction stops and the optimal molecular solution is obtained. P_m is a constant, i.e., the condition under which the reaction stops. Otherwise, continue to iterate the process above.

To achieve this, we can determine the optimal ζ^∗(k) and z^T∗(k) for each action in the current time slot. Substituting the solved equations back into (Equation 15) reduces its computational complexity and accelerates the convergence of the SNAP-DDPG algorithm.

4.3 Markov decision process construction

Given ζ^∗(k) and β^T∗(k) obtained in Section 4.2, bring in (Equation 19). (Equation 19) reduces to the a_k related adaptive offloading problem, denoted as

$\begin{array}{ll}\underset{a_i(k)}{\min }{\displaystyle {\sum }_k^K{c}^{*}(k)}& (21)\end{array}$

(Equations 17, 18) (22) where Equation 22 is a conditional constrain.

where K is the maximum of time slots in the system, satisfied with (Equation 18).

(Equation 21) simplifies to a sum of minimum energies with respect to action a_i(k). The system’s total cost is determined by the current marine environment state, confidence threshold, and device actions. These actions jointly trigger the system environment to transition into a new random state. Consequently, this paper models the problem as an MDP. We establish the MDP which is denoted as a tuple (S,A,P,R), where S is the state space, A is the action space, P is the state transfer probability matrix, R is the reward. The MDP state, action, and reward in this paper are as follows:

1. State: As images are detected and results are accumulated, the cumulative confidence of each device is dynamically changed over time through decision making. In order to fulfill the task requirements and satisfy the quality of service, the factors affecting the adaptive decision-making include η_i(k) and k. In addition, the number of lightweight object detection models executing on each device q_i(k) needs to be considered, represents the state of operation at the local device. B represents the real-time bandwidth status of the system, enabling dynamic adjustment decisions based on the bandwidth condition. Therefore, the state at time slot k is denoted by s_k, given by

$\begin{array}{ll}{s}_k=[q_i(k),{\eta }_i(k),k,B].& (23)\end{array}$

2. Action: Devices affect the environment through their actions. In this paper, the set of actions for all devices time slot k is an integer offloading decision vector a_k = {a₁(k),a₂(k),…,a_i(k)}, where a_i(k) denotes the number of times device i is offloaded at time slot k. The execution of actions should satisfy the constraints of q_k, as shown in Figure 3.

3. Satisfy the quality of service while minimizing the total cost and reducing the delay. The r_kin time slot k is

$\begin{array}{ll}{\displaystyle r_k=-\text{exp}({\omega }_2{c}^{*}(k))-\sum _{i\in I}{P}_i(k)-(\sum _{i\in I}({\eta }_T)}{\displaystyle -\sum _{i\in I}({\eta }_i(k))),}& (24)\end{array}$

where ω₂ represents the degree of focus between cost and delay and task completion, ω₂ > 0. c^∗(k) is the minimum cost by Subsection 4.2, and P_i(k) is the delay violation penalty, denoted as Equation 10. ${\displaystyle {\sum }_{i\in I}({\eta }_T)-{\displaystyle {\sum }_{i\in I}({\eta }_i(k))}}$ is the task completion penalty for each device between the confidence level at time slot k and the task metric.

4.4 Deep reinforcement learning solutions

The marine environment features high dynamicity and high-dimensional states. DDPG employs deep neural networks to approximate policy and value functions. It can handle high-dimensional state spaces. Through nonlinear mapping, it extracts key features to make effective offloading decisions.

4.4.1 Structure SNAP-DDPG

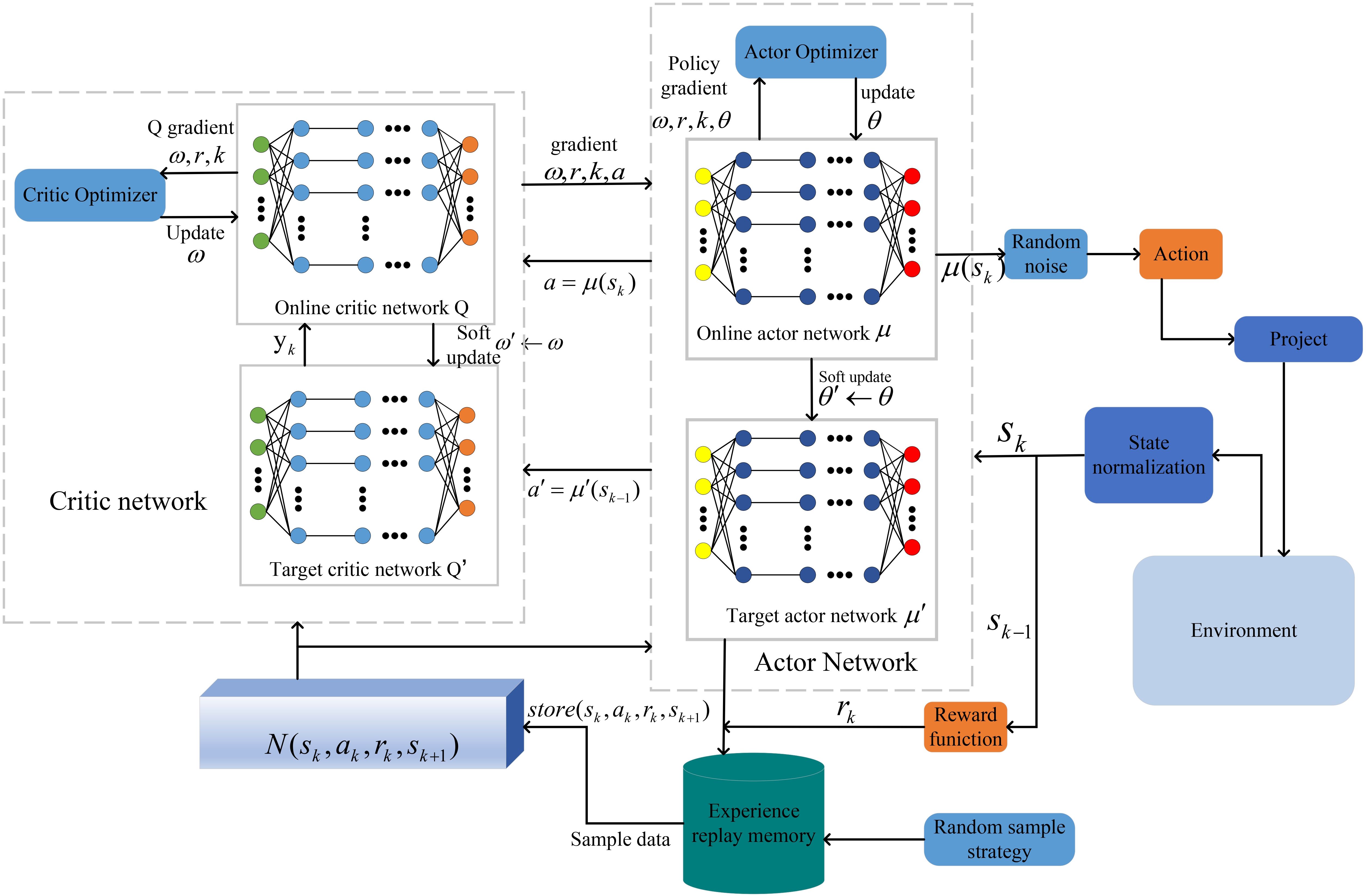
We propose a SNAP-DDPG algorithm to solve MDPs. The SNAP-DDPG algorithm uses the (ActorCritic) algorithm as the basic framework of the algorithm, and consists of online, target network and experience pool D. The DDPG network consists of an online actor network µ, an online critic network Q and a corresponding target network ${\mathit{\text{µ}}}^{\prime }$ and $Q^{\prime }$. The corresponding network parameters are $\omega ,{\omega }^{\prime },\theta ,{\theta }^{\prime }$. For the start of training, the experience pool D is emptied, and the random initialization parameters $\omega ,{\omega }^{\prime },\theta ,{\theta }^{\prime }$.

At the beginning of the DDPG algorithm, starting from time slot k, the agent of the system obtains the action a_k to be taken at that state by observing the current state of the environment, s_k, and according to the ϵ– greedy strategy.

The values of ϵ range from ϵ₀ to 1, ϵ₀ is a probability of exploration of ϵ decreases as the agent continues to be observed, with a decay factor △_ϵ ∈ (0,1), and there is a smooth transition from the probability of exploration to the probability of exploitation.

In order to further increase the randomness of learning and to increase the coverage of learning, a certain amount of random noise $\mathcal{N}$ is added to the actions. Where the current state action of the actor network is

$\begin{array}{ll}{a}_k=\mu (s_k|\theta )+\mathcal{N}.& (25)\end{array}$

In order to solve the problem of DDPG’s inability to handle discrete actions and to solve the problem of order-of-magnitude differences in the input variables. We propose a SNAP-DDPG algorithm.

We propose an action mapping approach. Mapping discrete actions into a continuous action space solves the problem that DDPG cannot handle discrete actions. During the initial process of the RL algorithm, we normalize the environment state. The maximum and minimum values of the training are stored in temporary memory by batch V training and the scaling factor is calculated. Addressing order-of-magnitude differences in input variables and improving training efficiency through normalization calculations. According to (Equation 23), the environment variable is set as $s_k=[q_i(k),{\eta }_i(k),k,B]$ as the state at time slot k, and the difference between the maximum and minimum values of each variable is used as the scaling factor, ${\varphi }_{qi(k)},{\varphi }_{{\eta }_i(k)},{\varphi }_k,{\varphi }_B$, to obtain the normalized environment variable $s_i(k^{\prime })=[q_i(k^{\prime }),{\eta }_i(k^{\prime }),k^{\prime },B^{\prime }]$. The specific steps of the algorithm are shown in Algorithm 1.

Algorithm 1. The SNAP-DDPG algorithm.

4.4.2 Implementation of the SNAP-DDPG

At the beginning of each event, the state of this RL is initialized to $s_1=[q_1,{\eta }_1,k_1,B_1]$. If all the tasks are full within the specified period, i.e., the total number of time slots for this event is less than $ma{x}_{i\in I}{K}_i,P_i(k)=0$. When the total number of time slots for the event is greater than $ma{x}_{i\in I}{K}_i$. u_k indicates the time slot status of the event, if u_k= 1, it means that the event ends at time slot k.

The system notifies each device of the new offloading decision based on the obtained action. At the end of time slot k, the agent computes the reward r_k (Equation 24) for action a_k and observes the new state s_k+1, and with the new cumulative confidence level η_k+1 updated by the cumulative object detection scheme on each device, the cumulative object detection scheme on each device, the new cached state q_k+1 can be updated based on q_k state. Judge the task completion status at the end of time slot k. If the task is completed, the system completion signal u_k= 1, if the task is not completed, the system completion signal u_k= 0. The communication overhead between the RL agent and the device can be considered negligible.

The new transition segments ($s_k,a_k,r_k,s_k{}_{+1},u_k$) are then added to the empirical memory in the SNAPDDPG, and a small batch of N experience need to be sampled from the memory in order to further compute the current target Q value, and thus the estimate of Target critic can be expressed as:

$\begin{array}{ll}{y}_k=r_k+\gamma Q^{\prime }(s_{k+1},{\mu }^{\prime }(s_{k+1}|{\theta }^{\prime })|{\omega }^{\prime })& (26)\end{array}$

where k is the time slot the current system is in, ${\mathit{\text{µ}}}^{\prime }(s_k{}_{+1}|{\theta }^{\prime })$ is the target actor’s action for time slot $k+1,{\theta }^{\prime },{\omega }^{\prime }$ are the network parameters of ${\mu }^{\prime }$ and $Q^{\prime }$, respectively, and γ is the discount factor.

Based on the output of online critic Q and the estimate of target critic $Q^{\prime }$ the loss function is obtained as

$\begin{array}{ll}L(\omega )=\mathbb{E}[{(y_k-Q(s_k,a_k|\omega ))}^2],& (27)\end{array}$

where $y_k-Q(s_k,a_k|\omega )$ denotes the timing difference error (TD-error), and then the parameters are updated according to the minimization loss function, which can be obtained by supervised learning of the mean-squared error loss (MES) function to find the gradient, given by

$\begin{array}{ll}{▽}_{\omega }L(\omega )=\mathbb{E}[2(y_k-Q(s_k,a_k|\omega )){▽}_{\omega }Q(s_k,a_k)].& (28)\end{array}$

Online critic network implements critic network parameters update according to the gradient rule of neural network, given by

$\begin{array}{ll}\omega \leftarrow \omega +\alpha {▽}_{\omega }L(\omega ),& (29)\end{array}$

where α is the learning rate of the online critic network.

Next, updating the actor network using the policy gradient method, given by

$\begin{array}{ll}{▽}_{\theta }\mu ={▽}_{\alpha }Q(s,a|\omega ){|}_{s=s_k,a=\mu (s_k)}{▽}_{\theta }\mu (s|\theta ){|}_{s=s_k}.& (30)\end{array}$

The parameters of the online actor network are updated by

$\begin{array}{ll}\theta \leftarrow \theta +\beta {▽}_{\theta }\mu ,& (31)\end{array}$

where β is the learning rate of online actor network. For SNAP-DDPG, the target network parameters are updated every certain number of steps and a soft update is used to prevent unstable convergence, the target network parameters are updated, given by

$\begin{array}{ll}\{\begin{array}{ll}\hfill & {\omega }^{\prime }\leftarrow \tau \omega +(1-\tau ){\omega }^{\prime }\hfill \\ \hfill & {\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime },\hfill \end{array}& (32)\end{array}$

where τ ∈ (0,1) denotes the soft update coefficient.

5 Simulation and discussion

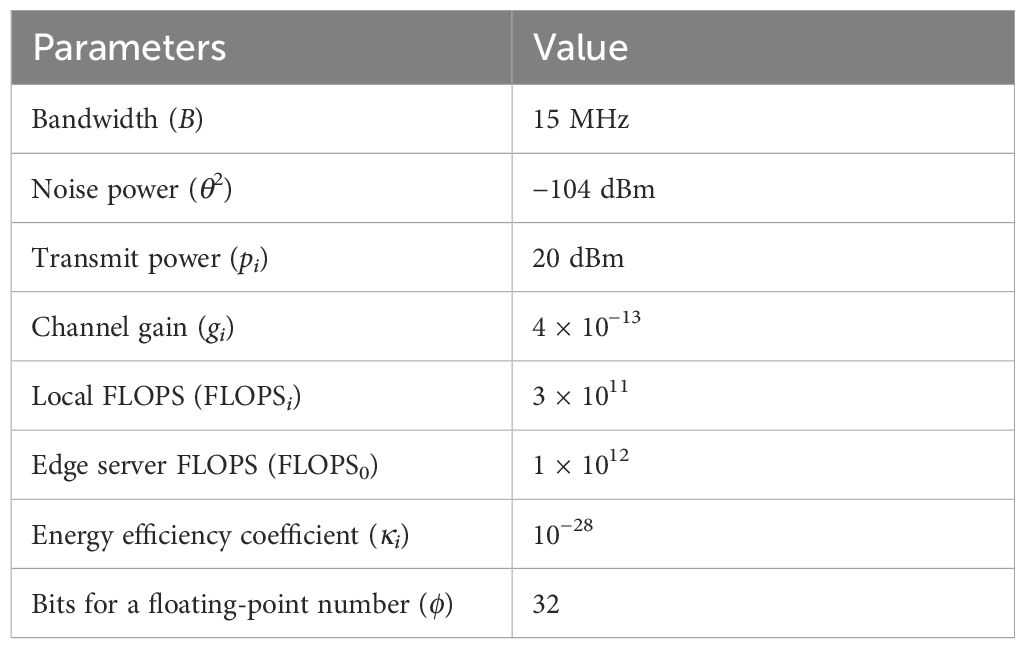
We consider three maritime mobile video collection devices performing independent tasks within a maritime AP’s coverage. In our example, YOLOv5s is the full model, and the YOLOv5s-based MobileNetv3 is the lightweight model (Zhang et al., 2021). Each device’s classification task involves cumulative confidence operations on a sequence of video frames until customer requirements are met. It is assumed that each device has the same task completion time in the number of time slots. Each device has the same confidence level requirement for its classification task, η_Tis set to (0.93,0.95,0.97), and the other system parameters are shown in Table 2. The selected data set includes 7,467 water surface images under diverse maritime areas, climatic conditions, and shooting times. It also covers 14 common object categories and focuses more on specific scenarios (Zhou et al., 2021). To train the marine target detection model, we constructed a dataset with 5,900 training samples, 740 validation samples, and 740 testing samples. The algorithm model is shown in Figure 5.

Table 2

Table 2. System parameters in simulation.

Figure 5

Figure 5. SNAP-DDPG algorithm structure.

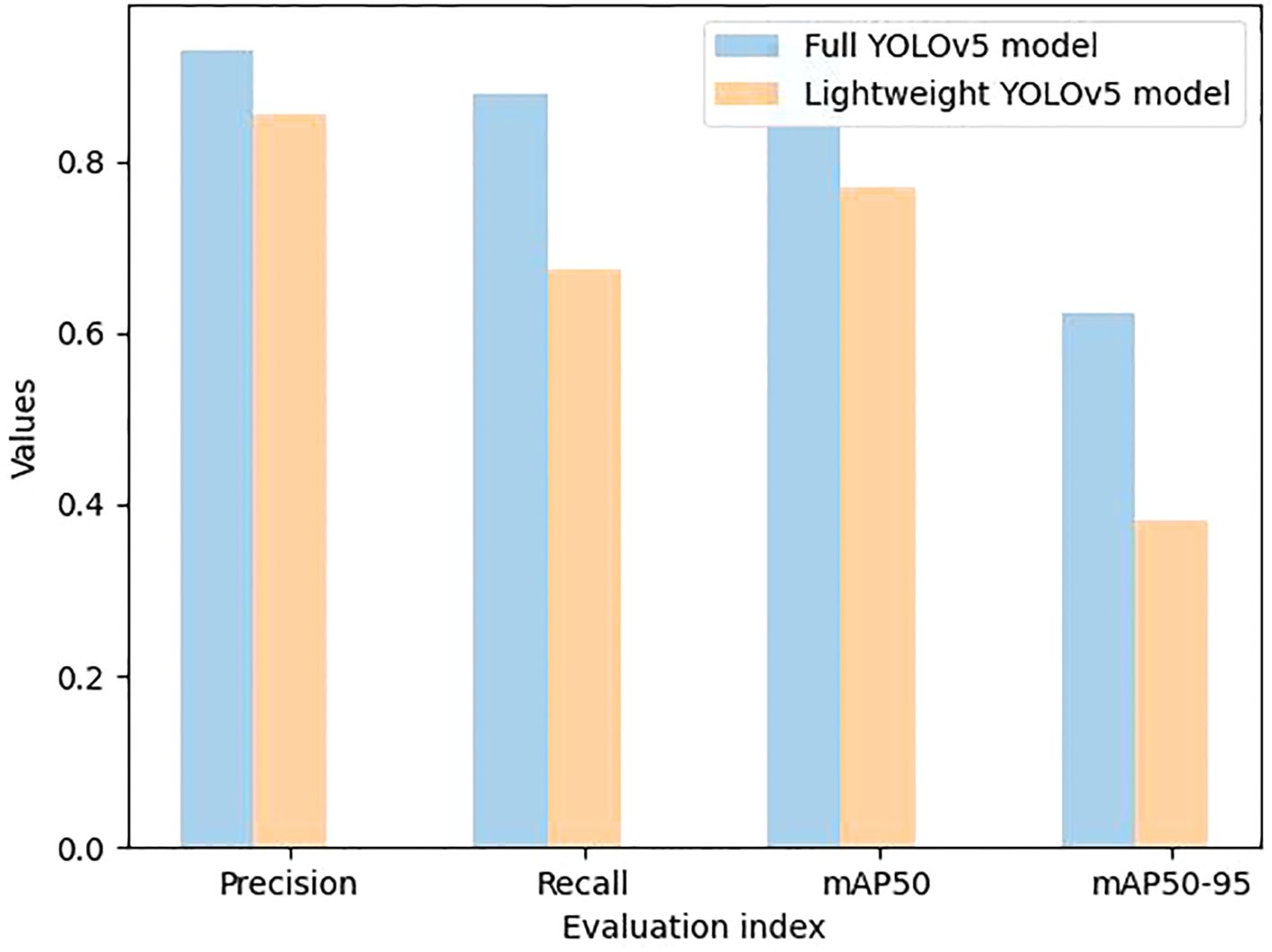
Comparing the two models in the system, the full model has 7,022,326 parameters and 214 layers, while the parameter of the lightweight model decreases to 5,024,100, which improves the inference speed of the model. The full model and the lightweight model are trained separately on the established dataset, and the precision, recall, class average precision, and other metrics can be obtained by training 200 rounds, as shown in the following Figure 6.

Figure 6

Figure 6. Model detection performance comparison.

Precision, recall, and mean average precision (mAP) were obtained through 300 training rounds, as shown in Figure 6. Although the YOLOv5s full model surpasses the YOLOv5s-based MobileNetv3 lightweight model in the number of model layers, parameters, and total computational cost (with computational costs of 15.94 FLOPs and 11.61 FLOPs, respectively), it outperforms the latter in terms of accuracy, recall, and mAP.

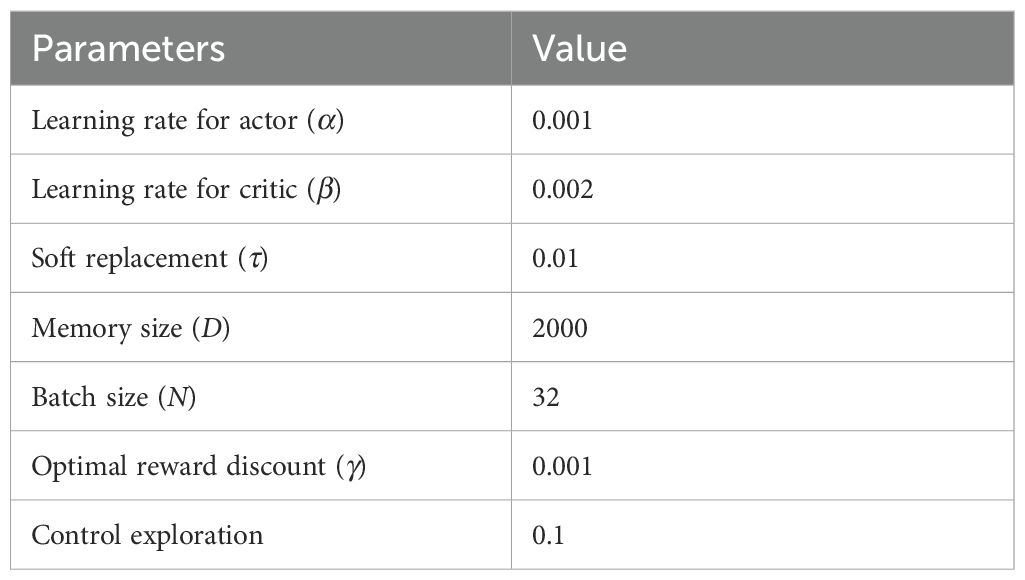
In the simulation setup, we set the time slot length as τ = 0.1, and in the case of an ideal network state, two computational offloads can be performed per time slot. Due to the constraints, the time slot size in the simulation in this paper is variable with respect to device resources but does not affect the subsequent simulation experiments. In the action space, each element in action $A=(a_1(k),a_2(k),.,a_i(k))$, represents the unloaded state of the corresponding device. In this paper, the 10 discrete unloading actions are as follows: (0,0,0), (0,0,1), (0,0,2), (0,1,0), (0,1,1), (0,2,0), (1,0,0), (1,0,1), (1,1,0), (2,0,0). We set weight ω₂ = 1 and delay penalty factor P = 1 in the reward function. Other Learning parameters are summarized in Table 3. The discrete action space is adapted to the algorithmic system proposed in this paper by projecting the discrete actions into a continuous interval.

Table 3

Table 3. Parameters in the SNAP-DDPG algorithm.

We evaluate the cumulative object detection schemes in the system and compare lightweight and full model schemes. For the pig training set produced in this paper, using the full model or the lightweight model, the object detection is really carried out in the data samples in j consecutive time periods, and the j object detection results are generated. According to the proposed object detection accumulation scheme, j consecutive object detection results are accumulated. Assume that a device produces a detection result in a time slot. In the average method, the confidence levels from 1 to j are expectation computed to obtain the cumulative confidence level of time slot j. In the max method, the confidence level with the largest confidence level before time slot j is selected as the cumulative confidence level of the current time slot k. The proposed method is shown in (Equations 9, 8). The results are shown in Figure 7.

Figure 7

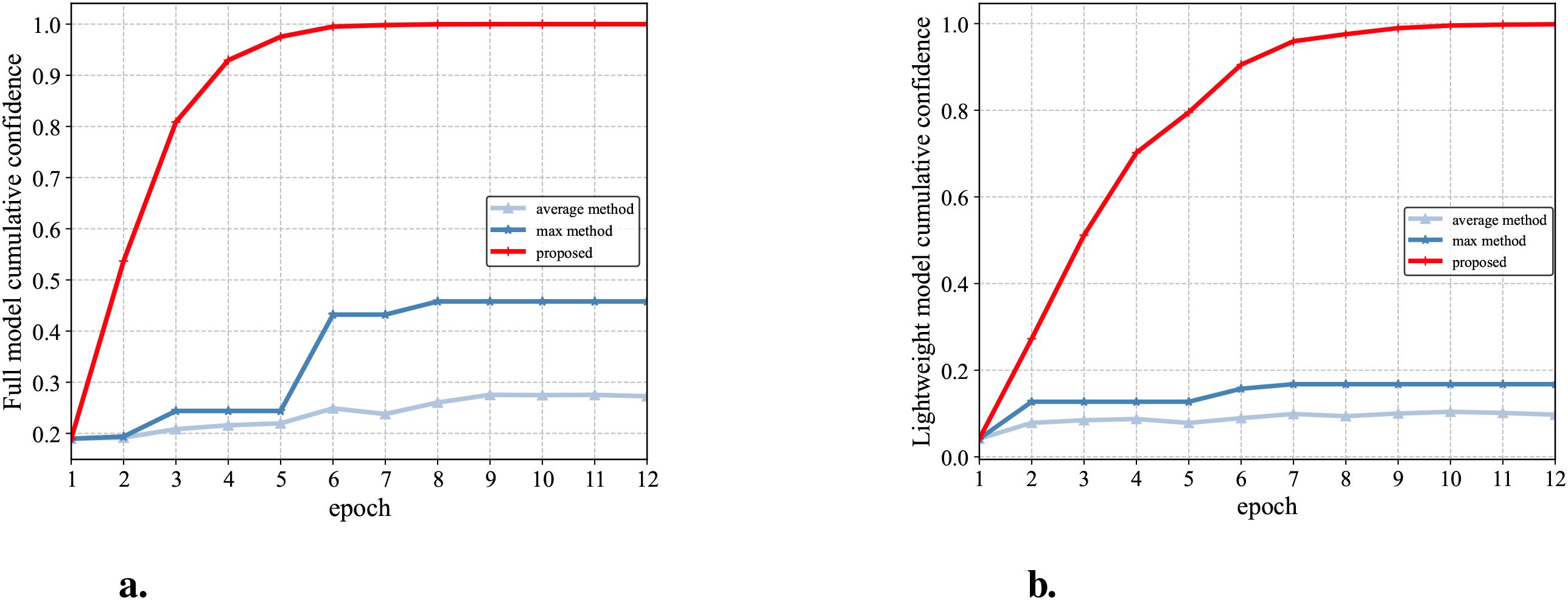
Figure 7. Comparison of the performance of (a) the full model and (b) the lightweight model for different cumulative object detection schemes.

As shown in Figure 7, the average method cannot correlate the information between images and can only ensure that the average detection accuracy remains stable and is not affected by accidental results. Max method will cause a sudden increase in confidence due to a certain result and also cannot correlate the information between images. However, the proposed method proposed in this paper is able to correlate image information in continuous time slots. The confidence level of the detection models in Figures 7a, b is close to 1 after round 10. The confidence level of both models is close to 1 after round 10. After practical verification, it is also obtained that the detection results of the detected objects are consistent with the results obtained at the confidence level of the scheme. By accumulating more target detection results, the probability of object detection category is improved.

Next, this study will specifically examine the effectiveness of random cumulative confidence schemes. A set of random consecutive video frames are placed into both the full model and the lightweight model to obtain a set of object detection results. As the number of data samples j increases, the cumulative confidence η(o_j,m), cumulative true class probability o_j,m, and true class probability z_j,mof the proposed cumulative detection scheme are shown in Figure 8.

Figure 8

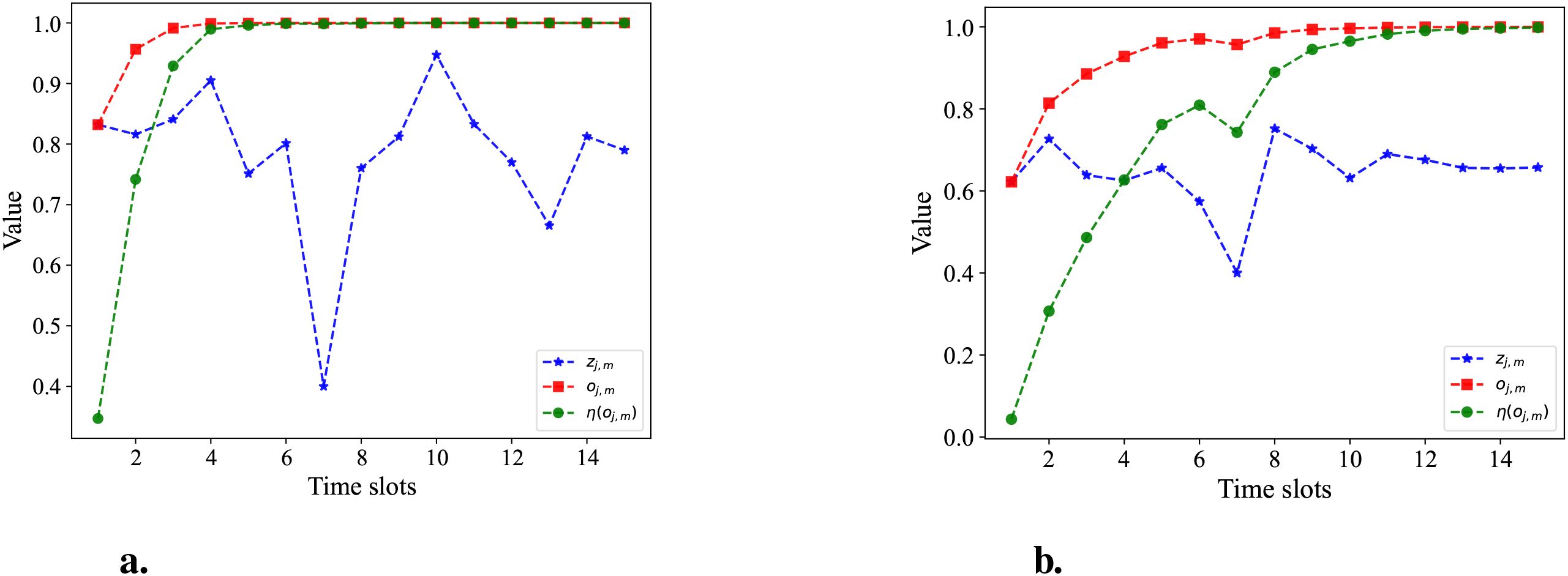
Figure 8. Comparing (a) the full model and (b) the lightweight model. The cumulative confidence and cumulative probability of detection vary over time slot.

From Figure 8, the accuracy of the lightweight model on the right is lower than that of the full model on the left. In the setup validation scenario, the cumulative confidence of Figure 8a tends to be close to 1 after 10 rounds, and even if there is a wrong detection in the seventh round of the scenario, the cumulative confidence is still able to get the correct detection result in the entire object detection application process, and the cumulative detection accuracy and cumulative confidence have an upward trend. For Figure 8b, the cumulative confidence has converged to 1 after the 6th round only, even if there is a misdetection in the detection and classification in the 7th round, but it does not affect the overall detection results. Compared to the lightweight model, the growth rate of cumulative confidence per round of the full model in Figure 8a is higher than that of the lightweight model in Figure 8b.

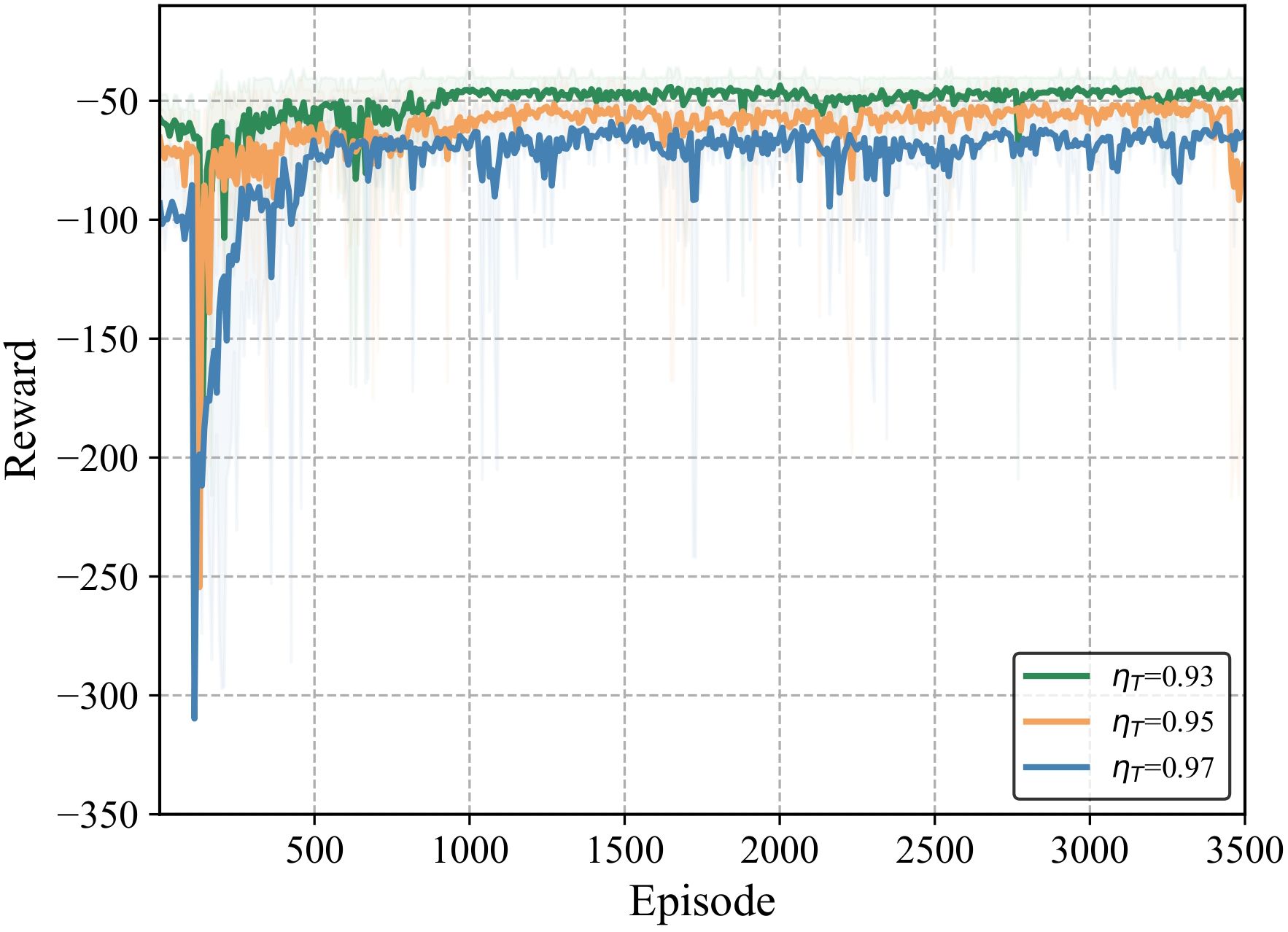
The selection of actions requires different strategies for various classification task metrics. Figure 9 represents the total rewards of each scene during the training process when ω₁ = 0.70 and η_T= 0.93, 0.95, and 0.97, respectively. The task confidence of each device is set to the same value for ease of analysis. The total reward grows fastest when η_T= 0.93 and converges around 500. In contrast, when η_T= 0.95, the total reward converges slower and converges after 700 rounds. Compared to the reward value at η_T= 0.93, the system has a smaller task requirement and a smaller cumulative picture sample requirement at η_T= 0.93. The system reaches convergence with a smaller total reward. The total reward for η_T= 0.97 converges the worst, with larger penalties for delayed violations before round 1,000, resulting in lower total reward values, and fluctuating more from rounds 1,500 to 2,000, before finally stabilizing at around 2,500.

Figure 9

Figure 9. Reward comparison with different values of η for ω₁ = 0.70.

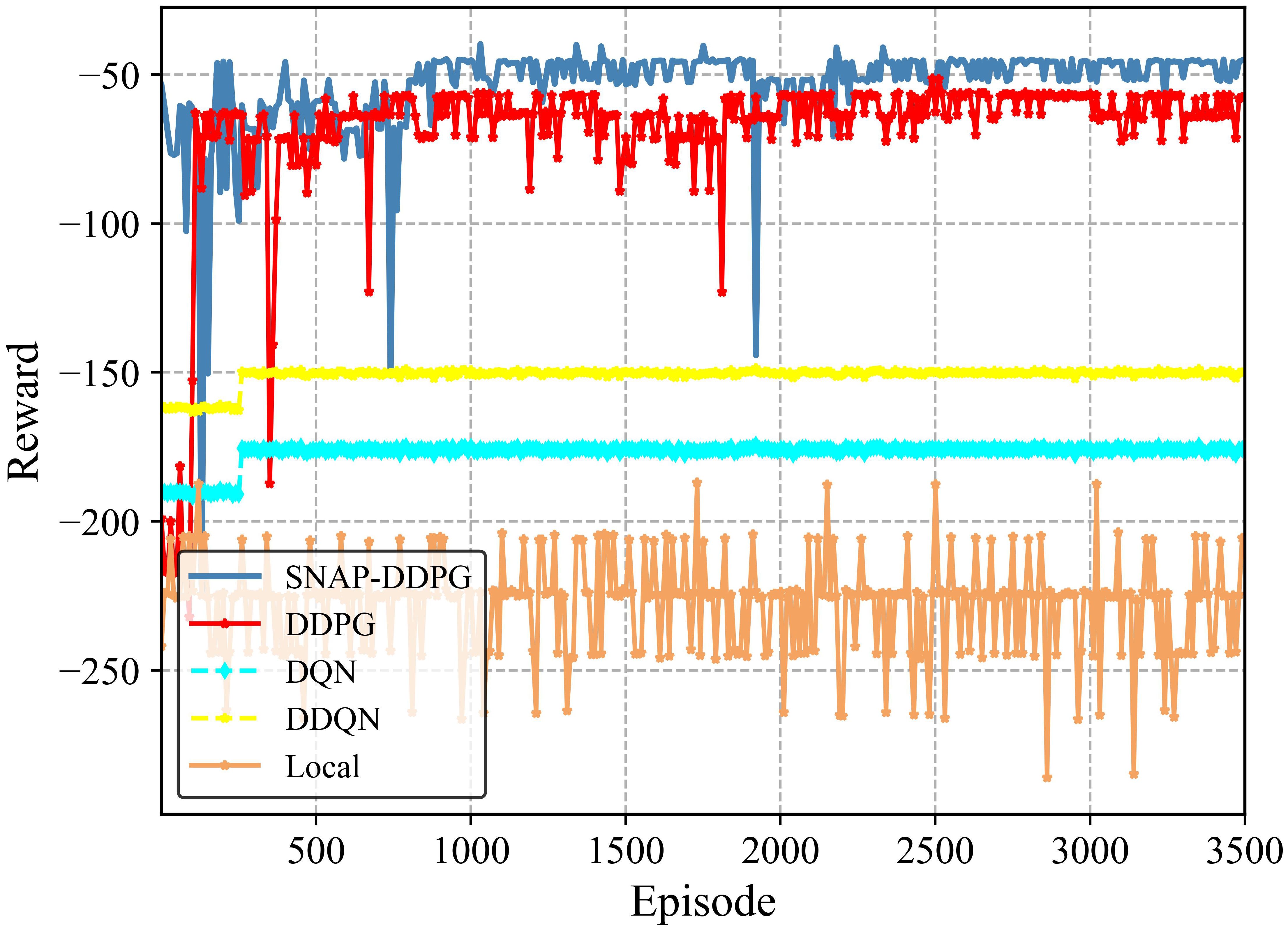
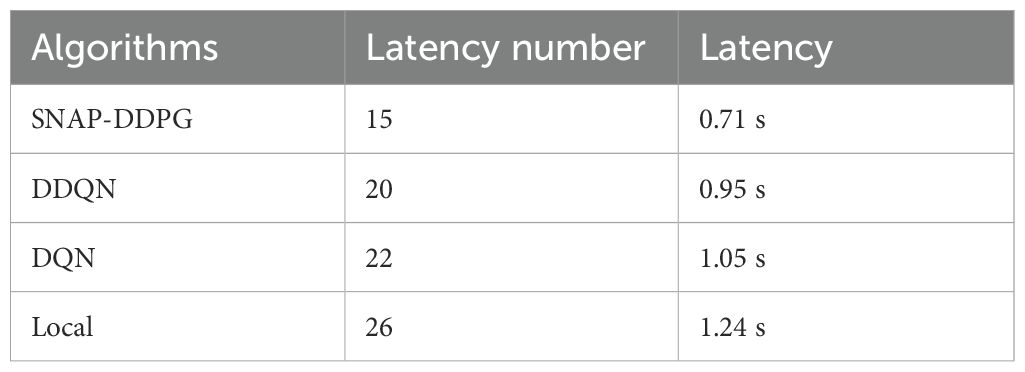
Figure 10 shows the reward performance of DQN, DDQN, DDPG, SNAP-DDPG, and local-only at η = 0.95. Due to limited marine local computing resources, local-only offloading needs many time slots to meet customer confidence requirements, so its reward is lower than the other three algorithms. Compared to SNAP-DDPG, DQN and DDQN updates, based on the current strategy, are prone to interference, leading to local convergence of around 500 episodes and limiting reward improvement. In contrast, SNAP-DDPG uses state normalization to reduce input parameter dimensionality differences and accelerate convergence. Compared to DDPG, SNAP-DDPG can better explore high-dimensional state spaces and achieve higher reward. The average running time slots for each algorithm at η = 0.95 are shown in Table 4.

Figure 10

Figure 10. Performance comparison under different algorithms with η = 0.95.

Table 4

Table 4. Task latency for different algorithms.

Figure 11 shows the variations of offloading counts and cumulative confidence over time slots under different network conditions. Compared with Figure 11b where the network is poor, Figure 11a enables faster confidence accumulation by offloading to invoke the full model. In contrast, in Figure 11b, the offloading strategy fluctuates with the network state and is adjusted by the SNAP-DDPG algorithm. It maintains local computing within time slots 6, 7, 10, 11 and 12, resulting in slow confidence growth and prolonged task completion times.

Figure 11

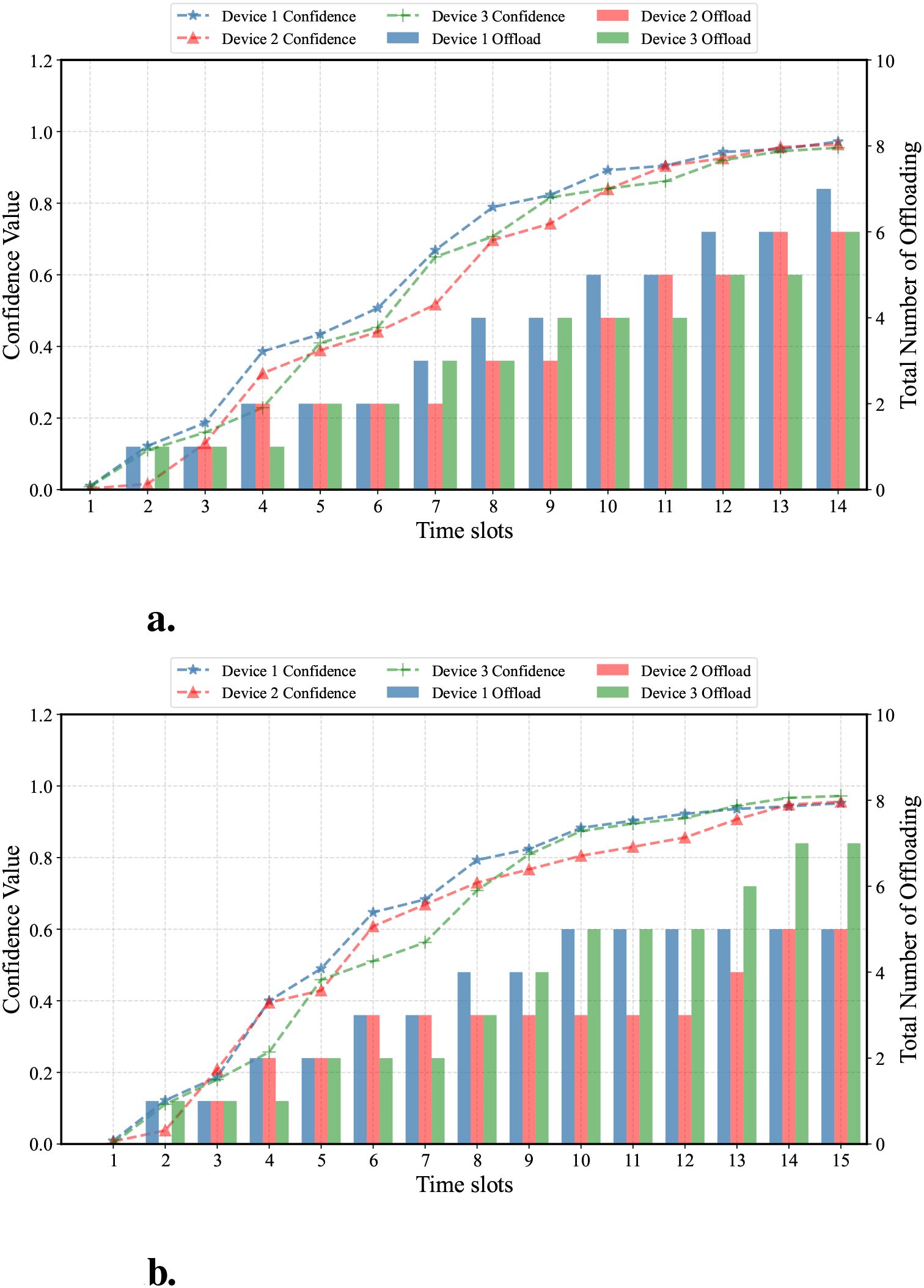
Figure 11. In a dynamic network, (a) is the number of offloaded tasks when the network is in good condition, varying over time slots (at time slot 5, the network is under-resourced), and (b) is the number of offloaded tasks when network resources are insufficient, also varying over time slots (at time slots 6, 7, 10, 11, and 12, the network is under-resourced).

Figure 12a illustrates the detection results obtained solely using the lightweight YOLOv5 model. Due to environmental factors, limitations inherent in the object detection model, and characteristics of the dataset, instances of missed detections and false positives may occur in specific video frames. As depicted in Figure 12b, by employing a cumulative confidence model to process the same scene, previously missed targets are subsequently identified through the accumulation of confidence scores over time. Conversely, falsely detected targets fail to meet the required confidence threshold and are therefore excluded from the detection.

Figure 12

Figure 12. The detection results (a) of the lightweight YOLOv5 model are compared with the detection results (b) of the adaptive offloading decisions for cumulative confidence models.

6 Conclusion

For image detection in MMEC scenarios, a cumulative confidence-driven joint scheduling strategy is proposed. An adaptive decision-making scheme for marine equipment is developed, factoring in object locations and the marine environment. It accumulates results to determine final detection confidence, supported by the SNAP-DDPG algorithm-based device policy. The simulation results verify that the framework maintains object detection confidence while cutting latency by 34.78%, providing a theoretical basis for CNN-based maritime tasks. In particular marine settings, the strategy boosts detection accuracy and cuts false-positive and false-negative rates compared to existing methods. It shows great potential in MIoT applications such as maritime target detection and UAV operations, where high reliability is crucial. Future work will center on designing service-rating strategies to enhance QoS, optimizing equipment task requirements in evaluation and segmentation networks, and incorporating spatial and temporal dimensions into target detection strategies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YS: Methodology, Writing – review & editing, Conceptualization. WL: Data curation, Formal Analysis, Writing – original draft. WX: Methodology, Writing – original draft. QM: Project administration, Writing – original draft. HP: Data curation, Methodology, Writing – original draft. LW: Project administration, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors would like to acknowledge Initiation Funding of Jimei University-Natural Sciences: ZQ2024099, the Jimei University Startup Research Project, Grant number ZQ2022015, Guidance Projects of Fujian Science Technology Agency: 2022H0022, the Project of the Xiamen Science and Technology Bureau: 2022CXY0317 to provide fund for conducting experiments.

Acknowledgments

The dataset in this paper is from Zhou et al. (2021). Thanks to the author for generously sharing it. We would also like to express our sincere appreciation to the editor and reviewers who provided valuable comments to help improve this paper. Additionally, we are grateful to the researchers who provided comparative methods.

Conflict of interest

Author LW was employed by the company Fujian Xinzhi Information Technology Co., LTD.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai Z., Lin Y., Cao Y., and Wang W. (2024). Delay-aware cooperative task offloading for Multi-UAV enabled edge-cloud computing. IEEE Trans. Mobile Computing 23, 1034–1049. doi: 10.1109/TMC.2022.3232375

Crossref Full Text | Google Scholar

Chen X., Wang M., Ling J., Wu H., Wu B., and Li C. (2024). Ship imaging trajectory extraction via an aggregated you only look once (YOLO) model. Eng. Appl. Artif. Intell. 130, 107742. doi: 10.1016/j.engappai.2023.107742

Crossref Full Text | Google Scholar

Chen X., Wei C., Xin Z., Zhao J., and Xian J. (2023). Ship detection under low-visibility weather interference via an ensemble generative adversarial network. J. Mar. Sci. Eng. 11, 2065. doi: 10.3390/jmse11112065

Crossref Full Text | Google Scholar

Cheng M., Zhu C., Lin M., and Zhu W.-P. (2024). “A MAPPO based scheme for joint resource allocation in uav assisted MEC networks,” in 2024 IEEE/CIC international conference on communications in China (ICCC) (Hangzhou, China: IEEE), 42–47.

Google Scholar

Du R., Liu C., Gao Y., Hao P., and Wang Z. (2022). Collaborative cloud-edge-end task offloading in NOMA-enabled mobile edge computing using deep learning. J. Grid Computing 20, 14. doi: 10.1007/s10723-022-09605-2

Crossref Full Text | Google Scholar

Du W., Ma J., and Yin W. (2023). Orderly charging strategy of electric vehicle based on improved PSO algorithm. Energy 271, 127088. doi: 10.1016/j.energy.2023.127088

Crossref Full Text | Google Scholar

Duan Y. and Wu J. (2023). Optimizing job offloading schedule for collaborative DNN inference. IEEE Trans. Mobile Computing 23, 3436–3451. doi: 10.1109/TMC.2023.3276937

Crossref Full Text | Google Scholar

Gai R., Chen N., and Yuan H. (2023). A detection algorithm for cherry fruits based on the improved YOLO-v4 model. Neural computing Appl. 35, 13895–13906. doi: 10.1007/s00521-021-06029-z

Crossref Full Text | Google Scholar

Heller D., Rizk M., Douguet R., Baghdadi A., and Diguet J.-P. (2022). “Marine objects detection using deep learning on embedded edge devices,” in 2022 IEEE international workshop on rapid system prototyping (RSP) (Shanghai, China: IEEE), 1–7.

Google Scholar

Jiang W., Han H., Feng D., Qian L., Wang Q., and Xia X.-G. (2025). Energy-efficient and accuracyaware DNN inference with IoT device-edge collaboration. IEEE Trans. Serv. Computing 18, 784–797. doi: 10.1109/TSC.2025.3536311

Crossref Full Text | Google Scholar

Li H., Wu S., Jiao J., Lin X.-H., Zhang N., and Zhang Q. (2023). Energy-efficient task offloading of edge-aided maritime UAV systems. IEEE Trans. Vehicular Technol. 72, 1116–1126. doi: 10.1109/TVT.2022.3205127

Crossref Full Text | Google Scholar

Liao Z., Hu W., Huang J., and Wang J. (2023). Joint multi-user DNN partitioning and task offloading in mobile edge computing. Ad Hoc Networks 144, 103156. doi: 10.1016/j.adhoc.2023.103156

Crossref Full Text | Google Scholar

Lin Z., Bi S., and Zhang Y.-J. A. (2021). Optimizing AI service placement and resource allocation in mobile edge intelligence systems. IEEE Trans. Wireless Commun. 20, 7257–7271. doi: 10.1109/TWC.2021.3081991

Crossref Full Text | Google Scholar

Liu R. W., Hu K., Liang M., Li Y., Liu X., and Yang D. (2023b). QSD-LSTM: Vessel trajectory prediction using long short-term memory with quaternion ship domain. Appl. Ocean Res. 136, 103592. doi: 10.1016/j.apor.2023.103592

Crossref Full Text | Google Scholar

Liu R. W., Lu Y., Guo Y., Ren W., Zhu F., and Lv Y. (2023c). Aioenet: All-in-one low-visibility enhancement to improve visual perception for intelligent marine vehicles under severe weather conditions. IEEE Trans. Intelligent Vehicles 9, 3811–3826. doi: 10.1109/TIV.2023.3347952

Crossref Full Text | Google Scholar

Liu Y., Yan J., and Zhao X. (2022). Deep reinforcement learning based latency minimization for mobile edge computing with virtualization in maritime UAV communication network. IEEE Trans. Vehicular Technol. 71, 4225–4236. doi: 10.1109/TVT.2022.3141799

Crossref Full Text | Google Scholar

Liu J., Zhang L., Li Y., and Liu H. (2023a). Deep residual convolutional neural network based on hybrid attention mechanism for ecological monitoring of marine fishery. Ecol. Inf. 77, 102204. doi: 10.1016/j.ecoinf.2023.102204

Crossref Full Text | Google Scholar

Lu Y., Guo Y., and Liang M. (2021). Cnn-enabled visibility enhancement framework for vessel detection under haze environment. J. advanced transportation 2021, 5598390. doi: 10.1155/2021/5598390

Crossref Full Text | Google Scholar

Munusamy A., Adhikari M., Khan M. A., Menon V. G., Srirama S. N., Alex L. T., et al. (2023). Edgecentric secure service provisioning in IoT-enabled maritime transportation systems. IEEE Trans. Intelligent Transportation Syst. 24, 2568–2577. doi: 10.1109/TITS.2021.3102957

Crossref Full Text | Google Scholar

Olorunshola O. E., Irhebhude M. E., and Evwiekpaefe A. E. (2023). A comparative study of YOLOv5 and YOLOv7 object detection algorithms. J. Computing Soc. Inf. 2, 1–12. doi: 10.33736/jcsi.5070.2023

Crossref Full Text | Google Scholar

Qi S., Lin B., Deng Y., Chen X., and Fang Y. (2024). Minimizing maximum latency of task offloading for multi-uav-assisted maritime search and rescue. IEEE Trans. Vehicular Technol. 73, 13625–13638. doi: 10.1109/TVT.2024.3384570

Crossref Full Text | Google Scholar

Qu K., Zhuang W., Wu W., Li M., Shen X., Li X., et al. (2023). Stochastic cumulative DNN inference with RL-aided adaptive IoT device-edge collaboration. IEEE Internet Things J. 10, 18000–18015. doi: 10.1109/JIOT.2023.3280746

Crossref Full Text | Google Scholar

Shakya A. K., Pillai G., and Chakrabarty S. (2023). Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 231, 120495. doi: 10.1016/j.eswa.2023.120495

Crossref Full Text | Google Scholar

Taylor C. J., Pomberger A., Felton K. C., Grainger R., Barecka M., Chamberlain T. W., et al. (2023). A brief introduction to chemical reaction optimization. Chem. Rev. 123, 3089–3126. doi: 10.1021/acs.chemrev.2c00798

PubMed Abstract | Crossref Full Text | Google Scholar

Teerapittayanon S., McDanel B., and Kung H.-T. (2016). “Branchynet: Fast inference via early exiting from deep neural networks,” in 2016 23rd international conference on pattern recognition (ICPR) (Cancun, Mexico: IEEE), 2464–2469.

Google Scholar

Teerapittayanon S., McDanel B., and Kung H.-T. (2017). “Distributed deep neural networks over the cloud, the edge and end devices,” in 2017 IEEE 37th international conference on distributed computing systems (ICDCS) (Atlanta, GA, USA: IEEE), 328–339.

Google Scholar

Vignesh S. and Dhamodaran S. (2024). “Unlocking the mysteries of the deep: Leveraging the power of mobilenet and YOLOv5 for efficient and accurate sea cucumber detection in underwater environments,” in 2024 international conference on recent innovation in smart and sustainable technology (ICRISST) (Bengaluru, India: IEEE), 1–8.

Google Scholar

Wang Z., Jin L., Wang S., and Xu H. (2022). Apple stem/calyx real-time recognition using YOLO-v5 algorithm for fruit automatic loading system. Postharvest Biol. Technol. 185, 111808. doi: 10.1016/j.postharvbio.2021.111808

Crossref Full Text | Google Scholar

Wang Z., Lin B., Ye Q., and Peng H. (2025). Two-tier task offloading for satellite-assisted marine networks: A hybrid stackelberg–bargaining game approach. IEEE Internet Things J. 12, 13047–13060. doi: 10.1109/JIOT.2024.3523527

Crossref Full Text | Google Scholar

Xiao Y., Xiao L., Wan K., Yang H., Zhang Y., Wu Y., et al. (2022). Reinforcement learning based energy-efficient collaborative inference for mobile edge computing. IEEE Trans. Commun. 71, 864–876. doi: 10.1109/TCOMM.2022.3229033

Crossref Full Text | Google Scholar

Xu W., Song Z., Gao Z., Lai L., Sun Y., and Luo W. (2024). Latency-aware MIoT service strategy in UAV-assisted dynamic MMEC environment. IEEE Internet Things J. 11, 22220–22231. doi: 10.1109/JIOT.2024.3383151

Crossref Full Text | Google Scholar

Yan D., Weng J., Huang S., Li C., Zhou Y., Su H., et al. (2022). Deep reinforcement learning with credit assignment for combinatorial optimization. Pattern Recognition 124, 108466. doi: 10.1016/j.patcog.2021.108466

Crossref Full Text | Google Scholar

Yang D., Solihin M. I., Zhao Y., Cai B., Chen C., and Riyadi S. (2024). “A YOLO benchmarking experiment for maritime object detection in foggy environments,” in 2024 IEEE 14th symposium on computer applications & Industrial electronics (ISCAIE) (Penang, Malaysia: IEEE), 354–359.

Google Scholar

Zhang X., Li N., and Zhang R. (2021). “An improved lightweight network MobileNetv3 based YOLOv3 for pedestrian detection,” in 2021 IEEE international conference on consumer electronics and computer engineering (ICCECE) (Guangzhou, China: IEEE), 114–118.

Google Scholar

Zhao C., Bao M., Liang J., Liang M., Liu R. W., and Pang G. (2025). Multi-sensor fusion-driven surface vessel identification and tracking using unmanned aerial vehicles for maritime surveillance. IEEE Trans. Consumer Electron. doi: 10.1109/TCE.2025.3527000

Crossref Full Text | Google Scholar

Zhen R., Ye Y., Chen X., and Xu L. (2023). A novel intelligent detection algorithm of aids to navigation based on improved YOLOv4. J. Mar. Sci. Eng. 11, 452. doi: 10.3390/jmse11020452

Crossref Full Text | Google Scholar

Zhou J. and Hua Z. (2022). A correlation guided genetic algorithm and its application to feature selection. Appl. Soft Computing 123, 108964. doi: 10.1016/j.asoc.2022.108964

Crossref Full Text | Google Scholar

Zhou Z., Sun J., Yu J., Liu K., Duan J., Chen L., et al. (2021). An image-based benchmark dataset and a novel object detector for water surface object detection. Front. Neurorobotics 15, 723336. doi: 10.3389/fnbot.2021.723336

PubMed Abstract | Crossref Full Text | Google Scholar

Zhu J. and Zhang T. (2024). “Multi-target tracking and detection on sea surface based on YOLOv5,” in 2024 3rd international conference on image processing and media computing (ICIPMC), 23–27.

Google Scholar