- 1Kinsmen Laboratory of Neurological Research, Department of Neuroscience, University of British Columbia, Vancouver, BC, Canada
- 2School of Computer Engineering, Nanyang Technological University, Singapore, Singapore
- 3Department of Electrical and Computer Engineering, University of British Columbia, Vancouver, BC, Canada
- 4Pacific Parkinson’s Research Centre, University Hospital, University of British Columbia, Vancouver, BC, Canada
- 5Department of Electrical and Computer Engineering, University of New Mexico, Albuquerque, NM, USA
When faced with visual uncertainty during motor performance, humans rely more on predictive forward models and proprioception and attribute lesser importance to the ambiguous visual feedback. Though disrupted predictive control is typical of patients with cerebellar disease, sensorimotor deficits associated with the involuntary and often unconscious nature of l-DOPA-induced dyskinesias in Parkinson’s disease (PD) suggests dyskinetic subjects may also demonstrate impaired predictive motor control.
Methods: We investigated the motor performance of 9 dyskinetic and 10 non-dyskinetic PD subjects on and off l-DOPA, and of 10 age-matched control subjects, during a large-amplitude, overlearned, visually guided tracking task. Ambiguous visual feedback was introduced by adding “jitter” to a moving target that followed a Lissajous pattern. Root mean square (RMS) tracking error was calculated, and ANOVA, robust multivariate linear regression, and linear dynamical system analyses were used to determine the contribution of speed and ambiguity to tracking performance.
Results: Increasing target ambiguity and speed contributed significantly more to the RMS error of dyskinetic subjects off medication. l-DOPA improved the RMS tracking performance of both PD groups. At higher speeds, controls and PDs without dyskinesia were able to effectively de-weight ambiguous visual information.
Conclusion: PDs’ visually guided motor performance degrades with visual jitter and speed of movement to a greater degree compared to age-matched controls. However, there are fundamental differences in PDs with and without dyskinesia: subjects without dyskinesia are generally slow, and less responsive to dynamic changes in motor task requirements, but in PDs with dyskinesia, there was a trade-off between overall performance and inappropriate reliance on ambiguous visual feedback. This is likely associated with functional changes in posterior parietal–ponto–cerebellar pathways.
Introduction
Prediction is a fundamental component of motor control. For instance, when catching a baseball it is necessary to predict where the ball will be at a given instant and how much force its impact will generate in order to prepare the hand for the catch. Central to motor prediction is the forward model, which enables prediction of the sensory effects of movement (1). Substantial evidence indicates that humans use forward models to predict the sensory consequences of their own actions (1–6), as well as to predict the dynamics of objects in the external environment (4, 7–11). Furthermore, forward models of object dynamics are necessary to guide visuo-motor coordination tasks, and can even override observed kinematic feedback (12, 13).
Predictive forward modeling becomes even more imperative as the reliability of visual feedback is compromised, for example in dim lighting, or disease states such as Parkinson’s disease (PD) where the visual system may be affected (14). Normally, human subjects account for the degree of sensory uncertainty during motor performance by de-weighting their reliance on sensory feedback when it is ambiguous (1, 6, 15–20), and instead more heavily rely on predictive forward models (6, 18, 20). However, when subjects are unable to use predictive motor control, the motor response no longer anticipates sensory feedback but rather reacts to it in an uncoordinated manner (21–24).
Motor performance in PD, at least in the early stages of the disease, is greatly improved by pharmacotherapy, and l-DOPA remains the gold standard of treatment in PD (25). However, l-DOPA-induced dyskinesias (LIDs) – excessive choreoathetoid involuntary movements – are a relatively common side effect of l-DOPA of which peak-dose LIDs are the most common type (26). Though LID pathophysiology remains unclear, behavioral studies suggest that rather than being a purely motor phenomenon, LIDs may be associated with deficits in sensorimotor control (27–29). For example, dyskinetic subjects have demonstrated increased variation in tracking velocity during a visually guided tracking task that was significantly reduced when visual feedback was withdrawn, suggesting an exaggerated motor response to sensory input (27). As dyskinetic subjects are often unaware of their involuntary movements (30), and have been shown to underestimate the distance their limb has moved (28), a component of sensorimotor deficits associated with LIDs may be attributed to impaired predictive motor control. For instance, a mismatch between predicted movement and actual movement may drive dyskinetic subjects to compensate for the sensory discrepancy with excessive movement. Deficits in predictive motor control are typically seen in diseases of the cerebellum (31–36), yet such deficits have also been demonstrated in PD (37, 38). There is evidence to support cerebellar involvement in LIDs (39), and altered activity and plasticity in the prefrontal cortex in dyskinetic subjects (40, 41) may contribute to altered sensorimotor control in LIDs.
If inadequate predictive motor control is an underlying feature of dyskinetic subjects’ motor performance, then a heightened reliance on sensory feedback should be especially prominent in conditions where healthy subjects rely more heavily on predictive forward models, such as when confronted with ambiguous visual feedback (6). Accordingly, we hypothesized that dyskinetic subjects would demonstrate an impaired ability to de-weight ambiguous visual feedback during a visually guided tracking task. We have purposely chosen a motor adaptation task, whereby subjects had to adapt to changing sensory information. We have recently demonstrated that overall, PD subjects are susceptible to sensory uncertainty during visually-guided tracking (42), but in that study we did not dichotomize dyskinetic and non-dyskinetic subjects. We have since recruited additional PD subjects while employing the same tracking task to assess the reliance on uncertain visual feedback of dyskinetic and non-dyskinetic PD (NDPD) subjects. As previous work has demonstrated linear dynamical system (LDS) models to be a sensitive marker of motor performance in PD (42, 43), here we use LDS models in addition to quantifying tracking error to assess tracking performance. By extracting the decay rate parameter from the LDS models during ambiguous tracking, we quantified subjects’ relative reliance on uncertain visual feedback.
Materials and Methods
Subjects
The Ethics Board of the University of British Columbia approved the study and all subjects gave written, informed consent. We recruited 19 patients with probable PD according to diagnostic criteria (44) and 10 age-matched control subjects without active neurological disorders. Exclusion criteria included known PD with dementia. PD subjects were Hoehn and Yahr stage 1–3 (45), and 9 subjects were dyskinetic PD (DPD) subjects and 10 were NDPD subjects. We did not screen subjects for the presence of depression or anxiety, however we excluded PD subjects with dementia and all subjects were cognitively able to follow the instructions and complete the tasks. Subject characteristics are shown in Table 1. All patients had overnight withdrawal of medications before the study for at least 12 h for l-DOPA and 18 h for dopamine agonists. We calculated the converted l-DOPA daily dosage as 100 mg l-DOPA = 125 mg of controlled-release l-DOPA, which was then added to the equivalents of dopamine agonists to give the l-DOPA equivalent daily dosage (LEDD), where 100 mg of l-DOPA = 1 mg of pramipexole, 6 mg of ropinirole, 10 mg of bromocriptine, 75 mg of l-DOPA plus entacapone. The presence of peak-dose LIDs was assessed up to 1.5 h after the l-DOPA challenge, where subjects received the equivalent of their morning l-DOPA dose given in the immediate release form. Peak-dose LIDs were defined by the presence of involuntary choreiform movements in any of the head/neck, trunk, and upper limbs of variable duration and in some cases were accompanied by dystonia. LID severity was assessed according to the Goetz Dyskinesia Rating Scale (46), and all DPD subjects had mild LID that were of minimal severity and did not interfere with voluntary motor acts (Goetz score = 1). Disease severity was assessed according to the Unified Parkinson’s Disease Rating Scale (UPDRS) motor score in the off medication state.
Study Paradigm
The large-amplitude tracking task used here has been previously described (42). Briefly, a Lissajous figure was presented on a screen measuring 1.62 m × 1.22 m with a red circular target (12 cm in diameter) in the center of the screen. Subjects stood approximately 55 cm in front of the screen, and tracked the moving target with their index finger, requiring movement about the wrist, elbow, and shoulder joints. We tested subjects in the standing position in order to facilitate larger amplitude movements more representative of everyday life that are often precluded in imaging studies. Additionally, evidence suggests LIDs may be of greater amplitude in the standing compared to the sitting position (47). In the baseline trials the target smoothly followed the Lissajous path, either at a slow tracking speed (average speed of 56.2 cm/s) or a fast tracking speed (average speed of 78.3 cm/s). In subsequent visually ambiguous conditions, the target jittered about the path while maintaining the path’s overall trajectory. In the ambiguous tracking conditions, subjects were instructed to attempt not to chase the jitter, but rather to attempt to track the desired target’s position, which maintained the overall Lissajous trajectory. Four levels of visual ambiguity were tested (0, 0.03, 0.05, 0.07) – representing the jitter root mean square (RMS) amplitude with respect to screen height (0, 0.0191, 0.0318, and 0.0445°), at two speeds, giving a total of eight conditions. The jitter was obtained by first starting with random Gaussian noise sampled at the frame rate of 60 Hz. Because we did not want excessive discontinuities in the visual pattern caused by high-frequencies, we then low-passed the random series at 20 Hz. Each condition was tested in three different trials, where a trial consisted of 30 s of tracking, a 12 s rest, followed by 30 s of tracking. The order of the trials began with the slow non-ambiguous condition followed by the fast non-ambiguous condition. The order of the remaining six ambiguous conditions was randomly selected. This same trial order of all eight tracking conditions was then repeated for the second and third trials. The trial order was the same for every subject. Subject DPD 9 was an exception and completed two trials of each condition due to complaints of fatigue. PD subjects performed this motor task in the morning when in the “off” medication state, and after a break for lunch subsequently repeated the task in the “on” medication state that same day.
Quantification of Manual Tracking
We used a Polhemus Fastrak (Polhemus, Colchester, VT, USA) six-degrees-of-freedom electromagnetic tracking system to record subject tracking. A stylus sensor was held in the palm of the subjects’ dominant hand and secured with tape. The tip of the stylus was aligned with the tip of the index finger in order to record subjects’ index finger position. A time series for displacement was recorded in the x, y, and z directions, and data was recorded at 10 Hz. We performed a robust linear regression analysis on the x and y sensor data during non-ambiguous tracking to determine the optimum affine transformation to map the sensor data coordinates to the Lissajous figure coordinates. We subsequently applied the same transformation to the ambiguous conditions on a subject-by-subject basis.
Quantification of Tracking Performance
Root mean square tracking error was calculated by subtracting the processed x and y sensor data of the index finger from the x and y target position along the baseline track, squaring the result for each time point, taking the mean for the squared values for each trial, and computing the square root of the result.
Analysis of motor performance using LDS models is being increasingly utilized in sensorimotor studies (16, 48–51) and has been previously used to rigorously characterize tracking performance in PD (42, 43). We computed LDS models of subjects’ tracking using system identification techniques (52) and extracted the decay rate parameter, which describes how quickly tracking performance returns to equilibrium after a perturbation. Intuitively, a higher decay rate can be considered akin to the tighter suspension of a sports car: tighter turning on a good road may be desirable, but when an uneven gravel (noisy) road is encountered, the ability to smooth out the bumps (i.e., de-weight the noise) is diminished. Thus during ambiguous tracking, higher decay rates can intuitively be interpreted as a greater response to ambiguous visual feedback (see Figure S1 in Supplementary Material). The natural logarithm of the decay rates were used to make the results more Gaussian distributed and this was subsequently used in all statistical analyses.
Statistical Analyses
MatLab (The MathWorks Inc., MA, USA) was used for all statistical analyses. In order to control for a training effect between tracking trials, we first performed paired t-tests on the pooled RMS error of all groups (DPD and NDPD off and on medication and control) between trial sets 1 and 2 and trial sets 2 and 3. We observed a training effect between trial set 1 and 2 that stabilized between trial set 2 and 3 (Figure 1), and trial 1 data were therefore omitted from all subsequent data analysis to ensure we were not examining motor learning in our visually guided tracking task but rather the effect of visual uncertainty after learning had occurred and stabilized.
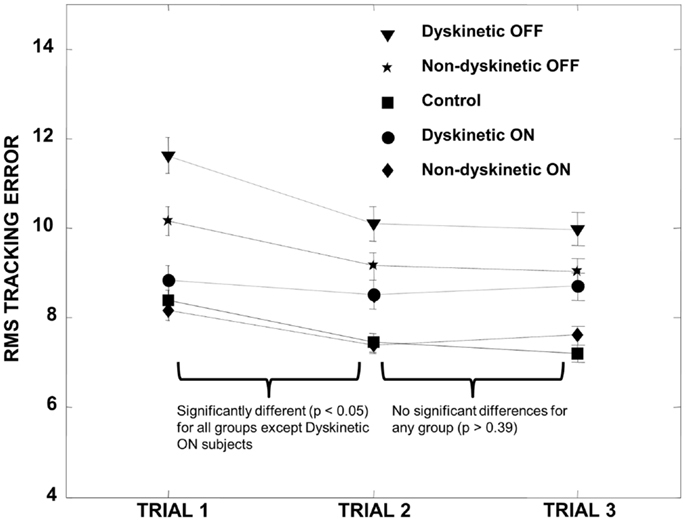
Figure 1. Training effect. All groups demonstrated a significant decrease in RMS error between trial 1 and trial 2 except for the DPD ON group (where the decrease was not significant), and the RMS error subsequently stabilized for all groups between trials 2 and 3. We therefore omitted trial 1 data in all subsequent calculations. Error bars represent the standard error.
We used mixed-model analysis of variance (ANOVA) to assess different effects on both overall RMS error as well as decay rate. In the first instance, we examined the effect of ambiguity, tracking speed, and drug status (i.e., ON or OFF l-DOPA), PD group (i.e., DPD or NDPD), and subject number as factors in the ANOVA. Since the same PD subjects were assessed before and after l-DOPA, ambiguity, tracking speed, and drug status were considered within subject factors and subject number was nested within the PD group factor.
To compare the PD subjects with Normal subjects, we also used a mixed-model analysis of variance (ANOVA), where ambiguity, tracking speed, group (i.e., N, DPD ON or OFF l-DOPA, or NDPD ON or OFF l-DOPA) and subject number were used as factors in the ANOVA. As before, ambiguity and tracking speed were considered within subject factors and subject number was nested within the group factor. We then repeated the above two ANOVA analyses with log(decay rate) instead of RMS error.
In order to examine the relationship between UPDRS and the effect of ambiguity on tracking performance, we calculated Spearman’s rank correlation coefficients between UPDRS and the difference in RMS error between the non-ambiguous and maximum ambiguous tracking conditions for each PD group, as well as between UPDRS and decay rate in each of the ambiguous tracking conditions. In order to better visualize the results of the ANOVA, a robust multivariate regression analysis was also performed, using RMS error or log(decay rate) as the dependent variable, and speed and ambiguity as the independent variables. Regression coefficients were obtained to indicate the portion of dependent variable explained by speed and ambiguity amplitude. Quality of LDS models’ was assessed by the Akaike information criterion (AIC) with a model quality score based on a trade-off between matching the data well and penalizing the use of an excessive number of model parameters. Significance for all comparisons was declared at p < 0.05. We estimated the stability of the regression coefficients and the group-wise RMS and log(decay rate) values by leave-one-out validation.
In order to further evaluate what features in visual input influenced finger movement, we decomposed finger velocity into its projection along different vectors. As shown in Figure 2, we looked at Finger velocity [i.e., the vector from FP(t) to FP(t + 1)], depicted as a Blue arrow; the cursor movement on the screen : green arrow, the desired velocity along the Lissajous path, ; the path from finger point to cursor point, green dotted arrow; and the path from the finger to the desired point: red dotted arrow. We used the “robustfit” function of MatLab to estimate the coefficients of a multivariate linear regression equation:
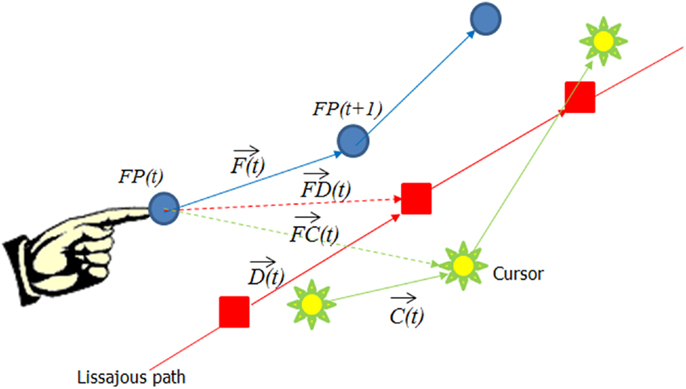
Figure 2. The decomposition of the finger movement vector into different constituent vectors. The blue arrow represents the finger velocity , the green arrow the cursor velocity , the red arrow the desired velocity , the green dotted arrow from the finger position to the cursor , and the red dotted arrow represents the vector from the finger to the desired point .
We then compared DPD subjects before medication and after medication (i.e., D-pre vs. D-post), NDPD before and after medication (ND-pre vs. ND-post), as well as the difference in finger movement trajectories with and without noise for all groups of patients.
Results
Subjects’ characteristics are shown in Table 1. There were no significant differences between age, UPDRS, disease duration, and LEDD (p > 0.05), though converted daily l-DOPA dosage was significantly higher for the DPD group. Analysis of RMS error between trials revealed that there was a significant decrease in the pooled RMS error between trial set 1 and trial set 2 (p < 0.00001) that stabilized between trial sets 2 and 3 (p = 0.7). The individual groups’ RMS error by trial is shown in Figure 1.
The results of the mixed-model ANOVA tests on RMS error are shown in Tables 2 and 3. When comparing DPD and NDPD subjects, ambiguity and tracking speed were significant independent factors on RMS error, as well as the interaction terms between ambiguity and tracking speed, PD group and drug status. When normal subjects were included in the analysis (Table 3), ambiguity, tracking speed, and group were all significant factors, as well as the interaction terms between ambiguity, speed, group, and subject. Similarly, when determining the effects on log(decay rate), ambiguity and speed were significant when comparing DPD and NDPD (Table 4), as well as the interaction between l-DOPA and PD group (Table 4). When control subjects were included in the analysis, significances were seen in the main effects of ambiguity, speed, and group, as well as the interaction effects of ambiguity and speed and group (Table 5).
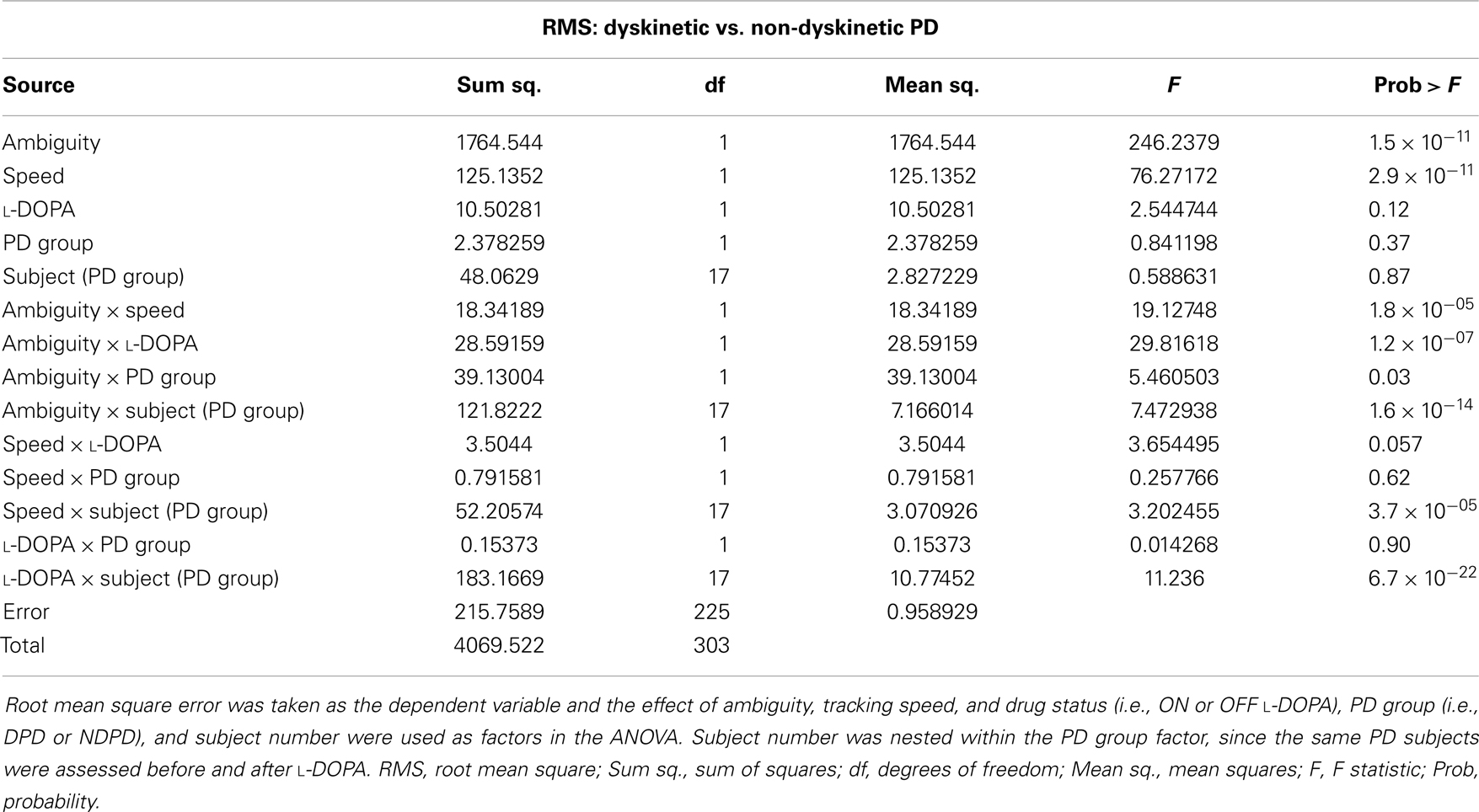
Table 2. Mixed-model analysis of variance (ANOVA) table to assess different effects on overall RMS error in PD subjects.
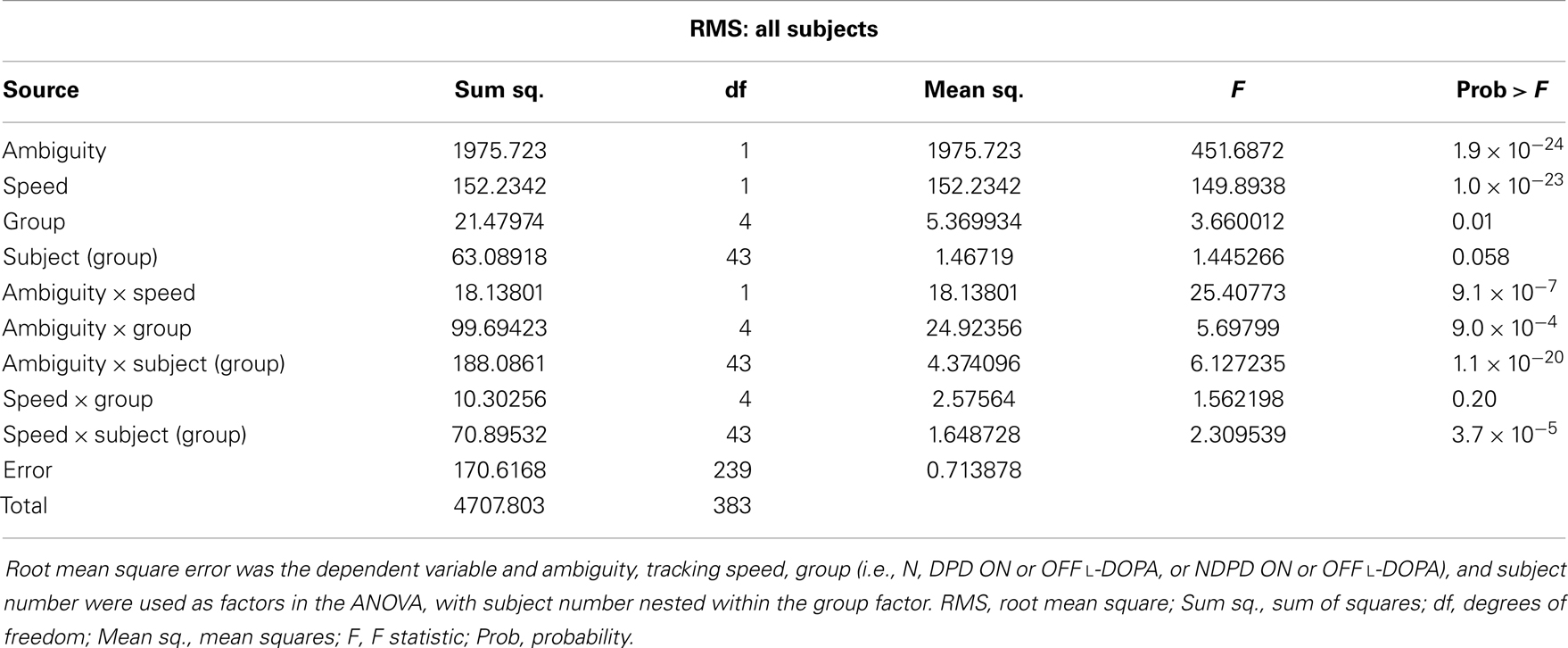
Table 3. Mixed-model analysis of variance (ANOVA) table to assess different effects on overall RMS error in all subjects.
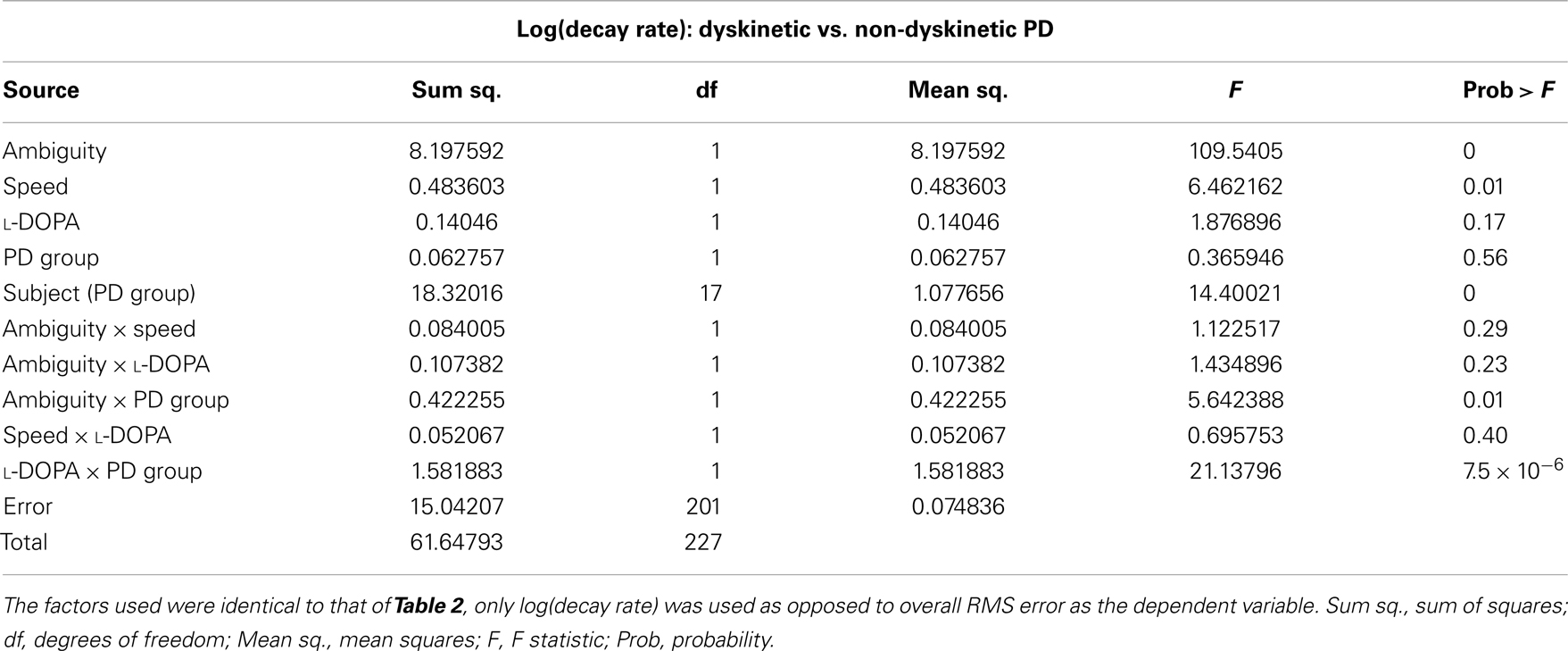
Table 4. Mixed-model analysis of variance (ANOVA) table to assess different effects on overall log(decay rate) in PD subjects.
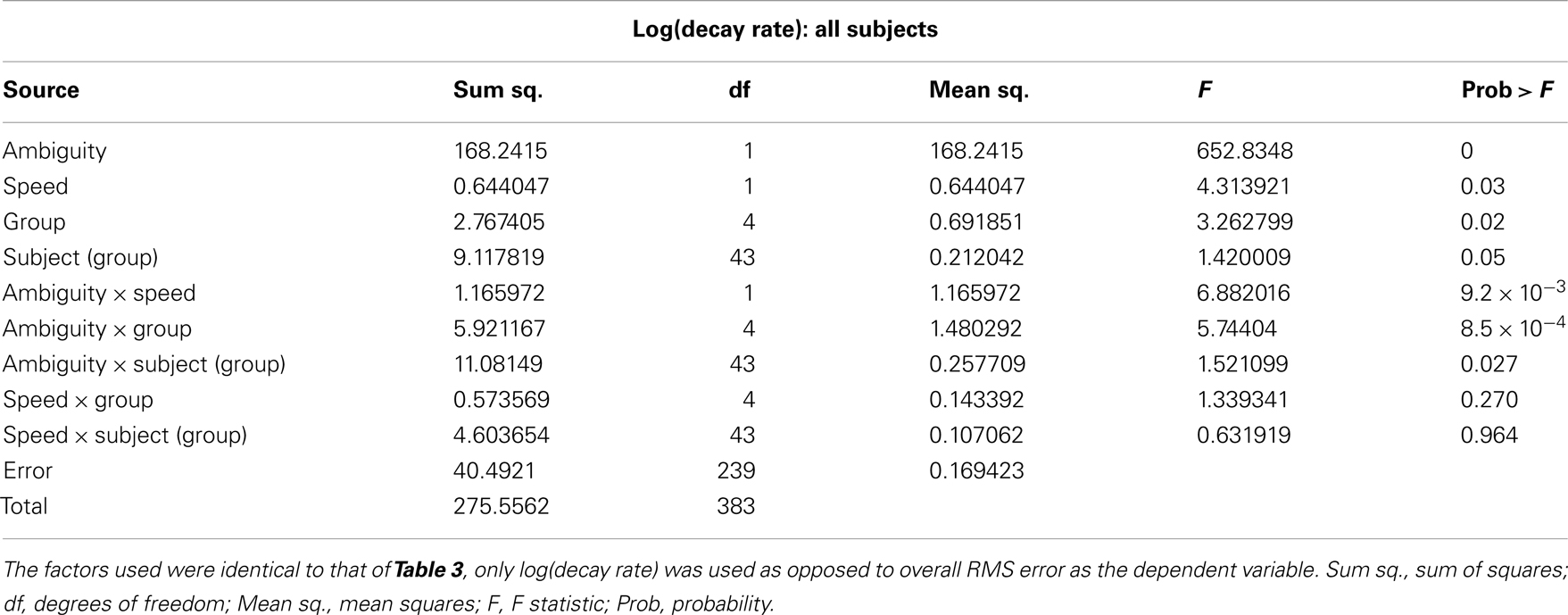
Table 5. Mixed-model analysis of variance (ANOVA) table to assess different effects on overall log(decay rate) in all subjects.
The differences in RMS error between non-ambiguous and maximum ambiguous tracking conditions were not significantly correlated with UPDRS scores at either tracking speed for either dyskinetic subjects or for non-dyskinetic subjects and p > 0.05.
The overall effect of increasing ambiguity and speed on overall tracking performance, and the l-DOPA effect, is illustrated in Figure 3. As expected, there were increases in RMS error with both speed and visual ambiguity. DPD subjects had the highest error, which was partially ameliorated by l-DOPA. In NDPD subjects, after medication, the tracking error approached that of control subjects.
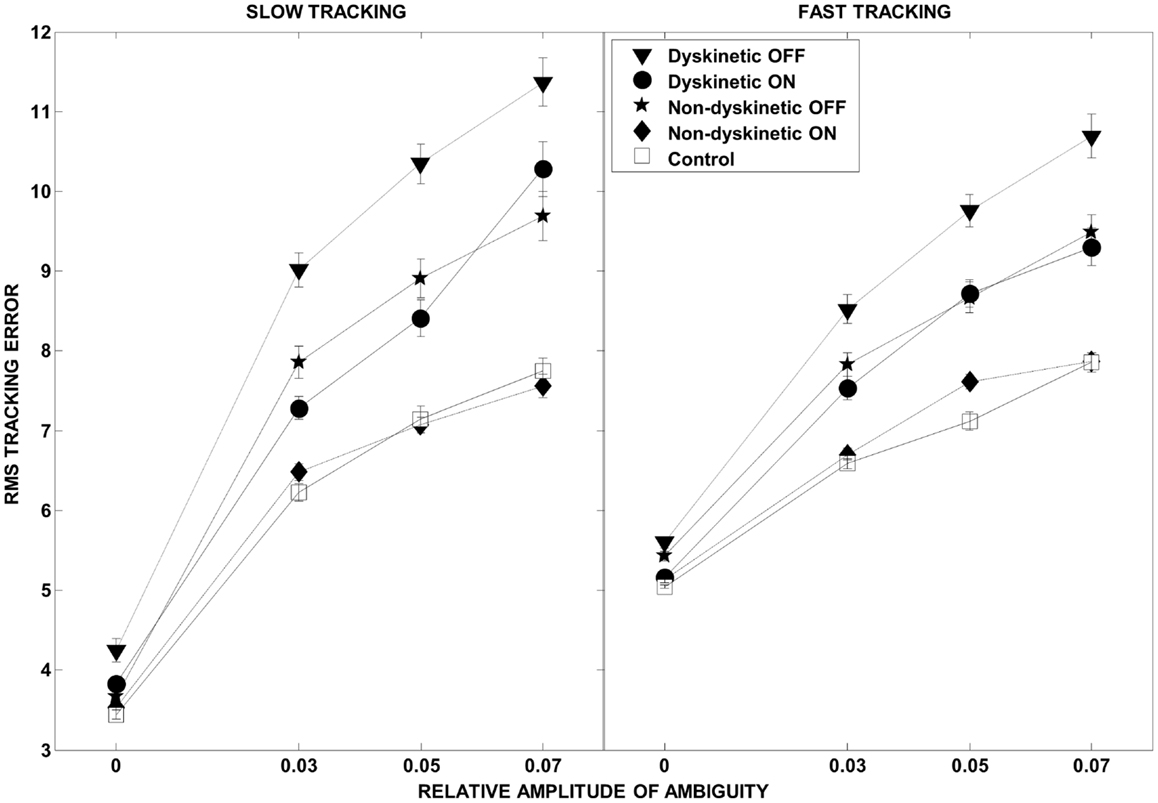
Figure 3. Root mean square error as a function of visual ambiguity and tracking speed. Differences in RMS error in the low tracking speed condition (left panel) and high tracking speed condition (right panel) are shown. Error bars were estimated by leave-one-out-validation.
The effect of visual ambiguity on the log of decay rate is shown in Figure 4. At slow speeds and higher levels of ambiguity, NDPD subjects had lower log(decay rates) than controls (left panel). However, at higher tracking speeds the NDPD subjects had similar or higher log(decay rates) as controls. In contrast, DPD subjects had higher values for log(decay rate) at high ambiguity levels at both speeds, a situation not ameliorated by medication.
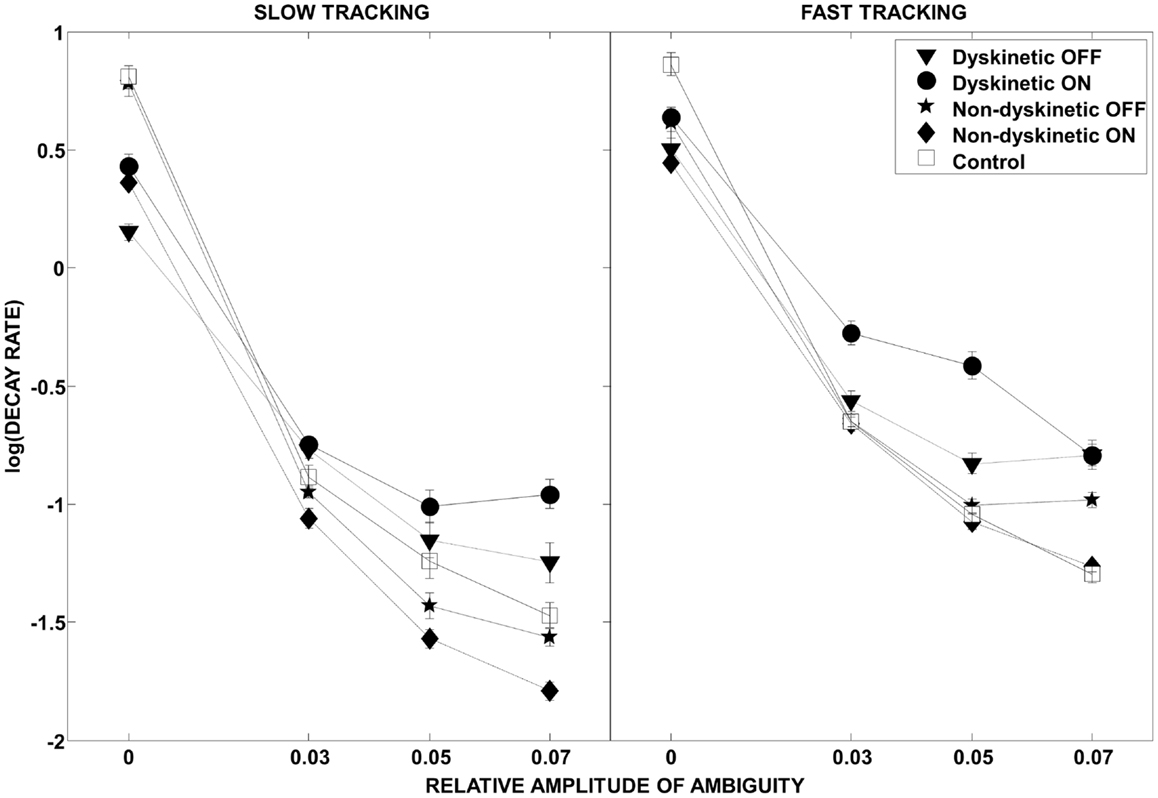
Figure 4. Log(decay rate) as a function of visual ambiguity and tracking speed. Differences in RMS error in the low tracking speed condition (left panel) and high tracking speed condition (right panel) are shown. Error bars were estimated by leave-one-out-validation.
The regression analysis illustrates the relative contribution of increasing ambiguity and speed to RMS error (Figure 5) and log(decay rate) (Figure S1 in Supplementary Material) by group. The speed and ambiguity regression coefficients captured by the model were highly significant for all groups (p < 10–5), and the between group differences in both speed and ambiguity regression coefficients were also highly significant (p < 10–5). Figure 5 demonstrates that increasing tracking speed and ambiguity contributed to the RMS error of DPD OFF subjects significantly more than for all other groups. Additionally, the susceptibility to speed and visual ambiguity is not normalized with medication for DPD ON subjects, but is roughly normalized for NDPD ON subjects. Figure S1 in Supplementary Material suggests that log(decay rate) is significantly affected by visual ambiguity in PD, but especially so for DPD subjects. l-DOPA had less of an effect on the sensitivity of log(decay rate) to tracking speed in DPD compared to NDPD subjects.
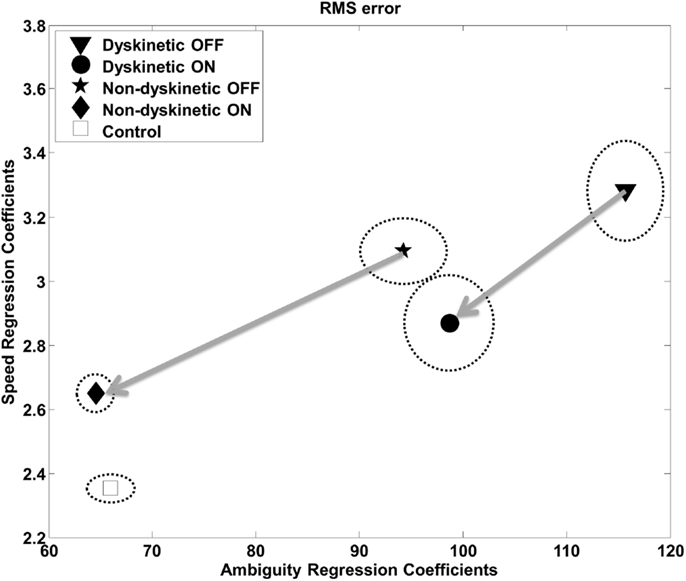
Figure 5. Regression analysis – RMS. The relative contribution of increasing target ambiguity and speed to RMS error is demonstrated. The design matrix for the regression included tracking speed, ambiguity columns, as well as nuisance covariates corresponding to individual subject and overall mean. The units can be considered arbitrary. The vertical and horizontal radii of the ellipses represent the standard error of the regression coefficients as estimated by leave-one-out validation. The arrows are from the same PD subjects OFF medication to ON medication, and thus show the effects of l-DOPA medication.
The Akaike’s final prediction error (FPE) and AIC used to assess the LDS models from ambiguous tracking conditions revealed robust tracking models. The means and standard deviations of the estimated LDS models’ FPE and AIC scores were ≤3.1 ± 2.0 and ≤1.8 ± 0.4 respectively, for all groups across all conditions, which is indicative of high model quality/fit. Furthermore, there were few outliers in the FPE and AIC values indicating validity of the modeling framework across subject groups.
In order to get an intuitive interpretation of the significantly different decay rates, we interrogated typical models from each group (i.e., models with eigenvalues close to the mean for each group) with one-dimensional sinusoidal inputs and additive noise similar to the experiment to determine the predicted tracking performance. Ideal tracking performance would occur in systems that ignore the noisy input and faithfully maintain sinusoidal tracking. Consistent with the RMS error results, the sinusoidal tracking improved with post-medication models in both dyskinetic and non-dyskinetic subjects. However, consistent with the statistical results, the dyskinetic model had an impaired ability to ignore the noisy visual cue, and was excessively reliant on noisy ambiguous visual feedback (Figure 6).
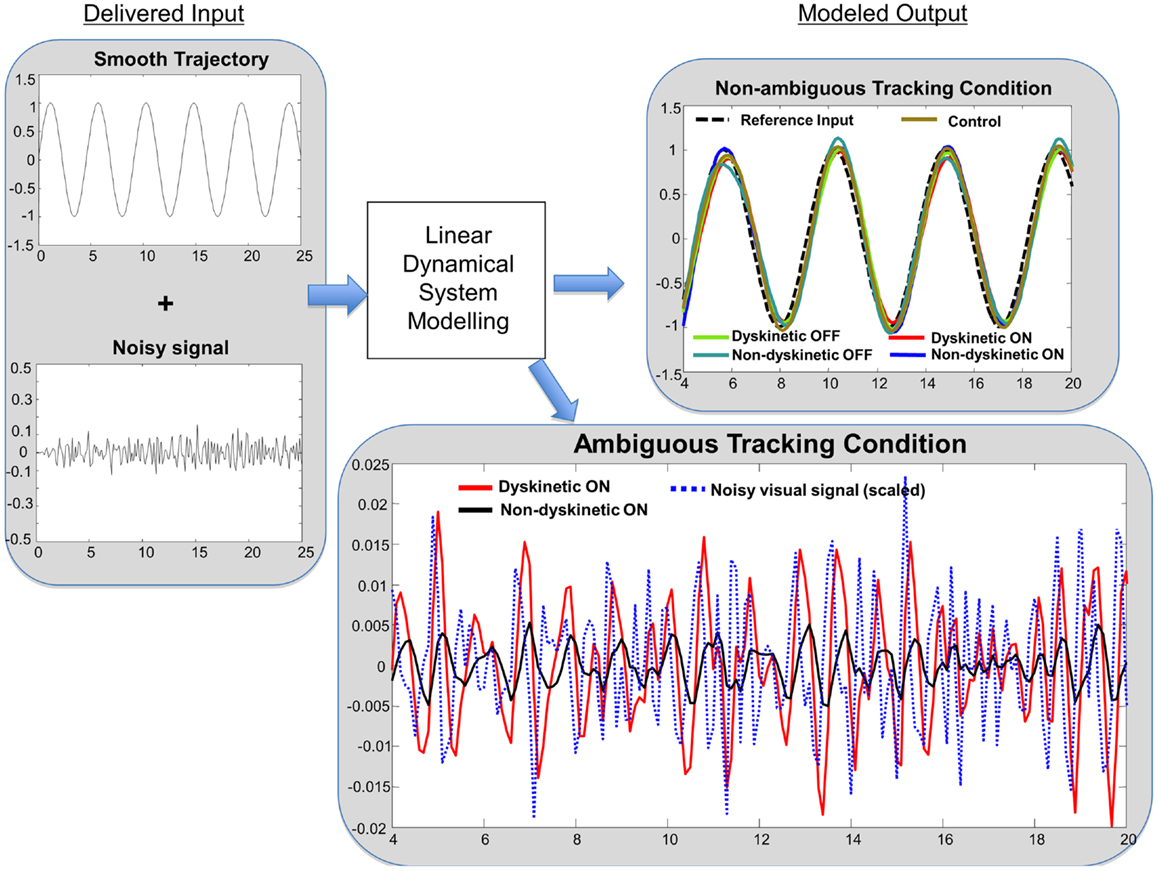
Figure 6. Linear dynamical system model simulation results. Left panel: tracking input is a combination of a smooth sinusoidal reference trajectory and bandpass filtered white noise. Right panel: subjects modeled tracking output in a smooth non-ambiguous tracking condition (upper box) and in a “noisy” ambiguous tracking condition (lower box). In the upper box, the modeled tracking output of a representative subject from each group is shown. The subjects’ output in non-ambiguous conditions is similar across groups. In the lower box, the effect of “noisy” ambiguous input on modeled output of a dyskinetic and a non-dyskinetic subject is shown. The increased decay rate of dyskinetic subjects on medication leads them to attempt to track the noise more significantly. The noisy visual signal is reduced to 15% of the actual magnitude for visualization purposes.
We observed the significant differences in the decomposition of the finger tracking data, depending upon whether or not jitter was present (Figure S2 in Supplementary Material). For only the DPD (D-pre and D-post) group, we found that contribution of – the vector from finger position to the desired position – increased (p = 0.036 and p = 0.026), while the contribution of – the desired trajectory – decreased when jitter was present (p = 0.002 and p = 0.005).
Discussion
We examined the ability of 9 dyskinetic and 10 NDPD subjects, as well as that of 10 age-matched control subjects, to de-weight uncertain sensory feedback and instead rely more heavily on predictive motor control during visually guided tracking. The relative contributions of increasing target ambiguity and speed (examined independently) to the RMS tracking error were the greatest for DPD subjects off medication (Figure 3). As expected, l-DOPA medication improved overall tracking performance for both PD groups, as evidenced by reduced RMS error with medication (Figure 3).
Dyskinetic subjects’ gross motor performance was worse in the Parkinsonian state than in the “on” medication state despite the presence of LIDs. This is consistent with the presence of mild LIDs experienced by DPD subjects that did not interfere with the completion of motor tasks, and the increased movement in the on-state compared to the Parkinsonian state that enabled improved overall motor performance. However in dyskinetic subjects, improved overall tracking performance came at a price: they were also more responsive to and reliant on non-informative visual cueing (Figure 6, right lower panel). We interpret our results in the context of established performance trade-offs in control theory, in which controllers that produce exceptionally fast, high-performance tracking under ideal circumstances are also extremely poor at disturbance rejection (that is, they experience high sensitivity to external or un-modeled noise processes). In a biological context, this is indicative of a system that relies more heavily on ambiguous sensory feedback and less on predictive motor control. This interpretation is further supported by the decomposition of the finger velocity . For DPD group only (i.e., D-pre and D-post), the contribution of the desired trajectory , to finger velocity, , was significantly reduced during jitter cases, implying that finger movement velocity was significantly degraded by jitter in these subjects. Interestingly, FD(t), i.e., where their finger was to where it should have been, significantly increased in the DPD group only, possibly reflecting an compensatory corrective motor movement after the realization that they had been misled by the jitter. The trends we observed in the LDS are consistent with the trends we observed through the regression analysis. The LDS model separates the contribution of the output due to the desired trajectory from the contribution of the output due to the additive jitter. The decreased reliance on in DPD subjects is consistent with the increased decay rate in the LDS – that is, the subjects are following the noise more than they were in the no-noise case.
It is important to note that the LDS models utilized here are deterministic. The numerical algorithm used to identify the LDS model, in fact, minimizes the residual between the actual output and the predicted output, in essence capturing as much information as possible from the input–output relationship and leaving only white noise. What would we see if the only differences between DPD and NDPD were that the DPD subjects had the same tracking performance but superimposed dyskinesias that were truly random fluctuating movements? The parameters of the models would be the same, but the residuals of the model, which reflect the part of the movement not accurately captured by the deterministic model, would be much higher in the DPD case. Yet we observed the opposite: the model residuals were not significantly higher in the DPD subjects (as reflected by the lack of significant differences in their model scores) and the parameters of the model were appreciably different. In fact, this raises an important issue, that a key interpretation of our findings is that LIDs may not be “random” at all as is normally assumed, but a deterministic response to various endogenous and exogenous stimuli that is normally appropriately de-weighted. This may explain why increasing sensitivity to stimuli such as that seen in anxiety (53), or increased vigilance due to cognitive or motor load (54) may increase dyskinesias.
Normally, forward models are used to predict sensory feedback, and the predicted feedback is subsequently compared to actual feedback when it becomes available after an inherent delay (55, 56). The difference between the actual and predicted sensory feedback is known as the sensory discrepancy or error, which is then used to update the forward model and in turn improve motor performance (1, 56). In fact, the concept of forward modeling has been extended from predicting the sensory consequences of movement to predicting the external environment (4, 7–13). For example, evidence indicates that human subjects utilize forward models of visual cues (11), of target motion during interception tasks (12, 13), and of the physical laws of gravitational acceleration (4, 9, 15). We quantified RMS tracking error as the difference between the subjects’ index finger position and the target position along the smooth Lissajous path at any given time point. During the non-ambiguous conditions of our tracking task, the sensory discrepancy is likely minimal as the predicted sensory feedback relating the subjects’ index finger position and the target position would be congruent, which is supported by the lack of differences in RMS tracking error between the groups in the baseline conditions (Figure 3). However, in the ambiguous tracking conditions the sensory discrepancy would be large due to the ambiguous jitter of the target. Human subjects have been shown to reliably predict the mean perturbation delivered from a variable distribution in reaching tasks (50, 57), and to do so according to Bayesian inference (17).
Though we did not explicitly test the use of Bayesian statistics in this study, the strategy of more heavily weighting the mean jitter amplitude and de-weighting the instantaneous uncertain jittering position of the target in order to predict the desired tracking position, corresponds to the optimal motor response in our task that minimizes RMS tracking error.
As expected, in our study, normal controls had the lowest overall tracking error of all groups (Figure 3). However, Figure 4 provides interesting insight into how this is achieved. During slow tracking and in high ambiguous situations, NDPD subjects had even lower decay rates than controls, suggesting that they were robust to the ambiguity – so much so that they excessively de-weighted the (still partially meaningful) visual information. However, in the high speed tracking condition, it becomes more critical to de-weight the visual information and the originally sluggish approach of the NDPD becomes the appropriate response – this is why NDPD patients ON medication and controls had essentially the same decay rates. These observations are consistent with other studies demonstrating that NDPD subjects do not overly respond to visual feedback (58), and that healthy human subjects internally account for sensory uncertainty and de-weight uncertain feedback during motor performance (1, 18, 20). In contrast, in both slow and fast tracking conditions, the DPD subjects demonstrated excessively high decay rates (Figure 4), implying faster dynamics, even though this resulted in excessive overall tracking error (Figure 2).
Thus, the inability of DPD subjects to de-weight ambiguous visual data that we observed may be based on excessive sensitivity to discrepancies between a (accurate) forward model and sensory feedback and/or an impaired forward model. The effect of l-DOPA medication may provide insight on this. In addition to reducing overall tracking error (Figure 3), l-DOPA medication made overall tracking error less susceptible to tracking speed and visual ambiguity (Figure 5), but had minimal effect on the log(decay rate)’s sensitivity to tracking speed and visual ambiguity (Figure S1 in Supplementary Material). If we assume that decay rate is related to corrective sub-movements and hence responses to discrepancy between models, this would imply that l-DOPA largely improves forward model accuracy (and hence reduced RMS error’s sensitivity to visual ambiguity and speed) while having minimal effect on the dynamics of the response to the errors between the forward model and sensory estimates (Figure 5).
A possible functional neuroanatomical correlate of the inability of DPD subjects to de-weight ambiguous visual feedback demonstrated in the present study is inadequate predictive cerebellar forward modeling. There is growing evidence of functional cerebellar changes occurring in PD (59–64) and in DPD (39) that supports this possibility. Furthermore, the cerebellum is known to have an integral role in predictive motor control, and predictive deficits that lead subjects to excessively respond to feedback are typically seen in cerebellar disease (21, 24, 31–34). Extensive evidence supports the use of forward models in human subjects (2–6), and neuroimaging, electrophysiology, and transcranial magnetic stimulation (TMS) studies provide strong evidence for the role of the cerebellum in forward modeling (31, 65–75). Interestingly, evidence from neuroimaging studies demonstrates significantly increased cerebellar activity in conditions of mismatch between predicted and actual feedback (66), and the degree of mismatch imposed by temporal delays has been correlated with cerebellar activity (76). Further evidence indicates that the cerebellar climbing fiber-Purkinje cell synapse may signal the error between the predicted and actual sensory feedback (71, 72, 77–80).
In addition to the cerebellum, the posterior parietal cortex (PPC) is believed to have an important role in predictive motor control (65). The role of the PPC in making on-line corrections (a process that requires forward models) during movement has been demonstrated in patients with lesions to this area and through the use of TMS (81, 82). TMS applied to the PPC of healthy human subjects prevented them from making fast on-line corrective movements to a target perturbation in a reaching task when vision of their arm was occluded, and they instead continued to reach to the initial target (81). As DPD subjects in our study were found to be overly responsive to the ambiguous visual feedback (as opposed to unresponsive PPC subjects), this may argue against altered PPC function explaining our results. Moreover, PPC stimulation has been related to motor awareness (83), and interestingly DPD patients can be unaware of their involuntary movements (30). Nonetheless it is possible that altered PPC activity contributed to the impaired predictive motor control of dyskinetic subjects, and as the PPC and cerebellum have reciprocal neuroanatomical connections (84, 85), it is likely that these two structures work together in using forward models to guide motor performance. Given that frontal “executive” dysfunction is well described in PD (86), it is tempting to speculate whether or not impaired frontal lobe dysfunction may contribute to the our observation of impaired forward models in PD. While this may explain, at least in part, the differences between PD subjects as a whole and controls, we do not believe that it could explain the differences between NDPD and DPD subjects we observed.
There is increasing evidence that although dyskinesias are present when DPD subjects are on medications, changes in motor function persist off medication (42). For example, Figure 3 demonstrates that DPD subjects OFF medication were significantly worse in overall tracking compared to NDPD subjects OFF medication. Animal models of PD suggest that unnatural pulsatile stimulation of dopaminergic receptors, occurring with intermittent dosing of l-DOPA, may induce plastic changes that contribute to the development of LIDs (87, 88). Interestingly, younger patients are more prone to developing LIDs (89), and this may be related to a greater degree of plasticity occurring in the younger brain. Additionally, neurochemical changes related to LIDs (90) are not limited to the basal ganglia. Nimura and colleagues (91) demonstrated that the binding potential of the cerebellar sigma receptors was positively correlated with LID scores but not with disease severity of PD patients undergoing pallidotomies; while Koch and colleagues (39) have demonstrated altered cerebellar plasticity in DPD subjects using TMS. Furthermore, we have found behavioral differences that differentiate dyskinetic from non-dyskinetic subjects in the off medication state that may be related to altered cerebellar functioning (42). Thus, the dyskinetic brain may exhibit altered cerebellar plasticity that manifests functionally as inadequate predictive motor control. Direct neuroanatomical pathways connecting the basal ganglia and the cerebellum have been found in primates (92, 93), providing a direct route for the administration of l-DOPA to interact with altered cerebellar structures.
There are a number of potential limitations to our study. First, there was a trend toward greater disease severity of dyskinetic than NDPD subjects, though the difference was non-significant (Table 1). Nonetheless, in order to fully address this, we examined the relationship between UPDRS and the increase in RMS between the non-ambiguous and maximum ambiguous tracking conditions, and no significant correlation for either DPD or NPDP subjects was found. Thus, the worsening of motor performance with increasing visual ambiguity was not associated with disease severity. Furthermore, UPDRS was not significantly correlated with decay rate for either PD groups, except for in the slow tracking condition (ambiguity level = 0.03), which was the only ambiguous tracking condition that lacked significant differences in mean decay rate between groups. Second, in addition to testing while on medication, we also tested PD subjects in the practically defined off medication state with 12 h of l-DOPA withdrawal and 18 h for dopamine agonists, and subjects were symptomatic upon study commencement. We note that this method of examining the practically defined off medication state in PD is universally utilized (94, 95), though we acknowledge that this may not reflect a truly depleted dopaminergic state. Furthermore, non-motor complications can occur with the off medication state (96), as well as pain that can be experienced by DPD patients (97), and such non-motor complications were not accounted for in this study. However, none of the subjects complained of pain and none of the subjects experienced non-motor complications requiring them to stop the study. Third, dyskinetic subjects can experience postural instability while on medication and experiencing LIDs (98), and we did not quantify postural instability between groups. However none of the subjects from either PD group complained of postural problems, and the lack of difference in overall accuracy in the baseline tracking condition of our task indicates that PD subjects were able to perform the task while standing equally well as healthy control subjects, and suggests any potential differences in postural instability did not significantly affect motor performance. Fourth, we did not examine potential differences in visual acuity between dyskinetic, non-dyskinetic, and control subjects. However, once again a lack of difference in RMS error in the baseline non-ambiguous conditions of the task suggests that any differences in visual acuity were not great enough to impact baseline motor performance. Fifth, it is theoretically possible that l-DOPA affected DPD and NDPD subjects with respect to eye movements. However, we note that (99) we found no changes in smooth pursuit gain during dose-related on–off fluctuations, so believe that this was not a factor here.
In conclusion, we demonstrate that DPD subjects are significantly more susceptible to visually ambiguous sensory input during a visually guided tracking task, and that the improvement in overall tracking performance with l-DOPA medication comes at a price for DPD subjects: an increased reliance on ambiguous visual feedback. The results indicate inadequate weighting of predictive motor control in DPD, which may be a significant contributor to pathophysiology of LIDs. We discuss possible cerebellar dysfunction in DPD as a neuroanatomical substrate of inadequate weighting of predictive motor control.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/Journal/10.3389/fneur.2014.00008/abstract
Figure S1. Regression analysis – log(decay rate). The regression was the same as for Figure 4, only the dependent variable used in the regression was log(decay rate).
Figure S2. Regression weights of the vector decomposition in Figure 2, comparing the situations with and without “jitter.”
References
1. Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science (1995) 269(5232):1880–2. doi:10.1126/science.7569931
2. Gritsenko V, Yakovenko S, Kalaska JF. Integration of predictive feedforward and sensory feedback signals for online control of visually guided movement. J Neurophysiol (2009) 102(2):914–30. doi:10.1152/jn.91324.2008
3. Kuo AD. An optimal control model for analyzing human postural balance. IEEE Trans Biomed Eng (1995) 42(1):87–101. doi:10.1109/10.362914
4. Merfeld DM, Zupan L, Peterka RJ. Humans use internal models to estimate gravity and linear acceleration. Nature (1999) 398(6728):615–8. doi:10.1038/19303
5. van Beers RJ, Sittig AC, Gon JJ. Integration of proprioceptive and visual position-information: an experimentally supported model. J Neurophysiol (1999) 81(3):1355–64.
6. Vaziri S, Diedrichsen J, Shadmehr R. Why does the brain predict sensory consequences of oculomotor commands? Optimal integration of the predicted and the actual sensory feedback. J Neurosci (2006) 26(16):4188–97. doi:10.1523/JNEUROSCI.4747-05.2006
7. Davidson PR, Wolpert DM. Motor learning and prediction in a variable environment. Curr Opin Neurobiol (2003) 13(2):232–7. doi:10.1016/S0959-4388(03)00038-2
8. Davidson PR, Wolpert DM. Widespread access to predictive models in the motor system: a short review. J Neural Eng (2005) 2(3):S313–9. doi:10.1088/1741-2560/2/3/S11
9. McIntyre J, Zago M, Berthoz A, Lacquaniti F. Does the brain model Newton’s laws? Nat Neurosci (2001) 4(7):693–4. doi:10.1038/89477
10. Schubotz RI. Prediction of external events with our motor system: towards a new framework. Trends Cogn Sci (2007) 11(5):211–8. doi:10.1016/j.tics.2007.02.006
11. Zupan LH, Merfeld DM, Darlot C. Using sensory weighting to model the influence of canal, otolith and visual cues on spatial orientation and eye movements. Biol Cybern (2002) 86(3):209–30. doi:10.1007/s00422-001-0290-1
12. Zago M, Bosco G, Maffei V, Iosa M, Ivanenko YP, Lacquaniti F. Internal models of target motion: expected dynamics overrides measured kinematics in timing manual interceptions. J Neurophysiol (2004) 91(4):1620–34. doi:10.1152/jn.00862.2003
13. Zago M, McIntyre J, Senot P, Lacquaniti F. Visuo-motor coordination and internal models for object interception. Exp Brain Res (2009) 192(4):571–604. doi:10.1007/s00221-008-1691-3
14. Harris J. Vision in Parkinson’s disease: what are the deficits and what are their origins? Neuroophthalmology (1998) 19(3):113–35. doi:10.1076/noph.19.3.113.7896
15. Angelaki DE, Shaikh AG, Green AM, Dickman JD. Neurons compute internal models of the physical laws of motion. Nature (2004) 430(6999):560–4. doi:10.1038/nature02754
16. Baddeley RJ, Ingram HA, Miall RC. System identification applied to a visuomotor task: near-optimal human performance in a noisy changing task. J Neurosci (2003) 23(7):3066–75.
17. Kording KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature (2004) 427(6971):244–7. doi:10.1038/nature02169
18. van Beers RJ, Baraduc P, Wolpert DM. Role of uncertainty in sensorimotor control. Philos Trans R Soc Lond B Biol Sci (2002) 357(1424):1137–45. doi:10.1098/rstb.2002.1101
19. Wei K, Kording K. Uncertainty of feedback and state estimation determines the speed of motor adaptation. Front Comput Neurosci (2010) 4:11. doi:10.3389/fncom.2010.00011
20. Wolpert DM, Ghahramani Z. Computational principles of movement neuroscience. Nat Neurosci (2000) 3(Suppl):1212–7. doi:10.1038/81497
21. Babin-Ratte S, Sirigu A, Gilles M, Wing A. Impaired anticipatory finger grip-force adjustments in a case of cerebellar degeneration. Exp Brain Res (1999) 128(1–2):81–5. doi:10.1007/s002210050821
22. Muller F, Dichgans J. Discoordination of pinch and lift forces during grasp in patients with cerebellar lesions. Exp Brain Res (1994) 101(3):485–92. doi:10.1007/BF00227341
23. Nowak DA, Hermsdorfer J. Grip force behavior during object manipulation in neurological disorders: toward an objective evaluation of manual performance deficits. Mov Disord (2005) 20(1):11–25. doi:10.1002/mds.20299
24. Nowak DA, Hermsdorfer J, Marquardt C, Fuchs HH. Grip and load force coupling during discrete vertical arm movements with a grasped object in cerebellar atrophy. Exp Brain Res (2002) 145(1):28–39. doi:10.1007/s00221-002-1079-8
25. Agid Y, Ahlskog E, Albanese A, Calne D, Chase T, De Yebenes J, et al. Levodopa in the treatment of Parkinson’s disease: a consensus meeting. Mov Disord (1999) 14(6):911–3. doi:10.1002/1531-8257(199911)14:6<911::AID-MDS1001>3.0.CO;2-H
26. Fahn S. The spectrum of levodopa-induced dyskinesias. Ann Neurol (2000) 47(4 Suppl 1):S2–9; discussion S11.
27. Liu X, Osterbauer R, Aziz TZ, Miall RC, Stein JF. Increased response to visual feedback of drug-induced dyskinetic movements in advanced Parkinson’s disease. Neurosci Lett (2001) 304(1–2):25–8. doi:10.1016/S0304-3940(01)01740-2
28. Moore AP. Impaired sensorimotor integration in parkinsonism and dyskinesia: a role for corollary discharges? J Neurol Neurosurg Psychiatry (1987) 50(5):544–52. doi:10.1136/jnnp.50.5.544
29. Wenzelburger R, Zhang BR, Pohle S, Klebe S, Lorenz D, Herzog J, et al. Force overflow and levodopa-induced dyskinesias in Parkinson’s disease. Brain (2002) 125(Pt 4):871–9. doi:10.1093/brain/awf084
30. Vitale C, Pellecchia MT, Grossi D, Fragassi N, Cuomo T, Di Maio L, et al. Unawareness of dyskinesias in Parkinson’s and Huntington’s diseases. Neurol Sci (2001) 22(1):105–6. doi:10.1007/s100720170066
31. Bastian AJ. Learning to predict the future: the cerebellum adapts feedforward movement control. Curr Opin Neurobiol (2006) 16(6):645–9. doi:10.1016/j.conb.2006.08.016
32. Beppu H, Nagaoka M, Tanaka R. Analysis of cerebellar motor disorders by visually-guided elbow tracking movement. 2. Contribution of the visual cues on slow ramp pursuit. Brain (1987) 110(Pt 1):1–18. doi:10.1093/brain/110.1.1
33. Beppu H, Suda M, Tanaka R. Analysis of cerebellar motor disorders by visually guided elbow tracking movement. Brain (1984) 107(Pt 3):787–809. doi:10.1093/brain/107.3.787
34. Day BL, Thompson PD, Harding AE, Marsden CD. Influence of vision on upper limb reaching movements in patients with cerebellar ataxia. Brain (1998) 121(Pt 2):357–72. doi:10.1093/brain/121.2.357
35. Lang CE, Bastian AJ. Cerebellar subjects show impaired adaptation of anticipatory EMG during catching. J Neurophysiol (1999) 82(5):2108–19.
36. Stein JF. Role of the cerebellum in the visual guidance of movement. Nature (1986) 323(6085):217–21. doi:10.1038/323217a0
37. Flowers K. Lack of prediction in the motor behaviour of parkinsonism. Brain (1978) 101(1):35–52. doi:10.1093/brain/101.1.35
38. Flowers K. Some frequency response characteristics of parkinsonism on pursuit tracking. Brain (1978) 101(1):19–34. doi:10.1093/brain/101.1.19
39. Koch G, Brusa L, Carrillo F, Lo Gerfo E, Torriero S, Oliveri M, et al. Cerebellar magnetic stimulation decreases levodopa-induced dyskinesias in Parkinson disease. Neurology (2009) 73(2):113–9. doi:10.1212/WNL.0b013e3181ad5387
40. Cerasa A, Morelli M, Augimeri A, Salsone M, Novellino F, Gioia MC, et al. Prefrontal thickening in PD with levodopa-induced dyskinesias: new evidence from cortical thickness measurement. Parkinsonism Relat Disord (2013) 19(1):123–5. doi:10.1016/j.parkreldis.2012.06.003
41. Cerasa A, Pugliese P, Messina D, Morelli M, Cecilia Gioia M, Salsone M, et al. Prefrontal alterations in Parkinson’s disease with levodopa-induced dyskinesia during fMRI motor task. Mov Disord (2012) 27(3):364–71. doi:10.1002/mds.24017
42. Stevenson JK, Oishi MM, Farajian S, Cretu E, Ty E, McKeown MJ. Response to sensory uncertainty in Parkinson’s disease: a marker of cerebellar dysfunction? Eur J Neurosci (2011) 33(2):298–305. doi:10.1111/j.1460-9568.2010.07501.x
43. Au WL, Lei N, Oishi MM, McKeown MJ. L-dopa induces under-damped visually guided motor responses in Parkinson’s disease. Exp Brain Res (2010) 202(3):553–9. doi:10.1007/s00221-010-2156-z
44. Gelb DJ, Oliver E, Gilman S. Diagnostic criteria for Parkinson disease. Arch Neurol (1999) 56(1):33–9.
45. Hoehn MM, Yahr MD. Parkinsonism: onset, progression and mortality. Neurology (1967) 17(5):427–42. doi:10.1212/WNL.17.5.427
46. Goetz CG, Stebbins GT, Shale HM, Lang AE, Chernik DA, Chmura TA, et al. Utility of an objective dyskinesia rating scale for Parkinson’s disease: inter- and intrarater reliability assessment. Mov Disord (1994) 9(4):390–4. doi:10.1002/mds.870090403
47. Fenney A, Jog MS, Duval C. Short-term variability in amplitude and motor topography of whole-body involuntary movements in Parkinson’s disease dyskinesias and in Huntington’s chorea. Clin Neurol Neurosurg (2008) 110(2):160–7. doi:10.1016/j.clineuro.2007.10.010
48. Cheng S, Sabes PN. Modeling sensorimotor learning with linear dynamical systems. Neural Comput (2006) 18(4):760–93. doi:10.1162/neco.2006.18.4.760
49. Donchin O, Francis JT, Shadmehr R. Quantifying generalization from trial-by-trial behavior of adaptive systems that learn with basis functions: theory and experiments in human motor control. J Neurosci (2003) 23(27): 9032–45.
50. Scheidt RA, Dingwell JB, Mussa-Ivaldi FA. Learning to move amid uncertainty. J Neurophysiol (2001) 86(2):971–85.
51. Thoroughman KA, Shadmehr R. Learning of action through adaptive combination of motor primitives. Nature (2000) 407(6805):742–7. doi:10.1038/35037588
52. Ljung L. System Identification: Theory for the User. NJ Upper Saddle River: Prentice hall (1999). 100 p.
53. Pontone GM, Williams JR, Anderson KE, Chase G, Goldstein SA, Grill S, et al. Prevalence of anxiety disorders and anxiety subtypes in patients with Parkinson’s disease. Mov Disord (2009) 24(9):1333–8. doi:10.1002/mds.22611
54. Durif F, Vidailhet M, Debilly B, Agid Y. Worsening of levodopa-induced dyskinesias by motor and mental tasks. Mov Disord (1999) 14(2):242–5. doi:10.1002/1531-8257(199903)14:2<242::AID-MDS1007>3.0.CO;2-W
55. van Sonderen JF, Denier van der Gon JJ, Gielen CC. Conditions determining early modification of motor programmes in response to changes in target location. Exp Brain Res (1988) 71(2):320–8.
56. Wolpert DM, Miall RC. Forward models for physiological motor control. Neural Netw (1996) 9(8):1265–79. doi:10.1016/S0893-6080(96)00035-4
57. Takahashi CD, Scheidt RA, Reinkensmeyer DJ. Impedance control and internal model formation when reaching in a randomly varying dynamical environment. J Neurophysiol (2001) 86(2):1047–51.
58. Liu X, Tubbesing SA, Aziz TZ, Miall RC, Stein JF. Effects of visual feedback on manual tracking and action tremor in Parkinson’s disease. Exp Brain Res (1999) 129(3):477–81. doi:10.1007/s002210050917
59. Ballanger B, Baraduc P, Broussolle E, Le Bars D, Desmurget M, Thobois S. Motor urgency is mediated by the contralateral cerebellum in Parkinson’s disease. J Neurol Neurosurg Psychiatry (2008) 79(10):1110–6. doi:10.1136/jnnp.2007.141689
60. Lewis MM, Slagle CG, Smith AB, Truong Y, Bai P, McKeown MJ, et al. Task specific influences of Parkinson’s disease on the striato-thalamo-cortical and cerebello-thalamo-cortical motor circuitries. Neuroscience (2007) 147(1):224–35. doi:10.1016/j.neuroscience.2007.04.006
61. Ni Z, Pinto AD, Lang AE, Chen R. Involvement of the cerebellothalamocortical pathway in Parkinson disease. Ann Neurol (2010) 68(6):816–24. doi:10.1002/ana.22221
62. Palmer SJ, Ng B, Abugharbieh R, Eigenraam L, McKeown MJ. Motor reserve and novel area recruitment: amplitude and spatial characteristics of compensation in Parkinson’s disease. Eur J Neurosci (2009) 29(11):2187–96. doi:10.1111/j.1460-9568.2009.06753.x
63. Rascol O, Sabatini U, Fabre N, Brefel C, Loubinoux I, Celsis P, et al. The ipsilateral cerebellar hemisphere is overactive during hand movements in akinetic parkinsonian patients. Brain (1997) 120(Pt 1):103–10. doi:10.1093/brain/120.1.103
64. Yu H, Sternad D, Corcos DM, Vaillancourt DE. Role of hyperactive cerebellum and motor cortex in Parkinson’s disease. Neuroimage (2007) 35(1):222–33. doi:10.1016/j.neuroimage.2006.11.047
65. Blakemore SJ, Sirigu A. Action prediction in the cerebellum and in the parietal lobe. Exp Brain Res (2003) 153(2):239–45. doi:10.1007/s00221-003-1597-z
66. Blakemore SJ, Wolpert DM, Frith CD. Central cancellation of self-produced tickle sensation. Nat Neurosci (1998) 1(7):635–40. doi:10.1038/2870
67. Imamizu H, Kuroda T, Miyauchi S, Yoshioka T, Kawato M. Modular organization of internal models of tools in the human cerebellum. Proc Natl Acad Sci U S A (2003) 100(9):5461–6. doi:10.1073/pnas.0835746100
68. Inoue K, Kawashima R, Satoh K, Kinomura S, Goto R, Koyama M, et al. PET study of pointing with visual feedback of moving hands. J Neurophysiol (1998) 79(1):117–25.
69. Ito M. Control of mental activities by internal models in the cerebellum. Nat Rev Neurosci (2008) 9(4):304–13. doi:10.1038/nrn2332
70. Kawato M, Kuroda T, Imamizu H, Nakano E, Miyauchi S, Yoshioka T. Internal forward models in the cerebellum: fMRI study on grip force and load force coupling. Prog Brain Res (2003) 142:171–88. doi:10.1016/S0079-6123(03)42013-X
71. Kettner RE, Mahamud S, Leung HC, Sitkoff N, Houk JC, Peterson BW, et al. Prediction of complex two-dimensional trajectories by a cerebellar model of smooth pursuit eye movement. J Neurophysiol (1997) 77(4):2115–30.
72. Kitazawa S, Kimura T, Yin PB. Cerebellar complex spikes encode both destinations and errors in arm movements. Nature (1998) 392(6675):494–7. doi:10.1038/33141
73. Miall RC, Christensen LO, Cain O, Stanley J. Disruption of state estimation in the human lateral cerebellum. PLoS Biol (2007) 5(11):e316. doi:10.1371/journal.pbio.0050316
74. Synofzik M, Lindner A, Thier P. The cerebellum updates predictions about the visual consequences of one’s behavior. Curr Biol (2008) 18(11):814–8. doi:10.1016/j.cub.2008.04.071
75. Tamada T, Miyauchi S, Imamizu H, Yoshioka T. Activation of the cerebellum in grip force and load force coordination: an fMRI study. Neuroimage (1999) S492.
76. Blakemore SJ, Frith CD, Wolpert DM. The cerebellum is involved in predicting the sensory consequences of action. Neuroreport (2001) 12(9):1879–84. doi:10.1097/00001756-200107030-00023
77. Andersson G, Armstrong DM. Complex spikes in Purkinje cells in the lateral vermis (b zone) of the cat cerebellum during locomotion. J Physiol (1987) 385:107–34.
78. Gellman R, Gibson AR, Houk JC. Inferior olivary neurons in the awake cat: detection of contact and passive body displacement. J Neurophysiol (1985) 54(1):40–60.
79. Simpson JI, Wylie DR, De Zeeuw CI. On climbing fiber signals and their consequence(s). Behav Brain Sci (1996) 19(3):384. doi:10.1017/S0140525X00081486
80. Oscarsson O. Functional organization of olivary projection to the cerebellar anterior lobe. In: Courville J, Lamarre DC, editors. The Inferior Olivary Nucleus: Anatomy and Physiology. New York: Raven (1980). p. 279–89.
81. Desmurget M, Epstein CM, Turner RS, Prablanc C, Alexander GE, Grafton ST. Role of the posterior parietal cortex in updating reaching movements to a visual target. Nat Neurosci (1999) 2(6):563–7. doi:10.1038/9219
82. Pisella L, Grea H, Tilikete C, Vighetto A, Desmurget M, Rode G, et al. An ‘automatic pilot’ for the hand in human posterior parietal cortex: toward reinterpreting optic ataxia. Nat Neurosci (2000) 3(7):729–36. doi:10.1038/76694
83. Desmurget M, Reilly KT, Richard N, Szathmari A, Mottolese C, Sirigu A. Movement intention after parietal cortex stimulation in humans. Science (2009) 324(5928):811–3. doi:10.1126/science.1169896
84. Clower DM, West RA, Lynch JC, Strick PL. The inferior parietal lobule is the target of output from the superior colliculus, hippocampus, and cerebellum. J Neurosci (2001) 21(16):6283–91.
85. Glickstein M. How are visual areas of the brain connected to motor areas for the sensory guidance of movement? Trends Neurosci (2000) 23(12):613–7. doi:10.1016/S0166-2236(00)01681-7
86. Owen AM, James M, Leigh PN, Summers BA, Marsden CD, Quinn NP, et al. Fronto-striatal cognitive deficits at different stages of Parkinson’s disease. Brain (1992) 115(Pt 6):1727–51. doi:10.1093/brain/115.6.1727
87. Calon F, Grondin R, Morissette M, Goulet M, Blanchet PJ, Di Paolo T, et al. Molecular basis of levodopa-induced dyskinesias. Ann Neurol (2000) 47(4 Suppl 1):S70–8.
88. Aubert I, Guigoni C, Hakansson K, Li Q, Dovero S, Barthe N, et al. Increased D1 dopamine receptor signaling in levodopa-induced dyskinesia. Ann Neurol (2005) 57(1):17–26. doi:10.1002/ana.20296
89. Kumar N, Van Gerpen JA, Bower JH, Ahlskog JE. Levodopa-dyskinesia incidence by age of Parkinson’s disease onset. Mov Disord (2005) 20(3):342–4. doi:10.1002/mds.20360
90. Troiano AR, de la Fuente-Fernandez R, Sossi V, Schulzer M, Mak E, Ruth TJ, et al. PET demonstrates reduced dopamine transporter expression in PD with dyskinesias. Neurology (2009) 72(14):1211–6. doi:10.1212/01.wnl.0000338631.73211.56
91. Nimura T, Ando T, Yamaguchi K, Nakajima T, Shirane R, Itoh M, et al. The role of sigma-receptors in levodopa-induced dyskinesia in patients with advanced Parkinson disease: a positron emission tomography study. J Neurosurg (2004) 100(4):606–10. doi:10.3171/jns.2004.100.4.0606
92. Bostan AC, Dum RP, Strick PL. The basal ganglia communicate with the cerebellum. Proc Natl Acad Sci U S A (2010) 107(18):8452–6. doi:10.1073/pnas.1000496107
93. Hoshi E, Tremblay L, Feger J, Carras PL, Strick PL. The cerebellum communicates with the basal ganglia. Nat Neurosci (2005) 8(11):1491–3. doi:10.1038/nn1544
94. Defer GL. Controversial issues concerning the initial treatment of Parkinson’s disease: L-Dopa or dopaminergic agonists? Rev Neurol (Paris) (1999) 155(1):43–5.
95. Langston JW, Widner H, Goetz CG, Brooks D, Fahn S, Freeman T, et al. Core assessment program for intracerebral transplantations (CAPIT). Mov Disord (1992) 7(1):2–13. doi:10.1002/mds.870070103
96. Chaudhuri KR, Schapira AH. Non-motor symptoms of Parkinson’s disease: dopaminergic pathophysiology and treatment. Lancet Neurol (2009) 8(5):464–74. doi:10.1016/S1474-4422(09)70068-7
97. Quinn NP, Koller WC, Lang AE, Marsden CD. Painful Parkinson’s disease. Lancet (1986) 1(8494):1366–9. doi:10.1016/S0140-6736(86)91674-0
98. Armand S, Landis T, Sztajzel R, Burkhard PR. Dyskinesia-induced postural instability in Parkinson’s disease. Parkinsonism Relat Disord (2009) 15(5):359–64. doi:10.1016/j.parkreldis.2008.08.007
Keywords: l-DOPA-induced dyskinesias, Parkinson’s disease, dynamical system models, visually guided tracking, visual uncertainty
Citation: Stevenson JKR, Lee C, Lee B-S, TalebiFard P, Ty E, Aseeva K, Oishi MMK and McKeown MJ (2014) Excessive sensitivity to uncertain visual input in L-DOPA-induced dyskinesias in Parkinson’s disease: further implications for cerebellar involvement. Front. Neurol. 5:8. doi: 10.3389/fneur.2014.00008
Received: 01 December 2013; Paper pending published: 21 December 2013;
Accepted: 10 January 2014; Published online: 04 February 2014.
Edited by:
Antonio Cerasa, Consiglio Nazionale delle Ricerche, ItalyReviewed by:
Giulia Donzuso, University “Magna Graecia” di Catanzaro, ItalyGennarina Arabia, University “Magna Graecia” di Catanzaro, Italy
Copyright: © 2014 Stevenson, Lee, Lee, TalebiFard, Ty, Aseeva, Oishi and McKeown. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin J. McKeown, Pacific Parkinson’s Research Centre, University Hospital, University of British Columbia, Purdy Pavilion, 2221 Wesbrook Mall, Vancouver, BC V6T 2B5, Canada e-mail:bWFydGluLm1ja2Vvd25AdWJjLmNh
 James K. R. Stevenson
James K. R. Stevenson Chonho Lee
Chonho Lee Bu-Sung Lee2
Bu-Sung Lee2 Kristina Aseeva
Kristina Aseeva Meeko M. K. Oishi
Meeko M. K. Oishi Martin J. McKeown
Martin J. McKeown