- 1School of Marine Electrical Engineering, Dalian Maritime University, Dalian, China
- 2China State Shipbuilding Corporation Limited, Beijing, China
This paper presents a distributed constant bearing guidance and model-free disturbance rejection control method for formation tracking of autonomous surface vehicles subject to fully unknown kinetic model. First, a distributed constant bearing guidance law is designed at the kinematic level to achieve a consensus task. Then, by using an adaptive extended state observer (AESO) to estimate the total uncertainties and unknown input coefficients, a simplified model-free kinetic controller is designed based on a dynamic surface control (DSC) design. It is proven that the closed-loop system is input-to-state stable The stability of the closed-loop system is established. A salient feature of the proposed method is that a cooperative behavior can be achieved without knowing any priori information. An application to formation control of autonomous surface vehicles is given to show the efficacy of the proposed integrated distributed constant bearing guidance and model-free disturbance rejection control.
1. Introduction
In recent years, there has been a surge of interest in distributed cooperative control of autonomous surface vehicles (ASVs). It can be envisioned that multiple ASVs enable vehicles to collaborate with each other to execute difficult missions, contributing to improved efficiency and effectiveness over a single one (Arrichiello et al., 2006; Cui et al., 2010; Peng et al., 2011, 2013, 2020, 2021a,b,c; Wang and Han, 2016; Li et al., 2018; Chen et al., 2020; Guo et al., 2020; Liu et al., 2020a,b, 2022; Zhang et al., 2020; Zhu et al., 2021, 2022; Gu et al., 2022a,b,c,d; Hu et al., 2022a,b; Rout et al., 2022). Recently, distributed control methods have been widely studied (see references, Cao and Ren, 2010; Wang et al., 2010; Zhang et al., 2011, 2012; Cui et al., 2012; Zhang and Lewis, 2012; Hong et al., 2013; Peng et al., 2014; Jiang et al., 2021). In Cao and Ren (2010), a distributed control method is proposed to deal with the formation control problem. In Jiang et al. (2021), a distributed model-free control method is designed using a data-driven fuzzy predictor and extended state observers for ASVs to achieve cooperative target enclosing. A distributed adaptive control method is presented to achieve the cooperative tracking with unknown dynamics in Zhang and Lewis (2012). In Cui et al. (2012), a distributed synchronized tracking control method is designed based on an adaptive neural network for ASVs. In Wang et al. (2010), a distributed control approach is designed to deal with the asymptotic tracking under disturbances generated by the exosystem. A distributed leader-follower control method is proposed using the output regulation theory and internal model principle in Hong et al. (2013). In Peng et al. (2014), a distributed adaptive control method is presented by using the state information of neighboring ASVs only. In Zhang et al. (2011), a distributed control method is presented by using the observer to achieve cooperative tracking. In Zhang et al. (2012), an adaptive distributed control technique is designed based on neural network to deal with the cooperative tracking problems. Its key advantage is that the group objective can be achieved via local information exchanges. Consensus-based distributed formation control schemes are presented in Ren (2007), Ren and Sorensen (2008), and Hu (2012). In Ren (2007), a consensus-based distributed control method is proposed to deal with the formation control problem. In Ren and Sorensen (2008), a consensus-based approach is designed to achieve the distributed formation control. In Hu (2012), a distributed consensus-based control method is designed to achieve global asymptotic consensus tracking.
As for autonomous surface vehicle systems, the modeling process is time-consuming and a large number of experiments is required for identifying model parameters. On the other hand, robustness against model uncertainty and ocean disturbances is critical for high-performance control of ASVs (Fossen, 2002; Skjetne et al., 2005; Tee and Ge, 2006; Li et al., 2008; Dai et al., 2012; Chen et al., 2013; How et al., 2013). To deal with this problem, adaptive backstepping and DSC techniques has been widely suggested; see the references (Fossen, 2002; Skjetne et al., 2005; Tee and Ge, 2006; Li et al., 2008; Dai et al., 2012; Chen et al., 2013; How et al., 2013). In Tee and Ge (2006), a stable tracking control method is proposed using backstepping and Lyapunov synthesis for multiple marine vehicles under the unmeasurable states. In Chen et al. (2013), a variable control structure based on backstepping and Lyapunov synthesis is designed for the positioning of marine vessels with the parametric uncertainties and ocean disturbances. In How et al. (2013), an adaptive approximation technique is designed using the backstepping to estimate the uncertainties. In Dai et al. (2012), an adaptive neural networks control method is designed based on the backstepping and Lyapunov synthesis with uncertain environment. In Skjetne et al. (2005), an adaptive recursive control method is designed using the backstepping and Lyapunov synthesis for marine vehicles with the unknown model parameters. Although the adaptive backstepping and DSC are recursive and systematic design methods, it does not offer the freedom to choose the parameter adaptive laws (Krstić et al., 1995). Besides, the identification process depends on the tracking error dynamics, and the transient performance cannot be guaranteed (Cao and Hovakimyan, 2007; Yucelen and Haddad, 2013).
Motivated by the above observations, this article presents a distributed constant bearing guidance and model-free disturbance rejection control method for formation tracking of ASVs subject to fully unknown kinetic model. Specifically, a distributed constant bearing guidance law is designed at the kinematic level to achieve a consensus task. Then, an AESO is constructed for estimating the model uncertainty and unknown ocean disturbances, which can achieve the uncertainty and disturbance estimation. Next, a controller module is developed by using a DSC technique. Simulation results are provided to show the efficacy of the proposed modular design integrated distributed constant bearing guidance and model-free disturbance rejection control method. The main contribution of the proposed control method are stated as follows. Firstly, the proposed design results in the decoupled estimation and control, where the estimation loop is faster than the control loop, yielding the improved transient performance. This contributes to the certainty equivalence control of multi-vehicle systems. Secondly, the security level of ASVs is enhanced by using an AESO to identify the total uncertainties. Finally, the salient feature of the proposed method is that a cooperative behavior can be achieved without knowing any priori information.
The rest of this paper is organized as follows: The problem formulation is presented in Section 2. Section 3 presents the distributed constant bearing guidance and model-free disturbance rejection control method. Section 4 provides simulation results to illustrate the designed model-free disturbance rejection control method for distributed formation tracking. Section 5 concludes this paper.
2. Problem formulation
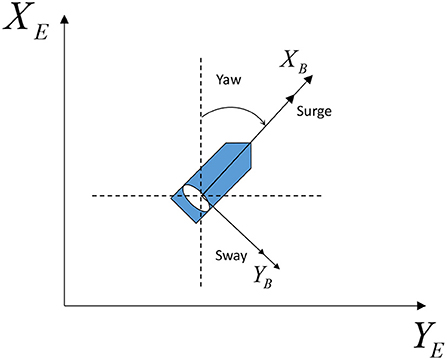
A three degree-of-freedom (DOF) dynamical model for ASVs in a horizontal plane as shown in Figure 1 can be expressed with kinematics (Fossen, 2002; Skjetne et al., 2005).
where
represents the earth-fixed position and heading; includes the body-fixed surge and sway velocities, and the yaw rate; denote the inertia matrix, coriolis/centripetal matrix, and damping matrix, respectively; denotes the control input; represents the disturbance vector caused by the wind, waves, and ocean currents.
Since the robot dynamics (1) contain unknown dynamics induced by model uncertainty and ocean disturbances, we rewrite the robot kinetics (1) as follows.
where
The control objective is to design a cooperative control law τi for ASVs with dynamics (1) to track a reference trajectory η0(t) such that
for some small constant δi.
We use the following assumption.
Assumption 1: The reference signals η0(t), , and are bounded.
3. Cooperative tracking
In this section, a modular design approach is presented to develop the cooperative formation controllers for ASVs. First, by using the designed AESO to estimate the total uncertainties and fully unknown input coefficients, a simplified model-free dynamic kinematic controller is designed with the aid of a dynamic surface control.
3.1. Controller design
Step 1. At first, a cooperative tracking error is defined as
where , and aij and ai0 are determined by the communication graph, if the ith ASV obtains the information of the jth, aij = 1; otherwise, aij = 0. The definition of ai0 is similar to aij.
Assumption 2: The augmented graph contains a spanning tree with the root node being the leader node n0.
Then, define a global formation tracking error ϵi as
Define as the Laplacian matrix of the graph and as the leader adjacency matrix, which leads to
where , , , and . Define aid = di + ai0, then, it follows from (1) that the time derivative of zi1 in (8) is obtained
where
A distributed constant-bearing guidance law αi1 is proposed as follows
where Δ is positive constant, and with kiη1 ∈ ℝ, kiη2 ∈ ℝ, and kiη3 ∈ ℝ being positive constants.
Let us suppose here that αi1 are unknown, and let it pass through a first-order filter as follows
where γi ∈ ℝ.
Then, the derivative of qi is obtained as
where qi = αi1 − νid.
Now using (15), we can conclude that
We can obtain that the bound of ||qi(t)|| satisfies the following inequality
where is a positive constant.
Step 2: To start with, define the velocity tracking error zi2 as
Take the time derivative of zi2 along (4) is
For the robot kinetics (4), an AESO is designed as
where , , and kiν1 ∈ ℝ, kiν2 ∈ ℝ, kiν3 ∈ ℝ, kis1 ∈ ℝ, kis2 ∈ ℝ, and kis3 ∈ ℝ are positive constants. , ŝi, , and are the estimates of νi, si, σi, and Λi, respectively.
Assumption 3: For unknown functions si and σi, there are and , such that and .
Let the parameter estimation be , and the prediction error be . Define and . It can be obtained with ai being the reconstruct error. Then, the error dynamics can be expressed as
To stabilize zi2, a model-free disturbance rejection control law is proposed as follows
where and and .
Substituting (21) into (18) yields
where ϱi is a positive constant.
The following lemma presents the stability of AESO error subsystem (20).
Lemma 1: Under Assumption 2, the AESO error subsystem (20), viewed as a system with the states being , , , and , the inputs being ṡi, , and is ISS.
Proof : Construct the Lyapunov function as
and the time derivatives of Vσi is
where and .
Since
renders
with θi ∈ (0, 1). Therefore, it can conclude that the error ϵi is bounded.
It follows from (20) that the dynamics of the and can be rewritten as
where , , and
with Aχi being Hurwitz. There exists a unique positive definite matrix Pχi, such that
Construct the Lyapunov function for system (27) as
The dynamics of the Vχi is
Since
renders
with ai2 ∈ (0, 1). It is concluded that the error subsystem (20) is ISS. There exists class function βi1 such that
with the gain function (Wang et al., 2006) given by
Recalling (11), (17), and (22), the error dynamics is addressed as
where qi = νid − αi1.
By using the coordinations of zi1 and ẑi2, the above subsystem (35) is only perturbed by and qi. Obviously, these two variables will vanish soon as time evolve by choosing the control parameters of predictors and filters.
Lemma 2: The error subsystem (35), viewed as a system with the states being zi1 and ẑi2 and the inputs being and qi, is ISS.
Proof : Construct a Lyapunov function as follows
Taking the time derivative of Vc along (35), it renders
Using the inequalities
it follows that
By selecting and , one has
Since
renders
There exists class function βi2 such that
where the gain functions are given by
with Pi2 = diag{Mi, 1}. The proof is completed.
3.2. Cascade stability
Theorem: Consider the closed-loop network system consisting of the vessels dynamics (1) (2), the AESO (19), the distributed constant-bearing guidance law (13), and the controller (21). If Assumptions 1–3 and ci > 0 are satisfied, all signals in the closed-loop system are bounded, and the global CFT error εi converges to a neighborhood around zero.
Proof : From Lemma 1, we have proved that subsystem (20) with states being and input being ṡi is ISS. From Lemma 2, it can be obtained that subsystem (35) with states being (zi1, ẑi2) and inputs being and qi is ISS. By Krstić et al. (1995), it proves that the cascade system formed by (20) and (35) with states being and the inputs being qi and ṡi is ISS. Since qi and ṡi is bounded by and , respectively. Then, the error signals and are all bounded. Observing that , it follows that zi2 is bounded.
Note that as t → ∞, βi1(·) and βi2(·) → 0, and it follows from (34) and (45) that zi1 is ultimately bounded by
Then, define as the minimal singular value of , and it follows from Assumption 2 that
From (47) and (48), εi is ultimately bounded as
4. An example
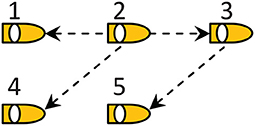
Consider a networked system consisting of five ASVs, and the communication topology is shown in Figure 2 with the ASV 2 being the leader. The parameters for each model ship are taken from Skjetne et al. (2005). The initial states of five ASVs are set to η1 = (0, 0, 0), η2 = (0, 12, 0), η3 = (0, −12, 0), η4 = (0, 24, 0), and η5 = (0, −24, 0). In order to better emerge the simulation effect, we add the desired deviations Δij between the ASVs as follows Δ12 = (12, 12, 0), Δ15 = (36, 0, 0), Δ23 = (8, 8, 0), and Δ34 = (8, −8, 0). The control parameters are chosen as kiη = diag{2, 2, 2}, kiν = diag{20, 20, 20}, kis = diag{100, 100, 100}, kiτ = diag{285, 338, 27.6}, and γi1 = 0.02. Define the path variable as ϑ, and the information of path is given in (49)
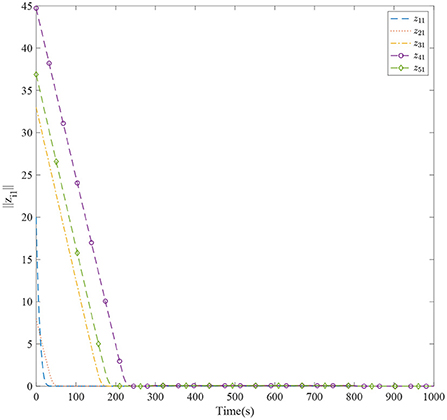
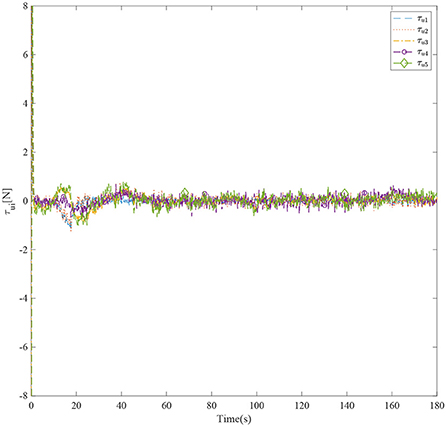
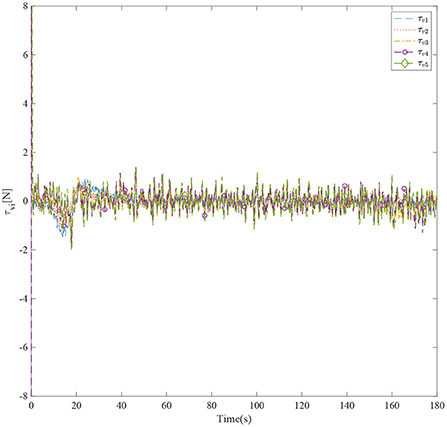
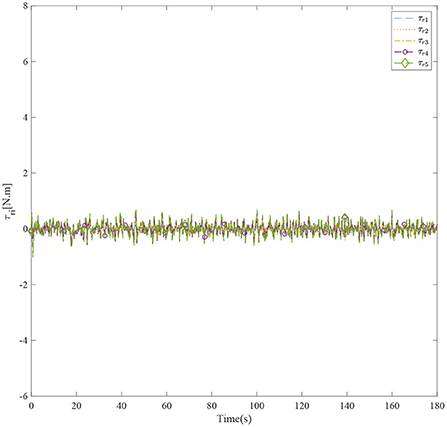
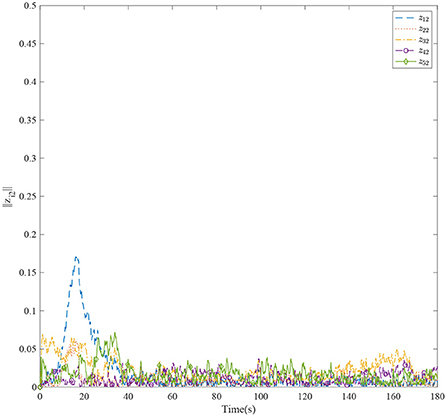
Figure 3 shows the formation trajectories of the five ASVs. It reveals that the a triangle formation can be well established without knowing any priori of the model parameters. Figure 4 shows the cooperative tracking error norms of zi1. It can be seen that the cooperative tracking errors ||zi1|| converge to a neighborhood of the origin. Figures 5–7 show the control inputs in terms of τui, τνi, and τri, respectively. It verifies that the control inputs are all bounded. The velocity tracking error norms of zi2 are shown in Figure 8. It can be seen that the velocity tracking errors ||zi2|| converge to a neighborhood of the origin.
5. Conclusions
In this paper, an integrated distributed constant bearing guidance and model-free disturbance rejection control method was presented for cooperative tracking of ASVs subject to fully unknown kinetic model. At the kinematic level, a distributed constant bearing guidance law is designed to achieve a formation task. By using AESO to estimate the total uncertainties and unknown input coefficients, a simplified model-free dynamic kinematic controller is designed with the aid of a dynamic surface control. The stability of the closed-loop cooperative system is proven. The application to formation control of autonomous surface vehicles is given to show the efficacy of the proposed model-free disturbance rejection control method for distributed formation tracking.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author contributions
Conceptualization, validation, investigation, and writing—review and editing: XN, SG, and ZX. Methodology and resources: XN, SG, and SF. Software and data curation: XN. Formal analysis and writing—original draft preparation: SG. All authors contributed to the article and approved the submitted version.
Conflict of interest
Author ZX was employed by China State Shipbuilding Corporation Limited.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer DM declared a shared affiliation with the authors XN, SG, and SF to the handling editor at the time of review.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arrichiello, F., Chiaverini, S., and Fossen, T. I. (2006). “Formation control of underactuated surface vessels using the Null-Space-Based behavioral control,” in IEEE/RSJ International Conference on Intelligent Robots & Systems IEEE (Beijing), 5942–5947. doi: 10.1109/IROS.2006.282477
Cao, C. Y., and Hovakimyan, N. (2007). Novel l1 neural network adaptive control architecture with guaranteed transient performance. IEEE Trans. Neural Netw. 18, 1160–1171. doi: 10.1109/TNN.2007.899197
Cao, Y., and Ren, W. (2010). Distributed formation control for fractional-order systems: dynamic interaction and absolute/relative damping. Syst. Control Lett. 59, 233–240. doi: 10.1016/j.sysconle.2010.01.008
Chen, L. P., Cui, R., and Yan, W. S. (2020). Adaptive neural network control of underactuated surface vessels with guaranteed transient performance: theory and experimental results. IEEE Trans. Indus. Electron. 67, 4024–4035. doi: 10.1109/TIE.2019.2914631
Chen, M., Ge, S. S., How, B. V. E., and Choo, Y. S. (2013). Robust adaptive position mooring control for marine vessels. IEEE Trans. Control Syst. Technol. 21, 395–409. doi: 10.1109/TCST.2012.2183676
Cui, R., Ge, S. S., How, B. V. E., and Choo, Y. S. (2010). Leader-follower formation control of underactuated autonomous underwater vehicles. Ocean Eng. 37, 1491–1502. doi: 10.1016/j.oceaneng.2010.07.006
Cui, R., Ren, B., and Ge, S. S. (2012). Synchronised tracking control of multi-agent system with high-order dynamics. IET Control Theory Appl. 6, 603–614. doi: 10.1049/iet-cta.2011.0011
Dai, S. L., Wang, C., and Luo, F. (2012). Identification and learning control of ocean surface ship using neural networks. IEEE Trans. Indus. Inform. 8, 801–810. doi: 10.1109/TII.2012.2205584
Fossen, T. I. (2002). Marine Control System, Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles. Marine Cyernetics, Trondheim, Norway.
Gu, N., Wang, D., Peng, Z., Li, T., and Tong, S. (2022a). Model-free containment control of underactuated surface vessels under switching topologies based on guiding vector fields and data-driven neural predictors. IEEE Trans. Cybern. 52, 10843–10854. doi: 10.1109/TCYB.2021.3061588
Gu, N., Wang, D., Peng, Z., and Wang, J. (2022b). Safety-critical containment maneuvering of underactuated autonomous surface vehicles based on neurodynamic optimization with control barrier functions. IEEE Trans. Neural Netw. Learn. Syst. doi: 10.1109/TNNLS.2021.3110014
Gu, N., Wang, D., Peng, Z., Wang, J., and Han, Q.-L. (2022c). Disturbance observers and extended state observers for marine vehicles: a survey. Control Eng. Pract. 2022:108258. doi: 10.1016/j.conengprac.2022.105158
Gu, N., Wang, D., Peng, Z. H., Wang, J., and Han, Q.-L. (2022d). Advances in line-of-sight guidance for path following of autonomous marine vehicles: an overview. IEEE Trans. Syst. Man Cybern. doi: 10.1109/TSMC.2022.3162862
Guo, X., Yan, W. S., and Cui, R. (2020). Modified line-of-sight guidance law with adaptive neural network control of underactuated marine vehicles with state and input constraints. IEEE Trans. Control Syst. Technol. 28, 1902–1914. doi: 10.1109/TCST.2020.2998798
Hong, Y., Wang, X., and Jiang, Z. (2013). Distributed output regulation of leader-follower multi-agent systems. Int. J. Robust Nonlin. Control 23, 48–66. doi: 10.1002/rnc.1814
How, B. V. E., Ge, S. S., and Choo, Y. S. (2013). Dynamic load positioning for subsea installation via adaptive neural control. IEEE J. Ocean. Eng. 35, 366–375. doi: 10.1109/JOE.2010.2041261
Hu, G. Q. (2012). Robust consensus tracking of a class of second-order multi-agent dynamic systems. Syst. Control Lett. 61, 134–142. doi: 10.1016/j.sysconle.2011.10.004
Hu, X., Wei, X., Kao, Y., and Han, J. (2022a). Robust synchronization for under-actuated vessels based on disturbance observer. IEEE Trans. Intell. Transp. Syst. 23, 5470–5479. doi: 10.1109/TITS.2021.3054177
Hu, X., Zhu, G., Ma, Y., Li, Z., Malekian, R., and Sotelo, M. A. (2022b). Event-triggered adaptive fuzzy setpoint regulation of surface vessels with unmeasured velocities under thruster saturation constraints. IEEE Trans. Intell. Transp. Syst. 23, 13463–13472. doi: 10.1109/TITS.2021.3124635
Jiang, Y., Peng, Z., Wang, D., Yong, Y., and Han, Q.-L. (2021). Cooperative target enclosing of ring-networked under-actuated autonomous surface vehicles based on data-driven fuzzy predictors and extended state observers. IEEE Trans. Fuzzy Syst. 30, 2515–2528. doi: 10.1109/TFUZZ.2021.3087920
Krstić, M., Kanellakopoulos, I., and Kokotovic, P. (1995). Nonlinear and Adaptive Control Design. New York, NY: John Wiley & Sons.
Li, J., Lee, P. M., Jun, B. H., and Lim, Y. K. (2008). Point-to-point navigation of underactuated ships. Automatica 44, 3201–3205. doi: 10.1016/j.automatica.2008.08.003
Li, T., Zhao, R., Chen, C. L. P., Fang, L., and Liu, C. (2018). Finite-time formation control of under-actuated ships using nonlinear sliding mode control. IEEE Trans. Cybern. 48, 3243–3253. doi: 10.1109/TCYB.2018.2794968
Liu, L., Wang, D., Peng, Z., and Han, Q.-L. (2022). Distributed path following of multiple under-actuated autonomous surface vehicles based on data-driven neural predictors via integral concurrent learning. IEEE Trans. Neural Netw. Learn. Syst. 32, 5334–5344. doi: 10.1109/TNNLS.2021.3100147
Liu, L., Wang, D., Peng, Z., Li, T., and Chen, C. L. P. (2020a). Cooperative path following of ring-networked under-actuated autonomous surface vehicles: algorithms and experiment results. IEEE Trans. Cybern. 50, 1519–1529. doi: 10.1109/TCYB.2018.2883335
Liu, L., Zhang, W., Wang, D., and Peng, Z. (2020b). Event-triggered extended state observers design for dynamic positioning vessels subject to unknown sea loads. Ocean Eng. 2020:107242. doi: 10.1016/j.oceaneng.2020.107242
Peng, Z., Liu, L., and Wang, J. (2021a). Output-feedback flocking control of multiple autonomous surface vehicles based on data-driven adaptive extended state observers. IEEE Trans. Cybern. 51, 4611–4622. doi: 10.1109/TCYB.2020.3009992
Peng, Z., Wang, D., Chen, Z., Hu, X., and Lan, W. (2013). Adaptive dynamic surface control for formations of autonomous surface vehicles with uncertain dynamics. IEEE Trans. Control Syst. Technol. 21, 513–520. doi: 10.1109/TCST.2011.2181513
Peng, Z., Wang, D., and Hu, X. (2011). Robust adaptive formation control of underactuated autonomous surface vehicles with uncertain dynamics. IET Control Theory Appl. 5, 1378–1387. doi: 10.1049/iet-cta.2010.0429
Peng, Z., Wang, D., Li, T., and Han, M. (2020). Output feedback cooperative formation maneuvering of autonomous surface vehicles with connectivity preservation and collision avoidance. IEEE Trans. Cybern. 50, 2527–2535. doi: 10.1109/TCYB.2019.2914717
Peng, Z., Wang, D., and Wang, J. (2021b). Data-driven adaptive disturbance observers for model-free trajectory tracking control of maritime autonomous surface ships. IEEE Trans. Neural Netw. Learn. Syst. 32, 5584–5593. doi: 10.1109/TNNLS.2021.3093330
Peng, Z., Wang, D., Zhang, H., and Sun, G. (2014). Distributed neural network control for adaptive synchronization of uncertain dynamical multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 25, 1508–1519. doi: 10.1109/TNNLS.2013.2293499
Peng, Z., Wang, J., Wang, D., and Han, Q.-L. (2021c). Automatic leader-follower persistent formation control for autonomous surface vehicles. IEEE Trans. Indus. Informatics 17, 732–745. doi: 10.1109/TII.2020.3004343
Ren, W. (2007). Consensus strategies for cooperative control of vehicle formations. IET Control Theory Appl. 1, 505–512. doi: 10.1049/iet-cta:20050401
Ren, W., and Sorensen, N. (2008). Distributed coordination architecture for multi-robot formation control. Robot. Auton. Syst. 56, 324–333. doi: 10.1016/j.robot.2007.08.005
Rout, R., Cui, R., and Yan, W. S. (2022). Sideslip-compensated guidance-based adaptive neural control of marine surface vessels. IEEE Trans. Cybern. 52, 2860–2871. doi: 10.1109/TCYB.2020.3023162
Skjetne, R., Fossen, T. I., and Kokotovic, P. V. (2005). Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 41, 289–298. doi: 10.1016/j.automatica.2004.10.006
Tee, K. P., and Ge, S. S. (2006). Control of fully actuated ocean surface vessels using a class of feedforward approximators. IEEE Trans. Control Syst. Technol. 14, 750–756. doi: 10.1109/TCST.2006.872507
Wang, C., Hill, D. J., Ge, S. S., and Chen, G. R. (2006). An ISS-modular approach for adaptive neural control of pure-feedback systems. Automatica 42, 723–731. doi: 10.1016/j.automatica.2006.01.004
Wang, X., Hong, Y., Huang, J., and Jiang, Z. P. (2010). A distributed control approach to a robust output regulation problem for multi-agent linear systems. IEEE Trans. Autom. Control 55, 2891–2895. doi: 10.1109/TAC.2010.2076250
Wang, Y.-L., and Han, Q.-L. (2016). Network-based fault detection filter and controller coordinated design for unmanned surface vehicles in network environments. IEEE Trans. Indus. Inform. 12, 1753–1765. doi: 10.1109/TII.2016.2526648
Yucelen, T., and Haddad, W. M. (2013). Low-frequency learning and fast adaptation in model reference adaptive control. IEEE Trans. Autom. Control 58, 1080–1085. doi: 10.1109/TAC.2012.2218667
Zhang, H., Lewis, F. L., and Das, A. (2011). Optimal design for synchronization of cooperative systems: state feedback, observer and output feedback. IEEE Trans. Autom. Control 56, 1948–1952. doi: 10.1109/TAC.2011.2139510
Zhang, H., Lewis, F. L., and Qu, Z. H. (2012). Lyapunov, adaptive, and optimal design techniques for cooperative systems on directed communication graphs. IEEE Trans. Indus. Electron. 59, 3026–3041. doi: 10.1109/TIE.2011.2160140
Zhang, H. W., and Lewis, F. L. (2012). Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics. Automatica 48, 1432–1439. doi: 10.1016/j.automatica.2012.05.008
Zhang, X.-M., Han, Q.-L., Ge, X., Ding, D., Ding, L., Yue, D., et al. (2020). Networked control systems: a survey of trends and techniques. IEEE/CAA J. Autom. Sin. 7, 1–17. doi: 10.1109/JAS.2019.1911651
Zhu, G., Ma, Y., Li, Z., Malekian, R., and Sotelo, M. (2021). Adaptive neural output feedback control for MSVs with predefined performance. IEEE Trans. Vehicul. Technol. 70, 2994–3006. doi: 10.1109/TVT.2021.3063687
Keywords: dynamic surface control, adaptive extended state observer, autonomous surface vehicle, model-free control, formation tracking
Citation: Niu X, Gao S, Xu Z and Feng S (2022) Distributed model-free formation control of networked fully-actuated autonomous surface vehicles. Front. Neurorobot. 16:1028656. doi: 10.3389/fnbot.2022.1028656
Received: 26 August 2022; Accepted: 13 September 2022;
Published: 29 September 2022.
Edited by:
Guibing Zhu, Zhejiang Ocean University, ChinaReviewed by:
Dongdong Mu, Dalian Maritime University, ChinaXin Hu, Ludong University, China
Yancai Hu, Shandong Jiaotong University, China
Copyright © 2022 Niu, Gao, Xu and Feng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shengnan Gao, Z2Fvc2hlbmduYW5AZGxtdS5lZHUuY24=
 Xiaobing Niu1
Xiaobing Niu1 Shengnan Gao
Shengnan Gao