- 1Department of Medical Engineering and Biotechnology, University of Applied Sciences Jena, Jena, Germany
- 2Department of Bioinformatics, Friedrich Schiller University Jena, Jena, Germany
- 3BioControl Jena GmbH, Jena, Germany
- 4Salata AG, Ritschenhausen, Germany
A dynamic coarse-grained model of microalgal growth considering light availability and temperature under discontinuous bioprocess operation was parameterized using experimental data from 15 batch cultivations of Nannochloropsis granulata in a pilot-scale tubular photobioreactor. The methodology applied consists of a consecutive two-step model parameter estimation using pooled, clustered and reorganized data to obtain initial estimates and multi-experiment fitting to obtain the final estimates, which are: maximum specific growth rate μmax = 1.56 d−1, specific photon half-saturation constant KS,ph = 1.89 , specific photon maintenance coefficient mph = 0.346 and the cardinal temperatures Tmin = 2.3°C, Topt = 27.93°C and Tmax = 32.59°C. Biomass productivity prediction proved highly accurate, expressed by the mean absolute percent error MAPE = 7.2%. Model-based numerical optimization of biomass productivity for repeated discontinuous operation with respect to the process parameters cultivation cycle time, inoculation biomass concentration and temperature yielded productivity gains of up to 35%. This optimization points to best performance under continuous operation. The approach successfully applied here to small pilot-scale confirms an earlier one to lab-scale, indicating its transferability to larger scale tubular photobioreactors.
1. Introduction
Microalgae as a phylogenetically non-related group of organisms are adapted to a wide variety of inhabited ecosystems (Hoffmann, 2010; Guarnieri and Pienkos, 2014). The mostly photosynthetically active organisms produce a number of substances, such as carotenoids and fatty acids, that are specific to primary producers. A number of them, such as ketocarotenoids (e.g., astaxanthin) or long-chain ω-3 fatty acids (e.g., eicosapentaenoic acid, C20:5, EPA), are of commercial interest to the food and feed industry (Posten, 2012; Minhas et al., 2016).
In comparison to plants, microalgae are in general structurally less complex and show higher area productivities (Derwenskus et al., 2018). Their gross biochemical composition can be influenced without genetic modifications (Gu et al., 2012; Draaisma et al., 2013). These specific characteristics cause growing interest in autotrophic biotechnological production processes based on microalgae. Their products are of particular interest to markets such as aquaculture, nutraceuticals and cosmetics (Khan et al., 2018; Malcata, 2018). This is accompanied by worldwide growing research efforts (Endres et al., 2018; Garrido-Cardenas et al., 2018; Lippi et al., 2018).
The commercial interest in the genus Nannochloropsis has risen since they accumulate high lipid contents per cell, high EPA contents and show comparatively high biomass productivities (Gouveia and Oliveira, 2009; Bartley et al., 2014). This eustigmatophyte has a rather small cell size of 2, …, 4 μm; cells are free-floating and easy to ingest by zooplankton and fish larvae, representing a major reason for its extensive use in aquaculture. As other microalgae, Nannochloropsis spp. contain variable contents of proteins (24, …, 52%), lipids (16, …, 50%), EPA (3, …, 5%), and carotenoids (0.4, …, 0.6%) (Chua and Schenk, 2017; Hulatt et al., 2017; Neumann et al., 2018). The biochemical composition shifts as a result of cellular adaptation to changing environmental conditions, such as light intensity, temperature, pH value and nutrient availability (Braun et al., 2014; Poliner et al., 2019). The cellular behavior influenced by these abiotic stimuli has been described for Nannochloropsis spp.; in particular effects on growth and biochemical composition have been reported (Pal et al., 2011; Wagenen et al., 2012; Wahidin et al., 2013). Here, the applied photobioreactor system sets specific conditions for the culture, e.g., with respect to photon availability (Schediwy et al., 2019).
Tubular photobioreactors are an important type among closed photobioreactor systems used for the phototrophic production of microalgal biomass worldwide (Takache et al., 2009; Grewe and Griehl, 2013; Karemore et al., 2015; Olaizola and Grewe, 2019). Biomass productivity and hence space-time yield (often referred to as volumetric yield) of a photoautotrophic bioprocess are influenced by many abiotic factors, which also change during the course of the day as well as throughout the cultivation cycle (Bernard et al., 2016). Light availability can vary by orders of magnitude along with biomass concentration, layer thickness and external light intensity and is therefore difficult to control, e. g. in outdoor discontinuous bioprocesses. Temperature can also vary in a wide range of 2, …, 30°C (Zittelli et al., 1999; Ras et al., 2013), in particular at larger scale, while pH is easier to control even in industrial applications.
The work presented here employs a dynamic coarse-grained model to describe the light and temperature dependent specific microalgal growth rate within a pilot-scale tubular photobioreactor in order to finally predict biomass growth and optimize biomass productivity. Within the model used, light-limited growth is described depending on the specific light availability rate qph. A similar approach has already been successfully applied to optimize steady-state biomass productivity within a lab-scale tubular photobioreactor under turbidostatic operation (Weise et al., 2019). The present work extends this approach to dynamic microalgal growth within discontinuous processes. While under turbidostatic operation qph can be controlled well, under discontinuous operation it can only be kept within reasonable ranges. This is investigated here for a repeated batch process, with the inoculation biomass concentration cX,0 and the cultivation cycle time tcyc as process parameters that can be influenced during operation.
The current work additionally includes temperature dependencies into the model. Therefore, the empirical Cardinal Temperature Model with Inflexion (CTMI), first introduced by Lobry et al. (1991), is employed. The CTMI was already successfully applied to describe microbial and microalgal temperature dependencies (Rosso et al., 1993; Bernard and Rémond, 2012; Barbera et al., 2019).
Therefore, the following growth kinetics model for the description of both dependencies, i. e. for light and temperature, was also used here (Equation 1) (Bernard and Rémond, 2012):
μopt(qph) [d−1] (Equation 2) represents the optimum specific growth rate for a specific light availability rate qph [] at the strain-specific optimum temperature Topt [°C], whilst ϕ(T) [-] (Equations 5 to 7) describes the influence of the temperature T [°C] on the optimum specific growth rate.
Equation (2) relies on a Monod-like function in which μmax [d−1] and KS,ph [] are the maximum specific growth rate and the specific half-saturation constant for photon availability, respectively. The specific photon maintenance coefficient mph [] represents the light energy used for purposes other than biomass synthesis (Pirt, 1986). This kinetics describes the experimentally observed saturation of the growth rate when light availability increases within the investigated range (Darvehei et al., 2018). Regarding Nannochloropsis spp., the literature reports maximum specific growth rates μmax in the range of 0.86, …, 1.6 d−1 (Sandnes et al., 2005; Spolaore et al., 2006). Specific photon availability rates qph are often found in the range of 0.25, …, 2.2 (under lit conditions; flat panel photobioreactors) (Zijffers et al., 2010; Kandilian et al., 2014; Janssen et al., 2018).
The biomass-specific photon availability rate qph (Equation 4) is calculated from process and geometrical characteristics, in particular from the biomass concentration cX [], the light intensity at the reactor surface I0 [], the illuminated reactor projection surface A [m2] and the total reactor liquid volume VL [m3]. The underlying relationships have been successfully applied and demonstrated in several publications (Bernard, 2011; Kliphuis et al., 2011; Blanken et al., 2016). Equation (4) applies only to light-limited growth conditions and was originally developed considering flat-panel photobioreactors (Schediwy et al., 2019). Therefore, the tubular reactor compartment is considered to be a flat-panel equivalent with an average light path length l∅ (Equation 3). Since VL has to be equal in both assumptions, the illuminated reactor projection surface is used for qph calculation in Equation (4).
Within Equation (4) qph [] is calculated using the light intensity at the reactor surface I0 [] of an individual reactor compartment multiplied by the illuminated reactor projection surface A [m2] of the respective compartment (z = 1, …, c) summarized over all compartments c, related to the total reactor liquid volume VL [m3] and the biomass concentration cX [] (Equation 4).
The temperature dependency ϕ(T) (within Equation 1) is described using the CTMI (Equations 5-7):
with
and
Outside Tmin and Tmax [°C], which represent the minimum and maximum temperature of the growth range, no growth is assumed (Equation 5). In order to obtain the inflected asymmetric shape of the CTMI, Topt values need to be closer to Tmax as to Tmin (Equation 7). Bernard and Rémond (2012) verified both the above model properties (Equations 5, 7), which are necessary for a successful model application in this context. Optimum growth temperatures are stated in the literature within a range of 20, …, 29 °C (Sukenik, 1991; Bartley et al., 2015; Abirami et al., 2017). However, to the best of our knowledge, no optimum growth temperature for N. granulata has been published yet.
Model parameter estimation was carried out in two consecutive steps: Initial parameter estimates were generated in a first step from pooled, clustered and reorganized data of the process. These initial estimates were then used in a second step for the final parameter estimation based on the original experimental time series data.
Based on the parameterized model, a numerical optimization regarding the biomass productivity Pr was carried out with respect to the process parameters inoculation biomass concentration cX,0, cultivation cycle time tcyc and temperature T. Also, suggestions are provided with respect to the transfer of the proposed approach to other tubular photobioreactors under repeated discontinuous operation.
2. Materials and Methods
2.1. Cultivation Conditions
The strain of Nannochloropsis granulata (Karlson et al., 1996) used in this study was previously isolated and its identity confirmed by 18s rDNA analysis carried out by SAG Göttingen. All experiments were performed using sterile brackish water medium with a salinity of 19 psu, a nitrate concentration of 12 mM and a phosphate concentration of 0.3 mM provided by Prof. Otto Pulz, IGV GmbH, Nuthetal, Germany. The composition of the artificial brackish water medium 1/2 ES1 (Enriched Seawater): NaCl 243.0 mM, MgSO4 · 7 H2O 29.3 mM, NaNO3 16.5 mM, MgCl2 · 6 H2O 12.7 mM, CaCl2 · 2 H2O 5.4 mM, KCl 5.3 mM, K2HPO4 · 3 H2O 0.8 mM, FeSO4 · 7 H2O 43.18 μM, MnCl2 · 4 H2O 2.02 μM, ZnSO4 · 7 H2O 0.30 μM, CuCl2 · 2 H2O 0.23 μM, H3BO4 0.16 μM, NaMoO4 · 2 H2O 0.09 μM and CoCl2 · 6 H2O 0.08 μM.
Both, nitrate and phosphate concentrations were measured using ready-to-use cuvette test kits (nitrate: WTW 252073; phosphate: WTW 252075, Xylem Analytics Germany, Weilheim, Germany) after centrifugation of samples at 4, 500*g for 20 min. Cell-free supernatant was diluted with double distilled water 1:100 for nitrate and 1:10 for phosphate analysis according to the manufacturer's instructions. Absorbance values and ion concentrations were determined in a photoLab® 6100 VIS Photometer (Xylem Analytics Germany, Weilheim, Germany). Nitrate and phosphate were added manually on demand from sterile stock solutions of NaNO3 (300 gl−1) and KH2PO4 (100 gl−1) if values fell below 50% of the initial medium concentrations ( = 1,021 mgl−1, = 98 mgl−1).
Maintenance cultures of N. granulata were kept in cell culture flasks at 14 °C and 50 light intensity (12 h light/12 h dark).
Preculturing was carried out in 1.7 l double jacked glass bubble columns (height to diameter ratio of 4), temperated at 22 °C and aerated at 0.1 vvm with a 2% CO2 to air ratio (v/v). Precultures where illuminated using fluorescent tubes (Philips Cool White, 36 W, eight tubes per column, horizontally arranged). The light intensities at the inner surfaces of the columns were on average 249 , measured by a spherical micro quantum sensor (US-SQS, Walz GmbH & Co KG, Ulm, Germany). During preculture, illumination was provided to the columns continuously for 24 h.
The 30 l photobioreactor was inoculated using precultures from four individual bubble columns which were originally inoculated by the same maintenance culture.
2.2. Experimental Set-Up
The experimental work carried out within this study was conducted using a 30 l pilot-scale tubular photobioreactor (PBR30, IGV GmbH, Nuthetal, Germany) consisting of a compartmented glass tube (borosilicate glass, inner diameter of 39.6 mm) and a stainless steel system vessel (see Figure 1). Illumination was provided permanently over 24 h to the glass tube of the reactor by fluorescent tubes (OSRAM Cool White, L 18 W/840) and five LED panels placed along the length of the compartmented glass tube (Figure 1). The LED panels had a spectral composition consisting of 95% red light (λ = 660 nm) and 5% blue light (λ = 440 nm).
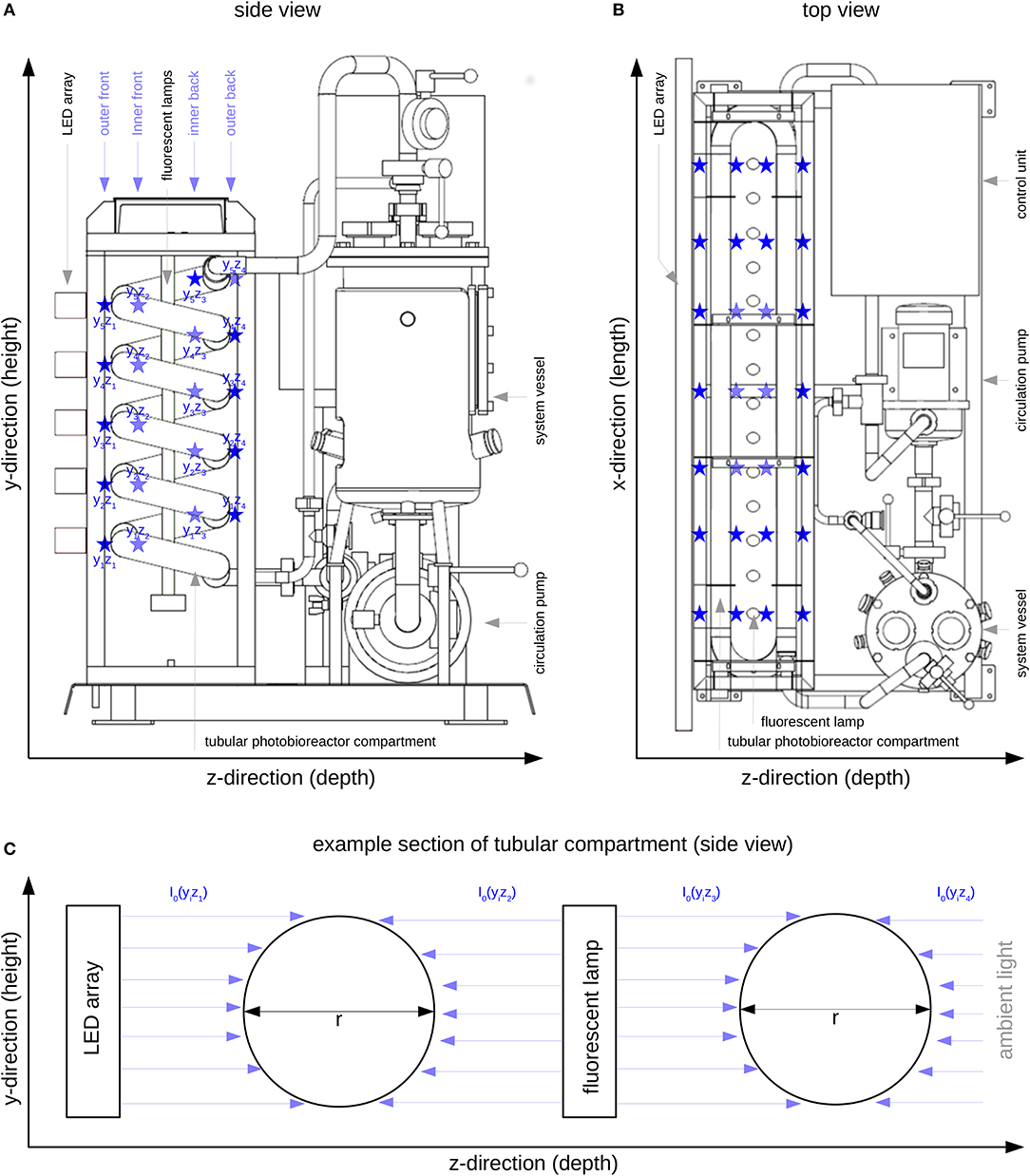
Figure 1. Tubular photobioreactor system PBR30 [IGV Institut für Getreideverarbeitung GmbH, Nuthetal, Germany]; Position of the LED array, the fluorescent lamps and the illuminated tubular reactor part; ⋆ I0 measuring positions (see also Table 1); (A): Side view; (B): Top view; (C): Representation of four modeled compartments in y/z-direction (referring to Figure 1A), I0(yizj) - surface light intensity of the respective compartment, yi - ith position in y-direction, zj - jth position in z-direction.
The illumination profile of the reactor's tubular glass part was recorded at 140 measuring positions (indicated by ⋆ in Figure 1 and Table 1) at 7 positions in x-direction (width), 5 positions in y-direction (height) and 4 positions in z-direction (depth). All measurements were carried out using the US-SQS described above. Since only minor variations in the light intensities in x-direction were observed (Figure 1B), values in this direction were averaged (see Table 1). The resulting 20 I0 values refer to their position in y/z-direction as indicated in Figure 1A. These values were used as surface light intensities of the respective reactor compartments within the modeling approach.
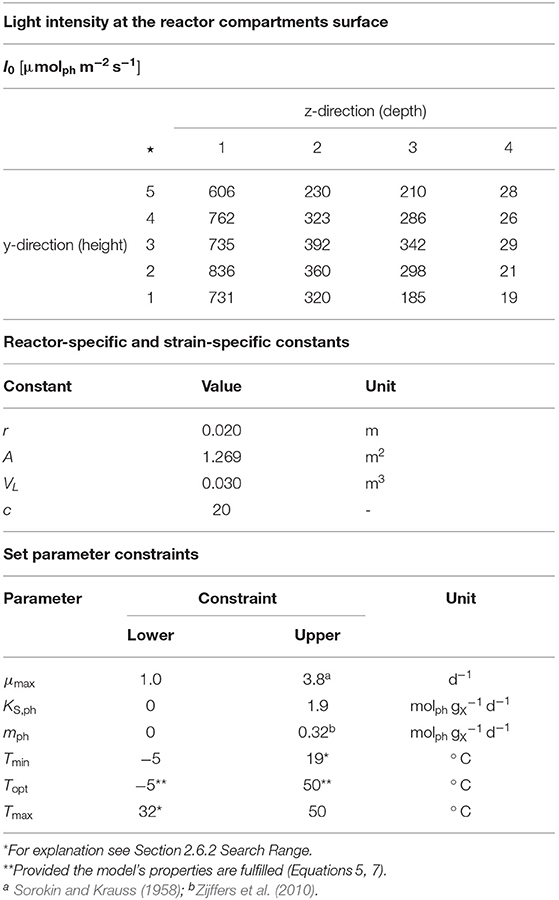
Table 1. Upper part: Light intensity at the reactor surface of the compartments used within the modeling approach, ⋆ Measuring positions (compare Figure 1A); Center part: Reactor-specific and strain-specific constants; Lower part: Set parameter constraints.
The pH value was controlled by the injection of pure CO2 at the intake side of the circulation pump using a limit controller (set-point pH 7.25; manipulated variable: solenoid-controlled valve; switch-point: pH 7.25; pH hysteresis: 0.05; on-delay: 5 s). The temperature was controlled using a cooling water circuit supplied by a water bath (F12, Julabo GmbH, Seelbach, Germany) and connected to the double jacket of the system vessel (limit comparator; hysteresis: 1 K). The circulation pump frequency was set to 35.7 Hz resulting in a suspension flow velocity of 0.72 m s−1 in the glass tubes.
2.3. Experimental and Modeling Approach
The experimental data used within this work was collected from altogether 15 cultivations which were carried out as a series of discontinuous (batch) bioprocesses in order to avert the lag phase at the start of the individual experiments (see Figure 2). Cultures were harvested partially by draining parts of the suspension and replacing it by fresh, steam sterilized medium (Figure 2). The experiments were designed to be conducted at constant illumination at the reactor surface I0 but by varying the inoculation biomass concentrations cX,0, the cultivation cycle times tcyc and the cultivation temperatures T (see Table 2-lower part and Figures 5A,B). Temperature variations during the cultivations, however, resulted from a limited cooling capacity of the reactor system under strongly differing ambient conditions.
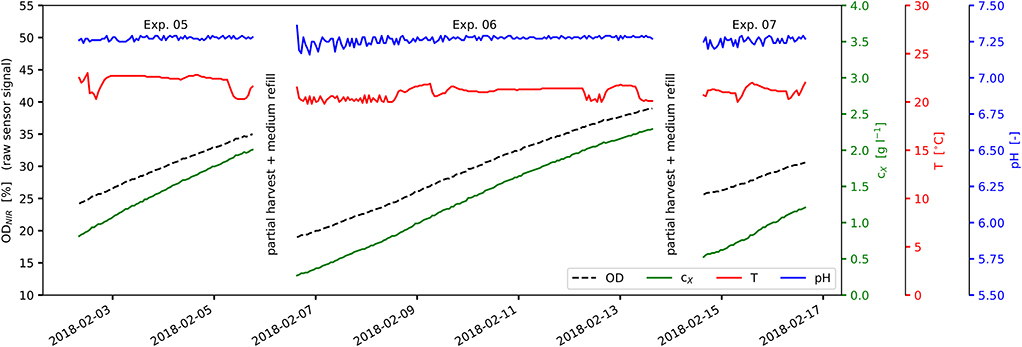
Figure 2. View of experimental process data: Experiments No. 05-07 as part of a series of repeated discontinuous cultivations; experiments are separated by partial harvest and medium refill; ODNIR, raw sensor signal ODNIR (black); cX, correlated biomass concentration (green); T, suspension temperature (red); pH, suspension pH value (blue).
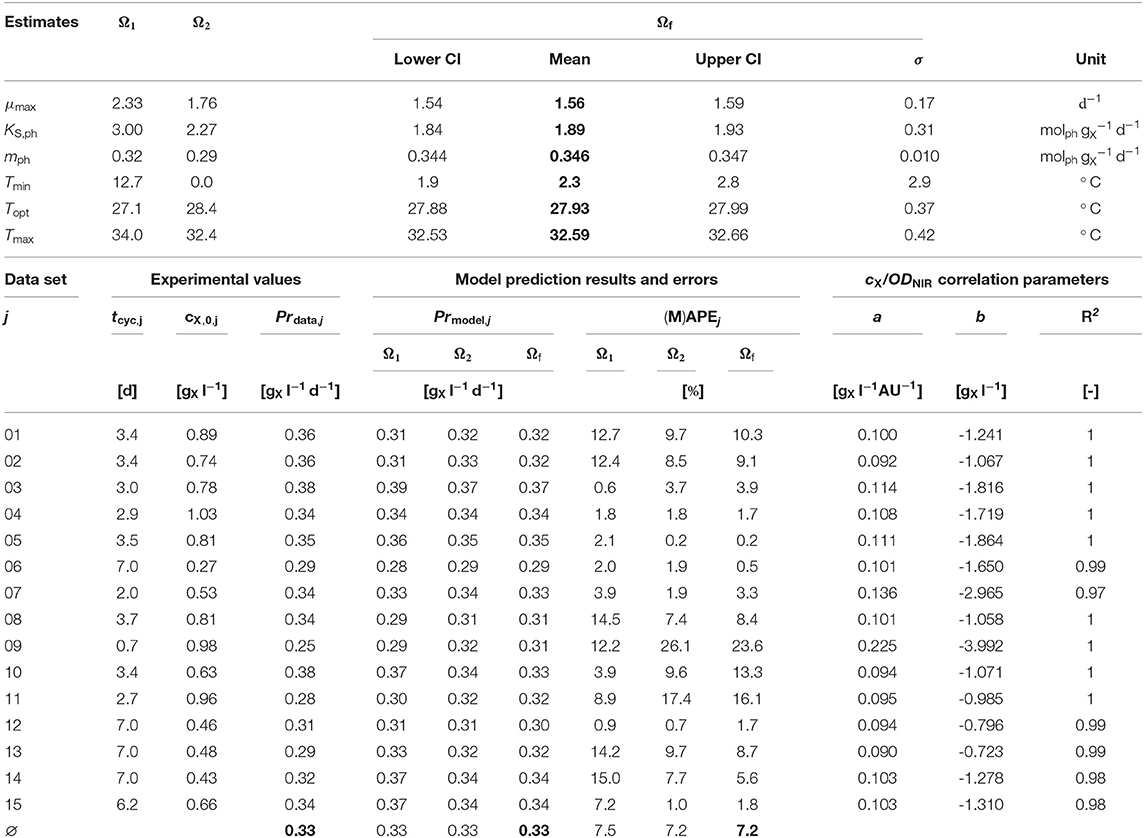
Table 2. Experimental and modeling results: Upper part: Initial Ω1, Ω2, and final estimates Ωf (mean values and jackknife 95 % confidence intervals (CI), if applicable); Lower part: Experimental values and model predictions, cX/ODNIR correlation parameters.
In order to carry out the modeling, the photobioreactor was subdivided into 20 glass tube compartments of equal size (z = 1, …, 20). Light intensity at the respective compartment surface was mapped as shown in Table 1 and remained constant during each individual experiment and across the experiments.
As described by Weise et al. (2019), I0 is considered to be a sum parameter for the light field description at the respective compartment surface. According to Equation (4) only light absorption is taken into account. Due to the actual reactor features (see Figure 1C), the light field is considered to illuminate the compartment yizj from only one side with equal intensity. In addition, because of the particular reactor arrangement, as shown in Figure 1C, each physical compartment is represented by two modeled compartments. The resulting photon fluxes (i.e., light intensity multiplied by surface area) within the modeled compartments were added and then related to the total biomass concentration and the reactor volume (see Equation 4).
2.4. Data Collection
During the experiments a number of variables were determined on-line and off-line. The on-line values of the optical density at near-infrared ODNIR, the pH and the temperature T were continuously measured and recorded by a 6-channel writer (JUMO Logoscreen 500 cf, Fulda, Germany). The sampling of the off-line values was carried out daily in the morning. The biomass concentration cX was determined as salt-free dry cell weight. Samples for the dry cell weight determination were homogenized, an aliquot of 10 ml was taken, centrifuged in pre-weighted glass tubes at 4.500 * g for 20 min; the resulting supernatant was discarded and the biomass pellet resuspended in 9 ml deionized water; this washing step was carried out twice. The pellets were dried at 105 °C for 24 h and weighed after cooling in a desiccator for 45 min. Measurements were carried out in duplicate.
The original experimental time series data are available as Supplementary Material.
2.5. Numerical Calculations
All computations were performed using the programming language python (version 3.6.5) and the additional packages astropy (version 3.0.4), numpy (version 1.15.0), pandas (version 0.23.4), SALib (version 1.3.8), scipy (version 1.1.0), and seaborn (version 0.9.0).
2.5.1. Biomass Concentration
cX [] was calculated from on-line ODNIR [AU] values using a linear correlation. Parameters a [] and b [] (see Table 2-lower part) have been estimated from off-line cX measurements for each individual experiments (original data not shown).
2.5.2. Averaged Approximated Growth Rate
The calculation of the averaged approximated growth rate [d−1] is carried out using the approximation of the ordinary differential equation of the biomass concentration for discontinuous bioprocesses (Equation 8). At first, the approximated growth rate μΔ(t) [d−1] is calculated employing the central difference approximation (Equation 9), which is subsequently smoothed using a moving average (Equation 10), where n is the total number of data points i between t − 1 h and t + 1 h. The employed central difference approximation linearizes the growth between the two observations and is therefore only applicable for small Δt (here: Δt = 2 h).
2.5.3. Biomass Productivity
The experimental biomass productivity for the respective experiment j was calculated as volumetric yield using the following Equation (11) (data point i, i = 0, n).
2.5.4. Model Validation by MAPE
The criterion used to evaluate the model's accuracy was the Mean Absolute Percent Error (MAPE) (Equation 12) (Mayer and Butler, 1993). It is calculated based on measured and modeled productivities considering all experiments (j = 1, …, m). When only a single experiment is considered (m = 1), MAPE is expressed as APE (Absolute Percent Error).
2.6. Parameter Estimation and Model Analysis
In order to parameterize the developed model, a parameter estimation procedure was carried out in two consecutive steps: The initial parameter estimation, following the methodology proposed by Bernard and Rémond (2012), was applied in a first step to generate initial parameter estimates which were then, in a second step, used as starting values for the final parameter estimation. Both stages of the consecutive parameter estimation were carried out using the same experimental (time series) data.
The initial parameter estimation (section 2.6.3) allows to efficiently screen through a wide parameter search range (see section 2.6.2) by fitting the growth kinetics directly to the reorganized data sets (see section 2.6.1). This was carried out in particular with respect to the temperature modeling in order for the unknown cardinal temperatures to converge. Since, however, the reorganization includes approximation and averaging of as well as clustering and selection, the returned results are potentially imprecise.
Therefore, the final parameter estimation (section 2.6.4) was carried out by fitting the model output to the original experimental time series data sets, employing the above mentioned initial estimates as starting values.
Based on the model, parameterized this way, the numerical biomass productivity optimization (section 2.6.6) was carried out with respect to the process parameters cX,0, tcyc, and T that are to be applied to the process.
2.6.1. Data Set Reorganization
In order to carry out the initial parameter estimation procedure described in the following section, a pooling, reorganization, clustering, and selection of the data was performed:
• Calculating the averaged approximated growth rates (according to Equation 10) for the ith data point of the jth experiment (j = 1, …, 15).
• Concatenating data sets for qph,i,j, and Ti,j from all 15 experiments into a new single data set.
• Reassigning the newly formed entries for and Ti that share the same qph value to a new kth data set which corresponds to this particular qph value (k = 1, …, s).
• Sorting each data set k obtained by its Ti,k values (for identical Ti,k values, corresponding values were averaged).
• Clustering the entire qph range into 10 equidistant clusters; assigning each data set k to its respective cluster.
• Selecting one data set per qph cluster that covers the widest individual Tk range (k = 1, …, 10).
The data sets (k = 1, …, 10) reorganized this way were then applied in the first part of the parameter estimation procedure.
2.6.2. Search Range
An adequate search range for the parameter estimation procedure was determined based on reasonable assumptions. In particular, the temperature range was constrained to -5.0, …, 50.0° C, based on the assumption that growth outside this range is not possible for the genus Nannochloropsis.
• Tmin ranges from −5.0°C (lower bound) to the lowest temperature for which experimental data is available (upper bound).
• Topt ranges from −5.0°C (lower bound) to 50.0 °C (upper bound), as long as the model's properties are fulfilled (see Equations 5, 7).
• Tmax ranges from the highest temperature for which experimental data is available (lower bound) to 50.0 °C (upper bound).
• μmax ranges from the highest value obtained from the experiments (lower bound) to the highest μmax value reported for microalgae (upper bound; see Table 1-lower part).
• KS,ph ranges from 0 (lower bound) to the highest qph value obtained from the experiments (upper bound).
• mph ranges from 0 (lower bound) to the highest mph value reported in the literature (upper bound; see Table 1-lower part).
2.6.3. Initial Parameter Estimation
Each data set k, reorganized as described above, contains growth rate values at temperatures Ti,k. Bernard and Rémond (2012) published a strategy that consists in the following: Identifying s + 3 parameters μopt,1, μopt,2, …, μopt,s, Tmin, Topt, Tmax (here s = 10, for the 10 cluster data sets) vectorised as θT, where the parameter μopt,k is the optimum growth rate at the optimum temperature Topt for the kth data set. Following their strategy, the underlying key assumption is that the cardinal temperatures (Tmin, Topt, Tmax) are common to all the data sets, whilst μopt,k is constant within the respective data set due to constant experimental lighting conditions qph,k. The unknown s + 3 parameter values were estimated in a first step by minimizing the optimization criterion J(θT) (Equation 13) (Bernard and Rémond, 2012). Within a second step, the remaining model parameters μmax, KS,ph and mph (vectorised as θqph) were estimated in a similar way (Equation 14). Both, Equations (13) and (14), were minimized with respect to the respective θ resulting in the minimum optimization criterion value J(Ω) for the optimum parameter vector Ω according to Equation (15).
The downhill-simplex method (Nelder-Mead method) used for the model parameter estimation procedure (scipy.optimize.fmin) was started from every possible parameter value combination within the search ranges described above. The T range was screened stepwise by ΔT = 5 °C, resulting in 70 initializations that match the model's properties (Equations 5, 7). The ranges for μmax, KS,ph and mph were screened using 10 equidistant values along each axis, resulting in 1,000 initializations. The method was set to perform a maximum of 200 iterations for each initialization. Computations were carried out using the standard settings of the above package regarding the convergence criteria of the method.
2.6.4. Final Parameter Estimation
Since the initial parameter estimation described above can provide results which are potentially imprecise due to the approximation and averaging of , the reorganization and clustering of the data sets k as well as the split parameter estimation of θT and θqph, a second and final parameter estimation step was carried out. Based on the ordinary differential equation of the biomass concentration for discontinuous bioprocesses (Equation 16), the original experimental time series data sets j (j = 1, …, 15) were simulated using the initial parameter estimates. Numerical integration was carried out employing the Euler method. The time series of cX were simulated for the i discrete time points ti,j and their corresponding temperatures Ti,j.
The objective of this final parameter estimation was to identify the m + 6 parameters cX,0,1, cX,0,2,…, cX,0,m, μmax, KS,ph, mph, Tmin, Topt, Tmax (here m = 15, for the 15 experiments) vectorised as θf, where the parameter cX,0,j is the inoculation biomass concentration cX,0 for the jth data set. The optimum parameter values were estimated by minimizing the optimization criterion J(θf) (Equation 17). The final optimum parameter vector Ωf (according to Equation 18) was determined in analogy to the initial parameter estimation as described above.
with
The Nelder-Mead method was also employed for this second step of the model parameter estimation procedure (scipy.optimize.fmin). The initially estimated parameter vectors were now used as start parameter vectors. The method was set to carry out a maximum of 200 iterations for each initialization. Again, the standard settings of the above package were used with respect to the convergence criteria.
Since the values of the parameters Tmin and Tmax to be estimated were expected to lie outside the experimental data range and to account for the relatively small number of experiments, the Delete-2-Jackknife analysis (astropy.stats.jackknife_stats) was used to indicate the 95 % confidence interval of the identified parameters of the vector Ωf (Efron and Tibshirani, 1993; Duchesne and MacGregor, 2001). Jackknife re-sampling was carried out by bootstrapping two respective data sets (experiments) from the data at a time.
2.6.5. Parameter Sensitivity Analysis
A variance-based sensitivity analysis according to Sobol (2001) was performed using the SALib.analyze.sobol in order to investigate the model's parameter sensitivities more deeply. This sensitivity analysis was done with respect to the biomass productivity as the main focus of this study. Within Equation (19), M represents the model output depending on the process parameters cX,0, tcyc and T as well as the model parameter vector θ (Zhang et al., 2017) consisting of μmax, KS,ph, mph, Tmin, Topt, and Tmax.
The Sobol method is based on the decomposition of the variance of the model output Var(M) (Equation 20) into summands of increasing dimensionality (Zhang et al., 2015, 2017). Vari is the partial variance corresponding to the first-order index of θi of the model output M, while Varij is the partial variance corresponding to the second-order index of the ith and jth parameter interaction (Zhang et al., 2015, 2017). k is the number of model parameters, here k = 6.
The sensitivity indices Si and Sij (Equations 21, 22) are calculated as ratios of the partial variances to the total variance (Zhang et al., 2015). Total-order indices STi are calculated following Equation (23) using Var~i which represents the variation of all parameters except θi (Homma and Saltelli, 1996; Sobol, 2001; Zhang et al., 2017). Si quantifies the effect of varying θi alone, while STi quantifies the effect of varying θi and includes all effects caused by its interactions with all other model parameters.
The Saltelli sampling scheme (SALib.sample.saltelli) was used to generate model parameter samples of the final model parameter estimates Ωf (section 2.6.4) varied by ±3σ (see Table 2-upper part). This scheme generates N · (2k + 2) samples (here N = 10,000; k = 5). The calculated indices were classified using thresholds. Indices contributing <0.01 to the model output variance are considered “non-sensitive,” while indices contributing ≥ 0.1 are considered “highly sensitive” (Tang et al., 2007).
Si and STi also potentially depend on the process parameters. The experimentally set cX,0 is associated with the present light availability, while the set T may influence the sensitivity of the three cardinal temperatures. Therefore, the sensitivity analysis was carried out for 9 combinations (scenarios) of cX,0 and T taking into account data corresponding to percentages of the respective experimental range [20% (“low”), 50% (“medium”), and 80% (“high”)].
2.6.6. Biomass Productivity Optimization
In order to optimize the biomass productivity Pr with respect to the described photobioreactor, a numerical optimization was carried out. The objective was to maximize Pr with respect to the process parameters cX,0, tcyc, and T. Numerical integration of Equation (16) was performed using the estimated model parameters (Ωf; Table 2-upper part) by employing lsoda of the ODEPACK (scipy.integrate.odeint). After each integration, Pr was calculated for the individual iteration steps using Equation (11). The process parameters cX,0, tcyc, and T were vectorised as θPr containing all possible process parameter combinations, while ΩPr contains the optimum process parameter combination with respect to Pr. The optimum process parameter values were estimated by minimizing the optimization criterion J(θPr) (Equations 24, 25) using also the downhill-simplex method (Nelder-Mead method; scipy.optimize.fmin). With respect to numerical integration and convergence criteria, standard settings of the above packages were used.
3. Results and Discussion
The experiments carried out and presented here consisted of a series of discontinuous (batch) cultivations. Single experiments were separated by partial harvest of the biomass suspension and replacement by new medium (see Figure 2). Inoculation biomass concentrations cX,0 and cultivation cycle times tcyc were varied between the experiments (see Figure 2 and Table 2-lower part). Temperature T as well as pH were recorded during the experiments (see Figures 2, 5A,B). The original experimental time series data and the reorganized data sets are available as Supplementary Material.
Light saturation was not observed during the experiments. The linear accumulation of biomass indicates limited lighting conditions (Figure 2). The light intensity at the photobioreactor surface varied between 19 and 836 (average: 337 ; see Table 1-upper part and Figure 1). These incident light intensities range from low values (100 Raso et al., 2011) to rather typical values at lab-scale (700 Pal et al., 2011; up to 850 Wagenen et al., 2012) for Nannochloropsis sp. With respect to the scalability toward outdoor production, higher incident light intensities of 1,500 to 2,000 are present on sunny days. These however are lowered due to the vertical arrangement of the glass tubes at industrial scale, the light absorption by greenhouse parts, etc. Therefore, the comparability and the transferability of presented model to industrial-scale outdoor conditions is limited unless further model extensions regarding higher variability in light and temperature, nightly biomass losses, etc. are carried out.
The inoculation biomass concentrations within this study (0.27,…, 1.03 ) are within a typical range for both, lab-scale and outdoor production of Nannochloropsis sp. in tubular photobioreactors (Olofsson et al., 2012; Pfaffinger et al., 2016; Pereira et al., 2018). The experimental variability regarding cX,0 is rather high within the investigated small pilot-scale experiments. However, biomass concentrations throughout the cultivation cycle time are found to be typical for large-scale and outdoor production of Nannochloropsis. cX ranged 0.27,…, 2.79 , reflecting usual inoculation and harvesting biomass concentrations, respectively. To the best of our knowledge, depending on the climatic zone, biomass concentrations of Nannochloropsis outdoor cultures within tubular photobioreactors rarely exceed 3 (Olofsson et al., 2012; Benvenuti et al., 2015) and do not exceed 5 (Zittelli et al., 1999). Therefore, the cX range observed here is comparable to larger-scale and outdoor processes.
Biomass productivity Pr was calculated for each experiment according to Equation (11) in order to evaluate the model's accuracy expressed as MAPE (see Table 2-lower part) and to use it for the biomass productivity optimization. The overall context of this work was to optimize Pr as part of a series of batch bioprocesses (i.e., repeated batch).
The devised two-stage consecutive parameter estimation procedure was carried out using the reactor-specific and strain-specific constants as well as the set parameter constraints shown in Table 1.
The initial parameter estimation converged to two valid solutions (Ω1 and Ω2, Table 2-upper part) depending on the start parameter combinations. Both solutions differ only strongly in the estimated value of Tmin.
Both initial parameter estimation vectors (Ω1 and Ω2) were used as start parameter combinations for the final parameter estimation. It was performed using the original time series data sets j (in contrast to the reorganized data sets k). The altogether six shared model parameters where estimated within multi-experiment fittings.
The final parameter estimation converged to the solution Ωf (Table 2-upper part, Figure 3) initialized from each of the two initial parameter combinations (Ω1 and Ω2). The ϕ(T) data shown in Figure 3A was normalized with respect to the corresponding estimated μopt (Figure 3B) according to Equation (1).
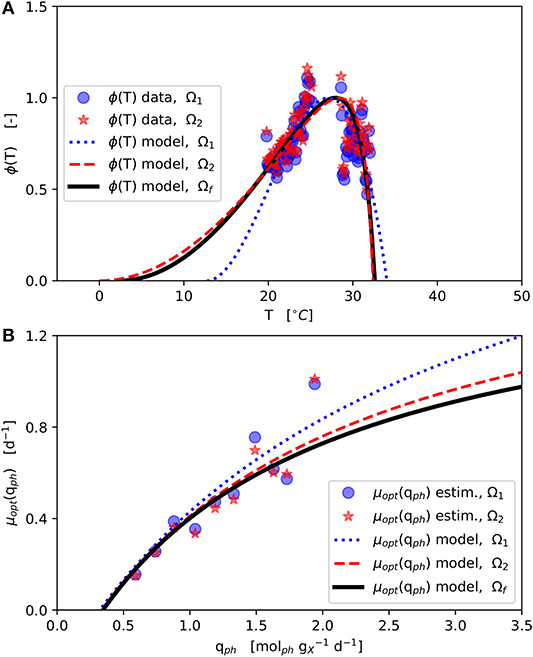
Figure 3. Model parameter estimation results: Initial parameter estimation provides solutions Ω1 and Ω2 and final parameter estimation solution Ωf (see Table 2–upper part); (A): CTMI estimation ϕ(T) vs. T (Equations 5–7); (B): Estimation μopt(qph) vs. qph (Equation 2).
The estimated values of Tmin and Tmax lie outside the range 19, …, 31 °C of available experimental data. Since the range between the estimated Tmin and the available data is much wider than the one between the estimated Tmax and the available data, in particular the Tmin estimation is afflicted with some uncertainty, which is further enforced by the asymmetric shape of the temperature function ϕ(T) as can be seen in Figure 3A showing the CTMI results. This is underlined by the jackknife 95 % confidence intervals CI and standard deviations σ of the estimated parameters (Table 2-upper part). While for all other parameters the σ values indicate relatively certain parameter estimations, σ for Tmin is at the same order of magnitude as the parameter's value.
The finally estimated cardinal temperatures for N. granulata (Tmin = 2.3°C, Topt = 27.93°C, Tmax = 32.59°C) lie within the specified parameter constraint ranges (Table 1) and match laboratory experience. The CTMI parameters estimated by Bernard and Rémond (2012) for the related species N. oceanica (data by Sandnes et al., 2005) showing a good degree of similarity (Tmin = −0.2°C, Topt = 26.7 °C, Tmax = 33.3 °C).
The results obtained here are supported by an optimum growth temperature range of 20, …, 29 °C given in the literature (Sukenik, 1991; Wagenen et al., 2012; Bartley et al., 2015; Abirami et al., 2017). Further, Wagenen et al. (2012) reported only very poor growth below 13.6 °C and above 32.3°C for N. salina. Also, Sukenik (1991) found that Nannochloropsis spp. failed to grow below 10 °C and above 38 °C. In view of the fact that the parameter estimation carried out here had only rough quantitative specifications with regard to the cardinal temperatures, the values calculated (Table 2-upper part) are in strong compliance with the literature. Sandnes et al. (2005) empirically described a light-dependent optimum cardinal temperature Topt for N. oceania (Sandnes et al., 2005). Although this combined effect of light and temperature is physiologically plausible, the functional relationship of these two variables was not observed for N. granulata within the own data.
The μopt values for Ω1 and Ω2 estimated increase monotonically with higher qph (Figure 3B). These estimates are subject to fluctuations but show no inhibition within the observed qph range. Therefore, a growth kinetics considering light limitation (Equation 2) without light inhibition was applied. The qph range observed during the experiments (0.59, …, 1.9 ) is comparable to qph values given by the literature (0.25, …, 2.2 ) (Zijffers et al., 2010; Kandilian et al., 2014; Janssen et al., 2018). In accordance with Equation (4) qph is calculated as a mean light availability rate of the whole culture suspension, considering the total culture volume VL. However, local light intensities differ due to light gradients within the culture suspension, which are not spatially resolved within the model. Despite this aggregation, the devised model predicts microalgal growth and biomass productivities precisely. The estimated photon maintenance coefficient mph = 0.346 is comparable to values reported for C. sorokiniana: 0.16 and D. tertiolecta: 0.32 (Zijffers et al., 2010). Pirt (1986) reported increasing mph values for photobioreactor set-ups with lower illuminated/non-illuminated culture volume ratios, which has to be considered during the transfer to different photobioreactor set-ups. The growth yield YX,ph [], calculated following, Pirt (1986) as YX,ph = μopt / (qph − mph), varied 0.45, …, 0.73 during the experiments (based on Figure 3B), which matches the YX,ph range of 0.2, …, 2.1 reported in the literature (Zijffers et al., 2010; Dillschneider et al., 2013; Schediwy et al., 2019). The estimated parameter μmax = 1.56 d−1 is comparable also to μmax ranges between 0.86, …, 1.6 d−1 as found in the literature (Sandnes et al., 2005; Spolaore et al., 2006; Weise et al., 2019).
The similar parameters indicate that the model structure in particular with respect to the light-limited growth modeling shows a good transferability for tubular photobioreactors that differ in scale, glass tube diameter and the mode of bioprocess operation, although the experimental and modeling approaches differed in many respects. In contrast to Weise et al. (2019), who considered constant temperature conditions (T = 22 °C) under steady-state turbidostatic bioprocess operation, experiments presented here were conducted under variable temperature conditions and have been scaled up by ≈ 7x regarding the reactor liquid volume VL, by 10x regarding the number of modeled compartments and by 2x regarding the glass tube diameter.
In order to transfer the devised model to other reactors and different scales, it is necessary to consider homogeneous one-sided illuminated glass tube compartments within the model, although the glass tubes may be illuminated homogeneously from both sides in the actual arrangement. Therefore in this context also, the physical compartments are to be decomposed mathematically into several theoretical ones. If these assumptions do not apply to the specific photobioreactor structure, the model cannot be transferred without further modification. The presented model considers basic geometric properties (e.g., inner tube radius, liquid reactor volume, illuminated reactor surface, etc.) of tubular photobioreactors. Using biomass productivity or reactor size as scale-up objectives, it is possible to estimate the dimensions (e. g. illuminated reactor surface) of a photobioreactor scale-up.
The presented model is implemented using the ordinary differential equation (ODE) for batch bioprocesses. In order to adapt the model for continuous cultivation, the ODE for batch bioprocesses can be extended by a dilution term. The growth kinetics, which are described by algebraic equations are not affected by this extension.
With respect to the model's sensitivity analysis, Figure 4 illustrates the first-order and total-order sensitivity indices of the model parameters across different scenarios. The comparatively small differences in the values of Si and STi indicate only limited interactions between the parameters, which was to be expected due to the model's structure (see Equations 1, 2, 7). The output of the model is highly sensitive (Si and STi ≥ 0.1) with respect to the parameters μmax and KS,ph. Both parameters combined contribute predominantly to the variance in the model output, since they describe the utilization of light as the sole energy source for phototrophic growth. The set cX,0 effects the sensitivities of KS,ph and mph. Since higher cX,0 reduce the qph, the photon half-saturation constant KS,ph becomes more sensitive. In addition, mph becomes sensitive (Si and STi ≥ 0.01) only at higher cX,0 (Figure 4).
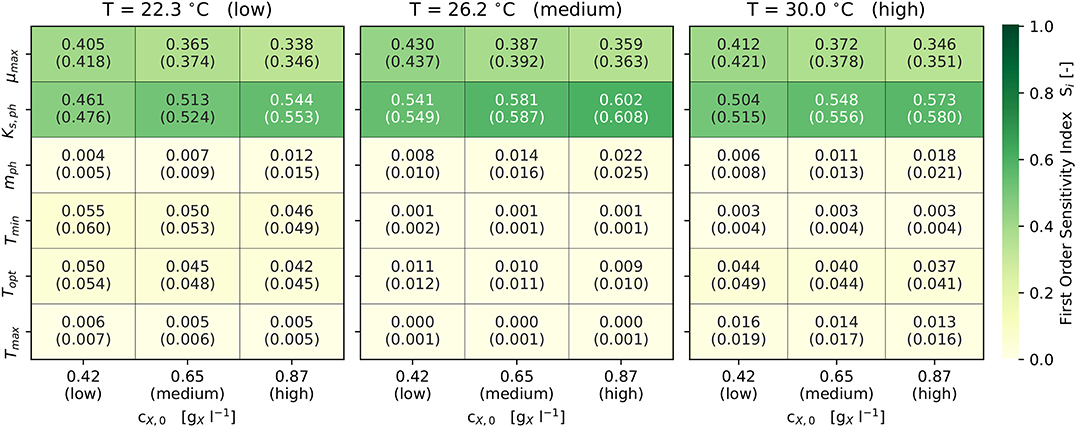
Figure 4. Results of the Sobol sensitivity analysis: First and (total) order sensitivity indices for Ωf ± 3σ and 9 scenarios (3 each for cX,0 and T).
Topt is sensitive (Si and STi ≥ 0.01) in all scenarios, while Tmin and Tmax are sensitive only at lower and higher temperatures. Also, Tmin and Tmax become non-sensitive at temperatures close to Topt. At temperatures away from Topt, the combined sensitivity of the three cardinal temperatures contributes up to 10 % (i.e., 0.1) to the model's output variance. The set cX,0 does not influence the sensitivity of the cardinal temperatures.
All experiments were carried out in the range 20, …, 25°C, except Experiment No. 10 at 31°C. Although the temperature inside the photobioreactor was actively controlled, diurnal rhythms in the ambient temperature resulted in temperature variations within individual experiments. These are displayed in Figure 5A using kernel density approximations (violins). The width of the individual violin represents the number of available data at the respective temperature value, while small pin-like tails of the violins indicate short-term outliers of the measured variable. In analogy, Figure 5B shows the distribution of the measured pH values of the respective experiments. Variations in temperature and pH value did not occur rapidly, as can be seen in Figure 2. Despite the variations in the observed temperature and pH ranges, using the specific approach applied here, the available data could be successfully processed in order to estimate model parameters and optimize process parameters at pilot-scale. Figure 5C provides violin plots that represent the absolute modeling error with respect to the biomass concentration time series using the estimated parameter vector Ωf. It can be seen that the modeling error rarely exceeds ± 0.15 .
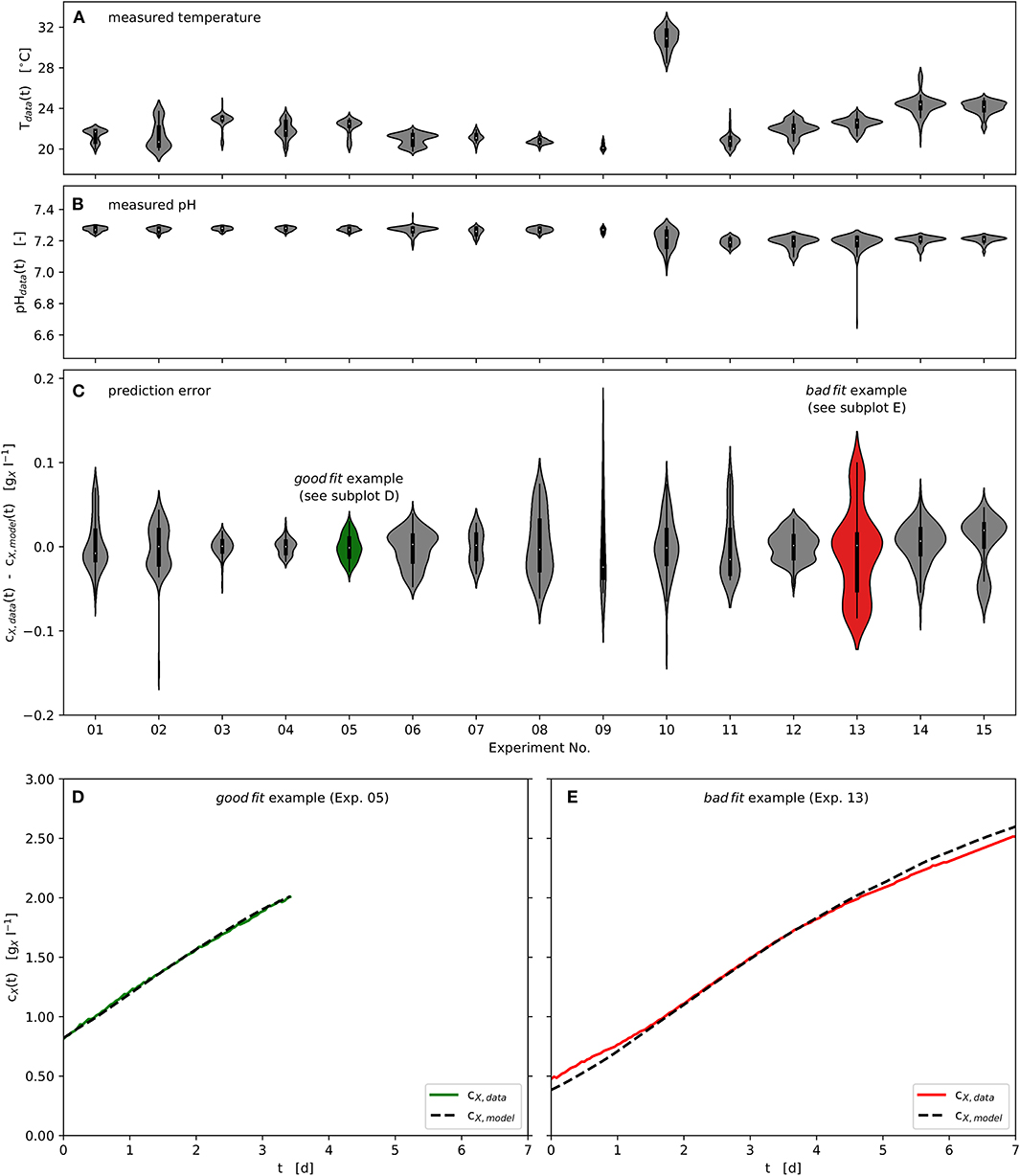
Figure 5. Experimental and modeling results: Time series of measured and modeled biomass concentration, measured temperature and pH; Violin plots: center point - median, box - interquartile range (IQR), whisker - 1.5 · IQR, kernel density estimation - number of observations; (A): Temperature distributions of the experimental time series data; (B): pH distributions of the experimental time series data; (C): Model prediction error distributions of the experimental time series data with respect to biomass concentration; (D): “good fit” example - representing lowest prediction error calculated, Experiment No. 05; (E): “bad fit” example - representing highest prediction error calculated, Experiment No. 13.
Furthermore, one good as well as one badly predicted experiment are highlighted in green (Experiment No. 05) and red (Experiment No. 13), as shown in Figure 5C. These two experiments are presented as time series in Figures 5D,E. Although the biomass concentration has been well predicted over much of the time (Figures 5D,E), some regions are underestimated or overestimated at the beginning and the end of the respective experiments (Figure 5E as example).
The prediction accuracy MAPE (Equation 12) of the target value biomass productivity Pr (Equation 11) improved over the course of the estimation procedures. Table 2-lower part provides an overview of these experimental and modeling results as well as the parameters a and b. The initial parameter estimation of Ω1 and Ω2 resulted in MAPE(Ω1) = 7.5% and MAPE(Ω2) = 7.2%, whilst the prediction accuracy after the final parameter estimation was MAPE(Ωf) = 7.2%. Therefore, the accomplished overall model prediction accuracy is very satisfactory, although the Absolute Percent Error of individual experiments (APEj) covers a wider range 0.1, …, 26.1%. Typical MAPE values for industrial and business data and their interpretation are: < 10% highly accurate forecasting, 10, …, 20% good forecasting, 20, …, 50% reasonable forecasting, > 50% inaccurate forecasting (Lewis, 1982; Moreno et al., 2013).
Based on the results of the parameter estimation procedure (Table 2-upper part), the parameterized model has been used to design an optimized bioprocess regime regarding the inoculation biomass concentration cX,0, the cultivation cycle time tcyc and the temperature T with respect to optimum biomass productivity Propt for a series of equal batch cultivations (repeated batches). Since, the specific light availability rate qph decreases monotonously along with biomass accumulation under constantly illuminated discontinuous bioprocess operation, qph is only influenced by alterable cX,0 and tcyc.
Following the above objective, a numerical optimization of Pr was conducted using Equations (24) and (25) as described in section 2.6.6. The biomass productivity optimization showed two major aspects: First, the optimum growth temperature equals the model parameter Topt = 27.93°C, which matches the intuitive expectation with regard to Equations (1) and (5). This applies independently of the lighting conditions according to the devised model. Second, the optimization results in a corner point optimum that points toward an insignificantly small cultivation cycle time tcyc → 0.
The developed approach therefore predicts the theoretical optimum biomass productivity Propt → 0.50 within the investigated bioreactor set-up for negligibly small cultivation cycle times with cX,0,opt → 1.07 , and hence the transition from discontinuous (e.g., batch, fed-batch or their repeated versions) to continuous (e.g., chemostat, turbidostat) bioprocess operation. The optimum inoculation biomass concentration cX,0,opt calculated this way corresponds to the steady-state biomass concentration of a settled chemostat bioprocess or to the optimum biomass concentration set-point of a turbidostat bioprocess, respectively (Weise et al., 2019). (Statement is no longer applicable due to the modifiaction of Equation 2). The above findings are also supported by Chen et al. (2012) who estimated cX,0,opt = 0.98 (Propt = 0.75 ) for a small-scale laboratory set-up, as well as Hulatt et al. (2017) finding Propt = 0.51 for a flat-panel photobioreactor, both under discontinuous operation. In addition, literature values for Pr at pilot-scale and industrial-scale show a range <0.1, …, 0.71 (de Vree et al., 2015; Pereira et al., 2018), confirming the feasibility of the Propt values obtained here.
A simulation of the original experiments was carried out using the actually applied cultivation cycles times tcyc of the experiments (see Table 2-lower part) as well as the optimized process parameters cX,0,opt and Topt (according to section 2.6.6). The model predicts a noticeable increase of Pr by 39% from 0.33 (see Table 2-lower part) to 0.46 .
The convergence toward the predicted optimum biomass productivity is asymptotic. This results in only minor additional gains in biomass productivity when moving from short-cycled discontinuous to continuous bioprocesses and requires a simultaneous adaptation of the inoculation biomass concentration cX,0. Within this context, Table 3 shows examples of the predicted Propt under discontinuous (repeated batch) bioprocess operation for fixed cultivation cycle times tcyc (1 d, 3.5 d, and 7 d) starting at the required inoculation biomass concentration cX,0 and under optimum temperature Topt. As a consequence, solely reducing tcyc from 7 d to 3.5 d would outweigh the increase in operational efforts by a higher Pr (0.37 → 0.46 ; with cX,0,opt 0.17 → 0.43 ) under discontinuous bioprocess operation.
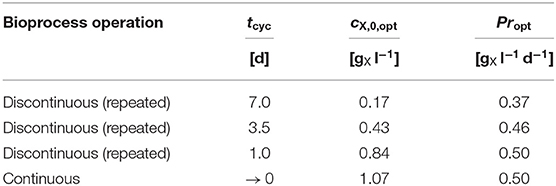
Table 3. Numerical optimization results: Model predicted Propt for different bioprocess operations and pre-set tcyc at Topt with the required cX,0,opt (see Figure 6A).
Figure 6A illustrates these relations in more detail by presenting the model's prediction with respect to biomass productivity Pr depending on the cultivation cycle time tcyc and the inoculation biomass concentration cX,0 for the optimum cultivation temperature Topt. According to the model's prediction, only moderately high biomass productivities are gained for cultivation cycle times greater ≈ 5 days, as well as for inoculation biomass concentrations above ≈ 1 (Figure 6A). Notably, the optimum productivity is reached at the shortest cultivation cycle time, which illustrates the said corner point optimum regarding the cultivation cycle time tcyc.
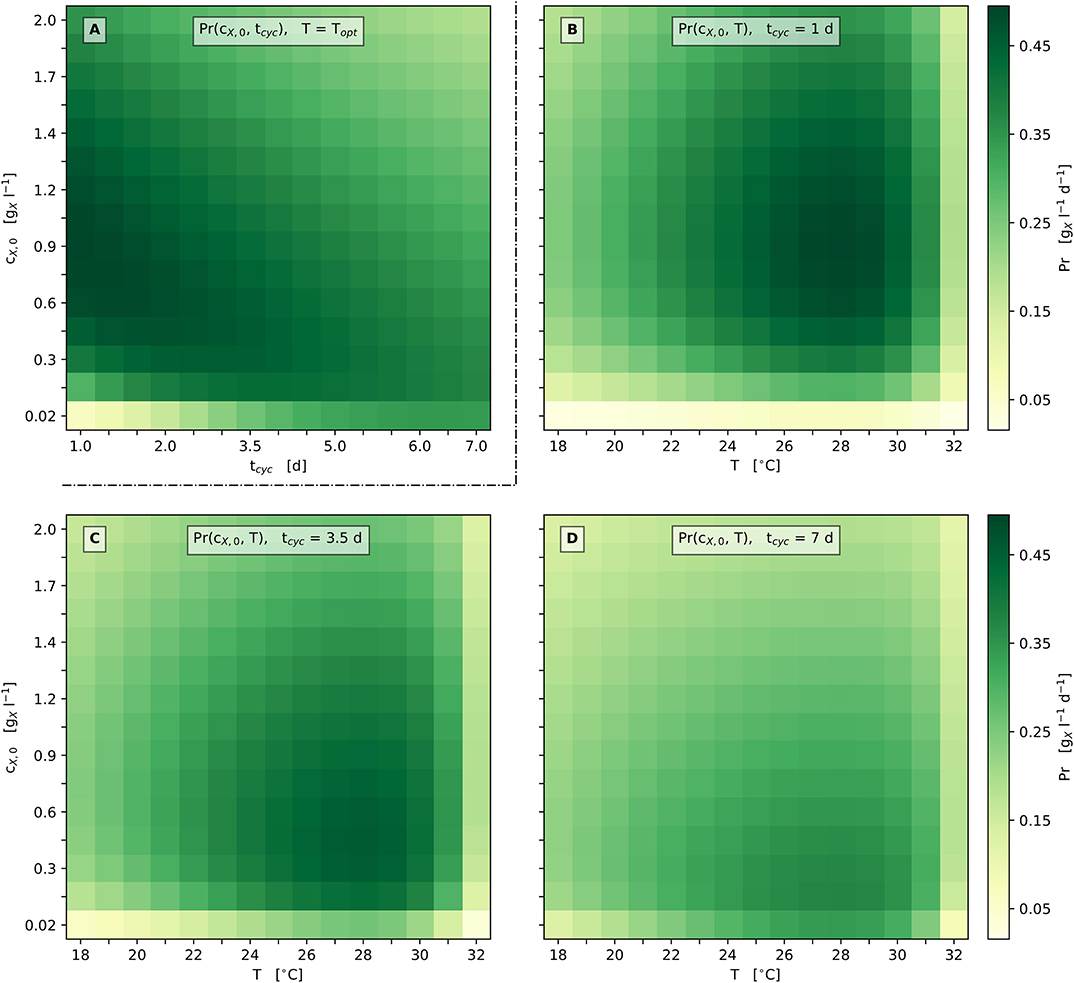
Figure 6. Heat map representation of model predicted biomass productivity; (A): Pr depending on tcyc and cX,0 at Topt; (B–D): Pr depending on T and cX,0 at set tcyc [1 d (B), 3.5 d (C), 7 d (D)].
In accordance with these findings, Figures 6B–D additionally provides graphical representations of the biomass productivity loss when varying the process parameters cX,0, tcyc and T. Figures 6B–D illustrate scenarios for three different cultivation cycle times: 1 d, 3.5 d (1/2 week), and 7 d (1 week) with respect to discontinuous bioprocess operation (repeated batch). Considerations regarding lag phases are neglected here, as can be seen in Figures 2, 5D,E. All three scenarios show a single optimum of biomass productivity at the respective optimum temperature Topt and the optimum inoculation biomass concentration cX,0,opt.
The predicted Propt increases by about 35% from 0.37 at tcyc = 7 d (cX,0,opt = 0.17 ) to 0.50 at tcyc = 1 d (cX,0,opt = 0.84 ). In general, the optimum biomass productivity Propt increases when the cultivation cycle time is shortened. In addition, when this time is shortened, a higher cX,0,opt is required to obtain the optimum productivity.
4. Conclusion
The work presented here provides a transferable methodology to model microalgal growth covering light availability and temperature based on experimental data from cultivation runs in a small pilot-scale tubular photobioreactor under discontinuous operation in order to subject it to biomass productivity analysis and optimization.
The established model with its estimated parameters accurately predicts light and temperature dependent growth of Nannochloropsis granulata. The parameter ranges are supported by the literature. In general, the model parameter Topt is much closer to Tmax than to Tmin, thus the CTMI displays a strong asymmetry. Temperatures above Topt therefore lead to a steep decline in the growth rate and also the biomass productivity. Since an accurate temperature control is hardly to provide under large-scale or outdoor conditions, these processes should be operated below the targeted Topt.
Model-based numerical biomass productivity optimization for repeated discontinuous operation points toward best performance under continuous operation. The optimization for repeated discontinuous operation yields reduction of cultivation cycle time and increase of inoculation biomass at optimum temperature. The calculated optimum inoculation biomass concentrations cX,0,opt and the corresponding optimum biomass productivities Propt are confirmed by different publications. Furthermore, biomass productivities for laboratory-scale, pilot-scale and industrial-scale reported in the literature support the feasibility of the Propt values obtained here. Applying these optimized process parameters would deliver a noticeable increase in biomass productivity.
The successful application of this approach here to small pilot-scale under discontinuous operation, following a previous investigation into lab-scale under continuous operation, indicates its potential transferability also to larger scale tubular photobioreactors covering both light and temperature dependent microalgal growth and biomass productivity.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
TW contributed to the conception and design of the study, the collection and assembly of data, the analysis and interpretation of the data, the drafting, critical revision and final approval of the article. CG contributed to the collection and assembly of data, the drafting, critical revision and final approval of the article and to obtaining funding. MP contributed to the conception and design of the study, the interpretation of the data, the drafting, critical revision and final approval of the article and to obtaining funding.
Funding
The authors gratefully acknowledge the financial support of this work by the Free State of Thuringia, Germany, and the European Union within the project nos. 2015 FE 9151, 2015 FE 9149, EFRE-OP 2014-2020. Additional financial support was provided by the University of Applied Sciences Jena.
Conflict of Interest
TW is collaborative doctoral candidate at the University of Applied Sciences Jena, Jena, Germany and the Friedrich Schiller University Jena, Jena, Germany. TW was employed by the University of Applied Sciences Jena, Jena, Germany and is now employed by the company BioControl Jena GmbH, Jena, Germany. CG is employed by the company Salata AG, Ritschenhausen, Germany. MP is professor at the University of Applied Sciences Jena, Jena, Germany. MP owns stock in the company BioControl Jena GmbH, Jena, Germany.
Acknowledgments
The technical assistance in culturing by G. Pogge (Salata AG, Ritschenhausen) is gratefully acknowledged. Further, the authors thank S. Henkel and D. Driesch (project partner BioControl Jena GmbH) as well as J. Demmel and J. M. Reinecke (University of Applied Sciences Jena, Department of Medical Engineering and Biotechnology) for very helpful discussions with respect to data analysis issues and also S. Schuster (Friedrich Schiller University Jena, Department of Bioinformatics) for assistance with respect to modeling issues.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2020.00453/full#supplementary-material
References
Abirami, S., Murugesan, S., Sivamurugan, V., and Sivaswamy, S. N. (2017). Screening and optimization of culture conditions of Nannochloropsis gaditana for omega 3 fatty acid production. J. Appl. Biol. Biotechnol. 5, 13–17. doi: 10.7324/JABB.2017.50303
Barbera, E., Grandi, A., Borella, L., Bertucco, A., and Sforza, E. (2019). Continuous cultivation as a method to assess the maximum specific growth rate of photosynthetic organisms. Front. Bioeng. Biotechnol. 7:274. doi: 10.3389/fbioe.2019.00274
Bartley, M. L., Boeing, W. J., Daniel, D., Dungan, B. N., and Schaub, T. (2015). Optimization of environmental parameters for Nannochloropsis salina growth and lipid content using the response surface method and invading organisms. J. Appl. Phycol. 28, 15–24. doi: 10.1007/s10811-015-0567-8
Bartley, M. L., Boeing, W. J., Dungan, B. N., Holguin, F. O., and Schaub, T. (2014). pH effects on growth and lipid accumulation of the biofuel microalgae Nannochloropsis salina and invading organisms. J. Appl. Phycol. 26, 1431–1437. doi: 10.1007/s10811-013-0177-2
Benvenuti, G., Bosma, R., Klok, A. J., Ji, F., Lamers, P. P., Barbosa, M. J., et al. (2015). Microalgal triacylglycerides production in outdoor batch-operated tubular PBRs. Biotechnol. Biofuels 8:100. doi: 10.1186/s13068-015-0283-2
Bernard, O. (2011). Hurdles and challenges for modelling and control of microalgae for co2 mitigation and biofuel production. J. Process Control 21, 1378–1389. doi: 10.1016/j.jprocont.2011.07.012
Bernard, O., Mairet, F., and Chachuat, B. (2016). “Modelling of microalgae culture systems with applications to control and optimization,” in Microalgae Biotechnology, eds C. Posten and S. F. Chen (Cham: Springer International Publishing), 59–87. doi: 10.1007/10_2014_287
Bernard, O., and Rémond, B. (2012). Validation of a simple model accounting for light and temperature effect on microalgal growth. Bioresour. Technol. 123, 520–527. doi: 10.1016/j.biortech.2012.07.022
Blanken, W., Postma, P. R., de Winter, L., Wijffels, R. H., and Janssen, M. (2016). Predicting microalgae growth. Algal Res. 14, 28–38. doi: 10.1016/j.algal.2015.12.020
Braun, R., Farre, E. M., Schurr, U., and Matsubara, S. (2014). Effects of light and circadian clock on growth and chlorophyll accumulation of Nannochloropsis gaditana. J. Appl. Phycol. 50, 515–525. doi: 10.1111/jpy.12177
Chen, Y., Wang, J., Liu, T., and L.Gao (2012). Effects of initial population density (IPD) on growth and lipid composition of Nannochloropsis sp. J. Appl. Phycol. 24, 1623–1627. doi: 10.1007/s10811-012-9825-1
Chua, E. T., and Schenk, P. M. (2017). A biorefinery for Nannochloropsis: induction, harvesting, and extraction of EPA-rich oil and high-value protein. Bioresour. Technol. 244, 1416–1424. doi: 10.1016/j.biortech.2017.05.124
Darvehei, P., Bahri, P. A., and Moheimani, N. R. (2018). Model development for the growth of microalgae: a review. Renew. Sustain. Energy Rev. 97, 233–258. doi: 10.1016/j.rser.2018.08.027
de Vree, J. H., Bosma, R., Janssen, M., Barbosa, M. J., and Wijffels, R. H. (2015). Comparison of four outdoor pilot-scale photobioreactors. Biotechnol. Biofuels 8:215. doi: 10.1186/s13068-015-0400-2
Derwenskus, F., Metz, F., Gille, A., Schmid-Staiger, U., Briviba, K., Schließmann, U., et al. (2018). Pressurized extraction of unsaturated fatty acids and carotenoids from wet Chlorella vulgaris and Phaeodactylum tricornutum biomass using subcritical liquids. GCB Bioenerg. 11, 335–344. doi: 10.1111/gcbb.12563
Dillschneider, R., Steinweg, C., Rosello-Sastre, R., and Posten, C. (2013). Biofuels from microalgae: photoconversion efficiency during lipid accumulation. Bioresour. Technol. 142, 647–654. doi: 10.1016/j.biortech.2013.05.088
Draaisma, R. B., Wijffels, R. H., Slegers, P. M., Brentner, L. B., Roy, A., and Barbosa, M. J. (2013). Food commodities from microalgae. Curr. Opin. Biotechnol. 24, 169–177. doi: 10.1016/j.copbio.2012.09.012
Duchesne, C., and MacGregor, J. F. (2001). Jackknife and bootstrap methods in the identification of dynamic models. J. Process Control 11, 553–564. doi: 10.1016/S0959-1524(00)00025-1
Efron, B., and Tibshirani, R. (1993). An Introduction to the Bootstrap (Monographs on Statistics and Applied Probability). Boca Raton, FL; London; New York, NY; Washington, DC: Chapman and Hall/CRC. Available online at: https://cds.cern.ch/record/526679/files/0412042312_TOC.pdf
Endres, C. H., Roth, A., and Brück, T. B. (2018). Modeling microalgae productivity in industrial-scale vertical flat panel photobioreactors. Environ. Sci. Technol. 52, 5490–5498. doi: 10.1021/acs.est.7b05545
Garrido-Cardenas, J. A., Manzano-Agugliaro, F., Acien-Fernandez, F. G., and Molina-Grima, E. (2018). Microalgae research worldwide. Algal Res. 35, 50–60. doi: 10.1016/j.algal.2018.08.005
Gouveia, L., and Oliveira, A. C. (2009). Microalgae as a raw material for biofuels production. J. Ind. Microbiol. Biotechnol. 36, 269–274. doi: 10.1007/s10295-008-0495-6
Grewe, C., and Griehl, C. (2013). “Chapter 8: The carotenoid astaxanthin from Haematococcus pluvialis,” in Microalgal Biotechnology: Integration and Economy, eds C. Posten and C. Walter (Berlin: De Gryuter), 129–143.
Gu, N., Lin, Q., Li, G., Tan, Y., Huang, L., and Lin, J. (2012). Effect of salinity on growth, biochemical composition, and lipid productivity of Nannochloropsis oculataCS 179. Eng. Life Sci. 12, 631–637. doi: 10.1002/elsc.201100204
Guarnieri, M. T., and Pienkos, P. T. (2014). Algal omics: unlocking bioproduct diversity in algae cell factories. Photosynth. Res. 123, 255–263. doi: 10.1007/s11120-014-9989-4
Hoffmann, M. (2010). Physiologische Untersuchungen parameterinduzierter Adaptionsantworten von Nannochloropsis salina in turbidostatischen Prozessen und deren biotechnologischer Potentiale (Ph.D. thesis). Christian-Albrechts-Universität Kiel, Büsum: Forschungs- und Technologiezentrum Westküste der Universität Kiel in Büsum.
Homma, T., and Saltelli, A. (1996). Importance measures in global sensitivity analysis of nonlinear models. Reliabil. Eng. Syst. Saf. 52, 1–17. doi: 10.1016/0951-8320(96)00002-6
Hulatt, C. J., Wijffels, R. H., Bolla, S., and Kiron, V. (2017). Production of fatty acids and protein by Nannochloropsis in flat-plate photobioreactors. PLoS ONE 12:e0170440. doi: 10.1371/journal.pone.0170440
Janssen, J. H., Driessen, J. L., Lamers, P. P., Wijffels, R. H., and Barbosa, M. J. (2018). Effect of initial biomass-specific photon supply rate on fatty acid accumulation in nitrogen depleted nannochloropsis gaditana under simulated outdoor light conditions. Algal Res. 35, 595–601. doi: 10.1016/j.algal.2018.10.002
Kandilian, R., Pruvost, J., Legrand, J., and Pilon, L. (2014). Influence of light absorption rate by Nannochloropsis oculata on triglyceride production during nitrogen starvation. Bioresour. Technol. 163, 308–319. doi: 10.1016/j.biortech.2014.04.045
Karemore, A., Ramalingam, D., Yadav, G., Subramanian, G., and Sen, R. (2015). “Photobioreactors for improved algal biomass production: analysis and design considerations,” in Algal Biorefinery: An Integrated Approach, ed D. Das (Cham: Springer International Publishing), 103–124. doi: 10.1007/978-3-319-22813-6_5
Karlson, B., Potter, D., Kuylenstierna, M., and Andersen, R. A. (1996). Ultrastructure, pigment composition, and 18s rRNA gene sequence for Nannochloropsis granulata sp. nov. (Monodopsidaceae, Eustigmatophyceae), a marine Ultraplankter isolated from the Skagerrak, northeast Atlantic ocean. Phycologia 35, 253–260. doi: 10.2216/i0031-8884-35-3-253.1
Khan, M. I., Shin, J. H., and Kim, J. D. (2018). The promising future of microalgae: current status, challenges, and optimization of a sustainable and renewable industry for biofuels, feed, and other products. Microb. Cell Factor. 17, 1–21. doi: 10.1186/s12934-018-0879-x
Kliphuis, A. M. J., Klok, A. J., Martens, D. E., Lamers, P. P., Janssen, M., and Wijffels, R. H. (2011). Metabolic modeling of Chlamydomonas reinhardtii: energy requirements for photoautotrophic growth and maintenance. J. Appl. Phycol. 24, 253–266. doi: 10.1007/s10811-011-9674-3
Lippi, L., Bähr, L., Wüstenberg, A., Wilde, A., and Steuer, R. (2018). Exploring the potential of high-density cultivation of cyanobacteria for the production of cyanophycin. Algal Res. 31, 363–366. doi: 10.1016/j.algal.2018.02.028
Lobry, J., Rosso, L., and Flandrois, J.-P. (1991). A FORTRAN subroutine for the determination of parameter confidence limits in non-linear Models. Binary 3, 86–93.
Malcata, F. (2018). Marine Macro- and Microalgae: An Overview. Boca Raton, FL: CRC Press. doi: 10.1201/9781315119441
Mayer, D., and Butler, D. (1993). Statistical validation. Ecol. Modell. 68, 21–32. doi: 10.1016/0304-3800(93)90105-2
Minhas, A. K., Hodgson, P, Barrow, C. J., and Adholeya, A. (2016). A review on the assessment of stress conditions for simultaneous production of microalgal lipids and carotenoids. Front. Microbiol. 7:546. doi: 10.3389/fmicb.2016.00546
Moreno, J. J. M., Pol, A. P., and Abad, A. S. (2013). Using the R-MAPE index as a resistant measure of forecast accuracy. Psicothema 25, 500–506. doi: 10.7334/psicothema2013.23
Neumann, U., Derwenskus, F., Gille, A., Louis, S., Schmid-Staiger, U., Briviba, K., et al. (2018). Bioavailability and safety of nutrients from the microalgae Chlorella vulgaris, Nannochloropsis oceanica and Phaeodactylum tricornutum in C57BL/6 Mice. Nutrients 10:E965. doi: 10.3390/nu10080965
Olaizola, M., and Grewe, C. (2019). “Commercial microalgal cultivation systems,” in Grand Challenges in Algae Biotechnology, eds A. Hallmann and P. Rampelotto (Cham: Springer International Publishing), 3–34. doi: 10.1007/978-3-030-25233-5_1
Olofsson, M., Lamela, T., Nilsson, E., Bergé, J. P., del Pino, V., Uronen, P., et al. (2012). Seasonal variation of lipids and fatty acids of the microalgae Nannochloropsis oculata grown in outdoor large-scale photobioreactors. Energies 5, 1577–1592. doi: 10.3390/en5051577
Pal, D., Khozin-Goldberg, I., Cohen, Z., and Boussiba, S. (2011). The effect of light, salinity, and nitrogen availability on lipid production by Nannochloropsis sp. Appl. Microbiol. Biotechnol. 90, 1429–1441. doi: 10.1007/s00253-011-3170-1
Pereira, H., Páramo, J., Silva, J., Marques, A., Barros, A., Maurício, D., et al. (2018). Scale-up and large-scale production of Tetraselmis sp. CTP4 (chlorophyta) for CO2 mitigation: from an agar plate to 100-m3 industrial photobioreactors. Sci. Rep. 8:5112. doi: 10.1038/s41598-018-23340-3
Pfaffinger, C. E., Schöne, D., Trunz, S., Löwe, H., and Weuster-Botz, D. (2016). Model-based optimization of microalgae areal productivity in flat-plate gas-lift photobioreactors. Algal Res. 20, 153–163. doi: 10.1016/j.algal.2016.10.002
Pirt, S. J. (1986). The thermodynamic efficiency (quantum demand) and dynamics of photosynthetic growth. N. Phytol. 102, 3–37. doi: 10.1111/j.1469-8137.1986.tb00794.x
Poliner, E., Cummings, C., Newton, L., and Farre, E. M. (2019). Identification of circadian rhythms in Nannochloropsis species using bioluminescence reporter lines. Plant J. 99, 112–127. doi: 10.1111/tpj.14314
Posten, C. (2012). “Introduction,” in Microalgal Biotechnology: Integration and Economy, eds C. Posten and C. Walter (Berlin: De Gryuter), 1–9. doi: 10.1515/9783110298321
Ras, M., Steyer, J.-P., and Bernard, O. (2013). Temperature effect on microalgae: a crucial factor for outdoor production. Rev. Environ. Sci. Biotechnol. 12, 153–164. doi: 10.1007/s11157-013-9310-6
Raso, S., van Genugten, B., Vermuö, M., and Wijffels, R. H. (2011). Effect of oxygen concentration on the growth of Nannochloropsis sp. at low light intensity. J. Appl. Phycol. 24, 863–871. doi: 10.1007/s10811-011-9706-z
Rosso, L., Lobry, J., and Flandrois, J. (1993). An unexpected correlation between cardinal temperatures of microbial growth highlighted by a new model. J. Theor. Biol. 162, 447–463. doi: 10.1006/jtbi.1993.1099
Sandnes, J. M., Källqvist, T., Wenner, D., and Gislerød, H. R. (2005). Combined influence of light and temperature on growth rates of Nannochloropsis oceanica: linking cellular responses to large-scale biomass production. J. Appl. Phycol. 17, 515–525. doi: 10.1007/s10811-005-9002-x
Schediwy, K., Trautmann, A., Steinweg, C., and Posten, C. (2019). Microalgal kinetics–a guideline for photobioreactor design and process development. Eng. Life Sci. 19, 830–843. doi: 10.1002/elsc.201900107
Sobol, I. (2001). Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 55, 271–280. doi: 10.1016/S0378-4754(00)00270-6
Sorokin, C., and Krauss, R. W. (1958). The effects of light intensity on the growth rates of green algae. Plant Physiol. 33, 109–113. doi: 10.1104/pp.33.2.109
Spolaore, P., Joannis-Cassan, C., Duran, E., and Isambert, A. (2006). Optimization of Nannochloropsis oculata growth using the response surface method. J. Chem. Technol. Biotechnol. 81, 1049–1056. doi: 10.1002/jctb.1529
Sukenik, A. (1991). Ecophysiological considerations in the optimization of eicosapentaenoic acid production by Nannochloropsis sp. (Eustigmatophyceae). Bioresour. Technol. 35, 263–269. doi: 10.1016/0960-8524(91)90123-2
Takache, H., Christophe, G., Cornet, J.-F., and Pruvost, J. (2009). Experimental and theoretical assessment of maximum productivities for the microalgae Chlamydomonas reinhardtii in two different geometries of photobioreactors. Biotechnol. Prog. 26, 431–40. doi: 10.1002/btpr.356
Tang, Y., Reed, P., Wagener, T., and van Werkhoven, K. (2007). Comparing sensitivity analysis methods to advance lumped watershed model identification and evaluation. Hydrol. Earth Syst. Sci. 11, 793–817. doi: 10.5194/hess-11-793-2007
Wagenen, J. V., Miller, T. W., Hobbs, S., Hook, P., Crowe, B., and Huesemann, M. (2012). Effects of light and temperature on fatty acid production in Nannochloropsis salina. Energies 5, 731–740. doi: 10.3390/en5030731
Wahidin, S., Idris, A., and Shaleh, S. R. M. (2013). The influence of light intensity and photoperiod on the growth and lipid content of microalgae Nannochloropsis sp. Bioresour. Technol. 129, 7–11. doi: 10.1016/j.biortech.2012.11.032
Weise, T., Reinecke, J. M., Schuster, S., and Pfaff, M. (2019). Optimizing turbidostatic microalgal biomass productivity: A combined experimental and coarse-grained modelling approach. Algal Res. 39:101439. doi: 10.1016/j.algal.2019.101439
Zhang, K., Ma, J., Zhu, G., Ma, T., Han, T., and Feng, L. (2017). Parameter sensitivity analysis and optimization for a satellite-based evapotranspiration model across multiple sites using moderate resolution imaging spectroradiometer and flux data. J. Geophys. Res. Atmos. 122, 230–245. doi: 10.1002/2016JD025768
Zhang, X.-Y., Trame, M., Lesko, L., and Schmidt, S. (2015). Sobol sensitivity analysis: a tool to guide the development and evaluation of systems pharmacology models. CPT Pharmacometr. Syst. Pharmacol. 4, 69–79. doi: 10.1002/psp4.6
Zijffers, J.-W. F., Schippers, K. J., Zheng, K., Janssen, M., Tramper, J., and Wijffels, R. H. (2010). Maximum photosynthetic yield of green microalgae in photobioreactors. Mar. Biotechnol. 12, 708–718. doi: 10.1007/s10126-010-9258-2
Zittelli, G. C., Lavista, F., Bastianini, A., Rodolfi, L., Vincenzini, M., and Tredici, M. (1999). Production of eicosapentaenoic acid by Nannochloropsis sp. cultures in outdoor tubular photobioreactors. J. Biotechnol. 70, 299–312. doi: 10.1016/S0168-1656(99)00082-6
Nomenclature
Keywords: microalgal cultivation, coarse-grained modeling, light limitation, temperature, biomass productivity optimization, Nannochloropsis
Citation: Weise T, Grewe C and Pfaff M (2020) Experimental and Model-Based Analysis to Optimize Microalgal Biomass Productivity in a Pilot-Scale Tubular Photobioreactor. Front. Bioeng. Biotechnol. 8:453. doi: 10.3389/fbioe.2020.00453
Received: 20 January 2020; Accepted: 20 April 2020;
Published: 13 May 2020.
Edited by:
Thomas Bartholomäus Brück, Technical University of Munich, GermanyReviewed by:
Clemens Posten, Karlsruhe Institute of Technology (KIT), GermanyJack Legrand, Université de Nantes, France
Copyright © 2020 Weise, Grewe and Pfaff. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tobias Weise, dG9iaWFzLndlaXNlQGVhaC1qZW5hLmRl
 Tobias Weise
Tobias Weise Claudia Grewe
Claudia Grewe Michael Pfaff
Michael Pfaff