Mathematical model for bone mineralization

Defective bone mineralization has serious clinical manifestations, including deformities and fractures, but the regulation of this extracellular process is not fully understood. We have developed a mathematical model consisting of ordinary differential equations that describe collagen maturation, production and degradation of inhibitors, and mineral nucleation and growth. We examined the roles of individual processes in generating normal and abnormal mineralization patterns characterized using two outcome measures: mineralization lag time and degree of mineralization. Model parameters describing the formation of hydroxyapatite mineral on the nucleating centers most potently affected the degree of mineralization, while the parameters describing inhibitor homeostasis most effectively changed the mineralization lag time. Of interest, a parameter describing the rate of matrix maturation emerged as being capable of counter-intuitively increasing both the mineralization lag time and the degree of mineralization. We validated the accuracy of model predictions using known diseases of bone mineralization such as osteogenesis imperfecta and X-linked hypophosphatemia. The model successfully describes the highly nonlinear mineralization dynamics, which includes an initial lag phase when osteoid is present but no mineralization is evident, then fast primary mineralization, followed by secondary mineralization characterized by a continuous slow increase in bone mineral content. The developed model can potentially predict the function for a mutated protein based on the histology of pathologic bone samples from mineralization disorders of unknown etiology.

Background

Defects in bone mineralization can result in reduced or excessive bone mineralization, which can lead to serious clinical manifestations, including bone deformities and fractures. Plasma levels of calcium and phosphate—ionic mineral constituents of bone hydroxyapatite mineral—as well as their key regulators parathyroid hormone, vitamin D and FGF23, are critically important for successful mineralization (Shimada et al., 2004; Morris et al., 2012). Numerous conditions which are not associated with abnormal levels of circulating calcium and phosphate are also known to result in hypo- or hypermineralization of bone matrix (Roughley et al., 2003). One example is osteogenesis imperfecta, a disease usually caused by mutations in collagen type I-encoding genes and characterized by increased bone mineralization (Roschger et al., 2008a; Forlino et al., 2011). The clinical phenotype of osteogenesis imperfecta can also be caused by mutations in genes encoding the proteins that are involved in collagen post-translational modifications such as bone morphogenetic protein 1 (BMP1), or the proteins that regulate bone mineralization by an as yet unknown mechanism (Marini et al., 2014). The mechanisms underlying the development of hypo- and hypermineralization of extracellular bone matrix when the plasma levels of calcium and phosphate are within the normal range are complex and not well understood.

Clinically, the mineralization process can be examined in bone biopsy samples, which are typically obtained from the iliac bone. When tetracycline labeling is performed prior to biopsy, it is possible to assess the mineralization process quantitatively using bone histomorphometry (Rauch, 2006). Key, well-accepted histomorphometric descriptors of the mineralization process include the average thickness of the layer of unmineralized organic bone matrix (osteoid thickness) and the duration of the lag time between the deposition of organic matrix and the start of mineralization (mineralization lag time). Using quantitative backscattered-electron imaging, it is also possible to determine the average density of mineralized bone (Roschger et al., 2008b), which among other measures indicates the proportion of the mineralized tissue mass contributed to by the mineral ions.

The molecular origin and mechanistic basis of bone hypo- and hypermineralization are incompletely understood; however, it is clear that the process of mineralization is tightly regulated and is highly nonlinear. The goal of this study was to develop a simplified mathematical model of a complex process that provides a description of basic steps in the mineralization process, including collagen production and maturation, delivery and degradation of inhibitors, as well as mineral nucleation and growth. To our knowledge, no mathematical model focused on bone mineralization process exists to date, however important work has been performed in modeling the role of mineralization process in determining the bone mineral distribution (Ruffoni et al., 2007); the process of dentinogenesis including dentin phosphoprotein-regulated mineralization (Niño-Barrera et al., 2013) as well as describing the mineralization-induced changes in mechanical properties of collagen (Crolet et al., 2005; Nikolov and Raabe, 2008; Barkaoui and Hambli, 2014). Using the intentionally simplified model which includes multiple complexities in a limited number of variables, we were able to capture the significant nonlinearity of the mineralization process. Modeling predictions regarding the roles of individual processes in generating abnormal mineralization patterns were compared to the phenotype of diseases having in major bone mineralization defects—namely osteomalacia diseases and osteogenesis imperfecta.

Model Development

We modeled the changes over time in the concentration of five key players in the mineralization process—the collagen matrix subdivided into naïve and mature matrix, the inhibitors of mineralization, the nucleation centers (nucleators), and the hydroxyapatite mineral—within a homogeneous unit volume of osteoid of ~1 μm³ in dimensions using a system of ordinary differential equations. The following considerations were used to identify the main model assumptions.

1. Physiologically, the formation of bone tissue begins with the secretion of an organic bone matrix by osteoblasts, which to a large extent (by weight and volume) consists of collagen type I (Christiansen et al., 2000). Once this naïve organic matrix is deposited into the extracellular compartment, it needs to be processed in order to accommodate mineralization—a process termed matrix maturation. This maturation phase includes cleavage of C- and N-terminal propeptides from the collagen molecule and collagen crosslinking and packaging (Knott and Bailey, 1998; Christiansen et al., 2000), as well as similar processing of noncollagenous proteins (Kaartinen et al., 2002). The process of extracellular matrix maturation lasts 10–14 days. For this model, we considered different steps of matrix maturation such as post-translational modification of collagen and noncollagenous matrix proteins, and collagen cross-linking as a maturation process, which normally occurs with a characteristic rate constant of k₁. In the model, a change in any step of post-translational modification or crosslinking is assumed to have an overall effect on matrix maturation by either facilitating or interfering with the normal process. We assumed that collagen matrix is produced by osteoblasts in a naïve form (x₁) that matures into a fully assembled mature collagen matrix (x₂). These relationships are described by Equations (1a) and (1b).

2. The mineralization of naïve matrix is prevented by the action of numerous inhibitors, which reside in the local bone extracellular microenvironment, or arrive from the circulation (Murshed and McKee, 2010). During matrix maturation, the inhibitors are degraded or inactivated to enable mineralization. For example, a potent small-molecule inhibitor of mineralization—inorganic pyrophosphate—is cleaved by alkaline phosphatase present on the osteoblast cell membrane (Murshed and McKee, 2010). The proteins of the SIBLING family (small integrin-binding ligand, N-linked glycoproteins) are also known for their role in the regulation of mineralization; for example, the SIBLING proteins osteopontin (OPN) and matrix extracellular phosphoglycoprotein (MEPE) are potent inhibitors of mineralization (Rowe et al., 2004; Jahnen-Dechent et al., 2008). The action of another SIBLING protein dentin matrix protein 1 (DMP1) is regulated by its state during matrix maturation. DMP1 acts an inhibitor of mineralization when it is in solution (He et al., 2005), but becomes a promoter of mineralization when absorbed onto collagen surfaces (Hunter and Goldberg, 1993; Hunter et al., 1996; He et al., 2003). We modeled the combined action of different inhibitors of mineralization (I), which were assumed to be released into the extracellular compartment near the cells (Murshed and McKee, 2010) and diffuse through immature collagen (Weinstock and Leblond, 1973) with the characteristic rate constant of v₁. Thus, inhibitor availability was modeled to be proportional to the amount of naïve collagen as described by the term v₁x₁ in the Equation (1c). The concentration of active inhibitors in mineralizing matrix gradually decreases both because of their degradation through enzymatic cleavage (Addison et al., 2008, 2010; Murshed and McKee, 2010; Barros et al., 2013) as well as removal by other processes that interfere with inhibitor function, such as binding, masking or trapping (He et al., 2005; David et al., 2011). In the model, inhibitor removal/reduction occurs with the rate constant of r₁ and is stimulated by the presence of mature collagen matrix and as described by the term r₁x₂I in the Equation (1c).

3. During the mineralization process calcium and phosphate precipitate to form hydroxyapatite [Ca₁₀(PO₄)₆(OH)₂] crystals within the organic bone matrix (Boskey and Posner, 1984). The location and orientation of individual crystals is not random, but rather is guided by the chemistry and structure of collagen and noncollagenous proteins and small proteoglycans initiating and regulating crystal nucleation and growth between and within collagen fibrils (George and Veis, 2008). Within the collagen fibril the mineral is formed in-between the assembled collagen molecules (intrafibrillar mineralization) (George and Veis, 2008). Interfibrillar crystals can be nucleated by the SIBLING proteins bone sialoprotein and DMP1 (Hunter and Goldberg, 1993; Hunter et al., 1996; He et al., 2003). We assumed that nucleation centers (N) are required to initiate mineral precipitation (Hunter and Goldberg, 1993; He et al., 2003), and that nucleators appear during matrix maturation. The number of nucleators per mature collagen molecule is k₂. We assumed that intrafibrillar and interfibrillar nucleators act in a similar way, therefore when k₂ = 1, there is only one intrafibrillar nucleator per 1 molecule of collagen, and when k₂ > 1, then there is a mix of intrafibrillar and interfibrillar nucleators. A resulting rate of nucleator appearance is proportional to matrix maturation given by Equation (1b) and is described by the term $k_2\frac{d{x}_2}{dt}$ in Equation (1d). We assume that after mineralization is initiated by a given nucleator, this nucleator becomes a mineral crystal and thus can maintain, but no longer can initiate mineral precipitation (Hunter et al., 1996). Therefore, when mineraization starts, the number of nucleators decreases as they become masked by the mineral. The rate of decrease of nucleators was assumed to be proportional to the rate at which mineralized crystals (y) appear (dy/dt), as well as to the concentration of nucleators present, as described by the term $r_2\frac{dy}{dt}N$ in Equation (1d).

4. The formation of mineral (y) was assumed to occur with a characteristic rate of k₃ and to be directly proportional to the number of nucleators and inversely related to the amount of inhibitors (Murshed and McKee, 2010). Although we modeled matrix mineralization in a homogenous assumption, it would be possible to relate the number of nucleators N to the number of mineral crystals within a given volume of the matrix, while the mineral growth rate k₃ to the growth of individual crystals. Particular considerations were given to the function describing the effect of inhibitors on mineral formation. We modeled mineralization rate by an equation of the form $\frac{dy}{dt}=k_{3}g(I)N$, where g(I) is a decreasing function of I which tends to 0 as I goes to infinity. Mineralization dynamics was qualitatively similar when g(I) was described by the piecewise function $g(I)=\{\begin{array}{c}-aI+b,x\le 1\\ 0,I>1\end{array}\}$ or the Hill type functions $g(I)=\frac{b}{b+e^{aI}}$ and $g(I)=\frac{b}{b+I^a}$, (data not shown). We chose a differentiable function amenable for biological interpretation $g(I)=\frac{b}{b+I^a}$ with a = 10 and b = 0.001. This function approaches 1 at I smaller than ~0.4, which represents the critical (nondimensionalized) value of I permitting mineralization in the system.

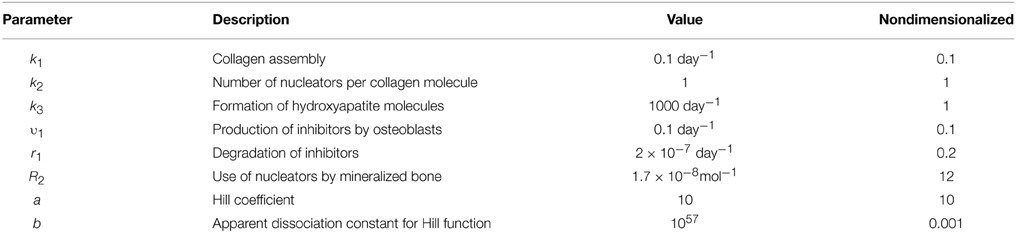
Based on these assumptions (Figure 1), the changes in the five components of the mineralizing bone matrix (Table 1) are described by the following system of ordinary differential Equations (1).

$\begin{array}{ll}\frac{d{x}_1}{dt}=-k_1{x}_1& \left(1\text{a}\right)\end{array}$

$\begin{array}{ll}\frac{d{x}_2}{dt}=k_1{x}_1& \left(1\text{b}\right)\end{array}$

$\begin{array}{ll}\frac{dI}{dt}=v_1{x}_1-r_1{x}_{2}I& \left(1\text{c}\right)\end{array}$

$\begin{array}{ll}\frac{dN}{dt}=k_2\frac{d{x}_2}{dt}-r_2\frac{dy}{dt}N& \left(1\text{d}\right)\end{array}$

$\begin{array}{ll}\frac{dy}{dt}=k_3\left(\frac{b}{b+I^a}\right)N& \left(1\text{e}\right)\end{array}$

FIGURE 1

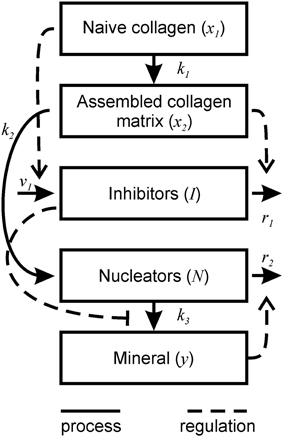
Figure 1. Schematic representation of bone mineralization described by the model. Thick lines represent the processes occurring during mineralization. Dotted lines represent the regulatory effects of different components on the mineralization process.

TABLE 1

Table 1. Variables used in Equation (1).

Estimation of Characteristic Values of the Variables and Parameters

To estimate collagen packing within 1 μm³ of matrix, we assume that a single molecule of triple-helical collagen is 1.4 nm in diameter and 300 nm in length based on estimates in the literature (Gross et al., 1955; George and Veis, 2008). Collagen molecules form fibrils of 70–90 nm in diameters, thus a single fibril contains ~3000 molecules (Hodge and Schmitt, 1960; George and Veis, 2008). We assume that fibrils have a ~10 nm coating of noncollagenous proteins and small proteoglycans, thus the cross-section of collagen fibrils is represented by circles of 110 nm diameter. In a hexagonal pattern circles have ~0.9069 packing density (Steinhaus, 1999), and hence, (0.9069 × 10⁶/(π × 55²) ~ 95.4 fibrils fit in a cross-section of 1 μm², and ~3.3 molecules fit in the 1 μm lengthwise. Therefore, in 1 μm³ of volume, there are 95.4 × 3.3 × 3000 = 9.4 × 10⁵ molecules of collagen.

To estimate the number of hydroxyapatite molecules, we started with a density of fully mineralized bone of 2.0 g/cm³ (Gong et al., 1964). Assuming that bone contains 70% mineral, the hydroxyapatite density is ~1.40 g/cm³ = 1.40 × 10⁻¹² g/μm³. Given the molecular weight of the hydroxyapatite molecule [Ca₁₀(PO₄)₆(OH)₂] of 1004 g/mol, 1004 g contains 6 × 10²³ molecules of hydroxyapatite. Therefore, 1 μm³ of mineralized matrix contains ~ 0.8 × 10⁹ molecules of hydroxyapatite.

The number of nucleators was first assumed to be of the same order of magnitude as the number of collagen molecules (k₂ = 1), and later we examined how changing the number of nucleators affects the outcome of the mineralization. It is difficult to estimate the number of inhibitors, since we pooled into this category factors that use different mechanisms to achieve a single function—inhibition of mineralization. These factors are much smaller in size than the collagen molecules; however, there is less physical space available for them, and therefore we assumed that the numbers of inhibitor molecules and collagen molecules are of the same order of magnitude.

The rate constant values were chosen based on the observation that two main phases are present during bone mineralization: a slow phase of matrix maturation and a relatively fast phase of matrix mineralization (Boskey and Posner, 1984; George and Veis, 2008; Murshed and McKee, 2010). To account for this dynamic, we assumed that the rates of matrix maturation and the related processes of inhibitor processing and nucleator production are slower than the rates of mineral precipitation and nucleator removal/reduction. Since collagen maturation takes place by ~10–14 days (Boskey and Posner, 1984; George and Veis, 2008), the rate of collagen assembly k₁ was estimated as 0.1 day⁻¹. We assumed the rate of inhibitor delivery to be v₁ = 0.1 day⁻¹ and the rate of inhibitor degradation to be r₁ = 2 × 10⁻⁷ day⁻¹ mol⁻¹. We assumed that when nucleators are available, and no inhibitors are present, mineralization occurs with a faster rate than collagen assembly k₃ = 1000 day⁻¹. An order of magnitude for the rate of the nucleator use by mineralization was r₂ = 1.5–2 × 10⁻⁸ mol⁻¹. The parameter values for the simulation of normal mineralization are given in Table 2. Further details for model nondimensionalization and numerical analysis are given in Supplementary Material.

TABLE 2

Table 2. Parameters used in Equations (1) and (2).

Results

First, we examined the pattern of temporal changes in the five variables for the parameters representing bone mineralization in a healthy subject (Tables 1, 2). Naïve collagen, which initially constituted 100% of all collagen in the system, was gradually assembled into mature collagen, resulting in 80% conversion within 20 days, and in complete maturation within 40–60 days (Figure 2A). Inhibitors initially present in the naïve matrix were sustained for the first 10 days and rapidly degraded with the appearance of mature collagen (Figure 2B). Nucleating centers produced with the mature collagen reached the maximum at ~10 days, and were removed with the offset of the mineralization (Figure 2B). After a lag time of ~10 days, the mineralization first progressed rapidly followed by a continuous slow mineral formation (Figure 2C). The normalized mineralization degree of 1 (i.e., full mineralization) was reached ~100 days after the deposition of naïve collagen. Thus, the model describes the lag time required for matrix maturation, the rapid mineralization offset, and the continuous slow increase in mineralization with time (Roschger et al., 2008b).

FIGURE 2

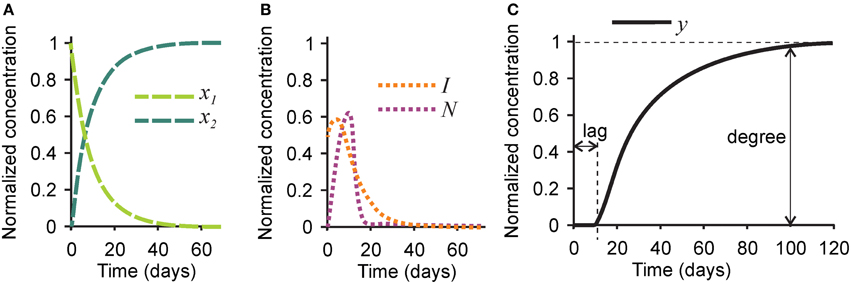
Figure 2. Changes in time in different players in the mineralization process in healthy bone. (A) The concentrations of naïve (x₁, light green) and mature (x₂, dark green) collagen matrix. (B) The concentration of the mineralization inhibitor (I, orange) and the nucleation centers (N, purple). (C) The concentration of mineral (y). Indicated are the mineralization lag time, measured as a time delay between time 0 and the onset of mineralization, and mineralization degree, measured as the amount of mineral at time = 100 days. For the simulation of healthy bone, the mineralization lag time is 10 days, and the mineralization degree is 1.

To model mineralization defects, we first examined the effect of the rate of hydroxyapatite formation k₃ on the mineralization outcome (Figure 3). Changes in k₃ predictably affected the rate of mineral formation, but also strongly and proportionally affected the degree of mineralization. A 3-fold decrease in the rate of hydroxyapatite formation k₃ resulted in a 3-fold decrease in mineralization degree (Figures 3A,B), while a 3-fold increase in k₃ led to a 3-fold increase in mineralization degree (Figures 3C,D). The robust effect of k₃ on the degree of mineralization is due to the fact that the removal of nucleators from the model is regulated by two independent parameters—the rate of hydroxyapatite formation (directly affected by k₃), and the efficiency of nucleator removal (r₂), which remains high even when k₃ is low. Therefore, when the rate of hydroxyapatite formation decreases, the time interval during which nucleators are present remains unchanged, resulting in a decrease in mineralization degree. Changes in k₃ did not affect the dynamics of collagen maturation or turnover of its inhibitors.

FIGURE 3

Figure 3. The effect of parameter affecting formation of hydroxyapatite crystals k₃ on the mineralization outcome. (A) The effect of decreasing k₃ 3-fold. (B) Comparison of the mineralization lag time and degree following decrease in k₃ to healthy mineralization. (C) The effect of increasing k₃ 3-fold. (D) Comparison of the mineralization lag time and degree following increase in k₃ to healthy mineralization. The same color scheme is used as in Figure 2.

Next we examined the role of parameters affecting the nucleators, the number of nucleators per mature collagen k₂, and rate of removal of nucleators caused by hydroxyapatite formation r₂ (Figure 4). Mineralization lag time was not affected by changes in k₂ and r₂, since the dynamics of collagen and inhibitors does not depend on these parameters (Figures 4C,F). A 3-fold decrease in the number of nucleators per mature collagen k₂ resulted in a 40% decrease in mineralization degree (Figures 4A,C), while a 3-fold increase in k₂ led to a 60% increase in the mineralization degree (Figures 4B,C). A 3-fold decrease in the rate of nucleator removal caused by hydroxyapatite formation r₂ resulted in an almost 2-fold increase in mineralization degree (Figures 4D,F), while a 3-fold increase in r₂ resulted in 40% decrease in mineralization degree (Figures 4E,F).

FIGURE 4

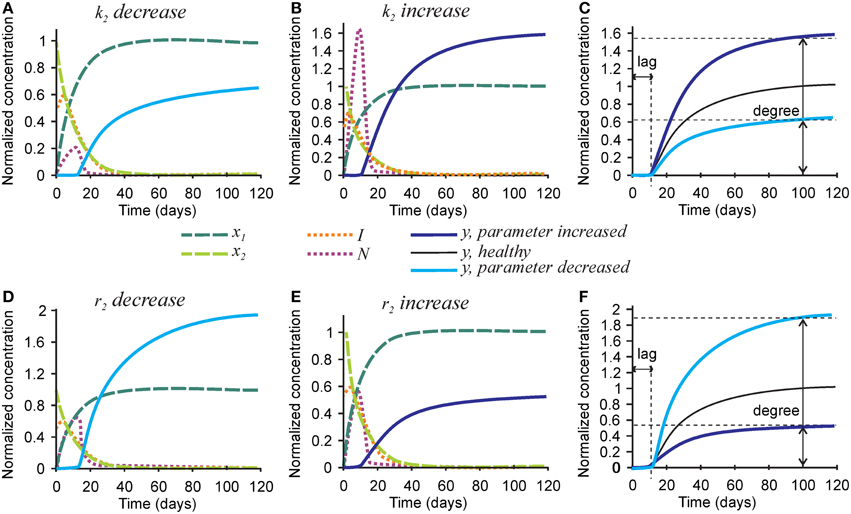
Figure 4. The effect of parameters affecting nucleator production and removal on the mineralization outcome. (A–C) The effect of decreasing 3-fold (A) or increasing 3-fold (B) the number of nucleators per crosslinked collagen (k₂). (C) Comparison of the mineralization lag time and degree in conditions affecting k₂ to healthy mineralization. (D–F) The effect of decreasing 3-fold (D) or increasing 3-fold (E) the rate of use of nucleators by mineralized bone (r₂). (F) Comparison of the mineralization lag time and degree in conditions affecting r₂ to healthy mineralization. The same color scheme is used as in Figure 2.

To examine the effect of parameters affecting the homeostasis of inhibitors on the mineralization outcome, we changed the rates of inhibitor production v₁ and degradation r₁ (Figure 5). Since Equations (1a) and (1b) are not affected by these parameters, no change in the degree or timing of collagen maturation was evident following changes in v₁ and r₁. The rate of inhibitor production v₁ was changed 10-fold since smaller changes only resulted in slight differences in the mineralization. A 10-fold decrease in the rate of inhibitor production v₁ resulted in a ~20% decrease in mineralization lag time and a similar 20% increase in mineralization degree (Figures 5A,C). A 10-fold increase in the rate of inhibitor production v₁ led to a 3-fold increase in mineralization lag time and a 40% decrease in mineralization degree (Figures 5B,C). The effect of changing the rate of inhibitor degradation r₁ on mineralization mirrored the effects of changing the rate of inhibitor production v₁, however, smaller, 3-fold alterations of r₁ were required to obtain noticeable effects on mineralization. A 3-fold decrease in r₁ resulted in a sustained inhibitor presence, a 2-fold increase in mineralization lag time and 40% decrease in mineralization degree (Figures 5D,F). A 3-fold increase in the rate of inhibitor degradation r₁ resulted in a 2-fold decrease in the mineralization lag time and 20% increase in mineralization degree (Figures 5E,F).

FIGURE 5

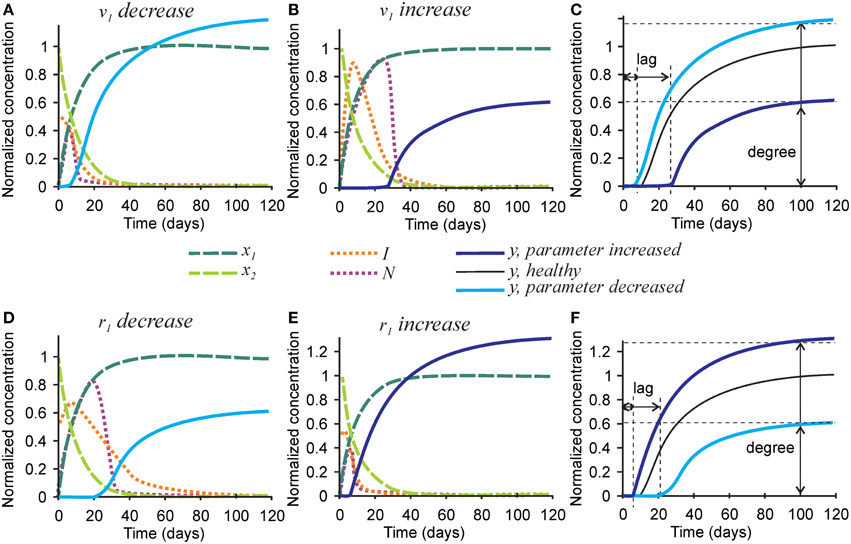
Figure 5. The effect of parameters affecting inhibitor production and degradation on the mineralization outcome. (A–C) The effect of decreasing 10-fold (A) or increasing 10-fold (B) the rate of inhibitor production (v₁). (C) Comparison of the mineralization lag time and degree in conditions affecting v₁to healthy mineralization. (D–F) The effect of decreasing 3-fold (D) or increasing 3-fold (E) the rate of inhibitor degradation (r₁). (F) Comparison of the mineralization lag and degree in conditions affecting r₁ to healthy mineralization. The same color scheme is used as in Figure 2.

Finally, we examined the effect of changing the parameters affecting initial collagen density x₁(0) and maturation k₁ on the mineralization outcome (Figure 6). Change in the initial density of naïve collagen x₁(0) represents an altered ability of osteoblasts to produce collagen, or altered collagen packing. A 3-fold decrease in x₁(0) resulted in a proportionally lower amount of mature collagen and the number of nucleators, leading to a 2-fold decrease in mineralization degree (Figures 6A,C). In addition, the inhibitor presence was sustained for a longer period of time leading to a 2-fold increase in mineralization lag time (Figure 6A). A 3-fold increase in x₁(0) led to a 3-fold increase in the amount of mature collagen and in the number of nucleators, which however translated to only a 70-80% increase in mineralization degree (Figures 6B,C).

FIGURE 6

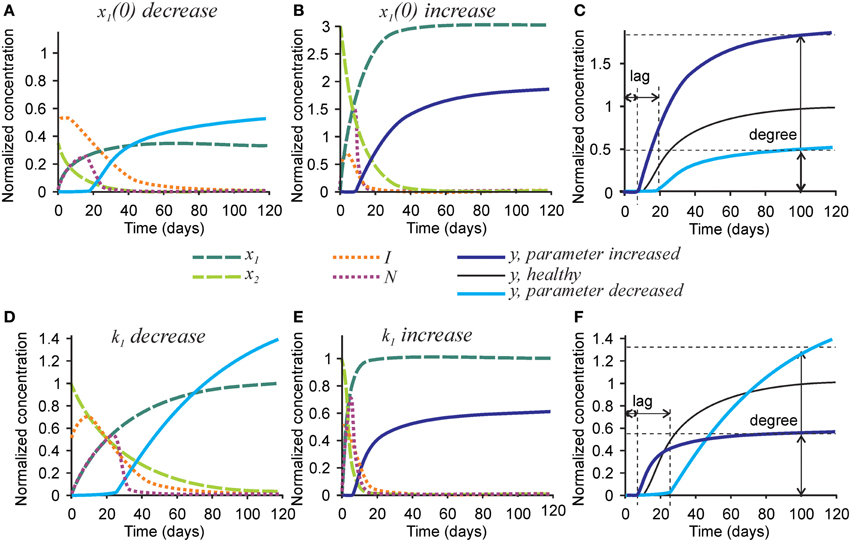
Figure 6. The effect of parameters affecting collagen maturation on the mineralization outcome. (A–C) The effect of decreasing 3-fold (A) or increasing 3-fold (B) the amount of naïve collagen deposited by osteoblasts at time = 0 (x₁(0)). (C) Comparison of the mineralization lag time and degree in conditions affecting x₁(0) to healthy mineralization. (D–F) The effect of decreasing 3-fold (D) or increasing 3-fold (E) the rate of collagen maturation (k₁). (F) Comparison of the mineralization lag and degree in conditions affecting k₁ to healthy mineralization. The same color scheme is used as in Figure 2.

A 3-fold decrease in the rate of collagen maturation k₁ resulted in the persistence of naïve collagen for up to 100 days and sustained inhibitor presence, leading to an almost 3-fold increase in mineralization lag time (Figure 6D). After mineralization started, it proceeded slower in the initial phase than in control conditions (Figures 6D,F). However, slow delivery of nucleators into the system resulted in a decrease in the rate of their removal (when nucleators are present at a low density, each of them can participate in mineralization for a longer time since they interfere less with each other). As a result, the mineralization rate did not decrease with time and a notably increased mineralization degree was reached (Figures 6D,F). A 3-fold increase in the rate of collagen maturation resulted in faster elimination of inhibitors and a slightly decreased mineralization lag time. The initial mineralization proceeded faster; however, because of faster removal of nucleators, it leveled off at lower overall mineralization degree (Figures 6E,F).

Discussion

The mathematical model for bone mineralization developed in this study captures the strongly nonlinear dynamics of mineralization, which starts from a lag phase when osteoid is present but no mineralization is evident, followed by fast primary mineralization, and subsequent secondary mineralization characterized by a continuous slow increase in bone mineral content (Roschger et al., 2008b). This dynamic was achieved in the model by assuming that (i) mineralization is suppressed in the presence of inhibitors, (ii) mineralization occurs fast, but requires the presence of nucleators, and (iii) nucleators formed during collagen maturation are removed from the system proportionally to the rate of mineralization. As a result, the lag phase allows for accumulation of nucleators, so that when inhibitors are reduced a large number of nucleators are present allowing mineralization to proceed rapidly. However, fast mineralization causes fast removal of nucleators leading to a substantial decrease in mineralization rate with time. We examined how changes in different parameters affect mineralization dynamics. The parameters describing the formation of hydroxyapatite crystals at the nucleating centers potently affected the degree of mineralization, while the parameters describing inhibitor homeostasis effectively changed the mineralization lag time. Of interest, a single parameter describing the rate of matrix maturation was capable of counter-intuitively increasing both the mineralization lag time and the degree of mineralization.

The model represents an intentional simplification of a complex mineralization process, as we focused on simultaneously capturing mineralization-related functions of many regulatory molecules. Therefore, the following limitations should be noted: (1) The model does not specify different steps of matrix maturation, such as post-translational modification of collagen and noncollagenous matrix proteins, and collagen crosslinking. (2) The action of a large number of chemically distinct inhibitors is pooled together as a single entity. (3) Similarly, the difference in action of intrafibrillar and interfibrillar nucleators is not described. (4) The model does not contain the physical limitation for the maximal amount of mineral that can be deposited into the matrix, and therefore its long-term predictions should be interpreted with caution. Model applicability at this stage is limited to situations when the changes in mineralization dynamics are dramatic, while further development of the model is required to predict more subtle changes over time such as occurring during development and in complex disorders of osteoporosis and diabetes.

To compare the model predictions to the phenotype of bone disorders known to result in abnormal mineralization, we examined hypomineralization in osteomalacia and hypermineralization in osteogenesis imperfecta. We used the proportion of osteoid (osteoid volume per bone volume OV/BV, and/or osteoid thickness O.Th.) as an indicator of mineralization lag time, and bone mineral density distribution (BMDD) (Roschger et al., 2008b) as a measure of mineralization degree to relate the disease mineralization phenotype observed on histomorphometric and BMDD analysis to model predictions.

Application of the Model to Osteomalacia

Osteomalacia arises in part because of a systemic deficiency in calcium and/or phosphate ions and the hormones responsible for their regulation—vitamin D and FGF23. It is characterized by an increase in mineralization lag time and a decrease in mineralization degree (Arnala et al., 2001; Roschger et al., 2003; Rabelink et al., 2011; Cheung et al., 2013). It is assumed that the main cause of osteomalacia is a decreased rate of hydroxyapatite formation (reflected by the parameter k₃ in the model) caused by a low level of calcium and/or phosphate. However, the model predicts that a decrease in k₃ accounts only for a strong decrease in mineralization degree, but cannot by itself affect the mineralization lag time (as mineral formation starts only after the lag phase is completed). In order to account for the strong increase in the mineralization lag time, it is necessary to assume additional direct or indirect effects of calcium/phosphate deficiency on inhibitor homeostasis. In fact, increases in local extracellular matrix mineralization inhibitors were also shown to contribute to the development of osteomalacia (Harmey et al., 2006; Barros et al., 2013; Millán, 2013). Inorganic calcium and phosphate are known to affect osteoblast differentiation (Beck et al., 2003; Dvorak et al., 2004), which could in turn result in changes in expression and processing of mineralization inhibitors. Deficiency in active 1,25-dihydroxyvitamin D (1,25(OH)2D) often associated with rickets (Takeda et al., 1997; Fukumoto, 2014) can affect the vitamin D receptor-mediated expression of mineralization inhibitors such as DMP1 (Nociti et al., 2014). Moreover, degradation of a strong inhibitor of mineralization—pyrophosphate (Addison et al., 2007)—is regulated by the concentration of phosphate, and both phosphate and pyrophosphate regulate expression of osteopontin (Harmey et al., 2006; Addison et al., 2007). In this context, removal/reduction of inhibitory osteopontin and its inhibitory peptides can be achieved by their extensive degradation by the enzyme PHEX (Addison et al., 2010; Barros et al., 2013). The model suggests that alteration of local inhibitor homeostasis is as important for the development of osteomalacia as is the direct effect of low calcium and phosphate on the rate of hydroxyapatite formation.

Application of the Model to Osteogenesis Imperfecta

Osteogenesis imperfecta (OI) is a disease characterized by high bone fragility associated with low bone mass as well as high mineral content in the bone tissue resulting in its brittleness (Roschger et al., 2008a). Mutations in genes coding for collagen type I—the usual cause of osteogenesis imperfecta—are associated with hypermineralization and normal mineralization lag time (Rauch et al., 2000). In the model, an increase in the number of nucleators per molecule of collagen (k₂) results in an increase in mineralization degree but does not affect the mineralization lag time. Therefore, the model suggests that the hypermineralization in OI caused by mutations in type I collagen-encoding genes is attributable to the increase in the number of nucleators per molecule of collagen. This prediction is consistent with a recent study that demonstrated that the hydroxyapatite crystal size is similar in OI and control bone tissue, thus implying that the increased mineral content in OI must be due to an increased density of mineral crystals (Fratzl-Zelman et al., 2014). Since in the model the density of nucleating centers corresponds to the density of mineral crystals, we conclude that the model correctly predicts hypermineralization in OI due to mutations in genes coding for collagen type I.

Of interest, there are two distinct forms of OI in which different mineralization phenotypes are described. In OI caused by mutations in cartilage-associated protein (CRTAP) a significant increase in the mineralization degree (Fratzl-Zelman et al., 2010) and a marked reduction in mineralization lag time (Morello et al., 2006) were observed. In contrast, mutations in the collagen type I C-propeptide cleavage site give rise to a hypermineralization accompanied by a simultaneous increase in the mineralization lag time (Lindahl et al., 2011).

CRTAP forms a complex with P3H1 and cyclophilin B which 3-hydroxylates the Pro986 residue of collagen alpha chains (Chang et al., 2010). It was reported that CRTAP deficiency results the deposition of abnormally structured collagen fibrils (variable in diameter, with irregular borders) in skin samples of OI patients due to CRTAP mutation (Valli et al., 2012). The model predicts that an increase in the initial collagen density (x₁(0)) can result in hypermineralization accompanied by a significant decrease in mineralization lag time. It is important to stress that the model describes the changes occurring in the already-deposited collagen, but not the rate of its deposition by osteoblasts, which is negatively affected by CTRAP mutation. It is indeed noticeable, that the distance between the collagen fibers in the skin of a patient with CRTAP mutation appear to be smaller (Valli et al., 2012). Thus, the CRTAP mutation likely affects the packing of collagen molecules simultaneously resulting in (i) an increase in trapping/masking and degradation of inhibitors, thus shortening the mineralization lag time, and (ii) an increase in the density of nucleators leading to an increase in mineralization degree.

Mutation in the collagen C-propeptide cleavage site disrupts extracellular collagen processing, resulting in decreased collagen maturation rate (Lindahl et al., 2011), represented in our model by the parameter k₁. In the model, decrease in k₁ uniquely gave rise to the phenotype of increase in both mineralization lag time and degree. Conversely, mutation in BMP1—an enzyme that cleaves C-propeptide off procollagen—also results in a decrease in collagen maturation, hyperosteoidosis and hypermineralization (Hoyer-Kuhn et al., 2013). Thus, our model predicted a correct, albeit counter-intuitive, mineralization phenotype resulting from a decrease in the collagen matrix maturation rate.

Conclusion

We have developed a simplified mathematical model that describes changes in the mineralization of bone matrix when individual processes occurring during mineralization are altered. We validated the accuracy of model predictions using bone diseases associated with dramatic changes in mineralization dynamics. During model development we used the data relevant to the mineralization process in human bone and applied the model to the analysis of human disorders of bone mineralization. In the future, this model can be applied for qualitative predictions of genotype/phenotype relationship in mouse models of bone mineralization, and it can be adapted to study mineralization of other calcified tissues, such as tooth dentin, cementum and enamel.

Author Contributions

SK, MDM, MM, and FR developed a biological framework of the model; LS, JG, EZ, MO, and SK constructed the model; LS, JG, EZ analyzed the model and generated the figures; SK prepared the first draft, all the co-authors read, critically revised, and approved the final manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The study was initiated and most of the work was completed during the Fifth Montreal Problem-Solving Workshop, August, 2013, which was supported by Network of Centre of Excellence Mprime, Group for Research in Decision Analysis (GERAD), the Matrix Dynamics Group, and Réseau de Recherche en santé Buccodentaire et Osseuse (RSBO). The completion of the project was supported by Natural Sciences and Engineering Research Council of Canada (NSERC) grant number RGPIN-2015-05579 to SVK.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fcell.2015.00051

References

Addison, W. N., Azari, F., Sørensen, E. S., Kaartinen, M. T., and McKee, M. D. (2007). Pyrophosphate inhibits mineralization of osteoblast cultures by binding to mineral, up-regulating osteopontin, and inhibiting alkaline phosphatase activity. J. Biol. Chem. 282, 15872–15883. doi: 10.1074/jbc.M701116200

CrossRef Full Text | Google Scholar

Addison, W. N., Masica, D. L., Gray, J. J., and McKee, M. D. (2010). Phosphorylation-dependent inhibition of mineralization by osteopontin ASARM peptides is regulated by PHEX cleavage. J. Bone Miner. Res. 25, 695–705. doi: 10.1359/jbmr.090832

PubMed Abstract | CrossRef Full Text | Google Scholar

Addison, W. N., Nakano, Y., Loisel, T., Crine, P., and McKee, M. D. (2008). MEPE-ASARM peptides control extracellular matrix mineralization by binding to hydroxyapatite: an inhibition regulated by PHEX cleavage of ASARM. J. Bone Miner. Res. 23, 1638–1649. doi: 10.1359/jbmr.080601

PubMed Abstract | CrossRef Full Text | Google Scholar

Arnala, I., Kemppainen, T., Kröger, H., Janatuinen, E., and Alhava, E. M. (2001). Bone histomorphometry in celiac disease. Ann. Chir. Gynaecol. 90, 100–104.

PubMed Abstract | Google Scholar

Barkaoui, A., and Hambli, R. (2014). Nanomechanical properties of mineralised collagen microfibrils based on finite elements method: biomechanical role of cross-links. Comput. Methods Biomech. Biomed. Eng. 17, 1590–1601. doi: 10.1080/10255842.2012.758255

PubMed Abstract | CrossRef Full Text | Google Scholar

Barros, N. M., Hoac, B., Neves, R. L., Addison, W. N., Assis, D. M., Murshed, M., et al. (2013). Proteolytic processing of osteopontin by PHEX and accumulation of osteopontin fragments in Hyp mouse bone, the murine model of X-linked hypophosphatemia. J. Bone Miner. Res. 28, 688–699. doi: 10.1002/jbmr.1766

PubMed Abstract | CrossRef Full Text | Google Scholar

Beck, G. R. Jr., Moran, E., and Knecht, N. (2003). Inorganic phosphate regulates multiple genes during osteoblast differentiation, including Nrf2. Exp. Cell Res. 288, 288–300. doi: 10.1016/S0014-4827(03)00213-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Boskey, A. L., and Posner, A. S. (1984). Bone structure, composition, and mineralization. Orthop. Clin. North Am. 15, 597–612.

PubMed Abstract | Google Scholar

Chang, W., Barnes, A. M., Cabral, W. A., Bodurtha, J. N., and Marini, J. C. (2010). Prolyl 3-hydroxylase 1 and CRTAP are mutually stabilizing in the endoplasmic reticulum collagen prolyl 3-hydroxylation complex. Hum. Mol. Genet. 19, 223–234. doi: 10.1093/hmg/ddp481

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheung, M., Roschger, P., Klaushofer, K., Veilleux, L. N., Roughley, P., Glorieux, F. H., et al. (2013). Cortical and trabecular bone density in X-linked hypophosphatemic rickets. J. Clin. Endocrinol. Metab. 98, E954–E961. doi: 10.1210/jc.2012-4133

PubMed Abstract | CrossRef Full Text | Google Scholar

Christiansen, D. L., Huang, E. K., and Silver, F. H. (2000). Assembly of type I collagen: fusion of fibril subunits and the influence of fibril diameter on mechanical properties. Matrix Biol. 19, 409–420. doi: 10.1016/S0945-053X(00)00089-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Crolet, J. M., Racila, M., Mahraoui, R., and Meunier, A. (2005). A new numerical concept for modeling hydroxyapatite in human cortical bone. Comput. Methods Biomech. Biomed. Eng. 8, 139–143. doi: 10.1080/10255840500156971

PubMed Abstract | CrossRef Full Text | Google Scholar

David, V., Martin, A., Hedge, A. M., Drezner, M. K., and Rowe, P. S. (2011). ASARM peptides: PHEX-dependent and -independent regulation of serum phosphate. Am. J. Physiol. Renal Physiol. 300, F783–F791. doi: 10.1152/ajprenal.00304.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Dvorak, M. M., Siddiqua, A., Ward, D. T., Carter, D. H., Dallas, S. L., Nemeth, E. F., et al. (2004). Physiological changes in extracellular calcium concentration directly control osteoblast function in the absence of calciotropic hormones. Proc. Natl. Acad. Sci. U.S.A. 101, 5140–5145. doi: 10.1073/pnas.0306141101

CrossRef Full Text | Google Scholar

Forlino, A., Cabral, W. A., Barnes, A. M., and Marini, J. C. (2011). New perspectives on osteogenesis imperfecta. Nat. Rev. Endocrinol. 7, 540–557. doi: 10.1038/nrendo.2011.81

PubMed Abstract | CrossRef Full Text | Google Scholar

Fratzl-Zelman, N., Morello, R., Lee, B., Rauch, F., Glorieux, F. H., Misof, B. M., et al. (2010). CRTAP deficiency leads to abnormally high bone matrix mineralization in a murine model and in children with osteogenesis imperfecta type VII. Bone 46, 820–826. doi: 10.1016/j.bone.2009.10.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Fratzl-Zelman, N., Schmidt, I., Roschger, P., Glorieux, F. H., Klaushofer, K., Fratzl, P., et al. (2014). Mineral particle size in children with osteogenesis imperfecta type I is not increased independently of specific collagen mutations. Bone 60, 122–128. doi: 10.1016/j.bone.2013.11.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Fukumoto, S. (2014). Phosphate metabolism and vitamin D. Bonekey Rep. 3, 497. doi: 10.1038/bonekey.2013.231

CrossRef Full Text | Google Scholar

George, A., and Veis, A. (2008). Phosphorylated proteins and control over apatite nucleation, crystal growth, and inhibition. Chem. Rev. 108, 4670–4693. doi: 10.1021/cr0782729

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, J. K., Arnold, J. S., and Cohn, S. H. (1964). Composition of trabecular and cortical bone. Anat. Rec. 149, 325–331. doi: 10.1002/ar.1091490303

PubMed Abstract | CrossRef Full Text | Google Scholar

Gross, J., Highberger, J. H., and Schmitt, F. O. (1955). Extraction of collagen from connective tissue by neutral salt solutions. Proc. Natl. Acad. Sci. U.S.A. 41, 1–7. doi: 10.1073/pnas.41.1.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Harmey, D., Johnson, K. A., Zelken, J., Camacho, N. P., Hoylaerts, M. F., Noda, M., et al. (2006). Elevated skeletal osteopontin levels contribute to the hypophosphatasia phenotype in Akp2(-/-) mice. J. Bone Miner. Res. 21, 1377–1386. doi: 10.1359/jbmr.060619

PubMed Abstract | CrossRef Full Text | Google Scholar

He, G., Dahl, T., Veis, A., and George, A. (2003). Nucleation of apatite crystals in vitro by self-assembled dentin matrix protein 1. Nat. Mater. 2, 552–558. doi: 10.1038/nmat945

PubMed Abstract | CrossRef Full Text | Google Scholar

He, G., Gajjeraman, S., Schultz, D., Cookson, D., Qin, C., Butler, W. T., et al. (2005). Spatially and temporally controlled biomineralization is facilitated by interaction between self-assembled dentin matrix protein 1 and calcium phosphate nuclei in solution. Biochemistry 44, 16140–16148. doi: 10.1021/bi051045l

CrossRef Full Text | Google Scholar

Hodge, A. J., and Schmitt, F. O. (1960). The charge profile of the tropocollagen macromolecule and the packing arrangement in native-type collagen fibrils. Proc. Natl. Acad. Sci. U.S.A. 46, 186–197. doi: 10.1073/pnas.46.2.186

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoyer-Kuhn, H., Semler, O., Schoenau, E., Roschger, P., Klaushofer, K., and Rauch, F. (2013). Hyperosteoidosis and hypermineralization in the same bone: bone tissue analyses in a boy with a homozygous BMP1 mutation. Calcif. Tissue Int. 93, 565–570. doi: 10.1007/s00223-013-9799-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunter, G. K., and Goldberg, H. A. (1993). Nucleation of hydroxyapatite by bone sialoprotein. Proc. Natl. Acad. Sci. U.S.A. 90, 8562–8565. doi: 10.1073/pnas.90.18.8562

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunter, G. K., Hauschka, P. V., Poole, A. R., Rosenberg, L. C., and Goldberg, H. A. (1996). Nucleation and inhibition of hydroxyapatite formation by mineralized tissue proteins. Biochem. J. 317(Pt 1), 59–64.

PubMed Abstract

Jahnen-Dechent, W., Schäfer, C., Ketteler, M., and McKee, M. D. (2008). Mineral chaperones: a role for fetuin-A and osteopontin in the inhibition and regression of pathologic calcification. J. Mol. Med. 86, 379–389. doi: 10.1007/s00109-007-0294-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaartinen, M. T., El-Maadawy, S., Räsänen, N. H., and McKee, M. D. (2002). Tissue transglutaminase and its substrates in bone. J. Bone Miner. Res. 17, 2161–2173. doi: 10.1359/jbmr.2002.17.12.2161

PubMed Abstract | CrossRef Full Text | Google Scholar

Knott, L., and Bailey, A. J. (1998). Collagen cross-links in mineralizing tissues: a review of their chemistry, function, and clinical relevance. Bone 22, 181–187. doi: 10.1016/S8756-3282(97)00279-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindahl, K., Barnes, A. M., Fratzl-Zelman, N., Whyte, M. P., Hefferan, T. E., Makareeva, E., et al. (2011). COL1 C-propeptide cleavage site mutations cause high bone mass osteogenesis imperfecta. Hum. Mutat. 32, 598–609. doi: 10.1002/humu.21475

PubMed Abstract | CrossRef Full Text | Google Scholar

Marini, J. C., Reich, A., and Smith, S. M. (2014). Osteogenesis imperfecta due to mutations in non-collagenous genes: lessons in the biology of bone formation. Curr. Opin. Pediatr. 26, 500–507. doi: 10.1097/MOP.0000000000000117

PubMed Abstract | CrossRef Full Text | Google Scholar

Millán, J. L. (2013). The role of phosphatases in the initiation of skeletal mineralization. Calcif. Tissue Int. 93, 299–306. doi: 10.1007/s00223-012-9672-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Morello, R., Bertin, T. K., Chen, Y., Hicks, J., Tonachini, L., Monticone, M., et al. (2006). CRTAP is required for prolyl 3-hydroxylation and mutations cause recessive osteogenesis imperfecta. Cell 127, 291–304. doi: 10.1016/j.cell.2006.08.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, H. A., Turner, A. G., and Anderson, P. H. (2012). Vitamin-D regulation of bone mineralization and remodelling during growth. Front. Biosci. (Elite. Ed). 4, 677–689. doi: 10.2741/E409

PubMed Abstract | CrossRef Full Text | Google Scholar

Murshed, M., and McKee, M. D. (2010). Molecular determinants of extracellular matrix mineralization in bone and blood vessels. Curr. Opin. Nephrol. Hypertens. 19, 359–365. doi: 10.1097/MNH.0b013e3283393a2b

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolov, S., and Raabe, D. (2008). Hierarchical modeling of the elastic properties of bone at submicron scales: the role of extrafibrillar mineralization. Biophys. J. 94, 4220–4232. doi: 10.1529/biophysj.107.125567

PubMed Abstract | CrossRef Full Text | Google Scholar

Niño-Barrera, J. L., Gutiérrez, M. L., and Garzón-Alvarado, D. A. (2013). A theoretical model of dentinogenesis: dentin and dentinal tubule formation. Comput. Methods Programs Biomed. 112, 219–227. doi: 10.1016/j.cmpb.2013.06.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Nociti, F. H. Jr., Foster, B. L., Tran, A. B., Dunn, D., Presland, R. B., Wang, L., et al. (2014). Vitamin D represses dentin matrix protein 1 in cementoblasts and osteocytes. J. Dent. Res. 93, 148–154. doi: 10.1177/0022034513516344

PubMed Abstract | CrossRef Full Text | Google Scholar

Rabelink, N. M., Westgeest, H. M., Bravenboer, N., Jacobs, M. A., and Lips, P. (2011). Bone pain and extremely low bone mineral density due to severe vitamin D deficiency in celiac disease. Arch. Osteoporos. 6, 209–213. doi: 10.1007/s11657-011-0059-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Rauch, F. (2006). Watching bone cells at work: what we can see from bone biopsies. Pediatr. Nephrol. 21, 457–462. doi: 10.1007/s00467-006-0025-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Rauch, F., Travers, R., Parfitt, A. M., and Glorieux, F. H. (2000). Static and dynamic bone histomorphometry in children with osteogenesis imperfecta. Bone 26, 581–589. doi: 10.1016/S8756-3282(00)00269-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Roschger, P., Fratzl-Zelman, N., Misof, B. M., Glorieux, F. H., Klaushofer, K., and Rauch, F. (2008a). Evidence that abnormal high bone mineralization in growing children with osteogenesis imperfecta is not associated with specific collagen mutations. Calcif. Tissue Int. 82, 263–270. doi: 10.1007/s00223-008-9113-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Roschger, P., Gupta, H. S., Berzlanovich, A., Ittner, G., Dempster, D. W., Fratzl, P., et al. (2003). Constant mineralization density distribution in cancellous human bone. Bone 32, 316–323. doi: 10.1016/S8756-3282(02)00973-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Roschger, P., Paschalis, E. P., Fratzl, P., and Klaushofer, K. (2008b). Bone mineralization density distribution in health and disease. Bone 42, 456–466. doi: 10.1016/j.bone.2007.10.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Roughley, P. J., Rauch, F., and Glorieux, F. H. (2003). Osteogenesis imperfecta–clinical and molecular diversity. Eur. Cell Mater. 5, 41–47. discussion: 7.

PubMed Abstract | Google Scholar

Rowe, P. S., Kumagai, Y., Gutierrez, G., Garrett, I. R., Blacher, R., Rosen, D., et al. (2004). MEPE has the properties of an osteoblastic phosphatonin and minhibin. Bone 34, 303–319. doi: 10.1016/j.bone.2003.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruffoni, D., Fratzl, P., Roschger, P., Klaushofer, K., and Weinkamer, R. (2007). The bone mineralization density distribution as a fingerprint of the mineralization process. Bone 40, 1308–1319. doi: 10.1016/j.bone.2007.01.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimada, T., Kakitani, M., Yamazaki, Y., Hasegawa, H., Takeuchi, Y., Fujita, T., et al. (2004). Targeted ablation of Fgf23 demonstrates an essential physiological role of FGF23 in phosphate and vitamin D metabolism. J. Clin. Invest. 113, 561–568. doi: 10.1172/JCI200419081

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinhaus, H. (1999). Mathematical Snapshots, 3rd Edn. New York, NY: Dover.

Google Scholar

Takeda, E., Yamamoto, H., Taketani, Y., and Miyamoto, K. (1997). Vitamin D-dependent rickets type I and type II. Acta Paediatr. Jpn. 39, 508–513. doi: 10.1111/j.1442-200X.1997.tb03629.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Valli, M., Barnes, A. M., Gallanti, A., Cabral, W. A., Viglio, S., Weis, M. A., et al. (2012). Deficiency of CRTAP in non-lethal recessive osteogenesis imperfecta reduces collagen deposition into matrix. Clin. Genet. 82, 453–459. doi: 10.1111/j.1399-0004.2011.01794.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinstock, M., and Leblond, C. P. (1973). Radioautographic visualization of the deposition of a phosphoprotein at the mineralization front in the dentin of the rat incisor. J. Cell Biol. 56, 838–845. doi: 10.1083/jcb.56.3.838

PubMed Abstract | CrossRef Full Text | Google Scholar