Simulation of the African ITCZ during austral summer seasons and ENSO phases: application of an RCM derived from stretched grid ESM

Introduction: Climate predictability across timescales in a changing climate presents a unique opportunity and challenges for state-of-the-art climate models. The use of regional climate models (RCMs) forced with interactively coupled Earth System Models (ESMs) for the sub-seasonal, seasonal, and decadal predictions is an actively growing research area.

Methods: The study explores a stretched-grid RCM constrained with an ESM which integrates a climate change signature. Spectral relaxation paradigm is applied to limit the climate drift within the range of the multi-model sea-surface temperature (SST) and sea-ice concentration (SIC) variability. The model retroactive ensemble simulations for November initialization are evaluated on the seasonal migration of the ITCZ during El-Niño and La-Niña phases, exploring both the spatial and zonal positions. The model is also evaluated on the ITCZ process’ characteristics that include the Hadley cell (HC), stream function and the subtropical jet stream (STJ) using quantitative methods.

Results: The RCM and the driving ESM demonstrate skillful performance in identifying the seasonal trajectory of both the spatial and zonal migration of the ITCZ during El-Niño and La-Niña. Moreover, the RCM also demonstrates a good skill in determining both the descending edge of the HC and the STJ with the highest mean percentage error of 16.3 and 7.5% for the HC and STJ latitudes, respectively.

Conclusions: The November initialization of the RCM skillfully simulates the seasonal migration of the ITCZ (and related characteristics) aligned to the observations and reanalysis datasets. Notwithstanding, the RCM manifests a tendency of more dynamic error growth relative to its driving ESM as the lead time increases. Furthermore, the RCM is also out of phase with a southerly shift of the stream function compared to the 500 hPa reanalysis stream function. The modeling framework offers process oriented and teleconnection studies. It also provides great potential for climate applications with suitable bias corrections techniques, albeit the source and mechanism of its dynamic error growth deserve further investigation.

1 Introduction

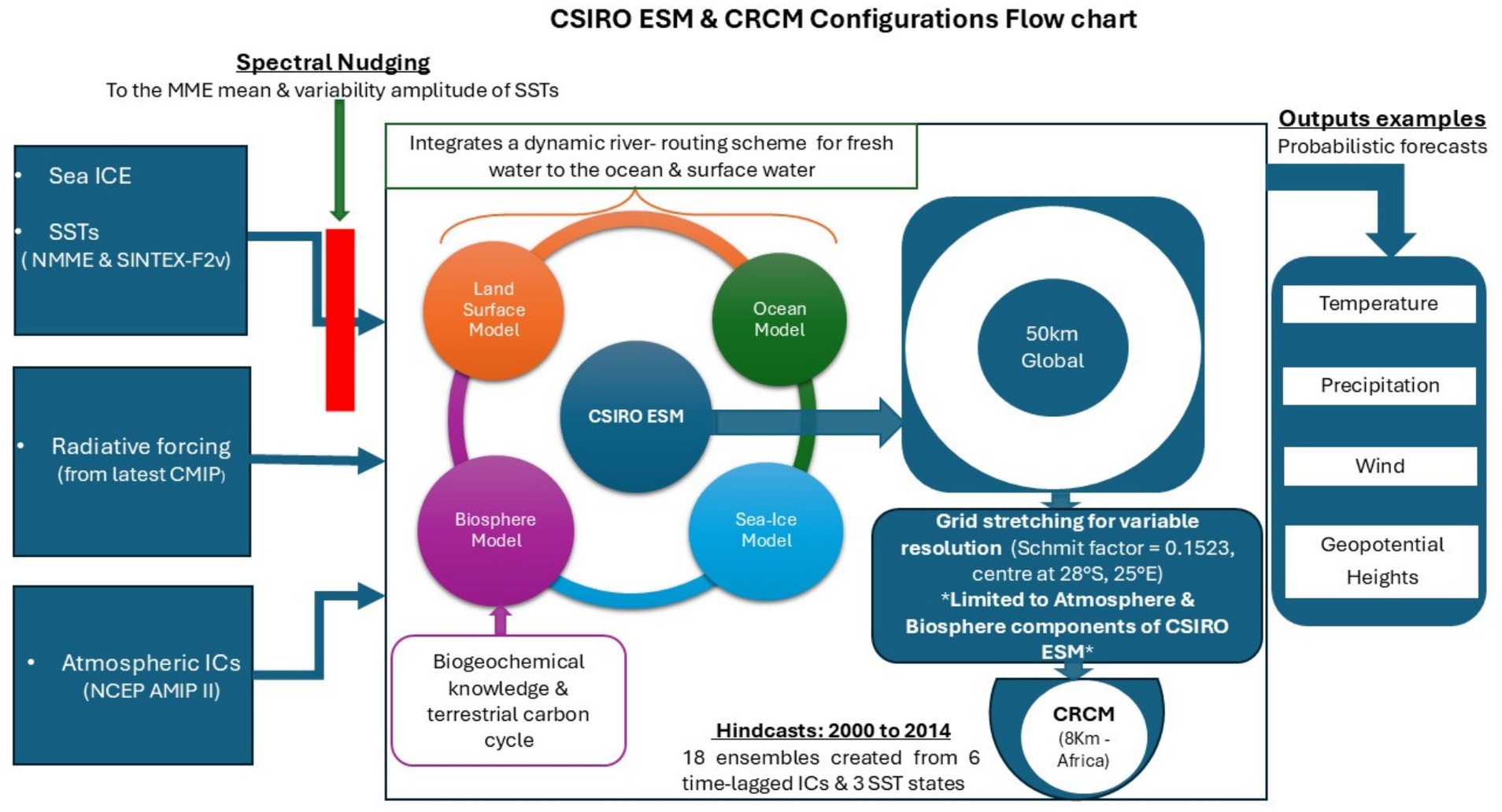
Climate variability in a changing climate heavily affects the economics and livelihoods in Africa and other parts of the world. The growing interest in scientific, operational and application communities for skillful predictions on sub-seasonal to interdecadal timescales presents unique opportunities and challenges for state-of-the-art climate models (Merryfield et al., 2020). On the seasonal time scale, climate prediction provides invaluable information and foreknowledge regarding the anomalous shifts of various meteorological fields and extreme events at several months lead time. These shifts depend on the various interactions between the atmosphere, slow variations of the oceans, and land surface which can be captured through the coupled earth system model (ESM) simulations (Engelbrecht et al., 2011). However, there has been a notable need for fully coupled regional ESM as mentioned by Giorgi (2019) alluding that one of the main challenges of running the coupled regional ESM is the computational cost even though it leads to advances in our understanding of the effects of climate change on the regional scale, amongst other benefits. But, applying the stretched grid on the global ESM provides a relatively low computational cost of running the regional ESM (Weber et al., 2023) with the benefit of having the high spatial resolution model outputs over the chosen grid stretching area whilst maintaining coarse spatial resolution elsewhere. Furthermore, this stretched grid provides advantageous consistency between the global and regional grids (Fox-Rabinovitz et al., 2006), enhancing their interactions without any need for lateral boundary conditions like is commonly done with the nested regional models.

The use of ESMs in southern Africa for seasonal prediction (specifically in operational environment) is limited, to date, due to their enormous computational cost and complexity. Notwithstanding, this computationally expensive numerical study becomes possible with the exponential expansion of the Centre for High Performance Computing (CHPC) computational facility in South Africa. In addition, the study is motivated by the recent development and numerous improvements of the Commonwealth Scientific and Industrial Research Organization (CSIRO) Earth System Model (hereafter CSIRO ESM). The CSIRO ESM interactively couples the atmosphere (McGregor and Dix, 2008), biosphere (Kowalczyk et al., 2013), ocean (Thatcher et al., 2015), and cryosphere (Gordon et al., 2002; O’Farrell, 1998) models with the knowledge of anthropogenic and aerosol forcings, and a spectral nudging and stretching technique (Thatcher and McGregor, 2010). The latter also enables the model to act as a stretched-grid regional climate model (hereafter CRCM) constrained with numerically consistent CSIRO ESM integrations albeit limiting CRCM’s capability to the models of the atmosphere and biosphere when a variable resolution is employed. The aim of the study is, therefore, to perform process-oriented evaluation and comparison of the CRCM’s 8 km resolution over continental Africa simulations against observations (reanalysis) and its driving CSIRO ESM’s 50 km resolution global quasi-uniform integrations treated here as baseline skills, respectively. The extended climate simulations (140 yrs) of the CSIRO ESM with various forcing strategies in the context of Antarctic sea-ice and Southern Ocean surface temperature trends were reported in a separate study (Beraki et al., 2020). The typical dynamical downscaling, using limited area models for seasonal climate predictions, was first attempted locally by Kgatuke et al. (2008) and more recently by Ratnam et al. (2016).

One of the key drivers of seasonal climate predictability is the El-Niño Southern Oscillation (ENSO) which has an influence on the global climate anomalies (Ma et al., 2017; Yin et al., 2022). The predictability of the ENSO on a 6–12-month lead time directly translates to the predictability of rainfall over most parts of West Africa, Southern Africa (Goddard et al., 2001; Mpheshea et al., 2025), and East Africa (Camberlin and Philippon, 2002; MacLeod et al., 2021) where the ENSO signal is strongly correlated with rainfall. The predictability of the ENSO and its interaction with the Hadley cell (HC) presents an opportunity for rigorous process model evaluation and benchmarking studies at both climate change and seasonal prediction time scales (Mahlobo et al., 2024). In particular, it allows for a test of how models simulate the temporal evolution of force fluxes as well as the models’ ability to respond to atmospheric forcings such as the ENSO and feedback from the ocean to the atmosphere (Alexander, 1992). The skill and reliability of model experiments, on specific meteorological processes, could be assessed based on how the model performs in representing the process and its related characteristics along with its response to the ENSO signal.

Furthermore, the study extends the process evaluation by emphasizing the ITCZ’s associated features and their linkages. The ITCZ is known to be the area of tropical surface wind convergence that coincides with the intense precipitation (Byrne et al., 2018; Chen et al., 2008; Jafari and Lashkari, 2023; Kang et al., 2018; Krishnamurti et al., 2013; Liu et al., 2015; Scott, 2013; Zhang et al., 2021). It has been the subject of investigation over the years in which various studies have applied different methods such as precipitation (Adam et al., 2016b; Byrne and Schneider, 2016b; Schneider, 2014; Sultan and Janicot, 2000; Xian and Miller, 2008), net energy input (Byrne and Schneider, 2016a; Frierson and Hwang, 2012; Keshtgar et al., 2020; Schneider, 2014), moist static energy (Byrne and Schneider, 2016b; Magnusdottir and Wang, 2008), wind convergence (Philander et al., 1996), low-level relative vorticity (Magnusdottir and Wang, 2008), cloud cover (Lashkari and Jafari, 2021b), and the out-going long-wave radiation (Byrne et al., 2018; Gu and Zhang, 2002) method to identify its location. According to Lashkari and Jafari (2021a) and Scott (2013), any index that reflects the uniqueness, seasonal shift to summer hemisphere, linkages with other related phenomena and existence of a continuous line can be used to identify the position of the ITCZ.

The ITCZ process is chosen for this regional modeling study because its positioning, together with its north/south migration, form part of the most important processes to study and analyze for improvements in the climate modeling research (Chen et al., 2008; Russotto and Ackerman, 2017). The HC and the subtropical jet stream (STJ) are critical characteristics of the ITCZ which are used to study its strength, width and area (Byrne et al., 2018; Byrne and Schneider, 2016a, 2016b; Ceppi et al., 2013). Furthermore, the zonally averaged Hadley circulation is known to be interlinked with the position of the ITCZ through the atmospheric energy balance between the Northern and Southern hemispheres (Moreno-Chamarro et al., 2020). Therefore, investigations of the relationship between the ITCZ, HC and STJ, in relation to ENSO, are significant components of regional and global weather and climate studies (Manney et al., 2021), especially considering the future impacts of climate on the strength, width and area of the ITCZ. Furthermore, the representation of the spatio-temporal evolution of the ITCZ translates to the model performance in simulating precipitation (Nicholson, 2009). In Southern Africa, the ITCZ’s position is linked to Southern Africa’s rainfall variability (Quagraine et al., 2019; Vindel et al., 2020). Specifically, the recent study by Randriatsara et al. (2022) uncovered that the onset and ending of the Southern African’s seasonal rainfall are affected by the position of the ITCZ. The north/south migration boundaries of the ITCZ typically varies between 20°N and 8°S over the Indian ocean (65°E–95°E) and its adjacent land masses, like Africa, and is very well linked to the South Asian monsoon (Schneider, 2014) amongst other regional teleconnections.

This work also reflects the developments in seasonal prediction, from using the statistical and General Circulation Models (GCMs), in southern African seasonal precipitation (see Landman et al. (2001) and Bartman et al. (2003) for more details) to the exploration of possible seasonal forecast skill improvement from the multi-model perspective (Landman and Beraki, 2012), followed by the coupling of the ocean and atmosphere general circulation models (Beraki et al., 2014; Landman et al., 2012), and lastly, the exploration of the fully coupled ESM with multiple climate forcing (Beraki et al., 2020). We are herein building on the latter with a modeling paradigm that also involves a variable resolution of the coupled ESM forcing for seasonal prediction.

The remainder of the paper is organized as follows: section 2 provides details about the data and methodology; covering the model description and set-up, the observational/reanalysis datasets used for evaluation and the metrics used for model performance. Section 3 presents the results and their discussion while section 4 concludes the findings of this study.

2 Data and methodology

2.1 Model description and set-up

The CSIRO ESM interactively couples the Conformal-Cubic Atmospheric Model (CCAM; McGregor and Dix, 2008), dynamic ocean model (Thatcher et al., 2015), sea-ice model (Gordon et al., 2002; O’Farrell, 1998) and sophisticated new generation land-surface model referred to as the CSIRO Atmosphere Biosphere Land Exchange (CABLE; Kowalczyk et al., 2013). The model employs a common reversibly staggered grid (McGregor, 2005), eliminating the coupling overhead associated with message passing among model components. This approach makes the simulations computationally economical since it negates the need for interpolation in every model time step commonly applied in other coupled models to reconcile grid type and resolution differences. In addition, the CSIRO ESM includes a prognostic aerosol scheme due to Mitchell et al. (1995), applied consistently with the emission inventories and radiative forcing specifications of the latest Coupled Model Intercomparison Project (CMIP; Taylor et al., 2012). It also integrates a dynamic river routing scheme of Arora and Harrison (2007) which feeds fresh water to the ocean and surface water. The model furthermore incorporates biogeochemical knowledge and elements of the terrestrial carbon cycle.

The study uses 15 yrs. (2000–2014) retroactive ensemble simulations built as a function of atmospheric states and ocean nudging; each integration runs for 6 months in length. This model configuration offers a better description of uncertainties that may arise from the initial and boundary forcings. In this regard, the CSIRO ESM is nudged, at its surface, to the Multi-Model Ensemble (MME) mean and variablity amplitude of the SSTs using spectral nudging (Thatcher and McGregor, 2009, 2010) to minimize the potential climate drift (large and unrealistic departures between the RCM and its driving model/s’ fields) (Omrani et al., 2012). This is a necessary step, to contain CSIRO ESM’s generated SSTs drift which will affect the RCM outputs. The MME SST forcing is obtained from North America (NMME) through the IRI data library, University of Pretoria Statistical Model (Landman et al., 2014), and SINTEX-F2v. of Japan Agency for Marine-Earth Science and Technology (JAMSTEC; Doi et al., 2016). The 18 CRCM ensemble members for hindcasts are created from the six scaled time-lagged initial conditions (ICs) in conjunction with the three SST states. The atmospheric ICs are acquired from the NCEP (National Centers for Environmental Prediction), Department of Energy (DOE) Atmospheric Model Intercomparison Project (AMIP) II Reanalysis (R2) data set (Kanamitsu et al., 2002). Each of these time-lagged perturbations are prescribed with the time varying CO₂ and Ozone boundary conditions.

In this experiment, the CSIRO ESM is run at C192 quasi-uniform (approximately about 50 km) global horizontal resolution and 25 vertical sigma layers. With a self-constraining stretched-grid paradigm, the CSIRO ESM runs, further, constrain the C192 variable spatial resolution of the same model by applying a Schmidt factor of 0.1523, centered over southern Africa (28°S, 25°E). This yields about 8 km finer horizontal resolution (CRCM) over continental Africa whilst maintaining coarse resolution elsewhere. The use of high-resolution (50 km) coupled forcing is found to be essential to maintain numerical stability and achieve balanced simulations of CRCM consistent with the driving CSIRO ESM. More description of CSIRO ESM can be found in Beraki et al. (2020) which elucidated the atmosphere–ocean-sea-ice interactions in response to different climate forcings and how these interactions affect the Southern Hemisphere’s circulation variability. Furthermore, CRCM is currently being experimentally used for seasonal prediction and its applications in renewable energy and precision Agriculture in South Africa. This study is the first effort to cover the process approach evaluation of this model set-up for seasonal timescales. Noteworthy, we are not aware of other initiatives that use similar modeling paradigm reported here for seasonal prediction over the African continent which has revealed a great potential for climate applications in an operational environment.

The evaluation is done on several months lead time hindcasts, generated from the November initialization. To minimize the loss of skill with the lead time (Brum and Schwanenberg, 2022), the seasons under consideration consist of the rolling 3 months seasons beginning with November. November was chosen for initialization because the main Southern Africa’s rainy season starts in November and ends in February, with a tendency of extending up to April (Macron et al., 2014; Pohl et al., 2009, 2018; Ullah et al., 2023; Vigaud et al., 2012). Madagascar, for example, experiences the wettest period between November and April (Randriatsara et al., 2022). Over Southern Africa, March to May (autumn) and September to November (spring) are the transitional seasons (Wang et al., 2021) that are not used in this study. November initialization is, furthermore, explored because it is aligned to Mamalakis et al. (2021) study of the ITCZ using a suite of Coupled Model Intercomparison Project, version 6 (CMIP6) global models (Eyring et al., 2016). The extreme North/South position of the ITCZ corresponds to peak austral winter/summer seasons (Zhang et al., 2021) respectively. These extreme positions provide the necessary seasonal boundary positions of the ITCZ over the African tropics and forms part of the reasons why summer (November) initialization is evaluated to identify the extreme southern position of the ITCZ. Figure 1 provides the schematic summary of the CSIRO ESM and CRCM model set-up configuration and interactions as applied in this research.

Figure 1

Figure 1. Schematic figure of the CSIRO ESM and CRCM model configurations.

2.2 Gridded observation and reanalysis datasets

The standard evaluation procedure is applied; the gridded observational/reanalysis datasets and model (CSIRO ESM and CRCM) hindcasts, for the period 2000–2014, were used to identify the seasonal ITCZ position and statistically compared the resulting positions. According to MacLachlan et al. (2015), a 14 years hindcasts is long enough to develop model climatology. A precipitation-based centroid method by Adam et al. (2016a) was used to identify the ITCZ position during El-Niño and La-Niña events. This method has recently been applied by Mischell and Lee (2022) to study the relationship between zonal ITCZ position and meridional temperature contrast. The maximum precipitation method was used to identify the ITCZ’s climatological position by identifying the latitude of maximum precipitation along each longitude as applied by Liu et al. (2020).

The observational datasets used include the gridded (0.5° × 0.5° grid) Climate Research Unit gridded Time Series version 4 (CRU TS v4; Harris et al., 2020) rainfall data and the Climate Hazards Group Infrared Precipitation with Stations version 2 (CHIRPS2.0) data at (0.05° × 0.05°) grid resolution (Funk et al., 2015). The (0.25° × 0.25°) European Centre for Medium-Range Weather Forecasts (ECMWF) fifth generation reanalysis (ERA5; Hersbach et al., 2020) dataset was also used.

CHIRPS, CRU and ERA5 datasets were used due to their value in model evaluation and interoperability as reflected by the past studies (Endris et al., 2021; Hassler and Lauer, 2021; Yimer et al., 2022). Li et al. (2021), for instance, applied them in their study on the ability of the CMIP6 models to simulate temperature and precipitation extremes. Furthermore, ERA5 dataset strongly correlates with CHIRPS & CRU (Gleixner et al., 2020) and it is also the best performing re-analysis data for statistical downscaling using analogue methods for meteorological variables (Horton, 2022). CHIRPS dataset has been proven by Burton et al. (2018) to be the best performing dataset for tropical Africa related studies. For fair comparability, we re-sampled higher resolution CHIRPS, ERA5, and Model datasets to similar (and coarser) resolution as CRU (0.5° × 0.5°) by applying the “samplegrid” operator from the Climate Data Operators (CDOs) (Schulzweida, 2023). The application of this operator does not require any interpolation schemes.

2.3 Model skill and reliability assessment

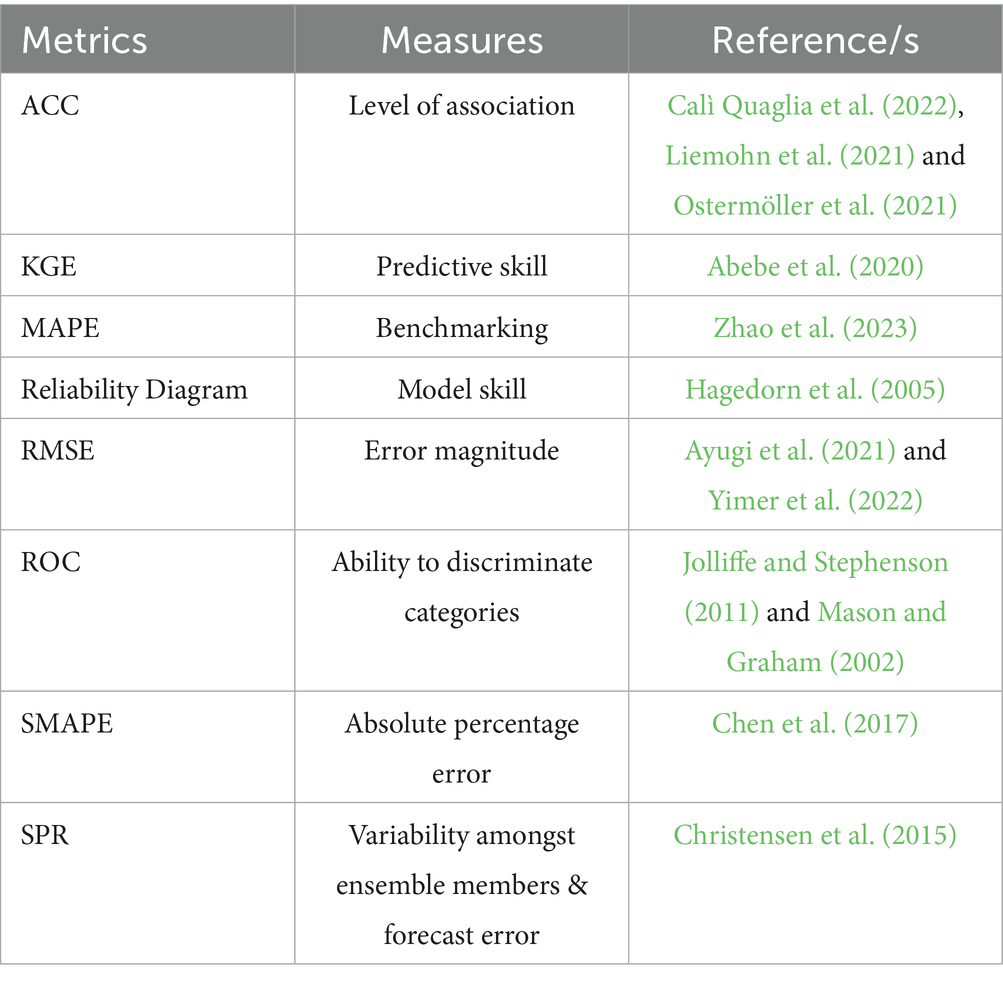
The study evaluates the model’s skill and reliability on its seasonal ITCZ simulation, including how the model performs in representing characteristics of the ITCZ such as the edge of the HC, the STJ and the stream function. To this effect, probabilistic and deterministic skill assessment metrics (Table 1) were used to assess the difference between forecasts and the reference precipitation data over the period (2000–2014). We assume that a forecast by each of the 18 ensemble members of CRCM is equally probable. A conversion of the ensemble forecast to probabilistic forecast allows use of the probabilistic validation measures such as the relative operating characteristics (ROC) curve and the Spread-error Ratio (SPR). ROC is applied to assess CRCM’s ability to discriminate amongst the above normal (AN), near normal (NN), and below normal (BN) seasonal precipitation forecasting categories. In this case AN and BN represent the upper and lower-tercile forecasts, respectively. It portrays the degree of correct probabilistic forecast discrimination (Jolliffe and Stephenson, 2011; Mason and Graham, 2002). Correct discrimination is quantified by the metric even if the forecast has a bias or calibration problems. The reliability diagram, on the other hand, evaluates the CRCM’s skill. It is used to reflect how well the forecast probabilities correspond to observation’s relative frequencies (Hagedorn et al., 2005) which is indicative of whether CRCM has over-confidence, under-confidence, conditional bias, or perfect reliability. Both the reliability diagram and ROC curves were calculated based on the CRCM’s grid-point predictions. The SPR metric is specifically chosen because it allows an assessment of variability among ensemble members and the forecast error (Wheatcroft, 2019). The benefits of SPR include its sensitivity to the reliability of a forecast without applying the event categories (Christensen et al., 2015) applied in ROC metric.

Table 1

Table 1. Summary of the evaluation metrics.

Deterministic performance metrics are also applied to quantify the correspondence between forecasts and reference data anomalies. The deterministic metrics used for evaluation include: the anomaly correlation coefficient (ACC), also known as a measure of association (Calì Quaglia et al., 2022; Liemohn et al., 2021; Ostermöller et al., 2021); the mean bias (MB, Chang et al., 2018; Liemohn et al., 2021); the root mean square error (RMSE) (Ayugi et al., 2021; Yimer et al., 2022). The Kling Gupta efficiency (KGE) introduced by Gupta et al. (2009) and later modified by Kling et al. (2012) allows an assessment of correlations between simulated and observed values, the prediction bias degree, and the variability in the modeled outputs. For example, it has been used to assess model performance in representing temporal dynamics of dry and wet bias, and dispersion (Abebe et al., 2020). The KGE values range from −0.4 to a maximum of unity (perfect skill) which reflects the model’s predictive skill in comparison to climatology (Abebe et al., 2020; Kling et al., 2012; Knoben et al., 2019). These KGE characteristics are a fit for purpose measure on whether the model can be used to explore the teleconnections between the seasonal ITCZ position and other rain bearing systems over southern Africa.

Further to the evaluation metrics explored, we have also tested CRCM’s performance on some of the main characteristics of the ITCZ. The evaluated characteristics include the edge of the HC, the multi-level (1,000 hPa to 100 hPa) stream function (Ψ) and the STJ. The identification of the HC, Ψ, and STJ was done following the python-based tropical width diagnostics software (PyTropD) as described in Adam et al. (2018), which can be consulted for further details on the relevant equations used and estimations made in identifying the edge of the HC, the STJ and mass-stream function. PyTropD has recently and successfully been applied by Menzel et al. (2024) in their study of the disconnect between the HC and STJ, and Gibson et al. (2024) for their study involving the winter precipitation change and how it relates to the shifts of the HC and the eddy driven jet. The mean absolute percentage error (MAPE) and symmetric mean absolute percentage error (SMAPE) between ERA5 reanalysis dataset and the CRCM’s outputs were calculated following Zhao et al. (2023) and Chen et al. (2017) respectively. MAPE is used here because it is part of the minimum standard metrics of the benchmarking framework as detailed by Isphording et al. (2024).

2.4 Selection of ENSO years

The seasonal Oceanic Niño Index (ONI) was used to identify the El-Niño and La-Niña phases. The ONI is based on 3 months running mean of SST anomalies in the Niño 3.4 Ocean region as obtained from the Extended Reconstructed SST version5 (ERSSTv5) (Huang et al., 2017). The El-Niño/La-Niña year as applied in this research, covers from November of the current calendar year (y₀) to April of the following calendar year (y₀ + 1). Therefore, NDJ (November–January) season consists of November and December from y₀ and January from y₀ + 1. DJF (December–February) consists of December from y₀ with January and February from y₀ + 1. JFM (January–March) and FMA (February–April) are from year y₀ + 1. Furthermore, a year is confirmed to be an El-Niño/La-Niña year provided the phase remains active in three of the four (NDJ, DJF, JFM, and FMA) rolling seasons. CSIRO ESM & CRCM are initialized in November and run for 6 months, which means November runs from y₀ provide predictions until April in y₀ + 1. Therefore, the active El-Niño years between 2000 and 2014 are 2002/03, 2004/05, 2009/10, and 2014/15 while the active La-Niña years are 2000/01, 2005/06, 2007/08, 2008/09, 2010/11, and 2011/12.

3 Results and discussion

According to WMO (2018), following definitions in Murphy (1993), a good forecast is the one that reflects consistency, quality and value. Therefore, KGE and its components address the consistency and skill of performance by CRCM while quality and reliability of the forecasts generated is addressed through the SPR. SPR is used to test the reliability (Monhart et al., 2019) of the forecasts issued over and above the reliability diagram. The model’s ability to discriminate between distinct categories of seasonal forecasts is done, through the ROC curve in combination with the KGE score, to provide a robust evaluation of the model’s skill.

Due to the differences in how the models (and ERA5) treat complex topography, CSIRO ESM and CRCM are evaluated for their performance only over the 10°E–40°E zonal area. This is because of multiple reasons including; the simplified topography in models, CHIRPS and CRU are land based (Funk et al., 2015; Harris et al., 2020), and very limited observational data is available over the mountainous topography for assimilation into CHIRPS (Arregocés et al., 2023; López-Bermeo et al., 2022) and CRU, resulting in poor performance over coastal and mountainous regions. The 10°E–40°E area avoids the oceanic area to the west (east) of 10°E (40°E) and the complex mountainous region with limited observations to the east of 40°E.

The ITCZ position to the west of 10°E (for both CHIRPS and CRU) aligns to the coastline because precipitation is higher over the coast and decreases going inland and into the ocean (Curtis, 2019; Ogino et al., 2016). This alignment to the coast is also because both CHIRPS and CRU datasets used in this work are land-based observations (no ocean observations) so the maximum precipitation will occur over the coastal area. This is the case whether maximum precipitation (Figure 2b) method or centroid method (Figures 3a–d) is used to identify the position of the ITCZ. The ITCZ position to the east of 40°E, on the other hand, reflects the precipitation enhanced by the complex topography interacting with the Arabian subtropical high pressure (ASHP) leading to the ITCZ refraction (Jafari and Lashkari, 2023; Lashkari and Jafari, 2021b, 2021a).

Figure 2

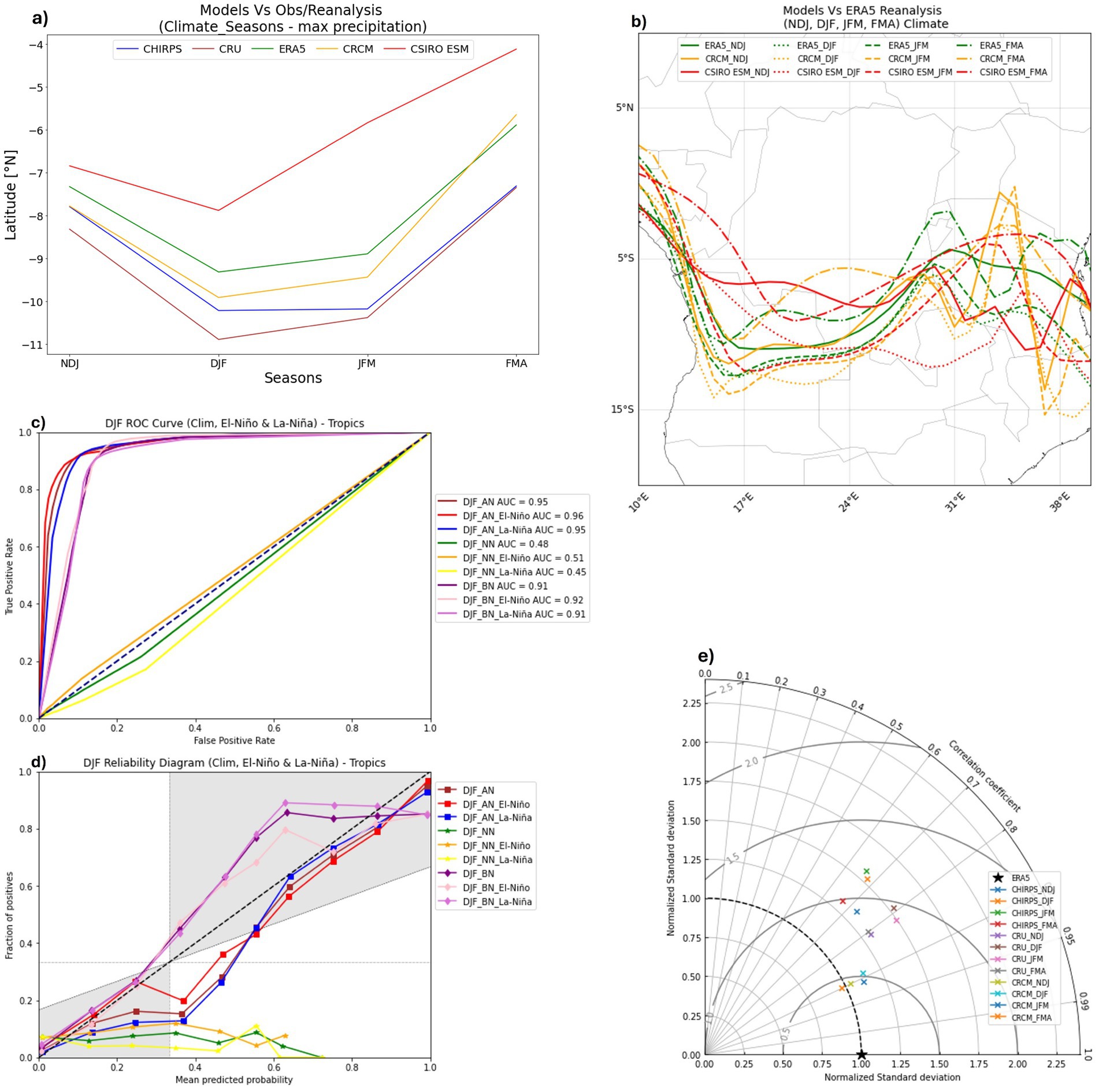
Figure 2. The zonal and spatial position of the ITCZ for: NDJ, DJF, JFM, and FMA represented by panels (a,b) respectively. CRCM’s ROC curve and reliability diagram over 10°–40°E and 20°N/S tropical area is presented by panels (c,d). The Taylor diagram for CRCM comparability with the different observational and reanalysis datasets, normalized by ERA5, is presented by panel (e).

Figure 3

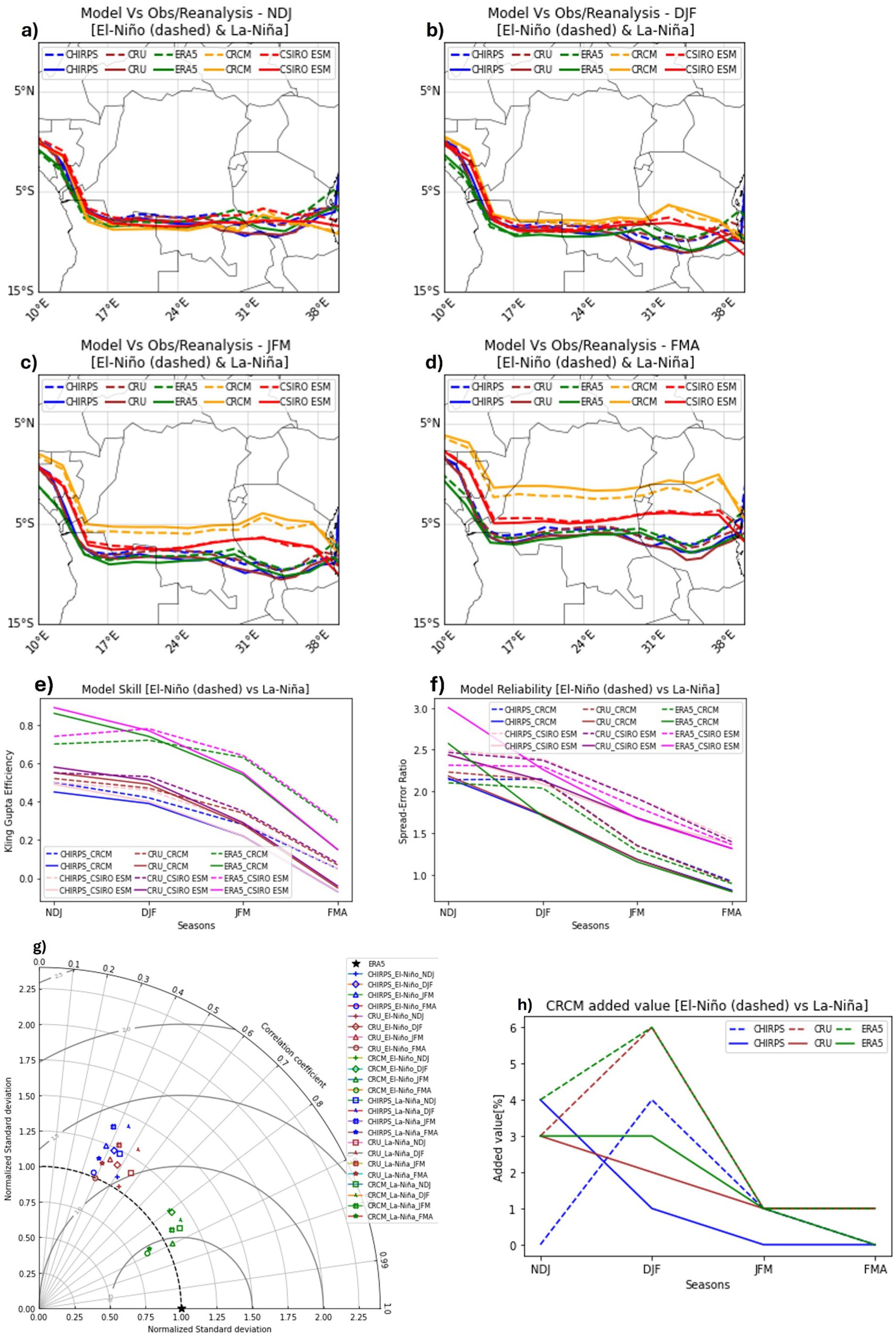
Figure 3. The representation of the spatial seasonal position of the ITCZ during El-Niño and La-Niña for NDJ, DJF, JFM, FMA seasons (a–d, respectively). The model skill and reliability (using KGE and SPR respectively) on the zonal (10°–40°E) position of the ITCZ during El-Niño/La-Niña seasons are presented by panels (e,f). The Taylor diagram in panel (g) shows how the model compares with the observations/reanalysis datasets for NDJ, DJF, JFM, and FMA seasons during El-Niño/La-Niña. Finally, panel (h) is a presentation of the added value (in percentage) by CRCM.

To quantify the benefits of CRCM dynamical downscaling from the CSIRO ESM, we first do a comparison of the CSIRO ESM and CRCM performance against the observations/reanalysis dataset for benchmarking and assessment of value addition by CRCM. The expectation is that CRCM should at least perform as best as CSIRO ESM (Isphording et al., 2024) with a provision of more regional details. The comparison between CSIRO ESM and CRCM is done through sections 3.1 and 3.2. In section 3.3, CRCM is independently evaluated on its performance on the ITCZ process’s characteristics. The benchmarking presentations style in Figures 2a,b, and Figures 3a–f are similar style to Figure 3 in Isphording et al. (2024).

3.1 Climatology performance

The figures and discussions in this section address CSIRO ESM and CRCM climatological performance on the zonal and spatial position of the ITCZ over 10–40°E longitudes using the maximum precipitation method and the question about CRCM’s ability to discriminate between above-normal (AN); near-normal (NN); and below-normal (BN) seasonal forecasting categories. The ability of CRCM to discriminate amongst the three categories is hereafter used as the basic proof of its capability to identify the ITCZ position through precipitation-based methods. The level of reliability of CRCM outputs is also discussed. All these are done for CRCM’s full climatology period (2000–2014), during the El-Niño, and La-Niña events between 2000 and 2014.

From Figures 2a,b, the CSIRO ESM and CRCM track the seasonally migrating climatological position of the ITCZ in line with both the observations (Figures 4a,b for spatial migration) and reanalysis data albeit CRCM reflecting a better performance than the CSIRO ESM. The spatial spearman correlations (at 99% significance level) between CRCM and the observation/reanalysis dataset varied from 0.66 (between CRCM and CHIRPS during JFM) to 0.91 (between CRCM and ERA5 during JFM), clearly reflected in Figure 2e as well. Figure 2a shows the zonal performance of the CSIRO ESM and CRCM against CHIRPS, CRU and ERA5 datasets for the period from November to April. CSIRO ESM and CRCM simulations can track the zonal climatological seasonal pattern of the ITCZ relative to the three test datasets (CHIRPS, CRU and ERA5). This performance is aligned to the expectation of consistency in grid-points interactions (Fox-Rabinovitz et al., 2006) between the global and regional resolutions wherein more regional details can be extracted without performance deterioration. CRCM has a northerly bias against CHIRPS and CRU while CSIRO ESM has a northerly bias against all the compared datasets (CHIRPS, CRU, ERA5 and CRCM). CRCM specifically tracks better, both zonally and spatially, with the ERA5 data than with CRU and CHIRPS possibly because ERA5 data inherently applies the same primitive equations as the weather and climate models beyond the actual observations acquired through data assimilation. For the zonal seasonal flow pattern, the southern-most latitudinal position of the ITCZ occurs during the DJF season. This seasonal shift is similarly suggested by Lauer et al. (2018), albeit for a different region.

Figure 4

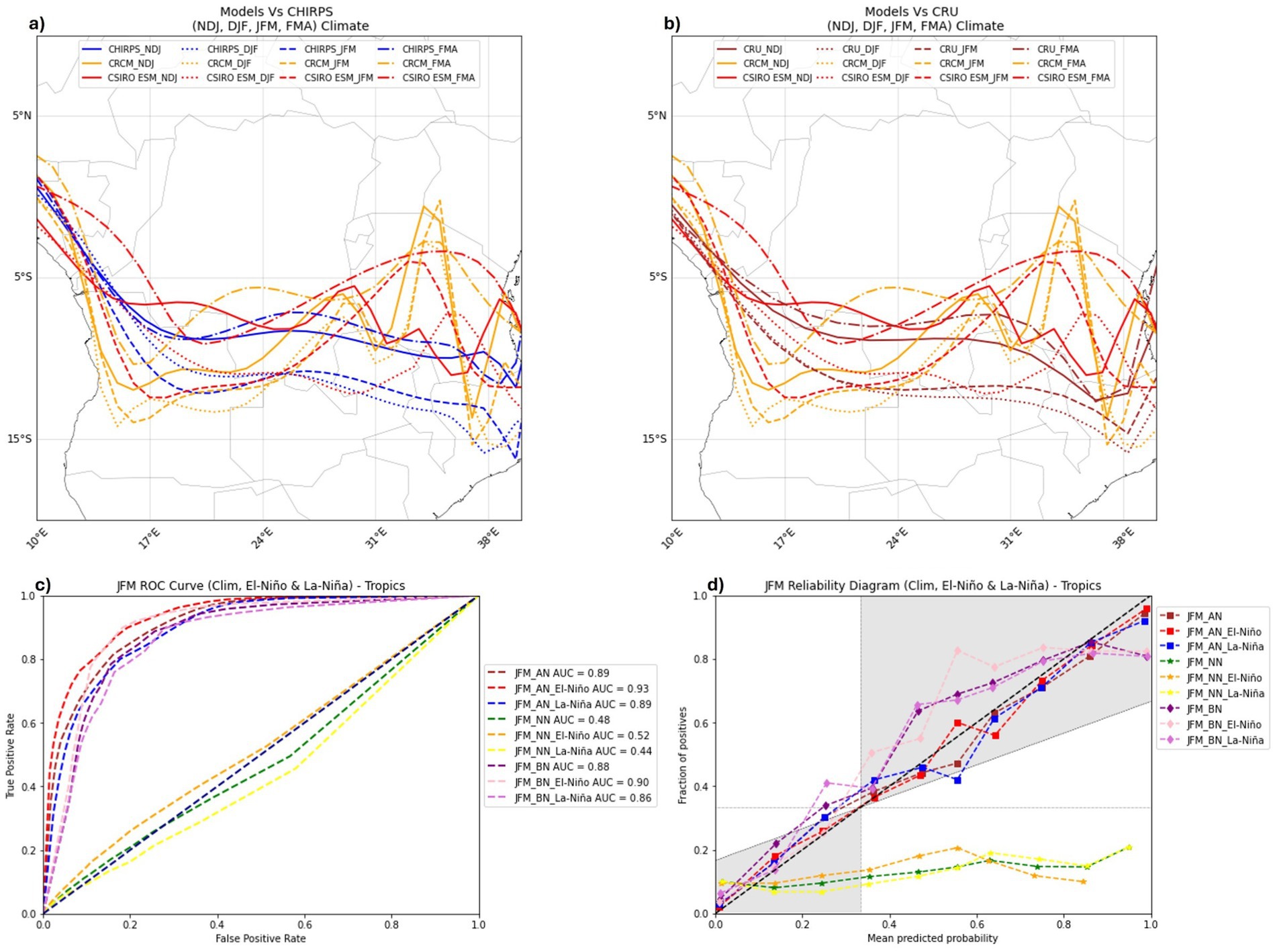
Figure 4. Climatological position of the seasonal ITCZ (NDJ, DJF, JFM, and FMA) based on the models (CSIRO ESM and CRCM) and CHIRPS (a), CRU (b) together with the JFM ROC curve (c) and Reliability diagram (d) CSIRO ESM.

The CRCM skill, assessed using the ROC curve against the CHIRPS dataset, found to be reasonable due to its comparable resolution to the CRCM, is shown in Figures 2, 4c. ROC is part of the metrics for evaluating climate model performance and it contributes toward the probability distribution metrics on benchmarking framework (Baker and Taylor, 2016). Figures 2, 4c shows the area under the curve (AUC) of between a minimum of 0.86 and a maximum 0.96 corresponding to JFM BN during La-Niña and DJF AN during El-Niño, respectively. These values indicate that CRCM can skillfully discriminate the AN and BN categories better than the NN (for which AUC ranges from 0.44 to 0.52) category. Furthermore, the seasonal forecast issued by CRCM is exceptionally reliable for the AN and BN categories while not reliable for the NN prediction (Figures 2, 4d). Considering that ITCZ is a high (intense) precipitation area and CRCM is skillfully reliable in high precipitation forecasting, it follows that CRCM is suitable for precipitation-based methods of identifying the ITCZ position. This capability to accurately represent high intensity precipitation events is an added value (Corney et al., 2013; Lindstedt et al., 2015) of running an ESM at a high resolution, an approach that is slightly modified by applying the stretched grid in this research. Furthermore, the reliability and ROC results imply that we can rely on the forecast for AN (even during El-Niño) or BN (during La-Niña) seasonal precipitation forecast for southern Africa which is known to experience mostly BN precipitation during El-Niño and AN precipitation during La-Niña (Guimarães Nobre et al., 2019; Lenssen et al., 2020).

A Taylor diagram compares several pairs of patterns: observations and model comparisons and tracking changes (in lead times) in model performance (Taylor, 2001). ERA5 was used as the reference dataset because of its resolution being between that of CHIRPS and CRU datasets and it has also been used to normalize CHIRPS, CRU, and CRCM standard deviations. Based on the Taylor diagram presented in Figure 2e, we note how strongly correlated ERA5, and CRCM predictions are (correlation coefficients that range from 0.89 to 0.91 at 99% confidence level); showing even similar standard deviations and root-mean square error values. On the other hand, slightly weaker correlations, higher standard deviations and higher root-mean square error values are observed for CHIRPS and CRU against CRCM predictions. In general, the Taylor diagram shows the weakening correlations between the observations/reanalysis with lead time and a high (between 1.0 and 1.6) but comparable normalized standard deviations amongst the datasets (CHIRPS, CRU, ERA5, and CRCM). The climatological error between CRCM and ERA5 is generally lower than 0.5° while it ranges from 0.75 to 1.2 between CRCM and CHIRPS/CRU. This indicates that CRCM is more aligned to ERA5 in both pattern recognition and the amplitude of variation.

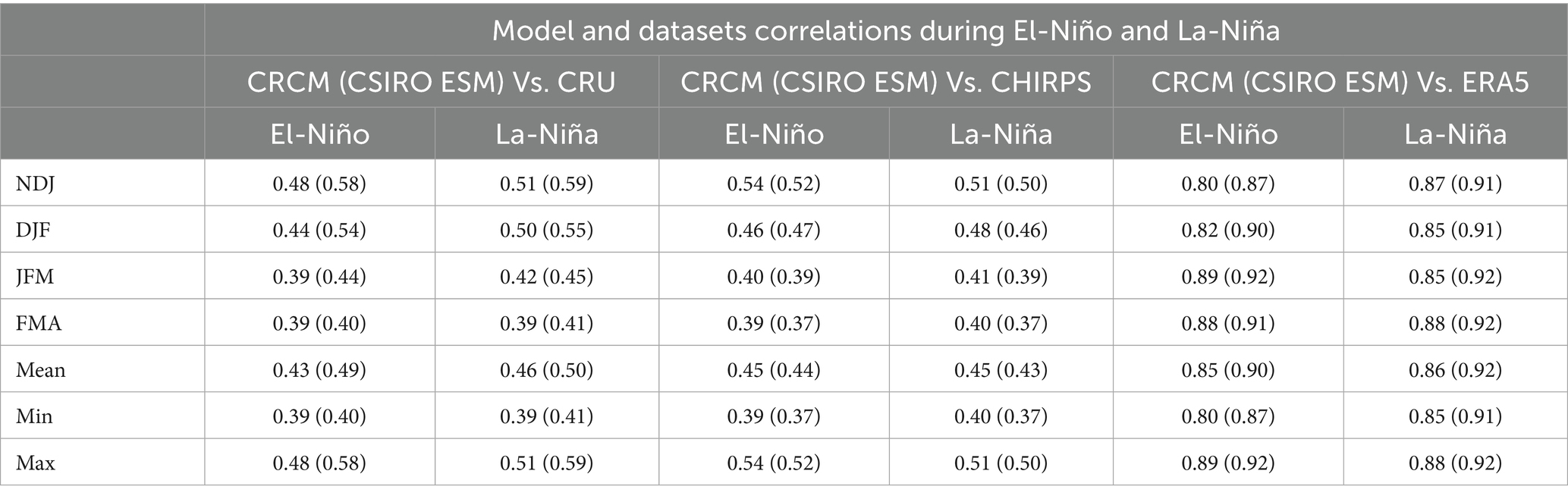
In terms of the observations/reanalysis datasets correlations, CHIRPS and CRU have a much higher correlation (>0.96) than CHIRPS correlated to ERA5, and CRU correlated to ERA5 (0.47–0.81 and 0.48–0.79 correlations, respectively), detailed correlations that cover both the El-Niño and La-Niña based correlations between CRCM (CSIRO ESM) and observations/reanalysis datasets are found in Table 2. Furthermore, this is reflected in the Taylor diagram (Figure 2e) where CHIRPS and CRU are packed together and separated from ERA5 datasets. These correlations are comparable to the CHIRPS correlated to CRU results found by Steinkopf and Engelbrecht (2022) for DJF when correlating CHIRPS, CRU, and ERA5 over the tropical (between 20°S and 20°N) Africa. The climatological normalized standard deviations amongst the observations/reanalysis and CRCM are all comparable throughout the seasons (maximum difference of <0.6) while the RMSE varies between 0.4 and 1.25°.

Table 2

Table 2. Correlations between CRCM (CSIRO ESM) and the observations/reanalysis datasets.

3.2 El-Niño and La-Niña performance

The analysis of the CSIRO ESM and CRCM performance over different rolling seasons (NDJ, DJF, JFM, and FMA) during the positive and negative phases of ENSO is shown in Figure 3. The centroid method was used for the identification of the spatial and zonal positions of the ITCZ.

CSIRO ESM and CRCM consistently track the seasonally migrating spatial position of the ITCZ in line with both the observations and reanalysis data during the El-Niño/La-Niña ENSO phases (Figures 3a–d). This tracking and CRCM’s performance on precipitation prediction (Figures 2, 4c,d) agrees with Nicholson (2009) on the consistency in model performance on precipitation and ITCZ position’s prediction. However, CRCM reflects a tendency of dynamic error growth relative to CSIRO ESM as the lead time increases (Figures 3c,d). This dynamic error growth could possibly be enhanced by the resolution at which CRCM is downscaled because it coincides with the grey zone (Lindstedt et al., 2015) for resolving deep convection like commonly happens along the ITCZ. The spatial spearman correlations between CRCM (CSIRO ESM) and individual observation/reanalysis dataset range from 0.39 (0.37) between CRCM (CSIRO ESM) and CHIRPS/CRU (CHIRPS) during FMA to 0.89 (0.92) between CRCM (CSIRO ESM) and ERA5 during JFM (JFM and FMA). These results (detailed in Table 2) show a marginally better spatial correlation between CSIRO ESM and CRU/ERA5 while comparable correlations exist between CRCM/CSIRO ESM and CHIRPS observations. This implies that CSIRO ESM performs better than CRCM against the low-resolution verifying datasets while both CSIRO ESM and CRCM perform equally well against the high-resolution observational verifying datasets.

CRCM (CSIRO ESM) skill (as measured by KGE and presented by Figure 3e) in predicting the seasonally changing position of the ITCZ during El-Niño varies between 0.05 for CHIRPS during FMA for both CSIRO ESM and CRCM and 0.72 (0.78) for ERA5 during DJF. On the other hand, the CRCM’s (CSIRO ESM) skill (KGE) in predicting the seasonally changing position of the ITCZ during La-Niña varies between a minimum of −0.07 (−0.07) for CHIRPS during FMA and a maximum of 0.86 (0.89) for ERA5 during NDJ. These values indicate that using CRCM (CSIRO ESM) to predict the spatial ITCZ position during El-Niño/La-Niña is, on average at 0.38 (0.39), which is greater than −0.4 and therefore implies that it is a far better performance than relying on the climatological response of the ITCZ position to the ENSO phases. This consistency of skill between CSIRO ESM and CRCM is aligned to the expectation in terms of the general performance between the RCM and its driving ESM as stated by Fox-Rabinovitz et al. (2006). Once again CSIRO ESM is skillfully better than CRCM against the low-resolution verifying datasets while they are equally skillful against high-resolution verifying datasets.

CRCM (CSIRO ESM) skill is with the level of reliability, measured by SPR and presented by Figure 3f, that varies between 0.89 (1.36) for ERA5 during FMA to 2.23 (2.50) for CRU (CHIRPS) during NDJ under the positive phase of ENSO while it varies between 0.80 (1.32) for ERA5 (ERA5/CRU) during FMA to 2.57 (3.01) for ERA5 during NDJ under the negative phase of ENSO. This indicates that, on average, CRCM (CSIRO ESM) gives a slightly better performance during La-Niña than it does during El-Niño even with an element of overconfidence (under dispersion) by CRCM. CRCM overconfidence also exists on the climatological seasonal position of the ITCZ (Figure 2d), especially for forecast probabilities of 40–90% for BN precipitation during the DJF and JFM.

Multiple studies, from as far back as the early 2000s (Landman et al., 2009) to as recent as the past 5 years (Scaife et al., 2019; Tapiador et al., 2020), have shown an interest in identifying the value added by the RCMs from the global circulation models (GCMs) and earth system models on the seasonal climate prediction scale. Some of these studies highlighted a need for the means to measure the added value, on the GCM/ESM, by the RCM. One such method used to assess the added value, as recommended by Gnitou et al. (2021), is by calculating the distance between the driving GCM/ESM and the corresponding RCM using any statistic. This method has also been used by Tamoffo et al. (2020) for process-based analysis of the added value making it suitable for application on the ITCZ process. Following Gnitou et al. (2021), we have chosen the KGE, a measure of the model skill, to assess the added value (AV) by CRCM (AV = KGE_{CSIRO ESM} minus KGE_CRCM) in identifying the position of the ITCZ. The added value by CRCM remains positive for all the seasons and up to as high as 4% (during La-Niña NDJ) and 6% (during El-Niño DJF) (Figure 3h). This shows a positive addition of value of up to 6% by CRCM from CSIRO ESM, indicating a great progress in African seasonal climate prediction using a dynamically downscaled ESM. This is even though some authors (Gnitou et al., 2021) would rather prefer a 10% and higher added value.

The Taylor diagram (Figure 3g) compares CHIRPS, CRU and ERA5 datasets to the CRCM predictions over the four rolling seasons (NDJ, DJF, JFM, FMA) to analyze the model performance. The ERA5 dataset was used as the reference dataset and normalizes the standard deviations of CHIRPS, CRU, and CRCM. The model’s fair track of the spatial ITCZ position is confirmed by the correlation coefficients that range from 0.39 to 0.89 at 99% confidence level. Furthermore, the Taylor diagram shows the weakening correlations between the observations/reanalysis with lead time except for CRCM against ERA5 where the correlation weakens into DJF but strengthens again in JFM and FMA. The standard deviations are comparable with Observation datasets showing lower standard deviations than CRCM in NDJ and DJF while ERA5 reanalysis shows lower standard deviation for all seasons except FMA (during El-Niño and La-Niña) wherein CRCM shows a lower standard deviation than ERA5 reanalysis. The RMSE is lower than 1.5° for all seasons and verifying datasets with the lowest RMSE occurring in FMA (CRCM during El-Niño and La-Niña) and JFM (CRCM during El-Niño) where it is less than 0.5°. These values, in comparison to Figure 2e, show that CRCM has a consistent performance between climatology and the ENSO phases. This CRCM performance on the ITCZ position reflects a very significant progress in regional dynamical climate modeling over southern Africa in terms of the onset and offset of seasonal precipitation which is linked to the position of the ITCZ (Randriatsara et al., 2022).

The observations/reanalysis datasets correlations during El-Niño show reasonably better association between CHIRPS and CRU (r ≥ 0.96) than CHIRPS-ERA5 & CRU-ERA5 correlations (0.47–0.81 and 0.48–0.79 respectively). These correlations are comparable to the CHIRPS-CRU and CRU-ERA5 correlations found by Steinkopf and Engelbrecht (2022) for DJF when correlating CHIRPS, CRU, and ERA5 over the tropical (between 20°S and 20°N) Africa.

The spatial spearman correlations between CRCM and individual observation/reanalysis dataset range between the lowest of 0.39 (CRCM and CRU during FMA) and highest of 0.88 (CRCM and ERA5 during FMA). CRCM diverges more than CSIRO ESM, with the lead time, from the observations/reanalysis (Figures 3a–d). This indicates the faster error growth by CRCM, in identifying the spatial ITCZ position, than CSIRO ESM further from the initialization time. With more focus on the flow pattern between CSIRO ESM/CRCM and observations/reanalysis datasets, it is evident that both CSIRO ESM and CRCM perform equally well in tracking the spatial ITCZ (Figures 3a–d) as also evidenced in the comparable correlations from Table 2. This agrees with the findings of Tapiador et al. (2020): it is now possible to run an ESM with a higher resolution and attain the same results as the RCM with an added advantage of avoiding most issues common with the RCMs.

3.3 HC, STJ, and stream function performance

This section presents the analysis of CRCM performance in detecting the regional edge of the HC, the regional STJ, and multi-level streamfunction at different lead times and ENSO phases. These characteristics form part of the teleconnections between the ITCZ (ascending edge of the HC, Faulk et al., 2017; Schwendike et al., 2014), descending edge of the HC and the STJ. Therefore, it is important to evaluate CRCM performance on these as part of the larger exploratory metrics (Pendergrass et al., 2020), especially considering the consistency of performance between the CSIRO ESM and CRCM as well as the skill and reliability of the CRCM on the position of the ITCZ.

The evaluation of CRCM was done with a focus on 10°E–40°E, covering the African tropics (between 20° North and South). This process-based model evaluation seeks to assess the predictive skill and explanatory values which provide a chance to improve process representation by the model (Steyn and Galmarini, 2008).

The differences on the descending edge of the HC latitude between ERA5 and CRCM vary from the highest of 24.3% (NDJ season during La-Niña) to the lowest of 3.5% (FMA season during La-Niña) (Figure 3f). The differences in the STJ latitude between ERA5 and CRCM vary between the highest of 7.5% (JFM season during La-Niña) and the lowest of 0.1% (DJF season during La-Niña). These MAPE values are within the error margin for a highly accurate to a good forecasting model (Montaño Moreno et al., 2013; Zhao et al., 2023). This means CRCM is performing well enough to study the width and area of the ITCZ.

SMAPE was used for the mean meridional zonal wind to eliminate the sensitivity of the results to outliers resulting from the high variability of the differences between the ERA5 reanalysis and CRCM winds prediction over Africa. The response of the model to lead time is visible between 740 hPa and 590 hPa (marked by purple dotted lines in Figure 5h) while no clear response is seen throughout all other levels. The model performance through these other levels is almost similar over all seasons. The CRCM reflects the consistently lower SMAPE from 300 hPa upwards and this result is aligned to the performance of the model in identifying the STJ latitude (Figure 5g), showing a maximum MAPE of 7.5% during JFM season. The changes (less than 3°) in the latitude position of the STJ as investigated here are aligned to the previous findings by Manney et al. (2021) that the STJ latitude changes relating to ENSO are within the 3°, over the southern hemisphere. Furthermore, we found that the STJ latitude shifts poleward during El-Niño while it shifts equatorward during La-Niña over the southern hemisphere and Africa. In comparison, the model performs better in identifying the STJ latitude (Figure 5g) than it does in identifying the edge of the HC (Figure 5f).

Figure 5

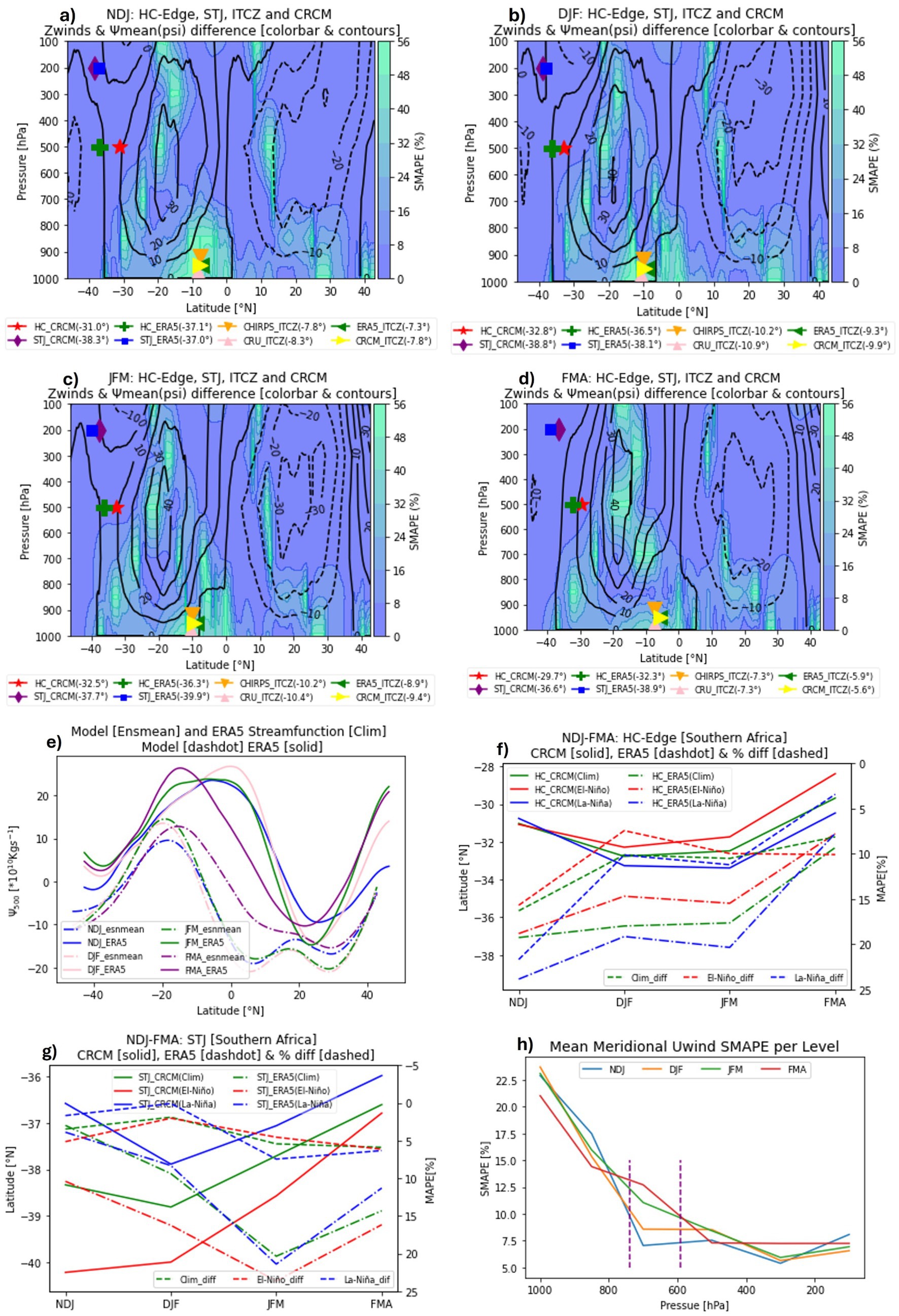
Figure 5. The climatological differences between the zonal wind from ERA5 and CRCM (ERA5 minus CRCM) as the color background (calculations based on wind measured in ms⁻¹), the stream function differences (ERA5 minus CRCM) as the contours (calculations based on stream function measured in *10¹⁰ Kgs⁻¹). Superimposed onto this color background and the contours are the climatological positions of the descending edge of the HC, ITCZ (ascending edge of the HC) and STJ as represented by ERA5 dataset and the model output (a–d) with their latitude positions in brackets. The 500 hPa climatological stream function (in *10¹⁰ Kgs⁻¹) using ERA5 dataset and CRCM outputs are presented by panel (e). The latitude for the descending edge of the HC and STJ, with their percentage difference, are presented by panels (f,g), respectively. Lastly, panel (h) presents the meridional SMAPE of the zonal wind per level with 740 hPa and 590 hPa lines (dotted purple lines).

The performance of the CRCM’s 500 hPa stream function was found to be out of phase with the ERA5’s 500 hPa stream function and mainly shifted southward even though it can correctly pick the pattern with minimal magnitude differences. The phase corrected presentation (Figure 5e) of the climatological 500 hPa stream function by CRCM (dash dotted lines) against the climatological 500 hPa stream function by ERA5 (solid lines) indicates similar pattern, with different magnitudes, and a minor southward shift. In consideration of this, it follows that CRCM can be used to study the strength of the ITCZ. There is a loss of skill, with lead time, by CRCM for both wind patterns and stream function (Figures 5a–d).

The descending edge of the HC is found to shift to the north of its climatological position during El-Niño while it shifts to the south of its climatological position during La-Niña (Figures 5a–d,f). This applies to both the ERA5 dataset and CRCM output. This HC shift is aligned to the shift of the zonal position of the ITCZ during the same phases of ENSO, especially from CHIRPS, CRU and ERA5 datasets. On the contrary, the latitude of the STJ has been found to shift to the south of its climatological position during El-Niño (for both ERA5 and CRCM output) while it shifts to the north of its climatological position in response to La-Niña (for CRCM while this is only the case for NDJ and JFM seasons for ERA5 dataset), Figures 5a–d,g. The descending edge of the HC (−32.8° by CRCM and −36.5° by ERA5) during DJF season is comparable to that from Mahlobo et al. (2018) (−36°) even though they used the ERA-Interim dataset. The response of the local HC to ENSO has previously been reported by Schwendike et al. (2014) who concluded that local Hadley circulation response to ENSO is much stronger than the local Walker circulation response to ENSO. According to Wolf et al. (2021), the ITCZ is a narrow band in which the northerly and southerly trade winds of Hadley circulation converge. This existing association between the HC structure and the ITCZ (Faulk et al., 2017) explains the intertwined shifting relationship between the edge of the HC and ITCZ in response to the ENSO phases.

Calculation of the mean ITCZ position, from different observations and reanalysis datasets, makes it possible to compare the ascending/descending edge from CRCM to the overall mean latitude for the ascending/descending edge of the HC over Africa, from various observation/reanalysis datasets. Table 3, summary of Figures 5a–d,f, indicates that the southernmost latitude for the ascending edge of the HC is found around 10.1°S (9.9°S) and descends around 36.5°S (32.8°S) during DJF, according to the mean ITCZ (CRCM). Similarly, the northernmost latitude for the ascending edge of the HC is found around 6.8°S (5.6°S) and descends around 32.3°S (29.7°S) during FMA as per the mean ITCZ (CRCM). The ITCZ position is also found within latitudes over which ERA5, and CRCM stream function differences are minimal (Figures 5a–d), making it possible to identify the ITCZ position using CRCM stream function (Figures 6, 7).

Table 3

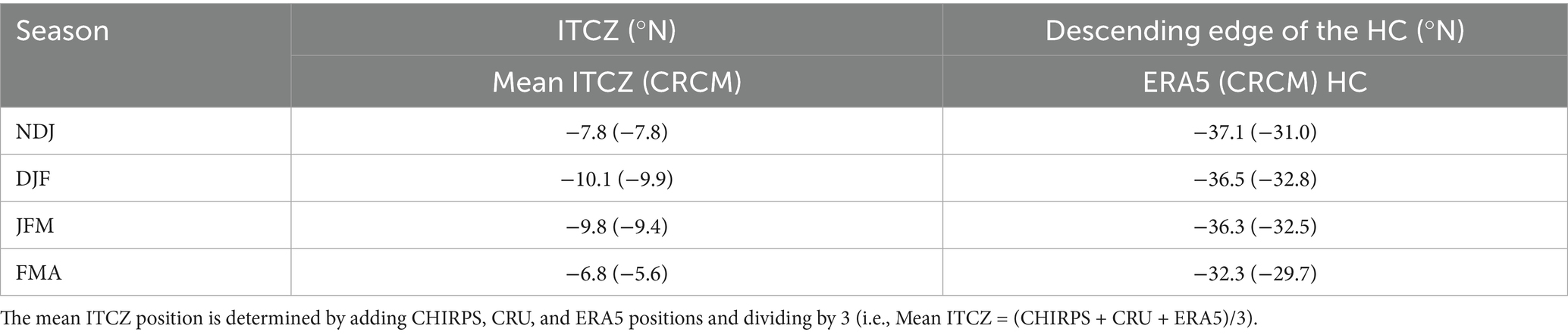
Table 3. The mean ITCZ position and descending edge of the HC from the observations and reanalysis datasets as well as CRCM outputs.

Figure 6

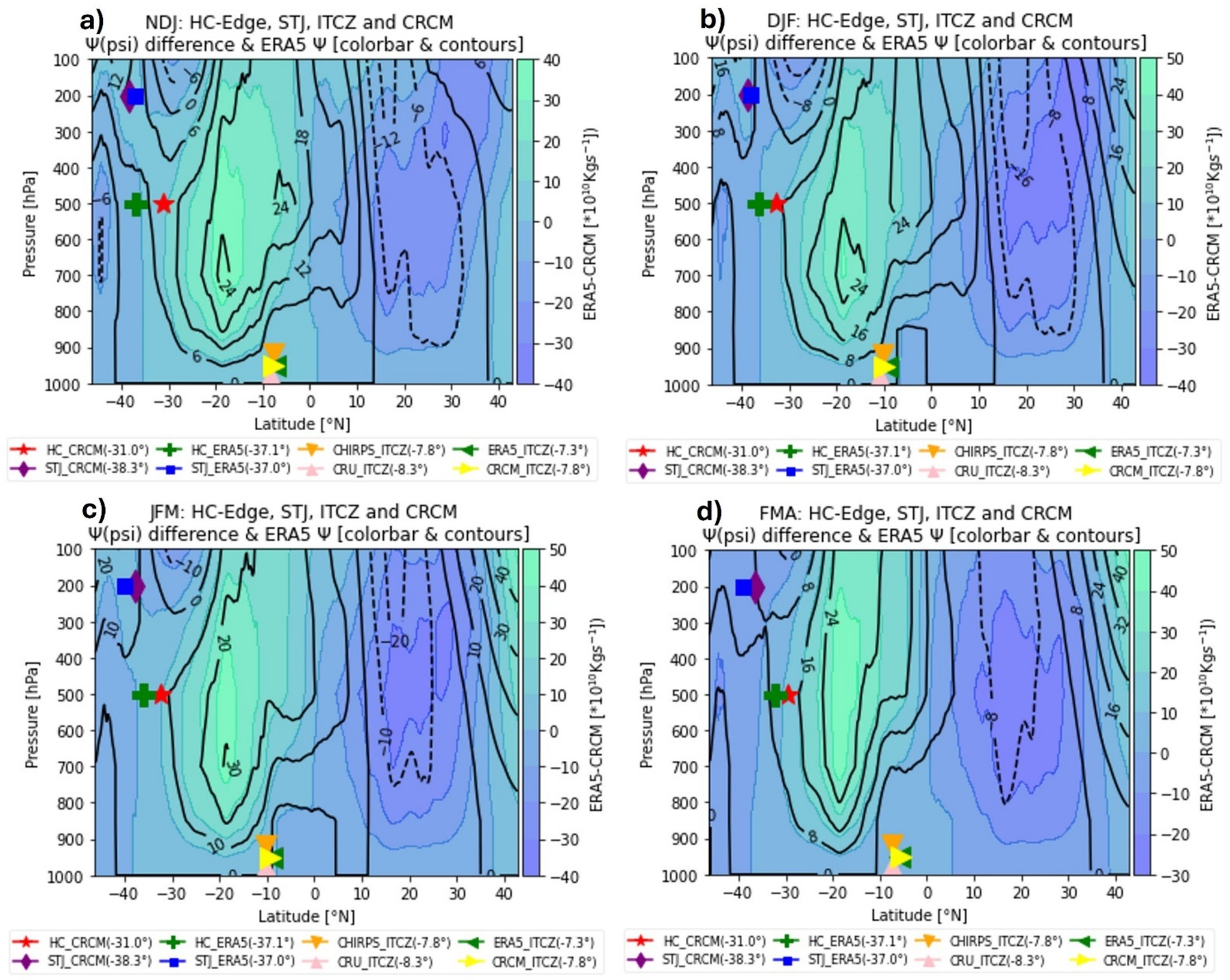
Figure 6. The climatological differences (prior to phase correction) between ERA5 and CRCM (ERA5-CRCM) stream function (Ψ) as the color background and the climatological stream function by ERA5 as the contours (in *10¹⁰ Kgs⁽⁻¹⁾) for NDJ - FMA seasons (a-d). Superimposed onto this color background and the contours are the climatological Latitude (in brackets) of the descending edge of the HC (HC-Edge), STJ, and ITCZ by CRCM (HC_CRCM, STJ_CRCM, and CRCM_ITCZ respectively) and by ERA5 (HC_ERA5, STJ_ERA5, and ERA5_ITCZ respectively) as well as ITCZ by CHIRPS (CHIRPS_ITCZ) and CRU (CRU_ITCZ).

Figure 7

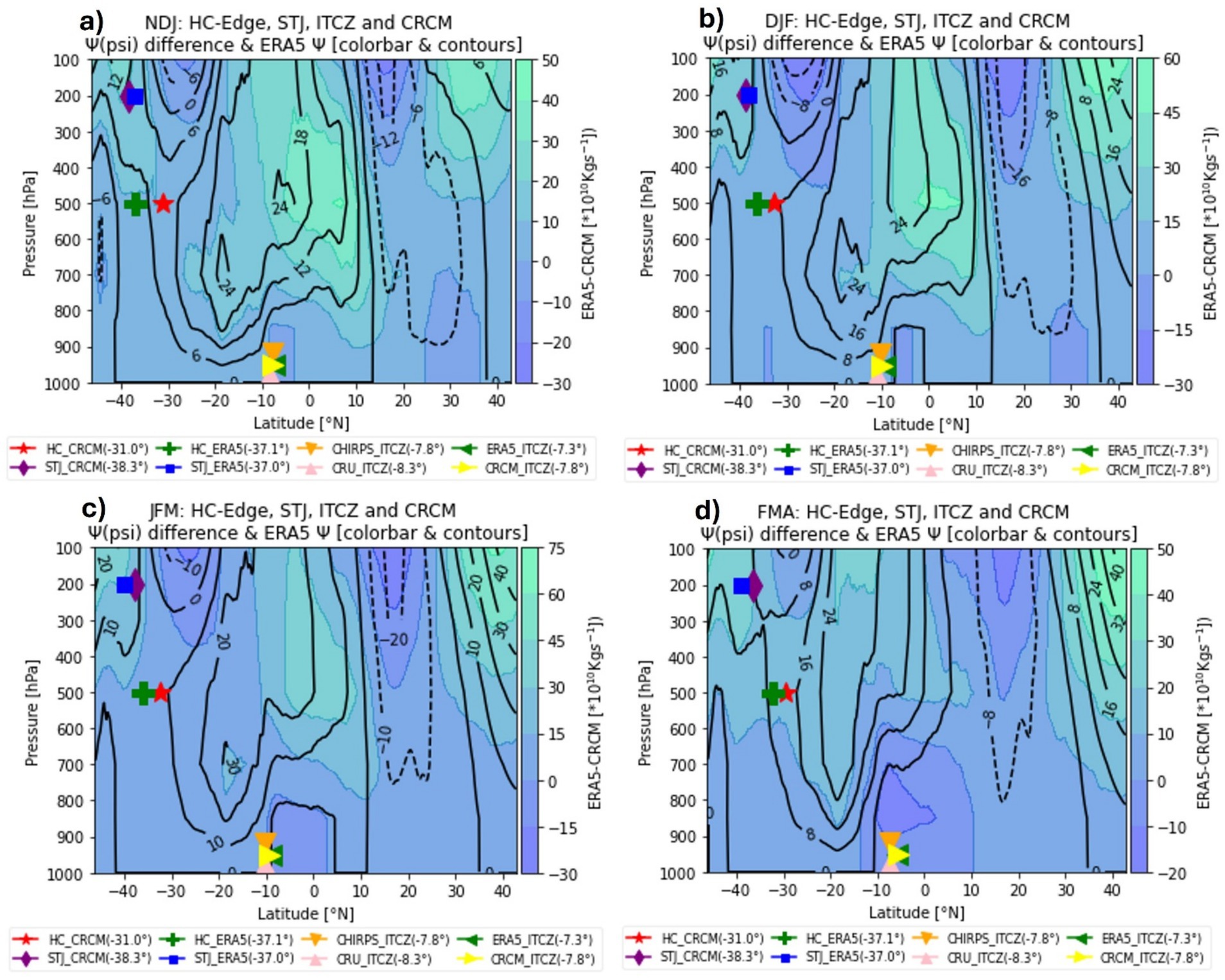
Figure 7. The climatological differences (post phase correction) between ERA5 and CRCM (ERA5-CRCM) stream function (Ψ) as the color background and the climatological stream function by ERA5 as the contours (in *10¹⁰ Kgs^(-1)) for NDJ - FMA seasons (a-d). Superimposed onto this color background and the contours are the climatological Latitude (in brackets) of the descending edge of the HC (HC-Edge), STJ, and ITCZ by CRCM (HC_CRCM, STJ_CRCM, and CRCM_ITCZ respectively) and ERA5 (HC_ERA5, STJ_ERA5, and ERA5_ITCZ respectively) as well as ITCZ by CHIRPS (CHIRPS_ITCZ) and CRU (CRU_ITCZ).

4 Conclusion

The study aimed to evaluate the performance of CRCM constructed through grid-stretching of the driving CSIRO ESM on its ability to discriminate amongst the three seasonal forecasting categories during El-Niño/La-Niña and hence its applicability on identifying the ITCZ process, using the precipitation-based methods, and its characteristics. Two precipitation-based methods (maximum precipitation and centroid methods) were used to identify the ITCZ seasonal position. Application of the maximum precipitation and centroid method on both the observations/reanalysis (CHIRPS, CRU and ERA5) and model (CSIRO ESM and CRCM) tracks the pattern of the seasonally changing position of the ITCZ. However, the ITCZ position identified using maximum precipitation method is found to be south (by more than 1°) of the ITCZ position identified by the centroid method. The climatological skill and reliability of CRCM is comparable to the skill and reliability of the driving CSIRO ESM. However, the skill of CRCM seems to decay faster than the driving CSIRO ESM as the lead time increases presumably due to dynamic error growth tendency. The model uses a spectral relaxation method to minimize a climate drift problem commonly witnessed in interactively coupled models. The variable grid resolution integrations may also inherit errors from the CRCM forcings at the time of animalization. Nonetheless, the source and mechanism of dynamic error growth is apparently complex and is deferred for future work.

The overall (NDJ to FMA mean) seasonal and climatological zonal average positions of the ITCZ determined from the maximum precipitation are found slightly south of the positions determined from the centroid method. Furthermore, it has been found that the position of the ITCZ during El-Niño occurs north of the position during La-Niña. CSIRO ESM and CRCM can identify and track the seasonally changing position of the ITCZ in line with the CHIRPS, CRU, and ERA5 datasets through the different ENSO phases. However, CRCM seems to have the opposite response of the ITCZ to the ENSO signal as its dynamical error grows.

CRCM is also proven skillful and reliable in isolating the AN and BN seasonal precipitation categories during El-Niño and La-Niña, respectively. This is a very important capability for seasonal forecasting over southern Africa where El-Niño is generally associated with BN precipitation while La-Niña is generally associated with AN precipitation. Furthermore, this makes CRCM most suitable for studying the ITCZ, an intense precipitation process, in totality.

Evaluating CRCM on the characteristics of the ITCZ process, it has been found that the model can track the shift of descending edge of the HC in response to the ENSO phases during the austral summer seasons. Furthermore, CRCM is aligned to ERA5 regarding the intertwined relationship between the HC and the ITCZ position. The position of the ITCZ is found within the latitudes in which ERA5 and CRCM stream function differences are minimal. This implies that it is possible to use CRCM to identify the ITCZ position using the stream function even against it being found to be out of phase with ERA5 stream function. Based on the MAPE and SMAPE, CRCM shows a better performance in tracking the STJ than it does in tracking the edge of the HC. The southernmost (northernmost) ascending edge of the HC occurs during DJF (FMA), according to the mean of observation/reanalysis datasets and CRCM outputs. The southernmost (northernmost) descending edge of the HC occurs during NDJ (FMA) as per ERA5 dataset while it occurs during DJF (FMA) according to CRCM outputs.

These results show that the application of the stretched grid on the ESM does, mostly, maintain the performance skill of the driving ESM while providing more regional details as reflected in other previous studies (Yhang et al., 2017) that investigated the specific contribution of the dynamical downscaling to regional research. This is more so considering that CSIRO ESM was previously proven to be skillful in seasonal and short-range timescales forecasting by Engelbrecht et al. (2011). The results further indicate CRCM’s ability to isolate high intensity rainfall areas during the southern hemispheres summer season; ITCZ is a high intensity precipitation process. This capability to isolate high intensity precipitation associated with the ITCZ has also been found to be the case with other models used under CMIP6 (Li et al., 2021).

Therefore, CRCM can be applied to study the teleconnections that exist between spatial or zonal ITCZ and the drivers of climate variability over southern Africa. It can also be used to study the width, strength and area of the ITCZ over the African continent. However, it is recommended, for the future studies beyond the goals of the current research, that the recent developments on a priori bias correction (APBC: Risser et al., 2024) and machine learning (Rampal et al., 2024) approaches amongst a variety of methods (Xu et al., 2019) to bias correction be explored to bias correct the CRCM outputs.

Finally, comparing the performance of CSIRO ESM and CRCM, there is a positive added value of up to 6% by CRCM in identifying large scale phenomena (process) like the ITCZ as demonstrated in this study. This indicates a valuable progress in improving the dynamic downscaling approach to seasonal forecasting over the African continent. Based on the comparable performance between CSIRO ESM and CRCM and in consideration of the computational costs, CSIRO ESM can be applied for operational purposes to save computational costs while CRCM should be used for the regional research studies which require more finer scale details as suggested by Tapiador et al. (2020).

The limitation of the study is the short, for robust El-Niño/La-Niña events analysis, hindcasts due to the computational costs of running this set-up. However, it is important to view this development in the context of the earth system modeling over the African continent; Africa being composed of mostly least developed countries, producing a 15 years hindcasts of a regional earth system model symbolizes a significant progress in coupled ESM with climate signature.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found at: https://cds.climate.copernicus.eu/datasets. Model output data can be requested from CSIR.

Author contributions

TR: Conceptualization, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft, Writing – review & editing. WL: Investigation, Supervision, Writing – review & editing. MM: Investigation, Supervision, Writing – review & editing. SN: Investigation, Supervision, Writing – review & editing. AB: Conceptualization, Investigation, Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the Council for Scientific and Industrial Research (CSIR) through the Department of Science and Innovation parliamentary grant (P1FCM00) received by the Climate and Air Quality Modelling group within the CSIR and the FOCUS-AFRICA project via the funding received from the European H2020 Research and Innovation program (Grant Agreement 869575).

Conflict of interest

AB was employed by ClimateSynth Solutions Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abebe, S. A., Qin, T., Yan, D., Gelaw, E. B., Workneh, H. T., Kun, W., et al. (2020). Spatial and temporal evaluation of the latest high-resolution precipitation products over the Upper Blue Nile River basin, Ethiopia. Water 12:3072. doi: 10.3390/w12113072

Crossref Full Text | Google Scholar

Adam, O., Bischoff, T., and Schneider, T. (2016a). Seasonal and interannual variations of the energy flux equator and ITCZ. Part I: zonally averaged ITCZ position. J. Clim. 29, 3219–3230. doi: 10.1175/JCLI-D-15-0512.1

Crossref Full Text | Google Scholar

Adam, O., Bischoff, T., and Schneider, T. (2016b). Seasonal and interannual variations of the energy flux equator and ITCZ. Part II: zonally varying shifts of the ITCZ. J. Clim. 29, 7281–7293. doi: 10.1175/JCLI-D-15-0710.1

Crossref Full Text | Google Scholar

Adam, O., Grise, K. M., Staten, P., Simpson, I. R., Davis, S. M., Davis, N. A., et al. (2018). The TropD software package (v1): standardized methods for calculating tropical-width diagnostics. Geosci. Model Dev. 11, 4339–4357. doi: 10.5194/gmd-11-4339-2018

Crossref Full Text | Google Scholar

Alexander, M. A. (1992). Midlatitude atmosphere–ocean interaction during El Niño. Part II: the northern hemisphere atmosphere. J. Clim. 5, 959–972. doi: 10.1175/1520-0442(1992)005<0959:MAIDEN>2.0.CO;2

Crossref Full Text | Google Scholar

Arora, V. K., and Harrison, S. (2007). Upscaling river networks for use in climate models. Geophys. Res. Lett. 34:L21407. doi: 10.1029/2007GL031865

Crossref Full Text | Google Scholar

Arregocés, H. A., Rojano, R., and Pérez, J. (2023). Validation of the CHIRPS dataset in a coastal region with extensive plains and complex topography. Case Stud. Chem. Environ. Eng. 8:100452. doi: 10.1016/j.cscee.2023.100452

Crossref Full Text | Google Scholar

Ayugi, B., Zhidong, J., Zhu, H., Ngoma, H., Babaousmail, H., Rizwan, K., et al. (2021). Comparison of CMIP6 and CMIP5 models in simulating mean and extreme precipitation over East Africa. Int. J. Climatol. 41, 6474–6496. doi: 10.1002/joc.7207

Crossref Full Text | Google Scholar

Baker, N. C., and Taylor, P. C. (2016). A framework for evaluating climate model performance metrics. J. Clim. 29, 1773–1782. doi: 10.1175/JCLI-D-15-0114.1

Crossref Full Text | Google Scholar

Bartman, A. G., Landman, W. A., and Rautenbach, C. J. D. W. (2003). Recalibration of general circulation model output to austral summer rainfall over southern Africa. Int. J. Climatol. 23, 1407–1419. doi: 10.1002/joc.954

Crossref Full Text | Google Scholar

Beraki, A. F., DeWitt, D. G., Landman, W. A., and Olivier, C. (2014). Dynamical seasonal climate prediction using an ocean-Atmosphere Coupled Climate Model Developed in Partnership between South Africa and the IRI. J. Clim. 27, 1719–1741. doi: 10.1175/JCLI-D-13-00275.1

Crossref Full Text | Google Scholar

Beraki, A. F., Morioka, Y., Engelbrecht, F. A., Nonaka, M., Thatcher, M., Kobo, N., et al. (2020). Examining the impact of multiple climate forcings on simulated southern hemisphere climate variability. Clim. Dyn. 54, 4775–4792. doi: 10.1007/s00382-020-05253-y

PubMed Abstract | Crossref Full Text | Google Scholar

Brum, M., and Schwanenberg, D. (2022). Long-term evaluation of the sub-seasonal to seasonal (S2S) dataset and derived hydrological forecasts at the catchment scale. EGUsphere [preprint]. doi: 10.5194/egusphere-2022-419

Crossref Full Text | Google Scholar

Burton, C., Rifai, S., and Malhi, Y. (2018). Inter-comparison and assessment of gridded climate products over tropical forests during the 2015/2016 El Niño. Philos. Trans. Roy. Soc. B Biol. Sci. 373:20170406. doi: 10.1098/rstb.2017.0406

PubMed Abstract | Crossref Full Text | Google Scholar

Byrne, M. P., Pendergrass, A. G., Rapp, A. D., and Wodzicki, K. R. (2018). Response of the intertropical convergence zone to climate change: location, width, and strength. Curr. Clim. Chang. Rep. 4, 355–370. doi: 10.1007/s40641-018-0110-5

PubMed Abstract | Crossref Full Text | Google Scholar

Byrne, M. P., and Schneider, T. (2016a). Energetic constraints on the width of the intertropical convergence zone. J. Clim. 29, 4709–4721. doi: 10.1175/JCLI-D-15-0767.1

Crossref Full Text | Google Scholar

Byrne, M. P., and Schneider, T. (2016b). Narrowing of the ITCZ in a warming climate: physical mechanisms. Geophys. Res. Lett. 43, 11–350. doi: 10.1002/2016GL070396

Crossref Full Text | Google Scholar

Calì Quaglia, F., Terzago, S., and von Hardenberg, J. (2022). Temperature and precipitation seasonal forecasts over the Mediterranean region: added value compared to simple forecasting methods. Clim. Dyn. 58, 2167–2191. doi: 10.1007/s00382-021-05895-6

PubMed Abstract | Crossref Full Text | Google Scholar

Camberlin, P., and Philippon, N. (2002). The east African march–may rainy season: associated atmospheric dynamics and predictability over the 1968–97 period. J. Clim. 15, 1002–1019. doi: 10.1175/1520-0442(2002)015<1002:TEAMMR>2.0.CO;2

Crossref Full Text | Google Scholar

Ceppi, P., Hwang, Y.-T., Liu, X., Frierson, D. M. W., and Hartmann, D. L. (2013). The relationship between the ITCZ and the southern hemispheric eddy-driven jet: ITCZ and jet latitude. J. Geophys. Res. Atmos. 118, 5136–5146. doi: 10.1002/jgrd.50461

Crossref Full Text | Google Scholar

Chang, L., Duc, H., Scorgie, Y., Trieu, T., Monk, K., and Jiang, N. (2018). Performance evaluation of CCAM-CTM regional airshed modelling for the New South Wales greater metropolitan region. Atmos. 9:486. doi: 10.3390/atmos9120486

Crossref Full Text | Google Scholar

Chen, B., Lin, X., and Bacmeister, J. T. (2008). Frequency distribution of daily ITCZ patterns over the Western–Central Pacific. J. Clim. 21, 4207–4222. doi: 10.1175/2008JCLI1973.1

Crossref Full Text | Google Scholar

Chen, C., Twycross, J., and Garibaldi, J. M. (2017). A new accuracy measure based on bounded relative error for time series forecasting. PLoS One 12:e0174202. doi: 10.1371/journal.pone.0174202

PubMed Abstract | Crossref Full Text | Google Scholar

Christensen, H. M., Moroz, I. M., and Palmer, T. N. (2015). Evaluation of ensemble forecast uncertainty using a new proper score: application to medium-range and seasonal forecasts. Q. J. R. Meteorol. Soc. 141, 538–549. doi: 10.1002/qj.2375

Crossref Full Text | Google Scholar

Corney, S., Grose, M., Bennett, J. C., White, C., Katzfey, J., McGregor, J., et al. (2013). Performance of downscaled regional climate simulations using a variable-resolution regional climate model: Tasmania as a test case. J. Geophys. Res. Atmos. 118, 11,936–11,950. doi: 10.1002/2013JD020087

Crossref Full Text | Google Scholar

Curtis, S. (2019). Means and long-term trends of global coastal zone precipitation. Sci. Rep. 9:5401. doi: 10.1038/s41598-019-41878-8

Crossref Full Text | Google Scholar

Doi, T., Behera, S. K., and Yamagata, T. (2016). Improved seasonal prediction using the S INTEX-F2 coupled model. J. Adv. Model. Earth Syst. 8, 1847–1867. doi: 10.1002/2016MS000744

Crossref Full Text | Google Scholar

Endris, H. S., Hirons, L., Segele, Z. T., Gudoshava, M., Woolnough, S., and Artan, G. A. (2021). Evaluation of the skill of monthly precipitation forecasts from global prediction systems over the greater horn of Africa. Weather Forecast. 36, 1275–1298. doi: 10.1175/WAF-D-20-0177.1

Crossref Full Text | Google Scholar

Engelbrecht, F., Landman, W., Engelbrecht, C., Landman, S., Bopape, M., Roux, B., et al. (2011). Multi-scale climate modelling over southern Africa using a variable-resolution global model. Water SA 37, 647–658. doi: 10.4314/wsa.v37i5.2

Crossref Full Text | Google Scholar

Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958. doi: 10.5194/gmd-9-1937-2016

Crossref Full Text | Google Scholar

Faulk, S., Mitchell, J., and Bordoni, S. (2017). Effects of rotation rate and seasonal forcing on the ITCZ extent in planetary atmospheres. J. Atmos. Sci. 74, 665–678. doi: 10.1175/JAS-D-16-0014.1

Crossref Full Text | Google Scholar

Fox-Rabinovitz, M., Côté, J., Dugas, B., Déqué, M., and McGregor, J. L. (2006). Variable resolution general circulation models: stretched-grid model intercomparison project (SGMIP). J. Geophys. Res. Atmos. 111:2005JD006520. doi: 10.1029/2005JD006520

Crossref Full Text | Google Scholar

Frierson, D. M. W., and Hwang, Y.-T. (2012). Extratropical influence on ITCZ shifts in slab ocean simulations of global warming. J. Clim. 25, 720–733. doi: 10.1175/JCLI-D-11-00116.1

Crossref Full Text | Google Scholar

Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., et al. (2015). The climate hazards infrared precipitation with stations—a new environmental record for monitoring extremes. Sci. Data 2:150066. doi: 10.1038/sdata.2015.66

PubMed Abstract | Crossref Full Text | Google Scholar

Gibson, P. B., Rampal, N., Dean, S. M., and Morgenstern, O. (2024). Storylines for future projections of precipitation over New Zealand in CMIP6 models. J. Geophys. Res. Atmos. 129:e2023JD039664. doi: 10.1029/2023JD039664

Crossref Full Text | Google Scholar

Giorgi, F. (2019). Thirty years of regional climate modeling: where are we and where are we going next? J. Geophys. Res. Atmos. 124, 5696–5723. doi: 10.1029/2018JD030094

Crossref Full Text | Google Scholar

Gleixner, S., Demissie, T., and Diro, G. T. (2020). Did ERA5 improve temperature and precipitation reanalysis over East Africa? Atmos. 11:996. doi: 10.3390/atmos11090996

Crossref Full Text | Google Scholar

Gnitou, G. T., Tan, G., Niu, R., and Nooni, I. K. (2021). Assessing past climate biases and the added value of CORDEX-CORE precipitation simulations over Africa. Remote Sens. 13:2058. doi: 10.3390/rs13112058

Crossref Full Text | Google Scholar

Goddard, L., Mason, S. J., Zebiak, S. E., Ropelewski, C. F., Basher, R., and Cane, M. A. (2001). Current approaches to seasonal to interannual climate predictions. Int. J. Climatol. 21, 1111–1152. doi: 10.1002/joc.636

Crossref Full Text | Google Scholar

Gordon, H. B., Rotstayn, L. D., McGregor, J. L., Dix, M. R., Kowalczyk, E. A., O’Farrell, S. P., et al. (2002). The CSIRO Mk3 Climate System Model. CSIRO Atmospheric Research, Technical paper (60).

Google Scholar

Gu, G., and Zhang, C. (2002). Cloud components of the intertropical convergence zone: cloud components of the intertropical convergence zone. J. Geophys. Res. Atmos. 107, ACL 4-1–ACL 4-12. doi: 10.1029/2002JD002089

Crossref Full Text | Google Scholar

Guimarães Nobre, G., Muis, S., Veldkamp, T. I. E., and Ward, P. J. (2019). Achieving the reduction of disaster risk by better predicting impacts of El Niño and La Niña. Prog. Disaster Sci. 2:100022. doi: 10.1016/j.pdisas.2019.100022

Crossref Full Text | Google Scholar

Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F. (2009). Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 377, 80–91. doi: 10.1016/j.jhydrol.2009.08.003

Crossref Full Text | Google Scholar

Hagedorn, R., Doblas-Reyes, F. J., and Palmer, T. N. (2005). The rationale behind the success of multi-model ensembles in seasonal forecasting—I. Basic concept. Tellus A. 57, 219–233. doi: 10.1111/j.1600-0870.2005.00103.x

Crossref Full Text | Google Scholar

Harris, I., Osborn, T. J., Jones, P., and Lister, D. (2020). Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 7:109. doi: 10.1038/s41597-020-0453-3

PubMed Abstract | Crossref Full Text | Google Scholar

Hassler, B., and Lauer, A. (2021). Comparison of reanalysis and observational precipitation datasets including ERA5 and WFDE5. Atmosphere 12:1462. doi: 10.3390/atmos12111462

Crossref Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

Crossref Full Text | Google Scholar

Horton, P. (2022). Analogue methods and ERA5: benefits and pitfalls. Int. J. Climatol. 42, 4078–4096. doi: 10.1002/joc.7484

Crossref Full Text | Google Scholar

Huang, B., Thorne, P. W., Banzon, V. F., Boyer, T., Chepurin, G., Lawrimore, J. H., et al. (2017). Extended reconstructed sea surface temperature, version 5 (ERSSTv5): upgrades, validations, and intercomparisons. J. Clim. 30, 8179–8205. doi: 10.1175/JCLI-D-16-0836.1

Crossref Full Text | Google Scholar

Isphording, R. N., Alexander, L. V., Bador, M., Green, D., Evans, J. P., and Wales, S. (2024). A standardized benchmarking framework to assess downscaled precipitation simulations. J. Clim. 37, 1089–1110. doi: 10.1175/JCLI-D-23-0317.1

Crossref Full Text | Google Scholar

Jafari, M., and Lashkari, H. (2023). Effect of Arabian subtropical high-pressure intensity on the ITCZ zonal displacement pattern in Northeast Africa. Theor. Appl. Climatol. 152, 135–149. doi: 10.1007/s00704-023-04365-9

PubMed Abstract | Crossref Full Text | Google Scholar

Jolliffe, I. T., and Stephenson, D. B. (Eds.). (2011). Forecast Verification: A Practitioner’s Guide in Atmospheric Science, 2nd edition (2nd ed.). John Wiley & Sons, Ltd.

Google Scholar

Kanamitsu, M., Ebisuzaki, W., Yang, S.-K., Hnilo, J. J., Fiorino, M., and Potter, G. L. (2002). NCEP-DOE AMIP-II reanalysis (R-2). Bull. Am. Meteorol. Soc. 83, 1631–1644. doi: 10.1175/BAMS-83-11-1631

Crossref Full Text | Google Scholar

Kang, S. M., Shin, Y., and Xie, S.-P. (2018). Extratropical forcing and tropical rainfall distribution: energetics framework and ocean Ekman advection. NPJ Clim. Atmos. Sci. 1:20172. doi: 10.1038/s41612-017-0004-6

Crossref Full Text | Google Scholar

Keshtgar, B., Alizadeh-Choobari, O., and Irannejad, P. (2020). Seasonal and interannual variations of the intertropical convergence zone over the Indian Ocean based on an energetic perspective. Clim. Dyn. 54, 3627–3639. doi: 10.1007/s00382-020-05195-5

PubMed Abstract | Crossref Full Text | Google Scholar

Kgatuke, M. M., Landman, W. A., Beraki, A., and Mbedzi, M. P. (2008). The internal variability of the RegCM3 over South Africa. Int. J. Climatol. 28, 505–520. doi: 10.1002/joc.1550

Crossref Full Text | Google Scholar

Kling, H., Fuchs, M., and Paulin, M. (2012). Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 424-425, 264–277. doi: 10.1016/j.jhydrol.2012.01.011

PubMed Abstract | Crossref Full Text | Google Scholar

Knoben, W. J. M., Freer, J. E., and Woods, R. A. (2019). Technical note: inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 23, 4323–4331. doi: 10.5194/hess-23-4323-2019

Crossref Full Text | Google Scholar

Kowalczyk, E., Stevens, L., Law, R., Dix, M., Wang, Y., Harman, I., et al. (2013). The land surface model component of ACCESS: description and impact on the simulated surface climatology. Aust. Meteorol. Oceanogr. J. 63, 65–82. doi: 10.22499/2.6301.005

Crossref Full Text | Google Scholar

Krishnamurti, T. N., Stefanova, L., and Misra, V. (2013). Tropical Meteorology: An Introduction. New York, Heidelberg, Dordrecht, and London: Springer. doi: 10.1007/978-1-4614-7409-8

Crossref Full Text | Google Scholar

Landman, W. A., and Beraki, A. (2012). Multi-model forecast skill for mid-summer rainfall over southern Africa. International J. Climatol. 32, 303–314. doi: 10.1002/joc.2273

Crossref Full Text | Google Scholar

Landman, W. A., DeWitt, D., Lee, D.-E., Beraki, A., and Lötter, D. (2012). Seasonal rainfall prediction skill over South Africa: One- versus Two-tiered forecasting systems. Weather and Forecasting. 27, 489–501. doi: 10.1175/WAF-D-11-00078.1

Crossref Full Text | Google Scholar

Landman, W. A., Kgatuke, M.-J., Mbedzi, M., Beraki, A., Bartman, A., and du Piesanie, A. (2009). Performance comparison of some dynamical and empirical downscaling methods for South Africa from a seasonal climate modelling perspective. Int. J. Climatol. 29, 1535–1549. doi: 10.1002/joc.1766

Crossref Full Text | Google Scholar

Landman, W. A., Mason, S. J., Tyson, P. D., and Tennant, W. J. (2001). Retro-active skill of multi-tiered forecasts of summer rainfall over southern Africa. Int. J. Climatol. 21, 1–19. doi: 10.1002/joc.592

Crossref Full Text | Google Scholar

Landman, W., Beraki, A., DeWitt, D., and Lötter, D. (2014). Sst prediction methodologies and verification considerations for dynamical mid-summer rainfall forecasts for South Africa. Water SA 40:615. doi: 10.4314/wsa.v40i4.6

Crossref Full Text | Google Scholar

Lashkari, H., and Jafari, M. (2021a). Annual displacement and appropriate index to determine ITCZ position in East Africa and the Indian Ocean regions. Meteorog. Atmos. Phys. 133, 1111–1126. doi: 10.1007/s00703-021-00797-y

Crossref Full Text | Google Scholar

Lashkari, H., and Jafari, M. (2021b). The role of spatial displacement of Arabian subtropical high pressure in the annual displacement of the ITCZ in East Africa. Theor. Appl. Climatol. 143, 1543–1555. doi: 10.1007/s00704-020-03475-y

Crossref Full Text | Google Scholar

Lauer, A., Jones, C., Eyring, V., Evaldsson, M., Hagemann, S., Mäkelä, J., et al. (2018). Process-level improvements in CMIP5 models and their impact on tropical variability, the Southern Ocean, and monsoons. Earth Syst. Dynam. 9, 33–67. doi: 10.5194/esd-9-33-2018

Crossref Full Text | Google Scholar

Lenssen, N. J. L., Goddard, L., and Mason, S. (2020). Seasonal forecast skill of ENSO teleconnection maps. Weather and Forecasting. 35, 2387–2406. doi: 10.1175/WAF-D-19-0235.1

Crossref Full Text | Google Scholar

Li, C., Zwiers, F., Zhang, X., Li, G., Sun, Y., and Wehner, M. (2021). Changes in annual extremes of daily temperature and precipitation in CMIP6 models. J. Clim. 34, 3441–3460. doi: 10.1175/JCLI-D-19-1013.1

Crossref Full Text | Google Scholar

Liemohn, M. W., Shane, A. D., Azari, A. R., Petersen, A. K., Swiger, B. M., and Mukhopadhyay, A. (2021). RMSE is not enough: guidelines to robust data-model comparisons for magnetospheric physics. J. Atmos. Sol.-Terr. Phys. 218:105624. doi: 10.1016/j.jastp.2021.105624

Crossref Full Text | Google Scholar

Lindstedt, D., Lind, P., Kjellström, E., and Jones, C. (2015). A new regional climate model operating at the meso-gamma scale: performance over Europe. Tellus A Dyn. Meteorol. Oceanogr. 67:24138. doi: 10.3402/tellusa.v67.24138

Crossref Full Text | Google Scholar

Liu, C., Liao, X., Qiu, J., Yang, Y., Feng, X., Allan, R. P., et al. (2020). Observed variability of intertropical convergence zone over 1998—2018. Environ. Res. Lett. 15:104011. doi: 10.1088/1748-9326/aba033

Crossref Full Text | Google Scholar

Liu, Y., Lo, L., Shi, Z., Wei, K.-Y., Chou, C.-J., Chen, Y.-C., et al. (2015). Obliquity pacing of the western Pacific intertropical convergence zone over the past 282,000 years. Nat. Commun. 6:10018. doi: 10.1038/ncomms10018

PubMed Abstract | Crossref Full Text | Google Scholar

López-Bermeo, C., Montoya, R. D., Caro-Lopera, F. J., and Díaz-García, J. A. (2022). Validation of the accuracy of the CHIRPS precipitation dataset at representing climate variability in a tropical mountainous region of South America. Phys. Chem. Earth Parts A B C 127:103184. doi: 10.1016/j.pce.2022.103184

Crossref Full Text | Google Scholar

MacLachlan, C., Arribas, A., Peterson, K. A., Maidens, A., Fereday, D., Scaife, A. A., et al. (2015). Global seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system: GloSea5: a high-resolution seasonal forecast system. Q. J. R. Meteorol. Soc. 141, 1072–1084. doi: 10.1002/qj.2396

Crossref Full Text | Google Scholar

MacLeod, D., Graham, R., O’Reilly, C., Otieno, G., and Todd, M. (2021). Causal pathways linking different flavours of ENSO with the greater horn of Africa short rains. Atmos. Sci. Lett. 22:e1015. doi: 10.1002/asl.1015

Crossref Full Text | Google Scholar

Macron, C., Pohl, B., Richard, Y., and Bessafi, M. (2014). How do tropical temperate troughs form and develop over southern Africa? J. Clim. 27, 1633–1647. doi: 10.1175/JCLI-D-13-00175.1

Crossref Full Text | Google Scholar

Magnusdottir, G., and Wang, C.-C. (2008). Intertropical convergence zones during the active season in daily data. J. Atmos. Sci. 65, 2425–2436. doi: 10.1175/2007JAS2518.1

Crossref Full Text | Google Scholar

Mahlobo, D. D., Ndarana, T., Grab, S., and Engelbrecht, F. (2018). Integrated climatology and trends in the subtropical Hadley cell, sunshine duration and cloud cover over South Africa. Int. J. Climatol. 39, 1805–1821. doi: 10.1002/joc.5917

Crossref Full Text | Google Scholar

Mahlobo, D., Engelbrecht, F., Ndarana, T., Abubakar, H. B., Olabanji, M. F., and Ncongwane, K. (2024). Analysis of the Hadley cell, subtropical anticyclones and their effect on south African rainfall. Theor. Appl. Climatol. 155, 1035–1054. doi: 10.1007/s00704-023-04674-z

Crossref Full Text | Google Scholar

Ma, J., Xie, S.-P., and Xu, H. (2017). Contributions of the North Pacific meridional mode to ensemble spread of ENSO prediction. J. Clim. 30, 9167–9181. doi: 10.1175/JCLI-D-17-0182.1

Crossref Full Text | Google Scholar

Mamalakis, A., Randerson, J. T., Yu, J.-Y., Pritchard, M. S., Magnusdottir, G., Smyth, P., et al. (2021). Zonally contrasting shifts of the tropical rain belt in response to climate change. Nat. Clim. Chang. 11, 143–151. doi: 10.1038/s41558-020-00963-x

Crossref Full Text | Google Scholar

Manney, G. L., Hegglin, M. I., and Lawrence, Z. D. (2021). Seasonal and regional signatures of ENSO in upper tropospheric jet characteristics from reanalyses. J. Clim. 34:1. doi: 10.1175/JCLI-D-20-0947.1

PubMed Abstract | Crossref Full Text | Google Scholar

Mason, S. J., and Graham, N. E. (2002). Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q. J. R. Meteorol. Soc. 128, 2145–2166. doi: 10.1256/003590002320603584

Crossref Full Text | Google Scholar

McGregor, J. L. (2005). Geostrophic adjustment for reversibly staggered grids. Mon. Weather Rev. 133, 1119–1128. doi: 10.1175/MWR2908.1

Crossref Full Text | Google Scholar

McGregor, J. L., and Dix, M. R. (2008). “An updated description of the conformal-cubic atmospheric model,” in High resolution numerical modelling of the atmosphere and ocean. eds. K. Hamilton and W. Ohfuchi (New York: Springer), 51–75.

Google Scholar

Menzel, M. E., Waugh, D. W., Wu, Z., and Reichler, T. (2024). Replicating the Hadley cell edge and subtropical jet latitude disconnect in idealized atmospheric models. Weather Clim. Dynam. 5, 251–261. doi: 10.5194/wcd-5-251-2024

Crossref Full Text | Google Scholar

Merryfield, W. J., Baehr, J., Batté, L., Becker, E. J., Butler, A. H., Coelho, C. A. S., et al. (2020). Current and emerging developments in subseasonal to decadal prediction. Bull. Am. Meteorol. Soc. 101, E869–E896. doi: 10.1175/BAMS-D-19-0037.1

Crossref Full Text | Google Scholar

Mischell, E., and Lee, J.-E. (2022). Observed zonal variations of the relationship between ITCZ position and meridional temperature contrast. Climate 10:30. doi: 10.3390/cli10030030

Crossref Full Text | Google Scholar

Mitchell, J. F. B., Davis, R. A., Ingram, W. J., and Senior, C. A. (1995). On surface temperature, greenhouse gases, and aerosols: models and observations. J. Clim. 8, 2364–2386. doi: 10.1175/1520-0442(1995)008<2364:OSTGGA>2.0.CO;2

Crossref Full Text | Google Scholar

Monhart, S., Zappa, M., Spirig, C., Schär, C., and Bogner, K. (2019). Subseasonal hydrometeorological ensemble predictions in small-and medium-size mountainous catchments: benefits of the NWP approach. Hydrol. Earth Syst. Sci. 23, 493–513. doi: 10.5194/hess-23-493-2019

Crossref Full Text | Google Scholar

Montaño Moreno, J. J., Palmer Pol, A., and Sesé Abad, A. (2013). Using the R-MAPE index as a resistant measure of forecast accuracy. Psicothema 25, 500–506. doi: 10.7334/psicothema2013.23

PubMed Abstract | Crossref Full Text | Google Scholar

Moreno-Chamarro, E., Marshall, J., and Delworth, T. L. (2020). Linking ITCZ migrations to the AMOC and North Atlantic/Pacific SST decadal variability. J. Clim. 33:13. doi: 10.1175/JCLI-D-19-0258.1

Crossref Full Text | Google Scholar

Mpheshea, L. E., Blamey, R. C., and Reason, C. J. C. (2025). The influence of ENSO-type on rainfall characteristics over southern Africa during the austral summer. Clim. Dyn. 63:161. doi: 10.1007/s00382-024-07489-4

Crossref Full Text | Google Scholar

Murphy, A. H. (1993). What is a good forecast? An essay on the nature of goodness in weather forecasting. Weather Forecast. 8, 281–293. doi: 10.1175/1520-0434(1993)008<0281:WIAGFA>2.0.CO;2

Crossref Full Text | Google Scholar

Nicholson, S. E. (2009). A revised picture of the structure of the “monsoon” and land ITCZ over West Africa. Clim. Dyn. 32, 1155–1171. doi: 10.1007/s00382-008-0514-3

PubMed Abstract | Crossref Full Text | Google Scholar

O’Farrell, S. P. (1998). Investigation of the dynamic sea ice component of a coupled atmosphere-sea ice general circulation model. J. Geophys. Res. Oceans 103, 15751–15782. doi: 10.1029/98JC00815

Crossref Full Text | Google Scholar

Ogino, S.-Y., Yamanaka, M. D., Mori, S., and Matsumoto, J. (2016). How much is the precipitation amount over the tropical coastal region? J. Clim. 29, 1231–1236. doi: 10.1175/JCLI-D-15-0484.1

Crossref Full Text | Google Scholar

Omrani, H., Drobinski, P., and Dubos, T. (2012). Spectral nudging in regional climate modelling: how strongly should we nudge? Q. J. R. Meteorol. Soc. 138, 1808–1813. doi: 10.1002/qj.1894

Crossref Full Text | Google Scholar

Ostermöller, J., Lorenz, P., Fröhlich, K., Kreienkamp, F., and Früh, B. (2021). Downscaling and evaluation of seasonal climate data for the European power sector. Atmosphere 12:304. doi: 10.3390/atmos12030304

Crossref Full Text | Google Scholar

Pendergrass, A. G., Gleckler, P. J., Leung, L. R., and Jakob, C. (2020). Benchmarking simulated precipitation in earth system models. Bull. Am. Meteorol. Soc. 101, E814–E816. doi: 10.1175/BAMS-D-19-0318.1

Crossref Full Text | Google Scholar

Philander, S. G. H., Gu, D., Lambert, G., Li, T., Halpern, D., Lau, N.-C., et al. (1996). Why the ITCZ is mostly north of the equator.pdf. J. Clim. 9, 2958–2972. doi: 10.1175/1520-0442(1996)009<2958:WTIIMN>2.0.CO;2

Crossref Full Text | Google Scholar

Pohl, B., Dieppois, B., Crétat, J., Lawler, D., and Rouault, M. (2018). From synoptic to interdecadal variability in southern African rainfall: toward a unified view across time scales. J. Clim. 31, 5845–5872. doi: 10.1175/JCLI-D-17-0405.1

Crossref Full Text | Google Scholar

Pohl, B., Fauchereau, N., Richard, Y., Rouault, M., and Reason, C. J. C. (2009). Interactions between synoptic, intraseasonal and interannual convective variability over southern Africa. Clim. Dyn. 33, 1033–1050. doi: 10.1007/s00382-008-0485-4

Crossref Full Text | Google Scholar

Quagraine, K. A., Hewitson, B., Jack, C., Pinto, I., and Lennard, C. (2019). A methodological approach to assess the co-behavior of climate processes over southern Africa. J. Clim. 32, 2483–2495. doi: 10.1175/JCLI-D-18-0689.1

Crossref Full Text | Google Scholar

Rampal, N., Hobeichi, S., Gibson, P. B., Baño-Medina, J., Abramowitz, G., Beucler, T., et al. (2024). Enhancing regional climate downscaling through advances in machine learning. Artif. Intell. Earth Syst. 3:230066. doi: 10.1175/AIES-D-23-0066.1

Crossref Full Text | Google Scholar

Randriatsara, H. H.-R. H., Hu, Z., Ayugi, B., Makula, E. K., Vuguziga, F., and Nkunzimana, A. (2022). Interannual characteristics of rainfall over Madagascar and its relationship with the Indian Ocean Sea surface temperature variation. Theor. Appl. Climatol. 148, 349–362. doi: 10.1007/s00704-022-03950-8

Crossref Full Text | Google Scholar

Ratnam, J. V., Behera, S. K., Doi, T., Ratna, S. B., and Landman, W. A. (2016). Improvements to the WRF seasonal hindcasts over South Africa by bias correcting the driving SINTEX-F2v CGCM fields. J. Clim. 29, 2815–2829. doi: 10.1175/JCLI-D-15-0435.1

Crossref Full Text | Google Scholar

Risser, M. D., Rahimi, S., Goldenson, N., Hall, A., Lebo, Z. J., and Feldman, D. R. (2024). Is bias correction in dynamical downscaling defensible? Geophys. Res. Lett. 51:e2023GL105979. doi: 10.1029/2023GL105979

Crossref Full Text | Google Scholar

Russotto, R. D., and Ackerman, T. P. (2017). Energy transport, polar amplification, and ITCZ shifts in the GeoMIP G1 ensemble. Atmos. Chem. Phys. 18, 2287–2305. doi: 10.5194/acp-18-2287-2018

Crossref Full Text | Google Scholar

Scaife, A. A., Camp, J., Comer, R., Davis, P., Dunstone, N., Gordon, M., et al. (2019). Does increased atmospheric resolution improve seasonal climate predictions? Atmos. Sci. Lett. 20:e922. doi: 10.1002/asl.922

Crossref Full Text | Google Scholar

Schneider, T. (2014). Migrations and dynamics of the intertropical convergence zone. Nat. Rev. 513:9. doi: 10.1038/nature13636

Crossref Full Text | Google Scholar

Schulzweida, U. (2023). CDO user guide. doi: 10.5281/ZENODO.10020800

Crossref Full Text | Google Scholar

Schwendike, J., Govekar, P., Reeder, M. J., Wardle, R., Berry, G. J., and Jakob, C. (2014). Local partitioning of the overturning circulation in the tropics and the connection to the Hadley and Walker circulations. J. Geophys. Res. Atmos. 119, 1322–1339. doi: 10.1002/2013JD020742

Crossref Full Text | Google Scholar

Scott, A. A. (2013). The intertropical convergence zone over the Middle East and North Africa: detection and trends. KAUST Research Repository. doi: 10.25781/KAUST-34778

Crossref Full Text | Google Scholar

Steinkopf, J., and Engelbrecht, F. (2022). Verification of ERA5 and ERA-interim precipitation over Africa at intra-annual and interannual timescales. Atmos. Res. 280:106427. doi: 10.1016/j.atmosres.2022.106427

Crossref Full Text | Google Scholar

Steyn, D. G., and Galmarini, S. (2008). Evaluating the predictive and explanatory value of atmospheric numerical models: between relativism and objectivism. Open Atmos. Sci. J. 2, 38–45. doi: 10.2174/1874282300802010038

Crossref Full Text | Google Scholar

Sultan, B., and Janicot, S. (2000). Abrupt shift of the ITCZ over West Africa and intra-seasonal variability. Geophys. Res. Lett. 27, 3353–3356. doi: 10.1029/1999GL011285

Crossref Full Text | Google Scholar

Tamoffo, A. T., Dosio, A., Vondou, D. A., and Sonkoué, D. (2020). Process-based analysis of the added value of dynamical downscaling over Central Africa. Geophys. Res. Lett. 47:e2020GL089702. doi: 10.1029/2020GL089702

Crossref Full Text | Google Scholar

Tapiador, F. J., Navarro, A., Moreno, R., Sánchez, J. L., and García-Ortega, E. (2020). Regional climate models: 30 years of dynamical downscaling. Atmos. Res. 235:104785. doi: 10.1016/j.atmosres.2019.104785

Crossref Full Text | Google Scholar

Taylor, K. E. (2001). Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 106, 7183–7192. doi: 10.1029/2000JD900719

Crossref Full Text | Google Scholar

Taylor, K. E., Stouffer, R. J., and Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498. doi: 10.1175/BAMS-D-11-00094.1

Crossref Full Text | Google Scholar

Thatcher, M., McGregor, J., Dix, M., and Katzfey, J. (2015). “A new approach for coupled regional climate modeling using more than 10,000 cores,” in Environmental software systems. Infrastructures, services and applications. eds. R. Denzer, R. M. Argent, G. Schimak, and J. Hřebíček (Cham: Springer), 599–607.

Google Scholar

Thatcher, M., and McGregor, J. L. (2009). Using a scale-selective filter for dynamical downscaling with the conformal cubic atmospheric model. Mon. Weather Rev. 137, 1742–1752. doi: 10.1175/2008MWR2599.1

Crossref Full Text | Google Scholar

Thatcher, M., and McGregor, J. L. (2010). A technique for dynamically downscaling daily-averaged GCM datasets using the conformal cubic atmospheric model. Mon. Weather Rev. 139, 79–95. doi: 10.1175/2010MWR3351.1

Crossref Full Text | Google Scholar

Ullah, A., Pohl, B., Pergaud, J., Dieppois, B., and Rouault, M. (2023). Intraseasonal descriptors and extremes in south African rainfall. Part II: summer teleconnections across multiple timescales. Int. J. Climatol. 43, 3799–3827. doi: 10.1002/joc.8059

PubMed Abstract | Crossref Full Text | Google Scholar

Vigaud, N., Pohl, B., and Crétat, J. (2012). Tropical-temperate interactions over southern Africa simulated by a regional climate model. Clim. Dyn. 39, 2895–2916. doi: 10.1007/s00382-012-1314-3

Crossref Full Text | Google Scholar

Vindel, J. M., Valenzuela, R. X., Navarro, A. A., and Polo, J. (2020). Temporal and spatial variability analysis of the solar radiation in a region affected by the intertropical convergence zone. Meteorol. Appl. 27:e1824. doi: 10.1002/met.1824

Crossref Full Text | Google Scholar

Wang, J., Guan, Y., Wu, L., Guan, X., Cai, W., Huang, J., et al. (2021). Changing lengths of the four seasons by global warming. Geophys. Res. Lett. 48. doi: 10.1029/2020GL091753

Crossref Full Text | Google Scholar

Weber, T., Cabos, W., Sein, D. V., and Jacob, D. (2023). Benefits of simulating precipitation characteristics over Africa with a regionally-coupled atmosphere–ocean model. Clim. Dyn. 60, 1079–1102. doi: 10.1007/s00382-022-06329-7

Crossref Full Text | Google Scholar

Wheatcroft, E. (2019). Interpreting the skill score form of forecast performance metrics. Int. J. Forecast. 35, 573–579. doi: 10.1016/j.ijforecast.2018.11.010

Crossref Full Text | Google Scholar

WMO (2018). Guidance on Verification of Operational Seasonal Climate Forecasts (2018th ed.). Geneva: World Meteorological Organization, 2.

Google Scholar

Wolf, F., Voigt, A., and Donner, R. V. (2021). A climate network perspective on the intertropical convergence zone. Earth Syst. Dyn. 12, 353–366. doi: 10.5194/esd-12-353-2021

Crossref Full Text | Google Scholar

Xian, P., and Miller, R. L. (2008). Abrupt seasonal migration of the ITCZ into the summer hemisphere. J. Atmos. Sci. 65, 1878–1895. doi: 10.1175/2007JAS2367.1

Crossref Full Text | Google Scholar

Xu, Z., Han, Y., and Yang, Z. (2019). Dynamical downscaling of regional climate: a review of methods and limitations. Sci. China Earth Sci. 62, 365–375. doi: 10.1007/s11430-018-9261-5

Crossref Full Text | Google Scholar

Yhang, Y.-B., Sohn, S.-J., and Jung, I.-W. (2017). Application of dynamical and statistical downscaling to east Asian summer precipitation for finely resolved datasets. Adv. Meteorol. 2017, 1–9. doi: 10.1155/2017/2956373

Crossref Full Text | Google Scholar

Yimer, S. M., Bouanani, A., Kumar, N., Tischbein, B., and Borgemeister, C. (2022). Assessment of climate models performance and associated uncertainties in rainfall projection from CORDEX over the eastern Nile basin, Ethiopia. Climate 10:95. doi: 10.3390/cli10070095

Crossref Full Text | Google Scholar

Yin, H., Wu, Z., Fowler, H. J., Blenkinsop, S., He, H., and Li, Y. (2022). The combined impacts of ENSO and IOD on global seasonal droughts. Atmosphere 13:1673. doi: 10.3390/atmos13101673

Crossref Full Text | Google Scholar

Zhang, H., Ma, X., Zhao, S., and Kong, L. (2021). Advances in research on the ITCZ: mean position, model bias, and anthropogenic aerosol influences. J. Meteorol. Res. 35, 729–742. doi: 10.1007/s13351-021-0203-2

Crossref Full Text | Google Scholar

Zhao, S., Fu, R., Anderson, M. L., Chakraborty, S., Jiang, J. H., Su, H., et al. (2023). Extended seasonal prediction of spring precipitation over the upper Colorado River basin. Clim. Dyn. 60, 1815–1829. doi: 10.1007/s00382-022-06422-x

PubMed Abstract | Crossref Full Text | Google Scholar