Data-Efficient Framework for Personalized Physiotherapy Feedback

1. Introduction

Physiotherapy is a rehabilitation activity that improves and restores physical function. The process can be labor-intensive, involving multiple face-to-face sessions with a physical therapist (PT) (Figure 1). In each therapy session, the PT and patient practice a large variety of movements with limited amount of time. An average post-stroke therapy session was found to be 36 min long, requiring patients to perform up to 17 types of movements (Lang et al., 2007). This amount of practice is an order of magnitude lower than what is expected to induce neural reorganization (Lang et al., 2009). Thus, the patient is required to continue the exercises themselves, without the corrective guidance from the PT (Tang et al., 2015).

FIGURE 1

Figure 1. Therapist (left) induces proper form of exercise on the patient (right).

While conventional face-to-face therapy is effective in treating many common injuries, access has become increasingly difficult for many individuals. Among many factors, the shortage of practitioners and physical distance were identified as major contributors (Schopp et al., 2000). This shortage is expected to worsen as the world population is aging at an unprecedented rate. At present, so-called developed countries are already considered aged, led by Japan (28%) and Italy (23%); developing countries are following this trend at an even faster pace (United Nations, 2019). As a result, countries are shifting long-term elderly care from institutions to home- and community-based services, and remote therapy has emerged as an accessible alternative to conventional therapy (Higo and Khan, 2015).

Remote therapy, or telehealth, is defined as the delivery of health-related services and information via telecommunications technologies (ICT) (Lee et al., 2018). Recent developments use immersive technologies, like augmented reality (AR) and virtual reality (VR) to simulate environments close to conventional therapy. An AR example is the popular augmented mirror setup that guides users through pre-recorded exercises. For example, Physio@Home demonstrates four shoulder exercises. The system tracks a user's joints and overlays them on the user's body, where a target shoulder angle is presented (Tang et al., 2015). A VR example is the simulation of a 3D environment to facilitate arm-reaching exercises. This system also tracks users' joint positions, while vibratory feedback is given when task performance is successful (Kato et al., 2015). These systems use simple single-limb models to reduce the cognitive load on the patient and the computational load on the system.

The existing systems use single-purpose frameworks, which can be cumbersome to calibrate for the variety of different exercises and users. We highlight three issues in particular. First, complex multi-joint movements are largely unexplored. Focus has been largely on isolated individual movements, such as finger motion, knee, and shoulder movements. Important whole-body movements, such as the sit-to-stand exercise, cannot be addressed. Second, patient-specific calibration is difficult to achieve. On the one hand, many systems rely on generic expert templates. The template may differ greatly from the target user's body type and physical condition, potentially suggesting painful postures. On the other hand, automatic calibration would require large amounts of personalized training data, which is impractical with the limited time available during a therapy session. Finally, the physical therapist's motor skills are completely ignored. Many systems are designed according to the information provided by the expert PT. Expert knowledge, such as what types of exercise and target angles are useful, but expert motor skills play an equally important role during therapy (Tang and Dillman, 2013).

The present study aims to develop a data-efficient framework for personalized physiotherapy exercises. This framework solves the identified problems by allowing arbitrary whole-body motions, using only few user-specific demonstrations available during collocated therapy. We approach this problem by utilizing a model called Gaussian Process Dynamical Model (GPDM) (Wang et al., 2008). GPDM is part of a family of latent variable models which can represent high-dimensional observation data in a low-dimensional latent space (Lawrence, 2005). GPDM, a dynamical variant, has been demonstrated to work well with human motion data. The key idea is to embed and organize meaningful task demonstrations in the same latent space. However, there is currently no principled way to compare characteristics between multiple demonstrations.

We propose simple modifications to the GPDM to extract meaningful feedback mechanisms for self-correction. In the context of motor skill learning, feedback refers to performance-related information that a learner receives for performing a task. Two types of augmented feedback are typically presented to a learner. One conveys knowledge of results (KR) while the other conveys knowledge of performance (KP) (Sunaryadi, 2016). From the modified latent space, we extract features that convey both types of feedback.

This paper describes proposed modifications to the GPDM for robust self-correction of whole-body physiotherapy exercises. We then demonstrate our model's utility on the sit-to-stand task, an important activity of daily living. Our work eliminates the need for cumbersome calibration or large amounts of user-specific data for a personalized self-exercise system. Using only a limited amount of personalized data, expert-level feedback can be easily obtained. We will start with mathematical formulations of the GPDM and proposed modifications, followed by a description of the data collection and processing procedures. Subsequently, we present the results of the modifications then discuss them in relation to similar studies. Finally, we conclude with a brief summary and outlook.

2. Materials and Methods

We first discuss the fundamental concepts of GPDM before introducing our proposed adjustments to the model. This is followed by details of the experiments and data-processing procedures performed for sit-to-stand motion data.

2.1. Gaussian Process Dynamical Model

The GPDM is a dynamical extension of the Gaussian Process Latent Variable Model (GPLVM), a class of latent variable models that allows non-linear generative mapping from latent space to observation space (Lawrence, 2005). The GPDM extends this model by introducing a dynamical prior in the latent space (Wang et al., 2008). For human motion, data is a sequence of poses indexed by discrete time t. The observation space is defined by a sequence of vector-valued poses ${\text{y}}_t\in {ℝ}^D$, while the latent space is defined by a corresponding lower-dimensional sequence ${\text{x}}_t\in {ℝ}^d$. Either can be written in the form

$\begin{array}{ll}{\text{x}}_t={\displaystyle \sum _i}{\text{a}}_i{\varphi }_i({\text{x}}_{t-1})+{\text{n}}_{x,t},& (1)\end{array}$

$\begin{array}{ll}{\text{y}}_t={\displaystyle \sum _j}{\text{b}}_j{\psi }_j({\text{x}}_t)+{\text{n}}_{y,t},& (2)\end{array}$

for weights A = [a₁, a₂, …] and B = [b₁, b₂, …], basis functions ϕ_i and ψ_j, and zero-mean white Gaussian noise n_x,t and n_y,t.

The GPDM is calculated by marginalizing over parameters of the mappings (i.e., A and B) and optimizing the latent coordinates of the training data. To obtain the data likelihood over the observations Y, we assume an isotropic Gaussian prior on each b_j and marginalize over B to obtain

$\begin{array}{ll}p(\text{y}|\text{X},\overline{\beta })=\frac{|\text{W}{|}^N}{\sqrt{{(2\pi )}^{ND}|{\text{K}}_Y{|}^D}}\text{exp}\left(-\frac{1}{2}\text{tr}({\text{K}}_Y^{-1}\text{Y}{\text{W}}^2{\text{Y}}^T)\right),& (3)\end{array}$

where $\text{Y}={\left[{\text{y}}_1,\dots ,{\text{y}}_N\right]}^T$ is a design matrix of poses, $\text{X}={\left[{\text{x}}_1,\dots ,{\text{x}}_N\right]}^T$ contains the corresponding latent coordinates, W ≡ diag(w₁, …, w_D) is a scaling matrix, and K_Y is a kernel matrix. The elements of the kernel matrix are defined by a kernel function, (_KY)i,j = k_Y(x_i, x_j), chosen to be the default “RBF + bias + white” (Lawrence, 2005). The density over the latent coordinates can be obtained in a similar manner. We assume an isotropic Gaussian prior on each a_i and marginalize over A to obtain

$\begin{array}{ll}p(\text{X}|\overline{\alpha })=\frac{p({\text{x}}_1)}{\sqrt{{(2\pi )}^{(N-1)d}|{\text{K}}_X{|}^d}}\text{exp}\left(-\frac{1}{2}\text{tr}({\text{K}}_X^{-1}{\text{X}}_{2:N}{\text{X}}_{2:N}^T)\right),& (4)\end{array}$

where ${\text{X}}_{2:N}={\left[x_2,\dots ,x_N\right]}^T$, K_X is the (N − 1) × (N − 1) kernel matrix constructed from ${\text{X}}_{1:N-1}={\left[{\text{x}}_1,\dots ,{\text{x}}_{N-1}\right]}^T$, and x₁ is given an isotropic Gaussian prior. The dynamics are chosen to be the default “RBF + linear + white” (Wang et al., 2008). The latent mapping, priors, and dynamics define a generative model for time series of the form

$\begin{array}{ll}p(\text{X},\overline{\alpha },\overline{\beta }|\text{Y})\propto p(\text{Y}|\text{X},\overline{\beta })p(\text{X}|\overline{\alpha })p(\overline{\alpha })p(\overline{\beta }),& (5)\end{array}$

where simple uninformative priors $p(\overline{\alpha })\propto {\prod }_i{\alpha }_i^{-1}$ and $p(\overline{\beta })\propto {\prod }_i{\beta }_i^{-1}$ are assumed. The GPDM is learned by minimizing the joint negative log-posterior of the unknowns $-\text{ln }p(\text{X},\overline{\alpha },\overline{\beta }|\text{Y})$.

The definition for GPDM in Equation (5) is trained using pose sequence Y, implying a single instance of motor behavior. However, Wang et al. also describe how the model can be extended to multiple sequences, explicitly modeling multiple instances simultaneously. To do so, the associated latent trajectories need to be embedded in a shared latent space. Now the observation space sequences {Y⁽¹⁾, …, Y^(P)} are still trained as a single data matrix, but each sequence is made independent by ignoring the temporal transitions between the last pose of sequence i − 1 and the first pose of sequence i. Consequently, the associated latent trajectories {X⁽¹⁾, …, X^(P)} become disconnected (Wang et al., 2008).

2.2. Organizing Latent Trajectories

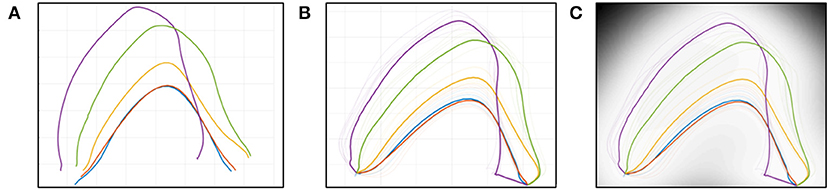
The original formulation of GPDM is insufficient for comparing multiple demonstrations. As is, we see a disorganized latent space where extraction of meaningful features becomes difficult (Figure 2A). We reorganize the space by introducing common reference points.

FIGURE 2

Figure 2. Latent space representation, (A) GPDM, (B) GPDM with CP, (C) with precision.

2.2.1. Common Pose

We hypothesize that the latent trajectories can be organized naturally by appending exact copies of common reference points to each motion sequence. We introduce the concept of a common pose (CP), which is appended to either end of each latent trajectory. The CP is calculated twice, based on the mean pose of trajectory end points. The first is done for the start of the motion sequence, and a second time for the end of the motion sequence. Formally, the common start pose is defined as

$\begin{array}{ll}C{P}_{start}=\frac{1}{P}{\displaystyle \sum _{p=1}^P}{\text{y}}_1^{(p)},& (6)\end{array}$

where P is the number of sequences. Similarly, the common end pose is defined as

$\begin{array}{ll}C{P}_{end}=\frac{1}{P}{\displaystyle \sum _{p=1}^P}{\text{y}}_N^{(p)},& (7)\end{array}$

where N is the number of poses in a sequence. The CP_start is appended to the start of each motion sequence Y^(p), while the CP_end is appended to the end. In our tests, we found that appending fifteen instances to each trajectory end works well.

2.2.2. Zone of Intermediate Poses

By connecting all latent trajectories through the common poses, any pair of trajectories creates an enclosed zone bounding all intermediate poses between them (Figure 2B). This Zone of Intermediate Poses (ZIP) has two useful properties for simple user feedback.

The geometric area of the ZIP is a measure of performance similarity in the latent space. A large area indicates dissimilar movement patterns; a small area indicates similar movement patterns; and zero area (coincident lines) indicates exact-matching movement patterns. The area given by the coordinates (x_i, y_i) of two connected trajectories is defined by Gauss's Area Formula:

$\begin{array}{ll}A=\frac{1}{2}{\displaystyle \sum _{i=1}^n}\left[x_i·(y_{i-1}-y_{i+1})\right],& (8)\end{array}$

where A is the area of the polygon and n is the total number of vertices. The first and last points that create the polygon connect to each other, defined as y₀ = y_n and y_n+1 = y₁. Since our definition of similarity explicitly uses an area formula, the latent space is necessarily two-dimensional.

Poses sampled within the ZIP yield a smooth pose sequence, due to the proximity of the trajectories. Each latent point has an associated level of uncertainty in the pose space, with higher precision yielding better pose estimates. Precision is highest on the training points, but decreases rapidly as points are sampled farther away. In our implementation, the uncertainty of each point in the pose space is visualized by gray-scale coloring in the latent space. High-precision poses are indicated by a light color, while low-precision poses are indicated by darker colors (Figure 2C).

2.3. User Performance Feedback

We propose two ways to present both types of augmented feedback. Knowledge of Results is presented through a performance score, while Knowledge of Performance is presented by visualization of corrective poses. In other words, users can confirm if their performance is improving, and if not, how to correct their mistakes.

2.3.1. Performance Score

The user is given a Performance Score to indicate the quality of performance, starting from base performance to the desired expert-induced motion. The Performance Score is defined as

$\begin{array}{ll}PS=1-\frac{A_{curr}}{A_{ref}},& (9)\end{array}$

where A_ref is the area between the baseline and desired trajectories; A_curr is the area between the current and desired trajectories; and both A_ref and A_curr are calculated using (8). This convention implies that the baseline condition is assigned a 0% score while a goal condition is assigned a 100% score. Generally, a user's progress starts from 0% and improves all the way to 100%. However, it is possible to perform worse than the baseline by misinterpreting the expert's instructions. In this case, the score can go below 0%. The possible scoring outcomes are visualized with their corresponding ZIP in Figure 3.

FIGURE 3

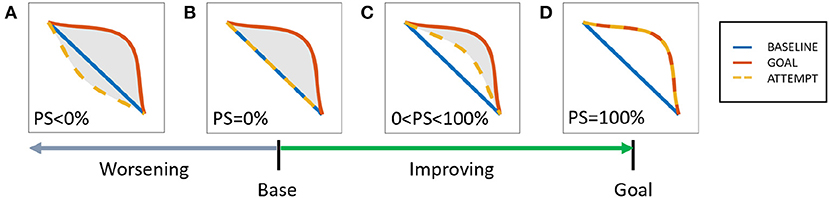
Figure 3. Area-based performance score system, possible scores (A) worsening: PS<0%, (B) base: PS = 0%, (C) improving: 0<PS<100%, (D) mastery: PS = 100%.

2.3.2. Corrective Action

Poses can be visualized by sampling points from the latent space. Self-correction is facilitated by sampling a trajectory from the ZIP. By tracing a line from a current trajectory to a desired trajectory, a smooth corrective pose sequence can be inferred.

2.4. Data Collection

2.4.1. Participants

Nine healthy adult males (age: 27.2 ± 1.5 years, weight: 62.7 ± 10.7 kg) were recruited for the role of subject (person who stands up), while one PT (30 years experience) was recruited for the role of expert (person who induces change). All participants gave informed consent to participate in the experiment.

2.4.2. Experiment Protocol

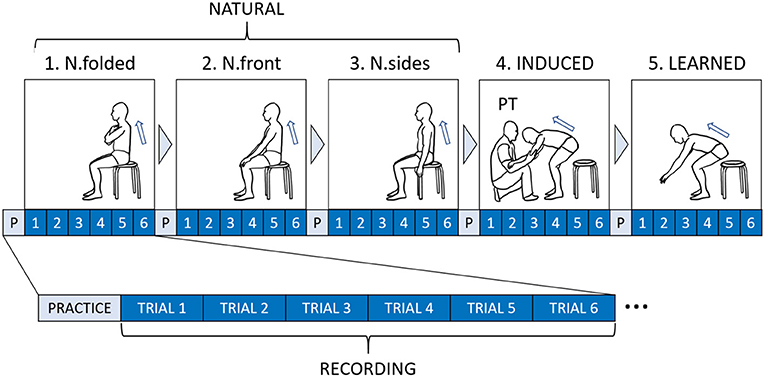
Each subject was asked to perform a number of conditions during their respective session. At the start of every condition, a subject is instructed to sit comfortably on an armless, backless chair of fixed height (0.45 m), while the knee is flexed to 90°. Before recording, a subject is given a few minutes to familiarize themselves with the movement of the current sit-to-stand condition. There are three types of conditions, performed in the following order:

1. NATURAL: A subject is asked to stand up naturally, i.e., a self-selected pace and strategy. This condition is further subdivided into three typical sit-to-stand conditions. These conditions are distinguished by the arm position: (1) N.folded: folded across the chest, (2) N.front: to the front on the knees, and (3) N.sides: to the sides.

2. INDUCED: The PT is asked to induce the desired sit-to-stand motion as usually performed for his patients. This form of guidance is characterized by a light touch on the arms, requiring the subject to use his own strength to stand up.

3. LEARNED: A subject is asked to recall the new strategy that was learned from the INDUCED condition. The subject is then asked to replicate the motion as close as possible to the taught movement. No additional instructions on timing or strategy was given.

Each subject performed all five conditions during their respective session, where each condition was repeated for six successful trials. A trial was considered a failure if data capture was affected in any way, e.g., occlusion of markers. A total of 270 successful trials (5 conditions × 6 trials × 9 subjects) were collected for analysis. The experiment protocol is summarized in Figure 4.

FIGURE 4

Figure 4. Experimental flow diagram for each subject.

2.4.3. Motion Capture Recording

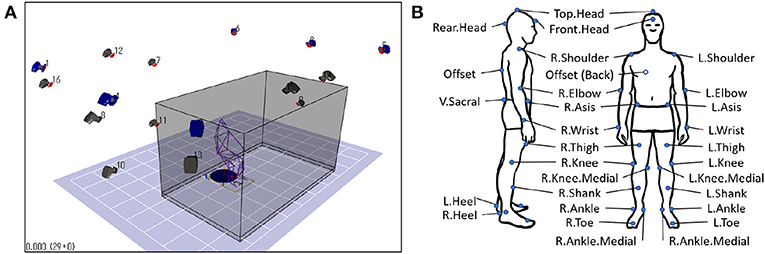
While the sit-to-stand tasks were being performed, the subject's whole-body motion was being recorded. The setup was an indoor MAC3D motion capture system (Motion Analysis Corp.), with 16 cameras mounted around the capture space (Figure 5A). The Cortex software from the same company provides the control panel for all devices and the tools for processing raw motion capture data.

FIGURE 5

Figure 5. Motion capture setup, (A) capture space, (B) Helen Hayes markerset.

Before data recording, 29 passive retroreflective markers were fitted to a subject's whole body, followed by a standard calibration procedure. The Helen Hayes marker set (Figure 5B) was used as a reference (Motion Analysis Corporation, 2006). During recording, the marker trajectories were sampled at 200 Hz with measurement units in millimeters. The x, y, z positions of each marker were continuously recorded, for a total of 87 channels (29 markers × 3 dimensions). An audible beep signals the subject when a trial starts and ends. The trial is ended a few seconds after the subject is fully standing.

2.4.4. Data Pre-processing

The marker data were first pre-processed before analysis, using built-in tools in Cortex (Motion Analysis Corp.) and custom code in Matlab (The MathWorks, Inc.). The procedures were performed in the following order:

1. Noise removal: Each trial was visually examined and corrected for occlusions and noise. The markers were then labeled and smoothed using a fourth-order Butterworth (6 Hz low-pass) filter.

2. Data translation: The coordinate system was standardized across trials. A common origin point was obtained using the static point between the R.Heel and L.Heel markers. The average point between the two markers were calculated, and the coordinates of all other markers were subtracted by this value. This procedure was performed for all trials individually.

3. Data normalization: To reduce inter-individual differences, the length units are normalized to a unitless value based on height (Hof, 1996; Bahrami et al., 2000). For each trial, all coordinate values are divided by the vertical component of the Top.Head marker.

4. Event standardization: Each trial was truncated to retain only the relevant portion of the sit-to-stand motion. A start and an end event were defined based on a stable reference marker (Tully et al., 2005). The start event is defined as the moment when the speed of the R.Shoulder marker is >0 in the sagittal plane, while the end event is defined as the moment when the R.Shoulder reaches its highest vertical position.

3. Results

A reorganized latent space was successfully extracted from the experiment data. Relevant properties of the new latent space are discussed in this section.

3.1. Latent Space Behavior

In conventional GPDM, multiple motor behaviors have no apparent relation in a shared latent space. This is true even when the same motor task is performed repeatedly. To organize the latent trajectories, we proposed to connect them according to known matching poses. Specifically, we appended reference common poses to both ends of each latent trajectory.

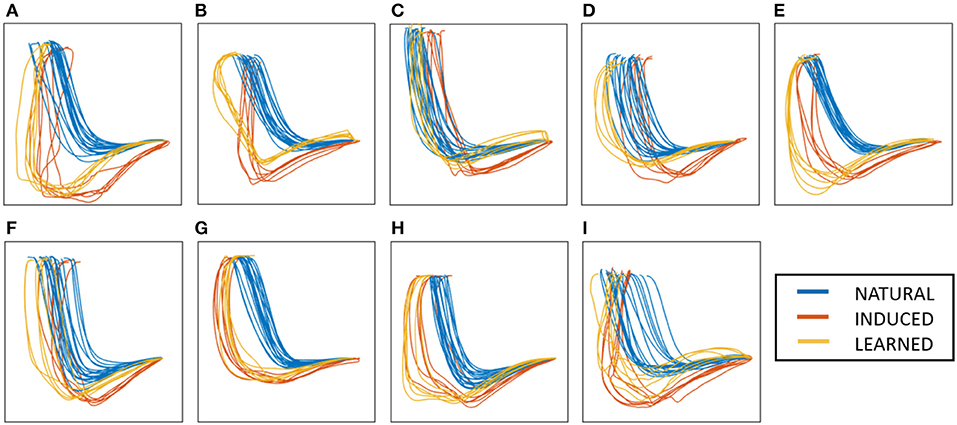
Results indicate that the latent trajectories have successfully connected at the common poses, CP_start and CP_end, found at either end. The trajectories of similar conditions stay close together, forming two subgroups. The NATURAL conditions stay close together, while the INDUCED and LEARNED conditions also stay close. However, the order within the subgroups vary among subjects. These results suggest that even small differences in the pose space can cause latent points to stay far apart. By connecting the trajectories through exactly matching poses, an organized latent space can be achieved. The extracted latent trajectories are shown in Figure 6.

FIGURE 6

Figure 6. Latent trajectory representation for all subjects (A–I).

3.2. Performance Score

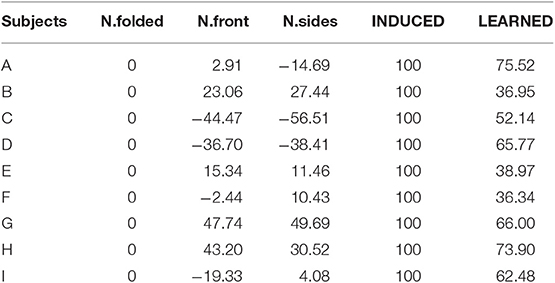
Knowledge of results (KR) is one of two types of augmented feedback shown to be positively linked to motor skill learning (Sunaryadi, 2016). We proposed the Performance Score (PS) as a measure of performance success. The score uses the normalized geometric area between two connected latent trajectories as a measure of similarity between a baseline and a desired behavior. We assigned N.folded as the baseline condition and INDUCED as the desired condition.

Results indicate that the INDUCED scores are always higher than the LEARNED scores, while the LEARNED scores are always higher than the NATURAL scores. This consistent ordering suggests that all subjects were able to remember and perform part of the expert-induced movement. While all LEARNED scores are positive, the N.front and N.sides conditions report some negative values. The inconsistent negative scores of the other NATURAL conditions suggest that the expert-advised movement is not naturally achieved. These results indicate that the Performance Score can capture the expected performance improvements. A summary of all scores is shown in Table 1.

TABLE 1

Table 1. Performance score summary.

3.3. Corrective Pose Sequence

Knowledge of performance (KP) is the other type of augmented feedback for motor skill learning (Sunaryadi, 2016). We proposed sampling from the Zone of Intermediate Poses (ZIP) as a simple yet robust solution for movement self-correction, since a smooth pose sequence can be visualized by simply sampling adjacent points from the latent space.

Results show that by sampling along a trajectory, known pose sequences can be reconstructed. For example, tracing a NATURAL trajectory and the INDUCED trajectory shows the prototypical pose sequences. We can see some distinction between the two conditions as the INDUCED poses are lower and more forward-leaning (Figure 7). Further, by sampling the ZIP between the LEARNED trajectory and the INDUCED trajectory, one can visualize the corrective pose sequence (Figure 8). These results indicate that the generative portion of GPDM is unaffected by our modification, while the formed ZIPs can be used to identify the erratic portions of movement.

FIGURE 7

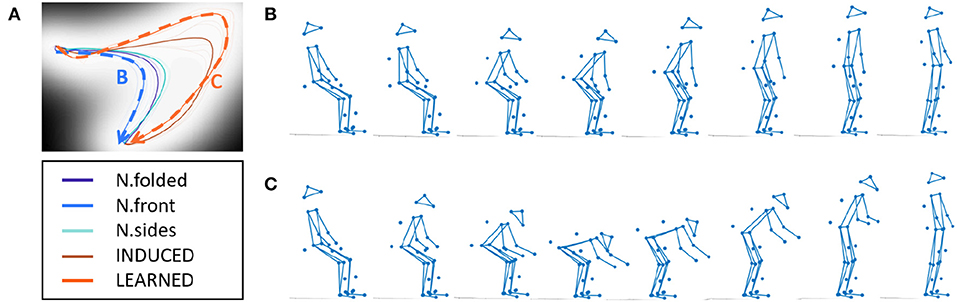
Figure 7. Reconstructing demonstrated poses, (A) latent space, (B) N.folded sequence, (C) INDUCED sequence.

FIGURE 8

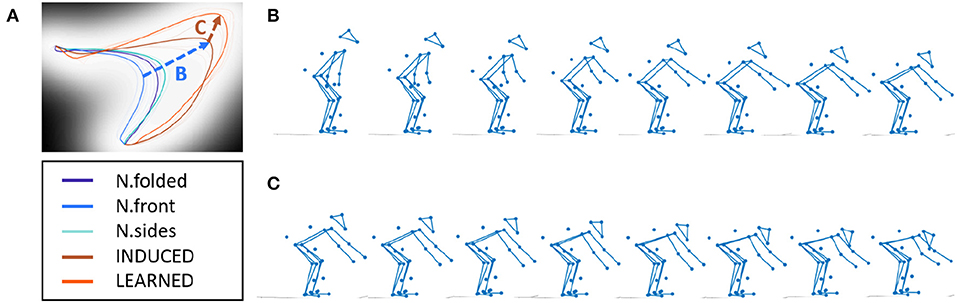
Figure 8. Inferring corrective poses, (A) latent space, (B) N.folded to LEARNED sequence, (C) LEARNED to INDUCED sequence.

4. Discussion

Our goal is to develop a data-efficient framework for personalized physiotherapy exercises. Our modified GPDM approach solves the common problems of existing telehealth applications, by providing personalized feedback for whole-body exercises, based on few expert-induced demonstrations. Specifically, two types of augmented feedback were extracted from the reorganized latent embedding, conveying both performance quality and the corrective action. By analyzing the feedback outcomes from sit-to-stand experiments, we confirmed the utility of our proposed method for an important physiotherapy exercise. In the discussion that follows, we compare our findings with related literature.

4.1. Latent Space Behavior

The introduction of the common pose solved the problem of relating multiple latent trajectories. The desired connecting effect is achieved because the common pose points “gather” nearby similar points. Effectively, the appended common poses reintroduce the still poses to both ends of the movement, i.e., subject is sitting still and standing still. The key differences with the original still poses are that they now match exactly and are shared by all sequences.

Multiple GPLVM studies demonstrate that multiple trajectories lie separately in the shared latent space, despite sharing common poses. One study modeled four golf swings from the same golfer, using conventional GPDM (Wang et al., 2008). Another study modeled sitting motion on surfaces of different heights, using Observation Driven GPLVM (Gupta et al., 2008). In both types of motion, the start poses are known to be the same pose, yet the latent starting points are represented by different points. One key difference with our target movement, i.e., sit-to-stand, is that the end pose is also known to be the same. This condition appears to be unique to our study.

4.2. Augmented Feedback

Our approach provides Knowledge of Results through the Performance Score, calculated as a function of the geometric area between two connected latent trajectories. Since the mapping from latent space to pose space is non-linear, the score does not necessarily convey the scale of progress, i.e., flexing a joint 50% more does not necessarily mean a subject improved by 50%. Other single-valued quantities for progress have been previously proposed, yet the scale of progress remains difficult to quantify exactly. Some examples include time to accomplish the task (Yang and Kim, 2002; Kato et al., 2015), joint flexion/extension angle (Piqueras et al., 2013), and root mean square error between poses (Anderson et al., 2013). Our proposed Performance Score has two advantages over the aforementioned metrics. First, it incorporates both spatial and sequential information. Second, calibration is not necessary when generalizing to other motions.

One interesting note regarding the Performance Score is that the area term in Equation (9) is a valid metric, i.e., distance function. Given any pair of connected latent trajectories, the four conditions of non-negativity, identity of indiscernibles, symmetry, and triangle inequality are all satisfied.

Our approach provides Knowledge of Performance through estimating the intermediate poses between two motor behaviors, allowing the user to visualize a corrective pose sequence. Due to the complexity of human motion, presenting the optimal amount and type of information is challenging. To reduce cognitive load, popular approaches use immersive technologies or only limb-specific movements. For example, some existing systems ask the user to move a target bone vertically and horizontally (Velloso et al., 2013) or move the shoulder laterally to a target number of degrees (Tang et al., 2015). Virtual reality applications, in particular, tend to be limited to upper-body movement for safety reasons. Our approach balances the amount of information captured and presented, by focusing only on the corrective poses of a whole-body model. Thus, removing the need to arbitrarily isolate body parts.

An important note regarding the corrective pose sequence is that it involves the visualization of the latent space, limiting the dimensionality to a maximum of three. Nonetheless, it would be of interest to discuss how different choices of dimensionality may affect our application. In particular, we highlight a three-dimensional example by Wang et al. (2008) and a nine-dimensional example by Damianou et al. (2016). In the first example, the original GPDM model was used to describe golf swing motion, and the latent space was set to three dimensions. The latent trajectories resulted in U-like shapes. In the second example, an extension of GPDM (dynamical variational GPLVM) was used to describe walking and running motions. In their model, the latent space was initially set to nine dimensions, but the model selects three “true” dimensions. Within the visualized three-dimensional space, each motion resulted in circular shapes with some distance between them.

We can see that relatively simple motions, such as golf swing, walking, and running, form “flat” trajectories. Despite being assigned three dimensions, the flat shapes of each motion suggest that these simple motions can be embedded in a two-dimensional space with some small loss. Although we can instead decide on a three-dimensional space for visualization, we argue that “navigating” a two-dimensional space can offer a more familiar experience. Since many commercial devices, such as smartphones and computer screens, offer a two-dimensional user interface, a user can more readily interact with the proposed system without the need to learn new forms of interaction. Thus, from the practical considerations discussed above, the simplest and most direct approach remains to be the two-dimensional representation.

4.3. Interpretation of Motor Knowledge

Subjects were found to interpret intervention differently after being guided by the PT. This difference can be observed by looking at the LEARNED condition, which is the subject's attempt to repeat the INDUCED movement. The PT's general strategy was observed to be guiding the subject lower and more forward than natural. However, some subjects undershoot while some overshoot the target motion. This behavior can be observed by plotting the body center of mass (CoM) in the sagittal plane (Figure 9). Further, the expert-INDUCED CoM trajectories were observed to be different across subjects. These results suggest that both treatment and subject response are personalized in practice.

FIGURE 9

Figure 9. Body center of mass in the sagittal plane for all subjects (A–I).

We observed that the subjects with the lowest LEARNED performance scores (i.e., subjects B, C, E, F in Table 1) were performing a posture called “augmented arm,” where arms are extended forward at shoulder height. We speculate that these subjects have the same interpretation of the therapist's intended change in motor behavior; thus, the same posture. Since this posture has the tendency to produce lower scores, such postures should be identified and avoided. This finding suggests that “low-score” postures may exist in other exercises as well, and identifying particular bad postures may help in self-correction. This posture may also be a reaction to counteract the slower motion induced by the PT, as it has been demonstrated to reduce standing up time (Kwong et al., 2014).

4.4. Alternative Models

Human motion can be modeled reasonably well in a few other ways. One can look at variants of GPDM, GPLVM, or deep learning techniques, which have the capacity to model a variety of high-dimensional dynamical data. We first discuss some extensions of GPDM and their application to different types of human motion. We also discuss two models which use conceptually different techniques to model dynamics.

GPDM has been demonstrated to work well with different types of whole-body motion. Wang et al. (2008) uses the GPDM to describe walking and golf swing movements, demonstrating the model's capability to model simple cyclic and acyclic motions. Chen et al. (2009) extends this concept by introducing a switching mechanism to account for motion sequences that involve switching dynamics, such as in salsa dancing. To our knowledge, a GPDM-based approach has not yet been applied to sit-to-stand motion, but we should note that Gupta et al. (2008) have applied it to the related stand-to-sit task. Together, these studies demonstrate the applicability of GPDM as a model for describing full-body motion, which can reasonably include sit-to-stand.

Hierarchical GPLVM (HGPLVM) can be considered an alternative implementation of dynamics for GPLVM. The main difference is that GPDM is autoregressive while HGPLVM is not. Instead, HGPLVM takes timestamps as inputs (Lawrence and Moore, 2007). This is advantageous if uniform sampling is difficult to achieve. But in the controlled environment of telehealth, such a precaution is not necessary. HGPLVM also offers the option to “decompose” the subject model into component parts, allowing an isolated view of selected parts. However, this increases the number of visualized subspaces and requires a decision on the appropriate decomposition for each target activity. While still considering whole-body information, the single latent space representation of GPDM is a more straightforward approach to visualization.

Deep learning models are widely considered as universal approximators, which can work well with a large variety of data (Hornik et al., 1989). Given enough data and resources, deep learning models can exceed the performance of whatever specific-purpose model. In fact, a single network can be demonstrated to generalize well to multiple types of human actions. A trained model can simultaneously perform classification and prediction of novel poses with very little computational cost (Butepage et al., 2017). The main downside with such a model is the amount of resources necessary to perform training. In the context of single subjects with limited sessions, such large amount of resources is simply unavailable.

4.5. Motion Data Format

Motion data is an attractive modality for telehealth since it can be naturally learned and can be measured remotely. However, high-quality captures of specific motor tasks can sometimes be expensive and logistically difficult to obtain. Thus, in several GPLVM-based works on human motion data, no motion experiments were actually performed. Instead, the popular CMU Graphics Lab Motion Capture Database (mocap.cs.cmu.edu) was often used. One practical note regarding the human models in these studies is the format used. The format used in the CMU database contains joint angle information instead of the marker coordinate information we used in our study.

Although both formats are functionally similar, formats that store joint angles typically need to define a skeleton. The main advantage to this is that bone segments can be calibrated to each user, and limb lengths can be fixed. On the other hand, we can also argue that coordinate-based formats are more accessible as sensors and algorithms themselves measure anatomical points. Currently, in-home telehealth applications often use the ubiquitous Kinect sensor (Microsoft Corp.) which tracks 3D skeletal landmarks of the users. As computer vision algorithms become more advanced, ordinary images and videos are increasingly used to extract similar coordinate-based anatomical key points as well (Cao et al., 2017).

4.6. Limitations

The consistent results found across all subjects highlight the ability of our proposed feedback framework to perform as intended. However, our approach was only demonstrated to work well in a controlled environment. Tests on a larger variety of users and motor tasks would be necessary to confirm its clinical utility. We discuss some of the methodological limitations, and how these limitations compare to related studies.

The proposed framework was tested on nine healthy subjects, where each subject performed a total of 270 trials for standing up motion (five conditions for six trials each). Other motion studies employing GPDM rather focus on a larger variety of movements with fewer samples each. For context, Wang et al. (2008) used the original GPDM formulation to model three different whole-body motions: two gait cycles from one subject, one gait cycle from four subjects, and four golf swings from one subject. A GPDM extension by Gupta et al. conducts two types of experiments. The first experiment models jumping jack, walking, and climbing a ladder with one subject and one instance each. The second experiment models four different sitting instances for one subject (Gupta et al., 2008).

Our framework was tested on sessions conducted by one professional therapist. Realistically, different PTs may have different individual preferences, and it would be interesting to investigate intervention strategies across multiple PTs. Currently, we made the simplifying assumption that a patient's attending PT can best prescribe the personalized exercises. Identifying the appropriate impairments and conditions for our system would be challenging and is outside the scope of the current study. A separate study with a larger cohort would be necessary for each target motor impairment.

Learning the GPDM involves numerical optimization in estimating the model unknowns $\left\{\text{X},\overline{\alpha },\overline{\beta }\right\}$. In our study, we needed to set both the number of learning iterations and the number of appended CPs. We found that setting a low number for both quantities saves on computational costs. In studies using GPLVM-based methods, the best working settings are generally reported without explanation. Some examples include iteration T = 15 for GPLVM (Lawrence, 2005), outer loop iteration I = 100 for GPDM (Wang et al., 2008), and no mention for Hierarchical-GPLVM (Lawrence and Moore, 2007). Notably, these methods have been demonstrated to generalize well despite few iterations and training samples.

5. Conclusion

This study aims to address some of the problems in existing telehealth systems. We first modified the GPDM algorithm, which allowed us to extract simple yet meaningful feedback mechanisms for self-correction in physiotherapy exercises. These mechanisms allow for whole-body movements and are personalized through expert-induced demonstrations. Our framework is appropriate for telehealth due to its ability to train a sensible model using only a small number of good examples. We confirmed its utility using sit-to-stand motion data, an important physiotherapy exercise.

We imagine that this research can take on two interesting directions. First, incorporating modalities other than motion can be used to extend the current framework. A multi-modal model can be an interesting approach to incorporate more assessment tools used by the PT. Second, our approach was designed with physiotherapy in mind, but it can be reasonably applied to arbitrary motor tasks where expert demonstrations are available, e.g., sports science. Instead of learning expert-induced movements, learning the expert motor skill itself is also an interesting possibility.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Ethics Statement

The studies involving human participants were reviewed and approved by the Nara Institute of Science and Technology Ethics Review Committee for research involving human participants. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

BL and TT conceived, designed, and performed the experiments. BL developed the software, analyzed the data, prepared tables and figures, and wrote the manuscript. All authors designed the study, contributed to data interpretation and manuscript revision, and read and approved the submitted version.

Funding

This work was supported in part by JSPS-KAKENHI grant number 18K19821 and the NAIST Big Data Project.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work made use of the Sheffield Machine Learning group's publicly-available package of GPLVM codes (https://github.com/SheffieldML/GPmat).

References

Anderson, F., Grossman, T., Matejka, J., and Fitzmaurice, G. (2013). “Youmove: enhancing movement training with an augmented reality mirror,” in Proceedings of the 26th Annual ACM Symposium on User Interface Software and Technology (St. Andrews, UK: ACM), 311–320.

Google Scholar

Bahrami, F., Riener, R., Jabedar-Maralani, P., and Schmidt, G. (2000). Biomechanical analysis of sit-to-stand transfer in healthy and paraplegic subjects. Clin. Biomech. 15, 123–133. doi: 10.1016/S0268-0033(99)00044-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Butepage, J., Black, M. J., Kragic, D., and Kjellstrom, H. (2017). “Deep representation learning for human motion prediction and classification,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Honolulu, HI), 6158–6166.

Google Scholar

Cao, Z., Simon, T., Wei, S.-E., and Sheikh, Y. (2017). “Realtime multi-person 2d pose estimation using part affinity fields,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Honolulu, HI), 7291–7299.

PubMed Abstract | Google Scholar

Chen, J., Kim, M., Wang, Y., and Ji, Q. (2009). “Switching gaussian process dynamic models for simultaneous composite motion tracking and recognition,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition (Miami Beach, FL: IEEE), 2655–2662.

Google Scholar

Damianou, A. C., Titsias, M. K., and Lawrence, N. D. (2016). Variational inference for latent variables and uncertain inputs in gaussian processes. J. Mach. Learn. Res. 17, 1425–1486. Available online at: http://www.jmlr.org/papers/v17/damianou16a.html

Google Scholar

Gupta, A., Chen, T., Chen, F., Kimber, D., and Davis, L. S. (2008). “Context and observation driven latent variable model for human pose estimation,” in 2008 IEEE Conference on Computer Vision and Pattern Recognition (Anchorage, AK: IEEE), 1–8.

Google Scholar

Higo, M., and Khan, H. T. (2015). Global population aging: unequal distribution of risks in later life between developed and developing countries. Glob. Soc. Policy 15, 146–166. doi: 10.1177/1468018114543157

CrossRef Full Text | Google Scholar

Hof, A. L. (1996). Scaling gait data to body size. Gait Posture 3, 222–223. doi: 10.1016/0966-6362(95)01057-2

CrossRef Full Text | Google Scholar

Hornik, K., Stinchcombe, M., and White, H. (1989). Multilayer feedforward networks are universal approximators. Neural Netw. 2, 359–366. doi: 10.1016/0893-6080(89)90020-8

CrossRef Full Text | Google Scholar

Kato, N., Tanaka, T., Sugihara, S., and Shimizu, K. (2015). Development and evaluation of a new telerehabilitation system based on VR technology using multisensory feedback for patients with stroke. J. Phys. Ther. Sci. 27, 3185–3190. doi: 10.1589/jpts.27.3185

PubMed Abstract | CrossRef Full Text | Google Scholar

Kwong, P. W., Ng, S. S., Chung, R. C., and Ng, G. Y. (2014). Foot placement and arm position affect the five times sit-to-stand test time of individuals with chronic stroke. Biomed. Res. Int. 2014:636530. doi: 10.1155/2014/636530

PubMed Abstract | CrossRef Full Text | Google Scholar

Lang, C. E., MacDonald, J. R., and Gnip, C. (2007). Counting repetitions: an observational study of outpatient therapy for people with hemiparesis post-stroke. J. Neurol. Phys. Ther. 31, 3–10. doi: 10.1097/01.NPT.0000260568.31746.34

PubMed Abstract | CrossRef Full Text | Google Scholar

Lang, C. E., MacDonald, J. R., Reisman, D. S., Boyd, L., Kimberley, T. J., Schindler-Ivens, S. M., et al. (2009). Observation of amounts of movement practice provided during stroke rehabilitation. Archiv. Phys. Med. Rehabil. 90, 1692–1698. doi: 10.1016/j.apmr.2009.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawrence, N. (2005). Probabilistic non-linear principal component analysis with gaussian process latent variable models. J. Mach. Learn. Res. 6, 1783–1816. Available online at: http://www.jmlr.org/papers/v6/lawrence05a.html

Google Scholar

Lawrence, N. D., and Moore, A. J. (2007). “Hierarchical gaussian process latent variable models,” in Proceedings of the 24th International Conference on Machine Learning (Corvallis, OR:ACM), 481–488.

Google Scholar

Lee, A. C., Davenport, T. E., and Randall, K. (2018). Telehealth physical therapy in musculoskeletal practice. J. Orthop. Sports Phys. Ther. 48, 736–739. doi: 10.2519/jospt.2018.0613

PubMed Abstract | CrossRef Full Text | Google Scholar

Motion Analysis Corporation (2006). EVaRT 5.0 User's Manual. Santa Rosa, CA: Motion Analysis Corporation.

Google Scholar

Piqueras, M., Marco, E., Coll, M., Escalada, F., Ballester, A., Cinca, C., et al. (2013). Effectiveness of an interactive virtual telerehabilitation system in patients after total knee arthroplasty: a randomized controlled trial. J. Rehabil. Med. 45, 392–396. doi: 10.2340/16501977-1119

CrossRef Full Text | Google Scholar

Schopp, L., Johnstone, B., and Merrell, D. (2000). Telehealth and neuropsychological assessment: new opportunities for psychologists. Prof. Psychol. Res. Pract. 31:179. doi: 10.1037/0735-7028.31.2.179

CrossRef Full Text | Google Scholar

Sunaryadi, Y. (2016). “The role of augmented feedback on motor skill learning,” in 6th International Conference on Educational, Management, Administration and Leadership (Bandung: Atlantis Press).

Google Scholar

Tang, A., and Dillman, K. (2013). Towards Next-Generation Remote Physiotherapy With Videoconferencing Tools. Technical report, University of Calgary.

Google Scholar

Tang, R., Yang, X.-D., Bateman, S., Jorge, J., and Tang, A. (2015). “Physio@ home: exploring visual guidance and feedback techniques for physiotherapy exercises,” in Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems (Seoul: ACM), 4123–4132.

Google Scholar

Tully, E. A., Fotoohabadi, M. R., and Galea, M. P. (2005). Sagittal spine and lower limb movement during sit-to-stand in healthy young subjects. Gait Posture 22, 338–345. doi: 10.1016/j.gaitpost.2004.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

United Nations (2019). World Population Ageing 2019: Highlights New York, NY: United Nations, Department of Economic and Social Affairs, Population Division.

Google Scholar

Velloso, E., Bulling, A., and Gellersen, H. (2013). “Motionma: motion modelling and analysis by demonstration,” in Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (Paris: ACM), 1309–1318.

Google Scholar

Wang, J., Fleet, D., and Hertzmann, A. (2008). Gaussian process dynamical models for human motion. IEEE Trans. Pattern Anal. Mach. Intell. 30:283. doi: 10.1109/TPAMI.2007.1167

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, U., and Kim, G. J. (2002). Implementation and evaluation of “just follow me”: an immersive, vr-based, motion-training system. Presence Teleoper. Virt. Environ. 11, 304–323. doi: 10.1162/105474602317473240

CrossRef Full Text | Google Scholar