Segments-aware universal adversarial perturbations purification on 3D point cloud classifiers

Introduction: 3D point cloud classifiers, while powerful for representing real-world objects and environments, are vulnerable to adversarial perturbations, particularly Universal Adversarial Perturbations (UAPs). These UAPs pose significant security threats due to their input-agnostic nature. Current purification methods exhibit critical limitations: they typically operate independently of the target classifier and treat perturbations as isolated points without considering the coherent, structural nature of UAPs in 3D point clouds (such as outlier-like shapes with continuous curvature). This fundamental oversight limits their effectiveness, primarily because distinguishing between genuine geometric features and structured adversarial patterns presents a significant challenge.

Methods: We propose a novel purification framework that leverages model interpretability to identify and remove adversarial regions in a holistic manner. Our approach uniquely identifies influential regions within adversarial samples that maximally impact the classifier's predictions. Recognizing that UAPs often manifest as structured segments rather than random points, we employ graph wavelet transforms to isolate suspicious curvature segments. These identified segments undergo a transplantation test where they are transferred to clean samples; segments are classified as adversarial if this transfer consistently induces misclassification. The identified adversarial regions are then removed to sanitize the point cloud. This model-guided, structure-aware approach treats UAPs as coherent structures rather than isolated perturbations.

Results: We conducted extensive experiments on two public 3D point cloud datasets using four different state-of-the-art classifiers. Our framework demonstrated remarkable improvements in robustness against various UAP attacks compared to existing purification methods. The results show significant accuracy recovery rates after purification, with consistent performance across different classifier architectures and attack methods. Our method particularly excels at preserving genuine geometric features while removing adversarial structures, maintaining high classification accuracy on clean samples while effectively neutralizing UAP threats.

Discussion: Our findings demonstrate that considering the structural nature of UAPs and leveraging model interpretability are crucial for effective defense. Unlike previous point-wise approaches, our framework's ability to identify and process coherent adversarial segments addresses the fundamental limitation in current purification methods. The transplantation test provides a reliable mechanism to distinguish between legitimate features and adversarial artifacts. This work highlights the importance of model-guided purification strategies and opens new directions for defending geometric deep learning systems against structured adversarial attacks. Future work could extend this approach to other geometric data representations and explore adaptive defense mechanisms against evolving attack strategies.

1 Introduction

3D point clouds are an ideal format for describing the real world, which consists of unorganized 3-dimensional coordinates, providing a direct representation of the surfaces of objects and environments captured by sensors such as LiDAR, structured light systems, or depth cameras. Starting from the analysis requirement of such data, 3D Point Cloud Classifiers has achieved extensive research attention and also shown outstanding performance on various applications, such as healthcare (Mozaffari-Kermani et al., 2014), self-driving cars (Badue et al., 2021), drones (Hassanalian and Abdelkefi, 2017), robotics (Pierson and Gashler, 2017), and many other applications (Zhu et al., 2024; Ma et al., 2022).

Among the various types of adversarial perturbations (Szegedy et al., 2014; Zhang et al., 2024; Hu et al., 2023; Khaddaj et al., 2023; Mo et al., 2024; Liu et al., 2023), Universal Adversarial Perturbations (UAPs) (Zhang et al., 2020) are considered to be one of the most threatening ones. Since UAPs can be applied to any input, so that poses a significant threat to the robustness and reliability of machine learning systems in real-world applications (Zhang et al., 2021). Basically, UAPs refer to a class of indistinguishable perturbations applied across an entire inputs. Unlike traditional adversarial attacks that generate perturbations specific to individual inputs, UAPs are crafted to be effective across a diverse range of inputs, making them particularly potent and challenging to defend against (Mopuri et al., 2019).

In response to this challenge, several notable purification techniques have been proposed to counteract UAPs in 3D point clouds. For instance, SOR (i.e., Statistical Outlier Removal) leverages explicit statistical rules to analyze local point density distributions, identifying and removing potential outliers that may contain perturbations. On the other hand, DUP-Net and IF-Defense exploit the generative capabilities of deep learning models by feeding suspicious point clouds into pre-trained networks for resampling, thereby producing refined, denoised versions.

However, a key limitation of these methods is their independence from the victim classifier's information. By relying solely on the intrinsic patterns of clean data for purification, they often yield sub-optimal defense performance. More importantly, in the context of 3D point clouds, UAPs typically manifest as coherent, outlier-like structures with continuous curvature and even semantic meaning, such as a ball or stick-shaped object (Naderi and Bajić, 2023). This characteristic complicates the distinction between legitimate geometry and adversarial perturbation, making it difficult for model owners to determine whether such shapes are genuine or malicious. Existing approaches largely overlook this structural nature of UAPs, instead focusing on individual points as the primary unit of analysis. As a result, they fail to fully capture and neutralize the holistic structure of adversarial perturbations, limiting their effectiveness in achieving comprehensive sanitization.

In this paper, we propose a novel purification framework that leverages model interpretability to identify and remove adversarial regions in 3D point clouds. Our method focuses on detecting the most influential regions in adversarial samples—those that significantly affect the model's prediction—as likely locations of perturbation. Our defense operates in a white-box scenario, where the defender has full access to the target model's architecture and parameters. Considering that UAPs often are outlier-like structures with continuous curvature, we apply graph wavelet transforms to extract suspicious curvature segments and treat these segments as the primary unit of analysis. Then, given the universal nature of UAPs, truly adversarial segments should induce misclassification when transferred to clean samples. We therefore classify a region as adversarial if its transplantation consistently degrades model performance. Once identified, these regions are removed to purify the original point cloud.

Our contributions are summarized as follows:

• Model-guided purification: The method uses the target model's own feedback (interpretability) to find the input regions most responsible for causing misclassifications, assuming these are the adversarial parts.

• Structural UAP analysis: It treats UAPs as coherent structures (not just points), using graph wavelets to find suspicious segments and verifying them with a novel transplantation test.

• Remarkable results: We evaluate our approach on two public real-world datasets and four 3D point cloud classifiers. The experimental results demonstrate the efficiency of our methods.

2 Related works

2.1 Adversarial perturbations on 3D point clouds

The Adversarial Perturbations was first introduced in Szegedy et al. (2014), which has demonstrated that the performance of a well-trained DNN can be significantly weakened by adversarial examples, which can be crafted by adding the human-imperceptible perturbation on the original examples.

Threateningly, the universal adversarial perturbations (UAPs), was developed. UAP is a fixed perturbation that can be added directly to various clean examples, resulting in misleading classification when these victim examples have been fed into a well-trained target model. UAP was first introduced by Moosavi-Dezfooli et al. (2017), in which they proposed an algorithm based on the image-dependent DeepFool attack (Moosavi-Dezfooli et al., 2016). The core idea is to calculate the minimum perturbation from each example to the decision boundary and iteratively accumulate these perturbations to find a universal perturbation. After that, Mopuri et al. (2017) introduced a method without access to target training data by maximizing the mean activations at multiple layers of the network when the input is the universal perturbation, which can only perform non-targeted attacks and the results are not as strong as (Moosavi-Dezfooli et al., 2017). Based on FFF, additional prior information about the data distribution is introduced to improve the fooling ability (Mopuri et al., 2019).

Moreover, Yang et al. (2019) used the Chamfer distance (instead of the ℓ₂-norm) between the original point cloud and the adversarial counterpart to extend the FGSM to 3D. One of the most potent attacks on 3D data is the Projected Gradient Descent (PGD), whose foundation is the pioneering work by Madry et al. (2017). Ma et al. (2020) proposed the Joint Gradient Based Attack (JGBA). They added an extra term to the objective function to defeat statistical outlier removal (SOR), a common defense against attacks.

Beyond these foundational methods, recent research has increasingly focused on enhancing the imperceptibility of input-specific attacks, ensuring the adversarial point clouds remain visually indistinguishable from their benign counterparts by preserving complex geometric properties. A significant trend in this area involves constraining perturbations to the object's underlying 2-manifold surface, preventing unnatural outliers. For instance, some work formulates a manifold attack that generates adversarial examples by learning to stretch a 2D parameter plane, which then deforms the 3D surface smoothly via a generative network (Tang et al., 2023b). Following a similar principle, other researchers have proposed enforcing manifold constraints through a bijective mapping to a parameter space; by preserving local properties in this simpler space, manifold-aware distortion on the 3D object is effectively mitigated (Tang et al., 2024).

Other innovative approaches tackle imperceptibility from different geometric perspectives. To address the issue of non-uniform point distributions caused by perturbations, the FLAT framework assesses uniformity changes by calculating the flux of the local perturbation vector field, adjusting perturbation directions to maintain visual consistency (Tang et al., 2025). Concurrently, research has also explored the effectiveness of directional perturbations. The Normal-Tangent Attack (NTA) framework, for example, moves beyond simple gradient guidance by creating a hybrid scheme that adaptively chooses perturbation directions—either along the surface normal or the tangent plane—based on the local curvature of the point cloud, thereby achieving a better balance between attack efficacy and imperceptibility (Tang et al., 2023a). These methods highlight a clear trajectory in the field toward creating more sophisticated and stealthy adversarial attacks.

2.2 Adversarial defense on 3D point clouds

There is no 3D point cloud adversarial defense method developed specifically for UAP, however, existing 3D point cloud adversarial defense methods can be used for UAP defense as well and are the only option from an engineering standpoint (Gao et al., 2023; Bian et al., 2024).

Zhou et al. (2019) utilized a statistical outlier removal (SOR) based defense method for point cloud data purification. The method is implemented as follows: for each point in the adversarial point cloud, its average distance from it's k nearest neighbors is calculated, and if this distance exceeds a threshold, the point is judged as an outlier and removed.

DUP-Net (Zhou et al., 2019) is a network architecture for defense against 3D adversarial point cloud attacks. Its main principle is to enhance the robustness of point cloud data by reconstructing the surface smoothness through Statistical Outlier Removal (SOR) and a data-driven upsampling network. DUP-Net first uses SOR to remove outliers that exceed a threshold, thereby reducing the number of noise points introduced by adversarial attacks. The second step is to reconstruct the surface smoothness of the point cloud using an upsampling network (Yu et al., 2018), which produces a denser point cloud that fills in critical points lost due to the attack and further restores the original structure of the point cloud. The total loss function combines the reconstruction loss and the rejection loss to ensure the accuracy of the denoising and up-sampling process.This dual mechanism of DUP-Net allows it to excel in defending against adversarial attacks and significantly improves the robustness of the point cloud classification model.

IF-Defense (Wu et al., 2020) is a 3D adversarial point cloud defense framework based on implicit function optimization designed to cope with both point perturbation and surface distortion attacks. Its core idea is to recover the attacked point cloud to a clean state through learning. Specifically, IF-Defense optimizes the coordinates of the input points by means of geometry-aware and distribution-aware constraints to restore the surface of the point cloud and remove perturbations in the point distribution. Its first step is to use SOR to remove outliers in the input point cloud. Then, two loss functions are used to optimize the coordinates of the remaining points to satisfy the geometric and distributional constraints. The geometry-aware loss function attempts to push points toward the surface to improve smoothness. To estimate the surface of an object, the authors trained an independent network of hidden functions (Peng et al., 2020; Mescheder et al., 2019). Since the output of the implicit function is continuous, the predicted surface is locally smooth. This reduces the effect of residual outliers. The second, distribution-aware loss function, encourages points to have a uniform distribution by maximizing the distance between each point and its k nearest neighbors. As a result, IF-Defense generates a smooth, uniformly sampled point cloud.

3 Methodology

3.1 Primary

Before presenting the details of our method, we first define the notation and formalize the goal of generating a universal adversarial perturbation (UAP). Specifically, we aim to find a fixed perturbation δ that, when added to most clean point clouds from the data distribution $\mathcal{P}$, causes the target model to misclassify them. Mathematically, this can be expressed as:

$\begin{array}{ll}f(P+\delta )\ne f(P)\text{for most }P~\mathbb{P},& (1)\end{array}$

where f(·) denotes the target classification model, and P represents a point cloud sampled from ℙ. The predicted label of P is denoted by y_p = f(P).

To better understand how such perturbations affect the model behavior, we now briefly describe the structure of the target model f. A point cloud $P={\left\{x_i\right\}}_{i=1}^N$ consists of N points in ℝ³, where each x_i represents the 3D coordinates of a point. The model f typically comprises multiple layers of neural network operations, which can be written as a composition of functions:

$\begin{array}{ll}f(P)=f^{(L)}(f^{(L-1)}(f^{(L-2)}(\cdots f^{(1)}(P)))),& (2)\end{array}$

where f^(l)(·) denotes the output of the l-th layer given input P. For simplicity, we use f^(l)(P) to refer to the feature representation at layer l.

This hierarchical structure allows us to analyze the propagation of adversarial effects through different layers of the model, which is essential for designing effective universal perturbations.

3.2 Threat model

Before detailing our methodology, it is crucial to define the operational scenario. We address a white-box defense setting. In this scenario, the defender has complete knowledge of the target classifier, f, which they aim to protect. This includes full access to the model's architecture, parameters (weights), and the ability to compute internal states and gradients, such as those required for Grad-CAM.

This assumption is practical for many real-world applications. For instance, a company deploying a proprietary 3D recognition model (e.g., in an autonomous vehicle or a quality control system) would have full access to its own model and would want to secure it against adversarial inputs from external sources. The attacker, on the other hand, may have generated the Universal Adversarial Perturbation (UAP) under black-box, gray-box, or white-box conditions. Our defense is agnostic to the attack's generation process but leverages the defender's white-box access to perform the purification.

This distinguishes our approach from model-agnostic (black-box) defenses like Statistical Outlier Removal (SOR), which do not utilize information from the victim classifier. By operating in a white-box context, our method can create a more tailored and effective defense by directly probing the model's response to identify and neutralize adversarial structures.

3.3 Pre-localization of suspicious areas

Against the fact that perturbations have a significant impact on the prediction results of the model, and without knowing which points are in the point cloud, our approach is to quantify the impact of all the points in the point cloud on the prediction results using model interpretability techniques, as shown in Figure 1.

Figure 1

Figure 1. Thermodynamic representation of the 3D point cloud with UAPs.

Grad-CAM (Selvaraju et al., 2017) is effective in revealing the model's decision-making rationale, identifying the data regions that the model focuses on when making classification decisions and their impact on the final result Grad-CAM can effectively reveal the decision basis of the model and identify the data areas that the model focuses on when making classification decisions and their influence on the final results. This can help us to initially identify areas of suspicious perturbation.

Since Grad-CAM was originally designed for 2D image-related models rather than 3D point cloud-related models, some modifications are necessary for Grad-CAM. For point cloud models, the process typically involves two stages: in the first stage, the model attempts to extract features from each point; in the second stage, due to the involvement of pooling layers, these features are further aggregated to extract the overall features of the point cloud. Considering that some models may include non-differentiable sampling or other operations in the second stage, we primarily use the features extracted in the first stage, i.e., per-point features. In this paper, unless otherwise specified, f^(l) represents per-point features, i.e., $f^{(l)}=\left\{x_i^{(l)}\right\}\in {ℝ}^{N\times d}$, where $x_i^{(l)}$ denotes the feature of point x_i at layer l of the model.

The attention of model f on point x_i in the point cloud is given by:

$\begin{array}{ll}{a}_i^{(l)}=||\frac{\partial C{E}_f(P,y_P)}{\partial x_i^{(l)}}{||}_2,& (3)\end{array}$

here, CE_f represents the cross-entropy loss computed on model f. For different tasks, the loss function may vary; here we use the most common point cloud classification task as an example.

The attention of model f on point x_i in the point cloud can be obtained using the following formula:

$\begin{array}{ll}{a}_i=\frac{1}{L^{\prime }}{\displaystyle \sum _{l=0}^{L^{\prime }}}\frac{a_i^{(l)}}{||\nabla f^{(l)}C{E}_f(P,y_P){||}_F},& (4)\end{array}$

here, L′ is the number of layers included in the first stage of the model. The denominator $\left|\right|\nabla f^{(l)}C{E}_f(P,y_P)|{|}_F$ is a normalization term, representing the gradient of f^(l) with respect to CE_f, and Frobenius norm is used for normalization.

After obtaining the attention coefficients, a straightforward approach is to sort all these coefficients and designate the top k percent of points as suspicious regions. However, considering the stealthiness required for adversarial attacks, universal adversarial perturbations often manifest as collections of points with continuous curvature (and usually semantic meaning), such as spherical or rod-like shapes. These shapes make it difficult for humans to discern whether they are naturally occurring features or malicious perturbations.

From the perspective of accuracy in removing perturbations, it is essential at this stage to align with the characteristics of universal adversarial perturbations by defining suspicious regions as clusters of high-attention points that exhibit continuous curvature. Therefore, a simple extractor based on graph wavelet transform is introduced to identify segments with continuous curvature, as shown in the following section.

3.4 Extraction of continuous curvature segments

For a point cloud $P={\left\{x_i\right\}}_{i=1}^N$, by calculating the Euclidean distance between each pair of points, we can construct a K-nearest neighbor graph, forming an isomorphic, unweighted, undirected graph G_P = (V, E), where V is the set of vertices corresponding to the points in the point cloud, and E is the set of edges. The construction method is as follows:

$\begin{array}{ll}E=\left\{(x_i,x_j)\mid x_i\in N_j\text{or }{x}_j\in N_i\right\},& (5)\end{array}$

here, N_i is defined as:

$\begin{array}{ll}{N}_i=\left\{x_j\mid d(x_i,x_j)<d_k\right\},& (6)\end{array}$

where d_k is the distance to the k-th nearest neighbor, measured using the Euclidean distance.

As a preparation of our graph wavelet, we perform farthest point sampling on the point cloud. The core idea is to start from a randomly chosen initial point and iteratively select the point that is farthest from the already selected points as the new sample point until the desired number of samples is reached. This method ensures that the selected points are as evenly distributed as possible across the entire point cloud space, thereby preserving the spatial structure information of the original data. Since the farthest points are always chosen, the final set of selected points maintains good uniformity throughout the space. Empirically, sampling 32 points from P using farthest point sampling is sufficient for most needs.

The next task is to construct continuous curvature segments centered around each sampled point. To achieve this, we first compute the normalized Laplacian matrix of the graph G_P:

$\begin{array}{ll}{\tilde{L}}_P=I-D_P^{-\frac{1}{2}}{A}_P{D}_P^{-\frac{1}{2}},& (7)\end{array}$

where A_P is the adjacency matrix corresponding to G_P, and D_P is the degree matrix, which is a diagonal matrix with the degrees of the corresponding nodes on its diagonal.

The Laplacian matrix ${\tilde{L}}_P$ is a semi-positive definite real symmetric matrix, and its eigenvalues lie in the interval [0, 2], making it easy to perform eigen-decomposition to obtain a set of mutually orthogonal bases:

$\begin{array}{ll}{L}_P=U\Lambda U^T,& (8)\end{array}$

where U represents the orthogonal matrix composed of feature vectors, and Λ is a diagonal matrix formed by the eigenvalues. Therefore, we can establish a filter bank using the eigenvalues as inputs to obtain wavelet coefficients, i.e.,

$\begin{array}{ll}{\psi }_{s,i}=U\Lambda (g_s(\lambda ))U^T{h}_i,& (9)\end{array}$

where g_s is the filter at scale s, and $h_i\in {ℝ}^N$ is a one-hot encoded vector that is 1 only at position i and 0 elsewhere, representing an impulse signal centered at node i on the graph. In wavelet transforms, to ensure signal recoverability, g_s is typically a band-pass filter, i.e., g_s(0) = 0 and $\underset{\lambda \to \infty }{lim}{g}_s(\lambda )\to 0$. Specifically, in engineering applications, g_s is often chosen as the Mexican hat function, which can be obtained through the second derivative of a Gaussian function. Additionally, for the simple task of extracting curvature segments, s can be fixed to a single value, indicating that only a suitable filter at a specific scale is needed rather than a multi-scale filter bank.

Specifically, ${\psi }_{s,i}\in {ℝ}^N$ can be interpreted as the contribution of node i to other nodes, or more specifically, the energy diffused from node i to node j. In terms of the practical significance of point cloud data, each ψ_{s, i} represents the local geometric structure and semantic context within the neighborhood of node i. Therefore, we can define the curvature segment ${\mathcal{P}}_i$ centered at i using a threshold ε:

$\begin{array}{ll}{\mathcal{P}}_i=\left\{x_j\mid {\psi }_{s,i}\left[j\right]>\epsilon \right\}.& (10)\end{array}$

By extracting the curvature segments corresponding to the points sampled via farthest point sampling, we proceed to calculate the attention score for each segment. For each curvature segment, we sum and average the attention scores a_i of all points within the segment to compute the overall attention score of the segment. After sorting these scores, we obtain the suspicious curvature segments and output them as the final suspicious regions.

3.5 Assessment of regions for UAPs presence

After obtaining the suspicious regions, the next task is to determine whether these regions are adversarial perturbations by leveraging the generalization capability of universal adversarial samples. To achieve this, we first overlay the suspicious region (denoted as $\mathcal{P}$) onto multiple normal point clouds, expressed as:

$\begin{array}{ll}\hat{P}=P+(\mathcal{P}\odot M),& (11)\end{array}$

where M is a mask matrix sampled randomly from a Bernoulli distribution, i.e., M~Bernoulli(0.2). The symbol ⊙ denotes the Hadamard product. Note that from the perspective of matrix computation, $\hat{P}$, P, and $\mathcal{P}$ need to be padded to a uniform size before this step, typically using 0-padding.

To enhance the accuracy of identifying suspicious regions, Gaussian noise is also used as an additional control group to further distinguish between adversarial effects and simple occlusion effects, i.e.,:

$\begin{array}{ll}\hat{P}=P+R,& (12)\end{array}$

where R~Gaussian(μ_p, Σ_n), and the noise parameters μ_p and Σ_n can be estimated from clean point clouds.

Note that for the same suspicious region $\mathcal{P}$, multiple samplings of M are performed to generate diverse classification results. Experiments show that the probability of correct classification caused by real universal adversarial perturbations is less than 0.3, which forms a significant contrast with normal regions.

3.6 Optional steps for purging UAPs

In the previous step, we have initially identified the UAPs, which makes the removal of UAPs simple and straightforward: remove the points or set the coordinates of the points to zero.

Specifically, by analyzing the number of point clouds deceived by the suspicious region $\mathcal{P}$ and the changes in confidence on the correct class, we can determine whether the input $\mathcal{P}$ has adversarial properties. A simple method is to make decisions based on threshold rules, but this approach makes it difficult to determine appropriate thresholds and which indicators are more important.

Therefore, a very simple classifier is trained using metrics collected from the control group and suspicious samples. Specifically, based on two key indicators—the misclassification rate (FR) and the confidence drop (Δconf), k-means clustering into 2 classes is performed. Since the control group is known not to be an adversarial perturbation, this clustering model can actually be used directly to distinguish adversarial perturbations.

Compared with traditional fixed-threshold methods, this mechanism can adaptively learn the feature distribution patterns of normal samples, effectively addressing the challenges of threshold parameter selection and multi-indicator weight balancing. To achieve this, first perform min-max normalization on the features $\varphi =\left[\overline{FR},\overline{{\Delta }_{conf}}\right]$ formed by the misclassification rate (FR) and the confidence drop (Δconf). Then, map the features to a high-dimensional space using a radial basis kernel function:

$\begin{array}{ll}\varphi =exp(-\gamma |\varphi -{\varphi }_i{|}^2),& (13)\end{array}$

where γ controls the sensitivity range of the kernel function and is fixed at 0.5. Next, randomly select 2 samples as initial cluster centers, denoted as $\left\{c_1^0,c_1^1\right\}$. For each sample ϕ_t, calculate its distance to each cluster center $\left\{c_1^0,c_1^1\right\}$ and assign it to the cluster corresponding to the nearest cluster center. The distance metric typically uses Euclidean distance. The probability that sample ϕ_i is assigned to the k-th cluster is expressed as:

$\begin{array}{ll}{r}_{ik}=\{\begin{array}{ll}1\hfill & \text{if }k=\arg {\min }_j\left|\right|\mathit{\varphi }-c_j|{|}^2,\hfill \\ 0\hfill & \text{else}.\hfill \end{array}& (14)\end{array}$

For each cluster, update its cluster center to the mean of all samples in that cluster. The new cluster center is represented as:

$\begin{array}{ll}{c}_k=\frac{{\displaystyle {\sum }_{i=1}^n}{r}_{ik}\varphi }{{\displaystyle {\sum }_{i=1}^n}{r}_{ik}}.& (15)\end{array}$

Repeat the calculation process for r_ik and c_k until the cluster centers converge or reach the maximum number of iterations. After obtaining the final cluster centers, for subsequent other suspicious regions, their normalized features $\left[\overline{FR},\overline{{\Delta }_{conf}}\right]$ can be directly extracted, and calculating the distance to the cluster centers can determine whether the region is an adversarial perturbation.

Once the suspicious region is determined to be an adversarial perturbation, it can be removed, typically using zero-padding.

4 Experiments

4.1 Settings

4.1.1 Environments

The experiments were conducted on a high-performance computing server. This server was equipped with an Intel Xeon Gold 6230R processor featuring 104 logical cores clocked at 4.000GHz, 128GB of RAM, and an NVIDIA A100 graphics processing unit. The experimental environment utilized the Ubuntu operating system and leveraged the CUDA 12.2 library for GPU acceleration. All experiments were implemented and executed using Python 3.10, based on the PyTorch deep learning framework, version 2.4.

4.1.2 Dataset

This study evaluates the proposed method using two publicly available datasets: ModelNet40 and ShapeNet. The ModelNet40 dataset comprises 12,311 CAD models categorized into 40 distinct object classes. These models are partitioned into a training set containing 9,843 samples and a test set with 2,468 samples. Covering a diverse range of domains including furniture, vehicles, and animals, the dataset provides both raw 3D mesh models and pre-processed point cloud representations, facilitating their use in various 3D analysis tasks.

ShapeNet, a considerably larger and more comprehensive dataset of 3D CAD models, was jointly published by Stanford University, Princeton University, and the Toyota Technological Institute. ShapeNet encompasses over 55 common object classes and provides detailed annotations for each model, including class labels, semantic segmentation, functional descriptions, and other attributes.

4.1.3 Victim model

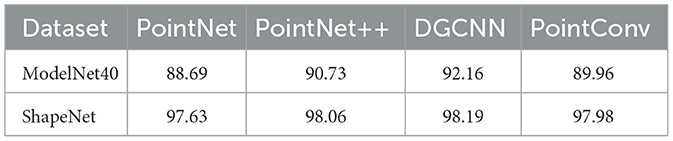
For experiments requiring a fixed-size input, 1024 points were uniformly sampled from the original point cloud data. As shown in Table 1, this study employs four widely-used 3D deep learning classifiers as victim models: PointNet (Qi et al., 2017a), PointNet++ (Qi et al., 2017b), DGCNN (Wang et al., 2019), and PointConv (Wu et al., 2019).

Table 1

Table 1. Classification accuracy of the target network on ModelNet40 and ShapeNet.

4.1.4 Attack methods

For evaluating defense performance against universal adversarial perturbations in 3D point clouds, we selected PointPBA-I and PointCBA (Zhou et al., 2020) from the existing literature on point cloud adversarial attacks.

Given the scarcity of publicly available UAP methods for 3D point clouds, we also developed two universal attack strategies based on the well-known FGSM (Goodfellow et al., 2014), APGD (Croce and Hein, 2020), and CW (Carlini and Wagner, 2017) attack principles. For all attacks, the universal perturbation was crafted using a randomly selected subset of 1,000 samples from the training set of the respective dataset (ModelNet40 or ShapeNet). The perturbation budget (number of adversarial points added) was set to 102, representing approximately 10% of the 1,024 points in a standard point cloud, unless specified otherwise in the attack budget experiments.

• PointPBA-I and PointCBA: These are state-of-the-art black-box attack methods. PointPBA (Point-based Boundary Attack) utilizes a simple yet effective binary search over the decision boundary, while PointCBA (Context-based Boundary Attack) enhances this by considering the geometric context of points. For our experiments, we adapted these input-specific attacks to generate a universal perturbation by iteratively accumulating the adversarial perturbations generated for each sample in our training subset and projecting the result back into the allowed perturbation space. We used the default hyperparameters from their respective papers, with an initial perturbation magnitude of 0.1 and 50 query iterations per sample.

• FGSM-based universal attack: The Fast Gradient Sign Method (FGSM) generates a perturbation in the direction of the sign of the gradient of the loss function. To create a universal perturbation, we employed an iterative version. In each iteration, a batch of training samples was passed through the target model, and the average gradient was computed. The universal perturbation δ was then updated by taking a small step in the direction of the sign of this average gradient. The process was repeated for 20 epochs over our training subset. The key parameters were:

– Step size (α): 0.007

– Perturbation bound (ϵ): 0.05 (L-infinity norm for point coordinates)

– Iterations: 20

• CW-based universal attack: The Carlini & Wagner (CW) attack is a powerful optimization-based attack that minimizes the perturbation distance while ensuring misclassification. We adapted it to generate a universal additive “adversarial object” (a small cluster of points). The optimization aims to find a set of points that, when added to any clean sample, maximizes the untargeted CW loss function. This optimization was performed iteratively over our training subset. The key parameters were:

– Learning rate: 0.01

– Confidence (κ): 0 (for untargeted attacks)

– Binary search steps: 9

– Max iterations: 100

• Auto-PGD (APGD)-based universal attack: Auto-PGD (APGD) is an extension of the classic Projected Gradient Descent (PGD) attack (Madry et al., 2017). Unlike PGD, APGD does not require a manually specified step size. Here, we set the Max Iterations to be 100.

4.1.5 Baselines

To provide a comprehensive comparison, we selected four state-of-the-art 3D point cloud denoising methods as baselines: PointCleanNet (PCN) (Rachmiel and Bruckstein, 2020), PointFilterNet (PFN) (Yuan et al., 2020), LPC (Implicit Gradient Defense) (Pang et al., 2020), and PointDP (Point Diffusion Purification) (Luo et al., 2021). For conciseness, these methods are denoted as PCN, PFN, LPC, and PDP, respectively.

• PCN (Rachmiel and Bruckstein, 2020): A data-driven approach designed to remove outliers and mitigate perturbations in point clouds. It first identifies and discards outlier samples, then projects perturbed points onto the estimated original surface by calculating correction vectors.

• PFN (Yuan et al., 2020): A filter network integrating filtering techniques with deep learning for point cloud denoising. PFN comprises two main components: an outlier recognizer and a denoiser, which generate distinct filter coefficients. Initially, the outlier recognizer produces coefficients to mitigate outlier disturbances, after which the denoiser iteratively refines the point cloud.

• LPC (Pang et al., 2020): Employs an implicit gradient defense mechanism against perturbations using a two-layer optimization framework. The outer loop minimizes the classification loss, while the inner loop introduces a declared node. This node reconstructs the point cloud via structured sparse coding, optimizing for the declared node to achieve purification.

• PDP (Luo et al., 2021): Utilizes a diffusion model for defending against adversarial attacks in 3D point cloud recognition. The primary objective is to purify adversarial perturbations through forward and inverse diffusion processes to recover the original clean point cloud.

• PointCVAR (Li et al., 2024): PointCVAR is the state-of-the-art outlier removal method using gradient-based attribution in deep learning for robust 3D point cloud classification task. This method can effectively filter out various types of noise points in point clouds.

4.1.6 Metrics

The primary evaluation metric used in this paper is classification accuracy (%). This metric quantifies the effectiveness of the proposed purification method by measuring the classification performance of victim models on point clouds after being subjected to universal adversarial perturbations and subsequent purification. A higher classification accuracy indicates more effective purification.

4.2 Comparative study

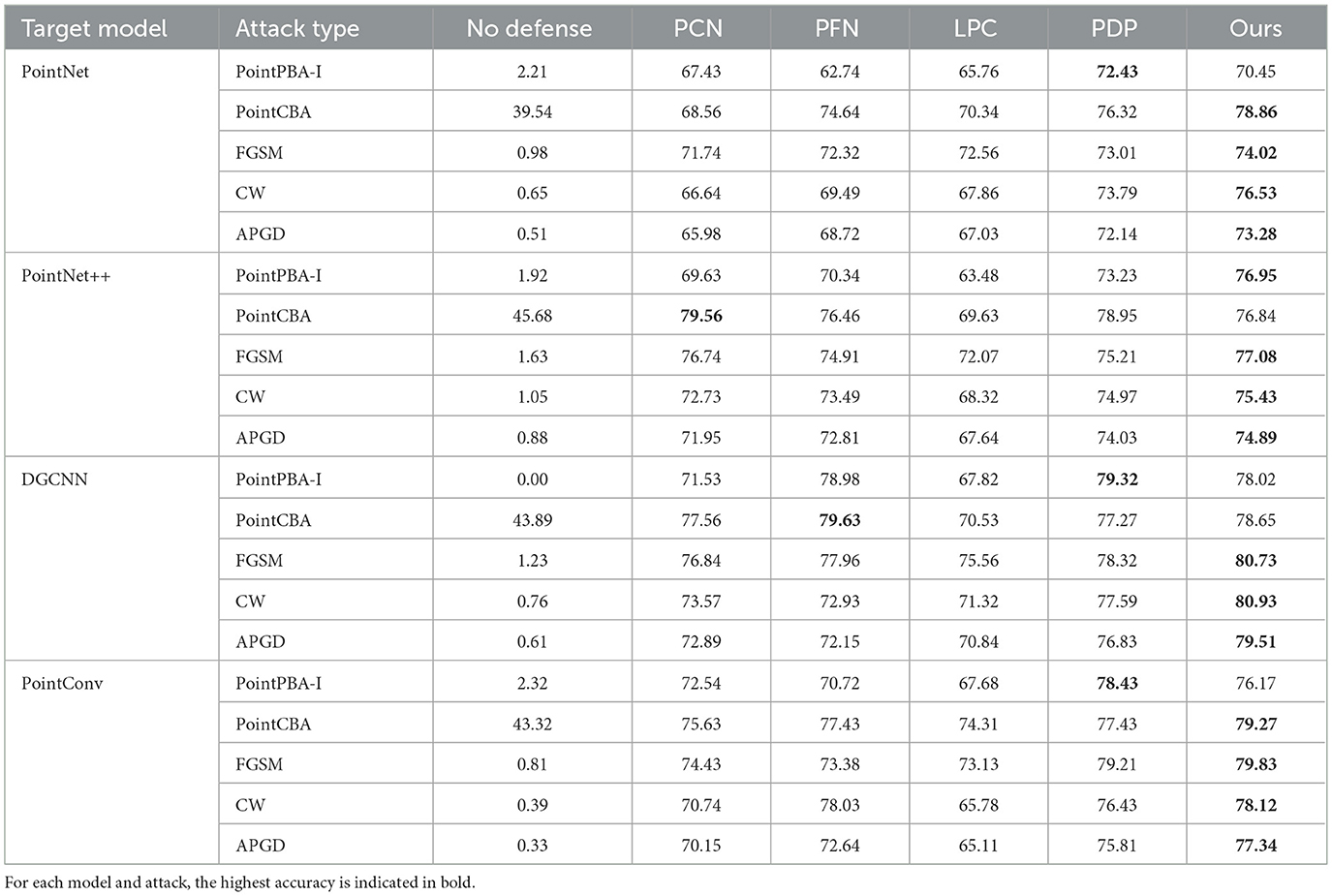
We first present a comparative analysis of the defense performance of our proposed method against the baselines (PCN, PFN, LPC, and PDP) under four different universal adversarial attack methods. The evaluation metric is classification accuracy. The test results on the ModelNet40 and ShapeNet datasets are summarized in Tables 2, 3, respectively.

Table 2

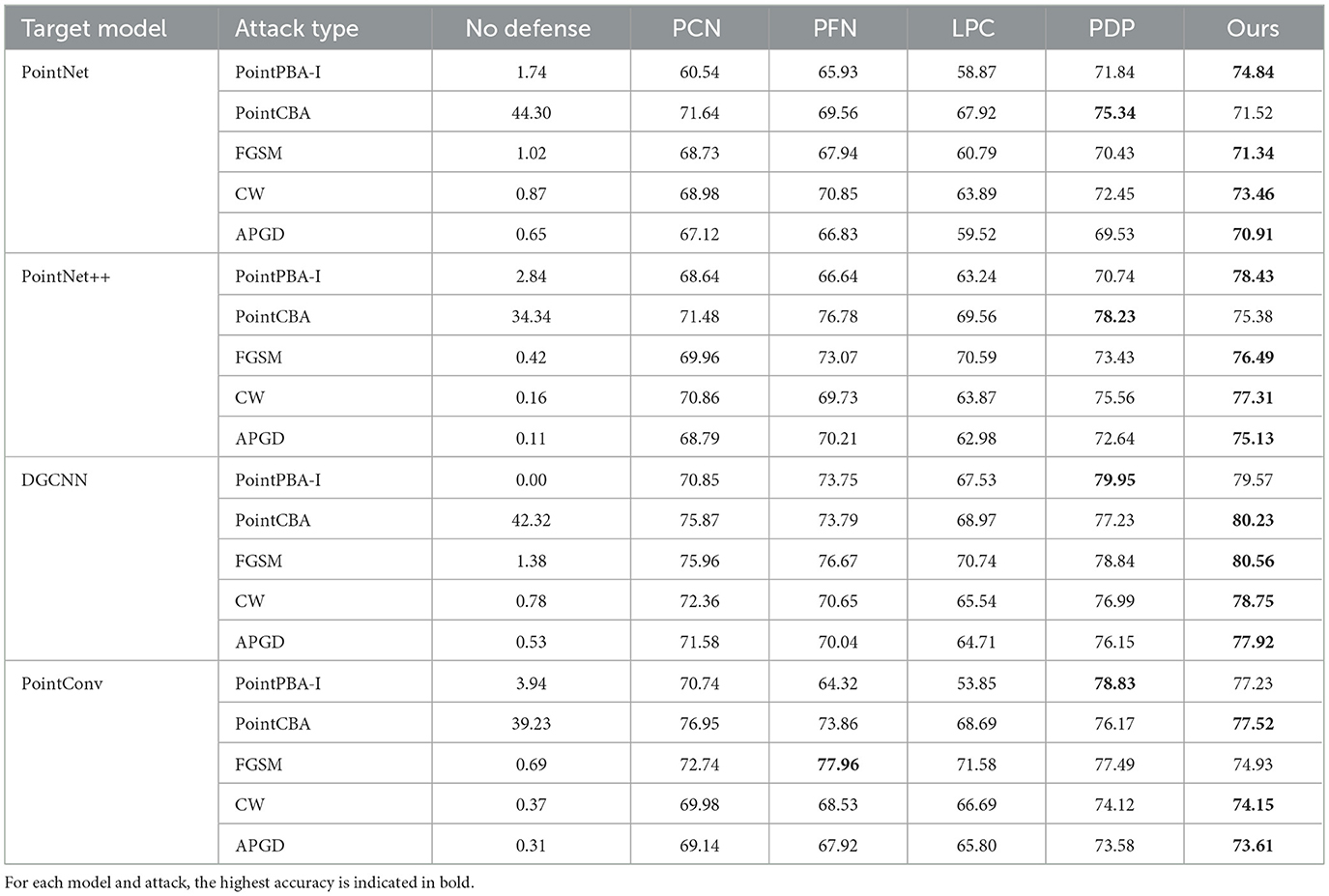
Table 2. Classification accuracy on the ModelNet40 dataset under different models and attack methods.

Table 3

Table 3. Classification accuracy on the ShapeNet dataset under different models and attack methods.

In the majority of cases, our proposed method demonstrates superior performance in defending against universal adversarial point clouds. The excellent performance of our method can be primarily attributed to two factors: (1) its reliance on model explainability, which enables precise region selection for the subsequent perturbation removal process. By deeply interpreting the model's decision-making and focusing on removing the most critical perturbations that significantly degrade performance, the efficiency of perturbation removal is enhanced. (2) the continuous curvature segment extraction method based on graph wavelet transforms aligns effectively with the characteristics of universal adversarial perturbations. Combining wavelet transforms with farthest point sampling allows for accurate identification and filtering of universal adversarial perturbations, leading to a more precise purification process.

As shown in Table 2, our method achieves an average classification accuracy of 76.35% across all ModelNet40 test scenarios, outperforming all baselines. The largest gains appear under the PointPBA-I attack, likely because PointPBA-I more severely disrupts the hierarchical structure of the original point clouds, steering model decisions toward adversarial features. Because our defense is grounded in model explainability, it more effectively identifies and mitigates such structural shifts. These results validate the effectiveness of an explainability-based defense for removing universal perturbations in point-cloud security. Across both ModelNet40 and ShapeNet, APGD drives the “No defense” accuracy near zero, while all defenses recover substantial performance; our method consistently achieves the highest robustness across PointNet, PointNet++, DGCNN, and PointConv, with PDP typically the runner-up and PCN/PFN/LPC trailing. Absolute accuracy under APGD varies by backbone, but strong defenses still reach roughly 70%–80% top-1 accuracy.

The defense performance of our method varies by attack. PointPBA-I is the most disruptive, yielding only 2.13% average accuracy on ModelNet40 without defense, yet our method restores it to 77.52%. By contrast, PointCBA is highly stealthy, leading to more limited accuracy improvements across all defenses.

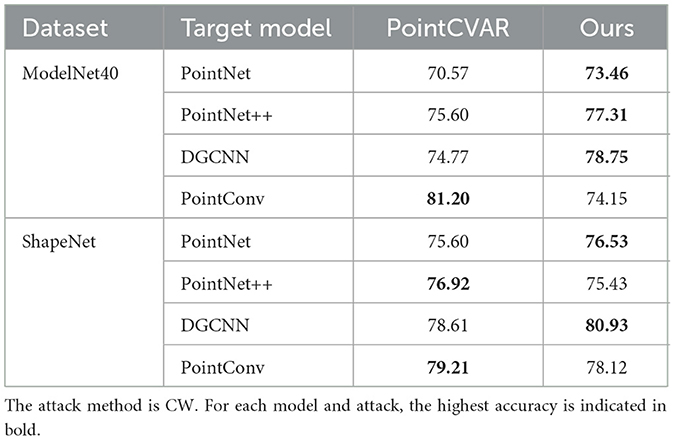
We also present a comprehensive performance comparison of our proposed method against PointCVAR, with the results detailed in Table 4. The evaluation spans two prominent datasets, ModelNet40 and ShapeNet, across four distinct target models. Our method demonstrates a consistent and marked improvement over PointCVAR in the majority of test cases. This trend of superior performance is also evident on the ShapeNet dataset for models like DGCNN and PointConv. It is, however, noteworthy that PointCVAR shows stronger performance in specific scenarios, namely with the PointConv model on ModelNet40 and the PointNet++ model on ShapeNet. Despite these exceptions, the overall results strongly indicate that our proposed method provides a more robust and generally effective solution across a diverse set of models and datasets.

Table 4

Table 4. Comparison of PointCVAR and our method on different datasets and models.

For specific individual models, the defense performance of our method also surpasses the baselines. Table 3 presents the classification accuracy of our method and the comparison methods under different attacks on the ShapeNet dataset. Our method achieves the highest classification success rate under three attack methods when tested on PointNet, PointNet++, and PointConv. On DGCNN, the average classification success rate reaches 79.58%, which is superior to the results obtained with other models. These results clearly indicate that the proposed method exhibits excellent performance and robustness against various universal perturbations.

4.3 Ablation study

To further evaluate the contribution of key components of our method, we conducted three ablation experiments on the two datasets (ModelNet40 and ShapeNet). The specific configurations for the ablation studies are as follows:

• Minus interpretability: In this setting, the suspicious region localization module, originally based on Grad-CAM model interpretability, is replaced with a random selection method. The input to the random selection method is simply the 3D spatial point coordinates, without relying on the suspicious regions identified through model interpretability.

• Minus Graph-Wavelet-voxel: This setting retains the model interpretability for suspicious region localization but removes the continuous curvature segment extraction process based on graph wavelet transforms. Instead, it is replaced by voxel-based processing for segment extraction.

• Minus Graph-Wavelet-ball: Similar to the previous setting, this retains model interpretability for localization and removes the graph wavelet transform-based segment extraction. It is replaced by a “Ball Query” method for segment extraction.

As shown in Tables 5, 6, the results for the control group (our full method) demonstrate that removing the model's interpretability significantly reduces the classification accuracy of the purified samples. This finding strongly suggests that model interpretability plays a crucial role in enhancing the defense effect against universal 3D point cloud perturbations. Additionally, when the continuous curvature segment extraction module is removed (using either voxel or Ball Query replacements), the model's classification accuracy also decreases, albeit to a lesser extent than when the model interpretability is removed entirely. The performance degradation in “Minus Graph-Wavelet-voxel” and “Minus Graph-Wavelet-ball” settings is less pronounced compared to “Minus Interpretability”.

Table 5

Table 5. Ablation experiments on the ModelNet40.

Table 6

Table 6. Ablation experiments on the ShapeNet.

The results highlight that removing the model interpretability module has a more substantial impact on reducing the defense effectiveness. The above findings underscore the critical role of the model interpretability module in our proposed method. Model interpretability not only provides effective guidance for identifying perturbation regions but also reveals the internal attention mechanisms of the model's decision-making process. By leveraging this attention information, it enhances the robustness and generalization ability of the model, thereby laying a strong foundation for defending against universal adversarial perturbations.

4.4 Defense on different attack budgets

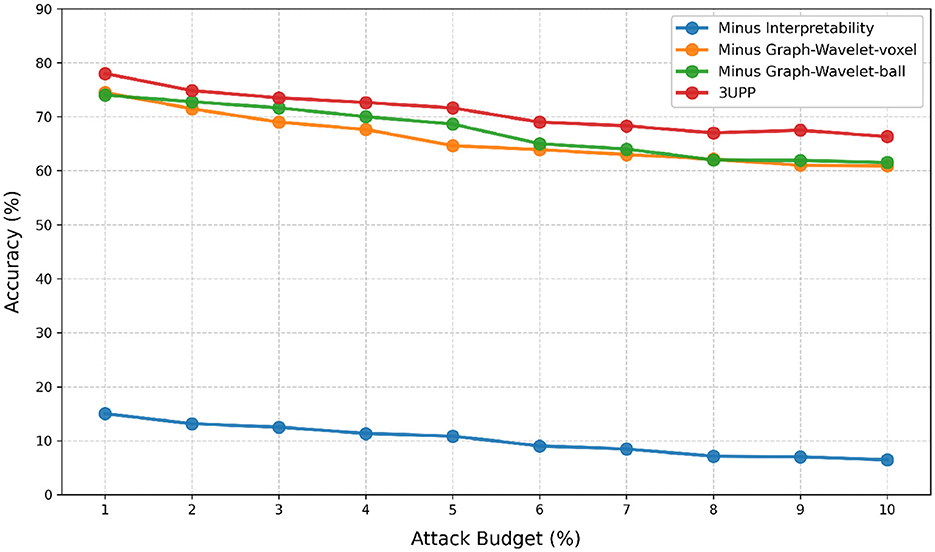
This section evaluates the impact of varying attack strengths on our defense approach. Different attack strengths are quantified by the perturbation budget, which is defined as the number of points that can be added to the original point cloud, expressed as a percentage (e.g., 5% or 10%) of the original point cloud size.

Figures 2, 3 present the ablation comparison and robustness analysis of our method tested on the ModelNet40 and ShapeNet datasets, respectively, under different attack budgets. The observations reveal that across all models, performance tends to decrease as the attack strength increases with the attack budget. However, our method consistently maintains the highest accuracy. On both datasets, the DGCNN model exhibits the best performance under our defense, achieving classification accuracies of 79.57% and 78.02% at a 2% attack budget, and 71.38% and 71.75% classification accuracies at a 10% attack budget.

Figure 2

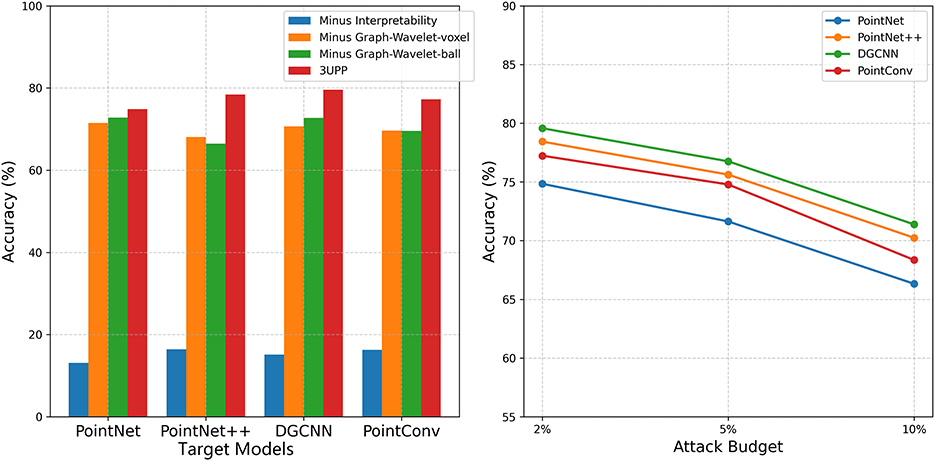
Figure 2. Ablation comparison and robustness analysis on the ModelNet40 with different attack budgets.

Figure 3

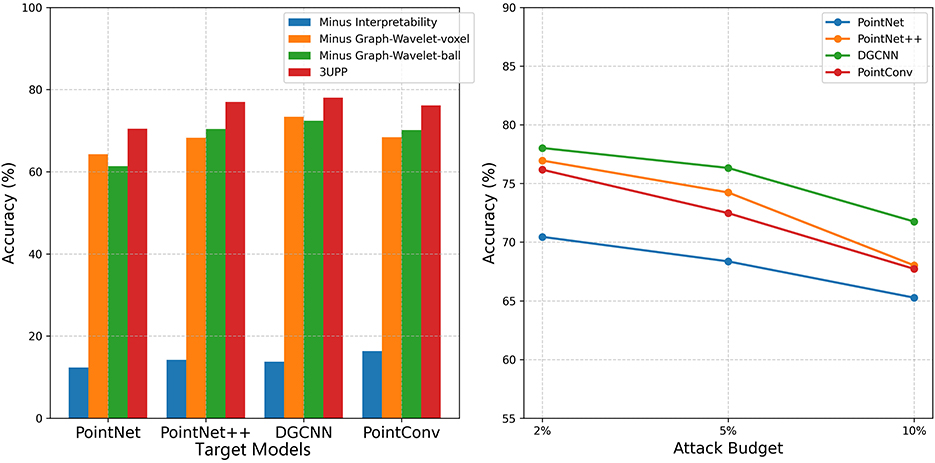
Figure 3. Ablation comparison and robustness analysis on the ShapeNet with different attack budgets.

Further testing against the PointNet model on ModelNet40, as shown in Figure 4, demonstrates that increasing the attack budget leads to increased perturbation strength, making the samples more vulnerable to attacks. Consequently, the effectiveness of the defense method decreases as the attack budget increases.

Figure 4

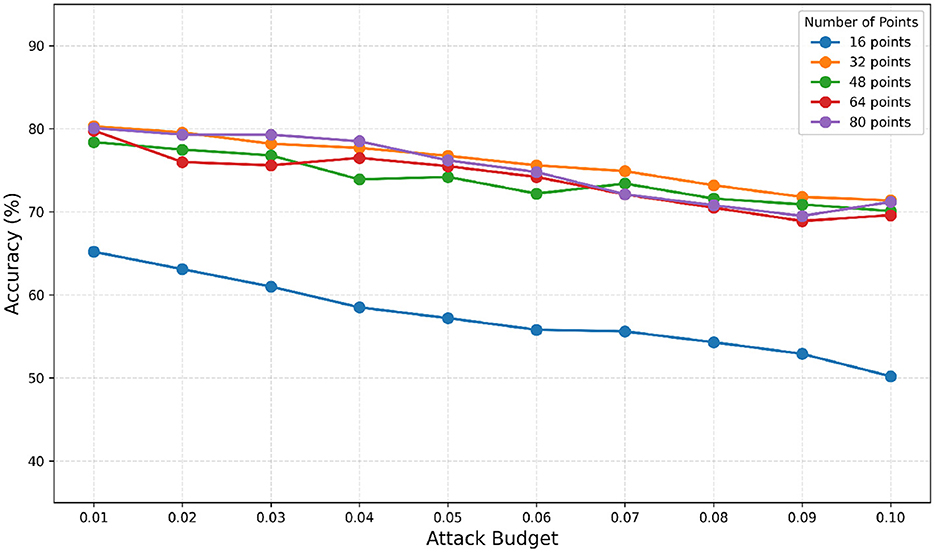
Figure 4. The influence of the number of FPS points relied on for extracting continuous curvature segments.

4.5 Hyper-parameter study

This section investigates the influence of the number of farthest points sampled during the continuous curvature segment extraction process on the performance of our method's defense, evaluated by the classification accuracy of the target model.

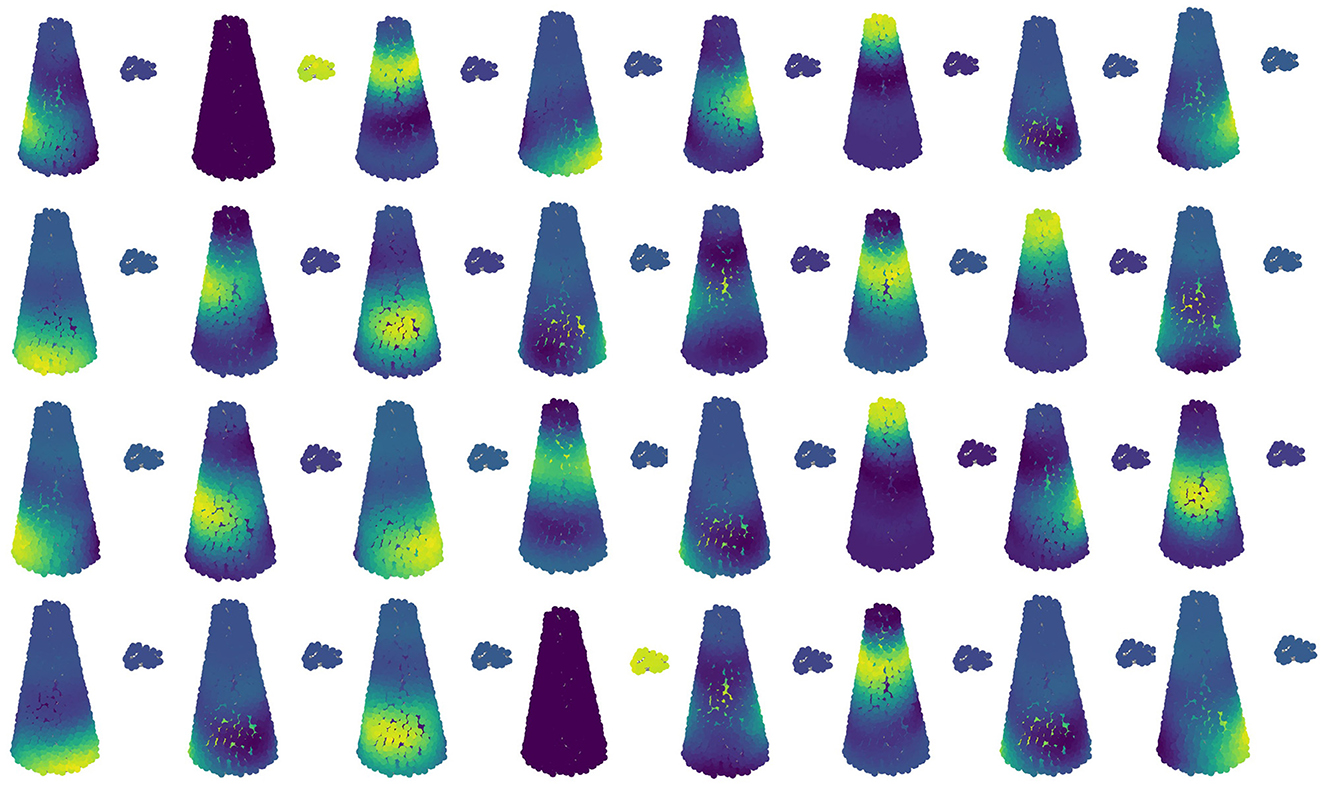
As illustrated in Figure 5, the experimental results on the ModelNet40 dataset indicate that increasing the number of sampling points does not significantly enhance the defense effect of our method, even though more continuous curvature segments are extracted. Conversely, the defense effect at slightly smaller sampling points is not considerably less effective. A possible explanation for this phenomenon is that when the number of sampling points reaches a certain threshold, it is sufficient to cover the key points on the surface of the point cloud data.

Figure 5

Figure 5. The impact of attack budget on PointNet and ModelNet40.

Due to the strong ability of our proposed defense strategy to remove generic perturbations, remarkable defense results can still be achieved even when fewer points (e.g., 32 points) are used for extracting continuous curvature segments.

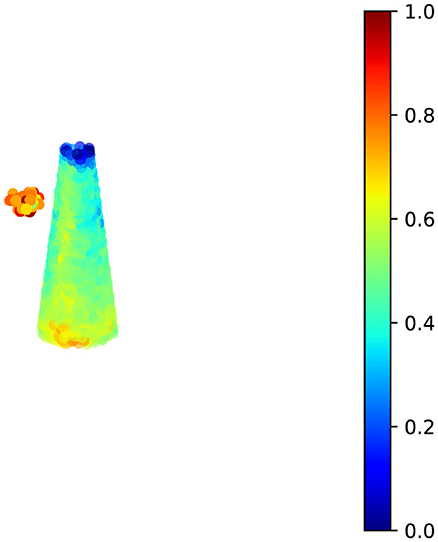
A visual representation of the continuous curvature fragments obtained by sampling the 32 farthest points is shown in Figure 6. It is observed that the selection of these farthest points effectively captures the generic perturbation. If the number of sampled points exceeds 32, the capture of the final generic perturbation is essentially equivalent to sampling 32 points. Therefore, 32 farthest points is considered an appropriate setting for the experiments.

Figure 6

Figure 6. Visualization of continuous curvature segments extraction.

A visual representation of all the continuous curvature fragments obtained by sampling the 32 farthest points is shown in Figure 6. It is observed that the existence of two farthest points perfectly captures the generic perturbation. If the number of sampled points reaches above 32, the final generic perturbation capture is essentially equal to sampling 32 points. Therefore, 32 farthest points is an appropriate setting in the experiment.

4.6 Defense on transfer-based attacks

The efficacy of our proposed defense mechanism against black-box transfer-based attacks is comprehensively illustrated in the provided Figure 7.

Figure 7

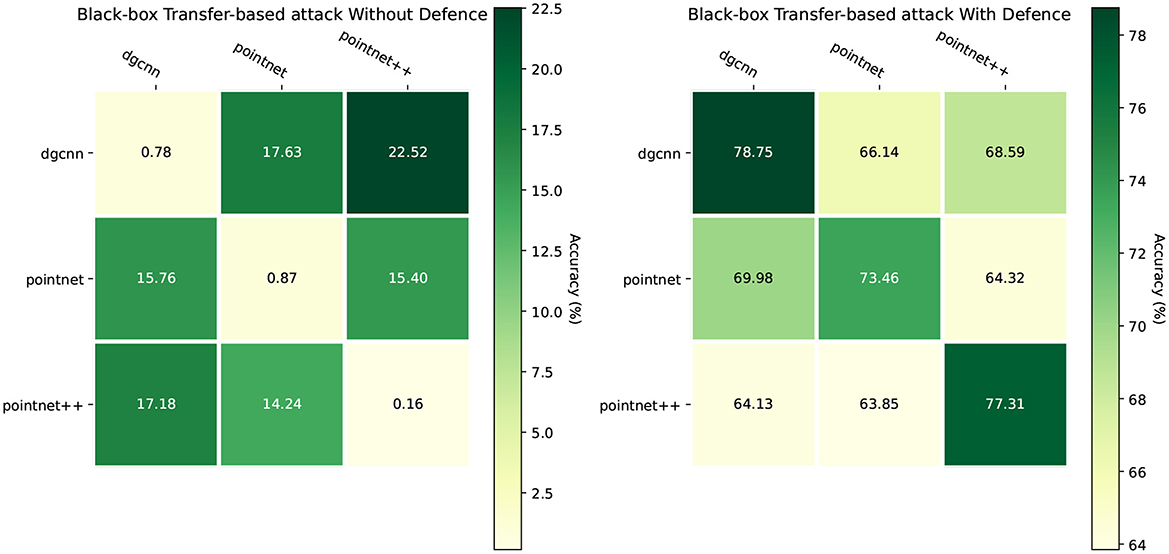
Figure 7. Black-box transfer-based attack without or with our proposed defense. The attack method is CW.

The left heatmap demonstrates the severe vulnerability of undefended models, where transfer attacks prove highly effective. The remaining classification accuracies are drastically reduced, consistently falling below 23% and often dropping to below 1% when the source and target model architectures are identical (e.g., 0.16% for PointNet++). This establishes a critical baseline, highlighting the insecurity of standard models. In stark contrast, the right heatmap reveals a dramatic improvement in model resilience upon applying our defense. The defended models consistently maintain high accuracy, with the lowest post-attack accuracy being 63.85%. Notably, accuracies on the diagonal, such as 78.75% for DGCNN and 77.31% for PointNet++, are significantly restored, showcasing the defense's strength even when the adversary has implicit knowledge of the model's architecture. This substantial elevation in performance across all source-target pairs confirms that our method provides robust protection, effectively neutralizing the threat of transfer-based attacks in a black-box setting.

5 Discussion

Our work has introduced a novel purification framework against Universal Adversarial Perturbations (UAPs), demonstrating that leveraging model interpretability is a highly effective defense strategy. This section discusses the method's specificity, its broader implications, and future research directions.

Our framework is intentionally designed for UAPs. The core assessment module, which validates a suspicious region by transplanting it onto multiple clean samples, fundamentally relies on the universal nature of the perturbation. This design is inherently less effective against input-specific attacks (e.g., PGD), as their perturbations are not crafted to be transferable. However, our method's utility is not strictly confined to UAPs. The successful defense against black-box transfer-based attacks, as shown in Figure 7, demonstrates that our model-guided approach can effectively identify and neutralize malicious geometric structures even without precise knowledge of the attack. This indicates a valuable degree of robustness in practical scenarios.

While we posit that a high-efficacy, specialized defense against a significant threat like UAPs is a valuable contribution, we recognize the limitations of our approach and propose the following future directions:

• Generalizing to input-specific attacks: Future work could focus on adapting the validation module to work for per-sample perturbations, perhaps by developing a learned metric for adversarial potential that does not rely on transplantation, or by creating a hybrid defense model.

• Reducing white-box reliance: Our method currently assumes full model access. Investigating its adaptation to gray-box or black-box scenarios, possibly by using surrogate models to approximate saliency, would greatly enhance its practical applicability.

• Broader task application: Extending this purification framework to more complex 3D tasks, such as object detection and semantic segmentation, remains a promising avenue for future research.

In summary, while specialized, our work provides a robust defense against a critical threat and offers a solid foundation for future advancements in 3D adversarial security.

6 Conclusion

In this paper, we introduced a 3D point cloud universal adversarial perturbation removal method based on model interpretability. The method involves calculating attention coefficients and locating suspicious regions using a Grad-CAM-based approach. It then extracts continuous curvature segments by combining graph wavelet transforms with attention coefficients to identify problematic regions. Leveraging the robust and generalization properties of universal adversarial perturbations, these identified perturbations are combined with benign samples through superposition. Finally, a binary classification model is employed to classify and remove these suspicious superposed samples, achieving the recognition and removal of universal adversarial perturbations. The experimental section applied this method to mainstream deep learning models for processing point cloud data and conducted comparative studies, ablation experiments, and hyper-parameter studies to validate its effectiveness. By analyzing samples with universal adversarial perturbations within the context of universal perturbation removal, the defense capability of this point cloud purification method was verified.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://paperswithcode.com/dataset/shapenet and https://paperswithcode.com/dataset/modelnet.

Author contributions

YG: Methodology, Writing – original draft, Writing – review & editing. XC: Software, Writing – original draft, Writing – review & editing. HL: Writing – original draft, Writing – review & editing. JX: Funding acquisition, Resources, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Fundamental Research Funds for the Central Universities (No. N2417008) and the National Natural Science Foundation of China (No. 62372096).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Badue, C., Guidolini, R., Carneiro, R. V., Azevedo, P., Cardoso, V. B., Forechi, A., et al. (2021). Self-driving cars: a survey. Expert Syst. Appl. 165:113816. doi: 10.1016/j.eswa.2020.113816

Crossref Full Text | Google Scholar

Bian, Y., Tian, S., and Liu, X. (2024). Mirrorattack: backdoor attack on 3D point cloud with a distorting mirror. arXiv preprint arXiv:2403.05847.

Google Scholar

Carlini, N., and Wagner, D. (2017). “Towards evaluating the robustness of neural networks,” in 2017 IEEE Symposium on Security and Privacy (SP) (IEEE), 39–57. doi: 10.1109/SP.2017.49

Crossref Full Text | Google Scholar

Croce, F., and Hein, M. (2020). “Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks,” in Proceedings of the 37th International Conference on Machine Learning.

Google Scholar

Gao, K., Bai, J., Wu, B., Ya, M., and Xia, S.-T. (2023). Imperceptible and robust backdoor attack in 3d point cloud. IEEE Trans. Inf. Forens. Secur. 19, 1267–1282. doi: 10.1109/TIFS.2023.3333687

Crossref Full Text | Google Scholar

Goodfellow, I. J., Shlens, J., and Szegedy, C. (2014). Explaining and harnessing adversarial examples. arXiv preprint arXiv:1412.6572.

Google Scholar

Hassanalian, M., and Abdelkefi, A. (2017). Classifications, applications, and design challenges of drones: a review. Progr. Aerospace Sci. 91, 99–131. doi: 10.1016/j.paerosci.2017.04.003

Crossref Full Text | Google Scholar

Hu, S., Liu, W., Li, M., Zhang, Y., Liu, X., Wang, X., et al. (2023). “Pointcrt: detecting backdoor in 3D point cloud via corruption robustness,” in Proceedings of the 31st ACM International Conference on Multimedia, 666–675. doi: 10.1145/3581783.3612456

Crossref Full Text | Google Scholar

Khaddaj, A., Leclerc, G., Makelov, A., Georgiev, K., Salman, H., Ilyas, A., et al. (2023). “Rethinking backdoor attacks,” in International Conference on Machine Learning (PMLR), 16216–16236.

Google Scholar

Li, X., Lu, J., Ding, H., Sun, C., Zhou, J. T., and Chee, Y. M. (2024). “Pointcvar: risk-optimized outlier removal for robust 3D point cloud classification,” in Proceedings of the AAAI Conference on Artificial Intelligence, 38. doi: 10.1609/aaai.v38i19.30129

Crossref Full Text | Google Scholar

Liu, D., Hu, W., and Li, X. (2023). Point cloud attacks in graph spectral domain: when 3D geometry meets graph signal processing. IEEE Trans. Pattern Anal. Mach. Intell. 46, 3079–3095. doi: 10.1109/TPAMI.2023.3339130

PubMed Abstract | Crossref Full Text | Google Scholar

Luo, Y., Li, J., Zheng, W., Fan, J., Li, Z.-J., and Yang, T. (2021). Diffusion-driven purification against adversarial attacks on 3D point cloud recognition. arXiv preprint arXiv:2111.00420.

Google Scholar

Ma, C., Meng, W., Wu, B., Xu, S., and Zhang, X. (2020). “Efficient joint gradient based attack against sor defense for 3D point cloud classification,” in Proceedings of the 28th ACM International Conference on Multimedia, 1819–1827. doi: 10.1145/3394171.3413875

Crossref Full Text | Google Scholar

Ma, X., Qin, C., You, H., Ran, H., and Fu, Y. (2022). Rethinking network design and local geometry in point cloud: a simple residual MLP framework. arXiv preprint arXiv:2202.07123.

Google Scholar

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. (2017). Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083.

Google Scholar

Mescheder, L., Oechsle, M., Niemeyer, M., Nowozin, S., and Geiger, A. (2019). “Occupancy networks: Learning 3d reconstruction in function space,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 4460–4470. doi: 10.1109/CVPR.2019.00459

Crossref Full Text | Google Scholar

Mo, X., Zhang, Y., Zhang, L. Y., Luo, W., Sun, N., Hu, S., et al. (2024). “Robust backdoor detection for deep learning via topological evolution dynamics,” in 2024 IEEE Symposium on Security and Privacy (SP) (IEEE), 2048–2066. doi: 10.1109/SP54263.2024.00174

Crossref Full Text | Google Scholar

Moosavi-Dezfooli, S., Fawzi, A., Fawzi, O., and Frossard, P. (2017). “Universal adversarial perturbations,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1765–1773. doi: 10.1109/CVPR.2017.17

Crossref Full Text | Google Scholar

Moosavi-Dezfooli, S., Fawzi, A., and Frossard, P. (2016). “Deepfool: a simple and accurate method to fool deep neural networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2574–2582. doi: 10.1109/CVPR.2016.282

Crossref Full Text | Google Scholar

Mopuri, K. R., Ganeshan, A., and Babu, R. V. (2019). Generalizable data-free objective for crafting universal adversarial perturbations. IEEE Trans. Pattern Anal. Mach. Intell. 41, 2452–2465. doi: 10.1109/TPAMI.2018.2861800

PubMed Abstract | Crossref Full Text | Google Scholar

Mopuri, K. R., Garg, U., and Radhakrishnan, V. B. (2017). Fast feature fool: a data independent approach to universal adversarial perturbations. arXiv preprint arXiv:1707.05572.

Google Scholar

Mozaffari-Kermani, M., Sur-Kolay, S., Raghunathan, A., and Jha, N. K. (2014). Systematic poisoning attacks on and defenses for machine learning in healthcare. IEEE J. Biomed. Health Inf. 19, 1893–1905. doi: 10.1109/JBHI.2014.2344095

PubMed Abstract | Crossref Full Text | Google Scholar

Naderi, H., and Bajić, I. V. (2023). Adversarial attacks and defenses on 3D point cloud classification: a survey. IEEE Access 11, 144274–144295. doi: 10.1109/ACCESS.2023.3345000

Crossref Full Text | Google Scholar

Pang, B., Zheng, X., Xu, S., Chen, C., Yan, J., and Ooi, B. C. (2020). “Implicit gradient defense for point cloud networks,” in European Conference on Computer Vision (Springer), 488–504.

Google Scholar

Peng, S., Niemeyer, M., Mescheder, L., Pollefeys, M., and Geiger, A. (2020). “Convolutional occupancy networks,” in European Conference on Computer Vision (Springer), 523–540. doi: 10.1007/978-3-030-58580-8_31

Crossref Full Text | Google Scholar

Pierson, H. A., and Gashler, M. S. (2017). Deep learning in robotics: a review of recent research. Adv. Robot. 31, 821–835. doi: 10.1080/01691864.2017.1365009

Crossref Full Text | Google Scholar

Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017a). “Pointnet: deep learning on point sets for 3D classification and segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 652–660.

Google Scholar

Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017b). “PointNet++: deep hierarchical feature learning on point sets in a metric space,” in Advances in Neural Information Processing Systems, 5099–5108.

Google Scholar

Rachmiel, T., and Bruckstein, A. M. (2020). Pointcleannet: Learning to denoise and remove outliers from point clouds. IEEE Trans. Pattern Anal. Mach. Intell. 43, 4230–4242. doi: 10.1111/cgf.13753

Crossref Full Text | Google Scholar

Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R., Parikh, D., and Batra, D. (2017). “Grad-cam: visual explanations from deep networks via gradient-based localization,” in Proceedings of the IEEE International Conference on Computer Vision, 618–626. doi: 10.1109/ICCV.2017.74

Crossref Full Text | Google Scholar

Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., et al. (2014). Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199.

Google Scholar

Tang, K., He, X., Peng, W., Wu, J., Shi, Y., Liu, D., et al. (2024). “Manifold constraints for imperceptible adversarial attacks on point clouds,” in AAAI, 5127–5135. doi: 10.1609/aaai.v38i6.28318

Crossref Full Text | Google Scholar

Tang, K., Huang, L., Peng, W., Liu, D., Wang, X., Ma, Y., et al. (2025). “Flat: flux-aware imperceptible adversarial attacks on 3D point clouds,” in ECCV, 198–215. doi: 10.1007/978-3-031-72658-3_12

Crossref Full Text | Google Scholar

Tang, K., Shi, Y., Lou, T., Peng, W., He, X., Zhu, P., et al. (2023a). Rethinking perturbation directions for imperceptible adversarial attacks on point clouds. IEEE Internet Things J. 10, 5158–5169. doi: 10.1109/JIOT.2022.3222159

Crossref Full Text | Google Scholar

Tang, K., Wu, J., Peng, W., Shi, Y., Song, P., Gu, Z., et al. (2023b). “Deep manifold attack on point clouds via parameter plane stretching,” in AAAI, 2420–2428. doi: 10.1609/aaai.v37i2.25338

Crossref Full Text | Google Scholar

Wang, Y., Sun, Y., Liu, Z., Sarma, S. E., Bronstein, M. M., and Solomon, J. M. (2019). Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. 38, 1–12. doi: 10.1145/3326362

Crossref Full Text | Google Scholar

Wu, W., Qi, Z., Li, X., Luo, M., Zhou, J., Lai, Y., et al. (2019). “Pointconv: deep convolutional networks on 3D point clouds,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 9625–9634. doi: 10.1109/CVPR.2019.00985

Crossref Full Text | Google Scholar

Wu, Z., Duan, Y., Wang, H., Fan, Q., and Guibas, L. J. (2020). If-defense: 3d adversarial point cloud defense via implicit function based restoration. arXiv preprint arXiv:2010.05272.

Google Scholar

Yang, J., Zhang, Q., Fang, R., Ni, B., Liu, J., and Tian, Q. (2019). Adversarial attack and defense on point sets. arXiv preprint arXiv:1902.10899.

Google Scholar

Yu, L., Li, X., Fu, C.-W., Cohen-Or, D., and Heng, P.-A. (2018). “Pu-net: point cloud upsampling network,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2790–2799. doi: 10.1109/CVPR.2018.00295

Crossref Full Text | Google Scholar

Yuan, S., Yang, J., Zhong, Y., Xie, Y., Guo, Y., and Zhang, J. (2020). “Pointfilternet: a filtering network for point cloud denoising,” in 2020 IEEE International Conference on Robotics and Automation (ICRA) (IEEE), 4601–4607.

Google Scholar

Zhang, C., Benz, P., Imtiaz, T., and Kweon, I. S. (2020). “Understanding adversarial examples from the mutual influence of images and perturbations,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 14521–14530. doi: 10.1109/CVPR42600.2020.01453

Crossref Full Text | Google Scholar

Zhang, C., Benz, P., Karjauv, A., and Kweon, I. S. (2021). “Data-free universal adversarial perturbation and black-box attack,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 7868–7877. doi: 10.1109/ICCV48922.2021.00777

Crossref Full Text | Google Scholar

Zhang, Z., Lin, M., Dai, E., and Wang, S. (2024). “Rethinking graph backdoor attacks: a distribution-preserving perspective,” in Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 4386–4397. doi: 10.1145/3637528.3671910

Crossref Full Text | Google Scholar

Zhou, H., Chen, K., Zhang, W., Fang, H., Zhou, W., and Yu, N. (2019). “Dup-net: denoiser and upsampler network for 3D adversarial point clouds defense,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 1961–1970. doi: 10.1109/ICCV.2019.00205

Crossref Full Text | Google Scholar

Zhou, H., Guan, J., Fan, J., Zhu, X., and Wu, Y. (2020). “Pointba: towards backdoor attacks in 3D point cloud,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 11477–11486.

Google Scholar

Zhu, Q., Fan, L., and Weng, N. (2024). Advancements in point cloud data augmentation for deep learning: a survey. Pattern Recognit. 153:110532. doi: 10.1016/j.patcog.2024.110532

Crossref Full Text | Google Scholar