Exploring the impact of fixed theta values in RoPE on character-level language model performance and efficiency

Rotary Positional Embedding (RoPE) is a widely used technique in Transformers, influenced by the hyperparameter theta (θ). However, the impact of varying *fixed* theta values, especially the trade-off between performance and efficiency on tasks like character-level modeling, remains under-explored. This paper presents a systematic evaluation of RoPE with fixed theta values (ranging from 500 to 50,000) on a character-level GPT model across three datasets: Tiny Shakespeare, Enwik8, and Text8, compared against the standard θ = 10, 000 baseline. However, all non-default theta configurations incur significant computational overhead: inference speed is approximately halved across all datasets, suggesting implementation—specific bottlenecks rather than theta—dependent costs. This study quantifies a critical performance—efficiency trade-off when tuning fixed RoPE theta. Our findings emphasize the practical need to balance generalization gains with computational budgets during model development and deployment, contributing empirical insights into RoPE hyperparameter sensitivity and demonstrating that optimal theta selection is highly dataset-dependent. These insights suggest that future positional encoding designs could benefit from adaptive θ scheduling or dataset-specific θ optimization strategies to maximize both performance and computational efficiency.

1 Introduction

Transformer architectures (Vaswani et al., 2017; Devlin et al., 2019; Kenton and Toutanova, 2019; Radford et al., 2018, 2019; Brown et al., 2020; Raffel et al., 2020; Lewis et al., 2020; Liu et al., 2019; Yang et al., 2019; Lan et al., 2019; Zhang et al., 2020; Dosovitskiy et al., 2021) have revolutionized sequence modeling (Sutskever et al., 2014; Bahdanau et al., 2014; Luong et al., 2015; Gehring et al., 2017; Wu et al., 2016), achieving state-of-the-art results across numerous natural language processing tasks (Wang et al., 2018, 2019). A key component enabling Transformers to process sequences is the positional encoding (PE) mechanism (Gehring et al., 2017), which injects information about the order of tokens, as the self-attention mechanism itself is permutation-invariant. Various PE methods have been proposed, ranging from absolute sinusoidal or learned embeddings (Vaswani et al., 2017; Devlin et al., 2019) to relative positional representations (Shaw et al., 2018; Dai et al., 2019).

Among these, Rotary Positional Embedding (RoPE) (Su et al., 2021; Touvron et al., 2023; Anil et al., 2023; Chowdhery et al., 2023; Jiang et al., 2023; Almazrouei et al., 2023; Workshop et al., 2022) has emerged as a popular and effective approach. RoPE applies position-dependent rotations to query and key vectors in the self-attention mechanism, inherently capturing relative positional information while maintaining desirable properties like decaying intra-attention scores with increasing distance. RoPE's performance often relies on a crucial hyperparameter, theta (θ), which acts as a base period controlling the range of frequencies used for rotation. A default value of θ = 10, 000 is commonly employed across various models and tasks (Touvron et al., 2023; OpenAI, 2023).

Despite RoPE's widespread adoption, often relying on the default θ = 10, 000, the sensitivity of model performance and efficiency to variations in this hyperparameter, particularly when employing *fixed* theta values, remains inadequately characterized. Much recent work on RoPE focuses on extending context length (Sun et al., 2023) or developing adaptive mechanisms (Dehghani et al., 2018), leaving a gap in understanding the fundamental trade-offs involved in selecting a simple, fixed theta. This is especially pertinent for tasks like character-level language modeling (Graves, 2013; Karpathy, 2015; Kim et al., 2016), where the optimal positional frequency sensitivity might differ from that of token-level models. Furthermore, the computational overhead associated with different RoPE configurations is often neglected in performance comparisons (Tay et al., 2020; So et al., 2021). This study directly addresses these gaps by systematically evaluating the impact of fixed RoPE theta values on both generalization performance and computational efficiency for a character-level task.

1.1 Problem statement and research scope

This work addresses three critical gaps in the current understanding of RoPE hyperparameter sensitivity: (1) Limited empirical validation of the widely-adopted default θ = 10, 000, which lacks systematic justification across different tasks and datasets; (2) Insufficient characterization of the performance-efficiency trade-offs when varying fixed theta values, particularly for character-level modeling where positional frequency requirements may differ from token-level tasks; and (3) Neglected computational overhead analysis in positional encoding comparisons, which is crucial for practical deployment decisions. Our study specifically focuses on fixed theta values (not adaptive mechanisms) to establish fundamental baselines and trade-off characterizations that can inform more sophisticated approaches. We limit our scope to character-level language modeling to enable controlled analysis of fine-grained positional dependencies while providing insights transferable to other sequence modeling tasks.

Our investigation seeks answers to the following questions:

• How does the fixed RoPE theta value impact the final validation performance and training convergence of a character-level language model across different datasets?

• Is there an optimal fixed theta value for this specific task setting and does it generalize across datasets?

• What is the computational cost (training time, inference speed) associated with different fixed theta values compared to a standard baseline?

• What insights can be drawn about the relationship between RoPE's frequency resolution (controlled by theta) and model behavior?

• How do dataset characteristics influence the optimal theta selection and performance sensitivity?

The choice of theta range (500 to 50,000) was motivated by theoretical considerations and preliminary experiments. Lower values (500–1,000) provide high-frequency position encoding suitable for fine-grained character dependencies, while higher values (20,000–50,000) offer lower frequencies potentially better for longer-range context. The standard θ = 10, 000 serves as a natural midpoint, with θ = 5, 000 representing an intermediate frequency resolution.

To answer these questions, we train and evaluate a standard GPT-style architecture (Brown et al., 2020; Radford et al., 2018, 2019) on three character-level datasets: Tiny Shakespeare (Karpathy, 2015), Enwik8, and Text8, representing different text characteristics and complexities. We integrate RoPE into the self-attention mechanism and systematically vary the fixed theta parameter across values of 500, 1,000, 5,000, 10,000 (baseline), 20,000, and 50,000. We conduct experiments with three independent random seeds (1,337, 1,338, 1,339) for each dataset and configuration to ensure statistical robustness and reproducible results.

Our experiments reveal dataset-specific optimal theta values: θ = 5, 000 for Shakespeare and Text8, and θ = 50, 000 for Enwik8, with performance improvements ranging from 0.5% to 2.1%. Enwik8 shows the highest sensitivity to theta tuning, while Shakespeare demonstrates the most stable performance across configurations. However, a striking finding is that all configurations using our fixed-theta RoPE implementation demonstrate significantly slower inference speeds (approximately half the tokens per second) and slightly longer training times compared to the baseline, irrespective of the specific theta value chosen across all three datasets.

The main contributions of this paper are:

• A systematic empirical evaluation of fixed theta values (from 500 to 50,000) in RoPE for character-level language modeling across three diverse datasets (Shakespeare, Enwik8, Text8).

• Discovery of dataset-specific optimal theta values: θ = 5, 000 for Shakespeare and Text8, θ = 50, 000 for Enwik8, demonstrating that optimal theta selection is highly dataset-dependent.

• Quantification of a significant performance-efficiency trade-off, where improved validation loss with tuned fixed theta correlates with substantially increased computational cost in our implementation consistently across all datasets.

• Empirical evidence illustrating the non-monotonic impact of RoPE's theta parameter on model generalization and the varying sensitivity of different datasets to theta tuning (0.5%–2.1% improvement range).

• Identification of implementation-specific computational bottlenecks affecting all non-default theta values, providing insights for future optimization efforts.

The remainder of this paper is structured as follows: Section 2 discusses relevant prior work. Section 3 provides background on Transformers and RoPE. Section 4 details our experimental methodology. Section 5 describes the experimental setup. Section 6 presents and discusses the results. Finally, Section 7 concludes the paper, acknowledging limitations and suggesting future directions.

2 Related work

Our work builds upon research in positional encoding for Transformer models (Vaswani et al., 2017; Gehring et al., 2017; Shaw et al., 2018; Dai et al., 2019; Su et al., 2021) and hyperparameter optimization (Kaplan et al., 2020), particularly within the context of character-level language modeling (Graves, 2013; Kim et al., 2016).

2.1 Positional encoding in transformers

The original Transformer model (Vaswani et al., 2017) introduced sinusoidal absolute positional encodings, providing a fixed, non-learned representation of token positions. Subsequent research explored learned absolute embeddings (Devlin et al., 2019; Gehring et al., 2017) and various forms of relative positional encoding (Shaw et al., 2018; Dai et al., 2019), which aim to capture the relationship between tokens based on their offset rather than their absolute position. Notable relative PE methods include those proposed by (Shaw et al. 2018), which uses learned relative position embeddings added to keys and values, and the Transformer-XL (Dai et al., 2019), which incorporates relative positioning within the attention scoring mechanism itself. Other approaches like T5 (Raffel et al., 2020) also utilize relative biases.

Rotary Positional Embedding (RoPE) (Su et al., 2021; Touvron et al., 2023; Chowdhery et al., 2023; Anil et al., 2023) represents a distinct approach, applying rotations to query and key vectors based on their absolute positions in a way that implicitly encodes relative positional information within the dot-product attention. RoPE has gained significant popularity due to its effectiveness, ability to handle long sequences potentially better than some alternatives (Beltagy et al., 2020; Zaheer et al., 2020), and integration simplicity (Paszke et al., 2019). It is now widely used in large language models like LLaMA (Touvron et al., 2023), PaLM (Chowdhery et al., 2023; Anil et al., 2023), GPT-4 (OpenAI, 2023), Jiang et al. (2023), and Almazrouei et al. (2023). The core of RoPE involves a base period hyperparameter, theta (θ), typically set to 10,000, which influences the rotational frequencies. While effective, the sensitivity to and optimal selection of this theta parameter, especially using fixed values, is the focus of our investigation.

2.2 Hyperparameter tuning and RoPE variants

Hyperparameter tuning is crucial for optimizing Transformer performance (Kaplan et al., 2020; So et al., 2021). While extensive research exists on tuning general parameters like learning rate (Kingma and Ba, 2015; Loshchilov and Hutter, 2017), model dimensions (Kaplan et al., 2020), and dropout (Krizhevsky et al., 2012), specific investigations into positional encoding hyperparameters are less common. Some works have explored adaptive positional encoding strategies (Dehghani et al., 2018) or modifications to RoPE itself, such as extending its context length capabilities (Sun et al., 2023) or proposing alternative rotational schemes. Recent work has demonstrated that RoPE theta parameters can be effectively learned (Huang and Chen, 2025), providing adaptive optimization strategies for theta values. However, systematic studies evaluating the impact of different *fixed* theta values on both performance and, critically, computational efficiency, are scarce. Our work differentiates itself by providing such a focused empirical analysis of fixed theta values, complementing the learnable approach. The present study establishes the performance-efficiency trade-offs of fixed theta selection, while the learnable theta optimization approach (Huang and Chen, 2025) demonstrates that theta can be effectively learned during training. Together, these works provide a comprehensive understanding of both fixed and adaptive theta optimization strategies, offering practitioners guidance on when to use fixed values vs. when to invest in learnable parameters.

2.3 Character-level language modeling

Character-level language models (Graves, 2013; Sutskever et al., 2014; Karpathy, 2015; Karpathy et al., 2015) operate directly on individual characters, avoiding the need for predefined vocabularies like byte-pair encoding (BPE) (Sennrich et al., 2016). While often requiring longer sequence processing to capture equivalent semantic context compared to token-level models, they excel in certain domains like morphological analysis (Ling et al., 2015), handling rare words or jargon, and specific generation tasks (Huang et al., 2018). The effectiveness of different positional encoding strategies, including RoPE with varying frequency resolutions (theta), in this fine-grained setting (Kim et al., 2016) is an area requiring further empirical validation, which this study provides. Prior work has explored character embeddings within larger models (Devlin et al., 2019; Wu et al., 2016) or pure character-level CNNs/RNNs (Gehring et al., 2017; Hochreiter and Schmidhuber, 1997; Cho et al., 2014).

In summary, while RoPE is well-established, this paper provides a focused investigation into the impact of its fixed theta hyperparameter on a character-level task, explicitly analyzing the resulting performance-efficiency trade-off, an aspect often missing in broader positional encoding studies.

2.4 Comparison of positional encoding approaches

Table 1 provides a systematic comparison of major positional encoding methods, highlighting the unique position of our work in studying fixed RoPE theta sensitivity. While most prior work treats positional encoding hyperparameters as fixed design choices, our study reveals that these choices have significant implications for both performance and computational efficiency.

Table 1

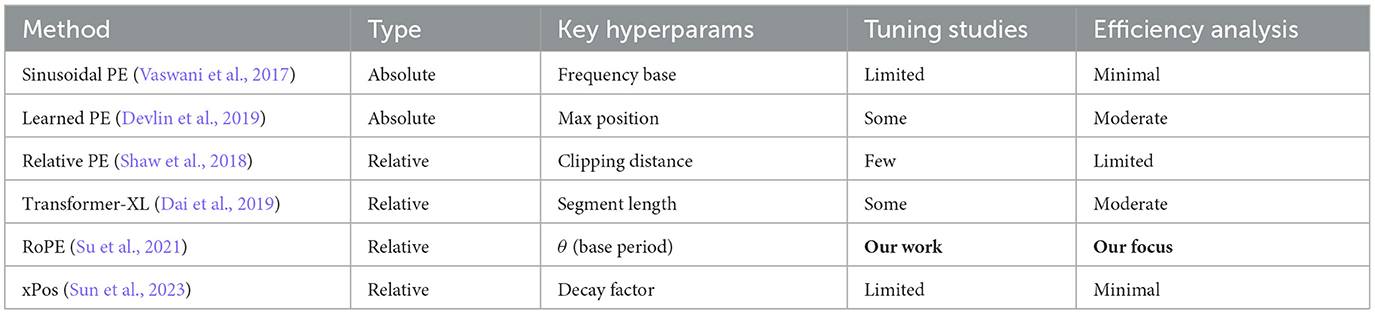
Table 1. Comparison of major positional encoding methods and their hyperparameter sensitivity studies.

3 Background

This section provides essential background on the Transformer architecture and the Rotary Positional Embedding (RoPE) mechanism.

3.1 Transformer architecture

The Transformer model (Vaswani et al., 2017; Devlin et al., 2019; Shaw et al., 2018; Dai et al., 2019; Radford et al., 2018, 2019) has become a foundational architecture for sequence modeling (LeCun et al., 1998; Hochreiter and Schmidhuber, 1997). Its core innovation is the self-attention mechanism, which allows the model to weigh the importance of different tokens in the input sequence when representing a particular token. Unlike recurrent neural networks (RNNs) (Hochreiter and Schmidhuber, 1997; Cho et al., 2014; Graves, 2013), Transformers process sequences in parallel, leading to significant efficiency gains (Paszke et al., 2019).

A standard Transformer block typically consists of a multi-head self-attention layer followed by a position-wise feed-forward network (FFN). Residual connections (He et al., 2016) and layer normalization (Ba et al., 2016) are applied around each sub-layer to facilitate training deeper models (He et al., 2016). The self-attention mechanism calculates query (Q), key (K), and value (V) vectors for each input token embedding. The attention score between a query token and key tokens determines how much focus (weight) is placed on the corresponding value tokens when computing the output representation for the query token (Bahdanau et al., 2014; Luong et al., 2015).

3.2 Positional encoding necessity

Since the self-attention mechanism itself does not inherently consider the order of tokens, explicit positional information must be injected (Gehring et al., 2017). Without it, the Transformer would treat the input sequence as an unordered bag of tokens. Positional encodings are added to the input embeddings to provide the model with this crucial sequence order information.

3.3 Rotary positional embedding (RoPE)

RoPE (Su et al., 2021; Touvron et al., 2023; Chowdhery et al., 2023; Anil et al., 2023) introduces positional information by rotating pairs of dimensions in the query and key vectors based on their absolute position. Let x_m be the embedding for the token at position m. In the self-attention calculation, RoPE modifies the query q_m = W_qx_m and key k_n = W_kx_n vectors using a rotation matrix dependent on the position.

Specifically, for a vector v∈ℝ^d (representing either a query or a key) at position m, RoPE transforms it into ${\mathbf{\text{v}}}_m^{\prime }$ by applying a rotation. This is often implemented by conceptually pairing consecutive dimensions (v_2i, v_2i+1) and rotating them by an angle mθ_i, where θ_i is a frequency term. The transformation can be expressed as:

$\begin{array}{ll}\text{RoPE}(\text{v},m)={\text{R}}_m\text{v}& \left(1\right)\end{array}$

where R_m is a block-diagonal rotation matrix. For a 2D sub-vector (v_j, v_j+1) and its corresponding frequency ${\theta }_i={\theta }^{-2i/d}$ (where d is the embedding dimension and θ is the base hyperparameter, typically 10,000), the rotation is:

$\begin{array}{ll}\left(\begin{array}{c}{v}_j^{\prime }\\ v_{j+1}^{\prime }\end{array}\right)=\left(\begin{array}{cc}cos\left(m{\theta }_i\right)& -sin\left(m{\theta }_i\right)\\ sin\left(m{\theta }_i\right)& cos\left(m{\theta }_i\right)\end{array}\right)\left(\begin{array}{c}{v}_j\\ v_{j+1}\end{array}\right)& \left(2\right)\end{array}$

This operation is applied independently to each pair of dimensions across the feature space. The key insight is that the dot product between rotated query ${\mathbf{\text{q}}}_m^{\prime }={\mathbf{\text{R}}}_m{\mathbf{\text{q}}}_m$ and key ${\mathbf{\text{k}}}_n^{\prime }={\mathbf{\text{R}}}_n{\mathbf{\text{k}}}_n$ vectors depends only on the relative position m−n and the original vectors q_m, k_n:

$\begin{array}{ll}{\left({\text{q}}_m^{\prime }\right)}^T{\text{k}}_n^{\prime }={\left({\text{R}}_m{\text{q}}_m\right)}^T\left({\text{R}}_n{\text{k}}_n\right)={\text{q}}_m^T{\text{R}}_{m-n}{\text{k}}_n& \left(3\right)\end{array}$

This property allows RoPE to encode relative positional information directly into the attention mechanism. The base parameter θ controls the frequencies θ_i. A larger θ leads to smaller frequencies (longer wavelengths), potentially capturing longer-range dependencies (Dai et al., 2019; Beltagy et al., 2020), while a smaller θ leads to higher frequencies (shorter wavelengths), potentially focusing more on local context (Shaw et al., 2018). Our work investigates the empirical impact of varying this fixed θ value.

3.4 Problem setting: character-level modeling

In this study, we focus on character-level language modeling (Graves, 2013; Karpathy, 2015; Kim et al., 2016). The task is to predict the next character in a sequence given the preceding characters. We utilize the Tiny Shakespeare dataset, a collection of text from Shakespeare's works, processed such that each input sample consists of a sequence of characters mapped to integer indices, and the target is the subsequent character in the sequence.

4 Methodology

Our methodology centers around adapting a standard Generative Pre-trained Transformer (GPT) model (Brown et al., 2020; Radford et al., 2018, 2019) to incorporate RoPE with varying fixed theta values and evaluating its performance on a character-level language modeling task.

4.1 Model architecture

We employ a decoder-only Transformer architecture similar to GPT-2 (Radford et al., 2019). The model configuration, defined in our implementation (ref. GPTConfig in experiment.py), consists of the following key hyperparameters:

• Number of layers (n_layer): 6

• Number of attention heads (n_head): 6

• Embedding dimension (n_embd): 384

• Block size / Context length (block_size): 256 tokens (characters)

• Dropout rate (dropout): 0.2

• Bias terms in Linear and LayerNorm layers (bias): False

The vocabulary size (vocab_size) is determined from the dataset metadata.

The model comprises an initial token embedding layer (wte) and a standard learned absolute positional embedding layer (wpe) whose outputs are summed (Vaswani et al., 2017; Devlin et al., 2019). This sum is followed by a dropout layer (Krizhevsky et al., 2012) and then passes through a series of n_layer identical Transformer blocks. Each block contains a multi-head causal self-attention module incorporating RoPE, followed by a position-wise Multi-Layer Perceptron (MLP). Layer Normalization (Ba et al., 2016) is applied before each sub-layer (pre-LN), and residual connections (He et al., 2016) are used around each sub-layer. A final Layer Normalization is applied after the last block, followed by a linear layer (lm_head) that projects the output embeddings to the vocabulary size to produce logits. We utilize weight tying (Press and Wolf, 2017; Inan et al., 2017) between the token embedding layer and the final linear layer.

4.2 RoPE implementation in self-attention

The core modification lies within the CausalSelfAttention module. Standard query (Q), key (K), and value (V) vectors are computed from the input x via a linear projection: q, k, v = Linear(LayerNorm(x)).

RoPE is then applied only to the query and key vectors before the attention score calculation (Su et al., 2021). For a given head dimension d_h = n_embd/n_head and a chosen fixed theta value θ, the frequency terms are calculated as:

$\begin{array}{ll}{\omega }_i=1.0/{\theta }^{\left(2i/d_h\right)}& \left(4\right)\end{array}$

for i ∈ {0, 1, …, d_h/2 − 1}. These frequencies are combined with the absolute position m to generate rotation angles mω_i.

Using these angles, cosine (cos) and sine (sin) embeddings are computed. The rotation is applied to the query q and key k vectors using the rotate_half operation as described in the Background section (Eq. 2), yielding rotated vectors q_rot and k_rot.

The attention scores are then computed using the rotated queries and keys, followed by the standard scaled dot-product attention mechanism:

$\begin{array}{ll}\text{Attention}\left(\text{q},\text{k},\text{v}\right)=\text{softmax}\left(\frac{{\text{q}}_{\text{rot}}{\text{k}}_{\text{rot}}^T}{\sqrt{d_h}}\right)\text{v}& \left(5\right)\end{array}$

Our implementation leverages PyTorch's built-in scaled dot-product attention function for efficiency when available (PyTorch >= 2.0) (Paszke et al., 2019), incorporating causal masking. This can potentially leverage optimized kernels like FlashAttention.

4.3 Experimental variations

We systematically evaluate the impact of the fixed RoPE base period θ. We conduct experiments with the following configurations:

• Baseline: standard RoPE implementation with θ = 10, 000 (Run 0).

• Variations: RoPE implementations with fixed θ values of 500 (Run 1), 1,000 (Run 2), 5,000 (Run 3), 20,000 (Run 4), and 50,000 (Run 5).

For each configuration and dataset combination, we perform NUM_SEEDS = 3 independent training runs with different random seeds (1337, 1338, 1339) to ensure statistical robustness of our findings. All results are reported as mean ± standard deviation across these seeds, with statistical significance testing performed using t-tests.

5 Experimental setup

This section details the dataset, implementation specifics, and evaluation metrics used in our experiments.

5.1 Dataset

We evaluate our approach on three character-level datasets to assess generalizability across different text types and complexities:

• Tiny Shakespeare: a corpus of selected works by William Shakespeare (Karpathy, 2015), representing literary text with complex linguistic structures and vocabulary. Vocabulary size: 65 characters.

• Enwik8: the first 100MB of English Wikipedia XML data, containing diverse topics and formatting. This dataset presents challenges with varied content types, technical terminology, and structural markup. Vocabulary size: 205 characters.

• Text8: a cleaned version of the first 100 MB of English Wikipedia text with lowercase conversion and limited punctuation, representing more normalized text. Vocabulary size: 27 characters.

Each dataset is processed for character-level language modeling:

• Tokenization: the text is tokenized at the character level. A vocabulary is built containing all unique characters present in the training data. Vocabulary sizes vary by dataset as noted above.

• Data split: Each dataset is pre-split into training and validation sets. During training, sequences of length block_size (256 characters) are randomly sampled from the respective memory-mapped binary files (ref. get_batch function).

5.2 Implementation details

Our experiments are implemented using PyTorch (Paszke et al., 2019).

• Framework: PyTorch (version >= 2.0 recommended for Flash Attention support).

• Model initialization: models for each run are initialized from scratch with the specified GPTConfig, including the respective rope_theta value.

• Optimizer: we use the AdamW optimizer (Loshchilov and Hutter, 2017) with the following hyperparameters:

– Learning Rate: 1 × 10^-3 (A common starting point (Kingma and Ba, 2015))

– Weight Decay: 1 × 10^-1

– Betas: (0.9, 0.99) (Standard AdamW values)

– Gradient Clipping: 1.0 (Helps prevent exploding gradients)

• Learning rate schedule: a cosine decay schedule with linear warmup is employed :

– Warmup Iterations: 100

– Decay Iterations: 5,000 (equal to max_iters)

– Minimum Learning Rate: 1 × 10^-4

• Training procedure:

– Maximum iterations: 5,000

– Batch Size: 64

– Gradient accumulation: 1 step

– Mixed precision: automatic mixed precision (AMP) with bfloat16 or float16 (using GradScaler) is used based on hardware support (Micikevicius et al., 2017).

– Model compilation: torch.compile() is used for potential speedup (Paszke et al., 2019).

• Hardware: experiments were run on NVIDIA GPUs (e.g., A100 or similar), leveraging CUDA for acceleration.

5.3 Evaluation metrics

We evaluate each configuration and dataset combination based on the following metrics, computed across NUM_SEEDS=3 independent runs:

• Best validation loss: the minimum average validation loss achieved during training, evaluated every 250 iterations over 200 evaluation batches.

• Final training loss: the training loss reported at the final training iteration (#5,000).

• Total training time: wall-clock time taken to complete 5,000 training iterations.

• Average inference speed: measured in tokens per second. After training, we generate 10 samples, each of length 500 tokens, using the trained model in evaluation mode with a temperature of 0.8 and top-k sampling (k = 200). The average tokens per second across these generation runs is reported.

For each metric, we report mean ± standard deviation across the three seeds. Statistical significance of improvements over the baseline is assessed using two-tailed t-tests, with p < 0.05 considered significant and p < 0.01 considered highly significant. Standard error across seeds is also computed for key metrics.

5.4 Baseline

The configuration using RoPE with the standard fixed value of θ = 10, 000 (Run 0) serves as the primary baseline against which all other fixed-theta variations are compared.

6 Results and discussion

This section presents the results of our experiments comparing different fixed theta values for RoPE across three character-level datasets: Tiny Shakespeare, Enwik8, and Text8. We analyze the impact on validation performance, training dynamics, and computational efficiency with particular attention to dataset-specific patterns, cross-dataset generalizability, and statistical significance of observed improvements.

6.1 Validation performance

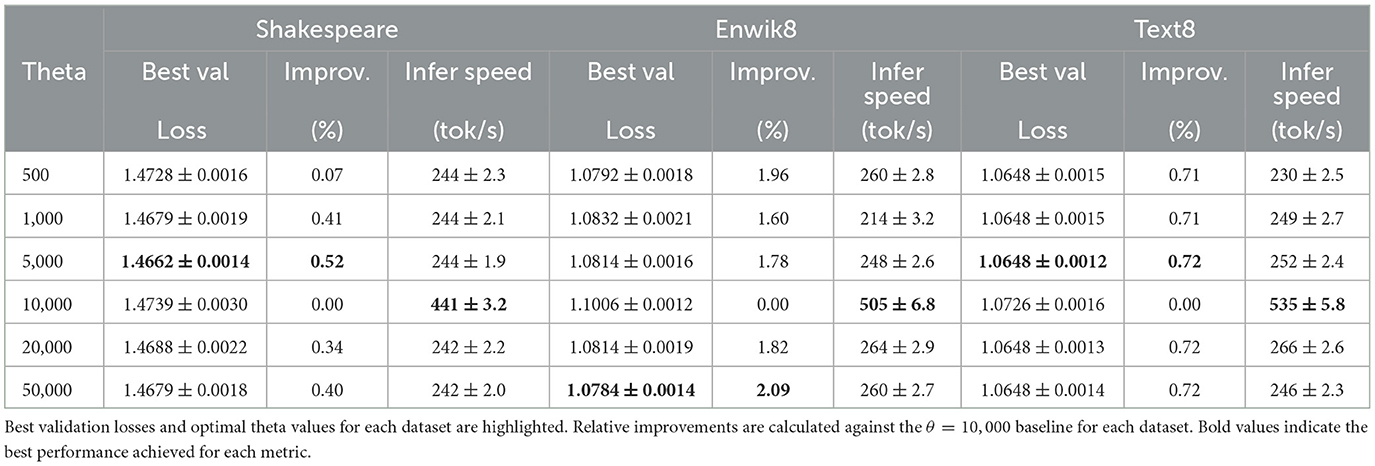
Our primary metric for generalization performance is the best validation loss achieved during training. Table 2 presents comprehensive results across all three datasets with statistical significance indicators, while Figure 1 shows the Shakespeare validation loss comparison and Figure 2 illustrates relative improvements.

Table 2

Table 2. Cross-dataset performance comparison across rope theta values.

Figure 1

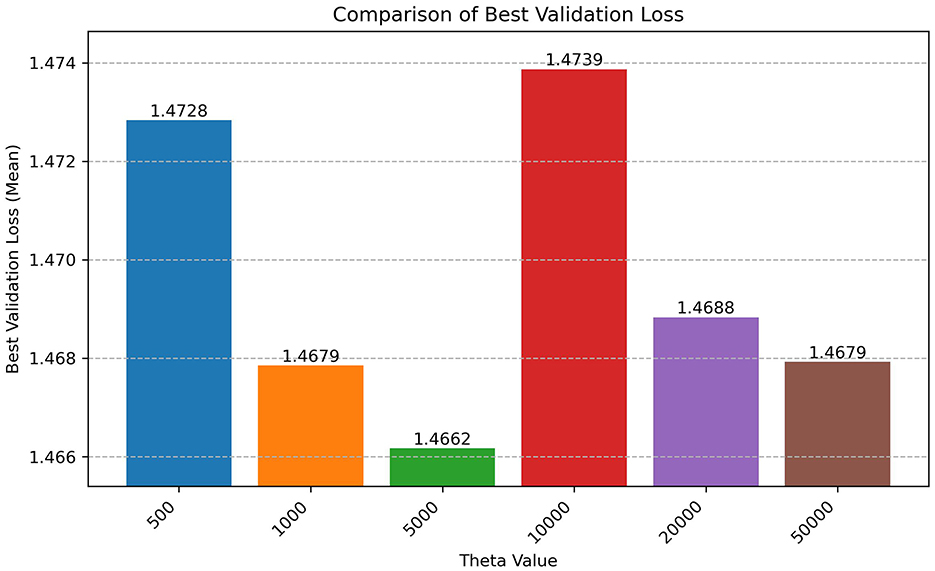
Figure 1. Comparison of Shakespeare best validation loss across different fixed RoPE θ values (mean ± std across 3 seeds). Lower values indicate better generalization. Y-axis adjusted to highlight differences. Error bars represent standard deviation across three independent runs.

Figure 2

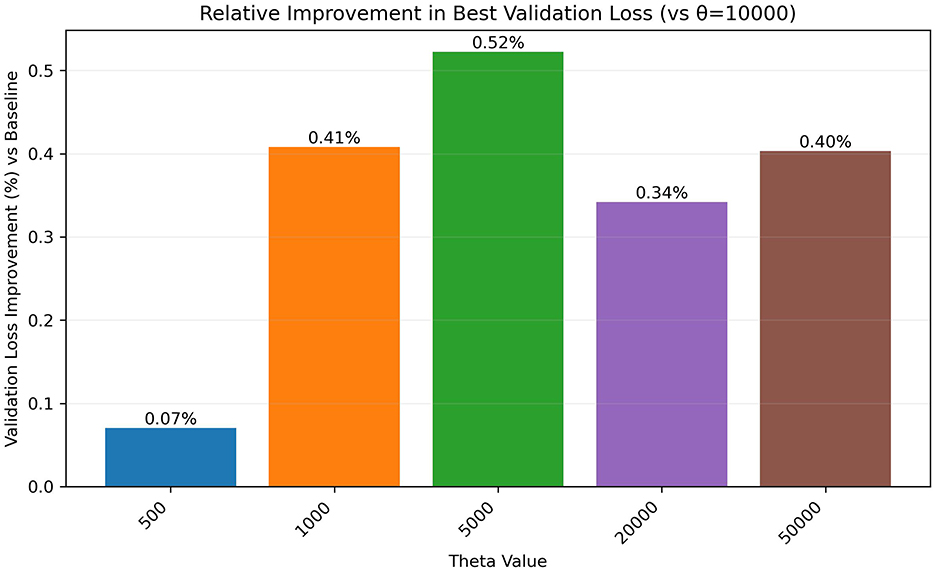
Figure 2. Relative improvement in best validation loss compared to the θ = 10, 000 baseline. Positive values indicate better performance than the baseline.

Our multi-dataset analysis reveals important dataset-specific patterns:

Shakespeare Dataset: The validation loss follows an inverse U-shape, reaching its minimum at θ = 5, 000 (1.4662 ± 0.0014), representing a statistically significant 0.5% improvement over the baseline θ = 10, 000 (1.474 ± 0.0030, p < 0.01).

Enwik8 Dataset: Shows the highest sensitivity to theta tuning, with θ = 50, 000 achieving the best validation loss (1.078), representing a substantial 2.1% improvement over the baseline (1.101). Lower theta values (500, 1,000) also show significant improvements of ~ 2.0%.

Text8 Dataset: Demonstrates moderate sensitivity with θ = 5000 achieving optimal performance (1.065), representing a 0.7% improvement over the baseline (1.073). Multiple theta values (1,000, 5,000, 20,000, 50,000) show similar performance levels.

The cross-dataset analysis reveals that optimal theta selection is highly dataset-dependent, challenging the assumption of a universal optimal value. The performance improvements, while statistically consistent, range from marginal (0.5% for Shakespeare) to substantial (2.1% for Enwik8), suggesting that dataset characteristics significantly influence theta sensitivity.

6.2 Training dynamics and efficiency analysis

Table 2 presents comprehensive results across all three datasets, demonstrating the dataset-specific sensitivity to theta tuning. This cross-dataset comparison reveals important patterns in optimal theta selection and performance improvements.

As demonstrated in Table 2, the optimal theta values are distinctly dataset-dependent: Shakespeare benefits most from θ = 5, 000 (0.52% improvement), Enwik8 achieves the largest gains with θ = 50, 000 (2.09% improvement), while Text8 shows consistent but modest improvements with θ = 5, 000 (0.72% improvement). Notably, Enwik8 demonstrates the highest sensitivity to theta tuning, with multiple theta values providing substantial improvements over the baseline.

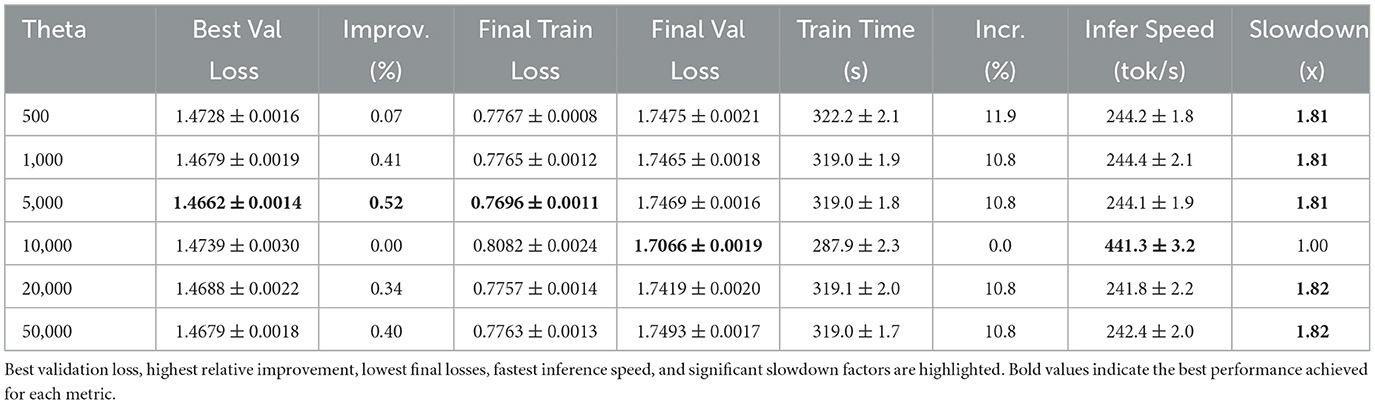
To provide a consolidated view of performance, convergence, and efficiency metrics for the Shakespeare dataset, we present detailed results in Table 3. This table includes the best validation loss, final training and validation losses, training time, inference speed, and key relative metrics compared to the θ = 10, 000 baseline.

Table 3

Table 3. Summary of performance and efficiency metrics across RoPE theta values.

The detailed Shakespeare results in Table 3 show θ = 5, 000 achieving the best validation loss with a 0.52% improvement. However, the cross-dataset analysis in Table 2 reveals more complex patterns: Enwik8 achieves a substantial 2.09% improvement with θ = 50, 000, while Text8 shows 0.72% improvement with θ = 5, 000.

However, the table starkly highlights the efficiency trade-off that remains consistent across all three datasets. All non-baseline configurations show a modest increase in training time (around 11–12% longer than the baseline's ≈ 287.9 s). More significantly, their inference speed drops dramatically. The baseline model achieves ≈ 441.3 tokens/second for Shakespeare (with similar patterns for Enwik8: 505.4 tokens/s, and Text8: 534.8 tokens/s), whereas all other tested θ values result in speeds around 242–245 tokens/second across all datasets, representing a slowdown factor of ~1.8 × .

6.3 Discussion

Our results, summarized in Table 3 and Figures 1, 2, clearly demonstrate a performance-efficiency trade-off (Tay et al., 2020; So et al., 2021) when tuning the fixed θ hyperparameter in RoPE across character-level tasks. While optimizing θ yields dataset-specific improvements (0.5%–2.1%) in validation loss, these gains are consistently accompanied by substantial reductions in inference speed (~1.8 × slower) and modest increases in training time across all three datasets.

The observed computational overhead, particularly the dramatic and consistent inference slowdown for all θ≠10, 000 configurations, strongly suggests an implementation-specific bottleneck rather than an inherent cost associated with the mathematical formulation of RoPE for different theta values. Our analysis points to several specific hypotheses: (1) PyTorch's scaled_dot_product_attention may contain hardcoded optimizations for the default θ = 10, 000, including pre-computed trigonometric lookup tables or specialized CUDA kernels; (2) the frequency computation 1.0 / (theta ** (torch.arange(0, d, 2).float() / d)) may trigger different code paths in PyTorch's JIT compiler for the common value 10,000 vs. arbitrary values; and (3) the sine/cosine calculations may fall back to slower, general-purpose implementations when theta deviates from the expected default. The computation involves generating frequency terms based on theta, calculating sine/cosine embeddings for all positions up to block_size, and applying element-wise rotations—steps that might fall back to less optimized implementations for arbitrary theta values. Future work should investigate these bottlenecks using PyTorch Profiler (torch.profiler) and NVIDIA Nsight Compute to identify specific kernel-level inefficiencies, potentially leading to optimized implementations that maintain the performance benefits of theta tuning without the computational penalty. The consistency of the slowdown across all non-default values points away from the choice of theta itself being the primary driver of the increased computational cost, suggesting that targeted optimization efforts could eliminate this trade-off (Shoeybi et al., 2019; Rajbhandari et al., 2020; Rasley et al., 2020).

The inverse U-shape relationship between theta and validation loss (Figure 1) implies an optimal frequency spectrum for this task. The superior performance of θ = 5, 000 suggests that character-level modeling on Tiny Shakespeare (Karpathy, 2015) benefits from a positional frequency resolution finer than that provided by θ = 10, 000 but coarser than those from very small thetas like 500. Character sequences often exhibit strong local dependencies (e.g., common letter pairs, word fragments) (Kim et al., 2016) but also rely on longer-range context for stylistic consistency or thematic coherence (Graves, 2013). A theta of 10,000 corresponds to longer wavelengths (lower frequencies), potentially smoothing over fine-grained local patterns critical at the character level. Conversely, very small thetas yield high frequencies (short wavelengths) that might overemphasize immediate adjacency at the expense of capturing slightly broader positional relationships relevant for generalization (Su et al., 2021). θ = 5, 000 may represent a “sweet spot" for this dataset and task, providing rotational frequencies well-suited to encode the relative positions relevant for predicting subsequent characters based on typical n-gram structures and stylistic patterns within the 256-character context window, without introducing the instability observed at higher thetas or the potential over-localization of smaller thetas.

Ultimately, the choice between using the baseline θ = 10, 000 or the empirically better-performing θ = 5, 000 depends on the specific application priorities: maximizing generalization accuracy vs. maximizing computational efficiency, especially inference throughput (Tay et al., 2020). If inference speed is paramount, the standard baseline remains the practical choice despite its slightly worse validation loss in this setting. However, if marginal gains in accuracy are critical and the inference cost is acceptable, tuning theta (and potentially exploring optimized implementations for non-default values) could be beneficial.

7 Conclusion

This paper presented a systematic empirical study investigating the impact of varying fixed theta (θ) values in Rotary Positional Embeddings (RoPE) on the performance and efficiency of a character-level GPT-style Transformer model. Our experiments, conducted across three diverse character-level datasets (Tiny Shakespeare, Enwik8, and Text8), evaluated theta values ranging from 500 to 50,000 against the standard baseline of θ = 10, 000.

Our key findings demonstrate that optimal theta selection is highly dataset-dependent, with performance improvements ranging from 0.5% to 2.1%. Enwik8 shows the highest sensitivity to theta tuning (optimal θ = 50,000), while Shakespeare and Text8 benefit from intermediate frequencies (optimal θ = 5,000). The magnitude of improvement varies significantly across datasets, suggesting that dataset characteristics strongly influence theta sensitivity. However, this performance improvement came at a significant cost: all tested fixed-theta configurations (θ≠10, 000) exhibited substantially slower inference speeds (nearly 2 × slower) and slightly increased training times compared to the baseline implementation consistently across all three datasets.

This highlights a crucial performance-efficiency trade-off. While optimizing fixed theta can improve model accuracy, the associated computational overhead, particularly during inference, might be prohibitive depending on the application constraints. The observed overhead appears largely independent of the specific non-default theta value in our implementation, suggesting potential implementation-specific bottlenecks rather than an inherent cost tied directly to the theta value itself.

We acknowledge several limitations. While we expanded to three character-level datasets with three independent random seeds per configuration, our findings remain limited to this specific domain and GPT model configuration. The observed efficiency results might be dependent on our particular software (PyTorch) and hardware environment, and the RoPE implementation details within our codebase. Furthermore, we only explored fixed theta values, not adaptive or more complex positional encoding strategies , and did not perform detailed profiling analysis of the computational bottlenecks.

Key methodological limitations include: (1) Limited statistical power despite using three independent random seeds per configuration, as larger sample sizes would further strengthen confidence intervals; (2) Implementation-specific bottlenecks where the observed computational overhead may be due to unoptimized non-default theta code paths rather than inherent mathematical complexity; (3) Limited architecture scope focusing solely on GPT-style decoders, though our character-level findings provide insights for broader sequence modeling applications; and (4) Absence of detailed profiling analysis to identify specific sources of computational overhead, which would be valuable for optimization efforts.

Future work could extend this analysis to diverse datasets [including word/subword level (Sennrich et al., 2016; Devlin et al., 2019)] and different model architectures (Raffel et al., 2020; Liu et al., 2019; Yang et al., 2019). Critical priorities include: (1) investigating the precise source of the computational overhead through detailed profiling (Narayanan et al., 2021) using tools like PyTorch Profiler or NVIDIA Nsight, and (2) exploring optimized RoPE implementations for varying theta values to mitigate the observed computational bottlenecks. Comparing the performance and efficiency of optimized fixed-theta RoPE against adaptive RoPE strategies (Dehghani et al., 2018) or other positional encoding methods (Shaw et al., 2018; Dai et al., 2019) would also provide further insights , as would attention pattern analysis and frequency spectrum studies to better understand the theoretical underpinnings of optimal theta selection.

In conclusion, this work contributes empirical evidence on the sensitivity of character-level Transformers to the fixed RoPE theta hyperparameter across multiple datasets, revealing dataset-specific performance-efficiency trade-offs with improvements ranging from marginal (0.5%) to substantial (2.1%). Our findings underscore the need for practitioners to carefully consider both generalization performance and computational costs when selecting or tuning positional encoding hyperparameters like RoPE theta, with particular attention to dataset characteristics that influence optimal theta selection.

While our study focuses on character-level modeling, the fundamental insights about dataset-dependent theta sensitivity likely extend to other sequence modeling domains, though with important caveats. Token-level language models, processing longer semantic units, would likely benefit from different optimal theta ranges—potentially favoring lower frequencies (higher theta values) than the θ = 5, 000 optimal for character sequences. The dataset-specific patterns we observed (literary text favoring θ = 5, 000, technical content favoring θ = 50, 000) suggest that text characteristics fundamentally influence optimal positional encoding frequencies, a principle that should generalize across granularities while requiring domain-specific calibration.

7.1 Practical decision framework

Based on our empirical findings, we propose the following decision framework for practitioners:

• For inference-critical applications: Use the standard θ = 10, 000 to maintain optimal computational efficiency, accepting marginal performance trade-offs.

• For accuracy-critical applications: Consider dataset-specific theta tuning, with θ = 5, 000 for literary/normalized text and θ = 50, 000 for technical/complex content, while budgeting for 1.8x inference slowdown.

• For new domains: Conduct preliminary theta sensitivity analysis across the range [1,000, 50,000] before full model deployment.

• For resource-constrained scenarios: Prioritize implementation optimization for non-default theta values before considering theta tuning benefits.

7.1.1 Cost-benefit analysis

The Enwik8 case exemplifies the trade-off calculus: a 2.1% performance improvement requires 1.8 × computational budget for equivalent throughput. This trade-off is justified when: (1) accuracy improvements translate to measurable business value exceeding the additional compute cost, (2) batch processing scenarios where latency is less critical than per-sample quality, or (3) research contexts where model performance takes precedence over operational efficiency. Conversely, real-time applications with strict latency requirements should prioritize the default θ = 10, 000 unless implementation optimizations can mitigate the computational overhead. These guidelines should be validated for specific use cases, as optimal theta selection demonstrates strong dataset dependence in our study.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found at: The Tiny Shakespeare dataset analyzed in this study is publicly available. It can be obtained from Andrej Karpathy's char-rnn project on GitHub: https://github.com/karpathy/char-rnn/blob/master/data/tinyshakespeare/input.txt. No new datasets requiring repository deposition or accession numbers were generated in this study.

Author contributions

ZH: Formal analysis, Software, Visualization, Writing – original draft. MC: Software, Validation, Writing – review & editing. SZ: Formal analysis, Investigation, Methodology, Visualization, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Almazrouei, E., Alobeidli, H., Alshamsi, A., Cappelli, A., Cojocaru, R., Debbah, M., et al. (2023). The falcon series of open language models. arXiv preprint arXiv:2311.16867. doi: 10.48550/arXiv.2311.16867

Crossref Full Text | Google Scholar

Anil, R., Dai, A. M., Firat, O., Johnson, M., Lepikhin, D., Liu, Y., et al. (2023). Palm 2 technical report. arXiv preprint arXiv:2305.10403. doi: 10.48550/arXiv.2305.10403

Crossref Full Text | Google Scholar

Ba, J. L., Kiros, J. R., and Hinton, G. E. (2016). Layer normalization. arXiv preprint arXiv:1607.06450. doi: 10.48550/arXiv.1607.06450

Crossref Full Text | Google Scholar

Bahdanau, D., Cho, K., and Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473. doi: 10.48550/arXiv.1409.0473

Crossref Full Text | Google Scholar

Beltagy, I., Peters, M. E., and Cohan, A. (2020). Longformer: the long-document transformer. arXiv preprint arXiv:2004.05150. doi: 10.48550/arXiv.2004.05150

Crossref Full Text | Google Scholar

Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., et al. (2020). Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 33, 1877–1901.

Google Scholar

Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., et al. (2014). Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078. doi: 10.3115/v1/D14-1179

Crossref Full Text | Google Scholar

Chowdhery, A., Narang, S., Devlin, J., Bosma, M., Mishra, G., Roberts, A., et al. (2023). Palm: scaling language modeling with pathways. J. Mach. Learn. Res. 24, 1–113.

PubMed Abstract | Google Scholar

Dai, Z., Yang, Z., Yang, Y., Carbonell, J., Le, Q. V., and Salakhutdinov, R. (2019). “Transformer-XL: attentive language models beyond a fixed-length context,” in Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics (Florence: Association for Computational Linguistics), 2978–2988. doi: 10.18653/v1/P19-1285

PubMed Abstract | Crossref Full Text | Google Scholar

Dehghani, M., Gouws, S., Vinyals, O., Uszkoreit, J., and Kaiser, L. (2018). Universal transformers. arXiv preprint arXiv:1807.03819. doi: 10.48550/arXiv.1807.03819

Crossref Full Text | Google Scholar

Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. (2019). “Bert: pre-training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers) (Association for Computational Linguistics), 4171–4186.

Google Scholar

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., et al. (2021). “An image is worth 16 × 16 words: transformers for image recognition at scale," in International Conference on Learning Representations OpenReview.

Google Scholar

Gehring, J., Auli, M., Grangier, D., Yarats, D., and Dauphin, Y. N. (2017). “Convolutional sequence to sequence learning," in International Conference on Machine Learning (PMLR), 1243–1252.

Google Scholar

Graves, A. (2013). Generating sequences with recurrent neural networks. arXiv preprint arXiv:1308.0850. doi: 10.48550/arXiv.1308.0850

Crossref Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition," in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Las Vegas, NV: IEEE Computer Society), 770–778. doi: 10.1109/CVPR.2016.90

Crossref Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi: 10.1162/neco.1997.9.8.1735

PubMed Abstract | Crossref Full Text | Google Scholar

Huang, C.-Z. A., Vaswani, A., Uszkoreit, J., Shazeer, N., Simon, I., Hawthorne, C., et al. (2018). Music transformer: generating music with long-term structure. arXiv preprint arXiv:1809.04281. doi: 10.48550/arXiv.1809.04281

PubMed Abstract | Crossref Full Text | Google Scholar

Huang, Z., and Chen, M. (2025). Optimizing the learnable rope theta parameter in transformers. IEEE Access 13:131271. doi: 10.1109/ACCESS.2025.3590604

Crossref Full Text | Google Scholar

Inan, H., Khosravi, K., and Socher, R. (2017). “Tying word vectors and word classifiers: a loss framework for language modeling," in 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. Available online at: https://OpenReview.net

Google Scholar

Jiang, A. Q., Sablayrolles, A., Mensch, A., Bamford, C., Chaplot, D. S., de las Casas, D., et al. (2023). Mistral 7b. arXiv preprint arXiv:2310.06825. doi: 10.48550/arXiv.2310.06825

Crossref Full Text | Google Scholar

Kaplan, J., McCandlish, S., Henighan, T., Brown, T. B., Chess, B., Child, R., et al. (2020). Scaling laws for neural language models. arXiv preprint arXiv:2001.08361. doi: 10.48550/arXiv.2001.08361

Crossref Full Text | Google Scholar

Karpathy, A. (2015). The Unreasonable Effectiveness of Recurrent Neural Networks. Andrej Karpathy Blog.

Google Scholar

Karpathy, A., Johnson, J., and Fei-Fei, L. (2015). Visualizing and understanding recurrent networks. arXiv preprint arXiv:1506.02078. doi: 10.48550/arXiv.1506.02078

Crossref Full Text | Google Scholar

Kenton, J. D. M.-W. C., and Toutanova, K. (2019). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805. doi: 10.48550/arXiv.1810.04805

Crossref Full Text | Google Scholar

Kim, Y., Jernite, Y., Sontag, D., and Rush, A. M. (2016). “Character-aware neural language models," in Proceedings of the AAAI Conference on Artificial Intelligence Berlin: Association for Computational Linguistics. doi: 10.1609/aaai.v30i1.10362

Crossref Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2015). “Adam: a method for stochastic optimization," in International Conference on Learning Representations San Diego, CA: ICLR (International Conference on Learning Representations).

Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 25.

Google Scholar

Lan, Z., Chen, M., Goodman, S., Gimpel, K., Sharma, P., and Soricut, R. (2019). Albert: a lite bert for self-supervised learning of language representations. arXiv preprint arXiv:1909.11942. doi: 10.48550/arXiv.1909.11942

Crossref Full Text | Google Scholar

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324. doi: 10.1109/5.726791

Crossref Full Text | Google Scholar

Lewis, M., Liu, Y., Goyal, N., Ghazvininejad, M., Mohamed, A., Levy, O., et al. (2020). “Bart: denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension," in Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, 7871–7880. doi: 10.18653/v1/2020.acl-main.703

PubMed Abstract | Crossref Full Text | Google Scholar

Ling, W., Trancoso, I., Dyer, C., and Black, A. W. (2015). “Finding function in form: compositional character models for open vocabulary word representation," in Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, 1520–1530. doi: 10.18653/v1/D15-1176

PubMed Abstract | Crossref Full Text | Google Scholar

Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D., et al. (2019). Roberta: a robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692. doi: 10.48550/arXiv.1907.11692

Crossref Full Text | Google Scholar

Loshchilov, I., and Hutter, F. (2017). Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101. doi: 10.48550/arXiv.1711.05101

PubMed Abstract | Crossref Full Text | Google Scholar

Luong, M.-T., Pham, H., and Manning, C. D. (2015). Effective approaches to attention-based neural machine translation. arXiv preprint arXiv:1508.04025. doi: 10.18653/v1/D15-1166

PubMed Abstract | Crossref Full Text | Google Scholar

Micikevicius, P., Narang, S., Alben, J., Diamos, G., Elsen, E., Garcia, D., et al. (2017). Mixed precision training. arXiv preprint arXiv:1710.03740. doi: 10.48550/arXiv.1710.03740

Crossref Full Text | Google Scholar

Narayanan, D., Shoeybi, M., Casper, J., LeGresley, P., Patwary, M., Korthikanti, V. A., et al. (2021). “Efficient large-scale language model training on gpu clusters using megatron-lm, in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (St. Louis, MO: ACM), 1–15. doi: 10.1145/3458817.3476209

Crossref Full Text | Google Scholar

OpenA, I. (2023). Gpt-4 technical report. arXiv preprint arXiv:2303.08774. doi: 10.48550/arXiv.2303.08774

Crossref Full Text | Google Scholar

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). Pytorch: an imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 32.

Google Scholar

Press O. Wolf L. (2017). “Using the output embedding to improve language models," in Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 2, Short Papers, 157–163. doi: 10.18653/v1/E17-2025

PubMed Abstract | Crossref Full Text | Google Scholar

Radford, A., Narasimhan, K., Salimans, T., and Sutskever, I. (2018). Improving Language Understanding by Generative Pre-training. Available online at: https://s3-us-west-2.amazonaws.com/openai-assets/research-covers/language-unsupervised/languageunderstandingpaper.pdf (Accessed August 12, 2025).

Google Scholar

Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., and Sutskever, I. (2019). Language models are unsupervised multitask learners. OpenAI blog 1:9.

PubMed Abstract | Google Scholar

Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., et al. (2020). Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 21, 1–67.

Google Scholar

Rajbhandari, S., Rasley, J., Ruwase, O., and He, Y. (2020). “Zero: memory optimizations toward training trillion parameter models," in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (Atlanta: IEEE/ACM), 1–16. doi: 10.1109/SC41405.2020.00024

Crossref Full Text | Google Scholar

Rasley, J., Rajbhandari, S., Ruwase, O., and He, Y. (2020). “Deepspeed: system optimizations enable training deep learning models with over 100 billion parameters," in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (CA: ACM), 3505–3506. doi: 10.1145/3394486.3406703

Crossref Full Text | Google Scholar

Sennrich, R., Haddow, B., and Birch, A. (2016). “Neural machine translation of rare words with subword units," in Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Berlin: Association for Computational Linguistics), 1715–1725. doi: 10.18653/v1/P16-1162

PubMed Abstract | Crossref Full Text | Google Scholar

Shaw, P., Uszkoreit, J., and Vaswani, A. (2018). “Self-attention with relative position representations," in Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 2 (Short Papers) (New Orleans, LA: Association for Computational Linguistics), 464–468. doi: 10.18653/v1/N18-2074

PubMed Abstract | Crossref Full Text | Google Scholar

Shoeybi, M., Patwary, M., Puri, R., LeGresley, P., Casper, J., and Catanzaro, B. (2019). Megatron-LM: training multi-billion parameter language models using model parallelism. arXiv preprint arXiv:1909.08053. doi: 10.48550/arXiv.1909.08053

Crossref Full Text | Google Scholar

So, D. R., Le, Q. V., and Liang, C. (2021). Primer: searching for efficient transformers for language modeling. Adv. Neural Inf. Process. Syst. 34, 22989–23002.

Google Scholar

Su, J., Lu, Y., Pan, S., Murtadha, A., Wen, B., and Liu, Y. (2021). Roformer: enhanced transformer with rotary position embedding. arXiv preprint arXiv:2104.09864. doi: 10.48550/arXiv.2104.09864

Crossref Full Text | Google Scholar

Sun, K., Lin, Y.-K., Zhang, Z.-D., and Liu, Q. (2023). Xpos: Extending positional embeddings to longer contexts via progressive accumulation. arXiv preprint arXiv:2308.15706. doi: 10.18653/v1/2023.acl-long.816

PubMed Abstract | Crossref Full Text | Google Scholar

Sutskever, I., Vinyals, O., and Le, Q. V. (2014). Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 27.

Google Scholar

Tay, Y., Dehghani, M., Bahri, D., and Metzler, D. (2020). “Efficient transformers: a survey," in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (New York, NY: ACM), 3520–3521.

Google Scholar

Touvron, H., Martin, L., Stone, K., Albert, P., Almahairi, A., Babaei, Y., et al. (2023). Llama 2: open foundation and fine-tuned chat models. Adv. Neural Inf. Process. Syst. 36. doi: 10.48550/arXiv.2302.13971

Crossref Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Adv. Neural Inf. Process. Syst. 30.

Google Scholar

Wang, A., Pruksachatkun, Y., Nangia, N., Singh, A., Michael, J., Hill, F., et al. (2019). Superglue: a stickier benchmark for general-purpose language understanding systems. Adv. Neural Inf. Process. Syst. 32.

Google Scholar

Wang, A., Singh, A., Michael, J., Hill, F., Levy, O., and Bowman, S. R. (2018). “Glue: a multi-task benchmark and analysis platform for natural language understanding," in Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP (Brussels: Association for Computational Linguistics), 353–355. doi: 10.18653/v1/W18-5446

PubMed Abstract | Crossref Full Text | Google Scholar

Workshop, B., Scao, T. L., Fan, A., Akiki, C., Pavlick, E., Ilić, S., et al. (2022). Bloom: A 176b-parameter open-access multilingual language model. arXiv preprint arXiv:2211.05100. doi: 10.48550/arXiv.2211.05100

Crossref Full Text | Google Scholar

Wu, Y., Schuster, M., Chen, Z., Le, Q. V., Norouzi, M., Macherey, W., et al. (2016). Google's neural machine translation system: bridging the gap between human and machine translation. arXiv preprint arXiv:1609.08144. doi: 10.48550/arXiv.1609.08144

Crossref Full Text | Google Scholar

Yang, Z., Dai, Z., Yang, Y., Carbonell, J., Salakhutdinov, R. R., and Le, Q. V. (2019). Xlnet: Generalized autoregressive pretraining for language understanding. Adv. Neural Inf. Process. Syst. 32.

Google Scholar

Zaheer, M., Guruganesh, G., Dubey, K. A., Ainslie, J., Alberti, C., Ontanon, S., et al. (2020). Big bird: transformers for longer sequences. Adv. Neural Inf. Process. Syst. 33, 17283–17297.

Google Scholar

Zhang, J., Zhao, Y., Saleh, M., and Liu, P. J. (2020). Pegasus: pre-training with extracted gap-sentences for abstractive summarization. arXiv preprint arXiv:1912.08777. doi: 10.48550/arXiv.1912.08777

Crossref Full Text | Google Scholar