Abstract
The advent of Industry 4.0 and the emerging Industry 5.0 have fundamentally transformed manufacturing systems, introducing unprecedented levels of complexity in production scheduling. This complexity is further amplified by the integration of cyber-physical systems, Internet of Things, Artificial Intelligence, and human-centric approaches, necessitating more sophisticated optimization methods. This paper aims to provide a more comprehensive perspective on the application of metaheuristic algorithms in shop scheduling problems within the context of Industry 4.0 and Industry 5.0. Through a systematic review of recent literature (2015–2024), we analyze and categorize various metaheuristic approaches, including Evolutionary Algorithms (EAs), swarm intelligence, and hybrid methods, that have been applied to address complex scheduling challenges in smart manufacturing environments. We specifically examine how these algorithms handle multiple competing objectives such as makespan minimization, energy efficiency, production costs, and human-machine collaboration, which are crucial in modern industrial settings. Our survey reveals several key findings: 1) hybrid metaheuristics demonstrate superior performance in handling multi-objective optimization compared to standalone algorithms; 2) bio-inspired algorithms show promising results in addressing complex scheduling and multi-objective manufacturing environments; 3) tri-objective and higher-order multi-objective optimization problems warrant further in-depth exploration; and 4) there is an emerging trend towards incorporating human factors and sustainability objectives in scheduling optimization, aligned with Industry 5.0 principles. Additionally, we identify research gaps and propose future research directions, particularly in areas such as real-time scheduling adaptation, human-centric optimization, and sustainability-aware scheduling algorithms. This comprehensive review provides insights for researchers and practitioners in the field of industrial scheduling, offering a structured understanding of current methodologies and future challenges in the evolution from Industry 4.0 to 5.0.
1 Introduction
The manufacturing industry is undergoing a profound transformation, characterized by rapidly expanding production scales and intensifying global competition. Traditional manufacturing approaches, heavily dependent on manual labor, are becoming increasingly inadequate in meeting the demands of modern industrial production. In response to these challenges, the emergence of cutting-edge technologies, including the Internet of Things (IoT), Artificial Intelligence (AI), and advanced automation systems, has provided unprecedented opportunities for manufacturing transformation (Mourtzis, 2020a; Mourtzis, 2022). These technological innovations have not only revolutionized production processes through enhanced automation and intelligence but have also optimized resource allocation, reduced operational costs, and significantly improved both efficiency and quality of products.
Shop scheduling represents a fundamental challenge in manufacturing systems and has been extensively studied in the literature. The core objective of scheduling is to optimally allocate limited production resources (e.g., machines, workers, materials) to various tasks while satisfying multiple constraints and objectives. While traditional scheduling approaches, based on human expertise and simplified mathematical models, have served well historically, they prove inadequate in addressing the complexity and dynamism of contemporary manufacturing environments characterized by volatile demand patterns and high uncertainty. Consequently, the integration of advanced information technologies and intelligent algorithms for scheduling optimization has emerged as a critical research focus.
In the evolution of industrial paradigms, Industry 4.0 emphasizes the comprehensive integration of information and communication technologies with cyberspace virtual systems, encompassing IoT, Cyber-Physical Systems, smart factories, and cloud computing, to enhance manufacturing automation and intelligence (Mourtzis, 2020b; Jain et al., 2022). Within the Industry 4.0 framework, shop scheduling faces both new opportunities and challenges (Ferreira et al., 2023). Data-driven scheduling optimization, intelligent decision support, and flexible production models have transformed production processes into more efficient and controllable systems. The vast amount of production data collected through IoT infrastructure enables the development of more accurate scheduling models. Furthermore, the integration of big data analytics and machine learning algorithms facilitates data-driven optimization, while smart factories and autonomous decision-making systems enable real-time production adjustments and anomaly detection, significantly enhancing system adaptability and efficiency.
With the continued advancement of Industry 4.0, it has become increasingly evident that, while technological progress has significantly enhanced productivity, achieving more comprehensive and sustainable industrial development requires greater consideration of human factors, environmental sustainability, and system resilience. Consequently, Industry 5.0 has emerged as an extension of Industry 4.0, adopting a more holistic approach that emphasizes human-centricity, sustainability, and resilience. This shift represents not merely a technological upgrade but a profound reevaluation and transformation of industrial production paradigms, aiming to establish a more harmonious, green, and flexible industrial ecosystem.
In this context, shop scheduling must evolve beyond technical optimization to incorporate human factors and social responsibility (Destouet et al., 2023). The human-centric manufacturing paradigm prioritizes worker wellbeing and satisfaction through smart wearable devices and health monitoring systems. Sustainable production practices focus on minimizing resource consumption and environmental impact through green manufacturing and circular economy principles. Additionally, resilient production systems are designed to withstand disruptions through flexible production networks and robust supply chain architectures. These emerging requirements have significantly increased the complexity of scheduling problems, necessitating the consideration of multiple objectives which often competing.
Metaheuristic algorithms have emerged as powerful tools for addressing these complex multi-objective scheduling challenges. These algorithms demonstrate remarkable effectiveness in handling large-scale problems with multiple competing objectives, offering flexible and efficient solutions that can adapt to varying production scenarios. Their success in solving complex and dynamic shop scheduling problems, coupled with their ability to balance multiple objectives across different production scales, has led to their increased adoption in manufacturing applications. Moreover, the integration of metaheuristics with Industry 4.0 and 5.0 technologies has opened new avenues for scheduling optimization, enabling more sophisticated approaches to improving production efficiency and quality. Compared to previous studies, this paper aims to provide a more comprehensive perspective on the application of metaheuristic algorithms in shop scheduling problems within the context of Industry 4.0 and Industry 5.0, making the following contributions:
(1) This paper focuses on the application of metaheuristic algorithms in multi-objective scheduling problems from 2015 to 2024, systematically evaluating the advantages and disadvantages of single algorithms and hybrid algorithms found in the existing literature.
(2) By conducting an in-depth analysis of the number of objectives across various studies, this paper explores scheduling goals in the context of Industry 5.0 and Industry 4.0, distilling the current scale of research objectives and the trends for future research goals.
(3) This paper provides an overview of the research progress on metaheuristic algorithms combined with Reinforcement Learning (RL) methods in scheduling problems, assesses the advantages of these combined approaches, and suggests potential directions for future research.
(4) Addressing the classification of scheduling problems, this paper summarizes and examines the current trends in scheduling issues from the perspectives of flow-shop and job-shop scheduling problems.
This comprehensive survey examines the application of metaheuristic algorithms in multi-objective shop scheduling within the Industry 4.0 and 5.0 frameworks. The paper is structured as follows: Section 2 provides an overview of multi-objective optimization concepts and methodologies. Section 3 presents a systematic classification of scheduling objectives in modern manufacturing environments. Sections 4, 5 analyze the application of metaheuristics in flow-shop and job-shop scheduling problems, respectively, including their variants. Section 6 explores the integration of metaheuristics with RL and other advanced techniques. Finally, Section 7 summarizes key findings and identifies promising directions for future research.
2 Multi-objective optimization
In contemporary manufacturing processes, multiple objectives often conflict with each other, such as product quality versus production cost, or production efficiency versus energy consumption. The complexity of modern manufacturing systems, particularly in the context of Industry 4.0 and 5.0, necessitates simultaneous optimization of multiple objectives, making multi-objective optimization a crucial research focus.
2.1 The essence of multi-objective optimization
Multi-objective optimization problems are characterized by the presence of multiple, often conflicting objectives where the optimization of one objective typically results in the degradation of others. This inherent trade-off necessitates finding solutions that achieve an acceptable balance among all objectives. The mathematical formulation of a Multi-objective Optimization Problem (MOP) can be expressed as follows:
Definition 1MOP (Coello, 2007) (Equation 1):where represents the decision variable vector in n-dimensional space, denotes the feasible solution space, and m represents the number of objective functions. maps the decision space to the objective space through m objective functions.
Definition 2Pareto Dominance Relationship:For two solutions and of MOP, dominates (denoted as ) if and only if and . Conversely, if dominates (denoted as ). In this context, is termed a non-dominated solution and a dominated solution relative to . The collection of all non-dominated solutions forms the Non-dominated Set.
Definition 3Pareto Optimal Solution (POS):A solution of the MOP is Pareto optimal if . Such solutions represent the best possible trade-offs among the multiple objectives.In the context of Multi-objective Evolutionary Algorithms (MOEA), the goal is to identify a set of Pareto optimal solutions, formally defined as (Equation 2):
Definition 4Pareto-optimal Front (POF) (Equation 3):Depending on the evolutionary mechanism, MOEA can be divided into three categories: decomposition-based MOEA, dominance relationship-based MOEA, and indicator-based MOEA.
2.1.1 Decomposition based multi-objective evolutionary algorithm
The core idea of the decomposition-based MOEA algorithm is to decompose a multi-objective problem into a set of single-objective optimization problems, and approximate the solution set of the multi-objective problem by solving the subproblems simultaneously. Among them, the commonly used decomposition methods include the following three: weighted sum approach, Tchebycheff approach and penalty-based boundary intersection approach.
The weighted sum approach was proposed by Hillermeier (2001) and it is a commonly used linear multi-objective aggregation method. The aggregation function of this method can be expressed as (Equation 4):where is the decision vector, and is the weight vector satisfying and .
As shown in Figure 1, take two objective values as an example, when the real Pareto front is convex, purple is the weight vector, the green solid line perpendicular to the purple weight vector is the contour line. Connecting the objective point and the origin in the objective space constitutes a vector, and the purpose of the aggregation function is to multiply this vector with the pair of weight vectors point by point. When the weight vector is unchanged, minimizing/maximizing the length value is optimizing the vector.
FIGURE 1

Weighted sum aggregation approach contours.
Tchebycheff approach is a nonlinear multi-objective aggregation method, proposed by the aggregation function is defined as (Equation 5):
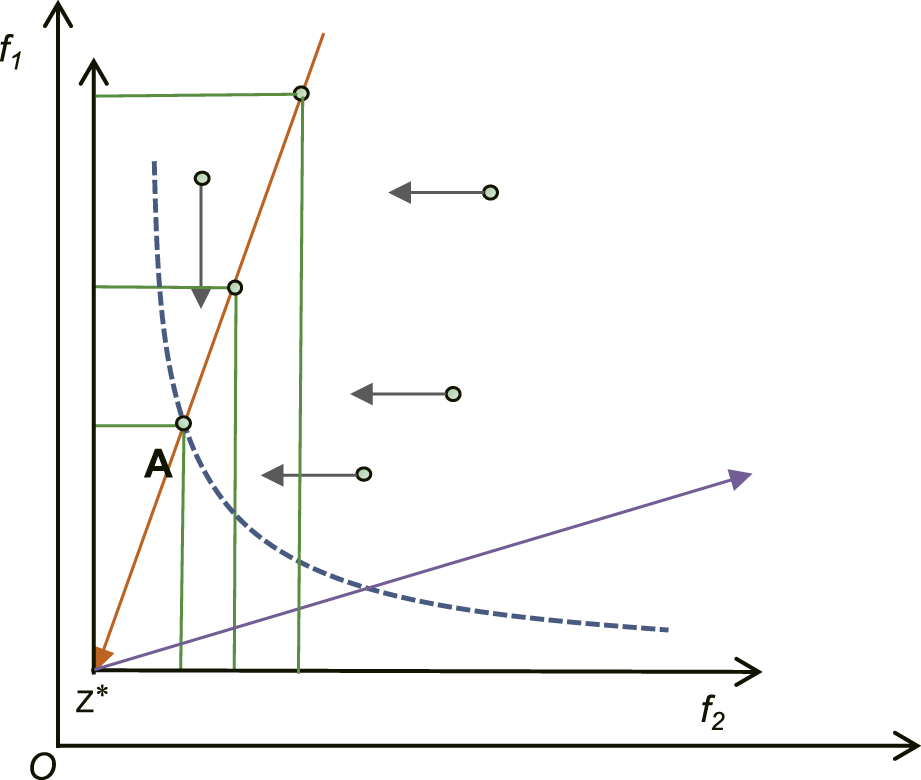
The Tchebycheff approach continuously forces individuals to approach a predetermined ideal point when transforming a multi-objective problem into a single-objective optimization by means of an aggregation function, which ultimately results in a Pareto optimal solution under the constraints. As shown in Figure 2, by definition the contour of each function in this method is a straight line parallel to that function, respectively; moreover, the intersection of two objective contours lies in the direction of the weight vector. In order to solve the problem that the solutions obtained by the standard Tchebycheff approach are not homogeneous, Qi et al. (2014) proposed the conversion of the reference vector into , which yields uniformly distributed solutions.
FIGURE 2
Tchebycheff approach contours.
The penalty-based boundary intersection approach was proposed by Zhang and Li (2007) which combines the Tchebycheff method and the penalty mechanism, which allows the solution to deviate from the direction of the weight vector, but a penalty will be imposed on the deviated solution. During the process of multi-objective optimization, the convergence and distribution of the solution can be controlled by adjusting the penalty parameter, so that the solution evolves directly along the direction of the weight vector, which is defined as follows:
Equation 6 give the calculation of the method. Where is a custom parameter and , which is used to control the magnitude of the weights and . In general and control the convergence and distributivity of the solution, respectively, and the larger is, the method focuses on . In other words, it tends to be distributed. Zhang and Li (2007) based on the idea of decomposition, they combine mathematical planning methods and Evolutionary Algorithms (EAs), convert a multi-objective optimization problem into a set of single-objective optimization problems, and seek the global optimal solution through the co-evolution of multiple sub-problems.
2.1.2 Pareto dominance based multi-objective evolutionary algorithm
Schaffer extended the simple Genetic Algorithm (GA) and proposed the Vector Evaluation Genetic Algorithm (Schaffer, 1985) (VEGA) in 1985, but the method cannot make trade-offs according to the attributes of each sub-objective, and it can only find the extreme points on the optimality boundary. In addition, the non-dominated solutions produced by VEGA are not necessarily globally non-dominated individuals. Fonseca and Fleming made use of the idea of sorting and proposed a kind of Multi-Objective Genetic Algorithm (MOGA) (Fonseca and Fleming, 1993), which determine the classification order of individuals based on the dominance relationship between them. Subsequently, Goldberg et al. (1993) proposed a dominance relationship-based MOEA method, which mainly uses a Pareto-based fitness allocation strategy to find all non-dominated individuals in an evolving population.
Currently, there is a great number of MOEA problems that use dominance relationship methods. The Non-dominated Sorting Genetic Algorithm (NSGA) proposed by Srinivas and Deb (1994) uses Goldberg’s idea directly. This algorithm is an improvement of the selection of the next-generation of sub-populations method based on GA, which stratifies each individual according to their dominance and non-dominance relationship before screening, which in turn makes the algorithm get the satisfactory results as possible on multiple objectives. Non-dominated Sorting Genetic Algorithm-II (NSGA-II) proposed by Deb et al. (2002), they uses fast non-dominated sorting on the basis of NSGA, which reduces the complexity of the algorithm and improves the running speed of the algorithm. Subsequently Jain and Deb (2014) proposed Non-dominated Sorting Genetic Algorithm-III (NSGA-III), which uses reference point based non-dominated sorting based on NSGA-II, this approach helps to identify the non-dominated solutions better in high dimensional objective space, NSGA-III is more suitable for the case where the number of objectives to be optimized is large. Zhang et al. (2014) employed a Pareto dominance-based strategy, proposed a hybrid sampling approach that combines VEGA with a fitness function grounded in novel Pareto dominance relationships, to balance the distribution and convergence of solutions. In addition, Gen et al. (2008) provided a comprehensive analysis of the advantages and applications of the GA. Figure 3 illustrates the development of MOEA based on dominance relationships.
FIGURE 3

Development of MOEA based on dominance relations.
In the MOEA based on dominance relationship, the evolutionary population is divided into several layers according to the dominance relationship. The first layer is the set of non-dominated individuals of the evolutionary population, the second layer is the set of non-dominated individuals after removing the first layer of individuals in the evolutionary population, the third layer is the set of non-dominated individuals after removing the first and second layer of individuals in the evolutionary population, and so on. When making the selection, the first layer of the non-dominated set is considered first, and individuals are selected from the first layer according to a certain strategy, and then individuals are considered to be selected sequentially in the other layers until the size requirement of the new evolutionary population is met. Figure 4 illustrates this process in detail.
FIGURE 4

Development of MOEA based on dominance relations.
2.1.3 Indicator based multi-objective evolutionary algorithm
Indicator based MOEA refers to the use of performance evaluation indictor in optimization algorithms to guide the search selection process of solutions. Based on the decision-making approach, MOEA can be classified into three categories: pre-decision techniques, interactive decision techniques and post-decision techniques.
Pre-decision techniques are those in which the decision maker has specified the preferences and objective weights of the problem before the optimization process begin. These preferences and weights are fixed during the optimization process and the algorithm searches based on these fixed preferences and weights. The advantage of pre-decision techniques is their simplicity and clarity, but the disadvantage is that some potential high-quality solutions may be ignored. The common pre-decision techniques are weighted sum method, constraint method and objective planning method.
Interactive decision-making techniques are those in which the decision maker interacts with the algorithm during the optimization process, adjusting preferences and objective weights step by step. This technique allows the decision maker to dynamically adjust the objectives during the optimization process to find a solution that better meets the practical requirements. Common interactive decision-making techniques are: stepwise preference adjustment, interactive multi-objective optimization and dynamic preference adjustment.
The post-decision technique means that at the end of the optimization process, the algorithm generates a set of Pareto optimal solutions from which the decision maker chooses the most satisfactory solution. The advantage of this technique is that the decision maker can make a decision after seeing all possible solutions, but the disadvantage is that it may need to deal with a large set of solutions. Some common post-decision techniques are: non-dominated sorting method, MOGA, Multi-Objective Particle Swarm Optimization (MOPSO) algorithm, Multi-Objective Differential Evolutionary algorithm.
Pre-decision techniques optimize with fixed objective weights and constraints, with the advantage of simplicity and clarity and ease of implementation, but may ignore potential high-quality solutions. Interactive decision-making techniques dynamically adjust preferences during the optimization process by providing real-time feedback and adjusting objective weights, which improves flexibility and adaptability, but may increase time costs. Post-decision techniques generate a set of Pareto optimal solutions after optimization, from which the most satisfactory solutions are selected, ensuring diversity and quality of solutions, but may need to deal with a large set of solutions, increasing the difficulty of decision-making. Depending on the size of the problem, these techniques can be applied in different methods.
3 Classification of scheduling optimization objectives
The selection of optimization objectives in shop scheduling problems fundamentally determines the effectiveness and practical applicability of scheduling solutions. This section presents a systematic classification and analysis of common scheduling objectives, which can be formalized as follows:
3.1 Time-based objectives
Makespan Minimization: The most fundamental objective in shop scheduling, defined as (Equation 7):where represents the completion time of job .
Total Weighted Completion Time: Considers job priorities through weights (Equation 8):where represents the weight of job .
3.2 Resource-based objectives
Energy Consumption: Modern scheduling increasingly emphasizes energy efficiency (Equation 9):where: represents processing energy for job on machine , represents idle energy consumption, and represents setup energy requirements.
Worker-related Objectives: Incorporating human factors (Equation 10):where represents workload of worker , and is idle time.
3.3 Quality-based objectives
Tardiness-related (Equation 11):where represents the due date of job .
Fuzzy Objectives: For uncertain environments (Equation 12):where represents triangular fuzzy numbers.
Analysis of the literature reveals several key trends in scheduling optimization objectives:
(1) Objective Prevalence: makespan minimization and energy consumption remain the most frequently studied objectives, reflecting their fundamental importance in production efficiency and sustainability.
(2) Multi-objective Complexity: the majority of studies focus on bi-objective optimization, with fewer addressing three or more objectives simultaneously. This trend reflects the inherent complexity of handling multiple competing objectives.
(3) Emerging Objectives: recent research shows increasing attention to: sustainability metrics (energy, emissions) and human factors (workload, fatigue).
(4) Integration Trends: modern studies increasingly combine traditional time-based objectives with resource and quality considerations, reflecting the complex requirements of contemporary manufacturing environments.
Table 1 summarise the studies related to each objective in detail. This classification demonstrates the evolution of scheduling objectives from simple time-based metrics to comprehensive multi-dimensional optimization problems that better reflect real world manufacturing challenges.
TABLE 1
| Problem | Reference | Objectives | The number of objectives | Algorithms | Category |
|---|---|---|---|---|---|
| FSP | Rahimi-Vahed and Mirghorbani (2006) | weighted average completion time, weighted average tardiness rate | 2 | SPEA-II | EA |
| FSP | Sekkal and Belkaid (2023) | makespan, total energy consumption | 2 | SA | EA |
| FSP | Vallejos-Cifuentes et al. (2019) | makespan, total energy consumption | 2 | MOGA | EA |
| FSP | Anjana et al. (2020) | duration time, average tardiness | 2 | NSGA-II, hybrid NSGA-II, PSO, hybrid PSO | EA |
| FSP | Hassanzadeh et al. (2016) | total weighted tardiness, makespan | 2 | MOPSO, NSGA-II | SI and EA |
| FSP | Tavakkoli-Moghaddam et al. (2007) | weighted average completion time, weighted average tardiness | 2 | IA, BFO | SI |
| FSP | Fekri et al. (2024) | makespan, total idle time of workers | 2 | GA, SA | EA |
| FSP | Dong et al. (2024) | fuzzy makespan, the average fuzzy due date agreement index | 2 | multi-objective non-dominated sorted GSA | PhA |
| HFSP | Engin and Yılmaz (2021) | agreement index, average agreement index, fuzzy makespan | 3 | improved GA | EA |
| HFSP | Wang et al. (2024) | makespan, total energy consumption, system stability | 3 | multi-objective discrete PSO | SI |
| HFSP | Schulz et al. (2019) | makespan, total energy cost, peak load | 3 | multi-stage iterative local search | EA |
| HFSP | Wang et al. (2023) | fuzzy makespan, total fuzzy energy consumption | 2 | improved NSGA-II | EA |
| HFSP | Geng et al. (2020) | worker makespan, total tardiness, workload balance | 3 | improved MA | SI |
| PFSP | Rajkumar and Jeen Robert (2019) | makespan, total flow time | 2 | SA, GA | EA |
| PFSP | Mishra et al. (2020) | makespan, tardiness cost | 2 | Jaya | SI |
| PFSP | Fasihi et al. (2023) | makespan, job tardiness | 2 | SA, GA | EA |
| PFSP | Motair (2021) | makespan, maximum tardiness | 2 | SA | EA |
| PFSP | Zhang et al. (2021) | makespan, maintenance cost | 2 | Pareto IG | EA |
| PFSP | Yüksel et al. (2020) | total delay, total energy consumption | 2 | multi-objective discrete PSO | SI |
| PFSP | Öztop et al. (2020) | makespan, total energy consumption | 2 | multi-objective IG | EA |
| PFSP | Ding et al. (2016) | energy consumption, carbon emissions | 2 | multi-objective IG | EA |
| DPFSP | Huang et al. (2022) | total flow time, total tardiness | 2 | two-stage evolutionary algorithm | EA |
| DPFSP | Fathollahi-Fard et al. (2024a) | makespan, energy consumption, the number of lost workdays | 3 | SA and TS | EA |
| DPFSP | Schulz et al. (2022) | makespan, carbon emissions | 2 | IG | EA |
| DPFSP | Lu et al. (2022) | makespan, total energy consumption | 2 | Pareto based collaborative multi-objective optimization algorithm | Human based |
| DPFSP | Chen et al. (2019) | makespan, total energy consumption | 2 | co-optimization algorithm | Human based |
| DHFSP | Rifai et al. (2021) | makespan, production cost, tardiness | 3 | ALNS | EA |
| DHFSP | Gao et al. (2024) | makespan, worker workload | 2 | enhanced elite retention strategy MOEA | EA |
| JSP | Zhang et al. (2024a) | makespan, total workload | 2 | ABC | PSO |
| JSP | González et al. (2022) | makespan, energy consumption | 2 | improved NSGA-II | EA |
| JSP | Afsar et al. (2022) | makespan, non-processing energy consumption | 2 | hybrid metaheuristics combine MA | SI |
| JSP | Wei et al. (2021) | total weighted tardiness, precocity, non-processing energy consumption, makespan | 4 | MOGA | EA |
| JSP | Li et al. (2020) | makespan, total precocity and tardiness | 2 | TLA | Human based |
| JSP | Xie et al. (2023) | tardiness, the number of transferred sub-batches | 2 | MOJA/D | SI |
| FJSP | Zhang et al. (2020) | makespan, total tardiness, total workload | 3 | distribute ACO | SI |
| FJSP | Shahsavari-Pour and Ghasemishabankareh (2013) | makespan, machine workload, total workload of all machines | 3 | hybrid GA and SA | EA |
| FJSP | Liu et al. (2021) | cost, energy consumption | 2 | VNS and GA | EA |
| FJSP | Li et al. (2014) | makespan, total workload of machine, workload of crucial machine | 3 | discrete ABC | SI |
| FJSP | Caldeira and Gnanavelbabu (2021) | makespan, total workload of machine, workload of crucial machine | 3 | discrete Jaya | SI |
| FJSP | Tan et al. (2021) | worker fatigue, makespan | 2 | improved NSGA-II | EA |
| Dist.FJSP | Shao et al. (2022) | total weighted tardiness, energy consumption | 2 | MA | SI |
| Dist.FJSP | Xu et al. (2021) | makespan, cost, quality, carbon emissions | 4 | GA and TS | EA |
| Dist.FJSP | Luo et al. (2020) | makespan, maximum workload, workload of the workers | 3 | improved MA | SI |
| Dist.FJSP | Li et al. (2018a) | makespan, total workload, early arrival/late arrival criteria | 3 | Pareto based hybrid TS | EA |
| Dyn.JSP | Wang et al. (2019) | discontinuity rate of new jobs, makespan deviation of the initial schedule, order deviation on the machine | 3 | improved PSO | SI |
| Dyn.FJSP | Liu et al. (2024) | makespan, workload imbalance | 2 | adaptive ALNS | EA |
| Dyn.FJSP | Zhang et al. (2013) | schedule efficiency, schedule stability | 2 | GA and TS | EA |
Literature objectives and algorithms.
Note: Abbreviations used in this table can be found in the Glossary section.
4 Metaheuristic algorithm in flow-shop scheduling problems
Metaheuristic optimization algorithms have emerged as powerful tools for solving complex global optimization problems, particularly in production scheduling. These algorithms excel in generating high-quality solutions within reasonable computational timeframes, making them especially valuable for planning, scheduling, and engineering design applications. Based on their underlying principles, metaheuristics can be broadly categorized into evolutionary mechanisms, physical principles, and swarm intelligence approaches.
To comprehensively analyze the research landscape, we conducted a systematic literature review using Web of Science from 2000 to 2024, focusing on metaheuristic algorithms in multi-objective Flow-shop Scheduling Problem (FSP) from 2015 to 2024.1
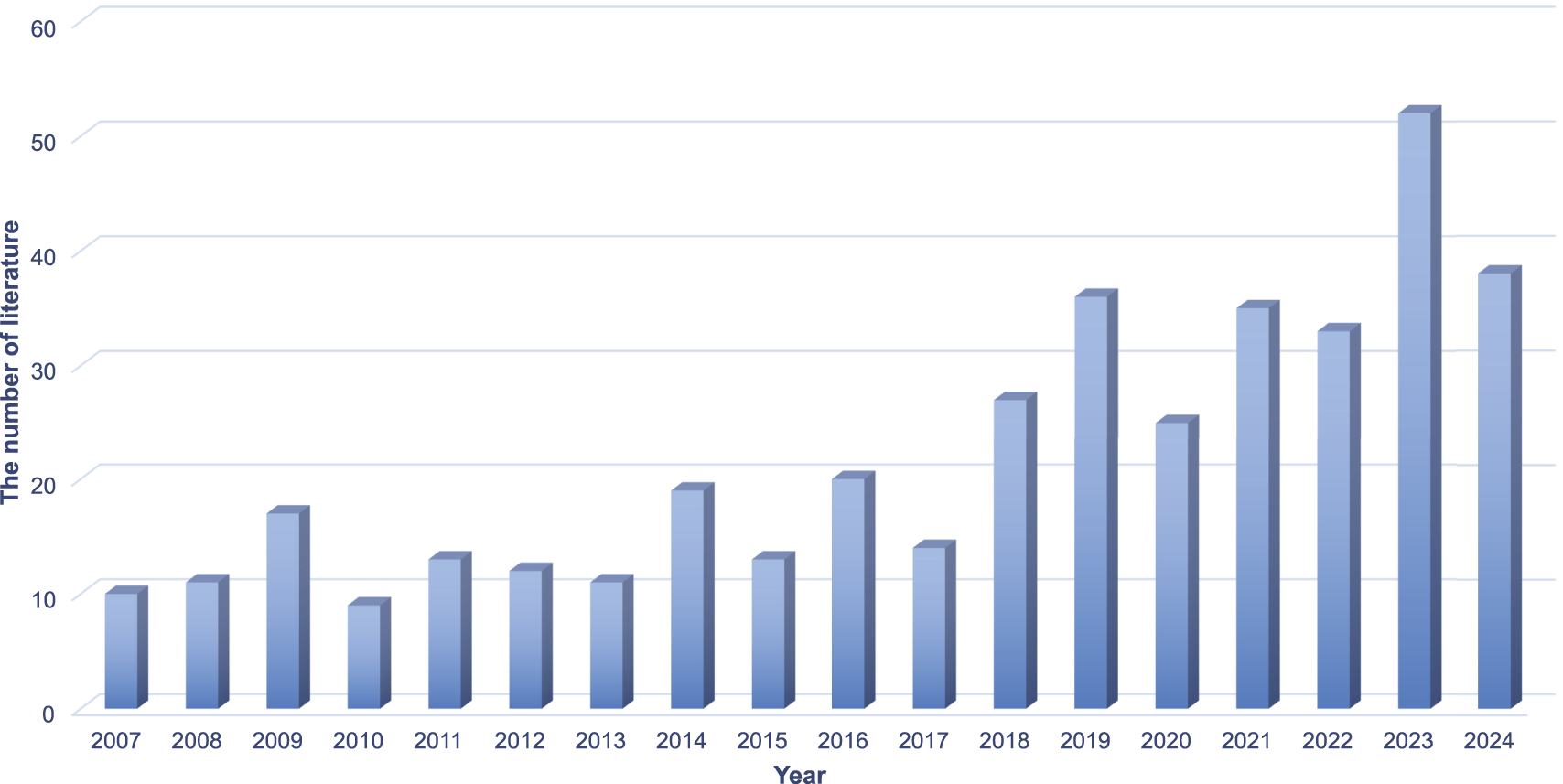
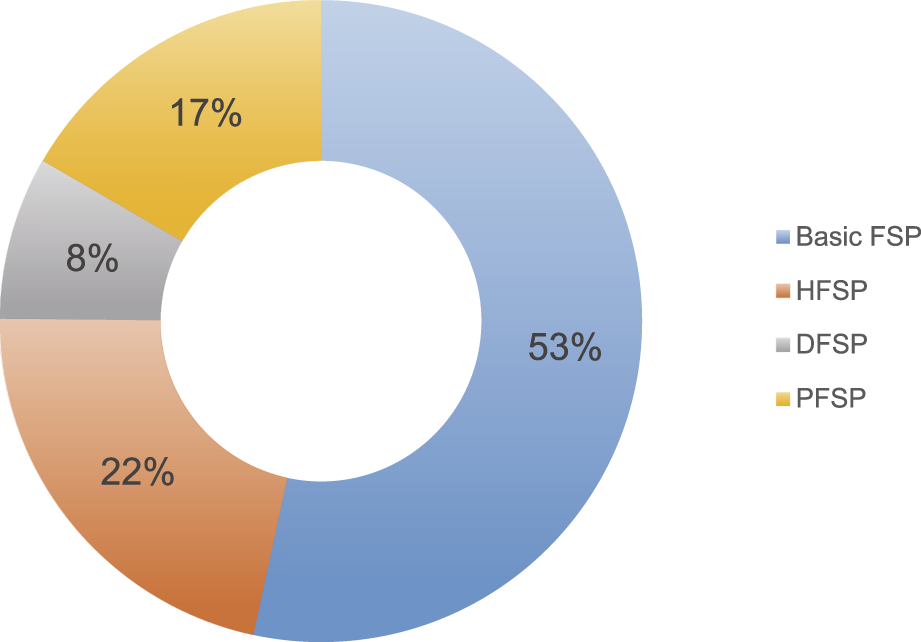
As illustrated in Figure 5, research activity in FSP reached its peak during 2019–2023, with 2023 recording over 50 publications. The trend analysis reveals a significant increase in academic attention since 2011, with particular intensity after 2020. Figure 6 further demonstrates that, beyond basic FSP, Hybrid Flow-shop Scheduling Problem (HFSP) and Permutation Flow-shop Scheduling Problem (PFSP) have garnered substantial scholarly interest.
FIGURE 5
Statistics on the number of metaheuristic algorithms solving muti-objective FSP and variant problems.
FIGURE 6
Proportion of metaheuristic algorithms solving muti-objective FSP and variant problems posted.
4.1 Flow-shop scheduling
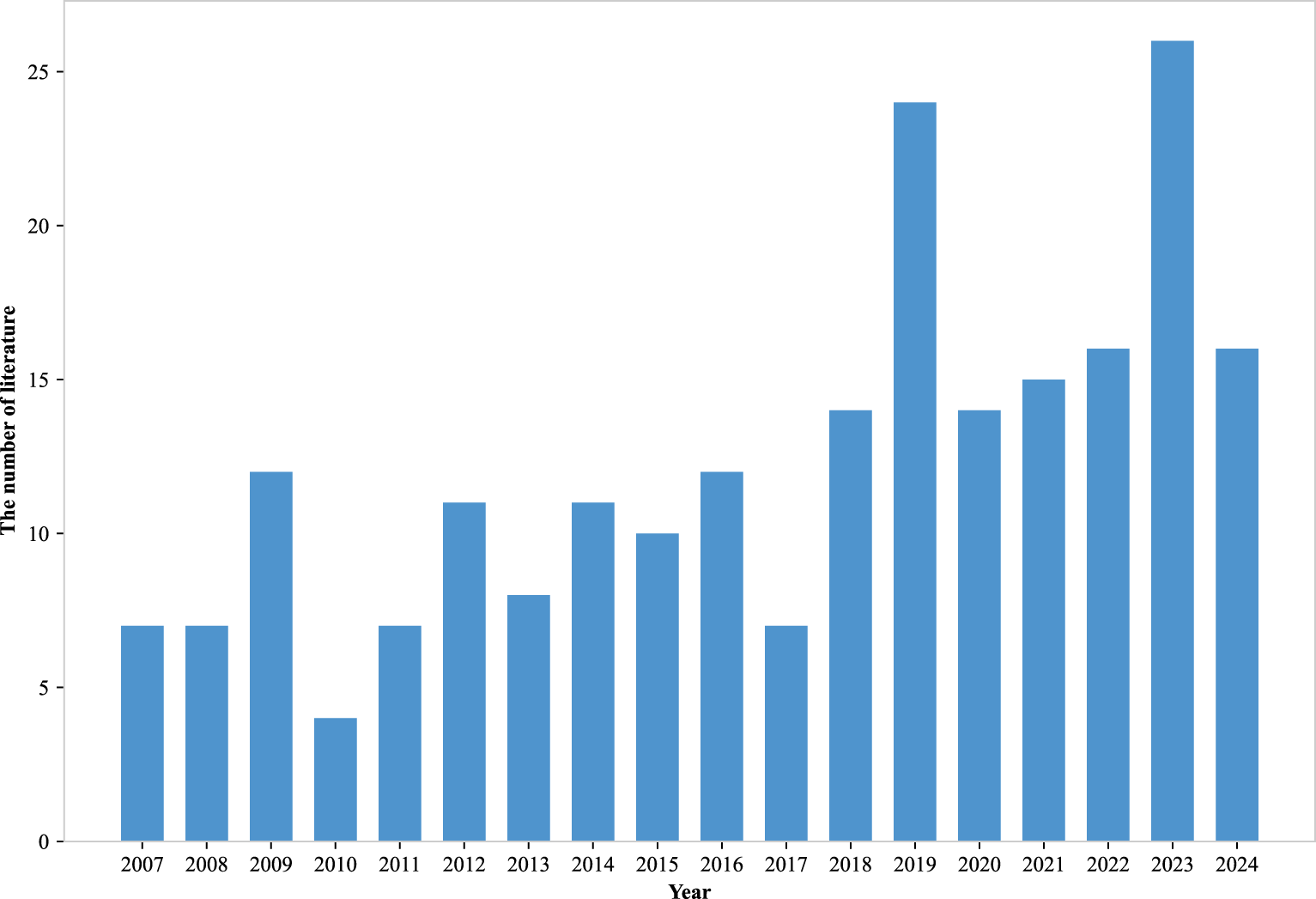
FSP represents a fundamental challenge in production scheduling, where the primary goal is to optimize the processing sequence of multiple jobs across a series of sequentially connected machines. As illustrated in Figure 7, research interest in multi-objective FSP has shown significant growth since 2019, reflecting the increasing complexity of modern manufacturing requirements.
FIGURE 7
The number of literature on metaheuristic algorithms solving muti-objective FSP and variant problems over the years.
4.1.1 Problem model
The problem can be formally defined as follows: Let
be a set of
jobs and
be a set of
machines. Each job
must be processed on all machines in the order
, with processing time
on machine
. The scheduling problem is subject to the following constraints:
(1) Each machine can process only one job at a time;
(2) Each job can be processed on only one machine at a time;
(3) The processing sequence is identical for all jobs;
(4) No preemption is allowed.
This chapter aims to construct a basic FSP model with the objectives of minimizing makespan and total flow time. Table 2 illustrates the parameter definitions for this problem.
TABLE 2
| Parameter | Statement |
|---|---|
| Set of jobs, consisting of jobs | |
| Set of machines, consisting of machines | |
| The -th operation of job | |
| Processing time of operation on machine | |
| The processing sequence of jobs | |
| The -th job in sequence | |
| All possible operation combinations | |
| Completion time of job on machine | |
| Completion time of operation on machine | |
| Binary variable, if operation is processed on machine ; otherwise | |
| Binary variable, if operation is processed exactly before operation ; otherwise |
Parameter descriptions.
Equations 15–18 represents the completion time of each job, while Equation 19 defines the processing sequence on each machine. Equation 20 ensures the feasibility of the operation sequence, and Equation 21 imposes constraints on job uniqueness. Similarly, Equation 22 enforces machine uniqueness, and Equations 23–25 specify non-negativity conditions. The optimization objectives of this model are defined in Equation 13, 14. Among these, Equation 13 represents the minimization of the makespan. As derived from Equations 15–18, the makespan is determined by , which corresponds to the completion time of the last job in the processing sequence on the last machine . Equation 15 defines the minimization of the total flow time, which is the sum of the completion times of all jobs.
4.1.2 Solution algorithm
The evolution of FSP research can be categorized into three main phases: classical optimization phase (pre-2010), modern manufacturing transition phase (2010–2020) and industry 5.0 and sustainability phase (2020-present).
Classical Optimization Phase (Pre-2010): Early research focused on fundamental scheduling objectives. Rahimi-Vahed and Mirghorbani (2006) designed an effective MOPSO considering minimizing the average weighted completion time and weighted average tardiness, which finds the local Pareto frontiers of the problem by employing ideal points to specify the position vectors of the dominant particles in the swarm. Tavakkoli-Moghaddam et al. (2007) in order to minimize the weighted average completion time and weighted average tardiness time, proposed a hybrid multi-objective algorithm based on Immune Algorithm (IA) and Bacterial Foraging Optimization Algorithm.
Modern Manufacturing Transition Phase (2010–2020): This period witnessed the convergence of various modern manufacturing constraints, integrating technological advancements. Rossit et al. (2022) proposed a decomposition-based MOEA to solve the multi-objective FSP with missing operations. The method employs a structured approach to decompose the solution space, ensuring diversity among initial solutions. Hassanzadeh et al. (2016) considered an multi-objective integrated production-distribution FSP with the objective of minimizing the total weighted tardiness and the makespan as the first objective function, and minimizing the sum of total weighted early completion times, total weighted number of late jobs, inventory cost and total delivery cost as the second objective function. Hao et al. (2017) proposed a Multi-objective Estimation of Distribution Algorithm to address stochastic JSP with uncertain processing times. The algorithm effectively balances the trade-off between expected mean completion time and total tardiness. By employing probabilistic model updates and Monte Carlo sampling, it ensures scheduling quality while enhancing computational efficiency. Branda et al. (2021) examined two metaheuristic algorithms combining GA and Harmony Search for solving the bi-objective problem of FSP. Anjana et al. (2020) considered a sequence-dependent setup time FSP with the objective of minimizing duration and average tardiness.
Industry 5.0 and Sustainability Phase (2020-Present): Current research emphasizes human-centric manufacturing and environmental considerations. Key developments include: energy efficiency and worker-centric optimization. Vallejos-Cifuentes et al. (2019) considered achieving energy savings without compromising the productivity of the manufacturing system and proposed an energy-aware FSP with process speed as the main energy related decision variable for a problem that targets production goals with energy efficiency. Boufellouh and Belkaid (2023) investigated the problem of energy saving FSP in the presence of blocking and collision-free transport constraints. For a manufacturing system with a sequential dependent setup times, Automatic Guided Vehicles (AGV), transport speed control and battery management constraints, an enhanced multi-objective Ant Colony Optimization (ACO) was developed for the scheduling problem. With the objective of simultaneously minimizing makespan and total energy consumption, the algorithm proposes a novel high-resolution search strategy, a heuristic AGV scheduling strategy and a critical path based energy saving improvement strategy. Sekkal and Belkaid (2023) considered the learning effect of workers and proposed FSP with learning efficiency. They developed a metaheuristic algorithm based on multi-objective Simulate Anneal (SA) with the minimisation of makespan and energy consumption as two objective functions, in which the search for solutions is enhanced by local search. Focusing on the multi-skilled characteristics of the workers, Fekri et al. (2024) proposed a GA and a SA with the objective of minimizing makespan and the total idle time of workers, and used a special Taguchi method for the parameter adjustment. It is finally concluded that the GA has better performance and efficiency than the SA for the multi-skill resource constrained FSP, but SA is superior to GA in terms of solution time. Dong et al. (2024) solved the multi-objective fuzzy block FSP based on learning and fatigue effects by combining the characteristics of the workers with the background of the FSP scheduling of the prefabricated pods modular cells. They used the objective of minimizing the fuzzy makespan and maximize the average fuzzy due-date agreement index, a multi-objective non-dominated Sorted Gravitational Search Algorithm (GSA) is proposed.
The evolution of FSP research reflects the field’s adaptation to emerging manufacturing paradigms, with increasing emphasis on sustainability, worker wellbeing, and system flexibility. Future research opportunities lie in integrating advanced technologies while maintaining computational efficiency and practical applicability.
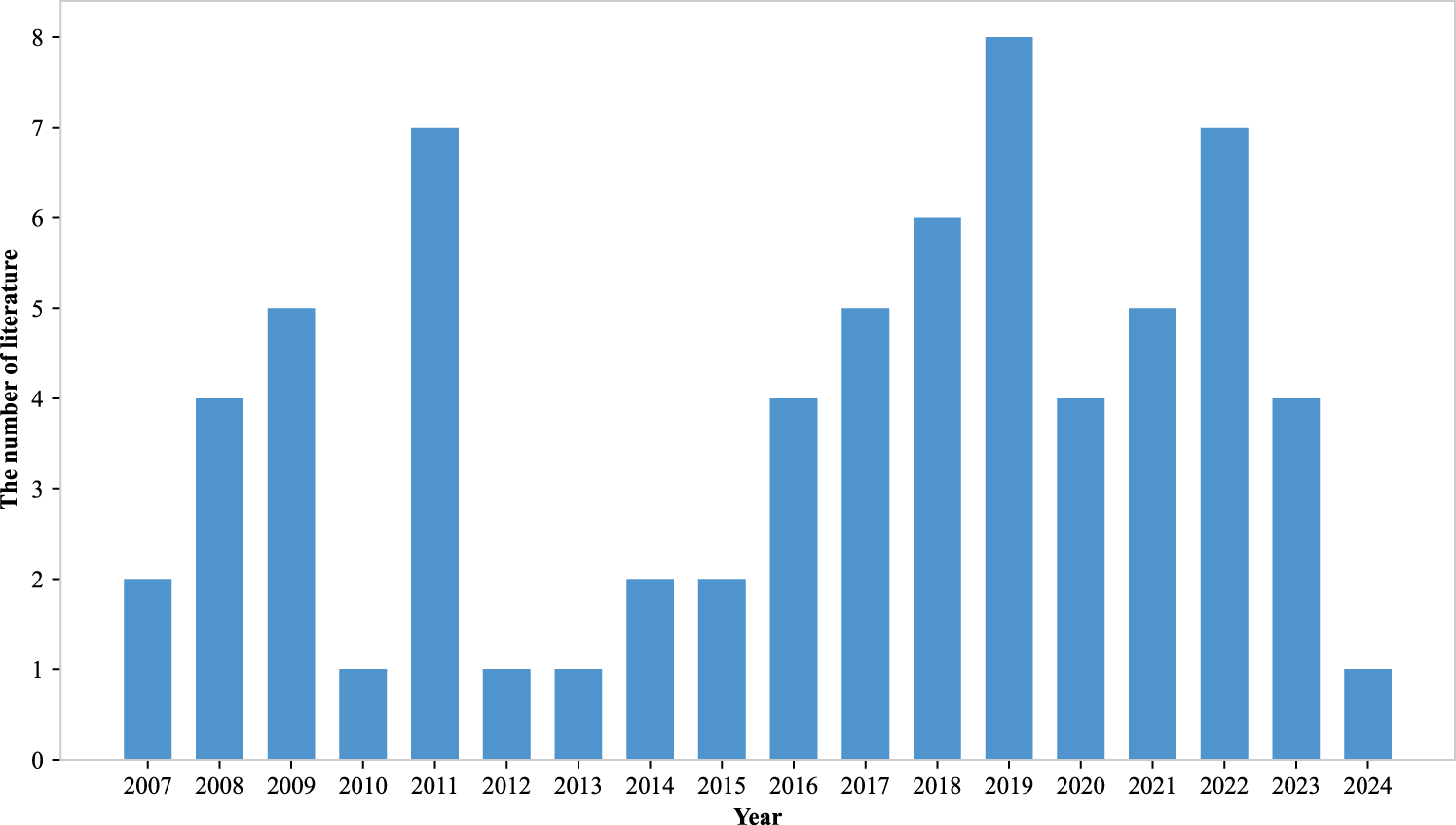
4.2 Permutation flow-shop scheduling
As shown in Figure 8, research interest in PFSP has exhibited significant volatility between 2007 and 2024, with notable peaks in 2019 and 2022.
FIGURE 8
The number of literature on metaheuristic algorithms solving muti-objective PFSP over the years.
4.2.1 Problem model
The PFSP can be described as follows: a set of jobs is processed on a set of machines in the same order. Each job has a series of corresponding operations on different machines, and the processing times for these operations are predetermined. The rules that must be followed in the workshop are that the processing order of each job on all machines is identical, and each machine must process all jobs in the same sequence. This chapter establishes a mathematical model with the objectives of minimizing makespan and energy consumption. Table 3 presents the detailed parameter list of this model.
TABLE 3
| Parameter | Statement |
|---|---|
| Job index, | |
| Machine index, | |
| Total number of jobs | |
| Total number of machines | |
| The fixed idle power of machine | |
| The total idle time of machine after processing all jobs | |
| Processing time of job on machine | |
| Completion time of job on machine |
Parameter descriptions.
Equations 26–28 define the objective functions of this model. Specifically, Equation 26 represents the first objective, which is the minimization of makespan. Equation 27 presents the second objective. The total energy consumption is calculated as the sum of the products of the idle time and the corresponding idle power for all machines. Equation 28 defines the computation of machine idle times. Equation 29 calculates the completion time of the first job on the first machine. Equation 30 computes the completion time of job on the first machine. Equation 31 determines the completion time of the first job on machine . Equation 32 calculates the completion time of job on machine . Equation 33 defines the maximum completion time for the job sequence.
4.2.2 Solution algorithm
Tajbakhsh et al. (2014) focused on a three-phase manufacturing system including machining, assembly and batch processing with the objective of minimizing makespan and the sum of early-to-delay costs. Based on the formulation of PFSP as a mixed integer mathematical model, a hybrid algorithm was designed to achieve efficient exploration of the solution space using a metaheuristic approach that combines the advantages of GA and Particle Swarm Optimization (PSO). Rajkumar and Jeen Robert (2019) proposed a hybrid multi-objective optimization algorithm based on GA and SA in order to solve the PFSP problem with the objective of minimizing makespan and the total flow time. The algorithm determines the near-optimal solution by assigning weights to each objective function.
The Jaya algorithm has also been used by scholars to study PFSP due to its advantages of simplicity, efficiency and scalability, Mishra et al. (2020) used the Jaya algorithm with the objective of minimizing makespan and tardiness cost to solve the PFSP problem. The algorithm converts the job preference vector into job ranking vector using maximum order value rule after randomly assigning priority to each job. In order to solve multi-objective, it uses a multi-attribute model based on Apriori method, and after comparing with SA. Zhang et al. (2021) considered preventive and corrective maintenance in manufacturing activities, and with the objective of minimizing makespan and maintenance cost, they designed a restarted iterative Pareto greedy algorithm. During the search process, the algorithm develops a restart mechanism to generate a new initial solution to prevent the algorithm from falling into a local optimum. Fasihi et al. (2023) proposed a two-step procedure by considering the reentrant PFSP with the objective of minimizing makespan and maximizing delay. The first step divides the population into sub-populations and applies GA in each sub-population to obtain the set of approximate Pareto frontier solutions. The second step unifies all the Pareto solution sets into a whole, using a multi-objective hybrid metaheuristic algorithm based on dominance relations.
Considering energy consumption and environmental constraints on manufacturing, Yüksel et al. (2020) proposed a new multi-objective discrete Artificial Bee Colony Algorithm (ABC) with the objective of minimizing both total delay and total energy consumption. By comparing it with metaheuristic algorithms such as traditional MOGA, variations of MOGA with local search, the algorithm is able to adapt to idle free FSP, blocking FSP, and Job-shop Scheduling Problem (JSP), or other higher level integrated manufacturing problems. Öztop et al. (2020) with the objective of minimizing makespan and total energy consumption, developed an enhanced constraint method to obtain a Pareto optimal solution. For small scale problems this algorithm obtains an approximation of the Pareto optimal bound using a small level. In addition, two multi-objective Integrated Gradients (IG) and a multi-objective variable block insertion heuristic algorithm were proposed for initial solution generation.
Ding et al. (2016) concerned about the direct relationship between energy consumption and carbon emissions, with the aim of improving the carbon efficiency of industrial factories and thus reducing the energy cost in the production process. Designed an optimization algorithm for the PFSP with the objective of minimizing the total carbon emissions and the makespan as the objective of the optimization algorithm. The algorithm is based on an extended Nawaz-Enscore-Ham (NEH) insertion procedure, and a multi-objective NEH algorithm and an improved multi-objective IG are designed to solve the problem. Wu and Che (2020) investigated the energy efficient no-waiting PFSP problem, and designed an adaptive multi-objective Variable Neighborhood Search (VNS) with the objective of minimizing makespan and total energy consumption. The algorithm designs two VNS structures to generate neighbours through insertion and swapping operations, and uses an adaptive mechanism to dynamically select the appropriate structure to handle the evolutionary direction of the current solution. Xin et al. (2021) designed an improved discrete Whale Optimization Algorithm (WOA) for PFSP with sequential dependence on setup time, considering that the energy consumption is related to the time of the job transfer process. The algorithm aims to minimize makespan and total energy consumption, and combines Differential Evolution (DE) and enhanced search strategy to improve the performance of the algorithm.
Recent research developments can be categorized into three main streams:
• Manufacturing System Integration: recent studies have expanded PFSP to incorporate real-world manufacturing complexities.
• Advanced Hybrid Approaches: modern PFSP solutions employ sophisticated hybrid algorithms. Such as hybrid GA and SA, Jaya algorithm and hybrid PSO and so on.
• Energy and Environmental Considerations: recent research has increasingly focused on sustainability objectives. For example, carbon emissions, energy consumption and machine availability and so on.
The evolution of PFSP research reflects increasing emphasis on practical manufacturing constraints and environmental considerations. This progression suggests a trend toward more comprehensive and sustainable scheduling solutions that balance traditional performance metrics with modern manufacturing requirements.
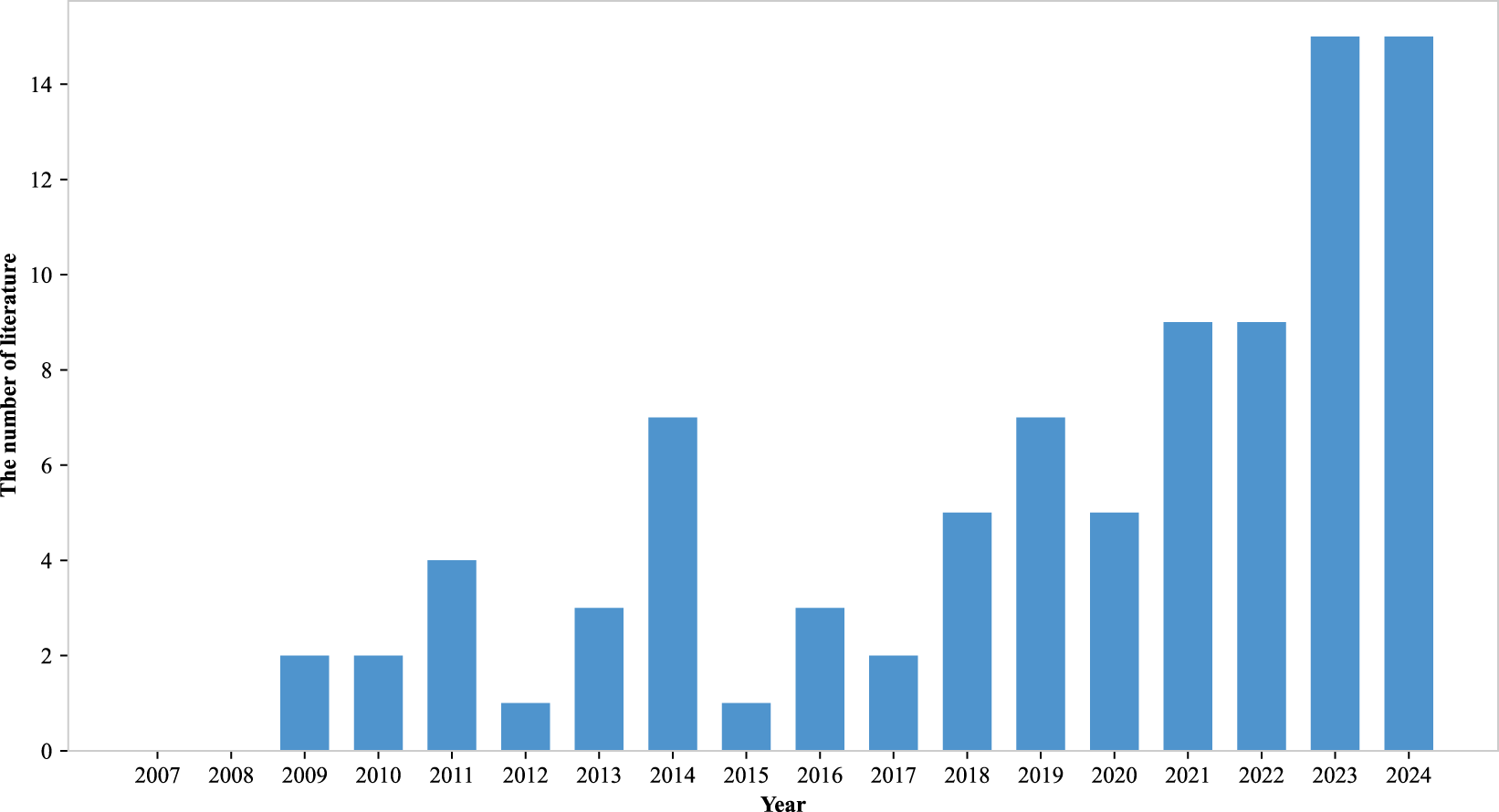
4.3 Hybrid flow-shop scheduling
As illustrated in Figure 9, research interest in HFSP has shown significant growth since 2020, reaching unprecedented levels in recent years. This surge reflects the increasing complexity and practical relevance of HFSP in modern manufacturing.
FIGURE 9
The number of literature on metaheuristic algorithms solving muti-objective HFSP and variant problems over the years.
4.3.1 Problem model
This chapter takes the HFSP with worker constraints as an example to establish a mathematical model. The problem can be described as follows: there are
consecutive stages, capable of processing
independent jobs that must be handled in the same sequential order. Each stage is equipped with
machines, and each machine can be operated by
workers. All jobs need to be scheduled according to certain optimization objectives. The problem involves addressing three sub-problems:
(1) Sequencing all operations based on operational constraints;
(2) Assigning machines to process the jobs;
(3) Allocating workers to operate the assigned machines.
Table 4 summarizes the parameters and their descriptions for this problem.
TABLE 4
| Parameter | Statement |
|---|---|
| Job index, | |
| Stage index, | |
| Machine index, | |
| Worker index, | |
| Sequential index of operations processed on the same machine, | |
| Sequential index of operations processed by the same worker, | |
| Number of jobs | |
| Number of stages | |
| Number of machines | |
| Number of workers | |
| Available worker set in stage | |
| Available machine set in stage | |
| Number of machines in stage | |
| Number of workers in stage | |
| Operation of job in stage | |
| Processing time of operation on machine by worker | |
| Completion time of operation in stage | |
| Completion time of job | |
| Cost when operation is processed on machine by worker | |
| Green indicator value of operation on machine by worker | |
| Energy consumption when operation is processed on machine by worker | |
| Noise when operation is processed on machine | |
| Recycling rate of tool chips when operation is processed on machine | |
| Safety coefficient when operation is processed on machine | |
| Decision variable, if is processed at the -th position on machine , then 1, otherwise 0 | |
| Decision variable, if is processed by worker on machine , then 1, otherwise 0 | |
| Decision Variable, if is processed by worker at the -th position, then 1, otherwise 0 | |
| A large enough integer |
Parameter descriptions.
The model aims to minimize the makespan and the total worker cost, as formulated in Equations 34, 35. Equation 36 ensures the precedence constraints for operations. Equation 37 enforces the sequencing constraints for operations on the same machine. Equation 38 ensures the sequencing constraints for operations assigned to the same worker. Equation 39 guarantees that each operation is processed by only one machine at any given time. Equation 40 ensures that each machine processes at most one operation at any given time. Equation 41 prevents gaps in the sequence of operations on the same machine, ensuring that no position is left empty before a position is fully occupied. Equation 42 ensures that each operation is handled by only one worker at any given time. Equation 43 guarantees that each worker handles at most one operation at any given time. Equation 44 prevents gaps in the sequence of operations assigned to the same worker, ensuring that no position is left empty before a position is fully occupied. Equation 45 ensures that each operation is performed by only one worker on one machine at a time. Equation 46 allows each worker to perform multiple operations on the same machine.
4.3.2 Solution algorithm
Behnamian et al. (2009) proposed a multi-objective HFSP with sequence-dependent setup times, focusing on minimizing makespan and the sum of job advance and delay times. Their approach consists of three stages: first, they use a random-keyed GA to approximate the Pareto front; second, they unify non-dominated solutions and enhance the front with a local search; and third, they apply an -constraint overlay hybrid metaheuristic, combining SA and VNS to refine the solutions further. Fadaei and Zandieh (2013) focused on sequence dependent family setup time for HFSP, considered the two objectives of minimizing makespan and total tardiness, and used three MOGA, subpopulation GA, and nondominated sequential GA to solve the above problems. Engin and Yılmaz, 2021) concerned about the time uncertainty HFSP problem due to human and other factors in the actual production process, proposed a multi-objective processor HFSP method based on fuzzy logic, which formulates the HFSP problem with fuzzy processing time and fuzzy due date. It involves three objectives of maximizing the minimum consistency index, maximizing the average consistency index and minimizing the maximum fuzzy makespan.
In real production process, energy consumption is one of the concerns of managers, Li et al. (2018b) proposed an energy-aware multi-objective optimization algorithm to solve the HFSP problem, which considers both minimizing makespan and energy consumption. This metaheuristic algorithm two vectors are used to represent the solution using machine assignment priority and scheduling, and four types of decoding methods are used to consider the two objectives simultaneously. Eight types of neighbourhood structures and an adaptive neighbourhood selection method are designed to speed up the search for a solution, effectively balancing the capabilities of global and local search through deep exploitation and exploration strategies. Hosseini (2017) focused on the difference between the manufacturing and assembly phases of a product and proposed a two phase HFSP, where they assumed the first phase to be a HFSP with the same parallel machines and the second phase was treated as assembly. The algorithm uses a two-stage MOGA to solve this problem with the objective of minimizing makespan and the sum of early and late arrivals of jobs. For the uncertain time manufacturing process, Wang et al. (2024) proposed the green HFSP in the case of emergency batch insertion. The problem adopts a multi-objective discrete ABC with the objectives of minimizing makespan, total energy consumption and system stability. The algorithm is able to significantly reduce the cost and substantially improve the accuracy and efficiency by testing and comparing it on small and large scale problems.
Schulz et al. (2019) focused on the importance of energy-aware scheduling and developed a new multi-stage iterative local search algorithm for energy-aware HFSP. The algorithm incorporates three energy saving strategies of reducing energy consumption, reducing energy cost using different energy prices and considering load balancing with the objective of minimizing makespan, total energy cost and peak load. The algorithm incorporates a tabu list, several time and energy dependent list scheduling algorithms, a right shift procedure and a reference point based fitness function to improve the quality of the solution. Chen et al. (2020) used a multi-objective mixed-integer planning model with the objective of minimizing makespan and power consumption. The algorithm uses a GA to obtain the Pareto solution set, and uses a multi-objective energy-efficient scheduling algorithm to compute the fitness value of each chromosome in GA. Wang et al. (2023) added variable machine speed constraints to the energy-efficient HFSP problem and proposed an energy-efficient fuzzy HFSP considering variable machine speeds, for which an extended NSGA-II was designed. The algorithm aims to minimize both fuzzy makespan and total fuzzy energy consumption, and generates an initial population through inverse learning, and a new strategy based on historical information to produce high-quality solutions.
In addition to the consideration of energy consumption, many scholars have also focused on human-centred manufacturing in the context of Industry 5.0. Geng et al. (2020) investigated multi-objective HFSP with dual resource constraints considering the dual flexibility characteristics of machines and workers. The problem was formulated with the objective of minimizing worker makespan, total tardiness and workload balance, and proposed an improved multi-objective Memetic Algorithm (MA) with parameters set by Taguchi method. This method significantly outperforms other algorithms in terms of convergence, diversity, and dominance of non-dominated solutions. Han et al. (2021) proposed a MOEA with seven heuristic decodings for HFSP considering workers constraints. The algorithm combines machine worker allocation priority rules with the optimization objective of minimizing makespan and total delay. It is demonstrated through numerical experiments that the algorithm enables the solution to achieve a balance between exploration and exploitation, and can reasonably solve the manufacturing problem.
Recent research has focused on several key aspects of HFSP: setup time considerations, energy-aware scheduling, human-centered manufacturing and uncertainty management. The evolution of HFSP research reflects a growing emphasis on practical manufacturing constraints while maintaining computational efficiency. Future research opportunities lie in integrating emerging technologies and addressing increasingly complex real-world scenarios, particularly in the context of smart manufacturing and Industry 5.0 requirements.
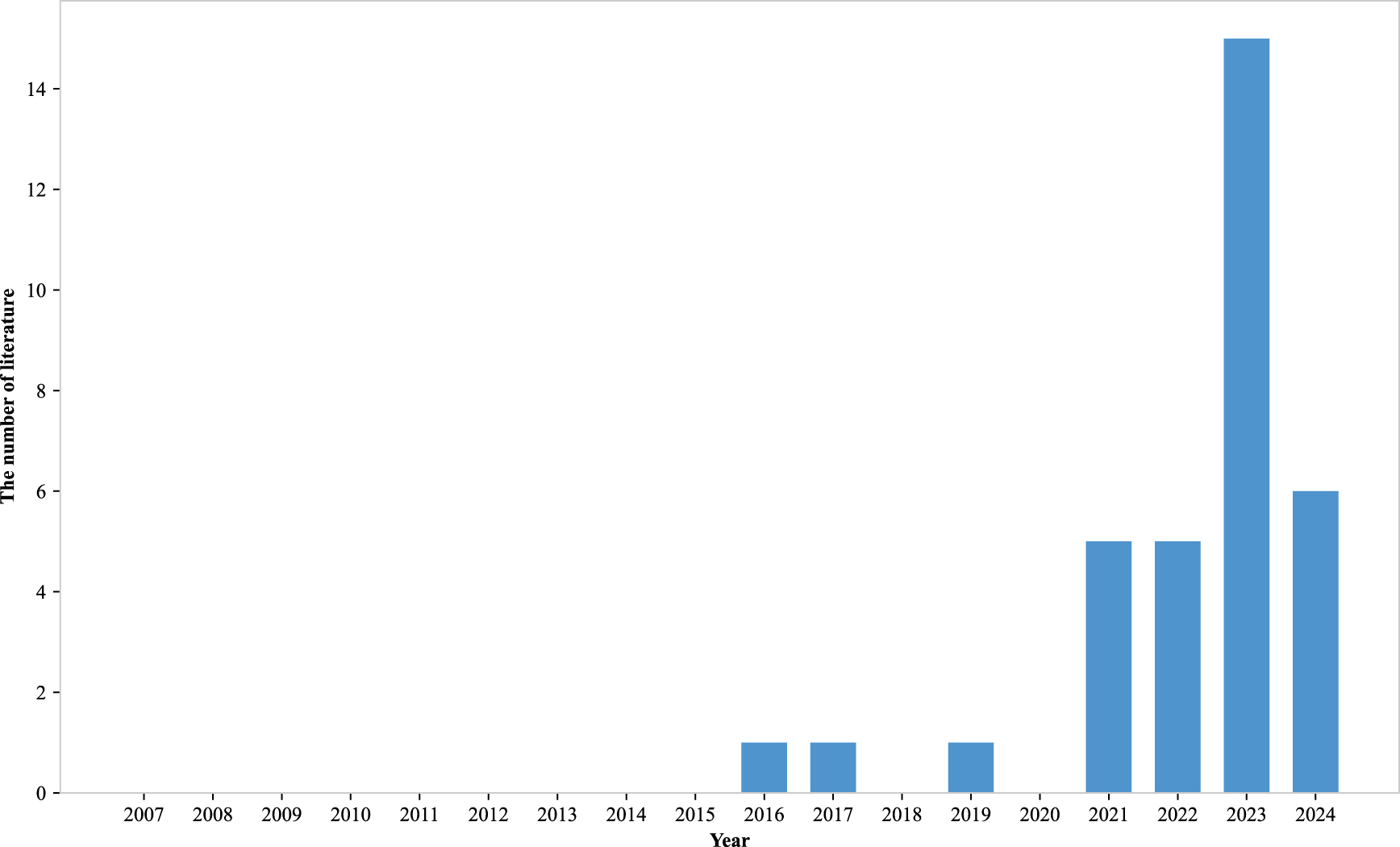
4.4 Distributed flow-shop scheduling
Distributed flow-shop scheduling problems encompasses three main variants: Distributed Flow-shop Problem (DFSP), Distributed Permutation Flow-shop Problem (DPFSP), and Distributed Hybrid Flow-shop Problem (DHFSP). In a DFSP system with factories, each containing a FSP, jobs are distributed across factories through specific allocation mechanisms.
As shown in Figure 10, research interest in distributed scheduling systems has grown significantly in recent years, which may be related to the expansion of manufacturing operations.
FIGURE 10
The number of literature on metaheuristic algorithms solving muti-objective DFSP and variant problems over the years.
4.4.1 Problem model
The DFSP can be described in detail as follows. It involves jobs and factories, each containing the same machines. Each job can only be processed on one machine, and each machine can process only one job at a time. Every job must be assigned to one of the factories, and all operations must be completed within the same factory, without transferring to another factory during this period. This chapter establishes a mathematical model with the objectives of minimizing makespan and total energy consumption. The detailed parameter list is presented as Table 5.
TABLE 5
| Parameter | Statement |
|---|---|
| Index of job, | |
| Index of machine, | |
| Index of factory, | |
| Index of processing speeds, | |
| The number of jobs | |
| The number of machines | |
| The number of factories | |
| The number of speeds | |
| The -th processing speed | |
| The number of jobs in the -th factory | |
| A complete schedule in the -th factory, | |
| The processing power of the job on machine in factory at speed per unit time | |
| The idle power of the machine in factory per unit time | |
| The standard process time of the -th job on the -th machine in the -th factory | |
| The actual process time of the -th job on the -th machine in the -th factory | |
| The idle time of the job in factory generate energy consumption | |
| The processing time of the job in factory generate energy consumption | |
| The completion time of job on machine in the factory | |
| A binary variable that takes value 1 if job occupies position in factory , and 0 otherwise | |
| A binary variable that takes value 1 if job is processed in factory , and 0 otherwise | |
| A binary variable that takes value 1 if job is processed in machine at speed , and 0 otherwise |
Parameter descriptions.
Equations 47, 48 represent the minimization of the two objectives. Equations 49, 50 ensure that each job is accurately assigned to one factory and exists only once within that factory. Equations 51, 53 indicate that each job can potentially be a predecessor or successor within the assigned factory, while avoiding priority conflicts. Equation 52 explains that all jobs should have the possibility of being assigned to the positions in each factory. Equations 54, 55 state that jobs are ready at time 0, and machines start working at time 0. Equations 56, 57 specify that a job can only begin after its predecessor in the same factory has completed processing on the machine. Equations 58–61 describe the calculation of completion times, starting from the first job processed on the first machine to the last job processed on the last machine. Equation 62 defines the actual processing time of a job. Equations 63, 64 specify the energy consumption of factory when machine operates in processing mode and standby mode, respectively.
4.4.2 Solution algorithm
Rifai et al. (2021) proposed an improved multi-objective Adaptive Large Neighborhood Search (ALNS) for the DPFSP by considering the effect of sequence-dependent setup time for the first time. The algorithm achieves an effective use of balancing and exploration by introducing new destruction and repair heuristics, optimizing the solution acceptance criterion and the non-dominated set update mechanism. Cai et al. (2018) proposed an improved NSGA-II for the DPFSP with transport and qualification constraints aiming to optimize the three objectives of fabrication time, maximum delay, and total cost (including transport and installation cost) simultaneously. The algorithm introduces a new solution representation, a population initialisation strategy, efficient crossover and mutation operators, and local search techniques.
Huang et al. (2022) proposed a two-stage evolutionary algorithm with the objective of minimizing the total flow time and total tardiness time. A two-stage structure is used, in the first stage of this algorithm to increase the population diversity through two constructive heuristics and four crossover and two mutation operators designed. In the second stage the first two populations are integrated to improve the performance of the algorithm by using the normalised objective function and two new crossover operators to extend the solution to the Pareto frontier. Fathollahi-Fard et al. (2024a) redefined the sustainable DPFSP using an online mixed-integer programming model. With the objective of minimizing makespan, energy consumption, and reducing the number of lost workdays, SA and Tabu Search (TS) were designed for the large scale problem. Fathollahi-Fard et al. (2024b) also proposed an ALNS for the sustainable DPFSP. The algorithm considers different modes of operation in which machines can run from manual to automatic, taking into account energy consumption, number of operators required and number of working days lost to training. In addition, the algorithm considers uncertainty problems including machine failures, variable processing times and the random arrival of new jobs.
Since carbon emissions will have a direct impact on the environment, Schulz et al. (2022) designed an IG for the DPFSP under large-scale instances in order to minimize makespan while reducing carbon emissions. Lu et al. (2022) investigated energy efficient scheduling for DPFSP with a finite buffer, aiming to minimize both the manufacturing time and the total energy consumption. They proposed a Pareto based collaborative multi-objective optimization algorithm. The algorithm reduces the total energy consumption through a speed scaling strategy, generates a high quality initial population using a collaborative initialisation strategy, and exploits the properties of the problem to develop a collaborative search operator and a knowledge based local search operator. Chen et al. (2019) investigated the energy efficient DPFSP with idle-free aiming to minimize both makespan and total energy consumption. For this problem, they designed a co-optimization algorithm. The algorithm uses two metaheuristics for population initialisation together to ensure the quality and diversity of the initial solutions. Multiple search operations are designed to collaborate in a competitive manner to enhance the exploration capability. Wang et al. (2022) proposed a method combining a multi-objective mixed integer programming model and a multi-objective WOA to solve the DFSP considering energy consumption. The method has the objective of minimizing the total energy consumption and makespan. For the base WOA, a new initialisation method, update operator and local search strategy are designed for this particular problem. When dealing with large scale problems, this combined approach is able to strike a good balance between computational cost and the quality of the solution.
Zhao et al. (2024) considered the problem of energy efficient DFSP with blocking, and proposed a multi-objective discrete DE with the objective of minimizing makespan and total energy consumption. The algorithm employs a local search strategy based on the knowledge of five operators is introduced to enhance the utilisation of the algorithm, and a non-critical path energy saving strategy is used to reduce energy consumption. In order to cope with environmental problems and to meet the demand of customised production, Yu F. et al. (2024) proposed a mixed integer linear programming model and a multi-objective MA for the study of DHFSP. The method simultaneously aims at minimizing the total delay and total energy consumption. The quality of the initial solution is improved by introducing a speed dependent decoding method, an initialisation strategy based on the problem characteristics, and a search strategy that enhances the local search capability, which guides the population to achieve effective exploration in the solution space. As the worker resources also affect the efficiency of scheduling in the actual production manufacturing process, Gao et al. (2024) studied the DHFSP with assembly to minimize the degree of imbalance between makespan and worker workload. To address the problem, a variation based local search method and an elite search method were proposed, and a MOEA with an enhanced elite retention strategy was developed. Xin et al. (2015) proposed an adaptive binary PSO in the process of solving the multi-skilled worker assignment problem in a complex assembly system in order to achieve a balance between assembly station and process workloads and to minimize the man cost.
Recent research has addressed various practical aspects: sequence-dependent setup time, energy efficiency, sustainability considerations, worker resource management and algorithmic innovations. These developments reflect the field’s evolution toward more comprehensive and practical scheduling solutions, incorporating environmental, worker-related, and efficiency considerations. Future research opportunities lie in addressing emerging challenges in distributed manufacturing environments, particularly in areas of real-time adaptation and system resilience.
The evolution of FSP and variant problems research reflects four key trends: Industry 4.0 integration, sustainability considerations, the development of hybrid algorithms and human-centered manufacturing. These developments reflect the field of evolution toward more comprehensive and practical scheduling solutions, incorporating environmental, worker-related, and efficiency considerations. Future research opportunities lie in addressing emerging challenges in smart manufacturing environments, particularly in areas of real-time adaptation and system resilience.
5 Metaheuristic algorithm in job-shop scheduling problems
Job-shop scheduling problems has established itself as a cornerstone of modern manufacturing, particularly valued for its flexibility and customization capabilities. Its applications span diverse industrial sectors, including precision machinery, aerospace manufacturing, and foundry operations (Tan et al., 2021; Wu et al., 2018; Gong et al., 2020). However, this versatility introduces significant complexity in resource utilization and productivity optimization, making it a focal point for academic research.
To comprehensively analyze the research landscape, we conducted a systematic literature review using Web of Science from 2000 to 2024, focusing on metaheuristic algorithms in multi-objective job-shop scheduling problems from 2015 to 2024.2
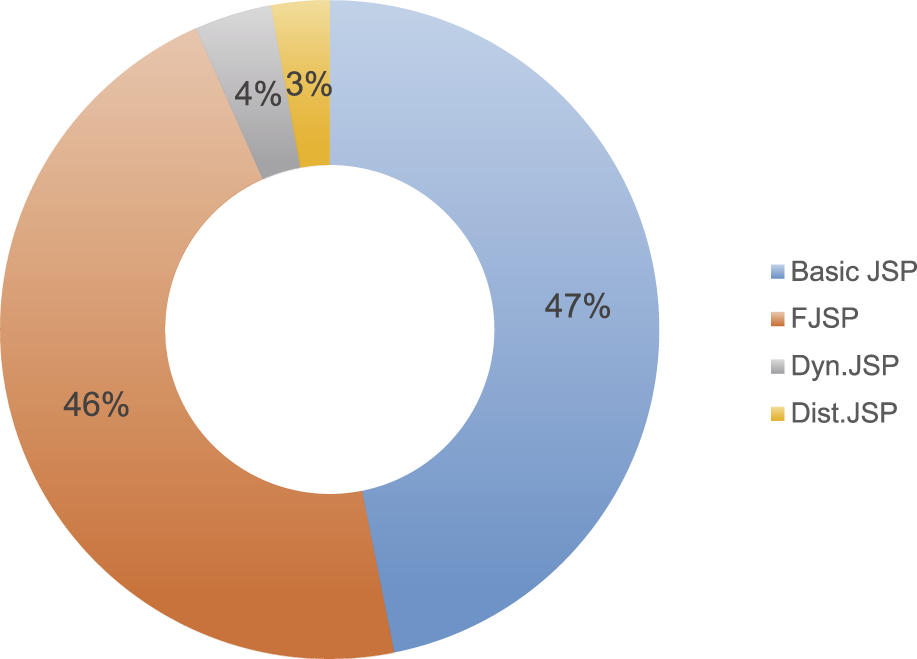
The analysis reveals several significant trends in job-shop scheduling problems research. As illustrated in Figure 11, there has been a marked increase in research activity since 2021, with sustained growth in publications across various JSP variants. Figure 12 demonstrates that Flexible Job-shop Scheduling Problem (FJSP) and Distributed Job-shop Scheduling Problem (Dist.JSP) have emerged as dominant research areas, likely due to their enhanced adaptability to modern production environments characterized by increasing complexity and variability.
FIGURE 11

Statistics on the number of metaheuristic algorithms solving muti-objective JSP and variants problems.
FIGURE 12
Proportion of metaheuristic algorithms solving muti-objective JSP and variant problems posted.
5.1 Job-shop scheduling
JSP, classified as NP-hard, finds widespread application in various industrial contexts, from automotive assembly to airport operations. As illustrated in Figure 13, research interest in JSP has shown significant growth since 2016, peaking in 2021, with continued momentum expected in this field.
FIGURE 13
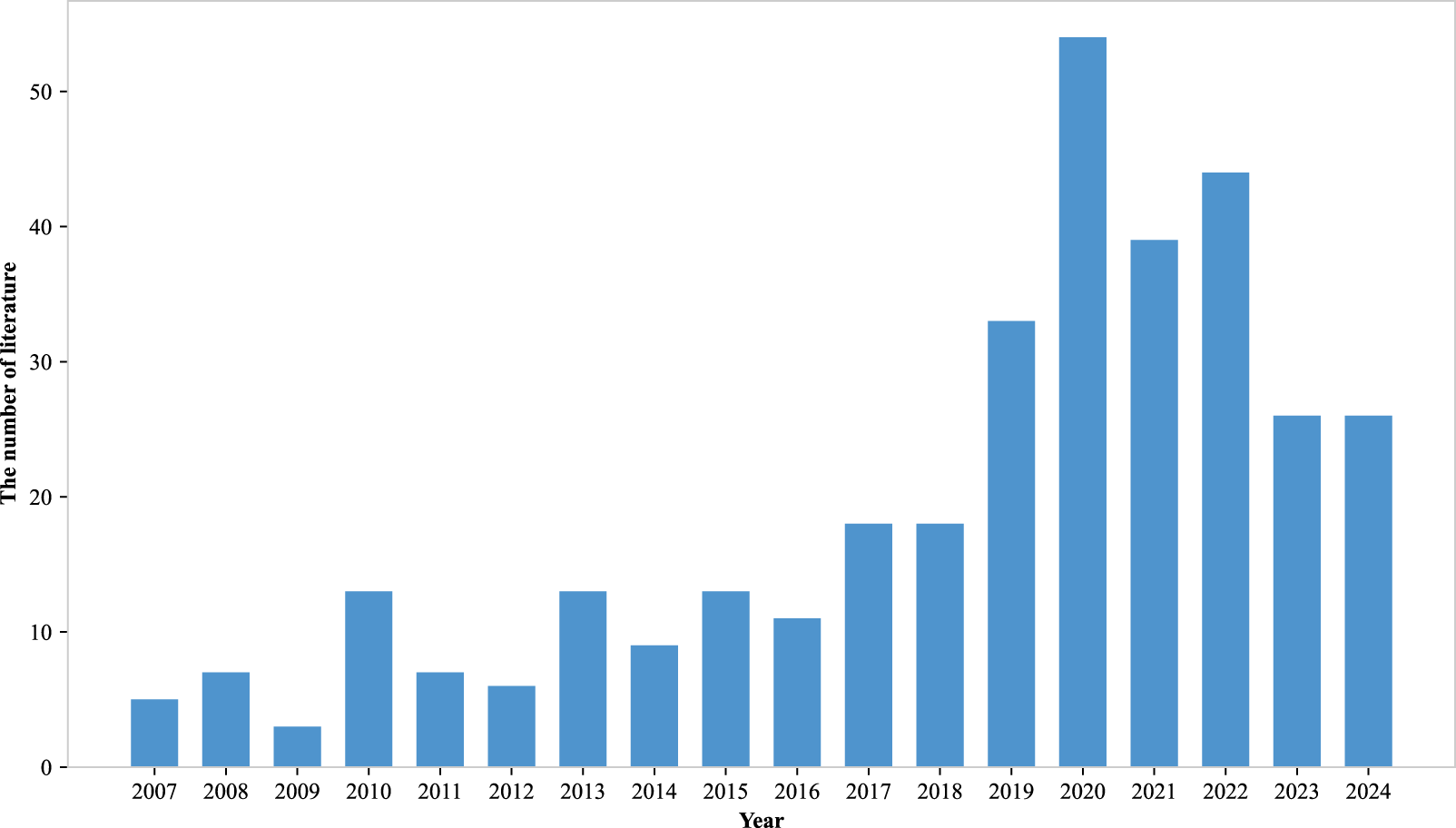
The number of metaheuristic algorithms solving muti-objective JSP literature over the years.
5.1.1 Problem model
To address the JSP, the following factors are typically considered:
(1) Processing sequence of jobs: each job must be processed on different machines in a specific order;
(2) Machine availability: some machines may be unavailable at specific times, which affects the scheduling of jobs;
(3) Job arrival time: certain jobs may not arrive at the workshop simultaneously, and their arrival times can influence the scheduling plan;
(4) Priority: some jobs may have higher priority than others, requiring preferential scheduling.
This chapter establishes a mathematical model with the objectives of minimizing makespan and total overtime. Table 6 presents the parameters and variables of the model.
TABLE 6
| Parameter | Statement |
|---|---|
| Job index, | |
| Operation index, | |
| Machine index, | |
| Time interval index, | |
| Number of jobs | |
| Number of operations for job | |
| Number of machines | |
| Number of available time intervals | |
| Maximum completion time for all jobs | |
| Operation of job | |
| Processing time of operation | |
| Completion time of operation | |
| Completion time of job | |
| Delivery date of job | |
| Time spent on operation in time interval | |
| Urgency factor for job | |
| Time spent on operation on machine | |
| Start time of operation on machine | |
| A sufficiently large positive number | |
| Start time of operation | |
| Binary variable, 1 if operation is processed in time interval , 0 otherwise | |
| Binary variable, 1 if operation on machine precedes operation , 0 otherwise | |
| Binary variable,1 if operation is processed on machine , 0 otherwise | |
| Binary variable,1 if the time interval is an overtime interval, 0 otherwise |
Parameter descriptions.
Among them, Equations 65, 66 represent the two objective functions, which are minimizing the total overtime and minimizing the makespan, respectively. Equation 67 defines the no-tardiness constraint. Equations 68, 69 constrain that an operation of a job can only start after its immediately preceding operation has been completed, and its start time must be no earlier than time zero. Equation 70 ensures that an operation cannot be interrupted once it starts. Equations 71, 72 indicate that an operation can be processed within one or more time intervals, with its processing time equal to the total time spent across these intervals. Equations 73, 74 constrain that each operation can be processed on only one machine, and each machine can process only one operation at a time.
5.1.2 Solution algorithm
GA have been extensively applied to address the challenges of the classical JSP (Cheng et al., 1996; Cheng et al., 1999). Davis proposed using GA to solve the classical JSP (Davis, 2014). Gonçalves et al. (2005) introduced a hybrid GA to tackle JSP. This method utilizes a chromosome representation based on random keys, where schedules are constructed according to priorities derived from GA. To enhance solution quality, parameterized active schedules are first generated, followed by the application of a local search heuristic for further optimization. Momenikorbekandi and Abbod (2023) proposed a metaheuristic hybrid Parthenogenetic Algorithm (PGA) for traditional JSP with the objective of minimizing makespan and delay time. The algorithm combines with ethnic selection GA and PGA to improve the search efficiency and the quality of the solution by introducing a racial selection mechanism and multiple selection operators. The parthenogenetic algorithm employs exchange, inversion, and insertion operators, while population selection utilizes four different selection operators: random selection, roulette wheel selection, sexual selection, and aging selection. Abedi et al. (2020) concerned with the fact that the speed of the machine has an impact on the productivity, considered JSP that carry out the necessary maintenance activities during the scheduling process. The problem with the objective of minimizing the total weighted delay time and the total energy consumption also determines the appropriate speed of the machine and the location of the maintenance activities. They proposed a multi-cluster, multi-objective MA. The algorithm assigns solutions to different sub-populations, and to better cover the solution space, the algorithm combines local search and advanced goal-oriented local search methods. In addition, an efficient non-dominated sorting method is developed for multi-objective optimization. For variable batch JSP, Xie et al. (2023) designed a decomposition-based multi-objective Jaya algorithm. The algorithm aims to achieve minimize tardiness and the least number of transferred sub-batches, based on which it combines forward and backward decoding strategies, problem-specific Jaya updating mechanisms, and local search strategies in order to better balance the exploration and exploitation of solutions. With the development of AI, robots provide new ideas to further improve the productivity of factories. Li et al. (2020) discussed JSP in a robotic cell, where the transport of jobs is handled by robots and the jobs need to be completed within a time window. They used a mixed integer planning model to formulate the problem and proposed a Teaching-based Learning Algorithm (TLA). The algorithm is able to simultaneously determine the operation assignments, the robot assignments to be used for the transport operations, and the robot movement order, aiming to minimize makespan and the overall early arrival and delay rates.
Nowadays, with the growing impact of the Industry 5.0 trend on the manufacturing industry, more and more scholars are exploring the constraints of environmental protection and worker scheduling in JSP as well. González et al. (2022) investigated the problem of minimizing both makespan and energy consumption in classical JSP. The energy model considered allows the machine to be in five states, i.e., off, standby, idle, setup, and processing. They proposed an NSGA-II based evolutionary algorithm combining local and heuristic search. Wei et al. (2021) investigated the problem of simultaneously minimizing makespan, total weighted tardiness and precocity, and non-processing energy consumption in JSP by proposing a algorithm based on unified NSGA. The algorithm incorporates a heuristic that incorporates MinMax and NEH for population initialisation. The algorithm is capable of generating a set of Pareto optimal solutions that enable production managers to select appropriate scheduling schemes based on priorities. González-Rodríguez et al. (2020) solved the fuzzy JSP by referencing fuzzy sets to deal with processing time uncertainty with the objective of minimizing makespan and total non-processing energy. They used a NSGA-II based approach combined with heuristic decoding operators that improves the robustness and applicability of the algorithm in practical applications. Since the processing and handling time of a job is affected by a number of uncertainties in the actual production process, Afsar et al. (2022) proposed a new hybrid metaheuristic approach with the objective of minimizing makespan and minimizing non-processing energy consumption. The method combines the design principles of MA, including an evolutionary component based on explicitness, a forbidden search for makespan and a heuristic search for non-processing energy, as well as a post-processing optimization based on linear programming. The collaborate of multiple algorithms is used to achieve reduced energy consumption and improved environmental sustainability without compromising service levels.
Zhang et al. (2024a) investigated a multi-objective JSP for manual loading and unloading tasks considering the human factor, and proposed a grid-based ABC with the goal of minimizing makespan and total workload. The algorithm combines the artificial bee colony algorithm and the grid technique to reduce the complexity of the problem using a decomposition method with earliest and shortest scheduling rule, and divides the target space into multiple cells by constructing a grid coordinate system to facilitate the localisation and evaluation of individuals. The algorithm also designed to generate observer bees based on a mathematical formulation of priority weights to improve information utilisation and algorithm exploration and development. Efficiency in the manufacturing process is also limited by worker’s ability to operate the machine, his work capacity, and the worker’s fatigue level, etc. Rodríguez-Espinosa et al. (2024) investigated multi-objective JSP considering overtime work in a make to order manufacturing company, aiming to minimize the total tardiness and overtime costs. They proposed an enhanced NSGA-II. To accelerate convergence, a problem-specific two-stage decoding scheme was designed and an adaptive mechanism was employed to maintain the stability of global convergence. In addition, a local search procedure is introduced to enhance solution exploration.
Recent advances in JSP research have addressed various practical considerations. These developments reflect the evolving nature of JSP research, incorporating increasingly complex real-world constraints while maintaining computational efficiency and practical applicability.
5.2 Flexible job-shop scheduling
FJSP represents a complex manufacturing scenario where each job comprises a sequence of operations with specific processing constraints. The defining characteristic of FJSP is its dual-layer decision making requirement: machine selection and process sequencing. Operations must follow sequential constraints and are non-preemptable, while each operation can be processed on multiple capable machines.
As shown in Figure 14, research interest in FJSP has grown significantly since 2019, indicating its continued relevance in modern manufacturing systems.
FIGURE 14
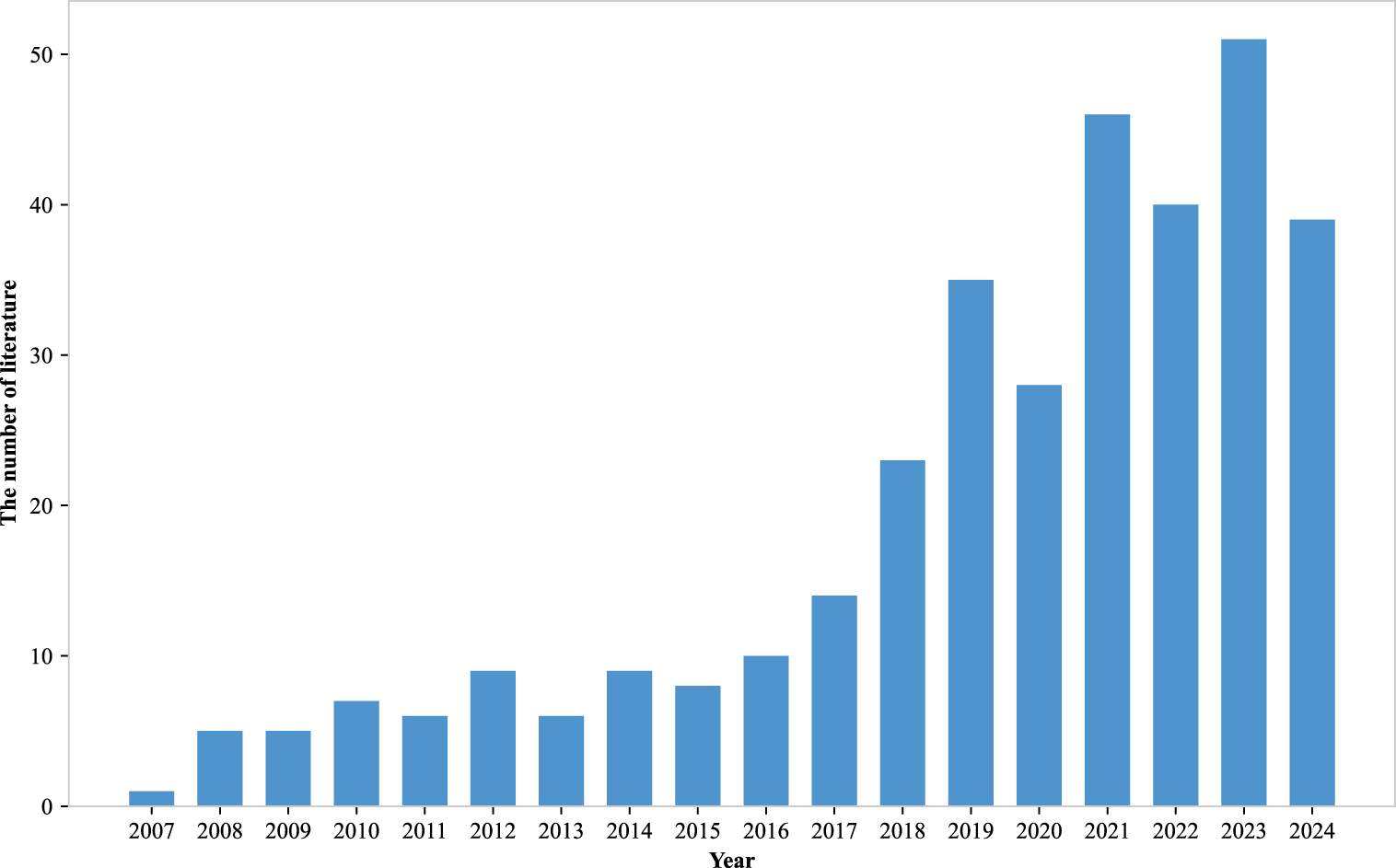
The number of literature on metaheuristic algorithms solving muti-objective FJSP over the years.
5.2.1 Problem model
Addressing FJSP requires not only determining the sequence of jobs but also assigning each operation to an appropriate processing machine, resulting in a complex set of constraints. This section presents a mathematical model formulated with the dual objectives of minimizing the makespan and the total machine delay time. Table 7 provides a detailed definition of the parameters for this problem.
TABLE 7
| Parameter | Statement |
|---|---|
| Job index | |
| Machine index | |
| Operation sequence index of the job | |
| Operation sequence index on the machine | |
| Total number of jobs | |
| Total number of machines | |
| Total number of operations for job | |
| Total number of operations processed on machine | |
| The set of available machines for the -th operation of job | |
| The -th operation of job | |
| The processing time of the -th operation of job on machine | |
| The -th operation processed on machine | |
| The processing time of the -th operation processed on machine | |
| If machine is selected to process operation , it is 1; otherwise, it is 0 | |
| If operation is completed, it is 1; otherwise, it is 0 | |
| If operation is completed, it is 1; otherwise, it is 0 |
Parameters descriptions.
Equation 75, 76 represents the objective function for minimizing the makespan and the total machine delay time. In Equation 76, if a solution assigns only one operation to machine , then . If no operation is assigned to machine , then . Equation 77 specifies the precedence of operations within the same job, where operation must be completed before operation can start. Equation 78 stipulates that when processing an operation, a machine must be selected from the available machine set for operation , and only one machine can be selected. For two operations, and , assigned to the same machine , if arrives before , the start time of must be greater than or equal to the completion time of , as shown in Equation 79. Similarly, in Equation 80, if arrives before , the start time of must also be greater than or equal to the completion time of . In the same manner, Equations 81 specify that all operations assigned to the same machine must satisfy the rules outlined in Equations 79, 80. Equation 82 defines the range of values for the machine selection decision variables, and Equations 83, 84 ensure that the completion time of any operation is greater than or equal to zero.
5.2.2 Solution algorithm
Gao et al. (2008) developed a hybrid GA to solve the FJSP with three objectives: minimizing the makespan, minimizing the maximum machine workload, and minimizing the total workload. Pezzella et al. (2008) introduced an integrated approach to tackle the FJSP, which combines various strategies for initial population generation, individual selection for reproduction, and the creation of new offspring. Shahsavari-Pour and Ghasemishabankareh (2013) proposed a hybrid algorithm combining the advantages of GA and SA for solving the multi-objective function optimization problem in FJSP. The algorithm directly deals with three objectives through a Pareto optimal solution approach: minimizing makespan, minimizing machine workload, and minimizing the total workload of all machines. The hybrid algorithm is able to provide higher quality solutions than existing methods in solving multi-objective problems while reducing computation time. Zhang et al. (2020) investigated FJSP with two neighbouring work areas for a problem involving the production of basic parts and subsequent assembly operations. In order to minimize makespan, total tardiness time and total workload, a distributed ACO is proposed to explore the Pareto frontier. In addition, the method was successfully applied to different scenarios of the ball valve production scheduling problem. Liu et al. (2021) provided a new algorithm which combine with VNS and GA for solving FJSP. The algorithm aims to improve productivity, reduce cost and energy consumption, and it proposes several improvement measures for the problems of slow convergence and low accuracy of traditional GA in solving FJSP. These include a mutation operator based on PSO, a hybrid heuristic initialisation strategy, a VNS based on an improved multilevel neighbourhood structure, and a real-number based chromosome representation, encoding, decoding and crossover method. These improvements improve the convergence performance and solution accuracy of the algorithm.
Li et al. (2014) proposed a novel discrete ABC in solving a multi-objective FJSP containing maintenance activities. The algorithm aims to optimize three main performance metrics: minimizing makespan, total machine workload and critical machine workload. The algorithm employs a unique problem solution representation, the application of TS for local search, an efficient initialisation scheme, an adaptive strategy to enhance the exploratory capabilities of the algorithm, and a specially designed decoding method to handle maintenance activities. An external Pareto archive set is employed for recording all the non-dominated solutions found. Kacem et al. (2002) proposed a Pareto-based hybrid approach combining fuzzy logic and EAs to address the FJSP. This method leverages the knowledge representation capability of fuzzy logic and the adaptability of EAs to optimize three objectives: minimizing the makespan, the total machine workload, and the workload of the most heavily utilized machine. Basiri et al. (2020) designed a hybrid intelligent algorithm for FJSP dealing with fuzzy time. The algorithm is optimized based on the Pareto solution set, considering constraints such as the number of un-predetermined parallel machines, sequence-dependent setup times, re-entrant workflows and fuzzy variables, and combines a simple weighted sum method and a technology preference method.
Industry 5.0 further extends the beautiful vision of Industry 4.0 for energy saving by focusing on sustainable development and environmental responsibility while emphasising on human-centred production methods. Luan et al. (2023) developed an enhanced NSGA-II for multi-objective energy-saving FJSP with the objective of minimizing makespan, total delay time and total energy consumption. This algorithm improves the accuracy of the current solution by performing different neighbourhood search procedures in the sparse solution space by performing different neighbourhood search procedures to increase the diversity of the population of children in the local search, thus improving the accuracy of the current solution. In addition, a weighted approach is used to select the desired compromise solution from the set of Pareto solutions in order to achieve a balance between multiple objectives. Burmeister et al. (2023) focused on FJSP with dynamic energy costs and proposed a multi-objective modelling algorithm based on NSGA-II. The algorithm aims to minimize makespan and energy cost, and bridges the gap in the existing literature that is limited to coarse-grained time periods by taking into account frequently changing real-time energy tariffs. He et al. (2022) focusing on FJSP with dual resource constraints of machines and workers, constructed a model considering both machine and worker constraints, with the aim of minimizing makespan and total delay. They developed an improved African Vultures Optimization Algorithm. A neighbourhood search operation was designed to further minimize makespan and total delay. Zhang et al. (2023b) focused on the post processing shop for parallel disassembly/reassembly workstations and FJSP, which needs to decide on the assignment and sequence of disassembly/reassembly jobs, the as well as the sequence of operations and workstation assignments for reprocessing operations. An enhanced Grey Wolf Optimizer is proposed to address the multi-objective FJSP in remanufacturing systems, aiming to minimize both makespan and energy consumption. The algorithm improves accuracy, computational efficiency, solution stability, and convergence performance by incorporating multiple local neighborhood search strategies, stochastic interference methods, and weighted distance updating mechanisms.
Tan et al. (2021) proposed an optimization model considering worker fatigue for FJSP with dual resource constraints, aiming to simultaneously reduce worker fatigue and increase productivity through joint scheduling of machines and workers. The model aims at minimizing maximum worker fatigue and makespan. This research not only provides practical scheduling tools for decision makers, but also brings fatigue awareness to machine and worker constrained flexible manufacturing systems, facilitating both worker health and productivity. Vital-Soto et al. (2023) developed an elite NSGA-II with innovative operators for a dual resource constrained FJSP considering machine and worker allocation and sorting. The algorithm is able to provide a set of Pareto optimal solutions that help the decision maker to evaluate the trade-offs between different objectives. The algorithm demonstrates its advantages in defining daily schedules, adjusting schedules, priority management, on-time delivery and balancing worker workloads.
With the advent of Industry 5.0, the field of FJSP is increasingly oriented toward energy efficiency and sustainable development. Researchers are placing greater emphasis on integrating factors such as energy consumption, worker fatigue, and environmental responsibility into the scheduling process, aiming to achieve sustainability objectives alongside enhanced production efficiency. Current studies employ various hybrid algorithms designed to address the limitations of traditional methods, thereby improving convergence speed and solution accuracy. This trend indicates that future research will place greater importance on the synergy between algorithmic innovation and practical applications, underscoring the necessity of developing efficient and environmentally friendly scheduling solutions in complex dynamic environments.
5.3 Dynamic job-shop scheduling
Manufacturing environments inherently contain uncertainties, making dynamic scheduling a crucial research direction that closely aligns with real-world production scenarios. Dynamic events in manufacturing can be categorized into four main types: job-related events, operations-related events, machine-related events and other operational events.
Within this domain, the Dynamic Flexible Job-shop Scheduling Problem (Dyn.FJSP) emerged as an extension of Dynamic Job-shop Scheduling Problem (Dyn.JSP), incorporating machine selection flexibility.
As illustrated in Figure 15, research interest in dynamic scheduling problems shows an upward trend, reflecting their increasing practical significance. The ability to respond rapidly to environmental changes while generating optimal scheduling solutions is paramount in this context.
FIGURE 15

The number of literature on metaheuristic algorithms solving muti-objective Dyn.JSP and variant problems over the years.
5.3.1 Problem model
The Dyn.FJSP with new job insertion considered in this chapter can be defined in detail as follows. There are sequentially arriving jobs to be processed on machines . Each job consists of operations, where represents the -th operation of job . Each operation can be processed on any machine selected from its compatible machine set . The processing time of operation on machine is denoted as . The arrival time and due date of job are represented as and , respectively. The actual completion time of operation is denoted as . The urgency level of job is indicated by , where a higher urgency level results in greater penalties for delays.
This chapter establishes a mathematical model with the objectives of simultaneously minimizing the total weighted tardiness and maximizing the average machine utilization. Table 8 presents the detailed parameters of this model.
TABLE 8
| Parameter | Statement |
|---|---|
| Total number of jobs | |
| Total number of machines | |
| Job | |
| Total number of operations belonging to job | |
| Machine | |
| Operation of job | |
| Set of available machines for operation | |
| Processing time of operation on machine | |
| Arrival time of job | |
| Due date of job | |
| Urgency degree of job | |
| The completion time of operation | |
| If operation is assigned on machine , it is 1; otherwise it is 0 | |
| If operation is a predecessor of , it is 1; If operation is a successor of , it is −1 |
Parameter descriptions.
Equation 85 represents the total weighted tardiness of all jobs, where urgency is used as the weight factor (i.e., the penalty factor) for delays. Equation 86 represents the reciprocal of the average machine utilization. Equation 87 indicates that the completion time of each operation must be non-negative. Equation 88 ensures that each operation can only be processed on one available machine. Equation 89 ensures that a job can only be processed after its arrival time. Equation 90 guarantees precedence constraints. Equation 91 ensures capacity constraints are satisfied.
5.3.2 Solution algorithm
When solving scheduling problems under the influence of dynamic events, it is particularly important to design algorithms that can respond quickly to changes in the environment and generate reasonable scheduling schemes in immediately. Chryssolouris and Subramaniam (2001) designed a GA for the Dyn.JSP with the objectives of average job tardiness and average job cost. In scheduling considering dynamic events, most scholars use rescheduling method, i.e., the newly inserted jobs are merged with the existing jobs to reschedule, this scheduling method will make the new scheduling scheme completely different from the old scheduling scheme. In addition, this rescheduling method may lead to stability degradation. Rangsaritratsamee et al. (2004) in order to improve the stability degradation caused by rescheduling and other problems, they proposed a multi-objective rescheduling method based on GA and local search algorithm. The method adopts stability as an additional performance measure based on the objective of minimizing makespan and delay, aiming to balance efficiency and stability. Random job arrivals are the most common class of dynamic events in the dynamic scheduling. Wang et al. (2019) proposed a rescheduling method that combines performance and stability considerations to address this type of Dyn.JSP. The method aims to minimize the discontinuity rate of new jobs, makespan deviation of the initial schedule and order deviation on the machine. Four matching strategies are modified to determine the rescheduling range. An improved PSO is proposed, which consists of a decoding scheme that considers machine unavailability constraints, a population initialisation method based on a new transformation mechanism, and a particle movement method that introduces positional variations and random inertia weights.
Compared to Dyn.JSP, Dyn.FJSP is more challenging in that it needs to consider not only the impact of dynamic events in the manufacturing process, but also the flexibility that jobs can be assigned to multiple machines for processing. Fattahi and Fallahi (2010) proposed a multi-objective mathematical model and a metaheuristic algorithm based on GA to address Dyn.FJSP, aiming at balancing the efficiency and stability of the schedule. Zhang et al. (2013) proposed a rescheduling approach based on hybrid GA and TS to solve Dyn.FJSP. They introduced a simulator to deal with the complexity of real-time events and the difficulty of representing them accurately in a mathematical model. Liu et al. (2024) proposed a multi-objective ALNS for the Dyn.FJSP of self-driving transportation in smart factories. The algorithm adopts a proactive responsive approach to cope with the dynamic interference of new job insertion. The algorithm formulates a two stage multi-objective mixed-integer planning model: the first stage aims to minimize makespan and workload imbalance; the second stage introduces instability minimisation to deal with the effects of disturbances.
From the above research, it can be concluded that in the field of dynamic scheduling, the design of algorithms that can quickly respond to dynamic events is particularly important, as it directly impacts the efficiency and stability of manufacturing environments. Researchers are focusing on employing rescheduling strategies to balance efficiency and stability, particularly in the context of multi-objective optimization, where the goal is to simultaneously enhance scheduling efficiency and robustness. The trend towards the adoption of hybrid algorithms and innovative strategies underscores the critical role of algorithmic innovation in improving scheduling performance.
5.4 Distributed job-shop scheduling
Modern manufacturing systems have evolved into complex networks of multiple interconnected job-shop scheduling problems, each characterized by distinct equipment, process capabilities, and resources. This evolution has exposed the limitations of traditional centralized scheduling approaches, highlighting the growing importance of distributed scheduling solutions. The field encompasses two main variants: Dist.JSP and its flexible counterpart, Distributed Flexible Job-shop Scheduling Problem (Dist.FJSP), distinguished by machine optionality.
As illustrated in Figure 16, research interest in Dist.JSP has shown a consistent upward trend, driven by industry demands for enhanced productivity and resource optimization. This trajectory suggests continued growth in this research domain.
FIGURE 16
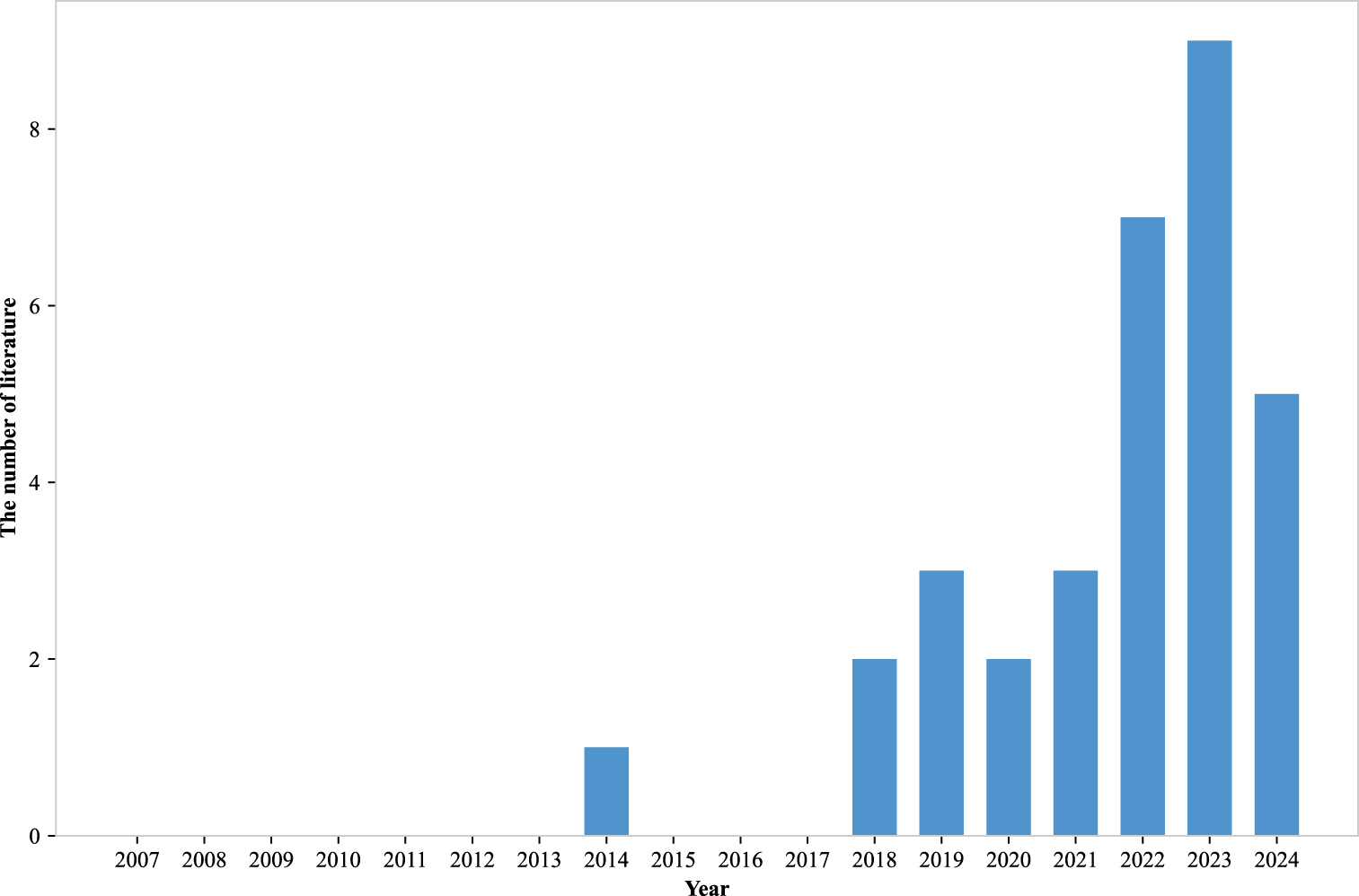
The number of literature on metaheuristic algorithms solving muti-objective Dist.JSP and variant problems over the years.
5.4.1 Problem model
In production and manufacturing systems, flexible scheduling strategies play a critical role in adapting to dynamic market demands and enhancing production flexibility. As a representative problem of multi-factory scheduling, Dist.FJSP is characterized by allowing each sub-factory to operate as an independent flexible job shop, responsible for processing specific parts of the overall production tasks. The resolution of Dist.FJSP involves addressing three key subproblems:
(1) The allocation of parts to processing factories;
(2) The matching of operations to processing machines;
(3) The optimization of operation scheduling within individual factories.
This chapter uses Dist.FJSP as an example to formulate a mathematical model aimed at minimizing makespan and total energy consumption. Table 9 presents the detailed parameters of this model.
TABLE 9
| Parameter | Statement |
|---|---|
| Total number of jobs | |
| Total number of operations for job | |
| Total number of factories | |
| Total number of machines in factory | |
| Job indices, | |
| Operation indices, | |
| Factory index, | |
| Machine index, | |
| Total number of machines across all factories | |
| Workload of factory | |
| The -th (or -th) operation of job (or ) | |
| Processing time of operation on machine in factory | |
| Transfer time of an operation between different machines within the same factory | |
| Transfer time of an operation between different factories | |
| Completion time of job (or ) | |
| Completion time of operation (or ) | |
| Energy consumption rate for operation on machine in factory | |
| Energy consumption rate for transportation | |
| Binary variable, equals 1 if operation is assigned to machine in factory , otherwise 0 | |
| Binary variable, equals 1 if operation is transferred between different machines within the same factory, otherwise 0 | |
| Binary variable, equals 1 if operation is transferred between different factories, otherwise 0 | |
| Total energy consumption for job processing | |
| Total energy consumption for transferring jobs between different machines within the same factory | |
| Total energy consumption for transferring jobs between different factories |
Parameter definitions.
Equations 92, 93 define the optimization objectives of the problem, which are minimizing the makespan and total energy consumption, respectively. Equation 94 ensures that each operation satisfies the precedence constraints. Equation 95 guarantees that each machine processes at most one operation at a time. Equation 96 ensures that each operation is processed on one machine in a single factory only once. Equation 97 restricts each operation to undergo only one transportation, either within or between factories.
5.4.2 Solution algorithm
Li et al. (2018a) proposed a Pareto based hybrid TS for multi-objective Dist.FJSP that simultaneously minimizes four objectives: makespan, maximum workload, total workload, and early arrival/late arrival criteria. The algorithm employs multiple methods to initialise the solution set, which take into account both problem characteristics and objective characteristics. In addition, five neighbourhood structures are used to balance the exploration and exploitation of solutions and a well-designed inverse method is proposed to optimize the early arrival/late arrival criteria. Luo et al. (2020) focus on the limitation that the job operations in the traditional Dist.FJSP can not be transferred between different factories, and propose a Dist.FJSP with transfers that allow operations to be to be processed between different factories. They proposed an efficient MA for this problem that aims to minimize makespan, maximum workload and total energy consumption. The algorithm devises several crossover and mutation operators as well as three efficient neighbourhood structures are developed to extend the search space and accelerate the convergence of the solution. Jia et al. (2024) focused on the problem of integrating optimization of production and distribution in a furniture supply chain, and proposed an integrated Dist.FJSP aiming to minimize makespan and total delay. They introduced a multi-objective Brain Storming Optimization algorithm based on the construction of a mixed integer mathematical planning model.
The widespread adoption of distributed factories in large and complex manufacturing industries will inevitably lead to a series of problems such as energy consumption and environmental impacts. Xu et al. (2021) proposed a multi-objective low carbon scheduling model, which takes the minimization of makespan, total cost, carbon emission and maximization of quality as the optimization objectives. A hybrid GA with three-layer coding and TS was developed, which combines the global search capability of GA and the local search capability of TS to effectively improve the solution performance. The method not only considers the three traditional subproblems of operation sequencing, job assignment and operation to machine assignment, but also introduces the characteristics of job outsourcing, which makes it more in line with the operation of real manufacturing enterprises. Shao et al. (2022) proposed a multi-objective MA based on multiple neighbourhoods aiming to optimize the total weighted tardiness and energy consumption for an energy-efficient Dist.FJSP with variable machine speeds. The algorithm designs two genetic global search operators to enhance the solution search capability and integrates several multi-neighbourhood strategies including intra and inter factories sequence adjustment, energy saving strategies and speed adjustment to enhance the exploration capability. To address the limitation that worker arrangement is not considered in Dist.FJSP, Luo et al. (2022) investigated Dist.FJSP with worker arrangement. To solve the problem, they proposed an improved MA based on the structure of NSGA-II, aiming to minimize the makespan of the machine, the maximum workload and the workload of the workers at the same time.
With the widespread adoption of distributed factories, research has increasingly focused on issues such as low-carbon scheduling and worker arrangement to enhance the energy efficiency and environmental sustainability of scheduling processes. This trend indicates a shift towards more complex real-world applications, emphasizing the integration of algorithmic innovation with practical operations to address the challenges faced by modern manufacturing industries.
The evolution of research on job-shop scheduling problems and its variants highlights four key trends: integration with Industry 5.0, the implementation of flexible manufacturing, the emergence of distributed manufacturing, and the advancement of hybrid algorithms. These trends underscore the ongoing evolution and adaptation of modern manufacturing systems in response to increasing complexity and diversity.
6 Combining metaheuristic algorithm and reinforcement learning for shop scheduling optimization
Despite the widespread application of metaheuristics in shop scheduling optimization, these algorithms face two significant limitations. First, their computational intensity and inability to retain optimization parameters necessitate repeated initialization, resulting in extended response times. Second, their limited generalization capability often requires parameter adjustments for different problem scales, hindering algorithmic transferability. Recent advances in AI, particularly RL, offer promising solutions to these challenges (Cheng et al., 2020).
6.1 Integration approaches in flow shop scheduling
Q-learning (Clifton and Laber, 2020) has emerged as a particularly effective model-free RL algorithm, offering several advantages including environment independent learning, structural simplicity, and efficient exploration exploitation balance through -greedy strategy. The Q-learning update rule can be expressed as (Equation 98):
Recent research has demonstrated successful integration of Q-learning with various metaheuristic algorithms. Zhang and Cai (2023) developed a dual population GA incorporating Q-learning to minimize makespan and delayed jobs. Their approach features multiple genetic operators and a sophisticated population evaluation method, where one population employs optimal search strategies while the other follows Q-learning guidance. Tao et al. (2023) proposed a NSGA-II with Q-learning for DPFSP. Firstly, an IG is used to generate the initial solution. Then, the NSGA-II is designed to optimize the bi-objective problem, and the algorithm parameters are dynamically adjusted by Q-learning. In addition, two kind of crucial factory based local search strategies, including insertion and exchange operations, are introduced to improve the quality of the solution. Zhang et al. (2024b) focused on the DHFSP in a heterogeneous shop and designed a multi-objective MA combining PSO and local search based on Q-learning to minimize makespan and total energy consumption. The algorithm employs a multi-group PSO to improve the fast convergence performance of the multidirectional solutions on the Pareto front, and two local search strategies are designed to further enhance the quality and diversity of the solutions. Q-learning is used to guide the VNS for a better balance of exploration and exploitation.
In the context of energy-efficient scheduling, Yu H. et al. (2024) conducted comprehensive research on multi-objective DPFSP, embedding Q-learning into multiple algorithms including ABC, GA, PSO, IG, and Jaya. Their work introduced five critical neighborhood structures, with the Q-learning enhanced Jaya algorithm demonstrating superior performance. Shao et al. (2024) addressed the challenges of uncertain processing times in DHFSP through a novel energy-efficient approach. Their algorithm combines: machine position-based scheduling rules, decomposition-based construction heuristics, problem-specific search operators and a two-phase framework incorporating metatraining and adaptive search. Zhang et al. (2023a) proposed a Q-learning based MOPSO for DFSP aiming to minimize makespan and total energy consumption. The algorithm enhances the convergence speed of PSO by dividing the particles into three subgroups, enabling it to reach three different regions of the Pareto front faster. Q-learning is used to guide VNS, balancing the exploration and exploitation functions. MOPSO uses exchange sequences to update the job sequence vector, and crossover and mutation to update the plant allocation vector to improve the rationality and efficiency of the algorithm.
Research indicates that Q-learning can be integrated with various metaheuristic algorithms, such as GA and PSO, to enhance their performance in addressing complex scheduling tasks. Particularly in the domains of energy-efficient scheduling and multi-objective optimization, the application of Q-learning demonstrates a favorable balance between exploration and exploitation, facilitating faster convergence to high-quality solutions.
6.2 Integration approaches in job shop scheduling
The integration of metaheuristics and RL has shown particular promise in job shop scheduling problems scenarios (Zhang et al., 2024c). Li et al. (2023) developed a sophisticated approach for energy-efficient HFSP, considering time-sharing tariffs and disconnection strategies. Their Q-learning enhanced NSGA-II algorithm demonstrates effective balance between exploration and exploitation.
He et al. (2021) proposed an effective multi-objective Jaya algorithm. The algorithm introduces a strategy based on gray entropy parallel analysis for evaluating and selecting solutions, and an opposition learning based strategy to enhance the algorithm’s search capability and convergence speed. The strategy of objection learning is integrated into the search operation and external archiving of Jaya to improve the diversity of solutions and avoid local optimum. This algorithm solves multi-objective JSP with the objective of minimizing makespan, total flow time and average tardiness. Abedi et al. (2020) studied Dyn.FJSP considering random job arrivals and machine failures with event-driven policy rescheduling. To solve the problem, they chose VNS as the rescheduling method with the objective of minimizing makespan and total delay, and dynamically updated the VNS parameters at each rescheduling point by a trained Artificial Neural Network. Li et al. (2022) proposed a RL based Multi-objective Evolutionary Algorithm Based on Decomposition for multi-objective FJSP with fuzzy processing time, aiming to minimize makespan and total machine workload. The algorithm generates high quality initial populations using three initial strategies, and employs a Q-learning based parameter adaptation strategy to guide the populations in selecting optimal parameters to increase diversity. In addition, VNS combined with RL guides the solution to choose the correct local search method.
Chen et al. (2023) proposed a predictive reactive dynamic/static rescheduling model for FJSP with ambiguous processing times, dynamic interrupts and variable processing speeds, aiming to optimize the three objectives of maximum completion time, total energy consumption and average protocol index. To address this problem, a multi-objective IA incorporating Q-learning was proposed to optimize the initial solution using an active decoding heuristic based on the interval insertion mechanism, to improve the exploration and exploitation capabilities through clone selected IA and Q-learning, respectively. Kamali et al. (2023) developed an algorithm to optimize the maximum completion time and the average protocol index for a multi-objective Dyn.FJSP, developed a bio-immune based multi-agent system that aims to simultaneously minimize the four objectives of makespan, total weighted tardiness, maximum machine workload and progress stability. In this algorithm, the immune intelligences are responsible for environment recognition, generating non-dominated schedules and selecting optimal schedules with self adaptive and flexible coordination capabilities. Tang et al. (2024) proposed an improved NSGA-III combined with RL for Dist.FJSP with transport resource constraints. The algorithm is designed with a heuristic rule based initialisation method and an IG decoding method, and the key parameters of NSGA-III are adaptively tuned using double Q-learning with an improved -greedy strategy.
In the field of job-shop scheduling problems, the integration of metaheuristic algorithms with RL has demonstrated both effectiveness and significance. By introducing novel evaluation strategies and dynamically adjusting parameters, these approaches enhance the search capabilities and convergence speeds of the algorithms. Furthermore, research addressing dynamic environments and uncertainty issues employs event-driven strategies and multi-agent systems to effectively facilitate dynamic rescheduling.
7 Conclusion and future perspectives
The evolution of manufacturing towards intelligent production has highlighted the limitations of traditional scheduling methods in addressing complex production environments. Metaheuristic algorithms have emerged as effective solution tools, demonstrating significant advantages in handling complex, multi-objective scheduling problems through their nature-inspired optimization approaches. Based on recent literature analysis, these methods have become a research hotspot in multi-objective shop scheduling, showing promising results in various applications.
7.1 Current status analysis
Under the background of Industry 4.0, most studies have concentrated on distributed and dynamic scheduling problems, with some research paying special attention to scheduling with transportation time constraints. In the era of Industry 5.0, a growing number of studies have started to consider the environmental impacts of manufacturing processes, alongside factors such as worker fatigue rates and skill levels. While the existing literature addresses various aspects, research on scheduling problems closer to real-world production scenarios, particularly in the domain of heterogeneous distributed scheduling involving workers, remains inadequate and requires further in-depth exploration.
As for research objectives, the optimization goals of multi-objective scheduling problems currently focus primarily on minimizing makespan, total energy consumption, and optimizing tardiness or earliness rates. Almost all studies emphasize makespan as a critical metric, however, the majority are limited to bi-objective optimization. Studies addressing tri-objective or multi-objective optimization remain relatively rare, indicating significant potential for advancing comprehensive optimization methods.
In addressing multi-objective scheduling problems, metaheuristic algorithms, with NSGA-II as a prominent example, dominate the field. Many studies adopt hybrid strategies that integrate multiple techniques, enhancing the exploration capabilities of algorithms while improving their exploitation of existing solutions. These approaches have achieved remarkable optimization results in multi-objective scheduling problems.
It is worth noting that most studies rely on job-based benchmark test cases for extended research on standard datasets, with only a small fraction utilizing real-world production cases. While benchmark test cases contribute to theoretical advancements, they often approach tasks at the job level, whereas actual production processes typically handle tasks at the order level. This mismatch underscores a gap between current testing methodologies and real-world production practices.
Additionally, in solving dynamic scheduling problems, metaheuristic algorithms often require frequent rescheduling, which incurs additional time costs. In the context of Industry 5.0, which emphasizes enhancing system resilience, RL has emerged as an essential complementary method. It effectively reduces the impact of frequent rescheduling while improving the overall adaptability and flexibility of scheduling systems.
7.2 Future research directions
Looking forward, several critical areas demand attention for advancing the field. First, research problems should expand beyond current paradigms to better align with actual production environments. The acceleration of Industry 5.0 necessitates increased focus on human-centric factors, including worker wellbeing and multi-skilled workforce deployment. This evolution requires a more nuanced approach to problem formulation and solution design.
The scope of optimization objectives needs broadening to reflect the multifaceted nature of modern manufacturing. While current bi-objective approaches have proven valuable, future research should embrace more comprehensive optimization objectives.
Dynamic scheduling represents another crucial frontier. Manufacturing environments face various uncertainties, from order modifications to equipment failures and workforce variations. Future research must develop robust approaches for handling these dynamic elements while maintaining system resilience. This includes designing adaptive strategies that can respond to real-time changes while ensuring production stability.
Methodologically, the integration of metaheuristic algorithms with RLpresents promising opportunities. While metaheuristics excel at finding approximate optimal solutions, they often struggle with large-scale problems and generalization. RL offers complementary strengths, particularly in strategy generalization and rapid decision-making. The integration of these two approaches holds promise for enabling researchers to develop more robust and practical scheduling solutions.
7.3 Implementation considerations
Success in advancing these research directions requires careful attention to implementation strategies. Researchers and practitioners should focus on:
• Adopting test cases that better reflect real-world scenarios: strengthening collaboration between academia and industry is essential for developing generalized test cases using real order data from manufacturing enterprises. This approach ensures that test scenarios are closer to actual production environments. By introducing diverse real-world order data and simulating realistic production processes and dynamic changes, such as order modifications and equipment failures, it is possible to provide more reliable and comprehensive performance evaluations. This ensures that algorithms not only demonstrate theoretical advantages but also excel in practical applications.
• Effective integration of RL and metaheuristic algorithms: to meet the demands of resilient manufacturing in Industry 5.0, it is recommended to effectively integrate RL with metaheuristic algorithms. Leveraging offline training and online application capabilities of RL, combined with the powerful search abilities of metaheuristic algorithms, can enable the development of more intelligent, flexible, and adaptable scheduling algorithms. These advanced approaches would facilitate efficient and stable optimization decisions in dynamically changing production environments.
• In-depth exploration of multi-objective research: for modern manufacturing, focusing on only two objectives often fails to comprehensively address the complexities of real-world requirements. Therefore, it is recommended to further explore optimization research involving three or more objectives. Expanding to multi-objective optimization is not only a necessary academic advancement but also a critical step in addressing the challenges of Industry 5.0.
Through these focused efforts, the field can move closer to achieving practical, efficient, and comprehensive scheduling solutions that meet the demands of modern manufacturing environments.
Statements
Author contributions
WZ: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing–review and editing. XB: Conceptualization, Data curation, Investigation, Methodology, Writing–original draft, Writing–review and editing. XH: Conceptualization, Funding acquisition, Methodology, Supervision, Writing–review and editing. MG: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Science and Technology Research Project of Henan Province (232102211049), Open Fund of Key Laboratory of Grain Information Processing and Control, Ministry of Education (KFJJ2023005), Zhengzhou Science and Technology Collaborative Innovation Project (21ZZXTCX19), and Open Fund of Institute for Complexity Science, Henan University of Technology (CSKFJJ-2024-29), and Scientific Research (C) of Japan Society of Promotion of Science (JSPS) (19K12148).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Glossary
- ABC
Artificial Bee Colony Algorithm
- ACO
Ant Colony Optimization
- AGV
Automatic Guided Vehicles
- AI
Artificial Intelligence
- ALNS
Adaptive Large Neighborhood Search
- BFO
Bacterial Foraging Optimization Algorithm
- DE
Differential Evolution
- DFSP
Distributed Flow-shop Problem
- DHFSP
Distributed Hybrid Flow-shop Problem
- Dist.FJSP
Distributed Flexible Job-shop Scheduling Problem
- Dist.JSP
Distributed Job-shop Scheduling Problem
- DPFSP
Distributed Permutation Flow-shop Problem
- Dyn.FJSP
Dynamic Flexible Job-shop Scheduling Problem
- Dyn.JSP
Dynamic Job-shop Scheduling Problem
- EA
Evolutionary Algorithm
- EAs
Evolutionary Algorithms
- FJSP
Flexible Job-shop Scheduling Problem
- FSP
Flow-shop Scheduling Problem
- GA
Genetic Algorithm
- GSA
Gravitational Search Algorithm
- HFSP
Hybrid Flow-shop Scheduling Problem
- IA
Immune Algorithm
- IG
Integrated Gradients
- IoT
Internet of Things
- JSP
Job-shop Scheduling Problem
- MA
Memetic Algorithm
- MOEA
Multi-objective Evolutionary Algorithms
- MOGA
Multi-Objective Genetic Algorithm
- MOJA/D
Multi-Objective Jaya Algorithm Based on Decomposition
- MOP
Multi-objective Optimization Problem
- MOPSO
Multi-Objective Particle Swarm Optimization
- NEH
Nawaz-Enscore-Ham
- NPGA
Niched Pareto Genetic Algorithm
- NSGA
Non-dominated Sorting Genetic Algorithm
- NSGA-II
Non-dominated Sorting Genetic Algorithm II
- NSGA-III
Non-dominated Sorting Genetic Algorithm III
- PAES
Pareto Archived Evolution Strategy
- PFSP
Permutation Flow-shop Scheduling Problem
- PGA
Parthenogenetic Algorithm
- PhA
Physics-based Algorithms
- POF
Pareto-optimal Front
- POS
Pareto-optimal Set
- PSO
Particle Swarm Optimization
- RL
Reinforcement Learning
- SA
Simulated Annealing
- SI
Swarm Intelligence
- SPEA
Strength Pareto Evolutionary Algorithm
- TLA
Teaching-Learning-Based Optimization
- TS
Tabu Search
- VEGA
Vector Evaluated Genetic Algorithm
- VNS
Variable Neighborhood Search
- WOA
Whale Optimization Algorithm
Footnotes
1.^The search query was structured as follows: TS=((metaheuristic* OR “meta-heuristic*” OR “nature-inspired algorithm*” OR “computational intelligence” OR “evolutionary algorithm*” OR “genetic algorithm*” OR “differential evolution” OR “evolution* strategy” OR “evolution* programming” OR “swarm intelligence” OR “particle swarm optimization” OR “ant colony optimization” OR “artificial bee colony” OR “firefly algorithm” OR “bat algorithm” OR “cuckoo search” OR “simulated annealing” OR “tabu search” OR “harmony search” OR “memetic algorithm*” OR “scatter search” OR “variable neighbourhood search” OR “iterated local search”) AND (“multi-objective” OR multiobjective OR “multi-criteria” OR multicriteria OR Pareto) AND (“flow shop” OR “flowshop” OR “flow-shop”) NOT (“job shop” OR “job-shop” OR “jobshop”)) AND PY=(2000–2024) AND DT=(Article).
2.^The search query was structured as follows: TS=((metaheuristic* OR “meta-heuristic*” OR “nature-inspired algorithm*” OR “computational intelligence” OR “evolutionary algorithm*” OR “genetic algorithm*” OR “differential evolution” OR “evolution* strategy” OR “evolution* programming” OR “swarm intelligence” OR “particle swarm optimization” OR “ant colony optimization” OR “artificial bee colony” OR “firefly algorithm” OR “bat algorithm” OR “cuckoo search” OR “simulated annealing” OR “tabu search” OR “harmony search” OR “memetic algorithm*” OR “scatter search” OR “variable neighbourhood search” OR “iterated local search”) AND (“multi-objective” OR multiobjective OR “multi-criteria” OR multicriteria OR Pareto) AND (“*job shop” OR “*job-shop” OR “*jobshop”)) AND PY=(2000–2024) AND DT=(Article).
References
1
Abedi M. Chiong R. Noman N. Zhang R. (2020). A multi-population, multi-objective memetic algorithm for energy-efficient job-shop scheduling with deteriorating machines. Expert Syst. Appl.157, 113348. 10.1016/j.eswa.2020.113348
2
Afsar S. Palacios J. J. Puente J. Vela C. R. Gonzalez-Rodriguez I. (2022). Multi-objective enhanced memetic algorithm for green job shop scheduling with uncertain times. Swarm Evol. Comput.68, 101016. 10.1016/j.swevo.2021.101016
3
Anjana V. Sridharan R. Ram Kumar P. (2020). Metaheuristics for solving a multi-objective flow shop scheduling problem with sequence-dependent setup times. J. Sched.23, 49–69. 10.1007/s10951-019-00610-0
4
Basiri M.-A. Alinezhad E. Tavakkoli-Moghaddam R. Shahsavari-Poure N. (2020). A hybrid intelligent algorithm for a fuzzy multi-objective job shop scheduling problem with reentrant workflows and parallel machines. J. Intelligent & Fuzzy Syst.39, 7769–7785. 10.3233/jifs-201120
5
Behnamian J. Fatemi Ghomi S. Zandieh M. (2009). A multi-phase covering pareto-optimal front method to multi-objective scheduling in a realistic hybrid flowshop using a hybrid metaheuristic. Expert Syst. Appl.36, 11057–11069. 10.1016/j.eswa.2009.02.080
6
Boufellouh R. Belkaid F. (2023). Multi-objective optimization for energy-efficient flow shop scheduling problem with blocking and collision-free transportation constraints. Appl. Soft Comput.148, 110884. 10.1016/j.asoc.2023.110884
7
Branda A. Castellano D. Guizzi G. Popolo V. (2021). Metaheuristics for the flow shop scheduling problem with maintenance activities integrated. Comput. & Industrial Eng.151, 106989. 10.1016/j.cie.2020.106989
8
Burmeister S. C. Guericke D. Schryen G. (2023). A memetic nsga-ii for the multi-objective flexible job shop scheduling problem with real-time energy tariffs. Flexible Serv. Manuf. J.36, 1530–1570. 10.1007/s10696-023-09517-7
9
Cai S. Yang K. Liu K. (2018). Multi-objective optimization of the distributed permutation flow shop scheduling problem with transportation and eligibility constraints. J. Operations Res. Soc. China6, 391–416. 10.1007/s40305-017-0165-3
10
Caldeira R. H. Gnanavelbabu A. (2021). A pareto based discrete jaya algorithm for multi-objective flexible job shop scheduling problem. Expert Syst. Appl.170, 114567. 10.1016/j.eswa.2021.114567
11
Chen J.-f. Wang L. Peng Z.-p. (2019). A collaborative optimization algorithm for energy-efficient multi-objective distributed no-idle flow-shop scheduling. Swarm Evol. Comput.50, 100557. 10.1016/j.swevo.2019.100557
12
Chen T.-L. Cheng C.-Y. Chou Y.-H. (2020). Multi-objective genetic algorithm for energy-efficient hybrid flow shop scheduling with lot streaming. Ann. Operations Res.290, 813–836. 10.1007/s10479-018-2969-x
13
Chen X.-l. Li J.-q. Xu Y. (2023). Q-learning based multi-objective immune algorithm for fuzzy flexible job shop scheduling problem considering dynamic disruptions. Swarm Evol. Comput.83, 101414. 10.1016/j.swevo.2023.101414
14
Cheng J. Yang B. Gen M. Jang Y. J. Liang C.-J. (2020). Machine learning based evolutionary algorithms and optimization for transportation and logistics. Comput. & Industrial Eng.143, 106372. 10.1016/j.cie.2020.106372
15
Cheng R. Gen M. Tsujimura Y. (1996). A tutorial survey of job-shop scheduling problems using genetic algorithms—i. representation. Comput. & Industrial Eng.30, 983–997. 10.1016/0360-8352(96)00047-2
16
Cheng R. Gen M. Tsujimura Y. (1999). A tutorial survey of job-shop scheduling problems using genetic algorithms, part ii: hybrid genetic search strategies. Comput. & Industrial Eng.36, 343–364. 10.1016/s0360-8352(99)00136-9
17
Chryssolouris G. Subramaniam V. (2001). Dynamic scheduling of manufacturing job shops using genetic algorithms. J. Intelligent Manuf.12, 281–293. 10.1023/a:1011253011638
18
Clifton J. Laber E. (2020). Q-learning: theory and applications. Annu. Rev. Statistics Its Appl.7, 279–301. 10.1146/annurev-statistics-031219-041220
19
Coello C. A. C. (2007). Evolutionary algorithms for solving multi-objective problems. Springer.
20
Davis L. (2014). “Job shop scheduling with genetic algorithms,” in Proceedings of the first international conference on genetic algorithms and their applications (New York: Psychology Press), 136–140.
21
Deb K. Pratap A. Agarwal S. Meyarivan T. (2002). A fast and elitist multiobjective genetic algorithm: nsga-ii. IEEE Trans. Evol. Comput.6, 182–197. 10.1109/4235.996017
22
Destouet C. Tlahig H. Bettayeb B. Mazari B. (2023). Flexible job shop scheduling problem under industry 5.0: a survey on human reintegration, environmental consideration and resilience improvement. J. Manuf. Syst.67, 155–173. 10.1016/j.jmsy.2023.01.004
23
Ding J.-Y. Song S. Wu C. (2016). Carbon-efficient scheduling of flow shops by multi-objective optimization. Eur. J. Operational Res.248, 758–771. 10.1016/j.ejor.2015.05.019
24
Dong R. Li J. Song D. Yang B. Zhou L. (2024). A multi-objective non-dominated sorting gravitational search algorithm for assembly flow-shop scheduling of marine prefabricated cabins. Mathematics12, 2288–7390. 10.3390/math12142288
25
Engin O. Yılmaz M. K. (2021). A fuzzy logic based methodology for multi-objective hybrid flow shop scheduling with multi-processor tasks problems and solving with an efficient genetic algorithm. J. Intelligent & Fuzzy Syst.42, 451–463. 10.3233/jifs-219203
26
Fadaei M. Zandieh M. (2013). Scheduling a bi-objective hybrid flow shop with sequence-dependent family setup times using metaheuristics. Arabian J. Sci. Eng.38, 2233–2244. 10.1007/s13369-013-0611-4
27
Fasihi M. Tavakkoli-Moghaddam R. Jolai F. (2023). A bi-objective re-entrant permutation flow shop scheduling problem: minimizing the makespan and maximum tardiness. Operational Res.23, 29. 10.1007/s12351-023-00770-0
28
Fathollahi-Fard A. M. Woodward L. Akhrif O. (2024a). A distributed permutation flow-shop considering sustainability criteria and real-time scheduling. J. Industrial Inf. Integration39, 100598. 10.1016/j.jii.2024.100598
29
Fathollahi-Fard A. M. Woodward L. Akhrif O. (2024b). A scenario-based robust optimization model for the sustainable distributed permutation flow-shop scheduling problem. Ann. Operations Res., 1–42. 10.1007/s10479-024-05940-7
30
Fattahi P. Fallahi A. (2010). Dynamic scheduling in flexible job shop systems by considering simultaneously efficiency and stability. CIRP J. Manuf. Sci. Technol.2, 114–123. 10.1016/j.cirpj.2009.10.001
31
Fekri M. Heydari M. Mahdavi Mazdeh M. (2024). Bi-objective optimization of flexible flow shop scheduling problem with multi-skilled human resources. Eng. Appl. Artif. Intell.133, 108094. 10.1016/j.engappai.2024.108094
32
Ferreira J. J. Lopes J. M. Gomes S. Rammal H. G. (2023). Industry 4.0 implementation: environmental and social sustainability in manufacturing multinational enterprises. J. Clean. Prod.404, 136841. 10.1016/j.jclepro.2023.136841
33
Fonseca C. M. Fleming P. J. (1993). Genetic algorithms for multiobjective optimization: formulation discussion and generalization. Icga (Citeseer)93, 416–423.
34
Gao J. Sun L. Gen M. (2008). A hybrid genetic and variable neighborhood descent algorithm for flexible job shop scheduling problems. Comput. & Operations Res.35, 2892–2907. 10.1016/j.cor.2007.01.001
35
Gao Q. Hu H. Liu J. Zhuang C. Ding H. Li H. (2024). Distributed assembly shop scheduling problem for complex products considering multiskilled worker assignment and transportation time. Int. J. Prod. Res., 1–23. 10.1080/00207543.2024.2383785
36
Gen M. Cheng R. Lin L. (2008). Network models and optimization: multiobjective genetic algorithm approach. Springer Science & Business Media.
37
Geng K. Ye C. Liu L. (2020). Research on multi-objective hybrid flow shop scheduling problem with dual resource constraints using improved memetic algorithm. IEEE Access8, 104527–104542. 10.1109/access.2020.2999680
38
Goldberg D. E. Deb K. Kargupta H. Harik G. (1993). “Rapid, accurate optimization of difficult problems using messy genetic algorithms,” in Proceedings of the fifth international conference on genetic algorithms (urbana, USA), 59–64.
39
Gonçalves J. F. de Magalhães Mendes J. J. Resende M. G. (2005). A hybrid genetic algorithm for the job shop scheduling problem. Eur. J. Operational Res.167, 77–95. 10.1016/j.ejor.2004.03.012
40
Gong G. Chiong R. Deng Q. Gong X. (2020). A hybrid artificial bee colony algorithm for flexible job shop scheduling with worker flexibility. Int. J. Prod. Res.58, 4406–4420. 10.1080/00207543.2019.1653504
41
González M. A. Rasconi R. Oddi A. (2022). Metaheuristics for multiobjective optimization in energy-efficient job shops. Eng. Appl. Artif. Intell.115, 105263. 10.1016/j.engappai.2022.105263
42
González-Rodríguez I. Puente J. Palacios J. J. Vela C. R. (2020). Multi-objective evolutionary algorithm for solving energy-aware fuzzy job shop problems. Soft Comput.24, 16291–16302. 10.1007/s00500-020-04940-6
43
Han W. Deng Q. Gong G. Zhang L. Luo Q. (2021). Multi-objective evolutionary algorithms with heuristic decoding for hybrid flow shop scheduling problem with worker constraint. Expert Syst. Appl.168, 114282. 10.1016/j.eswa.2020.114282
44
Hao X. Gen M. Lin L. Suer G. A. (2017). Effective multiobjective eda for bi-criteria stochastic job-shop scheduling problem. J. Intelligent Manuf.28, 833–845. 10.1007/s10845-014-1026-0
45
Hassanzadeh A. Rasti-Barzoki M. Khosroshahi H. (2016). Two new meta-heuristics for a bi-objective supply chain scheduling problem in flow-shop environment. Appl. Soft Comput.49, 335–351. 10.1016/j.asoc.2016.08.019
46
He L. Li W. Chiong R. Abedi M. Cao Y. Zhang Y. (2021). Optimising the job-shop scheduling problem using a multi-objective jaya algorithm. Appl. Soft Comput.111, 107654. 10.1016/j.asoc.2021.107654
47
He Z. Tang B. Luan F. (2022). An improved african vulture optimization algorithm for dual-resource constrained multi-objective flexible job shop scheduling problems. Sensors23, 90. 10.3390/s23010090
48
Hillermeier C. (2001). Generalized homotopy approach to multiobjective optimization. J. Optim. Theory Appl.110, 557–583. 10.1023/a:1017536311488
49
Hosseini S. M. H. (2017). A multi-objective genetic algorithm (moga) for hybrid flow shop scheduling problem with assembly operation. J. Industrial Syst. Eng.10, 132–154.
50
Huang Y.-Y. Pan Q.-K. Gao L. Miao Z.-H. Peng C. (2022). A two-phase evolutionary algorithm for multi-objective distributed assembly permutation flowshop scheduling problem. Swarm Evol. Comput.74, 101128. 10.1016/j.swevo.2022.101128
51
Jain A. K. Kumar S. Tayal S. (2022). Life cycle engineering in the era of industry 4.0[Dataset].
52
Jain H. Deb K. (2014). An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part ii: handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput.18, 602–622. 10.1109/tevc.2013.2281534
53
Jia Y. Zhou Y. Fu Y. (2024). A multi-objective brain storm optimization for integrated distributed flexible job shop and distribution problems. Heliyon10, e36318. 10.1016/j.heliyon.2024.e36318
54
Kacem I. Hammadi S. Borne P. (2002). Pareto-optimality approach for flexible job-shop scheduling problems: hybridization of evolutionary algorithms and fuzzy logic. Math. Comput. Simul.60, 245–276. 10.1016/s0378-4754(02)00019-8
55
Kamali S. R. Banirostam T. Motameni H. Teshnehlab M. (2023). An immune-based multi-agent system for flexible job shop scheduling problem in dynamic and multi-objective environments. Eng. Appl. Artif. Intell.123, 106317. 10.1016/j.engappai.2023.106317
56
Li J.-Q. Duan P. Cao J. Lin X.-P. Han Y.-Y. (2018a). A hybrid pareto-based tabu search for the distributed flexible job shop scheduling problem with e/t criteria. IEEE Access6, 58883–58897. 10.1109/access.2018.2873401
57
Li J.-Q. Pan Q.-K. Tasgetiren M. F. (2014). A discrete artificial bee colony algorithm for the multi-objective flexible job-shop scheduling problem with maintenance activities. Appl. Math. Model.38, 1111–1132. 10.1016/j.apm.2013.07.038
58
Li J.-Q. Sang H.-y. Han Y.-y. Wang C.-g. Gao K.-z. (2018b). Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions. J. Clean. Prod.181, 584–598. 10.1016/j.jclepro.2018.02.004
59
Li P. Xue Q. Zhang Z. Chen J. Zhou D. (2023). Multi-objective energy-efficient hybrid flow shop scheduling using q-learning and gvns driven nsga-ii. Comput. & Operations Res.159, 106360. 10.1016/j.cor.2023.106360
60
Li R. Gong W. Lu C. (2022). A reinforcement learning based rmoea/d for bi-objective fuzzy flexible job shop scheduling. Expert Syst. Appl.203, 117380. 10.1016/j.eswa.2022.117380
61
Li X. Yang X. Zhao Y. Teng Y. Dong Y. (2020). Metaheuristic for solving multi-objective job shop scheduling problem in a robotic cell. IEEE Access8, 147015–147028. 10.1109/access.2020.3015796
62
Liu J. Sun B. Li G. Chen Y. (2024). Multi-objective adaptive large neighbourhood search algorithm for dynamic flexible job shop schedule problem with transportation resource. Eng. Appl. Artif. Intell.132, 107917. 10.1016/j.engappai.2024.107917
63
Liu Z. Wang J. Zhang C. Chu H. Ding G. Zhang L. (2021). A hybrid genetic-particle swarm algorithm based on multilevel neighbourhood structure for flexible job shop scheduling problem. Comput. & Operations Res.135, 105431. 10.1016/j.cor.2021.105431
64
Lu C. Huang Y. Meng L. Gao L. Zhang B. Zhou J. (2022). A pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers. Robotics Computer-Integrated Manuf.74, 102277. 10.1016/j.rcim.2021.102277
65
Luan F. Zhao H. Liu S. Q. He Y. Tang B. (2023). Enhanced nsga-ii for multi-objective energy-saving flexible job shop scheduling. Sustain. Comput. Inf. Syst.39, 100901. 10.1016/j.suscom.2023.100901
66
Luo Q. Deng Q. Gong G. Guo X. Liu X. (2022). A distributed flexible job shop scheduling problem considering worker arrangement using an improved memetic algorithm. Expert Syst. Appl.207, 117984. 10.1016/j.eswa.2022.117984
67
Luo Q. Deng Q. Gong G. Zhang L. Han W. Li K. (2020). An efficient memetic algorithm for distributed flexible job shop scheduling problem with transfers. Expert Syst. Appl.160, 113721. 10.1016/j.eswa.2020.113721
68
Mishra A. K. Shrivastava D. Bundela B. Sircar S. (2020). “An efficient jaya algorithm for multi-objective permutation flow shop scheduling problem,” in Advanced engineering optimization through intelligent techniques: select proceedings of AEOTIT 2018 (Springer), 113–125.
69
Momenikorbekandi A. Abbod M. F. (2023). A novel metaheuristic hybrid parthenogenetic algorithm for job shop scheduling problems: applying an optimization model. IEEE Access11, 56027–56045. 10.1109/access.2023.3278372
70
Motair H. M. (2021). Exact and hybrid metaheuristic algorithms to solve bi-objective permutation flow shop scheduling problem. J. Phys. Conf. Ser.1818, 012042. IOP Publishing. 10.1088/1742-6596/1818/1/012042
71
Mourtzis D. (2020a). “Adaptive scheduling in the era of cloud manufacturing,” Scheduling in industry 4.0 and cloud manufacturing, 61–85.
72
Mourtzis D. (2020b). Simulation in the design and operation of manufacturing systems: state of the art and new trends. Int. J. Prod. Res.58, 1927–1949. 10.1080/00207543.2019.1636321
73
Mourtzis D. (2022). Advances in adaptive scheduling in industry 4.0. Front. Manuf. Technol.2, 937889. 10.3389/fmtec.2022.937889
74
Öztop H. Tasgetiren M. F. Eliiyi D. T. Pan Q.-K. Kandiller L. (2020). An energy-efficient permutation flowshop scheduling problem. Expert Syst. Appl.150, 113279. 10.1016/j.eswa.2020.113279
75
Pezzella F. Morganti G. Ciaschetti G. (2008). A genetic algorithm for the flexible job-shop scheduling problem. Comput. & Operations Res.35, 3202–3212. 10.1016/j.cor.2007.02.014
76
Qi Y. Ma X. Liu F. Jiao L. Sun J. Wu J. (2014). Moea/d with adaptive weight adjustment. Evol. Comput.22, 231–264. 10.1162/evco_a_00109
77
Rahimi-Vahed A. Mirghorbani S. (2006). A multi-objective particle swarm for a flow shop scheduling problem. J. Comb. Optim.13, 79–102. 10.1007/s10878-006-9015-7
78
Rajkumar R. Jeen Robert R. (2019). A hybrid algorithm for multi-objective optimization of minimizing makespan and total flow time in permutation flow shop scheduling problems. Inf. Technol. Control48, 47–57. 10.5755/j01.itc.48.1.20909
79
Rangsaritratsamee R. Ferrell W. G. Jr Kurz M. B. (2004). Dynamic rescheduling that simultaneously considers efficiency and stability. Comput. & Industrial Eng.46, 1–15. 10.1016/j.cie.2003.09.007
80
Rifai A. P. Mara S. T. W. Sudiarso A. (2021). Multi-objective distributed reentrant permutation flow shop scheduling with sequence-dependent setup time. Expert Syst. Appl.183, 115339. 10.1016/j.eswa.2021.115339
81
Rodríguez-Espinosa C. A. González-Neira E. M. Zambrano-Rey G. M. (2024). A simheuristic approach using the nsga-ii to solve a bi-objective stochastic flexible job shop problem. J. Simul.18, 646–670. 10.1080/17477778.2023.2231877
82
Rossit D. G. Nesmachnow S. Rossit D. A. (2022). A multiobjective evolutionary algorithm based on decomposition for a flow shop scheduling problem in the context of industry 4.0. Int. J. Math. Eng. Manag. Sci.7, 433–454. 10.33889/ijmems.2022.7.4.029
83
Schaffer J. D. (1985). Some experiments in machine learning using vector evaluated genetic algorithms. Nashville, TN (USA): Vanderbilt Univ.Tech. rep.
84
Schulz S. Neufeld J. S. Buscher U. (2019). A multi-objective iterated local search algorithm for comprehensive energy-aware hybrid flow shop scheduling. J. Clean. Prod.224, 421–434. 10.1016/j.jclepro.2019.03.155
85
Schulz S. Schönheit M. Neufeld J. S. (2022). Multi-objective carbon-efficient scheduling in distributed permutation flow shops under consideration of transportation efforts. J. Clean. Prod.365, 132551. 10.1016/j.jclepro.2022.132551
86
Sekkal D. N. Belkaid F. (2023). A multi-objective optimization algorithm for flow shop group scheduling problem with sequence dependent setup time and worker learning. Expert Syst. Appl.233, 120878. 10.1016/j.eswa.2023.120878
87
Shahsavari-Pour N. Ghasemishabankareh B. (2013). A novel hybrid meta-heuristic algorithm for solving multi objective flexible job shop scheduling. J. Manuf. Syst.32, 771–780. 10.1016/j.jmsy.2013.04.015
88
Shao W. Shao Z. Pi D. (2022). A multi-neighborhood-based multi-objective memetic algorithm for the energy-efficient distributed flexible flow shop scheduling problem. Neural Comput. Appl.34, 22303–22330. 10.1007/s00521-022-07714-3
89
Shao Z. Shao W. Chen J. Pi D. (2024). Mql-mm: a meta-q-learning-based multi-objective metaheuristic for energy-efficient distributed fuzzy hybrid blocking flow-shop scheduling problem. IEEE Trans. Evol. Comput., 1. 10.1109/tevc.2024.3399314
90
Srinivas N. Deb K. (1994). Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput.2, 221–248. 10.1162/evco.1994.2.3.221
91
Tajbakhsh Z. Fattahi P. Behnamian J. (2014). Multi-objective assembly permutation flow shop scheduling problem: a mathematical model and a meta-heuristic algorithm. J. Operational Res. Soc.65, 1580–1592. 10.1057/jors.2013.105
92
Tan W. Yuan X. Wang J. Zhang X. (2021). A fatigue-conscious dual resource constrained flexible job shop scheduling problem by enhanced nsga-ii: an application from casting workshop. Comput. & Industrial Eng.160, 107557. 10.1016/j.cie.2021.107557
93
Tang H. Xiao Y. Zhang W. Lei D. Wang J. Xu T. (2024). A dql-nsga-iii algorithm for solving the flexible job shop dynamic scheduling problem. Expert Syst. Appl.237, 121723. 10.1016/j.eswa.2023.121723
94
Tao X.-R. Pan Q.-K. Sang H.-Y. Gao L. Yang A.-L. Rong M. (2023). Nondominated sorting genetic algorithm-ii with q-learning for the distributed permutation flowshop rescheduling problem. Knowledge-Based Syst.278, 110880. 10.1016/j.knosys.2023.110880
95
Tavakkoli-Moghaddam R. Rahimi-Vahed A. Mirzaei A. H. (2007). A hybrid multi-objective immune algorithm for a flow shop scheduling problem with bi-objectives: weighted mean completion time and weighted mean tardiness. Inf. Sci.177, 5072–5090. 10.1016/j.ins.2007.06.001
96
Vallejos-Cifuentes P. Ramirez-Gomez C. Escudero-Atehortua A. Rodriguez Velasquez E. (2019). Energy-aware production scheduling in flow shop and job shop environments using a multi-objective genetic algorithm. Eng. Manag. J.31, 82–97. 10.1080/10429247.2018.1544798
97
Vital-Soto A. Baki M. F. Azab A. (2023). A multi-objective mathematical model and evolutionary algorithm for the dual-resource flexible job-shop scheduling problem with sequencing flexibility. Flexible Serv. Manuf. J.35, 626–668. 10.1007/s10696-022-09446-x
98
Wang G. Li X. Gao L. Li P. (2022). An effective multi-objective whale swarm algorithm for energy-efficient scheduling of distributed welding flow shop. Ann. Operations Res.310, 223–255. 10.1007/s10479-021-03952-1
99
Wang W. Zhang B. Jiang X. Jia B. Sang H. Meng L. (2024). Decomposition-based multi-objective approach for a green hybrid flowshop rescheduling problem with consistent sublots. Int. J. Prod. Res.62, 7904–7932. 10.1080/00207543.2024.2333943
100
Wang Y.-J. Wang G.-G. Tian F.-M. Gong D.-W. Pedrycz W. (2023). Solving energy-efficient fuzzy hybrid flow-shop scheduling problem at a variable machine speed using an extended nsga-ii. Eng. Appl. Artif. Intell.121, 105977. 10.1016/j.engappai.2023.105977
101
Wang Z. Zhang J. Yang S. (2019). An improved particle swarm optimization algorithm for dynamic job shop scheduling problems with random job arrivals. Swarm Evol. Comput.51, 100594. 10.1016/j.swevo.2019.100594
102
Wei H. Li S. Quan H. Liu D. Rao S. Li C. et al (2021). Unified multi-objective genetic algorithm for energy efficient job shop scheduling. IEEE Access9, 54542–54557. 10.1109/access.2021.3070981
103
Wu R. Li Y. Guo S. Xu W. (2018). Solving the dual-resource constrained flexible job shop scheduling problem with learning effect by a hybrid genetic algorithm. Adv. Mech. Eng.10, 1687814018804096. 10.1177/1687814018804096
104
Wu X. Che A. (2020). Energy-efficient no-wait permutation flow shop scheduling by adaptive multi-objective variable neighborhood search. Omega94, 102117. 10.1016/j.omega.2019.102117
105
Xie F. Li L. Li L. Huang Y. He Z. (2023). A decomposition-based multi-objective jaya algorithm for lot-streaming job shop scheduling with variable sublots and intermingling setting. Expert Syst. Appl.228, 120402. 10.1016/j.eswa.2023.120402
106
Xin B. Li Y. Yu J. Zhang J. (2015). An adaptive bpso algorithm for multi-skilled workers assignment problem in aircraft assembly lines. Assem. Autom.35, 317–328. 10.1108/aa-06-2015-051
107
Xin X. Jiang Q. Li S. Gong S. Chen K. (2021). Energy-efficient scheduling for a permutation flow shop with variable transportation time using an improved discrete whale swarm optimization. J. Clean. Prod.293, 126121. 10.1016/j.jclepro.2021.126121
108
Xu W. Hu Y. Luo W. Wang L. Wu R. (2021). A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission. Comput. & Industrial Eng.157, 107318. 10.1016/j.cie.2021.107318
109
Yu F. Lu C. Yin L. Zhou J. (2024). Modeling and optimization algorithm for energy-efficient distributed assembly hybrid flowshop scheduling problem considering worker resources. J. Industrial Inf. Integration40, 100620. 10.1016/j.jii.2024.100620
110
Yu H. Gao K. Li Z. Suganthan P. N. (2024). Energy-efficient multi-objective distributed assembly permutation flowshop scheduling by q-learning based meta-heuristics. Appl. Soft Comput.166, 112247. 10.1016/j.asoc.2024.112247
111
Yüksel D. Taşgetiren M. F. Kandiller L. Gao L. (2020). An energy-efficient bi-objective no-wait permutation flowshop scheduling problem to minimize total tardiness and total energy consumption. Comput. & Industrial Eng.145, 106431. 10.1016/j.cie.2020.106431
112
Zhang B. Che A. Wang Y. (2024a). Grid-based artificial bee colony algorithm for multi-objective job shop scheduling with manual loading and unloading tasks. Expert Syst. Appl.245, 123011. 10.1016/j.eswa.2023.123011
113
Zhang J. Cai J. (2023). A dual-population genetic algorithm with q-learning for multi-objective distributed hybrid flow shop scheduling problem. Symmetry15, 836. 10.3390/sym15040836
114
Zhang L. Gao L. Li X. (2013). A hybrid genetic algorithm and tabu search for a multi-objective dynamic job shop scheduling problem. Int. J. Prod. Res.51, 3516–3531. 10.1080/00207543.2012.751509
115
Zhang Q. Li H. (2007). Moea/d: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput.11, 712–731. 10.1109/tevc.2007.892759
116
Zhang S. Li X. Zhang B. Wang S. (2020). Multi-objective optimisation in flexible assembly job shop scheduling using a distributed ant colony system. Eur. J. Operational Res.283, 441–460. 10.1016/j.ejor.2019.11.016
117
Zhang W. Gen M. Jo J. (2014). Hybrid sampling strategy-based multiobjective evolutionary algorithm for process planning and scheduling problem. J. Intelligent Manuf.25, 881–897. 10.1007/s10845-013-0814-2
118
Zhang W. Geng H. Li C. Gen M. Zhang G. Deng M. (2023a). Q-learning-based multi-objective particle swarm optimization with local search within factories for energy-efficient distributed flow-shop scheduling problem. J. Intelligent Manuf.36, 185–208. 10.1007/s10845-023-02227-9
119
Zhang W. Li C. Gen M. Yang W. Zhang G. (2024b). A multiobjective memetic algorithm with particle swarm optimization and q-learning-based local search for energy-efficient distributed heterogeneous hybrid flow-shop scheduling problem. Expert Syst. Appl.237, 121570. 10.1016/j.eswa.2023.121570
120
Zhang W. Xiao G. Gen M. Geng H. Wang X. Deng M. et al (2024c). Enhancing multi-objective evolutionary algorithms with machine learning for scheduling problems: recent advances and survey. Front. Industrial Eng.2, 1337174. 10.3389/fieng.2024.1337174
121
Zhang W. Zheng Y. Ahmad R. (2023b). An energy-efficient multi-objective scheduling for flexible job-shop-type remanufacturing system. J. Manuf. Syst.66, 211–232. 10.1016/j.jmsy.2022.12.008
122
Zhang Z. Tang Q. Chica M. (2021). Maintenance costs and makespan minimization for assembly permutation flow shop scheduling by considering preventive and corrective maintenance. J. Manuf. Syst.59, 549–564. 10.1016/j.jmsy.2021.03.020
123
Zhao F. Zhang H. Wang L. Xu T. Zhu N. Jonrinaldi J. (2024). A multi-objective discrete differential evolution algorithm for energy-efficient distributed blocking flow shop scheduling problem. Int. J. Prod. Res.62, 4226–4244. 10.1080/00207543.2023.2254858
Summary
Keywords
metaheuristics, multi-objective optimization, scheduling problems, Industry 4.0, Industry 5.0, smart manufacturing, human-centric manufacturing
Citation
Zhang W, Bao X, Hao X and Gen M (2025) Metaheuristics for multi-objective scheduling problems in industry 4.0 and 5.0: a state-of-the-arts survey. Front. Ind. Eng. 3:1540022. doi: 10.3389/fieng.2025.1540022
Received
05 December 2024
Accepted
02 January 2025
Published
27 January 2025
Volume
3 - 2025
Edited by
Dimitris Zissis, Athens University of Economics and Business, Greece
Reviewed by
Aleksandar Trifunović, University of Belgrade, Serbia
Ioannis Avgerinos, Athens University of Economics and Business, Greece
Updates
Copyright
© 2025 Zhang, Bao, Hao and Gen.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenqiang Zhang, zhangwq@haut.edu.cn; Xinchang Hao, haoxc@outlook.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.