- Institute of Structural and Molecular Biology, Birkbeck College, London, UK
In studying the binding of host antibodies to the surface antigens of pathogens, the structural and functional characterization of antibody–antigen complexes by X-ray crystallography and binding assay is important. However, the characterization requires experiments that are typically time consuming and expensive: thus, many antibody–antigen complexes are under-characterized. For vaccine development and disease surveillance, it is often vital to assess the impact of amino acid substitutions on antibody binding. For example, are there antibody substitutions capable of improving binding without a loss of breadth, or antigen substitutions that lead to antigenic escape? The questions cannot be answered reliably from sequence variation alone, exhaustive substitution assays are usually impractical, and alanine scans provide at best an incomplete identification of the critical residue–residue interactions. Here, we show that, given an initial structure of an antibody bound to an antigen, molecular dynamics simulations using the energy method molecular mechanics with Generalized Born surface area (MM/GBSA) can model the impact of single amino acid substitutions on antibody–antigen binding energy. We apply the technique to three broad-spectrum antibodies to influenza A hemagglutinin and examine both previously characterized and novel variant strains observed in the human population that may give rise to antigenic escape. We find that in some cases the impact of a substitution is local, while in others it causes a reorientation of the antibody with wide-ranging impact on residue–residue interactions: this explains, in part, why the change in chemical properties of a residue can be, on its own, a poor predictor of overall change in binding energy. Our estimates are in good agreement with experimental results—indeed, they approximate the degree of agreement between different experimental techniques. Simulations were performed on commodity computer hardware; hence, this approach has the potential to be widely adopted by those undertaking infectious disease research. Novel aspects of this research include the application of MM/GBSA to investigate binding between broadly binding antibodies and a viral glycoprotein; the development of an approach for visualizing substrate–ligand interactions; and the use of experimental assay data to rescale our predictions, allowing us to make inferences about absolute, as well as relative, changes in binding energy.
Introduction
The identification and characterization of broadly neutralizing antibodies (bnAbs) to highly mutable pathogens such as HIV (1) and influenza (2, 3) has important consequences both for treatment and for vaccine development, but the structural understanding of antibody/antigen interactions is far from complete. An important area of focus is the impact on antibody binding of amino acid substitutions in the epitope—could mutation lead to escape?—or in the paratope—could binding be improved, without loss of breadth? Today, key residues are typically identified by means of alanine substitution assays, which determine ΔΔGbind, the change in the Gibbs free energy of binding caused by the substitution. These assays can be expensive and time consuming to conduct, particularly if the required antibody is not to hand, and can only provide a limited understanding of the contribution that individual residues make to the interaction. In particular, where exhaustive scans are conducted over the entire epitope, the sum of per-residue free-energy contributions inferred from alanine scanning is found to differ significantly from the wild-type (WT) free energy (4). Residues are therefore found to bind cooperatively, meaning that the contribution of individual residues is non-additive. Additionally, substitution assays cannot reliably identify the extent of intramolecular contacts. In particular, there are known examples of substitutions outside such contacts that significantly affect ΔΔGbind, and examples of contact residues that are not identified by alanine substitution (5). Thus, a crystal structure of the complex remains necessary.
In this report, we study the binding characteristics and sensitivity to mutations of three bnAbs to influenza for which structures and binding assays exist. We demonstrate that molecular dynamics (MD) and other computational techniques, running on widely available computer hardware, can be used to complement experimental results in order to gain a deeper insight into molecular interactions and can also predict the structural and chemical impact of substitutions.
Broadly neutralizing antibodies to influenza A hemagglutinin (HA), a surface glycoprotein implicated in host cell attachment, challenge the conventional wisdom that the B-cell response to influenza must always be governed by antigenic drift, and raise the possibility of broad-spectrum therapeutic treatment and of vaccines that could confer longer lasting protection (6). Such bnAbs were initially thought to be rare but have now been isolated in many studies. Examples exist that bind both to the HA globular head and to the stalk. The functional mechanism of stalk-binding bnAbs is largely through inhibition of cell membrane fusion, although other mechanisms such as antibody-dependent cell-mediated cytotoxicity may also play a part (7). While the stalk-binding antibodies characterized to date arise from several germlines, the VH1–69 germline is frequently found, and around 40 bnAbs arising from this germline have been described to date. Reported common features of these antibodies include binding through the heavy chain only; distinctive hydrophobic substitutions in HCDR2 and tyrosine(s) in HCDR3 (8).
In this study, we use MD simulations employing the energy method molecular mechanics with Generalized Born surface area (MM/GBSA) in combination with experimental results published previously by other groups. We examine three stalk-binding VH1–69 based bnAbs: CR6261, which neutralizes influenza A group 1 strains (3), CR9114, which neutralizes influenza A group 1 and group 2 strains as well as influenza B strains (9), and CR8020, which neutralizes group 2 strains only (10). We compare predictions obtained from MM/GBSA with experimental results, and with a computational service, ANCHOR, which was used in one of the experimental studies, and which, in the examples we study, is found to provide useful initial results for a small computational cost.
Molecular mechanics with Generalized Born surface area is an approximate method for inferring the change in Gibbs free energy, ΔG, caused by substrate/ligand binding (11). The method uses a thermodynamic cycle to infer the solvated free energy of association, which we shall refer to for brevity as ΔGbind. The inference is derived from calculations of the free energy of association in vacuum, ΔGbind,vac, and of the solvation energy ΔGsolv of the ligand, receptor, and complex, using the following equation:
The calculation averages results obtained from an ensemble of uncorrelated snapshots, collected from an MD simulation of the explicitly solvated complex and its components. ΔGsolv is determined by solving the linearized Generalized Born equation (to determine the electrostatic contribution) and by a term to account for enthalpic and entropic hydrophobic contributions: these contributions are typically taken to be linearly proportional to the solvent-exposed surface area and are calibrated with reference to experimentally determined hydration energies of small molecules. As Generalized Born is an implicit solvent model, solvent molecules are removed from the MD snapshot before the calculation of ΔGsolv is performed: this avoids the otherwise lengthy convergence times that would be required to smooth the fluctuations in solvent–solvent interactions. ΔGbind,vac can be expressed in terms of enthalpic and entropic contributions:
In this application, we adopt the commonly used approximation that, as the overall conformations of ligand and substrate are not substantially affected by the substitutions tested, the conformational entropy change caused by a substitution, ΔΔSbind,vac, is negligible. As we are principally interested in ΔΔG rather than ΔG, we do not calculate ΔSbind,vac. Our inferred values of ΔG will therefore not agree with experimentally determined values: however, within the limits of our approximation that ΔΔSbind,vac ≈ 0, determinations of ΔGbind may be compared in order to understand relative energies of interaction. ΔEbind,vac consists of the molecular mechanics contributions from bonded, electrostatic, and van der Waals interactions, determined from the receptor, ligand, and complex structures elicited from the MD simulation. Receptor, ligand, and complex structures may be determined from independent simulations, or, on the assumption that no significant conformational changes occur during binding, they may be extracted from a single trajectory of the complex. In our experience, the use of independent simulations greatly increases convergence times as frames from the separate simulations are not correlated: we therefore employ a single trajectory in this case.
We use MM/GBSA both to infer the overall value of ΔΔGbind for a given complex, and to determine the pairwise ΔΔGbind between individual residues in the epitope and paratope through a calculation known as energy decomposition. In this calculation, the binding free energy attributable to the interaction between a specific pair of residues is determined, from the Generalized Born equation, as the sum of the electrostatic and hydrophobic terms (the contribution to ΔΔGbind,vac from ΔΔSbind,vac, which we assume, as above, to be negligible, cannot be attributed to individual residue pairs and is not included in the calculation). Although it is subject to limits of error imposed by the approximations in the calculation, the determination of these pairwise energies allows an understanding of the interaction that is not available directly from experimental methods. ΔΔGbind predicted by MM/GBSA is typically found to be proportional to but not identical to experimentally determined ΔΔG, likely as a result of inconsistent energy functions in the explicit and implicit solvent terms underlying the MM/GBSA calculation (11–13). As some experimental assays are available for the complexes we study, we use these to rescale our predictions.
Molecular dynamics has provided valuable insights into the structural consequences of substitutions in Ab/influenza HA complexes (14, 15). Molecular mechanics with Poisson–Boltzmann surface area (MM/PBSA) and MM/GBSA have been used in at least one previous study to predict ΔΔGbind in an antibody/HA interaction that corresponded with experimental results (16). In this study, we develop novel interaction energy diagrams to facilitate such analysis and use MD in combination with MM/GBSA to develop insights into the binding characteristics of broad-spectrum stalk-binding antibodies by studying a range of substitutions and Abs. We examine and contrast several substitutions in the epitope and paratope, and we apply current best practice in MM/GBSA calculations by monitoring sample correlation and convergence of results. To our knowledge, this is the first comparative study of broadly binding antibodies to viral glycoprotein using MD.
Materials and Methods
Starting Structures
Starting structures, 3GBM (17), 4FQY (9), and 3SDY (10) (resolutions 2.7, 5.25, and 2.85 Å, respectively) were downloaded from the RCSA Protein Data Bank (18). Residues in antibody loops remote from the epitope for which no coordinates were reported were modeled with MODELLER (19). Protonation states consistent with physiological conditions were inferred by MolProbity (20). The trimeric biological construct was built in UCSF Chimera (21), using the author-defined biological unit, and the starting structure for simulation was created in AmberTools 15 tleap using the Amber ff12SB force field (22) and mbondi2 radius sets (23). Epitope substitutions were modeled in MODELLER using the single chain output by MolProbity, following which the same steps were taken to create the starting structure for simulation.
Explicit Solvent Simulations
For explicit solvent simulations, the structure was solvated in a truncated octahedral box using TIP3P water molecules. Na+ ions were added to neutralize the molecular charge. A minimum distance of 20 Å was enforced between the structure and the box boundary, leading to boxes of volume 6 × 106 Å3 containing a total of ~6 × 105 atoms. Simulations were conducted in Amber 14 using the GPU-based simulation engine (24–26).
Both the WT structure and structures with substitutions underwent an initial energy minimization stage at constant volume, consisting of 2,000 steps of the steepest descent method, followed by 2,000 steps of the conjugate gradient method. This was followed by two relaxation steps: 100 ps at constant volume with backbone atoms restrained by a force equivalent to 4.0 kcal/mol/Å during which the temperature was increased from 0 to 50 K using a Langevin thermostat; then 2000 ps at constant pressure using a Monte Carlo barostat and Langevin thermostat, with backbone atoms restrained by a force equivalent to 1.0 kcal/mol/Å. In this step, the temperature was increased from 50 to 310 K in the first 500 ps and then held at 310 K for the remainder.
Following the relaxation steps, the production run was conducted at constant pressure using a Monte Carlo barostat. The initial production step consisted of a 9 ns simulation and was followed by 20 independent simulations of 1 ns each. These simulations were started with position coordinates from the end of the initial 9 ns simulation, but randomized velocities, in order to de-correlate the output from successive samples (27). A short-range interaction cutoff distance of 8 Å was used throughout, and SHAKE was used to constrain hydrogens in all but the minimization step, allowing a 2 fs time step. iwrap was set to 1, wrapping atomic coordinates back into the primary box, in order to avoid coordinate overflow during the course of long simulations. Default values were used for other modeling parameters.
Snapshots were extracted from each of the 20 independent simulations for further calculations. To allow time for velocities to settle, the first snapshot was taken after 500 ps of simulation time. To minimize correlation between snapshots, subsequent snapshots were taken at times 100 ps apart, resulting in a total of five snapshots being extracted from each of the 20 simulations. The sampling interval of 100 ps was determined by examining the time required for the time-dependent autocorrelation function [as determined by the Python function numpy.correlate (28)] to reduce to 0, using MM/GBSA ΔG values obtained from more closely sampled snapshots (Figure 1A). The entire simulation of a structure (29 ns of simulation) took approximately 6 days on our Nvidia Titan/X GPU hardware.
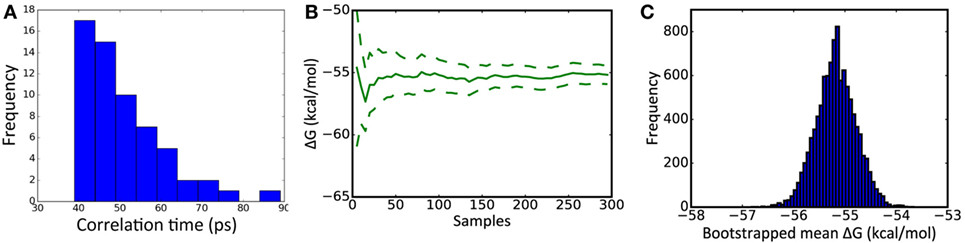
Figure 1. Key metrics underlying molecular mechanics with Generalized Born surface area (MM/GBSA) calculations. (A) Distribution of the correlation time of MM/GBSA ΔG energy estimates, calculated from 20 1 ns simulations yielding 60 snapshots. (B) Example cumulative estimate of ΔG as the number of samples is increased [dotted lines represent 95% confidence limits (see Analysis of MM/GBSA Calculations)]. (C) Example distribution of a mean ΔG obtained from 10,000 samplings of the underlying dataset. (B,C) are taken from the analysis of substitution CR8020 D19N.
Coordinate Analysis
Analysis of simulation coordinates was performed using cpptraj from Amber Tools 15. The 100 snapshots were analyzed for atomic contacts between HA1/HA2 and the Ab variable regions with a distance cutoff of 3.9 Å, sufficient for the identification of hydrogen bonds and other hydrophobic contacts. All corresponding residues were added to the list of potential contact residues regardless of the number of snapshots in which the contact was observed. The approach taken here is inclusive of the molecular conformations observed during the simulation. Hydrogen bonds were inferred between hydrogen atoms bonded to nitrogen or oxygen atoms, where the donor and acceptor heavy atoms concerned were less than 3.35 Å apart, and the acceptor-hydrogen-donor angle is greater than 135°. The hydrogen bond analysis was run over the same set of snapshots as for contact residues.
MM/GBSA Calculations
Energy calculations were conducted using MMPBSA.py from Amber Tools 15 (29). In accordance with typical practice (27), configurations in the bound and unbound states were assumed to be similar, and based on this assumption, unsolvated topology files for the bound and unbound species were prepared from the explicit solvent topology using ante-MMPBSA.py. The antibody bound to each monomer was treated independently, meaning that the set of 100 snapshots resulted in a total of 300 samples for implicit solvent simulations. These simulations were run in Amber 14’s sander under the control of MMPBSA.py using the Generalized Born model with igb = 2 (23). In this model, the non-polar contribution to ΔG is calculated as 0.005 kcal/mol for each 1 Å2 of solvent-accessible surface area. Salt concentration was set to 0.2 M, and other parameters followed Amber’s defaults. Pairwise free-energy decompositions (idecomp = 3) were obtained for all potential contact residues identified in the coordinate analysis. MM/GBSA analysis of a structure took approximately 6 h on a 20-core 2.5 GHz Intel Xeon E5-based server.
Analysis of MM/GBSA Calculations
The 100 ΔGbind values obtained for each of the three antibodies bound to the trimer were obtained via MMPBSA.py’s Python API and interleaved to form a single set of 300 results. Convergence was assessed by plotting the mean value obtained after from 10, 20, …, 300 results (Figure 1B). To form an unbiased estimate of the confidence limits, the resulting dataset was resampled 10,000 times: the confidence limits represent the range covered by 95% of the resulting means (Figure 1C).
As noted in the introduction, ΔΔGbind predicted by MM/GBSA is typically found to be proportional to but not identical to experimentally determined ΔΔG. Predicted values from each simulation were therefore plotted against experimental values (Figure S1 in Supplementary Material). The slopes of the lines were used to rescale the predictions.
ANCHOR Calculations
Structure files were uploaded to the ANCHOR server at http://structure.pitt.edu/anchor. For Ab heavy/light chain residue predictions, Protein 1 was set to the Ab chain, and Protein 2 to each of the two cognate HA chains in turn: the results were then summed. For HA residue predictions of CR9114 and CR6261, Protein 1 was set to either HA1 or HA2, and Protein 2 to the Ab heavy chain. For CR8020, results for both Ab chains were summed.
Influenza Sequence Variation
The sequence variation (SNP) module of the Influenza Research Database (30) was used to identify the variation of human HA subtypes H1, H3, and H5 (approximately 18,000, 13,000, and 450 strains, respectively) at key contact locations identified in this study. Precise numbers of strains compared varied from residue location to location depending on the extent of available sequences.
Software
The software underlying our methods is publicly available at https://github.com/williamdlees/AmberUtils (doi: 10.5281/zenodo.159170). The software streamlines the handling of substitutions; performs convergence limit calculations; and produces interaction diagrams as used in this report.
Results
Epitope and Paratope Determination
Epitopes and paratopes were inferred from contact residues (Figure 2). The epitopes of CR6261 and CR9114 cover similar regions, although that of CR6261 includes an additional region at the C- and N-termini of HA1. This region includes HA1 38, glycosylated in group 2 strains, which may account for its omission from the CR9114 epitope (9). Interactions with HA1 residues play a stronger part in the CR6261 complex than that of CR9114, with HA1 S291 forming a strong hydrogen bond to HFR3 D72 (predicted ΔGbind = −2.7 kcal/mol). In the CR9114 complex, interactions with the three tyrosines at CDR3 98–100 A provide stronger bonds to the N-terminus of HA2 than the single Y98 in CR6261. CR8020 binds closer to the viral membrane than the other two Abs. The HFR3 loop of CR8020 is not in contact with the antigen, but contacts are found in LCDR2 as well as the three HCDRs.
Figure 2. Averaged interactions between contact residues. Inferred hydrogen bonds are in red, other interactions in black. Line thickness is proportional to interaction energy. HA1 residues are indicated by *. Residue coloring reflects hydrophobicity at pH 7: red (pink) highly (slightly) hydrophobic, green neutral, blue hydrophilic. To ensure significance, and bearing in mind the overall confidence limits, only interactions with ΔG ≤ −1.0 kcal/mol are shown, and residues with no such interactions are omitted. All CDRs are in the heavy chain, except for LCDR2 in the CR8020 interface, which is explicitly marked.
In CR6261 and CR9114, MM/GBSA calculations predict binding energy in the paratope to be evenly spread between four regions of contact: the three HCDRs, and a loop in HFR3 with the tip at locations 72–75 (Table 1). In the epitopes, residues in Helix A account for ~50% of the predicted binding energy: other regions in HA2 account for a further 30%, and ~20% is accounted for by residues in HA1 at the membrane-distal end of the globular head. In CR8020, predicted binding energy is less evenly spread between the CDRs than in the other two complexes, with HCDR1 and HCDR3 accounting for 80% of the binding energy between them. In the epitope, approximately 50% of the predicted binding energy is accounted for by HA2 residues in a β-strand running between the membrane interface and Helix A.
Table 1. Percentage of the total Ab/epitope interaction energy attributable to the individual regions identified in the text.
Comparison of Predicted ΔΔGbind with Experimental Results
In addition to WT assays, we selected seven published assays in which substitutions were applied to the Ab or the epitope (Table 2). These were taken from three different studies: Avnir et al. (8) used the ANCHOR server to predict key residues in the CR6261 HCDRs before verifying results experimentally; Ekiert et al. (10) grew the virus in culture with CR8020 to generate escape mutants, while Dreyfus et al. (9) undertook an extensive panel of substitution assays to examine the impact of variants seen in the wild. In reaching this total of seven substitutions, for reasons of economy and to obtain a spread of results, we excluded a further nine assays of CR9114/H3N2 substitutions from Dreyfus et al. where ΔΔGbind was determined to be <1 kcal/mol, below the 95% confidence limits obtained in this study. We included one substitution, which was assayed in an H2 strain. Using MM/GBSA, we predicted ΔGbind for each substitution, and hence ΔΔGbind by comparing with the WT result. Experimental and predicted results are reasonably correlated (Table 2; Figure 3; Figure S1 in Supplementary Material). Error bars reflect the confidence limits in the MM/GBSA calculation, but do not reflect other sources of error such as those introduced by the approximations in our approach and underlying inaccuracies in the force fields. The mean difference between predicted and experimental ΔΔGbind was 0.6 kcal/mol, σ = 0.4 kcal/mol, hence in this application, we find that the technique can predict ΔΔGbind within approximately 1 kcal/mol.
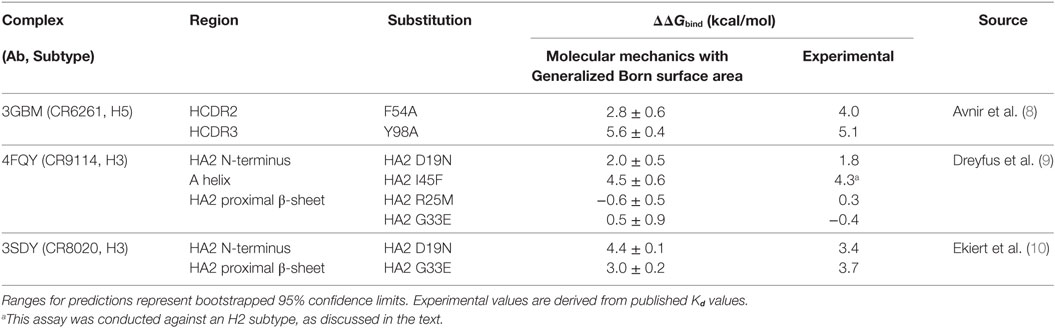
Table 2. Predictions of ΔΔGbind (relative to WT) for substitutions for which experimental values were found.
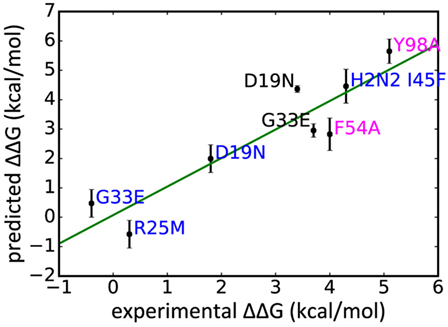
Figure 3. Experimentally derived ΔΔGbind for a range of substitutions compared with rescaled values predicted in this study, legend colored by Ab: CR9114 blue, CR6261 magenta, CR8020 black.
For the alanine substitutions in the CR6261 HCDRs, ΔΔGbind largely reflects subtraction of the substituted side chain (Figure 4), although compensatory changes to the structure mitigate the overall reduction in binding energy. In some other cases, substitutions with a further reaching impact were observed: in the case of the HA2 substitution D19N in the CR9114 complex, the simulation suggests a change in orientation of the Ab with respect to HA2 Helix A, causing a ripple of stronger and weaker interactions across the interface (Figure 5; Table S2 in Supplementary Material). An equally dispersed reaction was observed in the CR8020 complex with the substitution G33E. Here, a larger side chain is inserted into a congested region of the interface between the proximal region of HA2 and HCDR3. Changes to binding energies and residue distances in the region of the substitution itself were below the limits of error, but, in the MD simulation, the insertion is found to cause a realignment of the Ab that causes distances to other cognate CDRs to increase (Table 3), and this realignment is reflected in predicted pairwise ΔΔGbind (Figure 4).
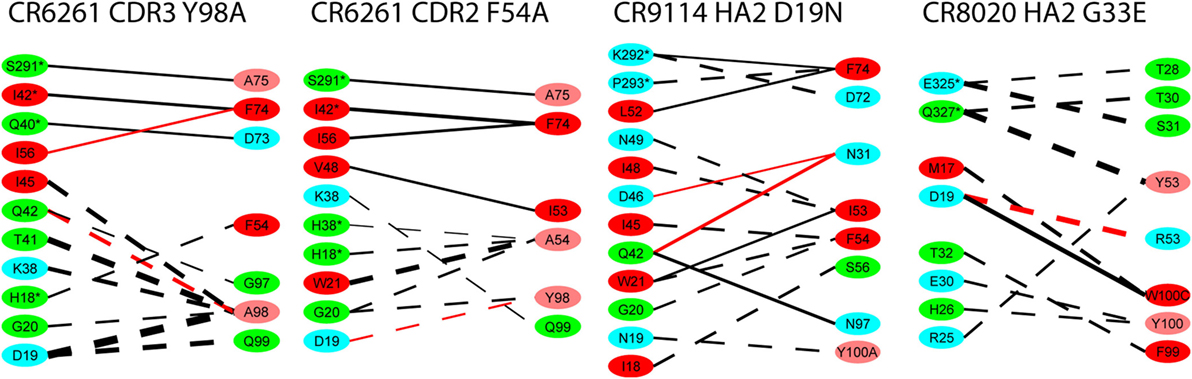
Figure 4. Interaction energy differences for selected substitutions. Layout and coloring are the same as for Figure 2, but here the thickness of the line represents the difference in interaction energy relative to the wild type. Dotted lines represent weaker interaction (reduced absolute ΔΔG) and solid lines represent stronger interaction. Only differences with an absolute value ≥1.0 kcal/mol are shown.
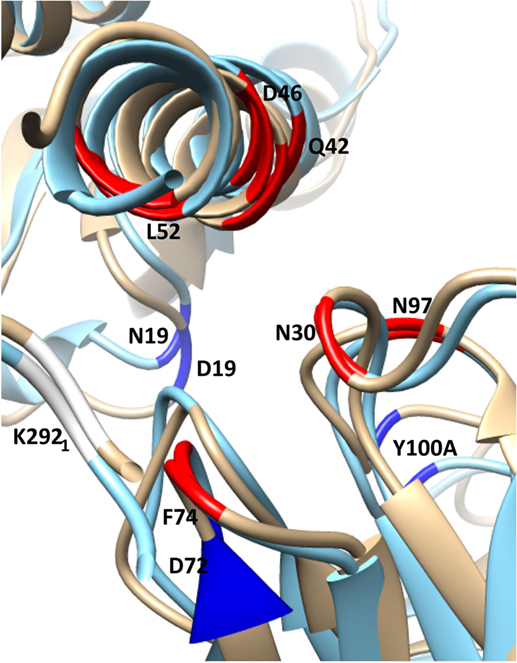
Figure 5. Selected residues with significant ΔΔGbind in the substitution D19N in the CR9114/H3N2 complex (wild-type chains are in gold, superposed with the substituted complex in blue). HA chains are in the top-left corner, Ab chains bottom-right. The structure is viewed along the axis of Helix A, looking toward the viral membrane. The locations of selected residues with stronger interaction in the presence of the substitution are shown in highlighted in red, weaker in dark blue. The weaker interaction between HA2 N19 and CDR3 Y100A allows the antibody’s orientation to shift anticlockwise along the Helix A axis, bringing CDR residues N30, N31, and N97 into closer contact with Helix A residues D46 and Q42. Furthermore, membrane-proximal Ab residues move away from Helix A, while membrane-distal residues move toward it. This latter adjustment weakens the interaction between HA1 K292 and FR3 D72, while strengthening interactions between FR3 F74 and HA1 K292, HA2 L 52.
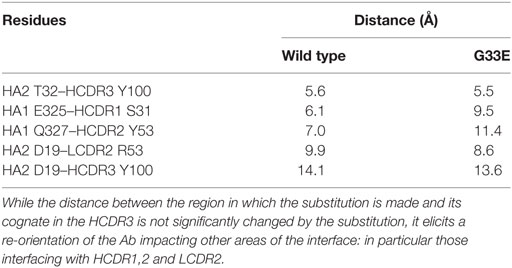
Table 3. Distances between CA atoms of selected residues, averaged over the final 2 ns of the initial production simulation of the CR8020 complex, with and without the substitution G33E.
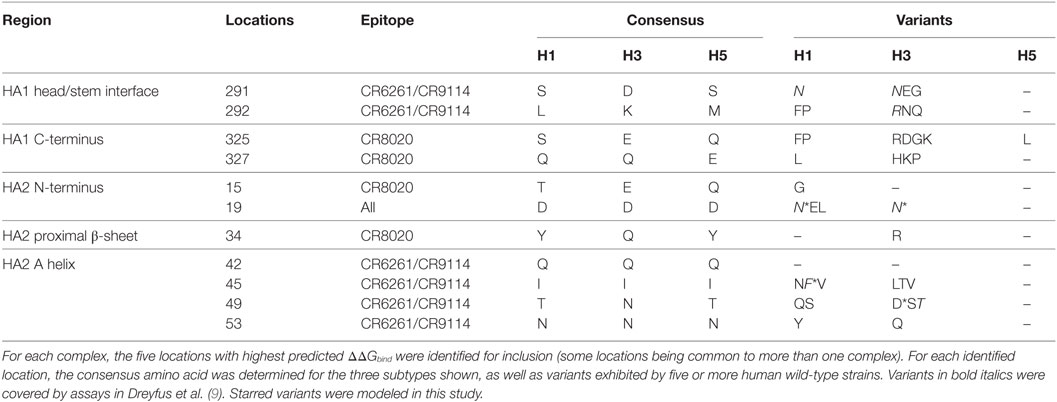
Variability of Key Residues in the HA Stalk
We used MM/GBSA analysis to assess substitutions observed in WT strains that we considered likely to have significant impact on ΔGbind. In key epitope locations identified from pairwise free-energy decompositions, we looked for variants found in at least five sequences deposited at http://fludb.org (Table 4), using the threshold of five as a protection against inaccurate sequencing calls or transcription errors. Notably, we found that HA2 F45 was present in 63 H1 sequences, while HA2 N19 was present in 5 H3 sequences (Table S1 in Supplementary Material). The impact of F45 and N19 on CR9114 binding has been addressed experimentally and by our work above. In addition to the simulations previously described, we simulated the impact of three novel substitutions for which assays have not previously been described: HA2 N49D in the CR9114/H3 complex; HA2 I45F in CR6261/H5; and E325R in CR8020/H3. The predicted ΔΔGbind associated with these three substitutions is comparable to that of experimentally determined escape mutants (Table 5).
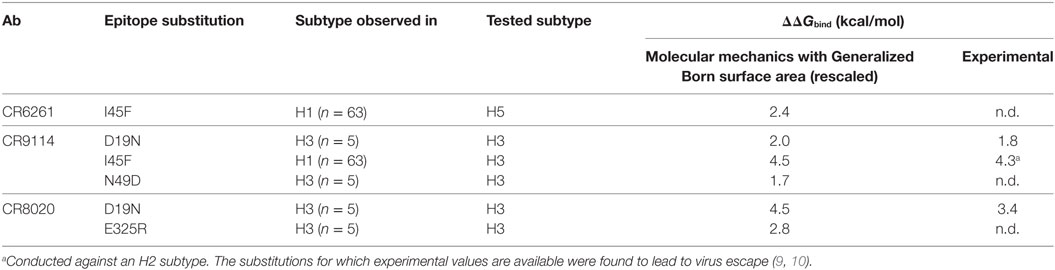
Table 5. Substitutions observed in wild-type strains that are predicted from assay and/or calculation to result in significant loss of binding energy.
Correspondence with ANCHOR Predictions
The ANCHOR server at http://structure.pitt.edu/anchor/ provides rapid computational estimates of residue contact free energies, using a combination of Coulombic electrostatic potential and a desolvation term based on interatomic contacts, derived empirically from analysis of protein structures (31). As mentioned previously, Avnir et al. (8) used ANCHOR to identify highly favorable contacts in antibody structures for further examination. We find general correspondence between MM/GBSA and ANCHOR in identifying such contacts (Figure 6), although some highly favorable contacts identified by MM/GBSA are not identified by ANCHOR: in particular, CR6261 CDR3 Y98 is predicted by ANCHOR to be have a lower contact free energy than CDR2 F54 (−2.0 and −3.0 kcal/mol, respectively) although in experimental assays Y98A reduced binding significantly more than F54A (ΔΔGbind −5.1 and −4.0 kcal/mol). In the CR8020 complex, ANCHOR does not predict any highly favorable contacts and predicts a contact free energy >−1 kcal/mol for S31 and Y100, which are predicted by MM/GBSA as highly favorable.
Figure 6. Comparison of predictions of residue contact free energies from molecular mechanics with Generalized Born surface area (MM/GBSA) with those of ANCHOR. Following Avnir et al. (8), Anchor predictions ≤−1 kcal/mol and >−3 kcal/mol are shaded amber, those ≤−3 kcal/mol are shaded red. For MM/GBSA, thresholds of −2 and −5 kcal/mol are used for the CR6261 and CR9114 complexes, and −5 and −10 kcal/mol for CR8020: these were found to provide the best correspondence between the two sets of results.
Discussion
It is now possible to conduct MD simulations of large protein structures on widely available computer hardware, allowing the combinatorial complexity inherent in the study of broad-binding Abs to highly mutable proteins to be explored more widely than would be feasible through experimental techniques alone. Computational techniques can also cast light on the pairwise interactions between residues, which cannot be directly inferred from experimental results. In the experimental work, we cite one study that used surface plasmon resonance (8), while two used biolayer interferometry (9, 10). We have shown that the MM/GBSA analysis can provide predictions of ΔΔGbind for antibodies in complex with influenza HA that are in good agreement with experimental results, and which approximate the accuracy with which biolayer interferometry can match results from surface plasmon resonance assays (32). We have used the technique to identify and explore substitutions of interest for which assay results are not available. The crystal structure of the CR9114 complex had a low resolution (5.7 Å), nevertheless we obtained comparable results: hence, although a structure is required for MM/GBSA analysis, it may in some cases be possible to work with structures of low resolution. The extended MD simulation may have served to refine the structure: alternatively, the low reported resolution may be attributable to flexible regions remote from the interface, such as the unbound light chain.
Molecular mechanics with Generalized Born surface area and MM/PBSA calculations embody approximations over and above those inherent in the MD force field, and they have been found more suited for some applications than for others. Several factors, both in the specific method employed and in its application, may contribute to success in this case. In terms of the method, we monitor convergence and minimize convergence times using independent short simulations. We rescale the predicted energy values to take account of force field inconsistencies inherent in MM/GBSA, using experimentally derived assay values. In terms of the application, the receptor and ligand in this system are large molecules with relatively stable backbone structures, supporting the assumptions that changes in conformational entropy will not be significant and that the system can be appropriately modeled with a single set of simulations rather than with separate simulations for the complex, the receptor and the ligand. Both complex and ligand are pure proteins, meaning that non-protein force fields (which are often not so well developed) are not required. Finally, we simulate single substitutions. Single substitutions are often examined in studies of bnAbs and can provide valuable insights into antibody development and the likelihood of escape; however, benchmarks of energy methods tend to focus on larger-scale substitutions.
The assumption that changes in conformational entropy are negligible remains problematic and may ultimately limit application of the technique. It is helpful in obtaining convergence as the entropy terms in MM/PBSA and MM/GBSA typically have the highest statistical uncertainty (11), but binding enthalpies typically do not correlate well with binding free energies, and the circumstances in which they do are not well understood (33). Changes in entropy can be difficult to determine experimentally, and the significance of entropy/enthalpy compensation is debated (34). Alchemical techniques (35), which maintain explicit solvation throughout and do not require explicit calculation of entropic terms, may ultimately supersede MM/PBSA and MM/GBSA. They are not widely supported on the GPU today, although support in Amber in a forthcoming release has been announced. In current implementations, they do not to our knowledge support per-residue energy decomposition.
In this study, we have not found it necessary to consider the free-energy contribution from ordered water in the interface, which has proved important in some small molecule calculations (11). However, the relatively planar nature of epitopes (36) may make the treatment of explicit water less important than it can be with the more strongly defined cavities typical in such interactions. In identifying contact residues, we have considered hydrogen bonds and other hydrophobic contacts. Longer-range interactions, such as caton–pi interactions, have been identified in some antibody/antigen complexes (37); however, with MM/GBSA, we did not find significant pairwise ΔΔGbind predicted between more distant residues in the complexes studied here.
Having identified key residues in the epitope with MM/GBSA, we were able to identify novel viral mutations observed in the field, that, based on a combination of experimental result and computational prediction, are predicted to lead to the escape of group 1 and group 2 strains from fusogenic inhibition by the bnAbs. We suggest that, when considering the breadth of a bnAb, low-frequency variants should be considered. Of the variants considered in this study, H1 D19N, I45F, and H3 D19N were isolated in multiple geographic locations and across multiple influenza seasons, while H3 N49D strains were isolated from five patients in New York over the course of a single season and H3 E325R was isolated in five patients located in three different cities in Japan over the course of a single season. The diversity of origin, coupled with, in all but one variant, its isolation from multiple subjects in the same city during a single season, suggests that the substitution is viable and hence may have potential to become dominant if there is sufficient antigenic pressure from natural or vaccine-induced Abs (38, 39). Given the potential number of such variants, computational methods such as those presented here may be needed to support such an analysis. Likewise, when assessing vaccine response, to minimize the chances of escape, the depth (i.e., the number of elicited antibodies associated with distinct epitopes or binding patterns) should be considered as well as the breadth.
While in many cases the impact of an epitope or paratope substitution may be relatively local and isolated in effect, in other cases, such as CR9114 HA2 D19N and CR8020 G33E, it can have widespread effects that would be difficult to predict from a list of key residues or understand from a substitution assay result on its own. bnAbs appear to rely less on founder or “anchor” residues than more targeted Abs, having greater evenness of contribution across CDR locations (40). In the case of the structures studied here, particularly CR6261 and CR9114, we can see such evenness of coverage in both the paratope and the epitope. As evenness of coverage increases, so does the likelihood of substitutions having complex, non-local impacts. Likewise, while the overall likelihood of escape may be minimized, the chances of a substitution in the epitope having a significant, albeit non-escaping, impact may increase. For these reasons, a thorough analysis of a broad-spectrum Ab is likely to be more demanding than that of a more highly targeted Ab, and predictions made on the basis of chemical properties or straightforward inferences of critical residues may not be reliable. While the HA stalk experiences substantially less variation than the globular head, the notion that it is “highly conserved” is based on an analysis of chemical similarity between residues (10, 17) and should not be taken to imply sequence or structural invariance.
Next-generation sequencing is allowing us to trace with detail the development of highly variable viruses and the antibodies that bind to them. There are no equivalently scalable approaches for determining antigenic development. Improvements in computer hardware and software make MD a credible tool to help bridge that gap. While MM/GBSA may over time be replaced by more self-consistent approaches, this study suggests that it can play a valuable role in binding studies today.
ANCHOR has been identified by other researchers as a tool that can identify key residues in an antigen/antibody complex, and in this work, we find reasonable overall correspondence between key residues identified by ANCHOR and those identified by MM/GBSA. Given that ANCHOR calculations on the two complexes ran in under a minute, the results are impressive, although some highly favorable contacts were not identified. More recent high-speed methods have employed multiscale methods to limit conformational sampling to the region in which a substitution occurs (41). Dourado and Flores (42), for example, restrict conformational sampling to the regions within 12 Å of a substitution. Our results suggest that, in the case of antibody interactions, better results might be obtained by extending sampling to cover the entire span of an epitope, which can exceed 45 Å (36).
Author Contributions
WL, DM, and AS codesigned the project. WL designed and performed simulations; wrote the manuscript. WL and LS analyzed and interpreted data. WL, LS, DM, and AS reviewed and edited the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Maya Topf and Mark Williams for their kind provision of additional computer resources.
Funding
This work was supported by the Wellcome Trust (grant 109162/Z/15/Z to LS).
Supplementary Material
The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fimmu.2017.00143/full#supplementary-material.
References
1. Scheid JF, Mouquet H, Feldhahn N, Seaman MS, Velinzon K, Pietzsch J, et al. Broad diversity of neutralizing antibodies isolated from memory B cells in HIV-infected individuals. Nature (2009) 458:636–40. doi:10.1038/nature07930
2. Okuno Y, Isegawa Y, Sasao F, Ueda S. A common neutralizing epitope conserved between the hemagglutinins of influenza A virus H1 and H2 strains. J Virol (1993) 67:2552–8.
3. Throsby M, van den Brink E, Jongeneelen M, Poon LLM, Alard P, Cornelissen L, et al. Heterosubtypic neutralizing monoclonal antibodies cross-protective against H5N1 and H1N1 recovered from human IgM+ memory B cells. PLoS One (2008) 3:e3942. doi:10.1371/journal.pone.0003942
4. di Cera E. Site-specific analysis of mutational effects in proteins. Adv Protein Chem (1998) 51:59–119. doi:10.1016/S0065-3233(08)60651-8
5. Greenspan NS, di Cera E. Defining epitopes: it’s not as easy as it seems. Nat Biotechnol (1999) 17:936–7. doi:10.1038/13590
6. Krammer F. Novel universal influenza virus vaccine approaches. Curr Opin Virol (2016) 17:95–103. doi:10.1016/j.coviro.2016.02.002
7. Krammer F, Palese P. Advances in the development of influenza virus vaccines. Nat Rev Drug Discov (2015) 14:167–82. doi:10.1038/nrd4529
8. Avnir Y, Tallarico AS, Zhu Q, Bennett AS, Connelly G, Sheehan J, et al. Molecular signatures of hemagglutinin stem-directed heterosubtypic human neutralizing antibodies against influenza A viruses. PLoS Pathog (2014) 10:e1004103. doi:10.1371/journal.ppat.1004103
9. Dreyfus C, Laursen NS, Kwaks T, Zuijdgeest D, Khayat R, Ekiert DC, et al. Highly conserved protective epitopes on influenza B viruses. Science (2012) 337(6100):1343–8. doi:10.1126/science.1222908
10. Ekiert DC, Friesen RHE, Bhabha G, Kwaks T, Jongeneelen M, Yu W, et al. A highly conserved neutralizing epitope on group 2 influenza A viruses. Science (2011) 333:843–50. doi:10.1126/science.1204839
11. Genheden S, Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin Drug Discov (2015) 10:449–61. doi:10.1517/17460441.2015.1032936
12. Wan S, Knapp B, Wright DW, Deane CM, Coveney PV. Rapid, precise, and reproducible prediction of peptide-MHC binding affinities from molecular dynamics that correlate well with experiment. J Chem Theory Comput (2015) 11:3346–56. doi:10.1021/acs.jctc.5b00179
13. Hou T, Wang J, Li Y, Wang W. Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations. J Chem Inf Model (2011) 51:69–82. doi:10.1021/ci100275a
14. Zhou R, Das P, Royyuru A. Single mutation induced H3N2 hemagglutinin antibody neutralization: a free energy perturbation study. J Phys Chem B (2008) 112(49):15813–20. doi:10.1021/jp805529z
15. Xia Z, Huynh T, Kang S-G, Zhou R. Free-energy simulations reveal that both hydrophobic and polar interactions are important for influenza hemagglutinin antibody binding. Biophys J (2012) 102:1453–61. doi:10.1016/j.bpj.2012.01.043
16. Leong P, Amaro RE, Li WW. Molecular dynamics analysis of antibody recognition and escape by human H1N1 influenza hemagglutinin. Biophys J (2015) 108:2704–12. doi:10.1016/j.bpj.2015.04.025
17. Ekiert DC, Bhabha G, Elsliger M-A, Friesen RHE, Jongeneelen M, Throsby M, et al. Antibody recognition of a highly conserved influenza virus epitope. Science (2009) 324:246–51. doi:10.1126/science.1171491
18. Berman HM, Battistuz T, Bhat TN, Bluhm WF, Bourne PE, Burkhardt K, et al. The protein data bank. Acta Crystallogr D Biol Crystallogr (2002) 58:899–907. doi:10.1107/S0907444902003451
19. Webb B, Sali A. Comparative protein structure modeling using MODELLER. Curr Protoc Bioinformatics (2014) 47:5.6.1–32. doi:10.1002/0471250953.bi0506s47
20. Chen VB, Arendall WB, Headd JJ, Keedy DA, Immormino RM, Kapral GJ, et al. MolProbity: all-atom structure validation for macromolecular crystallography. Acta Crystallogr D Biol Crystallogr (2010) 66:12–21. doi:10.1107/S0907444909042073
21. Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, et al. UCSF chimera – a visualization system for exploratory research and analysis. J Comput Chem (2004) 25:1605–12. doi:10.1002/jcc.20084
22. Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE, Simmerling C. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J Chem Theory Comput (2015) 11:3696–713. doi:10.1021/acs.jctc.5b00255
23. Onufriev A, Bashford D, Case DA. Exploring protein native states and large-scale conformational changes with a modified Generalized Born model. Proteins (2004) 55:383–94. doi:10.1002/prot.20033
24. Götz AW, Williamson MJ, Xu D, Poole D, Le Grand S, Walker RC. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. Generalized Born. J Chem Theory Comput (2012) 8:1542–55. doi:10.1021/ct200909j
25. Le Grand S, Götz AW, Walker RC. SPFP: speed without compromise – a mixed precision model for GPU accelerated molecular dynamics simulations. Comput Phys Commun (2013) 184:374–80. doi:10.1016/j.cpc.2012.09.022
26. Salomon-Ferrer R, Götz AW, Poole D, Le Grand S, Walker RC. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh Ewald. J Chem Theory Comput (2013) 9:3878–88. doi:10.1021/ct400314y
27. Genheden S, Ryde U. How to obtain statistically converged MM/GBSA results. J Comput Chem (2010) 31:837–46. doi:10.1002/jcc.21366
28. van der Walt S, Colbert SC, Varoquaux G. The NumPy array: a structure for efficient numerical computation. Comput Sci Eng (2011) 13:22–30. doi:10.1109/MCSE.2011.37
29. Miller BR, McGee TD, Swails JM, Homeyer N, Gohlke H, Roitberg AE. MMPBSA.py: an efficient program for end-state free energy calculations. J Chem Theory Comput (2012) 8:3314–21. doi:10.1021/ct300418h
30. Squires RB, Noronha J, Hunt V, García-Sastre A, Macken C, Baumgarth N, et al. Influenza research database: an integrated bioinformatics resource for influenza research and surveillance. Influenza Other Respir Viruses (2012) 6(6):404–16. doi:10.1111/j.1750-2659.2011.00331.x
31. Camacho CJ, Zhang C. FastContact: rapid estimate of contact and binding free energies. Bioinformatics (2005) 21:2534–6. doi:10.1093/bioinformatics/bti322
32. Abdiche Y, Malashock D, Pinkerton A, Pons J. Determining kinetics and affinities of protein interactions using a parallel real-time label-free biosensor, the Octet. Anal Biochem (2008) 377:209–17. doi:10.1016/j.ab.2008.03.035
33. Reynolds CH, Holloway MK. Thermodynamics of ligand binding and efficiency. ACS Med Chem Lett (2011) 2:433–7. doi:10.1021/ml200010k
34. Chodera JD, Mobley DL. Entropy-enthalpy compensation: role and ramifications in biomolecular ligand recognition and design. Annu Rev Biophys (2013) 42:121–42. doi:10.1146/annurev-biophys-083012-130318
35. Shirts MR, Mobley DL, Chodera JD. Chapter 4: Alchemical free energy calculations: ready for prime time? In: Spellmeyer DC, Wheeler R, editors. Annual Reports in Computational Chemistry. Elsevier (2013). p. 41–59. Available from: http://www.sciencedirect.com/science/article/pii/S1574140007030046
36. Rubinstein ND, Mayrose I, Halperin D, Yekutieli D, Gershoni JM, Pupko T. Computational characterization of B-cell epitopes. Mol Immunol (2008) 45:3477–89. doi:10.1016/j.molimm.2007.10.016
37. Chen SW, Van Regenmortel MHV, Pellequer J-L. Structure-activity relationships in peptide-antibody complexes: implications for epitope prediction and development of synthetic peptide vaccines. Curr Med Chem (2009) 16:953–64. doi:10.2174/092986709787581914
38. Lees WD, Moss DS, Shepherd AJ. Evolution in the influenza A H3 stalk – a challenge for broad-spectrum vaccines? J Gen Virol (2014) 95:317–24. doi:10.1099/vir.0.059410-0
39. Tharakaraman K, Subramanian V, Cain D, Sasisekharan V, Sasisekharan R. Broadly neutralizing influenza hemagglutinin stem-specific antibody CR8020 targets residues that are prone to escape due to host selection pressure. Cell Host Microbe (2014) 15:644–51. doi:10.1016/j.chom.2014.04.009
40. Pappas L, Foglierini M, Piccoli L, Kallewaard NL, Turrini F, Silacci C, et al. Rapid development of broadly influenza neutralizing antibodies through redundant mutations. Nature (2014) 516(7531):418–22. doi:10.1038/nature13764
41. Flores SC, Bernauer J, Shin S, Zhou R, Huang X. Multiscale modeling of macromolecular biosystems. Brief Bioinform (2012) 13:395–405. doi:10.1093/bib/bbr077
Keywords: influenza, hemagglutinin, broad-spectrum antibodies, molecular dynamics, MM/GBSA
Citation: Lees WD, Stejskal L, Moss DS and Shepherd AJ (2017) Investigating Substitutions in Antibody–Antigen Complexes Using Molecular Dynamics: A Case Study with Broad-spectrum, Influenza A Antibodies. Front. Immunol. 8:143. doi: 10.3389/fimmu.2017.00143
Received: 02 December 2016; Accepted: 30 January 2017;
Published: 15 February 2017
Edited by:
Marc H. V. Van Regenmortel, Centre national de la recherche scientifique (CNRS), FranceReviewed by:
Jean-Luc Pellequer, Alternative Energies and Atomic Energy Commission, FranceNeil S. Greenspan, Case Western Reserve University, USA
Copyright: © 2017 Lees, Stejskal, Moss and Shepherd. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adrian J. Shepherd, YS5zaGVwaGVyZEBtYWlsLmNyeXN0LmJiay5hYy51aw==
 William D. Lees
William D. Lees Lenka Stejskal
Lenka Stejskal David S. Moss
David S. Moss Adrian J. Shepherd
Adrian J. Shepherd