Fishermen Follow Fine-Scale Physical Ocean Features for Finance

The seascapes on which many millions of people make their living and secure food have complex and dynamic spatial features—the figurative hills and valleys—that influence where and how people work at sea. Here, we quantify the physical mosaic of the surface ocean by identifying Lagrangian Coherent Structures for a whole seascape—the U.S. California Current Large Marine Ecosystem—and assess their impact on the spatial distribution of fishing. We observe that there is a mixed response: some fisheries track these physical features, and others avoid them. These spatial behaviors map to economic impacts, in particular we find that tuna fishermen can expect to make three times more revenue per trip if fishing occurs on strong Lagrangian Coherent Structures. However, we find no relationship for salmon and pink shrimp fishing trips. These results highlight a connection between the biophysical state of the oceans, the spatial patterns of human activity, and ultimately the economic welfare of coastal communities.

Introduction

When quantifying the dynamics of coupled natural-human systems it is vital to consider the ways in which human activity occurs and where it is focused (Levin et al., 2013). For example, the spatial distribution of agriculture, urban expansion, and maritime shipping have respectively affected fire regimes in African savannas (Archibald et al., 2012), whole terrestrial food-webs (Faeth et al., 2005), and large-scale patterns of phytoplankton diversity (Hallegraeff, 1998). So too in fisheries, where the spatial distribution of fishing effort is both fundamental to the organization of marine food-webs (Essington et al., 2006) and to our calculations of sustainable fisheries production (Murawski et al., 2005). Indeed, almost all fisheries management actions are designed to influence the (spatial) behavior of fishermen (Branch et al., 2006; Hilborn, 2007), yet the issue of where they decide to fish and why, remains a key obstacle to achieving sustainable fisheries (Fulton et al., 2011; Hobday et al., 2011). This uncertainty is not for want of effort. Many disciplines have examined fishing location choice, from economics (Gordon, 1954; Holland and Sutinen, 2000) to anthropology (Orbach, 1977) to ecology (Hilborn and Ledbetter, 1979). From this work it is clear that fishermen behavior is at least partially explained by a desire to maximize individual well-being (via profits), but that this consideration alone is not the whole story. In the absence of a full understanding of the factors driving fishermen's spatial behavior, their actions will continue to surprise fisheries managers, potentially undermining management systems and jeopardizing the sustainability of fisheries (Fulton et al., 2011).

The choice of where to fish is in part determined by gradients in ocean properties such as temperature, salinity, and pollution, that persist over timescales equivalent to or greater than those of a fishing trip (Lehodey et al., 1997). These often sharp gradients are created by fronts of various kinds, including buoyancy currents, tidal mixing, shelf-slope/shelf-break flow, upwelling and boundary currents, and marginal ice zone fronts. Most fronts are characterized by a surface convergence, which contributes to the aggregation of nutrients and increases in primary production (Kahru et al., 2012). As a consequence, ocean fronts collectively define a dynamic mosaic of transient micro-habitats that numerous organisms use (MacKenzie et al., 2004), and are known to be “hot spots" of marine life (Bost et al., 2009; Godø et al., 2012; Scales et al., 2014; Woodson and Litvin, 2015). Fronts are observable in satellite derived maps of sea surface temperature, primary production and ocean color. However, cloud cover, flow discontinuities and noise, and low spatial resolution of satellite data present challenges for identifying the location of fronts (Ullman and Cornillon, 2000). To overcome these challenges, recent work has focused on the spatiotemporal extent of fronts identified by Lagrangian Coherent Structures (LCSs; frontal areas of convergence in the surface ocean, see Figure 1 and Supplementary Movie; Harrison and Glatzmaier, 2012). These are areas of attraction and repulsion, typically calculated for the surface ocean, which identify frontal structures in advected tracers (d'Ovidio et al., 2004; Lehahn et al., 2007). They have also been shown to correspond to biological activity. For example, it has been shown that the spatial distribution of planktonic organisms (Harrison et al., 2013), foraging frigate birds (Olascoaga et al., 2008), elephant seals (Della Penna et al., 2015), and baleen whales (Kai et al., 2009), correspond with the location of LCSs. However, while there exists evidence that fishing effort is colocated with LCSs (Prants et al., 2012), it remains unknown whether this is a systematic relationship across different marine systems and across fisheries, and also whether any relationship between LCSs and fishing influences catch rates and the revenue generated by fishing.

FIGURE 1

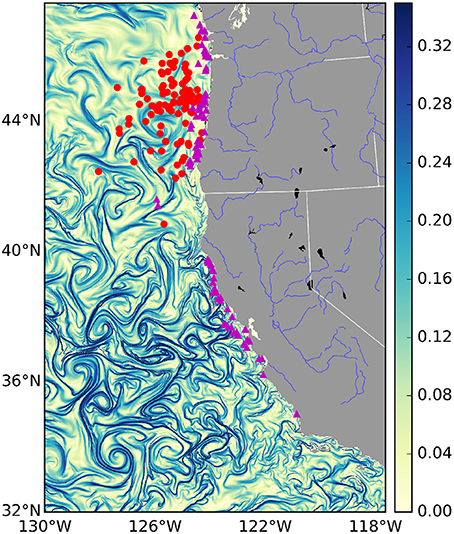
Figure 1. Finite-time Lyapunov Exponent values (d⁻¹) from the U.S. West Coast on January 1st 2009. Strong frontal activity or—Lagrangian Coherent Structures—are generally considered values > 0.1 d⁻¹. Overlaid are mock locations of several fishing events for different fisheries: the tuna fishery in red and the salmon fishery in purple. Due to privacy restrictions we will not show actual fishing locations, instead these are random points sampled from within the 95% kernel density contour of each fishery.

To understand whether fishermen track LCSs and whether doing so has economic impacts, we compiled data on the location of over 1,000 fishing vessels every hour in the U.S. California Current Large Marine Ecosystem (CCLME) for the period 2009–2013 produced from a Vessel Monitoring System (VMS), and collated corresponding fisheries catch and price data. We focused on the spatial dynamics of vessels operating in three commercially important fisheries: the albacore tuna (Thunnus alalunga) troll, chinook and coho salmon (Oncorhynchus tshawytscha and Oncorhynchus kisutch respectively) troll and pink shrimp (Pandalus jordani) trawl fisheries, which account for roughly 35, 45, and 50 million US dollars in annual revenue respectively (values from www.oceaneconomics.org/). Complementing this, we gathered oceanographic information for the same time period, from a 4-dimensional variational (4D-Var) data-assimilation Regional Ocean Modeling System (ROMS) solution to the US west coast (Moore et al., 2011a). This ROMS model operates at a higher spatial and temporal resolution than satellite altimetry data, which is commonly used to answer similar questions, and assimilates as much data as possible to make the best possible reconstruction of past oceanic conditions for the U.S. West Coast. We used the ROMS velocity fields to identify LCSs, and with these data, we assessed whether fishing events from the tuna, salmon and shrimp fisheries are associated with attracting LCSs, and whether this impacts the revenue generated by fishing.

Methods

To assess the relationship between the spatial distribution of fishing effort and the location of LCSs, we synthesized fisheries landings data. Using these data we then defined fisheries for the CCLME. Then, using spatially explicit vessel monitoring data for the tuna, salmon and pink shrimp fisheries, we identified fishing locations. In parallel to these analyses of fisheries data, oceanographic data produced from a regional ocean model were used to identify LCSs in the CCLME for the same time-period as covered by the fisheries data. Combining the two, we assessed whether vessels, operating in different fisheries, appear to search for and catch fish preferentially on LCSs. The following subsections expand on each of these steps.

Identifying Fisheries from Landings Data

Fisheries catch and price data were obtained from fish-tickets compiled through the Pacific Fisheries Information Network (PacFIN), and describe the time, location, catch and revenue of 340,466 trips, spanning 5,980 vessels for the time period 2009–2013. Using these data, we identified fisheries as groups of similar trips based on what was caught. These trip-groups are otherwise called métiers (mostly in Europe; Deporte et al., 2012). At its heart, a métier analysis groups trips based on the gear used, and the revenue and species composition of landings (Davie and Lordan, 2011; Boonstra and Hentati-Sundberg, 2016). This methodology requires choices in the way similarity among trips are measured, a clustering algorithm for grouping similar trips together, and scalability so that it can be applied to the 340,466 trips we had data for.

The first step was to calculate the similarity of every pair of trips, measured using the Hellinger distance D (Legendre and Legendre 2012). The Hellinger distance was calculated from the species composition of two fishing trips A and B as follows:

$\begin{array}{ll}{D}_{AB}=\sqrt{{\displaystyle \sum _{i=1}^S}{(a_i-b_i)}^2},& (1)\end{array}$

where a_i is the fraction of revenue derived from species i on trip A, b_i is the fraction of revenue derived from species i on trip B, and S is the total number of species collected in both trips. Hence, as the difference in revenue attributable to each of the S species increases, trips A and B become increasingly dissimilar. Applied to every pair of fishing trips results in a trip distance matrix.

The next step was to transform the Hellinger distance matrix into a similarity matrix. This was done by subtracting each element of the distance matrix from the maximum value of the whole matrix. From this similarity matrix, we identified métiers as groups of trips with similar target assemblages using the infoMap community detection algorithm (Rosvall and Bergstrom, 2008). This algorithm examines networks (which the similarity matrix represents, where nodes are trips and edges are trip similarity) for subgraphs more interconnected to one another than the network in which it is embedded.

Our dataset contained 340,466 unique trips, and due to computational limits, we were not able to implement the infoMap algorithm using a single matrix containing all pairwise trip similarities. To overcome this computational challenge, and obtain manageable matrix sizes, we first performed the métier analysis on one year's worth of landings data, for example 2010. Then for each trip in other years (e.g., 2009, 2011, 2012, and 2013), we identified which 2010 trip was “nearest” to it, in terms of species composition, using a k-nearest neighbors algorithm. Each trip in 2009, 2011, 2012, and 2013 then inherited the métier of its nearest 2010 trip. In this way, we managed to assign all trips from the whole dataset to specific métiers. We tested this method using different “base” years (i.e., different to 2010 in the above example), and found our results robust to this decision.

Linking Fishery Definitions to Vessel-Monitoring System Data

In total, the fisheries trip data contained numerous fisheries. We subsetted these data and focused our analysis on the albacore tuna, salmon and pink shrimp métiers. Pacific albacore tuna is a migratory species, caught relatively far from shore (see Figure 1: red dots) by towing artificial lures with barbless hooks or “trolling.” Of the three species we have studied, albacore tuna is the most likely to have a behavioral relationship with LCSs. Indeed there is strong anecdotal evidence that tuna fishermen look for frontal features when trolling for tuna (gained from personal communications with tuna fishermen). The salmon fishery consists mainly of chinook and coho salmon, which similarly to albacore tuna are caught by trolling, but are found mainly in areas closer to shore. Pink shrimp are associated with soft-sediment benthos, and are harvested by trawling nets along the sea-floor. As a consequence, of the three focal species, they are the least likely to be affected by surface LCSs, which will only impact the sea floor through the sinking of organic particles from phytoplankton blooms, which occurs over time-scales longer than considered here. Hence, we included shrimp precisely because LCSs are expected to have no relationship.

The locations of tuna, salmon and shrimp vessels were obtained from a Vessel Monitoring System (VMS) dataset provided by the National Marine Fisheries Service's Office of Law Enforcement (OLE). VMS is required for all vessels commercially fishing federally managed groundfish in the past 5 years. Many of these “groundfish” vessels operate in other fisheries and as a consequence the VMS data contained numerous tuna, salmon and shrimp trips. Vessel locations have an accuracy of approximately 500 meters and in total, we amassed 22 million GPS pings, hourly over the period 2009-2013, for 1,183 vessels. However, no contextual data is provided with the VMS data, for example when a vessel is in port, when it is fishing, or what kind of vessel it is. As a consequence, the first challenge with these data is to link them to the fisheries definitions obtained from the trip landings data, and then identify different spatial behaviors—searching for and catching fish vs. transiting—from the location time-series.

The first step to analyzing the VMS data was to identify trips. This was done in two steps. First, we assigned any VMS location less than 1.5km from the shore and stationary for greater than 3 hours as “in-port”. Distances to land were calculated using NOAA's GSHHG high-resolution geography dataset (Wessel and Smith, 1996). This resulted in a subset of the VMS data that included only “at-sea” locations. Then, trip-times (time-out and time-in) from the fisheries landing ticket data were matched with the at-sea VMS data points. This matching allowed us to assign a unique index for sets of VMS data-points associated with a distinct fishing trip. Furthermore, once the fisheries analysis of the landing ticket data was performed, we were also able to assign a fishery to each trip in the at-sea VMS data. Doing so identified what species was being harvested on each trip in the VMS database.

The last step was to link a NOAA Fisheries West Coast Groundfish Observer Program data to the at-sea VMS data, for the purpose of validating the spatial behavior segmentation (i.e., identifying when a vessel was fishing or not). This involved matching vessel identifiers and time-points in each database. These observer data included descriptions of the vessel, the location, and time-in and -out of a fishing set (i.e., the time when fishing happened) for 8,932 trips spanning 334 vessels over the period 2009–2013. We identified which at-sea VMS data points lay within these set-in/set-out time-spans, and used this information in validating the behavioral segmentation algorithm described below. Importantly, the NOAA observer data only covered a fraction of the trips in the at-sea VMS data, for example 13% of shrimp trips.

Vessel Monitoring System Data Behavioral Segmentation

The at-sea VMS data remained a collection of lat/lon time-series, grouped by trip and fishery. In order to identify when and where fishing occurred from these time-series, we developed an unsupervised behavioral segmentation algorithm, which works as follows. Vessel speed was calculated as the distance traveled per unit time between sequential location pings for all trips, making sure to also calculate the spatial mid-point between consecutive lat/lon points. Furthermore, for each trip, checks were made for extreme and unrealistic speeds. Then, for each vessel we subsetted trips by fishery, and calculated empirical speed distributions. To these empirical distributions we fitted Gaussian Mixture Models (GMM), varying in the number of components (i.e., modes) modeled. The “best” model was selected using Bayesian Information Criterion. The last step was to identify the 50th percentile value of the first Gaussian component of the best model. This speed value was used as a cut-off: any locations with speeds less than or equal to this value were assumed to be fishing-intended or fishing activity. This speed identifies the where the first component (i.e., fishing) becomes less likely than the second component (i.e., steaming). As an example, Figure S1 shows the empirical speed distributions, the best GMMs, and the cut-off speeds for a vessel that participated in a tuna, salmon and shrimp trip. All locations with speeds less than or equal to the cut-off, for that specific type of trip and for that vessel, were assumed to be fishing or fishing-intended events.

Vessel-speed criteria are commonly use to infer whether a VMS record corresponds to fishing activity (Murawski et al., 2005; Eastwood et al., 2007; Lee et al., 2010; Gerritsen and Lordan, 2011). For example, vessel speeds are commonly used to determine when trawling is in progress, with 8 knots considered to represent the upper limit of trawling speed for North Sea beam trawlers (Dinmore et al., 2003). Some authors who have used a similar approach have reported a significant number of false-positive results (where vessels were traveling at fishing speeds, but were not actually engaged in fishing). However, false-negative results tend to be rare. Indeed, previous work has included directionality in addition to speed, as determinants of fishing, but they only resulted in a very small improvement on speed alone (Mills et al., 2007). Further, unsupervised behavioral segmentation algorithms like ours are commonly used (Murawski et al., 2005; Gerritsen et al., 2012; Jennings and Lee, 2012), and although supervised classification methods are available (Joo et al., 2015), and access to the NOAA observer data meant we had the means to construct and test them, there are several caveats to the observer data (see paragraph below), and ultimately we would only be able to develop supervised methods for a small subset of fisheries due to data restrictions. Furthermore, these supervised classification methods would perform poorly for those fisheries to which they could not be trained (i.e., the tuna and salmon fisheries). As a consequence, we used a simple unsupervised approach based solely on speed that could be applied across fisheries. We used the NOAA observer data post-hoc to calculate the precision of our method, and we found it to perform well for all fisheries for which we could validate, averaging 83% (see Table 1; precision was calculated from the frequency of true-positives—locations that both the NOAA observer data and our algorithm identified as fishing.). Importantly, we accounted for the precision of our classification method using bootstrap methods in all subsequent statistical analyses, meaning our results are robust to the choice of using a simple unsupervised behavioral segmentation method.

TABLE 1

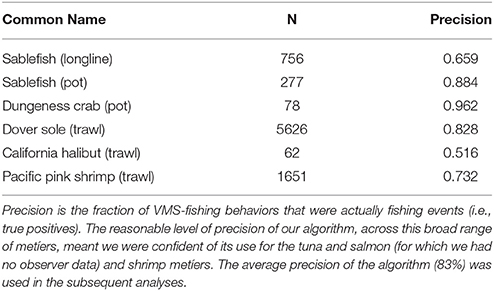
Table 1. The precision of the VMS segmentation algorithm, applied to different métiers that we had NOAA observer data for.

Another challenge that we came across, that affected our decision to use an unsupervised classification scheme, was systematic error in the start and end times of fishing in the NOAA observer data. For example, in Figure S2 we show a mock fishing trajectory where colored dots identify a fishing vessel's location, and the color the speed. We cannot show the tracks of a real fishing trajectory, but this mock-up copies exactly a problem seen throughout our data. Specifically, the NOAA observer set-in and set-out dates identify VMS locations that are not likely fishing events. In the top-panel of Figure S2, the dots surrounded by a grey-circle identify those VMS locations identified as fishing by the observer data. It is obvious that the observer data suggest this vessel is fishing, while steaming fast away from the true fishing location (the knot of points in blue). In contrast, our speed algorithm identifies what by eye are likely the true fishing locations (gray circles in the bottom panel of Figure S2). This potential error in the NOAA observer data contributed to our decision not to develop a supervised classification scheme.

Oceanographic Data

The spatial distribution of attracting LCSs for the whole U.S. California Current Large Marine Ecosystem, for the period 2009-2013, was estimated using modeled surface ocean currents produced from a 4-dimensional variational (4D-Var) data assimilation Regional Ocean Modeling System (ROMS) solution (Haidvogel et al., 2000, 2008; Shchepetkin and McWilliams, 2003, 2005). The ROMS model and domain is described in detail elsewhere (Moore et al., 2011a) so only a brief description is given here. The domain spans the region 134°W to 116°W and 31°N to 48°N, extending from midway down the Baja Peninsula to Vancouver Island at 1/10 degree (roughly 10 km) resolution, with 42 terrain-following levels resolving vertical structure in ocean properties. We chose to use surface currents from the high-resolution ROMS reanalysis to identify LCSs and corresponding fronts, instead of geostrophic velocity fields derived from satellite altimetry used in several previous studies of LCSs. We made this choice for several reasons: (i) the altimetry-based approach cannot be applied reliably in coastal regions, where the geostrophic balance no longer holds because of strong lateral and bottom boundaries and nearshore forcing; (ii) geostrophic surface currents derived from satellite altimetry are only available at coarser spatial resolution (at 1/4^o or roughly 25 km in our domain); (iii) altimetry accuracy decreases near the coast, where much fishing occurs, due to measurements being affected by the presence of land in the satellite footprint (i.e., <50 km from the shore).

The circulation of the US west coast is dominated by the California Current system, which is characterized by energetic mesoscale variability, and by pronounced seasonal upwelling driven by alongshore wind stress and offshore wind stress curl. High productivity in the California Current system is sustained by the supply of cool, nutrient-rich waters upwelled to the sunlit surface layer by alongshore winds. Coastal upwelling has a strong signature in sea surface temperature (SST) and chlorophyll concentration as illustrated in Figures S3, S4, which show the observed SST and chlorophyll concentration for August 23rd 2010. Figures S3, S4 also illustrate the complex circulation and intense mesoscale activity characterizing the dynamics of the California Current system circulation.

In order to build reliable estimates of past ocean conditions in this highly dynamic region and accurately represent the complex evolution of the true ocean state, the ROMS model uses 4D-Var data assimilation, which synthesizes numerous oceanic observations to produce the best linear unbiased estimate of the circulation of the California Current system (for an extensive description of the ROMS 4D-Var capability and implementation, see Moore et al., 2011a,b). For example, daily AVISO Sea Level Anomalies provide information of the sea surface height; and sea surface temperature data (SST) is obtained from numerous satellite platforms (i.e., AVHRR/PathFinder, AMSR-E, GOES and MODIS-Terra). The ROMS 4D-Var data assimilation system produces daily snapshots of the full 3-dimensional structure of the ocean extending from the surface to the ocean bottom. To utilize model information with the best agreement with past observations, we used the posterior circulation estimate, provided online here http://oceanmodeling.ucsc.edu/. Examples of the SST and surface velocity fields produced by the ROMS 4D-Var data assimilation system are shown in Figure S5, which should be compared to empirical observations for the same day shown in Figure S3 (surface temperature) and Figure S4 (surface chlorophyll) for a qualitative verification of its ability to reproduce past ocean conditions.

Lagrangian Coherent Structures

Using the ROMS modeled surface velocities, we identified the location of LCSs through time (Castruccio et al., 2013). These flow features are material curves that map filamentation and transport boundaries (Harrison et al., 2013). Fluid particles straddling a LCS will either diverge (repelling LCS) or converge (attracting LCS) in forward time (Haller and Yuan, 2000). LCSs thus delineate the boundary between dynamically distinct regions of the flow field, effectively allowing us to visualize the skeleton of turbulent transport (e.g., Haller, 2002; d'Ovidio et al., 2004; Shadden et al., 2005). Whereas the resolution of the ROMS velocities may appear relatively coarse compared to the spatial scales of fishing, the topological structure of surface ocean LCSs has been shown to be robust to noise and low spatial resolution velocity fields (Harrison and Glatzmaier, 2012). The spatial organization of LCSs has a large impact on the coastal environment not only because they influence the dispersion of tracers in the water but also because by separating dynamically distinct regions of flow, they can define fluid dynamical niches, which contribute to the structuring of marine ecosystems (d'Ovidio et al., 2004; Cotté et al., 2011). We focused on attracting LCSs because they identify regions of confluence and shear, and have been shown to correspond strongly with the location of fronts and the foraging behavior of marine top predators such as frigate birds (Kai et al., 2009), elephant seals (Della Penna et al., 2015), and baleen whales (Cotté et al., 2011).

There have been various proposed methods for identifying attracting LCSs. Among all these approaches, the definition of LCSs as ridges of the Finite-time Lyapunov Exponent (FTLE) field has been especially successful. Near LCSs, neighboring fluid parcels are strained by differing amounts by the flow field. These differences in stretching rates allow the detection of LCSs by Lyapunov exponents, which measures the rate of separation of infinitesimally close trajectories exhibiting exponential behavior with time (Nese, 1989). It is defined as:

$\begin{array}{ll}\lambda ={\displaystyle \underset{t\to \infty }{lim}}\frac{1}{t}ln\frac{{\delta }_t}{{\delta }_0},& (2)\end{array}$

where δ₀ and δ_t are the initial deviation and the deviation at time t, respectively. This concept has been previously introduced to the flow analysis (Haller and Yuan, 2000; Haller, 2001). FTLEs measures the maximum separation of close-by particles of a time-dependent flow field after a fixed, finite particle advection time. Here we have computed the FLTE on a regular grid with 1/80 degree horizontal resolution (approximatively 1km in the CCS). We naturally used the initial separation δ₀ of the particles equal to the grid spacing. The final separation δ_t is computed as the maximum separation after a particle advection time of 10 days, which is the typical mesoscale eddy-turnover time in the region. Large FTLE values identify regions where the stretching induced by mesoscale and submesoscale activity is strong and are typically organized in convoluted lines encircling submesoscale filaments. A line of local maxima of FTLE (more precisely, a ridge) can be used to predict the location of tracer fronts induced by horizontal advection and stirring; in other words, the location of LCSs. A snap-shot of the spatial distribution of backward FTLE values and the complementing probability distribution are shown in Figure 1 and Figure S6 respectively. Further, an animation showing the dynamic nature of FTLE fields is provided in the Supplementary Movie. These maps and the animation highlight the complex spatial patterns exhibited by LCSs (large FTLE values), and the probability distribution shows that FTLE values are roughly log-normally distributed, with a mode around 0.1d⁻¹. The LCS's ability to outline observed tracer patterns in geophysical flows is well illustrated by Figure S5 where LCSs align with frontal structures and filamentation in temperature.

Statistical Analysis of Fishing and Lagrangian Coherent Structures

The behaviorally segmented VMS data consists of a list of locations where fishing or fishing-intended activities occurred over the period 2009-2013. In total, these data included 3233 tuna, 2201 salmon and 7762 shrimp fishing locations. We then linearly interpolated in space and time the FTLE data, produced from the ROMS modeled velocity data, to these locations. The result is a unique FTLE value per fishing location. The next step was to generate a null dataset with which to compare VMS-FTLE values. Following the approach of (Cotté et al., 2011), for every fishing location estimated from the VMS data, a random location was chosen from within the 95% kernel polygon of the fishing location's parent fishery (see Figure S7 for maps showing the spatial distribution of fishing effort for each fishery). The kernel density estimation was performed on each fishery's fishing locations only, and results often identified numerous distinct polygons. In this case, random points were created by first choosing a polygon probabilistically, in proportion to its area, and then a choosing a location randomly from within that polygon. FTLE values were then linearly interpolated in space and time to each random point. The result is a set of random points in the “preferred fishing region” of each fishery. These random-FTLE distributions were then compared with the corresponding VMS-FTLE distributions.

In order to explore differences between the VMS and random-FTLE distributions, we performed Kolmogorov-Smirnov tests and G-tests of goodness-of-fit. The Kolmogorov-Smirnov test quantifies the significance of the largest difference between two cumulative density functions, whereas the G-test quantifies the significance of the difference in the frequency of particular events. Both Kolmogorov-Smirnov and G-tests were repeated 1,000 times, subsampling 83% of the VMS- and random-FTLE distributions to reflect the behavioral segmentation precision. For the G-test, we calculated the frequency of VMS- and random-FTLE points greater than or less than 0.1 d⁻¹, which is a threshold value that corresponds to frontogenesis timescales faster than 1 month—a time span that has been shown to be ecologically significant, attracting numerous taxa (d'Ovidio et al., 2004; Olascoaga et al., 2008; Kai et al., 2009).

We repeated this statistical comparison of VMS-FTLE and random-FTLE distributions, using a different random test. Here, instead of choosing random points from within the 95% contour of each fishery, we chose them randomly from within the whole U.S. CCLME domain. Like the fishery-specific random test, we performed Kolmogorov-Smirnov tests and G-tests of goodness-of-fit.

In addition to testing whether fishing was randomly associated with high FTLE values and LCSs, or not, we also explored whether fishing on high FTLE values impacts the revenue generated by a trip. To do so, we performed linear univariate regression analysis and fit linear mixed models with the maximum VMS-FTLE value per trip as the explanatory variable, and trip-revenue as the dependent variable. In the case of the linear mixed models, vessel length was additionally included as a fixed effect, and vessel-ID as a random effect. In order to estimate the significance of the regression parameters, we bootstrapped these analyses by taking only 83% of values, reflecting the expected behavioral segmentation precision, and repeating the regression analyses 1,000 times. This bootstrap approach allowed us to estimate a distribution and p-value for each regression parameter (i.e., the slope).

Results

The VMS-FTLE and random-FTLE distributions for the tuna, salmon and shrimp fisheries are shown in Figure 2. Values range from past −0.1 day⁻¹ to 0.5 day⁻¹, with median values for each fishery all around 0.1 day⁻¹. From these violin plots it is possible to identify systematic qualitative differences between the VMS-FTLE and random-FTLE values. For example, for the tuna fishery the VMS-FTLE median, 25th and 75th percentiles are all greater than the corresponding random-FTLE values. The Kolmogorov-Smirnov tests identified that the tuna and salmon VMS-FTLE distributions are significantly different from random, but that there is no significant difference between the shrimp VMS-FTLE and random-FTLE distributions (Figure 2; Kolmogorov-Smirnov p-values are given below the fishery names). In addition, we found that for the tuna, salmon and shrimp fisheries respectively, 57, 47.5, and 55% of fishing events happen on FTLE values ≥ 0.1day⁻¹, relative to 52, 50.5, and 54% of random events (see Figure 3A). The G-test p-values reflect those from the Kolmogorov-Smirnov tests, that is the fraction of fishing events occurring on FTLE values ≥ 0.1day⁻¹ in the tuna and salmon fisheries are significantly different from random, whereas in contrast, there is no significant difference for shrimp fishing. The differences between the VMS- and random FTLE values, for the tuna fishery, are 2–3 times less than those observed for foraging baleen whales (Cotté et al., 2011) (the fraction of baleen whales found on FTLE values greater than 0.1day⁻1 was roughly 10–15% greater than would be expected at random). This suggests that tuna fishermen are not tracking these surface frontal features as closely as baleen whales.

FIGURE 2

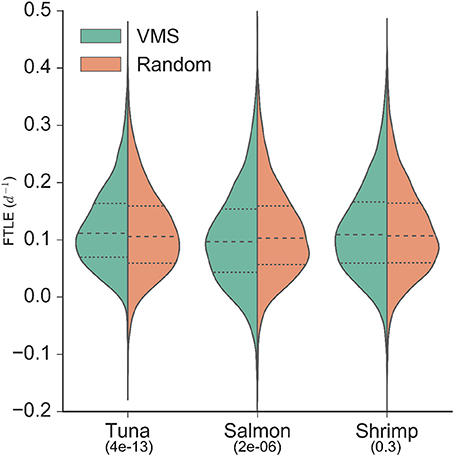
Figure 2. Distributions of backward finite-time Lyapunov exponent values from VMS (left of axis/green) and random (right of axis/orange; sampled from within the 95% density contour of each fishery) locations. Median values are identified by the dashed lines, and upper and lower quartiles are identified by the dotted lines. Kolmogorov-Smirnov p-values are indicated below fishery names, indicating the significance of the difference between the VMS- and random-distributions (i.e., only the shrimp fishery VMS-FTLE distribution is not significantly different from random).

FIGURE 3

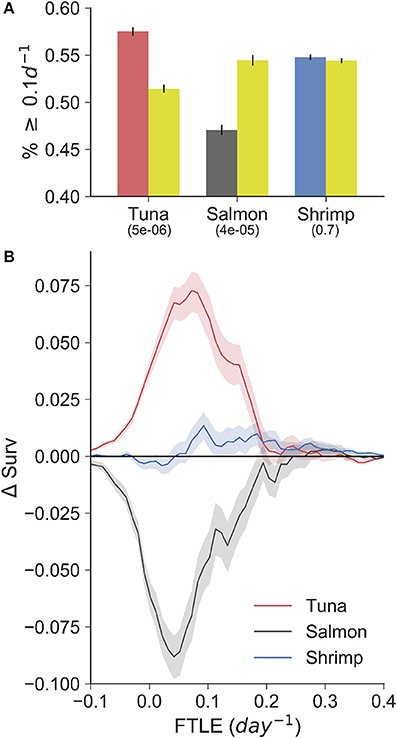
Figure 3. (A) Bar-plot showing the fraction of fishing (red-tuna, gray-salmon, blue-shrimp) and random (gold; sampled from within the 95% density contour of each fishery) points with a FTLE value greater than or equal to 0.1d⁻¹. G-test p-values are shown below each fishery label. (B) The difference in VMS- and random-FTLE survival functions (ΔSurv) for the three fisheries with 95% confidence intervals. These curves highlight that tuna fishermen search for and catch fish in areas of the ocean with FTLE values greater than would be expected by chance. In contrast, salmon fishermen are found preferentially in areas with low FTLE values.

To highlight the way in which these distributions differ from random, we calculated the difference in VMS- and random-FTLE survival functions, Δsurv, bootstrapping values with an 83% sample size to create confidence intervals that reflect the behavioral segmentation precision (in the case for shrimp, for which we had fishing observations, we used 75% precision: see Table 1). Survival functions identify the fraction of points with a certain FTLE value or greater (formally, they are 1 minus a cumulative density function), and the difference between the VMS- and random-survival functions identifies the magnitude and type of non-random association fishermen have with LCSs. For example, from the Δsurv curves shown in Figure 3B, it is evident that tuna fishing events always occur on FTLE values greater than would be expected from random, that is the red curve is always positive over the entire range of FTLE values. This strongly suggest that tuna fishermen preferentially search for and catch tuna on LCSs, as quantified by FTLEs.

In contrast to tuna fishing, salmon fishing always occurs on FTLE values less than would be expected from random, that is Δsurv values are negative. This can be interpreted in three ways. First, salmon fishermen may search for and catch fish in specific areas of the coast that have reduced frontal activity relative to nearby waters. Second, the spatial resolution of the ROMS model, from which the FTLE data were calculated, is not sufficient to resolve the physical features that salmon fishermen use to locate salmon. This is an important caveat to this work, and is expanded upon in the discussion. Third, salmon fishing may occur in places where LCSs were recently. We do not account for the possible time-lag between fishing and the presence of an LCS, but we can hypothesize that a time-lag would only happen if salmon track some trailing effect of LCSs. This is clearly possible, as the ecosystem effects of fluid convergence, caused by LCSs, will be integrated over space and time. In contrast to both tuna and salmon fishing, there is less difference between the shrimp VMS- and random-survival functions. In general, the shrimp Δsurv curve hugs the zero-line (the point at which there is no significant difference to random). Hence, when combined with non-significant p-values from the Kolmogorov-Smirnov and G-tests, this information confirms our expectation that shrimp fishing has no spatial correspondence with LCSs and surface frontal features.

The results of the whole-domain random test contrast strongly with those produced from the fishery-specific random test (compare Figure 3 and Figure S8). Here, all fisheries—tuna, salmon and shrimp—show negative Δsurv curves. This identifies that each of these fisheries operates in areas of the California Current with low FTLE values relative to the rest of the domain. It is an interesting oceanographic question to ask why this happens, but because our focus is on the spatial relationship between individual fishing events and specific FTLE features, and not with LME-scale biophysical patterns, we do not answer it in this paper. One point to note is that the qualitative differences between the Δsurv curves of each fishery are consistent across the fishery-specific and whole-domain tests. That is, the tuna curve is the least negative, the shrimp curve is an intermediate case and the salmon curve is the most negative. This qualitative consistency reflects the results of the fishery specific tests (i.e., that tuna fishermen track FTLE values that are relatively high when compared to shrimp and salmon fishermen).

These FTLE statistics reveal that tuna fishermen preferentially search for and catch fish in areas of high oceanic filamentation, in other words areas of the ocean with strong fronts. In contrast salmon fishing occurs in areas of low filamentation, and shrimp fishing occurs independently of the FTLE context. Do these behaviors translate into economic terms for fishermen? In order to answer this question we assessed the relationship between total revenue gained per trip (in log₁₀$) and the maximum FTLE value experienced whilst fishing, for every trip for each fishery (Figure 4). Our data consisted of 753 tuna, 670 salmon and 1907 shrimp trips (made by 94, 69, and 56 unique vessels respectively), and we found that for tuna fishing, there is a significant positive linear relationship between logarithmic trip revenue and the maximum FTLE value experienced while fishing. The slope of this linear relationship is 1.44 log$ per unit FTLE (with a standard error of 0.12 log$ per unit FTLE, calculated from bootstrapping the regression and subsampling the data by 83% to account for the segmentation precision). This univariate analysis implies that a tuna vessel that searches for and catches fish on a front with FTLE value 0.1 d⁻¹ can be expected to make roughly $3,500 on a single trip, while a vessel that catches fish on a front with FTLE value 0.4 d⁻¹ is expected to make $10,000 on a single trip, roughly three times the revenue. Flat and non-significant relationships were observed for salmon and shrimp trips indicating that trip revenue in these fisheries are not affected by the FTLE conditions experienced while fishing. These results are mirrored when trip revenue is substituted by trip landings (in units of mass: Figure S9), but they are not found when the expected FTLE experienced whilst fishing is used in place of the maximum (Figure S10; this highlights that the maximum FTLE experienced while fishing on a given trip is a better measure of catch success).

FIGURE 4

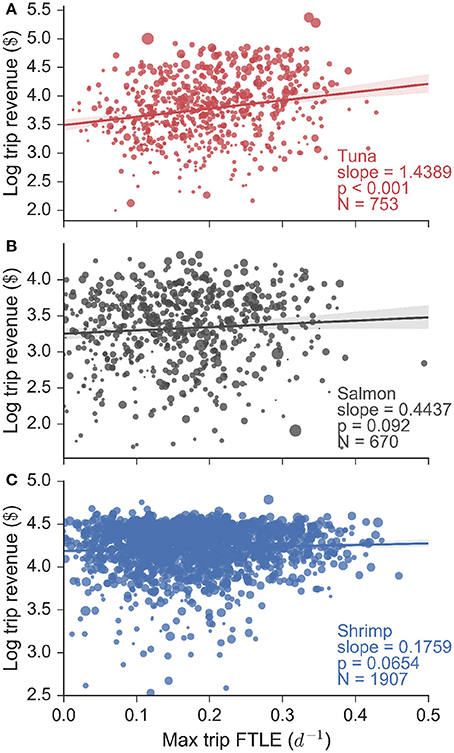
Figure 4. Logarithmic trip revenue (log$) as a function of the maximum finite-time Lyapunov exponent (FTLE) experienced while fishing on a particular trip, for all (A) tuna, (B) salmon, and (C) shrimp fisheries. Marker size is proportional to vessel length. We find a significant linear relationship for tuna fishing trips, indicating that tuna fishermen make more money the more they fish on fronts. This is confirmed using a linear mixture model that accounts for the effect of vessel size. Both the salmon and shrimp trips show flat and non-significant relationships.

Vessel size plays a role in determining trip revenue (Figure 4: marker size is proportional to vessel length), because larger vessels have more storage space and hence a greater capacity for bringing fish to harbor. Using generalized linear mixed models (bootstrapping results using subsamples similar to the univariate analysis) we indeed found that vessel size and tuna revenues are strongly and positively correlated (slope = 1.805, p-value < 0.001). However, we still also found a positive and significant (albeit secondary) effect of FTLE values on trip revenue (slope = 0.582, p-value < 0.001). In contrast, vessel size and FTLE values were not important determinants of salmon (slopes = 0.588, 0.344; all p-values > 0.05) or shrimp (slopes = −0.001, 0.369; all p-values > 0.05) trip revenues.

Discussion

Our results have identified a connection between fine-scale physical ocean features and the spatial patterns of human activity, and ultimately the economic welfare of fishermen. Specifically, our results infer that fishermen targeting albacore tuna track LCSs, as identified by large backward Finite-time Lyapunov exponents. This is reflected in the location of tuna fishing events, which are consistently found on LCSs, more so than would be expected at random, and also in the revenue gained by tuna fishermen. That there is significant positive correspondence between the spatial distribution of fine-scale (and ephemeral) physical features of the ocean and the income of fishermen is surprising, for there are many possible reasons why one fisherman might make more money than another (Fulton et al., 2011). For example, the institutional context, skill and experience, gear and weather all play a role in how much money a fishermen might make on any given trip (Hilborn, 1985; Bjarnason and Thorlindsson, 1993; Allison and Ellis, 2001). Thus, the clear signal of the physical ocean environment—the seascape—in the revenue garnered by tuna fishermen highlights the potential for strong natural-human coupling in the California Current system.

In contrast to tuna fishing events, we observed a negative relationship between salmon fishing and FTLE values, and no relationship for shrimp fishing. The absence of any relationship for shrimp fishing was expected, as shrimp fishing targets the benthos (Eales and Wilen, 1986), and as a consequence the surface physical structures described by FTLE values would not be expected to have an impact. However, the negative relationship seen in salmon fishing raises an important caveat of this work. It is impossible to tell whether this observation arises from an actual avoidance behavior of salmon fishermen, or whether this simply arises due to the inability for the ROMS model to resolve ocean processes close to shore, which is where salmon fishing typically occurs (see Figure 1). Although at the time of this work, the ROMS model data has a finer spatial resolution than satellite data, which is typically used to assess the impact of LCSs on predator foraging (e.g., Kai et al., 2009; Cotté et al., 2011; Della Penna et al., 2015), it is still too coarse to resolve coastal zone processes, which likely include even finer-scale physical ocean features than the LCS assessed here. For example, the FTLE value of 0.1d⁻¹ that we used has been adopted in previous works studying the relationship between marine top-predators and LCSs (e.g., Cotté et al., 2011). But these studies all focused on ocean regions far from shore (at least several tens of kilometers). Most likely, a different FTLE value will identify dominant frontal features in coastal zones. Hence, while 0.1d⁻¹ is appropriate for tuna fishing which occurs relatively far from shore, for studying the spatial behavior of vessels operating closer to shore, a different value should be identified using new higher resolution oceanographic information.

Indeed, the spatial scale at which fisherman behavior is assessed is a critical choice on the part of the investigator (Levin, 1992). Our choice to use the ROMS modeled data (produced at a spatial resolution of roughly 10km) allowed us to assess the impact of physical ocean features at this same spatial scale, that persist over timescales of roughly less than a month. If we were to have used higher spatial resolution data, we would have assessed the impact of even finer spatial scale and potentially more ephemeral physical ocean features on fishing. Importantly, at some fine scale there will cease to be any relationship. This is the spatial and temporal scale at which fishermen no longer are able to sense and react to the seascape. It is an interesting question to ask at what scale this is, and it likely relates to the technology that fishermen employ to search for fish. Because it is related to technology, this minimum spatiotemporal scale is likely decreasing, as vessels improve in speed and sensory ability.

In contrast to examining finer scale behaviors, one could coarse-grain the (ROMS) data, and assess the relationship between fishing and aggregate measures of the seascape. These coarse graining experiments have been used to examine the relationship between pelagic predators and relatively large areas of the ocean, characterized by different biophysical properties (Scales et al., 2017). Coarse graining experiments like these move the focus away from the behavior of individual fishermen and fishing vessels, and instead ask questions about where groups of vessels (fleets) operate. This is a vital consideration because while management typically focuses on directing the behavior of individual humans, their performance is often measured at the fleet level (Hilborn, 2007), and fleets themselves vary in their composition and in where their aggregate effort is directed (e.g., Figure S7;Boonstra and Hentati-Sundberg, 2016).

An important aspect of fisheries management that this study relates to is the impact of LCS-focused foraging on the organization and dynamics of the underlying marine food-web (Woodson and Litvin, 2015). Spatially focused foraging and consumption has been shown to impact fish stocks through a phenomenon known as “local depletion” (Bertrand et al., 2012), and in ecology these non-linearities in predator-prey interactions change the long-run mortality rate of prey, and the population growth rate of predators (Fryxell et al., 2007). This is important because the ecosystem models that we currently employ to quantify and predict the dynamics of marine ecosystems (e.g., Watson et al., 2015), possibly in the context of evaluating the potential response of management changes, use very simple linear mathematical functions to represent predator-prey encounter rates (e.g., the numerator in a Type II feeding function). These linear functions assume that prey are uniformly distributed over a given area, and predators move randomly over this area (Barbier and Watson, 2016). We know that in reality that this is not so, and our analysis confirms this. It is fair to say that all models are abstractions of reality; however, it is important to know the effect of these simplifying assumptions on the predictive skill of our ecosystem models. Our analysis suggests that more sophisticated predator-prey encounter functions that account for spatially focused foraging, and other important factors such as cooperation and advanced fishing technologies, are likely to provide new insights into fisheries dynamics (Fulton et al., 2011; Barbier and Watson, 2016).

One major policy tool that will benefit from improved understanding of the fine-scale spatial behavior of fishermen is marine spatial planning. Marine spatial planning takes many forms, for example Marine Protected Areas (MPAs) which have been widely adopted around the world (Edgar et al., 2014), and define areas of the ocean that are off-limits to fishing. Obviously, because vessels operating in different fisheries search for and catch fish in different places, MPAs will have a varying impact on people's income, depending on which fisheries they work in. Knowing in which oceanic regions and at what times of the year different fisheries operate is key to designing MPAs efficiently (Le Pape et al., 2014). Further, there are more sophisticated approaches to marine spatial planning, for example temporary closures (Brown et al., 2015), and policies directed at specific spatial behaviors, for example bycatch move-on rules (Dunn et al., 2014). Like MPAs, improved understanding of the spatial behavior of fishermen, at fine spatial and temporal resolution, will be critical to advancing these arguably more sophisticated forms of marine spatial planning.

Marine spatial planning extends to other ocean-industries, not just fishing. Indeed, much applied research is currently focused on “cross-sector” marine spatial planning, which aims to develop policies that optimize the (sustainable) use of the oceans by all sectors, for example fishing, aquaculture, shipping, tourism and oil and mineral extraction (Lester et al., 2013; Klinger et al., 2017). Like in the case of marine spatial planning geared solely for fisheries (e.g., MPAs), cross sector spatial policies will depend on a detailed quantification of spatial behavior. Importantly, this advanced understanding will not only improve our ability to design cross-sector policies for optimal/sustainable use of multiple ocean resources, but it will help us anticipate how people (like fishermen) will respond to these new policies (Klein et al., 2017). This is key to developing cross-sector policies that will provide opportunities for (economic) growth in the long-run, as the social and ecological organization of marine systems change (Klinger et al., 2018).

A final consideration for integrating detailed understanding of fishing spatial behavior into marine management is that fishermen typically work in numerous fisheries over a given year (Kasperski and Holland, 2013; Fuller et al., 2017). As a consequence, fishermen will move across, exploit and make money from different parts of a seascape at different parts of the year. Hence, they will have many relationships with different parts of the seascape. For example, a fisherman on the U.S. west coast that works in the albacore tuna fishery may also work in the dungeness crab fishery. As a consequence, high FTLE ocean features will be important to this fisherman during the tuna season, but not when they operate in the crab fishery. This is similar to agriculturalists that grow different crops in different parts of a landscape at different parts of the year. Indeed, just like in agricultural management (Iverson et al., 2014), spatial marine policies will be improved if they acknowledge that fishermen's diverse harvest portfolios connect different parts of seascapes (Hobday et al., 2011).

In summary, coastal management and marine spatial planning that recognizes and accounts for feedbacks between fishermen behavior and the dynamic and structured nature of seascapes is likely to meet with greater compliance and provide for stronger resilience in the face of cumulative anthropogenic impacts. Indeed, flexibility and resilience—the ability to cope with change (Folke, 2006)—are key properties of coastal human communities that managers are looking to bolster, especially in the context of impending shifts in species ranges expected with climate change (Pinsky et al., 2013). Furthermore, incorporating fine spatial-scale information into management policies is essential if we are to continue to improve the efficiency of fisheries (Hobday et al., 2011). Increased fisheries efficiency would lead to fishermen spending less time at sea, and as a consequence reduced risk of harm. Of course, in the interest of long-term sustainability this increase in efficiency should be matched by changes in governance institutions that prevent over harvest. Ultimately, given the coupled nature of social-ecological systems, integrating high resolution data on physical, chemical, ecological and social factors will improve both how and to what extent we use living natural resources (Wilen, 2004), leading to improved chances of prosperity now and in the future.

Author Contributions

JW, EF, FC, and JS all contributed data, designed the scientific approach, analyzed the data and wrote the manuscript.

Funding

JW and EF acknowledge the support of the NSF Dynamics of Coupled Natural-Human Systems grant GEO-1211972 and NSF GRFP: DGE-1148900 respectively.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Frank Davenport, Claudie Beaulieu for their help in preparing this manuscript. We would especially like to thank Brad Stenberg and the Pacific Fisheries Information Network (PacFIN), the Pacific States Marine Fisheries Commission, Kelly Spalding and the VMS Program at the National Marine Fisheries Service's Office of Law Enforcement, the NWFSC Observer Program, and Chris Edwards at UC Santa Cruz for providing the ROMS data. We also thank the Washington, Oregon and California Departments of Fish and Wildlife for sharing their data.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2018.00046/full#supplementary-material

Figure S1. The probability density function of speed from (A) tuna, (B) salmon, and (C) shrimp trips. Empirical distributions are shown in gray, the “best” fitted Gaussian Mixture Models in orange, and the cut-off speeds that are used to segment fishing and non-fishing behaviors is identified by the blue dashed line.

Figure S2. A mock-example of one trip. We are not allowed to show real fishing trajectories due to privacy constraints, so instead we created this mock-up based on a real example. Fishing vessel locations are identified by the colored dots (each separated by 5 min.) and speed (m/s) is identified by color. For this particular trip there are two searching/fishing events, identified by the clusters of slow-speed points. One problem we identified was that the NOAA observer data can sometimes be obviously erroneous. This is explained in the (Top), where the VMS locations circled in gray identify when the NOAA observer recorded that fishing is happening. For the top-most fishing event, there is clearly an overshoot. In contrast, our behavioral segmentation approach (Bottom) based on vessel speed is much more conservative.

Figure S3. Observed sea surface temperature provided by the Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA, Donlon et al., 2012). OSTIA uses satellite data provided by the GHRSST project, together with in-situ observations to determine the sea surface temperature. The analysis is produced daily at a resolution of 1/20^o (approximately 5 km).

Figure S4. Observed chlorophyll concentration (Maritorena et al., 2010) for May 23rd 2010, made using Level 3, daily, binned imagery from SeaWiFS, MODIS-Aqua, and Meris.

Figure S5. ROMS 4D-Var posterior estimate of Sea surface temperature (color shading) and surface velocity (vector) for May 23rd 2010. Attracting Lagrangian Coherent Structures (LCSs) are ridges of the Finite-time Lyapunov Exponent (FTLE) field, and are identified by the white lines.

Figure S6. Probability density function of finite-time Lyapunov values on Jan 1st 2009, for the ROMS US west coast modeled domain.

Figure S7. Fishing intensity (log₁₀ fishing days) for the tuna, salmon and shrimp métiers, calculated from the VMS data over the period 2009–2013.

Figure S8. Statistical analysis produced from the “whole-domain” random rest. (A) Bar-plot showing the fraction of fishing (red-tuna, blue-shrimp, gray-salmon) and random (gold) events with a FTLE value greater than or equal to 0.1d¹. G-test p-values are shown below each fishery label. (B) The difference in VMS- and random-FTLE survival functions (Δ Surv) for the three fisheries with 95% confidence intervals.

Figure S9. Logarithmic trip landing (log₁₀ lbs) as a function of the max finite-time Lyapunov exponent experienced while fishing on a given trip, for all (A) tuna, (B) salmon, and (C) shrimp trips. We find a significant linear relationship for tuna fishing trips, indicating that tuna fishermen make more money the more they fish on strong filaments. Both the salmon and shrimp trips show now (significant) relationships. Marker-size is proportional to vessel length.

Figure S10. Logarithmic trip revenue (log$) as a function of the expected finite-time Lyapunov exponent (FTLE) experienced while fishing on a particular trip, for all (A) tuna, (B) salmon, and (C) shrimp fisheries. Marker size is proportional to vessel length. We find no significant linear relationships for any of the fisheries studies.

References

Allison, E. H., and Ellis, F. (2001). The livelihoods approach and management of small-scale fisheries. Marine Policy 25, 377–388. doi: 10.1016/S0308-597X(01)00023-9

CrossRef Full Text | Google Scholar

Archibald, S., Staver, A. C., and Levin, S. A. (2012). Evolution of human-driven fire regimes in africa. Proc. Natl. Acad. Sci. U.S.A. 109, 847–852. doi: 10.1073/pnas.1118648109

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbier, M., and Watson, J. R. (2016). The spatial dynamics of predators and the benefits and costs of sharing information. PLoS Comput. Biol. 12:e1005147. doi: 10.1371/journal.pcbi.1005147

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertrand, S., Joo, R., Arbulu Smet, C., Tremblay, Y., Barbraud, C., and Weimerskirch, H. (2012). Local depletion by a fishery can affect seabird foraging. J. Appl. Ecol. 49, 1168–1177. doi: 10.1111/j.1365-2664.2012.02190.x

CrossRef Full Text | Google Scholar

Bjarnason, T., and Thorlindsson, T. (1993). In defense of a folk model: The ?skipper effect? in the icelandic cod fishery. Am. Anthropol. 95, 371–394. doi: 10.1525/aa.1993.95.2.02a00060

CrossRef Full Text | Google Scholar

Boonstra, W. J., and Hentati-Sundberg, J. (2016). Classifying fishers' behaviour. an invitation to fishing styles. Fish Fish. 17, 78–100. doi: 10.1111/faf.12092

CrossRef Full Text | Google Scholar

Bost, C.-A., Cotté, C., Bailleul, F., Cherel, Y., Charrassin, J.-B., Guinet, C., et al. (2009). The importance of oceanographic fronts to marine birds and mammals of the southern oceans. J. Marine Syst. 78, 363–376. doi: 10.1016/j.jmarsys.2008.11.022

CrossRef Full Text | Google Scholar

Branch, T. A., Hilborn, R., Haynie, A. C., Fay, G., Flynn, L., Griffiths, J., et al. (2006). Fleet dynamics and fishermen behavior: lessons for fisheries managers. Can. J. Fish. Aquat. Sci. 63, 1647–1668. doi: 10.1139/f06-072

CrossRef Full Text | Google Scholar

Brown, C. J., Abdullah, S., and Mumby, P. J. (2015). Minimizing the short-term impacts of marine reserves on fisheries while meeting long-term goals for recovery. Conserv. Lett. 8, 180–189. doi: 10.1111/conl.12124

CrossRef Full Text | Google Scholar

Castruccio, F. S., Curchitser, E. N., and Kleypas, J. A. (2013). A model for quantifying oceanic transport and mesoscale variability in the coral triangle of the indonesian/philippines archipelago. J. Geophys. Res. Oceans 118, 6123–6144. doi: 10.1002/2013JC009196

CrossRef Full Text | Google Scholar

Cotté, C., d'Ovidio, F., Chaigneau, A., Lévy, M., Taupier-Letage, I., Mate, B., et al. (2011). Scale-dependent interactions of mediterranean whales with marine dynamics. Limnol. Oceanogr. 56, 219–232. doi: 10.4319/lo.2011.56.1.0219

CrossRef Full Text | Google Scholar

Davie, S., and Lordan, C. (2011). Definition, dynamics and stability of métiers in the irish otter trawl fleet. Fish. Res. 111, 145–158. doi: 10.1016/j.fishres.2011.07.005

CrossRef Full Text | Google Scholar

Della Penna, A., De Monte, S., Kestenare, E., Guinet, C., and d'Ovidio, F. (2015). Quasi-planktonic behavior of foraging top marine predators. Sci. Reports 5:18063. doi: 10.1038/srep18063

PubMed Abstract | CrossRef Full Text | Google Scholar

Deporte, N., Ulrich, C., Mahévas, S., Demanèche, S., and Bastardie, F. (2012). Regional métier definition: a comparative investigation of statistical methods using a workflow applied to international otter trawl fisheries in the north sea. ICES J. Marine Sci. 69, 331–342. doi: 10.1093/icesjms/fsr197

CrossRef Full Text | Google Scholar

d'Ovidio, F., Fernández, V., Hernández-García, E., and López, C. (2004). Mixing structures in the mediterranean sea from finite-size lyapunov exponents. Geophys. Res. Lett. 31:L17203. doi: 10.1029/2004GL020328

CrossRef Full Text | Google Scholar

Dunn, D. C., Boustany, A. M., Roberts, J. J., Brazer, E., Sanderson, M., Gardner, B., et al. (2014). Empirical move-on rules to inform fishing strategies: a new england case study. Fish Fish. 15, 359–375. doi: 10.1111/faf.12019

CrossRef Full Text | Google Scholar

Eales, J., and Wilen, J. E. (1986). An examination of fishing location choice in the pink shrimp fishery. Marine Resour. Econom. 2, 331–351. doi: 10.1086/mre.2.4.42628909

CrossRef Full Text | Google Scholar

Eastwood, P., Mills, C., Aldridge, J., Houghton, C., and Rogers, S. (2007). Human activities in uk offshore waters: an assessment of direct, physical pressure on the seabed. ICES J. Marine Sci. 64, 453–463. doi: 10.1093/icesjms/fsm001

CrossRef Full Text | Google Scholar

Edgar, G. J., Stuart-Smith, R. D., Willis, T. J., Kininmonth, S., Baker, S. C., Banks, S., et al. (2014). Global conservation outcomes depend on marine protected areas with five key features. Nature 506, 216–220. doi: 10.1038/nature13022

PubMed Abstract | CrossRef Full Text | Google Scholar

Essington, T. E., Beaudreau, A. H., and Wiedenmann, J. (2006). Fishing through marine food webs. Proc. Natl. Acad. Sci. U.S.A. 103, 3171–3175. doi: 10.1073/pnas.0510964103

PubMed Abstract | CrossRef Full Text | Google Scholar

Faeth, S. H., Warren, P. S., Shochat, E., and Marussich, W. A. (2005). Trophic dynamics in urban communities. Bioscience 55, 399–407. doi: 10.1641/0006-3568(2005)055[0399:TDIUC]2.0.CO;2

CrossRef Full Text | Google Scholar

Folke, C. (2006). Resilience: the emergence of a perspective for social–ecological systems analyses. Global Environ. Change 16, 253–267. doi: 10.1016/j.gloenvcha.2006.04.002

CrossRef Full Text | Google Scholar

Fryxell, J. M., Mosser, A., Sinclair, A. R., and Packer, C. (2007). Group formation stabilizes predator–prey dynamics. Nature 449, 1041–1043. doi: 10.1038/nature06177

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuller, E. C., Samhouri, J. F., Stoll, J. S., Levin, S. A., and Watson, J. R. (2017). Characterizing fisheries connectivity in marine social ecological systems. ICES J. Marine Sci. 74, 2087–2096. doi: 10.1093/icesjms/fsx128

CrossRef Full Text | Google Scholar

Fulton, E. A., Smith, A. D., Smith, D. C., and van Putten, I. E. (2011). Human behaviour: the key source of uncertainty in fisheries management. Fish Fish. 12, 2–17. doi: 10.1111/j.1467-2979.2010.00371.x

CrossRef Full Text | Google Scholar

Gerritsen, H., and Lordan, C. (2011). Integrating vessel monitoring systems (vms) data with daily catch data from logbooks to explore the spatial distribution of catch and effort at high resolution. ICES J. Marine Sci. 68, 245–252. doi: 10.1093/icesjms/fsq137

CrossRef Full Text | Google Scholar

Gerritsen, H., Lordan, C., Minto, C., and Kraak, S. (2012). Spatial patterns in the retained catch composition of irish demersal otter trawlers: High-resolution fisheries data as a management tool. Fish. Res. 129, 127–136. doi: 10.1016/j.fishres.2012.06.019

CrossRef Full Text | Google Scholar

Godø, O. R., Samuelsen, A., Macaulay, G. J., Patel, R., Hjøllo, S. S., Horne, J., et al. (2012). Mesoscale eddies are oases for higher trophic marine life. PLoS ONE 7:e30161. doi: 10.1371/journal.pone.0030161

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, H. S. (1954). The economic theory of a common-property resource: the fishery. J. Polit. Econ. 62:124142. doi: 10.1086/257497

CrossRef Full Text | Google Scholar

Haidvogel, D. B., Arango, H., Budgell, W. P., Cornuelle, B. D., Curchitser, E., Di Lorenzo, E., et al. (2008). Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the regional ocean modeling system. J. Comput. Phys. 227, 3595–3624. doi: 10.1016/j.jcp.2007.06.016

CrossRef Full Text | Google Scholar

Haidvogel, D. B., Arango, H. G., Hedstrom, K., Beckmann, A., Malanotte-Rizzoli, P., and Shchepetkin, A. F. (2000). Model evaluation experiments in the north atlantic basin: simulations in nonlinear terrain-following coordinates. Dyn. Atmos. Oceans 32, 239–281. doi: 10.1016/S0377-0265(00)00049-X

CrossRef Full Text | Google Scholar

Hallegraeff, G. M. (1998). Transport of toxic dinoflagellates via ships ballast water: bioeconomic risk assessment and efficacy of possible ballast water management strategies. Marine Ecol. Progr. Series 168, 297–309. doi: 10.3354/meps168297

CrossRef Full Text | Google Scholar

Haller, G. (2001). Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D: Nonlinear Phenomena 149, 248–277. doi: 10.1016/S0167-2789(00)00199-8

CrossRef Full Text | Google Scholar

Haller, G. (2002). Lagrangian coherent structures from approximate velocity data. Phys. Fluids 14, 1851–1861. doi: 10.1063/1.1477449

CrossRef Full Text | Google Scholar

Haller, G., and Yuan, G. (2000). Lagrangian coherent structures and mixing in two-dimensional turbulence. Phys. D Nonlinear Phen. 147, 352–370. doi: 10.1016/S0167-2789(00)00142-1

CrossRef Full Text | Google Scholar

Harrison, C. S., and Glatzmaier, G. A. (2012). Lagrangian coherent structures in the california current system–sensitivities and limitations. Geophys. Astrophys. Fluid Dyn. 106, 22–44. doi: 10.1080/03091929.2010.532793

CrossRef Full Text | Google Scholar

Harrison, C. S., Siegel, D. A., and Mitarai, S. (2013). Filamentation and eddy-eddy interactions in marine larval accumulation and transport. Mar. Ecol. Prog. Ser. 472, 27–44. doi: 10.3354/meps10061

CrossRef Full Text | Google Scholar

Hilborn, R. (1985). Fleet dynamics and individual variation: why some people catch more fish than others. Can. J. Fish. Aquat. Sci. 42, 2–13. doi: 10.1139/f85-001

CrossRef Full Text | Google Scholar

Hilborn, R. (2007). Managing fisheries is managing people: what has been learned? Fish Fish. 8, 285–296. doi: 10.1111/j.1467-2979.2007.00263_2.x

CrossRef Full Text | Google Scholar

Hilborn, R., and Ledbetter, M. (1979). Analysis of the british columbia salmon purse-seine fleet: dynamics of movement. J. Fish. Board Can. 36, 384–391. doi: 10.1139/f79-058

CrossRef Full Text | Google Scholar

Hobday, A. J., Hartog, J. R., Spillman, C. M., and Alves, O. (2011). Seasonal forecasting of tuna habitat for dynamic spatial management. Can. J. Fish. Aquat. Sci. 68, 898–911. doi: 10.1139/f2011-031

CrossRef Full Text | Google Scholar

Holland, D. S., and Sutinen, J. G. (2000). Location choice in new england trawl fisheries: old habits die hard. Land Econ. 76, 133–149. doi: 10.2307/3147262

CrossRef Full Text | Google Scholar

Iverson, A. L., Marín, L. E., Ennis, K. K., Gonthier, D. J., Connor-Barrie, B. T., Remfert, J. L., et al. (2014). Do polycultures promote win-wins or trade-offs in agricultural ecosystem services? J. Appl. Ecol. 51, 1593–1602. doi: 10.1111/1365-2664.12334

CrossRef Full Text | Google Scholar

Jennings, S., and Lee, J. (2012). Defining fishing grounds with vessel monitoring system data. ICES J. Marine Sci. 69, 51–63. doi: 10.1093/icesjms/fsr173

CrossRef Full Text | Google Scholar

Joo, R., Salcedo, O., Gutierrez, M., Fablet, R., and Bertrand, S. (2015). Defining fishing spatial strategies from vms data: Insights from the world's largest monospecific fishery. Fish. Res. 164, 223–230. doi: 10.1016/j.fishres.2014.12.004

CrossRef Full Text | Google Scholar

Kahru, M., Di Lorenzo, E., Manzano-Sarabia, M., and Mitchell, B. G. (2012). Spatial and temporal statistics of sea surface temperature and chlorophyll fronts in the california current. J. Plankton Res. 34, 749–760. doi: 10.1093/plankt/fbs010

CrossRef Full Text | Google Scholar

Kai, E. T., Rossi, V., Sudre, J., Weimerskirch, H., Lopez, C., Hernandez-Garcia, E., et al. (2009). Top marine predators track lagrangian coherent structures. Proc. Natl. Acad. Sci. U.S.A. 106, 8245–8250. doi: 10.1073/pnas.0811034106

CrossRef Full Text | Google Scholar

Kasperski, S., and Holland, D. S. (2013). Income diversification and risk for fishermen. Proc. Natl. Acad. Sci. U.S.A. 110, 2076–2081. doi: 10.1073/pnas.1212278110

PubMed Abstract | CrossRef Full Text | Google Scholar

Klein, E. S., Barbier, M. R., and Watson, J. R. (2017). The dual impact of ecology and management on social incentives in marine common-pool resource systems. R. Soc. Open Sci. 4:170740. doi: 10.1098/rsos.170740

PubMed Abstract | CrossRef Full Text | Google Scholar

Klinger, D. H., Eikeset, A. M., Davíðsdóttir, B., Winter, A.-M., and Watson, J. R. (2018). The mechanics of blue growth: management of oceanic natural resource use with multiple, interacting sectors. Marine Policy 87, 356–362. doi: 10.1016/j.marpol.2017.09.025

CrossRef Full Text | Google Scholar

Klinger, D. H., Levin, S. A., and Watson, J. R. (2017). The growth of finfish in global open-ocean aquaculture under climate change. Proc. R. Soc. Lond. B Biol. Sci. 284:20170834. doi: 10.1098/rspb.2017.0834

CrossRef Full Text | Google Scholar

Le Pape, O., Delavenne, J., and Vaz, S. (2014). Quantitative mapping of fish habitat: a useful tool to design spatialised management measures and marine protected area with fishery objectives. Ocean Coast. Manag. 87, 8–19. doi: 10.1016/j.ocecoaman.2013.10.018

CrossRef Full Text | Google Scholar

Lee, J., South, A. B., and Jennings, S. (2010). Developing reliable, repeatable, and accessible methods to provide high-resolution estimates of fishing-effort distributions from vessel monitoring system (vms) data. ICES J. Marine Sci. 67, 1260–1271. doi: 10.1093/icesjms/fsq010

CrossRef Full Text | Google Scholar

Lehahn, Y., d'Ovidio, F., Lévy, M., and Heifetz, E. (2007). Stirring of the northeast atlantic spring bloom: A lagrangian analysis based on multisatellite data. J. Geophys. Res. Oceans 112:C08005. doi: 10.1029/2006JC003927

CrossRef Full Text | Google Scholar

Lehodey, P., Bertignac, M., Hampton, J., Lewis, A., and Picaut, J. (1997). El niño southern oscillation and tuna in the western pacific. Nature 389, 715–718. doi: 10.1038/39575

CrossRef Full Text | Google Scholar

Lester, S. E., Costello, C., Halpern, B. S., Gaines, S. D., White, C., and Barth, J. A. (2013). Evaluating tradeoffs among ecosystem services to inform marine spatial planning. Marine Policy 38, 80–89. doi: 10.1016/j.marpol.2012.05.022

CrossRef Full Text | Google Scholar

Levin, S., Xepapadeas, T., Crépin, A.-S., Norberg, J., De Zeeuw, A., Folke, C., et al. (2013). Social-ecological systems as complex adaptive systems: modeling and policy implications. Environ. Develop. Econ. 18, 111–132. doi: 10.1017/S1355770X12000460

CrossRef Full Text | Google Scholar

Levin, S. A. (1992). The problem of pattern and scale in ecology: the robert h. macarthur award lecture. Ecology 73, 1943–1967. doi: 10.1007/978-1-4615-1769-6_15

CrossRef Full Text | Google Scholar

MacKenzie, B. R., Almesjö, L., and Hansson, S. (2004). Fish, fishing, and pollutant reduction in the baltic sea. Environ. Sci. Technol. 38, 1970–1976. doi: 10.1021/es034297n

PubMed Abstract | CrossRef Full Text | Google Scholar

Mills, C. M., Townsend, S. E., Jennings, S., Eastwood, P. D., and Houghton, C. A. (2007). Estimating high resolution trawl fishing effort from satellite-based vessel monitoring system data. ICES J. Marine Sci. 64, 248–255. doi: 10.1093/icesjms/fsl026

CrossRef Full Text | Google Scholar

Moore, A. M., Arango, H. G., Broquet, G., Edwards, C., Veneziani, M., Powell, B., et al. (2011a). The regional ocean modeling system (roms) 4-dimensional variational data assimilation systems: part II–performance and application to the california current system. Progr. Oceanogr. 91, 50–73. doi: 10.1016/j.pocean.2011.05.003

CrossRef Full Text | Google Scholar

Moore, A. M., Arango, H. G., Broquet, G., Powell, B. S., Weaver, A. T., and Zavala-Garay, J. (2011b). The regional ocean modeling system (roms) 4-dimensional variational data assimilation systems: part I – system overview and formulation. Progr. Oceanogr. 91, 34–49. doi: 10.1016/j.pocean.2011.05.004

CrossRef Full Text | Google Scholar

Murawski, S. A., Wigley, S. E., Fogarty, M. J., Rago, P. J., and Mountain, D. G. (2005). Effort distribution and catch patterns adjacent to temperate mpas. ICES J. Marine Sci. 62, 1150–1167. doi: 10.1016/j.icesjms.2005.04.005

CrossRef Full Text | Google Scholar

Nese, J. M. (1989). Quantifying local predictability in phase space. Phys. D Nonlinear Phenomena 35, 237–250. doi: 10.1016/0167-2789(89)90105-X

CrossRef Full Text | Google Scholar

Olascoaga, M., Beron-Vera, F., Brand, L., and Kocak, H. (2008). Tracing the early development of harmful algal blooms on the west florida shelf with the aid of lagrangian coherent structures. J. Geophys. Res. Oceans 113:c12014. doi: 10.1029/2007JC004533

PubMed Abstract | CrossRef Full Text | Google Scholar

Orbach, M. K. (1977). Hunters, Seamen, and Entrepreneurs: The Tuna Seinermen of San Diego. Berkley, CA: University of California Press.

Google Scholar

Pinsky, M. L., Worm, B., Fogarty, M. J., Sarmiento, J. L., and Levin, S. A. (2013). Marine taxa track local climate velocities. Science 341, 1239–1242. doi: 10.1126/science.1239352

PubMed Abstract | CrossRef Full Text | Google Scholar

Prants, S. V., Uleysky, M. Y., and Budyansky, M. V. (2012). Lagrangian coherent structures in the ocean favorable for fishery. Dokl. Earth Sci. 447, 1269–1272. doi: 10.1134/S1028334X12110062

CrossRef Full Text | Google Scholar

Rosvall, M., and Bergstrom, C. T. (2008). Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. U.S.A. 105, 1118–1123. doi: 10.1073/pnas.0706851105

PubMed Abstract | CrossRef Full Text | Google Scholar

Scales, K. L., Hazen, E. L., Jacox, M. G., Edwards, C. A., Boustany, A. M., Oliver, M. J., et al. (2017). Scale of inference: on the sensitivity of habitat models for wide-ranging marine predators to the resolution of environmental data. Ecography 40, 210–220. doi: 10.1111/ecog.02272

CrossRef Full Text | Google Scholar

Scales, K. L., Miller, P. I., Embling, C. B., Ingram, S. N., Pirotta, E., and Votier, S. C. (2014). Mesoscale fronts as foraging habitats: composite front mapping reveals oceanographic drivers of habitat use for a pelagic seabird. J. R. Soc. Inter. 11:20140679. doi: 10.1098/rsif.2014.0679

PubMed Abstract | CrossRef Full Text | Google Scholar

Shadden, S. C., Lekien, F., and Marsden, J. E. (2005). Definition and properties of lagrangian coherent structures from finite-time lyapunov exponents in two-dimensional aperiodic flows. Phys. D Nonlinear Phenomena 212, 271–304. doi: 10.1016/j.physd.2005.10.007

CrossRef Full Text | Google Scholar

Shchepetkin, A. F., and McWilliams, J. C. (2003). A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate. J. Geophys. Res. Oceans 108:3090. doi: 10.1029/2001JC001047

CrossRef Full Text | Google Scholar

Shchepetkin, A. F., and McWilliams, J. C. (2005). The regional oceanic modeling system (roms): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 9, 347–404. doi: 10.1016/j.ocemod.2004.08.002

CrossRef Full Text | Google Scholar

Ullman, D. S., and Cornillon, P. C. (2000). Evaluation of front detection methods for satellite-derived sst data using in situ observations. J. Atmos. Oceanic Technol. 17, 1667–1675. doi: 10.1175/1520-0426(2000)017<1667:EOFDMF>2.0.CO;2

CrossRef Full Text | Google Scholar

Watson, J. R., Stock, C. A., and Sarmiento, J. L. (2015). Exploring the role of movement in determining the global distribution of marine biomass using a coupled hydrodynamic size-based ecosystem model. Progr. Oceanogr. 138(Pt B), 521–532. doi: 10.1016/j.pocean.2014.09.001

CrossRef Full Text | Google Scholar

Wessel, P., and Smith, W. H. (1996). A global, self-consistent, hierarchical, high-resolution shoreline. J. Geophys. Res. 101, 8741–8743. doi: 10.1029/96JB00104

CrossRef Full Text | Google Scholar

Wilen, J. E. (2004). Spatial management of fisheries. Marine Resour. Economics 19, 7–19. doi: 10.1086/mre.19.1.42629416

CrossRef Full Text | Google Scholar

Woodson, C. B., and Litvin, S. Y. (2015). Ocean fronts drive marine fishery production and biogeochemical cycling. Proc. Natl. Acad. Sci. U.S.A. 112, 1710–1715. doi: 10.1073/pnas.1417143112

PubMed Abstract | CrossRef Full Text | Google Scholar