Graphical Analysis of A Marine Plankton Community Reveals Spatial, Temporal, and Niche Structure of Sub-Communities

Species-rich communities are structured by environmental filtering and a multitude of associations including trophic, mutualistic, and antagonistic relationships. Graphs (networks) defined from correlations in presence or abundance data have the potential to identify this structure, but species with very high absence rates or abundances frequently near detection limits can result in biased retrieval of association graphs. Here we use graph clustering analysis to identify five sub-communities of plankton from the North Atlantic Ocean. We show how to mitigate the challenges of high absence rates and detection limits. The sub-communities are distinguished partially by their constituent functional groups: one group is dominated by diatoms and another by dinoflagellates, while the other three sub-communities are mixtures of phytoplankton and zooplankton. Diagnosing pairwise taxonomic associations and linking them to specific processes is challenging because of overlapping associations and complex graph topologies. Our approach presents a robust approach for identifying candidate associations among species through sub-community analysis and quantifying the aggregate strength of pairwise associations emerging in natural communities.

1 Introduction

Oceanic phytoplankton and copepods form species-rich communities at the base of the marine food web (Medlin et al., 2006; de Vargas et al., 2015; Fuhrman et al., 2015). These diverse communities can vary widely over space, time, and with environmental forcing. Species can be characterized by traits, which describe their maximal growth rate, trophic role, and biogeochemical function. Ultimately, the traits of species determine the optimal environmental conditions under which each species grows, and thrives, which is summarized as the species’ fundamental niche (Hutchinson, 1957). The selection of species from the broader species pool according to their niches is known as environmental filtering (Lebrija-Trejos et al., 2010). Associations - relationships and/or interactions - can develop between pairs, or groups, of co-occurring species and can influence growth rate and biomass to an extent that is not described by environmental forcing and niches alone. Depending on the intensity or quantity of these associations, they may have a significant effect on community compositions. In communities with strong associations between member species, community structure is an emergent phenomenon as a consequence of species traits, environmental forcing, and inter-species associations.

Graphical models (sometimes referred to as networks, or network models) are being developed as a tool to study ecological communities by identifying and visualizing a wide range of associations between pairs of taxa (Ings et al., 2009; Faust and Raes, 2012; Lima-Mendez et al., 2015; Sunagawa et al., 2015; Poisot et al., 2016; Zhou et al., 2018; Delmas et al., 2019). These associations can be directly observed interactions, such as pollination networks (Blüthgen et al., 2008), or inferred from abundance data using correlations or similar measures of similarity (Steele et al., 2011; Zhang, 2011; Friedman and Alm, 2012; Faust et al., 2012). A graph is composed of vertices (sometimes referred to as nodes), representing taxa, and edges, representing some connection between a pair of taxa. Consequently, one can define a community graph by examining the co-occurrence patterns between all pairs of taxa and determining if there is an association between the pair.

In a diverse community, it may be helpful to know about more than just pairwise associations. Clusters (referred to here as sub-communities) of co-occurring and interacting taxa may result in complex effects on biomass dynamics that are difficult to predict without detailed knowledge of the many potential pairwise associations. Knowledge of sub-communities can reveal information about groups of taxa who interact with the environment, or other groups, in a similar way (Girvan and Newman, 2002). Such sub-communities can be prescribed and defined by features such as functional or size class (e.g. Trombetta et al. (2020)). Alternatively, taxa can be automatically assigned to sub-communities using a clustering algorithm (e.g. Guidi et al. (2016)). Graphs may be directly decomposed into sub-graphs (Orman et al., 2011) to identify associations among groups of taxa who are close, or similar, in some way. These sub-graphs may assist in identifying interactions among trophic levels, hosts and parasites, or plant-pollinator relationships.

In the absence of direct evidence of interactions, observational data (such as abundance or presence-absence data) can be used to determine co-occurrence patterns and make inferences about the most significant pairwise associations. Co-occurrences may be affected by the direct effect of environmental filtering, pairwise interactions, or approximate equivalence of taxa within communities. Thus, it is desirable to account for environmental forcing in graphical analysis. Sometimes this has been done directly, by including environmental variables as vertices in the graph alongside the taxa, highlighting direct relationships (Steele et al., 2011; Eiler et al., 2012). This approach provides insight on the effect of environmental forcing upon the individual, at the cost of information on the impact of that forcing upon the relationships between taxa. Others have used community graphs, and sub-graphs, to investigate the impacts of community structure and species interactions on processes such as carbon export (Guidi et al., 2016) by identifying the sub-communities which are strongly associated with that process.

Here we use observations of more than 300 plankton taxa gathered over more than 60 years in the North Atlantic Continuous Plankton Recorder survey to develop a co-occurrence graph for marine plankton. Our analysis documents the community structure of plankton in the North Atlantic, enabling an investigation into positive and negative species associations, pairwise trophic interactions, and interactions among and within sub-communities. Observed sub-communities emerge as a consequence of environmental filtering and species interactions, so we analyze the spatial and temporal overlap between the sub-communities and the realized niche of sub-communities. We propose solutions to several challenges that arise when analyzing this kind of data. The data is sparse, consisting mostly of zero abundances, although an unknown number of these absences likely represent a failure to detect a taxon than a true absence. We can screen for potential interaction between taxa through the co-occurrence graph, and we propose that interactions between and within sub-communities can highlight potential interactions more clearly than pairwise co-occurrences. We show how spatial and temporal patterns of sub-community abundance can document significant differences between sub-communities, as well as similarities that may lead into seasonal succession. Finally, we demonstrate a negative correlation between niche distance and association measured by correlation between pairs of taxa, to quantify the relative importance of niche overlap relative to interactions in determining community structure.

Materials and Methods

2.1 Data

2.1.1 Biological Data

In this study we investigate the planktonic community in the region of the North Atlantic ocean bounded latitudinally by ~ 40°N to 65°N and longitudinally by ~70°W to 10°E, between 1958 and 2014. The biological data are derived from samples collected by the continuous plankton recorder (CPR) survey in this region (Hardy, 1939; Richardson et al., 2006; Johns et al., 2019). The CPR is a plankton sampling device that is towed at a standard depth of ~7 m (Hays and Warner, 1993) by ships of opportunity along regular shipping routes (Figure 1). Water continually enters the sampling device through a small square aperture (1.27×1.27 cm ≈ 1.61 cm²) and flows through an expanding tunnel and exits through the rear of the device. As the device is towed, the flow around the recorder rotates a small propeller which advances a fine silk filtering mesh within the device upon which plankton are continually filtered. The roll of mesh is divided into panels such that a single panel represents 3.1 m³ of water, and is equivalent to 18.5 km travelled (Warner and Hays, 1994). The relatively large size of the mesh (270 μm) means that some smaller plankton species are either under-counted or missed entirely (Richardson et al., 2006). As a consequence, many smaller plankton groups, notably nanoplankton and picoplankton, and their relationships are not included in this study.

FIGURE 1

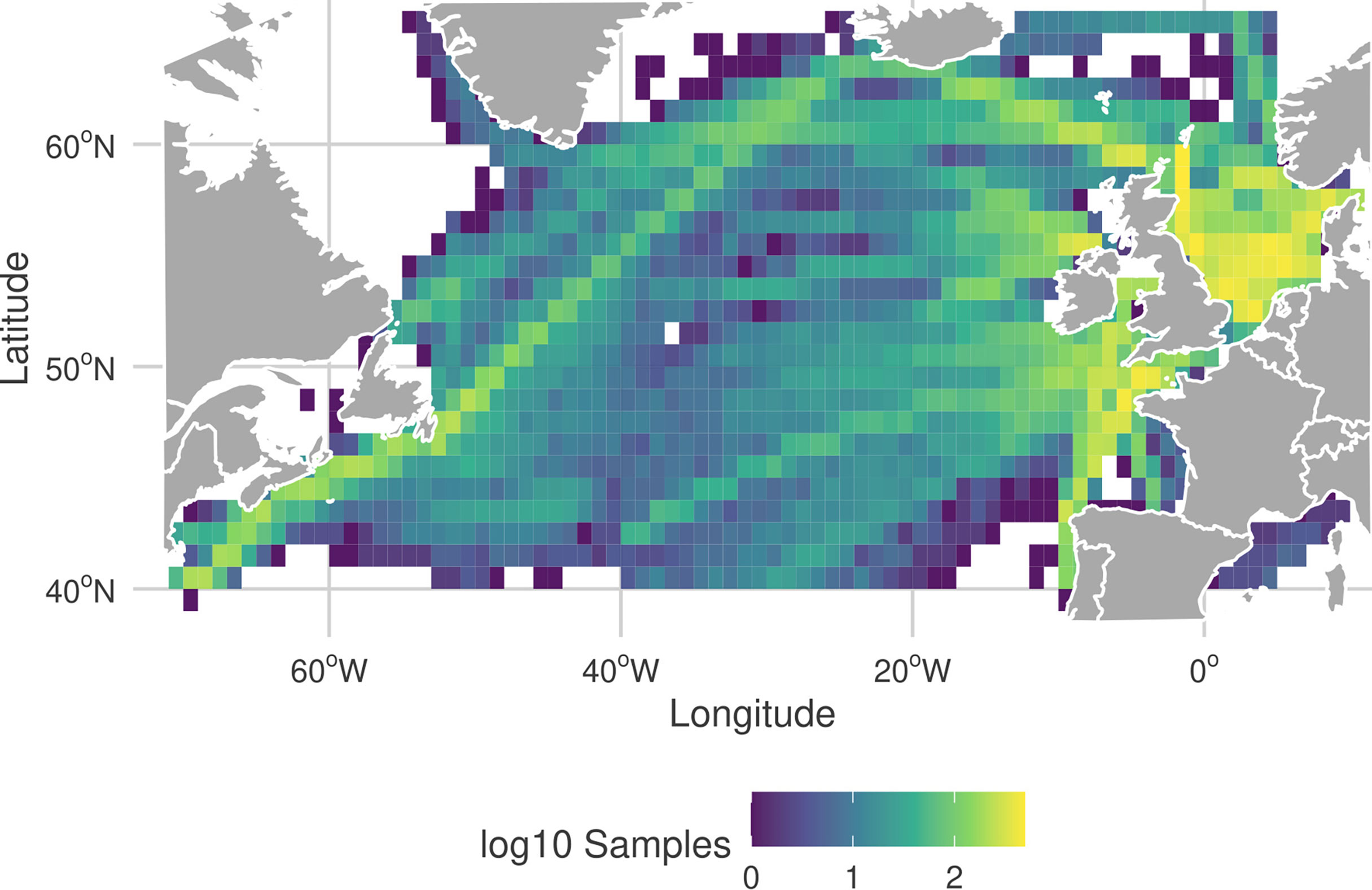
Figure 1 Frequency and location of the CPR samples in the North Atlantic region, from the filtered dataset used in this study. More yellow corresponds to a higher frequency of CPR observations in a 1°×1° grid cell. Color scale of the frequencies are on a log₁₀-scale.

The raw plankton count data from the CPR has been aggregated into monthly 1×1 degree boxes (Irwin et al., 2012; McGinty et al., 2018). The resultant CPR dataset consists of 110,000 samples and identifies 344 unique taxa (172 phytoplankton and 172 zooplankton), most of which are identified to species-level. The majority of taxa are very rare, appearing in fewer than 1% of samples. In order to reduce the sparsity of the data we removed taxa who appeared in fewer than 2.5% of samples, and since our goal is to describe patterns of co-occurrence and taxa associations, we removed samples which contained fewer than five unique taxa. The result is a dataset containing p=59 taxa over n=61,990 samples. Zooplankton represent 27 taxa within the reduced dataset, 22 of which are copepods. The copepods have been grouped by diet as either Herbivore (9), Omnivore (8), or Carnivore (4) according to their diet following Richardson et al. (2006). One copepod representing order Harpacticoida was not classified. The five remaining zooplankton taxa are grouped together. The remaining 32 taxa are phytoplankton and have been grouped into diatoms (20) and dinoflagellates (12). A breakdown of taxa in the reduced dataset is shown in Table S1 in the Supplementary Material. Taxonomic names follow those used by the CPR dataset.

2.1.2 Environmental Data

Environmental data were not collected contemporaneously with biological samples. In order to characterize planktonic and sub-community niches we combined the CPR data with environmental data from external sources. Macro-nutrient concentrations (nitrate, phosphate, silicate), oxygen saturation, salinity, and mixed layer depth (MLD) were collected from the World Ocean Atlas 2013 (Boyer et al., 2013). Sea surface temperature (SST) was collected from Hadley SST2 (Rayner et al., 2006), bathymetric depth from GEBCO (https://www.gebco.net), chlorophyll-a from GlobColour (https://www.globcolour.info), and sea surface photosynthetically available irradiance (PAR) was obtained from SeaWiFS (https://oceancolor.gsfc.nasa.gov). All environmental data is aggregated to the same 1°×1° grid cells as in the CPR data. Not all data is available across all years of the CPR dataset. As such, all 10 environmental variables are averaged over all available years for each dataset to generate monthly climatology, so that we were not including yearly variation in only a few of the covariates.

2.2 Inference of Graphical Models

We use a graph (sometimes referred to as a network) to represent relationships (associations) between different planktonic taxa in the North Atlantic. We will first compute a matrix of associations, $\widehat{T}=\left\{T_{ij}\right|i,j\in 1,\dots ,p\}$ from which we will then define a graph. A graph is defined by G=(V,E) where V={V_i | i=1,…,p} is the set of p vertices (representing taxa), E={(V_i,V_j) | T_ij≠0}⊆(V×V) is the set of edges (representing inferred relationships) (West, 2001). We can assign various attributes to V and/or E for example weights or sign to edges to indicate strength or type of association between pairs. A graph has an associated adjacency matrix $\widehat{A}$ with elements A_ij=1 if there is an edge between vertices i and j, 0 otherwise. In this work, vertices will represent the taxa from the CPR data (1 vertex per taxon). Edges will represent inferred relationships between the taxa. The inferred graph will be directed, so that the relationships will have direction and $\widehat{T}$, $\widehat{A}$ will be asymmetric. This direction of the relationships will indicate dependency. A directed edge from taxon i to taxon j such that the head of the arrow is at taxon j indicates that (the abundance of) taxon j is conditionally upon (the abundance of) taxon i. The degree of a vertex is defined as the total number of vertices connected to it, d(i)=∑_j,j≠iA_ij+∑_j,j≠iA_ji . The degree of a vertex accounts for both in-bound and out-bound relationships in directed graphs, and excludes the vertex itself.

Common methods for inferring graphical models require knowledge of the pairwise correlations or similarity between vertices (in this case taxa) (Faust and Raes, 2012), whether directly (Steele et al., 2011; Berry and Widder, 2014) or as part of a regression method (Meinshausen and Bühlmann, 2006). The most common correlation metric is the Pearson (sample) product-moment correlation coefficient. However, this is not suitable for non-normally distributed data (Calkins, 1974; Bishara and Hittner, 2012; Puth et al., 2014). For instance, plankton abundance data are typically approximately log-normally distributed as a consequence of exponential growth (Crow and Shimizu, 1987). Furthermore, sparse data, such as the CPR data, with many zeros resulting from a failure to detect taxa at low abundance (Mutshinda et al., 2022) (as well as true absences), are poorly summarized by Pearson correlation. To demonstrate the limitation of sparseness, we generated normally distributed data for two random variables with a range of known correlation values. We then replaced a proportion of the data, for each variable, with zeros either randomly, or by truncation (e.g. for 10% zeros, all values below the 10^th percentile are set to zero), for a series of sparsity levels and recalculated the Pearson’s correlation. The results, shown in Table 1, demonstrate that the Pearson’s correlation coefficient is damped for zero-inflated data. In particular, negative correlations are significantly damped for truncated data. As a consequence pairwise Pearson correlation will result in biased estimates yielding a clouded view of correlations.

TABLE 1

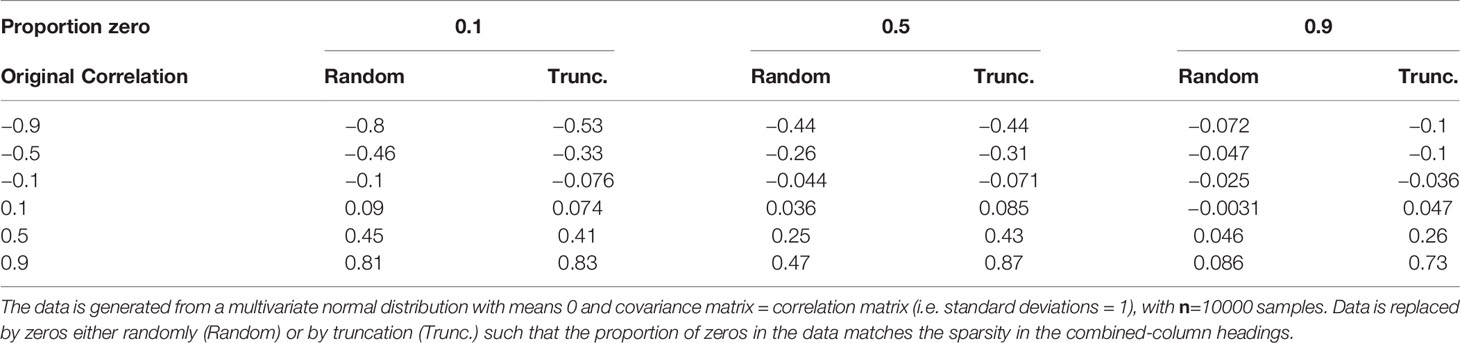
Table 1 Effect of different levels of sparsity (proportion of zeros) on the standard Pearson (sample) product-moment correlation coefficient.

To overcome the impacts of sparse data, we use the SPRING package for R (Yoon et al., 2019) to infer the plankton association graph. SPRING has three constituent components. First, the mixedCCA package of Yoon et al. (2020, 2021) is used to estimate the correlation matrix under the assumption that the data is truncated. Secondly, the estimated correlation matrix is used as an input to the Meinshausen and Bühlmann (2006) LASSO regression method to find the significant relationships, implemented in the Huge package (Zhao et al., 2012). Finally, the LASSO parameter, which controls the sparsity of the resulting graph, is selected using the StARS (Stability Approach to Regularization Selection) method (Liu et al., 2010).

In order to use SPRING we must make the assumption that sparsity in the CPR data is a result of truncation. Under this assumption, zeros are assumed to be non-zero and below some threshold value (perhaps as a consequence of measurement limitation), but recorded as zero. This is a reasonable assumption for the CPR data as several processes can lead to false zeros, including failure to capture individuals displaced by the bow wave, the large mesh in the sampling silk, and low abundance leading to sampling variation including a failure to detect the taxa (Richardson et al., 2006). Furthermore, the semi-quantitative counting method could result in missed observations.

The first component of SPRING, the mixedCCA package of Yoon et al. (2020, 2021)recovers correlations from sparse truncated data using the truncated non-paranormal (tNPN) model. The idea is to relate a random sample from a truncated distribution to an underlying multi-variate normal distribution $(\mathcal{N}(\mathbf{0},\widehat{\Sigma }),{\sigma }_{ii}=1)$ with a known correlation matrix, $\widehat{\Sigma }$ (referred to as the latent correlation matrix). This model is derived from, and is an extension to, the non-paranormal model of Liu et al. (2009) which relates multi-variate non-normally distributed data to an underlying multi-variate normal distribution. Yoon et al. (2020) define a bridge function between the sample Kendall’s Tau and the latent correlation matrix. We evaluated the ability of mixedCCA to recover correlations in sparse data (Table 2). We generated 2-dimensional multivariate log-normal data derived from 2-dimensional normal distributions with 0-mean and prescribed correlations. The simulated data was then truncated such that a prescribed proportion of the data is zero. Pearson and latent (tNPN) correlations were then computed and compared. We found that mixedCCA accurately recovered correlations at all sparsity levels.

TABLE 2

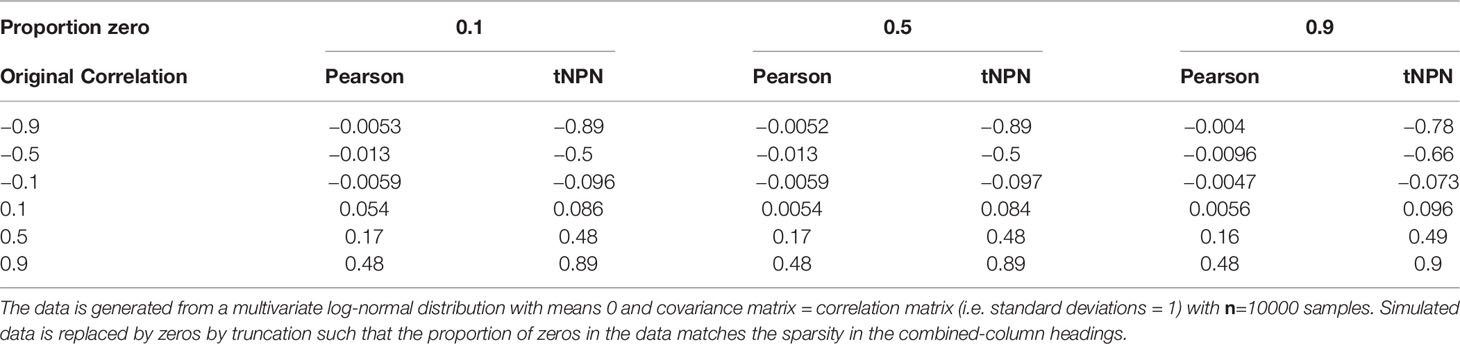
Table 2 Effect of different levels of sparsity (proportion of zeros) in the form of truncation on the standard Pearson (sample) product-moment correlation coefficient and the truncated non-paranormal correlation estimate $\widehat{\Sigma }$.

The estimated latent correlation matrix computed using the non-paranormal model assumption was used to compute a directed graph. A directed graph is defined by a non-symmetric adjacency matrix. The second component of SPRING implements a Meinshausen-Bühlmann neighborhood selection to detect significant associations (Meinshausen and Bühlmann, 2006). This takes the form of a LASSO regression (Tibshirani, 1996) which estimates a vector of association strengths, β^j, for each taxon, j:

$\begin{array}{ll}{\beta }^j=\underset{\beta \in {ℝ}^p,{\beta }_j=0}{\mathrm{argmin}}\left\{{\beta }^T\widehat{S}\beta -2{\beta }^T{s}^j+\lambda \Vert \beta {\Vert }_1\right\}& (1)\end{array}$

Here $\widehat{S}$ is the sample covariance matrix with j-th column s^j, p = 59 is the number of taxa, λ is the penalization parameter and controls the sparsity of the graph (see below). SPRING uses equation (1), and replaces the covariance matrix, $\widehat{S}$ with the estimated correlation matrix computed with mixedCCA, $\widehat{\Sigma }$. The β ^j vectors form the columns of a matrix, $\widehat{\beta }$ with elements β_ij which defines the graph. A non-zero β _ij will indicate that an edge, representing an association, between taxon i to taxon j i.e.: taxon j conditionally depends on taxon i.

A global λ-value is selected for the whole graph using StARS (Stability Approach to Regularization Selection) (Liu et al., 2010), which is implemented in the pulsar R package (Müller et al., 2016). StARS estimates the optimal λ from a λ-path, composed of a sequence of 100 increasing λ-values from the complete (all possible edges) to the empty (0 edges) graphs at the extrema. A set of graphs for each λ-value are computed from 50 sub-samples of the data, each sub-sample contains 80% of the data without replacement. The λ-value that results in the most stable (results in the least variation between graphs) non-empty graph is then selected as the global λ.

We ignore the magnitude of the association and define an unweighted, directed graph from the matrix:

$$\widehat{T}=\text{sign}\left(\widehat{\beta }\right).$$

A common approach to interpreting relationships from such a matrix is shown in Figure 1 of Faust and Raes (2012), summarized in Table 3. For example, in the case of T_ij=1, T_ji=−1 we have predation or parasitism. In this case, taxon j responds positively to taxon i whereas taxon i responds negatively to taxon j we could argue that individuals of taxon j consumes individuals of taxon i The graph object is then constructed from $\widehat{T}$ and analyzed using the igraph package for R (Csardi and Nepusz, 2006).

TABLE 3

Table 3 Interpretation of the sign of a pairwise association value from $\widehat{T}=\text{sign} \left(\widehat{\beta }\right)$, following Faust and Raes (2012), and number of edges (and pairs) of that association type in G.

2.3 Sub-Community Detection and Analysis

Data gaps and variability can result in the failure to detect pairwise associations and false discovery of relationships (Lima-Mendez et al., 2015; Yambartsev et al., 2016). For example, a pair of unconnected taxa who have an association in common are also likely to be associated. We seek to account for such missed connections, whilst also minimizing the effects of false connections.

We define sub-communities as edge-dense (relative to the whole graph) sub-graphs, i.e. groups of vertices who are highly connected. Sub-communities of taxa within the graph are identified using the Walk-trap algorithm (Pons and Latapy, 2005). The Walk-trap algorithm partitions a graph based upon the idea that random walks on a graph are likely to remain (or become trapped) within densely connected components. The algorithm computes a distance between pairs of vertices by estimating the probability that a random walk of length t starting from vertex itraverses vertex j. First, the graph is transformed into an undirected graph, with self-connection. This ensures that an isolated, connected, pair of vertices have zero distance and be detected as a sub-community. Next, compute the probability matrix ${\widehat{P}}^t$ here the elements, $P_{ij}^t$ are the probabilities of traversing from vertex i to vertex j in t steps. Finally, compute the Euclidean distance between the i-th and j-th rows of ${\widehat{P}}^t$.

The resulting distance, is then used to construct a dendrogram from which an optimal clustering that maximizes the modularity (Newman and Girvan, 2004; Newman, 2006) is selected. Orman et al. (2011) demonstrate that the Walk-trap algorithm consistently achieves good results in determining community structure in controlled artificial networks. Here, we set t = 4, which is the default value for the implementation in igraph; our testing did not find any significant differences in sub-community breakdown for higher values of t.

To analyze the behaviour of the resulting sub-communities (responses to environmental factors, and other sub-communities) we need to determine whether or not a given sub-community is present or not. One approach would be to assume that the sub-community is present if any of its members are present in a sample. Alternatively, consider only samples where all members of sub-community are present for sub-community presence. The first case would be too broad, and would include samples which may not be indicative of conditions favorable for the whole sub-community. Most of the samples would be included and it may be difficult to differentiate the behavior of each sub-community. In the latter case, it is likely that too few samples would be included for any robust analysis, especially for larger sub-communities. To find a middle ground between these two cases, a sub-community will be deemed to be present if at least 30%, with a minimum of 2, of its member taxa (rounded-down) are present. For example, a sub-community with 10 members would have a presence threshold of floor(10×0.3)= 3 members present. Following this definition we require a minimum size to sub-communities of five member taxa. Smaller sub-communities would require a greater proportion of the members to be detected in a sample for presence and may be more susceptible to their presence being controlled by a single taxon.

To test the statistical significance of the detected sub-communities, we verify that they are significantly edge-dense relative to the whole graph. We generate an edge-density distribution by computing edge-densities of random sub-graphs from the graph. 1,000,000 random sub-graphs will be constructed by (uniformly) randomly selecting vertices from the graph such that number of vertices in each random sub-graph falls within the range of sizes from the detected sub-communities. We will further test the strength of the sub-communities by computing the modularity (Newman and Girvan, 2004) of the graph subject to the resulting sub-community breakdown. Modularity is based upon the idea that we would not expect to see community structure in a random graph. It is a measure of the proportion of edges that connect to nodes of the same sub-community, minus that proportion if the edges were random. Modularity values for real-world graphs with strong community structure typically range between 0.3 to 0.7 (Newman, 2006; Steele et al., 2011). Another strong indicator of high edge-density is the presence of motifs, or complete (fully connected) sub-graphs. Presence of such motifs can be considered to be more strongly indicative of community structure than edge-density (Watts and Strogatz, 1998). The most common motif is the triangle, complete sub-graphs of order 3. Many methods to detect sub-communities make use of this idea, for example Prat-Pérez et al. (2012); Tsourakakis et al. (2017). Here we examine the distribution of triangles across the graph to evaluate the strength of the sub-community breakdown by calculating the proportion of triangles that are contained entirely within the sub-communities.

2.4 Niche Distance

One of the major challenges in interpreting community graphs is determining if the detected associations are real. For example, a pair of taxa may be associated mutualistically (Table 3), however this may actually be a consequence of sharing a similar niche, or being limited by the same resource. We examine the differences between taxa, or sub-communities, by comparing their niches. A taxon’s fundamental niche is defined as a hyper-volume in niche-space where the taxon can persist. To analyze how similarities, or differences, between taxa affects the community structure, in particular how they affect the associations between and within sub-communities, we calculate a matrix of pairwise mean niche distances. Two taxa with similar niches will have a small mean niche distance, whereas taxa with very different niches will have large mean niche distance. To compute niche distance, center and scale each physical and biological variable (by mean and standard deviation respectively) for all samples in the data. For only the samples in which each taxon is present, compute the mean niche vector by calculating the mean of each scaled variable. Finally, calculate the niche distance by computing the standard Euclidean distance between each pair of mean niche vectors. The result is a symmetric p × p matrix $\widehat{M}$ of niche distances where M_ij=M_ji is the niche distance between taxa i and j. We perform a linear regression for $\widehat{M}$ against $\widehat{\Sigma }$ to determine what role niche similarity plays in the detected relationships. From the residual variability we can start to determine whether the detected associations are real, and to what extent. By extending the concept of the niche to the sub-community-scale, we can compare sub-communities. We compute a sub-community niche by examining the range of environmental and biological variables over which the sub-community is deemed to be present (following the procedure for presence outlined above). We also calculate mean niche distances for the sub-communities in order to determine how similar the sub-communities might be.

3 Results and Discussion

3.1 North Atlantic Plankton Association Graph

Our graphical model of the North Atlantic plankton community structure, G, is a sparse directed graph with a vertex set, V, representing the 59 taxa, and an edge set, E⊆(V×V) , containing a total of 185 edges between the taxa. Two unconnected vertices: unidentified species from diatom genus Navicula, and unidentified species from copepod order Harpacticoida, are removed from G and excluded from any further analysis. This results in a reduced vertex set, V, containing 57 taxa with an edge-density of 5.8% (Figure 2). Mean and median vertex degree are 6.49 and 6 respectively, degree does not distinguish between edge direction. The taxon with highest degree is the dinoflagellate species Ceratium tripos (now renamed to Tripos muelleri) with 14 total edges, affecting eight taxa and affected by six taxa. High degree taxa are important and act as hub species who have a large influence on the structure and behavior of the community (Berry and Widder, 2014). The majority (169) of associations are positive, most of which form a mutualistic relationship pattern (Table 3, Faust and Raes (2012)). The remaining 16 associations are negative, split between competitive and amensal patterns. Negative associations were not observed between pairs of phytoplankton taxa. The ratio of positive associations to negative associations is consistent with similar studies, for example Lima-Mendez et al. (2015); Zhou et al. (2018).

FIGURE 2

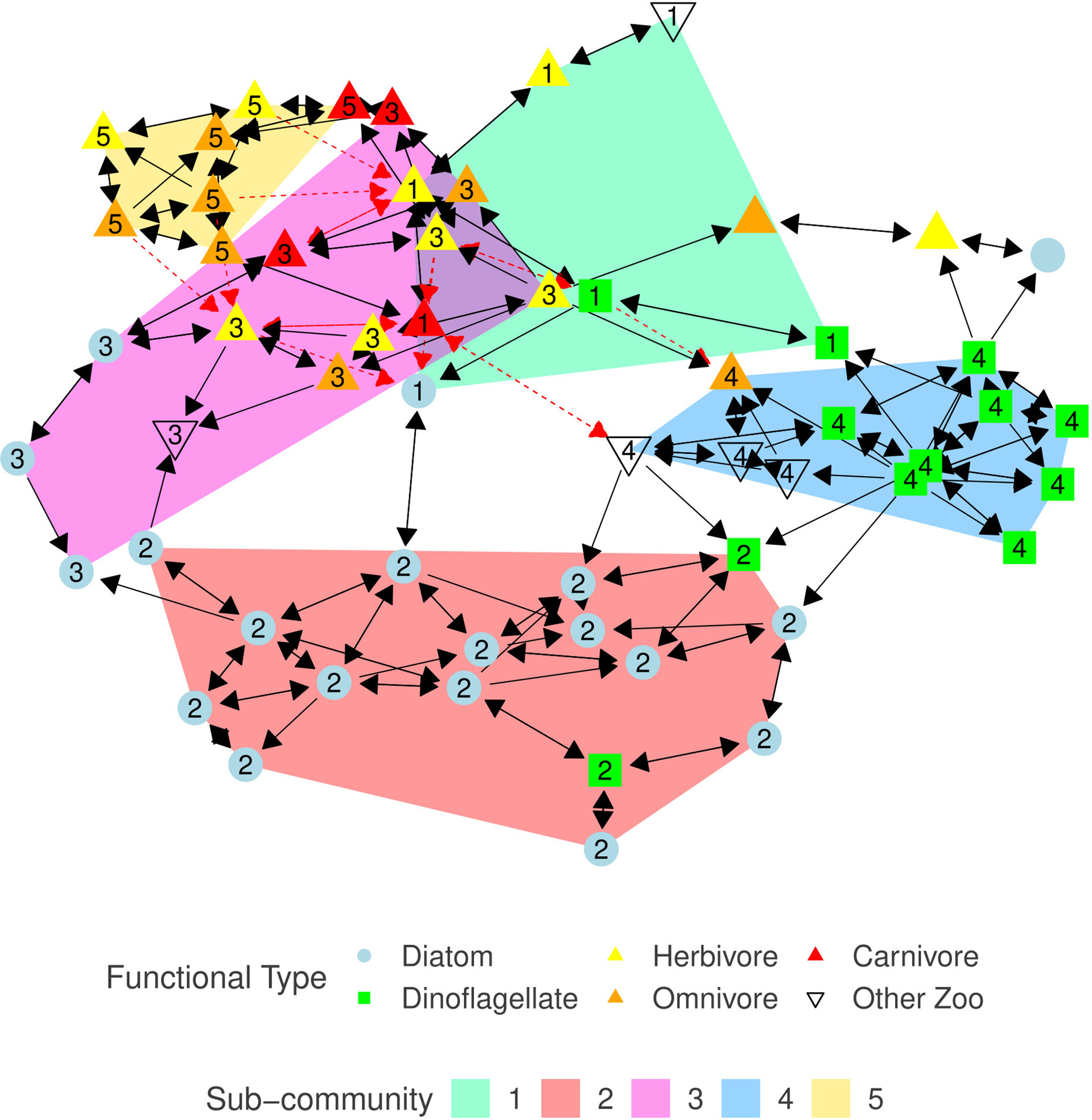
Figure 2 Plankton association graph, G=(V,E) , constructed from the CPR data using SPRING. Blue circles represent diatoms, green squares are dinoflagellates, up triangles represent zooplankton with the color indicating the copepods diet - yellow, orange, red correspond to herbivore, omnivore, and carnivore respectively, and uncolored down triangles represent other zooplankton classifications. Black solid arrows indicate a positive effect, red dashed arrows indicate a negative effect. Arrow direction from taxon x to y indicates that taxon y responds to the presence of taxon x. Vertex layout is determined using the Reingold-Fruchtermann force-directed algorithm (Fruchterman and Reingold, 1991). Shaded regions, and numeric labels (corresponding to the equivalent sub-graph index, G_i ), indicate sub-community membership (if any), for sub-communities containing at least five members; as calculated using the walk-trap algorithm.

3.2 Sub-Communities

The walk-trap community detection algorithm, applied to G , detects five distinct sub-communities, G₁−G₅ , with at least five members. Each taxon is assigned to at most one sub-community. Sub-community G₂ is entirely composed of phytoplankton (primarily diatoms), whereas G₅ is made-up of only zooplankton. Two dinoflagellates who are members of G₂ , species from the genera Gyrodinium and Exuviaella, have been observed in similar sub-community structures (Trombetta et al., 2020). All sub-communities contain more than one functional classification (Table 4; Supplementary Table S1). Although the vast majority of associations are mutualistic, the mixture of herbivorous copepods and phytoplankton in G₁ and G₃ combined with the documented described difficulty in detecting trophic grazing interactions through our association analysis suggests that there may be undetected trophic links in these sub-communities.

TABLE 4

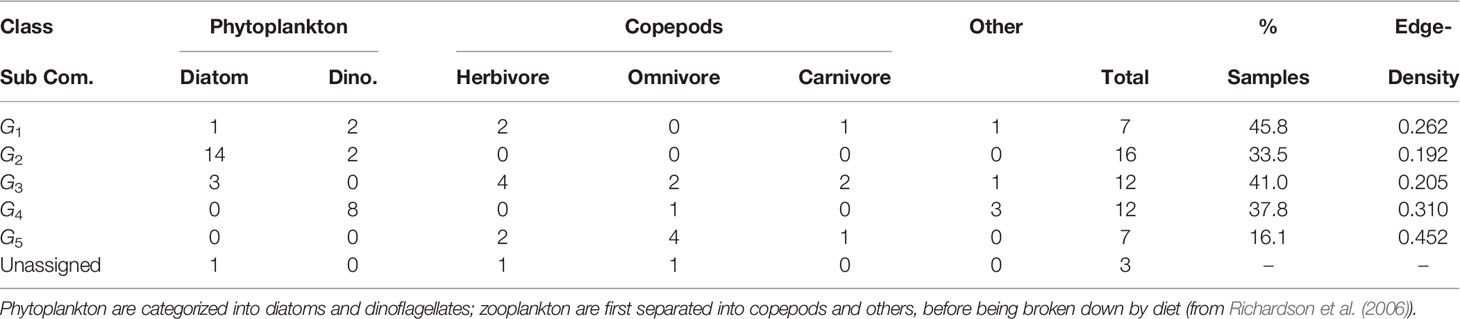
Table 4 Breakdown of functional classification of sub-community membership, total unique members, proportion of total samples in which each sub-community is observed, and edge-density for each sub-community.

The most frequently observed sub-community is G₁ (45.8% of all samples). G₅ is the rarest (16.1%) (Table 4). Three taxa are classified as unassigned, however they were within a sub-community with fewer than five members. Following our restrictions on sub-community size, this small group is removed from further sub-community niche and behavior analysis.

The edge-densities for each of the sub-communities range between 0.192 and 0.452 (Table 4), compared to 0.058 for G (excluding unconnected vertices). All sub-communities are significantly denser than the full graph (Figure 3) (p< 0.0005 - permutation test). Furthermore, we also find that 81.3% of triangles are contained within sub-communities, and 77.8% of all edges are between taxa within the same sub-community. This further indicates that these sub-graphs are edge-dense in comparison to G. The modularity of the graph given this sub-community breakdown is 0.59. Combining all of this indicates that this sub-community breakdown is a statistically significant breakdown of G.

FIGURE 3

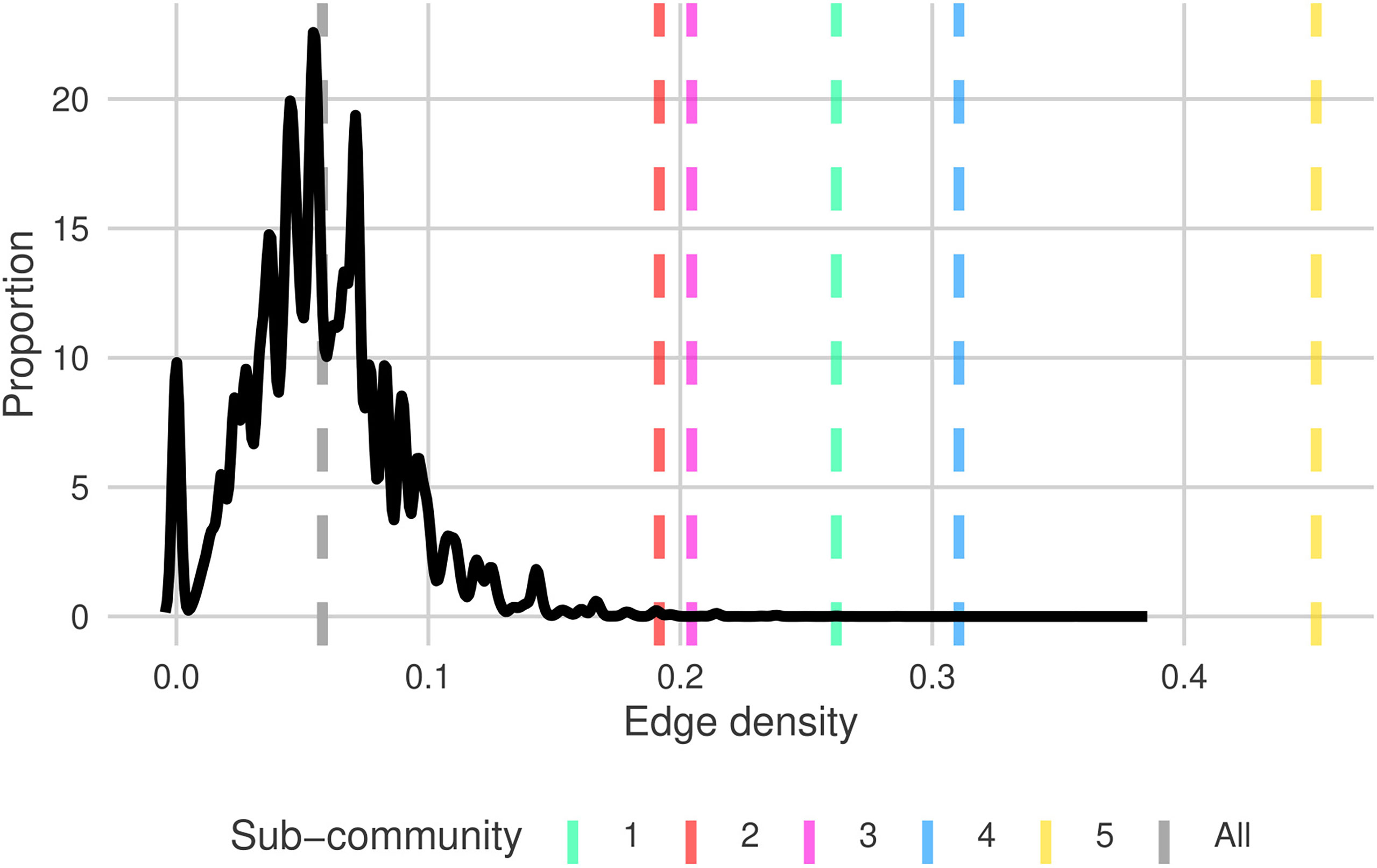
Figure 3 Distribution of edge densities for random sub-graphs of size ∈[7,16] (uniform random) from north Atlantic plankton community graph, G (solid black). Dashed grey and colored lines are the edge densities for G and each of the sub-communities G₁→G₅ , respectively. Sub-community line colors match the shaded regions in Figure 2.

3.3 Sub-Community Analysis

We identified a negative relationship between pairwise niche distance and estimated correlation, $\widehat{\Sigma }$ (Figure 4; Table 5). Pairs of taxa whose abundance patterns are positively correlated are likely to have very similar niches. The adjusted-R² values indicate that approximately 50% of the variability in estimated correlation can be explained by niche similarity. Niche distance is a good predictor for correlation strength. Correlations between pairs of taxa who share sub-community membership are mostly positive (287/297 pairs) and have similar niches (Table 6). Negatively correlated pairs of taxa have large mean niche distance. Correlations for pairs of taxa in different sub-communities are more variable (Figure 4), 45% of the correlations are negative.

FIGURE 4

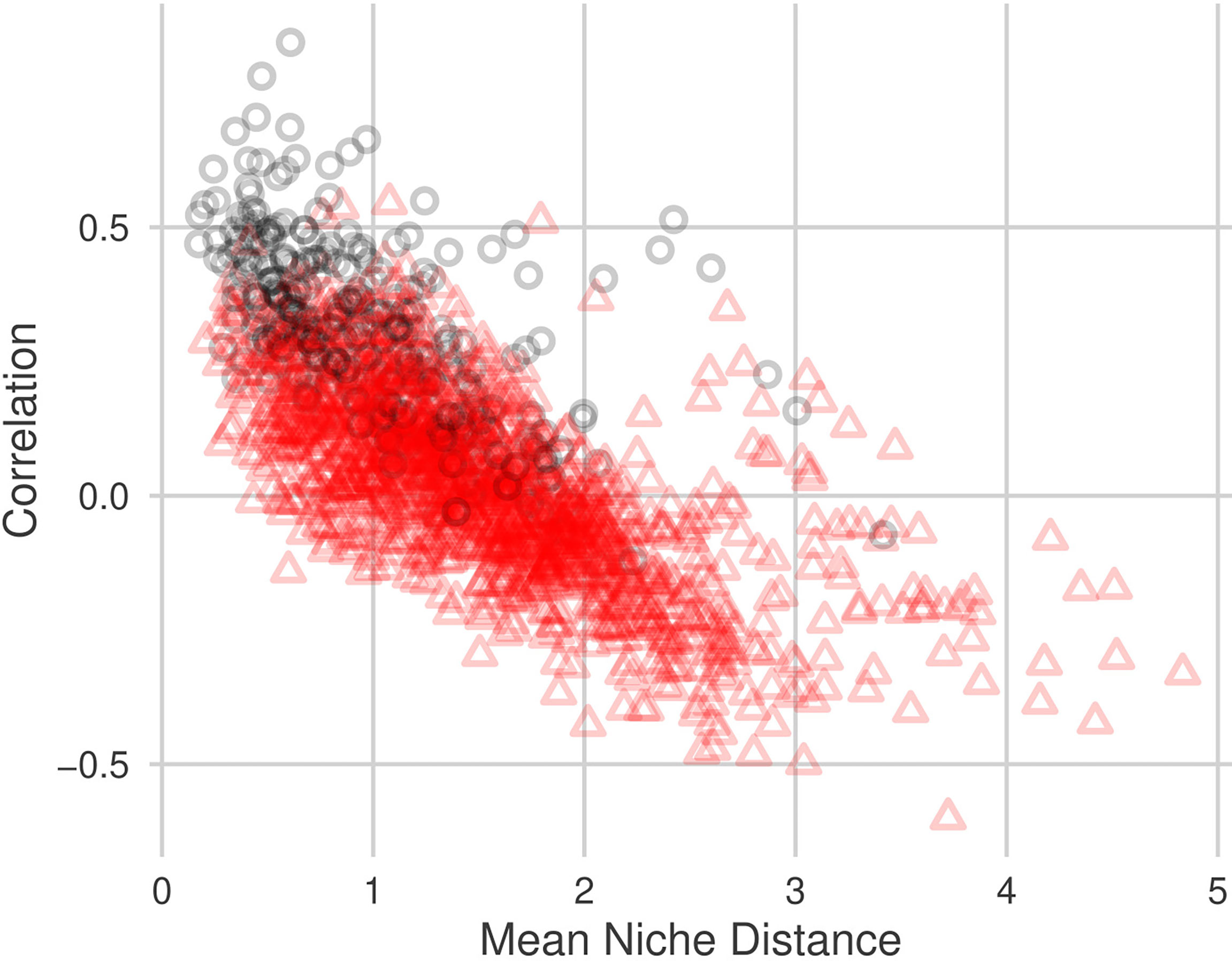
Figure 4 Relationship between pairwise mean niche distance and pairwise NPN correlation estimate, $\widehat{\Sigma }$. Black circles indicate that the taxa pair are within the same sub-community, red triangles indicate that the taxa pair are in different sub-communities. Niche distances were calculated using all 10 environmental variables described in Section 2.1.2.

TABLE 5

Table 5 Summaries (number of data points in subset n, intercept and gradient of linear model, adjusted-R² and p-value) of the simple linear models fitted to the correlation estimate with mean niche distance as predictor variable.

TABLE 6

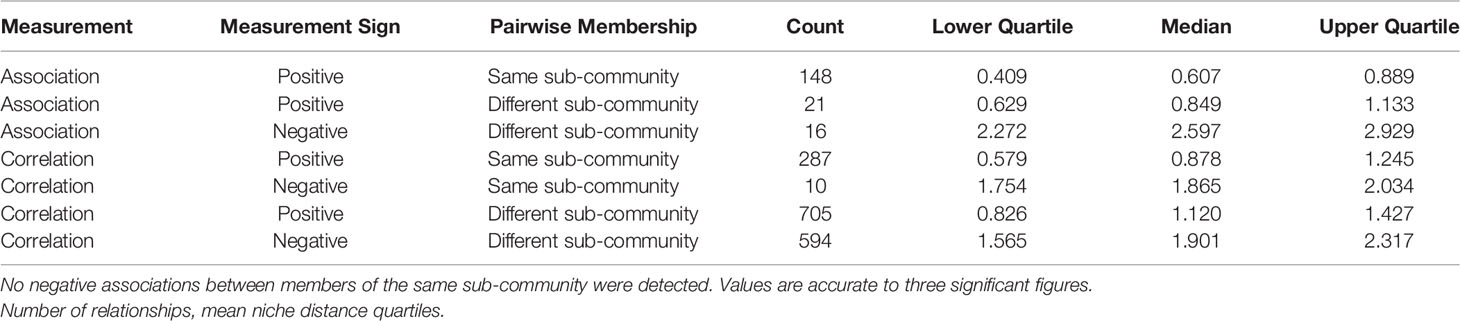
Table 6 Breakdown summary of mean niche distance by measurement (correlation or graph association), measurement sign (positive or negative relationship), and pairwise sub-community membership.

Associations between pairs of taxa within the same sub-community (G_i→G_i) are always positive. Most of these same sub-community pairs have low niche distance (120 pairs, 81%, with niche distance < 1). In contrast, niche distances between taxa who are members of different sub-communities (G_i→G_j) are more variable (Table 6). Pairs of taxa with positive associations tend to have very similar niches in general, more-so for pairs of taxa who share sub-community membership. In contrast, pairs of taxa who have distinct niches will typically have a negative association.

The five detected sub-communities are broadly split into three groups defined by their sub-community niches (Figures 5, 6). G₁ and G₂ have similar niches defined by a preference for cooler, more nutrient rich waters. G₂ can be described as a cold diatom group, its membership is predominantly diatoms. G₃ and G₄ who also have similar niches, tend to be found in warmer, more nutrient limited parts of the north Atlantic. G₅ has a similar temperature and nutrient niche to G₃ and G₄ however it has a narrower salinity niche and is associated with lower PAR. The association with lower PAR of G₅ matches the seasonality of this sub-community, we mostly observe this group in the winter months (Figure 7). A hierarchical clustering of mean niche distance further supports this grouping of sub-communities into (G₁,G₂), (G₃,G₄), and G₅ (Figure 6).

FIGURE 5

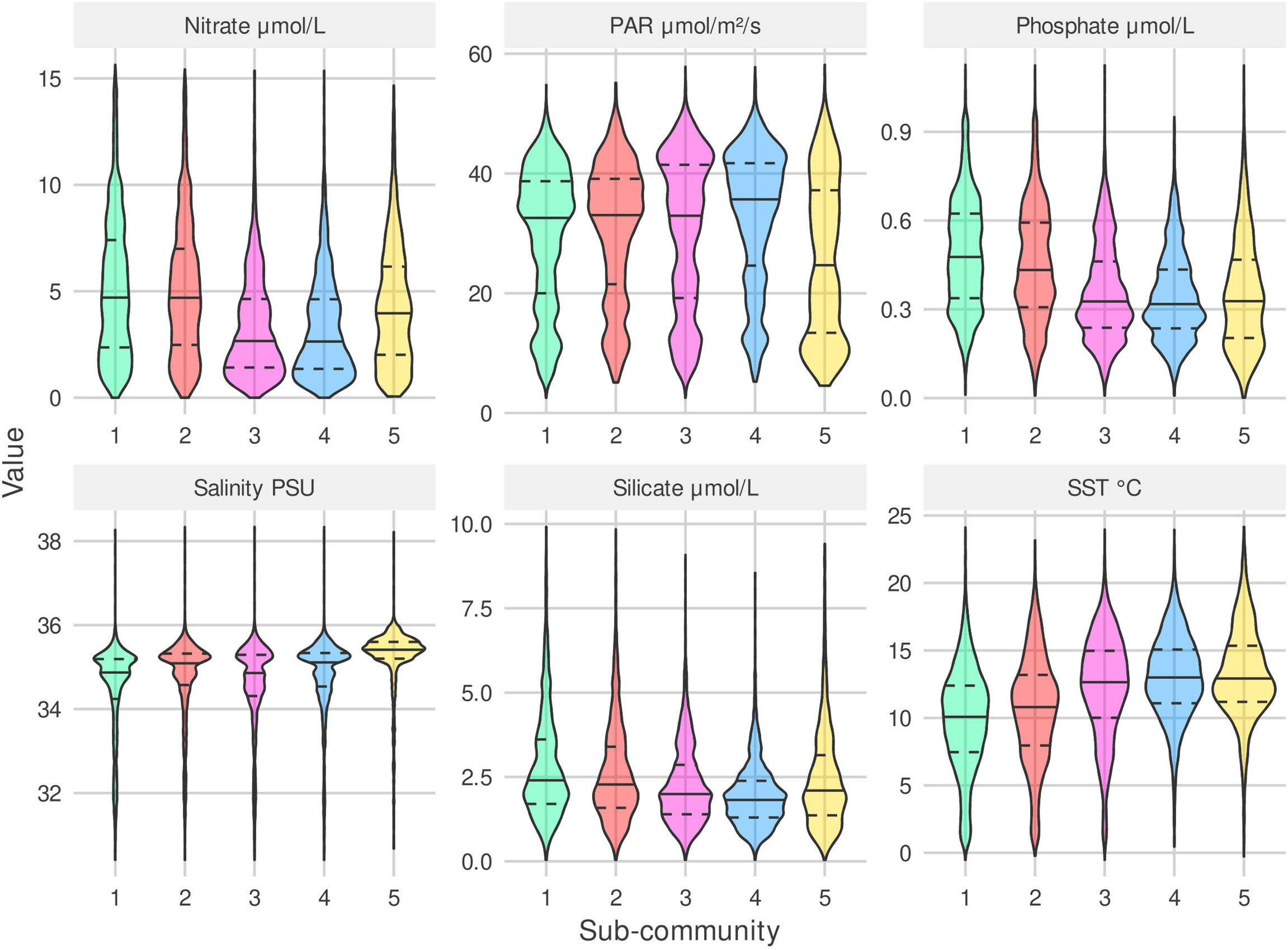
Figure 5 Sub-community niches. Violin plots (including median (solid), 25% and 75% percentiles(dashed)) for six environmental variables over samples where each sub-community is determined to be present (samples containing least 30% (rounded down) of a sub-community’s members). Sub-community colors and numeric-labels match the colored regions and labels of Figure 2.

FIGURE 6

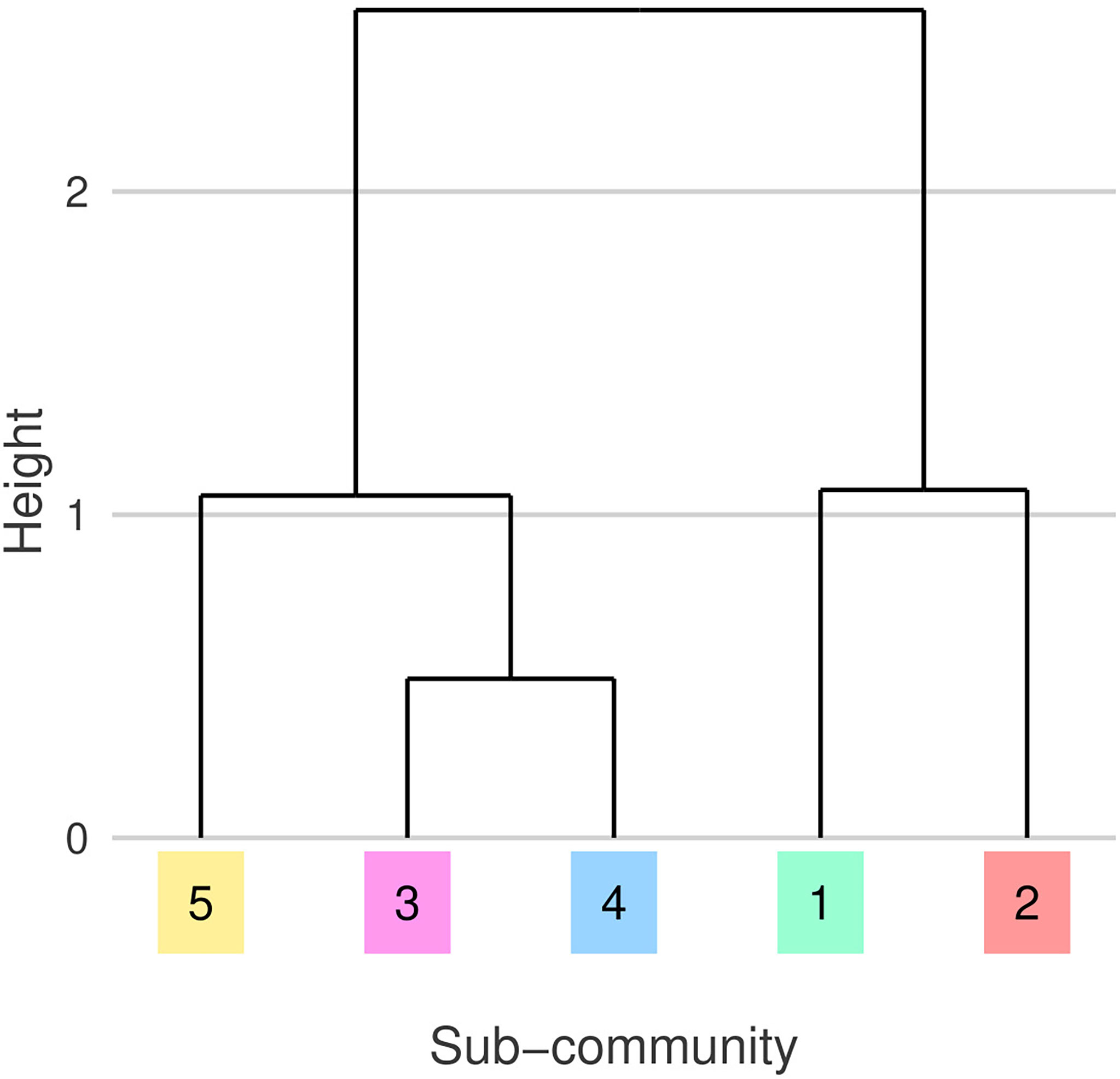
Figure 6 Dendrogram showing hierarchical clustering of mean niche distances between sub-communities, emphasizing similarity illustrated in Figure 5. Leaf colors and numeric-labels follow the shaded sub-community regions and labels from Figure 2.

The detected sub-communities are characterized by positive associations between pairs of taxa with a similar niche. On the sub-community-scale, niche similarity does not guarantee that the sub-communities will be closely associated. G₁ and G₂ have very similar niches but there is only a single bi-directional association between taxa from either sub-community (Figure 2). The same is true for sub-communities G₃ and G₄. Members of G₅ are only associated with G₁ and G₃ aside from associations within G₅.

By analyzing the seasonal cycles of each sub-community (Figure 7) we find that G₁ and G₂ are both observed most frequently during the spring bloom. Moreover, the peak month for observations of G₂ precedes the peak for G₁ by one month. We also frequently observe G₁ and G₂ in the same regions (Figure 8). Combined with the similar niches, this suggests that there is a seasonal succession of G₂ into G₁. A possible interpretation of this succession is that copepod members of G₁ graze upon the diatoms of G₂ . Both sub-communities are most frequently observed in the north-west of the sampling region. The diatom sub-community is more cosmopolitan than G₁ and is frequently found throughout the sampling region.

FIGURE 7

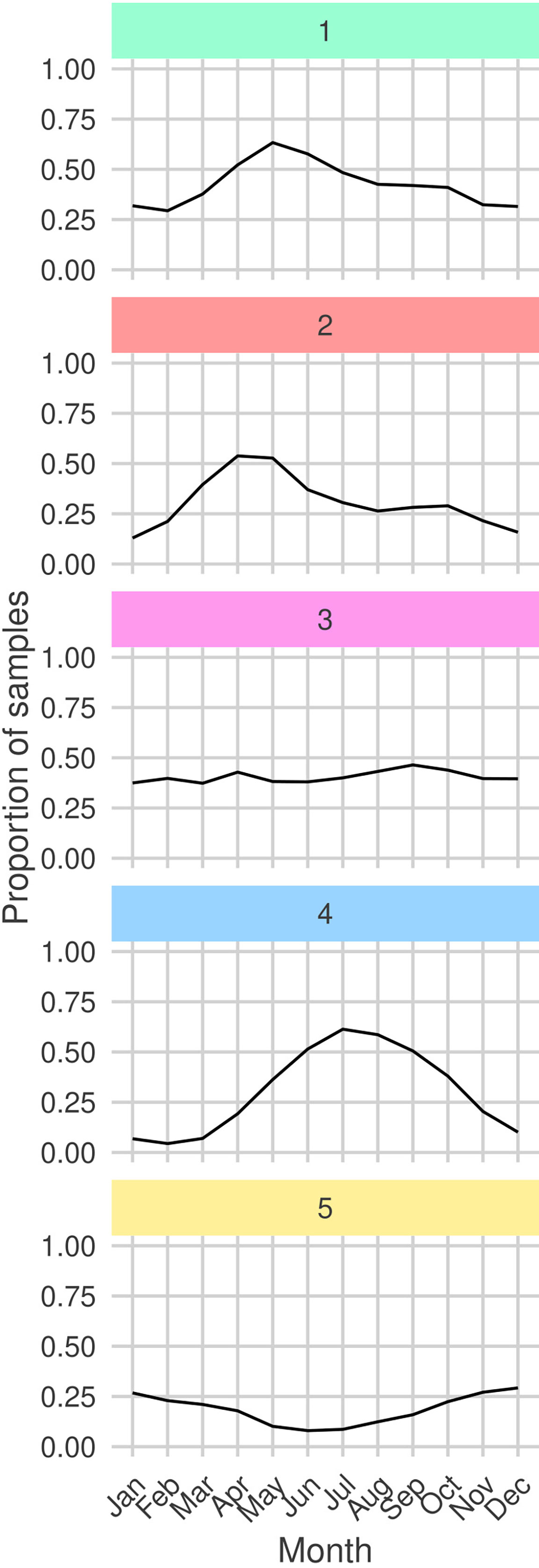
Figure 7 Proportion of total samples taken in each month in which each sub-community is determined to be present (samples containing least 30% (rounded down) of a sub-community’s members). Facet colors and numeric-labels follow Figure 2.

FIGURE 8

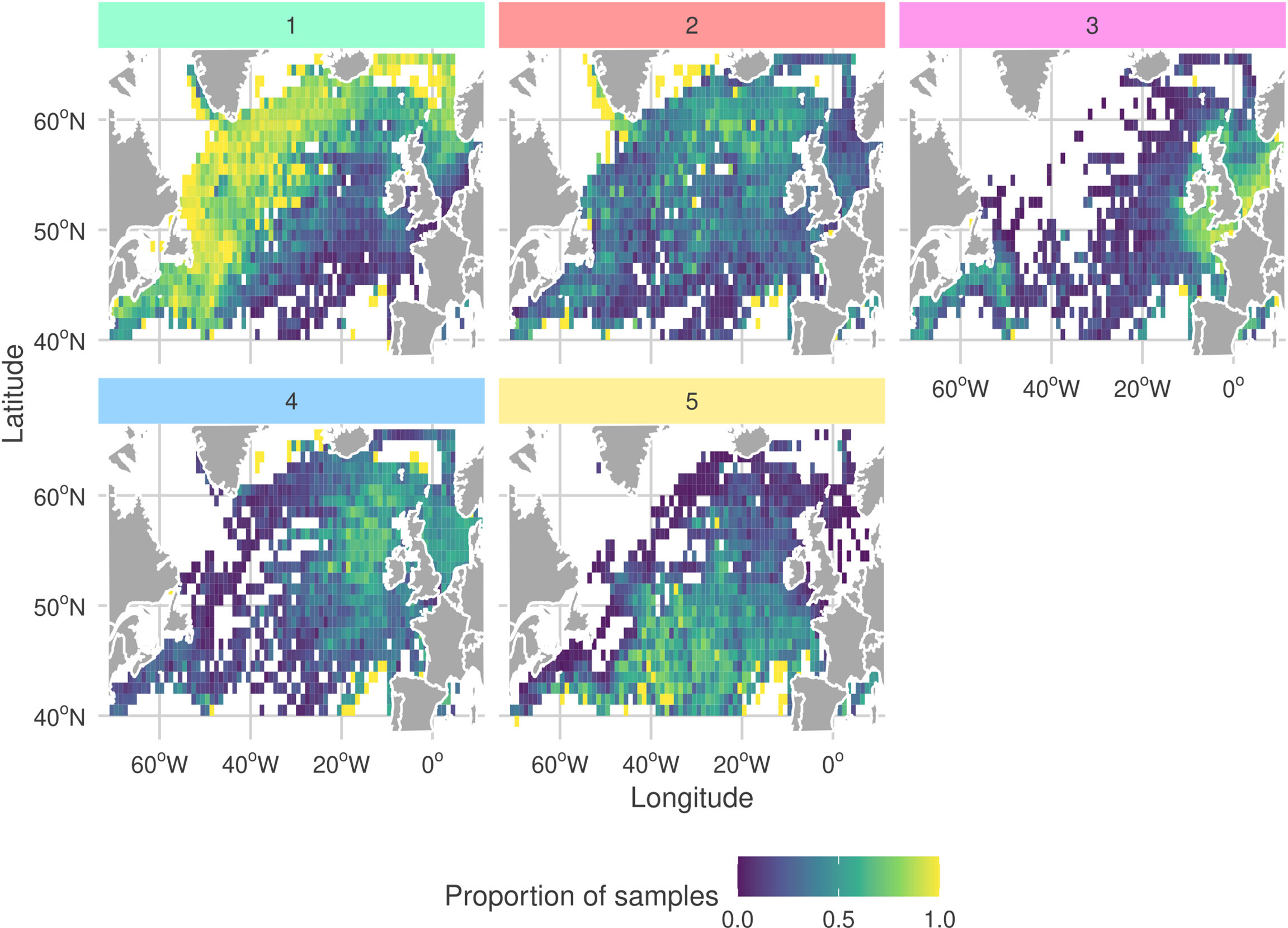
Figure 8 Proportion of samples at each CPR sampling site in which each sub-community was determined to be present (samples containing least 30% (rounded down) of a sub-community’s members). More yellow corresponds to a higher proportion of samples. To highlight spatial extent, only sites which included at least one observation of each sub-community are shown. Facet colors and numeric-labels follow Figure 2.

The dinoflagellate dominated sub-community, G₄ has the largest difference between peak and trough among the seasonal cycles of all sub-communities (Figure 7). It is most frequently observed in late-summer to early-autumn. In contrast, G₃ which has a similar niche is observed with relatively constant frequency throughout the year. G₃ is most commonly observed in coastal waters. In particular, it is frequently observed in the heavily sampled North Sea region. The dinoflagellate sub-community is found in similar regions but is more frequently observed in more open and shelf sea regions. This highlights that despite G₃ and G₄ having similar niches they are distinct sub-communities. This contrasts with the similar patterns between G₁ and G₂. G₄ is more mixed than the heavily diatom dominated G₂ and contains both phytoplankton and zooplankton.

The rarest sub-community, G₅ is most frequently observed during the winter. At the peak of its seasonal cycle, it is only observed in 25% of samples. It is most often observed towards the south of the sampling region, which is the least sampled area. The tendency to observe this sub-community in winter may explain why it has a low PAR and narrow salinity niche.

Association graphs have been used to infer interactions or relationships between species, such as plant-animal pollination network (Rodríguez-Rodríguez et al., 2017). We recommend caution when interpreting graphical models, as associations can arise from true interactions among species, but also as a result of niche overlap. In short, species may be associated because their growth is affected in similar ways by resource availability or environmental conditions, because they share a susceptibility or resilience to a common predator, or as a direct result of a positive or negative interaction. Changes in population density and environment changes may complicate recovery of interaction networks as interactions change over space and time (Poisot et al., 2014). We use the correlation between niche distance and association measures (Figure 4) to infer that about half of the strength of associations in our analysis is predicted by niche similarity. The presence or absence of any one pairwise interaction can’t be directly attributed to a particular cause, but the considerable residual variation in association strength leads us to expect that there are some true interactions in our graph and that the strongest interactions are most likely to be observed. The various kinds of interactions appear to be highly biased to mutualism with relatively few negative interactions detected (Table 3). The method recovers negative associations from simulated data with truncation and a high level of sparsity (Table 2), so our expectation is that the observed asymmetry reflects something real about the community. Facilitative interactions may be more evolutionarily stable than antagonistic interactions (Bronstein, 2009) which could partially explain the bias in our results. While it is possible that negative interactions are rare, we think it more likely that negative interactions are less likely to be strictly pairwise, perhaps because of the importance of generalist grazers, and that generalist negative interactions may be overprinted by niche selection leading to small magnitude associations that are difficult to detect.

4 Conclusion

The marine planktonic community is dynamic and highly structured. Member taxa are significantly affected by environmental forcing, which can control which taxa can thrive. There are complicated interactions between pairs, or groups, of frequently co-occurring taxa. The combined workflow of sparse graphical inference and sub-community analysis can provide insights into some of these effects on the community as a whole. These methods provide effective solutions to many challenges typically faced when analyzing co-occurrence datasets. In particular, difficulties associated with inference from sparse data can be effectively overcome. Good quality associations can be inferred using a truncated non-paranormal assumption. The impacts of false positive and false negative associations can be mitigated by grouping taxa into sub-communities, defined as (relatively) dense sub-graphs, based on the inferred associations using the walktrap algorithm.

The workflow presented here can be broken into three significant components. Each component was selected for its accuracy and performance, especially with sparse data. Firstly, the truncated non-paranormal model can be used to provide an estimate for pairwise correlations (Yoon et al., 2020). This method produces a reasonably accurate estimate to underlying correlations even in very sparse data (Table 2). Secondly, the correlation estimates are used as input to a penalized regression to generate the graph (Meinshausen and Bühlmann, 2006; Yoon et al., 2019). This approach allows for the development of a directed graph, which provides a more interpretable result (Table 3). Pairwise relationships are hard to detect, in particular negative associations are more difficult to detect than positive. Considering groups of similar, or heavily connected, taxa can highlight both associated taxa and potentially associated taxa. We partitioned the graph into sub-communities using the walktrap algorithm (Pons and Latapy, 2005), which performs well at detecting sub-communities on a graph (Orman et al., 2011). The tools used here can be adapted for use with zero-inflated compositional, or relative, abundance data, by use of a modified centered-log-ratio transform to the original data, included as a component of SPRING (Yoon et al., 2019).

Using these methods we have developed a graphical model of the North Atlantic planktonic community. Many features of the plankton community and component sub-communities were captured by the truncated paranormal model of Yoon et al. (2020). We anticipated discovering many pairwise positive-negative grazing associations, particularly between phytoplankton and zooplankton, but found none. This may be partially due to the difficulty in detecting negative associations in truncated data, or challenges of detecting predator-prey relationships from observational data. The lack of simple pairwise predator-prey relationships may be a real feature of a complex food-webs that are best understood by examining the aggregate effects of interactions that create sub-communities. By quantifying the effect of niche overlap, or niche similarity, on the strength of the associations we concluded that abiotic/environmental factors are not the sole drivers of variance in association strength, or correlation. Partitioning the graph into sub-communities allowed us to further detect bulk behaviors of the community. In general, these sub-communities displayed distinct niches, geographical extents, and seasonal dynamics, highlighting significant differences between these groups of taxa. By analyzing seasonal and spatial trends for these sub-communities, we have identified a potential seasonal succession from a diatom dominated sub-community into one that is dominated by copepods.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

JS and AI conceived and designed the analysis and computational experiment. JS performed the analysis. JS, AI, and ZF interpreted the results and wrote the paper. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Christian Müller for their guidance with setting up SPRING and its components. This work was supported by the Simons Collaboration on Computational Biogeochemical Modelling of Marine Ecosystems (CBIOMES, grant 549935 to AI).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.943540/full#supplementary-material

Supplementary Table S1 | Breakdown of taxa, prevalence, and sub-community membership, in the reduced CPR dataset. Order of taxa follows marinespecies.org (WoRMS Editorial Board, 2022). Names follow the CPR dataset (Richardson et al., 2006; Johns et al., 2019). Genus Exuviaella has now been classified as Prorocentrum, although they are counted separately in the CPR data as Exuviaella (Richardson et al., 2006). Genus Ceratium is now classified as Tripos, with species Ceratium tripos now renamed as Tripos muelleri (Bory de Saint-Vincent, 1826).

References

Berry D., Widder S. (2014). Deciphering Microbial Interactions and Detecting Keystone Species With Co-Occurrence Networks. Front. Microbiol. 5, 219. doi: 10.3389/fmicb.2014.00219

PubMed Abstract | CrossRef Full Text | Google Scholar

Bishara A. J., Hittner J. B. (2012). Testing the Significance of a Correlation With Nonnormal Data: Comparison of Pearson, Spearman, Transformation, and Resampling Approaches. psychol. Methods 17 (3), 399. doi: 10.1037/a0028087

PubMed Abstract | CrossRef Full Text | Google Scholar

Blüthgen N., Fründ J., Váquez D. P., Menzel F. (2008). What do Interaction Network Metrics Tell Us About Specialization and Bioligcal Traits? Ecology 89 (12), 3387–3399. doi: 10.1890/07-2121.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bory de Saint-Vincent M. (1826). “Essai D’une Classification Des Animaux Microscopiques,” in Histoire Naturelle, De L’encyclopédie Méthodique, tome II (Zoophytes), (Paris: Vve Agasse) 104, 515–543. Available at: https://www.biodiversitylibrary.org/page/9668780.

Google Scholar

Boyer T. P., Antonov J. I., Baranova O. K., Coleman C., Garcia H. E., Grodsky A., et al. (2013). World Ocean Database 2013. (Washington DC:NOAA Printing Office)

Google Scholar

Bronstein J. L. (2009). The Evolution of Facilitation and Mutualism. J. Ecol. 97 (6), 1160–1170. doi: 10.1111/j.1365-2745.2009.01566.x

CrossRef Full Text | Google Scholar

Calkins D. S. (1974). Some Effects of non-Normal Distribution Shape on the Magnitude of the Pearson Product Moment Correlation Coefficient. Rev. Interamericana Psicología 8 (3-4), 261–288. doi: 10.30849/rip/ijp.v8i3&4.708

CrossRef Full Text | Google Scholar

Crow E. L., Shimizu K. (1987). Lognormal distributions, Marcel Dekker New York.

Google Scholar

Csardi G., Nepusz T.. (2006). The Igraph Software Package for Complex Network Research. InterJournal Complex Syst. 1695 (5), 1–9.

Google Scholar

Delmas E., Besson M., Brice M.-H., Burkle L. A., Dalla Riva G. V., Fortin M.-J., et al. (2019). Analysing Ecological Networks of Species Interactions. Biol. Rev. 94 (1), 16–36. doi: 10.1111/brv.12433

CrossRef Full Text | Google Scholar

de Vargas C., Audic S., Henry N., Decelle J., Mahé F., Logares R., et al. (2015). Eukaryotic Plankton Diversity in the Sunlit Ocean. Science 348 (6237), 1261605. doi: 10.1126/science.1261605

PubMed Abstract | CrossRef Full Text | Google Scholar

Eiler A., Heinrich F., Bertilsson S. (2012). Coherent Dynamics and Association Networks Among Lake Bacterioplankton Taxa. ISME J. 6 (2), 330–342. doi: 10.1038/ismej.2011.113

PubMed Abstract | CrossRef Full Text | Google Scholar

Faust K., Raes J. (2012). Microbial Interactions: From Networks to Models. Nat. Rev. 10, 538–550. doi: 10.1038/nrmicro2832

CrossRef Full Text | Google Scholar

Faust K., Sathirapongsasuti J. F., Izard J., Segata N., Gevers D., Raes J., et al. (2012). Microbial Co-Occurrence Relationships in the Human Microbiome. PloS Comput. Biol. 8 (7), e1002606. doi: 10.1371/journal.pcbi.1002606

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedman J., Alm E. J. (2012). Inferring Correlation Networks From Genomic Survey Data. PloS comp.bio. 8 (9), 1–11. doi: 10.1371/journal.pcbi.1002687

CrossRef Full Text | Google Scholar

Fruchterman T. M. J., Reingold E. M. (1991). Graph Drawing by Force-Directed Placement. Software: Pract. Exp. 21 (11), 1129–1164. doi: 10.1002/spe.4380211102

CrossRef Full Text | Google Scholar

Fuhrman J. A., Cram J. A., Needham D. M. (2015). Marine Microbial Community Dynamics and Their Ecological Interpretation. Nat. Rev. 13, 133–146. doi: 10.1038/nrmicro3417

CrossRef Full Text | Google Scholar

Girvan M., Newman M. E. J. (2002). Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. 99 (12), 7821–7826. doi: 10.1073/pnas.122653799

CrossRef Full Text | Google Scholar

Guidi L., Chaffron S., Bittner L., Eviellard D., Larhlimi A., Roux S., et al. (2016). Plankton Networks Driving Carbon Export in the Oligotrophic Ocean’. Nature 532, 465–480. doi: 10.1038/nature16942

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardy A. C. (1939). Ecological Investigations With the Continuous Plankton Recorder. Object, Plan and Methods. Hull Bull. Mar. Ecol. 1, 1–57.

Google Scholar

Hays G. C., Warner A. J. (1993). Consistency of Towing Speed and Sampling Depth for the Continuous Plankton Recorder. J. Mar. Biol. Assoc. United Kingdom 73 (4), 967–970. doi: 10.1017/S0025315400034846

CrossRef Full Text | Google Scholar

Hutchinson G. E. (1957). Concluding Remarks. Cold Spring Harbor symposium quantitative Biol. 22, 415–427. doi: 10.1101/SQB.1957.022.01.039

CrossRef Full Text | Google Scholar

Ings T. C., Montoya J. M., Bascompte J., Blüthgen N., Brown L., Dormann C. F., et al. (2009). Ecological Networks – Beyond Food Webs. J. Anim. Ecol. 78, 253–269. doi: 10.1111/j.1365-2656.2008.01460.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Irwin A. J., Nelles A. M., Finkel Z. V. (2012). Phytoplankton Niches Estimated From Field Data. Limnology Oceanography 57 (3), 787–797. doi: 10.4319/lo.2012.57.3.0787

CrossRef Full Text | Google Scholar

Johns D., Broughton D., SAHFOS (2019) Continuous Plankton Recorder Survey (Cpr Survey V1.2). Available at: http://doi.dassh.ac.uk/data/1629.

Google Scholar

Lebrija-Trejos E., Pérez-García E. A., Meave J. A., Bongers F., Poorter L. (2010). Functional Traits and Environmental Filtering Drive Community Assembly in a Species-Rich Tropical System. Ecology 91 (2), 386–398. doi: 10.1890/08-1449.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Lima-Mendez G., Faust K., Henry N., Decelle J., Colin S., Carcillo F., et al. (2015). Determinants of Community Structure in the Global Plankton Interactome. Science 348 (6237), 1262073. doi: 10.1126/science.1262073

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu H., Lafferty J., Wasserman L. (2009). The Nonparanormal: Semiparametric Estimation of High Dimensional Undirected Graphs. J. Mach. Learn. Res. 10, 2295–2328.

Google Scholar

Liu H., Roeder K., Wasserman L. (2010). Stability Approach to Regularization Selection (Stars) for High Dimensional Graphical Models. Adv. Neural Inf. Process. Syst. (Red Hook, NY: Curran Associates, Inc.) 23, 1432–1440.

Google Scholar

McGinty N., Barton A. D., Record N. R., Finkel Z. V., Irwin A. J. (2018). Traits Structure Copepod Niches in the North Atlantic and Southern Ocean. Mar.Ecol.Prog.Ser. 601, 109–126. doi: 10.3354/meps12660

CrossRef Full Text | Google Scholar

Medlin L. K., Metfies K., Mehl H., Wiltshire K., Valentin K. (2006). Picoeukaryotic Plankton Diversity at the Helgoland Time Series Site as Assessed by Three Molecular Methods. Microbial Ecol. 52 (1), 53–71. doi: 10.1007/s00248-005-0062-x

CrossRef Full Text | Google Scholar

Meinshausen N., Bühlmann P. (2006). High-Dimensional Graphs and Variable Selection With the Lasso. Ann. Stat 34 (3), 1436–1462. doi: 10.1214/009053606000000281

CrossRef Full Text | Google Scholar

Müller C. L., Bonneau R., Kurtz Z. (2016). Generalized Stability Approach for Regularized Graphical Models. arXiv preprint arXiv:1605.07072. doi: 10.48550/arXiv.1605.07072

CrossRef Full Text | Google Scholar

Mutshinda C. M., Mishra A., Finkel Z. V., Widdicombe C. E., Irwin A. J. (2022). Bayesian Two-Part Modeling of Phytoplankton Biomass and Occurrence. Hydrobiologia 849 (5), 1287–1300. doi: 10.1007/s10750-021-04789-2

CrossRef Full Text | Google Scholar

Newman M. E. J. (2006). Modularity and Community Structure in Networks. Proc. Natl. Acad. Sci. 103 (23), 8577–8582. doi: 10.1073/pnas.0601602103

CrossRef Full Text | Google Scholar

Newman M. E. J., Girvan M. (2004). Finding and Evaluating Community Structure in Networks. Phys. Rev. E 69 (2), 026113. doi: 10.1103/PhysRevE.69.026113

CrossRef Full Text | Google Scholar

Orman G. K., Labatut V., Cherifi H. (2011). On Accuracy of Community Structure Discovery Algorithms. arXiv preprint arXiv:1112.4134. doi: 10.48550/arXiv.1112.4134

CrossRef Full Text | Google Scholar

Poisot T., Stouffer D. B., Gravel D. (2014). Beyond Species: Why Ecological Interaction Networks Vary Through Space and Time. Oikos 124 (3), 243–251. doi: 10.1111/oik.01719

CrossRef Full Text | Google Scholar

Poisot T., Stouffer D. B., Kéfi S. (2016). Describe, Understand and Predict: Why do We Need Networks in Ecology? Funct. Ecol. 30 (12), 1878–1882. doi: 10.1111/1365-2435.12799

CrossRef Full Text | Google Scholar

Pons P., Latapy M. (2005). “Computing Communities in Large Networks Using Random Walks,” in Computer and Information Sciences - ISCIS 2005. Eds. Yolum T., Güngör F., Gürgen C., Özturan (Berlin, Heidelberg: Springer Berlin Heidelberg), 284–293.

Google Scholar

Prat-Pérez A., Dominguez-Sal D., Brunat J. M., Larriba-Pey J.-L. (2012). “Shaping Communities Out of Triangles,” in Proceedings of the 21st ACM international conference on Information and knowledge management - CIKM 12 (NY: ACM Press). doi: 10.1145/2396761.2398496

CrossRef Full Text | Google Scholar

Puth M.-T., Neuhäuser M., Ruxton G. D. (2014). Effective Use of Pearson’s Product–Moment Correlation Coefficient. Anim. Behav. 93, 183–189. doi: 10.1016/j.anbehav.2014.05.003

CrossRef Full Text | Google Scholar

Rayner N. A., Brohan P., Parker D. E., Folland C. K., Kennedy J. J., Vanicek M., et al. (2006). Improved Analyses of Changes and Uncertainties in Sea Surface Temperature Measured in Situ Since the Mid-Nineteenth Century: The Hadsst2 Dataset. J. Climate 19 (3), 446–469. doi: 10.1175/JCLI3637.1

CrossRef Full Text | Google Scholar

Richardson A. J., Walne A. W., John A. W. G., Jonas T. D., Lindley J. A., Sims D. W., et al. (2006). Using Continuous Plankton Recorder Data. Prog.in Oceanogr 68, 27–74. doi: 10.1016/j.pocean.2005.09.011

CrossRef Full Text | Google Scholar

Rodríguez-Rodríguez M. C., Jordano P., Valido A. (2017). Functional Consequences of Plant-Animal Interactions Along the Mutualism-Antagonism Gradient. Ecology 98 (5), 1266–1276. doi: 10.1002/ecy.1756

PubMed Abstract | CrossRef Full Text | Google Scholar

Steele J. A., Countway P. D., Li X., Vigil P. D., Beman M. J., Kim D. Y., et al. (2011). Marine Bacterial, Archaeal and Protistan Association Networks Reveal Ecological Linkages. ISME 5, 1414–1425. doi: 10.1038/ismej.2011.24

CrossRef Full Text | Google Scholar

Sunagawa S., Coelho L. P., Chaffron S., Kultima J. R., Labadie K., Salazar G., et al. (2015). Structure and Function of the Global Ocean Microbiome. Science 348 (6237), 1261359. doi: 10.1126/science.1261359

PubMed Abstract | CrossRef Full Text | Google Scholar

Tibshirani R. (1996). Regression Shrinkage and Selection via the Lasso. J. R. Stat. Society: Ser. B (Methodological) 58 (1), 267–288. doi: 10.1111/j.2517-6161.1996.tb02080.x

CrossRef Full Text | Google Scholar

Trombetta T., Vidussi F., Roques C., Scotti M., Mostajir B. (2020). Marine Microbial Food Web Networks During Phytoplankton Bloom and non-Bloom Periods: Warming Favors Smaller Organism Interactions and Intensifies Trophic Cascade. Front. Microbiol. 11. doi: 10.3389/fmicb.2020.502336

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsourakakis C. E., Pachocki J., Mitzenmacher M. (2017). “Scalable Motif-Aware Graph Clustering,” in ‘Proceedings of the 26th International Conference on World Wide Web’ (Geneva: International World Wide Web Conferences Steering Committee). doi: 10.1145/3038912.3052653

CrossRef Full Text | Google Scholar

Warner A. J., Hays G. C. (1994). Sampling by the Continuous Plankton Recorder Survey. Prog. Oceanography 34 (2-3), 237–256. doi: 10.1016/0079-6611(94)90011-6

CrossRef Full Text | Google Scholar

Watts D. J., Strogatz S. H. (1998). Collective Dynamics of ‘Small-World’ Networks. Nature 393 (6684), 440–442. doi: 10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

West D. B.. (2001). Introduction to Graph Theory 2 (Prentice Hall Upper Saddle River, NJ).

Google Scholar

WoRMS Editorial Board (2022) World Register of Marine Species. Available at: https://www.marinespecies.orghttps://www.marinespecies.org/.

Google Scholar

Yambartsev A., Perlin M. A., Kovchegov Y., Shulzhenko N., Mine K. L., Dong X., et al. (2016). Unexpected Links Reflect the Noise in Networks. Biol. Direct 11 (52), 1–12. doi: 10.1186/s13062-016-0155-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoon G., Carroll R. J., Gaynanova I. (2020). Sparse Semiparametric Canonical Correlation Analysis for Data of Mixed Types. Biometrika 107 (3), 609–625. doi: 10.1093/biomet/asaa007

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoon G., Gaynanova I., Müller C. L. (2019). Microbial Networks in Spring - Semi-Parametric Rank-Based Correlation and Partial Correlation Estimation for Quantitative Microbiome Data. Front. Genet. 10, 516. doi: 10.3389/fgene.2019.00516

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoon G., Müller C. L., Gaynanova I. (2021). Fast Computation of Latent Correlations. J. Comput. Graphical Stat 30 (4), 1249–1256. doi: 10.1080/10618600.2021.1882468

CrossRef Full Text | Google Scholar

Zhang W. J. (2011). Constructing Ecological Interaction Networks by Correlation Analysis: Hints From Community Sampling. Net.Bio. 1 (2), 81–98. doi: 10.0000/issn-2220-8879-networkbiology-2011-v1-0008

CrossRef Full Text | Google Scholar

Zhao T., Liu H., Roeder K., Lafferty J., Wasserman L. (2012) The Huge Package for High-dimensional Undirected Graph Estimation in R. Journal of Machine Learning Research (JMLR) 13 (1), 1059–1062. http://jmlr.org/papers/v13/zhao12a.html

PubMed Abstract | Google Scholar

Zhou J., Richlen M. L., Sehein T. R., Kulis D. M., Anderson D. M., Cai Z. (2018). Microbial Community Structure and Associations During a Marine Dinoflagellate Bloom. Front. Microbiol. 9. doi: 10.3389/fmicb.2018.01201

CrossRef Full Text | Google Scholar