- 1Department of Biology, Faculty of Sciences, Kyushu University, Fukuoka, Japan
- 2School of Medicine, College of Medical, Pharmaceutical and Health Sciences, Kanazawa University, Kanazawa, Ishikawa, Japan
Analyzing the time-course of several viral infections using mathematical models based on experimental data can provide important quantitative insights regarding infection dynamics. Over the past decade, the importance and significance of mathematical modeling has been gaining recognition among virologists. In the near future, many animal models of human-specific infections and experimental data from high-throughput techniques will become available. This will provide us with the opportunity to develop new quantitative approaches, combining experimental and mathematical analyses. In this paper, we review the various quantitative analyses of viral infections and discuss their possible applications.
Introduction
Based on a decline in the viral load of human immunodeficiency virus type-1 (HIV-1) patients following the initiation of antiviral therapy, the turnover of HIV infected cells in vivo was estimated through mathematical modeling (Ho et al., 1995; Wei et al., 1995). Starting with these landmark papers, mathematical modeling has evolved into an important tool in modern virology. Developing a quantitative understanding of virus infection dynamics is useful for determining the pathogenesis and transmissibility of viruses, predicting the course of disease, and evaluating the effects of antiviral therapy in HIV (Perelson, 2002; Simon and Ho, 2003; Rong and Perelson, 2009), hepatitis B/C virus (HBV/HCV; Dahari et al., 2008, 2011; Rong and Perelson, 2010; Chatterjee et al., 2012) and influenza virus infection (Beauchemin and Handel, 2011; Murillo et al., 2013). The importance and significance of mathematical modeling work is slowly being recognized by virologists. In addition, in recent years, data from animal experiments have been analyzed using mathematical models (Igarashi et al., 1999; Chen et al., 2007; Dahari and Perelson, 2007; Dinoso et al., 2009; Klatt et al., 2010; Miao et al., 2010; Wong et al., 2010; Graw et al., 2011; Horiike et al., 2012; Pinilla et al., 2012; Oue et al., 2013). A synergistic approach, combining animal experiments and mathematical models, has strong potential applications for researching various viral infections. For example, to determine certain aspects of virus infection, such as sites of infection, target cells (Dinoso et al., 2009; Horiike et al., 2012), and viral gene functions (Sato et al., 2010, 2012; Pinilla et al., 2012), designing an animal experiment and estimating numerous parameters with a mathematical model are useful and important. In the future, to understand the pathophysiology of untreatable or (re-)emerging virus infections, and to effectively develop therapeutic strategies against these viruses, we need to establish a platform involving quantitative analyses that are based on data from animal experiments (Perelson, 2002; Simon and Ho, 2003; Dahari et al., 2008, 2011; Rong and Perelson, 2009, 2010; Beauchemin and Handel, 2011; Chatterjee et al., 2012; Murillo et al., 2013). In this paper, we briefly review a history of quantitative approaches to virology and discuss the possible applications of these in combination with animal experiments.
Quantification of Virus Infection Dynamics
Virological research has typically been conducted with a small number of experiments. For example, in order to investigate the fitness of virus strains, one typically measured viral loads (e.g., the amount of viral protein and viral infectivity) at a few times during infection and determined whether one strain produces significantly more virus than the other. However, the entire time-course of an infection reflects complex processes involving interactions between viruses, target cells, and infected cells. Therefore, viral load detection at one time point ignores the complexity of the aforementioned processes during an entire infection (Iwami et al., 2012b). It would be useful to translate virus infection quantitatively into the parameters identifying the multi-composed kinetics of viral infection from time-course data (Perelson, 2002; Simon and Ho, 2003; Dahari et al., 2008, 2011; Rong and Perelson, 2009, 2010; Beauchemin and Handel, 2011; Chatterjee et al., 2012; Murillo et al., 2013). Mathematical modeling of the entire time-course of infection would allow us to estimate several parameters underlying the kinetics of virus infection, including burst size and basic reproductive number (Nowak and May, 2000). These parameters cannot be directly obtained through experimental and clinical studies.
Human Immunodeficiency Virus and Simian Immunodeficiency Virus
On average it takes about, 10 years for an HIV infection to possibly progress to acquired immunodeficiency syndrome (AIDS; Richman, 2001). Because of this slow disease progression, HIV is classified as a slowly replicating virus (Coffin, 1995; Richman, 2001). Several studies have indicated that slow disease progression is not due to inactive viral replication, but is a result of aggressive viral replication and its clearance (Coffin, 1995; Ho et al., 1995; Wei et al., 1995; Perelson et al., 1996). Interestingly, these results were based on mathematical analyses of clinical data. Estimating the decline in viral load of patients following the initiation of antiviral therapy (or plasma removal by apheresis technique; Ramratnam et al., 1999) shows us that HIV is cleared from patients at a rapid rate, with a half-life of around 6 h (Ho et al., 1995; Wei et al., 1995; Perelson et al., 1996). This estimation of rapid virus turnover implies that HIV resistance to any single drug could quickly emerge, highlighting the importance of combination therapies as they reduce the chances of drug resistance developing (Coffin, 1995; Ho et al., 1995; Wei et al., 1995; Perelson et al., 1996; Perelson and Nelson, 1999).
The success of mathematical modeling, especially with respect to HIV infection dynamics has led to the development of a field called “viral dynamics” (Nowak and May, 2000; Perelson, 2002; Simon and Ho, 2003; Rong and Perelson, 2009) and has provided us with further quantitatively novel insights. In 1997, combinations of three antiretroviral drugs successfully reduced plasma HIV levels to below the limit of detection in clinical assays (50 copies of HIV RNA/ml; Perelson et al., 1997; Eisele and Siliciano, 2012). This approach, known as highly active antiretroviral therapy (HAART), is currently the primary choice of therapeutic intervention for HIV-1 infected patients, and dramatically decreases mortality associated with HIV-1 infection (Richman, 2001; Trono et al., 2010; Eisele and Siliciano, 2012). After the initiation of HAART, the viral load decays with an initially rapid and exponential decline, followed by a slower exponential decline (Perelson et al., 1997; Perelson, 2002; Murray et al., 2007; Keele et al., 2008; Palmer et al., 2008; Rong and Perelson, 2010). Modeling the effects of drug therapy allowed for the quantitation of virus clearance rates (Ho et al., 1995; Wei et al., 1995; Perelson et al., 1996), and the death rate of several cell types (e.g., the productively infected CD4+ T cells; Perelson et al., 1996, 1997; Markowitz et al., 2003), the productively long-lived infected cells (Perelson et al., 1997; Palmer et al., 2008), latently infected cells (Perelson et al., 1997; Zhang et al., 1999; Havlir et al., 2003; Palmer et al., 2008 and so on). This modeling also estimates the period of infectiousness for follicular dendritic cell-trapping viruses (Hlavacek et al., 2000), and assists with designing an optimal therapy (Murray et al., 2007; Rosenbloom et al., 2012). A simple assessment of HIV RNA data yields certain information, but mathematical approaches allow for the extraction of much more information from raw data. Some excellent reviews regarding the quantitation of HIV dynamics and its importance have been reported (Perelson and Nelson, 1999; Nowak and May, 2000; Perelson, 2002; Simon and Ho, 2003; Rong and Perelson, 2009).
Potent HAART effectively suppresses de novo replication of HIV but fails to eradicate an HIV-1 infection. Recent studies have revealed that HIV RNA persists over several years in most infected patients on suppressive HAART (Havlir et al., 2003; Palmer et al., 2008). Furthermore, virus loads rapidly rebound to pretreatment levels after discontinuation of HAART (Chun et al., 1999; Imamichi et al., 2001). These observations suggest the persistence of viral reservoirs during combination antiviral therapy. To completely cure HIV-1 infection, it is essential to identify these viral reservoirs and to eradicate them (Richman, 2001; Trono et al., 2010; Eisele and Siliciano, 2012). In addition to existing studies looking at peripheral blood (Chun et al., 1999; Imamichi et al., 2001; Sharkey et al., 2011), systemic analysis is required to elucidate the mechanisms underlying rebound of plasma viremia upon discontinuation of HAART. Because it is unethical to collect various tissues from patients, or to deplete certain cell populations in patients for analysis, the simian immunodeficiency virus (SIV)/macaque model (which has been useful in understanding HIV-1 infection) with HAART is suitable for investigating poorly understood aspects of HIV-1 infection (Dinoso et al., 2009; North et al., 2010; Horiike et al., 2012; Oue et al., 2013). Using the SIV/macaque model, for example, it has been recently reported that the cytotoxic effects of CD8+ T cells on virus-infected cells during HAART is limited despite suppression of viral load in vivo (Klatt et al., 2010; Wong et al., 2010). Similarly, analyzing the levels of viral RNA in plasma and infected cells (e.g., macrophage and resting memory CD4+ T cells) of certain tissues such as lung and lymph nodes in SIV-infected macaques using mathematical models might reveal the precise dynamics of the viral reservoir, and provide several valuable clues for HIV eradication in patients on HAART.
Hepatitis B Virus and Hepatitis C Virus
The theoretical framework for quantifying HIV infection has also been applied to understand the dynamics of HBV (Nowak et al., 1996; Lewin et al., 2001; Murray et al., 2006; Dahari et al., 2009b) and HCV (Neumann et al., 1998; Dixit et al., 2004; Guedj and Perelson, 2011; Guedj et al., 2012) infections during antiviral therapy. These approaches have estimated the key parameters of the viral life cycle such as the rate of virus production and clearance and the death rate of infected cells, that explained the mechanism of action of antiviral drugs such as interferon, ribavirin, and protease inhibitor against HCV (Neumann et al., 1998; Dixit et al., 2004; Guedj and Perelson, 2011; Guedj et al., 2012) and reverse transcriptase inhibitor against HBV (Nowak et al., 1996; Lewin et al., 2001; Murray et al., 2006; Dahari et al., 2009b). These analyses have mainly focused on extracellular viral dynamics based on clinical studies, while several researchers have investigated the intracellular replication of HCV (Dahari et al., 2007, 2009a; McLean et al., 2010; Nakabayashi, 2012) and HBV (Nakabayashi and Sasaki, 2011) based on experimentally established HBV/HCV cell culture system. These studies have provided novel insights into the detailed dynamics of intracellular HBV/HCV replication, and revealed some important processes of the HCV life cycle such as the subcellular localization of HCV RNA to the replication complex for RNA replication and viral assembly. The above findings are helpful in understanding HCV turnover and determining new drug targets with fewer side effects. A number of reviews have been published detailing the mathematical modeling of HCV infection (Dahari et al., 2008; Guedj et al., 2010; Rong and Perelson, 2010; Guedj and Perelson, 2011; Chatterjee et al., 2012).
Although mathematical models were successfully used to understand the viral dynamics of HBV/HCV during antiviral therapy, these models considered only one level of extracellular or intracellular viral replication. Recently, for HCV infection, several researchers have developed a new mathematical model, known as the multi-scale model, that combines extracellular virus infection dynamics with the key features of intracellular viral replication (Guedj and Neumann, 2010; Guedj et al., 2013; Rong et al., 2013). This model incorporates two different time scales: one is for viral replication within a cell, and the other is for free viral infection among cells. Using this model in conjunction with clinical trials, it is possible to verify the mechanism of action of direct-acting antiviral agents (DAAs) that target specific viral proteins in a cell. Estimating the effectiveness of DAAs using multi-scale model takes into account intracellular viral dynamics (Guedj et al., 2013; Rong et al., 2013). Additionally, the multi-scale model has the potential to describe the emergence of viral drug resistance against DAAs at an intracellular and extracellular level (Guedj and Neumann, 2010). In the era of developing DAAs, multi-scale models could provide a new theoretical framework that combines findings from several studies of intra- and extracellular viral dynamics; this can be applied to HBV, HIV (Althaus and De Boer, 2010), and influenza virus (Murillo et al., 2013).
Using animal and cell culture systems with mathematical models paves the way to investigate new vaccines against HCV. It would also assist with understanding the mechanisms of antiviral drug therapy. HBV vaccines are available, but there is no effective vaccine against HCV infection. The development of an effective HCV vaccine has been hampered by the high mutation rate of viral proteins, the genetic diversity of HCV, and the lack of usable small animal models for HCV infection (Houghton and Abrignani, 2005; Klenerman and Gupta, 2012). Recently, a uPA-TG/severe combined immunodeficiency (SCID) mouse model for HCV infection has been developed (Mercer et al., 2001). Although an authentic immune response against HCV does not occur in these models (and therefore cannot be directly suitable for vaccine studies), mathematical modeling could compensate for the lack of information regarding key processes of HCV immune interactions and promote further development of small animal models of HCV. These and other animal models could be alternatives to chimpanzees for investigating the effects of candidates drugs and vaccines against HCV (Bukh, 2012; chimpanzees are endangered species and now cannot be used for animal experiments). On the other hand, mathematical modeling of the immune response against HBV in patients has estimated the contribution of the host response for viral clearance (Ciupe et al., 2007a,b), and the optimal vaccination schedule (Gesemann and Scheiermann, 1995; Wilson et al., 2007). Taken together, the combination of a small animal model and mathematical modeling can overcome the ethical and financial limitations of clinical trials and help develop new effective therapies against HBV and HCV.
Influenza Virus
In epidemiology, many mathematical models have been developed and been used to determine the dynamics of influenza virus infections on the population level (Anderson, 1991; Ferguson et al., 2006; Hatchett et al., 2007; Beauchemin and Handel, 2011; Murillo et al., 2013). A small number of models have also been generated to describe influenza virus infections at the host level (Baccam et al., 2006; Miao et al., 2010; Dobrovolny et al., 2011; Pinilla et al., 2012; and at the individual cell level; Hatada et al., 1989; Heldt et al., 2012). The purpose of these models is to describe the time-course of influenza virus infections as accurately as possible. This allows for the calculation of the half-life of infected cells, the number of virus particles released per infected cell (i.e., the burst size), and the number of infected cells produced per infected cell (i.e., the basic reproductive number; Baccam et al., 2006; Beauchemin et al., 2008; Mitchell et al., 2011; Pinilla et al., 2012). This information has been used to understand the severity and duration of infections (Bocharov and Romanyukha, 1994; Hancioglu et al., 2007; Canini and Carrat, 2011), and has provided us with an optimal antiviral therapy (Baccam et al., 2006; Handel et al., 2007; Dobrovolny et al., 2011; Perelson et al., 2012).
Although influenza viruses have been studied extensively in vivo, it is difficult to determine the exact date of infection, influenza virus loads prior to a peak, and pre-hemagglutination inhibition antibody titers. All these factors are crucial in quantifying virus infection dynamics (Murphy et al., 1980; Carrat et al., 2008). Experimental infection of healthy volunteers with influenza viruses provides a unique opportunity to elucidate the dynamics of natural influenza infections. The first mathematical model proposed to describe the dynamics of influenza infections, using influenza A/Hong Kong/123/77 (H1N1), was conducted in 2006 (Baccam et al., 2006). This simple mathematical model revealed several important and novel quantities corresponding to biological processes of influenza virus infection (Mohler et al., 2005; Baccam et al., 2006; Schulze-Horsel et al., 2009; Smith et al., 2010; Beauchemin and Handel, 2011; Holder and Beauchemin, 2011; Murillo et al., 2013). For example, if a basic reproductive number (R0) was obtained, the critical inhibition rate (1 - 1/R0) could be estimated for protection against virus infection (Anderson, 1991; Iwami et al., 2012a,b). This implies that reducing viral growth with antiviral interventions, such as vaccines or drugs, could prevent viral spread in vivo. More biologically realistic mathematical models incorporating the eclipse phase of infected cells (Holder and Beauchemin, 2011; Pinilla et al., 2012), innate or adaptive immune responses (Bocharov and Romanyukha, 1994; Hancioglu et al., 2007; Handel et al., 2007; Miao et al., 2010; Canini and Carrat, 2011), and several distributed delays for each biological process (Holder and Beauchemin, 2011; e.g., a time from virus entry to progeny virus producing) have been developed. Furthermore, using a mathematical model, a relationship between virus and symptom dynamics during influenza infections has been described recently (Canini and Carrat, 2011). Reviews regarding quantitation of influenza virus dynamics and its importance have been published previously (Beauchemin and Handel, 2011; Murillo et al., 2013).
These quantitative analyses of influenza viruses have yielded useful insights (Bocharov and Romanyukha, 1994; Mohler et al., 2005; Baccam et al., 2006; Hancioglu et al., 2007; Handel et al., 2007; Schulze-Horsel et al., 2009; Miao et al., 2010; Smith et al., 2010; Canini and Carrat, 2011; Dobrovolny et al., 2011; Holder and Beauchemin, 2011; Perelson et al., 2012; Pinilla et al., 2012; Murillo et al., 2013). The development of reliable within-host models is critical in improving epidemiological models because the dynamics of viral shedding and symptoms following influenza virus infection are key factors (Ferguson et al., 2006; Hatchett et al., 2007; Murillo et al., 2013). However, a major difficulty, over-parameterization (Beauchemin and Handel, 2011), arises when only viral load data are available, especially in human volunteer studies. One possible approach to overcome this limitation is to conduct animal experiments using rhesus macaques (Watanabe et al., 2011), ferrets (Kiso et al., 2010), and mice (Imai et al., 2008; Martin and Wurfel, 2008; Morita et al., 2013), and to measure the time-course data for these analyses (Miao et al., 2010; Pinilla et al., 2012). It is possible that the number of uninfected and infected cells from the lung or respiratory tract can be measured. Although it is still currently not feasible to obtain sufficient time-course data during the acute phase of infections, we have recently developed a novel but simple mathematical model to robustly estimate virus replication rates (Ikeda et al., unpublished). In this model, a relatively few time-course data of both the number of uninfected cells and viral load is required. A new model and diverse data will promote knowledge of influenza virus infection dynamics, which is important for future research.
Other Viruses
Mathematical models have also been applied for understanding the dynamics of other virus infections. For example, during acute lymphocytic choriomeningitis virus (LCMV, which is a common infection of rodents and is best known for its application in immunological studies) infection, the dynamics of the specific CD8+ T-cell response such as proliferation and apoptosis rate was estimated in infected mice (De Boer et al., 2001). Quantitative analyses suggested that the specific CD8+ T-cell response is controlled via the number of CD8+ T-cells, rather than their individual function during persistent LCMV infection compared with those in acute LCMV infections (in fact, the immune response with a high killing effect is necessary to clear the LCMV infection; Graw et al., 2011). On the other hand, modeling and fitting data from patients revealed that the doubling time of cytomegaloviruses (CMV, which is assumed to cause asymptomatic infection in normal hosts) in human hosts is around 1 day, similar to that for HIV (Emery et al., 1999; Perelson, 2002). More recently, it has been revealed that viral productivity and transmissibility, but not cytotoxicity, differ among Enterovirus 71 (EV71, which is the causative agent of hand-foot-and-mouth disease and can trigger neurological disorders) strains in cell culture and could be associated with their epidemiological backgrounds (Fukuhara et al., 2013). Animal experiments using monkeys and mice are available to investigate the pathogenesis and symptoms of these and numerous other viruses (Farrell et al., 1997; De Boer et al., 2001; Arita et al., 2007, 2008; Graw et al., 2011; Sato et al., 2011). We have a chance to establish a platform that will allow for quantitative understanding of various virus infections based on animal experiments. Accumulation of knowledge regarding viral dynamics should be useful in understanding untreatable or (re-)emerging virus infections.
Conclusion
Studies of virus infection dynamics have significantly contributed to our understanding of many diseases. Merging animal experiment results with mathematical models is a desirable direction for virology research (Figure 1). In particular, quantifying viral dynamics in “humanized mice” (Shultz et al., 2007; Sato and Koyanagi, 2011), which are the most practical and relevant model available, will provide us with novel insights. Using humanized mice as models of specific human viral infections (Sato et al., 2010, 2011, 2012) or human diseases (Ishikawa et al., 2007), we were able to investigate mechanisms of disease symptoms (e.g., a relation between function of regulatory T cells and depletion of CD4+ T cells in HIV-1 infection), and the potency/mechanism of action for drug/host factors (e.g., an effect of anticancer drug in human T cell leukemia virus type-1 infection) based on virus infection dynamics. Mathematical models can be used to explore a complicated dynamical system of virus infection. Estimation of key parameters during a virus infection provides us with many details regarding the infection. If we can obtain these estimated parameters and calculate burst size and basic reproductive numbers, we could easily compare the dynamics of various viral infections. Qualitative data (in fact, most experiments are not designed from a quantitative point of view) are difficult to understand and compare with results from other studies. Based on the theoretical analysis of experimental data, we are able to determine optimum frequencies of sampling for the highest quality data possible. Once we establish a mathematical model and reasonably fit that model to experimental data, we can predict outcomes of animal experiments under different conditions and determine factors that control several phenomena during virus infection (e.g., peak of viral load and mode of virus spread) through simulations. Further associations between animal experiments and mathematical models are required to overcome untreatable diseases.
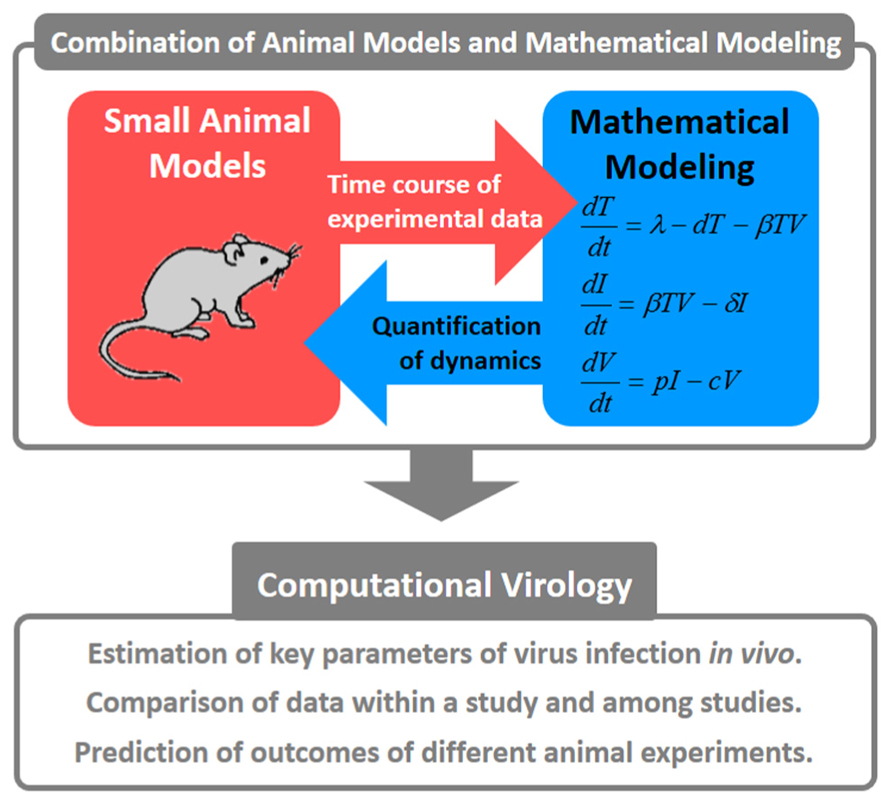
FIGURE 1. Concepts for combining animal models with mathematical modeling. These quantitative approaches are referred to as “computational virology.” This has the potential to provide novel insights into viral pathogenesis, the development of antiviral drugs, and the establishment of effective therapies against viral infections.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported, in part, by Kyushu University Interdisciplinary Programs in Education and Projects in Research Development (to Shingo Iwami); a grant-in-aid for Young Scientists B25800092 (to Shingo Iwami) from the Japan Society for the Promotion of Science (JSPS); and by the Aihara Innovative Mathematical Modeling Project, JSPS, through the “Funding Program for World-Leading Innovative R&D on Science and Technology (FIRST Program),” initiated by the Council for Science and Technology Policy (to Shingo Iwami) and a Kyushu University Fund (to Hiroki Ikeda).
References
Althaus, C. L., and De Boer, R. J. (2010). Intracellular transactivation of HIV can account for the decelerating decay of virus load during drug therapy. Mol. Syst. Biol. 6, 348. doi: 10.1038/msb.2010.4
Anderson, R. M. (1991). The Kermack–McKendrick epidemic threshold theorem. Bull. Math. Biol. 53, 3–32. doi: 10.1016/S0092-8240(05)80039-4
Arita, M., Ami, Y., Wakita, T., and Shimizu, H. (2008). Cooperative effect of the attenuation determinants derived from poliovirus sabin 1 strain is essential for attenuation of enterovirus 71 in the NOD/SCID mouse infection model. J. Virol. 82, 1787–1797. doi: 10.1128/JVI.01798-07
Arita, M., Nagata, N., Iwata, N., Ami, Y., Suzaki, Y., Mizuta, K., et al. (2007). An attenuated strain of enterovirus 71 belonging to genotype a showed a broad spectrum of antigenicity with attenuated neurovirulence in cynomolgus monkeys. J. Virol. 81, 9386–9395. doi: 10.1128/JVI.02856-06
Baccam, P., Beauchemin, C. A., Macken, C. A., Hayden, F. G., and Perelson, A. S. (2006). Kinetics of influenza A virus infection in humans. J. Virol. 80, 7590–7599. doi: 10.1128/JVI.01623-05
Beauchemin, C. A., and Handel, A. (2011). A review of mathematical models of influenza A infections within a host or cell culture: lessons learned and challenges ahead. BMC Public Health 11(Suppl. 1):S7. doi: 10.1186/1471-2458-11-S1-S7
Beauchemin, C. A., McSharry, J. J., Drusano, G. L., Nguyen, J. T., Went, G. T., Ribeiro, R. M., et al. (2008). Modeling amantadine treatment of influenza A virus in vitro. J. Theor. Biol. 254, 439–451. doi: 10.1016/j.jtbi.2008.05.031
Bocharov, G. A., and Romanyukha, A. A. (1994). Mathematical model of antiviral immune response III. Influenza A virus infection. J. Theor. Biol. 167, 323–360. doi: 10.1006/jtbi.1994.1074
Bukh, J. (2012). Animal models for the study of hepatitis C virus infection and related liver disease. Gastroenterology 142, 1279–1287. doi: 10.1053/j.gastro.2012.02.016
Canini, L., and Carrat, F. (2011). Population modeling of influenza A/H1N1 virus kinetics and symptom dynamics. J. Virol. 85, 2764–2770. doi: 10.1128/JVI.01318-10
Carrat, F., Vergu, E., Ferguson, N. M., Lemaitre, M., Cauchemez, S., Leach, S., et al. (2008). Time lines of infection and disease in human influenza: a review of volunteer challenge studies. Am. J. Epidemiol. 167, 775–785. doi: 10.1093/aje/kwm375
Chatterjee, A., Guedj, J., and Perelson, A. S. (2012). Mathematical modelling of HCV infection: what can it teach us in the era of direct-acting antiviral agents? Antivir. Ther. 17, 1171–1182. doi: 10.3851/IMP2428
Chen, H. Y., Di Mascio, M., Perelson, A. S., Ho, D. D., and Zhang, L. (2007). Determination of virus burst size in vivo using a single-cycle SIV in rhesus macaques. Proc. Natl. Acad. Sci. U.S.A. 104, 19079–19084. doi: 10.1073/pnas.0707449104
Chun, T. W., Davey, R. T. Jr., Engel, D., Lane, H. C., and Fauci, A. S. (1999). Re-emergence of HIV after stopping therapy. Nature 401, 874–875. doi: 10.1038/44755
Ciupe, S. M., Ribeiro, R. M., Nelson, P. W., Dusheiko, G., and Perelson, A. S. (2007a). The role of cells refractory to productive infection in acute hepatitis B viral dynamics. Proc. Natl. Acad. Sci. U.S.A. 104, 5050–5055. doi: 10.1073/pnas.0603626104
Ciupe, S. M., Ribeiro, R. M., Nelson, P. W., and Perelson, A. S. (2007b). Modeling the mechanisms of acute hepatitis B virus infection. J. Theor. Biol. 247, 23–35. doi: 10.1016/j.jtbi.2007.02.017
Coffin, J. M. (1995). HIV population dynamics in vivo: implications for genetic variation, pathogenesis, and therapy. Science 267, 483–489. doi: 10.1126/science.7824947
Dahari, H., Guedj, J., Perelson, A. S., and Layden, T. J. (2011). Hepatitis C viral kinetics in the era of direct acting antiviral agents and IL28B. Curr. Hepat. Rep. 10, 214–227. doi: 10.1007/s11901-011-0101-7
Dahari, H., Layden-Almer, J. E., Perelson, A. S., and Layden, T. J. (2008). Hepatitis C viral kinetics in special populations. Curr. Hepat. Rep. 7, 97–105. doi: 10.1007/s11901-008-0022-2
Dahari, H., and Perelson, A. S. (2007). Hepatitis C virus kinetics in chimeric mice during antiviral therapy. Hepatology 46, 2048–2049. doi: 10.1002/hep.21798
Dahari, H., Ribeiro, R. M., Rice, C. M., and Perelson, A. S. (2007). Mathematical modeling of subgenomic hepatitis C virus replication in Huh-7 cells. J. Virol. 81, 750–760. doi: 10.1128/JVI.01304-06
Dahari, H., Sainz, B. Jr., Perelson, A. S., and Uprichard, S. L. (2009a). Modeling subgenomic hepatitis C virus RNA kinetics during treatment with alpha interferon. J. Virol. 83, 6383–6390. doi: 10.1128/JVI.02612-08
Dahari, H., Shudo, E., Ribeiro, R. M., and Perelson, A. S. (2009b). Modeling complex decay profiles of hepatitis B virus during antiviral therapy. Hepatology 49, 32–38. doi: 10.1002/hep.22586
De Boer, R. J., Oprea, M., Antia, R., Murali-Krishna, K., Ahmed, R., and Perelson, A. S. (2001). Recruitment times, proliferation, and apoptosis rates during the CD8(+) T-cell response to lymphocytic choriomeningitis virus. J. Virol. 75, 10663–10669. doi: 10.1128/JVI.75.22.10663-10669.2001
Dinoso, J. B., Rabi, S. A., Blankson, J. N., Gama, L., Mankowski, J. L., Siliciano, R. F., et al. (2009). A simian immunodeficiency virus-infected macaque model to study viral reservoirs that persist during highly active antiretroviral therapy. J. Virol. 83, 9247–9257. doi: 10.1128/JVI.00840-09
Dixit, N. M., Layden-Almer, J. E., Layden, T. J., and Perelson, A. S. (2004). Modelling how ribavirin improves interferon response rates in hepatitis C virus infection. Nature 432, 922–924. doi: 10.1038/nature03153
Dobrovolny, H. M., Gieschke, R., Davies, B. E., Jumbe, N. L., and Beauchemin, C. A. (2011). Neuraminidase inhibitors for treatment of human and avian strain influenza: a comparative study. J. Theor. Biol. 269, 234–244. doi: 10.1016/j.jtbi.2010.10.017
Eisele, E., and Siliciano, R. F. (2012). Redefining the viral reservoirs that prevent HIV-1 eradication. Immunity 37, 377–388. doi: 10.1016/j.immuni.2012.08.010
Emery, V. C., Cope, A. V., Bowen, E. F., Gor, D., and Griffiths, P. D. (1999). The dynamics of human cytomegalovirus replication in vivo. J. Exp. Med. 190, 177–182. doi: 10.1084/jem.190.2.177
Farrell, H. E., Vally, H., Lynch, D. M., Fleming, P., Shellam, G. R., Scalzo, A. A., et al. (1997). Inhibition of natural killer cells by a cytomegalovirus MHC class I homologue in vivo. Nature 386, 510–514. doi: 10.1038/386510a0
Ferguson, N. M., Cummings, D. A. T., Fraser, C., Cajka, J. C., Cooley, P. C., and Burke, D. S. (2006). Strategies for mitigating an influenza pandemic. Nature 442, 448–452. doi: 10.1038/nature04795
Fukuhara, M., Iwami, S., Sato, K., Nishimura, Y., Shimizu, H., Aihara, K., et al. (2013). Quantification of the dynamics of enterovirus 71 infection by experimental-mathematical investigation. J. Virol. 87, 701–705. doi: 10.1128/JVI.01453-12
Gesemann, M., and Scheiermann, N. (1995). Quantification of hepatitis B vaccine-induced antibodies as a predictor of anti-HBs persistence. Vaccine 13, 443–447. doi: 10.1016/0264-410X(94)00010-K
Graw, F., Richter, K., Oxenius, A., and Regoes, R. R. (2011). Comparison of cytotoxic T lymphocyte efficacy in acute and persistent lymphocytic choriomeningitis virus infection. Proc. Biol. Sci. 278, 3395–3402. doi: 10.1098/rspb.2011.0453
Guedj, J., Dahari, H., Rong, L., Sansone, N. D., Nettles, R. E., Cotler, S. J., et al. (2013). Modeling shows that the NS5A inhibitor daclatasvir has two modes of action and yields a shorter estimate of the hepatitis C virus half-life. Proc. Natl. Acad. Sci. U.S.A. 110, 3991–3996. doi: 10.1073/pnas.1203110110
Guedj, J., Dahari, H., Shudo, E., Smith, P., and Perelson, A. S. (2012). Hepatitis C viral kinetics with the nucleoside polymerase inhibitor mericitabine (RG7128). Hepatology 55, 1030–1037. doi: 10.1002/hep.24788
Guedj, J., and Neumann, A. U. (2010). Understanding hepatitis C viral dynamics with direct-acting antiviral agents due to the interplay between intracellular replication and cellular infection dynamics. J. Theor. Biol. 267, 330–340. doi: 10.1016/j.jtbi.2010.08.036
Guedj, J., and Perelson, A. S. (2011). Second-phase hepatitis C virus RNA decline during telaprevir-based therapy increases with drug effectiveness: implications for treatment duration. Hepatology 53, 1801–1808. doi: 10.1002/hep.24272
Guedj, J., Rong, L., Dahari, H., and Perelson, A. S. (2010). A perspective on modelling hepatitis C virus infection. J. Viral Hepat. 17, 825–833. doi: 10.1111/j.1365-2893.2010.01348.x
Hancioglu, B., Swigon, D., and Clermont, G. (2007). A dynamical model of human immune response to influenza A virus infection. J. Theor. Biol. 246, 70–86. doi: 10.1016/j.jtbi.2006.12.015
Handel, A., Longini, I. M., and Antia, R. (2007). Neuraminidase inhibitor resistance in influenza: assessing the danger of its generation and spread. PLoS Comput. Biol. 3:e240. doi: 10.1371/journal.pcbi.0030240
Hatada, E., Hasegawa, M., Mukaigawa, J., Shimizu, K., and Fukuda, R. (1989). Control of influenza virus gene expression: quantitative analysis of each viral RNA species in infected cells. J. Biochem. 105, 537–546.
Hatchett, R. J., Mecher, C. E., and Lipsitch, M. (2007). Public health interventions and epidemic intensity during the 1918 influenza pandemic. Proc. Natl. Acad. Sci. U.S.A. 104, 7582–7587. doi: 10.1073/pnas.0610941104
Havlir, D. V., Strain, M. C., Clerici, M., Ignacio, C., Trabattoni, D., Ferrante, P., et al. (2003). Productive infection maintains a dynamic steady state of residual viremia in human immunodeficiency virus type 1-infected persons treated with suppressive antiretroviral therapy for five years. J. Virol. 77, 11212–11219. doi: 10.1128/JVI.77.20.11212-11219.2003
Heldt, F. S., Frensing, T., and Reichl, U. (2012). Modeling the intracellular dynamics of influenza virus replication to understand the control of viral RNA synthesis. J. Virol. 86, 7806–7817. doi: 10.1128/JVI.00080-12
Hlavacek, W. S., Stilianakis, N. I., Notermans, D. W., Danner, S. A., and Perelson, A. S. (2000). Influence of follicular dendritic cells on decay of HIV during antiretroviral therapy. Proc. Natl. Acad. Sci. U.S.A. 97, 10966–10971. doi: 10.1073/pnas.190065897
Ho, D. D., Neumann, A. U., Perelson, A. S., Chen, W., Leonard, J. M., and Markowitz, M. (1995). Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 373, 123–126. doi: 10.1038/373123a0
Holder, B. P., and Beauchemin, C. A. A. (2011). Exploring the effect of biological delays in kinetic models of influenza within a host or cell culture. BMC Public Health 11:S10. doi: 10.1186/1471-2458-11-S1-S10
Horiike, M., Iwami, S., Kodama, M., Sato, A., Watanabe, Y., Yasui, M., et al. (2012). Lymph nodes harbor viral reservoirs that cause rebound of plasma viremia in SIV-infected macaques upon cessation of combined antiretroviral therapy. Virology 423, 107–118. doi: 10.1016/j.virol.2011.11.024
Houghton, M., and Abrignani, S. (2005). Prospects for a vaccine against the hepatitis C virus. Nature 436, 961–966. doi: 10.1038/nature04081
Igarashi, T., Brown, C., Azadegan, A., Haigwood, N., Dimitrov, D., Martin, M. A., et al. (1999). Human immunodeficiency virus type 1 neutralizing antibodies accelerate clearance of cell-free virions from blood plasma. Nat. Med. 5, 211–216. doi: 10.1038/5576
Imai, Y., Kuba, K., Neely, G. G., Yaghubian-Malhami, R., Perkmann, T., van Loo, G., et al. (2008). Identification of oxidative stress and Toll-like receptor 4 signaling as a key pathway of acute lung injury. Cell 133, 235–249. doi: 10.1016/j.cell.2008.02.043
Imamichi, H., Crandall, K. A., Natarajan, V., Jiang, M. K., Dewar, R. L., Berg, S., et al. (2001). Human immunodeficiency virus type 1 quasi species that rebound after discontinuation of highly active antiretroviral therapy are similar to the viral quasi species present before initiation of therapy. J. Infect. Dis. 183, 36–50. doi: 10.1086/317641
Ishikawa, F., Yoshida, S., Saito, Y., Hijikata, A., Kitamura, H., Tanaka, S., et al. (2007). Chemotherapy-resistant human AML stem cells home to and engraft within the bone-marrow endosteal region. Nat. Biotechnol. 25, 1315–1321. doi: 10.1038/nbt1350
Iwami, S., Holder, B. P., Beauchemin, C. A., Morita, S., Tada, T., Sato, K., et al. (2012a). Quantification system for the viral dynamics of a highly pathogenic simian/human immunodeficiency virus based on an in vitro experiment and a mathematical model. Retrovirology 9, 18. doi: 10.1186/1742-4690-9-18
Iwami, S., Sato, K., De Boer, R. J., Aihara, K., Miura, T., and Koyanagi, Y. (2012b). Identifying viral parameters from in vitro cell cultures. Front. Microbiol. 3:319. doi: 10.3389/fmicb.2012.00319
Keele, B. F., Tazi, L., Gartner, S., Liu, Y., Burgon, T. B., Estes, J. D., et al. (2008). Characterization of the follicular dendritic cell reservoir of human immunodeficiency virus type 1. J. Virol. 82, 5548–5561. doi: 10.1128/JVI.00124-08
Kiso, M., Shinya, K., Shimojima, M., Takano, R., Takahashi, K., Katsura, H., et al. (2010). Characterization of oseltamivir-resistant 2009 H1N1 pandemic influenza A viruses. PLoS Pathog. 6:e1001079. doi: 10.1371/journal.ppat.1001079
Klatt, N. R., Shudo, E., Ortiz, A. M., Engram, J. C., Paiardini, M., Lawson, B., et al. (2010). CD8+ lymphocytes control viral replication in SIVmac239-infected rhesus macaques without decreasing the lifespan of productively infected cells. PLoS Pathog. 6:e1000747. doi: 10.1371/journal.ppat.1000747
Klenerman, P., and Gupta, P. K. (2012). Hepatitis C virus: current concepts and future challenges. Q. J. Med. 105, 29–32. doi: 10.1093/qjmed/hcr231
Lewin, S. R., Ribeiro, R. M., Walters, T., Lau, G. K., Bowden, S., Locarnini, S., et al. (2001). Analysis of hepatitis B viral load decline under potent therapy: complex decay profiles observed. Hepatology 34, 1012–1020. doi: 10.1053/jhep.2001.28509
Markowitz, M., Louie, M., Hurley, A., Sun, E., Di Mascio, M., Perelson, A. S., et al. (2003). A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J. Virol. 77, 5037–5038. doi: 10.1128/JVI.77.8.5037-5038.2003
Martin, T. R., and Wurfel, M. M. (2008). A TRIFfic perspective on acute lung injury. Cell 133, 208–210. doi: 10.1016/j.cell.2008.04.006
McLean, A. K., Luciani, F., and Tanaka, M. M. (2010). Trade-offs in resource allocation in the intracellular life-cycle of hepatitis C virus. J. Theor. Biol. 267, 565–572. doi: 10.1016/j.jtbi.2010.09.031
Mercer, D. F., Schiller, D. E., Elliott, J. F., Douglas, D. N., Hao, C., Rinfret, A., et al. (2001). Hepatitis C virus replication in mice with chimeric human livers. Nat. Med. 7, 927–933. doi: 10.1038/90968
Miao, H., Hollenbaugh, J. A., Zand, M. S., Holden-Wiltse, J., Mosmann, T. R., Perelson, A. S., et al. (2010). Quantifying the early immune response and adaptive immune response kinetics in mice infected with influenza A virus. J. Virol. 84, 6687–6698. doi: 10.1128/JVI.00266-10
Mitchell, H., Levin, D., Forrest, S., Beauchemin, C. A., Tipper, J., Knight, J., et al. (2011). Higher level of replication efficiency of 2009 (H1N1) pandemic influenza virus than those of seasonal and avian strains: kinetics from epithelial cell culture and computational modeling. J. Virol. 85, 1125–1135. doi: 10.1128/JVI.01722-10
Mohler, L., Flockerzi, D., Sann, H., and Reichl, U. (2005). Mathematical model of influenza A virus production in large-scale microcarrier culture. Biotechnol. Bioeng. 90, 46–58. doi: 10.1002/bit.20363
Morita, M., Kuba, K., Ichikawa, A., Nakayama, M., Katahira, J., Iwamoto R., et al. (2013). The lipid mediator protectin D1 inhibits influenza virus replication and improves severe influenza. Cell 153, 112–125. doi: 10.1016/j.cell.2013.02.027
Murillo, L. N., Murillo, M. S., and Perelson, A. S. (2013). Towards multiscale modeling of influenza infection. J. Theor. Biol. 332, 267–290. doi: 10.1016/j.jtbi.2013.03.024
Murphy, B. R., Rennels, M. B., Douglas, R. G. Jr., Betts, R. F., Couch, R. B., Cate, T. R. Jr., et al. (1980). Evaluation of influenza A/Hong Kong/123/77 (H1N1) ts-1A2 and cold-adapted recombinant viruses in seronegative adult volunteers. Infect. Immun. 29, 348–355.
Murray, J. M., Emery, S., Kelleher, A. D., Law, M., Chen, J., Hazuda, D. J., et al. (2007). Antiretroviral therapy with the integrase inhibitor raltegravir alters decay kinetics of HIV, significantly reducing the second phase. AIDS 21, 2315–2321. doi: 10.1097/QAD.0b013e3282f12377
Murray, J. M., Purcell, R. H., and Wieland, S. F. (2006). The half-life of hepatitis B virions. Hepatology 44, 1117–1121. doi: 10.1002/hep.21364
Nakabayashi, J. (2012). A compartmentalization model of hepatitis C virus replication: an appropriate distribution of HCV RNA for the effective replication. J. Theor. Biol. 300, 110–117. doi: 10.1016/j.jtbi.2012.01.023
Nakabayashi, J., and Sasaki, A. (2011). A mathematical model of the intracellular replication and within host evolution of hepatitis type B virus: understanding the long time course of chronic hepatitis. J. Theor. Biol. 269, 318–329. doi: 10.1016/j.jtbi.2010.10.024
Neumann, A. U., Lam, N. P., Dahari, H., Gretch, D. R., Wiley, T. E., Layden, T. J., et al. (1998). Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science 282, 103–107. doi: 10.1126/science.282.5386.103
North, T. W., Higgins, J., Deere, J. D., Hayes, T. L., Villalobos, A., Adamson, L., et al. (2010). Viral sanctuaries during highly active antiretroviral therapy in a nonhuman primate model for AIDS. J. Virol. 84, 2913–2922. doi: 10.1128/JVI.02356-09
Nowak, M. A., Bonhoeffer, S., Hill, A. M., Boehme, R., Thomas, H. C., and McDade H. (1996). Viral dynamics in hepatitis B virus infection. Proc. Natl. Acad. Sci. U.S.A. 93, 4398–4402. doi: 10.1073/pnas.93.9.4398
Oue, M., Sakabe, S., Horiike, M., Yasui, M., Miura, T., and Igarashi, T. (2013). No viral evolution in the lymph nodes of simian immunodeficiency virus-infected rhesus macaques during combined antiretroviral therapy. J. Virol. 87, 4789–4793. doi: 10.1128/JVI.03367-12
Palmer, S., Maldarelli, F., Wiegand, A., Bernstein, B., Hanna, G. J., Brun, S. C., et al. (2008). Low-level viremia persists for at least 7 years in patients on suppressive antiretroviral therapy. Proc. Natl. Acad. Sci. U.S.A. 105, 3879–3884. doi: 10.1073/pnas.0800050105
Perelson, A. S. (2002). Modelling viral and immune system dynamics. Nat. Rev. Immunol. 2, 28–36. doi: 10.1038/nri700
Perelson, A. S., Essunger, P., Cao, Y., Vesanen, M., Hurley, A., Saksela, K., et al. (1997). Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 387, 188–191. doi: 10.1038/387188a0
Perelson, A. S., and Nelson, P. W. (1999). Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 41, 3–44. doi: 10.1137/S0036144598335107
Perelson, A. S., Neumann, A. U., Markowitz, M., Leonard, J. M., and Ho, D. D. (1996). HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science 271, 1582–1586. doi: 10.1126/science.271.5255.1582
Perelson, A. S., Rong, L., and Hayden, F. G. (2012). Combination antiviral therapy for influenza: predictions from modeling of human infections. J. Infect. Dis. 205, 1642–1645. doi: 10.1093/infdis/jis265
Pinilla, L. T., Holder, B. P., Abed, Y., Boivin, G., and Beauchemin, C. A. (2012). The H275Y neuraminidase mutation of the pandemic A/H1N1 influenza virus lengthens the eclipse phase and reduces viral output of infected cells, potentially compromising fitness in ferrets. J. Virol. 86, 10651–10660. doi: 10.1128/JVI.07244-11
Ramratnam, B., Bonhoeffer, S., Binley, J., Hurley, A., Zhang, L., Mittler, J. E., et al. (1999). Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet 354, 1782–1785. doi: 10.1016/S0140-6736(99)02035-8
Rong, L., Guedj, J., Dahari, H., Coffield, D. J. Jr., Levi, M., Smith, P., et al. (2013). Analysis of hepatitis C virus decline during treatment with the protease inhibitor danoprevir using a multiscale model. PLoS Comput. Biol. 9:e1002959. doi: 10.1371/journal.pcbi.1002959
Rong, L., and Perelson, A. S. (2009). Modeling HIV persistence, the latent reservoir, and viral blips. J. Theor. Biol. 260, 308–331. doi: 10.1016/j.jtbi.2009.06.011
Rong, L., and Perelson, A. S. (2010). Treatment of hepatitis C virus infection with interferon and small molecule direct antivirals: viral kinetics and modeling. Crit. Rev. Immunol. 30, 131–148. doi: 10.1615/CritRevImmunol.v30.i2.30
Rosenbloom, D. I., Hill, A. L., Rabi, S. A., Siliciano, R. F., and Nowak, M. A. (2012). Antiretroviral dynamics determines HIV evolution and predicts therapy outcome. Nat. Med. 18, 1378–1385. doi: 10.1038/nm.2892
Sato, K., Izumi, T., Misawa, N., Kobayashi, T., Yamashita, Y., Ohmichi, M., et al. (2010). Remarkable lethal G-to-A mutations in vif-proficient HIV-1 provirus by individual APOBEC3 proteins in humanized mice. J. Virol. 84, 9546–9556. doi: 10.1128/JVI.00823-10
Sato, K., and Koyanagi, Y. (2011). The mouse is out of the bag: insights and perspectives on HIV-1-infected humanized mouse models. Exp. Biol. Med. 236, 977–985. doi: 10.1258/ebm.2011.010294
Sato, K., Misawa, N., Fukuhara, M., Iwami, S., An, D. S., Ito, M., et al. (2012). Vpu augments the initial burst phase of HIV-1 propagation and downregulates BST2 and CD4 in humanized mice. J. Virol. 86, 5000–5013. doi: 10.1128/JVI.07062-11
Sato, K., Misawa, N., Nie, C., Satou, Y., Iwakiri, D., Matsuoka, M., et al. (2011). A novel animal model of Epstein-Barr virus-associated hemophagocytic lymphohistiocytosis in humanized mice. Blood 117, 5663–5673. doi: 10.1182/blood-2010-09-305979
Schulze-Horsel, J., Schulze, M., Agalaridis, G., Genzel, Y., and Reichl, U. (2009). Infection dynamics and virus-induced apoptosis in cell culture-based influenza vaccine production: flow cytometry and mathematical modeling. Vaccine 27, 2712–2722. doi: 10.1016/j.vaccine.2009.02.027
Sharkey, M., Babic, D. Z., Greenough, T., Gulick, R., Kuritzkes, D. R., and Stevenson, M. (2011). Episomal viral cDNAs identify a reservoir that fuels viral rebound after treatment interruption and that contributes to treatment failure. PLoS Pathog. 7:e1001303. doi: 10.1371/journal.ppat.1001303
Shultz, L. D., Ishikawa, F., and Greiner, D. L. (2007). Humanized mice in translational biomedical research. Nat. Rev. Immunol. 7, 118–130. doi: 10.1038/nri2017
Simon, V., and Ho, D. D. (2003). HIV-1 dynamics in vivo: implications for therapy. Nat. Rev. Microbiol. 1, 181–190. doi: 10.1038/nrmicro772
Smith, A. M., Adler, F. R., and Perelson, A. S. (2010). An accurate two-phase approximate solution to an acute viral infection model. J. Math. Biol. 60, 711–726. doi: 10.1007/s00285-009-0281-8
Trono, D., Van Lint, C., Rouzioux, C., Verdin, E., Barré-Sinoussi, F., Chun, T. W., et al. (2010). HIV persistence and the prospect of long-term drug-free remissions for HIV-infected individuals. Science 329, 174–180. doi: 10.1126/science.1191047
Watanabe, T., Shinya, K., Watanabe, S., Imai, M., Hatta, M., Li, C., et al. (2011). Avian-type receptor-binding ability can increase influenza virus pathogenicity in macaques. J. Virol. 85, 13195–13203. doi: 10.1128/JVI.00859-11
Wei, X., Ghosh, S. K., Taylor, M. E., Johnson, V. A., Emini, E. A., Deutsch, P., et al. (1995). Viral dynamics in human immunodeficiency virus type 1 infection. Nature 373, 117–122. doi: 10.1038/373117a0
Wilson, J. N., Nokes, D. J., Medley, G. F., and Shouval, D. (2007). Mathematical model of the antibody response to hepatitis B vaccines: implications for reduced schedules. Vaccine 25, 3705–3712. doi: 10.1016/j.vaccine.2007.01.012
Wong, J. K., Strain, M. C., Porrata, R., Reay, E., Sankaran-Walters, S., Ignacio, C. C., et al. (2010). In vivo CD8+ T-cell suppression of SIV viremia is not mediated by CTL clearance of productively infected cells. PLoS Pathog. 6:e1000748. doi: 10.1371/journal.ppat.1000748
Keywords: virus infection, mathematical modeling, computer simulation, animal experiment, quantification
Citation: Iwami S, Koizumi Y, Ikeda H and Kakizoe Y (2013) Quantification of viral infection dynamics in animal experiments. Front. Microbiol. 4:264. doi: 10.3389/fmicb.2013.00264
Received: 13 June 2013; Accepted: 16 August 2013;
Published online: 10 September 2013.
Edited by:
Tomoyuki Miura, Kyoto University, JapanReviewed by:
Dorian McILroy, University of Nantes, FranceShinji Nakaoka, RIKEN Center for Integrative Medical Science Center, Japan
Copyright © 2013 Iwami, Koizumi, Ikeda and Kakizoe. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shingo Iwami, Department of Biology, Faculty of Sciences, Kyushu University, 6-10-1 Hakozaki, Higashi-ku, Fukuoka, Fukuoka 812-8581, Japan e-mail:c2l3YW1pQGt5dXNodS11Lm9yZw==

 Yoshiki Koizumi1,2
Yoshiki Koizumi1,2