- 1 Department of Neurology, Washington University School of Medicine, St. Louis, MO, USA
- 2 Department of Pediatrics, Washington University School of Medicine, St. Louis, MO, USA
- 3 Department of Radiology, Washington University School of Medicine, St. Louis, MO, USA
- 4 Department of Biomedical Engineering, Washington University School of Medicine, St. Louis, MO, USA
- 5 Department of Anatomy and Neurobiology, Washington University School of Medicine, St. Louis, MO, USA
Like many complex dynamic systems, the brain exhibits scale-free dynamics that follow power-law scaling. Broadband power spectral density (PSD) of brain electrical activity exhibits state-dependent power-law scaling with a log frequency exponent that varies across frequency ranges. Widely divergent naturally occurring neural states, awake and slow wave sleep (SWS), were used to evaluate the nature of changes in scale-free indices of brain electrical activity. We demonstrate two analytic approaches to characterizing electrocorticographic (ECoG) data obtained during awake and SWS states. A data-driven approach was used, characterizing all available frequency ranges. Using an equal error state discriminator (EESD), a single frequency range did not best characterize state across data from all six subjects, though the ability to distinguish awake and SWS ECoG data in individual subjects was excellent. Multi-segment piecewise linear fits were used to characterize scale-free slopes across the entire frequency range (0.2–200 Hz). These scale-free slopes differed between awake and SWS states across subjects, particularly at frequencies below 10 Hz and showed little difference at frequencies above 70 Hz. A multivariate maximum likelihood analysis (MMLA) method using the multi-segment slope indices successfully categorized ECoG data in most subjects, though individual variation was seen. In exploring the differences between awake and SWS ECoG data, these analytic techniques show that no change in a single frequency range best characterizes differences between these two divergent biological states. With increasing computational tractability, the use of scale-free slope values to characterize ECoG and EEG data will have practical value in clinical and research studies.
Introduction
The brain is a complex dynamic system in which the transient interaction between spatially segregated neural networks results in functional responses to both internal and external environments. These functional interactions produce emergent electrical activity that can be recorded at multiple levels, from that of individual neurons to that of more integrated activity recorded at the cortical surface or from the scalp. As shown for a large number of complex systems, the brain has been characterized both spatially and temporally by scale-free dynamics (Linkenkaer-Hansen et al., 2001; Stam and de Bruin, 2004; Bedard et al., 2006; Allegrini et al., 2009; Freeman and Zhai, 2009; Miller et al., 2009a; Chu-Shore et al., 2010; He et al., 2010; Safonov et al., 2010; Van De Ville et al., 2010; He, 2011). The recognition that the human brain electroencephalographic signal exhibits scale-free dynamics has resulted in reconsideration of the reliance of neural function on broadband, global frequency activity versus narrow, frequency specific oscillatory activity (Miller, 2010). Investigations of global measures of scale-free behavior using averaged data across multiple electrodes have suggested that these properties can be used as an index of neural state, and potentially of transitions between states (Freeman and Zhai, 2009; Chu-Shore et al., 2010; He et al., 2010; Van De Ville et al., 2010).
While there is a longstanding interest in defining state fluctuations in human neurophysiology on short time scales (microstates, see Fingelkurts and Fingelkurts, 2010; Van De Ville et al., 2010; Latchoumane and Jaeseung, 2011), the best defined stable neural state change is that seen between awake and asleep, where both clear behavioral and electrophysiological changes have been well characterized (Hobson and Pace-Schott, 2002; Saper et al., 2005; McCarley, 2007). This shift in neurobehavioral state is generally seen as representing a global change in brain state reflected not only in shifts in electrophysiological signaling, but also in metabolic activity (Braun et al., 1997; Maquet and Phillips, 1998). While a global shift to a changed neurophysiological state with a reduced level of metabolic activity is well established in slow wave sleep (SWS), recent work has shown local variation in sleep state (Dang-Vu et al., 2010; Mascetti et al., 2011; Vyazovskiy et al., 2011). Of the states represented in normal human sleep, the best characterized is that of SWS, in which recent studies of spatial dynamics have shown distinct changes in small-world network connectivity (Spoormaker et al., 2010; Larson-Prior et al., 2011). Similarly, investigation of temporal scale-free behaviors has revealed potentially stable shifts in power-law scaling between awake and SWS states (Freeman and Zhai, 2009; He et al., 2010).
Shifts in scale-free behavior with state can be compared using log–log plots of the power of brain electrical activity across the frequency spectrum, which have been shown to exhibit linear segments across decades of frequency (Linkenkaer-Hansen et al., 2001; Freeman and Zhai, 2009; Milstein et al., 2009; He et al., 2010). Fitting log transformed power data with a line provides a measurement of scale-free activity, where the slope is an index of the nature of the relationship. The power scale exponent provides information on the analyzed signal, with white noise having a slope of 0 (indicating no scale-free behavior), and pink noise a slope of negative one (indicating 1/f scale-free behavior). Measurements using EEG power have yielded exponent values of less than negative one, varying between −1 and −4 (Freeman and Zhai, 2009; Milstein et al., 2009; He et al., 2010). Such a relationship indicates that with measurements at lower frequencies, electrocorticographic (ECoG) power rises exponentially, attenuated only by our ability to both accurately measure low frequency ECoG without artifacts and to collect ECoG for long enough periods to adequately capture the lowest frequencies. With human scalp EEG, the ability to measure high frequency brain activity is also limited. Scalp electrodes measure the electrical field generated by neural activity at some distance from the cellular generators, through the skull and other tissues, which filter and attenuate the electrical signal measured at the scalp. Recording electrical activity directly from the brain through the placement of subdural electrodes on the cortical surface provides an opportunity for measuring brain activity closer to the generators, with increased signal amplitude improving and enabling the resolution of higher frequency brain activity necessary for optimal characterization of scale-free indices.
As has been noted in previous studies (Miller et al., 2009a) log–log transformed power-law dynamics in human brain are not well represented by a single global linear fit. While other investigators have described shifts in scale-free slopes with state, these changes have generally been investigated in relatively narrow frequency ranges rather than across the full measurable scale (Freeman and Zhai, 2009; He et al., 2010). Here, we report results of investigation of scale-free behavior across the full frequency range available to us using electrocorticography data in a pediatric population undergoing invasive monitoring for surgical evaluation of their intractable epilepsy. Using a data-driven approach, we examined the frequency ranges over which scale-free slopes could best distinguish the awake state from SWS. Exploring and characterizing the differences in indices of scale-free brain activity between these states is one approach to the study of fundamental mechanisms of brain function.
Materials and Methods
Subjects and ECoG Data
All subjects were consented for participation in this study under a protocol approved by the Washington University Human Research Protection Office. Parents gave written consent and the participants provided written assent. ECoG data from six patients with intractable epilepsy undergoing evaluation for surgical treatment of their epilepsy by identifying the site of focal seizure onset through neurosurgical placement of subdural electrodes according to clinical needs were used. Data were obtained from clinical ECoG recordings using subdural electrodes (either in grids or strips) on the cortical surface. The platinum electrodes (4 mm diameter, 2.3 mm exposed) spaced at 10 mm intervals were obtained from Ad-Tech (Racine, WI, USA).
Electrocorticographic data were recorded using a clinical EEG amplifier (Lamont Medical, Madison WI, USA) and Stellate Harmonie acquisition software (Montreal, Canada). Brain electrical activity was sampled from between 72 and 116 electrodes at 500 Hz (each subject had different electrode coverage). Reference and ground were either placed externally (mastoid) or internally to an electrode strip placed epidurally facing the skull. The amplifier had a 0.1 Hz low frequency hardware filter, and no high frequency filter was enabled.
ECoG Preprocessing
Data were collected over several days, providing multiple periods of both SWS and wakefulness. We use the capitalized “Awake” and “SWS” terms to represent the ECoG datasets obtained during clinical and electrographic awake and SWS periods respectively. SWS was selected out of the sleep data by viewing spectral changes as the subjects transitioned between sleep states, as well as the presence of up-down slow wave activity and sleep spindles. Five-minute sections were extracted from these longer data sets by visual inspection and chosen to be generally free of artifact and representative of ECoG from awake and SWS. In one subject a 2-h section representing the transition from the awake state through to SWS was extracted. No attempt to constrain motor or cognitive awake clinical activity was made, other than choosing sections of ECoG without significant movement artifact.
Analysis programs were implemented in Matlab (The MathWorks, Inc., Natick, MA, USA) after reading the data with EEG Lab (Delorme and Makeig, 2004). For a flowchart representing the ECoG preprocessing pathway see Figure 1A. The ECoG data were referenced to a common average, after excluding bad electrodes identified visually. A 30-s data interval was chosen for analysis, as 30 s is the standard period for clinical sleep staging (Iber et al., 2007). Ten consecutive 30 s intervals were cut from each 5 min dataset yielding 10 data sections per electrode for both Awake and SWS. For each 30-s interval for each electrode, the estimated baseline, calculated as the average of the signal, was subtracted. This baseline correction forces the zero-frequency (DC) component of the continuous Fourier Transform of the signal to zero while leaving the spectrum unchanged at all other frequencies. The effect on the Discrete Fourier Transform is to force the DC component to zero, to modify slightly frequencies near DC, and to leave higher frequencies virtually unchanged.
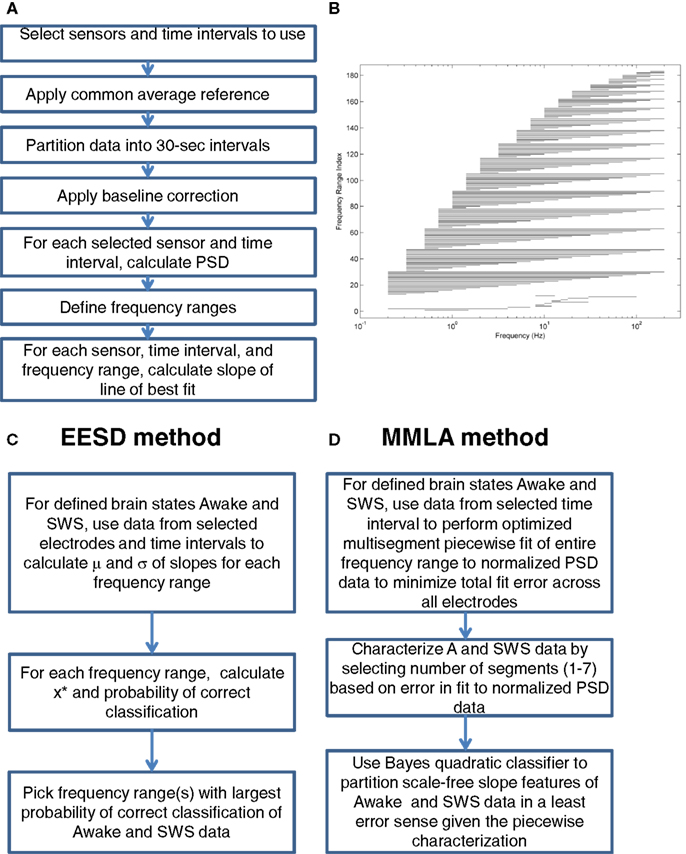
Figure 1. Analysis steps. (A) Preprocessing steps. (B) Frequency ranges. (C) EESD method. (D) MMLA method.
After baseline correction, 2048 frequency samples from 0.122 to 250 Hz were defined such that their logarithms were equally spaced. The method of Welch was used to calculate the power spectral density (PSD) at these frequencies (Welch, 1967). Because the frequency samples were not uniformly spaced, the slower Goertzel algorithm (Goertzel, 1958) is used by the pwelch call in the Matlab analysis scripts.
Least-squares straight-line fits to the logarithm of the PSDs were computed for each of 183 frequency ranges, the first 12 of which were “classical” bands and the last 171 of which systematically partition the overall frequency range, which is taken to be from 0.2 to 200 Hz, into ranges of varying lengths. Indexes 1–12 represent frequency bands that encompass the “canonical” EEG bands: 0.5–1.5 Hz (up-down), 0.2–4 Hz (delta), 4–7 Hz (theta), 8–12 Hz (alpha), 8–10 Hz (low alpha), 10–12 Hz (high alpha), 12–30 Hz (beta), 12–15 Hz (low beta), 15–18 Hz (intermediate beta), 18–30 Hz (high beta), 30–100 Hz (gamma), and 8–13 Hz (mu). The remaining 171 frequency ranges are constructed as follows. A set of 19 frequencies were chosen such that their logarithms are approximately equally spaced: 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, and 200 Hz. These frequencies were combined in all (19 × 18)/2 = 171 ways (indices 13 to 183, inclusive) as the minimum and maximum values of the frequency ranges. These frequency ranges are shown in Figure 1B, where the leftmost and rightmost points of each horizontal line represent the minimum and maximum frequencies included in the frequency range whose index is indicated on the vertical axis. The frequency range index is a shorthand way of referring to a range by a single number, primarily for programming purposes.
Equal Error State Discriminator Method
Taking the Awake and SWS data as distinct biological and cognitive states, a scheme was devised to determine the frequency ranges that best distinguished between these states using the 183 frequency ranges, so that no a priori assumptions about the most important frequency ranges influenced the search through frequency space. A summary of the equal error state discriminator (EESD) method is listed in Figure 1C. For a given subject, brain state, and electrode, the mean and SD of the fitted slopes were computed to form a histogram approximation to the distribution of slopes.
Let c ∈ {1, 2} be a class indicator for SWS (c = 1) and Awake (c = 2) data. Histograms of the frequency of occurrence of slopes were computed, displayed, and found to resemble Gaussian functions. The mean, μc, and SD, σc, were calculated for each class. The model probability density functions for the distributions of slopes are
Let
be a threshold such that if the calculated slope is below x*, then the estimated brain state would be SWS or Awake, whichever one has the smallest mean slope, μc, and if the calculated slope is above x* then the estimated brain state would be whichever has the largest mean slope. This yields an EESD, such that the probability of miscategorizing SWS for Awake is the same as miscategorizing Awake for SWS. The probability of correct state categorization was calculated first for all electrodes and then grouped by large (≥20 electrodes) grid.
Multivariate Piecewise Linear Fits
Each PSD is partitioned into an arbitrary number, D, of adjacent linear fit segments which together span the full PSD spectrum. All unique D-segment combinations are collected (from Figure 1B, indices 13–183). For each of these unique partitions, p, a fit error, Ep, is computed as the sum of the absolute differences between piecewise linear fits and the normalized PSD. That is,
where PSDst is the normalized PSD for electrodes in time interval t and PSDpst is the piecewise linear approximation of PSDst with regard to partitioning p. The algorithm then selects a frequency band partition, p, with the lowest value of Ep as the “best fit”. The full frequency spectrum is always fully covered by some combination of segments. Figure 2 illustrates the summation of individual line fit errors used to compute Ep. Each colored line segment represents the least error fit of a line segment to a given frequency range of a single channel and 30 s time interval’s PSD. Lines are colorized to indicate the degree of fit error. The total error for this partitioning is given by the summation of the error shown by each of these line segments.
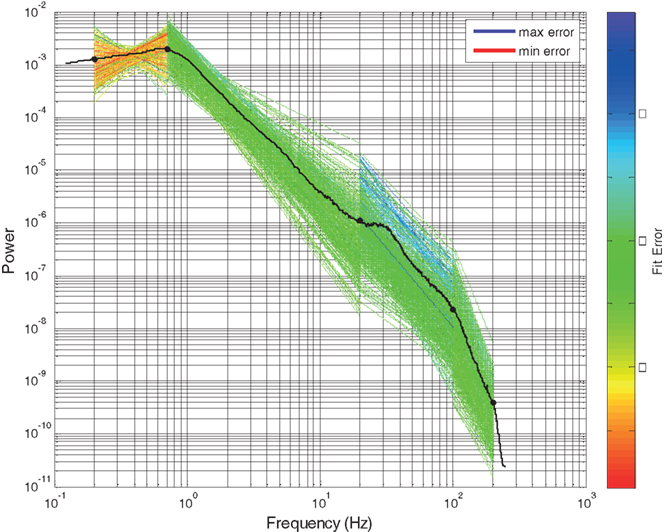
Figure 2. Four segment piecewise linear fit of scale-free slope for all electrodes in subject 1 in SWS. Each slope fit line is colored according to the line fit error, computed as the absolute difference between that line segment and the electrode specific PSD. The solid line is the global mean PSD of all electrodes averaged across all electrodes and time intervals. Y axis is log power. X axis is log frequency.
MMLA Method
The multivariate maximum likelihood analysis (MMLA) method uses the log-linear slopes of each fitted line segment over all electrode channels and time intervals for each PSD to determine an optimal partitioning of class categories ( frequency ranges). A summary of the MMLA method is listed in Figure 1D. Categories can be modeled by the NxD multivariate feature matrix F , where each of N observations of segment slope in some class A is represented as a D element row in series F and where D corresponds to the number of linear segments being considered. Class A is then modeled as this set of measured instances of the D-segment slope fit values.
After assigning each distinct state to a class category (Awake, SWS, etc.), the MMLA method was used to determine a decision surface in feature space. This decision surface acts as a category boundary such that each observation of a normally distributed class density can be identified with a minimum number of misclassifications.
The Bayes Classifier offers a straightforward method by which to implement maximum likelihood analysis and optimally partition class feature data that can be accurately parameterized. An inspection of slope-value histograms shows normal distribution of slope values when considering a single line fit segment’s characteristic across electrode channels and time intervals. For this reason, a Gaussian mixture model was selected to represent class characteristics in feature space, F. These Gaussian distributions can be fully specified as mean vector, μc, and covariance matrix, Σc for each class category c. It is straightforward to estimate these parameters as
and
for each class c = 1 … C, where x ci represents a D element vector. This corresponds to a single observation of D line segment slopes of class c. Nc is the total number of observations included in the training set for that class. In this analysis, two classes are considered, Awake and SWS. It follows from the definition of the Bayes Classifier with a Gaussian mixture model that a discriminant function can be computed as
where P(ωc) is the a priori probability of feature vector x belonging to class c. (The prior probabilities of each class are assumed to be equal.) The remainder of the equation is simply derived from the scaled and shifted expression of the multivariate normal density N (μ, Σ). When presented with a new observation, category assignment is determined by selecting class i for which di(x) > dj(x) for all i ≠ j. Following this same method, a decision surface which partitions feature space can be defined where di(x) = dj(x) for all i ≠ j.
Results
Subjects
A characterization of scale-free brain activity in awake and SWS states was performed with ECoG data from six pediatric (ages 8–17, two male, all right handed) subjects with intractable partial epilepsy. ECoG data provides substantially higher signal to noise ratios across broad frequency ranges compared with standard scalp EEG, as the brain signal is recorded subdurally on the cortical surface without filtering of the brain electrical signal by the skull. The higher signal amplitude obtained using ECoG recording allows investigation of upper gamma ranges not generally accessible in standard scalp-recorded EEG and improves the resolution of the brain electrical signal, which is 5–10 times higher amplitude than EEG recorded through scalp electrodes.
In most of the subjects investigated here, the majority of the electrodes were located outside the brain area that was surgically resected. Electrode coverage was determined by clinical needs. Table 1 provides information on the number and placement of electrodes for each of the six subjects participating in this study. A follow-up of greater than two years for all subjects found three are seizure free and a fourth showed seizure recurrence 4 years after surgery, exhibiting an extended period of freedom from seizure.
Electrocorticographic data from individual electrodes were excluded if excessive, non-physiologic noise was present, usually resulting from lack of ideal positioning on the cortical surface. No attempt was made to exclude the electrodes overlying the presumptive seizure onset zones or resected areas, which in all cases represented a minority of electrodes (all <10%, except in subject 4 where the resected tissue represented about one-third of the electrode coverage). Electrode numbers ranged between 72 and 116, and excluded electrodes ranged from 0 to 6, resulting in a total of 550 (72–114 per subject) electrodes across all subjects. Each ECoG time course over 5 min was broken into 10 time intervals for a total of 5500 PSD’s generated across all subjects in each Awake and SWS dataset.
Single Segment Linear Fits to PSD Data
Power spectral density data from a single 30 s interval from one subject and a single electrode in SWS (Figure 3) demonstrates the typical behavior seen across all datasets, where a log–log plot can be fit with a straight line over a range of frequencies (0.5–5 Hz illustrated). These log–log PSD plots, however, do not show the completely linear behavior expected with truly scale-free processes, rather they tend to show domains of linear behavior. At the two frequency extremes, this deviation can be explained by data acquisition conditions. At high frequencies (>200 Hz), where the signal power is low, the ECoG voltage merges with the noise characteristics of the measurement system (electrode, cabling, and amplifier noise) and thus includes non-neural signal sources. At low frequencies (<0.5 Hz), the amplifier high pass filter circuit truncates the rise of sub-1 Hz power seen in studies where DC amplifiers were used (He et al., 2010). Therefore, the frequency range evaluated in this study lies in a broad middle range (0.5–200 Hz) where the ECoG data represents brain activity rather than measurement artifacts. These middle frequency ranges include all of the classic frequency bands (up-down, delta, theta, alpha, beta, and gamma).
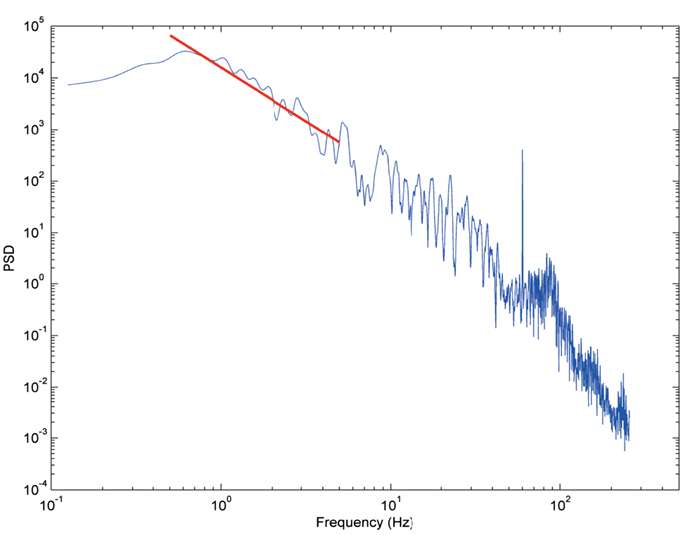
Figure 3. Typical PSD plot from subject 3 in SWS from a single 30 s time interval. Y axis is log power. X axis is log frequency. Red line indicates segment two slope fit (slope = −2).
As simple single linear fits did not adequately characterize the ECoG data, we chose to evaluate differences between Awake and SWS across the full broadband range rather than to focus on the classical band-limited frequencies or prechosen frequency ranges. This data-driven approach breaks up the frequency domain intervals into all possible combinations (171 plus 12 canonical frequency bands), without reflecting any preconceived ideas about the relative importance of specific frequency ranges.
Equal Error State Discriminator
The first analytic strategy, EESD, emphasizes classification based on equalizing the probability of each type of classification error, assuming Gaussian models for the distribution of slopes. A sample histogram from a single subject demonstrating the distribution of the slope values in Awake and SWS data is shown in Figure 4A and demonstrates the ability of this method to discriminate between electrical activities obtained during these two biologically distinct states. These data were used to calculate x*, which characterizes the probability of correct classification of the 30-s PSD from each electrode. An initial analysis was performed using both strip and grid electrodes (results not shown) with an improvement in performance seen when grouping by only grids, which samples more anatomically contiguous data as opposed to the more distant strip electrodes. The 10 frequency ranges with best discrimination accuracy (80–90%) are illustrated for each subject in Figure 4B. While the frequency ranges most useful for correct discrimination were not consistent across subjects, they tended to cluster within subjects. Further, those frequencies with greatest utility for categorization were not confined to any of the classical frequency bands used in staging sleep.
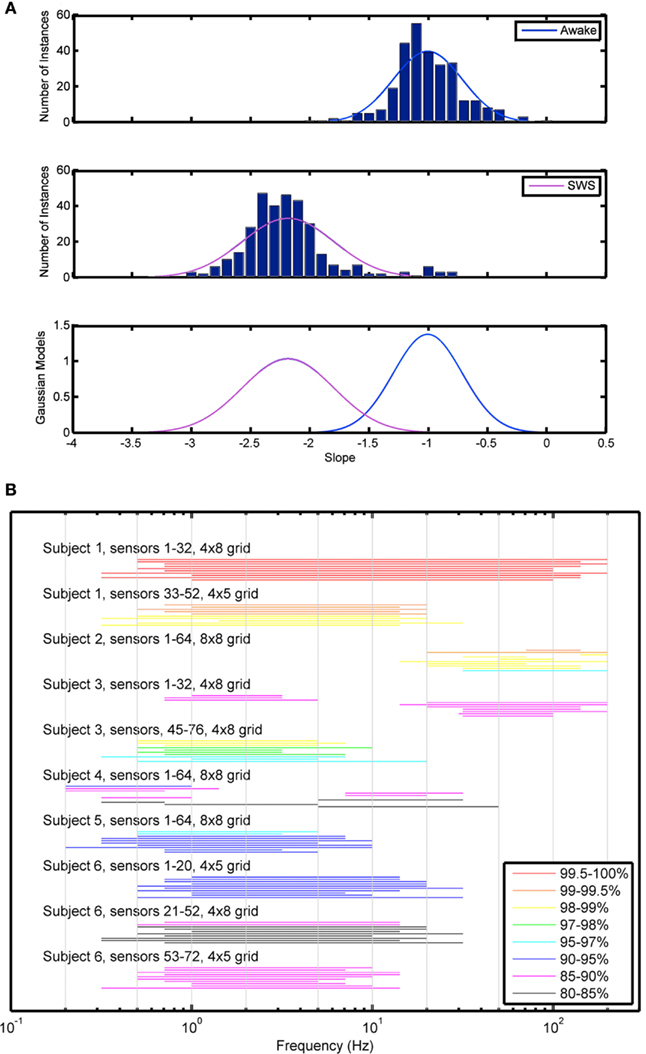
Figure 4. Equal error state discriminator method. (A) Sample histogram demonstrating histogram data used for characterization of scale-free slope data. (B) EESD method showing the top 10 frequency ranges associated with best categorization between Awake and SWS states by grid and subject.
Multiple Segment Piecewise Linear Fits to PSD Data
As our study was motivated by the notable changes in the linear nature of the log–log power spectral plots across the frequency spectrum, we chose to evaluate these data as combinations of piecewise linear fits that do not rely on a priori assumptions of prespecified frequency ranges. The PSDs were normalized to total power to emphasize the role of the scale-free slope across all electrodes. Linear fitting was then done analytically, using an optimization strategy in which adjacent frequency ranges are identified that minimize the error of fitting all possible combinations of frequency ranges across all the electrodes; each fit is not optimal for each electrode, but the frequency boundaries chosen are the best across all the electrodes in that state. This strategy identified where frequency boundaries in scale-free slope transitions occurred in particular Awake and SWS data.
Initial studies characterized the optimal number (1–8) of piecewise linear segments which provided the best overall fit to the data. We found that four segment fits provided, in both qualitative and quantitative terms (fit error improved less than 10% by including additional segments beyond four), the best piecewise linear fits. Figure 5 shows a comparison between optimization across the full frequency range (Figure 5A) relative to one in which a narrower frequency range (1–100 Hz) was chosen a priori (Figure 5B). In Figure 5B note that fitting to a prespecified frequency range of interest results in poor fits to residual frequency ranges. Visual inspection of these plots shows that the prespecified frequency range provides a poor fit for frequencies from 10 to 100 Hz, which are fit separately using the piecewise linear fit optimization approach.
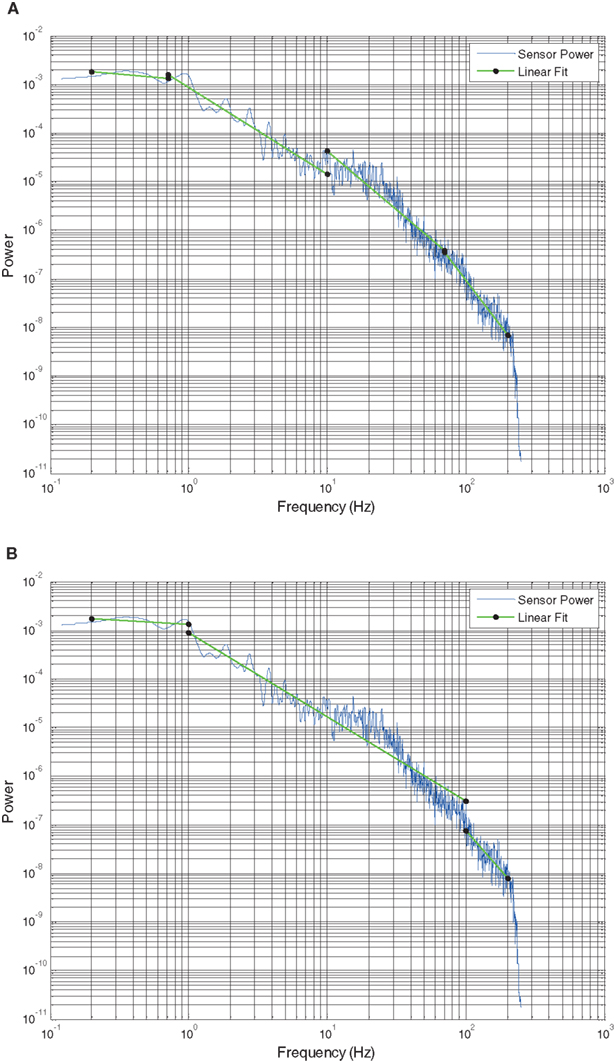
Figure 5. Power spectral density plots showing the PSD from subject 1 of a single electrode and 30 s time interval in blue. Green lines with endpoints show the (A) least error four slope segment fit and (B) three segment fit with the middle segment frequency range set to 1–100 Hz. Y axis is log power. X axis is log frequency.
Across subjects, these plots show several general themes (Figure 6). A global, normalized PSD is shown for comparison in blue (Awake) or red (SWS) for comparison. First, the general nature of negative slopes in segments two to four is present in almost all electrodes and segments. Such a general shape is valuable, as artifact-laden data does not always demonstrate an orderly progression across frequencies, and deviation from typical behavior may be a valuable way to exclude intervals of poor data from quantitative ECoG and EEG analyses. Second, in the lowest frequency segment (slope segment one), with a low frequency hardware filter present, the sign of the slopes is either positive- or negative-note the crossing of the lines indicating that some of the electrode by interval data has positive slope, while other lines have negative slopes. A positive slope indicates decreasing power at low frequency, which would seem to be at odds with a scale-free process, where a negative slope with increasing power at lower frequencies is characteristic. This is certainly due to the presence of the low frequency hardware filter (for similar data with a DC coupled EEG amplifier see He et al., 2010) and the diminution of the low frequency components due to the baseline correction, but the slope of segment one in Awake data is still usually negative across all subjects, indicating the difference is biological and not technical. The presence of higher power in the up-down frequency band actually pushes the slope mean from negative to positive in SWS (Figure 7A) and the percent of electrode-interval data with a positive value in segment one markedly decreases in the Awake data (Figure 7E). Such a feature may be helpful in scoring clinical sleep data, as this slope calculation can be performed with relatively short 30-s intervals.
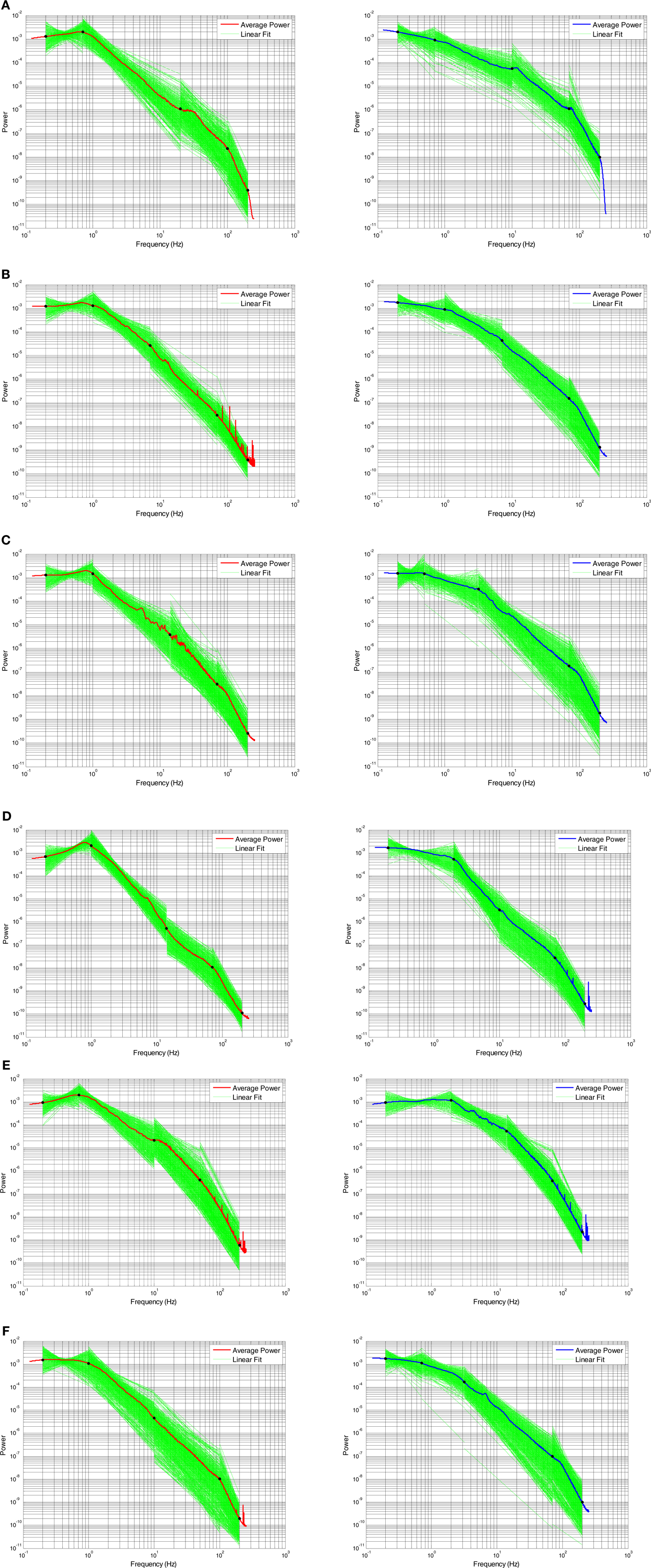
Figure 6. Four segment piecewise linear fits of PSD slopes by 30 s time interval and electrode plotted in green for each subject (one to six in order A–F, respectively) in both SWS (left column) and awake (right column) states. The red (SWS) and blue (awake) lines are global averages of normalized power averaged across all electrodes and time intervals.
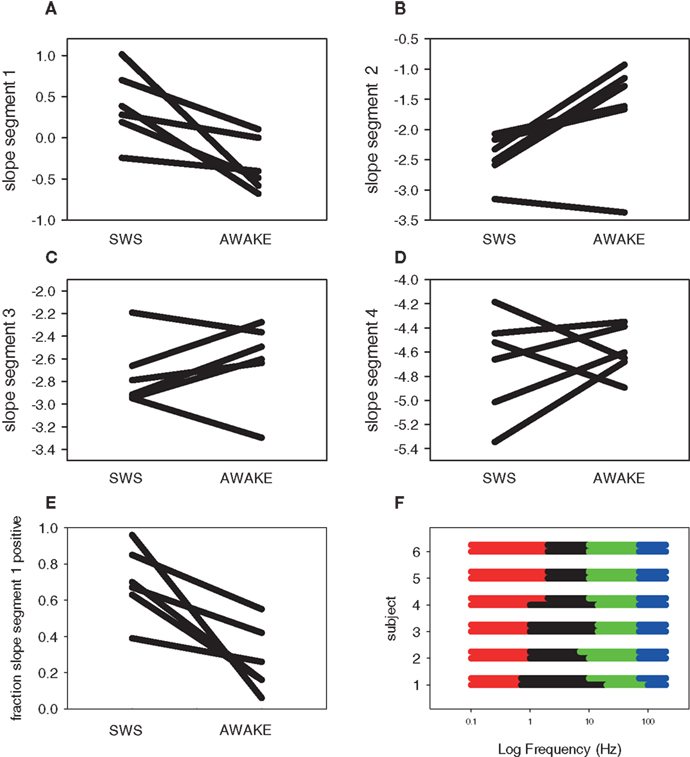
Figure 7. Summary data for scale-free four segment slopes in SWS and awake states. Each line is a separate subject. (A) Segment one slope (B) Segment two slope (C) Segment three slope (D) Segment four slope. (E) Fraction of positive segment one slopes. (F) Frequency ranges over which the four segment scale-free slopes were calculated by subject. The top line of each subject group is Awake; the bottom is SWS. Colors indicate segment: one (red), two (black), three (green), and four (blue).
The slope values from all four segments change between Awake and SWS (Figures 7A–D), though general features are apparent, even in six subjects. In general, mean slope values become more negative in progressively higher frequency segments, with slope segment numbers similar to those reported by others (Freeman and Zhai, 2009; Manning et al., 2009; Miller et al., 2009a; Milstein et al., 2009; He et al., 2010). The use of piecewise linear fits using multiple frequency segments also emphasizes that the values of the slope are not constant across the entire ECoG frequency spectrum and thus cannot be described by a single slope value, as typically seen in many other forms of scale-free data (geophysical, electrical, economic, geographic), but the general trend is consistent with a scale-free process. The frequency ranges chosen for the best segment fits are generally consistent (Figure 7F), indicating the stability of the fitting process across ECoG data from multiple subjects.
Multivariate Maximum Likelihood Analysis
To explore whether the use of multi-segment piecewise linear fits could further distinguish between neural states, an analysis scheme (MMLA) was developed. This method utilizes multivariate analysis with a Bayesian state discriminator to include slope data from multiple slope segments, adding higher dimensionality to the class models. The MMLA method utilizes the maximum likelihood method and non-linear decision boundaries to distinguish between states. The best performing MMLA state discriminator to distinguish between Awake and SWS data for the six subjects utilized segment one and segment two slope data (Figure 8A). Each point in Figure 8A shows a 30-s interval from a single electrode. MMLA performance was affected by the data from subject 4, which was different than the rest of the subject data (Figure 8B) in that a larger percentage of electrodes covered abnormal brain tissue. Nevertheless, SWS and Awake data were correctly distinguished in this subject.
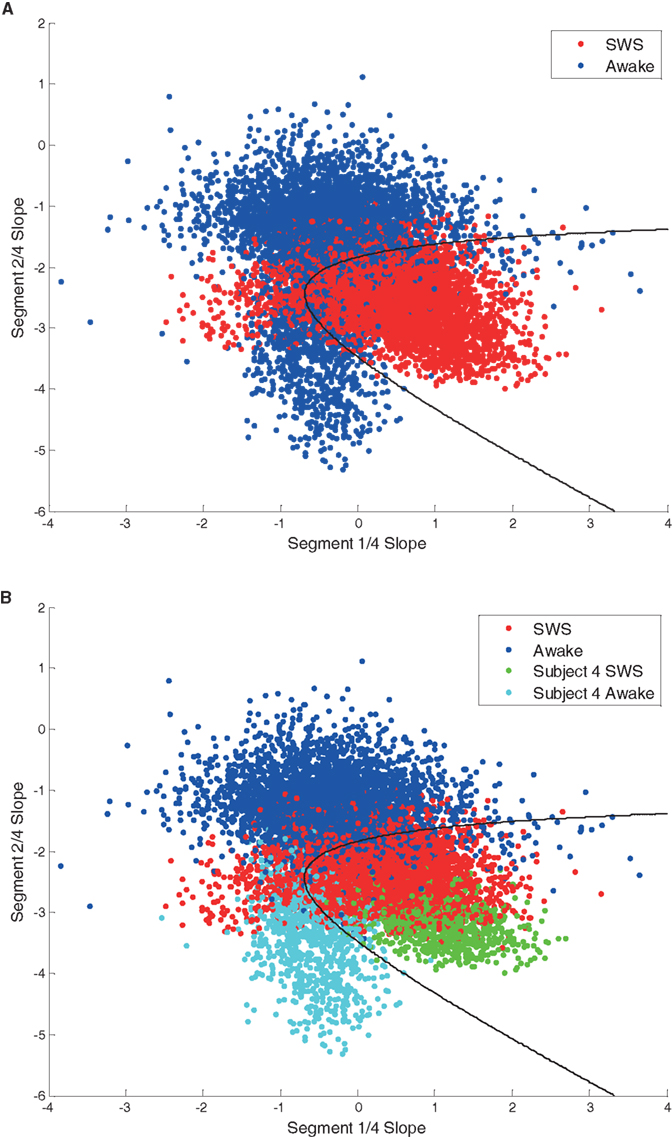
Figure 8. (A) Scatter plot of segment one and segment two scale-free slope values in awake (blue) and SWS (red). Each point represents 30 s data from one electrode. The black line represents a classifier decision boundary which best separates awake and SWS states in this feature space. MMLA performance was 0.84. (B) The same scatter plot with points from subject 4 highlighted in different colors. This coloring demonstrates that the subject 4 awake state cluster shows significant separation from the overall awake state group indicating heterogeneity between subjects.
Continuous ECoG Slope Data
Though we have focused on a direct comparison of two highly distinct neural states, the awake and SWS states, these same techniques can be employed in longer stretches of continuous ECoG data, to observe the properties of the slopes within states, and across state transitions. Figure 9 shows the slope calculations across a 2-h stretch of ECoG data from a single subject where the subject was initially awake, fell asleep, aroused and awoke, and again fell asleep with most of this 120 min period in some form of sleep. Note that these data were calculated with frequency ranges defined using the MMLA analytic method (Figure 10). In Figure 9B, we provide data on delta power changes over these state transitions.
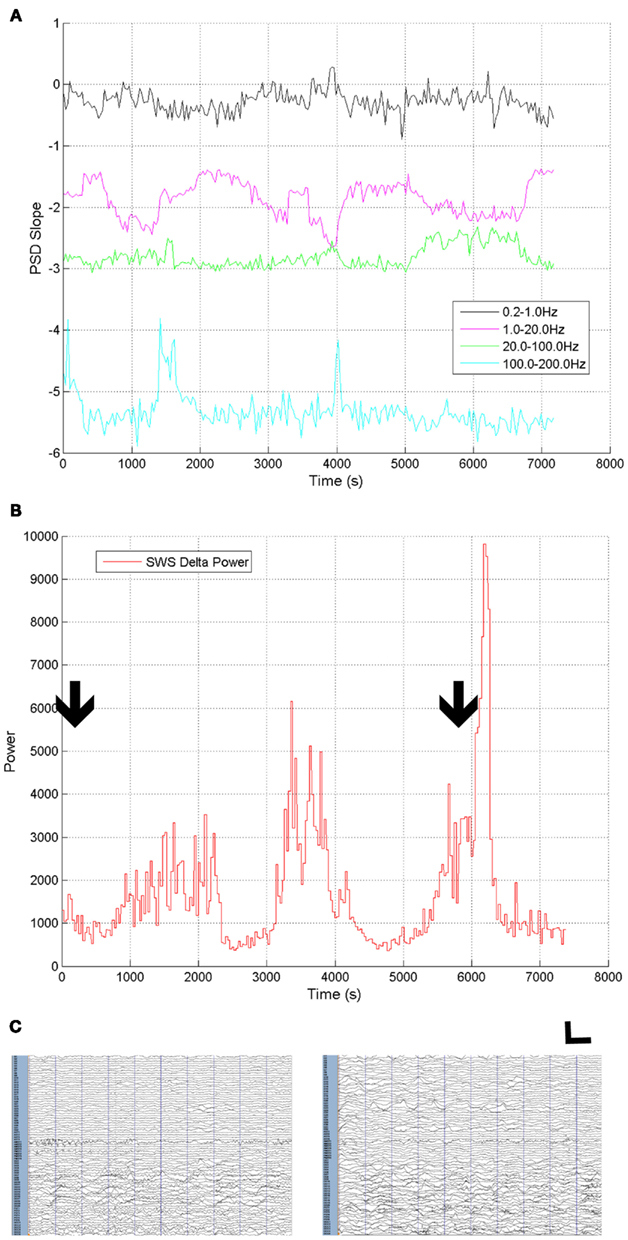
Figure 9. Changes in ECoG characteristics during state change over 2 h in subject 1. (A) Four segment scale-free slopes calculated with prespecified frequency ranges. (B) Delta and up-down frequency range power (0.5–4 Hz) over the same time period. Arrows indicate position often seconds of ECoG data shown in (C) left (awake) and right (SWS). ECoG data high pass filtered at 0.5 Hz. Vertical calibration bar indicates 2000 μV. Horizontal calibration bar indicates 1 s.
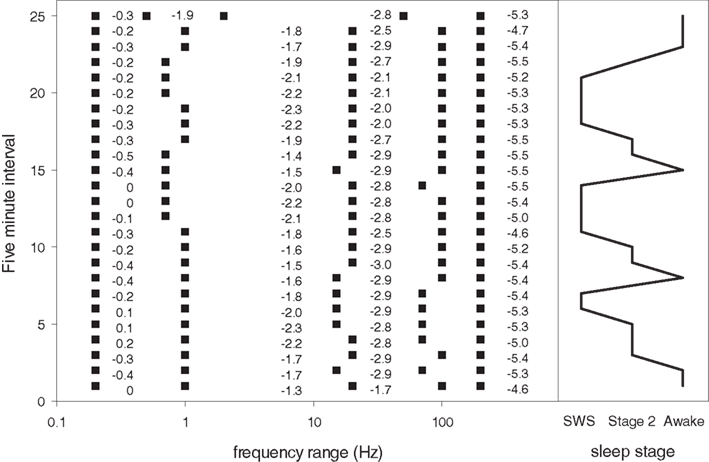
Figure 10. Frequency boundaries of four segment scale-free slope segment linear fits from 2 hours of continuous data during state changes in subject 1. Y axis shows frequency boundaries from 25 consecutive five minute intervals. X axis shows log frequency. Numbers indicate the value of the slope for each five minute interval within the frequency range endpoints indicated by the filled squares (all ranges start at 0.1 Hz and end at 200 Hz). Note the general stability of the frequency ranges chosen by MMLA across time and state. The right side of the figure shows the corresponding state (SWS, Awake, Stage 2).
Strikingly, there was no systematic relationship between state and the slope value of the highest frequency ranges despite the absence of overtly conscious cognitive activity in SWS, though two increases in slope during sleep were noted. Second, the slope of the lowest frequency segments one (0.2–1 Hz) and two (1–20 Hz) varied with the presence of the highest degree of 0.5–4 Hz power which includes up-down oscillations most prominent in SWS. Representative 10-s epochs of ECoG are also presented (Figure 9C). Note that the extent of visible ECoG slowing is variable across electrodes, even in the awake state, with clear slowing present in electrodes over posterior cortex (bottom of Figure 9C). Concern for this slowing on scalp EEG drove the posterior electrode placement, though the resection was performed far away in anterior temporal cortex, and the subject has been seizure free for greater than two years.
A movie of the slope segment fits linked temporally to the multi-segment scale-free slope data over the 2-h of ECoG data illustrated in Figure 9 is present on the Frontiers website (see Movie S1 in Supplementary Material) to further illustrate the relative temporal stability and the transitions inherent in the slope data. Note that the PSD segments are colorized to indicate the frequency ranges, with the actual slopes resulting from the linear fits time linked in the plot on the right. The similarity across time of even short segments (30 s) of log–log PSD plots is quite striking over time, and characteristic of human ECoG (see Figure 2A from He et al., 2010).
Discussion
Our analysis of a scale-free property of human ECoG has provided new insight into the characteristic of this property when the brain changes its state between awake and asleep. By choosing to allow the data to define the regions over which linear slopes could be fit to log–log plots of signal power by frequency, we show that ECoG spectra are not well characterized by a single linear fit across a defined set of frequencies, but are best described by a set of discrete linear fits across the full range of available frequencies. In agreement with Freeman and Zhai (2009), we show that the mean and SD of measured slope change across the entire frequency spectrum (EESD), are excellent determinants of state differences. In agreement with others (Miller et al., 2009a), we find an abrupt slope change at about 75 Hz in most subjects where the slope shifts to more negative values near −4. While we report data computed over 30 s intervals in this report, we also examined changes in shorter (10 s) intervals, finding similar behaviors and lending credence to the characterization of human brain activity as scale-free.
Scale-Free Slope Data and Characterization of SWS and Awake States
Clear differences in the scale-free slope values were observed between awake and SWS states, which allowed categorization of data from individual electrodes as SWS or awake state ECoG by two different, yet complementary methods. The EESD method characterized the frequency ranges that best categorized the data from the SWS and awake states within the constraint of having equal probabilities for each type of miscategorization. This method does not preselect a frequency range; rather it looks at all possibilities across the entire frequency range and reveals the most discriminative frequency ranges. That the ECoG signal, which is inherently non-stationary, can be described by a scale-free index shows that truly global measures can be used to analyze state changes over the entire brain. Scale-free slopes, however, may also be locally dynamic (He et al., 2010) and thus provide a source of contrast for utilization by brain–computer interfaces as well as characterizing local or regional cognitive processes.
The MMLA method emphasizes complete use of the available ECoG spectrum, optimizing the multi-segment slope fit across all electrodes and time intervals in a given state. This method compares the slopes of the PSD’s that have been normalized to total ECoG power. Two interesting features of this analysis emerge. First, with increasing frequency, the slopes of the segments increased, from positive to slightly negative in segment one up to more than negative four at the highest frequency segment. These changes reflect the fundamental biology of the ECoG PSD broadly across the brain. Second, the slopes of the highest frequency range, segment four (generally above 70 Hz), show little difference between awake and SWS neural states. Modulation of high frequencies (gamma, high gamma) has been implicated in many studies to be associated with cognitive processing, but gamma frequency power remains high in sleep (Valderrama et al., 2012). Although there was good reason to expect gamma frequency activity in awake states with ongoing behavior to be different than in SWS, no systematic differences in slope were present.
The largest differences between awake and SWS states were seen in slope segments one and two, the two lowest frequency ranges. At the lowest frequency values, the interaction of the hardware filter and the presence of up-down activity in the lowest frequency range actually flipped the expected negative segment one slope to a positive value in many electrodes. Since the Awake dataset, which was recorded under identical conditions as SWS, did not show this positive slope, the difference reflects the fundamental biology of the low frequency ECoG across changes in state. Indeed, including frequency ranges beyond 1–100 Hz provided a superior ability to distinguish between ECoG from awake and SWS states, indicating the importance of including frequency ranges beyond 1–100 Hz.
Interestingly, the very highest frequency data used in this study (up to 200 Hz) was not particularly helpful in distinguishing awake and asleep ECoG as all of the segment four slopes were around −4. Indeed, little variation in the slope could be seen with sleep onset, and transition into SWS. Though the ECoG electrodes are on the surface of the brain, they are relative macroelectrodes compared with depth electrodes, microwires, or higher density grids with smaller surface electrodes. Relatively low amplitude changes in power in discrete high frequency ranges can be resolved during cognitive tasks with careful recordings using similar subdural electrodes (Gaona et al., 2011), indicating that the lack of differences in slopes were not likely due to the inability to record low amplitude activity. Changes in power in discrete frequency bands that are not sizable enough to affect scale-free slope, however, may not resolvable if the differences are both anatomically local and short-lived, and reflect change in narrow frequency bands, since the present analysis emphasized slope changes across wide frequency ranges.
ECoG Power
Measurement of ECoG power over wide temporal scales, with transitions through neural states, is non-stationary; the means and SDs of the power distributions are not stable over time. Indeed, this non-stationarity of ECoG power is a fundamental characteristic of human ECoG and EEG. For our analysis of scale-free slopes, total power was normalized in the PSD from each electrode. Normalization limits the ability to see power changes, but represents a compromise to maximize the characterization of scale-free slope data. Whether task activity engages discrete frequency bands, or affects broadband activity through changes in total power remains an active area of inquiry (Manning et al., 2009; Miller et al., 2009b; He et al., 2010).
Within-electrode analyses will be needed to characterize possible power changes across state. Clearly, individual frequency bands profoundly change with state, best exemplified by the obvious qualitative difference between the presence of sleep spindles and up-down states in SWS. The ability to process long stretches of data available in ECoG studies will hopefully provide future insight into broadband power changes.
Limitations
Measurement of brain ECoG, necessarily an integration of synchronized brain activity reflecting the activity of millions of neurons for a signal to appear on the cortical surface, is currently limited by mathematical techniques for including the influences of arrhythmic activity. The foundation of this report and all others to date relies on the transformation of a time varying signal to the frequency domain that imposes the mathematical concept of a rhythmic, time varying signal. Such a measure is likely an inadequate index of brain activity where arrhythmic activity is a significant fractional part of ongoing spontaneous brain activity. Compared to the many other biological, geographical, geological, economic, and social science examples of scale-free activity, ongoing brain activity also has the special property of cross frequency coupling, where activity in discrete frequency bands is related to, and perhaps organizes, activity in other discrete frequency bands (He et al., 2010). The mechanisms underlying the generation of scale-free activity is currently a topic of intense investigation in many scientific disciplines, particularly in neuroscience.
All studies recording ECoG data from patients are limited by the necessity to provide brain coverage based upon clinical requirements, and the potential for recording from abnormal brain regions. In this study, while some data were recorded from electrodes overlying abnormal brain, the majority of the electrodes were located over brain tissue that was normal based on electrophysiological features. Thus, we believe that the decision to average across all electrodes overcame the contribution from those relatively few electrodes over resected brain tissue and over regions with abnormal activity.
In this report, we did not explore the rich spatial data also available in ECoG data sets. Others have reported a slight variation in scale-free slope in the awake state across cortical lobes (Milstein et al., 2009). In our EESD analysis, the improvement in performance of state categorization gained by grouping data from smaller anatomical regions (using the more contiguous ECoG data recorded separately from grids) may indicate systematic heterogeneity in the slope characteristics at different anatomical locations. Further studies will investigate whether such differences are present in slopes by anatomical location and across the long stretches of ECoG enabled by the use of clinical data.
Practical Issues
The ability to use scale-free indices to determine brain state from ECoG has several attractive properties. The computational efficiency of the creation of PSD’s, even with measurements from many electrodes, is increasingly tractable with current generation computers, and the extraction of simple summary statistics may make classification of ECoG and EEG data more automated and accurate, as well as being useful in characterizing and identifying pathological states.
The most compute intensive portion of the overall procedure is the computation of the PSD plots, which takes several hours for the entire dataset comprising 1 h total of ECoG data. Our deliberate choice of frequency samples that are not equally spaced, but whose logarithms are equally spaced, slows the computation of the PSD because it disallows the use of fast Fourier transform (FFT) methods (Welch, 1967) in favor of another method (Goertzel, 1958). Once the PSD’s are precomputed, the processing time is tens of minutes for the rest of the analysis across the six subjects. Much of this data can be processed in parallel, further decreasing computation times. Such improvement in compute times makes this analysis possible for clinical use.
These analytic strategies only represent initial attempts at characterization of scale-slopes of broadband ECoG, such techniques are applicable to clinical studies. The inherent similarity and relative stability of such data may provide an easy way to distinguish artifact, as sections of ECoG recordings with artifact often display substantially different PSD’s. Scale-free slope data is less affected by narrow band artifacts, and significant deviations from scale-free behavior may in fact be an excellent method of artifact detection.
The classification of awake and SWS state data has obvious clinical utility, and the use of scale-free slopes may provide an additional method for automated state scoring. Future studies will include trending of continuous data as reported in Figure 9. Such data may not only provide new methods for characterizing stable neural states, but also the nature and sharpness of state transitions. Such transitions could be global or local, with recent reports showing clear local differences in sleep state by region (Mascetti et al., 2011; Nir et al., 2011). The higher spatial sampling available in ECoG recordings may provide additional insight as to whether the brain performs state transitions globally or locally, in an orderly anatomic gradient or by brain sub-network.
A general characteristic of these scale-free slope data is its relative stability, emphasizing the scale-free nature of brain electrical activity. This general stability suggests that much of ongoing brain activity can be thought of as a scaffolding upon which cognitive activity rides, similar to the spontaneous fluctuations observed in BOLD fMRI (Raichle, 2010). Though such behavior is expected in truly scale-free processes, such stability is very useful in detecting when deviation from scale-free behavior might be artifactual, a key limitation in trying to perform computational studies on both clinical and research ECoG, or arises specifically from activity of locally concentrated active cognitive processes.
In exploring the differences between awake and SWS ECoG, these analytic techniques show that no changes in a single frequency range best characterizes differences between these two divergent biological states. Establishing the nature and values of scale-free slopes in ECoG data from awake and SWS states, the two most widely divergent neural states seen in normal daily brain activity, allows us to begin to develop a framework for the development of automated state classification using scale-free slopes. Establishing the extremes and variability in data across anatomic regions and subjects is necessary for tuning the analytic strategies for automated classification. The results of the current analysis will need to be extended to larger numbers of independent datasets to determine the ultimate value of using scale-free slope indices for such state classification, particularly across the more subtle changes in quiet non-REM sleep (stages 1–4), and distinguishing active sleep (REM) and awake ECoG data.
Many extensions to the current analytic methods are easily added. The current MMLA approach categorized single electrode data from single 30 s time intervals and does not integrate the information across all electrodes at a particular time point for a global state assignment. In addition, state assignments could be tuned using knowledge of the states surrounding the current time as changes in slope-free indices across state transitions shown in Figure 10 are better understood. Such potential additions would further improve performance of an automated state classifier. In the present report, however, our goal was to demonstrate the utility of characterizing awake and SWS brain activity using scale-free indices across the available frequency spectrum.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was supported by the McDonnell Foundation.
Supplementary Material
The Movie S1 for this article can be found online at http://www.frontiersin.org/Sleep_and_Chronobiology/10.3389/ fneur.2012.00076/abstract
Movie S1. Scale-free properties of ECoG Movie.AVI. Animation of PSD plots across 120 min of consecutive data during with separated into 5 min sections from start (S00) to finish (S24) during which subject 1 falls asleep (awake to several epochs of SWS illustrated in Figure 10). Colors in PSD data show frequency ranges linked to plot on right showing the segment slope values.
References
Allegrini, P., Menicucci, D., Bedini, R., Fronzoni, L., Gemignani, A., Grigolini, P., West, B. J., and Paradisi, P. (2009). Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80, 061914.
Bedard, C., Kroger, H., and Destexhe, A. (2006). Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 97, 118102.
Braun, A. R., Balkin, T. J., Wesenten, N. J., Carson, R. E., Varga, M., Baldwin, P., Selbie, S., Belenky, G., and Herscovitch, P. (1997). Regional cerebral blood flow throughout the sleep-wake cycle. An H2(15)O PET study. Brain 120, 1173–1197.
Chu-Shore, J., Westover, M. B., and Bianchi, M. T. (2010). Power law versus exponential state transition dynamics: application to sleep-wake architecture. PLoS ONE 5, e14204.
Dang-Vu, T. T., Schabus, M., Desseilles, M., Sterpenich, V., Bonjean, M., and Maquet, P. (2010). Functional neuroimaging insights into the physiology of human sleep. Sleep 33, 1589–1603.
Delorme, A., and Makeig, S. (2004). EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 134, 9–21.
Fingelkurts, A. A., and Fingelkurts, A. A. (2010). Short-term EEG spectral pattern as a single event in EEG phenomenology. Open Neuroimag. J. 4, 130–156.
Freeman, W., and Zhai, J. (2009). Simulated power spectral density (PSD) of background electrocorticogram (ECoG). Cogn. Neurodyn. 3, 97–103.
Gaona, C. M., Sharma, M., Freudenburg, Z. V., Breshears, J. D., Bundy, D. T., Roland, J., Barbour, D. L., Schalk, G., and Leuthardt, E. C. (2011). Nonuniform high-gamma (60-500 Hz) power changes dissociate cognitive task and anatomy in human cortex. J. Neurosci. 31, 2091–2100.
Goertzel, G. (1958). An algorithm for the evaluation of finite trigonomentric series. Am. Math. Mon. 65, 34–35.
He, B. J. (2011). Scale-free properties of the functional magnetic resonance imaging signal during rest and task. J. Neurosci. 31, 13786–13795.
He, B. J., Zempel, J. M., Snyder, A. Z., and Raichle, M. E. (2010). The temporal structures and functional significance of scale-free brain activity. Neuron 66, 353–369.
Hobson, J. A., and Pace-Schott, E. F. (2002). The cognitive neuroscience of sleep: neuronal systems, consciousness and learning. Nat. Rev. Neurosci. 3, 679–693.
Iber, C., Ancoli-Israel, S., Chesson, A. L., and Quan, S. F. (2007). The Aasm Manual for the Scoring of Sleep and Associated Events: Rules, Terminology, and Technical Specifications. Westchester, IL: American Academy of Sleep Medicine.
Larson-Prior, L. J., Power, J. D., Vincent, J. L., Nolan, T. S., Coalson, R. S., Zempel, J., Snyder, A. Z., Schlaggar, B. L., Raichle, M. E., and Petersen, S. E. (2011). Modulation of the brain’s functional network architecture in the transition from wake to sleep. Prog. Brain Res. 193, 277–294.
Latchoumane, C. F. V., and Jaeseung, J. (2011). Quantification of brain macrostates using dynamical nonstationarity of physiological time series. IEEE Trans. Biomed. Eng. 58, 1084–1093.
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., and Ilmoniemi, R. J. (2001). Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci. 21, 1370–1377.
Manning, J. R., Jacobs, J., Fried, I., and Kahana, M. J. (2009). Broadband shifts in local field potential power spectra are correlated with single-neuron spiking in humans. J. Neurosci. 29, 13613–13620.
Maquet, P., and Phillips, C. (1998). Functional brain imaging of human sleep. J. Sleep Res. 7, 42–47.
Mascetti, L., Foret, A., Bourdiec, A. S., Muto, V., Kusse, C., Jaspar, M., Matarazzo, L., Dang-Vu, T., Schabus, M., and Maquet, P. (2011). Spontaneous neural activity during human non-rapid eye movement sleep. Prog. Brain Res. 193, 111–118.
Miller, K. J. (2010). Broadband spectral change: evidence for a macroscale correlate of population firing rate? J. Neurosci. 30, 6477–6479.
Miller, K. J., Sorensen, L. B., Ojemann, J. G., and Den Nijs, M. (2009a). Power-law scaling in the brain surface electric potential. PLoS Comput. Biol. 5, e1000609.
Miller, K. J., Zanos, S., Fetz, E. E., Den Nijs, M., and Ojemann, J. G. (2009b). Decoupling the cortical power spectrum reveals real-time representation of individual finger movements in humans. J. Neurosci. 29, 3132–3137.
Milstein, J., Mormann, F., Fried, I., and Koch, C. (2009). Neuronal shot noise and Brownian 1/f2 behavior in the local field potential. PLoS ONE 4, e4338.
Nir, Y., Staba, R. J., Andrillon, T., Vyazovskiy, V. V., Cirelli, C., Fried, I., and Tononi, G. (2011). Regional slow waves and spindles in human sleep. Neuron 70, 153–169.
Safonov, L. A., Isomura, Y., Kang, S., Struzik, Z. R., Fukai, T., and Cateau, H. (2010). Near scale-free dynamics in neural population activity of waking/sleeping rats revealed by multiscale analysis. PLoS ONE 5, e12869.
Saper, C. B., Scammell, T. E., and Lu, J. (2005). Hypothalamic regulation of sleep and circadian rhythms. Nature 437, 1257–1263.
Spoormaker, V. I., Schroter, M. S., Gleiser, P. M., Andrade, K. C., Dresler, M., Wehrle, R., Samann, P. G., and Czisch, M. (2010). Development of a large-scale functional brain network during human non-rapid eye movement sleep. J. Neurosci. 30, 11379–11387.
Stam, C. J., and de Bruin, E. A. (2004). Scale-free dynamics of global functional connectivity in the human brain. Hum. Brain Mapp. 22, 97–109.
Valderrama, M., Crepon, B., Botella-Soler, V., Martinerie, J., Hasboun, D., Alvarado-Rojas, C., Baulac, M., Adam, C., Navarro, V., and Le Van Quyen, M. (2012). Human gamma oscillations during slow wave sleep. PLoS ONE 7, e33477. doi: 10.1371/journal.pone.0033477
Van De Ville, D., Britz, J., and Michel, C. M. (2010). EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc. Natl. Acad. Sci. U.S.A. 107, 18179–18184.
Vyazovskiy, V. V., Olcese, U., Hanlon, E. C., Nir, Y., Cirelli, C., and Tononi, G. (2011). Local sleep in awake rats. Nature 472, 443–447.
Keywords: electrocorticography, epilepsy, scale-free, sleep
Citation: Zempel JM, Politte DG, Kelsey M, Verner R, Nolan TS, Babajani-Feremi A, Prior F and Larson-Prior LJ (2012) Characterization of scale-free properties of human electrocorticography in awake and slow wave sleep states. Front. Neur. 3:76. doi: 10.3389/fneur.2012.00076
Received: 16 January 2012; Paper pending published: 16 February 2012;
Accepted: 18 April 2012; Published online: 12 June 2012.
Edited by:
Sean P. Drummond, University of California San Diego, USAReviewed by:
Sara J. Aton, University of Pennsylvania, USAMichael Czisch, Max Planck Institute of Psychiatry, Germany
Copyright: © 2012 Zempel, Politte, Kelsey, Verner, Nolan, Babajani-Feremi, Prior and Larson-Prior. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: John M. Zempel, Department of Neurology, Washington University School of Medicine, 660 South Euclid Box 8111, St. Louis, MO, 63110, USA. e-mail:emVtcGVsakBuZXVyby53dXN0bC5lZHU=

