- 1 Seton Brain and Spine Institute, University Medical Center at Brackenridge, Austin, TX, USA
- 2 Department of Psychology, The University of Texas at Austin, Austin, TX, USA.
Neurons display continuous subthreshold oscillations and discrete action potentials (APs). When APs are phase-locked to the subthreshold oscillation, we hypothesize they represent two types of information: the presence/absence of a sensory feature and the phase of subthreshold oscillation. If subthreshold oscillation phases are neuron-specific, then the sources of APs can be recovered based on the AP times. If the spatial information about the stimulus is converted to AP phases, then APs from multiple neurons can be combined into a single axon and the spatial configuration reconstructed elsewhere. For the reconstruction to be successful, we introduce two assumptions: that a subthreshold oscillation field has a constant phase gradient and that coincidences between APs and intracellular subthreshold oscillations are neuron-specific as defined by the “interference principle.” Under these assumptions, a phase-coding model enables information transfer between structures and reproduces experimental phenomenons such as phase precession, grid cell architecture, and phase modulation of cortical spikes. This article reviews a recently proposed neuronal algorithm for information encoding and decoding from the phase of APs (Nadasdy, 2009). The focus is given to the principles common across different systems instead of emphasizing system specific differences.
Phase Coding in Different Systems of the Brain
Ever since the correlation between the theta phases of pyramidal cell firing in the hippocampus and the position of the rat in a linear track was observed (O’Keefe and Recce, 1993), the question has lingered whether the phase of action potentials (APs) relative to local field potentials (LFPs) encode information or if this correlation is a mere epiphenomenon. Encoding implies that information available from the phase is decoded by neurons downstream, as their AP generation depends on this information. Numerous mechanisms have been proposed that could potentially generate phase precession relative to the theta oscillation. One class of models includes the dual oscillator interference model (O’Keefe and Recce, 1993; O’Keefe and Burgess, 2005; Blair et al., 2008) and the somato-dendritic dual oscillator model (Kamondi et al., 1998; Harris et al., 2002; Lengyel et al., 2003; Huhn et al., 2005). The key assumption in both models is that phase precession is generated by the interaction between two theta oscillations with slightly different frequencies. Another class of models focuses on the dendritic mechanisms (Magee, 2001), assumes a depolarization ramp (Mehta et al., 2002), or proposes network-level mechanisms (Jensen and Lisman, 1996; Tsodyks et al., 1996; Wallenstein and Hasselmo, 1997). Nevertheless, all of these models share the key assumption that the cause of phase precession is localized within the hippocampus. In contrast, we proposed an alternative model, which considers phase coding as originating from sensory processing, after which the code is transferred to the cortex where it is decoded and re-encoded before it is further propagated to the associated systems, including the entorhinal cortex (EC) and hippocampus (Nadasdy, 2009). Recent studies reporting AP phase modulation in the prefrontal (Montemurro et al., 2008; Kayser et al., 2009; Siegel et al., 2009), auditory (Kayser et al., 2009), visual (Montemurro et al., 2008), and EC (Hafting et al., 2008) are consistent with this view. Despite the differences in physiological characteristics, cell types, the input–output connectivity and predominant oscillation frequencies across these systems, we argue that the sensory, thalamo-cortical and limbic systems are sharing the common language of phase coding. In this review without the capacity of describing system specific implementations we overview the common mechanism of AP phase coding.
Action Potentials and SMO
When we record a neuron intracellularly while injecting different levels of current pulses, the current will drive the subthreshold membrane potential oscillations (SMOs) toward the threshold potential, evoking APs upon threshold crossing (Llinas et al., 1991). The larger the depolarizing current is, the more likely the membrane potential is to cross the threshold and generate APs. This is the mechanism by which the intensity of a sensory signal is converted to a firing rate code. Intriguingly, the level of input current in these experiments will not only affect the firing rate but also the phase of APs, as phases advance systematically with increasing depolarization, even after the firing rate has been saturated (Figure 1). Using the phase, neurons are endowed with a broader dynamic range for encoding information than they are with the firing rate. A similar sensory encoding scheme has been proposed and experimentally observed in the salamander retina (Gollisch and Meister, 2008). If neurons encode information using the phase of APs, how will that information be read out?
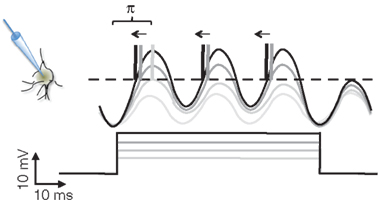
Figure 1. The scheme of intracellular current clamp recordings from a neuron being depolarized by different levels of current injection. As the level of depolarizing current increases (gray levels), the amplitude of subthreshold membrane potential oscillation increases with it. At the moments when the oscillations reach the threshold (dashed line), the neuron generates action potentials (vertical lines represent truncated action potentials). Near the threshold the action potential generation is probabilistic. The number of action potentials (0, 1, 3, 3) increases with the level of depolarization. At the same time, with the increasing current, the phases of action potentials relative to the membrane oscillations advance (left pointing arrows). The range of the phase change is bound to π. Note that while the number of action potentials saturates at 3, the phase still advances. (Scale bar is at bottom left.)
Oscillations: Temporal and Spatial Coherence of Neuronal Oscillations
The fluctuation of neuronal membrane potential around the mean without generating APs is known as SMO. This oscillation has a power spectrum with peaks at regionally specific resonant frequency bands, for instance olivary neurons ∼5 Hz (Devor and Yarom, 2002a), entorhinal cortical neurons 4–7 Hz (Giocomo et al., 2007), and cortical neurons ∼40 Hz (Llinas et al., 1991; Silva et al., 1991). The most likely sources of such oscillations are specific intrinsic conductances (White et al., 1998; Dickson et al., 2000; Fransen et al., 2004). However, the coherency of SMOs across neurons depends on electrotonic interactions between neurons (Devor and Yarom, 2002b). A number of mechanisms, including gap junctions, electrotonic synapses, ephaptic conductivity, and glial transfer (Yeh et al., 1996), have been proposed to mediate SMOs between neurons. These mechanisms allow the SMO to propagate in a radial spread or traveling waves, depending on the network architecture. Moreover, near-synchronized activity of interneurons impinging on different parts of principal cells may also sculpt such oscillations (Buzsaki and Chrobak, 1995).
Regardless of whether they are imposed or exchanged, we assume that these oscillations are not independent between neurons. Instead, oscillations of adjacent neurons stabilize themselves into a near-synchronized state. A number of studies confirmed the propagation of membrane oscillations and LFPs as either radial or traveling waves (Bringuier et al., 1999; Prechtl et al., 2000; Benucci et al., 2007; Lubenov and Siapas, 2009).
Based on the prevalence of SMOs, we further assume that the extracellular sum of such population-wide, near-synchronized rhythms contributes to the LFP. Although LFPs are considered to be derived from the sum of synaptic activity at the dendritic regions of neurons (Mitzdorf, 1985; Logothetis et al., 2001), a significant oscillatory component of LFP may also be derived from the sum of SMOs within a 250-μm (Katzner et al., 2009). This is supported by the shared theta frequency oscillation between intracellular SMOs and LFPs within the EC and in the frontal lobe (Alonso and Llinas, 1989; Llinas et al., 1991), as well as by the high correlation between LFP and intracellular SMO (Tanaka et al., 2009). The high correlation between LFP and SMO accomplishes a conceptual link between LFP and SMO and enables an important experimental shortcut of estimating the SMO based on the LFP.
The following two sections outline the principles of the phase-coding model.
Interference Principle
Subthreshold membrane potential oscillations play critical roles in phase coding during both encoding and decoding. The periodic amplification of the excitatory postsynaptic potentials (EPSP) by the SMO, which causes sensory neurons to convert input to AP phases during encoding, also makes the decoding-neurons highly selective for the timing of EPSPs. A presynaptically evoked EPSP that coincides with the depolarizing phase of the SMO is more potent in evoking APs than EPSPs outside of that time window. Due to the electrotonic propagation of SMO, there is a distance-dependent phase difference in membrane oscillations between most neurons, which, in a sufficiently large network, covers the entire 180° phase range. Thus, coincidences between input APs and SMO peaks are spatially restricted and neuron-specific. Conversely, for any input AP time there will be a neuron that is most activated by the AP–SMO coincidence. We call this the interference principle (Figure 2). The interference principle guarantees a consistent mapping of an input AP pattern on a spatial layout of neurons, which reproduces the original temporal pattern of APs (Nadasdy, 2009). For a faithful spatial reconstruction, we must furthermore assume an isomorphism between the sensory and target SMO fields. We remark that the interference principle should not be confused with the “oscillatory interference model” (O’Keefe and Burgess, 2005; Burgess et al., 2007).
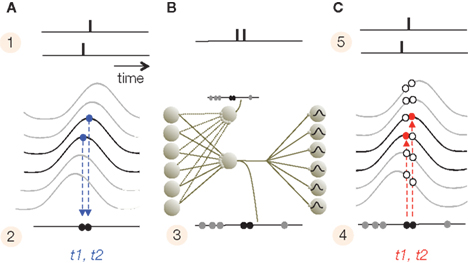
Figure 2. Interference principle. (A) The top panel illustrates the times of two APs generated by two adjacent neurons (1) after their alignments to the intracellular SMO (2). Because the only APs that survive are the ones that coincide with the peak of SMO, the propagating oscillation will convert the spatial distance between the two neurons into a slight delay (t1, t2) between the two APs (2). (B) At the transfer stage, due to convergent and divergent synaptic connections, APs from a subset of neurons will merge on a set of projection neurons with low thresholds. Projection neurons sharing input from the same pool will replicate the same compressed AP train (3). (C) The compressed code projects to a large pool of target neurons. Since target neurons have a similar propagating SMO, the projected APs will generate a new AP only on neurons where the AP precisely coincides with the SMO peak (4). This is the interference principle. The red circles represent these coincidences, while open circles are the mismatches. As a result, the APs pattern (t1, t2) recovered the original input pattern from (2).
The interference principle is applied twice, first when the sensory input is converted to the phase code (stage 1) and second at the target area (the cerebral cortex in mammals) where information is reconstructed from the phase code (stage 4). However, neurons that convert the input to phase may operate at a lower threshold than neurons that detect coincidences. The next section will summarize a four-stage model of information encoding and reconstruction. Then we will discuss possible realizations of the interference principle in sensory and limbic information processing that are consistent with a number of empirical data.
Four Stages of Information Encoding and Reconstruction
We propose that in all sensory systems, phase encoding and decoding takes place by a four-stage transformation. Stages 3 and 4 are also applicable to cortico-cortical information transfer. We will illustrate the four stages on the mammalian visual system, but the same principles can be generalized to other sensory systems.
(1) Latency encoding: sensory neurons sample the physical environment by converting energy to APs, which represent the intensity and the time of a receptor-specific feature. A third dimension is indirectly provided by the position of the sensory receptor relative to the entire array of sensory receptors, although the meaning of the position varies from one sensory modality to another. While, in the visual system, stimulus times are coarsely sampled due to the relatively slow adaptation of sensory receptors (>20 ms on vertebrates and ∼100 ms on primates; Glantz, 1991; Torre et al., 1995; Yeh et al., 1996; Rebrik et al., 2000; Holcman and Korenbrot, 2005), stimulus intensity is accurately represented by the frequency and latency of APs with a precision of <40 ms (Gollisch and Meister, 2008). Thus, the retinal ganglia use low (>25 ms) temporal resolution to encode sensory event times but high (<25 ms) temporal resolution to encode intensities (Koepsell et al., 2009). The important fact is that retinal ganglion cells register local luminance with a burst of one to six APs, where the burst frequency is proportional and latency is inversely proportional to the stimulus luminance (Figure 3A).
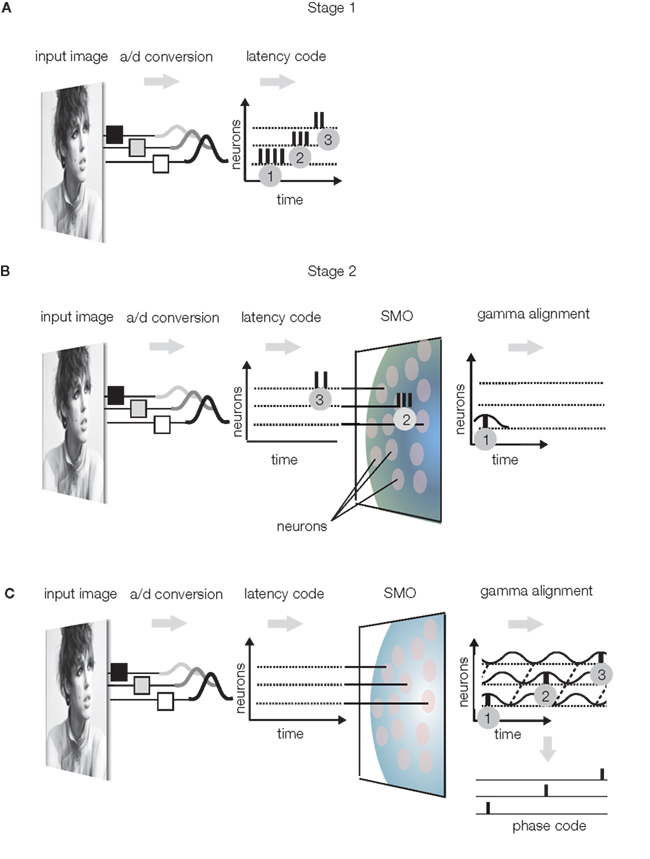
Figure 3. Sensory encoding. (A) Stage 1: Luminance changes in the visual input evoke bursts of APs in the retina, where the burst frequency is proportional and burst latency is inversely proportional to the luminance. Bursts are numbered in the order of generation time. (B) Stage 2: bursts are filtered by the SMOs of a layer of neurons. The SMOs propagate within the transversal plane with a radial spread and depolarize the neurons in a specific order. Only single AP components of bursts will pass the layer, specifically those APs that coincide with the SMO peaks of the given neuron. Gray patches represent neurons with SMOs. As a result, APs will be aligned to the intrinsic SMO of these neurons. (C) The complete burst sequence is converted to a sparse AP phase code, with the topography preserved. The latency of the action potential in SMO cycles is inversely proportional to the luminance and the spatial coordinate of the action potential generating neuron is encoded by the phase relative to any single instance of SMOs (phase code).
(2) Gamma alignment (alignment of APs to the SMO, however the frequency of SMO may not necessarily be gamma): Conversion of the latency code to a phase code involves aligning the APs to the local intracellular SMO. This conversion is naturally accomplished by the interference principle because, in response to the input AP burst, the first postsynaptic neuron will generate an AP only when the input AP coincides with the neuron’s SMO peak (Figure 3B). This will reduce the input burst to a single AP output. As a result of this “gamma alignment,” APs will be synchronized with the intracellular SMOs (Koepsell et al., 2009). With this simple operation, the originally independent stimulus dimensions of space, and quality will be converted to anatomical distances of neurons and AP time dimensions, where the time encodes not only quality but also the anatomical distance. To keep stimulus quality and space separated in time, APs will encode information on two different time scales: quality will be encoded by an integer number of gamma cycles preceding the AP (n × 25 ms), and the anatomical distance will be encoded by the phase within the gamma cycles (2 π ≈ 25 ms). Since the gamma alignment makes the phase of an AP specific to the neuron that generates it, the phase will associate the AP with the location of the neuron relative to the field of SMOs. Hence, phase will represent anatomical distance. Evidence supports that the spatial distance between ON and OFF ganglia generates a temporal difference between their burst firing during the early development of the retina that is controlled by propagating waves (Kerschensteiner and Wong, 2008). This space-time conversion in the visual system may generate temporary redundancy because space is represented twice, first by the anatomical distance between neurons and second by the phase. Therefore, the target topography of axonal projections is free to disperse because the phase unambiguously identifies the original location of the AP generating neuron. This saves the projection neurons from isomorphic projection of fine details and frees capacity to be utilized in the next stage to improve the reliability of transmission. (For motion processing, stimulus time replaces stimulus quality; Nadasdy, 2009).
(3) Compression: The major advantage of gamma alignment is that it allows all APs to be lossless compressed into a single or small number of channels/axons. By reducing the number of channels transferring different codes, the projection neurons are able to utilize the rest of the channels for transferring redundant codes, which in turn, enhances reliability. The redundant transfer is necessary for preserving the integrity of the code during long-range transmission to the cortex or between cortical areas. The compression of APs from multiple channels is accomplished by the massively divergent/convergent connections between presynaptic and postsynaptic neurons in the sensory nuclei of the thalamus (Figure 4). While synaptic convergence forces all APs from all projecting neurons to collapse onto a single/few channels/neurons, synaptic divergence distributes the same compressed AP code to multiple axons terminating in V1. Thus, the target area (V1) will receive a compressed code from each individual axon, while the parallel projection of the same APs via multiple axons will provide high redundancy. (For details on modeling the receptive field projections on V1 see Nadasdy, 2009). The next stage, reconstruction, is devoted to the decoding of the spatial information using the combined AP series with neuron-level specificity.
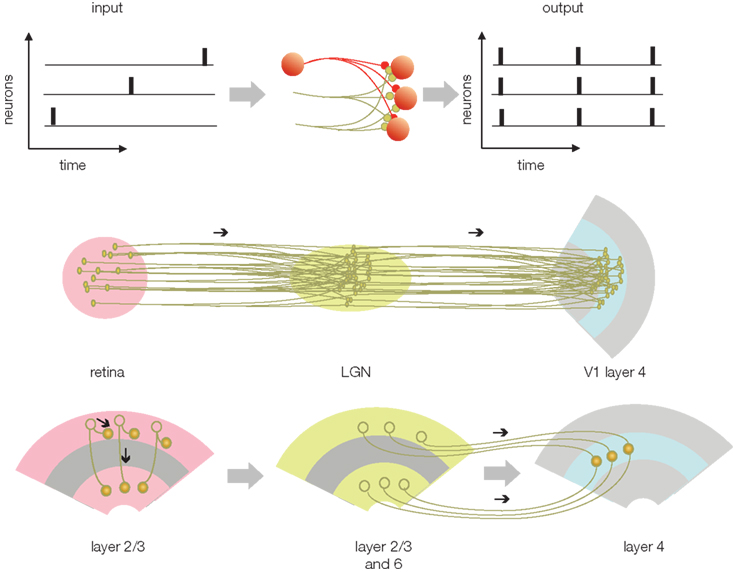
Figure 4. Transferring the phase code (from Figure 3) between structures. The upper left is the phase-encoded AP pattern from Figure 3C. In this code AP time represents the luminance of the image in the receptive field and the position of neuron represents geometry. When the phase code enters a structure that relays the information (middle), the divergent and convergent connections will cause the APs to be dispersed and projected on a set of output neurons. As a result of the dispersion, all of the APs from each connected neurons will be combined with all other APs. The output AP trains will represent the combined APs from all the neurons. On the one hand, this code is compressed at the cellular level because it contains all the APs from all the neurons. On the other hand, the code is redundant across neurons. Underneath, middle row is the potential correspondence with the retina, LGN, and V1. Bottom, potential correspondence of the compression and transfer scheme with the cortico-cortical information transfer.
(4) Reconstruction: This is the final stage where information is decoded from AP phases. The decoding, again, relies on the interference principle. The compressed code reaches cortical neurons, such as granule cells in a V1 column, through multiple parallel axons, each terminating on individual neurons. We assume that cortical neurons, like sensory neurons, generate spatially and temporally coherent SMOs that propagate in a radial fashion. For the sake of simplicity, we further assume that the frequency and spatial phase gradient of this SMO field are the same as the SMO field at the sensory organ. Although each layer-4 neuron receives the same AP sequence, individual APs within the sequence may originate from different sensory neurons. The task of the cortical network is to sort these APs according to their origin and route them to specific supragranular layer neurons that will reproduce the input activity pattern. This may seem like an extremely complicated task considering the combinatorial complexity, but it is easily accomplished using the interference principle. By projecting the input APs on the SMO field and letting their coincidences select the neurons capable of firing an AP, the network will generate a coherent spatio-temporal pattern (Figure 2). Provided there is topographical isomorphism between the input SMO field and the target SMO field, any given AP from the input sequence will precisely coincide with the SMO peak of a neuron that represents the same anatomical distance as the input neuron to which it was originally aligned in Stage 2 (Figure 5). As a result, the output of these neurons in the supragranular layer of the cortex will reproduce the original sensory input and form a sparse representation (high spatial specificity and low firing rate; Sakata and Harris, 2009).
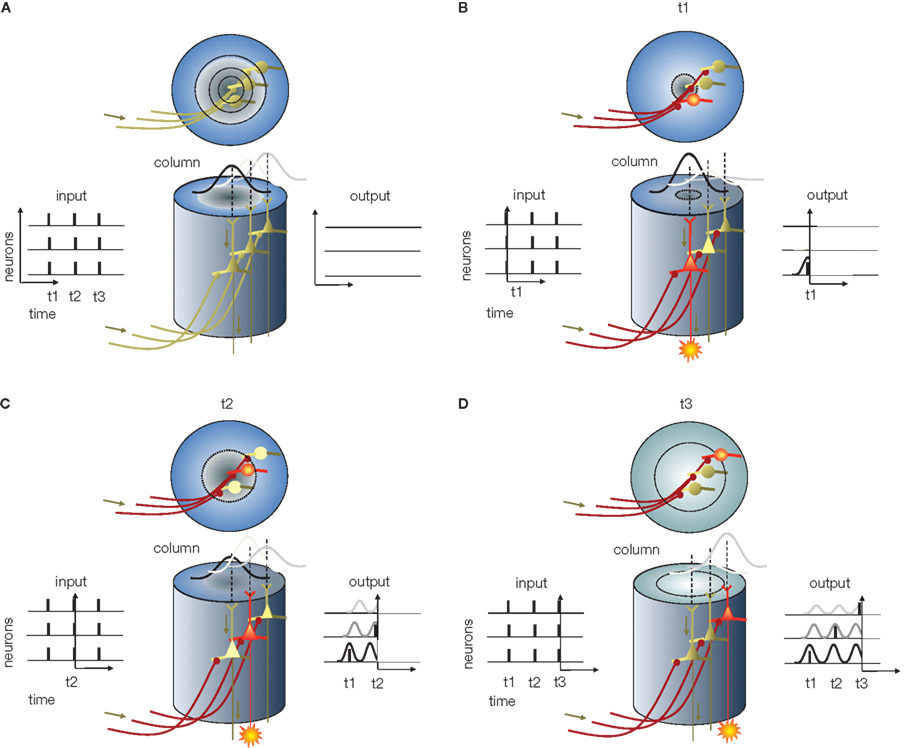
Figure 5. Information reconstruction from phase of APs in the cortical column, predicted based on the “interference principle. ” (A) Cortical column (center). The x–y plot at the left represents the input APs entering the column, and the x–y plot at the right represents the expected activity of cortical neurons. In all x–y plots x is time and y is neuron number. The column in this example, for the sake of simplicity, contains only three neurons – without layer specificity. Above the columns are top views. Circular rings represent the radial propagation of SMO. (B) The first volley of APs arrives at t1 (the output in Figure 4). Although the input depolarizes all receiving neurons (red axons), the only neuron in which the excitatory postsynaptic potential is able to generate an AP is the one at the center where the SMO is near a peak (red cell body). The AP generated by this neuron appears on the right x–y plot. (C) As time progresses, the first radial SMO wave reaches the periphery and the second wave starts while the second AP volley arrives (t2). Again, the input APs depolarize all the neurons. However, the only neuron capable of generating an AP is the one near peak SMO. Since the only neuron at peak SMO is the second neuron, located farther from the center, this neuron will generate an AP while the first is in the refractory period and the third’s membrane potential is still approaching SMO peak. As a result, a second AP appears in the diagram at t2. (D) When the third volley arrives at t3 and depolarizes all the postsynaptic neurons, the depolarization will coincide with the peak SMO in the third neuron, located at the periphery of the column. When this neuron fires an AP, it will be the third AP generated by the third neuron at t3. This sequence of events implements the “interference principle” by which the output of the neurons in the column reproduces the original input from the phase code as [AP1t1n1, AP2t2n2, AP3t3n3], where t is time and n is the neuron ID.
We emphasize that perfect reconstruction is neither the goal nor the final stage of information processing. When the sensory-cortical neurons reconstruct information from the phase code, they also add information to it. Reconstruction in the real brain is not an exact reproduction of the sensory information, since the input coming from the sensory thalamic nuclei is combined with inputs from a number of associated cortical areas. Rather, reconstruction is the stage at which important transformations, such as topographical and coordinate transformations and the combination of information from other cortical areas, take place. The reconstruction stage is also the starting point for cortico-cortical information transfer.
Computations with Phase Code
Above we described a conceptual model for neural encoding, information transmission, and decoding (for numerical simulations, see Nadasdy, 2009). For the sake of simplicity, we proved that information reconstruction from the phase code is nearly perfect within as few as four gamma cycles and 100 neurons, given the isomorphism of the SMO phase gradients at the sensory input and the target area (Nadasdy, 2009). Although this latter assumption may seem difficult to maintain under physiological conditions, there is substantial morphological and functional evidence in support of it. For example, multiple loops of the thalamo-cortical projection pathway through the thalamic reticular nucleus provide low- and high-frequency (gamma) links between the thalamus and cortex (Jones, 2002). Visual cortical areas 17 and 18 also synchronize to LGN with a 2.6-ms delay on anesthetized cats (Castelo-Branco et al., 1998). Moreover, a global retina-LGN-cortex synchronization is evident in the high gamma band (Castelo-Branco et al., 1998). On the one hand, incoherency between the encoding and decoding SMO fields would compromise phase coding. On the other hand, a systematic topographic (but not temporal) incoherency of SMO phase gradients between the encoding and decoding structures is where transformations and computations can be implemented. For example, transformations between retinal and head-centered and between head- and body-centered coordinates can be performed by gain fields (Zipser and Andersen, 1988) or by tuning the SMO field, which transforms the map of interferences. According to the phase-coding model, the location of AP–SMO coincidences, i.e., the interference pattern smoothly shifts depending on the relative phases of APs from concurrent inputs reaching the neuron. Moreover, an arsenal of interneurons is deployed to provide fine tuning of the SMO, not unlike to the hippocampus, where each interneuron type specifically calibrates the location and frequency of membrane resonance, thus tuning the SMO in individual neurons to the gradient of the larger SMO field (Cobb et al., 1995).
Different Solutions for Phase Coding
One of the critical features of phase coding is that it allocates different frequency bands for different types of information by utilizing the spatially and temporally coherent SMOs shared between coupled networks. One such frequency band is the range of phases within each oscillation period. The other frequency band is the frequency of SMO itself. It has been demonstrated that information can effectively be encoded and decoded by multiplexing the code in these two frequency bands (Nadasdy, 2009). The assignment of frequencies to features may vary across brain structures. Likewise, at the stage of sensory encoding and gamma alignment different scenarios are possible. The scenario we described earlier was that the spatial/anatomical location is encoded by phase and luminance is encoded by period cycles. However, these two features are interchangeable and phase can represent luminance and period cycles can represent the spatial/anatomical location. Within the visual system the magno, parvo, and konio cellular pathways represent the heterogeneity of these coding solutions. For instance, it is conceivable that since the magno cellular pathway is specialized to effectively transfer motion and orientation while the parvo cellular pathway transfers luminance and color with high spatial acuity, the former one encodes motion in phase, while the latter one encodes the spatial position or spatial frequency in phase. Thus, qualitative and spatial stimulus features are given different priorities in the different pathways of the visual system.
Another remarkable feature of phase coding is that with only a few parameter adjustments we can obtain different solutions to represent space and time. For example, if the cortical cytoarchitecture is homogeneous, such as in the EC, and if it allows an unconstrained propagation of SMO waves over multiple spatial SMO wavelengths, then multiple representations of the same input develop because of the spatial aliasing inherent to the interference principle (Nadasdy, 2009; also see a different solution by Burgess, 2008). Conversely, the same EC neuron exhibits spatial tuning to multiple, equidistant spatial locations, consistent with the definition of grid cells. The missing link between the spatial maps and network architecture could be the spatially and temporally periodic SMO field. Based on our simulations, the phase-coding model predicts that the phase-gradient map in the EC is coalescent with the topography of the grid cell map, i.e., with the matrix of grid cells that share space fields (Nadasdy, 2009).
The third important feature of phase coding becomes evident when we track the activity of a neuron relative to the SMO cycles under a dynamic input condition while also varying the propagation direction of the SMO field. This emulates the condition of recording place in a freely moving animal’s hippocampus and computing the phase of spikes relative to ongoing theta LFP oscillations. In similar experiments, the AP phase systematically advances relative to the theta cycles, defined as phase precession (O’Keefe and Recce, 1993; Skaggs et al., 1996; Harris et al., 2002). However, recording theta not only from a single electrode but also from a larger volume around the place cell should reproduce what we found by modeling. Namely, APs should always phase-lock to the intracellular SMO (Harvey et al., 2009), but the direction of phase precession (advancement vs. lagging) will depend on the propagation direction of global SMO/LFP field around the neuron (Nadasdy, 2009). The assumption of SMO field propagation is consistent with the observation of traveling waves in the hippocampus on freely moving rats (Lubenov and Siapas, 2009). The phase-lock between the APs and the intracellular SMO has been confirmed during behavior (Harvey et al., 2009). Combining SMO, LFP, and AP measurements from multiple neurons separated by different distances would elucidate the underlying network dynamics and test the interference principle.
Among the predictions that can be derived from the phase-coding model is the phase modulation of spikes in the cortex in relationship to stimulus or behavioral manipulations. We earlier argued that reconstruction takes place in the supragranular layer of the neocortex. According to our model, layers 2–3 and 4b pyramidal cells vigorously respond to the granule cell input only if the time of input APs coincides with the cell’s intracellular SMO peaks. In our simulations the optimal coincidence time window was ∼1 ms (Nadasdy, 2009). Empirically, however, this time window is a probability function, rather than a binary function, allowing neurons to fire less frequently when the input is away from the peak but still reaches threshold. When the stimulus is optimal for the neuron, the AP will be generated reliably near the intracellular SMO peak (LFP trough). The same neuron may also respond, although less likely, to a suboptimal stimulus. If the suboptimal stimulus is optimal for another neuron, it will drive that neuron at the exact intracellular SMO peak. However, due to the slight phase difference between the two intracellular SMO processes, the same depolarization that drives the other neuron at exact SMO peak will drive the first neuron at a slightly different SMO phase than would its own optimal stimulus. As a result we shall observe a modest phase difference between spikes of the same neuron when we vary the stimulus parameters within the receptive field. Studies are in progress to test this prediction. Prefrontal cortical neurons in a working memory task exhibit memory item dependent phase offset relative to the slow oscillations (Siegel et al., 2009). Other studies investigating the auditory and visual cortex found feature-dependent phase differences relative to theta in auditory (Kayser et al., 2009) and relative to alpha in primary visual cortex (Montemurro et al., 2008) and to gamma (Nadasdy and Andersen, 2009) also in primary visual cortex. It is also conceivable that the phases of local SMOs shift relative to the LFP, which integrates oscillations over a larger cell population (Harvey et al., 2009). We anticipate an increasing amount of data to arise in support of these so-far isolated examples in cortical recordings.
Concerns About the General Theory of Phase Coding
For phase coding and decoding to work, the subsystems of brain have to meet with specific dynamic conditions. One such condition is the high coherency between the SMOs at the encoding and decoding stages. For instance, the efficacy of visual information reconstruction in the cortex is highly dependent on the phase coherence between the LGN and V1. We postulated based on simulations that this coherency must approach a precision of 1 ms (Nadasdy, 2009), which is consistent with the coherency provided by the thalamo-cortical loop (Jones, 2002). The empirical precision of synchrony between cortical and LGN SMOs is yet to be determined. We also showed that the precise topographic mapping between the input and output is where the system can implement coordinate transformations between representations (Nadasdy, 2009).
The second condition is the compatibility of SMO frequencies across and within structures. While the hippocampal LFP is dominated by coherent theta and gamma oscillations, the hippocampal pyramidal cells express mainly theta frequency SMOs. If phase coding in the hippocampus relies on theta, it is not clear what role gamma oscillations may play. Likewise, entorhinal cortical neurons express theta frequency SMOs. In contrast, sensory organs and primary sensory areas are dominated by gamma oscillations. Notably, we observed visual feature-dependent spike phase modulation relative to the gamma band LFP and not to alpha, while other studies reported phase modulation relative to alpha band LFP (Belitski et al., 2008).
Although the correlation between SMO and LFP is high, they are not identical. The extent at which LFP is a good approximation of SMO is still unknown. The correlation between LFP and SMO is critical for the empirical testing of the phase-coding model and cries for defining the transfer function between population SMO and LFP.
Last, the noise tolerance of phase coding is unknown. Different types of noise need to be considered. One is the noise generated by the movement of sensory organs themselves, which affects the sensory sampling. Second is the noise level of intrinsic SMO oscillations. Third is the temporal incoherency between source and target structures. Fourth is the spatial incoherency between the neuronal source and target. While spatial incoherency can implement useful transformations in the reconstruction, the temporal incoherency is highly detrimental for the reconstruction. The effects of these concerns need to be investigated by simulations and tested empirically.
Questions Left Open
Because our understanding of the relationship between SMO and LFP is still incomplete, it leaves the question open: what is the timescale of phase modulation in the brain? The frequency of SMO and LFP consistently varies along the fronto-temporo-occipital axis, dominated by gamma in the occipital regions of the cortex, alpha in the frontal areas, and theta in the EC, hippocampal, and parahippocampal regions. In addition, gamma power is high and oscillations are phase-locked to hippocampal theta. Although hippocampal phase precession is defined relative to theta, we anticipate phase precession relative to gamma oscillations as well, while APs should be phase-locked to the intracellular gamma SMO. We also anticipate a similar relationship between EC theta and gamma. The phase modulation of spikes relative to alpha/theta LFP (Montemurro et al., 2008; Kayser et al., 2009) and relative to gamma LFP (Nadasdy and Andersen, 2009) in the visual cortex is still unclear. One of the most important questions is whether or not the interference principle would work at multiple timescales to allow information to be encoded relative to multiple frequency bands of ongoing oscillations and whether or not these frequency bands carry content-specific information. There is much to learn about the collective resonant property of the nervous system in the next few years that will complete our understanding of how the activity of millions of neurons is orchestrated, and this orchestration may happen in a much more deterministic fashion than the “noisy” brain models suggest.
Finally, as stated in the title, the phase-coding model suggests a critical revision of the concept of binding by synchrony. Accordingly, the key of preserving the integrity of the code across multiple stages of information transfer in the brain is the precise asynchrony of APs between neighbor neurons, as opposed to the zero-phase lag synchrony proposed earlier (Gray and Singer, 1989). We argued that a subtle but constant phase gradient of the propagating SMOs is critical for encoding and reconstructing the sensory information as well as to for performing different coordinate transformations on the sensory input to achieve context invariant object representations in the brain.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge Richard A. Andersen, Neil Burgess, and Paul Miller for invaluable comments on the original manuscript (Nadasdy, 2009) and the support from the National Eye Institute. We thank Sarah Gibson, Jason Ettlinger, and Hollie S. Thomas for proofreading.
Key Concepts
Subthreshold membrane potential oscillations
The fluctuation of neuronal membrane potential around the mean, while the neuron does not fire any action potentials.
When the original spatial information encoded at the source (sensory neurons/cortex), is transferred in a compressed fashion and reproduced at the target area (cortex) by principal neurons.
The phase-lock of the action potentials to the neuron’s own subthreshold membrane potential oscillation. The main frequency of oscillation is not necessarily gamma, but instead, often theta, alpha, or beta.
A dimensionality reduction of the neural code when action potentials from multiple presynaptic neurons, dispersed in time, converge on a neuron and the merged action potential sequence is transmitted to the next postsynaptic neuron on a single axon as a single spike train.
References
Alonso, A., and Llinas, R. R. (1989). Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature 342, 175–177.
Belitski, A., Gretton, A., Magri, C., Murayama, Y., Montemurro, M. A., Logothetis, N. K., and Panzeri, S. (2008). Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J. Neurosci. 28, 5696–5709.
Benucci, A., Frazor, R. A., and Carandini, M. (2007). Standing waves and traveling waves distinguish two circuits in visual cortex. Neuron 55, 103–117.
Blair, H. T., Gupta, K., and Zhang, K. (2008). Conversion of a phase- to a rate-coded position signal by a three-stage model of theta cells, grid cells, and place cells. Hippocampus 18, 1239–1255.
Bringuier, V., Chavane, F., Glaeser, L., and Fregnac, Y. (1999). Horizontal propagation of visual activity in the synaptic integration field of area 17 neurons. Science 283, 695–699.
Burgess, N. (2008). Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus 18, 1157–1174.
Burgess, N., Barry, C., and O’Keefe, J. (2007). An oscillatory interference model of grid cell firing. Hippocampus 17, 801–812.
Buzsaki, G., and Chrobak, J. J. (1995). Temporal structure in spatially organized neuronal ensembles: a role for interneuronal networks. Curr. Opin. Neurobiol. 5, 504–510.
Castelo-Branco, M., Neuenschwander, S., and Singer, W. (1998). Synchronization of visual responses between the cortex, lateral geniculate nucleus, and retina in the anesthetized cat. J. Neurosci. 18, 6395–6410.
Cobb, S. R., Buhl, E. H., Halasy, K., Paulsen, O., and Somogyi, P. (1995). Synchronization of neuronal activity in hippocampus by individual GABAergic interneurons. Nature 378, 75–78.
Devor, A., and Yarom, Y. (2002a). Coherence of subthreshold activity in coupled inferior olivary neurons. Ann. N. Y. Acad. Sci. 978, 508.
Devor, A., and Yarom, Y. (2002b). Electrotonic coupling in the inferior olivary nucleus revealed by simultaneous double patch recordings. J. Neurophysiol. 87, 3048–3058.
Dickson, C. T., Magistretti, J., Shalinsky, M. H., Fransen, E., Hasselmo, M. E., and Alonso, A. (2000). Properties and role of I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J. Neurophysiol. 83, 2562–2579.
Fransen, E., Alonso, A. A., Dickson, C. T., Magistretti, J., and Hasselmo, M. E. (2004). Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus 14, 368–384.
Giocomo, L. M., Zilli, E. A., Fransen, E., and Hasselmo, M. E. (2007). Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315, 1719–1722.
Glantz, R. M. (1991). Motion detection and adaptation in crayfish photoreceptors. A spatiotemporal analysis of linear movement sensitivity. J. Gen. Physiol. 97, 777–797.
Gollisch, T., and Meister, M. (2008). Rapid neural coding in the retina with relative spike latencies. Science 319, 1108–1111.
Gray, C. M., and Singer, W. (1989). Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. U.S.A. 86, 1698–1702.
Hafting, T., Fyhn, M., Bonnevie, T., Moser, M. B., and Moser, E. I. (2008). Hippocampus-independent phase precession in entorhinal grid cells. Nature 453, 1248–1252.
Harris, K. D., Henze, D. A., Hirase, H., Leinekugel, X., Dragoi, G., Czurko, A., and Buzsaki, G. (2002). Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cells. Nature 417, 738–741.
Harvey, C. D., Collman, F., Dombeck, D. A., and Tank, D. W. (2009). Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461, 941–946.
Holcman, D., and Korenbrot, J. I. (2005). The limit of photoreceptor sensitivity: molecular mechanisms of dark noise in retinal cones. J. Gen. Physiol. 125, 641–660.
Huhn, Z., Orban, G., Erdi, P., and Lengyel, M. (2005). Theta oscillation-coupled dendritic spiking integrates inputs on a long time scale. Hippocampus 15, 950–962.
Jensen, O., and Lisman, J. E. (1996). Hippocampal CA3 region predicts memory sequences: accounting for the phase precession of place cells. Learn. Mem. 3, 279–287.
Jones, E. G. (2002). Thalamic circuitry and thalamocortical synchrony. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 357, 1659–1673.
Kamondi, A., Acsady, L., Wang, X. J., and Buzsaki, G. (1998). Theta oscillations in somata and dendrites of hippocampal pyramidal cells in vivo: activity-dependent phase-precession of action potentials. Hippocampus 8, 244–261.
Katzner, S., Nauhaus, I., Benucci, A., Bonin, V., Ringach, D. L., and Carandini, M. (2009). Local origin of field potentials in visual cortex. Neuron 61, 35–41.
Kayser, C., Montemurro, M. A., Logothetis, N. K., and Panzeri, S. (2009). Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron 61, 597–608.
Kerschensteiner, D., and Wong, R. O. (2008). A precisely timed asynchronous pattern of ON and OFF retinal ganglion cell activity during propagation of retinal waves. Neuron 58, 851–858.
Koepsell, K., Wang, X., Vaingankar, V., Wei, Y., Wang, Q., Rathbun, D. L., Usrey, W. M., Hirsch, J. A., and Sommer, F. T. (2009). Retinal oscillations carry visual information to cortex. Front. Syst. Neurosci. 3:4. doi:10.3389/neuro.06.004.2009.
Lengyel, M., Szatmary, Z., and Erdi, P. (2003). Dynamically detuned oscillations account for the coupled rate and temporal code of place cell firing. Hippocampus 13, 700–714.
Llinas, R. R., Grace, A. A., and Yarom, Y. (1991). In vitro neurons in mammalian cortical layer 4 exhibit intrinsic oscillatory activity in the 10- to 50-Hz frequency range. Proc. Natl. Acad. Sci. U.S.A. 88, 897–901.
Logothetis, N. K., Pauls, J., Augath, M., Trinath, T., and Oeltermann, A. (2001). Neurophysiological investigation of the basis of the fMRI signal. Nature 412, 150–157.
Lubenov, E. V., and Siapas, A. G. (2009). Hippocampal theta oscillations are travelling waves. Nature 459, 534–539.
Magee, J. C. (2001). Dendritic mechanisms of phase precession in hippocampal CA1 pyramidal neurons. J. Neurophysiol. 86, 528–532.
Mehta, M. R., Lee, A. K., and Wilson, M. A. (2002). Role of experience and oscillations in transforming a rate code into a temporal code. Nature 417, 741–746.
Mitzdorf, U. (1985). Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol. Rev. 65, 37–100.
Montemurro, M. A., Rasch, M. J., Murayama, Y., Logothetis, N. K., and Panzeri, S. (2008). Phase-of-firing coding of natural visual stimuli in primary visual cortex. Curr. Biol. 18, 375–380.
Nadasdy, Z. (2009). Information encoding and reconstruction from the phase of action potentials. Front. Syst. Neurosci. 3:6. doi:10.3389/neuro.06.006.2009.
Nadasdy, Z., and Andersen, R. A. (2009). “Spike phase tuning in primary visual cortex,” in Society for Neuroscience Annual Meeting, Chicago, IL.
O’Keefe, J., and Burgess, N. (2005). Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells. Hippocampus 15, 853–866.
O’Keefe, J., and Recce, M. L. (1993). Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3, 317–330.
Prechtl, J. C., Bullock, T. H., and Kleinfeld, D. (2000). Direct evidence for local oscillatory current sources and intracortical phase gradients in turtle visual cortex. Proc. Natl. Acad. Sci. U.S.A. 97, 877–882.
Rebrik, T. I., Kotelnikova, E. A., and Korenbrot, J. I. (2000). Time course and Ca2+ dependence of sensitivity modulation in cyclic GMP-gated currents of intact cone photoreceptors. J. Gen. Physiol. 116, 521–534.
Sakata, S., and Harris, K. D. (2009). Laminar structure of spontaneous and sensory-evoked population activity in auditory cortex. Neuron 64, 404–418.
Siegel, M., Warden, M. R., and Miller, E. K. (2009). Phase-dependent neuronal coding of objects in short-term memory. Proc. Natl. Acad. Sci. U.S.A. 106, 21341–21346.
Silva, L. R., Amitai, Y., and Connors, B. W. (1991). Intrinsic oscillations of neocortex generated by layer 5 pyramidal neurons. Science 251, 432–435.
Skaggs, W. E., McNaughton, B. L., Wilson, M. A., and Barnes, C. A. (1996). Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6, 149–172.
Tanaka, N. K., Ito, K., and Stopfer, M. (2009). Odor-evoked neural oscillations in Drosophila are mediated by widely branching interneurons. J. Neurosci. 29, 8595–8603.
Torre, V., Ashmore, J. F., Lamb, T. D., and Menini, A. (1995). Transduction and adaptation in sensory receptor cells. J. Neurosci. 15, 7757–7768.
Tsodyks, M. V., Skaggs, W. E., Sejnowski, T. J., and McNaughton, B. L. (1996). Population dynamics and theta rhythm phase precession of hippocampal place cell firing: a spiking neuron model. Hippocampus 6, 271–280.
Wallenstein, G. V., and Hasselmo, M. E. (1997). GABAergic modulation of hippocampal population activity: sequence learning, place field development, and the phase precession effect. J. Neurophysiol. 78, 393–408.
White, J. A., Klink, R., Alonso, A., and Kay, A. R. (1998). Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J. Neurophysiol. 80, 262–269.
Yeh, T., Lee, B. B., and Kremers, J. (1996). The time course of adaptation in macaque retinal ganglion cells. Vision Res. 36, 913–931.
Keywords: neural code, oscillations, gamma, LFP, spike
Citation: Nadasdy Z (2010) Binding by asynchrony: the neuronal phase code. Front. Neurosci. 4:51. doi: 10.3389/fnins.2010.00051
Received: 15 February 2010;
Paper pending published: 01 May 2010;
Accepted: 18 June 2010;
Published online: 15 September 2010
Edited by:
Michael E. Hasselmo, Boston University, USAReviewed by:
Paul Miller, Brandeis University, USAMichael E. Hasselmo, Boston University, USA
Copyright: © 2010 Nadasdy. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Zoltan Nadasdy, Seton Brain and Spine Institute, University Medical Center at Brackenridge, 1400 N. IH35, Suite 300, Austin, TX 78701, USA.em9sdGFuQHZpcy5jYWx0ZWNoLmVkdQ==
