A Comparison between Mechanisms of Multi-Alternative Perceptual Decision Making: Ability to Explain Human Behavior, Predictions for Neurophysiology, and Relationship with Decision Theory

While there seems to be relatively wide agreement about perceptual decision making relying on integration-to-threshold mechanisms, proposed models differ in a variety of details. This study compares a range of mechanisms for multi-alternative perceptual decision making, including integration with and without leakage, feedforward and feedback inhibition for mediating the competition between integrators, as well as linear and non-linear mechanisms for combining signals across alternatives. It is shown that a number of mechanisms make very similar predictions for the decision behavior and are therefore able to explain previously published data from a multi-alternative perceptual decision task. However, it is also demonstrated that the mechanisms differ in their internal dynamics and therefore make different predictions for neuorphysiological experiments. The study further addresses the relationship of these mechanisms with decision theory and statistical testing and analyzes their optimality.

Introduction

Perceptual decision making involves selecting an appropriate action based on sensory evidence at an appropriate time. While there seems to be general agreement that perceptual decisions, at least those with response times that clearly exceed simple motor reaction times, involve some kind of integration-to-threshold mechanism, which accumulates sensory evidence until a decision boundary is crossed, there is still considerable debate about the details of the decision mechanism and their neural implementation. Furthermore, while an optimal algorithm for decisions between two alternatives based on sensory evidence that fluctuates over time is known: the sequential probability ratio test (SPRT; Wald, 1945), to date we only know an asymptotically optimal algorithm for decisions between more than two alternatives, which only applies to the asymptotic case of negligible error rates (Dragalin et al., 1999).

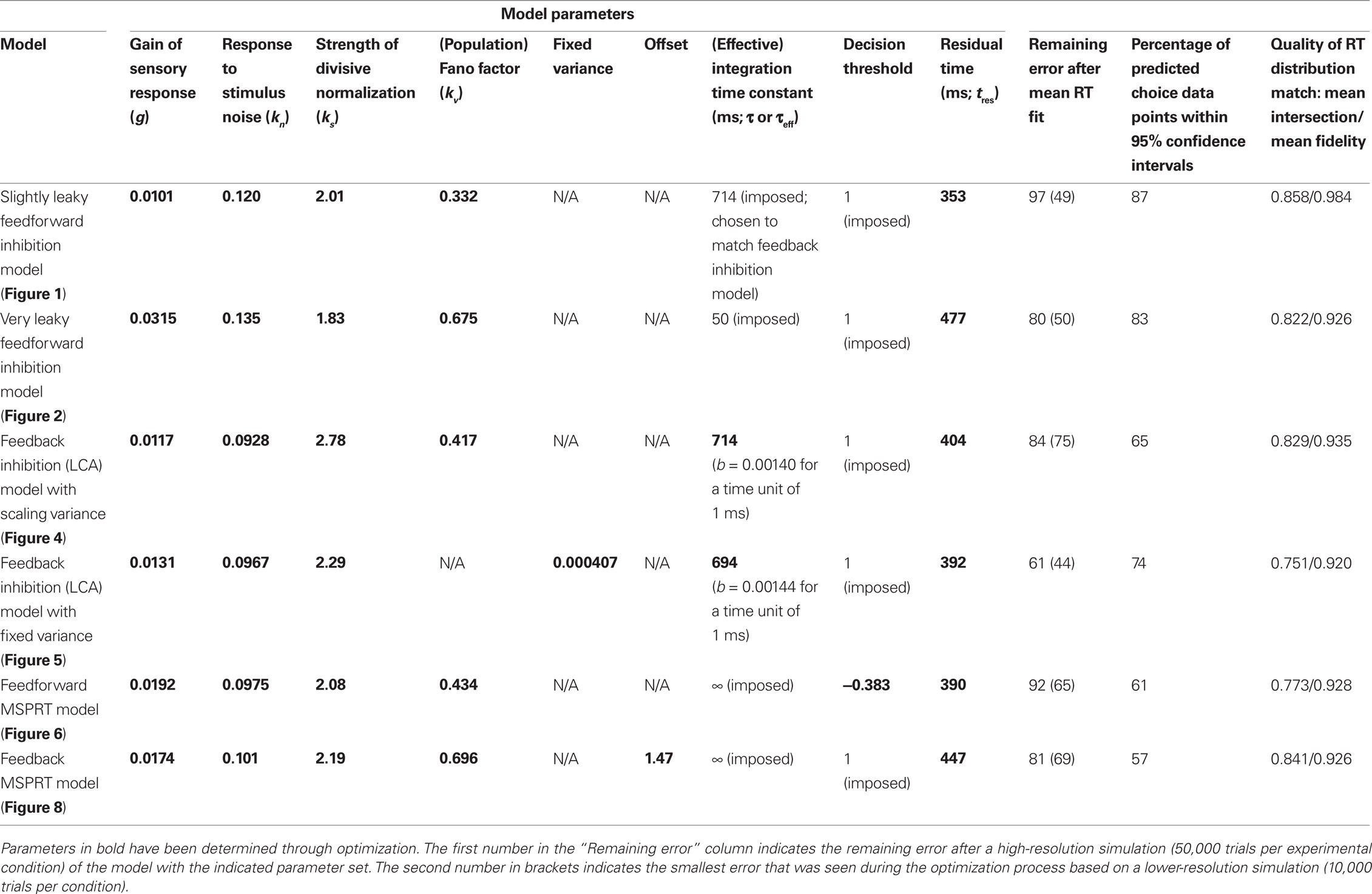
Niwa and Ditterich (2008) have presented a human behavioral dataset from a three-alternative random-dot motion direction-discrimination task, spanning a wide range of accuracy levels (from chance to perfect) and mean response times (with more than a second difference between the fastest and the slowest task condition). The observers made a judgment about the direction of the strongest motion component in a multi-component stimulus, allowing independent control of how much sensory evidence was provided for each of the alternatives and therefore an independent manipulation of speed and accuracy. Details on the behavioral dataset can be found in Niwa and Ditterich (2008). Briefly, human observers were watching a random-dot motion stimulus with three embedded coherent motion components, moving in three different directions all separated by 120°. The task was to identify the direction of the strongest motion component. The subjects were allowed to watch the stimulus as long as they wanted and responded with a goal-directed eye movement to one of three choice targets. Choices and response times were measured. On each trial the computer randomly picked a combination of coherences from 51 possible trial types. The symbols in Figure 1C show the choice data, mean response times (RTs) are shown in Figure 1B. The position on the horizontal axis indicates the coherence of the strongest motion component in the stimulus, the other two coherences are defined by the color of the symbol (see legend). In the choice plot circles represent correct choices, squares are choices of the direction of the intermediate motion component, and diamonds are choices of the direction of the weakest motion component. Figure 1C indicates that accuracy improved with stronger sensory evidence for making a particular choice (without changing the coherences of the components providing evidence for one of the alternative choices; same color in the plot), that the psychometric function was getting shallower the more distracting sensory evidence was present (from blue to red to green), and that the relative frequencies of the three possible choices followed the order of the coherences of the three motion components (circles above squares above diamonds). Figure 1B shows that responses were, on average, faster when stronger sensory evidence was presented for a particular choice (again without changing the coherences of the components providing evidence for one of the alternative choices; same color in the plot). One of the striking features of our behavioral dataset is that accuracy and mean RT can change independently. For example, all stimuli with three identical motion strengths are associated with choice performance at chance level, but the mean RTs are quite different for the different coherences (faster responses for higher coherence; see the leftmost blue, red, and green symbols in Figures 1B,C). Likewise, whereas mean RT was largely governed by the average of the two lower coherences (high degree of overlap between red and magenta symbols and green and cyan symbols in Figure 1B), accuracy was more sensitive to the individual coherences (larger separation between red and magenta circles and green and cyan circles in Figure 1C).

FIGURE 1

Figure 1. Slightly leaky feedforward inhibition model. (A) Structure of the model. Solid lines indicate excitatory connections, dashed lines inhibitory connections. (B) Fit of the model (lines) to the mean response time data (symbols). The coherence of the strongest motion component is plotted on the horizontal axis. The color codes for the strengths of the other two components. Data points within the light gray bars, which would normally all be aligned with the center of the bar, have been shifted horizontally for presentation purposes to reduce overlap. (C) Comparison between the model’s choice predictions (lines) and the behavioral data (symbols). The error bars indicate 95% confidence intervals. (D) Comparison between the model’s predictions for some RT distributions (blue lines) and the behavioral data (gray histograms).

In Niwa and Ditterich (2008) we have also demonstrated that both the datasets from individual subjects as well as the pooled dataset (which we are focusing on in this study) are consistent with a decision mechanism that assumes a race-to-threshold between three independent integrators, each of which accumulates a different linear combination of three relevant sensory signals. Our model made use of perfect integrators and feedforward inhibition was responsible for mediating competition between the alternative choices. However, many alternative models of multi-alternative perceptual decision making assume purely excitatory feedforward connections, propose feedback inhibition as the mechanism responsible for mediating competition between the choice alternatives, and involve imperfections of the integrators, like leakiness or saturation effects (Usher and McClelland, 2001; McMillen and Holmes, 2006; Bogacz et al., 2007; Beck et al., 2008; Furman and Wang, 2008; Albantakis and Deco, 2009).

It was therefore natural to ask whether our behavioral dataset was also consistent with some of these alternative model architectures. We chose to use one aspect of the behavioral dataset, the mean RTs, to fit these models and to test their predictive power for the remaining aspects of the dataset, the choice proportions and the RT distributions. As we will see, the behavioral data cannot distinguish well between different decision mechanisms. We therefore wanted to know whether different models would make different predictions for decision-related internal signals, which should allow a dissociation of the competing models based on neurophysiological experiments. Furthermore, we wanted to discuss how different model structures relate to decision theory, in particular the multihypothesis sequential probability ratio test (MSPRT; Dragalin et al., 1999). To be able to fit models to our data we will focus on abstract stochastic process models with only a small number of parameters rather than more complex biologically inspired models like Furman and Wang (2008) or Albantakis and Deco (2009), which require a different approach, but we will consider decision mechanisms based on both feedforward and feedback inhibition, integration with and without leakage, saturating integration, and non-linear mechanisms for a closer approximation of MSPRT (Bogacz and Gurney, 2007; Bogacz, 2009; Zhang and Bogacz, 2010). Finally, since MSPRT is only known to be optimal for the asymptotic case of negligible error rates, we wanted to address the optimality of different decision mechanisms over a wider range of error rates since human/animal decisions do not tend to be perfect.

Materials and Methods

Analysis of the Behavioral Data

Details on the data analysis can be found in Niwa and Ditterich (2008). The 95% confidence limits for the probabilities of making a particular choice are based on a method proposed by Goodman (1965).

Model of the Sensory Response to the Multi-Component Random-Dot Patterns

All of the models for explaining the behavioral data rely on the same representation of the sensory information as the input to the decision stage. As in Niwa and Ditterich (2008), the response of three pools of sensory neurons tuned to the three possible directions of coherent motion in the stimulus was modeled as three independent normal (Gaussian) random processes with means of

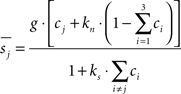
with j ranging from 1 to 3. Each stimulus is characterized by a set of three coherences c₁, c₂, and c₃. c_j is the coherence (between 0 and 1) of the motion component in the preferred direction of a particular pool of neurons. The first term of the sum in the numerator represents a strong linear response to coherent motion in the preferred direction. The second term reflects a weaker linear response to the noise component of the stimulus. The denominator reflects a divisive normalization process. Most of the models discussed here assume that the variance of each stochastic process scales linearly with its mean:

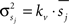
Only the LCA model with fixed variance assumes that the variances of the random processes are all the same and do not depend on the stimulus.

The means and the variances expressed by these formulas are means and variances per unit time, which we defined to be 1 ms. Thus, when performing a simulation with larger time steps, as we did (see below), both means and variances need to be multiplied accordingly when generating the random samples (by a factor of 5 for a time step of 5 ms).

Simulation of the Decision Models and Fit to the Mean Response Time Data

All models were simulated in MATLAB (The MathWorks, Natick, MA, USA) using the Stochastic Integration Modeling Toolbox developed by the author, which can be downloaded from http://master.peractionlab.org/software/. A temporal resolution of 5 ms was chosen for all simulations. Optimal model parameter sets were obtained through an optimization procedure using a multi-dimensional simplex algorithm (provided by MATLAB’s Optimization Toolbox). Simulations with 10,000 trials per experimental condition were run in parallel on a small computer cluster (using MATLAB’s Parallel Computing Toolbox and Distributed Computing Server) to minimize the sum of the squared differences between the mean RTs in the data and the mean RTs predicted by the model, taking the standard errors of the estimated means into account. We used the mean RTs for each combination of coherences, regardless of choice (15 data points). For the model these were obtained by calculating a weighted sum of the predicted mean RTs for the different choices based on the predicted probabilities of these choices. The set of model parameters yielding the smallest error (shown in brackets in the column “Remaining error” in Table 1) was then used to perform a higher-resolution simulation with 50,000 trials per condition for obtaining the behavior. The remaining error resulting from this simulation is shown in front of the brackets in the column “Remaining error” in Table 1. These simulations yield distributions of decision times. A fixed residual time t_res was added to convert these into distributions of response times. Leaky integrators are characterized by an exponential decay of their state toward 0 in the absence of any other input. How quickly an integrator decays is defined by the integration time constant τ. After τ the state has decayed to 37% of its initial value. Mathematically, the leakage shows up in the differential equation describing the integrator as a term that is proportional to the current integrator state with a negative sign:

TABLE 1

Table 1. Model parameters.

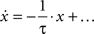
All of the simulations of models that were also used for making predictions for neurophysiology did not allow negative integrator states (indicated as “≥0” in the signal flow diagrams). This was implemented by setting an integrator state to 0 in any given time step if, without restrictions, it would have ended up with a negative state. Only the simulations of the model shown in Figure 6 did not prohibit negative integrator states since this model was excluded from further discussing its neurophysiological predictions due to its unrealistic predictions for the threshold crossing activity of the winning integrator (shown in Figure 6D). All of the shown trajectories of internal signals are based on simulations with 10,000 trials per condition.

Simulations for Comparing the Optimality of Different Decision Mechanisms

To obtain the relationship between error rate and mean sample size for each of the compared mechanisms, 20,000 trials were simulated for a variety of decision thresholds. For these simulations the integration range was unlimited, meaning that any integrator state was allowed, to provide a fair comparison between the feedforward and the feedback inhibition models and MSPRT, which also requires non-saturating integrators for a true implementation. For the feedforward inhibition mechanism the integrators x_k(k = 1…3) were updated in each time step n according to

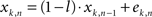
with l defining the leakiness of the integrators and e_k,n being the current sensory evidence (linear combinations of random samples). For the feedback inhibition mechanism the integrators were updated according to

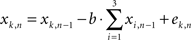
with b being the strength of the inhibitory feedback and e_k,n again being the current sensory evidence, which, in this case, are just the random samples.

Results

Models Based on Feedforward Inhibition

We will start with a model that is similar to the one presented in Niwa and Ditterich (2008). The structure of this model is shown in Figure 1A. Three independent integrators race against each other until the first one reaches a fixed decision threshold, which determines the choice and the decision time. Each of the integrators accumulates a different linear combination of three relevant sensory signals (with one sensory pool providing feedforward excitation and the other two pools providing feedforward inhibition). Each sensory pool shows a linear response to the coherent motion in its preferred direction as well as a weaker linear response to the noise (non-coherent) component of the stimulus. Simultaneous activation of multiple sensory pools by coherent motion induces divisive normalization, and the variance of the response of a sensory pool is proportional to its mean. The formulas describing the sensory response can be found in section “Materials and Methods.” The response time is determined by adding a constant residual (non-decision) time to the decision time. The model shown in Figure 1 is different from the one presented in Niwa and Ditterich (2008) in two aspects: the integrators are leaky and saturate. The leakiness was chosen to be identical to the one of a feedback inhibition model, which will be discussed later, to be able to make a direct comparison between both models. As we will see below, the feedforward inhibition model is able to explain the behavioral data for a wide range of integration time constants. The second modification is motivated by a biological constraint: since we want to look at model predictions for neurophysiological data later in this manuscript and since neural integrators cannot represent negative values by their firing rates, we imposed the constraint that the integrators cannot assume negative values. An upper limit is naturally given by the decision threshold. Since one of the model parameters can be chosen arbitrarily we defined the decision threshold to be 1. The starting point of the integration was chosen to be 1/3 of the decision threshold. This choice was informed by a preliminary analysis of recordings from the lateral intraparietal area (LIP) in monkeys performing the same task (Bollimunta and Ditterich, 2009), but is also consistent with the findings of Churchland et al. (2008). The exact location of the starting point turns out not to be too critical for being able to explain the behavioral data (data not shown). Figure 1B shows a fit of the model to the mean RT data. The symbols represent the data, the lines the model. The model parameters can be found in Table 1. This table also lists the remaining error after the fit as a goodness of fit measure with smaller numbers indicating a better fit. However, these numbers need to be taken with a grain of salt. All model calculations are based on simulations and even when simulating 50,000 trials per experimental condition this number shows a standard deviation of roughly 2.5 when repeating simulations with the same parameter set. Furthermore, the model fitting procedure had to be based on lower-resolution simulations (10,000 trials per condition), making the error during the optimization process even more variable. Once the mean RT data have been used for fitting the model, other aspects of the dataset can be used for testing the model. Figure 1C shows a comparison between the model’s predictions for the choice data (lines) with the actual choice data (symbols). Figure 1D compares the model’s predictions for the RT distributions (blue lines) with the actual RT distributions (gray histograms) for the four combinations of coherences for which we have the largest number of trials. The results indicate that adding some leakiness to the integrators and limiting the integration range to positive values (prohibiting negative integrator states) does not impact the model’s ability to account for the behavioral data.

We had previously demonstrated that a feedforward inhibition model was able to capture the behavior of monkeys performing a two-choice random-dot motion discrimination (Roitman and Shadlen, 2002) over a wide range of integration time constants (degrees of leakiness of the integrators; see section Simulation of the Decision Models and Fit to the Mean Response Time Data for an explanation; Ditterich, 2006). It turns out that the same is true for our human three-choice dataset. Figure 2A shows the results of fitting a model with the same structure as the one shown in Figure 1, but with very leaky integrators with an integration time constant of just 50 ms to the mean RT data. The model parameters can again be found in Table 1. Figures 2B,C show a comparison between the model’s predictions and the choice data and RT distributions. The match is not as good as the one for the longer integration time constant. In particular, the model’s mean RTs for the hardest trials are too long and the shape of the RT distributions approaches the typical exponential distribution of a probability summation model, a memory-free mechanism that keeps comparing incoming samples with a threshold until a threshold crossing occurs. However, overall, the results indicate that the behavioral data are consistent with a surprisingly wide range of integration time constants. To determine how other model parameters change with the integration time constant (τ) we fitted a number of models with different time constants to the mean RT data. The results are shown in Figure 2D. All model parameters but the strength of the divisive normalization (k_s; blue) changed systematically with τ (significant correlations with p < 0.01). As the leakiness increases (smaller τ) the strength of the sensory input (g; red solid line) has to increase as well as the Fano factor, the ratio between the variance of a sensory input and its mean (k_v; black solid line). However, g changes faster than k_v, leading to an improved signal-to-noise ratio (red dashed line) for smaller time constants. Being able to achieve the same performance requires better quality sensory signals when the integrators are not as efficient (leakier). At the same time, the residual time (t_res; magenta) also increases, meaning that the mean decision time is getting shorter for leakier integrators.

FIGURE 2

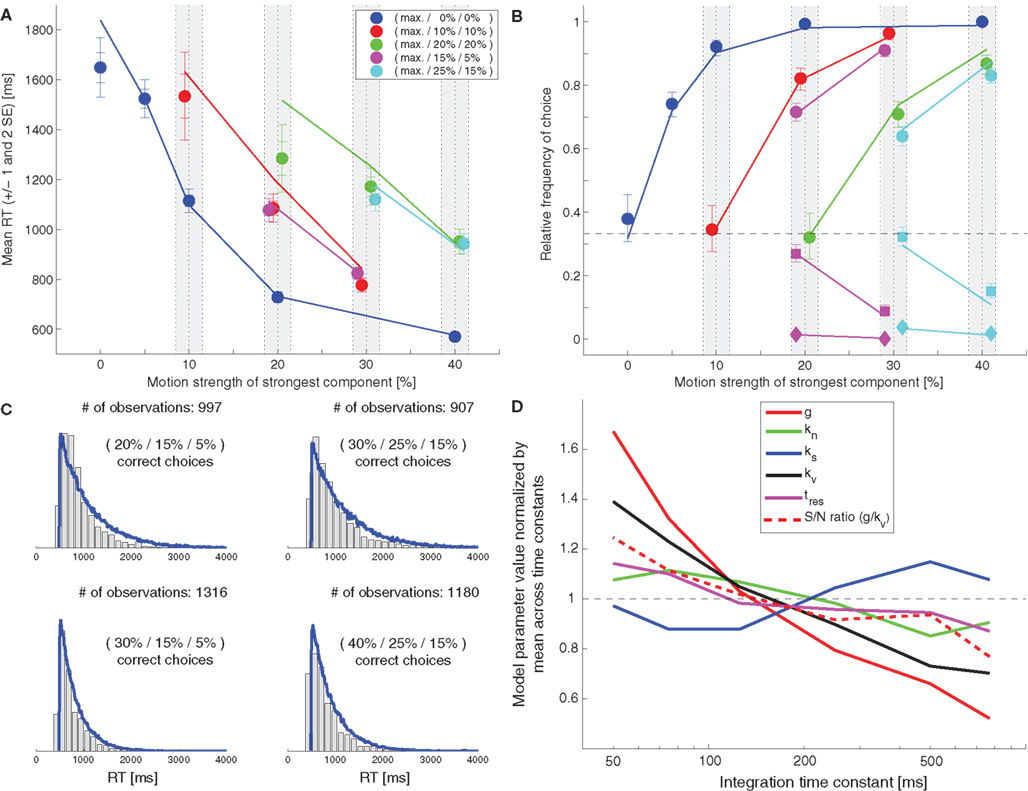
Figure 2. Very leaky feedforward inhibition model. (A) Fit of the model (lines) to the mean response time data (symbols). (B) Comparison between the model’s choice predictions (lines) and the actual data (symbols). (C) Comparison between the model’s predictions for some RT distributions (blue lines) and the behavioral data (gray histograms). (D) Dependency of remaining model parameters on the integration time constant. All parameters but the strength of the divisive normalization (k_s; blue) were significantly correlated with τ.

Models Based on Feedback Inhibition

Rather than basing the competition between the integrators on feedforward inhibition, the majority of published models of perceptual decisions between multiple alternatives rely on feedback inhibition. One of the most influential models in this area is the “leaky, competing accumulator (LCA) model” (Usher and McClelland, 2001). The structure of this model is shown in Figure 3A. Several leaky integrators compete against each other by laterally inhibiting their competitors. The integrators have an intrinsic leakiness (given by the inverse of the integration time constant τ) and inhibit each other with strength b. It has been pointed out that in the case of decisions between two alternatives a balanced LCA model (strength of inhibition equals leakiness of integrators) generates a decision behavior that is very similar to the one generated by a drift-diffusion model, which, in turn, is equivalent to a feedforward inhibition model (Bogacz et al., 2006). Here, we will also focus on the balanced version of a multi-alternative LCA model. A particularly interesting alternative implementation of this model is shown in Figure 3B. The need for tuning the network parameters in such a way that the intrinsic leak of the integrators matches the strength of the lateral inhibition disappears when the effective leakiness of the integrators is provided by an explicit inhibitory feedback rather than by intrinsic leakage. Mathematically, leaky integration simply means that the differential equation for the change of the state of the integrator has a term that is proportional to the current state with a negative coefficient. Whether this term is provided by an intrinsic leak of the integrator or by an external feedback does not matter. Thus, it is possible to start out with integrators whose intrinsic leakiness (yielding an intrinsic integration time constant τ_int) is substantially lower than the desired effective leakiness and to set the effective leakiness (yielding an effective integration time constant τ_eff) by feedback inhibition from the output of an integrator to its own input. A balance between the effective leakiness of the integrators and the strength of lateral inhibition means that the same amount of inhibitory feedback has to be provided from the output of an integrator to its own input as well as the inputs of all other integrators. Thus, this kind of inhibition can be provided by a common inhibitory signal that can be derived from the sum of all current states of the integrators. The structure of such a model (Figure 3B) is therefore very similar to the structure of more biologically inspired models that make use of a common pool of inhibitory interneurons (Furman and Wang, 2008; Albantakis and Deco, 2009).

FIGURE 3

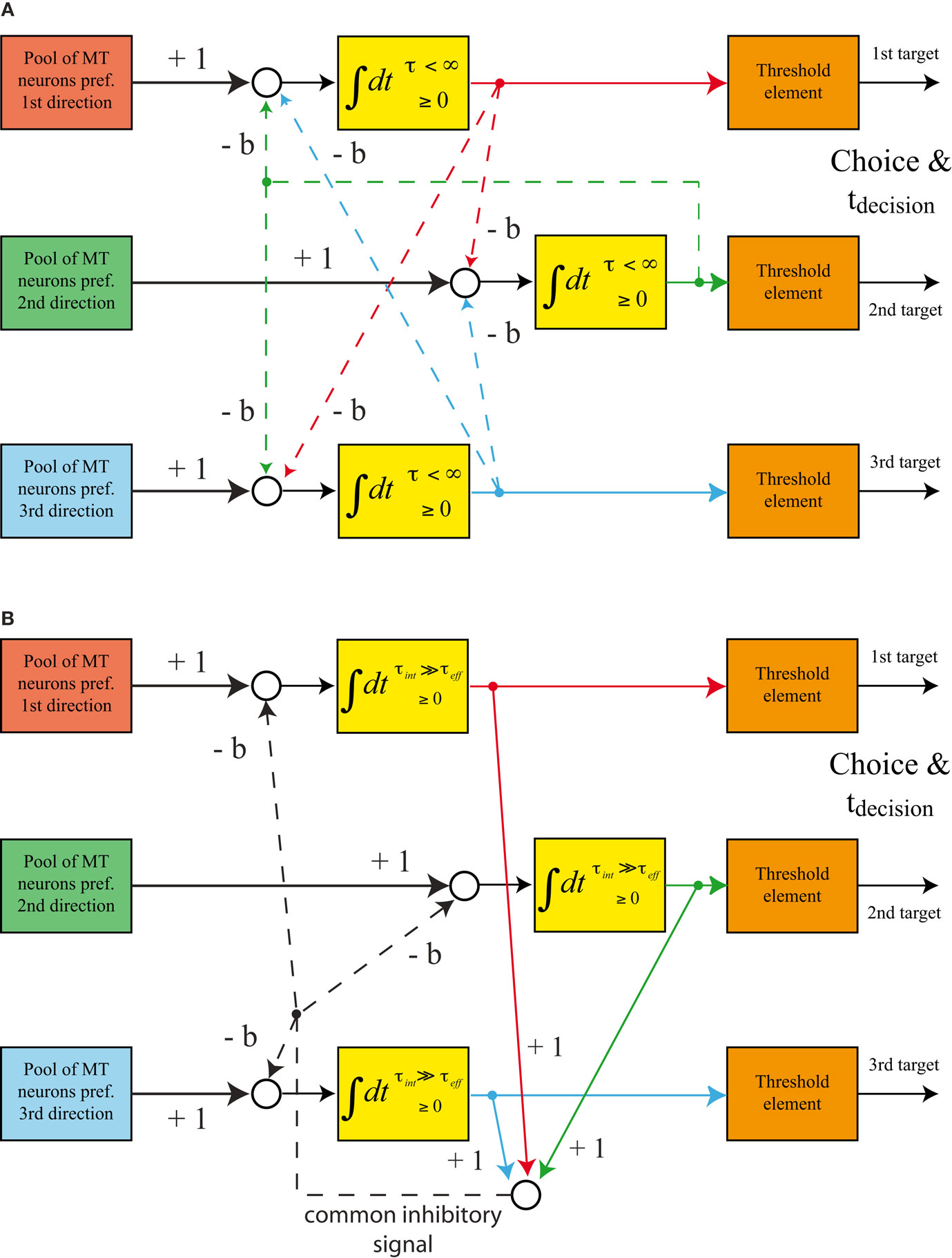
Figure 3. Structure of feedback inhibition models. (A) “Leaky, competing accumulator (LCA) model”: the integrators are intrinsically leaky, lateral inhibition is provided by individual feedback projections from the output of each integrator to the inputs of the other two integrators. (B) Alternative implementation of a balanced LCA model. The integrators’ intrinsic leak (determining τ_int) is substantially smaller than the effective leak (determining τ_eff) caused by the circuitry. The balance between leakiness and lateral inhibition is achieved by generating one common inhibitory feedback signal.

We were wondering whether our behavioral dataset was consistent with such a balanced LCA model. Using the same formalism for describing the sensory responses as the one used in the feedforward inhibition model, we again fitted the feedback inhibition model to the mean RT data (Figure 4A). The resulting model parameters can be found in Table 1. Figure 4B shows a comparison between the model’s predictions for the choice behavior (lines) and the actual choice data (symbols). The model’s predictions for some RT distributions (blue lines) are compared with the actual data (gray histograms) in Figure 4C. While the overall match seems slightly worse than in the case of the feedforward inhibition model, the results indicate that our behavioral dataset is consistent with both feedforward as well as feedback inhibition models of multi-alternative perceptual decision making.

FIGURE 4

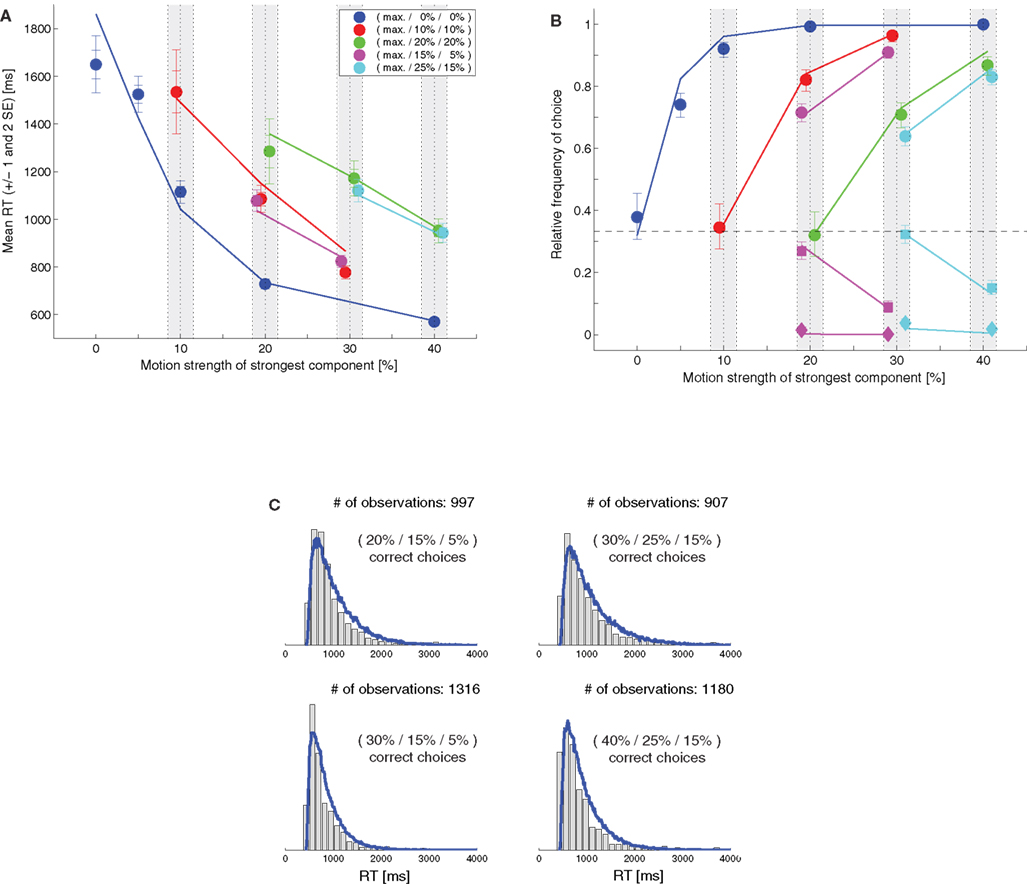
Figure 4. Feedback inhibition model with scaling variance. (A) Fit of the model (lines) to the mean response time data (symbols). (B) Comparison between the model’s choice predictions (lines) and the actual data (symbols). (C) Comparison between the model’s predictions for some RT distributions (blue lines) and the behavioral data (gray histograms).

As mentioned in the section “Introduction,” one of the striking features of our behavioral dataset is that in the case of three motion components with identical coherence faster mean RTs were observed for higher coherence. As we have pointed out in Niwa and Ditterich (2008), in the context of the feedforward inhibition model this observation can only be explained through changes in the variance of the combined sensory signals (e₁, e₂, and e₃ in Figure 1A) since the means are always 0 for three identical coherences. We therefore concluded that a significant scaling of the variance of the sensory signals with their mean has to be postulated. However, the situation is different in the case of the feedback inhibition model. The excitatory input to a particular integrator changes whenever the mean of the associated sensory signal changes. Thus, changes in the means only (without any changes of the variance) could, in principle, be driving the behavioral effects. To test whether such an alternative explanation would be consistent with our data we also fitted a version of the feedback inhibition model with fixed (rather than scaling) variance sensory signals. The results are shown in Figure 5A; the model parameters can be found in Table 1. Figures 5B,C show comparisons of the model’s predictions for choice and RT distributions with the actual data. The results indicate that a feedback inhibition model could explain the observed independent changes of accuracy and mean RT on the basis of changes of the mean sensory signals only without having to postulate additional changes of the variance (although, as we have seen in Figure 4, a scaling of the variance does not hurt).

FIGURE 5

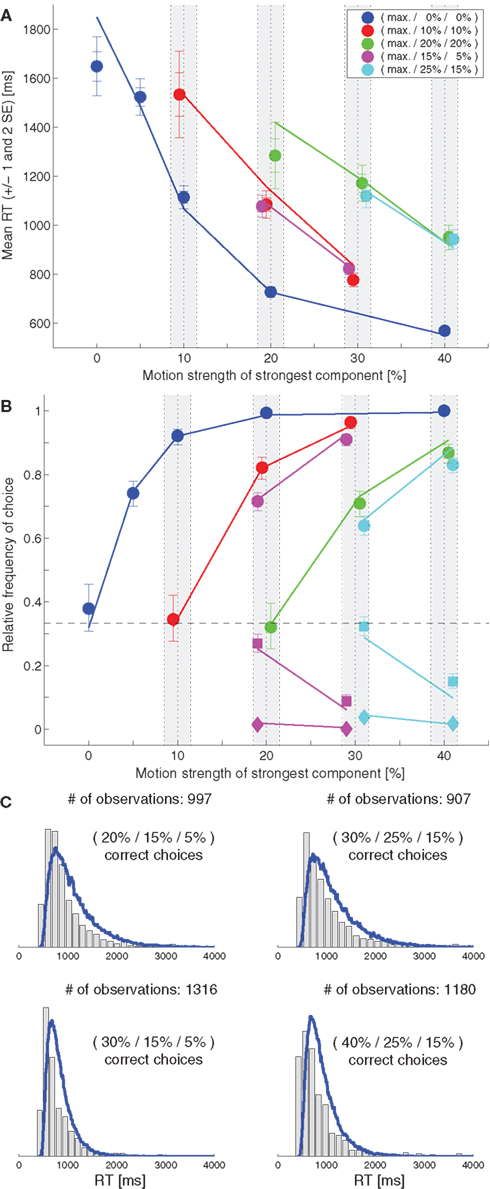
Figure 5. Feedback inhibition model with fixed variance. (A) Fit of the model (lines) to the mean response time data (symbols). (B) Comparison between the model’s choice predictions (lines) and the actual data (symbols). (C) Comparison between the model’s predictions for some RT distributions (blue lines) and the behavioral data (gray histograms).

Models Implementing or Approximating MSPRT

For choices between two alternatives Gold and Shadlen (2001) were able to demonstrate that, under reasonable assumptions about how sensory neurons represent the state of the sensory world, integrating the difference between the activities of two pools of opposing sensory neurons up to a decision threshold provides a good approximation of the SPRT, which has been shown to be optimal in the sense of minimizing the average decision time for any desired accuracy level (Wald, 1945). This is because the difference between the activities of the two sensory pools can be shown to be (roughly) proportional to the logarithm of the likelihood ratio between the two competing hypotheses based on the momentary sensory evidence. Assuming statistical independence, summing these differences over time yields a value proportional to the logarithm of the likelihood ratio based on the complete sensory evidence provided so far. According to SPRT the decision process should be terminated when this likelihood ratio exceeds a decision threshold.

While the optimal algorithm for decisions between more than two alternatives for any desired accuracy level is still unknown, an extension of SPRT, the MSPRT has been shown to be asymptotically optimal for negligible error rates (Dragalin et al., 1999). As will be discussed later in this manuscript, the models that we have been looking at so far do not implement MSPRT. However, Bogacz and Gurney (2007) have proposed that a circuit involving the basal ganglia could help implementing or at least approximating this algorithm. Dragalin et al. (1999) have proposed two versions of MSPRT: MSPRTa calculates the posterior probability of each hypothesis and stops the decision process when one of these exceeds a decision threshold; MSPRTb is based on multiple pairwise comparisons and stops the decision process when all likelihood ratios between a given hypothesis and all alternative hypotheses exceed a decision threshold. Bogacz and Gurney (2007) describe a potential implementation of MSPRTa. Cortex is assumed to integrate sensory evidence for each hypothesis independently and the basal ganglia are assumed to perform the calculations that are necessary for obtaining the posterior probabilities. The decision process is assumed to terminate when one of the posterior probabilities exceeds a critical threshold. The structure of such a model is shown in Figure 6A. Calculating the posterior probabilities involves obtaining the logarithm of a sum of exponentials. A truthful implementation of MSPRT would require the weight (g*) of the excitatory connections with the red, green, and blue arrowheads to change with the statistics of the sensory input. However, Bogacz and Gurney (2007) have demonstrated that the model is relatively robust with respect to how this weight is set. Here we only consider a model where these weights are set to 1. We used perfect integrators (since this is what a true implementation of MSPRT would require) and initialized them with a value of 0. The starting point of the integration can actually be chosen arbitrarily since it is easy to demonstrate that adding the same offset to the states of all integrators does not alter the result of calculating the posterior probabilities (see Bogacz and Gurney, 2007, Appendix D or Bogacz, 2009, Appendix E). The result of fitting this model to the mean RT data is shown in Figure 6B and the resulting model parameters can be found in Table 1. Note that the decision threshold is negative. This is because the logarithm of a probability is a negative number. Bogacz and Gurney (2007) have therefore proposed that the output of the basal ganglia should be the negative of this logarithm and that a threshold crossing would then occur when one of the outputs drops below a critical value. Figure 6C shows a comparison between this model’s predictions for the choice behavior and the actual choice data. As can be seen, our behavioral dataset seems also consistent with an MSPRT model.

FIGURE 6

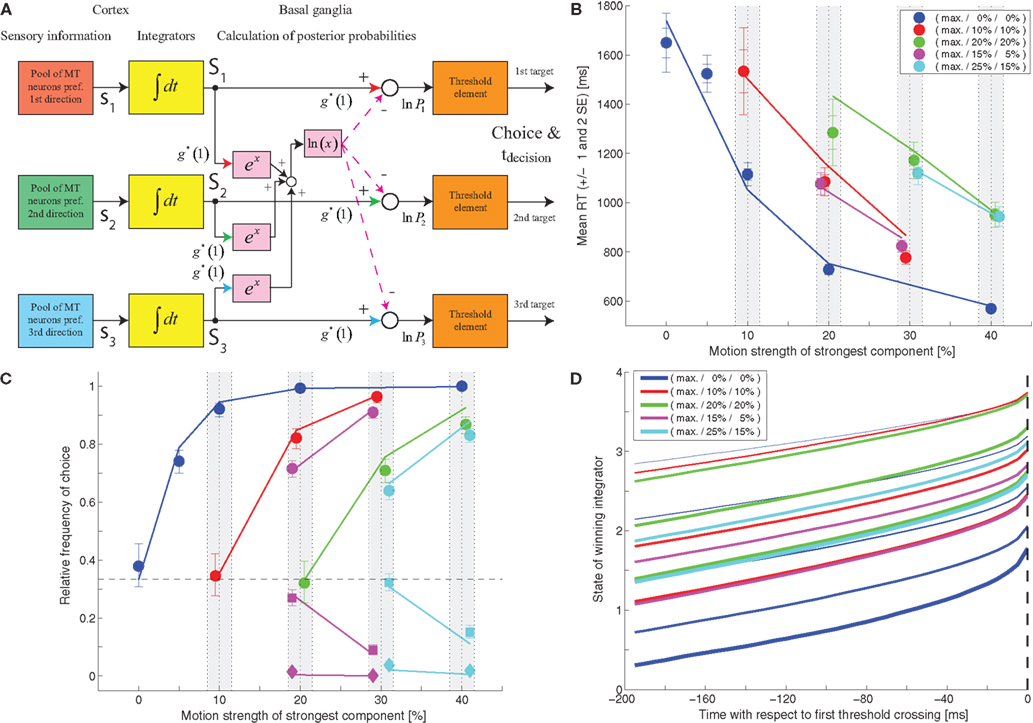
Figure 6. Feedforward MSPRT model. (A) Structure of the model. (B) Fit of the model (lines) to the mean response time data (symbols). (C) Comparison between the model’s choice predictions (lines) and the actual data (symbols). (D) Model predictions for the state of the winning integrator just prior to decision threshold crossing. Line width codes for the coherence of the strongest motion component (thicker = higher coherence), line color codes for the other two motion strengths. The integrator state at threshold crossing is very different for different combinations of motion coherence.

This feedforward implementation of MSPRT, however, makes a prediction that is incompatible with experimental observations that have been made in non-human primates performing random-dot motion discrimination tasks. Figure 6D shows the model’s prediction for the state of the winning integrator immediately prior to the decision threshold crossing for different combinations of motion coherences. The dashed vertical line marks the time of the threshold crossing. It is obvious that, at this point in time, the state of the winning integrator spans a wide range for different coherence combinations. This is because the thresholding is not performed on the state of the integrator, but on the output of the circuit calculating the posterior probabilities. In contrast, recordings from parietal cortex of monkeys performing such tasks, which have revealed neurons that appear to reflect the state of the integrator, suggest that the activity of the winning integrator is very stereotyped around the time when the decision is made (Roitman and Shadlen, 2002; Churchland et al., 2008; Bollimunta and Ditterich, 2009). Aware of this issue, Bogacz (2009) has considered an alternative implementation: rather than having the basal ganglia circuit operate downstream from the cortical integrators, it could also be part of a cortico-cortical feedback loop. Thus, if the circuit could be arranged such that the integrators themselves carry the information about the posterior probabilities, the thresholding could be moved back to the cortical level.

Figure 7A shows a feedback implementation of MSPRT that closely follows the suggestion in Bogacz (2009). What does this mechanism calculate compared to the mechanism shown in Figure 6A? The feedforward mechanism in Figure 6A takes an integrated sensory evidence signal S_i, multiplies it with g*, and subtracts the logarithm of the sum of the exponentials of all integrated evidence signals, again multiplied by g*, to obtain the logarithm of the posterior probability P_i:

FIGURE 7

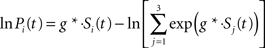
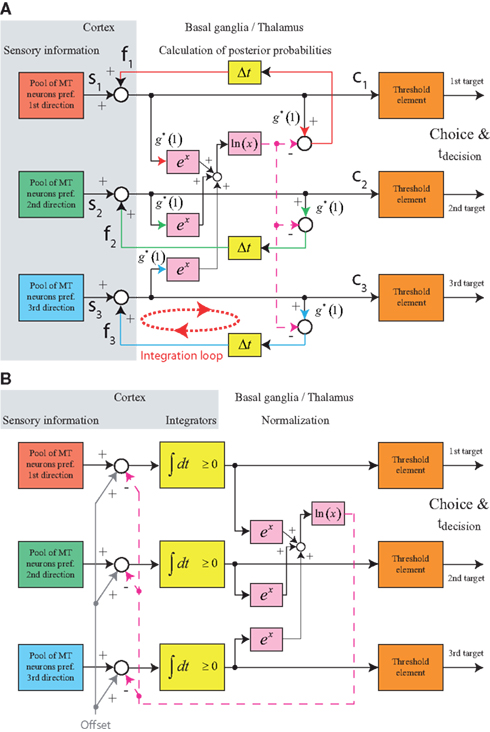
Figure 7. Structure of feedback MSPRT models. (A) Feedback implementation of MSPRT following Bogacz (2009). The basal ganglia are part of a cortico-cortical feedback loop that provides an excitatory feedback signal representing the logarithm of the posterior probability. Note that in this implementation the integration of the sensory evidence is mediated by the cortico-cortical feedback loop involving the basal ganglia. The yellow boxes with “Δt” in them indicate some time delay in the feedback loop. (B) Alternative feedback implementation of MSPRT. The feedback signals in (A) have been separated into an excitatory component responsible for integrating the sensory evidence and an inhibitory component responsible for normalizing the posterior probabilities. This implementation no longer requires the basal ganglia to participate in the temporal accumulation process. Furthermore, an excitatory offset has been added to the inputs of all integrators to move the operating point of the circuit into the positive range (recall that the logarithm of a probability is a negative value). As long as the same offset is added to the input of all integrators, this does not affect the result of calculating the posterior probabilities. Thus, each integrator now carries the sum of the logarithm of the posterior probability and the offset. The integrators now also have the property that they cannot represent negative values (like the integrators in the earlier models).

Thinking of this as a discrete time process, which will make it easier to compare it with the feedback process, the integrals over the sensory signals up to time t would be replaced by sums of sensory samples up to some index n:

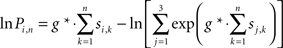
Let us now have a look at the mechanism in Figure 7A. As demonstrated in the Appendix, for a g* of 1 the feedback signal f_i,n is always the logarithm of the posterior probability from the previous iteration ln P_i,n−1. The summation nodes update these with the current sensory evidence and the feedback loops again normalize the results. Note that in this implementation the accumulation of the sensory evidence (temporal integration) is performed by the feedback loops involving the basal ganglia.

However, the integration does not necessarily have to be performed by the cortico-cortical loop involving the basal ganglia. A closer inspection of the feedback signals reveals that they are composed of two additive components: an excitatory component with a gain of 1 for feeding back each individual signal and a shared inhibitory component that carries the logarithm of the sum of exponentials. The individual excitatory component simply ensures perfect integration and can be separated from the shared inhibitory component, removing the function of temporal integration from the basal ganglia loop and using it only for the normalization process. Such an implementation is shown in Figure 7B. Another modification has been applied to this implementation. Recall that the logarithm of a probability is a negative number. However, we want the integrators to operate in a positive range. To achieve this, we are adding an identical excitatory offset to the inputs of all integrators. Remember that adding an identical offset to all integrators does not change the outcome of the posterior probability calculation (see above). This circuit has in interesting property: Assume that the actual decision thresholds are fixed. (We set them to 1 as in the earlier models.) To change the effective decision threshold the excursion from the starting point of integration to the actual threshold has to be adjusted. In this circuit this is achieved by changing the additive offset, since the combination of the additive offset with the feedback circuit takes care of automatically setting the starting point of integration. Why is this? Let us assume that the integrators start out with any arbitrary activity A. What exactly A is does not matter as long as the activation of all integrators is identical. This leads to an inhibitory feedback signal of size ln[3 exp(A)] = A + ln 3. In the absence of sensory input the integrators therefore receive an excitatory input of size “Offset” and an inhibitory input of size A + ln 3. Thus, the current integrator activity is subtracted and the integration starting point is set at Offset − ln 3.

Figure 8A shows a fit of the model in Figure 7B to the mean RT data, again using a more realistic integrator that cannot assume negative values. The parameter values can be found in Table 1. Figures 8B,C compare the model’s predictions for choice behavior and RT distributions with the actual data. The automatically set starting point of integration turns out to be roughly 0.38 (see Figure 11), which is not unrealistic and similar to the imposed starting point of 0.33, which has been applied to all other models on the basis of neurophysiological observations in animal experiments.

FIGURE 8

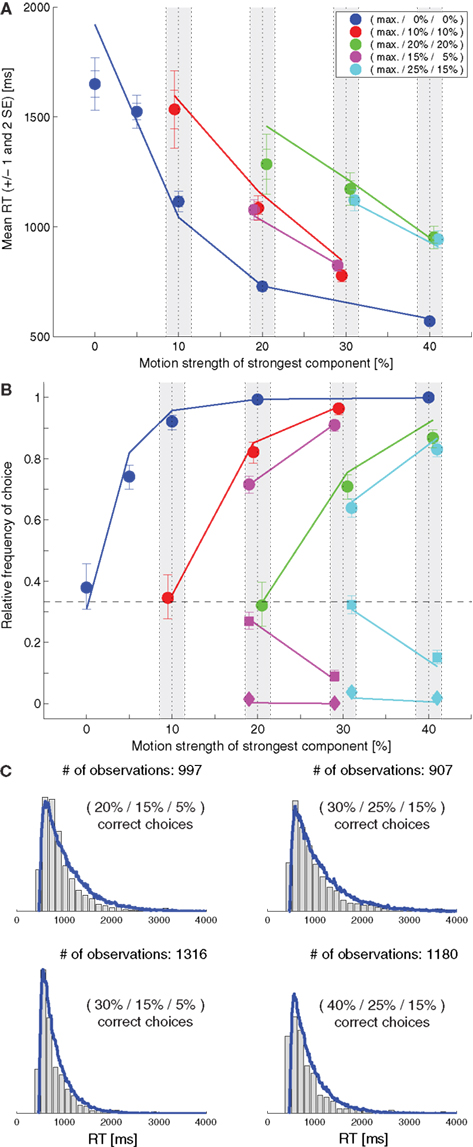
Figure 8. Results of the feedback MSPRT model (shown in Figure 7B). (A) Fit of the model (lines) to the mean response time data (symbols). (B) Comparison between the model’s choice predictions (lines) and the actual data (symbols). (C) Comparison between the model’s predictions for some RT distributions (blue lines) and the behavioral data (gray histograms).

Predictions for Neurophysiology

What we have seen so far is that the pattern of behavioral data that we have observed in our multi-alternative perceptual decision-making task seems to be consistent with a number of integration-to-threshold model structures that involve a broad range of integration time constants, feedforward as well as feedback inhibition mechanisms, as well as linear and non-linear mechanisms for combining signals across alternatives. Since it seems to be virtually impossible to discriminate between these different options based on the behavioral data alone, the question arises whether other types of data would help with this discrimination. What I am going to demonstrate in the following is that, although the models make almost identical predictions for behavior, the predictions for how the internal state of the system should evolve over time are quite different. Thus, invasive recordings in animal models that aim at tapping into the state of the integrator (like Roitman and Shadlen, 2002; Churchland et al., 2008) should be helpful in discriminating the alternatives.

We will be looking at a number of measures for assessing the internal dynamics of a decision mechanism: how the activity of the integrator associated with the strongest motion component evolves over time, how the summed activity of all integrators evolves over time, and how the states of the two integrators associated with the two larger motion coherences move through state space over time. Figure 9 shows all of these measures for the feedforward inhibition model presented in Figure 1. The left column indicates the expected trajectories during the first 200 ms after integration onset (ignoring the outcome of the decision); the right column presents the expected trajectories during the last 200 ms before the decision threshold crossing (for correct trials only). Different trajectories are associated with different combinations of coherences, with the width of the line representing the coherence of the strongest motion component and the color representing the coherences of the other two components.

FIGURE 9

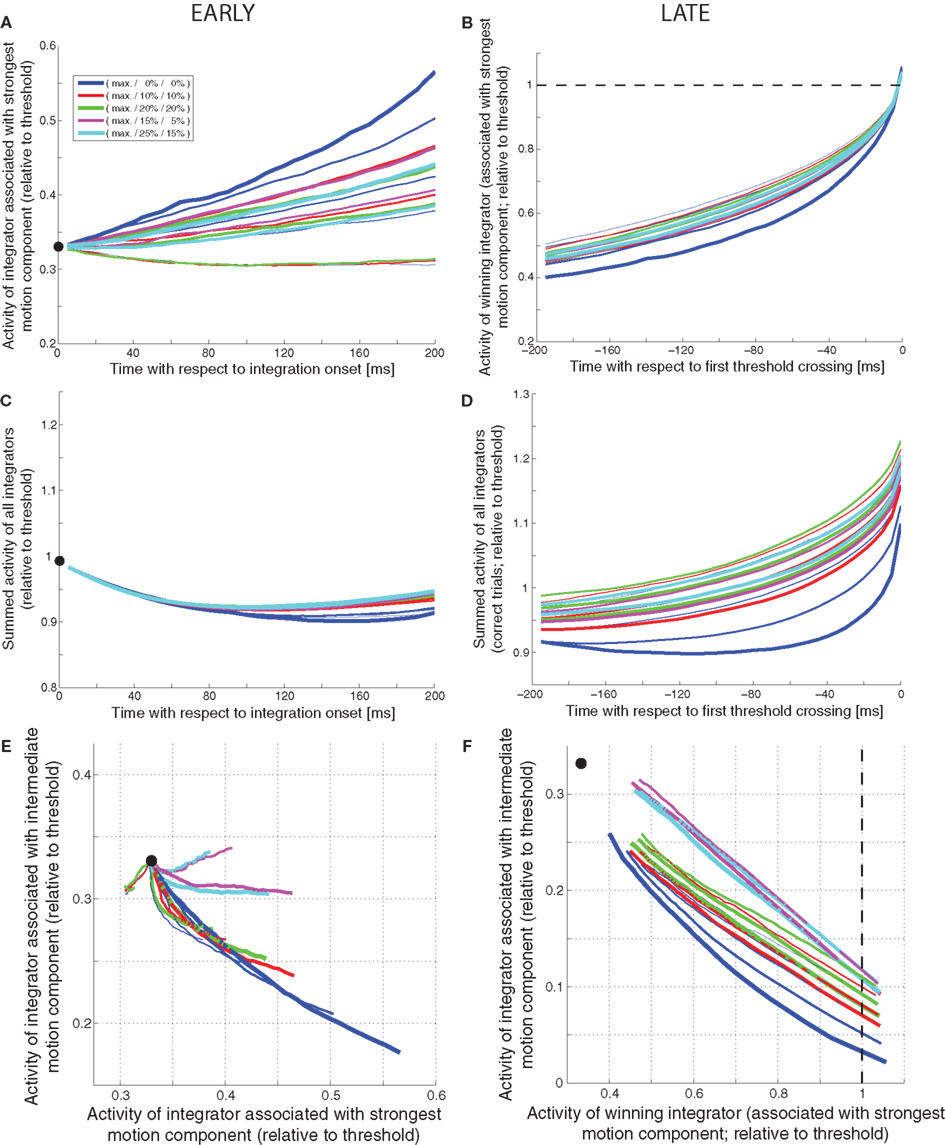
Figure 9. Internal dynamics of feedforward inhibition mechanism (shown in Figure 1). (A) Expected activity (relative to threshold) of the integrator associated with the strongest motion component during the first 200 ms after integration onset. The thickness of the line represents the coherence of the strongest motion component (thicker = higher coherence), the color codes for the coherences of the other two components (see legend). The black dot marks the starting point of integration. (B) Expected activity of the integrator associated with the strongest motion component during the last 200 ms before threshold crossing on correct trials. The dashed line indicates the decision threshold. (C) Expected sum of the activities of all integrators during the first 200 ms. (D) Expected sum of the activities of all integrators during the last 200 ms on correct trials. (E) Expected movement through state space (states of the integrators associated with the two stronger motion components) during the first 200 ms. (F) Expected movement through state space during the last 200 ms.

How can these measures be used to differentiate between different decision mechanisms? How, for example, can we dissociate a slightly leaky feedforward inhibition mechanism (Figure 1) from a very leaky feedforward inhibition mechanism (Figure 2)? As shown in Figure 9A, the slightly leaky mechanism predicts early trajectories that are roughly linear ramps with different slopes for different combinations of coherences. The very leaky mechanism on the other hand, as shown in Figure 10A, predicts that the integrator assumes different steady states for different combinations of coherences. Likewise, the slightly leaky mechanism predicts continuously rising late trajectories (Figure 9B), whereas the very leaky mechanism again predicts different steady states during the second to last 100 ms before the threshold crossing (Figure 10B). Is there a way to tell a feedback inhibition mechanism with scaling variance (Figure 4) from one with fixed variance (Figure 5)? Figure 10C shows the early expected summed activity of all integrators for the scaling variance model. It can be seen that for trials with only a single coherent motion component (blue lines) the summed activity is expected to be lowest for the highest coherence (thicker lines below thinner lines). On the contrary, Figure 10D shows that in the fixed variance case the summed activity is expected to be highest for the highest coherence (thicker blue lines above thinner blue lines). Can we also tell a feedforward inhibition model (Figure 1) from a feedback inhibition model (Figure 2)? Figure 9F shows how a feedforward inhibition mechanism (regardless of the leakiness) approaches the decision threshold: the activity of the integrator associated with the intermediate motion component keeps falling as the activity of the winning integrator keeps rising. In contrast, Figure 10E shows the situation for the feedback inhibition mechanism (regardless of whether the variance scales or not): the integrator associated with the intermediate motion component tends to assume different steady states as the winning integrator approaches threshold. Finally, how can we tell a feedback MSPRT mechanism (Figure 8) from any of the mechanisms based on linear combinations of signals (regardless of feedforward or feedback inhibition)? With the exemption of high coherence single component trials, most of the presented decision mechanisms predict a continuous increase in the summed activity of all integrators during the last 200 ms before threshold crossing. Only two mechanisms are different: the very leaky feedforward inhibition mechanism (Figure 2), which predicts a roughly flat sum up to approx. 50 ms before threshold crossing when the sum starts rising continuously, and the feedback MSPRT mechanism (Figure 8), which also predicts a roughly flat sum up to approx. 100 ms before threshold crossing when the sum tends to start dropping (see Figure 10F). Thus, although all of the discussed decision mechanisms predicted virtually indistinguishable behavior, the predictions for the internal dynamics are quite different. These differences are summarized in Table 2.

FIGURE 10

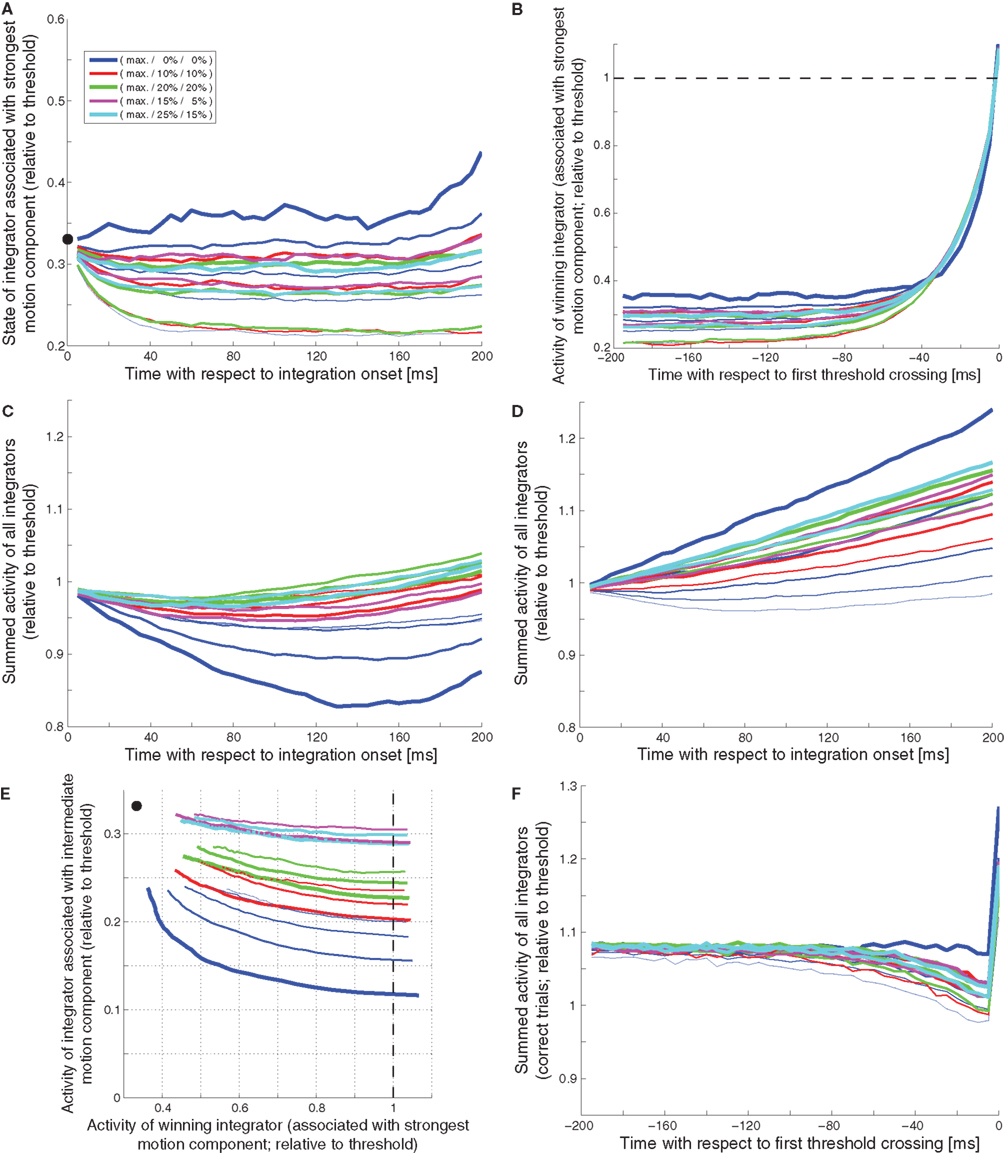
Figure 10. Deviating internal dynamics of other decision mechanisms. (A) Very leaky feedforward inhibition model (Figure 2): Early activity of leading integrator. (B) Very leaky feedforward inhibition model (Figure 2): Late activity of winning integrator. (C) LCA model with scaling variance (Figure 4): Early summed activity of all integrators. (D) LCA model with fixed variance (Figure 5): Early summed activity of all integrators. (E) LCA model with scaling variance (Figure 4): Late state space. (F) Feedback MSPRT model (Figure 8): Late summed activity of all integrators.

TABLE 2

Table 2. Comparison of internal model dynamics.

Figure 11 shows the early state space trajectories for the feedback MSPRT model (Figure 8). Qualitatively, these trajectories are similar to the ones predicted by most of the other decision mechanism. The reason for showing these trajectories is to demonstrate the result of the automatic setting of the integration starting point by the feedback mechanism as has been discussed above.

FIGURE 11

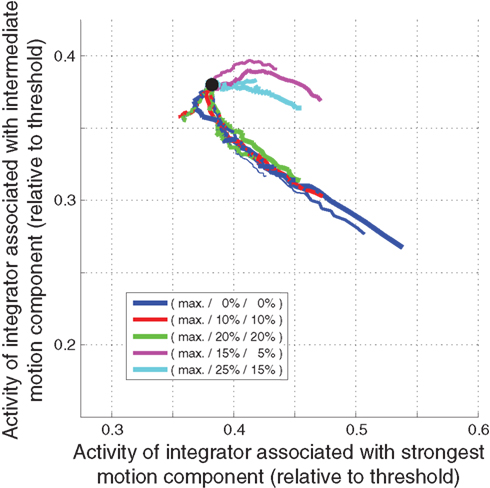
Figure 11. Early state space of the feedback MSPRT model (shown in Figures 7B and 8). Note that the integration starting point (approx. 0.38) is set by the feedback mechanism and not imposed as in the other models.

Another difference between the considered decision models pertains to the correlation between the input signals to the integrators. This correlation structure could potentially show up in spike time correlations between simultaneously recorded neurons representing the states of two different integrators (de la Rocha et al., 2007; Ostojic et al., 2009). There are too many unknowns (see section Discussion) to make a quantitative prediction for the expected correlations, but we will discuss the qualitative pattern that should be seen if correlations can be observed at all. A hallmark of the feedforward inhibition mechanism shown in Figure 1A is that a sensory signal that provides excitatory input to one of the integrators also provides inhibitory input to the other integrators. Thus, pairs of integrators share an anti-correlated input component that could show up as a reduced likelihood of (nearly) simultaneous spiking of neurons belonging to different integrator populations. In contrast, in the feedback inhibition mechanisms shown in Figure 3 different integrators only share inhibitory input. Thus, these positively correlated input components could show up as an increased likelihood of simultaneous spiking of neurons belonging to different integrator populations. In the feedback MSPRT mechanism shown in Figure 7A the feedback signals to the different integrators are largely independent and we therefore would not expect any significant correlation between the spike timing of neurons belonging to different integrator populations. In contrast, the integrators in the alternative implementation shown in Figure 7B share both an excitatory offset input as well as an inhibitory feedback input. The input signals to different integrators are therefore expected to be positively correlated, which could again show up as an increased likelihood of simultaneous spiking of neurons belonging to different integrator populations.

Relationship with Decision Theory

We have seen that a variety of integration-to-threshold models are apparently able to explain behavioral data from multi-alternative perceptual decision making, but what is it that these mechanisms are calculating and what is the relationship between the underlying algorithms and decision theory? Making a decision has two essential aspects: deciding when one has collected enough evidence for being able to make an informed choice, which we will refer to as the “stopping rule,” and choosing one out of a limited set of alternative hypotheses, which we will refer to as the “decision rule.” For example, when making a decision between two possible alternatives based on sequential sampling of sensory evidence, it has been demonstrated that the SPRT is the optimal algorithm in the sense of minimizing the mean sample size for any given desired accuracy level (Wald, 1945). In this case the stopping rule is to terminate the decision process when the likelihood ratio for the two alternatives exceeds a particular critical threshold that depends on the desired accuracy. And the decision rule is to pick the alternative with the larger likelihood.

To address the relationship between the discussed multi-alternative decision mechanisms and decision theory, I will start out developing an argument that is analogous to what Gold and Shadlen (2001) have done for the case of two alternatives: we will see that under certain circumstances the integration of the difference between the activities of two pools of sensory neurons yields a result that is proportional to the log-likelihood ratio between two hypotheses. To keep the argument as simple as possible, let us consider a slightly less complex problem than what the discussed experimental task requires: assume that the brain is listening to the outputs of three pools of sensory neurons, which are emitting random samples that can be described as originating from a stochastic process. The mean of one of these processes μ⁺ is slightly larger than the means of the other two, which are identical (μ⁻; this is the simplification). The brain’s job is to find out which of the three streams is the one with the larger mean. Thus, there are three possible hypotheses H₁, H₂, and H₃ with H_i meaning that stream i is the one with the larger mean:

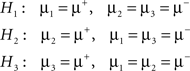
Each time step k we observe a sample x_k from the first stream, a sample y_k from the second stream, and a sample z_k from the third stream. In the following we will consider two special cases: (1) all stochastic processes are Poisson and (2) all stochastic processes are normal with equal variance.

Let us first look at the Poisson case. The conditional probabilities of observing a sample x_k given the different hypotheses are

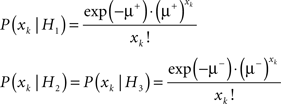
The conditional probabilities for the samples from the other two streams can be written analogously. We can thus establish a number of log-likelihood ratios:

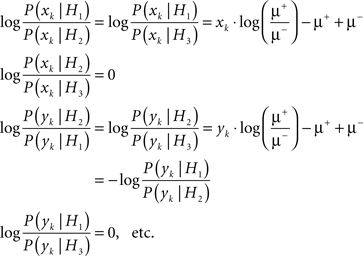
Assuming statistical independence between the samples obtained from the different streams, the total log-likelihood ratios for a set of observations (x_k, y_k, z_k) can be written as

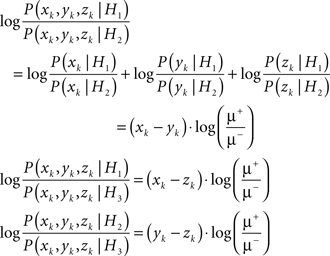
Furthermore, assuming statistical independence between successive observations, the log-likelihood ratios based on the sensory observations up to time index n can be written as

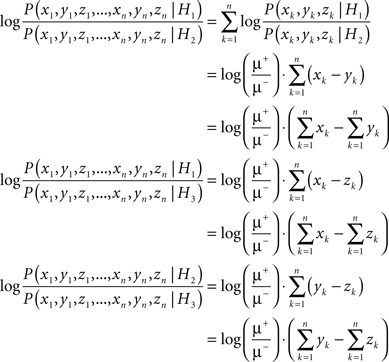
This means that the log-likelihood ratio between two hypotheses is proportional to the sum of the differences between the samples obtained from two sensory streams or, in the continuous case, to the integral over the difference between two sensory streams. Equivalently, it is also possible to sum/integrate each stream independently and then calculate the difference afterward. The proportionality factor, which we will refer to as g*, in the case of Poisson processes is 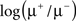. Thus, we see that the same principal result that was developed by Gold and Shadlen (2001) for the 2AFC case, namely that the log-likelihood ratio between two hypotheses is proportional to the integral of the difference between the activities of two pools of sensory neurons, also holds for multiple alternatives.

Let us now consider the case of normal processes with equal variance. Under these circumstances the conditional probabilities for observing an individual sample can be written as

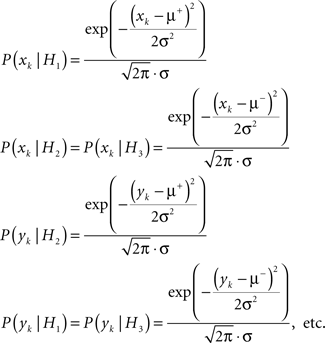
Following the same steps as in the case of the Poisson processes above, one arrives at the following final expressions:

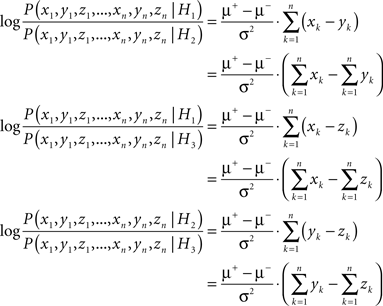
Thus, the same principal result holds, but the proportionality factor g* is now .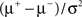

Given these results, what is it that the feedforward inhibition model (Figure 1A) computes? It calculates the integrals over

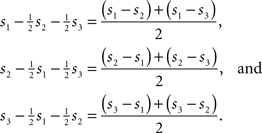
Assuming that the outputs of the sensory pools can be approximated by either Poisson processes or by normal processes with roughly equal variance and ignoring imperfections of the integrators, the integrators then carry signals that are roughly proportional to the average log-likelihood ratio between one hypothesis and the other two hypotheses. The integration process stops once one of these values exceeds a threshold and the corresponding hypothesis is picked. This is what McMillen and Holmes (2006) have referred to as a max-vs-average test. Note that this is different from what MSPRT does. Recall that there are two versions of MSPRT: MSPRTa, which stops when the posterior probability of one hypothesis exceeds a threshold and picks the corresponding hypothesis, and MSPRTb, which stops when all of the likelihood ratios between a given hypothesis and all alternatives exceed a threshold and picks the corresponding hypothesis. This is what McMillen and Holmes have referred to as a max-vs-next test. What does the calculation of the posterior probability look like? Assuming flat priors, each posterior can be expressed as the corresponding likelihood multiplied by some factor. Since the posterior probabilities have to sum to 1 (one of the hypotheses has to be true and only one of them can be true at a time), this factor has to be 1 divided by the sum of the likelihoods. Thus the posteriors can be written as

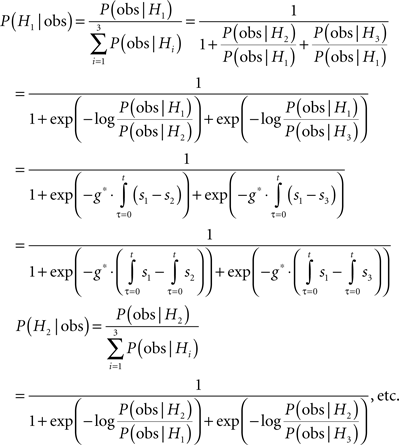
Here, “obs” stands for all sensory observations. Note that implementing this algorithm would require either 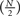integrators for N alternatives (leading to an explosion in the number of required integrators with increasing number of alternatives) if the system wanted to keep track of all possible differences or N integrators for N alternatives if each sensory signal were integrated independently, plus calculating exponentials.

For a thorough comparison between the LCA model and MSPRT please see McMillen and Holmes (2006). Briefly, the authors demonstrated that, similar to our feedforward inhibition model, the LCA model also approximates a max-vs-average test.

Why is it that the mechanism shown in Figure 6A implements/approximates MSPRT? The calculation looks quite different from the formula for the posterior probabilities shown above. We can rewrite the posterior probability of the first hypothesis as

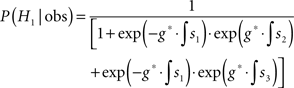
Multiplying both the numerator as well as the denominator by exp (g* • ∫s₁) yields

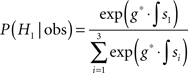
Taking the logarithm yields

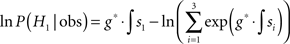
This is what the circuit shown in Figure 6A computes. It therefore implements MSPRTa.

Optimality of the Discussed Decision Mechanisms at Different Accuracy Levels

Multihypothesis sequential probability ratio test has been shown to be optimal in the sense of minimizing sample size or decision time for the asymptotic case of negligible error rates. However, when facing difficult decisions, humans or animals often do not operate in a regime of no or almost no errors. For example, our human subjects had an error rate of 20%. Our monkeys tend to be closer to a 30% error rate (Bollimunta and Ditterich, 2009). It is still unknown what the optimal multi-alternative decision algorithm in such a regime is. We therefore wanted to perform an empirical comparison of the optimality of the different decision mechanisms that are being discussed here for a range of biologically plausible error rates. The decision mechanisms had to solve the following challenging problem: From listening to three streams of random numbers they had to find out which of the streams had a slightly higher mean than the other two. All of the random processes were normal processes with a variance of 1. One of them had a mean of 0.1, the other two means were 0. The decision threshold was varied systematically to obtain the relationship between mean sample size and error rate for error rates ranging from roughly 1% to 40% for each of the decision mechanisms. Figure 12A shows a comparison between the optimality of a feedforward inhibition mechanism (“FFW”, red), a feedback inhibition mechanism (“FB”, green), MSPRTa (blue), and MSPRTb (black). FFW and FB showed identical performance. The same was true for the two MSPRT algorithms. For low error rates, the MSPRT algorithms clearly outperformed the integration-to-threshold mechanisms based on linear combinations. However, for error rates of 20% and more the performance was virtually indistinguishable. This indicates that an implementation based on linear combinations (using either feedforward or feedback inhibition) might no longer have a serious optimality disadvantage compared to MSPRT when looking at a biologically more relevant accuracy regime. Figure 12B shows how the optimality of the feedforward inhibition mechanism changes with the integration time constant. As can be seen, the optimality quickly declines with increasing leakiness of the integrators. The feedback inhibition mechanism’s optimality, on the other hand, is largely insensitive to changes in the leakiness of the integrators (Figure 12C).

FIGURE 12

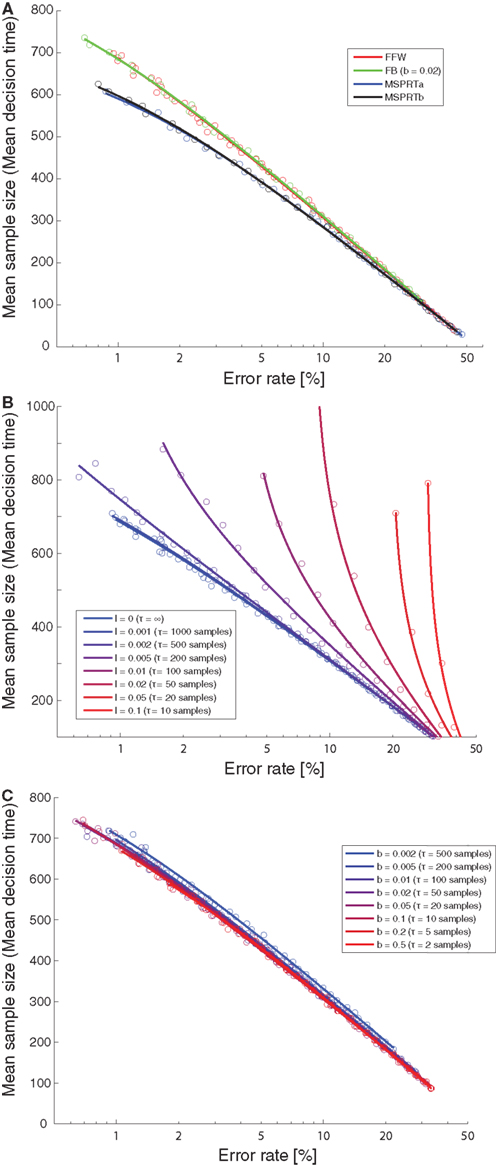
Figure 12. Optimality of decision mechanisms. (A) Mean sample size (decision time) as a function of error rate for different decision mechanisms. A feedforward inhibition mechanism (“FFW”, red) and a feedback inhibition mechanism (“FB”, green) are compared with MSPRTa (blue) and MSPRTb (black). The circles are the simulation results, the lines are all fits of the form mean sample size = α + log(β + γ error rate) (with α, β, and γ free parameters), which provided good empirical fits for all simulations. (B) Effect of leakiness of the integrators on optimality of the feedforward inhibition mechanism. The leakiness ranges from 0 (perfect integration; blue) to very leaky (integration time constant of 10 samples; red). As can be seen, the optimality quickly declines with increasing leakiness. See (A) for an explanation of the circles and the lines. (C) Effect of leakiness of the integrators on optimality of the feedback inhibition mechanism. The leakiness ranges from slightly leaky (integration time constant of 500 samples; blue) to very leaky (integration time constant of two samples; red). As can be seen, over a wide range of time constants, the optimality is insensitive to the leakiness of the integrators. See (A) for an explanation of the circles and the lines.

Discussion

In this manuscript we have examined a number of different integration-to-threshold mechanisms that could potentially underlie perceptual decisions between multiple alternatives. These mechanisms included integrators with and without leakage, competition mechanisms based on either feedforward or feedback inhibition, and both linear and non-linear mechanisms for combining signals across alternatives. Overall, we have seen that these mechanisms can produce virtually indistinguishable decision behavior, which can make it difficult to impossible to distinguish between different alternative implementations based on behavioral data alone, at least with the dataset from our perceptual decision task. On the other hand, we have seen that these mechanisms make quite different predictions for the internal dynamics during the decision process. Thus, it is likely that high-resolution neural recordings will be helpful in figuring out which implementation is actually being used by the brain. Furthermore, we have discussed what kind of statistical tests are being implemented or approximated by these mechanisms and we have seen that the optimality advantage of the MSPRT tends to disappear once error rates on the order of 20% are being reached. In the following, we will be discussing the observations that have been made in this study and how they relate to previous work in more detail.

Similarity of the Decision Behavior Predicted by Different Integration-to-Threshold Mechanisms

For perceptual decisions between two alternatives it has been shown previously that a balanced LCA model can mimic the choice behavior of a drift-diffusion model, which is equivalent to a feedforward inhibition model (Bogacz et al., 2006). Similarly, McMillen and Holmes (2006) have pointed out that, in the case of decisions between multiple alternatives, the LCA model approximates a max-vs-average test, which is, as demonstrated in this manuscript, the statistical test that is being implemented/approximated by the feedforward inhibition model. It is therefore perhaps not too surprising that feedforward and feedback inhibition models can also mimic each other’s decision behavior in multi-alternative perceptual decision making and that both of these mechanisms can explain our behavioral dataset (Niwa and Ditterich, 2008).

For choices between two alternatives I had shown previously that feedforward inhibition mechanisms with a wide range of integration time constants are able to account for the choice behavior observed in a random-dot motion discrimination task (Ditterich, 2006). Similarly, we have seen here that the same is also true for decisions between more than two alternatives. What is becoming clear from both of these studies and what makes intuitive sense is that, although a wide range of integration time constants can produce very similar behavior, the fidelity or signal-to-noise ratio (SNR) of the sensory evidence signal has to change with the leakiness. A very leaky (feedforward) integration mechanism requires better quality (less noisy) sensory evidence signals for achieving the same performance (accuracy) than perfect or only slightly leaky integrators, but can do so in a shorter period of time (shorter mean decision times). Therefore, if the SNR is known, the integration time constant can, in principle, be determined from the decision behavior. I have used this type of argument in Ditterich (2006) to make the claim that, for the 2AFC case, the SNR required by an integration mechanism with a long integration time constant was closer to the expected SNR of a pool of extrastriate visual neurons representing the motion information than the SNR required by a very leaky integration mechanism. We currently have recordings of the sensory evidence signal from monkeys performing the same task as our human subjects under way and we expect these recordings to be helpful in addressing the integration time constant question for the multi-alternative case.

What is perhaps a bit more surprising is that the implementations of MSPRT that we have looked at in this study, which actually perform different statistical tests, also produced very similar decision behavior. Whereas, as already mentioned above, the feedforward inhibition mechanism and LCA approximate a max-vs-average test, MSPRT comes in two flavors and either performs a max-vs-next test (MSPRTb) or evaluates the posterior probability of each hypothesis (MSPRTa). Although our experimental task was designed such that we had control over how much sensory evidence was provided for each of the alternatives and although the experimental protocol included trials with different amounts of sensory evidence for the two not-maximally supported hypotheses, the dataset seems consistent with both max-vs-average-style as well as MSPRT-style mechanisms.

Overall, the observation that different multi-alternative decision mechanisms are difficult to differentiate on the basis of behavioral data alone seems consistent with a recent study by Leite and Ratcliff (2010), which also revealed a relatively high degree of mimicking when modeling data from a multi-alternative letter discrimination task. This does not necessarily mean that these mechanisms can mimic each other for any given parameter set. It might still be possible to design a clever experiment that drives these mechanisms into an operating range where the mimicking breaks down.

Do any of the Discussed Decision Mechanisms Provide a Better Account of our Behavioral Dataset than others?

We have used the strategy to fit the models on the basis of the mean response time (RT) data and to compare the models’ predictions for choice behavior and RT distributions with the actual data. Since all model predictions had to be simulated and since the required computing time had to be limited, the results are necessarily noisy. The reported model parameter sets are the ones that provided the smallest error during the optimization procedure, but due to the simulation-induced noise they probably deviate somewhat from the true optimum. It is therefore difficult to use smaller deviations in the remaining error after the fit to argue in favor of or against particular models. This becomes obvious when looking at the slightly leaky feedforward inhibition model, which achieved the second smallest error during the fitting procedure, but ended up with the largest error after the final higher-resolution simulation (see Table 1). The model with the lowest remaining error both during and after the fit was the LCA model with fixed variance. A visual inspection of the fits does not provide any major qualitative differences. All of the models tended to show a bigger difference in mean RT between stimuli with equal distracting coherences (red and green in the figures) and stimuli with unequal distracting coherences (magenta and cyan in the figures) than the dataset. Why do the models predict faster responses for unequal distracting coherences than for equal coherences (with the same mean)? The closer race between the two leading integrators in the unequal coherence case tends to cut off some slower correct responses that are still possible in the not so close race in the equal coherence case. This conditionalization effect, the integrator associated with the strongest motion component can only win the race if the integrator associated with the intermediate motion component has not crossed threshold yet, leads to an overall speedup of the responses. A variance of the sensory signals that scales with the mean tends to increase the size of this effect. This is potentially why the only discussed model with a fixed variance provided a slightly better fit to the mean RT data.

To address how well a model predicts the choice behavior I have decided to assess the proportion of predicted choice data points that are located within the 95% confidence intervals of the actual data. This assessment shows a slightly clearer ranking of the models than the quality of the mean RT fit. The feedforward inhibition models provided the best accuracy predictions (approx. 85%), followed by the feedback inhibition models (approx. 70%), and the MSPRT models (approx. 60%; see Table 1). The LCA model with scaling variance and the MSPRT models tended to predict somewhat better choice performance than was actually observed.

For quantifying the similarity of probability distributions a large number of potential measures have been proposed (Cha, 2007). I have picked two relatively simple measures that, as Vegelius et al. (1986) have pointed out, have a number of desirable properties: the “proportional similarity” (Vegelius et al., 1986) or “intersection” (Cha, 2007), which is simply the shared area of two compared histograms and therefore ranges from 0 (no overlap) to 1 (identical distributions), and the “Hellinger coefficient” (Vegelius et al., 1986) or “fidelity” (Cha, 2007), which uses the geometric mean of two corresponding histogram bins rather than the minimum, but also ranges from 0 (for no overlap) to 1 (identical distributions). While there are minor differences in the results provided by these two measures, both agree in ranking the slightly leaky feedforward inhibition model as providing the best account of the RT distribution shape (roughly 85% overlap) and the LCA model with fixed variance as the one providing the worst account (roughly 75% overlap). However, the differences are certainly not major. Thus, to summarize the results of comparing the behavioral data with the predictions of different decision mechanisms, I would be hesitant to reject any of the considered models on the basis of the behavioral data alone.

Neurophysiological Predictions Based on the Internal Dynamics of the Decision Models

Since it is apparently extremely difficult to differentiate between alternative decision mechanisms on the basis of behavioral data alone, the question arises whether other types of measurements could be more informative. To address this question, we have analyzed the internal dynamics of the competing mechanisms. We have looked at how the activity of individual integrators is expected to evolve over time, how the summed activity of all integrators is expected to evolve over time, and how the pair of activities of two of the integrators is expected to evolve over time (state space analysis). The results, summarized in Table 2, indicated that by taking all of these measures into account it should be much easier to tell the difference between various decision mechanisms. Such an analysis requires recordings of the activity of individual integrators with high temporal resolution and therefore currently can only be obtained using invasive recording techniques. Previous non-human primate work suggests that such data can likely be obtained from behaving animals (Roitman and Shadlen, 2002; Churchland et al., 2008) and we are currently in the process of recording from monkeys that are performing the same task as our human subjects (Bollimunta and Ditterich, 2009). In a previous analysis of neural data recorded from monkeys performing perceptual decisions between two alternatives I had considered different variants of feedforward inhibition mechanisms, but no feedback inhibition mechanisms (Ditterich, 2006). The observation that neural data can be helpful in distinguishing models that cannot be distinguished on the basis of behavioral data has recently also been made by Purcell et al. (2010) when analyzing monkeys’ visual search behavior and associated neural activity in the frontal eye fields.

When looking at the predicted model dynamics, it is not always easy to come up with intuitive explanations for the observed differences in the trajectories. This is because the trajectories are not only determined by the average activity of the inputs to the integrators, but also by the presence of absorbing boundaries, the clipping of negative integrator states, and the presence of noise. The tendency of a very leaky integrator to approach different steady state levels (shown in Figures 10A,B) results from an equilibrium between its intrinsic leakiness and the amount of input it receives. Figures 10C,D show a difference in the summed activity of all integrators between a feedback inhibition model with scaling variance and one with fixed variance. Where does this difference come from? An inspection of the trajectories of the individual integrators (not shown) indicates that the leading integrator shows a steeper rise in the fixed variance case than in the scaling variance case and that the losing integrators show a steeper fall in the scaling variance case than in the fixed variance case. This is because the noise associated with the strong input is higher in the scaling variance case than in the fixed variance case. At the same time the noise associated with the weaker inputs is lower in the scaling variance case than in the fixed variance case. This is because the fixed variance needs to resemble a variance that is associated with some intermediate coherence in the scaling variance case to match the overall SNR. To produce the same behavior the same fraction of trajectories needs to be absorbed by the boundary of the winning integrator in some specified time interval. Since the trajectories are much more variable in the high noise case, the average trajectory needs to be shallower to make this happen. The integration of noise in combination with the clipping of negative integrator states keeps the integrator at more positive values for higher noise, leading to a shallower fall of the trajectories of the losing integrators. The phenomenon shown in Figure 10E results from a combination of a very gradual decrease of the activity of the integrator associated with the intermediate motion strength and an accelerating increase of the activity of the winning integrator. The decrease in the summed activity prior to threshold crossing shown in Figure 10F results from accelerating decreases of the activities of both losing integrators as the winning integrator approaches the threshold.

Neurophysiological Predictions Based on the Correlation Structure of Internal Signals

The required information for analyzing the internal dynamics can be obtained from recording the firing rate of individual neurons. However, multi-electrode recording techniques are increasing in popularity and the question arises whether simultaneous recordings of multiple neural signals could potentially provide further information. The decision mechanisms that have been discussed in this study do not only differ in terms of the predicted dynamics of how integrator states should evolve over time, but also in terms of the correlation structure of the signals that are being integrated. This raises the question whether this correlation structure could potentially be picked up in simultaneous neural recordings. The general principle would be to simultaneously record from two neurons that carry information about the current states of two different integrators. If these two integrators receive inputs that are positively correlated there is hope that this correlation might also show up in the structure of the exact spike timing as an increased likelihood of simultaneous spiking (de la Rocha et al., 2007; Ostojic et al., 2009). On the other hand, a negative correlation between input signals might show up as a reduced likelihood of (nearly) simultaneous spiking. However, there are also a number of (largely unknown) caveats. What we have been treating as single stochastic signals in our models (for example, the state of an integrator or the sensory evidence signal for a particular direction of motion) are in reality distributed signals that are carried by larger populations of neurons. However, we can only record the signals carried by individual neurons and not the total population activity. Furthermore, what shows up as single wires in our signal flow diagrams are in reality connections between two populations of neurons, which can have quite different connectivity patterns, ranging from very sparse to very dense. How likely it is that any given pair of neurons taken from two different populations will show a correlation pattern that should exist at the population level is therefore unknown. However, assuming that a correlation can indeed be observed, the sign of the correlation should provide further evidence for or against certain decision mechanisms. We have seen that a negative correlation would be consistent with a feedforward inhibition mechanism like the one shown in Figure 1A (shared input signals with different signs), whereas a positive correlation would be indicative of a shared feedforward or feedback signal of the same sign, like an LCA model or a feedback MSPRT model would predict. Such simultaneous recordings are currently also under way in our laboratory.

Major Sources of Noise in the Decision Process

Different opinions have been voiced about the major source of noise that is driving the perceptual decisions. One extreme view would be that the noise mainly originates at the sensory end of the process: random fluctuations of the neural representation of the sensory evidence are largely driving the system. I have made an argument along these lines in Ditterich (2006) for the 2AFC version of the random-dot discrimination task. The observation that the total SNR of the signals feeding into the integrators, as estimated from a feedforward inhibition model, were on the order of the expected SNR of pools of MT neurons (informed by neurophysiological measurements) suggested that there was not much room for additional noise feeding into the integrators. The other extreme view would be that the noise that is being contributed by the sensory representation is small compared to the noise that is being contributed by other (background) inputs to the integrators. The question whether the variances of the signals feeding into the integrators need to change systematically with the presented stimulus addresses this issue to some degree, since inputs to the integrators that do not carry information about the sensory stimulus should not change their variance when the stimulus changes. We had pointed out previously that a feedforward inhibition mechanism can only explain the observed independent changes in accuracy and mean RTs if the variances of the signals feeding into the integrators changed systematically with the stimulus (Niwa and Ditterich, 2008). Thus, if the behavior should turn out to be mediated by a feedforward inhibition mechanism, there would be strong evidence for sensory noise being the major noise source in the process. However, in this study I have demonstrated that a feedback inhibition mechanism can explain the observed behavior regardless of whether the variances scale with the stimulus or not. Thus, if it should turn out that the decision is being mediated by a feedback inhibition mechanism, the question regarding the major noise source would remain open. Note, however, that I have also shown that a feedback inhibition mechanism with scaling variance and a feedback inhibition mechanism with fixed variance have different internal dynamics. Neurophysiological data might therefore help with answering this question.

Relationship Between Discussed Decision Models, Decision Theory, and Statistical Tests

For perceptual decisions between two alternatives it has previously been demonstrated that a feedforward inhibition mechanism is a good approximation of the optimal decision algorithm, the SPRT (Gold and Shadlen, 2001). And since a balanced LCA model can mimic the drift-diffusion model, which is equivalent to a feedforward inhibition model, it also provides a good approximation of SPRT (Bogacz et al., 2006). For decisions between more than two alternatives the optimal algorithm for any desired accuracy is still not known, but the MSPRT has been shown to be optimal for negligible error rates (Dragalin et al., 1999). LCA, when applied to multiple alternatives, approximates a statistical test, a max-vs-average test, that is, different from MSPRT (McMillen and Holmes, 2006). As demonstrated here, a max-vs-average test is also implemented/approximated by the feedforward inhibition mechanism. We have seen that for Poisson processes and for normal processes with equal variance the integral over the difference between samples taken from two sensory streams can be directly proportional to the log-likelihood ratio between two hypotheses. Deviations from this scheme, for example, normal processes with different variances, will lead to some deviation from this direct proportionality. However, since the output of a pool of sensory neurons is likely to be relatively well-described by a Poisson process, we expect a neural version of our feedforward inhibition mechanism to provide a pretty good approximation of the max-vs-average test. It is therefore not too surprising that the feedforward inhibition mechanism and balanced LCA can also mimic each other in the multi-alternative case.

To summarize, I have demonstrated that a variety of integration-to-threshold mechanisms for multi-alternative decision making can make very similar predictions for decision behavior. However, I have also shown that there is hope to be able to discriminate between competing mechanisms on the basis of combined behavioral and neurophysiological experiments because of different predictions of these mechanisms for the internal dynamics and potentially for the correlation structure of simultaneously recorded neural signals. Furthermore, we have seen that while the discussed decision mechanisms implement or approximate different types of stochastic tests, the optimality advantage of the MSPRT for small error rates tends to disappear as error rates on the order of 20% are approached. Thus, a neural implementation of a max-vs-average test rather than MSPRT might not be a major disadvantage when operating in the regime of non-negligible error rates.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This material is based on research sponsored by the Air Force Research Laboratory, under agreement number FA9550-07-1-0205. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright notation thereon. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the Air Force Research Laboratory or the U.S. Government.

References

Albantakis, L., and Deco, G. (2009). The encoding of alternatives in multiple-choice decision making. Proc. Natl. Acad. Sci. U.S.A. 106, 10308–10313.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Beck, J. M., Ma, W. J., Kiani, R., Hanks, T., Churchland, A. K., Roitman, J., Shadlen, M. N., Latham, P. E., and Pouget, A. (2008). Probabilistic population codes for Bayesian decision making. Neuron 60, 1142–1152.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bogacz, R. (2009). “Optimal decision-making theories,” in Handbook of Reward and Decision Making, ed. J.-C. T. Dreher (Oxford: Academic Press), 375–397.

Bogacz, R., Brown, E., Moehlis, J., Holmes, P., and Cohen, J. D. (2006). The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol. Rev. 113, 700–765.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bogacz, R., and Gurney, K. (2007). The basal ganglia and cortex implement optimal decision making between alternative actions. Neural Comput. 19, 442–477.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bogacz, R., Usher, M., Zhang, J., and McClelland, J. L. (2007). Extending a biologically inspired model of choice: multi-alternatives, nonlinearity and value-based multidimensional choice. Philos. Trans. R. Soc. Lond., B., Biol. Sci. 362, 1655–1670.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bollimunta, A., and Ditterich, J. (2009). Neural mechanisms underlying perceptual decisions between multiple alternatives. In Program No 6526 2009 Neuroscience Meeting Planner Chicago, IL: Society for Neuroscience.

Cha, S.-H. (2007). Comprehensive survey on distance/similarity measures between probability density functions. Int. J. Math. Model. Meth. Appl. Sci. 1, 300–307.

Churchland, A. K., Kiani, R., and Shadlen, M. N. (2008). Decision-making with multiple alternatives. Nat. Neurosci. 11, 693–702.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

de la Rocha, J., Doiron, B., Shea-Brown, E., Josic, K., and Reyes, A. (2007). Correlation between neural spike trains increases with firing rate. Nature 448, 802–806.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ditterich, J. (2006). Stochastic models of decisions about motion direction: behavior and physiology. Neural Netw. 19, 981–1012.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dragalin, V. P., Tartakovsky, A. G., and Veeravalli, V. V. (1999). Multihypothesis sequential probability ratio tests – Part I: Asymptotic optimality. IEEE Trans. Inf. Theory 45, 2448–2461.

CrossRef Full Text

Furman, M., and Wang, X. J. (2008). Similarity effect and optimal control of multiple-choice decision making. Neuron 60, 1153–1168.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gold, J. I., and Shadlen, M. N. (2001). Neural computations that underlie decisions about sensory stimuli. Trends Cogn. Sci. 5, 10–16.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goodman, L. A. (1965). On simultaneous confidence intervals for multinomial proportions. Technometrics 7, 247–254.

CrossRef Full Text

Leite, F. P., and Ratcliff, R. (2010). Modeling reaction time and accuracy of multiple-alternative decisions. Atten. Percept. Psychophys. 72, 246–273.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McMillen, T., and Holmes, P. (2006). The dynamics of choice among multiple alternatives. J. Math. Psychol. 50, 30–57.

CrossRef Full Text

Niwa, M., and Ditterich, J. (2008). Perceptual decisions between multiple directions of visual motion. J Neurosci 28, 4435–4445.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ostojic, S., Brunel, N., and Hakim, V. (2009). How connectivity, background activity, and synaptic properties shape the cross-correlation between spike trains. J. Neurosci. 29, 10234–10253.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Purcell, B. A., Heitz, R. P., Cohen, J. Y., Schall, J. D., Logan, G. D., and Palmeri, T. J. (2010). Neurally constrained modeling of perceptual decision making. Psychol. Rev. doi: 10.1037/a0020311

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Roitman, J. D., and Shadlen, M. N. (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci. 22, 9475–9489.

Pubmed Abstract | Pubmed Full Text

Usher, M., and McClelland, J. L. (2001). The time course of perceptual choice: the leaky, competing accumulator model. Psychol. Rev. 108, 550–592.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vegelius, J., Janson, S., and Johansson, F. (1986). Measures of similarity between distributions. Qual. Quant. 20, 437–441.

CrossRef Full Text

Wald, A. (1945). Sequential tests of statistical hypotheses. Ann. Math. Stat. 16, 117–186.

CrossRef Full Text

Zhang, J., and Bogacz, R. (2010). Optimal decision making on the basis of evidence represented in spike trains. Neural Comput. 22, 1113–1148.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text