A Self-Calibrating, Camera-Based Eye Tracker for the Recording of Rodent Eye Movements

Much of neurophysiology and vision science relies on careful measurement of a human or animal subject’s gaze direction. Video-based eye trackers have emerged as an especially popular option for gaze tracking, because they are easy to use and are completely non-invasive. However, video eye trackers typically require a calibration procedure in which the subject must look at a series of points at known gaze angles. While it is possible to rely on innate orienting behaviors for calibration in some non-human species, other species, such as rodents, do not reliably saccade to visual targets, making this form of calibration impossible. To overcome this problem, we developed a fully automated infrared video eye-tracking system that is able to quickly and accurately calibrate itself without requiring co-operation from the subject. This technique relies on the optical geometry of the cornea and uses computer-controlled motorized stages to rapidly estimate the geometry of the eye relative to the camera. The accuracy and precision of our system was carefully measured using an artificial eye, and its capability to monitor the gaze of rodents was verified by tracking spontaneous saccades and evoked oculomotor reflexes in head-fixed rats (in both cases, we obtained measurements that are consistent with those found in the literature). Overall, given its fully automated nature and its intrinsic robustness against operator errors, we believe that our eye-tracking system enhances the utility of existing approaches to gaze-tracking in rodents and represents a valid tool for rodent vision studies.

Introduction

A number of eye tracking technologies are currently in use today for neurophysiology research, including video-oculography (Mackworth and Mackworth, 1959), scleral search coils (Robinson, 1963; Remmel, 1984), and electro-oculography (Shackel, 1967). In research with non-human primates, eye-tracking approaches are dominated by implanted search coils where a high-level of accuracy is required, and video-based tracking, where convenience and non-invasiveness are desired.

Rodents are increasingly recognized as a promising model system for the study of visual phenomena (Xu et al., 2007; Griffiths et al., 2008; Niell and Stryker, 2008; Jacobs et al., 2009; Lopez-Aranda et al., 2009; Zoccolan et al., 2009), because of their excellent experimental accessibility. Although scleral search coils can be used in rodents (Chelazzi et al., 1989, 1990; Strata et al., 1990; Stahl et al., 2000), because of the small size of their eyes, implanting a subconjuctival coil (Stahl et al., 2000) or gluing a coil to the corneal surface (Chelazzi et al., 1989) can interfere with blinking and add additional mass and tethering forces to the eye, potentially disrupting normal eye movement (Stahl et al., 2000). In addition, coil implants require a delicate surgery and can easily lead to damage or irritation to the eye when permanently implanted.

In contrast, video eye trackers are completely non-invasive. However, they typically rely on a calibration procedure that requires the subject to fixate on a series of known locations (e.g., points on a video display). Rodents, while able to perform a variety of eye movements, are not known to reliably fixate visual targets, making traditional video eye tracking unsuitable for use on members of this order.

To circumvent this problem, Stahl and colleagues (Stahl et al., 2000; Stahl, 2004) have devised an alternative calibration approach to video eye-tracking. This method involves rotating a camera around a head-fixed animal in order to estimate the geometric properties of its eye, based on the assumption that the cornea is a spherical reflector. Stahl has shown that this video-based tracking of mice oculomotor reflexes is as reliable as scleral search coil-based tracking (Stahl et al., 2000). Stahl’s method has the advantage of not requiring the animal’s co-operation during the calibration phase and is likely the most commonly used approach to video eye-tracking in rodents. However, the requirement to manually move the camera around the animal makes the method time consuming and difficult to master, since the operator must make a large number of precise movements to line up eye-features on a video monitor, and must take a number of measurements while the animal’s eye can potentially move. Moreover, with this method, some geometric properties of the eye that are critical for the calibration procedure are not directly measured during calibration and are instead derived from data available in the literature. Finally, since the method relies on “live” interaction between an operator and an awake subject, it is difficult to quantify the validity of the calibration and to ensure that an error has not occurred (i.e., by repeating the calibration several times and estimating its precision).

Here, we modify and extend the method of Stahl and colleagues (Stahl et al., 2000; Stahl, 2004) using computer-controlled motorized stages and in-the-loop control to rapidly and accurately move a camera and two infrared illuminators around a stationary rodent subject to estimate eye geometry in a fully automated way. By using computer-in-the-loop measurements we are able to greatly speed up the calibration process, while at the same time replacing certain assumptions in the original method with direct measurements and avoiding some unnecessary (and time consuming) calibration steps. In this report we demonstrate the method’s utility for tracking rodent eye movements; however, this method would prove useful to track eye movements in any other species that do not spontaneously fixate visual targets.

Materials and Methods

Our eye-tracking system relies on a calibration procedure that measures the geometric arrangement of the eye and pupil relative to the camera, so that gaze angle can be estimated directly from the position of the pupil image on the camera’s image sensor. This system relies on the fact that, if a subject’s eye cannot be moved to a known angle, it is geometrically equivalent to rotate the camera about the eye’s center while the eye is stationary. Since this calibration procedure is based on the approach described by Stahl and colleagues (Stahl et al., 2000; Stahl, 2004), we have adopted ( wherever possible, in our figures and equations) the same notation used in these previous studies, so to make more understandable where one approach differs from the other.

As in Stahl et al. (2000), our approach relies on two key assumptions, which are both well supported by the available literature about the rodent eye geometry (Hughes, 1979; Remtulla and Hallett, 1985). First, we assume that the corneal curvature is approximately spherical, which implies that the reflected image of a distant point light source on the cornea will appear halfway along the radius of the corneal curvature that is parallel to the optic axis of the camera (see below for details). Second, we assume that the pupil rotates approximately about the center of the corneal curvature. As will be described below, the first assumption allows estimation of the center of the corneal curvature relative to the camera in three dimensions. The second assumption allows estimation of the radius of the pupil’s rotation relative to the eye’s center by moving our camera around the eye.

System Components

Figure 1 shows a schematic diagram of our eye-tracking system. A gigabit ethernet (GigE) camera with good near-infrared (NIR) quantum efficiency (Prosilica GC660; Sony ExView HAD CCD sensor) was selected to image the eye. An extreme telephoto lens (Zoom 6000, Navitar) with motorized zoom and focus was affixed to the camera. The camera and lens were held using a bracket affixed to the assembly at its approximate center of mass. A NIR long-pass filter with 800 nm cutoff (FEL0800, Thorlabs, Inc.) was attached to the lens to block visible illumination. A pair of 2.4 W 880 nm LED illuminators (0208, Mightex Systems) were attached to the camera assembly such that they were aligned with the camera’s horizontal and vertical axes, respectively. These illuminators were controlled using a serial 4-channel LED controller (SLC-SA04-S, Mightex Systems).

The camera/lens/illuminator assembly was attached to a series of coupled motion stages, including a rotation stage (SR50CC, Newport), a vertical linear stage with 100 mm travel range (UTS100CC, Newport), and a horizontal stage with 150 mm travel range (UTS150CC, Newport). A counterbalance weight was affixed to the horizontal stage to offset the weight of the cantilevered camera assembly and ensure that the stage’s offset weight specifications were met. Motion control was achieved using a Newport ESP300 Universal Motion Controller (Newport). Figure 1B shows the three degrees of freedom enabled by this set of stages: (1) vertical translation; (2) horizontal translation; and (3) rotation of the camera assembly about a vertical axis passing through the lens at about 115 mm from the camera’s sensor. In the course of calibration, these stages allow the camera to be translated up and down, panned left and right, and (more importantly for the calibration purpose) to make pseudo-rotations about a point at an arbitrary distance in front of the camera. Such pseudo-rotations are achieved by combining a right (left) translation with a left (right) rotation of the camera assembly about its axis of rotation, as shown in Figure 1C. After each pseudo-rotation, the distance between the camera’s sensor and the center of the pseudo-rotation changes. As a consequence, the size of the imaged eye changes. In our calibration, we compensate for such a change, by scaling the position/size of the tracked eye features (e.g., the pupil position on the image plane) by a factor that is equal to the ratio of the distances between the camera assembly and the center of the pseudo-rotation, before and after the pseudo-rotation is performed (i.e., the ratio between d and d′ in the example shown in Figure 1C).

FIGURE 1

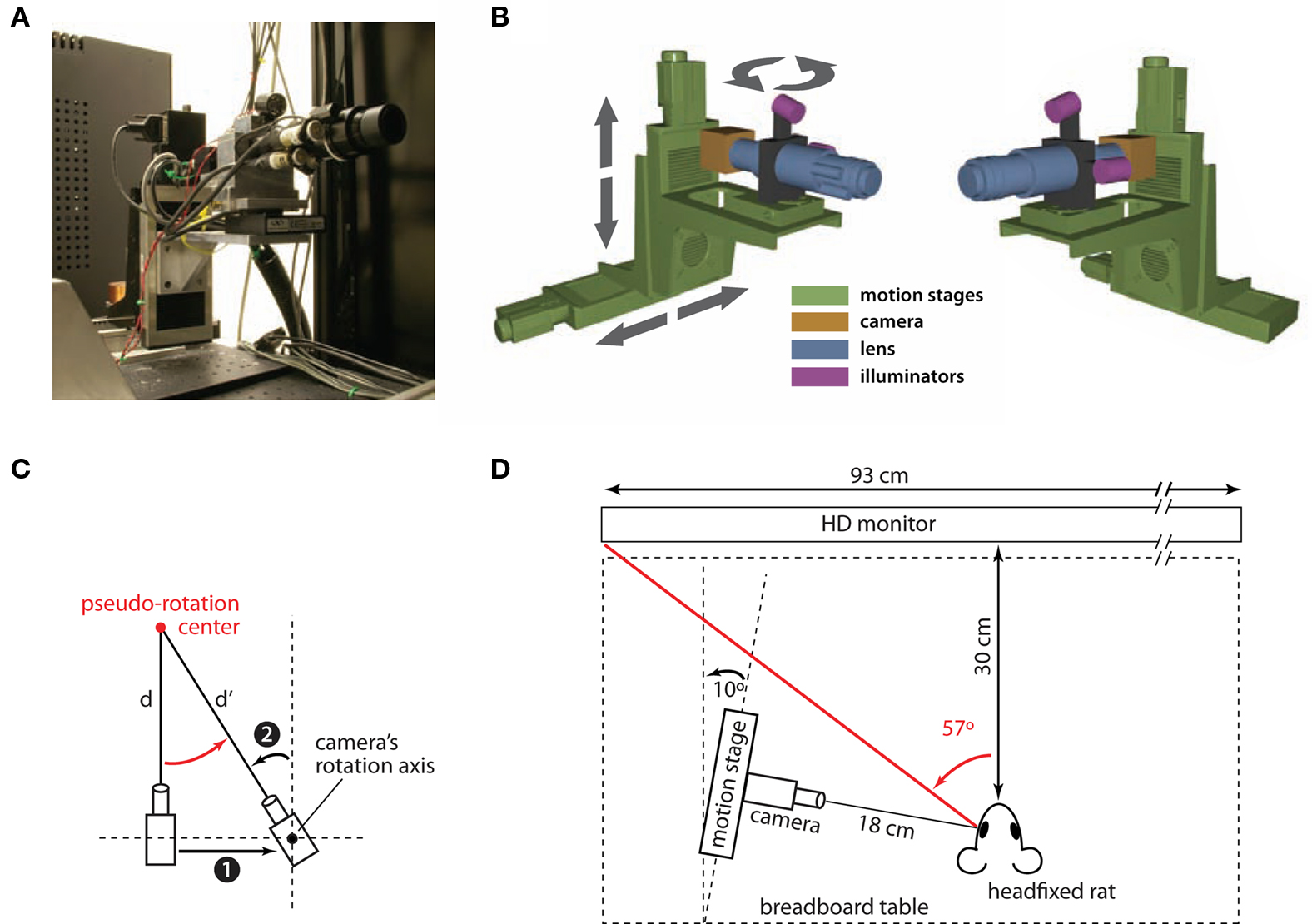
Figure 1. Schematic diagram of the eye-tracking system. (A) A photograph of the eye tracking system, showing the camera assembly (camera, lens, and infrared LED illuminators) mounted on the motorized stages used to move the camera around the eye of the subject during the calibration procedure (see Materials and Methods). (B) Two 3-dimensional renderings of the eye-tracking system (viewed from two different angles). The colors emphasize the four main components of the system: motorized stages (green), camera (yellow), lens (blue), and illuminators (magenta). The arrows show the motion direction of the linear and rotary motorized stages. (C) The diagram (showing a top view of the camera assembly) illustrates how a horizontal translation of the camera to the right (1) can be combined with a left rotation of the camera about its rotation axis (2) to achieve a pseudo-rotation (red arrow) about a point (red circle) at an arbitrary distance d from the camera itself. This drawing also illustrates how, following the pseudo-rotation, the distance between the camera and the center of the pseudo-rotation changes from d to d′. (D) Diagram showing the position of the camera assembly relative to the imaged eye of the head-fixed rat. The distance of the animal from the screen used for stimulus presentation and the amplitude of the rat’s left visual hemifield are also shown.

The eye tracker was mounted onto an optical breadboard table and placed to the left of a head-fixed rat, at approximately 18 cm from his left eye (see Figure 1D). The horizontal linear stage (bottom stage in Figure 1B) was rotated of 10° from the sagittal plane of the animal (see Figure 1D). This exact arrangement is not critical to the correct operation of the eye tracker. However, this setup places the animal’s pupil at approximately the center of the image plane to avoid losing the pupil during large saccades. Additionally, the eye tracker only minimally occludes the left visual hemifield of the animal, leaving completely free the frontal (binocular) portion of the visual field. In our setup, 114° of the un-occluded frontal portion of the visual field was occupied by a 42-inch HDTV monitor positioned 30 cm from the animal that was used to present visual stimuli (see Figure 1D).

Pupil and Corneal Reflection Localization

Images from the camera were transmitted to a computer running a custom-written tracking software application. Early experiments with a commercial eye tracking system (EyeLink II, SR research) found its tracking algorithm to be unsatisfactory for our application on a number of dimensions. First, the simple (and proprietary) thresholding algorithm is intended for use with human eyes and was easily confused by the animal’s fur and required unrealistically ideal lighting conditions. Second, the interleaved nature of the commercial eye tracker’s pupil and corneal reflection (CR) tracking (i.e., pupil tracked on even frames, CR on odd frames) led to large errors when the animal made rapid translational eye movements during chewing (e.g., “bruxing,” Byrd, 1997). Finally, the EyeLink software computes and provides to the user a CR-corrected pupil signal, but does not allow the user direct access to the pure CR signal, which is essential to our calibration procedure. To overcome these problems we implemented a custom multi-stage algorithm to simultaneously track the pupil and CR, relying on the circularity of these objects (see Figure 2A). Such an algorithm is based on different state-of-the-art circle detection methods that are among the fastest (Loy and Zelinsky, 2002) and more robust (Li et al., 2005, 2006) in the computer vision and eye-tracking literature.

FIGURE 2

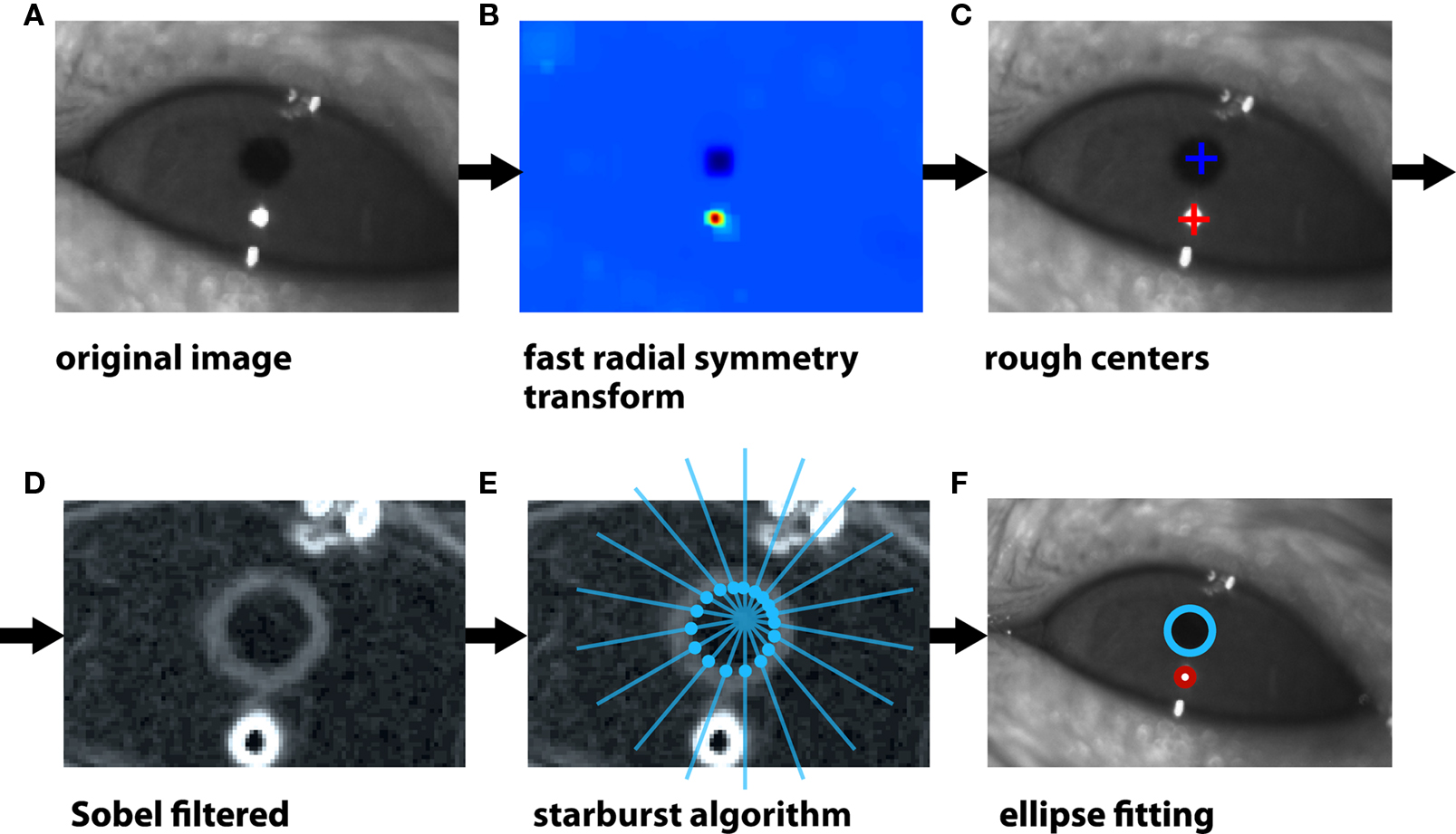
Figure 2. Illustration of the algorithm to track the eye’s pupil and corneal reflection spot. (A) The image of a rat eye under infrared illumination. The dark circular spot is the pupil, while the bright round spot is the reflection of the infrared light source on the surface of the cornea (i.e., the corneal reflection, CR). Other, non-circular reflection spots are visible at the edges of the eyelids. (B) The color map shows the image areas in which the presence of circular features is more likely according to a fast radial symmetry transform. The rough location of both the pupil and CR is correctly extracted. (C) Following the application of the fast radial symmetry transform (see B), the rough centers of the pupil (blue cross) and CR (red spot) are found. (D) A Sobel (edge finding) transform is applied to the image of the eye to find the boundaries of the pupil (gray ring) and CR (white ring). Note that the eye is shown at higher magnification in this panel (as compared to A–C). (E) The previously found rough center of the pupil (see C) is used as a seed point to project a set of “rays” (blue lines) toward the boundary of the pupil itself. The Sobel-filtered image is sampled along each ray and when it crosses a given threshold (proportional to its standard deviation along the ray), an intersection between the ray and the pupil boundary is found (intersections are shown as blue, filled circles). The same procedure is used to find a set of edge points along the CR boundary. (F) An ellipse is fitted to the boundary points of the pupil (blue circle) and CR (red circle) to obtain a precise estimate of their centers.

First, a Fast Radial Symmetry transform (Loy and Zelinsky, 2002) was applied (using a range of candidate sizes bracketing the likely sizes of the pupil and CR) to establish a rough estimate of the centers of the pupil and CR (see Figure 2C) by finding the maximum and minimum values in the transformed image (see Figure 2B). These rough centers were then used as seed points in a modified version of the “starburst” circle finding algorithm (Li et al., 2005, 2006). This algorithm has the advantages of being tolerant to any potentially suboptimal viewing condition of the tracked eye features (e.g., overlapping pupil and CR), and computationally undemanding (fast). Briefly, a Sobel (edge finding) transform (González and Woods, 2008) was applied to the image (see Figure 2D) and a series of rays were projected from each seed point resampling the Sobel-transformed magnitude image along each ray (see Figure 2E). For each ray, the edge of the pupil or CR was found by finding the first point outside of a predefined minimum radius that crossed a threshold based on the standard deviation of Sobel magnitude values (see Figure 2E). These edge points were then used to fit an ellipse (Li et al., 2005; see Figure 2F).

To further accelerate the overall algorithm, we can avoid computing the relatively more expensive fast radial symmetry transform on every frame, using the previous pupil and CR position estimates from the previous frame to seed the “starburst” algorithm for the current frame. In this scenario, the fast radial symmetry transform is performed only on a fraction of frames (e.g., every five frames), or in the event the starburst algorithm fails to find a sufficiently elliptical target. The full algorithm is able to run at a frame rate in excess of 100 Hz using a single core of a 2.8-GHz Xeon processor, with faster rates being possible when multiple cores are utilized. In practice, our current system is limited by the camera and optics used, to a frame rate of approximately 60 Hz, which is the highest frame rate that affords acceptable exposure given the available illumination. If needed, higher frame rates are in principle possible through the use of a faster camera and/or more powerful illumination/optics. Code for our software system is available in a publicly accessible open source repository¹.

Principle of Operation

The goal of our eye-tracking system is to estimate the pupil’s elevation θ and azimuth φ (see Figure 3A) from the position of the pupil image on the camera’s image sensor. This is achieved by measuring the distance Δy of the pupil P from the eye’s equator plane (i.e., the plane that is perpendicular to the image plane and horizontally bisects the eye), and the distance Δx of the pupil’s projection on the eye’s equator plane from the eye’s meridian plane (i.e., the plane that is perpendicular to the image plane and vertically bisects the eye; for details, see Figure 3A). The position of the equator and meridian planes can be reliably measured by alternatively switching on the two infrared light sources that are horizontally and vertically aligned to the camera’s sensor. In fact, when the vertically aligned (side) light source is turned on, its reflection on the corneal surface (CR) marks the position of the equator plane (Figure 3B), and Δy can be measured as the distance between P and CR (Figure 3C). Vice-versa, when the horizontally aligned (top) light source is turned on, its reflection on the corneal surface marks the position of the meridian plane (Figure 3D) and Δx can be measured as the distance between P and CR (Figure 3E).

FIGURE 3

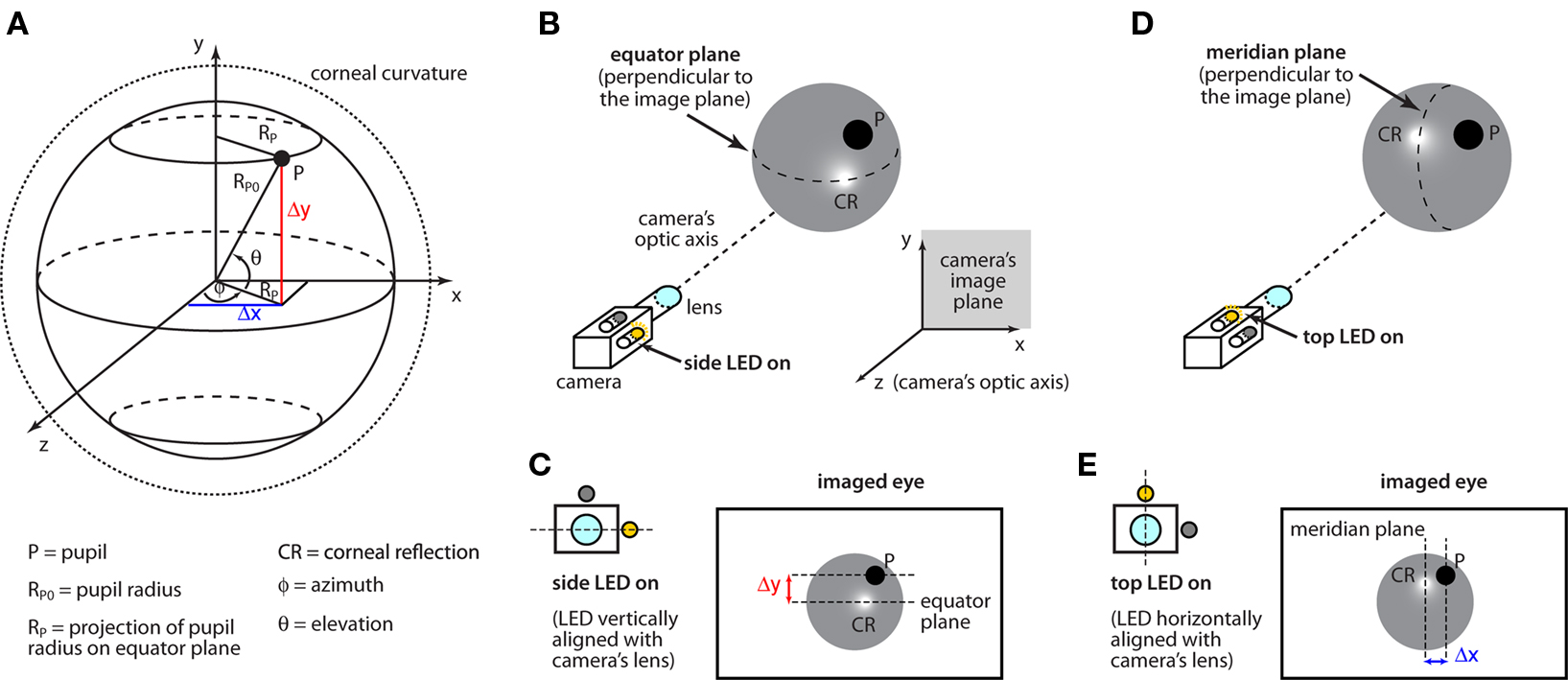
Figure 3. Eye coordinate system and measurements. (A) The pupil (P) moves over the surface of a sphere (solid circle) of radius R_P0. Such a sphere is contained within a larger sphere – the extension of the corneal curvature (dotted line). The two spheres are assumed to have the same center (see text). The pupil position is measured in a polar coordinate system, whose origin is in the center of the corneal curvature. The orientation of the reference system is chosen such that the z axis is parallel to the optic axis of the camera and, therefore, the (x, y) plane constitutes the camera’s image plane (see inset in B). The goal of the eye-tracking system is to estimate the pupil’s elevation (θ) and azimuth (φ). This is achieved by measuring the distance Δy of the pupil from the equator plane (i.e., the plane that is perpendicular to the image plane and horizontally bisects the eye), and the distance Δx of the pupil’s projection on the equator plane from the meridian plane (i.e., the plane that is perpendicular to the image plane and vertically bisects the eye). (B) In our imaging system, two infrared LEDs flank the imaging camera. When the side LED (which is vertically aligned with the camera’s lens) is turned on, its reflection on the corneal surface (CR) marks the position of the equator plane. (C) Δy is measured as the distance between P and CR, when the side LED is turned on. (D) When the top LED (which is horizontally aligned with the camera’s lens) is turned on, its reflection on the corneal surface (CR) marks the position of the meridian plane. (E) Δx is measured as the distance between P and CR, when the top LED is turned on.

Given the eye’s geometry, the measurements of Δy and Δx can be used to calculate the pupil’s elevation and azimuth using the following trigonometric relationships (see Figure 3):

and

provided that R_P0 (the radius of rotation of the pupil relative to the eye’s center) is known. R_P0, in turn, can be obtained through the following calibration procedure.

Calibration Steps

Camera/eye alignment

In this step, the center of the camera’s image sensor/plane is aligned with the center of the imaged eye (Figure 4). As pointed out by Stahl et al. (2000), this alignment is not strictly necessary for the calibration procedure to succeed (a rough alignment would be enough). In practice, however, centering the eye on the image plane is very convenient because it maximizes the range of pupil positions that will fall within the field of view of the camera. Since the cost of performing this alignment is negligible in our motorized computer-controlled system (it takes only a couple of seconds), centering the eye on the image plane is the first step of our calibration procedure.

FIGURE 4

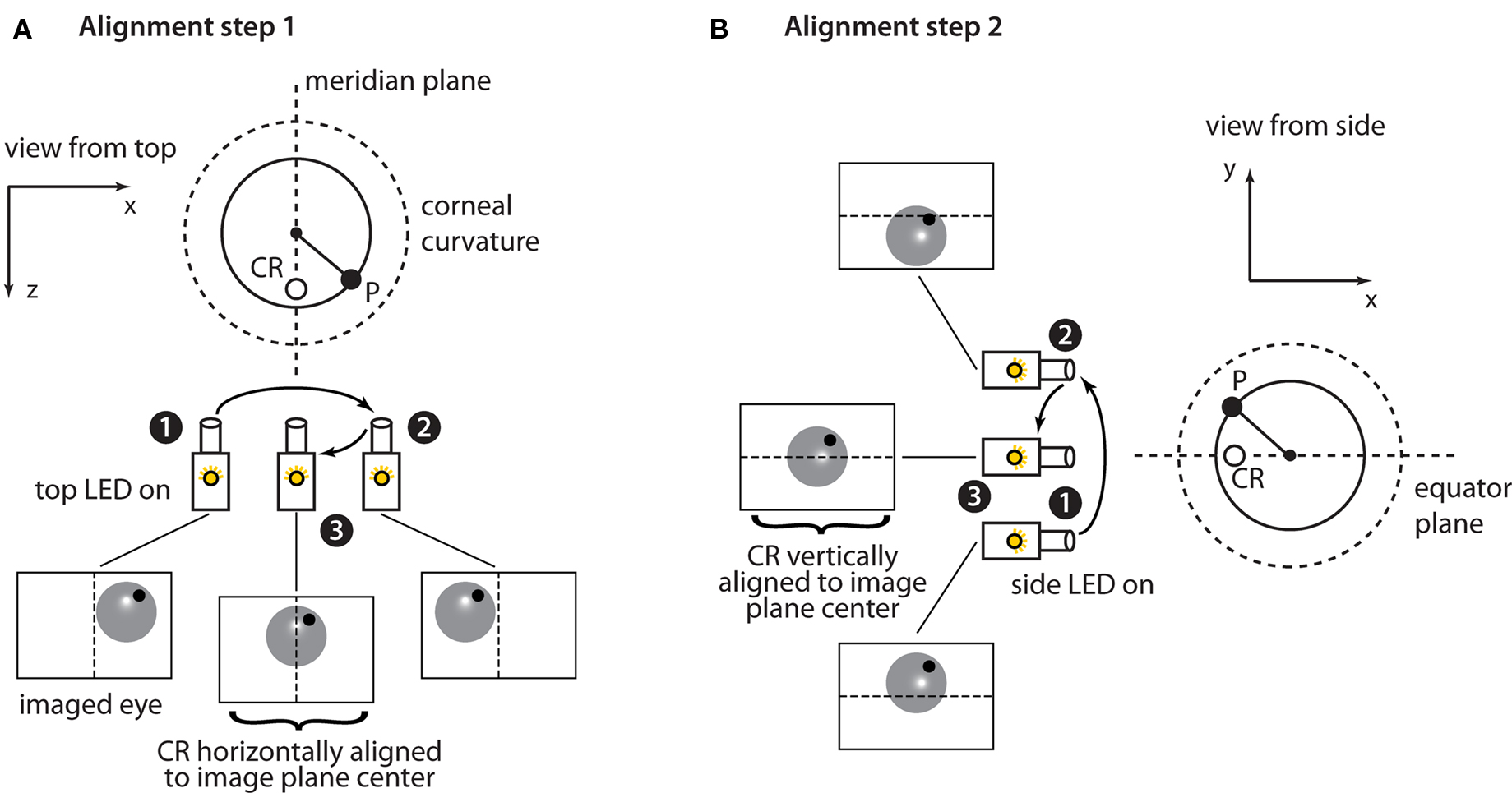
Figure 4. Horizontal and vertical alignment of the eye with the center of the camera’s sensor. (A) When the horizontally aligned (top) infrared LED is turned on a corneal reflection (CR) spot (empty circle) appears halfway along the radius of the corneal curvature (dashed line) that is parallel to the optic axis of the camera. The filled circle shows the pupil position. The large dashed circle shows the corneal curvature/surface. Assuming that the camera’s sensor is initially not aligned with the center of the eye (e.g., in position 1), the location of CR can be used as a landmark of the eye’s meridian plane to achieve such an alignment by moving the camera’s assembly horizontally. The camera is first translated a few mm (from position 1 to position 2) to determine the mm/pixels conversion factor and then makes an additional translation (from position 2 to position 3) that aligns the CR with the center of the horizontal axis of the camera’s sensor. Note that because the cornea behaves as a spherical mirror the CR marks the position of the eye’s meridian plane throughout all horizontal displacements of the camera’s assembly (i.e., the position of the empty circle is the same when the camera is in position 1, 2, and 3). (B) A similar procedure to the one described in (A) is used to vertically align the camera’s sensor to the eye’s equator plane. In this case, the vertically aligned (side) infrared LED is turned on so that the CR marks the position of the eye’s equator plane. A similar process is then repeated along the vertical axis.

First, the camera’s image plane is horizontally aligned to the eye’s meridian plane (Figure 4A). To achieve this, the horizontally aligned (top) illuminator is turned on (Figure 4A). Due to the geometry of the cornea, this produces a reflection spot on the cornea (CR) aligned with the eye’s meridian plane (see Figure 4 legend for details). To center the camera’s image plane on the CR spot, the camera is translated a small amount (from position 1 to position 2 in Figure 4A) and the displacement of the CR in pixels is measured to determine the mm/pixels conversion factor and the direction in which the camera should be moved to obtain the desired alignment. These measurements are then used to translate the camera so that the CR is aligned with the horizontal center of the image plane (final translation from position 2 to position 3 in Figure 4A). A similar procedure is used to vertically align the camera’s image plane to the eye’s equator plane (Figure 4B). To achieve this, the vertically aligned (side) illuminator is turned on and the process is repeated along the vertical axis. At the end of this calibration step the camera’s optical axis points directly at the center of the corneal curvature.

Estimation of the 3D center of the corneal curvature

In this step, we determine the distance from the camera’s center of rotation to the center of the corneal curvature. This distance measurement, in combination with the horizontal and vertical alignment achieved in the previous step, defines the location of the center of the corneal curvature in three dimensions. To measure this quantity, we rely on the fact that the cornea is approximately a spherical reflector and thus the CR spot (empty circles in Figure 5) will always appear halfway along the radius of the corneal curvature that is parallel to the optic axis of the camera (assuming that the camera’s sensor and the light source are horizontally aligned, as in our imaging system). A consequence of this arrangement is that if we rotate the camera about a virtual point in space in front of the camera, the shift in the observed CR spot within the camera image will vary systematically depending on whether the virtual point of rotation is in front of (Figure 5A), behind (Figure 5B), or aligned with (Figure 5C) the center of corneal curvature. If we rotate the camera about a point in front of the eye (Figure 5A), the location of the CR within the camera image will be displaced in the direction of the rotation (i.e., to the left for leftward rotations and right for rightward). Similarly, if we rotate the camera about a point behind the eye (Figure 5B), the CR will be displaced in a direction opposite of the rotation (right for leftward rotations, etc). This apparent displacement occurs because rotations about a point other than the center of the corneal surface shifts the camera’s field of view relative to the stationary eye. Only if the virtual rotation point of the camera is superimposed on the center of the corneal curvature will the CR spot remain stationary in the camera image across any rotation. Thus, to estimate the distance to the center of the corneal curvature, we measured the displacement Δ_CR of the CR spot in response to a series of five +15° rotations about virtual points at a range of candidate distances, and −15° rotations about points at the same candidate distances, and then fit a line to the differences between the +15° displacements and −15° rotations. The zero intercept of this line corresponds to the distance of the virtual point of rotation that results in no displacement of the CR and reveals the center of the corneal curvature (i.e., the condition shown in Figure 5C). At the end of this calibration step, the camera is aligned with the horizontal and vertical centers of the eye, and can be rotated about the center of the corneal curvature.

FIGURE 5

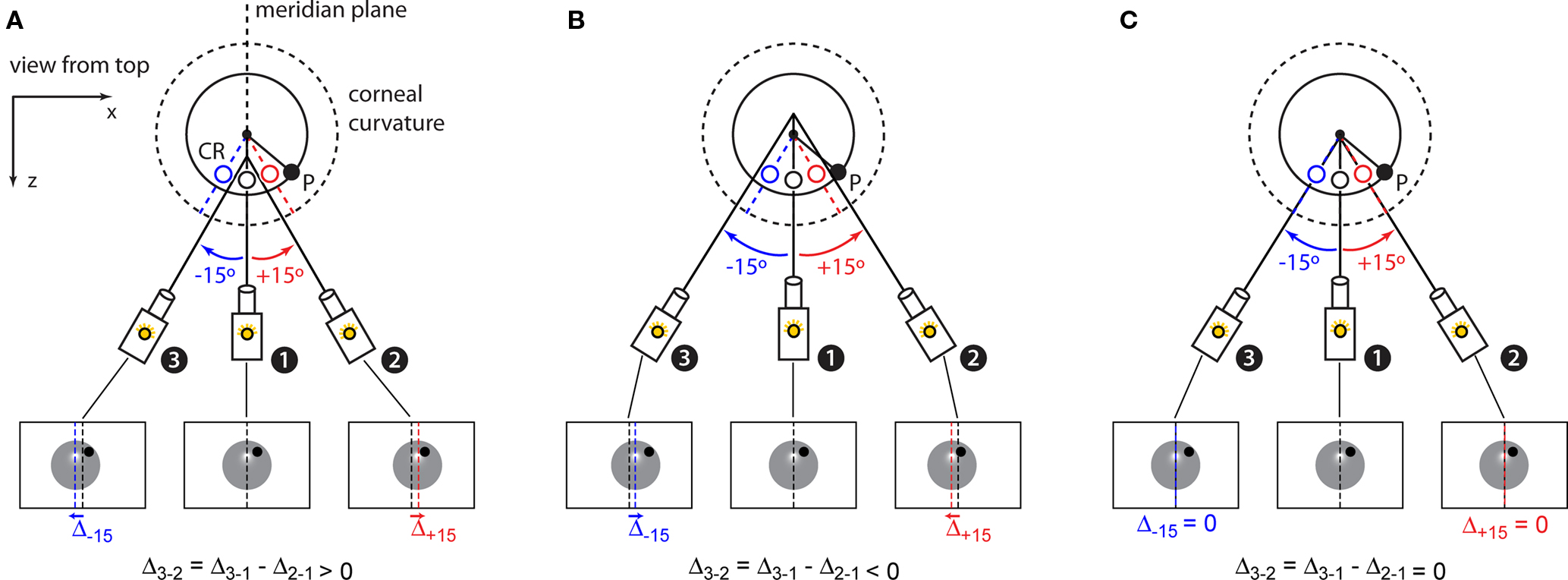
Figure 5. Estimation of the 3D center of the corneal curvature. (A) At the end of the previous calibration steps (see Figure 4), the camera is in position 1, i.e., with the eye centered on the camera’s sensor. Motorized stages allow pseudo-rotations of the camera about a distant point along its optic axis (solid lines) by combining a horizontal translation with a rotation (see Figure 1C). If such a rotation happens about a point in front of the center of the corneal curvature the corneal reflection (CR) produced by the horizontally aligned (top) infrared LED will appear offset (red and blue open circles) of its location at the camera’s starting point (black empty circle). Specifically, positive (counter-clockwise from the top, red) and negative (clockwise, blue) pseudo-rotations result in a rightward and leftward displacements of the CR respectively. Therefore, the difference (Δ_3-2) between the displacement of the CR produced by the positive (red arrow) and negative (blue arrow) camera rotations will be positive. (B) When the camera is rotated about a virtual point (along its optic axis) behind the center of the corneal curvature the CR will be displaced medially and Δ_3-2 will be negative. (C) If the camera rotates about a virtual point that is aligned to the center of the corneal curvature both the right (red arrow) and left (blue arrow) 15° rotations will produce no displacement of the CR and Δ_3-2 will be null.

Estimation of the radius of pupil rotation

The final step in calibrating the system is to estimate the distance from the center of the corneal curvature to the pupil (i.e., the radius of rotation of the pupil R_P0; see Figure 3A), which lies some distance behind the corneal surface. Measuring R_P0 is necessary to convert the linear displacement of the pupil into angular coordinates (see Eqs.1 and 2), while the distance of the pupil from the corneal surface is not relevant to our calibration procedure and, therefore, is not measured. Here an assumption is made that the eye rotates approximately about the center of the corneal curvature (Hughes, 1979; Remtulla and Hallett, 1985). In standard calibration methods for video eye trackers, this parameter is estimated by moving the eye to known angles and measuring the displacement of the pupil on the image sensor. Here, we do the reverse: we rotate the camera about the eye to known angles and measure the pupil’s displacement.

More specifically, the measurement of R_P0 is performed in two steps. First, the projection of R_P0 on the equator plane (R_P; see Figure 3A) is measured by switching on the horizontally aligned (top) infrared illuminator and measuring the distance Δx between the pupil position and the eye’s meridian plane (which is marked by the CR spot; see Figures 3A,D,E) when the camera is rotated to five known angles Δφ about the center of eye (one of such rotations is shown in Figure 6A). The resulting displacements Δx(Δφ) are then fit to the following equation (using a least squares fitting procedure):

FIGURE 6

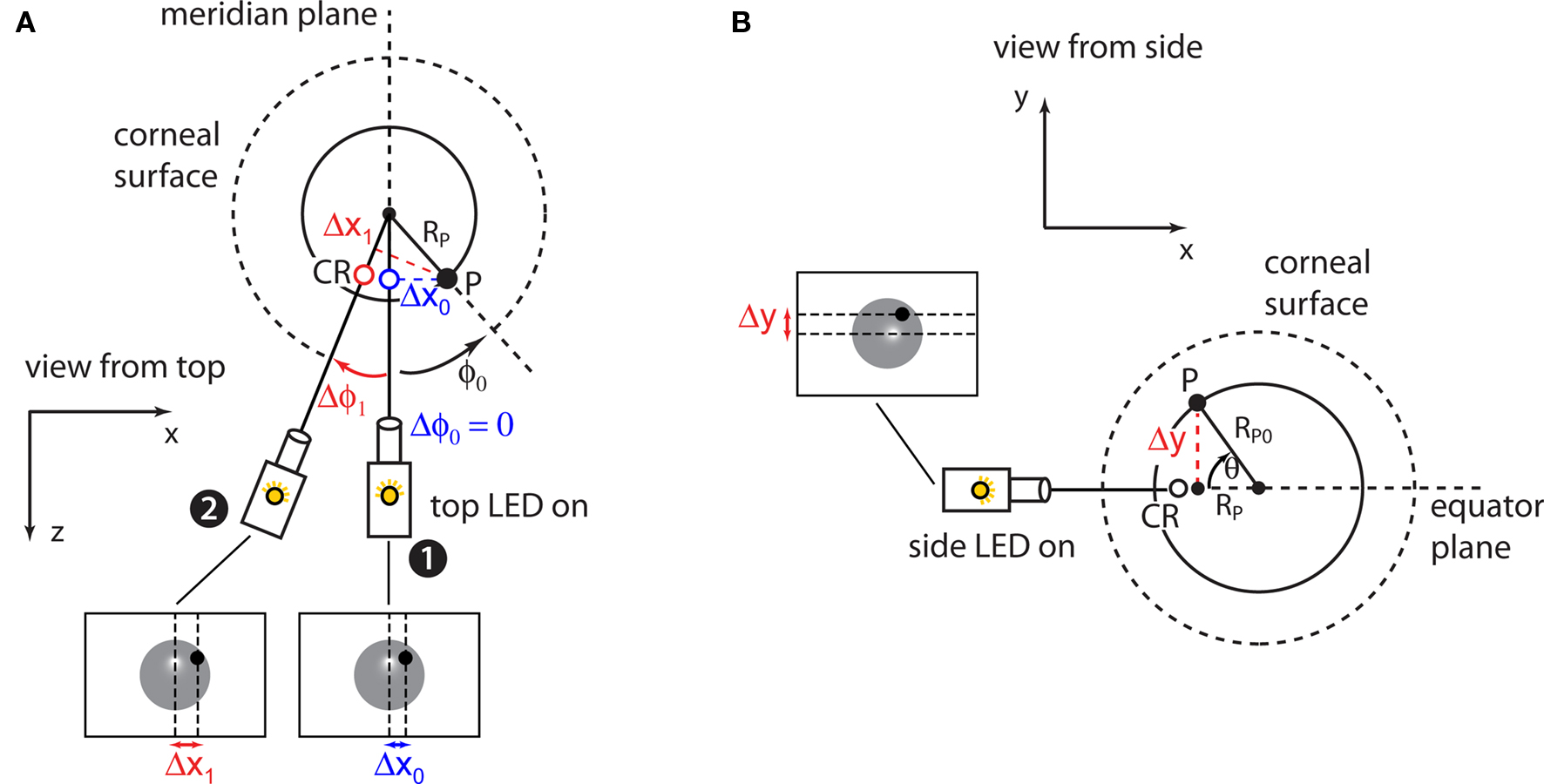
Figure 6. Estimation of the radius of pupil rotation. (A) At the end of the previous calibration steps (see Figures 4 and 5) the camera is in position 1, i.e., its sensor and the eye are aligned and the camera can be rotated about the center of the eye (small black circle). Additionally, illumination from the horizontally aligned (top) infrared LED results in a corneal reflection (CR; blue circle) that marks the meridian plane of the eye. Generally, the pupil (P; black circle) will not be aligned with the eye’s meridian plane (i.e., it will not point straight to the camera). This displacement can be described as an initial angle φ₀ (black arrow) between the eye’s meridian plane and R_P (the projection of the radius of rotation of the pupil R_P0 on the eye’s equator plane; see also Figure 3) and an initial distance Δx₀ between the pupil and the eye’s meridian plane. When the camera is rotated to an angle Δφ₁ about the center of the eye (red arrow), the distance Δx₁ between the pupil and the eye’s meridian plane will depend on both Δφ₁ and the pupil initial angle φ₀ (see Eq. 3 in Methods). (B). Once RP is known by the fit to Eq. 3 (see Materials and Methods), RP0 can be easily obtained by switching on the vertically aligned (side) infrared LED and measuring the distance Δy of the pupil from the eye’s equator plane (marked by the resulting CR spot; empty circle). In general, such a distance will not be null due to an initial elevation θ (black arrow) of the pupil from the equator plane.

where the two fitting parameters R_P and φ₀ are, respectively, the projection of R_P0 on the equator plane and the initial angle between the pupil and the eye’s meridian plane (see Figure 6A). Noticeably, this fitting procedure allows estimating R_P without the need of aligning the pupil to the CR spot (which would make φ₀ null in Eq. 3), since both R_P and φ₀ are obtained as the result of the same fit, and without the need of limiting the rotations of the camera to small angles Δφ. This marks an improvement over the method originally described by Stahl et al. (2000), where pupil and CR spot needed to be roughly aligned so that φ₀ ≈ 0, and Δφ needed to be small so that sin(Δφ) could be approximated with Δφ (see Discussion).

Next, R_P0 is computed by switching on the vertically aligned (side) illuminator and measuring the distance Δy between the pupil and the eye’s equator plane (which is marked by the CR spot; see Figures 3A–C). Since R_P is known from the fit to Eq. 3, R_P0 can be obtained from the following equation (see Figure 6B):

This method requires that the pupil be stationary while the measurements are collected; however, the required duration that the pupil be stationary is limited only by the speed of the stages and the frame rate of the camera. In practice, rats fixate their eyes for long periods of time (at least tens of seconds, see Figures 8A and 9B) allowing ample time for the calibration procedure. Moreover, if the subject moves their eyes during calibration, the process can easily be repeated due to the speed and autonomy of the method.

Post-Calibration Operation

Following calibration, the motion stages carrying the camera are powered-down, the vertically aligned (side) LED is permanently shut off, and the horizontally aligned (top) LED is illuminated. Gaze angles are then computed according to Eqs 1 and 2, with the (x,y) position of the CR from the top LED serving a reference for both the equator and meridian planes. This is possible because the x coordinate of the CR produced by the top LED lies on the meridian plane (see Figure 3E), while its y position is offset by a known value from the equator plane (compare Figures 3C,E). This offset is computed once, when the side LED is turned on, during the final step of the calibration procedure (see previous section). The relative offset of the CR spots produced by the top and side LEDs is constant (i.e., if the eyeball shifts, they will both shift of the same amount). Therefore, once the offset is measured, only one of the two LEDs (the top in our case) is sufficient to mark the position of both the equator and meridian planes. Because the corneal is approximately a spherical reflector, the gaze angles determined relative to the CR reference are relatively immune to small translational movements of the eye relative to the camera.

Simulated Eye

To validate the system’s accuracy, a simulated eye was constructed that could be moved to known angles. A pair of goniometer stages (GN2, Thorlabs, Inc.) were assembled such that they shared a common virtual rotation point 0.5 inches in front of the stage surface allowing rotation in two axes about that point. A 0.25-inch radius reflective white non-porous high-alumina ceramic sphere (McMaster Carr) was glued to a plastic mounting platform using a mandrel to ensure precise placement of the sphere at the goniometer’s virtual rotation point. A shallow hole was drilled into the sphere and subsequently filled with a black epoxy potting compound which served as a simulated pupil. The entire goniometer/eye apparatus was then firmly bolted down the table of the experimental setup at a distance from the camera approximating that of a real subject.

The resulting simulated eye served as a good approximation to a real eye. In particular, when one of the LED infrared sources of our imaging system was turned on, its reflection on the surface of the ceramic sphere (the simulated cornea) produced a bright reflection spot (the simulated CR spot). Both the simulated pupil and CR spot could be reliably and simultaneously tracked by our system, as long as the LED source did not point directly at the pupil. In such a cases, no reflection of the LED source could be observed, since the simulated pupil was opaque (this is obviously not the case for a real eye). As a matter of fact, the only limitation of our simulated eye was that it could not simulate conditions in which the CR spot would overlap the pupil. The effectiveness of our tracking algorithm to deal with such situations was tested by imaging real eyes of head-fixed rodents (see next section).

Test with Head-Fixed Rats

Two Long Evans rats and one Wistar rat were used to test the ability of our system to track the gaze of awake rodents and deal with any potentially suboptimal viewing conditions encountered in imaging a real eye (e.g., overlapping of the pupil and CR spot). All animal procedures were performed in compliance with the Harvard University Institutional Animal Care and Use Committee. Animals were head-fixed relative to the experimental setup by attaching a stainless steel head-post fixture to the skull, which mated with a corresponding head holder that was fixed to the table of the experimental setup. The animal’s body was held in a cloth sling suspended by elastic cords that provided support for the body while not providing any rigid surface to push off and place strain on the implant. Animals were gradually acclimated to the restraint over the course of 2 weeks prior to the experiments presented here.

Results

Validation with a Simulated Eye

To test the accuracy of our system, a simulated eye capable of being moved to known angles was used (see Materials and Methods). The simulated eye was placed approximately 18 cm in front of the lens of our eye-tracking system, which was calibrated using the procedure described above. To test the reproducibility of the calibration procedure, we repeated the calibration 10 times, and examined the estimates of the distance from the eye center to the pupil (R_P0) and the distance from eye center to the camera’s axis of rotation (d). R_P0 was estimated to be 6.438 mm (consistent with the known dimensions of the 0.25-inch radius sphere), with a standard deviation of 0.060 mm. The distance d was measured at 369.46 mm, with a standard deviation 0.33 mm. Both measurements suggest variation on the order of one part per thousand.

After completing the calibration, the eye was rotated so that the simulated pupil on its surface was moved to a grid of known locations (i.e., simulated gaze angles) and the eye tracker’s output was recorded. Figure 7 shows measured gaze directions relative to a grid of known positions of the simulated pupil. Such measurements could not be obtained for all possible grid positions, since, by construction, the simulated eye did not allow simulating conditions in which the CR spot would overlap the pupil (see Materials and Methods for details). For each pupil rotation for which the simulated pupil and CR spot were both visible, the gaze measurements were repeated 10 times and the average was recorded (red crosses in Figure 7). As shown by the figure, across a range of 10–15° of visual angles, the system estimated the gaze angle with good accuracy (i.e., <0.5° errors) and precision (0.09° standard deviation).

FIGURE 7

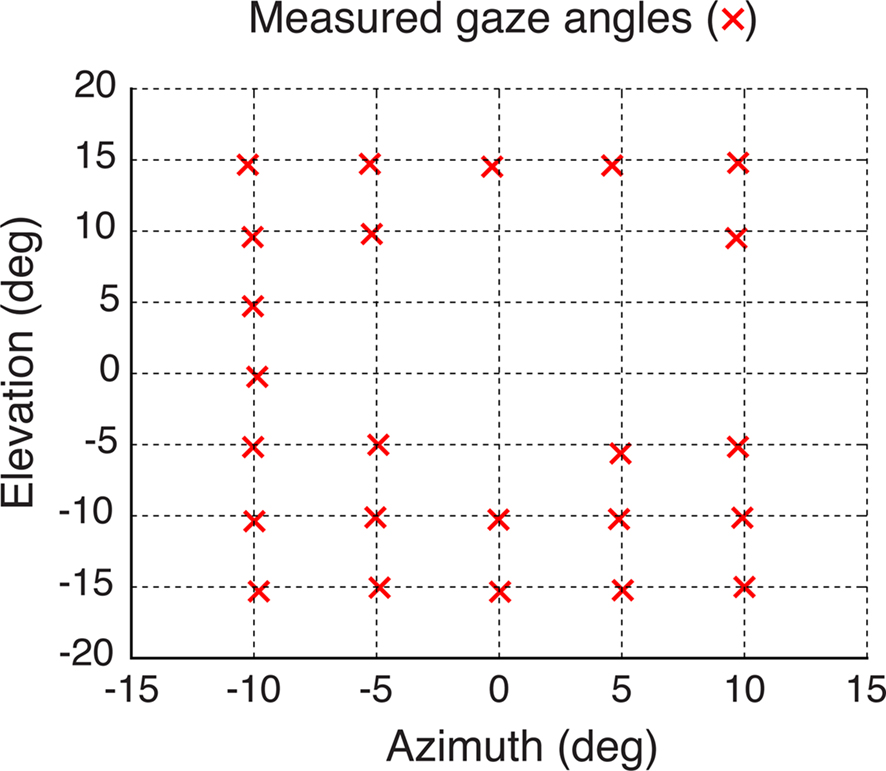
Figure 7. Validation of the eye-tracking system using an artificial eye. The artificial eye was rotated to a grid of known azimuth and elevation angles (intersections of the dashed lines) while the pupil on its surface was tracked. Pupil gaze measurements were repeated 10 times and their average values were drawn (red crosses) superimposed over the grid of know gaze angles to show the accuracy of the eye-tracking system. Missing measurements (i.e., grid intersections with no red crosses) refer to pupil rotations that brought the LED infrared source to shine directly onto the opaque simulated pupil, resulting in a missing CR spot (see Materials and Methods).

Eye Movements in an Awake Rat

To verify that our system was able to track the pupil position of a real rodent eye, we calibrated and measured eye movements in two awake (head-fixed) pigmented rats. The calibration procedure resulted in an average estimate of the center-of-rotation to pupil radius (R_P0) of 2.623 mm (averaging six measurements obtained from one animal), which is roughly consistent with the size of animal’s eye and with published ex vivo measurements of eye dimensions (Hughes, 1979).

Estimation of R_P0 allowed real-time measurement of the azimuth and elevation angles of the animal’s pupil (see Eqs 1 and 2). Consistent with previous reports (Chelazzi et al., 1989) we observed a variety of stereotypic, spontaneous eye movements (see Figure 8A). In particular, as described in previous literature, we found that saccades were primarily directed along the horizontal axis with small vertical components. Saccade amplitudes as large as 12° were observed with the median amplitude of all observed saccades being 3.6°. The mean inter-saccadic interval was 137.9 s though inter-saccadic intervals as short as 750 ms were also seen.

FIGURE 8

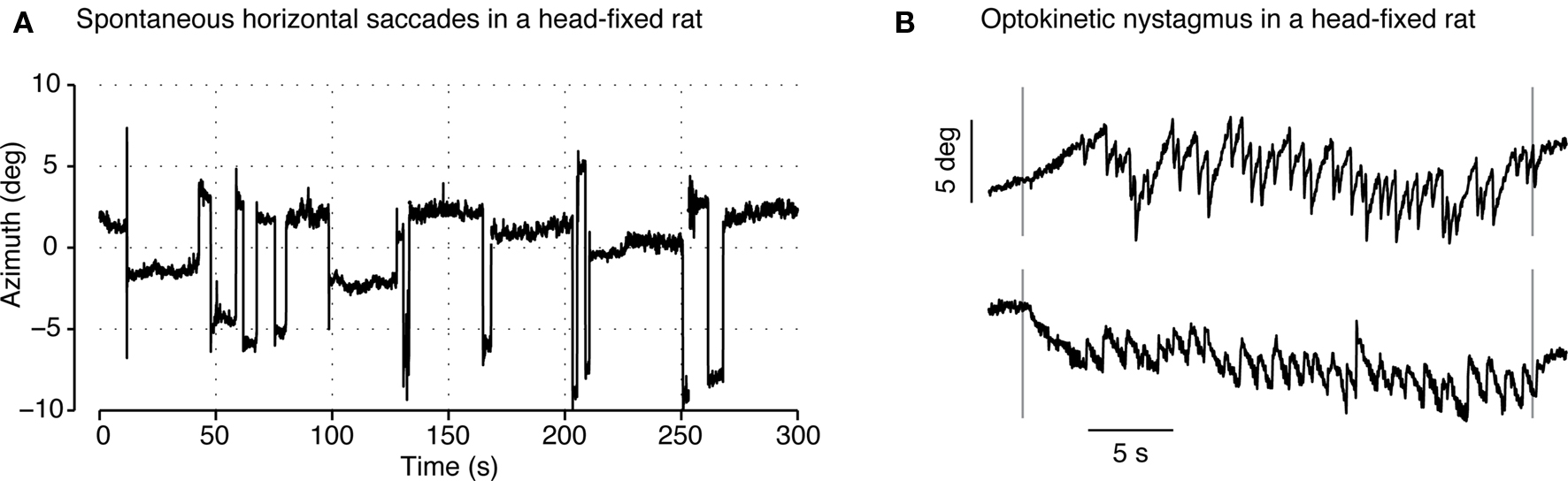
Figure 8. Validation of the eye-tracking system in a head-fixed rat. (A) Several minutes of the azimuth (i.e., horizontal) gaze angle tracking in a head-fixed rat. During this period the animal made several saccades (with an amplitude of approximately 5°) interleaved with fixation periods lasting tens of seconds. (B) Horizontal gaze angle recorded during the presentation of a 0.25 cycles per degree sinusoidal grating moving at 5.0°/s in the leftward (top) or rightward (bottom). Vertical lines indicate the appearance and disappearance of the grating. Optokinetic nystagmus, composed of a drift in gaze angle following the direction of grating movement and corrective saccade, is visible during both trials.

As a further basic test of eye movement behavior, we presented the subject with a drifting sinusoidal grating stimulus (0.25 cycles per degree, 5.0°/s) designed to evoke optokinetic nystagmus (OKN: Hess et al., 1985; Stahl et al., 2000; Stahl, 2004). OKN is composed of two phases: a slow drifting movement of the eye that follows the direction of movement and speed of the stimulus, and a fast corrective saccade in the opposite direction. Successive transitioning between these two phases, as seen during OKN, results in a saw-tooth-like pattern of eye movement. The slow and fast OKN phases were quantified by measuring the closed-loop gain (drift speed/stimulus speed) and open-loop gain (saccade speed/stimulus speed). Figure 8B shows the recorded horizontal gaze angle during the presentation of a leftward drifting (top) and rightward drifting grating (bottom). Traces show the characteristic drift and corrective saccade pattern associated with OKN. Furthermore, closed-loop (0.75 ± 0.19) and open-loop (9.46 ± 4.20) gains, measured across 10 trials in the pigmented rats, were in agreement with previous reports (closed-loop: 0.9, open-loop: 9.0; Hess et al., 1985).

We also tested the efficacy of our system to track eye movements of an awake (head-fixed) albino rat. In general, the unpigmented eye of albino rodents poses some challenges to pupil tracking algorithm, because, due to greater reflectivity of the retinal surface and leakage of light through the unpigmented iris and globe, the pupil appears as a bright, rather than dark object (see Figure 9A). Nevertheless, since our image-processing pipeline depends on a radial-symmetry approach (see Pupil and Corneal Reflection Localization) rather than simpler schemes (such as thresholding), we were able to make minor modifications that enabled effective tracking of a bright pupil. Specifically, rather than selecting the lowest and highest values of the fast radial symmetry transform (Loy and Zelinsky, 2002) to find the CR and pupil, respectively (see Figure 2B), we instead selected the two highest valued patches from this transform (i.e., the two bright image regions exhibiting the highest degree of radial symmetry as measured by the fast radial symmetry transform). The brighter of the two patches identified in this way is then assumed to be the CR (blue circle in Figure 9A), and the other is assumed to be the pupil (red circle in Figure 9A). The remainder of the processing pipeline proceeded as described in the Section “Materials and Methods.” Following this minor modification of our tracking algorithm, we were able to calibrate our system and successfully track the saccades of the albino rat (see Figure 9B), albeit at a slower sampling rate than what obtained for pigmented rats (compare to Figure 8A).

FIGURE 9

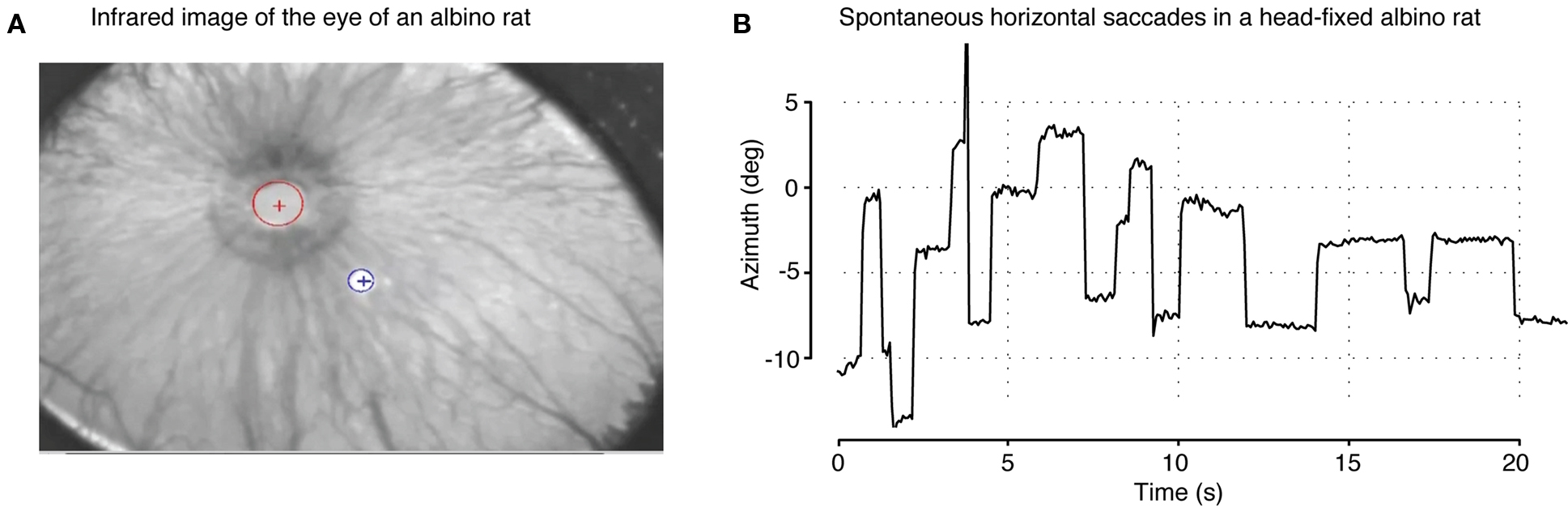
Figure 9. Modification of the eye-tracking system for use with an albino animal. (A) An infrared (IR) image of the eye of an albino rat. A key difference with albino animals (compare to Figure 2A) is that the IR image of the pupil is dominated by “bright pupil” effects (light reflected back through the pupil) due to a more reflective unpigmented retinal epithelium and significant illumination through the unpigmented iris. The red and blue circle/cross indicates, respectively, the position of the pupil and corneal reflection spot. (B) Examples of spontaneous saccades measured in an albino rat (comparable to Figure 8A).

Discussion

Eye-tracking systems are an essential tool to conduct vision experiments in awake subjects. For instance, neuronal receptive fields in cortical visual areas can only be studied if the gaze direction of the subject is measured in real-time with reasonable accuracy so that visual stimuli can be presented reproducibly in any given visual field location. Irrespective of the technology used (e.g., a scleral search coil or a camera-based eye tracker), the calibration of an eye tracking system is typically achieved by requiring the subject to saccade to visual targets over a grid of known visual field locations. Obviously, this is possible only in species (such as primates) that spontaneously saccade to external visual targets. To date, this limitation has not represented a major issue since the great majority of vision studies in awake animals have been conducted in monkeys.

However, rodents are increasingly recognized as a valuable model system for the study of various aspects of visual processing (Xu et al., 2007; Griffiths et al., 2008; Niell and Stryker, 2008, 2010; Jacobs et al., 2009; Lopez-Aranda et al., 2009; Zoccolan et al., 2009). In particular, one study (Zoccolan et al., 2009) has shown that rats are capable of invariant visual object recognition, an ability that could depend on rather advanced representations of visual objects similar to those found in the highest stages of the primate ventral visual stream. Investigation of such high-level visual areas in rodents will require performing neuronal recordings in awake animals. Hence, the need for a convenient, accurate, easy-to-use, and relatively inexpensive eye tracking technology that can work in afoveate rodents that do not reliably saccade to visual targets. The eye-tracking system described in this article fulfills this need combining the advantages of non-invasive video tracking with a fully automated calibration procedure that relies exclusively on measuring the geometry of the eye.

The idea of measuring the geometrical properties of the eye to establish a map between the linear displacement of the pupil on the image plane and its rotation about the center of the eye (i.e., the gaze angle) is not new. In fact, this approach was proposed and successfully applied by Stahl and colleagues (Stahl et al., 2000; Stahl, 2004) to calibrate a video-based eye tracking system that recorded mouse eye movements, and is likely the most commonly used approach to video eye-tracking by the rodent eye movements community. Although inspired by the work of Stahl and colleagues (Stahl et al., 2000; Stahl, 2004) and based on the same principles, our system differs from Stahl and colleague’s method in many regards and overcomes several of its limitations.

First, the calibration procedure originally proposed by Stahl and colleagues (Stahl et al., 2000; Stahl, 2004) requires performing a long sequence of calibration steps by hand (i.e., a large number of precise rotations/translations of the imaging apparatus relative to the animal). Therefore, manual operation of Stahl and colleague’s calibration procedure is necessarily slow, difficult to repeat and verify, and subject to operator error.

In contrast, in our design the camera/illuminator assembly is mounted on a set of computer-controlled motion stages that allow its translation and rotation relative to the head-fixed animal. The use of a telephoto lens with high magnification power (see Materials and Methods) allows the camera to be placed at a range of tens of centimeters from the subject causing minimal mechanical interference with other equipment. More importantly, the whole calibration procedure is implemented as a sequence of computer-in-the-loop measurements (i.e., is fully automated) with no need for human intervention. As a result, the calibration is fast (∼30 s for the total procedure), precise, and easily repeatable. The speed of our approach minimizes the risk that the animal’s eye moves during a critical calibration step (which could invalidate the calibration’s outcome) since each individual step takes just a few seconds. In addition, the automated nature of our measurements makes it easy to repeat a calibration step if an eye movement occurs during the procedure. More generally, the precision (i.e., self-consistency) of the calibration’s outcome can be easily assessed through repetition of the calibration procedure (see Results and below).

Finally, in contrast to the method proposed by Stahl and colleagues (Stahl et al., 2000; Stahl, 2004) our calibration procedure directly measures a fuller set of the relevant eye properties, avoiding several shortcuts taken in Stahl’s approach. This is possible because of the use of a vertically aligned (side) illuminator in addition to the horizontally aligned (top) illuminator used by Stahl and colleagues (Stahl et al., 2000; Stahl, 2004). This allows a direct measurement of the vertical distance Δy of the pupil from the equator plane (see Figure 6B) and subsequent estimation of R_P0 (see Eq. 4) without making any assumption about the radius of the cornea as required by Stahl’s procedure (Stahl, 2004). Moreover, our method avoids time-consuming and unnecessary calibration steps, such as aligning the pupil and CR spot (see Materials and Methods), and does not impose any limitation on the amplitude of the camera’s rotations about the eye during calibration, since no approximations of sine functions with their arguments are needed (see Materials and Methods).

Our eye-tracking system was tested using both an artificial eye and two head-fixed rats. In both cases, the calibration procedure yielded precise, reproducible measurements of the radius of rotation of the pupil R_P0 (see Results). Repeated calibration using the artificial eye (with known R_P0) validated the accuracy of our procedure. Similarly, the estimated R_P0 of our rats showed a good consistency with values reported in literature (Hughes, 1979). The artificial eye also demonstrated the capability of our system to faithfully track gaze angles over a range of ±15° of visual angles with an average accuracy better than 0.5°. To test the tracking performance in vivo, we used a paradigm designed to elicit optokinetic responses and found that the amplitude and gain of these responses were within the range of values measured using scleral search coils (Hess et al., 1985). Finally, consistent with previous reports (Chelazzi et al., 1989), we found that rats make a variety of spontaneous eye movements including saccades greater than 10° in amplitude.

Limitations and Future Directions

Compared to scleral search-coils, our system has all of the common limitations found in video tracking systems, e.g., an inability to track radial eye movement components and generally lower sampling rate (though this limit could be overcome through the use of a faster camera). However, as opposed to search-coil methods, our approach has the important advantage of being non-invasive and circumvents the risk of damaging the small rodent eye and interfering with normal eye movement (Stahl et al., 2000). Consequently, our system can be repeatedly used on the same rodent subject, with no limitation on the number of eye-movement recording sessions that can be obtained from any given animal.

Although our system was tested on pigmented rats, we do not expect any difficulties using it to track eye movements of pigmented mice. Although different in size, the eyes of rats and mice have similar morphology and refractive properties (Remtulla and Hallett, 1985). Moreover, our approach is based on the method originally designed by Stahl and colleagues (Stahl et al., 2000; Stahl, 2004), who successfully developed and tested their video-based eye tracking system on pigmented mice.

Although most scientists engaged in the study of rodent vision do work with pigmented strains, we also tested how effectively our system would track the pupil of an albino rat. With some adjustment to our tracking algorithm, our system was able to track an unpigmented eye, albeit at a slower sampling rate and lower reliability (see Figure 9B). Additional work, such as tuning and accelerating the algorithm or optimizing the lighting conditions, would be necessary for effective tracking of unpigmented eyes. However, we do not anticipate significant difficulties. The modified “albino mode” for the eye-tracking software is included in our open code repository² and, while not fully optimized, could serve as a starting point for any parties interested in further optimizing the method for albino animals.

One further current limitation of our system is that it tracks only one eye. However, this limitation can easily be overcome by using two identical systems, one on each side of the animal. Since the system operates at a working distance greater than 25 cm, there is a great deal of flexibility in the arrangement of the system within an experimental rig. Furthermore, if the assumption is made that both eyes are the same or similar size, simply adding a second, fixed camera would suffice to obtain stereo tracking capability.

Another drawback of the system described here is that it requires the subject to be head-fixed in order to operate. While this is a hard requirement in our current implementation, it is conceivable that this requirement could be at least partially overcome by simultaneously tracking the head position of a rat and training the animal to remain with a given working volume. In addition, one can imagine methods where the geometry of an animal’s eye is estimated using the system described here but where “online” eye tracking is accomplished with smaller (e.g., cell phone style) head-mounted cameras.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank N. Oertelt, C. Paul-Laughinghouse, and B. Radwan for technical assistance. This work was supported by the National Science Foundation (IOS-094777) and the Rowland Institute at Harvard. Davide Zoccolan was partially supported by an Accademia Nazionale dei Lincei – Compagnia di San Paolo Grant.

Footnotes

1. ^http://github.com/coxlab/eyetracker
2. ^http://github.com/coxlab/eyetracker

References

Byrd, K. (1997). Characterization of brux-like movements in the laboratory rat by optoelectronic mandibular tracking and electromyographic techniques. Arch. Oral Biol. 42, 33–43.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chelazzi, L., Ghirardi, M., Rossi, F., Strata, P., and Tempia, F. (1990). Spontaneous saccades and gaze-holding ability in the pigmented rat. II. Effects of localized cerebellar lesions. Eur. J. Neurosci. 2, 1085–1094.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chelazzi, L., Rossi, F., Tempia, F., Ghirardi, M., and Strata, P. (1989). Saccadic eye movements and gaze holding in the head-restrained pigmented rat. Eur. J. Neurosci. 1, 639–646.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dongheng Li, David Winfield, Derrick J. Parkhurst, “Starburst: A hybrid algorithm for video-based eye tracking combining feature-based and model-based approaches,” IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPRW’05) – Workshops, 2005. Available at: http://www.computer.org/portal/web/csdl/doi/10.1109/CVPR.2005.531

CrossRef Full Text

González, R. C., and Woods, R. E. (2008). Digital Image Processing. Upper Saddle River, NJ: Pearson/Prentice Hall.

Griffiths, S., Scott, H., Glover, C., Bienemann, A., Ghorbel, M., Uney, J., Brown, M., Warburton, E., and Bashir, Z. (2008). Expression of long-term depression underlies visual recognition memory. Neuron 58, 186–194.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hess, B. J., Precht, W., Reber, A., and Cazin, L. (1985). Horizontal optokinetic ocular nystagmus in the pigmented rat. Neuroscience 15, 97–107.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hughes, A. (1979). A schematic eye for the rat. Vision Res. 19, 569–588.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jacobs, A. L., Fridman, G., Douglas, R. M., Alam, N. M., Latham, P. E., Prusky, G. T., and Nirenberg, S. (2009). Ruling out and ruling in neural codes. Proc. Natl. Acad. Sci. U.S.A. 106, 5936–5941.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, D., Babcock, J., and Parkhurst, D. J. (2006). “openEyes: a low-cost head-mounted eye-tracking solution,” in ETRA’06: Proceedings of the 2006 Symposium on Eye Tracking Research and Applications. New York: ACM Press.

Li, D., Winfield, D., and Parkhurst, D. J. (2005). “Starburst: a hybrid algorithm for video-based eye tracking combining feature-based, and model-based approaches,” in Proceedings of the IEEE Vision for Human–Computer Interaction Workshop at CVPR, 1–8.

Lopez-Aranda, M. F., Lopez-Tellez, J. F., Navarro-Lobato, I., Masmudi-Martin, M., Gutierrez, A., and Khan, Z. U. (2009). Role of layer 6 of V2 visual cortex in object-recognition memory. Science 325, 87–89.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Loy, G., and Zelinsky, A. (2002). “A fast Radiaul symmetry transform for detecting points of interest,” in Proceedings of the 7th European Conference on Computer Vision, Vol. 2350, 358–368.

Mackworth, J. F., and Mackworth, N. H. (1959). Eye fixations on changing visual scenes by the television eye-marker. J. Opt. Soc. Am. 48, 439–445.

CrossRef Full Text

Niell, C. M., and Stryker, M. P. (2008). Highly selective receptive fields in mouse visual cortex. J. Neurosci. 28, 7520–7536.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Niell, C. M., and Stryker, M. P. (2010). Modulation of visual responses by behavioral state in mouse visual cortex. Neuron 65, 472–479.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Remmel, R. S. (1984). An inexpensive eye movement monitor using the scleral search coil technique. IEEE Trans. Biomed. Eng. 31, 388–390.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Remtulla, S., and Hallett, P. E. (1985). A schematic eye for the mouse, and comparisons with the rat. Vision Res. 25, 21–31.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Robinson, D. A. (1963). A method of measuring eye movement using a scleral search coil in a magnetic field. IEEE Trans. Biomed. Eng. 10, 137–145.

Pubmed Abstract | Pubmed Full Text

Shackel, B. (1967). Eye movement recording by electro-oculography,” in Manual of Psychophysical Methods, eds P. H. Venables and I. Martin. (Amsterdam: North-Holland), 229–334.

Stahl, J. S. (2004). Eye movements of the murine P/Q calcium channel mutant rocker, and the impact of aging. J. Neurophysiol. 91, 2066–2078.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stahl, J. S., van Alphen, A. M., and De Zeeuw, C. I. (2000). A comparison of video and magnetic search coil recordings of mouse eye movements. J. Neurosci. Methods 99, 101–110.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Strata, P., Chelazzi, L., Ghirardi, M., Rossi, F., and Tempia, F. (1990). Spontaneous saccades and gaze-holding ability in the pigmented rat. I. Effects of inferior olive lesion. Eur. J. Neurosci. 2, 1074–1084.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Xu, W., Huang, X., Takagaki, K., and Wu, J. Y. (2007). Compression and reflection of visually evoked cortical waves. Neuron 55, 119–129.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zoccolan, D., Oertelt, N., DiCarlo, J. J., and Cox, D. D. (2009). A rodent model for the study of invariant visual object recognition. Proc. Natl. Acad. Sci. U.S.A. 106, 8748–8753.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text