A commentary on
Response time distributions in rapid chess: a large-scale decision making experiment
by Sigman, M., Etchemendy, P., Slezak, D. F., and Cecchi, G. A. (2010). Front. Neurosci. 4:60. doi: 10.3389/fnins.2010.00060
Adjusting our behavior to the changing demands of the environment requires flexible decision mechanisms. In an analysis of more than 91,000 chess games, an original research effort now suggests that performance is correlated with a player’s ability to adjust its decision criteria to meet the varying degrees of complexity observed throughout a match (Sigman et al., 2010).
Chess has always captivated not only to those who play it, but also mathematicians and computer scientists who are often drawn to the challenge of designing artificial intelligence algorithms capable of matching or even surpassing human cognition (Shannon, 1950; Turing, 1950). Traditionally, those trying to understand the cognitive processes related to chess have brought players within laboratory settings that allow studying such things as eye movements and pattern recognition abilities (Chase and Simon, 1973; Charness et al., 2001). A new approach, however, has taken the study of chess and decision making to new level by realizing that the enormous databases generated by storing the thousands of games played online every day can help uncover subtle but insightful statistical trends (Blasius and Tönjes, 2009).
Sigman and colleagues analyzed how response time (RT) changed according to the number of moves played into the game. The resulting mean RT profile clearly showed that openings and endgames are played much faster than the middle game, a pattern that most chessists know from experience (see also Hyatt, 1984). This general trend was present among all contestants, but a revealing result emerged when the authors compared time usage of low (<1400) and high-rated (>1900) players: strong players spend even less time on the openings and endings, and invest significantly more time reflecting on middle game moves. The wider RT range of high-rated players suggested a more flexible policy of time management. Supporting this view, Sigman and collaborators found that, not only mean RT showed larger modulations throughout a match, but also the spread of the RT distributions for each move number was wider among strong players.
But, what is the main factor shaping the general trend of slow moves at the middle, and fast ones at the opening and endgame? One possibility is that the time invested on a given move is determined by the complexity of the board position. Players intuitively know that position complexity grows as the match progresses from the opening into the middle game. To estimate how complexity changed as games unfolded, the authors came up with a clever trick. Instead of calculating just the total number of legal moves, certainly a raw measure of board complexity, they weighted each possible move by a factor reflecting how often it appeared in a database of more than 650,000 games. Results show that for the first 20 moves the weighted number of options, which can be thought of as the board entropy, grow linearly with the number of played moves. The increase in board complexity thus offers a plausible explanation for the increasing decision times observed as matches advance from the opening into the middle game.
But the entropy calculations revealed something unexpected: board complexity remained high also throughout the endgame, while players progressively sped up their decisions. Board complexity was clearly not the only factor determining RT at the second half of the match. The decrease in decision time probably reflected a new setting on the speed–accuracy tradeoff inherent to every decision (Ratcliff, 1978; Luce, 1986; Palmer et al., 2005). As remaining time ticked away, players increasingly favored fast over precise but slower moves.
For decisions that must be reached within a limited time frame, as most of them are, a tight correlation exists between accuracy and the time invested deciding. Increasing precision is always possible, at the expense of longer deliberation times. To estimate the accuracy of chess decisions, the authors used open-source software that calculated how position score changed after every move. This score, positive if board position is favorable to white, accounted not only for material advantage, but also for board subtleties such as open files and piece mobility.
Gaining full advantage of their large database, the authors calculated how score and remaining time combined to determine a player’s winning likelihood. This analysis showed that the main factor determining the match outcome shifts from material advantage to time advantage as remaining time decreases. In 3 min games, for example, when remaining time is between 20 and 30 s, an 8 s advantage on the clock is equivalent to having an extra knight on the board. It was clear from these results that under time pressure fast moves become more effective than good moves requiring extra time.
But what is the mechanism allowing a chess player to modulate the speed–accuracy tradeoff and hence decision time? The authors did not propose a particular model, but we can think of a chess decision as the process of finding out whether a given move is good enough or not. To do this, a player could assign a subjective value to each possible response movement. But to refine its initial assessment of choices the player must calculate how this value would change after the most likely response from the opponent (Figure 1). Repeating the evaluation process for long sequences of moves would assure a deeper assessment of choices, but would also consume more time. The evaluation process has to stop at some point if a player is not to spend its allotted time on a single move. This could be achieved by setting an acceptance criterion on the accumulated value, and selecting the sequence to first hit this bound.
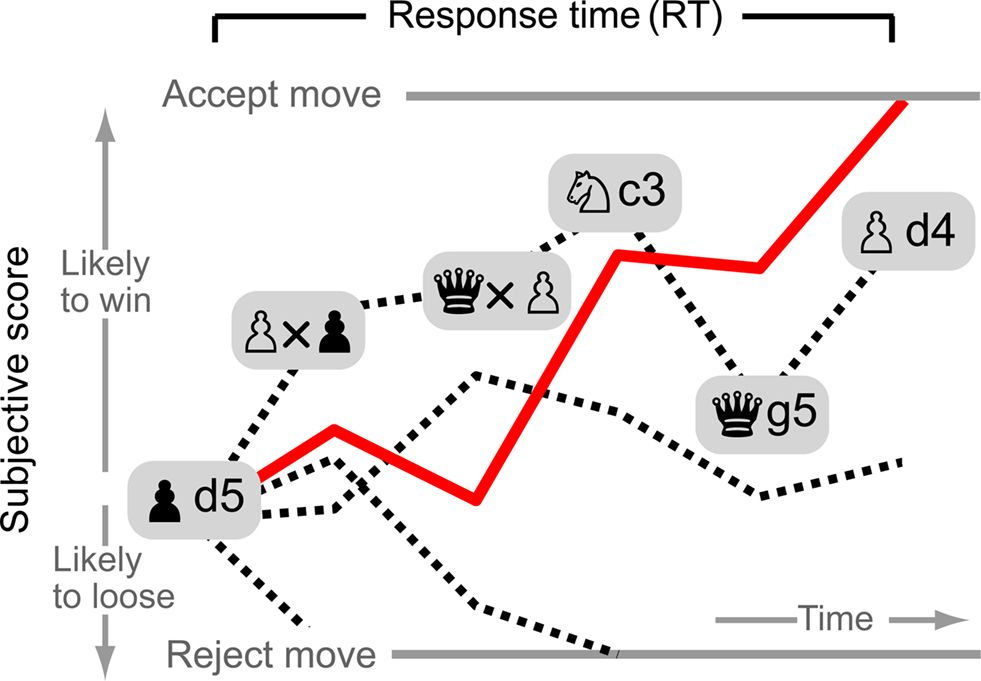
Figure 1. A decision mechanism in chess. After an opponent’s move (d5), a player evaluates his choices by assigning a goodness value (subjective score) to each possible response. He must then calculate how the score will change after a sequence of moves involving the most likely opponent’s responses. When accumulated score, that is, the summed value of each move within a sequence, reaches an acceptance criterion, the move initiating the sequence is played on the board. Deeper calculations, at the expense of longer response times, could be achieved by elevating the acceptance criterion. How the human brain assigns values to chess moves is still largely unknown, but in addition to raw piece value, its evaluation function likely incorporates variables such as elapsed time (Churchland et al., 2008), long term plans, and the opponent’s estimated strength.
According to this decision model, lowering the acceptance criterion would generate faster RTs, at the expense of a less profound evaluation of the choices. Ideally, the decision bound should be adjusted according to board complexity and remaining time. It is known, in fact, that the criterion value must be raised in relation to the number of choices in order to maintain a constant level of performance (Usher et al., 2002). This would explain why players make slower decision as the entropy of board increases. Several simplifying assumptions of this decision algorithm need rigorous testing. To spare an extra mechanism for determining evaluation order, move sequences are assumed to be calculated in parallel. Additionally, only the height of the decision criterion determines RT, so the model assumes no bound on the number of evaluated moves. As it is, openings would be analyzed the same way as the middle games, an assumption that might not hold for those players able to play “by the book,” i.e., relying on proven sequences of moves. In its simplest form, however, this decision model could potentially account for some of the uncovered statistical trends, namely, the linear relation of RT mean and standard deviation, as well as the long tails of RT distributions.
Chess expertise likely depends on a number of cognitive skills such as fast pattern recognition to quickly grasp the geist of a position, or the capacity to hold long sequences of moves in working memory (Simon and Chase, 1973). The results of Sigman and colleagues now indicate that a hallmark of strong chess players, and successful decision making, is the ability to constantly adjust the decision criteria to meet the changing demands of accuracy, complexity, and remaining time.
References
Blasius, B., and Tönjes, R. (2009). Zipf’s law in the popularity distribution of chess openings. Phys. Rev. Lett. 103, 218701.
Charness, N., Reingold, E. M., Pomplun, M., and Stampe, D. M. (2001). The perceptual aspect of skilled performance in chess: evidence from eye movements. Mem. Cogn. 29, 1146–1152.
Churchland, A. K., Kiani, R., and Shadlen, M. N. (2008). Decision making with multiple alternatives. Nat. Neurosci. 6, 693–702.
Palmer, J., Huk, A. C., and Shadlen, M. N. (2005). The effect of stimulus strength on the speed and accuracy of a perceptual decision. J. Vis. 5, 376–404.
Sigman, M., Etchemendy, P., Slezak, D. F., and Cecchi, G. A. (2010). Response time distributions in rapid chess: a large-scale decision making experiment. Front. Neurosci. 4:60. doi: 10.3389/fnins.2010.00060
Citation: de Lafuente V (2011) Flexible decisions and chess expertise. Front. Neurosci. 5:4. doi: 10.3389/fnins.2011.00004
Received: 07 December 2010;
Accepted: 05 January 2011;
Published online: 25 January 2011.
Copyright: © 2011 de Lafuente. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence:bGFmdWVudGVAdW5hbS5teA==
