- 1 Laboratoire Psychologie de la Perception, CNRS, Université Paris Descartes, Paris, France
- 2 Equipe Audition, Département d’Etudes Cognitives, Ecole Normale Supérieure, Paris, France
- 3 Institut des Systèmes Intelligents et de Robotique, Université Pierre et Marie Curie-Paris 06, Paris, France
- 4 Center for Hearing and Communication Research, Karolinska Institutet, Stockholm, Sweden
- 5 Department of Clinical Neuroscience, Karolinska University Hospital, Stockholm, Sweden
Computational modeling is increasingly used to understand the function of neural circuits in systems neuroscience. These studies require models of individual neurons with realistic input–output properties. Recently, it was found that spiking models can accurately predict the precisely timed spike trains produced by cortical neurons in response to somatically injected currents, if properly fitted. This requires fitting techniques that are efficient and flexible enough to easily test different candidate models. We present a generic solution, based on the Brian simulator (a neural network simulator in Python), which allows the user to define and fit arbitrary neuron models to electrophysiological recordings. It relies on vectorization and parallel computing techniques to achieve efficiency. We demonstrate its use on neural recordings in the barrel cortex and in the auditory brainstem, and confirm that simple adaptive spiking models can accurately predict the response of cortical neurons. Finally, we show how a complex multicompartmental model can be reduced to a simple effective spiking model.
1 Introduction
An increasing number of studies in systems neuroscience rely on computational modeling to understand how function emerges from the interaction of individual neurons. Although the neuron models used in these studies are usually well established models [e.g., Hodgkin–Huxley (HH), integrate-and-fire models, and variations], their parameters are generally gathered from a number of measurements in different neurons and preparations. For example, the model of Rothman and Manis (2003), an established biophysical model of neurons in the cochlear nucleus (CN) of the auditory brainstem, includes ionic channels with properties measured in different neurons of the CN of guinea pigs, combined with a sodium channel and an Ih current derived from previous measurements in mammalian neurons in other areas (including the thalamus). This situation is hardly avoidable for practical reasons, but it raises two questions: (1) channel properties from heterogeneous neuron types, species or ages may not be compatible, and (2) there could be functionally relevant correlations between parameter values within the same neuron type (e.g., maximal conductances), which would be missed if the information about channels came from several independent neurons. Therefore, it seems desirable to obtain models which are fitted for specific neurons.
If these models are to be used for network modeling, then the main goal is to predict the spike trains in response to an arbitrary input. Recently, it was found that simple phenomenological spiking models, such as integrate-and-fire models with adaptation, can predict the response of cortical neurons to somatically injected currents with surprising accuracy in spike timing (Jolivet et al., 2004; Brette and Gerstner, 2005; Gerstner and Naud, 2009; Kobayashi et al., 2009). A number of techniques have been used to fit specific models to electrophysiological recordings, in particular in the context of the recent INCF Quantitative Single-Neuron Modeling competition (Jolivet et al., 2008), but they are not generic, which limits their practical applicability. This is a difficult optimization problem for two reasons. Firstly, because of the threshold property, any matching criterion between the target spike train and the model spike train is necessarily discontinuous with respect to the model parameters (Brette, 2004), which discards many efficient optimization algorithms. Secondly, a single evaluation of the criterion for a given set of parameter values involves the simulation of a neuron model over a very long time. Therefore, this model fitting problem requires an optimization technique that is both flexible and very efficient.
We have developed a model fitting toolbox (Rossant et al., 2010) for the spiking neural network Brian (Goodman and Brette, 2009). Brian is an open-source simulator1 written in Python that lets the user define a model by directly providing its equations in mathematical form. To achieve efficiency, we used vectorization techniques and parallel computing. In particular, optimization can run on a graphics processing unit (GPU), an inexpensive chip available on most modern computers and containing multiple processor cores. In this review, we start by giving an overview of our optimization technique and we demonstrate its use on neural recordings in the barrel cortex and in the auditory brainstem. We also show how a complex multicompartmental model can be reduced to a simple effective spiking model.
2 Methods
2.1 Vectorized Optimization
Our technique is illustrated in Figure 1. The experimental data consists of current-clamp recordings, with fluctuating currents mimicking in vivo synaptic activity (Figure 1A). In this example (consisting of barrel cortex recordings from the INCF competition), the same current was injected several times in the same neuron (A1 and A2, regular spiking cell) and in different neurons (B1, fast spiking cell). Figure 1B shows the Python script used to run the optimization procedure. The spiking neuron model is defined by its mathematical equations (here, a simple integrate-and-fire model) and the parameter values are to be optimized so that the model spike trains are as close as possible to the recorded spike trains, which is assessed by a criterion. We chose the gamma factor (Jolivet et al., 2008), used in the INCF competition, which is based on the number of coincidences between the two spike trains, within a fixed temporal window (δ = 4 ms in our figures). Other criteria could be used, but in any case the criterion is a discontinuous function of the model parameters, because model spike trains are themselves discontinuous functions of the parameters. This is a strong constraint: it requires us to use a global optimization algorithm that does not directly use gradient information, for example genetic algorithms. These are computationally intensive, because the criterion must be evaluated on a large number of parameter values, and each evaluation consists of many operations (at least as many as the number of recording samples in the traces). Processing each set of parameters serially is computationally inefficient because (1) in Python, each instruction has a small fixed computational cost (the “interpretation overhead”) which adds up to a substantial cost if each set of parameters is processed separately, and (2) with serial computations we cannot make use of multiple processors. To maximize efficiency without compromising flexibility (the possibility of easily defining any model, as shown in Figure 1B), we developed vectorization techniques, which allows us to use the Brian simulator with minimal interpretation overhead (Brette and Goodman, 2010), and to run the optimization algorithm in parallel. Vectorization consists in simultaneously simulating many neurons defined by the same model but with different parameters, using vector operations to update their variables (that is, using a single Python instruction to perform the same computation on multiple items of data).
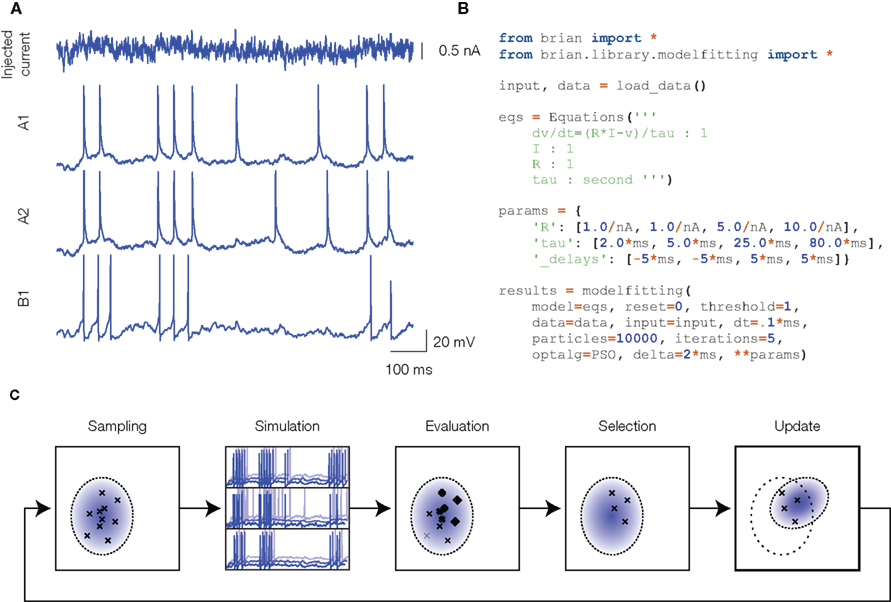
Figure 1. Overview of the model fitting technique. (A) Experimental data: a fluctuating current is injected into the neuron (top) and the responses are recorded (only spike trains are used). The first two traces correspond to two different trials in the same cortical neuron, the third trace is the response of another neuron. (B) Python script to fit an integrate-and-fire model to the experimental data: the model is defined in its mathematical form, and initial parameter values are specified. (C) Illustration of the optimization procedure using the CMA-ES algorithm. A large number of parameter values are drawn from a distribution (sampling). Neurons with these parameters are simultaneously simulated in a vectorized way (simulation). Multiple target traces are simultaneously optimized (three traces here). The prediction error for all neurons is estimated (evaluation), and the best ones are selected (selection). The distribution of the best ones is then used to update the distribution of parameters for the next iteration (update).
Figure 1C illustrates one step of the optimization algorithm. In this figure, we describe the CMA-ES algorithm (Hansen and Ostermeier, 2001), but other global optimization algorithms can be used (for example we used the particle swarm algorithm in Rossant et al., 2010). A large number of neurons are simulated in a vectorized way: they are defined by the same model but their parameter values are different. The current state of the optimization procedure is specified by a (Gaussian) distribution of parameter values. Parameter values for all the neurons to be simulated are randomly drawn from this distribution. The neural responses to the fluctuating current are simulated and compared to the target experimental spike trains. The best neurons are selected, and their parameter values are used to update the parameter distribution. It is straightforward to simultaneously optimize models for different recordings (e.g., A1, A2, and B1 in Figure 1A): the neuron population is simply subdivided in as many groups as target recordings. When the number of simultaneously simulated neurons is greater than a few thousand neurons, the Brian simulator (which is written in Python, an interpreted language) performs only marginally worse than custom compiled C code (Brette and Goodman, 2010). But this performance can be greatly increased by distributing the optimization over multiple processors.
2.2 Distributed Computing
The most computationally expensive part of the optimization is simulating the neuron population. Since the neurons do not communicate with each other, it is straightforward to distribute their simulations over several processors, as illustrated in Figure 2. One machine acts as a “master” and centralizes the optimization. An iteration starts with the master sending the current parameter distribution to all machines (“workers”). This is a negligible data transfer because the distribution is fully specified by the means and the covariance matrix. The workers independently draw parameter values from the distribution and simulate a population of neurons with these parameters. Each worker then evaluates the performance and selects the best neurons. The parameter values from these local selections are sent back to the master. Again, this is a small data transfer. The master collects all best neurons and updates the parameter distribution, which is sent back to the workers at the next iteration. Since the exchange of information between processors is minimal, the work can be efficiently distributed across several processors in a single machine, or across multiple machines connected over a local network or even over the internet. We use a Python package called Playdoh to distribute the optimization process2, which is based on the standard Python multiprocessing package. Performance scales approximately linearly with the number of processors (Rossant et al., 2010).
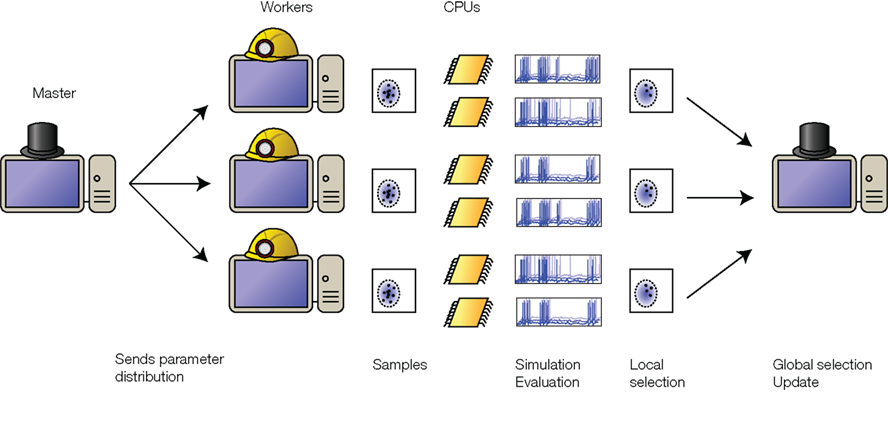
Figure 2. Distributed optimization. The “master” machine sends the distribution of parameters to the “worker” machines. Each worker simulates a population of neurons with parameters drawn from this distribution, evaluates their prediction performance (possibly making use of multiple CPUs on each machine), selects the best ones, and sends them back to the master. The master then collects the best neurons from all the workers, calculates their distribution, and updates the parameter distribution. The updated distribution is sent back to the workers for the next iteration.
2.3 GPU Implementation
Graphics processing units are specialized chips available on most modern computers, which can be used for high-performance parallel computing (Owens et al., 2007). These chips consist of up to 512 processor cores which run separate threads in parallel. Programming GPUs is rather specialized, and in order to obtain maximal performance the structure of the program has to be matched to the design of the hardware. For example, GPUs are designed for single input, multiple data (SIMD) parallelism, meaning that the same operation is simultaneously applied to many different items of data. Memory access is faster when threads read or write contiguous memory blocks. This design is very well adapted to vectorized operations, which we use in our optimization technique. Our model fitting toolbox automatically takes advantage of GPUs, as illustrated in Figure 3. The user writes Python code providing equations as strings, as shown in Figure 1, and the toolbox automatically generates GPU C++ code at runtime (using the techniques discussed in Goodman, 2010), which is compiled and executed on the GPU using the PyCUDA package (Klöckner et al., 2009). With 240-core GPUs, we achieved a 50–80×-speed improvement using a single GPU (and multiple GPUs can be installed in a single machine or over a cluster for further speed improvements).
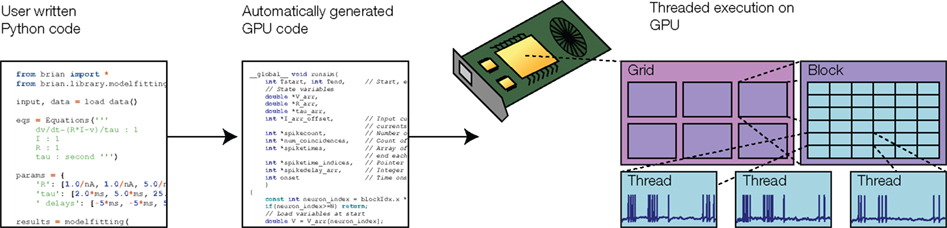
Figure 3. Simulation on graphics processing unit (GPU). Model code is transformed into GPU-executable code and compiled at runtime. The GPU simulates the neurons with one execution thread per neuron, each with a specific set of parameter values. GPU threads are organized into blocks, and blocks are organized into grids. The division into blocks and grids controls the memory access patterns in the GPU hardware.
3 Results
3.1 Fitting Models of Cortical and Brainstem Neurons
Figure 4 shows the application of our procedure to an in vitro intracellular recording of a cortical pyramidal cell from the 2009 Quantitative Single-Neuron Modeling competition (challenge A, first trace). In these recordings, fluctuating currents were injected into the soma and the elicited spike trains were used to fit various models. The most accurate one on the training data was the MAT-model (Kobayashi et al., 2009), which won the INCF competition: it predicted about 86% of reliable spikes (spikes that are repeatedly observed in different trials) with 4 ms precision. It is essentially an integrate-and-fire model with adaptive threshold: the threshold is a sum of two adaptive components, which increase by a fixed amount after each spike and relax to an equilibrium value with different time constants. Other sorts of integrate-and-fire models with adaptation (either as an adaptive current or an adaptive threshold) also performed very well (see also Rossant et al., 2010). On the test data, the simpler adaptive integrate-and-fire model performed better than the MAT-model (79 vs. 66%), which indicates overfitting, but this is presumably because we had to split the competition traces into training and test traces, resulting in little available data for the fitting. Interestingly, more complex models did not perform better. In particular, the adaptive exponential integrate-and-fire model (Brette and Gerstner, 2005; AdEx) did not give better results although spike initiation is more realistic (Fourcaud-Trocme et al., 2003; Badel et al., 2008). This surprising result is explained by the fact that the optimized slope factor parameter (δT) was very small, in fact almost 0 mV, meaning that spike initiation was as sharp as in a standard integrate-and-fire model. This is consistent with the fact that spikes are sharp at the soma (Naundorf et al., 2006; McCormick et al., 2007), sharper than expected from the properties of sodium channels alone, because of the active backpropagation of spikes from the axon initiation site (Hu et al., 2009; Platkiewicz and Brette, 2010). The Izhikevich (2003) model, a two-variable model with the same qualitative properties as the AdEx model, did not perform as well. This could be because spike initiation is not sharp enough in this model (Fourcaud-Trocme et al., 2003) or because it is based on the quadratic model, which approximates the response of conductance-based models to constant currents near threshold, while the recorded neurons were driven by current fluctuations. We also fitted the HH model to the response of a fast spiking cortical cell, by optimizing the maximal conductances and the capacitance. The performance was much worse than that of an integrate-and-fire model (35 vs. 80%), even though the number of free parameters was slightly larger. One possibility is that the channel properties in the HH models did not match those of the cells and should have been optimized as well – although this increases the number of free parameters and therefore the quality of the optimization. But a likely possibility is that the sharpness of spikes cannot be well reproduced by a single-compartment HH model (Naundorf et al., 2006), even though it can by reproduced by a more complex multicompartmental HH model (McCormick et al., 2007; Hu et al., 2009). This suggests that, as a phenomenological model of cortical neurons, the single-compartment HH model might be less accurate than a simpler integrate-and-fire model.
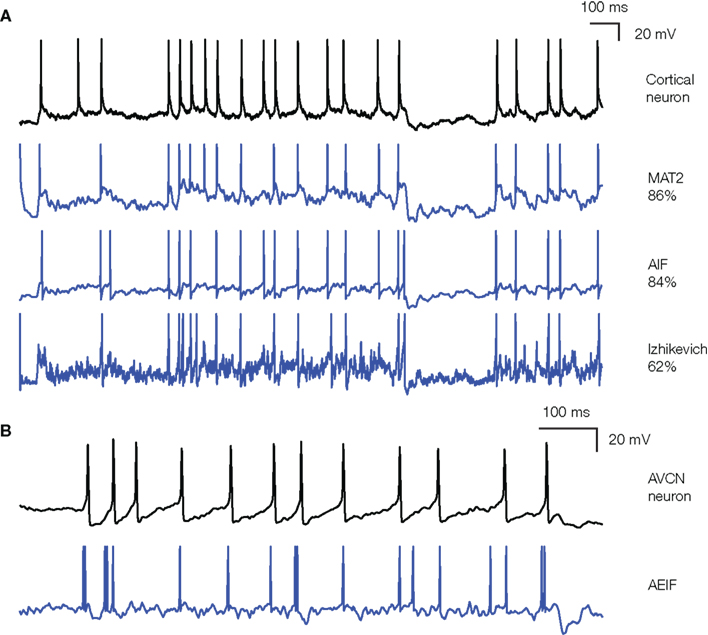
Figure 4. Fitting spiking models to electrophysiological recordings. (A) The response of a cortical pyramidal cell to a fluctuating current (from the INCF competition) is fitted to various models: MAT (Kobayashi et al., 2009), adaptive integrate-and-fire, and Izhikevich (2003). Performance on the training data is indicated on the right as the gamma factor (close to the proportion of predicted spikes), relative to the intrinsic gamma factor of the neuron (i.e., proportion of common spikes between two trials). Note that the voltage units for the models are irrelevant (only spike trains are fitted). (B) The response of an anteroventral cochlear nucleus neuron (brain slice made from a P12 mouse, see Methods in Magnusson et al., 2008) to the same fluctuating current is fitted to an adaptive exponential integrate-and-fire [Brette and Gerstner, 2005; note that the responses do not correspond to the same portion of the current as in (A)]. The cell was electrophysiologically characterized as a stellate cell (Fujino and Oertel, 2001). The performance was Γ = 0.39 in this case (trial-to-trial variability was not available for this recording).
We also applied our model fitting technique to a recording of a neuron in the anteroventral CN of the auditory brainstem (brain slice made from a P12 mouse, see Methods in Magnusson et al., 2008). In this case, it appeared that simple models were less accurate than for cortical neurons (Figure 4B shows a fit to an adaptive exponential integrate-and-fire model Brette and Gerstner, 2005). One reason might be that neurons in the CN are more specialized than cortical neurons, with specific morphology (Wu and Oertel, 1984) and strong non-linear conductances (Golding et al., 1999), which make them very sensitive to coincidences in their inputs (McGinley and Oertel, 2006). Interestingly, the performance of a biophysical HH model of CN neurons (Rothman and Manis, 2003) was even worse, when we optimized the maximal conductances of the various ionic channels. It could be that other channel parameters should also be optimized (time constants, reversal potentials, etc.), or that spike initiation is not well reproduced in single-compartment HH models.
3.2 Reducing Complex Biophysical Models to Simple Phenomenological Models
Our model fitting tools can also be used to reduce a complex biophysical model to a simpler phenomenological one, by fitting the simple model to the spike train generated by the complex model in response to a fluctuating input. We show an example of this technique in Figure 5 where a multicompartmental model of a cortical neuron, used in a recent study of spike initiation (Hu et al., 2009), is reduced to an integrate-and-fire model with adaptive threshold (Platkiewicz and Brette, 2010). In this example, the simpler model predicted 90% of spikes (Γ = 0.90) with a 4-ms precision. This surprising accuracy may be due to the fact that active backpropagation of action potentials from the initiation site to the soma makes spike initiation very sharp (McCormick et al., 2007), as in an integrate-and-fire model. Indeed, it can be seen in Figure 8 of Platkiewicz and Brette (2010), where threshold properties of this multicompartmental model were studied, that spikes are produced precisely when the membrane potential exceeds the (dynamic) threshold.

Figure 5. Reduction of a complex biophysical model to a phenomenological spiking model. The response of a multicompartmental cortical neuron model (Hu et al., 2009) to a fluctuating current is simulated (A), and fitted by an integrate-and-fire model with adaptive threshold (B), as defined in (Rossant et al., 2010). The threshold is in green and the membrane potential in blue (note that the voltage unit for the model is arbitrary). The simpler spiking model could predict about 90% of spikes with a 4-ms precision (Γ = 0.9).
4 Discussion
We have developed efficient parallel algorithms for fitting arbitrary spiking neuron models to electrophysiological data, which are now freely available as part of the Brian simulator3. These algorithms can take advantage of GPUs, which are cheap pieces of hardware available on many desktop PCs and laptops. They can also run on the multiple computers running in a lab, without specific hardware or complex configuration. This computational tool can be used by modelers in systems neuroscience, for example, to obtain empirically validated models for their studies. Because the technique requires only a few minutes of current-clamp recording, another interesting application would be to examine diversity in neural populations, to examine for example the variability and correlations of parameters (maximum conductances, time constants, and so forth). Other model fitting techniques have been previously described by several authors, most of them based on maximum likelihood (Paninski et al., 2004, 2007; Huys et al., 2006), but these are generally model-specific whereas our approach is generic. Besides, maximum likelihood techniques are designed for cases when neuron responses are very variable between trials and can only be described in a probabilistic framework. On the contrary, the optimization approach we chose is best suited for current-clamp recordings in slices, in which neural responses are precisely reproducible (Mainen and Sejnowski, 1995).
Our results confirm that integrate-and-fire models with adaptation are a good description of the response of cortical neurons to somatically injected currents. Complex multicompartmental models of cortical neurons could also be accurately reduced to such simple models. This is surprising for two reasons. Firstly, neurons have many ionic channels with specific properties and it would be surprising that they are not relevant for the input–output properties of neurons. However, it is known that detailed conductance-based models with widely diverse ion channel characteristics can in fact have the same properties at the neuron level (Goldman et al., 2001). Our technique only produces a phenomenological or “effective” description of neural responses, without trying to explicitly model all the contributing ionic mechanisms. We can speculate that the presence of a variety of ionic channels makes it possible for the cell to tune its integrative properties through the action of modulation or intrinsic plasticity, which are not included in the effective description. Another important aspect to bear in mind is that we only addressed the response of neurons to somatically injected currents, while dendritic properties are certainly very important for the function of cortical neurons (Stuart et al., 1999). Interestingly, simple models did not perform as well at predicting the spike trains of neurons in the auditory brainstem, presumably because they express strong non-linear ionic channels, e.g., Ih (Rothman and Manis, 2003). Secondly, spike initiation in integrate-and-fire models is very sharp, unlike in HH models, and this is known to impact the response of neuron models to fluctuating inputs (Fourcaud-Trocme et al., 2003), so it might seem surprising that integrate-and-fire models predict the responses of cortical neurons so well. However, in real cortical neurons, spike initiation is in fact very sharp, unlike in single-compartment HH models (Naundorf et al., 2006; Badel et al., 2008). This property results from the active backpropagation to the soma of spikes initiated in the axon hillock (McCormick et al., 2007). Complex multicompartmental HH models can reproduce this property, as well as threshold variability (Hu et al., 2009; Platkiewicz and Brette, 2010), but single-compartment ones cannot. This explains why integrate-and-fire models are surprisingly effective descriptions of spike initiation in cortical neurons – if adaptation is also included, in particular threshold adaptation (Platkiewicz and Brette, 2010).
Our model fitting toolbox can be extended in several ways. Different optimization algorithms could be implemented, but more interestingly different error criterions could be chosen. For example, one could fit the intracellular voltage trace rather than the spike trains, or try to predict the value of the spike threshold (Azouz and Gray, 2000; Platkiewicz and Brette, 2010). Finally, although our technique primarily applies to neural responses to intracellular current injection, it could in principle be applied also to extracellularly recorded responses to time-varying stimuli (e.g., auditory stimuli), if spike timing is reproducible enough, for example in the bushy cells of the CN (Louage et al., 2005).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the European Research Council (ERC StG 240132) and by Vetenskapsrådet (grant no. 80326601).
Key Concepts
Phenomenological spiking model
An effective neuron model with accurate input–output properties (the output being spike trains), but where the underlying biophysical mechanisms are not explicitly represented (e.g., integrate-and-fire model), as opposed to a biophysical model (e.g., Hodgkin–Huxley model).
Python is a high-level programming language. Programs can be run from a script or interactively from a shell (as in Matlab). It is often used for providing a high-level-interface to low level code. The Python community has developed a large number of third party packages, including NumPy and SciPy which are commonly used for efficient numerical and scientific computation.
Vectorization is a technique for achieving computational efficiency in high-level languages. It consists of replacing repeated operations by single operations on vectors (e.g., arithmetic operations) that are implemented in a dedicated efficient package (e.g., NumPy for Python).
Graphics processing units or GPUs are specialized chips available on most modern computers (originally for graphics rendering), which can be used for high-performance parallel computing. These chips consist of up to 512 processor cores working in parallel.
Global optimization is the minimization or maximization of a function of several variables, using algorithms such as genetic algorithms, particle swarm optimization, differential evolution.
Footnotes
References
Azouz, R., and Gray, C. (2000). Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc. Natl. Acad. Sci. U.S.A. 97, 8110.
Badel, L., Lefort, S., Brette, R., Petersen, C. C. H., Gerstner, W., and Richardson, M. J. E. (2008). Dynamic I-V curves are reliable predictors of naturalistic pyramidal-neuron voltage traces. J. Neurophysiol. 99, 656–666.
Brette, R., and Gerstner, W. (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637–3642.
Brette, R., and Goodman, D. F. (2010). Vectorised algorithms for spiking neural network simulation. Neural. Comput. (in press).
Fourcaud-Trocme, N., Hansel, D., van Vreeswijk, C., and Brunel, N. (2003). How spike generation mechanisms determine the neuronal response to fluctuating inputs. J. Neurosci. 23, 11628–11640.
Fujino, K., and Oertel, D. (2001). Cholinergic modulation of stellate cells in the mammalian ventral cochlear nucleus. J. Neurosci. 21, 7372–7383.
Golding, N. L., Ferragamo, M. J., and Oertel, D. (1999). Role of intrinsic conductances underlying responses to transients in octopus cells of the cochlear nucleus. J. Neurosci. 19, 2897–2905.
Goldman, M. S., Golowasch, J., Marder, E., and Abbott, L. F. (2001). Global structure, robustness, and modulation of neuronal models. J. Neurosci. 21, 5229–5238.
Goodman, D., and Brette, R. (2009). The Brian simulator. Front. Neurosci. 3:2. doi: 10.3389/neuro.01.026.2009
Goodman, D. F. M. (2010). Code generation: a strategy for neural network simulators. Neuroinformatics 8, 183–196.
Hansen, N., and Ostermeier, A. (2001). Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 9, 159–195.
Hu, W., Tian, C., Li, T., Yang, M., Hou, H., and Shu, Y. (2009). Distinct contributions of na(v)1.6 and na(v)1.2 in action potential initiation and backpropagation. Nat. Neurosci. 12, 996–1002.
Huys, Q. J. M., Ahrens, M. B., and Paninski, L. (2006). Efficient estimation of detailed single-neuron models. J. Neurophysiol. 96, 872–890.
Jolivet, R., Kobayashi, R., Rauch, A., Naud, R., Shinomoto, S., and Gerstner, W. (2008). A benchmark test for a quantitative assessment of simple neuron models. J. Neurosci. Methods 169, 417–424.
Jolivet, R., Lewis, T. J., and Gerstner, W. (2004). Generalized integrate-and-fire models of neuronal activity approximate spike trains of a detailed model to a high degree of accuracy. J. Neurophysiol. 92, 959–976.
Jolivet, R., Schrmann, F., Berger, T. K., Naud, R., Gerstner, W., and Roth, A. (2008). The quantitative single-neuron modeling competition. Biol. Cybern. 99, 417–426.
Klöckner, A., Pinto, N., Lee, Y., Catanzaro, B., Ivanov, P., Fasih, A., Sarma, A. D., Nanongkai, D., Pandurangan, G., and Tetali, P. (2009). PyCUDA: GPU run-time code generation for high-performance computing. Arxiv preprint arXiv 0911.3456.
Kobayashi, R., Tsubo, Y., and Shinomoto, S. (2009). Made-to-order spiking neuron model equipped with a multi-timescale adaptive threshold. Front. Comput. Neurosci. 3:9. doi: 10.3389/neuro.10.009.2009
Louage, D. H. G., van der Heijden, M., and Joris, P. X. (2005). Enhanced temporal response properties of anteroventral cochlear nucleus neurons to broadband noise. J. Neurosci. 25, 1560–1570.
Magnusson, A. K., Park, T. J., Pecka, M., Grothe, B., and Koch, U. (2008). Retrograde GABA signaling adjusts sound localization by balancing excitation and inhibition in the brainstem. Neuron 59, 125–137.
Mainen, Z., and Sejnowski, T. (1995). Reliability of spike timing in neocortical neurons. Science 268, 1503.
McCormick, D. A., Shu, Y., and Yu, Y. (2007). Neurophysiology: Hodgkin and Huxley modelstill standing? Nature 445, E12; discussion E2–E3.
McGinley, M. J., and Oertel, D. (2006). Rate thresholds determine the precision of temporal integration in principal cells of the ventral cochlear nucleus. Hear. Res. 216–217, 52–63.
Naundorf, B., Wolf, F., and Volgushev, M. (2006). Unique features of action potential initiation in cortical neurons. Nature 440, 1060–1063.
Owens, J. D., Luebke, D., Govindaraju, N., Harris, M., Kruger, J., Lefohn, A. E., and Purcell, T. J. (2007). A survey of general-purpose computation on graphics hardware. Comput. Graph. Forum 26, 80–113.
Paninski, L., Pillow, J., and Lewi, J. (2007). Statistical models for neural encoding, decoding, and optimal stimulus design. Prog. Brain Res. 165, 493–507.
Paninski, L., Pillow, J. W., and Simoncelli, E. P. (2004). Maximum likelihood estimation of a stochastic integrate-and-fire neural encoding model. Neural. Comput. 16, 2533–2561.
Platkiewicz, J., and Brette, R. (2010). A threshold equation for action potential initiation. PLoS Comput. Biol. 6, e1000850. doi: 10.1371/journal.pcbi.1000850
Rossant, C., Goodman, D. F. M., Platkiewicz, J., and Brette, R. (2010). Automatic fitting of spiking neuron models to electrophysiological recordings. Front. Neuroinformatics 4:2. doi: 10.3389/neuro.11.002.2010
Rothman, J. S., and Manis, P. B. (2003). The roles potassium currents play in regulating the electrical activity of ventral cochlear nucleus neurons. J. Neurophysiol. 89, 3097–3113.
Keywords: python, spiking models, simulation, optimization, parallel computing
Citation: Rossant C, Goodman DFM, Fontaine B, Platkiewicz J, Magnusson AK and Brette R (2011) Fitting neuron models to spike trains. Front. Neurosci. 5:9. doi: 10.3389/fnins.2011.00009
Received: 29 October 2010;
Accepted: 13 January 2011;
Published online: 23 February 2011.
Edited by:
Henry Markram, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Werner Van Geit, Okinawa Institute of Science and Technology, JapanCopyright: © 2011 Rossant, Goodman, Fontaine, Platkiewicz, Magnusson and Brette. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Romain Brette obtained a PhD in Computational Neuroscience from the Paris VI University in France. He did postdoctoral studies in Alain Destexhe’s group in Gif-sur-Yvette (France) and Wulfram Gerstner’s group in Lausanne (Switzerland). He is now an associate professor of computational neuroscience at Ecole Normale Supérieure, Paris. His group investigates spike-based neural computation, theory, and simulation of spiking neuron models, with a special focus on the auditory system.cm9tYWluLmJyZXR0ZUBlbnMuZnI=





