- 1 Department of Mathematics, University of Houston, Houston, TX, USA
- 2 Department of Biology and Biochemistry, University of Houston, Houston, TX, USA
Neurons integrate inputs from thousands of afferents. Similarly, some experimental techniques record the pooled activity of large populations of cells. When cells in these populations are correlated, the correlation coefficient between the collective activity of two subpopulations is typically much larger than the correlation coefficient between individual cells: The act of pooling individual cell signals amplifies correlations. We give an overview of this phenomenon and present several implications. In particular, we show that pooling leads to synchronization in feedforward networks and that it can amplify and otherwise distort correlations between recorded signals.
1 Introduction
To characterize the neural code it is essential to understand how information is represented in the collective response of neurons. The correlation between cell pairs is a fundamental statistic that can be extracted from concurrent recordings of multiple cells. It has therefore frequently been used to characterize the dependence between neuronal responses. Cells at different stages of processing, from periphery (Mastronarde, 1983; Meister et al., 1995; Schneidman et al., 2006), through sensory (Zohary et al., 1994; Kohn et al., 2009) and motor areas (Lee et al., 1998) display correlated firing. Correlations can be important in sensory coding (Romo et al., 2003; Jones and Gabbiani, 2010), can carry information about movement direction (Nicolelis et al., 1995; Maynard et al., 1999; Kilavik et al., 2009), and can significantly affect the amount of information in neuronal responses (Zohary et al., 1994; Abbott and Dayan, 1999; Sompolinsky et al., 2001; Averbeck et al., 2006). However, the strength of these dependencies, and the impact they may have on the neural code are hotly debated (Ecker et al., 2010; London et al., 2010; Renart et al., 2010). It is therefore essential to understand the mechanisms that shape correlations between neurons in a population.
The total input to a cortical neuron often represents the pooled activity of hundreds to thousands of afferent cells. Similarly, voltage sensitive dye (VSD) and multi-unit (MU) recordings can represent the pooled activity of many nearby cells (Gray et al., 1995; Grinvald and Hildesheim, 2004). Here, we discuss the effects of such pooling on correlations and explore several implications.
Correlations can be dramatically amplified by pooling: Weak correlations between pairs of cells in two populations can result in high correlations between the summed activity of these two populations (Bedenbaugh and Gerstein, 1997; Chen et al., 2006; Renart et al., 2010; Rosenbaum et al., 2010). An illustration is provided in Figure 1A: Two electrodes each record the ensemble activity of a population of weakly correlated cells. Even in the absence of overlap, the recorded signals are much more strongly correlated than the activity of individual cells. The same effect can cause strong correlations between the activity of two neurons that receive inputs from a population of weakly correlated cells. Correlations between excitatory and inhibitory cells can modulate this effect, but only when excitation and inhibition are nearly perfectly balanced (Hertz, 2010; Renart et al., 2010; Rosenbaum et al., 2010).
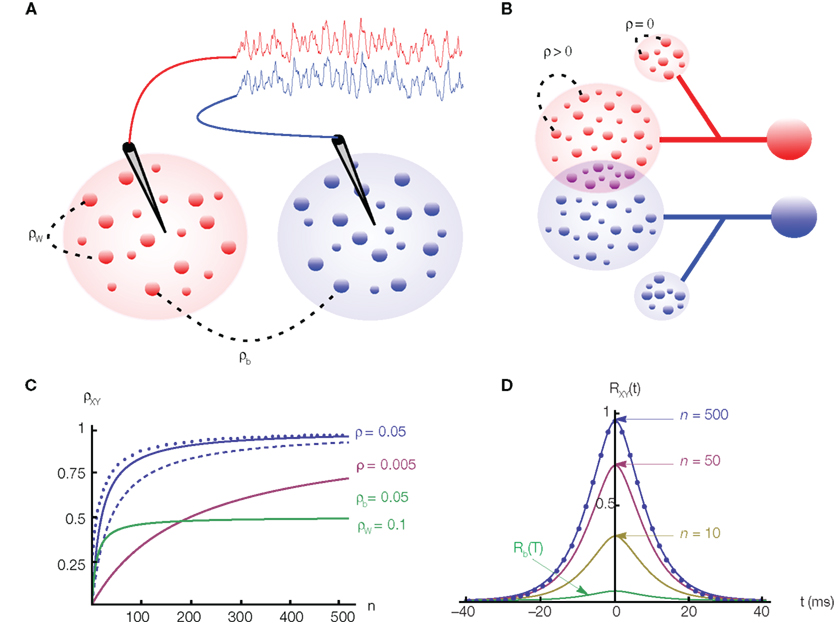
Figure 1. The effects of correlations on pooled signals. (A) Two electrodes record from non-overlapping populations. Cells from separate (same) populations are correlated with coefficient ρb (ρw). The traces above the populations were obtained by convolving the pooled spike trains with an exponential kernel. Here ρb = ρw = 0.050 and n = 500. Although ρb is small, the traces are strongly correlated. (B) Two cells receiving input from overlapping populations. Each of the two subpopulations on the left contain n cells. All pairs of cells within these subpopulations are correlated with coefficient ρ. The two cells on the right share np of their inputs from these subpopulations (purple intersection). Additionally, each cell receives nq uncorrelated inputs (smaller populations on top and bottom). (C) The dependence of the pooled correlation, ρXY, on population size, n, for the examples in (A,B). Green line corresponds to population model (A) with ρb = 0.05 and ρw = 0.1, while the blue line corresponds to (B) with ρ = 0.05 and p = q = 0 (solid line); p = 0 and q = 1 (dashed line); p = 0.25 and q = 0 (dotted line). A moderate amount of overlap between the populations or independent inputs do not significantly affect the pooled correlation when n is large. The pink line corresponds to model (A) with ρb = ρw = 0.005. (D) The cross-correlation function from the population model in (A) with Rb(t) = Rw(t) = 0.05e−t|/5(1 + |t|/5) and for various values of n. The case n = 500 corresponds to the traces in (A) and the filled circles are from simulations.
This amplification of correlations has a simple mathematical explanation and has been noticed a number of times in different contexts (Bedenbaugh and Gerstein, 1997; Super and Roelfsema, 2005; Chen et al., 2006; Stark et al., 2008; Renart et al., 2010). We review, synthesize, and extend several existing results that pertain to this phenomenon and discuss several implications. In particular, we show that the effects of pooling on correlations is the primary mechanism responsible for the synchronization of feedforward chains. We also show that the effects of pooling can conceal the stimulus dependence of correlations as measured by MU recordings and otherwise distort relations between recorded signals.
2 The Impact of Pooling on Correlations
We start by examining the effects of pooling in a simple setting where two signals each represent the summed activity of a population. We will first look at how pooling affects the correlation coefficient between such signals, and then examine the impact on their cross-correlation function.
The Impact of Pooling on Correlation Coefficients
We represent the activity of cells in two populations by 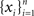 and
and 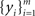 respectively, where xi and yi are random numbers that can represent spike counts or some other scalar measure of neuronal response. The pooled activity from the two populations is assumed to be
respectively, where xi and yi are random numbers that can represent spike counts or some other scalar measure of neuronal response. The pooled activity from the two populations is assumed to be 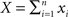 and
and 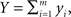 which can represent the total input spike counts to a pair of downstream cells. The following discussion applies to any pair of signals that represent an approximately linear combination of individual cell activity.
which can represent the total input spike counts to a pair of downstream cells. The following discussion applies to any pair of signals that represent an approximately linear combination of individual cell activity.
To simplify the exposition we assume homogeneity in the populations: All variables have the same variance, σ2 = var(xi) = var(yi), and the populations have equal size, n = m. To illustrate the impact of correlations between individual variables, i.e., the xi’s and yi’s, on the pooled quantities, X and Y, we consider two idealized population models. As discussed below, the effects of pooling are similar under more general assumptions (Rosenbaum et al., 2010).
The first population model (Figure 1A) captures the fundamental effects of pooling on correlations between two populations. For simplicity, we assume that the populations are non-overlapping. The correlation coefficients between two cells from separate populations (the between correlations) are denoted by ρb = cov(xi, yj)/σ2. The correlation coefficients between pairs from the same population (the within correlations) are ρw = cov(xi, xk)/σ2 = cov(yi, yk)/σ2, for i ≠ k. The correlation coefficient between the pooled variables is then given by (Bedenbaugh and Gerstein 1997; Rosenbaum et al., 2010)
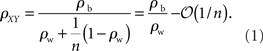
Hence, for large n, the correlation between the pooled signals approaches the ratio of the between and within correlations (see Figure 1C). More generally, |ρXY| ≥ |ρb| so that pooling amplifies correlations for any value of n.
If the recordings are from two subsets of a larger, homogeneous population then ρb = ρw = ρ. When pooling from a smaller number of neurons, ρXY = nρ + (ρ2), and pooled activity increases approximately linearly with population size (Renart et al., 2010). For large populations correlations saturate and ρXY = 1−(1/n).
This analysis also provides simple bounds on pairwise correlations in a population. For example in the population model considered in Figure 1A, the fact that |ρXY| < 1 combined with Eq. (1) tells us that that |ρb| ≤ |ρw| + (1/n). That is, pairwise correlations between two populations are bounded by the correlations within the two populations. As the input population size grows, this bound becomes tighter and ρb cannot be much larger than ρw.
The second population model (Figure 1B), illustrates the case when X and Y represent the activity of overlapping populations. We assume that a proportion p of the n recorded cells in a population are shared between the populations. This implies that cov(xi,yj)/σ2 = 1 for n p separate xi, yj pairs. The remaining n (n − np) pairs have correlation ρ = cov(xi, yj)/σ2. For simplicity, assume that the within correlations are the same as the between correlations: ρ = cov(xi, yj)/σ2= cov(xi, xk)/σ2 = cov(yi, yk)/σ2 for i ≠ k. We also include inputs from two external, statistically independent populations, modeled by m = qn independent variables. Hence, 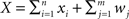 and
and 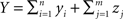 where zj and wj are independent from all other variables, i.e., cov(wj,u) = 0 for all u ≠ wj and cov(zj,u) = 0 for all u ≠ zj. The correlation coefficient between the pooled variables is then given by (Rosenbaum et al., 2010)
where zj and wj are independent from all other variables, i.e., cov(wj,u) = 0 for all u ≠ wj and cov(zj,u) = 0 for all u ≠ zj. The correlation coefficient between the pooled variables is then given by (Rosenbaum et al., 2010)
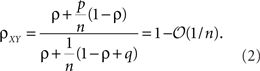
Overlap between the two populations, as well as uncorrelated input, does not significantly affect the pooled correlation, ρXY, when n is large (see Figure 1C). For smaller values of n and when ρ is small, correlations are dominated by overlap and ρXY ≈ p.
The equations discussed above have been studied in the context of multiunit recordings (Bedenbaugh and Gerstein, 1997) and VSD signals (Chen et al., 2006). They can be generalized to arbitrary heterogeneous populations (Rosenbaum et al., 2010) yielding an equation that is nearly identical to Eq. (1) with ρb and ρw replaced by weighted averages of the correlations between and within each population. Thus, the main ideas that we discuss are not fundamentally impacted by heterogeneity. In Figure 1C, we illustrate the dependence of ρXY on the population size, n, for the population models discussed above.
The Impact of Pooling on Cross-Correlation Functions
It is frequently of interest to determine correlations over different timescales (Bair et al., 2001; Smith and Kohn, 2008). For instance, the filtering of recorded spike trains by synapses or recording devices can affect the timescale over which correlations occur (Tetzlaff et al., 2008; Rosenbaum et al., 2010; Tetzlaff and Diesmann, 2010) and downstream cells with short membrane time constants may be more sensitive to tightly synchronous inputs (Moreno et al., 2002; Gutnisky and Josić, 2010). Assuming two signals, x(t) and y(t), are jointly stationary, this temporal correlation structure is captured by the cross-correlation function (Perkel et al., 1967),
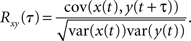
Due to stationarity, var(y(t)) = var(y(t + τ)) so that −1 < Rxy(τ) < 1 is simply the correlation coefficient between the random variables x(t) and y(t + τ). Thus, the impact of pooling on cross-correlation functions can be understood in terms of the results in the previous section.
We derive the analog of Eq. (1) for cross-correlation functions. Assume that 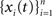 and
and 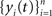 are populations of stationary stochastic processes with σ2 = var(xi(t)) = var(yi(t)),
are populations of stationary stochastic processes with σ2 = var(xi(t)) = var(yi(t)), 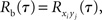 and
and 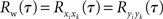 for i ≠ k. The cross-correlation function between the pooled processes,
for i ≠ k. The cross-correlation function between the pooled processes, 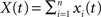 and
and 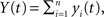 is given by
is given by
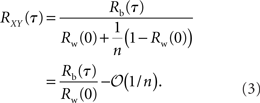
This equation can be related to Eq. (1) intuitively by recalling that RXY(τ) is the correlation coefficient between X(t) = Σixi(t) and Y(t + τ) = Σiyi(t + τ). The “between” correlations in this case are given by the correlation coefficient between xi(t) and yj(t + τ), i.e., Rb(τ) = cov(xi(t), yj(t + τ))/σ2. Similarly, the “within” correlations are given by Rw(0) = cov(xi(t), xj(t))/σ2 = cov(yi(t + τ), yj(t + τ))/σ2.
From Eq. (3) we see that pooling scales the entire cross-correlation function by Rw(0) + (1 − Rw(0))/n so that correlations over all time lags are scaled by the same factor. We also see that the cross-correlation function is generally amplified by pooling in the sense that |RXY(τ)| ≥ |Rb(τ)|. For homogeneous populations, where Rb(τ) = Rw(τ) = R(τ), the zero-lag cross-correlation, RXY(0), approaches 1 for large n, as illustrated in Figure 1D.
3 Pooling Induces Synchronization in Feedforward Networks
Layered feedforward networks (Figure 2), provide a simple setting to study the propagation of neuronal activity (Kumar et al., 2010). In general, neurons in the deeper layers of such networks tend to synchronize (Diesmann et al., 1999; van Rossum et al., 2002; Litvak et al., 2003; Reyes, 2003; Tetzlaff et al., 2003; Doiron et al., 2006; Kumar et al., 2008). Propagation of synchronous activity is important for some neural codes (Abeles, 1991; Abeles et al., 1994; Diesmann et al., 1999), but the tendency of feedforward to synchronize in feedforward networks generally reduces information encoded in deeper layers (van Rossum et al., 2002; Kumar et al., 2010).
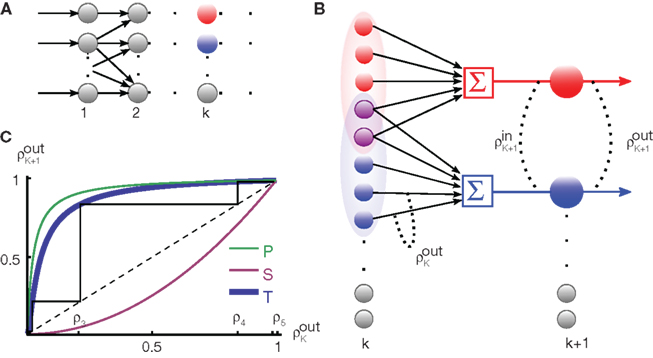
Figure 2. The effect of pooling in feedforward networks. (A) A schematic diagram of a feedforward network with random connectivity. Each layer consists of N cells. Each cell in layer k + 1 receives a fixed number of randomly selected inputs from layer k. (B) The stages of processing in the network pictured in (A). Outputs from layer k are pooled to form the input to each cell in layer k + 1. These inputs are, in turn, decorrelated by the cells in layer k + 1. The combined effect can lead to large gains in correlation from layer-to-layer. (C) Iteration of the dynamical model described in the text. The green line represents the pooling map P, the pink line is the decorrelating transfer map, S (here chosen to be S(ρ) = ρ2). The solid blue line represents their composition, T = S ± P, which maps output correlations from layer k to output correlations from layer k + 1. The solid black line shows the trajectory obtained by iterating the map with 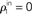 , ne = 600, ni = 400, p = 0.05.
, ne = 600, ni = 400, p = 0.05.
The amplification of correlations due to pooling underlies the development of synchrony in feedforward networks. This effect can be understood using the diagram in Figure 2B: The input to layer k + 1 is obtained by pooling the output of layer k, leading to a large gain in correlations. This pooled input is then passed through the cells of layer k + 1. Due to cellular dynamics and the effects of thresholding, a layer of neurons typically reduces correlations, especially when the cells are operating in a fluctuation dominated regime (Shea-Brown et al., 2008; Rosenbaum and Josić, 2011). However, the correlating effects of pooling will often outweigh the decorrelating effects of cellular dynamics. Correlations between cells in layer k + 1 will therefore be greater than those in layer k.
The development of synchrony can be illustrated more quantitatively using a mean-field model. We follow a construction similar to those in Aviel et al. (2003), Tetzlaff et al. (2003), but highlight the effects of pooling. In addition, we oversimplify the input–output correlation transfer of a neuron. For a more detailed study of the interplay between correlation transfer and firing rates of cells, see Tetzlaff et al. (2003). Consider a randomly connected feedforward network with excitatory and inhibitory cells, and denote the input correlations to and output correlations from cells in the kth layer by 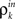 and
and 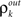 respectively. In a network with random connectivity, the number of inputs to a cell in a layer, as well as the overlap in the pools projecting to two cells are random quantities. We replace these quantities with their means to obtain a tractable model. Hence each cell receives input from exactly ne excitatory and ni inhibitory cells, and each pair of cells share a fraction p of their excitatory and inhibitory input pools.
respectively. In a network with random connectivity, the number of inputs to a cell in a layer, as well as the overlap in the pools projecting to two cells are random quantities. We replace these quantities with their means to obtain a tractable model. Hence each cell receives input from exactly ne excitatory and ni inhibitory cells, and each pair of cells share a fraction p of their excitatory and inhibitory input pools.
The inputs to layer k + 1 are obtained by pooling the outputs from layer k. The effect of this pooling on the correlation, 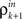 , between the inputs to layer k + 1 is captured by a mapping P such that
, between the inputs to layer k + 1 is captured by a mapping P such that 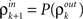 . This mapping can be derived using Eq. (4) (see Tetzlaff et al., 2003; Rosenbaum et al., 2010),
. This mapping can be derived using Eq. (4) (see Tetzlaff et al., 2003; Rosenbaum et al., 2010),
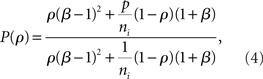
where β measures the balance of excitation and inhibition. Assuming for simplicity that excitation and inhibition have equal synaptic weights, β = ne/ni. As illustrated in Figure 2C, P is strongly correlating when ne and ni are large and β ≠ 1. To complete the dynamical model, we must map input correlations to output correlations. As a simplifying approximation, we assume that 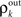 only depends on
only depends on 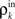 and write
and write 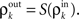 As mentioned above, the mapping from input to output correlations is typically decorrelating, i.e., |S(ρ)| ≤ |ρ|. The composite map, T = S ± P, combines the correlating effects of pooling and the decorrelating effects of cell transfer. This mapping induces the discrete dynamical system,
As mentioned above, the mapping from input to output correlations is typically decorrelating, i.e., |S(ρ)| ≤ |ρ|. The composite map, T = S ± P, combines the correlating effects of pooling and the decorrelating effects of cell transfer. This mapping induces the discrete dynamical system, 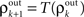 that describes the propagation of correlations across layers (Aviel et al., 2003; Tetzlaff et al., 2003; Rosenbaum et al., 2010).
that describes the propagation of correlations across layers (Aviel et al., 2003; Tetzlaff et al., 2003; Rosenbaum et al., 2010).
The correlating effects of pooling typically outpace the decorrelating effects of cell filtering so that T is correlating (see Figure 2C). Precise balance between excitation and inhibition (β = 1) can prevent runaway synchrony in this simple dynamical model, but this cancelation is difficult to achieve in feedforward networks of spiking cells due to the fragile stability of this asynchronous state (Rosenbaum et al., 2010). However, recurrent networks can dynamically stabilize the asynchronous state under certain conditions (Renart et al., 2010).
We argue that the development of synchrony in large feedforward networks is primarily due to the pooling of correlated inputs. Overlapping inputs introduce correlations in early layers, but the layer-to-layer increase in correlations downstream is primarily a result of pooling and not overlap. This point is illustrated by comparing a network with overlapping inputs (Figure 3A) to a network without overlap (Figure 3B). In Figure 3B, correlations are introduced in the input to the first layer, whereas in Figure 3A input to the first layer are uncorrelated, but correlations are introduced to the second layer by overlap. Comparing layer k in Figure 3B to layer k + 1 in Figure 3A, we see that spiking in the two networks becomes correlated at about the same rate, suggesting that pooling, not overlap, is the mechanism most responsible for the gain in correlations across layers.
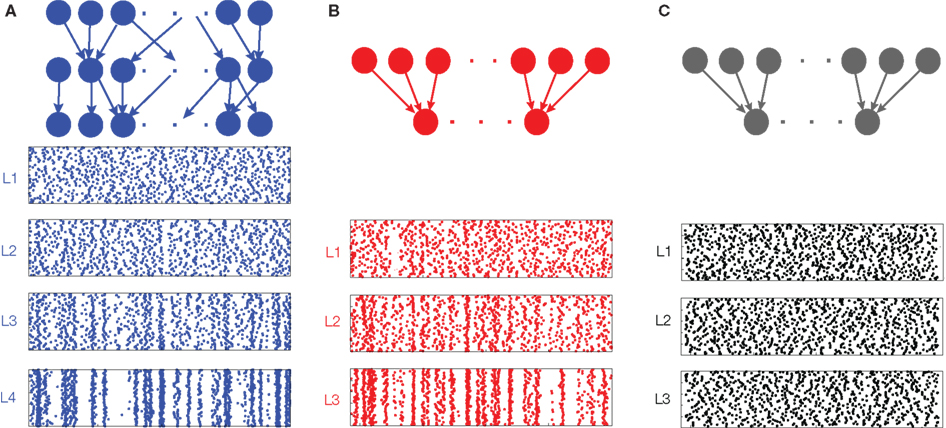
Figure 3. Development of synchrony in feedforward networks. (A) Spike rasters from a simulation of a randomly connected feedforward network. Each cell receives ne = 1400 excitatory and ni = 600 inhibitory inputs. In addition, two cells in a layer share, on average, a proportion p = 0.05 of their inputs. Each cell in layer 1 receives an independent Poisson excitatory input, so that outputs from the first layer are uncorrelated. (B) A feedforward network with no overlap. Each cell receives the same number of inputs as in (A), but there are no shared inputs (p = 0). Correlated inputs are introduced to the first layer,  to match the level of correlation introduced by overlap in the input to layer 2 in (A). (C) A feedforward network with no overlap receiving independent input. All model parameters are the same as in (B). However, the input to the first layer is uncorrelated
to match the level of correlation introduced by overlap in the input to layer 2 in (A). (C) A feedforward network with no overlap receiving independent input. All model parameters are the same as in (B). However, the input to the first layer is uncorrelated  , and synchrony does not develop. The spike count correlation over a window of width 50 ms averaged over all pairs is ρ = 0.02, 0.18, and 0.59 for layers 2, 3, and 4 in (A); and ρ = 0.03, 0.21, and 0.63 for layers 1, 2, and 3 in (B). Cells in all other layers are not correlated.
, and synchrony does not develop. The spike count correlation over a window of width 50 ms averaged over all pairs is ρ = 0.02, 0.18, and 0.59 for layers 2, 3, and 4 in (A); and ρ = 0.03, 0.21, and 0.63 for layers 1, 2, and 3 in (B). Cells in all other layers are not correlated.
The fact that pooling dominates overlap in synchronizing feedforward networks can also be explained quantitatively by appealing to Eq. (4). The effect of overlap in the input population is of order (1/ne, 1/ni) when upstream correlations are non-zero, but pooling has an order unity effect, and is therefore the dominant factor in determining input correlations when input populations are large and upstream correlations are non-zero.
In Figure 3 we see that the activity in deeper layers is not only highly correlated, but tightly synchronous. We can explain this fact by appealing to Eq. (3) which shows that if the “within” and “between” correlation coefficients at lag zero are not significantly different, then RXY(0) approaches unity (see Figure 1D) for large input populations. In a feedforward network, this effect is compounded across layers and cells in deeper layers will tend to spike synchronously.
Synchrony in feedforward networks has received much attention, especially in the context of the propagation of pulse packets (Diesmann et al., 1999; Kumar et al., 2008). While synchrony may benefit temporal codes, it can make rate coding difficult (van Rossum et al., 2002). The tuning of feedforward networks for rate or temporal coding and the impact on information transmission is reviewed in Kumar et al. (2010). An alternative to the present approach is to use Fokker-Planck equations to describe the evolution of the size and shape of pulse packets (Câteau and Fukai, 2001; Doiron et al., 2006). Closer to the present approach, one can develop probabilistic models of randomly connected feedforward networks of binary threshold neurons (Nowotny and Huerta, 2003). However, this approach makes the effects of pooling difficult to isolate.
The lack of recurrence in feedforward networks makes them more amenable to mathematical analysis. However, biophysically realistic layered neuronal networks are embedded within larger, recurrent networks. Moreover, connectivity between cells is not random. Additional structure can lead to richer dynamics and functionality. For instance, the inclusion of disynaptic inhibitory circuits (which amounts to adding lateral inhibitory-to-excitatory and inhibitory-to-inhibitory connections to the purely feedforward network) allows the network to selectively propagate only strongly synchronous inputs (Kremkow et al., 2010). Hence, the details of the feedforward network architecture can significantly impact the propagation of synchronous activity.
4 Impact of Pooling on VSD and MU Recordings
We next explore the effects that pooling can have on recorded signals. First, we show that pooling can mask stimulus dependent changes in spiking correlations. Second, we show that poor discrimination between cells when sorting spikes can artificially increase measured correlations.
4.1 Pooling Can Conceal Stimulus Dependent Changes in Correlation
A stimulus (Kohn and Smith, 2005; de la Rocha et al., 2007; Gutnisky and Dragoi, 2008; Churchland et al., 2010), as well as the behavioral state of the animal (Riehle et al., 1997; Greenberg et al., 2008; Cohen and Maunsell, 2009; Kilavik et al., 2009) can modulate the firing rates and correlations in neuronal responses. Stimulus dependent changes in correlation can have a significant impact on the neural code (Shamir and Sompolinsky, 2004; Josić et al., 2009). However, such changes may be masked in recordings that reflect the pooled activity of large groups of cells.
As discussed above, the correlation, ρXY, between the pooled signals from two large populations of cells reflects the ratio of the “between” and “within” correlations (ρb and ρw), but does not reflect the actual scale of these pairwise correlations. Thus, changes in correlation structure that scale ρb and ρw by the same factor are difficult to detect by looking at the correlation between the pooled recordings.
To illustrate this effect, we consider a simple, experimentally motivated model. Using VSDs, Chen et al. (2006) imaged the response of primary visual cortex in monkey during an attention task. The imaged area was divided into 64 pixels, each pixel capturing the pooled activity of n ≈ 104 neurons. To model such recordings we assume that, in the presence of a stimulus, the firing rate of individual cells decays with the distance from the center of the retinotopic image of that stimulus. When a stimulus is absent, the background firing rate is assumed constant. Additionally, the correlation between the responses of two neurons increase with their firing rates (see de la Rocha et al., 2007; Shea-Brown et al., 2008) and correlations decay exponentially with cell distance (Smith and Kohn, 2008; see however Poort and Roelfsema, 2009; Ecker et al., 2010). In particular, we assume that the correlation between two cells at distance d is given by ρxy = e−αd for some α > 0. See Rosenbaum et al. (2010) for more details about our model and derivations.
We consider the recordings from two pixels, X and Y. In response to a stimulus, correlation between cells in the pixels increase due to an increase in firing rates, however all pairwise correlations are increased by the same factor so that the ratio of between and within correlations is unchanged. Thus, the correlation between the recordings is nearly unchanged by the presence of a stimulus when n is large. More precisely, the correlation between the pooled signals is of the form ρXY = e−αD (1/n) where D is the distance between the pixels (Rosenbaum et al., 2010). This holds whether a stimulus is present or not. Thus, even significant stimulus dependent changes in correlations could be masked in the recorded signals. This overall trend is consistent with the results in Chen et al. (2006; compare Figure 4B to their Figure 2F).
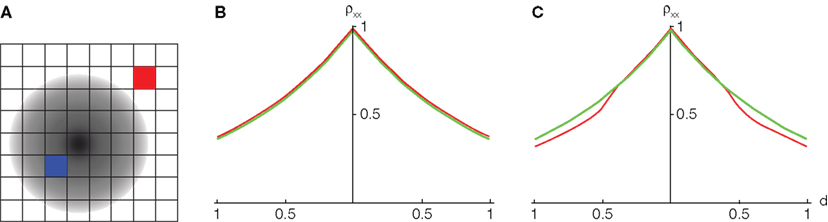
Figure 4. The effect of pooling on recordings of stimulus dependent correlations. (A) A diagram of our model. Signals X(t) and Y(t) are recorded from two pixels (red and blue squares). The activity in response to a stimulus is shown as a gradient centered at some pixel (the center of the retinotopic image of the stimulus). (B) The prediction of the correlation between two pixels obtained using the model considered in the text with stimulus present (red) and absent (green). We assumed that one pixel is located at the stimulus center (d1 = 0). A stimulus dependent change in correlations is undetectable. (C) Same as in (C), except that the activity of cells not tuned to the stimulus is decreased by 50% in the presence of stimulus. Compare to Figure 2F in Chen et al. (2006).
However, in Supplementary Figure 3 of Chen et al. (2006) the presence of a stimulus apparently results in a slight decrease in correlations between more distant pixels. In Figure 4C this effect is reproduced using the model described above with the additional assumption that the activity of cells not tuned to a stimulus is suppressed in the presence of that stimulus. The imaged area was divided into 64 pixels, each pixel capturing the pooled activity of n ≈ 104 neurons (See Figure 4A). The effect can also be reproduced by assuming that the spatial correlation decay constant, α, increases when a stimulus is present.
As this example shows, care needs to be taken when inferring underlying correlation structures from pooled activity. The statistical structure of the recordings can depend on pairwise correlations between individual cells in a subtle way, and different underlying correlation structures may be difficult to distinguish from the pooled signals. The fine structure of correlations may be similarly masked if recordings from many cells are used in obtaining estimates. However, as downstream neurons are driven by the pooled input from many afferents, they may also be insensitive to the precise structure of pairwise correlations.
4.2 Pooling Amplifies Correlations when Spikes are Poorly Discriminated in Multi-Cell Recordings
Spike sorting methods are used to assign action potentials recorded by a single electrode to different cells. Insufficient separation may result in treating spikes from different cells as coming from a single cell (Lewicki, 1998). Thus the response attributed to a single cell can reflect the pooled activity of a small population. Errors in spike sorting can therefore affect estimates of correlations (Gerstein, 2000; Pazienti and Grün, 2006; Ecker et al., 2010; Cohen and Kohn, private communication).
To illustrate this effect, consider an example where m + n cells with equal spike count variance, σ2, are recorded using an extracellular electrode (or several electrodes). Assume that the spikes from m of the cells are mistakenly attributed to a single cell and spikes from the other n are mistakenly attributed to a separate single cell, so that the experimenter sees two cells where there are actually m + n. For simplicity, assume that the spike count correlation between all of the cells is identically ρ. Then the correlation, ρrec, between the recorded spike counts is given by
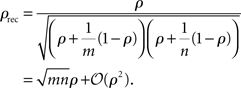
Thus, when cells are weakly correlated, the correlation coefficient between the recorded spike counts is a factor of 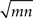 larger than the actual spike count correlation. In practice, it is unlikely that m and n would be large, but even in the simplest case where two cells are mistaken for one and another cell is isolated correctly (m = 2, n = 1), the recorded correlation is a factor of
larger than the actual spike count correlation. In practice, it is unlikely that m and n would be large, but even in the simplest case where two cells are mistaken for one and another cell is isolated correctly (m = 2, n = 1), the recorded correlation is a factor of 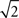 larger than the actual correlation.
larger than the actual correlation.
5 Discussion
We have illustrated how pooling can impact correlations between the inputs to pairs of cells, as well as recordings that represent the summed activity of neuronal populations. These effects have been discussed in a variety of settings (Bedenbaugh and Gerstein, 1997; Super and Roelfsema, 2005; Chen et al., 2006; Stark et al., 2008; Renart et al., 2010), and similar ideas were also developed for the variance alone (Salinas and Sejnowski, 2000; Moreno-Bote et al., 2008). The saturation of the signal-to-noise ratio with increasing population size observed in Zohary et al. (1994) has a similar origin. We have extended these results by generalizing the population models and by giving a combined analysis of the effects of pooling and overlap (Rosenbaum et al., 2010). We also reviewed the impact of pooling on the development of synchrony in feedforward networks and the interpretation of results obtained from recordings of population activity. While pooling increases correlations, it may also mask stimulus dependent changes in correlations because of saturation.
Although feedforward connectivity appears constraining, neuronal architectures may harbor hidden feedforward structures (Ganguli et al., 2008; Goldman, 2009; Murphy and Miller, 2009). However, there are other mechanisms that can modulate correlated activity which we did not address here. For instance, recurrent connections between cells can increase or decrease correlations (Schneider et al., 2006; Ostojić et al., 2009; Renart et al., 2010). Moreover, the activity of groups of neurons may become entrained to network oscillations, thus resulting in more synchronous firing (Womelsdorf et al., 2007). A full understanding of the statistics of population activity will require an understanding of how these mechanisms interact to shape the spatiotemporal properties of the neural response.
In addition to looking at the impact of pooling on correlation coefficients, we also looked at the impact on cross-correlation functions. We found that correlations are amplified by the same factor at all time lags. This effect gives rise to tight synchrony between spiking in deeper layers of feedforward networks.
Although all equations remain valid in the presence of negative correlations, we did not consider them here. Negative correlations can be introduced to the inputs of two cells by negatively correlated afferents or by positively correlated excitatory and inhibitory inputs (Renart et al., 2010). Pooling can amplify negative correlations. However, negative and positive correlations can also cancel between signals that represent the collective activity of cell populations. Only when positive and negative contributions are precisely balanced will such cancelation be exact. Theoretical and experimental studies suggest that such a decorrelated state may be stable in neuronal networks (Ecker et al., 2010; Hertz, 2010; Renart et al., 2010). The non-negative definiteness of covariance matrices also imposes theoretical bounds on their magnitude. Additionally, there are bounds on the magnitude of negative input correlations that can result from correlations between excitatory and inhibitory afferents. These bounds are discussed in the context of pooling in Rosenbaum et al. (2010).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Adam Kohn, Brent Doiron, Eric Shea-Brown, and Jaime de la Rocha for helpful discussions and comments. We also thank the reviewers and the handling editor for numerous useful suggestions. This work was supported by NSF Grant DMS-0817649 and a Texas ARP/ATP award.
Key Concepts
The Pearson correlation coefficient is a measure of dependence between two random quantities. The correlation coefficient between spike counts is frequently used to quantify the statistical dependence between two spike trains. The degree of correlation can impact stimulus coding and network dynamics.
A neuron combines inputs from thousands of afferent cells. Similarly, signals obtained using some recording techniques represent the combined activity of many neurons. We refer to this act of combining cellular activity as “pooling.” Here we assume that the pooled signal represents approximately a linear combination of the component signals.
The spiking activity of neurons can be correlated over a broad timescale. The cross-correlation function quantifies the degree of correlation between two signals over different time lags. In particular, the cross-correlation function evaluated at a time lag τ represents the correlation between one signal at time t and the other at time t + τ.
Within versus between correlations
When looking at the correlation between the pooled activity of two subpopulations, it is necessary to distinguish correlations between elements of the same population (within correlations) from correlations between elements of different populations (between correlations).
A layered network of neurons in which cells in a layer only receive inputs from cells in a previous layer. Frequently, neurons in deeper layers of such networks spike synchronously. Such synchronization is primarily due to the effects of pooling.
Stimulus dependent changes in correlation
The structure and magnitude of correlations in a population of cells can change in response to stimuli, as well as changes in behavioral states. Such changes in correlation can modulate information encoded in the cells’ spike trains. We show that these changes can be masked by the effects of pooling.
References
Abbott, L., and Dayan, P. (1999). The effect of correlated variability on the accuracy of a population code. Neural Comput. 11, 91–101.
Abeles, M. (1991). Corticonics: Neural Circuits of the Cerebral Cortex. New York, NY: Cambridge University Press.
Abeles, M., Prut, Y., Bergman, H., and Vaadia, E. (1994). Synchronization in neuronal transmission and its importance for information processing. Prog. Brain Res. 102, 395–404.
Averbeck, B., Latham, P., and Pouget, A. (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci. 7, 358–366.
Aviel, Y., Mehring, C., Abeles, M., and Horn, D. (2003). On embedding synfire chains in a balanced network. Neural Comput. 15, 1321–1340.
Bair, W., Zohary, E., and Newsome, W. (2001). Correlated firing in macaque visual area MT: time scales and relationship to behavior. J. Neurosci. 21, 1676.
Bedenbaugh, P., and Gerstein, G. (1997). Multiunit normalized cross correlation differs from the average single-unit normalized correlation. Neural Comput. 9, 1265–1275.
Câteau, H., and Fukai, T. (2001). Fokker-planck approach to the pulse packet propagation in synfire chain. Neural Netw. 14, 675–685.
Chen, Y., Geisler, W., and Seidemann, E. (2006). Optimal decoding of correlated neural population responses in the primate visual cortex. Nat. Neurosci. 9, 1412–1420.
Churchland, M., Yu, B., Cunningham, J., Sugrue, L., Cohen, M., Corrado, G., Newsome, W., Clark, A., Hosseini, P., Scott, B., Bradley, D. C., Smith, M. A., Kohn, A., Movshon, J. A., Armstrong, K. M., Moore, T., Chang, S. W., Snyder, L. H., Lisberger, S. G., Priebe, N. J., Finn, I. M., Ferster, D., Ryu, S. I., Santhanam, G., Sahani, M., and Shenoy, K. V. (2010). Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat. Neurosci. 13, 369–378.
Cohen, M., and Maunsell, J. (2009). Attention improves performance primarily by reducing interneuronal correlations. Nat. Neurosci. 12, 1594–1600.
de la Rocha, J., Doiron, B., Shea-Brown, E., Josić, K., and Reyes, A. (2007). Correlation between neural spike trains increases with firing rate. Nature 448, 802–806.
Diesmann, M., Gewaltig, M., and Aertsen, A. (1999). Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529–533.
Doiron, B., Rinzel, J., and Reyes, A. (2006). Stochastic synchronization in finite size spiking networks. Phys. Rev. E. 74(3 Pt 1), :030903.
Ecker, A., Berens, P., Keliris, G., Bethge, M., Logothetis, N., and Tolias, A. (2010). Decorrelated neuronal firing in cortical microcircuits. Science 327, 584–587.
Ganguli, S., Huh, D., and Sompolinsky, H. (2008). Memory traces in dynamical systems. Proc. Natl. Acad. Sci. 105, 18970.
Gerstein, G. (2000). Cross-correlation measures of unresolved multi-neuron recordings. J. Neurosci. Methods 100, 41–51.
Gray, C., Maldonado, P., Wilson, M., and McNaughton, B. (1995). Tetrodes markedly improve the reliability and yield of multiple single-unit isolation from multi-unit recordings in cat striate cortex. J. Neurosci. Methods 63, 43–54.
Greenberg, D., Houweling, A., and Kerr, J. (2008). Population imaging of ongoing neuronal activity in the visual cortex of awake rats. Nat. Neurosci. 11, 749–751.
Grinvald, A., and Hildesheim, R. (2004). VSDI: a new era in functional imaging of cortical dynamics. Nat. Rev. Neurosci. 5, 874–885.
Gutnisky, D., and Dragoi, V. (2008). Adaptive coding of visual information in neural populations. Nature 452, 220–224.
Gutnisky, D., and Josić, K. (2010). Generation of spatiotemporally correlated spike trains and local field potentials using a multivariate autoregressive process. J. Neurophysiol. 103, 2912.
Hertz, J. (2010). Cross-correlations in high-conductance states of a model cortical network. Neural Comput. 22, 427–447.
Jones, P., and Gabbiani, F. (2010). Synchronized neural input shapes stimulus selectivity in a collision-detecting neuron. Curr. Biol. 20, 2052–2057.
Josić, K., Shea-Brown, E., Doiron, B., and de la Rocha, J. (2009). Stimulus-dependent correlations and population codes. Neural Comput. 21, 2774–2804.
Kilavik, B., Roux, S., Ponce-Alvarez, A., Confais, J., Grün, S., and Riehle, A. (2009). Long-term modifications in motor cortical dynamics induced by intensive practice. J. Neurosci. 29, 12653.
Kohn, A., and Smith, M. (2005). Stimulus dependence of neuronal correlation in primary visual cortex of the macaque. J. Neurosci. 25, 3661.
Kohn, A., Zandvakili, A., and Smith, M. (2009). Correlations and brain states: from electrophysiology to functional imaging. Curr. Opin. Neurobiol. 19, 434–438.
Kremkow, J., Perrinet, L., Masson, G., and Aertsen, A. (2010). Functional consequences of correlated excitatory and inhibitory conductances in cortical networks. J. Comput. Neurosci. 28, 1–16.
Kumar, A., Rotter, S., and Aertsen, A. (2008). Conditions for propagating synchronous spiking and asynchronous firing rates in a cortical network model. J. Neurosci. 28, 5268.
Kumar, A., Rotter, S., and Aertsen, A. (2010). Spiking activity propagation in neuronal networks: reconciling different perspectives on neural coding. Nat. Rev. Neurosci. 11, 615–627.
Lee, D., Port, N., Kruse, W., and Georgopoulos, A. (1998). Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. J. Neurosci. 18, 1161.
Lewicki, M. (1998). A review of methods for spike sorting: the detection and classification of neural action potentials. Network 9, 53–78.
Litvak, V., Sompolinsky, H., Segev, I., and Abeles, M. (2003). On the transmission of rate code in long feedforward networks with excitatory-inhibitory balance. J. Neurosci. 23, 3006–3015.
London, M., Roth, A., Beeren, L., Häusser, M., and Latham, P. (2010). Sensitivity to perturbations in vivo implies high noise and suggests rate coding in cortex. Nature 466, 123–127.
Mastronarde, D. (1983). Correlated firing of cat retinal ganglion cells. I. Spontaneously active inputs to X-and Y-cells. J. Neurophysiol. 49, 303.
Maynard, E., Hatsopoulos, N., Ojakangas, C., Acuna, B., Sanes, J., Normann, R., and Donoghue, J. (1999). Neuronal interactions improve cortical population coding of movement direction. J. Neurosci. 19, 8083.
Meister, M., Lagnado, L., and Baylor, D. (1995). Concerted signaling by retinal ganglion cells. Science 270, 1207–1210.
Moreno, R., de la Rocha, J., Renart, A., and Parga, N. (2002). Response of spiking neurons to correlated inputs. Phys. Rev. Lett. 89, 288101.
Moreno-Bote, R., Renart, A., and Parga, N. (2008). Theory of input spike auto- and cross-correlations and their effect on the response of spiking neurons. Neural Comput. 20, 1651–1705.
Murphy, B., and Miller, K. (2009). Balanced amplification: a new mechanism of selective amplification of neural activity patterns. Neuron 61, 635–648.
Nicolelis, M., Baccala, L., Lin, R., and Chapin, J. (1995). Sensorimotor encoding by synchronous neural ensemble activity at multiple levels of the somatosensory system. Science 268, 1353.
Nowotny, T., and Huerta, R. (2003). Explaining synchrony in feed-forward networks: are mcculloch-pitts neurons good enough? Biol. Cybern. 89, 237–241.
Ostojić, S., Brunel, N., and Hakim, V. (2009). How connectivity, background activity, and synaptic properties shape the cross-correlation between spike trains. J. Neurosci. 29, 10234–10253.
Pazienti, A., and Grün, S. (2006). Robustness of the significance of spike synchrony with respect to sorting errors. J. Comput. Neurosci. 21, 329–342.
Perkel, D., Gerstein, G., and Moore, G. (1967). Neuronal spike trains and stochastic point processes: II. Simultaneous spike trains. Biophys. J. 7, 419–440.
Poort, J., and Roelfsema, P. (2009). Noise correlations have little influence on the coding of selective attention in area v1. Cereb. Cortex 19, 543.
Renart, A., de la Rocha, J., Bartho, P., Hollender, L., Parga, N., Reyes, A., and Harris, K. D. (2010). The asynchronous state in cortical circuits. Science 327, 587–590.
Reyes, A. (2003). Synchrony-dependent propagation of firing rate in iteratively constructed networks in vitro. Nat. Neurosci. 6, 593–599.
Riehle, A., Grün, S., Diesmann, M., and Aertsen, A. (1997). Spike synchronization and rate modulation differentially involved in motor cortical function. Science 278, 1950.
Romo, R., Hernández, A., Zainos, A., and Salinas, E. (2003). Correlated neuronal discharges that increase coding efficiency during perceptual discrimination. Neuron 38, 649–657.
Rosenbaum, R., and Josić, K. (2011). Mechanisms that modulate the transfer of spiking correlations. Neural Comput. 23, 1261–1305.
Rosenbaum, R., Trousdale, J., and Josić, K. (2010). Pooling and correlated neural activity. Front. Comput. Neurosci. 4:9.
Salinas, E., and Sejnowski, T. (2000). Impact of correlated synaptic input on output firing rate and variability in simple neuronal models. J. Neurosci. 20, 6193–6209.
Schneider, A., Lewis, T., and Rinzel, J. (2006). Effects of correlated input and electrical coupling on synchrony in fast-spiking cell networks. Neurocomputing 69, 1125–1129.
Schneidman, E., Berry, M., Segev, R., and Bialek, W. (2006). Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440, 1007–1012.
Shea-Brown, E., Josić, K., de la Rocha, J., and Doiron, B. (2008). Correlation and synchrony transfer in integrate-and-fire neurons: basic properties and consequences for coding. Phys. Rev. Lett. 100, 108102.
Smith, M., and Kohn, A. (2008). Spatial and temporal scales of neuronal correlation in primary visual cortex. J. Neurosci. 28, 12591–12603.
Sompolinsky, H., Yoon, H., Kang, K., and Shamir, M. (2001). Population coding in neuronal systems with correlated noise. Phys. Rev. E. 64, 051904.
Stark, E., Globerson, A., Asher, I., and Abeles, M. (2008). Correlations between groups of premotor neurons carry information about prehension. J. Neurosci. 28, 10618–10630.
Super, H., and Roelfsema, P. (2005). Chronic multiunit recordings in behaving animals: advantages and limitations. Prog. Brain Res. 147, 263–282.
Tetzlaff, T., Buschermöhle, M., Geisel, T., and Diesmann, M. (2003). The spread of rate and correlation in stationary cortical networks. Neurocomputing 52, 949–954.
Tetzlaff, T., and Diesmann, M. (2010). Analysis of Parallel Spike Trains, Chapter 6. New York, NY: Springer, 103–127.
Tetzlaff, T., Rotter, S., Stark, E., Abeles, M., Aertsen, A., and Diesmann, M. (2008). Dependence of neuronal correlations on filter characteristics and marginal spike-train statistics. Neurocomputing 20, 2133–2184.
van Rossum, M., Turrigiano, G., and Nelson, S. (2002). Fast propagation of firing rates through layered networks of noisy neurons. J. Neurosci. 22, 1956–1966.
Womelsdorf, T., Schoffelen, J., Oostenveld, R., Singer, W., Desimone, R., Engel, A., and Fries, P. (2007). Modulation of neuronal interactions through neuronal synchronization. Science 316, 1609–1612.
Keywords: correlation, pooling, synchrony, feedforward networks
Citation: Rosenbaum R, Trousdale J and Josić K (2011) The effects of pooling on spike train correlations. Front. Neurosci. 5:58. doi: 10.3389/fnins.2011.00058
Received: 15 January 2011;
Paper pending published: 07 February 2011;
Accepted: 07 April 2011;
Published online: 28 April 2011.
Edited by:
Philipp Berens, Max Planck Institute for Biological Cybernetics, GermanyReviewed by:
Markus Diesmann, RIKEN Brain Science Institute, JapanTom Tetzlaff, Norwegian University of Life Sciences, Norway
Copyright: © 2011 Rosenbaum, Trousdale and Josić. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Robert Rosenbaum, University of Houston, Mathematics, 4800 Calhoun Road, Houston, 77004, TX, USA,cm9iZXJ0ckBtYXRoLnVoLmVkdQ==
James Trousdale, University of Houston, Mathematics, Houston, 77004, TX, USA,anJ0cm91c2RAbWF0aC51aC5lZHU=


