- 1 Department of Psychology, Cognitive, Perceptual and Brain Sciences, University College London, London, UK
- 2 Department of Psychology, Tel-Aviv University, Tel-Aviv, Israel
- 3 Department of Psychology, Birkbeck College, London, UK
- 4 Department of Psychology, Stanford University, Stanford, CA, USA
Recent research has investigated the process of integrating perceptual evidence toward a decision, converging on a number of sequential sampling choice models, such as variants of race and diffusion models and the non-linear leaky competing accumulator (LCA) model. Here we study extensions of these models to multi-alternative choice, considering how well they can account for data from a psychophysical experiment in which the evidence supporting each of the alternatives changes dynamically during the trial, in a way that creates temporal correlations. We find that participants exhibit a tendency to choose an alternative whose evidence profile is temporally anti-correlated with (or dissimilar from) that of other alternatives. This advantage of the anti-correlated alternative is well accounted for in the LCA, and provides constraints that challenge several other models of multi-alternative choice.
Introduction
Models of Decision Making and Evidence Integration
Decision making in daily activities, such as identifying a word or finding a flatmate, most often requires a choice among multiple alternatives. Nevertheless, most of the research on the neural basis of decision making so far has focused on binary choice, both in experimental psychology (Laming, 1968; Link and Heath, 1975; Ratcliff, 1978; Vickers, 1970; Usher and McClelland, 2001; Ratcliff and Smith, 2004; Bogacz et al., 2006; Ratcliff and McKoon, 2008) and in neuroscience (Heekeren et al., 2004; Gold and Shadlen, 2007; Ratcliff et al., 2007; Wang, 2008; Albantakis and Deco, 2009; Donner et al., 2009; Rorie et al., 2010). This research has shown that the decision making mechanism takes multiple samples of noisy evidence and integrates them to a response criterion, determining both what alternative is chosen and the timing of the decision. This mechanism gives a natural explanation for the speed–accuracy tradeoff (observers can trade speed for accuracy: with more time available, one can take more samples of the evidence, resulting in more accurate decisions), and it can produce optimal decisions (fastest mean-RT for a specified error-rate; Wald, 1947; Gold and Shadlen, 2001, 2002; Bogacz et al., 2007). Furthermore, neurophysiological evidence for this mechanism has been reported, showing that neurons in area LIP exhibit ramped activity that corresponds to the integrated evidence. In a perceptual decision making task using the free-response paradigm, wherein participants respond (and thereby stop the presentation of evidence) at a time of their own choosing, the physiological evidence supports the assumption that responses occur when the accumulated evidence reaches a fixed criterial level or integration bound (Hanes and Schall, 1996; Horwitz and Newsome, 2001; Shadlen and Newsome, 2001; Roitman and Shadlen, 2002).
A number of computational models have been proposed, implementing this choice mechanism for binary decisions (see next section for multi-alternative decision models), in a variety of ways. One of these models, often labeled the drift–diffusion model (Stone, 1960; Laming, 1968; Ratcliff, 1978; Ratcliff and Rouder, 1998; Ratcliff and McKoon, 2008), treats evidence accumulation as a stochastic process, in which a single variable tracks the cumulative difference between the momentary stimulus support for one hypothesis and the support for the competing hypotheses. A close relative of this model (Mazurek et al., 2003), and the variant of the diffusion model we consider here, has been used to model physiological data. This model employs two accumulators racing each other to a decision criterion. Each accumulator is excited by the evidence for one alternative and inhibited by the evidence for the other via feed-forward inhibition. These models that are driven by relative evidence can be distinguished from the classical accumulator, or what we will call the race model, in which only positive evidence for each alternative accumulates in a race toward a decision bound (Vickers, 1970; Brown and Heathcote, 2008). A third type of model, including the leaky competing accumulator (LCA) model (Usher and McClelland, 2001; Bogacz et al., 2007, see also related attractor models; Wang, 2002; Wong and Wang, 2006; Albantakis and Deco, 2009) also assumes one accumulator for each alternative, but the accumulators compete with each other via lateral inhibition and are subject to leakage or decay of accumulated activation.
These models differ in a number of dynamical properties that affect the weighting of the evidence across time and the temporal range of evidence integration. These dynamic properties have sometimes been investigated in tasks where the experimenter controls the duration of a stimulus observation period, with responses required immediately at the end of this period. This version of the decision task is sometime labeled the interrogation paradigm (Bogacz et al., 2006). The use of an integration bound or decision criterion is assumed by all models for the free-response paradigm, in which participants respond when they feel ready. For the interrogation paradigm, however, the inclusion of a bound can truncate evidence accumulation prematurely, leading to sub-optimal performance. Indeed, it has often been assumed that there is no decision bound in this case, and the decision is made in favor of the accumulator with the highest activation at the end of the observation interval (Ratcliff, 1978; Usher and McClelland, 2001; Brown and Heathcote, 2008). Under this assumption, the race and diffusion models are identical (up to a rescaling of the noise level), as they predict a uniform integration of the evidence across time. The LCA can function in one of three modes, depending on the balance between evidence-leak and lateral inhibition (Usher and McClelland, 2001; Bogacz et al., 2007). As illustrated in Figure 1A, when the leak is stronger than the inhibition, the LCA is leak-dominant; evidence accumulated early in an observation period tends to leak away, so that the choice tends to be determined by information coming late in the stimulus observation interval (recency). When the inhibition is stronger than the leak, the process is inhibition dominant (Figure 1B). In this case, information coming early in the observation period can give one accumulator an advantage, thus determining the choice outcome (primacy). The third regime holds in the special case that leak and inhibition are in a perfect balance. In this case, information from all time points receives equal weight, and the process exhibits neither recency nor primacy.
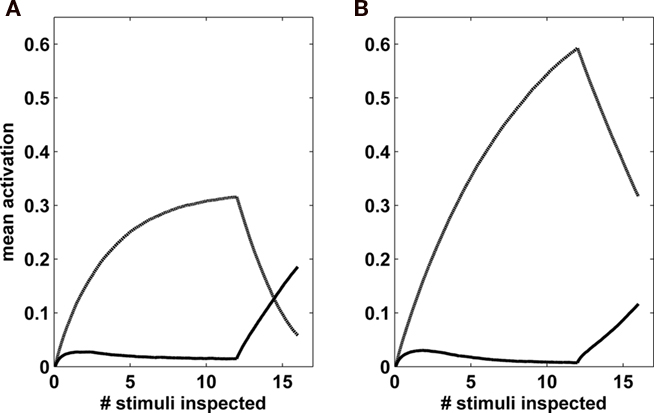
Figure 1. Leaky competing accumulator activations in a binary task, in which the total evidence to both alternatives is equal, but is modulated in time, so that the first accumulator (dashed line) receives more evidence at the beginning (first 12 frames), while the second one (solid line), receives more evidence at the end (last 4 frames). (A): leak dominance (leak = 0.022, inhibition = 0.01); (B): inhibition dominance (leak = 0, inhibition = 0.025). In the first case, the accumulator receiving more evidence at the end would be chosen; in the second, the accumulator receiving more evidence at the beginning would be chosen. Reproduced from Usher and McClelland (2001).
The race and diffusion models can account for primacy in interrogation paradigms, if it is assumed that participants actually do employ a decision bound in the interrogation paradigm, such that evidence accumulation stops when the bound is reached, if this occurs before the end of the stimulus observation period (Ratcliff, 2006; Kiani et al., 2008). We follow Bogacz et al. (2006) in calling such a boundary an absorbing boundary, since the consideration of evidence is assumed to cease when this boundary is reached (i.e., the trajectory sticks at boundary). We follow Kiani et al. (2008) in using the term bounded diffusion model when the bound is applied to the relative evidence variable of the diffusion model, and we use the label bounded-race model for the corresponding version of a race model, when these models are applied to the interrogation paradigm. In addition to predicting a primacy effect (as reported in Kiani et al., 2008), this assumption allows these models to account for experimental data showing bounded accuracy with increasingly long stimulus durations in the interrogation paradigm (Ratcliff, 2006), as the decision bound effectively limits stimulus integration.
In the LCA model, a limitation on temporal integration can result from the effects of leak and inhibition, even in the absence of an absorbing decision boundary. While such a boundary is used in the LCA to model data in the free-response paradigm, it is not needed to account for the leveling off of accuracy in the interrogation paradigm (Usher and McClelland, 2001), and the model assumes that observers continue to integrate as long as the evidence presentation continues. The LCA does, however, include an important non-linearity, in the form of a floor on activation (called a reflecting boundary by Zhang et al., 2009) that prevents activations from becoming negative, as we shall discuss in more detail in the next section.
The aim of the present article is to develop an experimental protocol that can distinguish the predictions of these models. We focus on the bounded diffusion and bounded-race models and contrast their predictions with those of the LCA (The attractor models of Wang, 2002; Wong and Wang, 2006; Albantakis and Deco, 2009 are like the LCA but more complex; we will return to consider them in the discussion). We use a task in which participants must choose between more than two alternatives. This requires an extension of the models to the multi-alternative situation, which we now consider.
Models of Multi-Alternative Choice
The first step in extending the models to multi-alternative choice is to assume a separate accumulator for each alternative (see Figure 2). Within the LCA or the race model, this extension is straightforward (Vickers, 1970; Usher and McClelland, 2001; Usher et al., 2002; Brown and Heathcote, 2005, 2008).
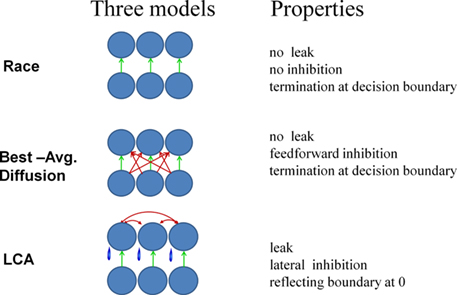
Figure 2. Neural implementation of perceptual choice models for the interrogation paradigm (top row): Pure race model; (middle row) Niwa and Ditterich (2008) diffusion model; (bottom row) LCA model (Usher and McClelland, 2001). Green arrows correspond to excitation and red to inhibition. Blue “tears” represent leakage in the LCA model.
In the n-choice race model, each alternative is assigned to a separate accumulator, and each accumulates evidence according to the following stochastic differential equation:

Here the quantity dxm represents the change in activation of accumulator m, Im represents the external input, and N(0, σ) represents processing noise thought to be intrinsic to the accumulators. This noise process, included in all the models, is assumed to be Gaussian, with 0 mean and SD σ.
In the n-choice LCA, each alternative is also assigned to a separate accumulator. The property of relative evidence integration is achieved through lateral inhibition, and the accumulators are also subject to leakage. The activation level of accumulator m is updated with each simulation time-step according to:
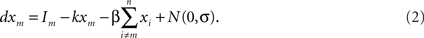
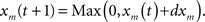
Here k is the leak, β the inhibition, and the other terms are as before. The Max-function in the second line of the equation implements a lower bound or floor imposed on the activations. It differs from the (upper) absorbing boundary in the bounded diffusion and race models because integration is not terminated when the bound is reached. Indeed, because the activation of the accumulator may possibly grow positive as subsequent evidence comes in, this lower bound is called a reflecting boundary. The inclusion of the reflecting bound was motivated by the fact that neural activity can never go below a minimum level (Usher and McClelland, 2001, p. 14 and Appendix A; see also Bogacz et al., 2007).
For the special case when k = β = 0, the LCA reduces to a classical race or pure accumulator model as long as all activations are greater than 0. When k and β are both non-zero but equal, the leak and inhibition are said to be balanced, and the linearized 2-alternative version of this model is equivalent to the classical drift–diffusion model (Bogacz et al. 2006).
It is less obvious how to extend the diffusion model to multi-alternative choice. One approach has been suggested by Niwa and Ditterich, 2008 (see also Roe et al., 2001 for a similar scheme). For the case of three alternatives, three accumulators race toward a common decision criterion. The input to each accumulator, however, is the net evidence signal for that accumulator, defined as the evidence for the alternative the accumulator represents minus the evidence against it, which is in turn defined as the average of the evidence for the other two alternatives. Accordingly, the differential equation for the m-th accumulator is1:
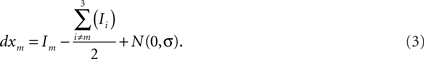
There are a number of other possible ways to extend the diffusion models to multiple choice (Churchland et al., 2008; Bogacz, 2009; Ditterich, 2010), and we will consider several of these in our Section “Discussion.” Here we focus primarily on the three models described above (illustrated in Figure 2), using the names race, diffusion, and LCA. Note that in our analysis we will examine the role of an absorbing decision bound in both the race and the diffusion model, but as in earlier work no such bound will be employed in our analysis of the LCA model.
These models differ in the efficiency with which they utilize stimulus information (i.e., the level of accuracy that can be achieved by accumulating information corrupted by a given level of noise for a given amount of internal time; e.g., Usher and McClelland, 1995; Figure 7). It is hard to distinguish them on this basis, however, because the level of noise in the process is not known, and must be treated as a free parameter. We demonstrate here that it is possible to distinguish the LCA from the other models on a different basis, namely, the ways in which they are affected by changes in evidence over time and by correlations and anti-correlations in the evidence for the different alternatives.
Using Non-Stationary Evidence to Distinguish between Choice Models
Our effort to distinguish the models relies on a protocol in which the stimulus contains non-stationary evidence (see also Usher and McClelland, 2001; Huk and Shadlen, 2005), such that there are intervals with stronger and weaker evidence for each of the three alternatives (Figure 3). We will consider choices among three alternatives whose average evidence is the same (i.e., they are equally attractive on average), but the evidence for two of the three options, A (blue) and B (green) is temporally correlated (or similar) and anti-correlated with the evidence for the third option C (red).
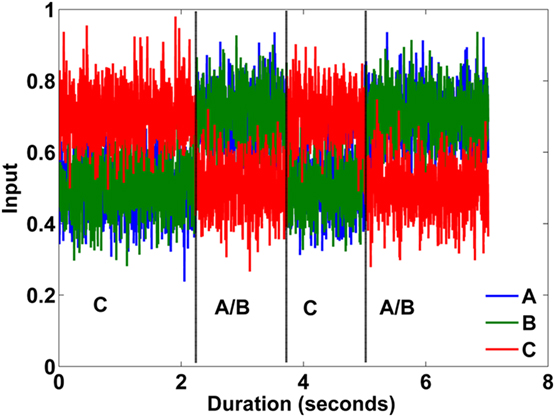
Figure 3. The non-stationary evidence to three alternatives in a single trial with 7 s duration. The evidence includes Gaussian noise on top of a changing baseline. A-blue, B-green, C-red (evidence reversals are marked by vertical black lines).
To obtain such a process, we create two evidence phases that alternate back and forth within a trial. At the beginning of each trial, one phase is chosen at random, and then the phases alternate at random intervals, with the likelihood of alternating phase increasing with the duration of the current phase (the resulting phase duration distribution from this stochastic process is depicted in Figure 4). Within each phase (1 or 2) there is a mean value of the evidence for each alternative m (designated μm1 and μm2; Table 1) and Gaussian noise with SD 0.1429 is added to the instantaneous value of the evidence (in the examples of Figure 3 the input noise was reduced to 0.075, to facilitate the graphical presentation).
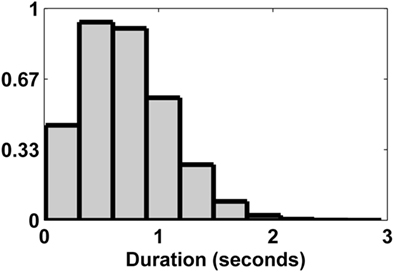
Figure 4. Density distribution that determines the time of switching from one phase to the other (see Figure 3).
Below we present computer simulations that examine the predictions of the three models on the choice between these three alternatives. As we will see the models make distinct predictions about the probability to choose the dissimilar alternative, motivating an experiment that we then use to test these predictions.
Materials and Methods
Computer Simulations
Evidence alternation protocol
The transitions between the two phases of evidence (Tables 1 and 2; Figure 4) are based on a Markov process with a transition rate that increases at long intervals. In particular after staying to phase j for n time-steps the probability of switching to phase k is p(n) = 5 × 10−5 × n. This transition formula resulted in the distribution of phase durations that is shown in Figure 4. Within each phase, for each alternative m, Gaussian noise with SD σin (set to be 0.1429 – the value used in the experiment reported below – corresponding to variability in evidence on a time scale faster than the characteristic Markov switch time), was added on top of the mean value of the evidence (designated μm1 and μm2, see Figure 3, for an illustration of the input and Table 1 for the exact mean values that were used). The evidence values were restricted between 0 and 1, which correspond to minimal and maximal brightness values (in the RGB scale), in the subsequent experiment.
Stimulus duration
Each simulation time-step corresponded to 13.3 ms (or 1 frame on a 75-HZ refresh rate monitor). The stimulus duration was uniformly chosen from the range 375–750 time-steps (or 5–10 s). Note that the duration of the last phase is truncated by the end of the trial, making the distribution of last phase durations different from the distribution shown in Figure 4.
Accumulator initialization and choice policy
In all three models, accumulators were initialized at 0 at the start of each simulated trial. For race and diffusion, if the bound was reached, the accumulator that reached the bound was chosen as the response on that trial. When the bound was not reached, or in the LCA where there is no bound, the alternative chosen is the one that is most active when the stimulus input is terminated.
Information integration in the three models
Race. The race model involved three independent accumulators. Each of them (m) was updated according to Eq. 1 above.
Only three free parameters are needed in this model: The SD of the processing noise (σ), a stimulus sensitivity parameter s, and the activation value corresponding to the upper absorbing bound, A. In accordance with our behavioral experiment, the inputs Im vary in each time frame due to signal noise according to a Gaussian with mean s × μmi (with μmi corresponding to the evidence for alternative m during phase-i (Table 1) and with SD = s σin: Im ∼ N(s × μmi, s × σin), where s is a sensitivity parameter that multiplies luminance levels to map them into accumulator input (note the processing noise sigma is not multiplied by s). In all simulations s = 1, except for the simulation in Figure 8, where it was a free parameter (to fit experimental data) with its optimized value of s = 1.33. The behavior of the model as the absorbing bound A is varied is the focus of many of the simulations, and the range of values considered with be discussed as we present the simulations.
Diffusion. The diffusion model was implemented using the same processing noise, sensitivity, and absorbing bound parameters as in the race model. The activation state of each accumulator m was updated according to Eq. 3. Similar to the race model the sensitivity parameter s was held constant at 1 except in the simulation of Figure 8, where the optimized value was s = 1.09 and, as with the race model, the behavior of this model as A was varied is discussed as we present the simulations.
Leaky competing accumulator. In most of the simulations, the LCA model was implemented using five free parameters including β, k, and σ, which stand for the values of inhibition, leak, and processing noise (see Eq. 2). The inputs Im are computed as N(s × μmi + I0, s × σin), where s is a sensitivity parameter as before and I0 is an additive input affecting all of the accumulators. This last parameter modulates the degree to which the model is affected by the reflecting boundary at 0; when the value of I0 is large, activations tend to remain positive, avoiding the reflecting boundary. In some of the simulations (Figure 6), we only varied the first three LCA parameters, while the other two were set to I0 = 0.3 and s = 1. In Figure 8 I0 and s were free parameters and their optimized values were 0.1 and 1.22 respectively.
Model fitting
For optimization we used the toolbox developed by Bogacz and Cohen (2004), which estimates the parameters of a model based on least squares. The advantage of the method employed by Bogacz and Cohen (2004) is that it extends the multi-dimensional simplex algorithm in order to better handle noisy functions (simulation-based models). The cost function that the optimization routine minimizes is defined as: 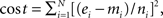 where mi are the statistics of the model, ei the statistics obtained from the experiment and N the number of the statistics that are fitted. A normalization factor, ni, is introduced for each statistic i. This is to ensure that all data points contribute equally to the cost function despite differences in the scale across the statistics. As described in detail in Bogacz and Cohen (2004), the selection of the value of the normalization factor varies across the different stages of the optimization process to maximize efficiency. During the initial stages of the optimization process (i.e., searching for starting points and first optimization), ni takes the value of the average value of the empirical statistics (ei). At the final stage of the process (i.e., tuning of parameters) ni becomes the SD of statistic i, obtained after running the model with the same parameters 10 times. In order to compare the quantitative fits of the three models we used the Bayesian information criterion (BIC), which takes into account both the goodness of fit and the complexity of the model. The BIC penalizes the extra free parameters much more strongly than other similar measures (e.g., Akaike information criterion). The BIC is computed as ln(σε)2 + (k/n)ln(n), where (σε)2 is the error variance, k is the number of free parameters and n is the number of data points.
where mi are the statistics of the model, ei the statistics obtained from the experiment and N the number of the statistics that are fitted. A normalization factor, ni, is introduced for each statistic i. This is to ensure that all data points contribute equally to the cost function despite differences in the scale across the statistics. As described in detail in Bogacz and Cohen (2004), the selection of the value of the normalization factor varies across the different stages of the optimization process to maximize efficiency. During the initial stages of the optimization process (i.e., searching for starting points and first optimization), ni takes the value of the average value of the empirical statistics (ei). At the final stage of the process (i.e., tuning of parameters) ni becomes the SD of statistic i, obtained after running the model with the same parameters 10 times. In order to compare the quantitative fits of the three models we used the Bayesian information criterion (BIC), which takes into account both the goodness of fit and the complexity of the model. The BIC penalizes the extra free parameters much more strongly than other similar measures (e.g., Akaike information criterion). The BIC is computed as ln(σε)2 + (k/n)ln(n), where (σε)2 is the error variance, k is the number of free parameters and n is the number of data points.
Experiment
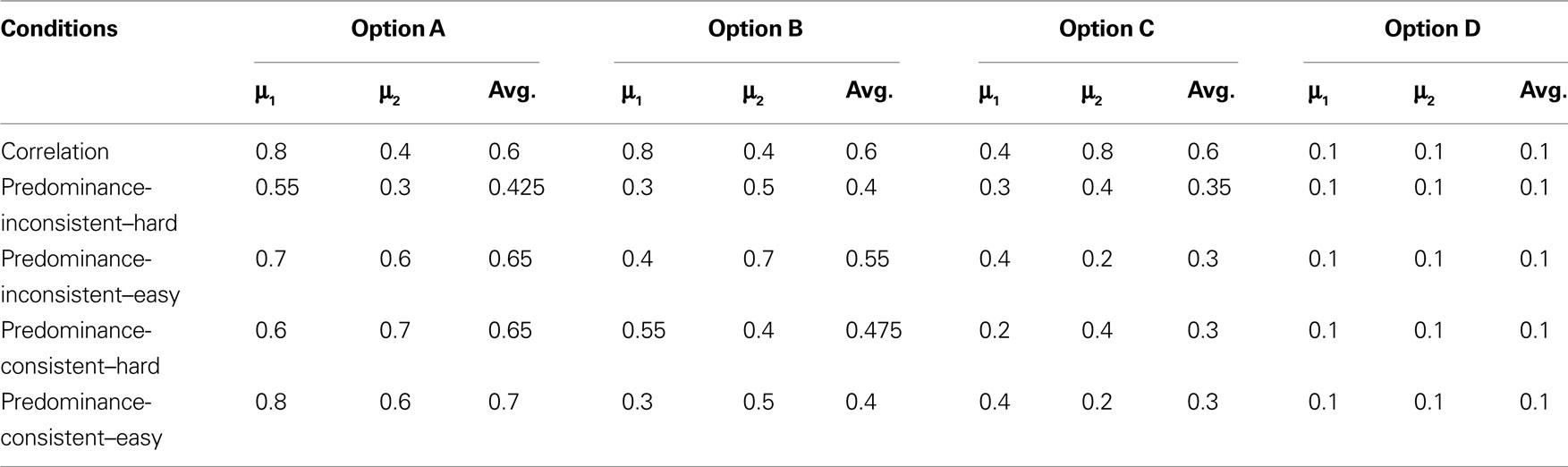
A total of eight conditions were interleaved in the experiment. Each condition involved four alternatives of varying brightness, with mean brightness specified for each of the two phases. The critical condition was the correlation condition previously discussed and illustrated in Figure 3. Seven filler conditions were also used. Here we report only the four of the filler conditions which were such that there was always one alternative with the highest integrated evidence (treated as the correct response and used to determine the participant feedback). The precise stimulus value in the critical condition and the four conditions with a correct response are shown in Table 2 (the three remaining filler conditions are given in Table A1 in Appendix). These conditions are labeled, inconsistent–hard, inconsistent–easy, consistent–hard, and consistent–easy, where consistent indicates that the evidence favors one of the alternatives at all time (consistent evidence), and inconsistent that the evidence favors different alternatives at different times. The other three filler conditions have two or more alternatives with equal integrated values. As the manipulation relevant to these fillers is not the focus of this investigation we do not report the choice results for these conditions (but see Discussion), and we provide their full specification in the Appendix (Table A1).
Observers
Sixteen participants recruited from the University College London subject pool were tested over two sessions.
Stimulus
The brightness was non-stationary, based on a stochastic transition between two phases. In phase 1, the brightness of each patch (m) was sampled (at each time frame) from a normal distribution, N(μm1, σin), while in phase 2 it was sampled from N(μm2, σin) (σin = 0.1429), where the μm1,2 values, for each option (m) and condition, are shown in Table 2. One of the four patches (D) was so dim that it was virtually never chosen, with the effect that the experiment effectively involves only three meaningful choice alternatives. The extra dim spot was added to balance the positions of the meaningful alternatives around the corners of an imaginary square. For the dim patch (D), the brightness fluctuation SD was only 0.01. The screen positions of the A, B, C, and D alternatives were randomized.
Each trial started randomly with either phase 1 or phase 2. The transition times from the one phase to the other were selected from the distribution in Figure 4 (see also Figure 3 for an input example, in the correlation condition). In total, for each condition, 50 trials were presented (25 at each session). At the critical correlation condition the integral of the evidence had the same average across the two regimes. However, because the duration of the trials is limited, a small imbalance can occur, such that the alternative(s) that receive(s) more support at the beginning also receive(s) the most support on 65% of the trials. In the other four conditions (called predominance conditions), A was always the brightest option. These conditions differed in (a) the margin of evidence supporting the A alternative (ranging from 0.025 to 0.30) and (b) whether the advantage for the A alternative was consistent throughout the trial or was reversed in one of the two phases. Note the margin of evidence was lower overall in the inconsistent conditions, compared with the consistent conditions.
Although the stimuli were presented on a monitor without applying a Gamma correction, the measurement of the monitor non-linearity with a photometer showed that the deviation from linearity was very small in the range (0.4–0.8). Gaussian noise added to the stimulus value could cause brightness to fall above 0.8, however, and the largest brightness value allowed was 1.0. See the Section “Appendix” for details and for simulations that show that the results are not affected by the monitor non-linearity.
Procedure
The sessions were run on different days with a maximum of a week difference. Before the beginning of the experiment a brief explanation of the task was given and the participant was presented with 5–10 examples of the stimulus. The input values for these trials were randomly chosen. Immediately after the introductory trials, 25–50 trials sampled from the experimental conditions were presented for practice (the introductory and practice trials were given in the first session only). The practice period ended when no error-beeps occurred for five consecutive trials (see below), but no earlier than 25 trials and no later than 50 trials. The main experiment had 200 trials per session (400 trials overall) and 8 conditions (50 trials for each condition). The 200 trials for each session were broken into 5 blocks (40 trials each). Trials within each session were randomized across all eight stimulus conditions. After each block participants were shown their accuracy score up to that point in the experiment and took a short break (1–5 min).
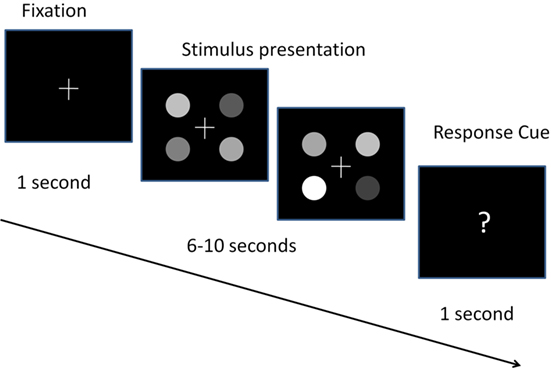
Each trial began with the presentation of a fixation cross. After 1 s, four patches appeared on the screen around the fixation cross, in a square formation. The brightness of each patch fluctuated across time (the brightness was updated every 13.3 ms, corresponding to the frame rate of the monitor) and the participants had to select the patch that was the brightest overall (see Figure 7). The duration of the stimulus presentation was chosen randomly from a uniform distribution between 5 and 10 s. Upon termination of the stimulus presentation the participants had 1 s to make a response. If the participant failed to respond within this interval, a “Response deadline missed” screen was shown and the next trial started. For incorrect responses (in the predominance conditions, see Table 2) the participants received negative (error) feedback (beep sounds). For correct responses in these conditions and for trials in the correlation condition no feedback was given. The correct option in each trial was defined based on the average input brightnesses (average of μ1 and μ2, in Table 2).
Results
Simulation Study
We start with an informal illustration of the models’ choice pattern with two example stimuli chosen from the correlation condition which is shown in Figure 3. Input parameters and simulation protocol is described in Section “Materials and Methods.” To keep the illustration simple, no processing noise is used (σ = 0; but we vary σ in the formal simulations below) and the stimulus noise is reduced (from 0.1429 to 0.04). For this illustration only, we also constrain the total presentation time to be such that it gives an equal amount of time to the two phases of evidence. In Figure 5 (left panels) we show the response of the pure race model – the model that simply accumulates incoming information. We consider two contrasting cases: In the first, the stimulus starts with evidence that favors alternatives A and B. In the second, the stimulus starts with evidence that favors C.
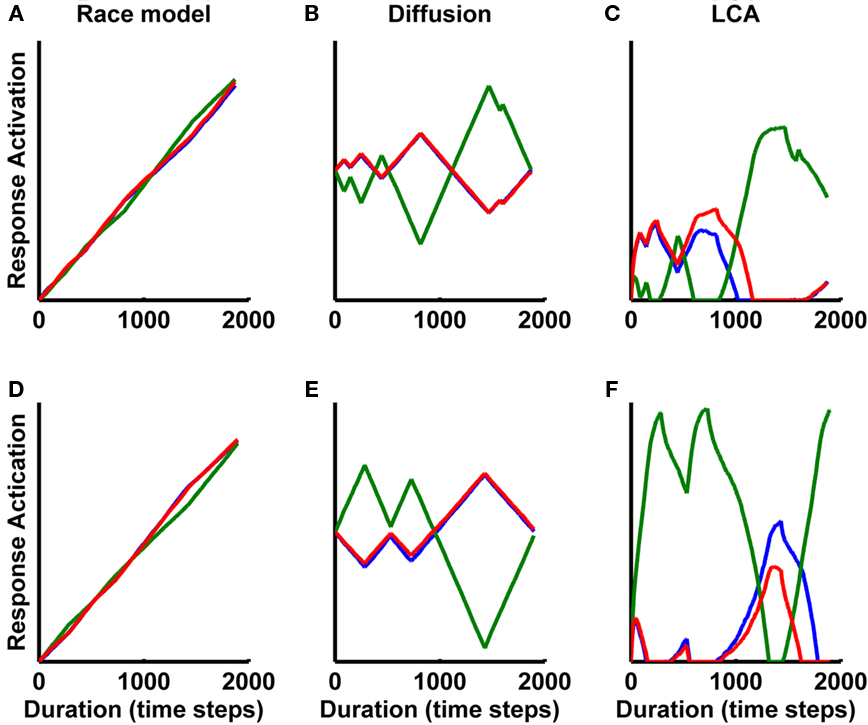
Figure 5. Single trial activations for race (left panels), diffusion (middle panels), and LCA (right panels) for initial evidence supporting [(A,B) (top panels)] and supporting [(C) (bottom panels)]. The same two random streams (top/bottom panels) of evidence were used for all the models shown in this figure. Blue and red curves show the activations for the two correlated options (A,B) while the green curve shows the activation for the anti-correlated option (C). The processing noise (σ) is zero while the stimulus noise is reduced to 0.04.
One can observe that, toward the end of the observation period, the activations of the accumulators converge, since all receive the same amount of input overall. At earlier integration times, however, one can see intervals where one of the correlated alternatives {A or B} dominates or where the uncorrelated alternative C dominates. If an absorbing bound is reached before the end of the observation period (as assumed by Kiani et al., 2008), one finds that the likelihood of the dissimilar option to win is approximately 0.5, since the A and B activations (red and blue) are almost identical and therefore will be equally likely to cross the criterion at about the same time and thus split their wins. If extra noise (not correlated with the evidence) is introduced, then the likelihood to choose the dissimilar alternative decreases toward the chance level (0.33).
In the middle and right panels of Figure 5, we present the response of the diffusion model and the non-linear inhibition dominant LCA (β = 0.019, k = 0.015), using the same two example stimulus sequences that were used for the race model in the left panels.
The activations for the diffusion model correspond to the differences between the activations of the accumulators in the race model. Looking directly at these differences, one can clearly observe moments in which either C or one of {A or B} dominates the choice. Again, since the total evidence to the three accumulators is equal, the three diffusion processes end up at the same level. If an absorbing bound is reached, this is likely to favor the alternative associated with the stimulus presented at the beginning of the trial; on average, then, C is likely to be chosen about 50% of the time. As before, with higher noise C may be chosen less than 50% of the time.
The situation is different for the non-linear LCA, when inhibition is larger than leak so that the process is inhibition dominant. Here in the right panels we observe a clear advantage for the dissimilar option, C. Due to the non-linearity at zero activation, the low evidence phases of the anti-correlated option C are not suppressed as much as they would be in the linear diffusion model or if their activation were allowed to go below 0. Also, since A and B are low when C is high, while A and B are both high together, the mutual inhibition causes A and B to suppress each other when they are high, while when C is high it receives no such suppression. This asymmetry allows the activation of C to rise more quickly than the activations of A and B, and tends to give C an advantage over A and B. As a result, within a particular range of parameter values, the LCA predicts a tendency to decide in favor of the dissimilar option more than 50% of the time, independent of whether the stimulus starts with A/B (as in the top panel) or with C (as in the bottom panel). As we shall see in more detail below, this phenomenon – an order-independent dissimilarity advantage – is not exhibited by either of the other models under consideration, but can be exhibited both by human participants and by the LCA.
In order to demonstrate these differences in the conditions that are in force in our behavioral experiment, we present a second simulation study. We ran simulations with stimuli of the type illustrated in Figure 3, driving the accumulators with inputs in accordance with the visual stimulation protocol used in the behavioral experiment. Note that the trials in the behavioral experiment differ from the single trial illustrations in Figure 5, where the total duration of the stimulus was set up to result in equal amount of time for the two phases. As noted in Section “Materials and Methods,” with a stimulus starting with one type of evidence, and then switching at random intervals, and with the trial ending at an independently chosen time, the evidence associated with the first event is more likely to be larger overall (this bias weakens and eventually disappears as the total length of the observation interval increases). For the protocol used in the experiment, the proportion of trials that have C predominance in trials that start with C is 0.65. However, note that the degree of preponderance is moderate: the ratio between the integrated evidence corresponding to the two phases (A/B vs. C) only ranges in the interval 0.9–1.1.
We ran sets of 2000 simulation trials with such stimuli, for each of the three models (race, diffusion and LCA) with no processing noise (σ = 0; Figure 6, top panels) and high processing noise (σ = 0.6; Figure 6, bottom panels). For the race and the diffusion model, we examined the impact of an absorbing decision boundary (Kiani et al., 2008); if the decision criterion is reached before stimulus termination, the evidence is not integrated after that time. We varied the boundary over a wide range to understand its effects. The fraction of C-choices is shown as a function of decision boundary for the diffusion model (Figure 6, left) and the race model (Figure 6, middle). For the LCA, we plot the fraction of C-choices as a function of the ratio between leak (which was fixed at k = 0.0457) and inhibition, which varies in the range (0.00043, 0.08571) (Figure 6, right). For each model we show three curves. The green curve corresponds to the trials where the initial evidence favors the dissimilar option C, the blue curve is obtained from the trials in which the early evidence favors the similar options A and B; the red curve is the average of the two other curves.
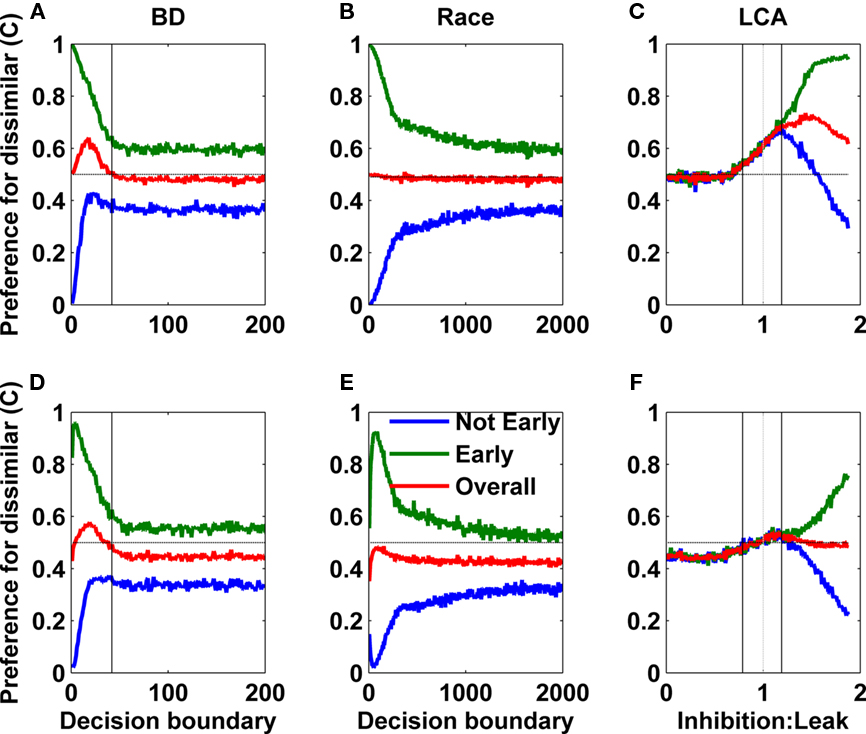
Figure 6. Predictions for the bounded diffusion and race models and the LCA model with zero (σ = 0, top) and high (σ = 0. 6, bottom) levels of processing noise. The green curve shows the choice probability for (C) in trials when it is favored at the beginning; blue shows the same when (A,B) are favored at the beginning, and the red curve is the average of the other two. For the diffusion model (left panels) and the race model (middle panels) these probabilities are graphed as a function of the decision boundary position. For the LCA (right panels) they are shown as a function of the inhibition/leak ratio.
For low levels of processing noise, we observe that in most models, the total fraction of C-choices is at the 50% range for some range of parameters (red lines, top panels) while with higher processing noise the mean preference for C can go below 50% (red lines, bottom panels). In both the race and the diffusion models, we observe that the fraction of C-choices is above 50% when the evidence starts favoring C (green lines), and below 50% when the evidence starts favoring A and B (blue lines), which is consistent with the fraction of trials that have more A/B or more C evidence, overall. Note that, while true chance level is 33%, a 50% baseline is predicted by any model that decides on the basis of a random sample of momentary evidence, as the correlated alternatives are splitting their wins. On the other hand, since for the stimuli used here, the fraction of trials that have C predominance in trials that start with C is 0.65, a perfect integrator should converge to this choice value. Indeed this value is reached with high decision boundary values in both the race and diffusion models.
An important deviation from the primacy pattern shown by the race and diffusion models occurs in the non-linear LCA, where we see an order-independent advantage for the dissimilar alternative. With low noise, and when the inhibition-leak imbalance is small (Figure 6, top right panel, range between vertical black lines), the probability of choosing C is independent of whether the initial evidence favors Figure 6C (green curve) or Figures A,B (blue curve) and is higher than 50%. This arises from the advantage that the dissimilar option gains from the non-linear dynamic as previously discussed in relation to the single trial trajectories in Figure 5.
The area to the right of the gray vertical line corresponds to inhibition becoming more than a little bit stronger than leak. Here the green (strong evidence for C at the beginning) and blue (weak evidence for C at the beginning) are initially both maintained above 50%, but start to progressively diverge as the relative strength of inhibition increases further. Eventually for inhibition much higher than leak, the LCA shows a strong primacy (large difference between green and blue lines), like in the diffusion/race models. For the LCA as well as the other models, the impact of an increase in processing noise is to push the fraction of C-choices down, toward the 33% chance level (Figure 6, bottom panels). In summary, we see that with low levels of processing noise, and in a particular range of the ratio between inhibition and leak, the LCA shows an advantage for the uncorrelated alternative over the correlated alternatives, even when the uncorrelated alternatives receive stronger activation at the beginning of the trial.
There is a situation within the diffusion model in which the C-choice is made on more than 50% of trials. This occurs in the diffusion model for low decision boundary (left of the vertical black line, at bound =42, in the left panels of Figure 6). The low decision boundary strongly favors stimuli with larger initial support. It especially favors C, however, because the diffusion associated with the dissimilar option (Figure 6, left panels) raises with higher rate (green curve) and thus it is more likely to hit the decision boundary at the beginning of the trial than when the trial begins with greater support for the similar options A/B, which mutually suppress each other and thus have lower slopes. These differences produce the result that, averaging over trials where the evidence supports C first and those where it supports A and B first (red curves in left panels) the probably of choosing C can be greater than 50%. Crucially, though, the probability of choosing C is never above 50% in trials where the evidence associated with A and B is stronger at the beginning, so that the model never exhibits the order-independent advantage for C that we can observe in the LCA model. Thus a distinctive prediction of the non-linear LCA is that P(C) can exceed 50%, both for the trials when C starts with stronger evidence, as well as for those when it starts with weaker evidence. This prediction takes place for low additional noise (σ) and with inhibition moderately stronger than leak (close to the gray vertical line in Figure 6, right panel).
To summarize, we have explored a novel input protocol for three-alternative choice in which the evidence is non-stationary and temporally modulated, and which allows us to examine the effect of temporal correlations in the evidence for the various alternatives. We showed that the LCA (with inhibition > leak) can predict an advantage beyond 50% for the dissimilar option, which is independent of evidence at the stimulus onset and is a result of inhibition dominance, combined with non-linear dynamics. This distinctive pattern – the probability of choosing the dissimilar option more than 50%, independent of order of presentation – distinguishes the LCA from the race and diffusion variants. Both of these patterns are examined in the following experiment.
Experiment
The experimental protocol closely parallels the simulation protocol. Stimuli corresponded to four circular patches of fluctuating brightness (Caspi et al., 2004; Ludwig et al., 2005), and the participants were asked upon stimulus termination to select the patch that was the brightest overall (Figure 7).
The evidence protocol and the conditions are described in the experimental methods. The first four conditions correspond to stimuli with evidence that favors a predominant alternative (two with consistent and two with inconsistent evidence), while the fifth condition corresponds to the correlated evidence discussed above (see Table 2).
Mean choice
The choice pattern did not change across the two sessions [the session factor was not significant in a 2 (consistent/inconsistent) × 2 (easy/hard)× 2(sessions) repeated measures ANOVA: F(1,15) = 0.99, MSE = 0.008, p = 0.34], and thus all the results we report are collapsed across the sessions. A paired-samples t-test was also conducted to compare the preference for C (anti-correlated alternative) in the correlation condition, across the two sessions. There was no significant difference in preference for C in session 1 (M = 0.53, SD = 0.20) and session 2 (M = 0.58, SD = 0.19); t(15) = −1.13, p = 0.28. The mean choice pattern (averaged across the 16 participants) in the five conditions in Table 2 (see Experimental Method) is shown in Figure 8. The left panel (symbols with error bars) shows the mean accuracy for conditions 2–5 (predominant conditions), in terms of probability to choose the predominant (A) option. The right panel shows the choice likelihood for the dissimilar alternative C, in condition 1(correlation). We observe that, on average, the participants chose the predominant option (A) more than 50% of the time in both inconsistent conditions (paired t-tests: p < 0.001 in both conditions); however, accuracy in both of these conditions was relatively low. For the consistent–hard and consistent–easy conditions, where the correct option dominated at all moments in a given trial, the subjects achieved very high accuracy. In particular, there was a big discrepancy between inconsistent–easy and consistent–hard, in favor of the latter condition [22 ± 13% SD; t(15) = 6.46; p < 0.001]. This large difference in accuracy indicates that consistent information (i.e., evidence not reversing in time) has a positive impact on choice accuracy beyond what would be expected based simply on the integrated evidence advantage for the correct alternative; this advantage is 0.025, 0.1, 0.175, 0.3, in the four filler conditions, I–H, I–E, C–H, C–E, respectively.
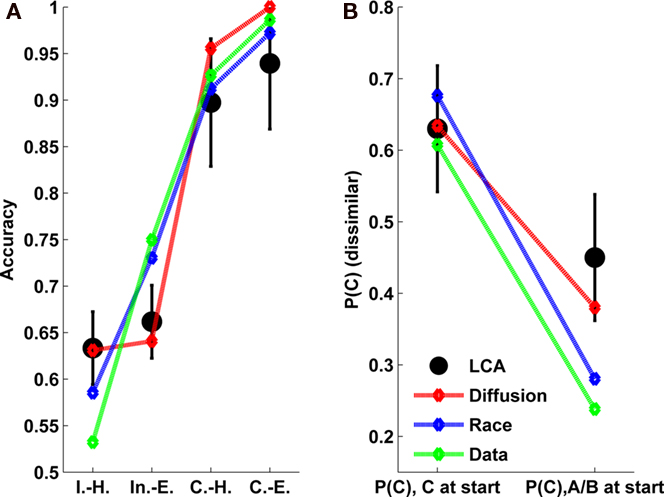
Figure 8. The average choice for the best (A) option for the first four conditions (left) and the choice of the dissimilar (B) option, in the correlation condition (right). Experimental results are shown with black circles (error bars correspond to 95% CI) while model fits with dashed lines (Red-LCA; blue-diffusion, green-race).
Turning now to the correlation condition (Figure 8, right panel), we see that the participants chose the dissimilar option (C), more than 50% of the time when the stimulus starts with a C-phase (p < 0.01), and, equally important, that they still chose C close to 50%, even when the stimulus starts with an A/B phase (and when C has only a 0.35 likelihood to receive more input than A or B).
As we shall see below, there are large individual differences across participants. Nevertheless, it may be useful to consider how well the different models can fit the data averaged across all participants, as a starting point for understanding how well the models capture participants performance in this task. We fitted the race, diffusion, and the LCA models to the data shown in Figure 8 (see Materials and Methods for details on the optimization technique). For the race and diffusion models we varied three parameters: decision criterion, processing noise (σ), and sensitivity (s), while for LCA we varied leak (k), inhibition (β), input sensitivity (s), I0, and processing noise (σ). The results of the fits are shown as colored lines in Figure 8 while the optimized parameters and the BIC values for each model are given in Table 3.

Table 3. Model parameters to optimized fits (Figure 9).
While all the models account for the general choice pattern (accuracy increasing in the filler conditions from I–H to C–E), and a preference for the dissimilar alternative in the correlation condition, they differ in their quantitative goodness of fit. The LCA has the lowest BIC scores (this includes a penalty of 3.58 for 2 extra degrees of freedom) of 26.4, followed by the diffusion model with a BIC of 29.2, and last is the race model with the BIC of 33. According to Raftery (1995, Table 6) BIC differences that are between 2 and 6 points provide positive support (0.75 < p <= 0.95) for the model with the lowest BIC score, while differences between 6 and 10 give strong support (0.95 < p <= 0.99). As one can see in Figure 8, the better fits of the LCA are due to the fact that it is the only model that does not overestimate the accuracy in the inconsistent–easy condition and does not underestimate the preference for the dissimilar alternative, P(C), in trials that start with evidence favoring A/B. Unlike the LCA, the race and the diffusion model require a low decision bound to obtain good fits. This low bound results in a strong primacy pattern (Kiani et al., 2008). A primacy pattern with approximate magnitude of 10% (i.e., smaller magnitude compared to the diffusion model with boundary, which predicts a primacy of 20%), is present in the data of the inconsistent conditions. For example, in the I-E and I-H conditions the accuracy, when the trial starts with evidence supporting the correct option is 69 and 72%, respectively, compared to 58 and 62% when the trial starts with evidence supporting the incorrect alternative (both ps < 0.05). This excessive primacy pattern leads the race and diffusion models to strongly underestimate P(C) in trials starting with contrary evidence.
Unlike the race and the diffusion model, the LCA accounts for primacy as a result of moderate inhibition dominance, without the need for an absorbing decision bound, and is able to better account for the choice data in the correlation condition. The BIC advantage for the LCA is only moderate relative to the diffusion model. Furthermore, the choice-preference for the dissimilar alternative in the correlated condition is subject to significant individual differences. Thus, it is possible that the average choice is not the best measure to use in assessing how well the models can capture the performance of individual participants. In the next section we examine how the various models can account for these individual differences.
Individual differences in the correlation condition
In Figure 9 (upper-left) we report the C-choice pattern for each participant in a 2D plot, in which the x-axis corresponds to the preference for the dissimilar option, P(C), in the trials where A/B received stronger input at the beginning of the trial, while the y-axis corresponds to P(C), when it received stronger evidence at the beginning of stimulus presentation. Each o-symbol corresponds to the mean choice pattern of a participant and error bars correspond to 90% confidence intervals.
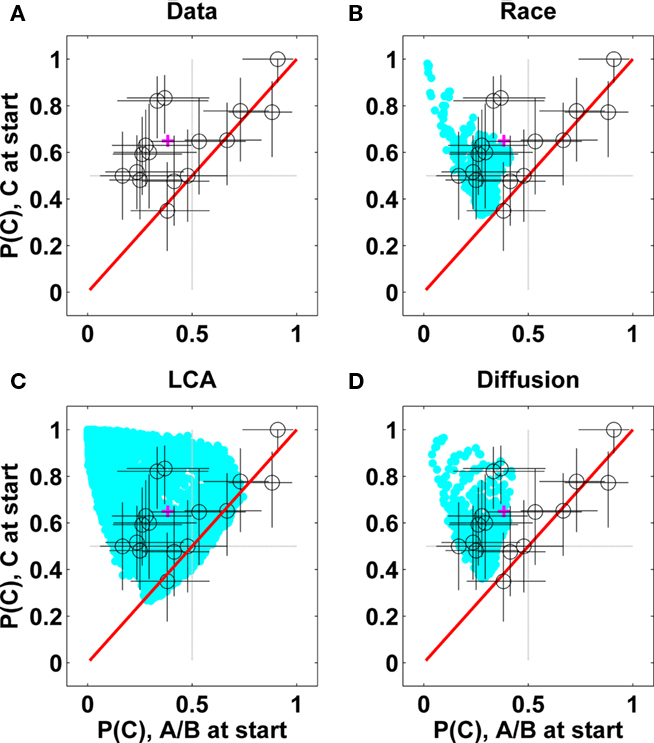
Figure 9. Individual choice for the dissimilar alternative, P(C), in the correlation condition of the experiment (upper-left) and in the models (others panels). Open-circles show the fraction of C-choices for each participant (error bars are 90% confidence intervals). The pink cross at (0.35, 0.65), indicates where the preference of a perfect integrator should be, based on the input statistics. The model predictions are shown with cyan.
The red-diagonal line in Figure 9 indicates the range of choice patterns expected if the choice mechanism is not sensitive to the initial evidence. Eight out of 16 subjects conform to that pattern and for five of them in the top right, P(C) is significantly greater than 50% in both conditions. The other eight participants (in the upper-left quarter) showed an increased preference for C when it received stronger input in the beginning. The magenta cross [at point (0.35, 0.65)] indicates where the preference of a perfect integrator should lie since, given the limited duration of the trials, the options that receive strong evidence in the beginning will receive more total evidence 65% of the time. We next examine how the three choice models can account for these individual differences in the choice of the C alternative.
Model predictions (for the race, diffusion and the LCA, indicated by cyan dots on the figure) were generated by systematically varying the parameters in each model. For the diffusion/race models this involved varying the variance of the Gaussian noise, σ, and the evidence value corresponding to the decision criterion on a 2-D grid. For these two models noise was varied in the interval (0.1, 4) with increments of 0.1 while the threshold was varied in the interval (5, 400) with increments of five for the diffusion and in the interval (10, 1600) with increment 40 for race. Overall 3200 points were derived for each of these models. For LCA, the predictions in Figure 11 were derived using two sets of simulations. In the first set we varied four parameters (a 4-D grid): inhibition (0–0.384, step = 0.024), leak (0–0.192, step = 0.012), I0 (0–2, step = 0.5), and processing noise σ (0–3, step = 0.5). In the second set of LCA simulations, I0 was constant at 0.3, processing noise σ was set to zero and six levels (three low and three high) of leak were used (0.0076, 0.0051, 0.0038, 0.0305 0.0457, 0.0610). For each leak level, inhibition started equal to leak and increased with a step of 0.00014 for 150 values. This set of parameters was chosen on the basis of the simulations reported above, as well as novel exploratory simulations, as they covered the relevant behaviors in the models. For example, the noise parameter did not exceed 3, so as to maintain accuracy levels in the range obtained in the experiment, and the value of the inhibition parameter in the LCA did not exceed 0.384; stronger inhibition would cause evidence early in the trial to predominate to the extent that it produces decisions that are too fast and of a too low level of accuracy.
Consistent with the simulations reported above, (Figure 6, right panels), we find that the non-linear LCA is the only model that is able to predict an order-independent advantage for the dissimilar alternative, as exhibited by the four participants whose choice pattern falls near the diagonal in the upper-right quadrant of Figure 9 (it must be noted, however, that none of the models accounts for the extreme participant near the (1, 1) corner). Data points on the upper-right portion of the main diagonal correspond to choice rates higher that 50% in favor of the dissimilar option, C, both when the evidence starts with a C-phase and when it does not. As previously discussed, this pattern is exhibited by the LCA with low noise, in the area of modest inhibition dominance (left of the second vertical lines in Figure 6 right panels). As previously noted, a perfect integrator would choose C with a rate of 65%, when the trial begins with C > (A/B) and with a rate of 35% when the trial begins with (A/B) > C. The ability of the LCA to predict data points on the upper diagonal implies that the models choice (like the participants in the upper-right quadrant) can be insensitive both to primacy and to the small differences in overall evidence. This is the case in the LCA with leak dominance (where early evidence has little weight), and for the LCA with moderate inhibition dominance.
Additionally, LCA (with higher internal noise; see Figure 6, bottom-right panel) is the only model able to account for the C-choices of the other three participants near (0.5, 0.5), who show a preference for the dissimilar option of about 50%, but are still invariant to initial evidence. To account for the individual differences in C-choice probability among these participants, the LCA mainly varies the amount of processing noise in the simulation. This leads to a simple prediction. The five “low-noise suspects” (participants with data in the upper-right quadrant) should have a higher accuracy in the predominant trials, compared with the three “high-noise suspects” [those near the center of the figure, with P(C) close to 50% regardless of the identity of the first stimulus]. This prediction is confirmed: 83% (±7%) vs. 73% (±6%), for low-noise vs. high-noise suspects, respectively. As illustrated in Figure 9, the diffusion and the race models cannot account for the C-choices of the eight participants on the diagonal. As Figure 8 suggests, diffusion and race both predict that when C initially receives stronger evidence it will be preferred more than when A/B receive stronger initial evidence. Therefore both the models are restricted to the upper-left quarter of Figure 9.
Finally the third group of subjects (in the upper-left quadrant) show a primacy pattern which can be explained qualitatively by all three models, with the race slightly worse for the two data points near (x = 0.4, y = 0.8). The LCA can encompass a wider range of patterns, spanning the participants whose performance falls near y = 0.5 in Figure 9. The choice values for these participants are consistent with the LCA model with moderate noise and stronger inhibition dominance (inhibition right of the second black line in Figure 6, right-bottom panel).
In order to better understand how the LCA parameters affect the choice pattern, in the simulation presented in Figure 9 (left-bottom panel), we replot in Figure 10 the LCA predictions with a color code that reflects the inhibition/leak ratio (a), the absolute leak value (b), and the noise level (c). One can observe several regularities: (i) recency dominance (inhibition much weaker than leak) is associated with the area near the (0.5, 0.5) location (blue, left panel), (ii) strong inhibition dominance is associated with the stripe near the negative diagonal in the upper-left quadrant (red in left panel, blue in the middle panel), (iii) balanced or moderate inhibition dominance and low noise (yellow in left panel, blue in right panel) is associated with the area near the diagonal in the upper-right quadrant. Points in this vicinity are associated with a tendency to choose the dissimilar alternative, with no dependency on the early evidence, and (iv) high processing noise (red areas on the right panel) is associated with the region near the main diagonal in the lower left quadrant (noise reduces the probability to choose the dissimilar option). These findings are consistent with the analysis of the simulation study presented earlier (Figure 6).
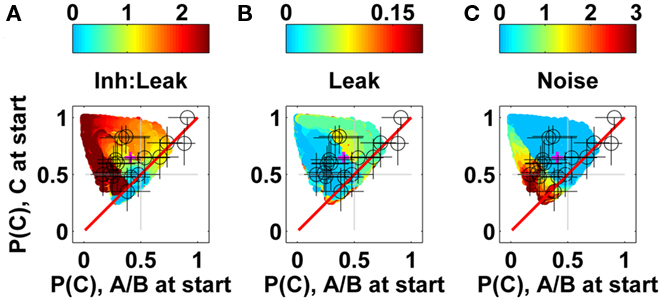
Figure 10. Mapping of LCA predictions to parameter values. (A) The color of each filled circle corresponds to the inhibition to leak ratio; (B) the color of each point shows the leak level; (C) the color of each filled circle shows the level of the processing noise.
Discussion
We have contrasted a number of models for multi-alternative choice. All the models belong to the sequential sampling framework, which assumes that observers take multiple samples of evidence and integrate them over time. These models differ, however, on the stopping rule for evidence integration, on the inclusion of leakage and competition, and on the presence of a lower reflecting boundary on activation. While it has proven difficult to distinguish the models based on perceptual choice data obtained with stationary stimuli (see also Ditterich, 2010; but see Leite and Ratcliff, 2010; Teodorescu and Usher, in preparation), here we found that it is possible to make steps toward distinguishing them using non-stationary evidence with temporal correlations.
First, we did find that, in trials with predominant evidence, the participants are biased toward evidence at the start of the stimulus onset (69 and 72%, for I–E and I–H, respectively, compared to 58 and 62%, for late evidence trials) and that they show an increased accuracy for conditions without evidence reversals. This result is consistent with models that assume a limited range of integration, such as the bounded diffusion (Huk and Shadlen, 2005; Kiani et al., 2008) or the unbalanced non-linear LCA with inhibition dominance (Usher and McClelland, 2001; Bogacz et al., 2007). The latter is also consistent with perturbation studies, showing the effects of transient changes in evidence to be higher when applied early on during the observation interval (Huk and Shadlen, 2005; Figure 10B). While both LCA and bounded integration can explain such effects, Huk and Shadlen (2005) noted that “bounded integration is not sufficient to explain the weak impact of later pulses on the LIP responses” (p. 3027) and suggest attractor dynamics (Wang, 2002) – a mechanism that shares much with the inhibition dominant LCA – as one mechanism that could account for the residual effect.
The central result of our investigation involves our critical correlation condition, involving choice between three alternatives that receive an (approximately) equal amount of integrated evidence averaged across two alternative temporal phases. Two options (A, B) are quite similar in their temporal profile of the evidence, while option C is dissimilar, or anti-correlated, with the temporal profile of evidence for A and B. The main result is that, for many participants, the anti-correlated option is chosen quite often, regardless of which evidence phase (the phase favoring A and B, or the phase favoring C) came first during a given trial of our experiment. This finding parallels the similarity effect reported by Tversky (1972) in the domain of multi-attribute choice, where two alternatives that have high preference value on one dimension (e.g., laptop screen size) loose out to a third alternative that has a high preference value on another dimension (e.g., the laptop’s weight). Indeed, in other work, we have accounted for this similarity effect using the same mechanism that produces the advantage for the uncorrelated alternative in the present experiment2.
For the present results, the LCA gave the best account of the combined data, with the diffusion model next and the race model further behind. In particular, the race and diffusion model overestimate the accuracy in the inconsistent–easy condition, and the effect of the first evidence phase on the probability of choosing the dissimilar alternative (Figure 8); in particular, both models strongly underestimated the probability of choosing the dissimilar alternative when evidence starts contrary to it.
As the pattern of choices of the uncorrelated alternative was subject to considerable individual differences, we also examined how the models can account for the patterns exhibited by different individual participants. First, we find that some of the participants (ellipse, in Figure 9 upper-left) showed a preference for the dissimilar option (C) that is larger for stimuli that start with evidence that favors that option than for stimuli where the initial evidence favors the A and B options. This pattern can be accounted for in all three models and it can also be accounted for by a perfect integrator, since the preponderance of evidence tends to favor the option that starts the trial. Second, we find that the pattern of individual performance is better covered by the LCA. These participants showed little or no sensitivity to order effects (red-diagonal). This pattern is difficult to explain under the race and diffusion models (they can do so only if the overall proportion of C-choices is very low, by assuming high-noise levels), but is easily explained by the LCA. Two properties of LCA model work together to produce a preference for the uncorrelated option with little or no primacy bias (Figure 6, upper-right, between the two vertical lines): moderate inhibition dominance and non-linear dynamics (preventing activation from going below 0). It should be noted, though, that none of the models accounted for the performance of one participant, who preferred the C alternative so strongly that he chose it on nearly every trial regardless of which phase came first. A goal for future research will be to understand whether a future variant of the LCA, or some other model of the decision process best explains this participant’s data pattern. Some such possible models are considered in the next section.
The apparent advantage of the LCA over the race and diffusion models needs to be further qualified by the fact that the LCA model had more free parameters (four in LCA, compared with two in race and diffusion, given that in Figure 9 sensitivity was set to one for all models), and this could therefore explain its higher flexibility in accounting for individual differences. In this regard, it is worth noting that all of the models share one mechanism and its associated parameter – intrinsic processing noise. The race and diffusion models add an absorbing boundary mechanism, and this mechanism can allow them to account in part for the data. Instead of this, the LCA adds leakage, inhibition, and a reflecting boundary at 0 activation and each of these mechanisms is associated with an additional free parameter (the I0 parameter is associated with the reflecting boundary, since the choice of I0 influences the distribution of occasions on which the reflecting boundary is reached). Though the LCA model certainly is more complex and does have more free parameters, the data indicate that the additional flexibility it provides is helpful to account for the range of patterns observed in the data. This does not, of course, imply that the particular assumptions of the LCA are the only ones possible. It is possible that there are ways of increasing flexibility in other models that would allow them, also, the needed additional flexibility. We now turn to a consideration of a range of model variants under current consideration, including several variants of the diffusion model.
Alternative Accounts and Future Directions
We first consider whether it might be possible to modify the bounded diffusion model to account for the preference some participants show for the uncorrelated alternative in the correlation condition, in the absence of a primacy effect. In the LCA, this preference depends, in part, on the presence of a reflecting boundary at an activation value of 0. Here we consider whether including a similar reflecting lower boundary in the bounded diffusion model would allow it to account for this feature of the data as well (Zhang et al., 2009). We carried out simulations to explore the ability of such a model to account for the individual difference data in Figure 8. As shown in Figure 11 (right panels), the reflecting lower bound does help the diffusion model to extend its choice pattern toward the diagonal and the (0.7, 0.7) point. The reflecting bound helps the diffusion model because the activation of the dissimilar alternative is kept at zero in cases where it would otherwise have been inhibited below this value, thereby allowing it to quickly regain activation when it is receiving the strongest support from the stimulus. The model is still less robust than the LCA in accounting simultaneously for the results in the filler conditions and the correlation condition. To show this we plot in Figure 11 the predictions of the LCA and non-linear diffusion model for parameters that at the same time predict differences in accuracy between the consistent–hard and inconsistent–easy conditions, which are smaller or larger than 0.24 (0.24 was the population average, with a SD of 0.12). We observe that while both models account equally for the participants with small differences, the diffusion model has problems accounting for the data of participants that show larger differences, which require a low decision bound, resulting in strong primacy. Nevertheless, the bounded diffusion model with reflecting boundary goes quite some way in the direction of encompassing all of the data, and certainly deserves further consideration in subsequent research.
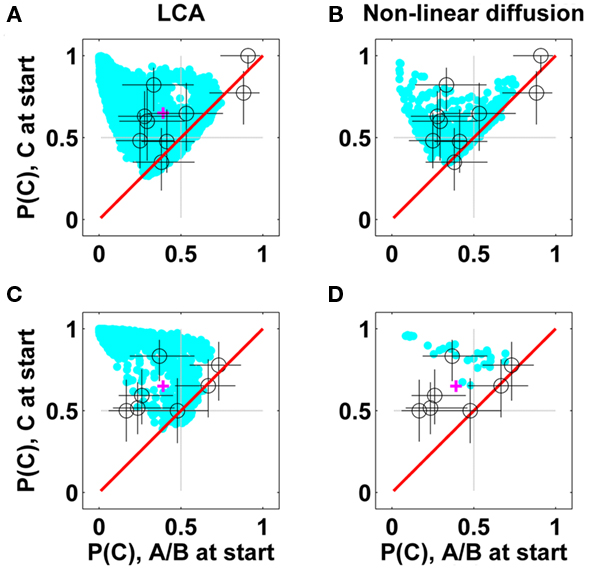
Figure 11. Predictions for LCA (left panels) and non-linear diffusion with a reflecting lower bound (right panels). The predictions presented in the top panels satisfy the constrain Accuracy (Cons.-Hard) – Accuracy (Incons.-Easy) < 0.24, and in the bottom panels Accuracy (Cons.-Hard) – Accuracy (Incons.-Easy) > 0.24.
A second modification of the diffusion model (Niwa and Ditterich, 2008) is to replace the absorbing upper boundary with a reflecting upper boundary. Such a mechanism has been suggested in the 2AFC task by Zhang and Bogacz (2010). As we demonstrate in the Section “Appendix,” transforming the upper decision boundary into a reflecting one (i.e., a diffusion model between two reflecting boundaries) reduces the models ability to account for the similarity effect. This happens because the dissimilar alternative, C, has a higher chance to hit the reflecting upper boundary (because its positive/negative drift is larger) and thus it accumulates less activation than it would in the absence of the reflecting boundary.
Third, the type of diffusion model we have considered here assumes that the evidence in support of each alternative equals the direct support minus the average support for the other alternatives. Unlike in other versions of this model (Niwa and Ditterich, 2008; Ditterich, 2010) we did not assume an input dependent variance. Future work will be needed to examine the impact of such variance to the choice in the task we examined. Furthermore, an alternative extension of the diffusion model to n-alternatives has been suggested by McMillen and Holmes, 2006 (see also Bogacz et al., 2007; McMillen and Behseta, 2010) and is equivalent to the multi-hypothesis sequential ratio test (MSPRT; see also Bogacz, 2009; Ditterich, 2010). In this model, N accumulators integrate evidence independently and at each moment, the quantity L is computed, where L is the state of the accumulator with the maximum activity minus the activity of the next highest accumulator. When L exceeds a threshold a decision is made. This approach is asymptotically optimal but its neural realization is complex requiring the online computation of the max and the next-max functions. Unlike the diffusion model we focused on here, this (max-next) diffusion model can account better for the tendency to choose the dissimilar option in our correlated conditions (the predictions fall in between the results of the diffusion and of LCA (in Figure 9). This is due to the fact that the decision criterion is applied to the two maximally activated alternatives, and this penalizes alternatives that have correlated evidence (their support goes up together). We see the LCA as a natural biological approximation of this near optimal choice model, without requiring a complex architecture or a complex computational algorithm. Indeed, competition among any number of alternatives can closely approximate the max-next computation. This happens since in LCA, all the choice units compete with each other, but the weak units drop out of the process due to the non-linearity at zero activation, leaving the ones that have the strongest evidence to compete at the end (Bogacz et al., 2007), and thus it does not require a change of weights with set size. Additional implementations of the MSPRT have been recently proposed (Bogacz and Gurney, 2007; Bogacz, 2009; Ditterich, 2010; McMillen and Behseta, 2010). Further work is needed to examine the predictions these models would make for choices with correlated evidence.
There are a number of additional models that have been recently used to account for physiological and behavioral data in multi-choice tasks with moving dots stimuli. One such model was proposed by Churchland et al. (2008). In this model, binary choices (opposite motion direction) is modeled as a diffusion process, but four-alternative choice with two orthogonal motion directions (e.g., classifying the motion of the dots in one out of four directions: up-left, up-right, down-left, down-right) is modeled as an independent race between the two diffusions, one for each of the orthogonal directions. This model accounts for the slowdown in RT with larger set size, but it has not been tested on critical stimuli that contain ambiguous evidence, and in which race and diffusion models have contrasting predictions (see Niwa and Ditterich, 2008; Teodorescu and Usher, in preparation). Another recent model for multiple choice was proposed by Furman and Wang (2008). This model accounts for multi-choice decisions of moving dots stimuli, via a continuous line attractor model, in which center-surround connectivity implements competing attractors around the direction continuum, and accounts, in this way, for similarity effects. Note also that the attractor model of choice (Wong and Wang, 2006) is closely related to the LCA model, and thus under certain parameter regimes it may have quite similar behavioral predictions [see also Ditterich, 2010, for an implementation of a balanced LCA using a model similar to Wang, 2002].
As a final alternative, we consider the possibility that participants may shift their attention among the alternatives, either covertly or overtly via eye movements. We have not considered how such shifts would affect the integration of information, and this matter certainly deserves consideration in future investigations. It is possible that that the attended alternative could exert a stronger influence on the corresponding accumulator (Krajbich et al., 2010), and/or that shifts of attention could reset the integrators. If there were also a tendency to direct attention to the momentarily brightest (or one of the two brightest) alternatives, these factors could potentially lead to a preference for the uncorrelated alternative. We leave it to future research to consider whether a full account of the results we have reported here can be given in a model that incorporates these or other ideas about how fluctuations in attention or eye movements might affect the evidence accumulation process.
Conclusion
In a recent article in this journal, which compared a variety of models for multi-alternative choice, Ditterich (2010) concluded that they all account well for the behavioral data, but that they can be distinguished using physiological measurements. Here we showed that a more complex behavioral evidence protocol can also provide an improved tool for distinguishing among choice mechanisms. In the end, however, it seems likely that a full understanding of the mechanisms of choice will require combining behavioral and physiological (or imaging) methods.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Air Force Research Laboratory (FA9550-07-1-0537). We also wish to thank Roy de Kleijn for bringing to our attention a mistake in the original report of the experimental values we reported in our first manuscript.
Footnotes
- ^In the Niwa and Ditterich (2008) model, the noise variance is input dependent. Here we use a simpler variant of this model, with input-independent noise variance.
- ^In previous work (Usher and McClelland, 2004; Tsetsos et al., 2010) we have shown that the LCA can account for three preference reversal effects (similarity, attraction and compromise) in multi-attribute choice. In that work, we assumed a non-linear and asymmetric value function, characterized by loss-aversion (higher slope for losses than for gains) borrowed from Prospect Theory (Tversky and Kahneman, 1991). This asymmetric value function was only needed for accounting for the compromise/attraction effect and not for the similarity effect, which in fact is reduced in size by loss aversion. In the present paradigm, we found no compromise or attraction effect (unreported filler conditions), indicating that in processing of brightness, “advantages” and “disadvantages” are not subject to such an asymmetry.
References
Albantakis, L., and Deco, G. (2009). The encoding of alternatives in multiple-choice decision-making. Proc. Natl. Acad. Sci. U.S.A. 106, 10308–10313.
Bogacz, R. (2009). “Optimal decision making theories,” in Handbook of Reward and Decision Making, eds J.-C. Dreher, L. (Oxford: Academic Press), 375–397.
Bogacz, R., Brown, E., Moehlis, J., Cohen, J. D., and Holmes, P. (2006). The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced- choice tasks. Psychol. Rev. 113, 700–765.
Bogacz, R., and Cohen, J. D. (2004). Parametrization of connectionist models. Behav. Res. Methods Instrum. Comput. 36, 732.
Bogacz, R., and Gurney, K. (2007). The basal ganglia and cortex implement optimal decision making between alternative actions. Neural Comput. 19, 442–477.
Bogacz, R., Usher, M., Zhang, J., and McClelland, J. L. (2007). Extending a biologically inspired model of choice: multi-alternatives, nonlinearity and value-based multidimensional choice. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 1655.
Brown, S., and Heathcote, A. (2005). A ballistic model of choice response time. Psychol. Rev. 112, 117–128.
Brown, S. D., and Heathcote, A. (2008). The simplest complete model of choice response time: linear ballistic accumulation. Cogn. Psychol. 57, 153–178.
Caspi, A., Beutter, B. R., and Eckstein, M. P. (2004). The time course of visual information accrual guiding eye movement decisions. Proc. Natl. Acad. Sci. U.S.A. 101, 13086.
Churchland, A. K., Kiani, R., and Shadlen, M. N. (2008). Decision-making with multiple alternatives. Nat. Neurosci. 11, 693–702.
Ditterich, J. (2010). A comparison between mechanisms of multi-alternative perceptual decision making: Ability to explain human behavior, predictions for neurophysiology, and relationship with decision theory. Front. Decis. Neurosci. 4:184. doi: 10.3389/fnins.2010.00184
Donner, T. H., Siegel, M., Fries, P., and Engel, A. K. (2009). Build-up of choice-predictive activity in human motor cortex during perceptual decision-making. Curr. Biol. 19, 1581–1585.
Furman, M., and Wang, X. J. (2008). Similarity effect and optimal control of multiple-choice decision making. Neuron 60, 1153–1168.
Gold, J. I., and Shadlen, M. N. (2001). Neural computations that underlie decisions about sensory stimuli. Trends Cogn. Sci. (Regul. Ed.) 5, 10–16.
Gold, J. I., and Shadlen, M. N. (2002). Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron 36, 299–308.
Gold, J. I., and Shadlen, M. N. (2007). The neural basis of decision making. Annu. Rev. Neurosci. 30, 535–574.
Hanes, D. P., and Schall, J. D. (1996). Neural control of voluntary movement initiation. Science 274, 427.
Heekeren, H. R., Marrett, S., Bandettini, P. A., and Ungerleider, L. G. (2004). A general mechanism for perceptual decision-making in the human brain. Nature 431, 859–861.
Horwitz, G. D., and Newsome, W. T. (2001). Target selection for saccadic eye movements: prelude activity in the superior colliculus during a direction-discrimination task. J. Neurophysiol. 86, 2543.
Huk, A. C., and Shadlen, M. N. (2005). Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. J. Neurosci. 25, 10420.
Kiani, R., Hanks, T. D., and Shadlen, M. N. (2008). Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J. Neurosci. 28, 3017.
Krajbich, I., Armel, C., and Rangel, A. (2010). Visual fixations and the computation and comparison of value in simple choice. Nat. Neurosci. 13, 1292–1298.
Leite, F. P., and Ratcliff, R. (2010). Modeling reaction time and accuracy of multiple-alternative decisions. Attent. Percept. Psychophys. 72, 246.
Link, S. W., and Heath, R. A. (1975). A sequential theory of psychological discrimination. Psychometrika 40, 77–105.
Ludwig, C. J., Gilchrist, I. D., McSorley, E., and Baddeley, R. J. (2005). The temporal impulse response underlying saccadic decisions. J. Neurosci. 25, 9907.
Mazurek, M. E., Roitman, J. D., Ditterich, J., and Shadlen, M. N. (2003). A role for neural integrators in perceptual decision making. Cereb. Cortex 13, 1257.
McMillen, T., and Behseta, S. (2010). On the effects of signal acuity in a multi-alternative model of decision making. Neural. Comput. 22, 539–580.
McMillen, T., and Holmes, P. (2006). The dynamics of choice among multiple alternatives. J. Math. Psychol. 50, 30–57.
Niwa, M., and Ditterich, J. (2008). Perceptual decisions between multiple directions of visual motion. J. Neurosci 28, 4435.
Ratcliff, R., Hasegawa, Y. T., Hasegawa, R. P., Smith, P. L., and Segraves, M. A. (2007). Dual diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. J. Neurophysiol. 97, 1756.
Ratcliff, R., and McKoon, G. (2008). The diffusion decision model: theory and data for two-choice decision tasks. Neural. Comput. 20, 873–922.
Ratcliff, R., and Rouder, J. N. (1998). Modeling response times for two-choice decisions. Psychol. Sci. 9, 347–356.
Ratcliff, R., and Smith, P. L. (2004). A comparison of sequential sampling models for two-choice reaction time. Psychol. Rev. 111, 333–367.
Roe, R. M., Busemeyer, J. R., and Townsend, J. T. (2001). Multialternative decision field theory: A dynamic connectionst model of decision making. Psychol. Rev. 108, 370–392.
Roitman, J. D., and Shadlen, M. N. (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci. 22, 9475.
Rorie, A. E., Gao, J., McClelland, J. L., and Newsome, W. T. (2010). Integration of sensory and reward information during perceptual decision-making in lateral intraparietal cortex (LIP) of the Macaque monkey. PLoS ONE 5, e9308. doi: 10.1371/journal.pone.0009308
Shadlen, M. N., and Newsome, W. T. (2001). Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol. 86, 1916.
Tsetsos, K., Usher, M., and Chater, N. (2010). Preference reversal in multiattribute choice. Psychol. Rev. 117, 1275–1291.
Tversky, A., and Kahneman, D. (1991). Loss aversion in riskless choice: a reference-dependent model. Q. J. Econ. 1039–1061.
Usher, M., and McClelland, J. L. (1995). “On the time course of perceptual choice: A model based on principles of neural computation,” in Technical Report PDP.CNS.95.5, Center for the Neural Basis of Cognition (Pittsburgh, PA: Carnegie Mellon University).
Usher, M., and McClelland, J. L. (2001). The time course of perceptual choice: The leaky, competing accumulator model. Psychol. Rev. 108, 550–592.
Usher, M., and McClelland, J. L. (2004). Loss aversion and inhibition in dynamical models of multialternative choice. Psychol. Rev. 111, 757–769.
Usher, M., Olami, Z., and McClelland, J. L. (2002). Hicks law in a stochastic race model with speed-accuracy tradeoff. J. Math. Psychol. 46, 704–715.
Vickers, D. (1970). Evidence for an accumulator model of psychophysical discrimination. Ergonomics 13, 37–58.
Wang, X. J. (2002). Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36, 955–968.
Wong, K. F., and Wang, X. J. (2006). A recurrent network mechanism of time integration in perceptual decisions. J. Neurosci. 26, 1314.
Zhang, J., and Bogacz, R. (2010). Bounded Ornstein–Uhlenbeck models for two-choice time controlled tasks. J. Math. Psychol. 54, 322–333.
Keywords: multiple alternatives, diffusion, leaky integration, inhibition, perceptual decisions
Citation: Tsetsos K, Usher M and McClelland JL (2011) Testing multi-alternative decision models with non-stationary evidence. Front. Neurosci. 5:63. doi: 10.3389/fnins.2011.00063
Received: 18 October 2010; Accepted: 19 April 2011;
Published online: 04 May 2011.
Edited by:
Shu-Chen Li, Max Planck Institute for Human Development, GermanyReviewed by:
Roozbeh Kiani, Stanford School of Medicine, USAPatrick Simen, Princeton University, USA
Eric Shea-Brown, University of Washington, USA
Copyright: © 2011 Tsetsos, Usher and McClelland. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Marius Usher, Department of Psychology, Tel-Aviv University, Ramat Aviv, Israel. e-mail:bWFyaXVzQHBvc3QudGF1LmFjLmls