- 1 Helen Wills Neuroscience Institute, University of California Berkeley, Berkeley, CA, USA
- 2 Department of Psychiatry and Biobehavioral Sciences, University of California Los Angeles, Los Angeles, CA, USA
- 3 Brain Research Institute, University of California Los Angeles, Los Angeles, CA, USA
- 4 Department of Psychology, University of California Los Angeles, Los Angeles, CA, USA
- 5 Department of Psychology, Imaging Research Center, University of Texas at Austin, Austin, TX, USA
- 6 Department of Neurobiology, Imaging Research Center, University of Texas at Austin, Austin, TX, USA
The application of statistical machine learning techniques to neuroimaging data has allowed researchers to decode the cognitive and disease states of participants. The majority of studies using these techniques have focused on pattern classification to decode the type of object a participant is viewing, the type of cognitive task a participant is completing, or the disease state of a participant’s brain. However, an emerging body of literature is extending these classification studies to the decoding of values of continuous variables (such as age, cognitive characteristics, or neuropsychological state) using high-dimensional regression methods. This review details the methods used in such analyses and describes recent results. We provide specific examples of studies which have used this approach to answer novel questions about age and cognitive and disease states. We conclude that while there is still much to learn about these methods, they provide useful information about the relationship between neural activity and age, cognitive state, and disease state, which could not have been obtained using traditional univariate analytical methods.
1. Introduction
Recent advances in functional MRI (fMRI) analysis techniques have enabled cognitive neuroscientists to ask a new set of questions about the neural basis of cognitive states. Predictive analytical tools in particular have led to a spate of studies demonstrating that it is possible to decode cognitive and disease states from neuroimaging data. In a sense, these tools allow a rudimentary version of “mind reading,” by making it possible to infer what a participant is viewing or what cognitive processes a participant is engaged in without any external evidence (O’Toole et al., 2007). Many of these studies classify the cognitive states of participants into two more categories. For example, one of the earliest functional studies to use a predictive analysis to decode fMRI data found that the type of object participants were viewing (faces, cats, houses, chairs, scissors, shoes, or bottles) could be successfully predicted from knowing the pattern of activation each object category elicited on separate runs of data (Haxby et al., 2001). This study took advantage of multivariate techniques to quantitatively compare patterns of activation across object categories. Not long after this groundbreaking study, sophisticated techniques adapted from statistics and computer science were applied to functional neuroimaging data to ask similar questions. Cox and Savoy (2003) implemented a pattern recognition analysis, in which a “statistical machine” was trained to learn and classify patterns of neural data into discrete categories. They found that this statistical machine was able to correctly classify objects from 10 different categories, even if the training and testing sessions were held on different days and if the exemplars used during test were different from those on which the machine was trained (Cox and Savoy, 2003). These pattern classification studies and others like them have allowed us to better understand the distributed and overlapping yet distinct patterns of activity associated with certain categories of objects (Haxby et al., 2001; Cox and Savoy, 2003).
Since these early studies, many others have used machine learning techniques to decode the current cognitive state of participants (for reviews, see Haynes and Rees, 2006; Norman et al., 2006). While many of these studies used classifiers that were trained on a subset of data within a participant and then tested on separate data from that same participant, some studies have demonstrated that there is enough similarity across participants engaged in similar mental processes that it is possible to classify cognitive states across participants as well (i.e., by training a pattern classification machine on N-1 participants and testing it on the left-out participant). Classifying across participants has been successfully applied both to categorize what object participants are viewing (Mourão-Miranda et al., 2005; Shinkareva et al., 2008) as well as what cognitive task a participant is performing (Poldrack et al., 2009). When classifying what task a participant was performing (including tasks as varied as response inhibition, risky decision making, and semantic judgments), it was found that classification accuracy was almost as high across participants (80%) as classifying different runs within participants (90%). This finding led to the conclusion that patterns of activation during different cognitive processes are consistent across participants, at least for the kinds of tasks examined in this study (Poldrack et al., 2009).
Given the finding that brain states may be consistent across individuals, machine learning techniques have been expanded for clinical purposes. The chance for human error makes automatic detection of disease states an appealing endeavor. Therefore, research has been conducted with the intent of using anatomical brain images to classify patients. These techniques have been successfully implemented to classify the brains of patients with Alzheimer’s disease (AD) and mild cognitive impairment (MCI; Duchesne et al., 2005; Fan et al., 2008), carriers of the Huntington’s disease (HD) gene who are pre-symptomatic (Klöppel et al., 2008, 2009; Rizk-Jackson et al., 2011), and patients either at risk for or diagnosed with schizophrenia or psychosis (Davatzikos et al., 2005; Sun et al., 2009; Koutsouleris et al., 2010), depression (Fu et al., 2008), autism (Ecker et al., 2010a,b), and attention deficit hyperactivity disorder (ADHD; Zhu et al., 2005). These studies have demonstrated that certain neurological disorders can be characterized by a systematic deterioration or deformation of brain tissue.
While most studies exploring predictive analyses with neuroimaging data have focused on pattern classification, there is a small but emerging body of literature implementing regression analysis to decode continuous participant characteristics from neuroimaging data. Regression-based predictive analyses can predict the values of continuous variables from neuroimaging data, such as age (Ashburner, 2007; Cohen et al., 2010; Franke et al., 2010), cognitive characteristics (Cohen et al., 2010; Chu et al., 2011; Kahnt et al., 2011; Valente et al., 2011), or neuropsychological characteristics (Duchesne et al., 2009; Wang et al., 2010; Rizk-Jackson et al., 2011). In this focused review we discuss the recent development of regression-based predictive analytical tools for examining the neural basis of cognitive organization and their potential advantages over traditional univariate analytical methods. We begin by describing the methods used to decode continuous variables from neuroimaging data. Next, we provide examples of different types of variables that can be decoded using these regression-based methods and how these methods allow for a greater understanding of the neural state underlying individual differences in age, normal cognition, and disease. Last, we give suggestions for future research and applications of these tools.
2. Predictive Decoding Methods
The goal of predictive decoding is to predict some aspect of cognitive function from neuroimaging data; as noted above, most studies have done this in the context of classification (i.e., assigning the participant to one of a discrete number of cognitive states), but there is increasing interest in prediction of continuous values (i.e., regression). In the imaging literature, significant correlations between behavior and activation are often described as reflecting “prediction,” but a fundamental insight from the field of statistical learning (which is focused on the development of tools for statistical prediction) is that the fit of a model to a particular dataset will generally overestimate the ability to predict the values of new observations (e.g., Hastie et al., 2001). This is due to “overfitting,” in which the model fits both the signal as well as the noise in the data. The more complex the model the more likely it is to suffer from overfitting, although even simple linear models will generally fit better to the dataset on which they were developed as compared to a new sample from the same population.
For this reason, in order to demonstrate true “prediction,” one must assess the ability of the model to make predictions about new observations that were not included in the initial sample. To do so, machine learning techniques can be applied. For example, a machine can be “trained” on a sample of data, in which it is given the patterns of input data that are associated with a specific value of an outcome variable (i.e., age). Next, that machine can be “tested” on previously unseen data by being given input data and being asked to predict, based on the patterns noted in the training data set, the unknown value of the outcome variable. The success of a machine can be assessed by comparing the predicted outcome values to the known outcome values in novel data (i.e., with a Pearson correlation).
Rather than collecting an entirely new sample on which to test the prediction, it is more common with functional neuroimaging data to use a “cross-validation” strategy in which one trains the model on subsets (or “folds”) of the entire sample and then tests the accuracy of predictions for the “left-out” observations. There are a number of strategies that one can use for cross-validation, such as training on half of a participant’s data and testing on the second half or training on all the data from a subset of participants and testing on the remaining participants. While it is common to leave one participant out and train the machine on N-1 participants (doing so N times so that each participant has been left-out once), our experience has shown that for regression modeling it is best to use a relatively small set of folds (e.g., four equal groups of participants; Cohen et al., 2010; Rizk-Jackson et al., 2011). Using a small number of folds prevents the overfitting that can occur when the leave-one-out method is applied to small sample sizes (Kohavi, 1995). In practice, this means training the machine on three-fourths of participants and testing the machine on the remaining one-fourth. This procedure is done four times so that all participants have been left-out once. Using this method, it is very important that the distribution of the to-be-predicted variable does not differ between these folds (known as “balanced cross-validation”; Kohavi, 1995). In other words, if the goal of the machine is to predict participant age, each of the four folds should have equal ages on average.
Another challenge in predicting behavioral or other measures from whole-brain neuroimaging data is that the number of predictor variables (or “features”; in this case, voxels) is generally much larger than the number of observations (which could be participants, trials, or other events depending on the nature of the study). These are known generically as “large p, small n” problems. The general linear model (which is generally used in a “mass univariate” approach for fMRI analysis) breaks down when there are more variables than data points because there is no longer a unique solution to the least squares optimization problem. One alternative is to reduce the dimensionality of the data (e.g., using the first few principal components as variables, or selecting a small subset of features/voxels), but a more common approach is to use methods from statistics and computer science that have been specifically developed to perform high-dimensional classification and regression. A full explication of these methods is outside the scope of this paper; for systematic reviews, see Alpaydin (2004), Duda et al. (2001), or Hastie et al. (2001).
In general, these high-dimensional regression methods work by placing additional constraints on the possible solutions, such as enforcing sparse solutions (i.e., ensuring that only a small number of features have non-zero coefficients, or that only a small number of observations are used). For example, in ridge regression (Hoerl and Kennard, 1970), a regression solution is estimated that minimizes the error in the training data, with the constraint that the sum of the squared weights across the features should be minimized (as opposed to standard regression, where there are no constraints on the regression weights). Support vector regression imposes a similar constraint on the sum of squared weights. In addition, whereas standard linear regression is estimated by minimizing the squared error between predicted and actual values for all observations, in support vector regression the error is counted only for values that fall outside of a “tube” around the regression line, and the regression solution is determined by this (relatively small) number of observations, which are known as “support vectors.” Although support vector machines have become very popular due to the availability of robust toolboxes, many other approaches also exist which use other forms of regularization and which may work better under some circumstances. Relevance vector machines (Tipping, 2001) are similar to support vector machines, but they use Bayesian estimation and generally find solutions that are much sparser than those found by support vector machines. Gaussian process regression (Rasmussen and Williams, 2006) is another Bayesian regression method that is formally related to relevance vector machines; both of these methods generally perform well on fMRI data, but in some cases may take a very long time to estimate. In general, all of the methods discussed here are able to scale to very large numbers of features (e.g., hundreds of thousands of voxels) and are relatively resistant to overfitting, which means that they can generalize well to new data sets.
3. Predicting Cognitive States
3.1. Initial Studies
The field of regression-based predictive analyses is still in its infancy, and as a result many of the existing studies are exploratory and test multiple methods and parameters or practical applications of such techniques. In one early application of decoding data, Ashburner (2007) was successfully able to predict participant age from anatomical scans registered using a new technique he was proposing (DARTEL). Because changes in brain shape with age can be difficult to register, this analysis tested two different types of registration techniques. He found that neuroimaging data from brains registered using the two techniques he tested were similarly able to predict participant age, implying that both techniques could successfully register brains across development.
Two recent papers have been published detailing the methods the two groups utilized to earn first and second place in the 2007 Pittsburgh Brain Activity Interpretation Competition, with the stated goal being “to infer subjective experience from a rigorously collected data set of fMRI data associated with dynamic experiences in a virtual reality environment with a quantitative metric of success” (http://www.lrdc.pitt.edu/ebc/2007/competition.html; Chu et al., 2011; Valente et al., 2011). Data were fMRI scans from participants playing a virtual reality game, in which a number of objective variables (i.e., time spent viewing faces or speed) and subjective variables (i.e., participant ratings) were collected. Using different regression methods (kernel ridge regression, relevance vector regression), both groups were successfully able to predict a number of continuous variables from the neural data with which they were provided. Objective variables were better predicted than subjective ratings for both groups, possibly because the objective variables were more reliable or because they were collected during the task, while the subjective ratings were collected after the task (Chu et al., 2011; Valente et al., 2011).
Most of the literature exploring regression-based predictive analyses focuses on methodology or a demonstration of the ability to decode participant characteristics from neural data. Another genre of studies has used predictive regression for a clinical purpose: to predict clinically relevant variables from anatomical scans of various groups of patients (see Section 4 below). Additionally, a small number of studies have been published that used the existing methodology to answer theoretical questions about underlying cognitive organization that could not be answered using traditional univariate methods. The next three sections of this review will discuss three of those basic research studies as a demonstration of the diverse types of research questions that can be answered with regression-based predictive analyses, and what advantages they have over more standard analyses.
3.2. Response Inhibition Case Study
In a recent study, we took advantage of predictive analyses to answer specific questions about the cognitive process of response inhibition. A network of cortical and basal ganglia regions has been identified as being critical for response inhibition, including the right inferior frontal gyrus (IFG), right pre-supplementary motor area (preSMA), and right subthalamic nucleus (STN). Neuroimaging studies consistently implicate these three regions, the right IFG most consistently, along with others such as the anterior insula, anterior cingulate cortex (ACC), parietal cortex, and striatum, as active during successful response inhibition (Konishi et al., 1998; Garavan et al., 1999, 2002; Liddle et al., 2001; Menon et al., 2001; Rubia et al., 2001, 2003; Buchsbaum et al., 2005; Aron and Poldrack, 2006; Chevrier et al., 2007; Boehler et al., 2010; Congdon et al., 2010; Kenner et al., 2010; for reviews, see Aron et al., 2004; Chikazoe, 2010). Further, lesion and transcranial magnetic stimulation (TMS) studies have demonstrated that these regions are necessary for response inhibition (Aron et al., 2003; Chambers et al., 2006, 2007; Floden and Stuss, 2006; Chen et al., 2009). Crucially, there is evidence that successful response inhibition is related to the intensity of neural activity in a network of brain regions, including the right IFG, preSMA, STN, and striatum (Aron and Poldrack, 2006; Rubia et al., 2007; Cohen et al., 2010; Congdon et al., 2010). Additionally, children and adolescents are poorer at response inhibition than adults (Schachar and Logan, 1990; Archibald and Kerns, 1999; Williams et al., 1999; Brocki and Bohlin, 2004) and are often found to have less activity during successful response inhibition in regions of the proposed response inhibition network, including the right IFG (Bunge et al., 2002; Durston et al., 2002; Rubia et al., 2006, 2007; but see Booth et al., 2003; Braet et al., 2009). This relationship between age, response inhibition ability, and neural activity in the purported response inhibition network has been taken to indicate that this network specifically underlies response inhibition ability. However, it has also been proposed that this relationship may actually reflect other underlying processes, such as response time variability (Bellgrove et al., 2004; Lijffijt et al., 2005). Earlier research used correlational analyses; with correlations it was not possible to determine whether the relationship between age and stop-signal reaction time (SSRT) was due to response inhibition ability or another variable, such as response time variability. Given this major analytical limitation we used predictive analyses to decode age, response inhibition ability, response time, and response time variability from neural data during successful motor response inhibition (Cohen et al., 2010). By identifying which kinds of information were encoded under which task conditions, we were able to provide a more direct link between behavioral variability and the underlying mental and neural processes that drive that variability.
We administered the stop-signal task (Logan, 1994) to participants, in which an intended motor response to a primary stimulus (go response) must be rapidly suppressed after a “stop-signal” that occurs on a subset of trials at a variable delay following the onset of the primary stimulus (Figure 1). The outcome variable of the stop-signal task is the SSRT, which is the estimated time that a participant needs in order to be able to inhibit his or her intended response (computed using the race model of Logan and Cowan, 1984). Predicted values for each variable were obtained using four-fold cross-validation, in which our participants were split randomly into four equal groups that did not significantly differ in the variables we were attempting to predict [age, SSRT, go response time (GoRT), and SD of go response time (SDRT)]. The statistical machine was trained on three of the four groups and tested on the fourth, using all iterations of the data. We compared three different machine learning techniques (linear Gaussian process regression, squared exponential Gaussian process regression, and linear support vector regression) and found that all three methods produced similar results. The statistical significance of the results was established by repeatedly re-running the analyses with the predicted variables randomized across participants, in order to obtain an empirical null hypothesis distribution, against which we compared the actual observations.
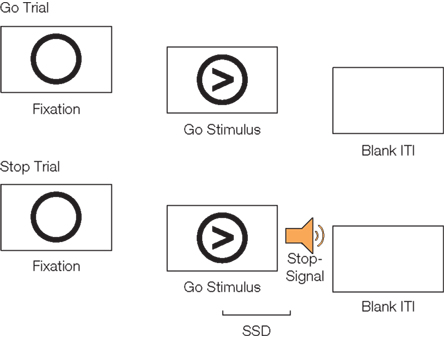
Figure 1. Schematic of go trials and stop trials on the stop-signal task. On go trials, participants respond with a button press to the direction of an arrow. On stop trials, participants hear a tone (the stop-signal) at a variable delay after the go stimulus appears (the stop-signal delay; SSD) and attempt to inhibit their motor response. Figure adapted from Cohen et al. (2010).
We found that SSRT was successfully predicted from neural activity during successful response inhibition as compared to successful response execution, but not from activity during other task contrasts (including go trials vs. baseline and successful vs. unsuccessful stop trials). We were also able to successfully decode age from the successful response inhibition contrast but not from others. GoRT and SDRT could not be decoded from any task contrasts. These results provide a direct link between individual differences in response inhibition ability and the neural processes involved in successful response inhibition, while at the same time disconfirming the hypothesis that these individual differences in inhibitory behavior are reflective of some aspect of the execution process. Interestingly, this specificity was true even though we found correlations using univariate methods in the neural data with age, SSRT, SDRT, and GoRT during successful response inhibition. This discrepancy between significant correlations and unsuccessful prediction may reflect the fact that the correlations were driven by a small number of observations or that they reflect false positives.
To further support our conclusion that individual differences in age and SSRT were specifically related to response inhibition processes, we found that the most predictive voxels of age and SSRT during successful response inhibition (the top 10%) were similar to each other. Critically, some of these voxels for age and SSRT fell within regions of the response inhibition network (specifically the IFG, preSMA, and STN; Figure 2).
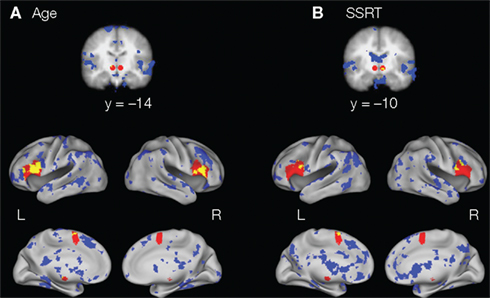
Figure 2. Regions in the response inhibition network (IFG, preSMA, and STN; in red) and the 10% of voxels that are most predictive of (A) age and (B) SSRT during successful response inhibition (in blue). As can be seen in yellow (the conjunction of the two maps), regions within the IFG, preSMA, and STN are positively predictive of age and negatively predictive of SSRT, indicating that these regions are important for successful response inhibition and that this network changes with age.
This study demonstrates the utility of using a predictive analysis to more completely understand a cognitive process, in this case response inhibition. There has been debate in the literature as to whether SSRT truly reflects inhibitory control ability or if it actually reflects another process, such as response time variability. While correlation-based and effect-sized based univariate analyses have demonstrated a link between response time variability and impaired inhibitory control (Bellgrove et al., 2004; Lijffijt et al., 2005), our predictive analysis found that SDRT could not be decoded from neural data during successful response inhibition. This finding supports the conclusion that SSRT, but not SDRT, is related to inhibitory control ability, at least in a healthy developmental population during motor response inhibition. Taking advantage of a predictive analysis we were able to conclude, therefore, that SSRT and SDRT are actually independent processes, a finding that is supported by a lack of a relationship between those two variables in our participants (r = −0.07, p = 0.69). It is important to note that our results are specific to our population; it is possible that in impulsive populations there is a different relationship between response time variability and inhibitory control ability, a possibility that can be empirically explored by applying the same techniques to a new population of participants.
3.3. Resting State Network Case Study
Another recent study investigated how neural changes with development are predictive of age by focusing on functional patterns of activation during rest as opposed to a specific cognitive process such as response inhibition (Dosenbach et al., 2010). Examining the spontaneous neural fluctuations and connections between regions at rest has been proposed to be a useful manner with which to study baseline neural networks, especially in populations that may have difficulty completing tasks, such as young children or patient populations. The goal of this study was to determine what regions and interregional connections were most important when predicting age. Using support vector regression in a large sample of children and adults aged 6–35, the support vector machine was trained to predict “brain age,” or the functional maturity level of each participant’s brain using the “leave-one-out” method.
Dosenbach et al. (2010) were able to successfully predict age from the neural data. Additionally, they found that highly predictive connections between brain regions that were positively correlated with age were significantly longer than those connections that were negatively correlated with age. While these strengthening connections were found throughout the entire cortex, they were most often along the anterior–posterior axis. That result is consistent with results using graph theory analyses of resting state data that have found that long-range connections get stronger and short-range connections get weaker throughout development (for a review, see Power et al., 2010). Moreover, it was found that the connections within multiple networks that have been found to be functionally connected at rest were important for predicting age, the cingulo--opercular network in particular. Individual neural regions that had the greatest predictive power included the right anterior prefrontal cortex and the precuneus. This study provides an important first step toward characterizing the developmental trajectories of functional connectivity within and between brain networks.
3.4. Decision Making Case Study
In another recent study that applied machine learning techniques to the decoding of continuous variables, the roles of specific brain regions involved in decision making were examined (Kahnt et al., 2011). The goal of the study was to determine which neural regions are most important when predicting stimulus value and variability of value. Participants were trained to learn the value of a reward associated with three distinct dimensions of a multi-dimensional stimulus (shape, color, and coherence of moving dots). Each dimension was associated with three levels of reward (e.g., diamond = 0.10 €, octagon = 0.20 €, and dodecagon = 0.30 €). The associations between dimension and reward were counterbalanced across participants. After training on each dimension separately, participants were scanned while being tested on the overall value of a multi-dimensional stimulus (e.g., green diamond with 95% coherence of the moving dots). The overall stimulus value was defined as the mean of the three independent values and the stimulus variability was defined as the variance of the three independent values (Figure 3A).
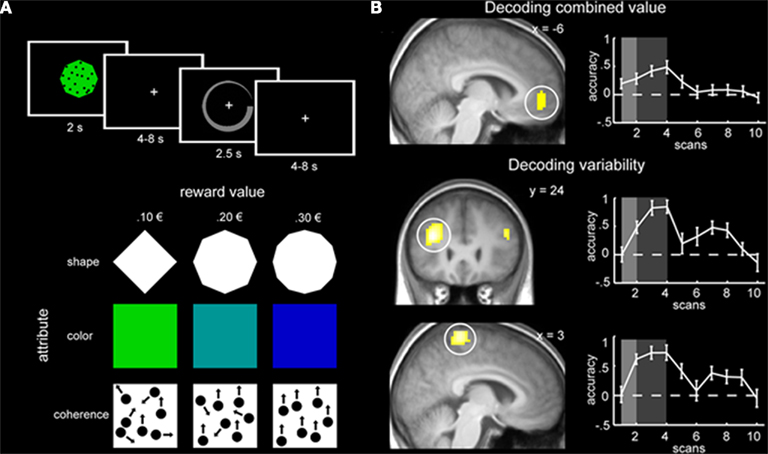
Figure 3. (A) Experimental design of the multi-attribute decision making task. Each stimulus consisted of three dimensions and participants had to make a decision about the stimulus value by indicating value on a circular rating scale (top panel). The three dimensions were shape, color, and coherence of moving dots; each dimension had three levels with different values (bottom panel). (B) Regions with significant prediction accuracy in the VMPFC for stimulus value (top panel) and the DLPFC and DMPC for stimulus variability (bottom two panels). Graphs on the right plot prediction accuracy across the trial. Figure taken from Kahnt et al. (2011).
Support vector regression was utilized in a within participants design (the machine was trained on three scanning runs and tested on a fourth). The authors used a searchlight approach, in which they trained and tested their machine on voxels falling within a sphere (with a four voxel radius) centered at each voxel in the brain. They calculated prediction accuracy at each voxel by standardizing the correlation coefficient between the actual value and predicted value of both stimulus value and stimulus variability, resulting in prediction accuracy maps across the whole-brain for each participant (Kahnt et al., 2011).
Across all participants, it was found that activity in ventromedial prefrontal cortex (VMPFC) was significantly predictive of stimulus value, while activity in dorsolateral prefrontal cortex (DLPFC) and dorsomedial parietal cortex (DMPC) was significantly predictive of stimulus variability (Figure 3B). Crucially, the authors found that these results could not be explained by stimulus attributes or response speed variability. To demonstrate that, they trained a classifier to learn the difference between different stimuli that were associated with the same reward value. Classification performance was at chance in the VMPFC (p = 0.50), indicating that stimulus value, not stimulus attributes, is decoded in the VMPFC. Moreover, regressing out participant response speed did not change the results. Lastly, the authors conducted traditional univariate analyses and did not find correlations between stimulus value and VMPFC activity or stimulus variability and DLPFC or DMPC activity. While previous research has found that both medial PFC and DLPFC were associated with multi-attribute decision making (Zysset et al., 2006), the univariate methods utilized could not distinguish between the specific aspects of decision making identified using predictive analytical tools (Kahnt et al., 2011).
The results of this study demonstrate that different aspects of multi-attribute decision making are associated with activity in dissociable regions in the brain (i.e., value assessment in the VMPFC and variability assessment in the DLPFC; Kahnt et al., 2011). The authors were able to expand our knowledge of how multi-attribute decision making is distributed in the brain beyond what could be learned using more traditional univariate methods.
4. Predicting Disease States
Much time and many resources have been spent attempting to identify biomarkers for and automate the diagnosis of psychiatric diseases. While disease classification has been implemented for a wide range of disorders, including schizophrenia (Davatzikos et al., 2005; Sun et al., 2009; Koutsouleris et al., 2010), depression (Fu et al., 2008), autism (Ecker et al., 2010a,b), and ADHD (Zhu et al., 2005), this review will focus on the automatic diagnosis of degenerative brain disorders, since there have been attempts to not only classify, but to implement regression-based predictive analyses with these disorders. For example, there have been attempts to ascertain patterns of degeneration that mark the transition from healthy aging to MCI to AD. It has been demonstrated that anatomical scans of the brains of patients with AD can be reliably differentiated from brain scans of age-matched healthy controls (classification accuracy 94.3%; Fan et al., 2008). Additionally, patients with MCI, in some cases a precursor to AD, have successfully been classified (with 100% accuracy) as those whose cognitive functioning stayed stable, declined, or improved over a 12-month period (as operationalized by score on the mini--mental state examination, MMSE; Duchesne et al., 2005). Moreover, it has been demonstrated that patients with MCI whose brains were classified as AD (as opposed to healthy) displayed a greater decline in cognitive functioning (MMSE score) over a 12-month period than did MCI patients whose brains were classified as healthy (mean decline = −2.31 vs. −0.30; p = 0.03; Fan et al., 2008). These techniques have also been applied to classify the brains of people who will develop HD but who are currently pre-symptomatic. It has been found that the brains of patients who are closer to disease onset (estimated onset within 5 years) can be correctly classified as pre-HD (classification accuracy = 69%, p = 0.002), while the brains of patients who are likely to remain pre-symptomatic for greater than 5 years cannot (classification accuracy at chance; Klöppel et al., 2009). In general, it has been found that pre-HD patients that are more likely to be misclassified are those with greater years to onset (21.2 vs. 12.0; Rizk-Jackson et al., 2011).
Recent studies have attempted to predict disease-related continuous variables from neural data using regression-based machine learning. Duchesne et al. (2009) attempted to predict MMSE score from anatomical scans. Baseline and change in MMSE scores are often used to detect MCI and to diagnose probable AD. Scores are generally fairly stable across 1–2 years in healthy participants, but decline with the onset of cognitive impairment and dementia. Using principal component analysis with robust linear regression and a leave-one-out approach, it was found that MMSE score assessed 1 year after a baseline anatomical scan could be predicted from that baseline scan (correlation predicted vs. actual: r = 0.31, p = 0.03). Furthermore, decoding MMSE scores was more accurate in participants whose scores declined than in participants whose scores remained stable (correlation predicted vs. actual for decliners only:r = 0.80, p < 0.0001; Duchesne et al., 2009).
A later study confirmed the ability to successfully decode MMSE scores (the average score from three time points over a 6-month period) from gray matter patterns in baseline anatomical scans in healthy participants, patients with MCI, and patients with AD using both support vector regression and relevance vector regression with leave-one-out cross-validation (correlation predicted vs. actual at least r = 0.75 for best fit support and relevance vector regression machines; Wang et al., 2010). This study also found that the score on another neuropsychological test, the Boston naming test (BNT), could be predicted from baseline anatomical scans, although not as successfully (maximum correlation predicted vs. actual:r = 0.59). Furthermore, in participants whose MMSE scores declined over a six month period, future MMSE scores could be predicted from the gray matter of baseline anatomical scans (correlation predicted vs. actual: r = 0.54). Importantly, the prediction improved only marginally when the machine was trained on white matter and cerebral spinal fluid maps as well, implying that most of the information about level of dementia is contained in gray matter (Wang et al., 2010). A last study found that both support vector regression and relevance vector regression were successfully able to predict age in healthy adults (aged 19–86; correlation predicted vs. actual: r = 0.92). Participant scans and information were taken from a large, publicly available database (the IXI database), thus there was a large enough sample to be able to train the machines on 410 participants and test them on separate datasets of over 100 participants each (untrained participants from the IXI database and participants whose data had been collected by the current investigators for previous studies). Critically, when this same classifier (trained on healthy adults) was tested on participants with AD (from the Alzheimer’s Disease Neuroimaging Initiative database), the estimated age of the AD patients was significantly higher than their actual age (10 years, p < 0.001; Franke et al., 2010).
Huntington’s disease is another disorder marked by neural degeneration that has been studied using predictive analysis techniques. HD is appealing to study because of its known genetic basis (a CAG triplet on the Huntingtin gene) with very high penetrance. Moreover, the age of onset can be estimated fairly accurately based on current age and number of repeats of the CAG triplet (Langbehn et al., 2004). A recent study in our laboratory found that a support vector regression machine with four-fold cross-validation could successfully predict the number of years to onset of HD in pre-symptomatic HD gene carriers (as estimated from age and number of CAG repeats) when training the machine on anatomical gray matter maps (both across the entire brain and within the caudate nucleus of the basal ganglia) and on a diffusion-weighted white matter map of the whole-brain (minimum reported correlation predicted vs. actual years to onset: r = 0.49, corrected p = 0.02; Rizk-Jackson et al., 2011). Interestingly, while classification of HD vs. non-HD was very good using a simple linear discriminant analysis model with a small number of basal ganglia features, a simple linear regression model on the same features was not effective for decoding years to onset; instead, only the more complex support vector regression model was able to successfully predict estimated years to onset, suggesting that the relevant information is carried in regions across the brain.
5. Future Directions
Predictive analytical techniques can help to elucidate the relationships between neural activity and age, cognitive state, and disease state. While classification methods have been instrumental in increasing our understanding of how cognitive states are generally represented in the brain, regression-based methods can further examine the neural patterns underlying individual differences. This type of analysis is still in its infancy, thus expanding the ways in which it can be applied to functional neuroimaging data has great potential.
As is clear from the majority of studies utilizing regression-based machine learning that compare the results of different machines (Ashburner, 2007; Cohen et al., 2010; Franke et al., 2010; Wang et al., 2010; Chu et al., 2011; Valente et al., 2011) there are differences in the effectiveness of different approaches, but the relative strengths and weaknesses have yet to be fully characterized. It is doubtful that there is a single technique that will be best for every data set, but the general characteristics of brain MRI data may be more amenable to some methods as compared to others. Another area where more work is needed is the determination of optimal procedures for significance testing of predictive decoding results. A number of studies reported descriptive results (i.e., correlation coefficients) without reporting significance values (Ashburner, 2007; Dosenbach et al., 2010; Franke et al., 2010; Wang et al., 2010; Chu et al., 2011; Valente et al., 2011). Studies from our lab have used permutation testing (Cohen et al., 2010; Rizk-Jackson et al., 2011), which we believe provides the closest possible solution to a ground-truth type I error rate, but this technique is very computationally intensive and only possible in reasonable time using large computing clusters. Lastly, multiple methods for determining the importance of different brain regions in driving classification results have been utilized, including reporting the weights of each feature (i.e., voxel) that the machine used (Cohen et al., 2010; Dosenbach et al., 2010; Chu et al., 2011; Valente et al., 2011), a searchlight approach (Kahnt et al., 2011), or restricting analyses to regions of interest (Duchesne et al., 2009; Rizk-Jackson et al., 2011). Each of these may provide different answers to the same question.
Aside from methodological considerations, there are many novel ways in which predictive analytical techniques can be applied to ask questions about the cognitive state of individuals. Regression-based predictive methods can be utilized to determine the root of individual differences in cognitive processes, both within the normal range of functioning and in impaired individuals. For example, finding that the right IFG is highly predictive of SSRT during successful response inhibition (Cohen et al., 2010) supports the theory that the right IFG may underlie motor control (Aron, in press). Moreover, if that same region is predictive of one’s ability to exert other forms of control (i.e., emotional control or control over risky behavior), that would support the theory that the right IFG underlies multiple forms of self-control (Cohen et al., in press).
Clinically, predictive analytical tools are currently being applied to the brains of patients with neurodegenerative diseases. Ultimately being able to identify biomarkers for early detection of degenerative diseases using predictive analyses would help increase the possibility of early intervention and provide measures of the effectiveness of that intervention. For example, it is known that the neuropathology in HD appears at least 10 years before the onset of neurological symptoms. A biomarker for this degeneration would be a very useful surrogate outcome for treatments during that pre-symptomatic period. Additionally, determining which neural regions are more indicative of progression toward disease may increase our understanding of that disease. As an example, structural scans of the medial temporal lobe were found to be highly predictive of classification as probable AD or MCI (Duchesne et al., 2005) and were able to predict MMSE scores (Duchesne et al., 2009), supporting previous research emphasizing the importance of these neural regions in the progression of AD. Such techniques could be applied to other disorders in which less is known regarding the specific neural changes that underlie them, such as autism or ADHD. Discovering neural regions that specifically predict such disorders would be an important step toward being able to better diagnose and treat them. For example, if a regression-based predictive analysis demonstrates that different neural regions predict response inhibition ability in healthy participants as compared to patients with ADHD it would give clues as to the etiology of ADHD, as would determining which neural regions are best able to predict level of impulsivity or real-world correlates of functioning in patients with ADHD.
In conclusion, the decoding of continuous behavioral variables from neuroimaging is still in its infancy, but it holds substantial promise for furthering our ability to understand both normal and abnormal cognitive functioning and development, as well as healthy and disease states.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by the US Office of Naval Research (N00014-07-1-0116), the National Institute of Mental Health (5R24 MH072697), the National Institute of Mental Health Intramural Research program, the National Institute of Drug Abuse (5F31 DA024534-02), and the Consortium for Neuropsychiatric Phenomics (NIH Roadmap for Medical Research grants UL1DE019580, RL1DA024853, and PL1MH08327).
Key Concepts
Statistical tools implementing a form of learning in which predictions about new observations can be made based on existing data.
When applied to neuroimaging data, using multivariate patterns of activity in existing data to decode a participant’s cognitive or disease state.
Training statistical machines to learn patterns in a dataset that can be associated with an outcome variable for the purpose of later using that machine to predict the outcome variable in novel data.
Regression-based predictive analyses
The implementation of regression analysis to decode continuous participant characteristics, such as age, from neuroimaging data.
Training a model on a subset of data and then testing that model on the “left-out” observations.
The predictor variables in predictive analyses; with neuroimaging data, each voxel or component that goes into the training dataset is a feature.
High-dimensional regression methods
Predictive analytical methods that predict continuous variables, such as ridge regression, support vector regression, relevance vector regression, and Gaussian process regression.
References
Alpaydin, E. (2004). Introduction to Machine Learning (Adaptive Computation and Machine Learning). Cambridge, MA: MIT Press.
Archibald, S. J., and Kerns, K. A. (1999). Identification and description of new tests of executive functioning in children. Child Neuropsychol. 5, 115–129.
Aron, A., Fletcher, P., Bullmore, E., Sahakian, B., and Robbins, T. (2003). Stop-signal inhibition disrupted by damage to right inferior frontal gyrus in humans. Nat. Neurosci. 6, 115–116.
Aron, A., Robbins, T., and Poldrack, R. (2004). Inhibition and the right inferior frontal cortex. Trends Cogn. Sci. (Regul. Ed.) 8, 170–177.
Aron, A. R. (2010). From reactive to proactive and selective control: developing a richer model for stopping inappropriate responses. Biol. Psychiatry. doi:10.1016/j.biopsych.2010.07.024. [Epub ahead of print].
Aron, A. R., and Poldrack, R. A. (2006). Cortical and subcortical contributions to stop signal response inhibition: role of the subthalamic nucleus. J. Neurosci. 26, 2424–2433.
Bellgrove, M. A., Hester, R., and Garavan, H. (2004). The functional neuroanatomical correlates of response variability: evidence from a response inhibition task. Neuropsychologia 42, 1910–1916.
Boehler, C. N., Appelbaum, L. G., Krebs, R. M., Hopf, J. M., and Woldorff, M. G. (2010). Pinning down response inhibition in the brain–conjunction analyses of the stop-signal task. Neuroimage 52, 1621–1632.
Booth, J. R., Burman, D. D., Meyer, J. R., Lei, Z., Trommer, B. L., Davenport, N. D., Li, W., Parrish, T. B., Gitelman, D. R., and Mesulam, M. M. (2003). Neural development of selective attention and response inhibition. Neuroimage 20, 737–751.
Braet, W., Johnson, K. A., Tobin, C. T., Acheson, R., Bellgrove, M. A., Robertson, I. H., and Garavan, H. (2009). Functional developmental changes underlying response inhibition and error-detection processes. Neuropsychologia 47, 3143–3151.
Brocki, K. C., and Bohlin, G. (2004). Executive functions in children aged 6 to 13: a dimensional and developmental study. Dev. Neuropsychol. 26, 571–593.
Buchsbaum, B. R., Greer, S., Chang, W.-L., and Berman, K. F. (2005). Meta-analysis of neuroimaging studies of the Wisconsin card-sorting task and component processes. Hum. Brain Mapp. 25, 35–45.
Bunge, S. A., Dudukovic, N. M., Thomason, M. E., Vaidya, C. J., and Gabrieli, J. D. E. (2002). Immature frontal lobe contributions to cognitive control in children: evidence from fMRI. Neuron 33, 301–311.
Chambers, C. D., Bellgrove, M., Stokes, M., Henderson, T., Garavan, H., Robertson, I., Morris, A., and Mattingley, J. (2006). Executive “brake failure” following deactivation of human frontal lobe. J. Cogn. Neurosci. 18, 444–455.
Chambers, C. D., Bellgrove, M. A., Gould, I. C., English, T., Garavan, H., McNaught, E., Kamke, M., and Mattingley, J. B. (2007). Dissociable mechanisms of cognitive control in prefrontal and premotor cortex. J. Neurophysiol. 98, 3638–3647.
Chen, C.-Y., Muggleton, N. G., Tzeng, O. J. L., Hung, D. L., and Juan, C.-H. (2009). Control of prepotent responses by the superior medial frontal cortex. Neuroimage 44, 537–545.
Chevrier, A. D., Noseworthy, M. D., and Schachar, R. (2007). Dissociation of response inhibition and performance monitoring in the stop signal task using event-related fMRI. Hum. Brain Mapp. 28, 1437–1458.
Chikazoe, J. (2010). Localizing performance of go/no-go tasks to prefrontal cortical subregions. Curr. Opin. Psychiatry 23, 267–272.
Chu, C., Ni, Y., Tan, G., Saunders, C. J., and Ashburner, J. (2011). Kernel regression for fMRI pattern prediction. Neuroimage 56, 662–673.
Cohen, J. R., Asarnow, R. F., Sabb, F. W., Bilder, R. M., Bookheimer, S. Y., Knowlton, B. J., and Poldrack, R. A. (2010). Decoding developmental differences and individual variability in response inhibition through predictive analyses across individuals. Front. Hum. Neurosci. 4:47. doi: 10.3389/fnhum.2010.00047
Cohen, J. R., Berkman, E. T., and Lieberman, M. D. (in press). “Ventrolateral PFC as a self-control muscle and how to use it without trying,” in Principles of Frontal Lobe Functions, 2nd Edn, eds D. T. Stuss, and R. T. Knight (New York, NY: Oxford University Press, Inc.).
Congdon, E., Mumford, J. A., Cohen, J. R., Galvan, A., Aron, A. R., Xue, G., Miller, E., and Poldrack, R. A. (2010). Engagement of large-scale networks is related to individual differences in inhibitory control. Neuroimage 53, 653–663.
Cox, D. D., and Savoy, R. L. (2003). Functional magnetic resonance imaging (fMRI) “brain reading”: detecting and classifying distributed patterns of fMRI activity in human visual cortex. Neuroimage 19(2 Pt 1), 261–270.
Davatzikos, C., Shen, D., Gur, R. C., Wu, X., Liu, D., Fan, Y., Hughett, P., Turetsky, B. I., and Gur, R. E. (2005). Whole-brain morphometric study of schizophrenia revealing a spatially complex set of focal abnormalities. Arch. Gen. Psychiatry 62, 1218–1227.
Dosenbach, N. U. F., Nardos, B., Cohen, A. L., Fair, D. A., Power, J. D., Church, J. A., Nelson, S. M., Wig, G. S., Vogel, A. C., Lessov-Schlaggar, C. N., Barnes, K. A., Dubis, J. W., Feczko, E., Coalson, R. S., Pruett, J. R., Barch, D. M., Petersen, S. E., and Schlaggar, B. L. (2010). Prediction of individual brain maturity using fMRI. Science 329, 1358–1361.
Duchesne, S., Caroli, A., Geroldi, C., Collins, D. L., and Frisoni, G. B. (2009). Relating one-year cognitive change in mild cognitive impairment to baseline MRI features. Neuroimage 47, 1363–1370.
Duchesne, S., Caroli, A., Geroldi, C., Frisoni, G. B., and Collins, D. L. (2005). Predicting clinical variable from MRI features: application to MMSE in MCI. Med. Image Comput. Comput. Assist. Interv. 8(Pt 1), 392–399.
Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern Classification, 2nd Edn. New York, NY: John Wiley and Sons, Inc.
Durston, S., Thomas, K. M., Yang, Y., Ulug, A. M., Zimmerman, R. D., and Casey, B. J. (2002). A neural basis for the development of inhibitory control. Dev. Sci. 5, F9–F16.
Ecker, C., Marquand, A., Mourão-Miranda, J., Johnston, P., Daly, E. M., Brammer, M. J., Maltezos, S., Murphy, C. M., Robertson, D., Williams, S. C., and Murphy, D. G. M. (2010a). Describing the brain in autism in five dimensions–magnetic resonance imaging-assisted diagnosis of autism spectrum disorder using a multiparameter classification approach. J. Neurosci. 30, 10612–10623.
Ecker, C., Rocha-Rego, V., Johnston, P., Mourão-Miranda, J., Marquand, A., Daly, E. M., Brammer, M. J., Murphy, C., and Murphy, D. G. MRC AIMS Consortium. (2010b). Investigating the predictive value of whole-brain structural MR scans in autism: a pattern classification approach. Neuroimage 49, 44–56.
Fan, Y., Batmanghelich, N., Clark, C. M., and Davatzikos, C., and Alzheimer’s Disease Neuroimaging Initiative. (2008). Spatial patterns of brain atrophy in MCI patients, identified via high-dimensional pattern classification, predict subsequent cognitive decline. Neuroimage 39, 1731–1743.
Floden, D., and Stuss, D. T. (2006). Inhibitory control is slowed in patients with right superior medial frontal damage. J. Cogn. Neurosci. 18, 1843–1849.
Franke, K., Ziegler, G., Klöppel, S., and Gaser, C., and Alzheimer’s Disease Neuroimaging Initiative. (2010). Estimating the age of healthy subjects from T1-weighted MRI scans using kernel methods: exploring the influence of various parameters. Neuroimage 50, 883–892.
Fu, C. H. Y., Mourão-Miranda, J., Costafreda, S. G., Khanna, A., Marquand, A. F., Williams, S. C. R., and Brammer, M. J. (2008). Pattern classification of sad facial processing: toward the development of neurobiological markers in depression. Biol. Psychiatry 63, 656–662.
Garavan, H., Ross, T., Murphy, K., Roche, R., and Stein, E. (2002). Dissociable executive functions in the dynamic control of behavior: inhibition, error detection, and correction. Neuroimage 17, 1820–1829.
Garavan, H., Ross, T. J., and Stein, E. A. (1999). Right hemispheric dominance of inhibitory control: an event-related functional MRI study. Proc. Natl. Acad. Sci. U.S.A. 96, 8301–8306.
Hastie, T., Tibshirani, R., and Friedman, J. (2001). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York, NY: Springer Publishing Company, Inc.
Haxby, J. V., Gobbini, M. I., Furey, M. L., Ishai, A., Schouten, J. L., and Pietrini, P. (2001). Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science 293, 2425–2430.
Haynes, J.-D., and Rees, G. (2006). Decoding mental states from brain activity in humans. Nat. Rev. Neurosci. 7, 523–534.
Hoerl, A. E., and Kennard, R. W. (1970). Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12, 55–67.
Kahnt, T., Heinzle, J., Park, S. Q., and Haynes, J.-D. (2011). Decoding different roles for vmPFC and dlPFC in multi-attribute decision making. Neuroimage 56, 709–715.
Kenner, N. M., Mumford, J. A., Hommer, R. E., Skup, M., Leibenluft, E., and Poldrack, R. A. (2010). Inhibitory motor control in response stopping and response switching. J. Neurosci. 30, 8512–8518.
Klöppel, S., Chu, C., Tan, G. C., Draganski, B., Johnson, H., Paulsen, J. S., Kienzle, W., Tabrizi, S. J., Ashburner, J., and Frackowiak, R. S. J., and PREDICT-HD Investigators of the Huntington Study Group. (2009). Automatic detection of preclinical neurodegeneration: pre symptomatic Huntington disease. Neurology 72, 426–431.
Klöppel, S., Draganski, B., Golding, C. V., Chu, C., Nagy, Z., Cook, P. A., Hicks, S. L., Kennard, C., Alexander, D. C., Parker, G. J. M., Tabrizi, S. J., and Frackowiak, R. S. J. (2008). White matter connections reflect changes in voluntary-guided saccades in pre-symptomatic Huntington’s disease. Brain 131(Pt 1), 196–204.
Kohavi, R. (1995). “A study of cross-validation and bootstrap for accuracy estimation and model selection,” in Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence (San Francisco, CA: Morgan Kaufmann Publishers), 1137–1143.
Konishi, S., Nakajima, K., Uchida, I., Sekihara, K., and Miyashita, Y. (1998). No-go dominant brain activity in human inferior prefrontal cortex revealed by functional magnetic resonance imaging. Eur. J. Neurosci. 10, 1209–1213.
Koutsouleris, N., Gaser, C., Bottlender, R., Davatzikos, C., Decker, P., Jäger, M., Schmitt, G., Reiser, M., Möller, H.-J., and Meisenzahl, E. M. (2010). Use of neuroanatomical pattern regression to predict the structural brain dynamics of vulnerability and transition to psychosis. Schizophr. Res. 123, 175–187.
Langbehn, D. R., Brinkman, R. R., Falush, D., Paulsen, J. S., and Hayden, M. R., and International Huntington’s Disease Collaborative Group. (2004). A new model for prediction of the age of onset and penetrance for Huntington’s disease based on CAG length. Clin. Genet. 65, 267–277.
Liddle, P., Kiehl, K., and Smith, A. (2001). Event-related fMRI study of response inhibition. Hum. Brain Mapp. 12, 100–109.
Lijffijt, M., Kenemans, J. L., Verbaten, M. N., and van Engeland, H. (2005). A meta-analytic review of stopping performance in attention-deficit/hyperactivity disorder: deficient inhibitory motor control? J. Abnorm. Psychol. 114, 216–222.
Logan, G. D. (1994). “On the ability to inhibit thought and action: a users’ guide to the stop signal paradigm,” in Inhibitory Processes in Attention, Memory, and Language, eds D. Dagenbach, and T. H. Carr (San Diego, CA: Academic Press), 189–240.
Logan, G. D., and Cowan, W. B. (1984). On the ability to inhibit thought and action: a theory of an act of control. Psychol. Rev. 91, 295–327.
Menon, V., Adleman, N. E., White, C. D., Glover, G. H., and Reiss, A. L. (2001). Error-related brain activation during a go/nogo response inhibition task. Hum. Brain Mapp. 12, 131–143.
Mourão-Miranda, J., Bokde, A. L. W., Born, C., Hampel, H., and Stetter, M. (2005). Classifying brain states and determining the discriminating activation patterns: support vector machine on functional MRI data. Neuroimage 28, 980–995.
Norman, K. A., Polyn, S. M., Detre, G. J., and Haxby, J. V. (2006). Beyond mind-reading: multi-voxel pattern analysis of fMRI data. Trends Cogn. Sci. (Regul. Ed.) 10, 424–430.
O’Toole, A. J., Jiang, F., Abdi, H., Pénard, N., Dunlop, J. P., and Parent, M. A. (2007). Theoretical, statistical, and practical perspectives on pattern-based classification approaches to the analysis of functional neuroimaging data. J. Cogn. Neurosci. 19, 1735–1752.
Poldrack, R. A., Halchenko, Y. O., and Hanson, S. J. (2009). Decoding the large-scale structure of brain function by classifying mental states across individuals. Psychol. Sci. 20, 1364–1372.
Power, J. D., Fair, D. A., Schlaggar, B. L., and Petersen, S. E. (2010). The development of human functional brain networks. Neuron 67, 735–748.
Rasmussen, C. E., and Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. Cambridge, MA: MIT Press.
Rizk-Jackson, A., Stoffers, D., Sheldon, S., Kuperman, J., Dale, A., Goldstein, J., Corey-Bloom, J., Poldrack, R. A., and Aron, A. R. (2011). Evaluating imaging biomarkers for neurodegeneration in pre-symptomatic Huntington’s disease using machine learning techniques. Neuroimage 56, 788–796.
Rubia, K., Russell, T., Overmeyer, S., Brammer, M. J., Bullmore, E. T., Sharma, T., Simmons, A., Williams, S. C. R., Giampietro, V., Andrew, C. M., and Taylor, E. (2001). Mapping motor inhibition: conjunctive brain activations across different versions of go/no-go and stop tasks. Neuroimage 13, 250–261.
Rubia, K., Smith, A., Brammer, M., and Taylor, E. (2003). Right inferior prefrontal cortex mediates response inhibition while mesial prefrontal cortex is responsible for error detection. Neuroimage 20, 351–358.
Rubia, K., Smith, A. B., Taylor, E., and Brammer, M. (2007). Linear age-correlated functional development of right inferior fronto-striato-cerebellar networks during response inhibition and anterior cingulate during error-related processes. Hum. Brain Mapp. 28, 1163–1177.
Rubia, K., Smith, A. B., Woolley, J., Nosarti, C., Heyman, I., Taylor, E., and Brammer, M. (2006). Progressive increase of frontostriatal brain activation from childhood to adulthood during event-related tasks of cognitive control. Hum. Brain Mapp. 27, 973–993.
Schachar, R., and Logan, G. D. (1990). Impulsivity and inhibitory control in normal development and childhood psychopathology. Dev. Psychol. 26, 710–720.
Shinkareva, S. V., Mason, R. A., Malave, V. L., Wang, W., Mitchell, T. M., and Just, M. A. (2008). Using fMRI brain activation to identify cognitive states associated with perception of tools and dwellings. PLoS ONE 3, e1394. doi: 10.1371/journal.pone.0001394
Sun, D., van Erp, T. G. M., Thompson, P. M., Bearden, C. E., Daley, M., Kushan, L., Hardt, M. E., Nuechterlein, K. H., Toga, A. W., and Cannon, T. D. (2009). Elucidating a magnetic resonance imaging-based neuroanatomic biomarker for psychosis: classification analysis using probabilistic brain atlas and machine learning algorithms. Biol. Psychiatry 66, 1055–1060.
Tipping, M. E. (2001). Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 1, 211–244.
Valente, G., Martino, F. D., Esposito, F., Goebel, R., and Formisano, E. (2011). Predicting subject-driven actions and sensory experience in a virtual world with relevance vector machine regression of fMRI data. Neuroimage 56, 651–661.
Wang, Y., Fan, Y., Bhatt, P., and Davatzikos, C. (2010). High-dimensional pattern regression using machine learning: from medical images to continuous clinical variables. Neuroimage 50, 1519–1535.
Williams, B. R., Ponesse, J. S., Schachar, R. J., Logan, G. D., and Tannock, R. (1999). Development of inhibitory control across the life span. Dev. Psychol. 35, 205–213.
Zhu, C. Z., Zang, Y. F., Liang, M., Tian, L. X., He, Y., Li, X. B., Sui, M. Q., Wang, Y. F., and Jiang, T. Z. (2005). Discriminative analysis of brain function at resting-state for attention--deficit/hyperactivity disorder. Med. Image Comput. Comput. Assist. Interv. 8(Pt 2), 468–475.
Keywords: predictive analysis, fMRI, high-dimensional regression, multivariate decoding, machine learning
Citation: Cohen JR, Asarnow RF, Sabb FW, Bilder RM, Bookheimer SY, Knowlton BJ and Poldrack RA (2011) Decoding continuous variables from neuroimaging data: basic and clinical applications. Front. Neurosci. 5:75. doi: 10.3389/fnins.2011.00075
Received: 01 February 2011;
Accepted: 16 May 2011;
Published online: 15 June 2011.
Edited by:
Silvia A. Bunge, University of California Berkeley, USACopyright: © 2011 Cohen, Asarnow, Sabb, Bilder, Bookheimer, Knowlton and Poldrack. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Jessica R. Cohen, University of California, Berkeley, Helen Wills Neuroscience Institute, 132 Barker Hall, Berkeley, 94720, CA, USA,anJjb2hlbkBiZXJrZWxleS5lZHU=





