- 1 Department of Technologies and Health, Istituto Superiore di Sanitã, Rome, Italy
- 2 Institute of Biology, Otto-von-Guericke University, Magdeburg, Germany
- 3 Istituto Nazionale di Fisica Nucleare, Rome, Italy
We demonstrate bistable attractor dynamics in a spiking neural network implemented with neuromorphic VLSI hardware. The on-chip network consists of three interacting populations (two excitatory, one inhibitory) of leaky integrate-and-fire (LIF) neurons. One excitatory population is distinguished by strong synaptic self-excitation, which sustains meta-stable states of “high” and “low”-firing activity. Depending on the overall excitability, transitions to the “high” state may be evoked by external stimulation, or may occur spontaneously due to random activity fluctuations. In the former case, the “high” state retains a “working memory” of a stimulus until well after its release. In the latter case, “high” states remain stable for seconds, three orders of magnitude longer than the largest time-scale implemented in the circuitry. Evoked and spontaneous transitions form a continuum and may exhibit a wide range of latencies, depending on the strength of external stimulation and of recurrent synaptic excitation. In addition, we investigated “corrupted” “high” states comprising neurons of both excitatory populations. Within a “basin of attraction,” the network dynamics “corrects” such states and re-establishes the prototypical “high” state. We conclude that, with effective theoretical guidance, full-fledged attractor dynamics can be realized with comparatively small populations of neuromorphic hardware neurons.
Introduction
Neuromorphic VLSI copies in silicon the equivalent circuits of biological neurons and synapses (Mead, 1989). The aim is to emulate as closely as possible the computations performed by living neural tissues exploiting the analog characteristics of the silicon substrate. Neuromorphic designs seem a reasonable option to build biomimetic devices that could be directly interfaced to the natural nervous tissues.
Here we focus on neuromorphic recurrent neural networks exhibiting reverberating activity states (“attractor states”) due to massive feedback. Our main motivation is the belief that neural activity in mammalian cortex is characterized by “attractor states” at multiple spatial and temporal scales (Grinvald et al., 2003; Shu et al., 2003; Holcman and Tsodyks, 2006; Fox and Raichle, 2007; Ringach, 2009) and that “attractor dynamics” is a key principle of numerous cognitive functions, including working memory (Amit and Brunel, 1997; Del Giudice et al., 2003; Mongillo et al., 2003), attentional selection (Deco and Rolls, 2005), sensory inference (Gigante et al., 2009; Braun and Mattia, 2010), choice behavior (Wang, 2002; Wong et al., 2007; Furman and Wang, 2008; Marti et al., 2008), motor planning (Lukashin et al., 1996; Mattia et al., 2010), and others. To date, surprisingly few studies have sought to tap the computational potential of attractor dynamics for neuromorphic devices (Camilleri et al., 2010; Neftci et al., 2010; Massoud and Horiuchi, 2011).
The more elementary forms of attractor dynamics in networks of biologically realistic (spiking) neurons and synapses are theoretically well understood (Amit, 1989, 1995; Fusi and Mattia, 1999; Renart et al., 2004). This is particularly true for bistable attractor dynamics with two distinct steady-states (“point attractors”). Attractor networks can store and retrieve prescribed patterns of collective activation as “memories.” They operate as an “associative memory” which retrieves a prototypical “memorized” state in response to an external stimulus, provided the external perturbation does not push the state outside the “basin of attraction.” The “attractor state” is self-correcting and self-sustaining even in the absence of external stimulation, thus preserving a “working memory” of past sensory events. Besides being evoked by stimulation, transitions between attractor states may also occur spontaneously, driven by intrinsic activity fluctuations. Spontaneous activity fluctuations ensure that the energetically accessible parts of state space are exhaustively explored.
Thanks to this theoretical understanding, the system designer has considerable latitude in quantitatively shaping bistable attractor dynamics. By sculpting the effective energy landscape and by adjusting the amount of noise (spontaneous activity fluctuations), he can control how the network explores its phase space and how it responds to external stimulation (Mattia and Del Giudice, 2004; Marti et al., 2008). The kinetics of network dynamics, including response latencies to external stimulation, can be adjusted over several orders of magnitude over and above the intrinsic time-scale of neurons and synapses (Braun and Mattia, 2010).
Below, we demonstrate step-by-step how to build a small neuromorphic network with a desired dynamics. We show that the characteristics of bistable attractor dynamics (“asynchronous activity,” “point attractors,” “working memory,” “basin of attraction”) are robust, in spite of the small network size and the considerable inhomogeneity of neuromorphic components. Moreover, we demonstrate tunable response kinetics up to three orders of magnitude slower (1 s vs. 1 ms) than the time-constants that are expressly implemented in the neuromorphic circuits.
Some of these results have been presented in a preliminary form (Camilleri et al., 2010).
Materials and Methods
A Theory-Guided Approach
We are interested in attractor neural networks expressing noisy bistable dynamics. Networks of this kind are well understood and controlled in theory and simulations. Here, we describe a theory-guided approach to implementing such networks in neuromorphic VLSI hardware.
A compact theoretical formulation is essential to achieve the desired dynamics in hardware. Such a formulation helps to validate neuron and synapse circuits, to survey the parameter space, and to identify parameter regions of interest. In addition, a theoretical framework helps to diagnose hardware behavior that diverges from the design standard.
Note that here we are interested in stochastic activity regimes that are typically not encountered in electronic devices. Boolean circuitry, sensing amplifiers, or finite-state machines all exhibit deterministic behavior. In contrast, the stochastic dynamical systems at issue here respond in multiple ways to identical input.
Accordingly, the behavior of neuromorphic hardware must be characterized in the fashion of neurophysiological experiments, namely, by accumulating statistics over multiple experimental trials. Comparison to theoretical predictions proves particularly helpful with regard to the characterization of such stochastic behavior.
Finally, the massive positive feedback that is implemented in the network not only begets a rich dynamics, but also amplifies spurious effects beyond the intended operating range of the circuitry. Comparison to theory helps to identify operating regimes that are not contaminated materially by such effects.
The starting point of our approach – mean-field theory for integrate-and-fire neurons (Renart et al., 2004) with linear decay (Fusi and Mattia, 1999) – is summarized in the next section.
Mean-Field Theory
Fusi and Mattia (1999) studied theoretically and in simulation networks of integrate-and-fire neurons with linear decay and instantaneous synapses (similar to those implemented on our chip). We use their formulation to explore the parameter space and to identify regions of bistable dynamics. The dynamics we are considering for the neuronal membrane potential V(t) (below the firing threshold θ) are described by the equation:
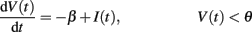
V(t) is constrained to vary in the interval [0, θ]. When V(t) reaches the threshold θ, it is reset to zero, where it remains during the absolute refractory period τarp.
The authors show that, if a neuron receives a Gaussian current I(t) with constant mean μ and variance σ2, the stationary neuronal spiking rate νout = Φ(μ, σ) has a sigmoidal shape with two asymptotes. Given σ, for low values of μ, Φ approaches 0, while for high values of μ, Φ approaches 1/τarp. For given μ, Φ increases with increasing σ. The assumption of a Gaussian process holds if the number of incoming spikes is large, if spike times are uncorrelated, and if each spike induces a small change in the membrane potential. This set of assumptions is often termed the “diffusion limit.”
We consider a neuron receiving n uncorrelated input spike trains, each with a mean rate equal to νin. In the “diffusion limit” our neuron will receive an input current I(t) with mean and variance:
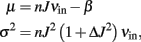
where J is the synaptic efficacy, ΔJ2 is the variance of J and β is the constant leakage current of the neuron. These equations state that both μ and σ are functions of the mean input rates νin, thus the response function Φ(μ, σ) can be written as νout = Φ(νin).
We now consider an isolated population of N identical and probabilistically interconnected neurons, with a level of connectivity c. c is the probability for two neurons to be connected, thus the number of inputs per neuron is cN. If we assume that the spike trains generated by the neurons are uncorrelated, and that all neurons have input currents with the same μ and σ (mean-field approximation), and we keep J small and N large, then the “diffusion approximation” holds and the previous equations for μ and σ (with n = cN) are still valid. We can then use, for neurons in the population, the same transfer function Φ defined above, possibly up to terms entering μ and σ due to external input spikes to the considered population.
In our population all the neurons are identical and hence the mean population response function is equal to the single-neuron response function Φ(ν). Since the neurons of the population are recurrently connected, i.e., a feedback loop exists, νin ≡ νout = ν, resulting in a self-consistency equation ν = Φ(ν) in a stationary state, whose solution(s) define the fixed point(s) of the population dynamics.
In the more complex case of p interacting populations, the input current of each population is characterized by a mean μ and a variance σ2, which is obtained by summing over the contributions from all populations. The stable states of the collective dynamics may be found by solving a system of self-consistency equations:
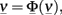
where 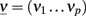 and Φ = (Φ1 … Φp).
and Φ = (Φ1 … Φp).
Effective Response Function
The solution to the self-consistency equation does not convey information with regard to the dynamics of the system away from the equilibrium states. To study these dynamics we should consider the open-loop transfer function of the system.
In the case of a single isolated population, the open-loop transfer function is simply Φ. It can be computed theoretically, as we have shown in the previous section, or it can be measured directly from the network, provided that one can “open the loop.” Experimentally this is a relatively simple task: it corresponds to cutting the recurrent connections and substituting the feedback signals with a set of externally generated spike trains at a frequency νin. By measuring the mean output firing rate of the population νout one can obtain, the open-loop transfer function νout = Φ(νin).
In Mascaro and Amit (1999), the authors extended the above approach to a multi-population network and devised an approximation which allows, for a subset of populations “in focus,” to extract an Effective Response Function (ERF) 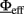 which embeds the effects of all the other populations in the network. As will be described later on, we have applied these concepts to our multi-population hardware network. The key ideas are summarized below.
which embeds the effects of all the other populations in the network. As will be described later on, we have applied these concepts to our multi-population hardware network. The key ideas are summarized below.
Consider a network of p interacting populations, of which one population (say, no. 1) is of particular interest. Following (Mascaro and Amit, 1999), the ERF of population no. 1 may be established by “cutting” its recurrent projections and by replacing them with an external input (cf. Figure 3). As before, with the isolated population, this strategy introduces a distinction between the intrinsic activity of population no. 1 (termed 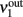 ) and the extrinsic input delivered to it as a substitute for the missing recurrent input (termed
) and the extrinsic input delivered to it as a substitute for the missing recurrent input (termed 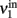 ). Next, the input activity
). Next, the input activity 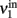 is held constant at a given value and the other populations are allowed to reach their equilibrium values
is held constant at a given value and the other populations are allowed to reach their equilibrium values 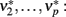
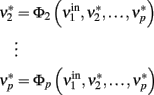
The new equilibrium states 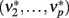 drive population no. 1 to a new rate:
drive population no. 1 to a new rate:
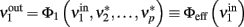
where 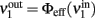 is the ERF of population no. 1.
is the ERF of population no. 1.
By capturing the recurrent feedback from all other populations, the ERF provides a one-dimensional reduction of the mean-field formulation of the entire network. In particular, stable states of the full network dynamics satisfy (at least approximately) the self-consistency condition of the ERF:
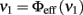
The ERF is a reliable and flexible tool for fine-tuning the system. It identifies fixed points of the activity of population no. 1 and provides information about its dynamics (if it is “slow” compared to the dynamics of the other populations).
The Neuromorphic Chip
The core of our setup is the FLANN device described in detail in Giulioni (2008), Giulioni et al. (2008). It contains neuromorphic circuits implementing 128 neurons and 16,384 synapses and is sufficiently flexible to accommodate a variety of network architectures, ranging from purely feed-forward to complex recurrent architectures. The neuron circuit is a revised version of the one introduced by Indiveri et al. (2006) and implements the integrate-and-fire neuron with linear decay described above.
The synapse circuit triggers, upon arrival of each pre-synaptic spike, a rectangular post-synaptic current of duration τpulse = 2.4 ms. The nature of each synaptic contact can be individually configured as excitatory or inhibitory. The excitatory synapses can be further set to be either potentiated or depressed. According to its nature each synapse possesses an efficacy J equal to either Jp for excitatory potentiated synapses, Jd for excitatory depressed ones or Ji for inhibitory synapses. In what follows we will express the value of J as a fraction of the range [0, θ] of the neuronal membrane potential. Accordingly, an efficacy of J = 0.01 θ implies that 100 simultaneous spikes are required to raise V(t) from 0 to θ. Similarly, we express the leakage current β in units of θs−1. Thus, a value of β = 200 θ s−1 implies that 1/200 s = 5 ms are required to reduce V(t) from θ to 0 (disregarding any incoming spikes).
The membrane potential of each neuron integrates post-synaptic currents from a “dendritic tree” of up to 128 synapses. Spiking activity is routed from neurons to synapses by means of the internal recurrent connectivity, which potentially provides for all-to-all connectivity. Spiking activity sent to (or coming from) external devices is handled by an interface managing an Address-Event Representation (AER) of this activity (Mahowald, 1992; Boahen, 2000). All AER interfaces, described in Dante et al. (2005) and Chicca et al. (2007) are compliant with the parallel AER standard.
The nominal values of all neuron and synapse parameters are set by bias voltages, resulting in effective on-chip parameters which will vary due to device mismatch. Each synapse can be configured to accept either local or AER spikes, and it can be set as excitatory or inhibitory, and potentiated or depressed, thus implementing a given network topology by downloading a certain configuration to the on-chip synapses. To disable a synapse, we configure it to receive AER-input and simply avoid providing any such input from the external spike activity. To stimulate and monitor the chip activity, we connect it to the PCI-AER board (Dante et al., 2005), which provides a flexible interface between the asynchronous AER protocol and the computer’s synchronous PCI (Peripheral Component Interconnect) standard. Controlled by suitable software drivers, the PCI-AER board can generate arbitrary fluxes of AER spikes and monitor on-chip spiking activity.
Several aspects of the circuitry implemented in the FLANN device were disabled in the present study. Notably, these included the spike-frequency adaptation of the neuron circuit and the self-limiting Hebbian plasticity (Brader et al., 2007) of the synapse circuit.
The Network
The architecture of the network we have implemented and studied is illustrated in Figure 1. It comprises several populations of neurons, some with recurrent connectivity (on-chip) and some without (off-chip). Two excitatory populations with 48 neurons each constitute, respectively, an “attractor population” Eatt and a “background population” Ebkg. In addition, there is one inhibitory population I of 31 neurons. These three populations are recurrently connected and are implemented physically on the neuromorphic chip. All on-chip neurons share the same nominal parameter values, with a leakage current β = 200 θs−1 and an absolute refractory period τarp = 1.2 ms. Two additional excitatory populations (E1AER, E2AER) and one further inhibitory population (IAER) project to the on-chip populations in a strictly feed-forward manner. These three populations are implemented virtually (i.e., as spike fluxes delivered via the AER generated by the PCI-AER sequencer feature).
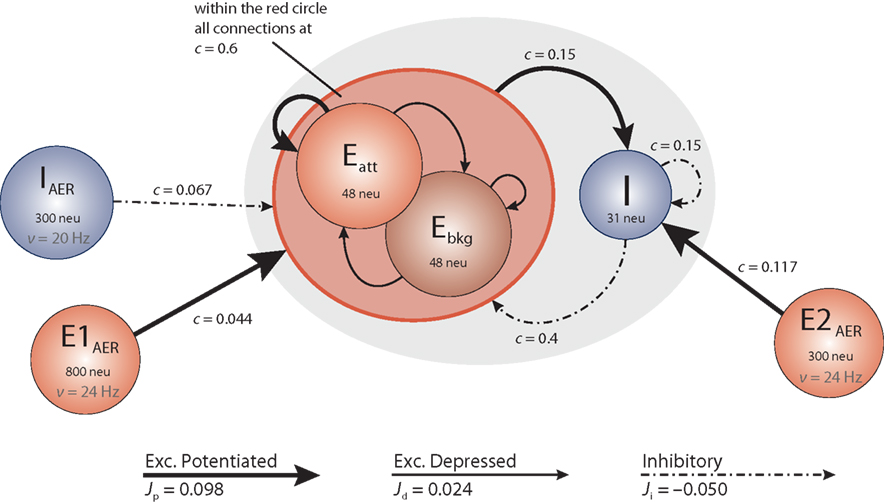
Figure 1. Network architecture. Each circle represents a homogeneous population of neurons. The gray oval includes the on-chip populations: two excitatory populations Eatt and Ebkg (48 neurons each) and one inhibitory population I (31 neurons). Off-chip populations E1AER (800 neurons), E2AER (300 neurons), and IAER (300 neurons) are simulated in software. Connectivity is specified in terms of the fraction c of source neurons projecting to each target neuron. Projections are drawn to identify synaptic efficacies as excitatory potentiated (Jp), excitatory depressed (Jd), or inhibitory (Ji).
The on-chip excitatory populations Eatt and Ebkg are recurrently and reciprocally connected with a connectivity level c = 0.6. They differ only in their degree of self-excitation: Eatt recurrent feedback is mediated by excitatory potentiated synapses, while all the other synapses connecting on-chip excitatory populations are set to be depressed. Due to stronger self-excitation, Eatt is expected to respond briskly to increased external stimulation from E1AER. In contrast, Ebkg is expected to respond more sluggishly to such stimulation. Later, in Section “Tuning feedback,” we study the network response for different levels of self-excitation obtained varying the fraction of potentiated synapses per projection. The recurrent inhibition of I is fixed at c = 0.15. The excitatory projections from Eatt and Ebkg onto the inhibitory population I are fixed at c = 0.15. In return, the inhibitory projections of I onto Eatt and Ebkg are set at c = 0.4, respectively.
On-chip synapses of the same kind share the same voltage biases. Thus the synaptic efficacies, expressed as a fraction of the dynamic range of the membrane potential (see above), are Jp = 0.098 and Jd = 0.024 for potentiated and depressed excitatory synapses, respectively, and Ji = −0.050 for inhibitory synapses.
Due to the small number of neurons in each population, an asynchronous firing regime can be more easily maintained by immersing the on-chip populations in a “bath” of stochastic activity – even if sparse synaptic connectivity can allow for asynchronous firing with constant external excitation as predicted by van Vreeswijk and Sompolinsky (1996) and observed in a neuromorphic VLSI chip by D’Andreagiovanni et al. (2001). To this end, each neuron of the excitatory populations Eatt and Ebkg receives external excitation from E1AER (840 Hz = 35·24 Hz) and external inhibition from IAER (480 Hz = 20·24 Hz). Similarly, each neuron of the inhibitory population I receives external excitation from E2AER (700 Hz = 35·20 Hz). External (AER) spike trains are independent Poisson processes. During various experimental protocols, the off-chip activity levels are modulated.
Mapping to Neuromorphic Hardware
To implement the target network depicted in Figure 1 on the FLANN device, neuron, and synapse parameters must be brought into correspondence with the theoretical values. This is not an easy task, because analog circuits operating in a sub-threshold regime are sensitive to semiconductor process variations, internal supply voltage drops, temperature fluctuations, and other factors, each of which may significantly disperse the behavior of individual neuron and synapse circuits.
To compound the problem, different parameters are coupled due to the way in which the circuits were designed (Giulioni et al., 2008). For instance, potentiated synaptic efficacy depends on both the depressed synaptic efficacy bias and the potentiated synaptic efficacy bias. As sub-threshold circuits are very sensitive to drops in the supply voltage, any parameter change that results in a slight voltage drop will also affect several other parameters. Even for the (comparatively small) chip in question, it would not be practical to address this problem with exhaustive calibration procedures (e.g., by sweeping through combinations of bias voltages).
We adopted a multi-step approach to overcome these difficulties. In the first step, we use “test points” to certain individual circuits in order to monitor various critical values on the oscilloscope (membrane potential, pulse length, linear decay β, etc.). In subsequent steps, we performed a series of “neurophysiological” experiments at increasing levels of complexity (individual neurons and synapses, individual neuron response function, open-loop population response functions), which will be described in detail below.
Implementing the desired connectivity between circuit components presents no particular difficulty, as the configuration of the synaptic matrix is based on a digital data-stream handled by a dedicated microcontroller.
Synaptic Efficacy
To assess the effective strength of the synaptic couplings, it is essential to know the distribution of efficacies across synaptic populations. We conducted a series of experiments to establish the efficacies of excitatory (potentiated and depressed) and inhibitory synapses. The results are summarized in Figure 2 (left panel). The basic principle of these measurements is to stimulate an individual synapse with pre-synaptic regular spike trains of different frequencies and to establish how this affects the firing activity of the post-synaptic neuron. Specifically, for a post-synaptic neuron with zero drift rate β = 0 and no refractory period τarp = 0, the synaptic efficacy Jsyn (for small Jsyn) is approximated by:
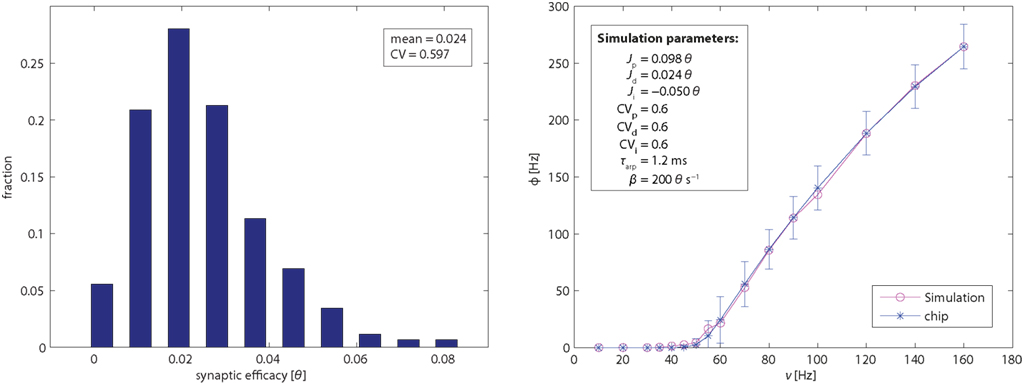
Figure 2. Left panel: distribution of efficacy in 1,024 excitatory depressed synapses, expressed as fractions of the dynamic range of the membrane potential (i.e., from the reset potential 0 and to the firing threshold θ). Right panel: single-neuron response function. Mean and SE of neuromorphic neurons (blue symbols with error bars). The variability is due primarily to device mismatch in the leakage current β and in the absolute refractory period τarp. Mean of simulation results (red symbols) for an ideal neuron and 120 synapses drawn from a Gaussian distribution of efficacies (see inset and text for details). CV stands for the coefficient of variation of the efficacy distributions.
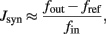
where fout is post-synaptic output frequency, fref is post-synaptic baseline activity, and fin is pre-synaptic input frequency.
If the measured spike trains are sufficiently long (≥0.5 s), this procedure gives reasonably accurate results. Note that this measurement characterizes the analog circuitry generating post-synaptic currents and therefore does not depend on the routing of pre-synaptic spikes (i.e., internally via recurrent connections or externally via the AER). To measure the efficacy of excitatory synapses, it is sufficient to initialize the desired configuration (potentiated or depressed) and to apply the desired pre-synaptic input. To measure the efficacy of inhibitory synapses, the post-synaptic neuron has to be sufficiently excited to produce spikes both with and without the inhibitory input. To ensure this, a suitable level of background excitation (fref) has to be supplied via an excitatory synapse of known strength.
Knowing the dispersion of synaptic efficacies will prove important for the experiments described below (e.g., in determining the value of ΔJ2). Note also that the variability of the efficacy is not related to the location of the synapse on the matrix (not shown), thus all post-synaptic neurons receive spikes mediated by synapses with similar distribution of efficacies.
Duration of Synaptic Current
Synaptic efficacy is the product of the amplitude and the duration of the synaptic pulse. To disambiguate these two factors, we experimentally determined the actual duration of individual synaptic currents. To this end, we took advantage of current saturation due to overlapping synaptic pulses. The synapse circuit initiates a post-synaptic current pulse immediately upon arrival of the pre-synaptic spike. If another spike arrives while the pulse remains active, the first pulse is truncated and a new pulse initiated. This truncation reduces synaptic efficacy at high pre-synaptic spike frequencies.
The duration of synaptic pulses was τpulse = 2.4 ms with a SD of 0.58 ms. To determine the actual duration for individual synapses, we stimulated pre-synaptically with periodic spikes of frequency νpre and monitored post-synaptic firing νpost, setting both leakage current β and absolute refractory period τarp to zero. With these settings, post-synaptic firing saturates when synaptic pulses overlap to produce a constant continuous current. The true pulse duration τpulse may then be computed as the inverse of the pre-synaptic frequency at which saturation is reached: τpulse = 1/νpre.
Duration of Refractory Period
To measure the absolute refractory period τarp of individual neurons, we availed ourselves of a special feature of the neuron circuit which allows a direct current to be delivered to each neuron. For a given input current, we compared the inter-spike intervals (ISI) obtained for zero and non-zero values of τarp. The difference between those values revealed the true value of the absolute refractory period.
The dispersion in the value of τarp was ≈10% (average τarp = 1.2 ms and SD 0.11 ms). This degree of variability is sufficient to affect single-neuron response functions (see below).
Leakage Current
In principle, the leakage current β of individual neurons can also be determined experimentally (e.g., by nulling it with a direct current). In practice, however, it proved more reliable to establish β in the context of the single-neuron response function (see below).
Single-neuron Response Function
The response function of a neuron describes the dependence of its firing rate on pre-synaptic input. To establish this function for an individual FLANN neuron, we configured 40 synapses of its dendritic tree as excitatory/depressed, 40 synapses as excitatory/potentiated, and 30 synapses as inhibitory. All synapses were activated via AER with independent Poisson spike trains. In particular, 70 synapses (depressed and inhibitory) were activated with fixed Poisson rates of 20 Hz (to maintain a baseline operating regime), while 40 synapses (potentiated) were stimulated with Poisson rates ranging from 10 to 160 Hz (to vary excitatory input). For each input rate, an associated output rate was established and the results (mean and SD over 100 individual neurons) are shown in Figure 2 (right panel). For the chosen parameter values, output firing exhibited a monotonically increasing and slightly sigmoidal dependence on excitatory input. For comparison, Figure 2 (right panel) also shows the response function of a simulated neuron model (with all parameters set to their nominal values). The sigmoidal shape of the transfer function will turn out to be crucial for obtaining bistable dynamics with recurrently connected populations (see further below).
Once an estimate of the synaptic efficacies and τarp is obtained, the match between the empirical and simulated single-neuron response function allows us to extract a good estimate of β. Thus, by comparing the leftmost part of the curve with simulation data, we could determine the effective value of β for each neuron. All simulations were performed with an efficient event-driven simulator.
The comparison between single-neuron response function and its theoretical or simulated counterpart is an important aggregate test of a neuromorphic neuron and its synapses (i.e., the synapses on its “dendritic tree”). Passing this test safeguards against several potential problems, among them crosstalk between analog and digital lines, excessive mismatch, or other spurious effects. In addition, this comparison stresses the AER communication between the FLANN chip and the PCI-AER board. In short, the single-neuron response function provides a good indication that the hardware components, as a whole, deliver the expected neural and synaptic dynamics.
Note that there are a number of unavoidable discrepancies between the hardware experiment, on the one hand, and theory/simulation, on the other hand. These include device mismatch among neurons and synapses, violations of the conditions of the “diffusion limit,” finite duration of synaptic pulses (causing the saturation effects discussed above), non-Gaussian distribution of the synaptic efficacies, as it results from Figure 2 (left panel), and any deviations from the predictions for instantaneous synaptic transmission (Brunel and Sergi, 1998; Renart et al., 2004), and others. For the present purposes, it was sufficient to avoid egregious discrepancies and to achieve a semi-quantitative correspondence between hardware and theory/simulation.
Measuring the Effective Response Function
Measuring the ERF of a population of hardware neurons provides valuable information. While the predictions of theory and simulation are qualitatively interesting, they are quantitatively unreliable. This is due, firstly, to the unavoidable discrepancies between experiment and theory (mentioned above) and, secondly, to the compounding of these discrepancies by recurrent network interactions. We therefore took inspiration from the theoretical strategy to develop a procedure to estimate the ERF directly on-chip. This constitutes, we believe, a valuable contribution to the general issue of how to gain predictive control of complex dynamical systems implemented in neuromorphic chips.
To establish the ERF for population Eatt in the context of the network (Figure 1), we modified the connectivity as illustrated in Figure 3. Specifically, the recurrent connections of Eatt were cut and replaced by a new excitatory input Eext. From the point of view of a post-synaptic neuron in Eatt, any missing pre-synaptic inputs from fellow Eatt neurons were replaced one-to-one by pre-synaptic inputs from Eext neurons. This was achieved by the simple expedient of reconfiguring recurrent synapses within Eatt as AER synapses and by routing all inputs to these synapses from Eext neurons, rather than from Eatt neurons. All other synaptic connections were left unchanged.
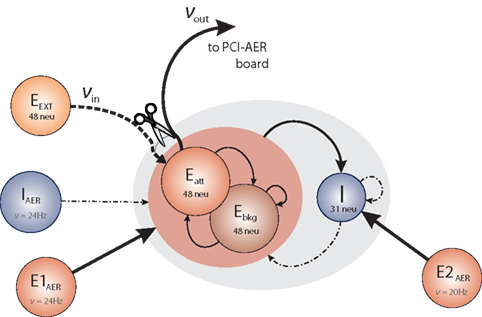
Figure 3. Modified network architecture to measure the effective response function of population Eatt. Recurrent connections within Eatt are severed and their input replaced by input from external population Eext. In all other respects, the network remains unchanged. The effective response function is νout = Φ(νin).
Controlling the activity νin of Eext neurons, we monitored the resulting activity νout of Eatt neurons. Performing a sweep of νin values, established the ERF of Eatt, which is illustrated in Figure 4 (left panel). Note that, during the entire procedure, populations E1AER, E2AER, and IAER maintained their original firing rates, while populations Ebkg and I were free to adjust their activity.
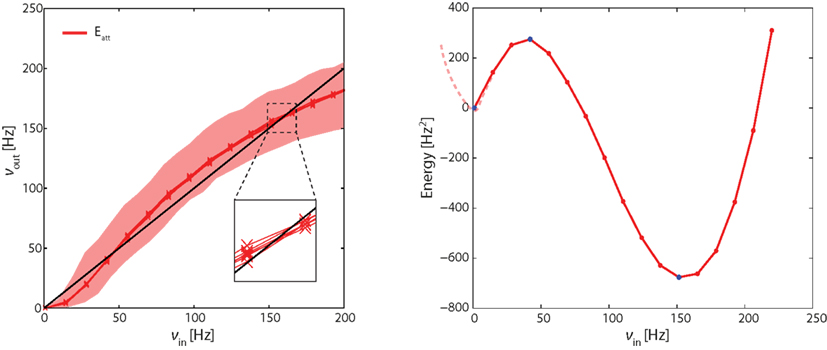
Figure 4. Left panel: effective response functions (ERF) of population Eatt measured on-chip (see Figure 3). Each red lines represents an average over neurons in Eatt. Different red lines represent different probabilistic assignments of connectivity (see text). Also indicated is the range of activities obtained from individual neurons (shaded red area). Intersections between ERF and the diagonal (black line) predict fixed points of the network dynamics (stable or unstable). Note that these predictions are approximate (inset). Right panel: “Double-well” energy landscape derived from the ERF (see text for details). Energy minima (maxima) correspond to stable (unstable) fixed points of the network dynamics.
In Figure 4, each red curve shows the average activity in Eatt as a function of νin. Different red curves show results from six different “microscopic” implementations of the network (i.e., six probabilistic assignations of the connectivity of individual neurons and synapses). The fact that the bundle of red curves is so compact confirms that the network is stable across different “microscopic” implementations. The shaded red area gives the total range of outcomes for individual neurons in Eatt, attesting to the considerable inhomogeneity among hardware neurons.
The effective response function Φeff in the left panel of Figure 4 predicts three fixed points for the dynamics of the complete network (i.e., in which the severed connections are re-established). These fixed points are the intersections with the diagonal (νin = νout, black line) at approximately 0.5, 40, and 160 Hz. The fixed points at 0.5 and 160 Hz are stable equilibrium points and correspond to stable states of “low” and “high” activity, respectively. The middle fixed point at 40 Hz is an unstable equilibrium point and represents the barrier the network has to cross as it transitions from one stable state to another.
The choice of excitatory J is the compromise between two needs: first we want the higher fixed point to be stable against finite-size fluctuations, which would favor high values of J, on the other hand we want to both keep the lower fix point simultaneously stable, and to avoid the network being trapped into globally synchronous state, which points toward low values of J.
If we consider the difference Δν = νin − νout as a “driving force” propelling activity toward the nearest stable point, we can infer an “energy landscape” from the ERF by defining “energy” as:
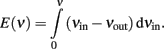
The result (Figure 4, right panel) is a typical “double-well” landscape with two local minima at 0.5 and 160 Hz (two stable fixed points), which are separated by a local maximum at 40 Hz (unstable fixed point). In predicting the relative stability of the two fixed points, one has to consider both the height of the energy barrier and the amplitude of noise (essentially the finite-size noise), which scales with activity. For example, while the transition from “low” to “high” activity faces a lower barrier than in the reverse direction, it is also driven by less noise. As a matter of fact, under our conditions, the “low” activity state turns out to be less stable than the “high” state.
Furthermore inhibitory neurons are a needed ingredient to increase the attractor stability (Mattia and Del Giudice, 2004).
Results
Our neuromorphic network exhibits the essential characteristics of an attractor network. Here we demonstrate, firstly, hysteretic behavior conserving the prior history of stimulation (section entitled “Working memory”), secondly, stochastic transitions between meta-stable attractor states (“Bistable dynamics”) and, thirdly, self-correction of corrupted activity states (“Basins of attraction”). In addition, we characterize the time-course of state transitions (“Transition latencies”) and performance experimental bifurcation analysis (“Tuning feedback”).
Working Memory
Attractor networks with two (or more) meta-stable states show hysteretic behavior, in the sense that their persistent activity can reflect earlier external input. This behavior is termed “working memory” in analogy to the presumed neural correlates of visual working memory in non-human primates (see for instance Zipser et al., 1993; Amit, 1995; Del Giudice et al., 2003). The central idea is simple: a transient external input moves the system into the vicinity of one particular meta-stable state; after the input has ceased, this state sustains itself and thereby preserves a “working memory” of the earlier input.
Our starting point is the network depicted in Figure 1, which possesses meta-stable states of “low” and of “high” activity (see Methods). The normal level of external stimulation is chosen such that spontaneous transitions between meta-stable states are rare. To trigger transitions, an additional external input (“kick”) must be transiently supplied. To generate an excitatory (inhibitory) input transient, the mean firing rate of E1AER (IAER) is increased from the baseline frequency νE1 = 24 Hz as described in the following paragraphs. Here, input transients are applied to all Eatt neurons and only to Eatt neurons. The effect of stimulating both Eatt and Ebkg neurons is reported further below (“Basins of attraction”).
The effect of excitatory and inhibitory input transients (“kicks”) to Eatt is illustrated in Figure 5. Its central panel depicts average firing of Eatt and Ebkg neurons during four successive “kicks,” two excitatory and two inhibitory. The first excitatory “kick” is weak (t = 0.5 s, νE1 = 34 Hz) and modifies the Effective Response Function (ERF) only slightly, so that Eatt increases only marginally. After the “kick” the original ERF is restored and Eatt returns to the “low” meta-stable state (Figure 5, bottom left inset).
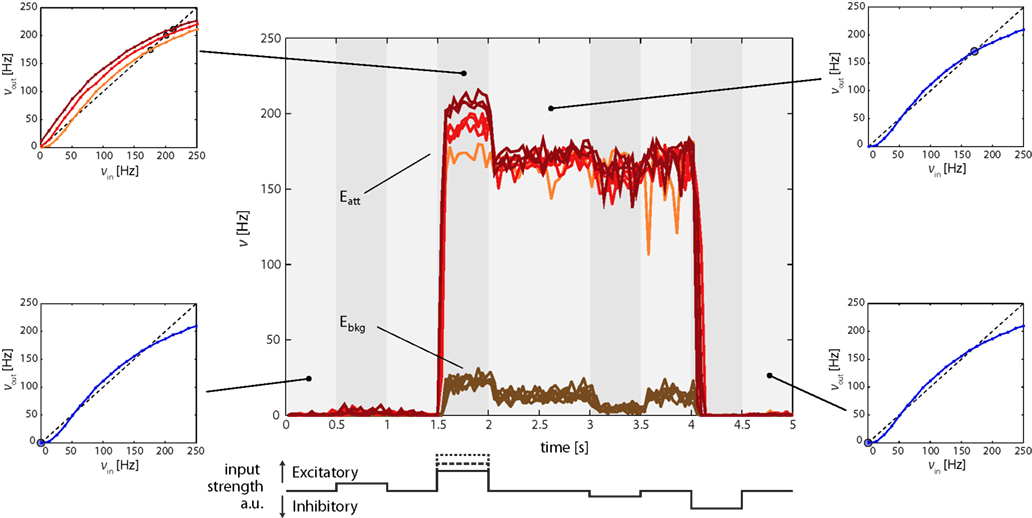
Figure 5. Firing rates of Eatt and Ebkg in response to multiple input transients (“kicks,” central figure). Excitatory (inhibitory) transients are created by square-pulse increments of E1AER (IAER) activity. The timing of input transients is illustrated beneath the central figure: 0.5 and 1.5 s mark the onset of sub-threshold (νE1 = 34 Hz) and supra-threshold (νE1 = 67, 84, or 115 Hz) excitatory “kicks,” 3 and 4 s that of sub- and supra-threshold inhibitory “kicks.” Sub-threshold “kicks” merely modulate activity of the current meta-stable state. Supra-threshold “kicks” additionally trigger a transition to the other meta-stable state. All observations are predicted by the analysis of effective response functions (ERFs, insets on either side of central figure) measured on-chip. In the absence of input transients, the default ERF predicts two meta-stable fixed points, one “low” state (blue dot, bottom insets) and one “high” state (blue dot, top right inset). In the presence of input transients, the ERF is altered (orange, red, and burgundy curves, top-left inset) and the position of the meta-stable “high” state is shifted (orange, red, and burgundy dots).
The second excitatory “kick” is more hefty (t = 1.5 s, νE1 = 67, 84, or 115 Hz) and dramatically increases Eatt and (to a lesser degree) Ebkg activity. The reason is that a stronger “kick” deforms the ERF to such an extent that the “low” state is destabilized (or even eliminated) and the system is forced toward the “high” state (with ν > 170 Hz, Figure 5, top-left inset). Thus, the recurrent interactions of the network (far more than the external “kick” itself) drive the network to a “high” state. After the “kick,” the original ERF is once again restored. However, as the network now occupies a different initial position, it relaxes to its “high” meta-stable state (Figure 5, top right inset), thereby preserving a “working memory” of the earlier “kick.”
In a similar manner, inhibitory “kicks” can induce a return transition to the “low” meta-stable state. In Figure 5, a weak inhibitory “kick” was applied at t = 3 s and a strong inhibitory “kick” at t = 4 s. The former merely shifted the “high” state and therefore left the “working memory” intact. The latter was sufficiently hefty to destabilize or eliminate the “high” state, thus forcing the system to return to the “low” state.
Figure 5 also illustrates the different behaviors of Eatt and Ebkg. Throughout the experiment, activity of the background population remains below 30 Hz. The highest level of Ebkg is reached while the input from Eatt is strong, that is, while Eatt occupies its “high” state. Differences between Eatt and Ebkg highlights, therefore, the overwhelming importance of the different recurrent connectivity in allowing for multiple meta-stable states.
The meta-stable states are robust against activity fluctuations and small perturbations, a manifestation of the attractor property. However, even in the absence of strong perturbations like the above kicks, large spontaneous fluctuations of population activity can drive the network out from an attractor state and into another, as illustrated in the next section.
Bistable Dynamics
An important characteristic of attractor networks is their saltatory and probabilistic dynamics. This is due to the presence of spontaneous activity fluctuations (mostly due to the finite numbers of neurons) and plays an important functional role. Spontaneous fluctuations ensure that the energy landscape around any meta-stable state is explored and that, from time to time, the system crosses an energy barrier and transitions to another meta-stable state. The destabilizing influence of spontaneous fluctuations is counter-balanced by the deterministic influence of recurrent interactions driving the system toward a minimal energy state. The stochastic dynamics of attractor networks is thought to be an important aspect of neural computation. Below, we describe how spontaneous transitions between meta-stable states may be obtained in a neuromorphic hardware network.
Once again, we consider our network (Figure 1) with “low” and “high” meta-stable states. In contrast to the “working memory” experiments described above, we elevate and keep fixed E1 activity to νE1 = 33 Hz. The additional excitation increases the amplitude of spontaneous fluctuations such that meta-stable states are made less stable and spontaneous transitions become far more frequent (cf. double-well energy landscape in Figure 4, right panel).
Network activity was allowed to evolve spontaneously for 30 s and a representative time-course is illustrated in Figure 6. The instantaneous firing rate of Eatt neurons (red curve) alternates spontaneously between “low” and “high” states, spending comparatively little time at intermediate levels. The spiking of individual neurons (blue raster) reveals subtle differences between the two meta-stable states: in the “low” state, activity is driven largely by external stimulation and inter-spike intervals are approximately Poisson-distributed (coefficient of variation CV = 0.82), whereas, in the “high” state, activity is sustained by feedback and inter-spike intervals are approximately Gaussian-distributed (CV = 0.29). In both cases, the network maintains an asynchronous state as confirmed by the power spectra of the population activity (see Figure 7).

Figure 6. Spontaneous activity of Eatt neurons: population average (red curve) and 48 individual neurons (blue spike raster). Excitatory input from E1AER was raised to ν = 33 Hz, such as to make less stable the low activity state. The population activity jumps spontaneously between meta-stable “low” and “high” states. This results in a bimodal distribution of activity, as shown in the histogram on the right. Note that the average activity of individual neurons differs markedly, due to mismatch effects.
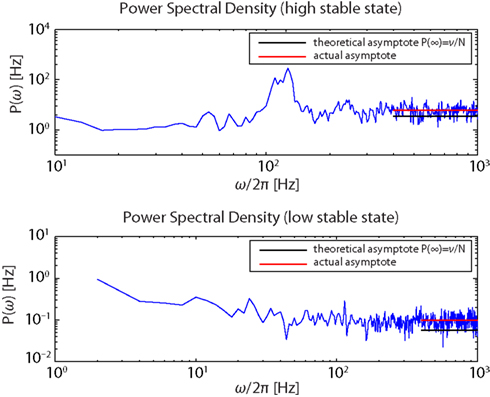
Figure 7. Power spectra of the firing activity of population Eatt in the “high” (upper panel) and the “low” (lower panel) stable states.
The simultaneous evidences of a flat spectral density for high ω together with the structure of the spectral resonances, centered at multiples of ν, is consistent with established theoretical expectations for a globally asynchronous state (Spiridon and Gerstner, 1999; Mattia and Del Giudice, 2002).
The measured asymptotic values lie slightly above their theoretical counterparts, suggesting that spikes of different neurons co-occur a bit more frequently than expected. This is likely due to the strength of the synaptic efficacies as they were determined based on the constraints discussed in the Methods (D’Andreagiovanni et al., 2001).
The origin of spontaneous fluctuations is well understood: they are due to a combination of noisy external input, of the randomness and sparseness of synaptic connectivity, and of the finite number of neurons in the network (van Vreeswijk and Sompolinsky, 1996; Brunel and Hakim, 1999; Mattia and Del Giudice, 2002).
The balance between spontaneous fluctuations and deterministic energy gradients provides a tunable “clock” for stochastic state transitions. In the present example, the probability of large, transition-triggering fluctuations is comparatively low, so that meta-stable states persist for up to a few seconds. Note that this time-scale is three orders of magnitude larger than the time-constants implemented in circuit components (e.g., 1/β = 5 ms).
In spite of the comparatively slow evolution of the collective dynamics, transitions between meta-stable states complete, once initiated, within milliseconds. This is due to the massive positive feedback, with each excitatory neuron receiving spikes from 57 (48 · 0.6 2; see Figure 1) other excitatory neurons. This feedback ensures that, once the energy barrier is crossed, activity rapidly approaches a level that is appropriate to the new meta-stable state.
Transition Latencies
The experiments described so far exemplify two escape mechanisms from a meta-stable state: a deterministic escape triggered by external input and a probabilistic escape triggered by spontaneous fluctuations which is consistent with Kramers’ theory for noisy crossings of a potential barrier (Risken, 1989).
We examined the distribution of “escape times” following an onset of external stimulation. The protocol adopted was similar to Figure 5, but involved only a single input transient (“kick”) lasting for 3 s. Although we studied transitions in both directions, we only report our findings for transitions from the low spontaneous state to the high meta-stable state induced by stimulation (see top-left inset in Figure 5). In this direction, the transition latency (or “escape time”) was defined as the time between stimulus onset and Eatt activity reaching a threshold of ν = 50 Hz.
Representative examples of the evolution of activity in response to weaker (νE1 = 34 Hz) or stronger (νE1 = 41 Hz) “kicks” are illustrated in the central panel of Figure 8. It is evident that weaker “kicks” result in longer, more broadly distributed latencies, whereas stronger “kicks” entail shorter, more narrowly distributed latencies. The respective latency distributions produced by weaker and stronger “kicks” are shown in the left and right panels of Figure 8 (as well being superimposed over the central panel).
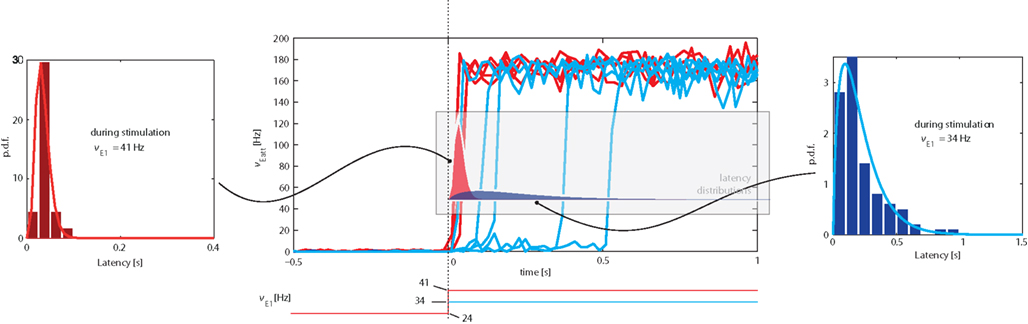
Figure 8. Central Panel: superposition of average Eatt activity, transitioning from the “low” spontaneous state to the “high” stable state induced by stimulation (increase of E1 activity from baseline of νE1 = 24 Hz). Blue tracks correspond to weaker (νE1 = 34 Hz), red tracks to stronger stimulation (νE1 = 41 Hz). Lateral panels: distributions of latencies between the onset of stimulation and the transition time (defined as Eatt activity reaching ν = 50 Hz). Stronger stimulation results in short, narrowly distributed latencies, weaker stimulation in long, broadly distributed latencies. Note the different time-scales of lateral insets. The same latency distributions are superimposed over the central panel.
The difference between the two latency distributions reflects the difference between the underlying mechanism: a stronger “kick” disrupts the energy landscape and eliminates the “low” meta-stable state, forcing a rapid and quasi-deterministic transition, whereas a weaker “kick” merely modifies the landscape to increase transition probability.
Tuning Feedback
So far, we have described the network response to external stimulation. We now turn to examine an internal parameter – the level of recurrent feedback – which shapes the network’s dynamics and endows it with self-excitability. We will show that the network response to an external stimulus can be modulated quantitatively and qualitatively by varying internal feedback.
The present experiments were conducted with a network similar to that of Figure 1, except that the fraction f of potentiated synapses (among recurrent Eatt synapses) was varied in the range 0.65–1.0. The results are summarized in terms of a bifurcation diagram (the set of meta-stable states as a function of f; Figure 10) and in terms of the average transition latencies (Figure 9).
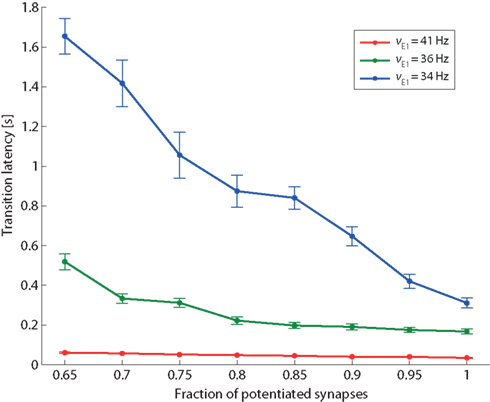
Figure 9. Transition latency and recurrent connectivity. Latency of transition from low spontaneous state of Eatt activity to its high meta-stable state induced by stimulation (same protocol as Figure 8), as a function of the recurrent connectivity of population Eatt (fraction of potentiated synapses) and of the strength of external stimulation (νE1 increasing from a baseline of 24 Hz to an elevated level of either 34, 36, or 41 Hz (blue, green, and red curves, respectively).
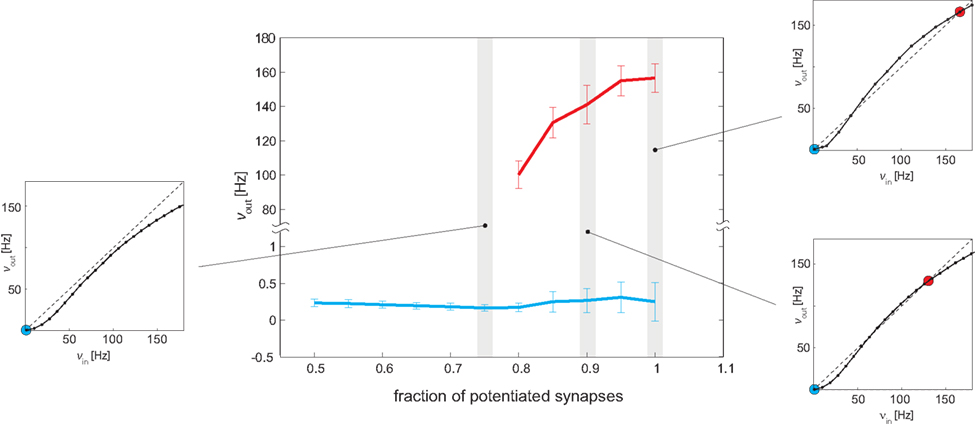
Figure 10. Bifurcation diagram. Central panel: measured Eatt activity (mean and SE) of meta-stable states, as a function of the strength of recurrent connectivity (fraction f of potentiated synapses in recurrent Eatt connectivity). A “low” meta-stable state (blue line and error bars) exists for all levels of recurrency. A “high” meta-stable state appears for strong levels of recurrency (bifurcation point ≈0.77). Side panels: all observations are predicted by the analysis of effective response functions (ERFs, insets on either side) measured on-chip. For weak recurrency of f = 0.75, the ERF predicts a “low” meta-stable state (blue dot, left inset), for intermediate recurrency of f = 0.9, it predicts a “low” and a “high” state (blue and red dots, bottom right inset), and for high recurrency of f = 1, it predicts that “low” and “high” states are separated more widely (blue and red dots, top right inset).
To establish a bifurcation diagram (analogous to the theoretical one introduced in Amit and Brunel, 1997), we used a protocol similar to Figure 5 and measured the firing of Eatt after the end of a strong “kick” (νE1 = 41 Hz, duration 0.5 s). The results are illustrated in Figure 10. For low levels of recurrency (f < 0.8), only the “low” meta-stable state is available and after the “kick” Eatt activity rapidly returns to a level below 0.5 Hz (blue curve). For high levels of recurrency (f ≥ 0.8), the network exhibits both “high” and “low” meta-stable states in the absence of stimulation. Just beyond the bifurcation point (f ∼ 0.8) the high meta-stable state is about 100 Hz (red points); due to the finite-size effect after a variable amount of time, the network spontaneously returns to the “low” state (blue curve). Both the activity level and the stability (persistence time) of the “high” state increase with the degree of recurrency, as expected. Indeed, the sigmoidal shape of the effective transfer function and the height of the barrier in the energy landscape become more pronounced (see insets in Figure 10).
In addition to the qualitative effect of establishing a “high” meta-stable state, stronger feedback influences the network also in quantitative ways. One such quantitative effect is expected to be an acceleration of response times to external stimulation. To demonstrate this, we return to the protocol of Figure 8 and measure transition latencies (“escape times”) in response to three levels of external stimulation (νE1 = 34, 36, and 41 Hz). The dependence of transition latencies on the strength of recurrency is shown in Figure 9.
As expected, the responsiveness of the network to external stimulation can be tuned over a large range of latencies by varying the strength of recurrent feedback.
It is also noted that the sensitivity of the transition latencies to f decreases as the external stimulus increases (compare the slopes of the three curves in Figure 9).
Basins of Attraction
The “basin of attraction” of a given attractor is defined as the set of all the initial states from which the network dynamics spontaneously evolve to that attractor. The size of the basins of attraction established the “error correction” ability of the network: a stimulus implementing a “corrupted” version of the neural activities in the attractor state leads, provided it is in the basin of attraction, to a fully restored attractor state. In other words, the network behaves as a “content addressable memory” in the sense suggested by Hopfield (1982).
Specifically, we define a “corruption level” C and deliver a transient external input (“kick”) to a subset of 48(1 − C) neurons in Eatt and a subset of 48C neurons in Ebkg. Accordingly, for C = 0, a “kick” is delivered exclusively to Eatt neurons and, for C = 1, the “kick” impacts only Ebkg neurons. This ensures that for different levels of corruption (i.e., different distances from the attractor states in which all 48 neurons in Eatt are highly active) the total afferent input to the network is kept constant. Once the input transient has passed, the network is again governed by its intrinsic dynamics. If these dynamics restore the “high” meta-stable state of Eatt (which also entails “low” activity in Ebkg), we say that the network has “recognized” the corrupted input pattern. If the dynamics lead to some other activity pattern, we speak of a “recognition failure.”
A representative example of the network’s response to a “kick” of 500 ms duration and a corruption level C = 0.5 is illustrated in Figure 11. The instantaneous activities of the stimulated and non-stimulated subsets of Eatt neurons (orange and gray curves, respectively) are seen to be very similar, except during a short period following the onset of the “kick.” During this period, the activity of non-stimulated neurons may lag slightly behind that of the stimulated neurons, by the time it takes for them to be recruited by the stimulated ones.
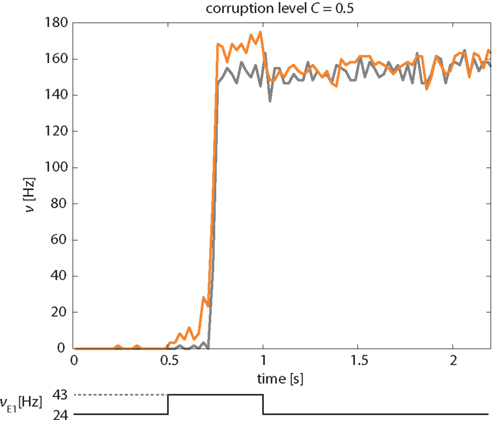
Figure 11. Correction of “corrupted” input pattern. An external stimulus (increase of νE1 from 24 to 43 Hz) is applied selectively to half of Eatt and half of the Ebkg neurons (corruption level C = 0.5). The network corrects this “corrupted” input and transitions into the “high” meta-stable state with both stimulated and non-stimulated Eatt neurons (orange and gray curves, respectively). Activity of Ebkg neurons remains below 30 Hz (not shown).
With this protocol, we measured “recognition” probability as a function of corruption level C (Figure 12). For low values of C, the network recognizes the “corrupted” input reliably and enters into the “high” attractor state.
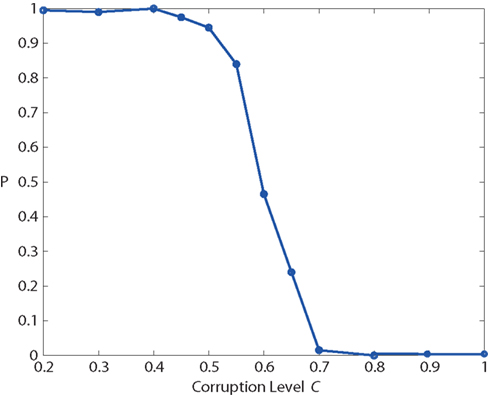
Figure 12. Basin of attraction: recognition probability P, as a function of input corruption C, measured with the protocol of Figure 11. For corruption levels C > 0.65, P falls below 25%, which implies that recognition fails in more than 75% of the trials.
For values of C above 0.65, the “recognition” probability falls below 25%, so that the network fails to recognize the input pattern in more than 75% of the trials. The sharp drop of the sigmoidal P(C) curve marks the boundary of the basin of attraction around the “high” state. Note that this curve depends also on the strength of the external input transient (not shown).
Discussion
We show how bistable attractor dynamics can be realized in silicon with a small network of spiking neurons in neuromorphic VLSI hardware. Step-by-step, we describe how various emergent behaviors can be “designed into” the collective activity dynamics. The demonstrated emergent properties include:
• asynchronous irregular activity,
• distinct steady-states (with “low” and “high” activity) in a sub-population of neurons,
• evoked state transitions that retain transient external input (“working memory”),
• self-correction of corrupted activity states (“basin of attraction”),
• tunable latency of evoked transitions,
• spontaneous state transitions driven by internal activity fluctuations,
• tunable rate of spontaneous transitions.
Standard theoretical techniques predict the single-neuron response function, which in turn determines the equilibrium states of the collective dynamics under the “mean-field” approximation (see Section Mean-field theory). In the case of a multi-population network, an Effective Response Function (ERF) for one or more populations of interest can be extracted with the help of further approximations.
The ERF provides the central hinge between network architecture and various aspects of the collective dynamics. It predicts quantitatively the number and location of steady-states in the activity of selected populations, both for spontaneous and for input-driven activity regimes. In addition, within the scope of the relevant approximations, the ERF describes qualitatively the energy landscape that governs the activity dynamics. Accordingly, it also gives an indication about kinetic characteristics such as transition latencies.
Establishing a proper correspondence between theoretical parameters and their empirical counterparts in an analog, neuromorphic chip is fraught with difficulties and uncertainties. For this reason, we do not stretch theory to the point of directly predicting the network’s behavior in silicon (in contrast to the route taken by Neftci et al., 2011). Instead, we implement the theoretical construction of the ERF in hardware and establish this important function empirically. The ERF so obtained encapsulates all relevant details of the physical network, including effects due to mismatch, violation of the diffusion limit, etc. Thus, we rely on an effective description of the physical network, not on a tenuous correspondence to an idealized network. Equipped with these tools (mean-field theory, characterization scripts, empirical ERF), our neuromorphic hardware becomes an easily controllable and reliable system on which we show how the concepts of mean-field theory may be used to shape various aspects of the network’s collective dynamics.
Wider Objectives
The computational possibilities of neural activity dynamics are gradually becoming better understood. Our wider objective is to translate neuroscientific advances in this area to neuromorphic hardware platforms. In doing so, we hope to build step-by-step the technological and theoretical foundations for biomimetic hardware devices that, in the fullness of time, could be integrated seamlessly with natural nervous tissues.
Reverberating states of neocortical activity, also called “attractor states,” are thought to underlie various cognitive processes and functions. These include working memory (Amit and Brunel, 1997; Del Giudice et al., 2003; Mongillo et al., 2003), recall of long-term memory (Hopfield, 1982; Amit, 1995; Hasselmo and McClelland, 1999; Wang, 2008), attentional selection (Deco and Rolls, 2005), rule-based choice behavior (Fusi et al., 2007; Vasilaki et al., 2009), sensory integration in decision making (Wang, 2002; Wong et al., 2007; Furman and Wang, 2008; Marti et al., 2008; Braun and Mattia, 2010), and working memory in combination with delayed sensory decision making (Laing and Chow, 2002; Machens et al., 2005), among others.
Dynamical representations involving attractor states are not restricted to the “point attractors” we have considered here (Destexhe and Contreras, 2006; Durstewitz and Deco, 2008). For example, there is evidence to suggest that “line attractors” may underlie some forms of working memory and path integration (Machens et al., 2005; Trappenberg, 2005; Chow et al., 2009). Chaotic attractors have long been proposed to subserve perceptual classification in certain sensory functions (Skarda and Freeman, 1987). More generally, both spontaneous and evoked activity in mammalian cortex may well be characterized by “attractor hopping” at multiple spatial and temporal scales (Grinvald et al., 2003; Shu et al., 2003; Fox and Raichle, 2007; Durstewitz and Deco, 2008; Ringach, 2009).
Thus, the stochastic dynamics of a multi-attractor system offer both a comparatively stereotyped, low-dimensional representation of high-dimensional inputs, and a statistical distribution of possible responses. This motivates the emphasis that we have placed on the stochastic aspects of the collective dynamics of our hardware network. The classification of sensory events at multiple spatial and temporal scales might require “nested attractor” dynamics in a neuromorphic VLSI device. In a “nested” scenario, reverberating activity patterns spanning multiple spatial and temporal scales are generated by many individually bistable attractor modules interacting in a hierarchical network architecture (Gigante et al., 2009; Braun and Mattia, 2010).
The energy landscape of a “nested” system would be considerably more complex than the one described here (Braun and Mattia, 2010). It should be imagined with multiple high-dimensional valleys within valleys, ridges, and saddles permitting state transitions. To match the sensory time-scales of interest, the dynamics of such a system could be tuned in much the same way as the simplistic attractor system of the present work (i.e., by adjusting ERFs and noise levels).
Yet another challenging perspective is to build attractor representations in an adaptive manner, by means of activity-driven plasticity. Even at the level of theory, surprisingly few studies have addressed this important issue (Amit and Mongillo, 2003; Del Giudice et al., 2003). The 16,384 synapses of the FLANN chip exhibit a bistable, spike-driven plasticity (Fusi et al., 2000) that, in principle, would be well suited for this purpose (Del Giudice et al., 2003). Although the present study did not make use of this feature, we consider it imperative to face this challenge with neuromorphic hardware and have taken some initial steps in this direction (Corradi, 2011).
State of the Field
Neuromorphic engineering is a broad and active field seeking to emulate natural neural processes with CMOS hardware technology for robotic, computational, and/or medical applications.
Recently, two groups have implemented “continuous attractor” dynamics in neuromorphic VLSI (Neftci et al., 2010; Massoud and Horiuchi, 2011). The two networks in question (comprising 32 and 124 neurons, respectively) realized a continuous-valued memory of past sensory input by means of excitatory-inhibitory interactions between nearest neighbors. The resulting winner-take-all dynamics permitted the authors to represent and update a sensory state with incremental input (Trappenberg, 2005). The hardware used by these groups is comparable to ours in that it combines fixed synapses with the neuronal circuit of Indiveri et al. (2006).
The main difference to our study concerns the handling of noise and mismatch. To minimize drift in the continuous attractor dynamics (Massoud and Horiuchi 2011), suppress finite-size noise with a synchronous and regular firing regime, while authors of Neftci et al. (2010) propose an initial precise calibration phase to reduce the mismatch that greatly affects the performance of their system. In contrast, we take advantage of both mismatch and finite-size noise to create a stochastic dynamics. As we have shown, the time-scale of this dynamics can be finely controlled by setting the balance between deterministic forces (energy landscape) and stochastic factors (finite-size noise).
To our knowledge, there have been no further demonstrations of self-sustained activity and working memory with neuromorphic VLSI hardware. Other neuromorphic applications concern biomimetic sensors such as “silicon cochleas” (Chan et al., 2007; Hamilton et al., 2008; Wen and Boahen, 2009) or “silicon retinas” (Boahen, 2005; Zaghloul and Boahen, 2006; Lichtsteiner et al., 2008; Kim et al., 2009; Liu and Delbruck, 2010), implementations of linear filter banks (Serrano-Gotarredona et al., 2006), receptive field formation (Choi et al., 2005; Bamford et al., 2010), echo-localization (Shi and Horiuchi, 2007; Chan et al., 2010), or selective attention (Indiveri, 2008; Serrano-Gotarredona et al., 2009).
Scaling up
As mentioned, our wider objectives include spiking neural networks that operate in real-time and that can be interfaced with living neural tissues. At present, it is not evident which technological path will lead to the network sizes and architectures that will eventually be required for interesting computational capabilities. However, neuromorphic VLSI is a plausible candidate technology that offers considerable scope for further improvement in terms of circuits, layout, autonomy, and silicon area. Multi-chip architectures with a few thousand spiking neurons and plastic synapses may come within reach in the near future (Federici, 2011). Such networks could accommodate multiple attractor representations and complex energy landscapes. We note here in passing that moving to larger networks would imply softer constraints on the choice of the synaptic connectivity (see Methods), thereby allowing more biologically plausible firing rates for the higher meta-stable states.
Several consortia are building special-purpose platforms that in principle could able to host large, attractor-based networks. These include the neuromorphic Neurogrid (Boahen, 2007) system, which aims to simulate up to one million neurons in real-time, the BrainScaleS project (Meier, 2011), which relies on wafer scale technology and promises 160,000 neurons with 40 million plastic synapses operating several thousand times faster than natural networks. In addition, the SpiNNaker project (Furber and Brown, 2009) proposes a fully digital, ARM-based simulation of approximately 20,000 Izhikevich neurons and spike-time-dependent synapses and the EU SCANDLE project, which uses a single, off-the-shelf FPGA to accommodate one million neurons (Cassidy et al., 2011). Finally, a fully digital VLSI chip has recently been presented by the DARPA-funded SyNAPSE project. Designed with 45 nm technology, it comprises 256 neurons and 65,000 plastic synapses (Merolla et al., 2011; Seo et al., 2011).
Of course, a fully digital implementation would quietly abandon the original vision of a “synthesis of form and function” in neuromorphic devices (Mahowald, 1992). Nevertheless, in view of the rapid progress in digital tools and fabrication processes, this may well be the most appropriate route for most applications. However, for applications requiring an implantable device operating in real-time, a mixed-signal approach founded on analog CMOS circuits seems likely to remain a viable alternative.
Conclusion
We demonstrate, with a network of leaky integrate-and-fire neurons realized in neuromorphic VLSI technology, that two distinct meta-stable states of asynchronous activity constitute attractors of the collective dynamics. We describe how the dynamics of these meta-stable states – an unselective state of low activity and a selective state of high activity – can be shaped to render transitions either quasi-deterministic or stochastic, and how the characteristic time-scale of such transitions can be tuned far beyond the time-scale of single-neuron dynamics. This constitutes an important step toward the flexible and robust classification of natural stimuli with neuromorphic systems.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank G. Indiveri and D. Badoni for their support in designing the chip, S. Bamford for helping in writing the software, and E. Petetti for his technical assistance. This work was supported by the EU-FP5 project ALAVLSI (IST2001-38099), EU-FP7 project Coronet (ICT2009-269459), and the BMBF Bernstein Network for Computational Neuroscience. In addition, P. Camilleri was supported by the State of Saxony-Anhalt, Germany.
References
Amit, D. J. (1995). The hebbian paradigm reintegrated, local reverberations as internal representation. Behav. Brain Sci. 18, 617–657.
Amit, D. J., and Brunel, N. (1997). Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb. Cortex 7, 237–252.
Amit, D. J., and Mongillo, G. (2003). Spike-driven synaptic dyanamics generating working memory states. Neural. Comput. 15, 565–596.
Bamford, S. A., Murray, D. A., and Willshaw, D. J. (2010). Large developing receptive fields using a distributed and locally reprogrammable address-event receiver. IEEE Trans. Neural Netw. 21, 286–304.
Boahen, K. A. (2007). Neurogrid Project. Available at: http://www.stanford.edu/group/brainsinsilicon/goals.html
Boahen, K. A. (2000). Point-to-point connectivity between neuromorphic chips using address-events. IEEE Trans. Circuits Syst. II 47, 416–434.
Brader, J. M., Senn, W., and Fusi, S. (2007). Learning real-world stimuli in a neural network with spike-driven synaptic dynamics. Neural. Comput. 19, 2881–2912.
Braun, J., and Mattia, M. (2010). Attractors end noise: twin drivers of decisions and multistability. Neuroimage 52, 740–751.
Brunel, N., and Hakim, V. (1999). Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural. Comput. 11, 1621–1671.
Brunel, N., and Sergi, S. (1998). Firing frequency of integrate-and-fire neurons with the finite synaptic time constants. J. Theor. Biol. 195, 87–95.
Camilleri, P., Giulioni, M., Mattia, M., Braun, J., and Del Giudice, P. (2010). “Self-sustained activity in attractor networks using neuromorphic VLSI,” in Neural Networks (IJCNN), The 2010 International Joint Conference, Barcelona, 1–6.
Cassidy, A., Andreou, A. G., and Georgiou, J. (2011). “Design of a one million neuron single FPGA neuromorphic system for real-time multimodal scene analysis,” in Information Sciences and Systems Conference (CISS), Baltimore, 1–6.
Chan, V., Jin, C. T., and van Schaik, A. (2010). Adaptive sound localisation with a silicon cochlea pair. Front. Neurosci. 4:196.
Chan, V., Liu, S. C., and van Schaik, A. (2007). AER EAR: a matched silicon cochlea pair with address event representation interface. IEEE Trans. Circuits Syst. I 54, 48–59.
Chicca, E., Dante, V., Whatley, A. M., Lichtsteiner, P., Delbruck, T., Indiveri, G., Del Giudice, P., and Douglas, R. J. (2007). Multi-chip pulse based neuromorphic systems: a general communication infrastructure and a specific application example. IEEE Trans. Circuits Syst. I 54, 981–993.
Choi, T. Y. W., Merolla, P. A., Arthur, J. V., Boahen, K. A., and Shi, B. E. (2005). Neuromorphic implementation of orientation hypercolumns. IEEE Trans. Circuits Syst. I 56, 1049–1060.
Chow, S. S., Romo, R., and Brody, C. D. (2009). Context-dependent modulation of functional connectivity: secondary somatosensory cortex to prefrontal cortex connections in two-stimulus-interval discrimination tasks. J. Neurosci. 29, 7238–7245.
Corradi, F. (2011). Dinamica ad attrattori in una rete di neuroni spiking su chip VLSI neuromorfi (unpublished). Master’s thesis, University of Rome ‘Sapienza’, Rome.
D’Andreagiovanni, M., Dante, V., Del Giudice, P., Mattia, M., and Salina, G. (2001). “Emergent asynchronous, irregular firing in a deterministic analog VLSI recurrent network,” in Proceedings of the World Congress on Neuroinformatics, ed. F. Rattey (Vienna: AGESIM/ASIM Verlag), 478–486.
Dante, V., Del Giudice, P., and Whatley, A. M. (2005). The Neuromorphic Engineer Newsletter. Available at: http://neural.iss.infn.it/Papers/Pages_5-6_from_NME3.pdf
Deco, G., and Rolls, T. S. (2005). Sequential memory: a putative neural and synaptic dynamical mechanism. J. Cogn. Neurosci. 17, 294–307.
Del Giudice, P., Fusi, S., and Mattia, M. (2003). Modeling the formation of working memory with networks of integrate-and-fire neurons connected by plastic synapses. J. Physiol. Paris 97, 659–681.
Destexhe, A., and Contreras, D. (2006). Neuronal computations with stochastic network states. Science 314, 85–90.
Durstewitz, D., and Deco, G. (2008). Computational significance of transient dynamics in cortical networks. Eur. J. Neurosci. 27, 217–227.
Federici, L. (2011). Dinamica stocastica di decisione in una rete di neuroni distribuita su chip VLSI (unpublished). Master’s thesis, University of Rome ‘Sapienza’, Rome.
Fox, M. D., and Raichle, M. E. (2007). Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 8, 700–711.
Furber, S., and Brown, A. (2009). “Biologically-inspired massively-parallel architectures – computing beyond a million processors,” in Proceedings of ASCD International Conference on Application of Concurrency to System Design, Augsburg, 3–12.
Furman, M., and Wang, X.-J. (2008). Similarity effect and optimal control of multiple-choice decision making. Neuron 60, 1153–1168.
Fusi, S., Annunziato, M., Badoni, D., Salamon, A., and Amit, D. J. (2000). Spike-driven synaptic plasticity: theory, simulation, VLSI implementation. Neural. Comput. 12, 2227.
Fusi, S., Asaad, W. F., Miller, E. K., and Wang, X.-J. (2007). A neural circuit model of flexible sensorimotor mapping: learning and forgetting on multiple timescales. Neuron 54, 319–333.
Fusi, S., and Mattia, M. (1999). Collective behavior of networks with linear(VLSI) integrate-and-fire neurons. Neural. Comput. 11, 633.
Gigante, G., Mattia, M., Braun, J., and Del Giudice, P. (2009). Bistable perception modeled as competing stochastic integrations at two levels. PLoS Comput. Biol. 5, e1000430.
Giulioni, M. (2008). Networks of Spiking Neurons and Plastic Synapses: Implementation and Control. St. Julian’s, Malta. Available at: http://neural.iss.infn.it/Papers/PhD_thesis.pdf
Giulioni, M., Camilleri, P., Dante, V., Badoni, D., Indiveri, G., Braun, J., and Del Giudice, P. (2008). “A VLSI network of spiking neurons with plastic fully configurable stop-learning synapses,” in Proceedings of IEEE International Conference on Electronics Circuits and Systems, 678–681.
Grinvald, A., Arieli, A., Tsodyks, M., and Kenet, T. (2003). Neuronal assemblies: single cortical neurons are obedient members of a huge orchestra. Biopolymers 68, 422–436.
Hamilton, T. J., Jin, C., van Schaik, A., and Tapson, J. (2008). An active 2-d silicon cochlea. IEEE Trans. Biomed. Circuits Syst. 2, 30–43.
Hasselmo, M. E., and McClelland, J. L. (1999). Neural models of memory. Curr. Opin. Neurobiol. 9, 184.
Holcman, D., and Tsodyks, M. (2006). The emergence of up and down states in cortical networks. PLoS Comput. Biol. 2, e23.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558.
Indiveri, G. (2008). Neuromorphic VLSI models of selective attention: from single chip vision sensors to multi-chip systems. Sensors 8, 5352–5375.
Indiveri, G., Chicca, E., and Douglas, R. (2006). A VLSI array of low-power spiking neurons and bistable synapses with spike-timing dependent plasticity. IEEE Trans. Neural Netw. 17, 211–221.
Kim, D., Fu, Z. M., and Culurciello, E. (2009). A 1-mw CMOS temporal-difference AER sensor for wireless sensor networks. IEEE Trans. Electron Devices 56, 2586–2593.
Laing, C. R., and Chow, C. C. (2002). A spiking neuron model for binocular rivalry. J. Comput. Neurosci. 12, 39–53.
Lichtsteiner, P., Posch, C., and Delbruck, T. (2008). A 128×128 120 dB 15 μs latency asynchronous temporal contrast vision sensor. IEEE J. Solid State Circuits 43, 566–576.
Lukashin, A. V., Amirikian, B. R., Mozhaev, V. L., Wilcox, G. L., and Georgopoulos, A. P. (1996). Modeling motor cortical operations by an attractor network of stochastic neurons. Biol. Cybern. 74, 255–261.
Machens, C. K., Romo, R., and Brody, C. D. (2005). Flexible control of mutual inhibition: a neural model of two-interval discrimination supporting methods. Science 307, 1121–1124.
Mahowald, M. (1992). VLSI Analogs of Neuronal Visual Processing: A Synthesis of Form and Function. Ph.D. thesis, California Institute of Technology, Pasadena, CA.
Marti, D., Deco, G., Mattia, M., Gigante, G., and Del Giudice, P. (2008). A fluctuation-driven mechanism for slow decision processes in reverberant networks. PLoS ONE 3, e2534.
Mascaro, M., and Amit, D. J. (1999). Effective neural response function for collective population states. Network 10, 251–373.
Massoud, T., and Horiuchi, T. (2011). A neuromorphic VLSI head direction cell system. IEEE Trans. Circuits Syst. 58, 150–163.
Mattia, M., and Del Giudice, P. (2002). Population dynamics of interacting spiking neurons. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 66, 051917.
Mattia, M., and Del Giudice, P. (2004). Finite-size dynamics of inhibitory and excitatory interacting spiking neurons. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 70, 052903.
Mattia, M., Ferraina, S., and Del Giudice, P. (2010). Dissociated multi-unit activity and local field potentials: a theory inspired analysis of a motor decision task. Neuroimage 52, 812–823.
Meier, K. (2011). BrainScaleS Project. Available at: http://brainscales.kip.uni-heidelberg.de/public/index.html
Merolla, P., Arthur, J., Akopyan, F., Imam, N., Manohar, R., and Modha, D. S. (2011). “A digital neurosynaptic core using embedded crossbar memory with 45pj per spike in 45nm,” in IEEE Custom Integrated Circuits Conference, IEEE, San Jose.
Mongillo, G., Amit, D. J., and Brunel, N. (2003). Retrospective and prospective persistent activity induced by hebbian learning in a recurrent cortical network. Eur. J. Neurosci. 18, 2011–2024.
Neftci, E., Chicca, E., Indiveri, G., Cook, M., and Douglas, R. J. (2010). “State-dependent sensory processing in networks of VLSI spiking neurons,” in International Symposium on Circuits and Systems, ISCAS 2010 (IEEE), Paris, 2789–2792.
Neftci, E., Chicca, E., Indiveri, G., and Douglas, R. (2011). A systematic methods for configuring VLSI networks of spiking neurons. Neural. Comput. 23, 2457–2497.
Renart, A., Brunel, N., and Wang, X.-J. (2004). “Mean-field theory of irregularly spiking neuronal populations and working memory in recurrent cortical networks,” Computational Neuroscience A Comprehensive Approach, ed J. Feng (Boca Raton: Chapman et Hall/Crc), 431–490.
Ringach, D. L. (2009). Spontaneous and driven cortical activity: implications for computation. Curr. Opin. Neurobiol. 19, 439–444.
Seo, J., Brezzo, B., Liu, Y., Parker, B. D., Esser, S. K., Montoye, R. K., Rajendran, B., Tierno, J. A., Chang, L., Modha, D. S., and Friedman, D. J. (2011). “A 45nm CMOS neuromorphic chip with a scalable architecture for learning in networks of spiking neurons,” in IEEE Custom Integrated Circuits Conference, San Jose.
Serrano-Gotarredona, R., Oster, M., Lichtsteiner, P., Linares-Barranco, A., Paz-Vicente, R., and Gomez-Rodriguez, F. (2009). Caviar: a 45k neuron, 5m synapse, 12g connects/s AER hardware sensory processing learning actuating system for high-speed visual object recognition and tracking. Trans. Neural Netw. 20, 1417–1438.
Serrano-Gotarredona, R., Serrano-Gotarredona, T., Acosta-Jimenez, A., and Linares-Barranco, B. (2006). A neuromorphic cortical-layer microchip for spike- based event processing vision systems. IEEE Trans. Circuits Syst. I 53, 2548–2566.
Shi, R. Z., and Horiuchi, T. K. (2007). A neuromorphic VLSI model of bat interaural level difference processing for azimuthal echolocation. IEEE Trans. Circuits Syst. I 54, 74–88.
Shu, Y., Hasenstaub, A., and McCormick, D. A. (2003). Turning on and off recurrent balanced cortical activity. Nature 423, 288–293.
Skarda, C. A., and Freeman, W. J. (1987). How brains make chaos in order to make sense of the world. Behav. Brain Sci. 10, 161–195.
Spiridon, M., and Gerstner, W. (1999). Noise spectrum and signal transmission through a population of spiking neurons. Network 10, 257–272.
Trappenberg, T. (2005). “Continuous attractor neural networks,” in Recent Developments in Biologically Inspired Computing, eds L. N. de Castro, and F. J. Von Zuben (Idea Group Publishing), Oxford, 398–425.
van Vreeswijk, C. A., and Sompolinsky, H. (1996). Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726.
Vasilaki, E., Fusi, S., Wang, X.-J., and Senn, W. (2009). Learning flexible sensori-motor mappings in a complex network. Biol. Cybern. 100, 147–158.
Wang, X.-J. (2002). Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36, 955–968.
Wen, B., and Boahen, K. (2009). A silicon cochlea with active coupling. IEEE Trans. Biomed. Circuits Syst. 3, 444–455.
Wong, K., Alexander, C. H., Shadlen, M. N., and Wang, X.-J. (2007). Neural circuit dynamics underlying accumulation of time-varying evidence during perceptual decision making. Front. Comput. Neurosci. 1:6.
Zaghloul, K. A., and Boahen, K. (2006). A silicon retina that reproduces signals in the optic nerve. J. Neural Eng. 3, 257–267.
Keywords: attractor dynamics, neuromorphic chips, working memory, stochastic dynamics, spiking neurons
Citation: Giulioni M, Camilleri P, Mattia M, Dante V, Braun J and Del Giudice P (2012) Robust working memory in an asynchronously spiking neural network realized with neuromorphic VLSI. Front. Neurosci. 5:149. doi: 10.3389/fnins.2011.00149
Received: 30 August 2011; Paper pending published: 16 October 2011;
Accepted: 29 December 2011; Published online: 02 February 2012.
Edited by:
Julius Georgiou, University of Cyprus, CyprusReviewed by:
Saber Moradi, ETH Zurich, SwitzerlandHoracio Rostro Gonzalez, University of Cyprus, Cyprus
Sridharan Devarajan, Stanford University, USA
Andrew Cassidy, International Business Machines, USA
Copyright: © 2012 Giulioni, Camilleri, Mattia, Dante, Braun and Giudice. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Paolo Del Giudice, Department of Technologies and Health, Istituto Superiore di Sanità, V.le Regina Elena 299, 00161 Rome, Italy. e-mail:cGFvbG8uZGVsZ2l1ZGljZUBpc3MuaW5mbi5pdA==
† Massimiliano Giulioni and Patrick Camilleri have contributed equally to this work.

 Patrick Camilleri2†
Patrick Camilleri2†
