- Institute for Infocomm Research, Agency for Science, Technology and Research, Singapore
Detecting motor imagery activities versus non-control in brain signals is the basis of self-paced brain-computer interfaces (BCIs), but also poses a considerable challenge to signal processing due to the complex and non-stationary characteristics of motor imagery as well as non-control. This paper presents a self-paced BCI based on a robust learning mechanism that extracts and selects spatio-spectral features for differentiating multiple EEG classes. It also employs a non-linear regression and post-processing technique for predicting the time-series of class labels from the spatio-spectral features. The method was validated in the BCI Competition IV on Dataset I where it produced the lowest prediction error of class labels continuously. This report also presents and discusses analysis of the method using the competition data set.
1. Introduction
Self-paced brain-computer interfaces (BCIs) have received increasing attention in recent years in the BCI community (Mason and Birch, 2000; Blankertz et al., 2002; Millan and Mourino, 2003; Scherer et al., 2008; Zhang et al., 2008). Conventionally, BCIs often require the users to follow a specific computer-generated cue before performing a specific mental control task. By contrast, self-paced BCIs allow the users to perform the control at will at anytime, by detecting specific brain signals associated with the mental control at each and every time point (Blankertz et al., 2002, 2007, 2008a). Providing the user with continuous control is also important for efficient control and user-training applications: first, it means that the user can perceive the system’s response in a continuous and real-time manner so as to plan the mental task to activate desired BCI actions; second, it enables real-time feedback training in which the users (ALS patients; Kübler et al., 2005), for example) can learn to regulate brain waves so as to improve the BCI performance.
Various EEG modalities have been demonstrated for self-paced BCIs, such as P300 (Zhang et al., 2008), motor imagery (Townsend et al., 2004), or finger movement related signals (Mason and Birch, 2000). In this work we focus on motor imagery (MI) which is the mental rehearsal of a motor act without any real motor output. It provides an important means for the BCIs that directly compensate lost motor functions for physically disabled (Pfurtscheller et al., 1997). It has also been shown that naïve subjects can operate a MI-BCI (Blankertz et al., 2006).
Numerous signal processing and pattern recognition techniques have been developed for classification of two or multiple MI classes (e.g., imaginary movements of left hand, right hand, tongue, or foot). For example, the common spatial pattern method (CSP; Pfurtscheller et al., 1997) and its various extensions (Lemm et al., 2005; Blankertz et al., 2008b; Wu et al., 2008) are widely used for extracting discriminative spatial (or joint spatio-spectral) patterns that contrast the power features of spatial patterns in different MI classes. For tackling multi-class problems, an information theoretic feature extraction method (Grosse-Wentrup and Buss, 2008) and other extensions of CSP (Dornhege et al., 2003, 2004) have been proposed. And various classifiers have also been studied for MI classification (Müller et al., 2003).
In self-paced MI-BCIs, the system not only needs to differentiate between specific MI activities, but also it has to detect them against a not-so-well-controlled class called non-control which is the aggregate of all user states other than the MI activities. For example in Millan and Mourino (2003), a local neural classifier was used to reject non MI signals. In Townsend et al. (2004), CSP features were combined with a linear discriminant analysis method to produce a scalar feature, which determined the user-state (e.g., left hand MI or NC) via thresholds. Special processing of the output incorporating a dwell and refractory period was also studied. More recently, it was reported in Scherer et al. (2008) that able-bodied subjects were able to navigate through a virtual environment using a self-paced MI-BCI with three bi-polar EEG channels only. It worked by combining two classifiers: one for discrimination between MI tasks and the others for detecting specific motor activities in the brain. It was also reported that the second classifier was sensitive to the non-stationarity of EEG, and this may indicate how challenging it is to differentiate MMI EEG against NC.
In this paper we present and study a MI detection method that won the first place in the BCI Competition IV, Dataset I. In particular, we develop a robust machine learning technique for spatio-spectral feature extraction and selection to differentiate multi-class MI and NC. We also employ a non-linear regression machine to predict the class labels at each time from the EEG features. And we propose a non-linear regression method to post-process the time-series of predicted class labels so as to improve prediction accuracy. We conduct an offline analysis using 5-fold cross-validation on the calibration data. The method yields a mean-square-error (MSE) for class label prediction in the range from 0.20 to 0.29 for the subjects. The method then produces an average MSE of 0.38 on the evaluation data.
The rest of the paper is organized as follows. Section 2 briefly describes the EEG data. Section 3 overviews the system and presents detailed descriptions of the essential components. We study the system using the EEG data in Section 4, and present the conclusion in Section 5.
2. Materials and Methods
2.1. The EEG Data
The proposed method was evaluated using the BCI Competition IV Dataset I (Blankertz et al., 2007), which was recorded from 4 human subjects performing motor imagery tasks. A few computer-generated artificial data were also present in the dataset, though they are not considered both in this study and in the competition. The EEG recordings included a total of fifth-nine channels that mostly were distributed over or around sensorimotor areas. Each subject contributed in two sessions: a calibration session and an evaluation session (Scherer et al., 2008).
In the calibration session, each subject chose to perform two classes of motor imagery tasks from left hand, right hand, or foot imaginary movements. At the beginning of each task, a visual cue was displayed in a computer screen to the subject who then started to perform a motor imagery task accordingly for 4 s. Each subject performed a total of 200 motor imagery tasks that were balanced between the two classes. The motor imagery tasks were interleaved with breaks of 4-s long. The evaluation session followed a different protocol. The subjects followed the soft voice commands from an instructor to perform motor imagery tasks of varying time length between 1.5 and 8 s. Consecutive tasks were also interleaved with a varying time length interval also between 1.5 and 8 s.
The four human subjects are referred to as “a,” “b,” “f,” and “g.” For the sake of computational efficiency, we use the 100-Hz version of the data in this work.
2.2. The Self-Paced BCI
2.2.1. Overview
As illustrated in Figure 1, the system consists of three processing components, namely, m-class feature extraction based on the filter-bank common spatial pattern (FBCSP) technique (Ang et al., 2008), information theoretic feature selection and non-linear regression for sample-based prediction, and post-processing. The input is a stream of multi-channel EEG waveforms, while the output is a sequence of scalar values in the range of [−1 1]. And the output is expected to approximate the ordinal class labels at each time point: −1 for the first motor imagery class (MI-1), 0 for NC, and 1 for the second motor imagery class (MI-2). Please note that the accuracy of the system is measured by the mean-square-error between the outputs and the true class labels.
Figure 1. Online processing system. It consists of three processing steps to map continuous EEG data into a final output in the range of [−1 1]. Here FBCSP stands for filter-bank common spatial pattern (see Section 2), and TDNN for time-delay neural network (see Section 4).
The first two processing components work on individual windowed EEG data that we refer to as EEG epochs. Basically, the epochs are created by a shifting short-time window of a specific length (we will discuss the window length later) running through the data stream. The ending point of the window is the current sample whose class label is to be predicted. The third component, i.e., post-processing, looks into not only the current short-time window, but also the history of EEG data so as to improve the prediction. The following subsections will describe the three components successively.
2.2.2. m-class FBCSP for feature selection
The primary phenomenon of MI EEG is event-related desynchronization (ERD) or event-related synchronization(ERS; Pfurtscheller et al., 1997; Müller-Gerking et al., 1999), the attenuation, or increase of the rhythmic activity over the sensorimotor cortex generally in the μ (8–14 Hz) and β (14–30 Hz) rhythms. The ERD/ERS can be induced by both imagined movements in healthy people or intended movements in paralyzed patients (Dornhege et al., 2004; Kübler et al., 2005; Grosse-Wentrup and Buss, 2008).It is noteworthy that another neurological phenomenon called Bereitschafts potential is also associated with MI EEG but non-oscillatory (Blankertz et al., 2003). In this works we consider ERD/ERS features only.
Feature extraction of ERD/ERS is, however, a challenging task due to its poor, low signal to noise ratio. Therefore, spatial filtering in conjunction with frequency selection (via processing in either temporal domain or spectral domain) in multi-channel EEG has been highly successful for increasing the signal to noise ratio (Ramoser et al., 2000; Lemm et al., 2005; Dornhege et al., 2006; Blankertz et al., 2008b; Zhang et al., 2011). This technique of m-class FBCSP is developed from Ang et al. (2008), but account for the NC class.
Suppose there is an EEG epoch given in form of a matrix
where nc is the number of channels, and nt is the number of time samples.
The precise frequency band which is responsive to MI activities can vary from one subject to another. From the viewpoint of learning, multiple possible frequency bands have to be examined. Therefore, we process the EEG epoch using an array of filter-banks, each of them is a particular band-pass filter and all together they cover a continuous frequency range, e.g., from 4 to 32 Hz. In this work, a total of 8 zero-phase filters based on Chebyshev Type II filters are built with central frequencies from 8 to 32 Hz at a constant interval in the logarithm domain. Consequently, the center frequencies are respectively 8, 9.75, 11.89, 14.49, 17.67, 21.53, 26.25, and 32 Hz. The filters have a uniform Q factor (bandwidth-to-center frequency) of 0.33 as well as an order of 4.
Let us use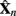 
to denote a processed EEG epoch by an arbitrary filter-bank, say the n-th one. A set of spatial filters then apply to the matrix to extract the spatio-spectral characteristics of MI activities in that frequency band. Each spatial filter transforms 
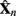into a time-series of the same length by
where nm is the index of the spatial filter, t:1 ≤ t ≤ nt is the index of time sample, and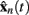 
is the column vector of matrix X n at time t.
The principle of the spatial filtering is to maximize the contrast between two classes in y in terms of Rayleigh coefficient
where R1 and R2 are the covariance matrices of all epochs of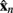 
in the two classes respectively.
The maximization of the Rayleigh coefficient is achieved by solving the following generalized eigenvalue problem (Ramoser et al., 2000)
The system selects the maximal 2 and the minimal 2 eigenvalues and the corresponding eigenvectors for w.
It should be noted that the feature used for BCI are the short-time power of the filtered signal y
where l defines the length of the short-time window.
Different from the conventional 2-class BCIs, the present system has to account for MI classes in addition to NC. And it takes a pair-wise approach. The first pair compares MI-1 vs. MI-2. The second and the third pairs compare MI-1 vs NC and MI-2 vs NC respectively. The construction of the spatial filters for MI-1 vs. MI-2 is performed with the original CSP method, while the spatial filters for the other two pairs are obtained in a different way as below.
To contrast MI-1 vs NC or MI-2 vs NC, we need to account for large within-class variations in NC, where the brain activity is not as well controlled as in motor imagery. Therefore, we consider that NC epochs can be further categorized into sub-states or modes. And each sub-state may exhibit different spatio-spectral characteristics, and form a particular cluster in EEG observations. Therefore, we employ a clustering approach to identify the sub-states of NC EEG epochs. First, we reduce the dimensionality of EEG by principal component analysis (PCA), and we use the energy vector u from the top few PCA components to represent each NC epoch: (the filter-bank index n is dropped for simplicity)
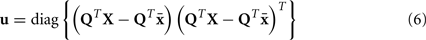
where 
denotes the mean value vector of x in an epoch, and Q is the matrix of top eigenvectors for the maximal eigenvalues. Then we cluster the feature vectors of u from all the training data using the standard k-means algorithm into nk clusters, by minimizing the total intra-cluster variance.
where k denotes the index of the k-th cluster of NC epochs, and Sk denotes the set of all feature vector indices belonging to the cluster and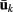 
is their mean feature vector. We will examine different sub-state number nk in the experiment later.
To contrast a motor imagery class, say MI-1, against NC, we have to compare each and every sub-state in NC against MI-1. Again, we use the same CSP method that now maximizes the Rayleigh coefficient between a NC sub-state and MI-1.
With all the CSP filters constructed for the three class-pairs in every filter-bank, we will run them and aggregate the outcomes to form a joint, raw feature vector for each input EEG epoch. It can be seen that the size of the raw feature vector is partially determined by the number of clusters for learning NC. Then we consider how to further select a robust feature vector from the raw feature vector and map it to the desired output in the next subsection.
2.2.3. Information theoretic feature selection and regression
We denote the raw feature vector variable by A, and the selected feature vector variable by Aη. And consider that generally the class label as a discrete random variable C with value from 1 to Nc. We will use aη and c to represent a particular selected feature vector and its class label.
For modeling the dependency between Aη and C, the mutual information is an important quantity that measures the mutual dependence of the two variables according to information theory (Papoulis, 1984). Mathematically, it is given by
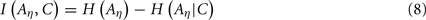
where H(Aη) denotes the entropy of the random feature vector, and H(Aη | C) is the conditional entropy
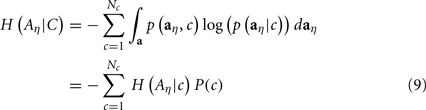
From the viewpoint of information theory, the optimum feature set is the one that carries the most mutual information about the class label. This is exactly the idea of the maximum mutual information (MMI) criterion, which has been established as the basis for discriminative learning procedures in various machine learning techniques. Therefore, our system seeks the optimal feature vector Aη which maximizes the mutual information.
The objective above involves joint probability density functions (PDFs) that need to be estimated from a given training data set. Please note that, to simplify the descriptions, we will omit the symbol η in the expressions unless otherwise specified.
Using kernel density estimation, the PDF of a is given by
where a i is a training sample of the feature vector, and φ is a smoothing kernel that takes a Gaussian form here.
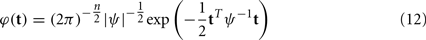
where ψ is the covariance matrix that is assumed diagonal and estimated from training data according to the normal optimal smoothing strategy (Bowman and Azzalini, 1997).
We can then adopt a method proposed in Viola and Wells (1997) to approximate the entropy H(A) with a given set of samples.
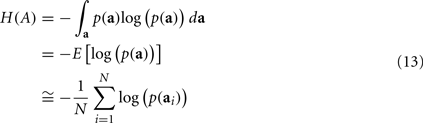
Combining the above equations, the entropy of the random vector A can be approximated by
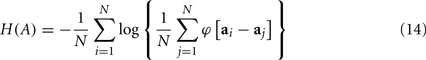
The within-class entropy H(A | c) can be similarly estimated with the training samples from the class c only.
With the above developments, we can compute the mutual information estimate for any subset of features. And we will select the subset which yields the largest mutual information estimate.
Now we consider the mapping from the features to the desired outputs of class labels as a regression problem. The features are linearly normalized to the range [−1 1] using their empirical upper and lower bounds. To account for possibly non-linearity in the mapping, we employ a generalized regression neural network with non-linear hidden neurons. Briefly, the network consists of three layers of neurons: the second (hidden) layer contains radial basis function neurons, while the third layer has linear neurons with normalized inputs (Wasserman, 1993). This mapping can be cast as a general regression neural network (GRNN). Here in this work we use the SD of all the training set features for the spread parameter that basically defines the kernel width for the radial basis functions.
2.2.4. Post-processing and optimization
The above procedure addresses the problem of predicting class labels from individual EEG segments. On the other hand, post-processing of the predicted label series allows us to explore information in the dynamics of brain activities and corresponding EEG observations. Particularly, we introduce a time-delay neural network (TDNN; Clouse et al., 1997). Here the network has three layers: the input layer acts as a 4-s buffer of epoch-based label predictions from training data; the output is the sequence of desired true label sequence in the same time frame; and the hidden layers consists of a few neurons with radial basis transfer functions. Again, this network can be cast as a GRNN.
There are two parameters to be optimized during system calibration, including the time interval for motor imagery segment extraction for training; the number of sub-states for NC segments clustering (hereafter nNC). It is worthwhile to note that the training data usually are still trial-based for calibration, and we may take advantage of the timing information to extract most effective time intervals related to motor imagery EEG. Particularly, the system will examine the following time intervals: four 2-s-long intervals starting at 0.5, 1, 1.5, and 2 s from the trial-start cue, and three 2.5-s-long intervals starting at 0.5, 1, 1.5 s from the cue. For the submission to competition, we used a 5-fold cross-validation to optimize the two parameters in a subject-dependent manner.
Since the true class labels are from the limited number set {−1, 0, 1}, the output of the system is finally cut to the range of [−1 1]. This, however, did not produce any significant effects in the performance measure in our tests below.
3. Results
First we would like to present the results of cross-validation before post-processing. For the sake of computational efficiency, the prediction of class label is performed every 0.1 s.
Figure 2 plots the mean-square-error (MSE) of regression with respect to the selection of time interval Titv for training the feature extractor (see Section 1). Note that for each subject and each time interval, the MSE presented in the graph is the lowest MSE with the optimal Titv. Interestingly, it can be seen that all of the lower MSEs were achieved by 2.5-s-long intervals instead of 2-s-long ones. Overall, the interval of 1.5–4.0 s gave rise to the smallest regression error. Nonetheless, it seems that the regression error is not very sensitive to the selection of time interval, as the variation of the error on each subject’s data is small across different time intervals.
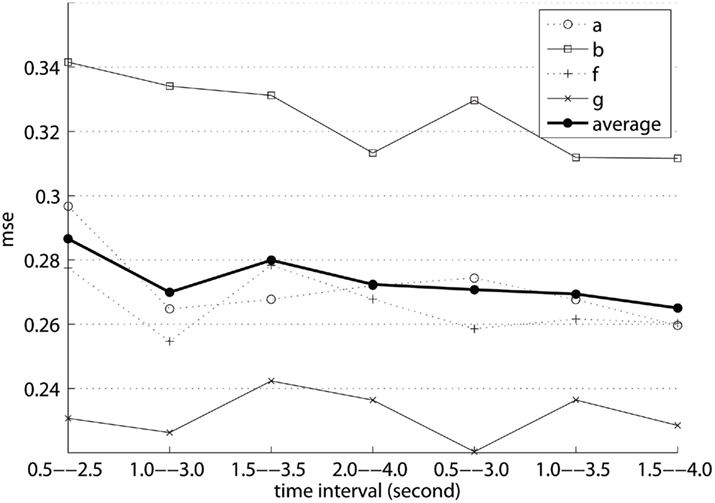
Figure 2. Mean-square-error of class label prediction with respect to the time interval of a motor imagery trial extracted for training data.
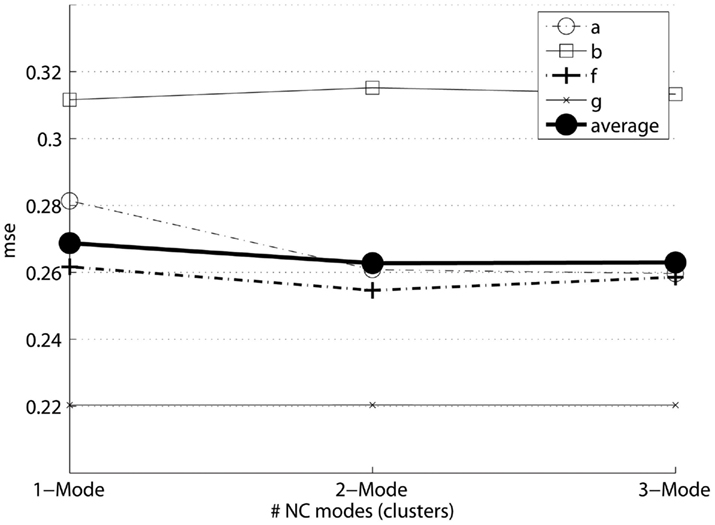
Figure 3 plots MSE with respect to nk: the number of NC sub-states (modes, or clusters) in calibration. Note that for each subject and each nk, the MSE presented in the graph comes from the time interval with the lowest MSE. And, there is a slightly decrease in the error on two subjects (“a” and “f”) by 2-mode NC learning.
Figure 3. MSE with respect to number of NC sub-states (modes) in learning.
Now let us assess the post-processing technique. With the best time interval and NC sub-state number obtained from the study above, the MSEs before and after the post-processing are compared in Table 1. It can be seen that on every subject, the technique effectively reduced MSE by 0.02 or 0.03, which is approximately 10% of the original MSE.
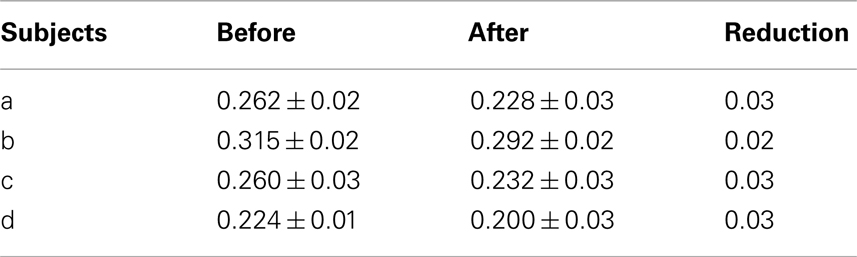
Table 1. MSE before and after post-processing. Mean and STD of MSE over 5-fold cross-validation are shown here for each subject.
Finally, we would like to give the evaluation results, which we submitted to the competition, on the independent data sets (i.e., the evaluation sets in the competition) in Table 2.
Table 2. MSE on the evaluation data sets.
4. Discussion
In summary, we have presented a computational method for motor imagery detection. It can extract and learn effective spatio-spectral features to discriminate between three EEG classes including non-control and 2 motor imagery classes. It is expected that the use of dwell and refractory periods (c.f. Townsend et al., 2004) may further improve the performance. Furthermore, comparing the performance on the calibration data and that on the evaluation data, it seems that the performance degrades significantly. And this is due to the effect of session-to-session transfer that often cause considerable changes in the EEG characteristics, especially in the competition data where the calibration and the evaluation sessions employed different protocols. Finally, since this method uses an autonomous learning framework such that it does not rely on ad hoc tuning, it can serve as a favorable baseline for future research in motor imagery detection.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank the organizers (BCI competition IV; http://www.bbci.de/competition/iv/) and the providers of the BCI Competition Dataset I (Blankertz et al., 2007).
References
Ang, K. K., Chin, Z. Y., Zhang, H., and Guan, C. (2008). “Filter bank common spatial pattern (fbcsp) in brain-computer interface,” in International Joint Conference on Neural Networks (IJCNN2008), Hong Kong, 2391–2398.
Blankertz, B., Curio, G., and Müller, K.-R. (2002). Classifying single trial EEG: towards brain-computer interfacing. Adv. Neural Inf. Process. Syst. 14, 157–164.
Blankertz, B., Dornhege, G., Krauledat, M., Müller, K.-R., and Curio, G. (2007). The non-invasive Berlin brain-computer interface: fast acquisition of effective performance in untrained subjects. Neuroimage 37, 539–550.
Blankertz, B., Dornhege, G., Krauledat, M., Müller, K.-R., Kunzmann, V., Losch, F., and Curio, G. (2006). The Berlin brain-computer interface: EEG-based communication without subject training. IEEE Trans. Neural Syst. Rehabil. Eng. 14, 147–152.
Blankertz, B., Dornhege, G., Schafer, C., Krepki, R., Kohlmorgen, J., Müller, K.-R., Kunzmann, V., Losch, F., and Curio, G. (2003). Boosting bit rates and error detection for the classification of fast-paced motor commands based on single-trial EEG analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 11, 127–131.
Blankertz, B., Losch, F., Krauledat, M., Dornhege, G., Curio, G., and Müller, K.-R. (2008a). The Berlin brain-computer interface: accurate performance from first-session in BCI-naïve subjects. IEEE Trans. Biomed. Eng. 55, 2452–2462.
Blankertz, B., Tomioka, R., Lemm, S., Kawanabe, M., and Müller, K.-R. (2008b). Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process. Mag. 25, 41–56.
Bowman, A. W., and Azzalini, A. (1997). Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations. New York: Oxford University Press.
Clouse, D. S., Giles, C. L., Horne, B. G., and Cottrell, G. W. (1997). Time-delay neural networks: representation and induction of finite-state machines. IEEE Trans. Neural Netw. 8, 1065–1070.
Dornhege, G., Blankertz, B., Curio, G., and Müller, K.-R. (2003). Increase information transfer rates in BCI by csp extension to multi-class. Adv. Neural Inf. Process. Syst. 16.
Dornhege, G., Blankertz, B., Curio, G., and Müller, K.-R. (2004). Boosting bit rates in noninvasive EEG single-trial classifications by feature combination and multiclass paradigms. IEEE Trans. Biomed. Eng. 51, 993–1002.
Dornhege, G., Blankertz, B., Krauledat, M., Losch, F., Curio, G., and Müller, K.-R. (2006). Combined optimization of spatial and temporal filters for improving brain-computer interfacing. IEEE Trans. Biomed. Eng. 53, 2274–2281.
Grosse-Wentrup, M., and Buss, M. (2008). Multiclass common spatial patterns and information theoretic feature extraction. IEEE Trans. Biomed. Eng. 55, 1991–2000.
Kübler, A., Nijboer, F., Mellinger, J., Vaughan, T. M., Pawelzik, H., Schalk, G., McFarland, D. J., Birbaumer, N., and Wolpaw, J. R. (2005). Patients with ALS can use sensorimotor rhythms to operate a brain-computer interface. Neurology 64, 1775–1777.
Lemm, S., Blankertz, B., Curio, G., and Müller, K.-R. (2005). Spatio-spectral filters for robust classification of single trial EEG. IEEE Trans. Biomed. Eng. 52, 1541–1548.
Mason, S. G., and Birch, G. E. (2000). A brain-controlled switch for asynchronous control applications. IEEE Trans. Rehabil. Eng. 47, 1297–1307.
Millan, J. D. R., and Mourino, J. (2003). Asynchronous bci and local neural classifiers: an overview of the adaptive brain interface project. IEEE Trans. Neural Syst. Rehabil. Eng. 11, 159–161.
Müller, K.-R., Anderson, C. W., and Birch, G. E. (2003). Linear and non-linear methods for brain-computer interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 11, 165–169.
Müller-Gerking, J., Pfurtscheller, G., and Flyvbjerg, H. (1999). Designing optimal spatial filtering of single trial EEG classification in a movement task. Clin. Neurophysiol. 110, 787–798.
Papoulis, A. (1984). Probability, Random Variables, and Stochastic Processes, 2nd Edn. New York: McGraw-Hill.
Pfurtscheller, G., Neuper, C., Flotzinger, D., and Pregenzer, M. (1997). EEG-based discrimnation between imagination of right and left hand movement. Clin. Neurophysiol. 103, 642–651.
Ramoser, H., Müller-Gerking, J., and Pfurtscheller, G. (2000). Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans. Rehabil. Eng. 8, 441–446.
Scherer, R., Lee, F., Schlögl, A., Leeb, R., Bischof, H., and Pfurtscheller, G. (2008). Toward self-paced brain-computer communication: navigation through virtual worlds. IEEE Trans. Biomed. Eng. 55, 675–682.
Townsend, G., Graimann, B., and Pfurtscheller, G. (2004). Continuous EEG classification during motor imagery – simulation of an asynchronous bci. IEEE Trans. Neural Syst. Rehabil. Eng. 12, 258–265.
Viola, P., and Wells, W. M. III. (1997). Alignment by maximization of mutual information. Int. J. Comput. Vis. 24, 2.
Wu, W., Gao, X., Hong, B., and Gao, S. (2008). Classifying single-trial EEG during motor imagery by iterative spatio-spectral patterns learning (isspl). IEEE Trans. Biomed. Eng. 55, 1733–1743.
Zhang, H., Chin, Z. Y., Ang, K. K., Guan, C., and Wang, C. (2011). Optimum spatio-spectral filtering network for brain-computer interface. IEEE Trans. Neural Netw. 22, 52–63.
Keywords: self-paced brain-computer interface, motor imagery
Citation: Zhang H, Guan C, Ang KK, Wang C and Chin ZY (2012) BCI competition IV – data set I: learning discriminative patterns for self-paced EEG-based motor imagery detection. Front. Neurosci. 6:7. doi: 10.3389/fnins.2012.00007
Received: 20 December 2011;
Paper pending published: 05 January 2012;
Accepted: 14 January 2012;
Published online: 06 February 2012.
Edited by:
Benjamin Blankertz, Berlin Institute of Technology, GermanyReviewed by:
Steven Lemm, Technische Universität Berlin, GermanyGuido Nolte, Fraunhofer FIRST, Germany
Copyright: © 2012 Zhang, Guan, Ang, Wang and Chin. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Haihong Zhang, Institute for Infocomm Research, Agency for Science, Technology and Research, 1 Fusionopolis Way, #21-01 Connexis (South Tower), Singapore 138632. e-mail: hhzhang@i2r.a-star.edu.sg