Dopaminergic control of the exploration-exploitation trade-off via the basal ganglia

We continuously face the dilemma of choosing between actions that gather new information or actions that exploit existing knowledge. This “exploration-exploitation” trade-off depends on the environment: stability favors exploiting knowledge to maximize gains; volatility favors exploring new options and discovering new outcomes. Here we set out to reconcile recent evidence for dopamine’s involvement in the exploration-exploitation trade-off with the existing evidence for basal ganglia control of action selection, by testing the hypothesis that tonic dopamine in the striatum, the basal ganglia’s input nucleus, sets the current exploration-exploitation trade-off. We first advance the idea of interpreting the basal ganglia output as a probability distribution function for action selection. Using computational models of the full basal ganglia circuit, we showed that, under this interpretation, the actions of dopamine within the striatum change the basal ganglia’s output to favor the level of exploration or exploitation encoded in the probability distribution. We also found that our models predict striatal dopamine controls the exploration-exploitation trade-off if we instead read-out the probability distribution from the target nuclei of the basal ganglia, where their inhibitory input shapes the cortical input to these nuclei. Finally, by integrating the basal ganglia within a reinforcement learning model, we showed how dopamine’s effect on the exploration-exploitation trade-off could be measurable in a forced two-choice task. These simulations also showed how tonic dopamine can appear to affect learning while only directly altering the trade-off. Thus, our models support the hypothesis that changes in tonic dopamine within the striatum can alter the exploration-exploitation trade-off by modulating the output of the basal ganglia.

1. Introduction

When deciding what to do next, we face the dilemma of choosing between actions with a well-known outcome or of choosing actions whose outcome is unsure, but potentially better. This trade-off between exploiting or exploring depends on the current state of the world. A stable world favors exploiting existing knowledge; a volatile world favors exploring new options and discovering new outcomes. Whatever sets the trade-off in the brain is thus likely to be driven by information about the stability of the environment. Moreover, that signal must affect the computation in brain circuits responsible for action selection. Here we set out to find if a plausible candidate neuromodulator for the trade-off signal, dopamine, could feasibly change behavior between exploration and exploitation through affecting its main target neural system, the basal ganglia.

Why should we consider the exploration-exploitation trade-off problem separately from the problem of learning how to choose actions? Formal models of reinforcement learning posit a conceptual separation between a system that learns the value of each action through reinforcement and a system that transforms those values into a probability distribution for action selection (Sutton and Barto, 1998). The underlying rationale for this separation is that choosing actions to optimally maximize reinforcement would require perfect knowledge of the value distribution; but, in reality, such a value distribution is constructed from finite data in a finite time from a non-stationary world, and is necessarily incomplete. Therefore, a separate action selection system allows on-the-fly tuning of how to best use the gathered value data, given the current state of the world. Figure 1 illustrates how this is quantified by a single parameter β that tunes between transforming into a “flat” probability distribution, thereby favoring exploration, and transforming into a peaked probability distribution, thereby favoring exploitation.

FIGURE 1

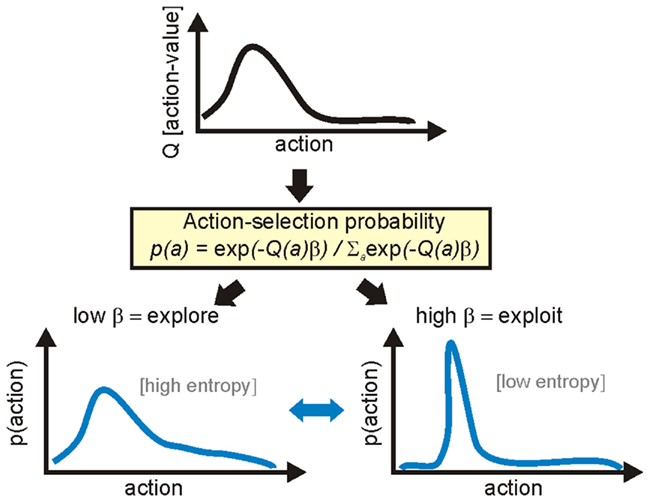
Figure 1. Formalization of the exploration-exploitation trade-off. In formal models of reinforcement learning there is a conceptual separation between learning the value of each action, and transforming those values into a probability distribution function (PDF) for action selection. Through ongoing experience, the agent learns the current value of each action (top). This value distribution is transformed into a PDF for action selection, illustrated here as a continuous transform using the classic softmax function. The inverse temperature parameter β tunes between broad and peaked transforms of the value distribution, respectively promoting exploration of action space or exploitation of current knowledge. Thus, the exploration-exploitation trade-off is set by the current value of β.

As this trade-off parameter must carry information about the state of the world and act globally through the action selection system, it is reasonable to suppose that neuromodulators carry this information in the brain (Doya, 2002; Krichmar, 2008). While evidence points to a role for noradrenaline in tuning between explorative and goal-directed attention (Usher et al., 1999; Doya, 2002; Cohen et al., 2007), there is a growing body of work pointing to dopamine as the carrier of this trade-off for action selection (Kakade and Dayan, 2002). Chronic changes in tonic dopamine levels across the prefrontal cortex and striatum affect the ability to exploit learnt knowledge separately from the ability to acquire that knowledge (Frank et al., 2009; Beeler et al., 2010). Separately, we have shown that a subset of midbrain dopamine neurons have outcome-driven phasic activity that predicts whether the subject exploits or explores in the immediate future (Humphries and Redgrave, 2010). Thus both changes in dopamine concentration and the firing of the dopamine neurons has been directly linked to encoding the exploration-exploitation trade-off.

Separately, from converging behavioral, electrophysiological, and clinical evidence, the fore- and mid-brain basal ganglia have been identified as the principal action selection system in the brain (see, e.g., Mink, 1996; Redgrave et al., 1999; Kimchi and Laubach, 2009; Humphries and Prescott, 2010), consisting of a repeated canonical circuit that instantiates a mechanism for selecting between competing inputs (Gurney et al., 2001a; Frank et al., 2004; Humphries et al., 2006; Leblois et al., 2006a; Girard et al., 2008). This has led to many attempts to map portions of the basal ganglia circuit to the formal action selection methods in reinforcement learning algorithms (for review see Joel et al., 2002; Khamassi et al., 2005).

Linking together dopamine and the basal ganglia is that the principal site of dopamine’s action is within the striatum, the main input structure of the basal ganglia. The striatum contains up to an order of magnitude greater density of both D1- and D2-type receptor families than any other brain structure (Dawson et al., 1986; Charuchinda et al., 1987; Diop et al., 1988; Richfield et al., 1989). As well as controlling synaptic plasticity (Shen et al., 2008), the activation of these dopamine receptors on the striatal projection neuron modulates its short-term excitability (Moyer et al., 2007; Surmeier et al., 2007; Humphries et al., 2009).

We therefore hypothesize that dopamine can alter the exploration-exploitation trade-off by modulating action selection via its effect on the basal ganglia circuit. Here we aim to test this hypothesis in computational models of the full basal ganglia circuit, by seeing whether or not the actions of dopamine within the striatum can cause a change in the level of exploration or exploitation in the ensuing action selection. If so, this would provide, first, a mechanistic explanation reconciling the existing evidence for dopamine’s control of the exploration-exploitation trade-off with the existing evidence for basal ganglia control of action selection, and, second, a mapping of this neural substrate to reinforcement learning algorithms.

To do so, we first advance a simple, yet new, interpretation of how the basal ganglia output encodes action selection. We suggest that it is plausible to interpret the basal ganglia’s vector of outputs as defining a probability distribution function for action selection, consistent with recent evidence for its encoding of saccade target selection (Basso and Wurtz, 2002; Kim and Basso, 2010). A corollary of this hypothesis is that it allows a straightforward quantification of how dopamine’s simulated effects in the striatum change this probability distribution, facilitating direct comparisons with the formal models of the exploration-exploitation trade-off in reinforcement learning algorithms (Figure 1).

2 Materials and Methods

2.1 The Basal Ganglia Model

The basal ganglia are a group of inter-connected subcortical nuclei, which receive massive convergent input from most regions of cortex, and output to targets in the thalamus and brainstem. We have previously shown how this combination of inputs, outputs, and internal circuitry implements a neural substrate for a selection mechanism (Gurney et al., 2001a,b, 2004; Humphries et al., 2006). Figures 2A,B illustrates the macro- and micro-architecture of the basal ganglia, highlighting three key ideas underlying the computational models: that the projections between the neural populations form a series of parallel loops – channels – running through the basal ganglia from input to output stages (Alexander and Crutcher, 1990); that the total activity from cortical sources converging at each channel of the striatum encodes the salience of the action represented by that channel (Samejima et al., 2005; Kimchi and Laubach, 2009); and that the basal ganglia encode action selection by a process of disinhibition – the reduction of the basal ganglia’s tonic inhibitory output to neurons in the target regions (Chevalier and Deniau, 1990).

FIGURE 2

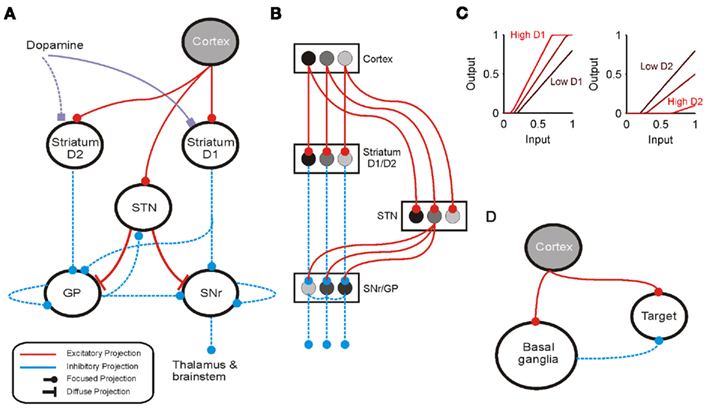
Figure 2. Architecture of the basal ganglia model. (A) The basal ganglia circuit. Cortical input reaches both the GABAergic striatum and the glutamatergic subthalamic nucleus (STN). The striatum is divided into two populations of projection neurons, respectively expressing the D1- or D2-type dopamine receptors. These populations send their principal projections to the substantia nigra pars reticulata (SNr) and the globus pallidus (GP); the GP also receives a collateral from a subset of the D1-SNr projections. Both receive input from the STN; the GP reciprocates that projection. Both send local projections that inhibit neighboring neurons. Constant inhibitory output from SNr reaches widespread targets in the thalamus and brainstem. (B) The main circuit can be decomposed into two copies of an off-center, on-surround network. Cortical inputs representing competing actions are organized into separate groups of co-active cortical neurons. These groups project to corresponding populations in striatum and STN. In the D1-SNr pathway, the balance of focused inhibition from striatum and diffuse excitation from STN results in the focused reduction of inhibitory output from SNr. In the D2-GP pathway, a similar overlap of projections to GP exists, but the feedback from GP to the STN acts as a self-regulating mechanism for the activity in STN, which ensures that overall basal ganglia activity remains within operational limits irrespective of the number of actions (Gurney et al., 2001b). Three parallel loops – channels – are shown in both pathways; gray-scale indicates example activity levels to illustrate the relative contributions of the nuclei. Note that, for clarity, full connectivity is only shown for the second channel. (C) Modulation of the striatal projection neuron input-output function by dopamine receptor activation: left, D1; right, D2. (D) Cortical inputs to the basal ganglia are copies of principal projections to thalamus, superior colliculus, and brainstem, where they reconverge with basal ganglia output.

We used the population-level implementation of this model from Gurney et al. (2004). The average activity of all neurons comprising a channel’s population changed according to

where τ is a time constant and I is summed, weighted input. We used τ = 40 ms. The normalized firing rate y of the unit was given by a piecewise linear output function

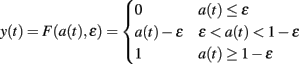
with threshold ∈.

The following describes net input I_i and output y_i for the ith channel of each structure, with n channels in total. Net input was computed from the outputs of the other structures, except cortical input c_i to channel i of striatum and STN. The striatum was divided into two populations, one of projection neurons with the D1-type dopamine receptor, and one of projection neurons with the D2-type dopamine receptor. Many converging lines of evidence from electrophysiological, mRNA transcription, and lesion studies support this functional split into D1- and D2-dominant projection neurons and, further, that the D1-dominant neurons project to SNr, and the D2-dominant neurons project to GP (Gerfen et al., 1990; Surmeier et al., 2007; Matamales et al., 2009; Humphries and Prescott, 2010).

The model simulated opposite effects of activating D1 and D2 receptors on striatal projection neuron activity: D1 activation increased the efficacy of their input in driving activity; D2 activation decreased the efficacy of their input (Moyer et al., 2007; Humphries et al., 2009). Let the relative activation of D1 and D2 receptors by tonic dopamine be λ₁, λ₂ ∈ [0, 1]: then the increase in efficacy due to D1 receptor activation was given by (1 + λ₁); the decrease in efficacy due to D2 receptor activation was given by (1 − λ₂). Though simple, these models made the population respectively more and less sensitive to input with increasing dopamine (Figure 2C), consistent with the overall effect of D1 and D2 activation on striatal projection neuron excitability shown by complete models of dopamine’s effects on ion channels and synaptic inputs (Moyer et al., 2007; Humphries et al., 2009). Typically we considered the case where activation of D1 and D2 receptors changes together, such that λ = λ₁ = λ₂; for the results in Figure 4 we studied the effects of separately changing D1 and D2 activation.

The full model was thus given by Gurney et al. (2004):

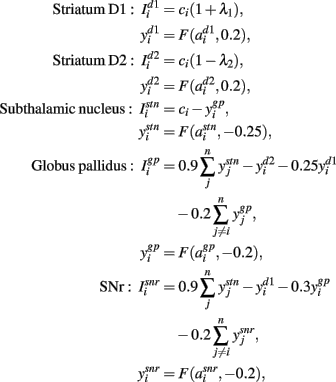
The negative thresholds ensured that STN, GP, and SNr have spontaneous tonic output (Humphries et al., 2006).

Unless otherwise specified, we used the following simulation design. We used n = 10 channels to represent a possible action set to select between. Each input vector c was sampled from a Gamma distribution Γ(2, 0.1). Inputs c_i were delivered at 1 s, and all simulations were run until they reached equilibrium or until 10 s had elapsed. Equilibrium was specified as the change in total activity, summed over the whole model, being less than 10⁻⁴ on consecutive time-steps. We used exponential Euler to numerically solve this system, with a time-step of 1 ms.

2.1.1. Translation model of D2 activation

The models of dopamine receptor activation we used have multiplicative effects on a population’s input-output function, both translating the function and altering its gain. However, detailed models of dopamine effects on short-term excitability changes of striatal projection neurons suggest that the overall effect of D2 activation is to translate the neuron’s input-output function, but not alter its gain (Moyer et al., 2007; Humphries et al., 2009). In turn, this suggests that our D2 model should be subtractive, not multiplicative. Thus, we also tested an alternative model of striatal D2 population activity:

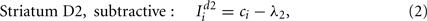
2.2. Target Nuclei

The basal ganglia output to multiple target nuclei, including the ventrolateral, ventromedial, intralaminar, and mediodorsal thalamic nuclei, the superior colliculus, and numerous regions in the upper brainstem, including the mesencephalic reticular formation (Cebrian et al., 2005). In these nuclei, the basal ganglia output potentially reconverges directly (Royce, 1983; Levesque et al., 1996a,b; Pare and Smith, 1996) or with a copy (Weyand and Gafka, 1998; McHaffie et al., 2001) of the cortical input to the basal ganglia (Figure 2D). Where these signals reconverge, the basal ganglia output is effectively setting a dynamic threshold for selection: the necessary strength of cortical input to activate the target nucleus is a function of basal ganglia output, which is itself a function of that cortical input. We thus examined how basal ganglia output shapes the cortically driven output of these target nuclei, to understand how action selection signals are propagated through the brain.

The basal ganglia model was extended by the addition of a nominal target nucleus. We studied two models of the target nucleus as basal ganglia output may have different effects on different target regions, depending on the number and location of synapses on the target dendrites. First, we examined a standard subtractive inhibition model:

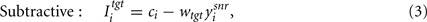
where w_tgt ∈ [0, 1] is the normalized weight of the connection between the SNr and the target nucleus.

Second, we considered that, if the GABAergic synapses originating from the SNr mainly fall on the soma and proximal dendrites, as they do in ventromedial thalamus (Bodor et al., 2008), then they will shunt excitatory inputs arriving at more distal locations on the dendritic tree. This potentially implements a divisive inhibition of firing rate in some neuron classes (Prescott and Koninck, 2003; Brizzi et al., 2004), though not all (Holt and Koch, 1997; Ulrich, 2003). We modeled this divisive effect as:

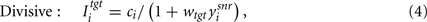
where w_tgt ∈ [1, 10] gives the strength of divisive inhibition on the target nucleus’ input.

In both subtractive and divisive cases, we used the same rectified output model for the target nucleus:

and we explored the effects of different values of the threshold ∈^tgt (see Results).

2.3. Learning Model

We sought to link the role of striatal dopamine in affecting the basal ganglia output to potentially measurable effects in subjects’ choice behavior. To do so, we simulated a probabilistic two-choice forced selection task, using a reinforcement learning model in which the basal ganglia model performed the action selection step. By testing this combined model under different levels of striatal dopamine we sought to detect the signature of dopaminergic control over the exploration-exploitation trade-off in the behavioral performance. Moreover, we would be able to address how the exploration-exploitation trade-off interacts with ongoing learning.

The conceptual form of the task was taken from Frank et al. (2004, 2007), as this has proved an excellent probe for the effects of altered dopamine on human choice behavior. Three stimuli pairs (A,B), (C,D), and (E,F) are presented in random sequence, each stimulus of the pair corresponding to some semantically meaningless symbol. Subjects are probabilistically rewarded for choosing one of each pair, with probabilities: A (0.8), B (0.2); C (0.7), D (0.3); E (0.6), F (0.4). Thus the subjects are expected to learn to choose stimuli A, C, and E over B, D, and F when each pair is presented.

We simulated learning of this task with a trial-by-trial Q-learning model. On each trial t, a pair of stimuli was presented, stimulus s chosen, and reward r_t ∈ [0, 1] obtained with the probabilities given above. The value of that stimulus was then updated by Q(s) ← Q(s) + α[r_t − Q(s)], with learning rate α. All models had α = 0.1, from the fits to subject behavior in Frank et al. (2007). Every simulated subject had a specified level of tonic dopamine λ, and had Q-values all initialized to zero; following (Frank et al., 2007), each simulated subject was run for 360 trials, seeing each stimulus pair 120 times in random order. We simulated 40 subjects per dopamine level.

When choosing the stimulus, we considered the Q-values corresponding to the presented pair as the inputs (c₁, c₂) to a two-channel basal ganglia model. Conceptually, this simulates either that action-values are learnt in orbitofrontal or medial prefrontal cortex (Schultz et al., 2000; Sul et al., 2010) and transmitted to striatum, or that action-values are computed directly in the striatum from converging cortical inputs (Samejima et al., 2005). We then ran this basal ganglia model to equilibrium, and converted its output into a probability distribution function for action selection (see Results and Figure 3 for details). The chosen response to the stimulus pair was then randomly selected from this probability distribution.

FIGURE 3

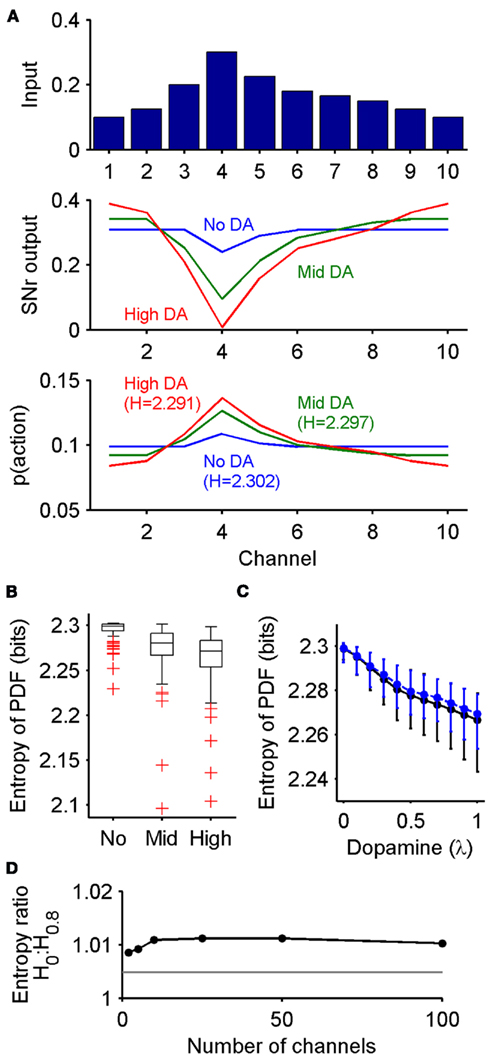
Figure 3. Dopaminergic control of exploration-exploitation via the output of the basal ganglia. (A) Basal ganglia output implements an exploration-exploitation trade-off. Top: distribution of inputs to the basal ganglia model across the 10 channels. Middle: corresponding distribution of SNr output at equilibrium, under three dopamine conditions (No: 0, Mid: 0.4, High: 0.8). Bottom: conversion of output to probability distribution function (PDF) for action selection. The higher the dopamine level, the more peaked the PDF, indicating enhanced exploitation. H: entropy (in bits) of the PDF; note that small magnitude differences in entropy reflect large differences in both the SNr output and PDFs. (B) Robustness of dopamine’s effect on the exploration-exploitation trade-off. Boxplots show the distribution of the action selection PDF’s entropy across 100 samples of input vectors, each sample run through the model for the three dopamine levels (0, 0.4, 0.8). Whiskers are 1.5IQR (interquartile range), red symbols indicate outliers. (C) Relationship between dopamine proportion and entropy of the PDF. Black line, default multiplicative effect D2 receptor model; blue line, model with subtractive effect of D2 receptor activation on striatal input. Symbols are median values; bars are interquartile range. (D) Effect of the number of channels on dopamine’s control of the PDF’s entropy. We plot the ratio of the median entropy for the no dopamine H₀ and high dopamine H_0.8 conditions. The gray line is the ratio (1.0048) of the entropies for the example no dopamine and high dopamine condition PDFs in (A), plotted to show that every median ratio indicates a greater change in the entropy of the probability distribution than this example.

3. Results

3.1. Basal Ganglia Implementation of the Probability Distribution for Action Selection

We begin by proposing that we can interpret the basal ganglia’s output as a population code for the probability distribution function over the set of possible actions in some domain. One example would be over the possible set of saccade targets in the retinotopic map, where the encoding of target selection in SNr (Hikosaka et al., 2000; Basso and Wurtz, 2002) sets the probability of saccadic movement to that target through its output to the superior colliculus (Kim and Basso, 2010); other domains potentially encoded by basal ganglia output include the set of orienting movements and locomotion directions (Krauzlis et al., 2004; Felsen and Mainen, 2008), and the set of possible arm movements (Leblois et al., 2006b).

A fundamental assumption of basal ganglia theories is that reduction of its tonic inhibitory output is the signal for selection (Mink, 1996; Redgrave et al., 1999; Hikosaka et al., 2000). Therefore, we interpret the inverse of the relative levels of inhibitory output from the basal ganglia to be proportional to the probability of selection. The probability of taking action A_i given the corresponding normalized SNr output is then: 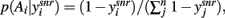where the sum in the denominator is taken over the n actions. We read-out this distribution when the basal ganglia model has reached equilibrium after the onset of the input values (Figure 3A), taken to indicate the end result of computation on those updated action-values. In this way, we can view the computation of the basal ganglia as exactly equivalent to them performing a transform of action-values into the probability distribution of action selection (Figure 1).

3.2. Dopamine Sets Exploration-Exploitation Trade-Off in Basal Ganglia Output

Under this probabilistic interpretation, our model predicts that the level of dopamine receptor activation in the striatum does change the output of the basal ganglia to favor exploration or exploitation. Figure 3A shows that, in response to the same set of action-value inputs, increasing dopamine increases the peak of the action selection probability distribution 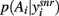around the action with the greatest value. Increasing dopamine has thus increased exploitation of known action-values.

We find that this effect of dopamine is highly robust. For each of 100 randomly sampled input vectors, we computed 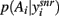at equilibrium for the whole range of dopamine receptor activation. To measure how peaked 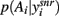was, and thus how much it signaled exploitation over exploration, we computed its entropy H = −Σⁿp(A_i) log₂ p(A_i): low H indicates a more peaked distribution, high H indicates a flatter distribution (Figure 1). Figure 3B shows that the entropy of the action selection probability distribution reliably decreased with increasing dopamine, thus indicating a reliable increase in exploitation.

Figure 3C shows that the distribution’s entropy fell monotonically across the whole range of striatal dopamine receptor activation. Figure 3C also shows that this was true even if we used an alternative subtractive model for D2 receptor activation (equation 2), which accounted for the linear translation of striatal projection neuron output by D2 activation predicted by detailed individual neuron models (Moyer et al., 2007; Humphries et al., 2009). (As this subtractive model did not qualitatively change the output of the basal ganglia, we do not consider it further here).

The above results were obtained with a ten-channel model. However, it is not clear how many channels participate in the basal ganglia microcircuit, illustrated in Figure 2B, that underpins the action selection computation (Alexander and Crutcher, 1990; Middleton and Strick, 2000). Neither is it clear whether the channels are a fixed anatomical entity, as in a somatotopic map (Hoover and Strick, 1999), or are flexibly recruited by cortical input to the basal ganglia, through synaptic plasticity at the cortico-striatal and cortico-subthalamic synapses (Horvitz, 2009). We thus tested the effect of the number of input channels on dopamine’s control of the action selection probability distribution’s entropy, repeating the above 100 input vector protocol for models ranging between 2 and 100 channels.

We found that increasing dopamine robustly decreased the entropy of the probability distribution across the whole range of tested channels. Figure 3D shows that the ratio of median entropies found for the no dopamine (H₀) and high dopamine (H_0.8) simulations was always greater than one, indicating that there was always a fall of entropy with increasing dopamine, irrespective of the number of channels. Thus, our model predicts that, as encoded in basal ganglia output, moving from low to high levels of tonic striatal dopamine robustly tunes between exploration and exploitation in action selection.

3.3. Striatal D1 Receptor Activation Dominates Trade-Off

We then wanted to understand the relative contribution to the dopaminergic control of exploration-exploitation by the different dopamine receptors in the striatum. We thus tested the D1 and D2 receptor activation pairs (λ₁, λ₂) across their full ranges λ₁, λ₂ ∈ [0, 1]. Using the same set of 100 randomly sampled input vectors, we ran the model for each input vector using each of the dopamine parameter pairs, and again computed the entropy of 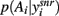at equilibrium following each input.

We found that the dopaminergic control of the probability distribution’s entropy was dominated by activation of the D1 receptor. Figure 4 shows that, for any choice of D2 receptor activation, increasing the D1 receptor activation always decreased the entropy of the action selection probability distribution. Increasing D2 receptor activation did not reliably change the entropy of the distribution, and always had a smaller effect than a change in D1 receptor activation. Thus, the model predicts that striatal D1 receptor activation is the key basal ganglia contributor to the hypothesized dopaminergic control of the exploration-exploitation trade-off.

FIGURE 4

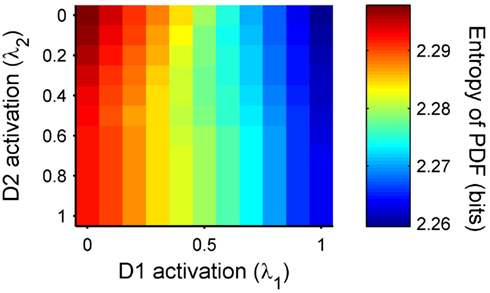
Figure 4. Relative dopaminergic receptor control of exploration-exploitation via the output of the basal ganglia. Each square shows the median entropy of the action selection probability distributions computed from 100 sample input vectors, each sample run through the model with that pair of dopamine receptor activation parameters (λ₁, λ₂). The top-left to bottom-right diagonal corresponds to equal dopamine levels – hence the medians correspond to those in Figure 3C.

3.4. Dopamine Sets Exploration-Exploitation Trade-Off in Basal Ganglia Targets

Having established that our model predicts that striatal dopamine controls the exploration-exploitation trade-off encoded in the output of the basal ganglia, we turned to the question of whether that control is maintained over the basal ganglia’s targets. Thus here we derive the probability of action selection from the output of the target nuclei.

In the target nuclei, basal ganglia output reconverges with a copy of its own cortical input (Pare and Smith, 1996), and shapes the target nuclei’s activity. For example, falling inhibition from a specific locus of the SNr seems to be a prerequisite for the development of cortically driven activity in the intermediate layers of the superior colliculus that provides the motor command for a saccade to a specific target (Hikosaka et al., 2000). Following this example, we assume that higher levels of activity in the target nucleus indicate more probable selection of that action, as is the case in superior colliculus for saccade targets and orienting (Krauzlis et al., 2004; Felsen and Mainen, 2008; Kim and Basso, 2010). Therefore, we interpret the relative levels of output from the target nucleus to be proportional to the probability of selection. The probability of taking action A_i given the corresponding target nucleus output is then: 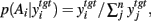where the sum in the denominator is taken over the n actions.

We found that this action selection probability function, derived from the target nuclei, also can be modulated by striatal dopamine levels. Figure 5A shows that, using a subtractive inhibition model (equation 3) for basal ganglia’s effects on the target nucleus, we can choose its parameters (w_tgt= 0.6, ∈^tgt= −0.2) such that the resulting distribution 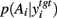becomes progressively more peaked for increasing dopamine levels. Thus, the dopaminergic control of exploration-exploitation trade-off can be effective in the basal ganglia’s target nuclei (Figure 5A), by the shaping of their cortical input by basal ganglia outflow.

FIGURE 5

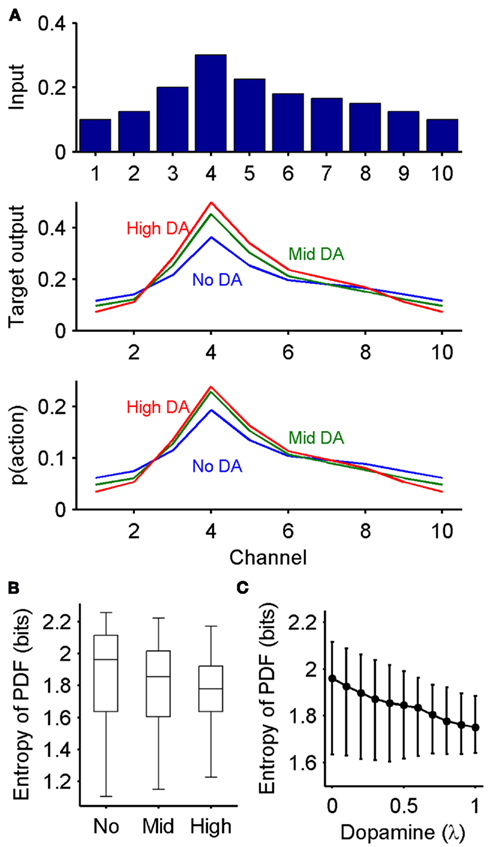
Figure 5. Dopaminergic control of exploration-exploitation via the targets of the basal ganglia. (A) Output of the basal ganglia targets also implements an exploration-exploitation trade-off. Top: distribution of inputs to the basal ganglia model across the 10 channels. Middle: corresponding distribution of target nucleus output at equilibrium, under three dopamine conditions (0, 0.4, 0.8). Bottom: conversion of target nucleus output to probability distribution function (PDF) for action selection. The higher the dopamine level, the more peaked the PDF, indicating enhanced exploitation. (B) Robustness of dopamine effect on the exploration-exploitation trade-off via the target nucleus. Boxplots show the distribution of the action selection PDF’s entropy across 100 samples of input vectors, each sample run through the model for the three dopamine levels (0, 0.4, 0.8). Whiskers are 1.5IQR. (C) Relationship between dopamine proportion and entropy of the PDF. Bars are interquartile range. All these simulations were run using target nucleus parameters ∈^tgt = −0.2 and w_tgt= 0.6.

We found that this effect of dopamine is also highly robust. Using the same protocol as the previous section, Figure 5B shows that the entropy of the target nucleus’ action selection probability distribution reliably decreased with increasing dopamine, thus indicating a reliable increase in exploitation. Figure 5C shows that the distribution’s entropy fell monotonically across the whole range of striatal dopamine receptor activation. Thus, our model predicts that, as encoded in the output of the basal ganglia’s target nuclei, moving from low to high levels of tonic striatal dopamine can robustly tune between exploration and exploitation in action selection.

3.5. Dopamine’s Effect Depends on Strength of Basal Ganglia Outflow

We examined how the key parameters of the target nucleus affect the basal ganglia’s control over its output: the threshold of target nucleus activity ∈^tgt and the weight of input from the basal ganglia w_tgt. These are unknown and likely to differ between different basal ganglia target nuclei. For example, thalamic neurons are tonically active in vivo, suggesting they are best modeled by a negative output threshold, but intermediate layer superior colliculus neurons are not, suggesting a threshold closer to zero. Thus, we assessed changes in these parameters to understand how basal ganglia output may differentially affect its target nuclei.

We tested parameter pairs (w_tgt, ∈^tgt) across the intervals w_tgt ∈ [0.1, 1] and ∈^tgt ∈ [0, −0.3], using the subtractive inhibition model (equation 3). We first generated a set of 100 randomly sampled input vectors. For each parameter pair, we tested the set of input vectors for each of three levels of dopamine: none (λ = 0), moderate (λ = 0.4), and high (λ = 0.8). For each dopamine level, we again computed the entropy of 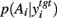from the output of the target nucleus at equilibrium to assess its relative promotion of exploration (low entropy) or exploitation (high entropy).

To assess the effect of striatal dopamine on the output of the target nucleus for that parameter pair, we computed a one-way ANOVA to test if dopamine level significantly interacted with the entropy of 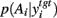across the input vector set. We then used a Tukey HSD post hoc test to determine the direction of the significant changes in entropy with changing dopamine levels, tested at p = 0.05. Hence we used just three dopamine levels to ensure the multiple comparisons of the Tukey HSD test were not overly penalized.

We found that for many combinations of output threshold and input weight the entropy of the target output’s probability distribution 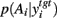was significantly, monotonically decreased by increasing dopamine (Figure 6A), in exactly the same way as the example of the previous section (Figure 5B). There thus exists a set of target nuclei models for which their output is shaped by the basal ganglia’s output such that increasing dopamine increases exploitation in action selection.

FIGURE 6

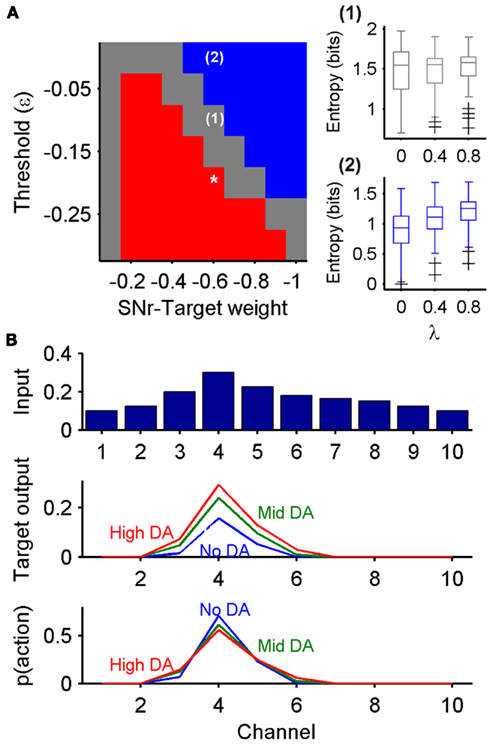
Figure 6. Dopaminergic control of exploration-exploitation depends on strength of basal ganglia control over target structures. (A) Striatal dopamine’s effect on the entropy of the probability distribution function (PDF) from the target nucleus, using subtractive inhibition by SNr input. Each square indicates the direction of effect for a combination of threshold and weight parameter values. Red: significant negative correlation between dopamine and entropy (square marked *is the parameter pair from Figure 5); blue: significant positive correlation between dopamine and entropy [example distributions of entropy given for pair marked (2)]; gray: no significant effect [example given for pair marked (1)]. (B) Example of dopamine having a reversed effect on the action selection PDF derived from the target nucleus’ output: increasing striatal dopamine flattened the PDF, promoting exploration [example outputs for the parameter pair marked (2) in (A)].

However, to our surprise, we found that some combinations of output threshold and input weight could alter the direction of entropy change (Figure 6A). A subset of threshold and weight combinations showed no significant effect of dopamine on the entropy of 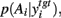suggesting that, for these target nuclei models, changes in SNr output was canceled out by cortical input. Moreover, there was also a subset of threshold and weight combinations for which the effect of dopamine was reversed: increasing dopamine significantly, monotonically increased the entropy of 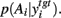Figure 6B shows an example of this effect on 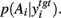Thus, there also exists a set of target nuclei models for which the effect of dopamine on the basal ganglia’s output entropy is reversed in the target nucleus’ output: when reading out the probability distribution from these target nuclei models, increasing dopamine increases exploration in action selection.

3.6 Dopamine’s Effect Depends on the Type of Basal Ganglia Inhibition

We examined the effect of changing the type of inhibition of the target nucleus on the control of its output by changing striatal dopamine levels. In the previous section, we examined a model in which basal ganglia output was subtractive for its target nuclei, in keeping with standard models of inhibitory control of population activity. However there is also the possibility that, due to the placement of synapses on somas and dendrites of neurons in the target nuclei, basal ganglia output shunts excitatory inputs to the target nucleus (see section 2.2). We thus tested a divisive input version of the target nucleus model (equation 4), using the same protocol as the previous section to assess the effect of dopamine on the entropy of 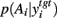across all target nucleus’ parameter pairs (w_tgt ∈ [1, 10], ∈^tgt ∈ [0, −0.3]). We found that all combinations of output threshold and divisive weight retained dopamine’s effect on the probability distribution’s entropy between basal ganglia output and target output. Thus, if the basal ganglia output does have a divisive effect on target nucleus input, then the model predicts that dopaminergic control of the exploration-exploitation trade-off is that increasing tonic striatal dopamine decreases exploration.

3.7 Exploration-Exploitation and Learning Interact on a Forced Two-Choice Experiment

Finally, we sought to bridge the gap between the predictions of neural activity changes from these computational models and predictions of measurable effects on behavior under experimental conditions. Frank and colleagues have extensively studied the effects of both mild dopaminergic modulators and single nucleotide polymorphisms of dopamine genes on choice performance by healthy human subjects (Frank and O’Reilly, 2006; Frank et al., 2007). In this prior work, the focus has been principally on how differences in striatal D1 and D2 receptor activation may alter rates of learning from positive and negative outcomes. Here we considered how choice behavior may be modulated by differences in tonic striatal dopamine, and consequently how the exploration-exploitation trade-off interacts with an ongoing learning process.

To do so, we used a reinforcement learning model to simulate performance on a probabilistic selection task (Frank et al., 2004, 2007). We simulated this task for 40 subjects in each of three tonic dopamine conditions (hypodopaminergic, normal, and hyperdopaminergic). Such conditions might be created by administration of a general dopamine precursor drug (such as L-DOPA; Frank and O’Reilly, 2006), or by separating populations according to their alleles of the dopamine transporter gene DAT1 (Dreher et al., 2009), or by separate patient groups (Frank et al., 2004). The model results illustrated the need for three rather than just two (low/high) dopamine conditions.

Each simulated subject was presented with a random sequence of three stimulus pairs (which we labeled AB, CD, and EF), and was rewarded for their stimulus selection with probabilities: A (0.8), B (0.2); C (0.7), D (0.3); E (0.6), F (0.4). We used a Q-learning model to update trial-by-trial action-values according to the subject’s choice and received reward (see Methods). On each trial the action selection step was done using the basal ganglia model. (We emphasize that all results here were thus obtained by modeling dopamine’s tonic effect on excitability in the striatum, and not the proposed role of phasic dopamine signals in reinforcement learning; Schultz et al., 1997). The pairs of action-values for the current stimulus pair were input to a two-channel model, and the probability distribution function 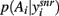derived from the output of the SNr at equilibrium. The response was then randomly chosen using this distribution.

We found that dopamine’s effect on the exploration-exploitation trade-off was detectable by simply measuring the probability of action choice. For each of the three pairs, we computed the probability that the most-often rewarded stimulus (A,C,E) was chosen over all trials. Figure 7A shows that across all simulated subjects this probability was significantly affected by dopamine level for all three pairs (AB: F = 5.44, p = 0.0055; CD: F = 22.56, p = 5.2 × 10⁻⁹; EF: F = 5.62, p = 0.0047; one-way ANOVA and Tukey HSD post hoc test at p < 0.05). Moderate dopamine levels resulted in the highest choice probability for all three pairs, suggesting that moderate dopamine led to the most exploitative behavior. Thus, this task simulation showed that dopamine’s effect on exploration-exploitation at the output of the basal ganglia could be detectable at the level of behavior; however, the results also appeared to disagree with prior simulations using random inputs (Figure 3) – we return to this below.

FIGURE 7

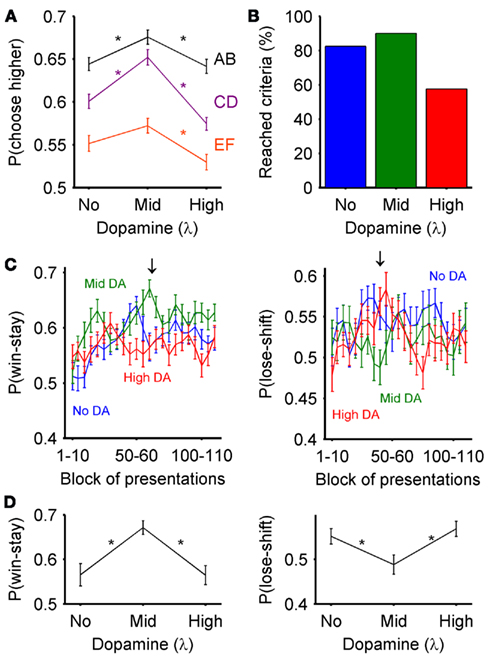
Figure 7. Predicted behavioral effects of dopaminergic control of exploration-exploitation during learning. (A) The effect of dopamine level on the probability of choosing the most-likely rewarded of each pair (A, C, and E) over the entire set of trials. Plotted are mean ± SEM over all subjects for that dopamine level; asterisks indicate a significant difference in choice probability (one-way ANOVA, and Tukey HSD post hoc test at p < 0.05). Dopamine levels: none (λ = 0), moderate (λ = 0.4), and high (λ = 0.8). (B) The effect of dopamine level on the number of subjects reaching criterion performance during the set of trials. (C) Dopamine level effect on the evolution of the probability of win-stay and lose-shift over the set of stimulus presentations. The probability of win-stay and lose-shift were computed for each block of ten presentations of each stimulus pair, giving 30 presentations total per block; the blocks were computed every five presentations (1–10, 5–15, and so on). Plotted are mean ± SEM over all subjects for that dopamine level. The arrows indicate the presentation blocks shown in (D). (D) Largest effect of dopamine level on the probability of win-stay and lose-shift. These blocks were those with the largest range of mean probability – they also corresponded to the blocks with the smallest p-value from the ANOVA. Plotted are mean ± SEM over all subjects for that dopamine level; asterisks indicate a significant difference in choice probability (one-way ANOVA, and Tukey HSD post hoc test at p < 0.05).

We noted that dopamine level, though only able to affect action choice on each trial via its effect on the basal ganglia model, also manifested significant effects on two measures that a priori would seem to indicate dopamine affects learning and strategy. First, we recorded when the simulated subjects reached the criterion performance levels set by Frank et al. (2007): over at least one block of 60 trials the probability of choosing stimulus A was 65%, stimulus C was 60%, and stimulus E was 50%. We found that there was a notable effect of dopamine level on the number of simulated subjects reaching this criterion performance by the end of the task (Figure 7B), particularly that only 57.5% of subjects in the high dopamine condition reached criterion performance. If detected in a behavioral experiment, such a result would suggest a direct effect of tonic dopamine on learning the task’s probability structure, but we know that this did not occur: dopamine did not affect the learning algorithm in this model. Rather, our simulation results suggest that such an effect of tonic dopamine on performance would be indirect and produced via the effect of tonic dopamine on the exploration-exploitation trade-off.

Second, we recorded each subject’s probabilities of performing win-stay and lose-shift strategies. On each presentation of a stimulus pair, a win-stay strategy repeats the stimulus choice if it was rewarded on the previous presentation, whereas a lose-shift strategy changes the stimulus choice after not being rewarded on the previous presentation. We computed p(win-stay) and p(lose-shift) for blocks of ten presentations of the 3 stimulus pairs, overlapping by 5 presentations (so presentations 1–10, 5–15, 10–20, and so on). We found that both win-stay and lose-shift probabilities changed over the learning of the task (Figure 7C). Nonetheless there were clear, but different, stages of the task where win-stay and lose-shift probabilities were significantly affected by dopamine level. Figure 7D shows that, for the presentation block with the largest probability range, moderate levels of dopamine had significantly different p(win-stay) and p(lose-shift) to the other dopamine levels, favoring higher win-stay and lower lose-shift probabilities. If detected in a behavioral experiment, such a result would suggest a direct effect of tonic dopamine on trial-by-trial adjustments to feedback, and thus on either or both of learning from feedback and behavioral strategy, but we know this did not occur: dopamine did not affect the learning algorithm in this model. Again, our simulation results suggest that such an effect of tonic dopamine on trial-by-trial learning would be indirect and produced via the effect of tonic dopamine on the exploration-exploitation trade-off.

Why then, in both the probabilities of action choice and the probabilities of win-stay and lose-shift, do the simulations show that moderate dopamine levels maximize exploitation, whereas the simulation results above show that high dopamine maximizes exploitation? Figure 8A shows that the probabilities of action selection derived from the basal ganglia model output did indeed evolve so that the PDF for moderate dopamine levels was comparatively more peaked for the duration of the task, and hence more exploitative, than other dopamine levels; this difference was large enough to be reflected in the gross behavioral statistics (Figure 7A).

FIGURE 8

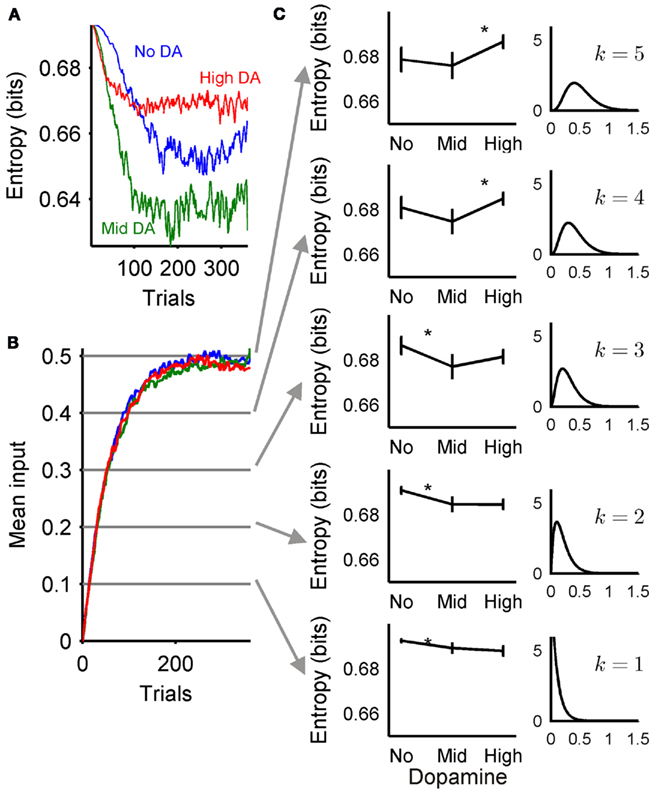
Figure 8. Exploration-exploitation trade-off changes over learning. (A) Entropy of the probability distribution function (PDF) for action selection 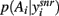over all trials, plotted as the mean over all subjects in each dopamine condition. As in previous figures, lower entropy indicates a more peaked action selection PDF, and hence greater exploitation. (B) Mean input values to the basal ganglia model over all trials, plotted as the mean over all subjects in each dopamine condition; colors are as in (A). (C) Dopamine’s effect on exploration-exploitation trade-off changes with increasing input in a two-choice model. Each left-hand plot shows the entropy of the action selection PDF for 100 two-element input vectors sampled from the gamma distributions shown on the right. Each distribution corresponds to the mean input value indicated in (B); given the shape k and scale (þeta = 0.1) of the gamma distribution, the mean is kθ. Entropy plots are mean ± 2 SEM over all input samples for that dopamine level. Asterisks indicate a significant difference in entropy between those dopamine conditions (one-way ANOVA, and Tukey HSD post hoc test at p < 0.05).

We found that it was the changes in the mean input to the basal ganglia model during the task that caused these changes in output, which ultimately caused moderate dopamine levels to be the most exploitative. Figure 8B shows how the mean value of the inputs to the model – the mean of the pair of action-values – increased over time, and reached the expected asymptote around 0.5 as the probabilities of each pair were successfully learnt (the mean of each pair – AB, CD, EF – was 0.5). To test the effect of this input, we generated sets of 100 input vectors from five distributions corresponding to five increasing mean input levels over the task (Figure 8C), and tested each set of input vectors in a two-channel basal ganglia model for each of three levels of dopamine. Figure 8C shows that, with increasing mean input, dopamine’s effect on a two-channel basal ganglia model changed from low dopamine being comparatively explorative to high dopamine being comparatively explorative. Consequently, as the task progressed, moderate dopamine remained consistently exploitative in comparison. However, when similarly using sets of input vectors drawn from the five distributions, the output of a ten-channel basal ganglia model always had a decreasing PDF entropy from low to high dopamine (as in Figure 3), and thus increased exploitation with increasing dopamine, regardless of the mean input level (results not shown). Thus, maximum exploitation for moderate dopamine was a consequence of the two-choice task structure.

4. Discussion

We set out to test the hypothesis that dopamine can alter the exploration-exploitation trade-off by modulating action selection via its effect on the basal ganglia circuit. To do so, we first advanced the idea that we can interpret the basal ganglia output vector as a probability distribution function for action selection, consistent with recent evidence for its encoding of saccade target selection (Basso and Wurtz, 2002; Kim and Basso, 2010). We showed in computational models of the full basal ganglia circuit that, under this interpretation, the actions of dopamine within the striatum can correspondingly change the basal ganglia’s output to favor the level of exploration or exploitation encoded in the action selection probability distribution. The models robustly predict that increasing tonic striatal dopamine decreases the level of exploration encoded in the probability distribution. Thus, by reading out the action selection probability distribution from the basal ganglia output, the model predicts tonic striatal dopamine plays the role of the exploration-exploitation trade-off parameter in formal models of reinforcement learning algorithms (Figure 1).

As this basal ganglia output then reconverges with a copy of the basal ganglia’s cortical input in its target nuclei, we then tested whether this trade-off encoding by dopamine is maintained in the output of the basal ganglia’s targets. By reading out the target nucleus’ output as the probability distribution for action selection, we found that our models predict striatal dopamine also controls the exploration-exploitation trade-off in that distribution. This was robust to almost every combination of target nucleus model parameters, and to whether the basal ganglia contributed subtractive or divisive inhibition over the target nucleus. Thus, the models predict that the hypothesized control of the exploration-exploitation trade-off by striatal dopamine is highly robust.

4.1. Implications for Neural Substrates of Voluntary Behavior

However, the models suggest that the exact relationship between dopamine levels and the exploration-exploitation trade-off depends on the strength and type of inhibitory control by the basal ganglia over its targets. For subtractive inhibition, some combinations of input weight and output threshold allowed the changes in basal ganglia’s output entropy to be translated directly into changes in the target nucleus’ output entropy. But for other combinations of weight and threshold the changes in basal ganglia’s output entropy were reversed in the output of the target nucleus. As these parameters are likely to differ between target regions, it suggests that dopamine may have different correlations with the continuum of exploratory and exploitative behavior depending on the exact nature of the task.

Beeler et al. (2010) found that chronically hyperdopaminergic mice were able to learn the shifting cost of lever presses to obtain reward, but were unable to exploit this knowledge to maximize reward. Their results thus suggest that high tonic dopamine levels evoked explorative behavior compared to normal tonic dopamine levels. Our model results suggest that this is consistent with the basal ganglia output having a strong inhibitory control over the target nuclei involved in this task, such that higher striatal dopamine promotes explorative behavior.

Our model also predicts that changes in D1 receptor activation are key to changing the exploration-exploitation trade-off via the basal ganglia: changing D2 activation had little effect on the trade-off. This is consistent with Frank et al. (2009) finding that subjects with DRD2 gene polymorphisms, expressing different binding potentials for striatal D2 receptors (Hirvonen et al., 2004), did not show differences in their exploratory behaviors on a time interval estimation task.

4.2. Interaction of Learning and Exploration-Exploitation Trade-Off

We were also able to show that striatal dopamine’s effect on the exploration-exploitation trade-off via the basal ganglia output could manifest as a measurable effect on subject performance during learning. In simulations of a probabilistic selection task (Frank et al., 2004, 2007), we found a significant difference between dopamine conditions in the probability of choosing the stimulus with the highest likelihood of reward. Moderate levels of tonic dopamine resulted in the highest choice probability, and thus the most exploitative behavior.

Though a plausibly testable prediction of the model, we do not wish to make strong predictions here. To keep simulations tractable, we assessed only the action selection PDF derived from the output of the SNr, but our prior results already showed that the exact direction of dopamine’s effect on the exploration-exploitation trade-off may be changed if we read-out the PDF from the basal ganglia’s target instead. Moreover, the Q-learning model may not accurately reflect how human subjects approach this task, though Frank and O’Reilly (2006) and Frank et al. (2007) have had some success fitting Q-learning models to human data on these tasks. Nonetheless, our results have shown that the exploration-exploitation effect of tonic dopamine in the striatum is in principle possible to read-out from behavioral performance on a well-studied psychological task.

Moreover, these learning simulations showed two difficulties in separating the potential effects of tonic dopamine on learning and decision making using behavioral tasks. First, we found that changes in some behavioral measures strongly suggest that tonic dopamine level influences learning. With high tonic dopamine levels, simulated subjects were poor at reaching criterion performance for learning the task, suggesting that high tonic dopamine directly impairs learning of the task structure. Tonic dopamine levels also influenced the probability of the subjects performing win-stay and lose-shift strategies, suggesting that tonic dopamine affects learning from feedback or the choice of behavioral strategy. However, by construction, we know that neither of these dopamine effects were true: tonic dopamine in our model only directly affected the exploration-exploitation trade-off and not any aspect of learning, such as synaptic plasticity. Consequently, our results show how tonic dopamine’s effects on the exploration-exploitation trade-off could lead to differential learning during a task, but without involvement of tonic dopamine in the learning process. Thus, although phasic release of dopamine in the striatum has a well-established role in learning (see below), effects of tonic dopamine on learning could be explained by its effect on the exploration-exploitation trade-off.

Second, the model also revealed a clear difficulty in extrapolating from psychological task paradigms to natural settings. That moderate dopamine levels resulted in maximum exploitation in the learning simulations seemed to flatly contradict the prior results (Figure 3). However, we showed that the effect of dopamine on the action selection PDF changed during the learning of the task because of the increase in mean input to the basal ganglia: low dopamine was most explorative at the start, then high dopamine thereafter, and consequently moderate dopamine was always comparatively more exploitative. Moreover, this effect was only found when using a two-channel model, simulating the forced two-choice task with only two salient stimuli. Thus our results show how a forced two-choice task could predict a different effect of dopamine level on the exploration-exploitation trade-off than would appear in more naturalistic setting with a broader set of choices.

4.3. Integrating with Encoding in Other Neural Structures

The proposed role of tonic striatal dopamine in setting the exploration-exploitation trade-off is separable from the properties encoded by the phasic activity of midbrain dopamine neurons. Many dopamine neurons encode a prediction error (Schultz et al., 1997; Redgrave and Gurney, 2006) in their phasic activity evoked by behavioral outcomes or outcome-predictive stimuli. The resulting phasic change in dopamine concentration in the forebrain is hypothesized to provide the gating signal for synaptic plasticity (Reynolds et al., 2001; Shen et al., 2008). Thus, phasic activity is key to long-term learning of action-value or action-outcome associations, whereas here we have examined the role of dopamine’s effects on short-term excitability changes. It remains the subject of future work to study the mechanisms linking the outcome-evoked phasic firing of dopamine neurons to the correlated short-term changes in the exploration-exploitation trade-off (Humphries and Redgrave, 2010).

Prefrontal cortical activity in humans (Daw et al., 2006; Behrens et al., 2007) and primates (Khamassi et al., 2011) appears to contribute to the regulation of exploratory behaviors based on tracking the stability of the environment. In particular, anterior cingulate cortex activity tracks task performance through signaling both positive and negative prediction errors in both the subject’s performance (e.g., breaking eye fixation) and in the choice outcome (e.g., choosing the wrong option; Quilodran et al., 2008). Behrens et al. (2007) found that differences in anterior cingulate cortex activity between subjects correlates with differences in learning rate, suggesting that these task monitoring signals are used to modulate meta-parameters of learning. Thus, these signals may also be the source of input to the midbrain dopamine neurons, perhaps via the shell of striatum (Humphries and Prescott, 2010), where, multiplexed with recent reward information (Humphries and Redgrave, 2010), they are used to update the exploration-exploitation trade-off.

5. Conclusion

We have provided evidence for the hypothesis that tonic dopamine levels in the basal ganglia can control the trade-off between exploration and exploitation in action selection. Our models provide the mechanistic explanation that striatal dopamine changes are sufficient to exercise this control, reconciling the existing evidence for dopamine’s control of the exploration-exploitation trade-off with the existing evidence for basal ganglia control of action selection. Finally, we have advanced a mapping of this neural substrate to formal reinforcement learning algorithms, in which the basal ganglia are computing the probability distribution transform of the action-value distribution, and that the trade-off parameter in this transform is encoded by tonic dopamine.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by: L’Agence Nationale de Recherche “NEUROBOT” project (Mark D. Humphries); the Centre National de la Recherche Scientifique “IMAVO” PEPII project (Mehdi Khamassi); and the EU Framework 7 “IM-CLEVER” project (Kevin Gurney).

References

Alexander, G. E., and Crutcher, M. D. (1990). Functional architecture of basal ganglia circuits: neural substrates of parallel processing. Trends Neurosci. 13, 266–272.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Basso, M. A., and Wurtz, R. H. (2002). Neuronal activity in substantia nigra pars reticulata during target selection. J. Neurosci. 22, 1883–1894.

Pubmed Abstract | Pubmed Full Text

Beeler, J. A., Daw, N., Frazier, C. R. M., and Zhuang, X. (2010). Tonic dopamine modulates exploitation of reward learning. Front. Behav. Neurosci. 4:170. doi:10.3389/fnbeh.2010.00170

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Behrens, T. E. J., Woolrich, M. W., Walton, M. E., and Rushworth, M. F. S. (2007). Learning the value of information in an uncertain world. Nat. Neurosci. 10, 1214–1221.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bodor, A. L., Giber, K., Rovo, Z., Ulbert, I., and Acsady, L. (2008). Structural correlates of efficient GABAergic transmission in the basal ganglia-thalamus pathway. J. Neurosci. 28, 3090–3102.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brizzi, L., Meunier, C., Zytnicki, D., Donnet, M., Hansel, D., D’Incamps, B. L., and Vreeswijk, C. V. (2004). How shunting inhibition affects the discharge of lumbar motoneurones: a dynamic clamp study in anaesthetized cats. J. Physiol. (Lond.) 558, 671–683.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cebrian, C., Parent, A., and Prensa, L. (2005). Patterns of axonal branching of neurons of the substantia nigra pars reticulata and pars lateralis in the rat. J. Comp. Neurol. 492, 349–369.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Charuchinda, C., Supavilai, P., Karobath, M., and Palacios, J. M. (1987). Dopamine D2 receptors in the rat brain: autoradiographic visualization using a high-affinity selective agonist ligand. J. Neurosci. 7, 1352–1360.

Pubmed Abstract | Pubmed Full Text

Chevalier, G., and Deniau, J. M. (1990). Disinhibition as a basic process in the expression of striatal function. Trends Neurosci. 13, 277–280.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohen, J. D., McClure, S. M., and Yu, A. J. (2007). Should I stay or should I go? how the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 933–942.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Daw, N. D., O’Doherty, J. P., Dayan, P., Seymour, B., and Dolan, R. J. (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–879.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dawson, T. M., Gehlert, D. R., McCabe, R. T., Barnett, A., and Wamsley, J. K. (1986). D-1 dopamine receptors in the rat brain: a quantitative autoradiographic analysis. J. Neurosci. 6, 2352–2365.

Pubmed Abstract | Pubmed Full Text

Diop, L., Gottberg, E., Briere, R., Grondin, L., and Reader, T. A. (1988). Distribution of dopamine D1 receptors in rat cortical areas, neostriatum, olfactory bulb and hippocampus in relation to endogenous dopamine contents. Synapse 2, 395–405.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doya, K. (2002). Metalearning and neuromodulation. Neural Netw. 15, 495–506.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dreher, J.-C., Kohn, P., Kolachana, B., Weinberger, D. R., and Berman, K. F. (2009). Variation in dopamine genes influences responsivity of the human reward system. Proc. Natl. Acad. Sci. U.S.A. 106, 617–622.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Felsen, G., and Mainen, Z. F. (2008). Neural substrates of sensory-guided locomotor decisions in the rat superior colliculus. Neuron 60, 137–148.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Frank, M. J., Doll, B. B., Oas-Terpstra, J., and Moreno, F. (2009). Prefrontal and striatal dopaminergic genes predict individual differences in exploration and exploitation. Nat. Neurosci. 12, 1062–1068.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Frank, M. J., Moustafa, A. A., Haughey, H. M., Curran, T., and Hutchison, K. E. (2007). Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proc. Natl. Acad. Sci. U.S.A. 104, 16311–16316.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Frank, M. J., and O’Reilly, R. C. (2006). A mechanistic account of striatal dopamine function in human cognition: psychopharmacological studies with cabergoline and haloperidol. Behav. Neurosci. 120, 497–517.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Frank, M. J., Seeberger, L. C., and O’Reilly, R. C. (2004). By carrot or by stick: cognitive reinforcement learning in parkinsonism. Science 306, 1940–1943.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerfen, C., Engber, T., Mahan, L., Susel, Z., Chase, T., Monsma, F., and Sibley, D. (1990). D1 and D2 dopamine receptor-regulated gene expression of striatonigral and striatopallidal neurons. Science 250, 1429–1432.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Girard, B., Tabareau, N., Pham, Q. C., Berthoz, A., and Slotine, J.-J. (2008). Where neuroscience and dynamic system theory meet autonomous robotics: a contracting basal ganglia model for action selection. Neural Netw. 21, 628–641.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gurney, K., Prescott, T. J., and Redgrave, P. (2001a). A computational model of action selection in the basal ganglia I: a new functional anatomy. Biol. Cybern. 85, 401–410.

CrossRef Full Text

Gurney, K., Prescott, T. J., and Redgrave, P. (2001b). A computational model of action selection in the basal ganglia II: analysis and simulation of behaviour. Biol. Cybern. 85, 411–423.

CrossRef Full Text

Gurney, K. N., Humphries, M., Wood, R., Prescott, T. J., and Redgrave, P. (2004). Testing computational hypotheses of brain systems function using high level models: a case study with the basal ganglia. Network 15, 263–290.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hikosaka, O., Takikawa, Y., and Kawagoe, R. (2000). Role of the basal ganglia in the control of purposive saccadic eye movements. Physiol. Rev. 80, 953–978.

Pubmed Abstract | Pubmed Full Text

Hirvonen, M., Laakso, A., Nagren, K., Rinne, J. O., Pohjalainen, T., and Hietala, J. (2004). C957T polymorphism of the dopamine D2 receptor (DRD2) gene affects striatal DRD2 availability in vivo. Mol. Psychiatry 9, 1060–1061.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Holt, G. R., and Koch, C. (1997). Shunting inhibition does not have a divisive effect on firing rates. Neural Comput. 9, 1001–1013.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hoover, J. E., and Strick, P. L. (1999). The organization of cerebellar and basal ganglia outputs to primary motor cortex as revealed by retrograde transneuronal transport of herpes simplex virus type 1. J. Neurosci. 19, 1446–1463.

Pubmed Abstract | Pubmed Full Text

Horvitz, J. C. (2009). Stimulus-response and response-outcome learning mechanisms in the striatum. Behav. Brain Res. 199, 129–140.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Humphries, M. D., Lepora, N., Wood, R., and Gurney, K. (2009). Capturing dopaminergic modulation and bimodal membrane behaviour of striatal medium spiny neurons in accurate, reduced models. Front. Comput. Neurosci. 3:26. doi:10.3389/neuro.10.026.2009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Humphries, M. D., and Prescott, T. J. (2010). The ventral basal ganglia, a selection mechanism at the crossroads of space, strategy, and reward. Prog. Neurobiol. 90, 385–417.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Humphries, M. D., and Redgrave, P. (2010). “Midbrain dopamine neurons encode an exploration/exploitation trade-off,” in 2010 Neuroscience Meeting Planner, Program No. 916.3 (San Diego: Society for Neuroscience).

Humphries, M. D., Stewart, R. D., and Gurney, K. N. (2006). A physiologically plausible model of action selection and oscillatory activity in the basal ganglia. J. Neurosci. 26, 12921–12942.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Joel, D., Niv, Y., and Ruppin, E. (2002). Actor-critic models of the basal ganglia: new anatomical and computational perspectives. Neural Netw. 15, 535–547.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kakade, S., and Dayan, P. (2002). Dopamine: generalization and bonuses. Neural Netw. 15, 549–559.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Khamassi, M., Lacheze, L., Girard, B., Berthoz, A., and Guillot, A. (2005). Actor-critic models of reinforcement learning in the basal ganglia: from natural to arificial rats. Adapt. Behav. 13, 131–148.

CrossRef Full Text

Khamassi, M., Wilson, C., Rothe, R., Quilodran, R., Dominey, P. F., and Procyk, E. (2011). “Meta-learning, cognitive control, and physiological interactions between medial and lateral prefrontal cortex,” in Neural Bases of Motivational and Cognitive Control, eds R. B. Mars, J. Sallet, M. F. S. Rushworth, and N. Yeung (Cambridge, MA: MIT Press), 351–370.

Kim, B., and Basso, M. A. (2010). A probabilistic strategy for understanding action selection. J. Neurosci. 30, 2340–2355.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kimchi, E. Y., and Laubach, M. (2009). Dynamic encoding of action selection by the medial striatum. J. Neurosci. 29, 3148–3159.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Krauzlis, R. J., Liston, D., and Carello, C. D. (2004). Target selection and the superior colliculus: goals, choices and hypotheses. Vision Res. 44, 1445–1451.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Krichmar, J. L. (2008). The neuromodulatory system: a framework for survival and adaptive behavior in a challenging world. Adapt. Behav. 16, 385–399.

CrossRef Full Text

Leblois, A., Boraud, T., Meissner, W., Bergman, H., and Hansel, D. (2006a). Competition between feedback loops underlies normal and pathological dynamics in the basal ganglia. J. Neurosci. 26, 3567–3583.

CrossRef Full Text

Leblois, A., Meissner, W., Bezard, E., Bioulac, B., Gross, C. E., and Boraud, T. (2006b). Temporal and spatial alterations in GPi neuronal encoding might contribute to slow down movement in parkinsonian monkeys. Eur. J. Neurosci. 24, 1201–1208.

CrossRef Full Text

Levesque, M., Charara, A., Gagnon, S., Parent, A., and Deschenes, M. (1996a). Corticostriatal projections from layer V cells in rat are collaterals of long-range corticofugal axons. Brain Res. 709, 311–315.

CrossRef Full Text

Levesque, M., Gagnon, S., Parent, A., and Deschenes, M. (1996b). Axonal arborizations of corticostriatal and corticothalamic fibers arising from the second somatosensory area in the rat. Cereb. Cortex 6, 759–770.

CrossRef Full Text

Matamales, M., Bertran-Gonzalez, J., Salomon, L., Degos, B., Deniau, J.-M., Valjent, E., Herve, D., and Girault, J.-A. (2009). Striatal medium-sized spiny neurons: identification by nuclear staining and study of neuronal subpopulations in BAC transgenic mice. PLoS ONE 4, e4770. doi:10.1371/journal.pone.0004770

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McHaffie, J. G., Thomson, C. M., and Stein, B. E. (2001). Corticotectal and corticostriatal projections from the frontal eye fields of the cat: an anatomical examination using WGA-HRP. Somatosens. Mot. Res. 18, 117–130.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Middleton, F. A., and Strick, P. L. (2000). Basal ganglia and cerebellar loops: motor and cognitive circuits. Brain Res. Brain Res. Rev. 31, 236–250.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mink, J. W. (1996). The basal ganglia: focused selection and inhibition of competing motor programs. Prog. Neurobiol. 50, 381–425.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moyer, J. T., Wolf, J. A., and Finkel, L. H. (2007). Effects of dopaminergic modulation on the integrative properties of the ventral striatal medium spiny neuron. J. Neurophysiol. 98, 3731–3748.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pare, D., and Smith, Y. (1996). Thalamic collaterals of corticostriatal axons: their termination field and synaptic targets in cats. J. Comp. Neurol. 372, 551–567.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prescott, S. A., and Koninck, Y. D. (2003). Gain control of firing rate by shunting inhibition: roles of synaptic noise and dendritic saturation. Proc. Natl. Acad. Sci. U.S.A. 100, 2076–2081.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Quilodran, R., Rothe, M., and Procyk, E. (2008). Behavioral shifts and action valuation in the anterior cingulate cortex. Neuron 57, 314–325.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Redgrave, P., and Gurney, K. (2006). The short-latency dopamine signal: a role in discovering novel actions? Nat. Rev. Neurosci. 7, 967–975.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Redgrave, P., Prescott, T. J., and Gurney, K. (1999). The basal ganglia: a vertebrate solution to the selection problem? Neuroscience 89, 1009–1023.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Reynolds, J. N., Hyland, B. I., and Wickens, J. R. (2001). A cellular mechanism of reward-related learning. Nature 413, 67–70.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Richfield, E. K., Penney, J. B., and Young, A. B. (1989). Anatomical and affinity state comparisons between dopamine D1 and D2 receptors in the rat central nervous system. Neuroscience 30, 767–777.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Royce, G. J. (1983). Cortical neurons with collateral projections to both the caudate nucleus and the centromedian-parafascicular thalamic complex: a fluorescent retrograde double labeling study in the cat. Exp. Brain Res. 50, 157–165.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Samejima, K., Ueda, Y., Doya, K., and Kimura, M. (2005). Representation of action-specific reward values in the striatum. Science 310, 1337–1340.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schultz, W., Tremblay, L., and Hollerman, J. R. (2000). Reward processing in primate orbitofrontal cortex and basal ganglia. Cereb. Cortex 10, 272–284.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shen, W., Flajolet, M., Greengard, P., and Surmeier, D. J. (2008). Dichotomous dopaminergic control of striatal synaptic plasticity. Science 321, 848–851.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sul, J. H., Kim, H., Huh, N., Lee, D., and Jung, M. W. (2010). Distinct roles of rodent orbitofrontal and medial prefrontal cortex in decision making. Neuron 66, 449–460.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Surmeier, D. J., Ding, J., Day, M., Wang, Z., and Shen, W. (2007). D1 and D2 dopamine-receptor modulation of striatal glutamatergic signaling in striatal medium spiny neurons. Trends Neurosci. 30, 228–235.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press.

Ulrich, D. (2003). Differential arithmetic of shunting inhibition for voltage and spike rate in neocortical pyramidal cells. Eur. J. Neurosci. 18, 2159–2165.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Usher, M., Cohen, J. D., Servan-Schreiber, D., Rajkowski, J., and Aston-Jones, G. (1999). The role of locus coeruleus in the regulation of cognitive performance. Science 283, 549–554.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Weyand, T. G., and Gafka, A. C. (1998). Corticostriatal and corticotectal neurons in area 6 of the cat during fixation and eye movements. Vis. Neurosci. 15, 141–151.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text