- Institute for Learning and Brain Sciences, University of Washington, Seattle, WA, USA
The basal ganglia play a fundamental role in decision-making. Their contribution is typically modeled within a reinforcement learning framework, with the basal ganglia learning to select the options associated with highest value and their dopamine inputs conveying performance feedback. This basic framework, however, does not account for the role of cholinergic interneurons in the striatum, and does not easily explain certain dynamic aspects of decision-making and skill acquisition like the generation of exploratory actions. This paper describes basal ganglia acetylcholine-based entropy (BABE), a model of the acetylcholine system in the striatum that provides a unified explanation for these phenomena. According to this model, cholinergic interneurons in the striatum control the level of variability in behavior by modulating the number of possible responses that are considered by the basal ganglia, as well as the level of competition between them. This mechanism provides a natural way to account for the role of basal ganglia in generating behavioral variability during the acquisition of certain cognitive skills, as well as for modulating exploration and exploitation in decision-making. Compared to a typical reinforcement learning model, BABE showed a greater modulation of response variability in the face of changes in the reward contingences, allowing for faster learning (and re-learning) of option values. Finally, the paper discusses the possible applications of the model to other domains.
Introduction
Recent years have witnessed an amazing advancement in our understanding of the basal ganglia circuit. This progress has been made possible by the convergence of neuroscientific data with increasingly sophisticated computational models of the circuit. Despite these advances, a number of structural and functional characteristics of the basal ganglia remain unaccounted for, such as the microstructure of the striatum, the role of behavioral variability for skill acquisition, and the balance of exploration and exploitation in decision-making. This paper describes a new model of the acetylcholine system in the striatum that furthers our current understanding of the basal ganglia and provides a unified explanation for these phenomena.
The remainder of this paper is organized into four sections. The first section will provide a brief overview of functional anatomy of the basal ganglia, their role of in decision-making, and some currently problematic aspects of basal ganglia functions. The second section will describe the proposed framework and a neurocomputational models that implements it. The third section will detail the results of two decision-making tests that were performed to verify our framework’s predictions. Finally, the implications of our framework will be discussed.
Functional Anatomy of the Basal Ganglia
Because this paper will often refer to specific aspects of the basal ganglia physiology, this section will provide a brief overview of their functional anatomy. The basal ganglia are a set of interconnected nuclei located at the center of the brain, and they play an important role in many cognitive functions, including working memory (McNab and Klingberg, 2008), reasoning (Stocco and Anderson, 2008), learning (Packard and Knowlton, 2002), and even language (Friederici, 2006; Prat and Just, 2011) The nuclei in the circuit form part of a series of loops from and to the cortex (Alexander et al., 1986). Within the circuit, the striatum serves s the input nucleus, receiving projections from the entire cortex. On the other hand, the pars reticulata of the substantia nigra (SNr) and the internal part of the globus pallidus (GPi) serve as the output nuclei, which project to and control the activity of the thalamic nuclei that project to the frontal lobes. Thus, the basal ganglia are placed in the ideal location to control behavior by regulating signals to the frontal cortex.
The current understanding of the arrangement of the nuclei within the circuit dates back to Albin et al. (1989), and is summarized in Figure 1. According to their framework, the output of the circuit is the result of two competing pathways: a direct pathway that originates in the striatonigral (SN) cells of the striatum, and an indirect pathway that originates in the striatopallidal (SP) cells and proceeds through the external globus pallidus and the sub-thalamic nucleus. A “hyperdirect” pathway that proceeds from the cortex to the thalamus through the sub-thalamic nucleus also exists, but researchers are divided as to its exact functions (see Gurney et al., 2001; Nambu et al., 2002; Frank et al., 2007, for three alternative accounts), and will not be discussed further in this paper.
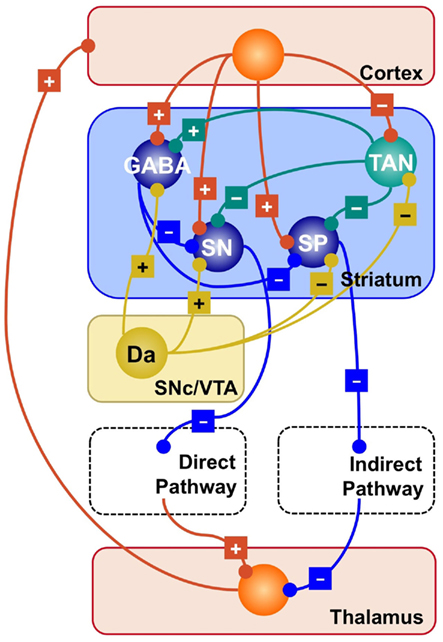
Figure 1. Simplified representation of the striatal circuitry within the basal ganglia system. Excitatory projections are marked with a “+”; inhibitory projections with a “−.” Glutamatergic neurons and projections are represented in red; GABA-ergic, in blue; Dopaminergic, in yellow; cholinergic, in green. SP, striatopallidal projection neuron; SN, striatonigral projection neuron; GABA, GABA-ergic interneuron; TAN, tonically active (cholinergic) neuron; Da, dopaminergic neuron.
Researchers generally agree that basal ganglia perform a selection of possible signals by means of competing excitatory and inhibitory pathways. These competing signals are thought to originate in the striatum in response to cortical excitatory inputs. Responses originating in the striatum are thought to represent a subset of possible “actions” that are associated to the incoming cortical signals. What exactly constitutes an “action” depends on the contents of the signals being passed to the frontal lobes; thus, depending on the context, actions might consist of decisions (Barto, 1995), working memory updates (Frank et al., 2001), or motor programs (Berns and Sejnowski, 1998).
Basal Ganglia and Decision-Making
The crucial link between action selection and decision-making is provided by the dopamine pathways that converge on the striatum (see Figure 1). Dopamine is a neurotransmitter that promotes synaptic plasticity in the corticostriatal synapses, thus determining the degree of association between cortical inputs and SN and SP responses (Wickens et al., 1996; Calabresi et al., 2000). Importantly, the release of dopamine has a direct but non-trivial relationship to the rewards connected to an action.
Dopamine is normally released in response to primary rewards, such as food. However, when a primary reward becomes reliably associated to a predictive cue, dopamine neurons cease to fire in response to the reward itself, and instead begin responding to the cue. Consider, for example, a classic conditioning experiment where a monkey receives a drop of juice a few moments after seeing a visual cue (Schultz et al., 1993). Dopamine neurons initially increase their firing rate in response to the juice. However, after the monkey has learned that the juice is anticipated by a visual cue, dopamine neurons fire when the cue is presented, but not when the juice is delivered. Conversely, when the cue is presented but the juice is later omitted, dopamine release is reduced instead (Schultz et al., 1993; Schultz, 1998).
This pattern of data can be accounted for by assuming that dopamine reflects the difference between real and expected rewards. In artificial intelligence, such an error term is used in reinforcement learning algorithms to learn the expected value (i.e., the amount of reward) of an action (Sutton, 1988; Sutton and Barto, 1998). This mechanism offers an elegant theory for interpreting how the basal ganglia can discover the true “value” of each possible action based on its previous rewards, and thus selecting the best action available.
The reinforcement learning framework can be easily transported in the domain of decision-making by treating the possible options for a decision as alternative actions. In this case, the response of SN and SP cells in the striatum reflects the amount of reward that is expected by each option, and dopamine response represents the difference between the expected and real payoff of a decision. In neuroimaging studies of decision-making, for example, activity in the striatum correlates with a decision’s perceived expected payoff (Delgado et al., 2003; O’Doherty, 2004; Schönberg et al., 2007) or its success probability (Tricomi et al., 2004; Delgado et al., 2005), and even with individual differences in the preference between alternative decision options (Tom et al., 2007). The connection between decision-making and reinforcement learning becomes even stronger when one considers iterative decision-making paradigms, where the true value of each option needs to be learned through repeated selections. Thus, although alternatives exist (Gonzalez et al., 2003; Fum and Stocco, 2004), reinforcement learning models of the basal ganglia have been frequently applied to decision-making tasks (Frank et al., 2004; Frank and Claus, 2006; Biele et al., 2009).
In summary, the basal ganglia can be understood as a neural mechanism for selecting actions based on previous reward. This framework can be successfully applied to the field of decision-making, where it has proven successful in account for a wide range of behavioral and neuroimaging data in human decision-making.
Three Problems in Current Basal Ganglia Research
The reinforcement learning framework has been successful at explaining the role of the basal ganglia not only in decision-making, but also in other domains, such as procedural learning (Barto, 1995; Suri and Schultz, 1998; Frank et al., 2001; Packard and Knowlton, 2002) and working memory (O’Reilly and Frank, 2006; McNab and Klingberg, 2008). Despite this success, a number of problems still remain that need to be addressed. This section will review three of these issues that deal with physiology, learning, and decision-making. The following sections will provide evidence that the same mechanism (i.e., modulation of response variability by striatal cholinergic interneurons) represents a solution to all three, apparently unrelated, problems, and sheds further light on the connection between basal ganglia and decision-making.
The role of acetylcholine in the striatum
All models of the basal have to make simplifying assumptions about the physiology of the striatum. By making these assumptions, however, one runs the risk of sacrificing some structural characteristics that are crucial to basal ganglia function. Here, we argue that one of these crucial features is the role of interneurons in the microcircuitry of the striatum.
Figure 1 provides a visual summary of the connections between different types of neurons in the striatum. Roughly speaking, it contains two classes of cells; (a) Projection neurons, which comprise the SN and SP neurons discussed above; and (b) Striatal interneurons, which can be further divided into cholinergic interneurons and different sub-types of GABA-ergic interneurons (Bolam et al., 2000; Tepper and Bolam, 2004).
Cholinergic interneurons form a circuit that is neurochemically separated from the rest of the striatum, which is mostly made up by GABA-ergic (i.e., inhibitory) synapses. Because they are characterized by an elevated firing rate at rest, they are also known as tonically active neurons (TANs). TANs influence both other interneurons and projection neurons, therefore playing a central and strategic role in orchestrating the activity of the striatum.
While projection neurons ultimately determine the competition between direct and indirect pathways, striatal interneurons play a crucial role in modulating the response of projection neurons by exerting a powerful inhibitory influence (Tepper and Bolam, 2004).
Despite their remarkable properties, cholinergic interneurons are often omitted in computational models of the basal ganglia, with the exception of those models designed to capture specific physiological properties (Tan and Bullock, 2008; Humphries et al., 2009, 2010). In fact, many of the computational cognitive models of the basal ganglia (Barto, 1995; Beiser and Houk, 1998; Suri and Schultz, 1998; Frank et al., 2001; Gurney et al., 2001) assume that the striatum is made only of projection neurons, and that their activity is limited by some indirect mechanism – for instance, by artificially imposing a limit on the number of SN and SP cells that can be active at any given time (e.g., Frank et al., 2001).
When TANs had been included in a model, they were found to play an important functional role for cognition and behavior. For instance, in Stocco et al. (2010) TANs were needed to exert context-dependent inhibition of unwanted actions. In their model, the basal ganglia actions can be thought of as production rules; for each “rule,” the TANs specify the condition (e.g., the context upon which actions should be applied) and projection neurons determine the “action.” Thus, this model embodies the idea that TANs’ activations are context-dependent and direct the activity of projection neurons (as suggested, for instance, by Apicella, 2007). Alternatively, in Ashby and Crossley’s (2011) model, TANs modulate learning and skill acquisition by keeping non-relevant striatal projection neurons outside the scope of dopamine-based Hebbian learning.
This paper puts forward a hypothesis on the functional role of cholinergic interneurons that unifies these previous accounts. According to this hypothesis, by controlling the amount of inhibition exerted on projection neurons, TANs effectively control the number of possible actions to be performed at each moment, thus restricting the possible actions to either the optimal response or widening the range to different (optimal and non-optimal) responses. Furthermore, this paper suggests that the range of possible selections depends on dopamine-based reward signals, with TANs increasing the range of possible actions when previously learned routines lose their effectiveness.
Behavioral variability during skill acquisition
A second problem with existing views of basal ganglia function concerns our current view of the basal ganglia role in learning. For examples, there is considerable amount of evidence suggesting that the basal ganglia contribute to the acquisition of procedural skills (Cohen and Squire, 1980; Knowlton et al., 1996; Packard and Knowlton, 2002; Seger and Cincotta, 2005; Yin and Knowlton, 2006), although the precise mechanisms by which they are acquired are still debated. For instance, some researchers believe that skills are permanently encoded in the basal ganglia (Anderson, 2007), while others believe that they are encoded in the basal ganglia initially, but eventually re-encoded in the form of corticocortical pathways (Pasupathy and Miller, 2005; Stocco et al., 2010). Still, others believe that the basal ganglia simply facilitate the acquisition of skills in form of corticocortical connections (Ashby et al., 2007, 2010). Despite their differences, all these theories share a common view of the basal ganglia as a fast learning system, which quickly detects and encodes associations between patterns of signals occurring in different cortical areas.
Given that the basal ganglia are an evolutionary old structure, one might expect that this interpretation would hold across species, especially in instances where complex skill acquisition is relevant. Instead, this view is at odds with what is known of the basal ganglia role in one of the most studied examples of complex skill acquisition in animals, birdsong learning (Brainard and Doupe, 2002). During the song learning phase, birds produce vocalizations trying to match a tutor’s template song. While learning eventually results in the acquisition of a crystallized and stable song, during the learning process birds explore different vocalizations until they converge on the template. The learning process is supported by various nuclei of the songbird’s brain (Brainard and Doupe, 2002; Nottebohm, 2005; Aronov et al., 2008), including the bird’s equivalent of the basal ganglia – the anterior forebrain pathway (AFP; Nottebohm, 2005). Contrary to what would be expected on the bases of studies on mammals and primates, damage to the bird’s AFP does not impair the acquisition of a song; instead, it severely diminishes the final song’s quality by reducing the variety of vocalizations produced during the learning process (Gardner et al., 2005; Olveczky et al., 2005). These findings suggest that the AFP controls variability during the acquisition of a birdsong, rather than mediating its encoding as a fixed routine.
In summary, a conceptual contradiction seems to exist between the role of the basal ganglia in skill acquisition in humans and in birdsong learning. The current consensus in skill acquisition research is that the ganglia support learning by rapidly acquiring stimulus–response associations. Research on birdsong learning, however, suggests that the basal ganglia provide random variations in the patterns of learned vocal responses, instead of fixing them into stable patterns as suggested by the skill acquisition view. Given the fact that both types of learning depend on the same structure, it would be desirable to have a single framework that accounts for both.
Although the exact mechanism by which variability is introduced into vocalizations is unknown (and it might be ultimately underpinned by a different and specific neural mechanism), this paper puts forward the hypothesis that the generation of variability during songbird learning is mediated by striatal cholinergic interneurons. In particular, the framework proposed in this paper attempts to solve this contradiction by modeling the striatum as a two-level system. At the lower level, dopamine release is used to associate cortical inputs with proper responses; this level accounts for the fast acquisition of fixed behavioral responses during skill acquisition. At the upper level, acetylcholine modulates the number of responses that can be applied at each moment, manipulating the degree of competition between possible actions and, in turn, the variability of behavioral responses. In turn, this mechanism can be used generate variability in a songbird’s vocalizations during the learning process.
Exploration and exploitation in decision-making
Response variability plays an important role in decision-making as well, and its exact nature and origin represents the last issue addressed in this section. In their basic form, reinforcement learning models of the basal ganglia consider only one parameter in the selection of an action (namely, its expected value), and would not consider other parameters such as the uncertainty of its own estimates (Doya, 2008).
However, instead of blindly trusting one’s own internal estimates of reward, animals and humans agents balance between exploitation and exploration, i.e., making decisions based on the current knowledge of the environment or explore novel options and courses of actions. In this context, exploitation refers to a policy where a decision-maker always selects the option that, in the past, has been associated with the highest rewards; and exploration indicates the deviations from this strict policy to re-explore sub-optimal or previously unexplored options. Exploration is related to response variability because, when an agent explores new options (instead of sticking with the ones that are currently deemed the best), the variability of its own behavior increases.
There are a number of circumstances where exploration can be more beneficial than exploitation. Consider, for instance, the case of a mouse navigating in search of food in a new maze: being the environment novel, the rat benefits from examining the existing alternatives before settling for one in particular. Exploration is also advantageous when contingencies between actions and rewards suddenly change. Every creature lives in a changing, dynamic environment, where a successful behavioral routine might suddenly become inappropriate. For instance, a rat might learn that a path through the maze is blocked, and a bird might learn that its current song does not attract females (Or, for that matter, a scientist might find out that a certain theory does not explain a new set of data). When the environment changes, the rewarding values of actions that have been previous learned in the past become untrustworthy, and alternative course of actions must be explored.
Conversely, circumstances exist where capitalizing on the learned values (LV) of each action is advantageous. This is the case, for instance, when the surrounding environment is stable, and all the possible options have been explored thoroughly.
The balance between exploration and exploitation is related to the problem of how much trust an agent should put into its own knowledge of the environment. Intuitively, it makes sense for an agent to explore more when it is uncertain about the state of the environment. A number of authors have suggested that, as dopamine conveys information about the difference between predicted and expected rewards, other neurotransmitters could encode the amount of confidence an agents has about its own estimates. Such a role has been proposed, for instance, in the case of norepinephrine (Aston-Jones and Cohen, 2005b; Bouret and Sara, 2005; Yu and Dayan, 2005; Dayan and Yu, 2006).
This paper puts forward the hypothesis that the balance between exploration and exploitation can be interpreted in terms of the amount of response variability originating in the striatum. Variability is ultimately controlled by cholinergic interneurons and modulated by dopamine, providing a way to capture exploration in decision-making with the same parameters and inputs that are available to reinforcement learning models of the basal ganglia.
Summary
We have reviewed three existing problems with the current understanding of basal ganglia function, i.e., the problem of accounting for striatal microcircuitry, the problem of reconciling the role of the basal ganglia in skill acquisition and in birdsong learning, and the problem of how response variability in controlled in decision-making. This article explores the hypothesis that the cholinergic interneurons (i.e., TANs) in the striatum provide a common response for these problems, and that their role can be seen as modulating response variability on the basis of expected rewards. The next sections will further specify this hypothesis as implemented in a computational model, and describe its application to a decision-making task.
Materials and Methods
The theory behind the framework makes the following three assumptions: (1) in the basal ganglia, each action is represented by specific set of neurons in the striatum; (2) the incoming cortical projections transmit information about the current state of the environment; and (3) the activity of striatal neurons is a function of their strength of association with the cortical patterns (which, in turn, is a function of the previous history of rewards). In reinforcement learning terms, the cortical inputs constitute the state of the system S, and the various pools of neurons that are activated by S represents the set of possible actions a1… aN. Because the associations between S and each pool of units is a history of reward, the activations A1, A2, … AN of the neurons reflect their expected value V, i.e., Ai ∼ Vi.
A rational system will base the probability of choosing each action on the distribution of activations among all the possible actions, choosing the most active ones the most often. A standard way to capture this is to transform each value into a corresponding probability by means of a Boltzmann distribution:

Where p(ai) is the probability of selecting action ai, Vi is the value (i.e., expected reward) of action i, and T is a global parameter, known as temperature, that regulates how deterministic the choice between competing actions is. The parameter T can be seen as a means to balance between exploration and exploitation: as T approximates zero, decisions converge deterministically toward the highest-value action, while larger values of T produce increasingly more uniform distributions of probabilities across different actions and lead to more unpredictable choices.
It is problematic to relate the activation of neurons encoding an action ai to the quantity eV(i)/T. In the Boltzmann equation, the denominator T has the functional role of magnifying the differences between different values of V. Within a neural framework, however, one must work within simple additive quantities. One way to capture the effect of temperature is through a adaptive inhibitory threshold. The mechanism works as follows. Figure 2 illustrates a simple, idealized case where three actions (A, B, and C) are encoded by the three different neurons. The activation of each cell is represented by the height of the corresponding bar. In particular, the full length of each bar represents the total excitatory inputs; the black line represents a common inhibitory input; and the black top of a bar, above the black line, represents the amount of activation remaining after subtracting the inhibitory effect. This remaining activation (the dark, top parts of each bar) is the quantity entered into Eq. 1.
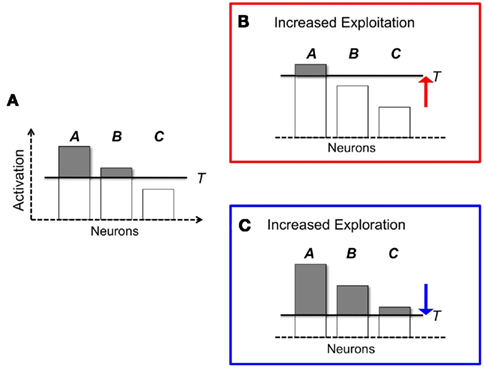
Figure 2. How widespread inhibition modulates response variability. The panels depict three hypothetical situation where three neurons are active, corresponding to three possible, responses (A, B, C). Each neuron’s activation is represented by the height a corresponding bar; widespread inhibition T is represented as a horizontal line. In (A) widespread inhibition T limits the selection to options A and B. The final selection will be determined by their relative activations above threshold (dark gray part of the bars). (B,C) represent different versions of the same situation, where the exploration/exploitation tradeoff is modulated by the raising [(A) increased exploitation] or lowering [(B) increase exploration] the inhibitory thresholds T.
The amount of competition between alternative options can be modulated raising or lowering the dark line, i.e., the shared inhibitory input. For instance, one can increase exploration by lowering inhibition, as shown in Figure 2C. Alternatively, one can increase exploitation by raising the inhibitory value until only the most active option A is considered (Figure 2B). In fact, lowering or raising inhibition permits to finely calibrate the relative magnitudes of each option.
Thus, we have established a correspondence between the term T in a Boltzmann equation and a widespread inhibitory signal across projection neurons. The second term corresponds to a widespread inhibitory neural input, which should be roughly constant across neurons encoding for competing actions. Cholinergic interneurons seem particularly adapt to provide such a widespread inhibitory signal, because they provide a very dense cholinergic innervation of the striatum, which is amplified by their control of GABA-ergic interneurons (Koós and Tepper, 2002; Bonsi et al., 2011), and because their activity is correlated (Morris et al., 2004). Thus, this paper suggests that one of the their functional roles is to modulate noise in action selection at the level of the striatum, playing a computational role akin to the T parameter in the Boltzmann equation.
One might wonder which circumstances make variability desirable. In general, response variability (i.e., exploration) can be seen as a mechanism to foster learning, and variability should increase in situations that demand a refinement of knowledge of the environment. Two intuitive examples of such situations are when an agent initially learns the values of available options, and when changes in the environments cause strong violations of the expected payoffs of an options (e.g., “expected” and “unexpected” uncertainty, according to Yu and Dayan, 2005). An alternative way of framing this problem is to see response variability and exploration as inversely proportional to the confidence an agent has in its own knowledge; the more reliable the knowledge, the less advantageous it is to explore the values of different options.
Confidence (or, alternatively, uncertainty) in one’s own current knowledge can be gathered from performance feedback. In the striatum, performance feedback is conveyed by dopamine neurons, whose firing rate is proportional to the difference between expected and actual rewards (Schultz, 1998, 2002). For example, a positive dopamine response signals that the actual outcomes are larger than expected. Such a signal implies that the previous choice was correct. Under such circumstances, the probability of making the same choice should increase and, correspondingly, exploration should be reduced. On the contrary, a negative dopamine signal implies that previous estimates were incorrect, and alternative decisions should be explored.
In addition to conveying performance feedback, dopamine also modulates synaptic plasticity (Wickens et al., 1996; Calabresi et al., 2000b). Thus, a positive dopamine response strengthens the synapses between cortical inputs and projection neurons, making the response more likely to occur. At the same time, dopamine strengthens the response of at least certain types of interneurons, such as fast-spiking interneurons (Bracci et al., 2002) to the same cortical inputs, thus increasing the level of inhibition, and limiting the number of potential active neurons.
By linking variability to dopamine response, this framework establishes a straightforward method for controlling the balance of exploration and exploitation based on internal measures of behavioral performance.
Implementing and Testing the Framework: The BABE Model
The previous section has established the connection between the activity of striatal inhibitory interneurons and the variability in decision-making. This section provides experimental support for the validity of this framework by describing a neurocomputational model, named basal ganglia acetylcholine-based entropy (BABE), that embodies it, and by proving its validity through simulations of decision-making tasks. In order to test the viability of the proposed framework, the BABE model was tested on a decision-making task that stresses the importance of response variability and adaptive behavior in reinforcement-based decision-making. The next sections will first introduce the experimental task, then the model designed to perform it (and its comparison to other models), and finally the results of two tests of its performance.
The task
The task consists of a simplified version of the probabilistic selection (PS) task, first introduced by Frank et al. (2004) to study the role of dopamine and basal ganglia in decision-making.
In the original task, participants were repeatedly presented with pairs of Japanese Hiragana characters, and required to choose one character from each pair by pressing a key on the keyboard. For simplicity, we will indicate each character with one of the Latin letters A through F. Selecting each character resulted in a feedback message (either “Correct” ors “Incorrect”) that was presented visually to the participant. Each character was associated with a different probability of yielding a “Correct” outcome. The participants’ goal was to select from each pair the character that was more likely to be “correct.”
The stimuli were presented as Hiragana characters in order to look unfamiliar to the original sample of American participants, and thus be difficult to verbalize. This prevented participants from reverting to strategies that relied on declarative memory (such as explicit encoding and recall of previous decisions), and pushed them toward a more “implicit” and reinforcement-driven decision strategy instead.
Three possible pairs of characters combinations were given, which we will indicate as AB, CD, and EF. Within each pair, one of the characters (A, C, and E) had a high probability of being “correct,” and the other (B, D, and F) had a low probability. However, feedback was always binary so that participants had to discover the different probabilities associated with each option by repeatedly sampling each character in the pair. The probabilities were varied across characters, as showed in Table 1.

Table 1. Summary of the different trial types (“Pairs”) used in the PS task and the probability of each stimulus being associated with a reward.
Although it was designed to verify specific experimental predictions (such as the differential effects of dopamine for high- and low-probability stimuli) that lay beyond the scope of this paper, the task represents an ideal test-bed for our framework for three reasons. First, it was explicitly designed to be implicit in nature and depend on a procedural learning system that most authors (Cohen and Squire, 1980; Knowlton et al., 1996; Packard and Knowlton, 2002; Seger and Cincotta, 2005) associate with the basal ganglia, thus providing a natural application of our computational results to the real world. Second, it is an iterative multi-option decision-making paradigm, and thus it belongs to a class of tasks that are frequently used in the decision neuroscience literature (Bechara et al., 1994; Bowman and Turnbull, 2004; Fellows and Farah, 2005). Third, it manipulates both the reward probability associated to each option (from A’s 80% to B’s 20%) and the levels of reward discriminability within each pair (from the high discriminability pair AB to the low-discriminability pair EF).
To facilitate the testing of our framework, one crucial modification has been applied to the PS task. In the simulated version, the model is free to indicate each of the six possible options as a response for each pair. While this modification makes each pair presented akin to a simple pair-specific cue (as there is nothing left in the pair AB that explicitly limits the possible choices to A and B only), it permitted to let the model develop its own internal representations of the decision context, without having to directly encode it in the architecture.
The model
Developing a model to test this framework requires putting together three different components. First, one needs to have a simple but plausible model of the cortico-basal ganglia loop, reflecting the major anatomical features of the circuit. Second, one needs to connect the basal ganglia circuit to a plausible reinforcement learning system, so that it can learn which actions to perform in response to environmental stimuli. These first two components are common to virtually every existing reinforcement learning model of the basal ganglia. The third component is instead specific to our framework and a few other models only (Stocco et al., 2010; Ashby and Crossley, 2011), and consists of a layer of striatal interneurons, providing the diffuse inhibition that modulates variability.
The next section will briefly describe the architecture of the BABE model, how it relates to the basal ganglia functional anatomy, and how it performs the PS task. The model’s architecture is illustrated in Figure 4, while Figure 5 provides a visual rendition of its real implementation. A complete description of the model’s implementation and dynamics can be found in the Appendix.
The cortico-basal ganglia system
The main component of the BABE model is the cortico-basal ganglia system. This system is responsible for selecting an option (i.e., either A or B) when given a particular decision (i.e., the pair AB). Thus, it can be thought of as the analogous of the “actor” in the actor–critic framework (Barto, 1995).
The system was designed to be simple while respecting the general anatomy of its biological counterpart. It includes two pools of neurons supposed to represent cortical areas, which are named “Context” and “Time” layers (see Figure 4). The Context layer represents the current decision context, i.e., the current pair of stimuli that are presented in a trial of the PS task (AB, CD, or EF). This layer can be thought of as a working memory region holding contextual information (hence the name), and receiving input (e.g., visual inputs of the characters presented on the screen) from posterior sensory regions (left unmodeled). The Time layer maintains a representation of the time course of each decision-making trial. As a trial progresses, neuronal activation moves across the “Time” layer from front to back. Thus, when a new decision-making trial is presented, only one neuron in the first row will be active; when the model provides a response, only one neuron in the second row will be active; and, finally, when feedback is delivered, one neuron in the third row will be active.
Both the Time and the Context layers in turn project to the dorsal striatum, which is made up of three interrelated sets of neurons: a set of tonically active (i.e., cholinergic) interneurons, labeled as “TAN”; and two set of striatal projection neurons, representing the striatonigral (“SN”) and striatopallidal (“SP”) cells, respectively. This section will focus on the role of the SN and SP units, while TAN interneurons will be discussed later.
Although SN and SP cells have ultimately opposite effects within the basal ganglia circuitry, their competition does not manifest itself at the level of the striatum. SN and SP cells do make large inhibitory connections between each other, but these connections are extremely weak (Jaeger et al., 1994). Instead, as outlined in the Introduction, SN and SP cells send inhibitory projections to the other nuclei downstream in the basal ganglia hierarchy, originating the direct pathway and the indirect pathway (Albin et al., 1989; DeLong, 1990). Both pathways eventually converge on the pars reticulata of the SNr and the GPi, two nuclei that control the medial and dorsal nuclei of the thalamus and their projections to the cortex. Although both the direct and the indirect pathways are made of inhibitory projections, their different number of segments results in SN cells having a net excitatory effect on the thalamus, and the SP cells having a net inhibitory action. Because of their effects downstream on the circuit, these two types of neurons are thought to signal either the execution (SN cells) or the vetoing (SP cells) of one particular action or motor program. For example, in the successful prefrontal–basal ganglia working memory model (PBWM; Frank et al., 2001; O’Reilly and Frank, 2006) the two groups of neurons are explicitly referred to as “Go” and “No Go” cells.
Since the competition between the SN and SP cells of the striatum plays an important role in our framework, the distinction between the two groups of cells has been maintained in the model. The exact arrangement of the direct and indirect pathways, however, has been simplified. In particular, the output nuclei of the basal ganglia (SNr and GPi) and the intermediate nuclei of the indirect pathway (e.g., external part of the globus pallidus and the sub-thalamic nucleus) have been omitted, so that the SN and SP cells project directly to the model thalamus (see Figure 4). This simplification is justified by the fact the further information processing that might occur in these nuclei (e.g., Bar-Gad et al., 2000) is not relevant for the scope of this paper, and would not affect the localist representation format used in this model.
To maintain the correct direction of the effect of the two pathways, SN neurons were modeled as sending excitatory (instead of inhibitory) signals to the thalamus, while the model SP neurons send inhibitory projections (see Figure 3). A similar simplification scheme has been previously used in other basal ganglia models (Frank et al., 2001). Also, the hyperdirect pathway that proceeds from the cortex to the output nuclei through the sub-thalamic nucleus has also been left out of the BABE model. These parts of the circuit play a significant functional role in the biological basal ganglia circuit, and in particular in response inhibition (see, for instance, Frank et al., 2007) and action selection (Gurney et al., 2001; Nambu et al., 2002). However, response inhibition does not play a significant role in this research, and action selection has been simplified as a Boltzmann selection algorithm. Thus, the omitted parts of the circuit are not relevant to the topics discussed in this paper.
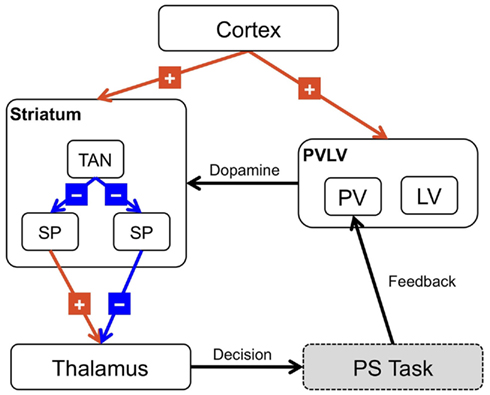
Figure 3. Architecture of the BABE model. Excitatory projections are marked with a “+”; inhibitory projections with a “−”; black arrows represent modulatory or control signals. SP, striatopallidal projection neurons; SN, striatonigral projection neurons; TAN, striatal tonically active neurons (i.e., cholinergic interneurons).
Finally, it is worth mentioning that the biological basal ganglia circuit also includes feedback projections that proceed from lower to higher nuclei in the circuit tree. For instance, there are projections from the thalamus to the striatum (Sidibé et al., 2002; Smith et al., 2004), from the thalamus to cholinergic interneurons (Lapper and Bolam, 1992), and from the globus pallidus to GABA-ergic striatal interneurons (Bevan et al., 1998). These ascending projections are thought to play an import control function (Redgrave et al., 1999). Because the arrangement of circuit has been simplified, our model includes only a simple feedback system represented by excitatory projections from the model thalamus to the SN and SP cells. These pathways are important to allow the BABE model to converge toward stable states.
Representation of context and choices in the cortex and basal ganglia
The BABE model encodes decisions and actions in a simple localist fashion, so that each particular pair of stimuli (the decision context) and the each possible choice (the actions) are represented by a single model neuron. A real biological system is unlikely to revert to such a brittle representation scheme, but localist representations have the advantage of simplifying the model to terms that are easier to analyze, implement, and to visualize. In fact, many proposed models of the basal ganglia adopt localist or quasi-localist representations (Barto, 1995; Suri and Schultz, 1999; Frank et al., 2001; Gurney et al., 2001; O’Reilly and Frank, 2006). Furthermore, large-scale biological models can be build to approximate computations described by localist networks (Eliasmith and Anderson, 2003), and the computational principles of this framework can be generalized to other representation schemes. Thus, the use of localist representations does not compromise the soundness of our conclusions.
In the representation scheme used for the simulations, each of the three pair of stimuli in the simulated task (AB, CD, and EF) is represented by the activation of a single neuron in a set of three. Therefore, each pair is encoded as an individual decision cue. The same representation format is used for both the “decision context” and the “time context,” with the difference that the time context contains enough units to represent each stimulus pair across different phases of a trial (see Figure 4). Each of the six possible stimulus choices (A through F) is represented by a corresponding unit in the SN and SP cells and in the Thalamus.
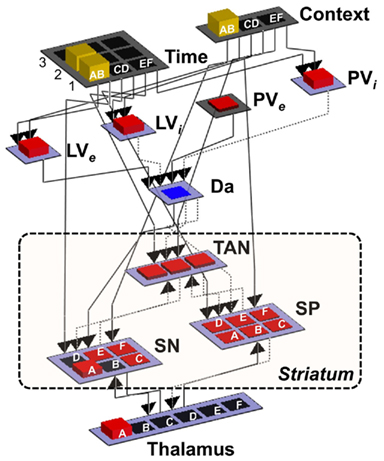
Figure 4. Implementation of the BABE model. Separated pools of neurons represent gray matter nuclei and cortical regions; the height and color of the each unit represents the amount of neuronal activation. Dotted arrows represent inhibitory projections, while solid lines represent excitatory projections. Context, cortical region representing the current decision context (i.e., one of the pairs AB, CD, or EF); Time, cortical region representing the current phase in the decision trial; LVe, LVi, PVe, PVi, components of the PVLV reinforcement learning system (see main text for details); Da, dopaminergic neurons; SP, striatopallidal projection neurons; SN, striatonigral projection neurons; TAN, striatal tonically active neurons (i.e., cholinergic interneurons).
The reinforcement learning system
The BABE model uses the PVLV system developed by O’Reilly et al. (2007) as its reinforcement learning system (akin to the “critic” in an actor–critic architecture). In PVLV, the dopamine response is the sum of the signals computed by two subsystems, the primary value (PV) and the learned value (LV) component (see Figure 3). The PV system learns over time the degree of predictability between a primary reward and the state of the environment where the reward is delivered. The LV component, instead, learns the degree of predictability between a state of the environment and the future primary rewards that will be delivered, based on how predictably the given state will lead to the state where rewards are delivered.
Each of the two subsystems is further divided into two parts, an excitatory part (PVe, LVe) and an inhibitory one (PVi, LVi, see Figure 4). Within each sub-system, the excitatory part learns faster than the inhibitory part. The activity of PVe reflects the immediate reward being delivered at a given state. As the primary reward becomes firmly associated to the condition where it is delivered, the contribution of PVi increases and cancels out that of PVe. Therefore, the more a reward is expected, the less effective it is. At the same time, LVe learns to associate the value of the reward to those conditions and states of the environment that are ultimately conducive to its delivery. As a result, the excitatory activity of a primary reward shifts back in time to the earliest state that is reliably associated to it. Finally, the LVi system slowly learns to expect and cancel out the activity of LVe. The response of dopamine neurons is a function of the sum of the contribution of both the PV and the LV inhibitory and excitatory components (see Appendix for a complete description of the equations governing the system).
Although being somewhat unusual because not based on a Temporal Difference algorithm (Sutton, 1988), PVLV is as successful as any other reinforcement learning model in reproducing the distinctive features of dopamine neurons response. These features include the decrease in the activity of dopamine neurons as the reward becomes predictable, and their response’s shifting back in time to predictive cues. Furthermore O’Reilly et al. (2007) have proposed a convincing anatomical substrate for each of the PVLV components, while the physiological substrates of most neurobiological models based on TD-learning have been called into question (Joel et al., 2002). In particular, the LV system has been proposed to correspond to the computations of the ventral striatum, thus suggesting an anatomical connection with the computations occurring in the basal ganglia (O’Reilly et al., 2007) and providing a physiological ground for using it in our simulation. Finally, PVLV has been previously used as the primary learning system in other basal ganglia models (Frank and Claus, 2006; O’Reilly and Frank, 2006).
Striatal interneurons
The most crucial part of the BABE model is represented by the layer of cholinergic TANs, labeled “TAN” in Figures 3 and 4. As discussed above, these neurons provide both direct and indirect inhibition for striatal SN and SP neurons, thus controlling their response to excitatory cortical inputs.
At the onset of behaviorally relevant stimuli, TANs show a sudden increase in firing rate, which is followed by a sudden pause in activity. Although acetylcholine has complex modulatory effects on striatal projection neurons (e.g., Calabresi et al., 2000a), experimental evidence suggests that its main effect is inhibitory, and that it is the transient pause in cholinergic activity that allows projection neurons to fire (Morris et al., 2004; Reynolds and Wickens, 2004; Reynolds et al., 2004; Pakhotin and Bracci, 2007; Bonsi et al., 2011). In fact, it has been suggested that the primary purpose of TANs is to detect specific contexts where routine actions (encoded within striatal projection neurons) need to be applied (Apicella, 2007).
In addition to responding to cortical signals, striatal cholinergic neurons are also sensitive to reward (Morris et al., 2004) and their response is modulated by dopamine inputs (Bolam et al., 2000; Reynolds et al., 2004; Tepper and Bolam, 2004). Thus, they represent the ideal substrate for modulating variability in the way outlined by our framework.
In the real striatum, TAN modulate the activity of projection neurons both directly (e.g., Pakhotin and Bracci, 2007; See Figure 1) and indirectly, via their influence on GABA-ergic interneurons (e.g., Koós and Tepper, 2002; See also Figure 1). This control network was simplified in the model and reduced to a single pool of TANs, whose functional role incorporates elements of GABA-ergic interneurons, such as the strong inhibitory influence over SN and SP cells. The control of projection neurons was achieved by setting the initial weights of synapses from TANs to SN and SP neurons to such values that no cortical signal can activate a projection neuron unless TAN activation drops from baseline. Their elevated tonic activity of cholinergic interneurons was modeled by setting the synapses between cortical cells (i.e., state and time layers) and TANs to initially elevated values, so that even minimal cortical stimulation is sufficient to keep them tonically active. In these synapses, learning occurs by reducing (instead of increasing) the strength of synapses from cortical inputs of interest. This mechanism was sufficient to reproduce the decrease of TAN activity at the onset of significant inputs (see the Appendix for a more detailed description of the learning algorithm).
Tonically active neurons also receive projections from dopamine neurons (Kubota et al., 1987; Lavoie et al., 1989). Dopamine modulates the response of TANs in a complex way, activating both excitatory, D1-like (Aosaki et al., 1998) and inhibitory, D2-like (DeBoer et al., 1996; Pisani et al., 2000) receptors. Simulations of these effects suggest that, as in the case of cortical projections, dopamine release produces initial excitatory burst of TAN activity, which is followed by a phasic pause (Tan and Bullock, 2008). To capture this effect, dopamine projections were modeled as inhibitory. As outlined in the framework, the model dopamine modulates the synaptic plasticity of cortical projections to TAN, so that their inhibitory influence is reduced by dopamine depletion (i.e., actual rewards are smaller than expected) and increased by dopamine release (i.e., actual rewards are larger than expected; See Appendix for details).
Finally, experimental evidence suggests that that maybe TANs (Tepper and Bolam, 2004; Tepper and Plenz, 2006; Bonsi et al., 2011; Chuhma et al., 2011, but see Sullivan et al., 2008 for contrary evidence) and at least some types of GABA-ergic interneurons (Ibáñez-Sandoval et al., 2010; Tepper et al., 2010) receive inhibitory projections from striatal projection neurons. These projections were modeled as simple inhibitory projections from SN and SP cells to TANs (see Figure 4). In agreements with what is generally known about lateral inhibition in the striatum (Jaeger et al., 1994), these synapses are weak; nonetheless, their feedback signals is plays an important functional role in making the circuit converge toward a stable state.
Results
The previous sections have outlined a theory according to which striatal cholinergic interneurons contribute to learning by modulate variability in decision-making. The theory is embodied in a neurocomputational model of the basal ganglia where a pool of simulated cholinergic interneurons is introduced to modulate the activity of the striatal cells that control the execution of an action.
To verify our hypothesis, the BABE model was compared to a reduced version that shares the same architecture and parameters, but that does not include the layer of interneurons. In this reduced version the dorsal striatum is entirely composed of SN and SP projection neurons, which are the direct and only target of cortical stimulation. This architecture is common to other models of the basal ganglia, such as PBWM (Frank et al., 2001; O’Reilly and Frank, 2006) and FROST (Ashby et al., 2005).
In addition to the removal of the TAN units, two additional changes were made to the reduced model. First, a k-winner-takes-all (kWTA) algorithm was added to the SN and SP groups. The kWTA algorithm maintains the first k most active units, and sets to zero the activation values of the rest, reducing the competition between active units. The kWTA procedure is often used in computational models of the basal ganglia to mimic internal lateral inhibition (Frank et al., 2001; O’Reilly and Frank, 2006), and in preliminary simulations was found to improve the reduced model’s performance significantly. In our simulations, k = 41. The second change consisted in replacing the original rate-code activation function of the SN and SP neurons with a more conventional sigmoid function (see Appendix for details); again, this was found to improve the performance of the model although reducing somewhat its biological plausibility.
Note that, even without the modulation of TANs, the reduced version still performs a rudimentary form of exploration/exploitation tradeoff. This is due to the fact that the Boltzmann selection rule (Eq. 1, see also Appendix) tends to select an option in proportion to its expected value (biological models of action selections, such as Gurney et al., 2001, also tend to do the same). Thus, as the estimated value of an option increases, that option will be selected more and more often. The following tests will show, however, how the addition of TANs significantly improves this mechanism, making the BABE more flexible than a traditional reinforcement learning model.
The full and reduced versions of the BABE model were then compared in two tests of performance. Each tests consisted of 100 simulated runs of each model. During each run, one version of the model (either the full or the reduced version, in alternating fashion) was generated anew and performed a series of trials with PS task. During each trial, one of the three stimulus pairs (AB, CD, or EF) was randomly presented to the model. The model was then let converge to a stable pattern of Thalamus activations, which was interpreted as indicating one of the choices A, B, … F. Finally, a decision outcome (either “Correct” or “Incorrect”) was internally generated based on the success probability associated with the given response (see Table 1), and presented to the model to provide the reward signal necessary for learning. Each trial was terminated when the decision outcome was presented to the model, and each run was terminated as soon as the model reached a predefined performance criterion. The performance criterion was different for the two tests (see next sections for details). A complete description of the computational steps occurring during a simulated decision-making trial is provided in the Appendix.
Test 1: BABE Advantage in Learning and Re-Learning
The first test was designed to verify whether the introduction of a layer of interneurons does indeed facilitate learning and re-learning. The rationale for the test is that, by modulating the initial exploration, the BABE model should discover the best options faster, and converge on them quicker than the reduced model. Also, the BABE model’s advantage should be greater during re-learning, since the reduced version has to progressively learn to devalue what was previously the best action before refraining from using it.
To verify these predictions, a test suite was developed where the model interacted with the task until its performance was indicative of having successfully learned the best option for each pair. The criterion for successful learning was that, for each pair of stimuli AB, CD, and EF, the model should have picked the better of the two options (A, C, and E, respectively) with a probability equal or superior to the option’s probability of resulting in a correct trial. For instance, in the case of the pair AB, A is the best option and has an 80% chance of yielding a “Correct” result; thus, learning was considered successful for the AB pair when the model selected A at least 80% of the times. The probability of selecting an option was calculated over a moving window of the past 10 selections where the option appeared, and a separate moving window was kept and updated for each pair.
As soon as the model has reached the criterion for all pairs, the reward contingencies were suddenly changed, so that the least successful stimulus within a pair (B, D, and F, respectively) was now given the most successful one’s probabilities, and vice versa. For example, in the case of the pair AB, the change resulted in B being the correct choice 80% (and A only 20%) of the times. The model was let to interact with the task until it had reached the criterion again.
We predicted that the full version of the model would learn faster than the reduced version during the initial phase. The rationale for this prediction is that the full version of the model should be faster at shifting from exploration to exploitation, thus selecting from the best options more frequently and reaching the criterion faster.
In addition, we predicted that the reduced version of the model would learn more slowly during the re-learning phase than during the initial phase; on the other hand, we expect to find little or no difference between learning and re-learning for the full version of the BABE model. The rationale for this prediction is that, in the reduced model, the amount of exploration is simply proportional to the current value of an option (because selection is simplified as a Boltzmann rule), and the model learns by gradually revising each option’s value estimate until they reach their true values. Therefore, when the reward probabilities within each pair are swapped, the reduced model has first to unlearn its current estimates of each option’s value before learning the new ones. For instance, in the AB pair, the value of A has to be revised downwards from a learned 80% reward probability to a mere 20%, and B has to be revised upwards from 20 to 80%. Before the model samples with equal frequency from A and B, they both have to reach an estimated value of 50%. The full model, on the other hand, reacts to the contingency reversal by quickly reverting to exploring all the other options, thus not requiring additional time to relearn.
Results
Figure 5 illustrates the results of the test. The two panels represent the performances of the reduced (left) and full (right) versions of the BABE model. Within each individual plot, the bars represent the number of trials at which the learning criterion was passed for each of the three pairs during the two learning phases; gray bars represent the initial learning phase, and dark bars represent the re-learning phases following reversal. The data were analyzed using a mixed-effects ANOVA model where the number of trials to reach the criterion were the dependent measure, and the Model (full vs. reduced), Trial Type (AB, CD, EF), and Condition (Learning vs. Re-learning) were the independent measures.
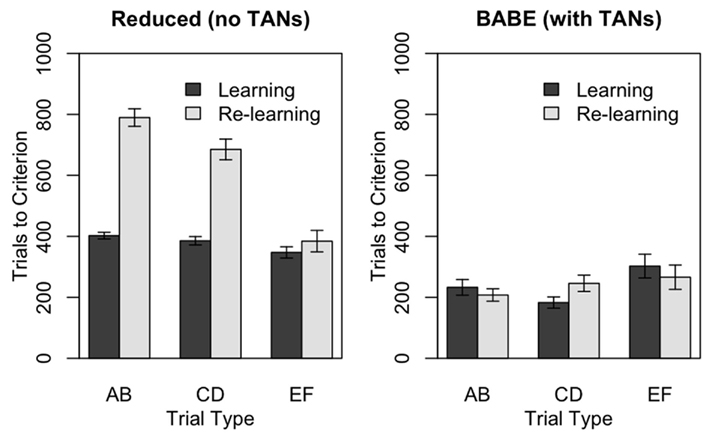
Figure 5. Performance of the reduced version (left) and of the full version (right) of the BABE model. Bars represent the number of trials needs to reach the criterion in the PS task, during either the initial learning phase (“Learning,” dark gray) or after the reversal of stimuli probabilities (“Re-learning,” light gray). Values represent means ± SEs.
The analysis showed that all the main effects and all the interactions were significant (F > 11.52, p < 0.0001). A separate ANOVA performed on the reduced model data showed that, as predicted, the reduced model was slower to achieve the criterion during the re-learning then during the learning phase [F(1,100) = 151.48, p < 0.0001]; that it was faster to converge on the criterion for the smaller-contrast trial types [i.e., EF was learned faster than CD, and CD faster than AB: F(2,200) = 59.37, p < 0.0001]; and that the difference between trial types was magnified during re-learning [F(1,100) = 22.65, p < 0.0001]. In the full version of the BABE model, on the other hand, there was no difference in performance between the learning and the re-learning phases (F < 0.001), while the significant effect of Trial Type [F(1,100) = 3.83, p < 0.03] was due to EF trials being learned slower than the other two.
In summary, the introduction of cholinergic interneurons to modulate the response variability results in a significant improvement in decision-making performance. Consistent with the framework outlined herein, the model can use the difference between expected and predicted rewards to explore new options and thus adapt in a changing environment.
Test 2: Modulation of Variability and Success Expectations
The first test has established that introducing cholinergic interneurons improves the model’s performance in a decision-making task. However, our framework specifically claims that the performance improvement is due to better and more adaptive modulation of response variability. This claim implies that (a) The model should modulate response variability in response to a change in the reward contingencies (such as the reversal of success probabilities); and (b) That performance improvements should correlate negatively with response variability.
A second test was performed to verify these predictions. During this test, each model performed the PS task until it had successful learned the best response for the AB trials. Success in learning was assessed using the same criterion as in the previous test, i.e., by checking whether the best option (A before reversal, and B after) was chosen at least 80% of the times in the previous 10 trials. Upon reaching the criterion, the success probabilities within each pair were swapped. Performance of the model was then recorded until it had performed an additional 100 AB-type trials. Although CD and EF trials were still randomly intermixed with AB trials, this test focuses on AB trials only, as they are those where the difference between the full and reduced versions of the BABE model become more apparent in re-learning (see Figure 5).
Results
In order to analyze the modulation of response variability, the activity of SN and SP cells was recorded at each trial, and the group entropy H was calculated separately for the SN and SP cells. Entropy is used in information theory as a measure of the information content of a message: the higher the entropy level, the lower the amount of information that is conveyed. Entropy is also used in thermodynamics as a measure of uncertainty of the state of a physical system: the higher the entropy, the more chaotic and unpredictable is the system. In the case of SN and SP cells, entropy provides a convenient way to relate the state of activation of striatal projection neurons to the uncertainty of the final behavioral response made by the model. When many SN cells are active at the same time, entropy is high, implying that the information available in the system is low (as there is no clear preference for one action over the others) and the system is less predictable (different response might be selected). Similarly, when only few SN cells are active, entropy is low, implying that the information available is elevated (there is a clear preference for one action) and the final behavioral response is more predictable. Because of this properties, entropy provides a convenient way to relate a physical property of the model striatum (the pattern of activation in projection neurons) to uncertainty and behavioral response variability (the action that would eventually be selected).
Entropy was calculated as follow:
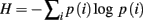
Where p(i) is the probability of neuron i encoding the final response, which was estimated by dividing each cell’s activation value over the sum of all the activation values of SN or SP units.
To accommodate random chaotic variations during a model’s interaction, the values of H for each run of each model were normalized, so that they had a mean of 0 and a SD of 1. The normalization was needed because the two models (and each run of each model) have different baseline entropy levels. The normalization process removes this baseline differences while preserving the time course of entropy across the task and the modulation of entropy in response to the reversal of contingencies. Note that, although entropy can only be a positive quantity, its normalized version can take both positive and negative values (because its mean is constrained to be 0). To track the variations of entropy over time, the entire time series of 130 trails (30 preceding and 100 following the reversal) was divided into blocks of 10 trials each, and the averages for each block calculated.
The results of this analysis are shown in Figure 6. In the figure, the data from the reduced model is on the left, and data from the full version of the model is on the right; within each plot, points and lines in dark gray represent values for SP cells, and those in light gray represent values for SN cells. The vertical dotted line represents the moment where the probabilities were reversed.
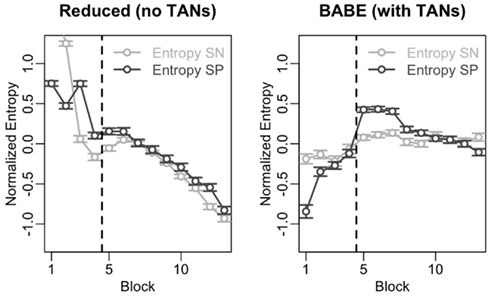
Figure 6. Time course of the entropy level in the SN and SP cells across the 13 blocks of Test 2 for the reduced (left) and full version (right) of the BABE model. The dark gray lines and circles represent entropy in the SP cells; the light lines and circles represent entropy in the SN cells. Points represent mean values, and the vertical line indicates the point where the success contingencies were reversed during the test.
In the figure, entropy follows different time courses for the two models. In fact, entropy in both SN and SP cells correlates negatively with time in the reduced model (Spearman’s r > 0.85, p < 0.0002) but not in the case of the full version of the BABE model. This decline of entropy with time might be the cause for the greater difficulty shown by the reduced version to learn the correct options after the reversal (see previous section and Figure 5).
Despite exhibiting different time courses, both models are capable of modulating entropy in response to changing contingencies, as shown by the increase in entropy after reversal and as assessed by a series of t-tests (t > 4.66, p < 0.001). To assess whether the models differ, entropy modulation in both SN and SP cells was estimated as the difference between the highest entropy value after the reversal and the value immediate before the reversal. An ANOVA was then performed using the modulation estimates as the dependent variable, the neuron type (SN vs. SP) and the model (Full vs. Reduced version) as the independent variables, and model run as the error term. The results of the ANOVA showed that the full BABE model’s modulation of entropy was larger than the reduced version’s [F(1,87) = 20.42, p = 0.0002], but that there was no main effect of neuron type, and no interaction [F < 2.58, p > 0.1]. Thus, the full version of the BABE model shows a larger modulation of entropy in response to the reversal of success probabilities.
To make a stronger case for the claim that the model’s modulation of variability (as indexed by the entropy in SN and SP cells) occurs in response to changes in success probabilities, each model’s entropy level for SN and SP cells was regressed over performance, calculated as the probability of selecting the most-rewarding option (A before reversal, B after reversal) in a particular block. To make the data as comparable as possible, the first and the last two blocks were excluded from the analysis. The exclusion was due to the fact that the first block is affected by the large difference in the initial entropy between the two models (see Figure 6), while in the last two blocks the full model’s performance has grown significantly higher than the reduced version’s (p < 0.001). Therefore, blocks 2 through 11 permitted a fairer comparison between the two models.
Figure 7 illustrates the results of this analysis in form of scatterplots, with entropy on the x-axis and performance on the y-axis. As in Figure 6, the data from the reduced model is on the left, and data from the full version of the model is on the right; within each plot, points and lines in dark gray represent values for SN cells, and those in light gray represent values for SP cells. As predicted, performance does not inversely correlate with entropy in the reduced model; in fact, the slope of the regression line was positive for both SN and SP cells [even if not significantly so in the case of SN: β = 1.00, t(8) = 0.95, p = 0.37; and β = 1.38, t(8) = 2.44, p = 0.04, respectively]. On the contrary, performance was a reliable predictor of entropy in the case of the full version of the BABE model, with poorer performance being significantly associated to more entropy in both SN and SP cells [β = −0.67, t(8) = −2.52, p = 0.04; and β = −2.00, t(8) = –4.24, p = 0.004, respectively].
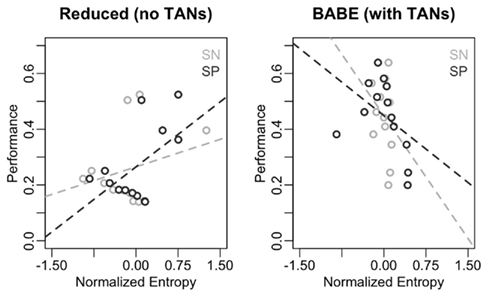
Figure 7. Correlations between performance and entropy levels for the reduced (left) and full version (right) of the BABE model. Performance (for the AB pairs only) is the abscissa, and entropy on the ordinate; The dark circles represent the SP cells; the dark dotted lines represents the regression lines for the SP cells; the light lines and circles represent entropy the SN cells; the dark dotted lines represents the regression lines for the SN cells.
In summary, the results of this test have shown that the introduction of cholinergic interneurons results in a modulation of response variability that is larger in response to changes in the reward contingences, more directly coupled with immediate performance, and less dependent on the amount of experience with the task, allowing for a quicker adaptive response in the face of changing contingencies.
Discussion
This paper presented a theory on how cholinergic interneurons (also known as TANs) in the striatum contribute importantly to decision-making by adaptively modulating the variability of action and option selection. The theory was implemented in a neurocomputational model of the basal ganglia circuit (called BABE) that was tested using an iterative decision-making task. The results showed that, compared to a reduced version that does not include modulation from acetylcholine interneurons, the BABE model is faster at learning, more capable of re-learning in response to perceived changes in action–reward contingencies, and more successful at balancing between exploration and exploitation in the face of a changing environment.
Role of Striatal Interneurons
The proposed framework accounts for the role of striatal interneurons in the striatum, and in particular cholinergic interneurons, therefore providing a more biologically accurate characterization of striatal functions and computations. Although cholinergic interneurons have been previously included in detailed models of basal ganglia physiology (e.g., Wickens et al., 1991; Tan and Bullock, 2008; Humphries et al., 2009, 2010), their role has been overlooked by most of the models of the basal ganglia role in to cognition (Barto, 1995; Beiser and Houk, 1998; Suri and Schultz, 1998, 1999; Amos, 2000; Frank et al., 2001; Gurney et al., 2001; Ashby et al., 2005, 2007; O’Reilly and Frank, 2006). A few models have accounted for cholinergic contributions, but have conceived of them in different, although not mutually exclusive, ways. For example, Stocco et al. (2010) suggested that the TANs provide a mechanism to limit striatal responses to specific contexts, and Ashby and Crossley (2011) proposed that cholinergic interneurons make reinforcement learning more precise by restricting the number of neurons where dopamine induces synaptic plasticity. Since both models rely on the cholinergic interneurons modulating their inhibition on projection neurons, they are both compatible with the proposed framework. Theoretical integration of these different functions of cholinergic interneurons is an interesting future direction to extend the BABE model.
Skill Acquisition and Birdsong Learning
One of the advantages of the proposed framework is that it reconciles two alternative views of the role of basal ganglia in skill learning, i.e., the view that the basal ganglia rapidly form stimulus–response associations, and the view that they provide variability in behavior (as in the case of birdsong learning). The BABE model claims that the two types of contribution occur at the same time, and are related to two different neurotransmitters (dopamine vs. acetylcholine) and two different types of neurons (projection neurons vs. interneurons) in the striatum, thus providing a framework where the two views can co-exist. In particular, this paper has proposed that the generation of variability in songbird vocalization during the learning phase is underpinned by acetylcholine and its effects on striatal interneurons. Under this hypothesis, the eventual, “crystallized” phase where a songbird’s song is fixed and stereotyped can be seen as the final exploitation of acquired knowledge in decision-making, while the generation of variable vocalization during the learning phase can be seen as the result of increased exploration among possible options.
Exploration and Exploitation
An important and novel contribution of this paper is that it accounts for how exploration and exploitation are balanced during decision-making. This account is set apart from other theories by employing the very same signals (e.g., dopamine) and circuitry (e.g., competing SN and SP cells) that are already present in other reinforcement learning models of the basal ganglia (Frank et al., 2001; Joel et al., 2002; O’Reilly and Frank, 2006). In contrast, previous biological models of the balance between exploration and exploitation relied on the introduction of somewhat novel mechanisms, such as, for example, introducing an uncertainty signal based on norepinephrine (Doya, 2002; Yu and Dayan, 2005; Dayan and Yu, 2006). One possibility is that different brain signals contribute to the modulate response variability, with acetylcholine relating variability to on-line performance measures (as in this the proposed framework) and norepinephrine relating response variability to other factors, such as general arousal (e.g., Aston-Jones and Cohen, 2005a,b).
Existing experimental evidence suggests that exploratory actions are based, in part, on contributions from prefrontal cortex (Daw et al., 2006). The current model is not inconsistent with these findings, as ultimately the computations performed in the basal ganglia result in a projection of information to the prefrontal cortex through the thalamus (Alexander et al., 1986; Albin et al., 1989; DeLong, 1990). Furthermore, it is worth noting that balancing between exploration and exploitation is a basic biological need, and can be observed in animals (e.g., in rats: Penner and Mizumori, 2012) whose prefrontal circuitry is not as sophisticated as in humans. Thus, the association between exploratory decisions and prefrontal cortex activation in humans might be due to some explicit, deliberative process instead of the automatic, reinforcement-based mechanism described herein. This explanation is consistent with the idea that prefrontal cortex and the basal ganglia both contribute to human decision-making, but that, while the basal ganglia implements a “model-free” system that selects actions based on their perceived values, the richest representations of prefrontal cortex also enable a “model-based” form of reinforcement learning that selects actions based on an internal representations of their consequences (Daw et al., 2005, 2011; Gläscher et al., 2010). Within this duel-system framework, exploration might originate in the prefrontal cortex as a means of building an internal model of the results of each action, which are subsequently used to modulate action selection in the basal ganglia loops. This dual-model approach, however, does not rule out the existence of simpler mechanism to modulate exploratory decision within the striatal microcircuitry, akin to the one described in this paper.
Extensions and Applications of the Model
In its current formulation, the model has a number of limitations. For instance, the model only includes cholinergic interneurons, and does not include the contribution of GABA-ergic interneurons. In fact, there are various types of GABA-ergic interneurons in the striatum, which have important modulatory effects on striatal function (Bonsi et al., 2011) and might interact with cholinergic interneurons as well (Sullivan et al., 2008). Also, the model accounts only for the inhibitory effect of acetylcholine, while this neurotransmitter has complex effects on its post-synaptic targets and on synaptic plasticity (Calabresi et al., 2000a). Finally, the model currently does not have a realistic system for action selection, which is simplified as a Boltzmann selection algorithm among those options whose corresponding cells are active. A more realistic system should include a biological mechanism determining a single action to be executed, probably by including the hyperdirect pathway (Gurney et al., 2001; Nambu et al., 2002).
Despite its limitations, the generality of the proposed framework makes it possible to integrate it with other models and architectures and apply it to other domains. For instance, basal ganglia models have been successfully applied to model behavioral impairments in Parkinson’s disease (Frank, 2005; Stocco et al., 2010). Because Parkinson’s disease originates from a depletion of dopamine in the basal ganglia (Jankovic, 2008), reinforcement learning models have provided a natural and successful framework to account for this impairment. Our model, however, provides a more complete account of neuromodulation in the striatum, and can be used, for instance to account for the positive effects of anti-cholinergic drugs in the treatment of the disease (Jankovic, 2008; Jankovic and Aguilar, 2008).
Also, two existing models of basal ganglia (PBWM; Frank et al., 2001; and the Conditional Routing model, Stocco et al., 2010) are based on the proposition that the basal ganglia play an even more general role in cognition than action selection. In PBWM, the basal ganglia control the access of working memory; and in the Conditional Routing model, the basal ganglia dynamically modify how signals are transferred to cortical regions. In both models, the basal ganglia allow for a rapid re-organization of brain activity, making them capable of performing unusually complex tasks. Within these models, modulation of response variability does not only result in exploration of the best options, but also in the explorations of novel ways to perform complex tasks. Thus, in principle, the cholinergic modulatory system could be used to explain how novel and creative lines of thoughts are generated in human cognition. Within the decision-making literature, this could be used to explain, for example, reward-based switches between alternative decision strategies within the same task (Stocco et al., 2009).
In summary, the proposed framework provides a simple yet powerful way to account for how response variability (and, in turn, exploration and exploitation) is modulated within the basal ganglia circuit. When applied to decision-making tasks, the framework results in significant performance improvements and greater behavioral flexibility. Future extensions of the BABE model will include applications to domains other than decision-making, providing a general mechanism for understanding action selection and information routing in the brain.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnote
- ^The value of k was determined as the smaller integer that guarantees that at least one neuron encodes the same choice (A, B,…F) in both SN and SP cells. A smaller value of k could lead the model to situations where there is no competition between the indirect and direct pathway, thus violating one of the core features of the functional anatomy of the basal ganglia.
References
Albin, R. L., Young, A. B., and Penney, J. B. (1989). The functional anatomy of basal ganglia disorders. Trends Neurosci. 12, 366–375.
Alexander, G. E., DeLong, M. R., and Strick, P. L. (1986). Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu. Rev. Neurosci. 9, 357–381.
Amos, A. (2000). A computational model of information processing in the frontal cortex and basal ganglia. J. Cogn. Neurosci. 12, 505–519.
Anderson, J. R. (2007). How can the Human Mind Occur in the Physical Universe? 1st Edn. New York, NY: Oxford University Press.
Aosaki, T., Kiuchi, K., and Kawaguchi, Y. (1998). Dopamine D1-like receptor activation excites rat striatal large aspiny neurons in vitro. J. Neurosci. 18, 5180–5190.
Apicella, P. (2007). Leading tonically active neurons of the striatum from reward detection to context recognition. Trends Neurosci. 30, 299–306.
Aronov, D., Andalman, A. S., and Fee, M. S. (2008). A specialized forebrain circuit for vocal babbling in the juvenile songbird. Science 320, 630–634.
Ashby, F. G., and Crossley, M. J. (2011). A computational model of how cholinergic interneurons protect striatal-dependent learning. J. Cogn. Neurosci. 23, 1549–1566.
Ashby, F. G., Ell, S. W., Valentin, V. V., and Casale, M. B. (2005). FROST: a distributed neurocomputational model of working memory maintenance. J. Cogn. Neurosci. 17, 1728–1743.
Ashby, F. G., Ennis, J. M., and Spiering, B. J. (2007). A neurobiological theory of automaticity in perceptual categorization. Psychol. Rev. 114, 632–656.
Ashby, F. G., Turner, B. O., and Horvitz, J. C. (2010). Cortical and basal ganglia contributions to habit learning and automaticity. Trends Cogn. Sci. (Regul. Ed.) 14, 208–215.
Aston-Jones, G., and Cohen, J. D. (2005a). Adaptive gain and the role of the locus coeruleus-norepinephrine system in optimal performance. J. Comp. Neurol. 493, 99–110.
Aston-Jones, G., and Cohen, J. D. (2005b). An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu. Rev. Neurosci. 28, 403–450.
Bar-Gad, I., Havazelet-Heimer, G., Goldberg, J. A., Ruppin, E., and Bergman, H. (2000). Reinforcement-driven dimensionality reduction – a model for information processing in the basal ganglia. J. Basic Clin. Physiol. Pharmacol. 11, 305–320.
Barto, A. G. (1995). “Adaptive critics and the basal ganglia,” in Models of Information Processing in the Basal Ganglia, eds J. C. Houk, J. L. Davis, and D. G. Beiser (Cambridge, MA: MIT Press), 215–232.
Bechara, A., Damasio, A. R., Damasio, H., and Anderson, S. W. (1994). Insensitivity to future consequences following damage to human prefrontal cortex. Cognition 50, 7–15.
Beiser, D. G., and Houk, J. C. (1998). Model of cortical-basal ganglionic processing: encoding the serial order of sensory events. J. Neurophysiol. 79, 3168–3188.
Berns, G. S., and Sejnowski, T. J. (1998). A computational model of how the basal ganglia produce sequences. J. Cogn. Neurosci. 10, 108–121.
Bevan, M. D., Booth, P. A., Eaton, S. A., and Bolam, J. P. (1998). Selective innervation of neostriatal interneurons by a subclass of neuron in the globus pallidus of the rat. J. Neurosci. 18, 9438–9452.
Biele, G., Rieskamp, J., and Gonzalez, R. (2009). Computational models for the combination of advice and individual learning. Cogn. Sci. 33, 206–242.
Bolam, J. P., Hanley, J. J., Booth, P. A., and Bevan, M. D. (2000). Synaptic organisation of the basal ganglia. J. Anat. 196(Pt 4), 527–542.
Bonsi, P., Cuomo, D., Martella, G., Madeo, G., Schirinzi, T., Puglisi, F., Ponterio, G., and Pisani, A. (2011). Centrality of striatal cholinergic transmission in basal ganglia function. Front. Neuroanat. 5:6. doi: 10.3389/fnana.2011.00006
Bouret, S., and Sara, S. J. (2005). Network reset: a simplified overarching theory of locus coeruleus noradrenaline function. Trends Neurosci. 28, 574–582.
Bowman, C. H., and Turnbull, O. H. (2004). Emotion-based learning on a simplified card game: the Iowa and Bangor Gambling Tasks. Brain Cogn. 55, 277–282.
Bracci, E., Centonze, D., Bernardi, G., and Calabresi, P. (2002). Dopamine excites fast-spiking interneurons in the striatum. J. Neurophysiol. 87, 2190–2194.
Brainard, M. S., and Doupe, A. J. (2002). What songbirds teach us about learning. Nature 417, 351–358.
Calabresi, P., Centonze, D., Gubellini, P., Pisani, A., and Bernardi, G. (2000a). Acetylcholine-mediated modulation of striatal function. Trends Neurosci. 23, 120–126.
Calabresi, P., Gubellini, P., Centonze, D., Picconi, B., Bernardi, G., Chergui, K., Svenningsson, P., Fienberg, A. A., and Greengard, P. (2000b). Dopamine and cAMP-regulated phosphoprotein 32 kDa controls both striatal long-term depression and long-term potentiation, opposing forms of synaptic plasticity. J. Neurosci. 20, 8443–8451.
Chuhma, N., Tanaka, K. F., Hen, R., and Rayport, S. (2011). Functional connectome of the striatal medium spiny neuron. J. Neurosci. 31, 1183–1192.
Cohen, N. J., and Squire, L. R. (1980). Preserved learning and retention of pattern-analyzing skill in amnesia: dissociation of knowing how and knowing that. Science 210, 207–210.
Daw, N. D., Gershman, S. J., Seymour, B., Dayan, P., and Dolan, R. J. (2011). Model-based influences on humans’ choices and striatal prediction errors. Neuron 69, 1204–1215.
Daw, N. D., Niv, Y., and Dayan, P. (2005). Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci. 8, 1704–1711.
Daw, N. D., O’Doherty, J. P., Dayan, P., Seymour, B., and Dolan, R. J. (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–879.
Dayan, P., and Yu, A. J. (2006). Phasic norepinephrine: a neural interrupt signal for unexpected events. Network 17, 335–350.
DeBoer, P., Heeringa, M. J., and Abercrombie, E. D. (1996). Spontaneous release of acetylcholine in striatum is preferentially regulated by inhibitory dopamine D2 receptors. Eur. J. Pharmacol. 317, 257–262.
Delgado, M. R., Locke, H. M., Stenger, V. A., and Fiez, J. A. (2003). Dorsal striatum responses to reward and punishment: effects of valence and magnitude manipulations. Cogn. Affect. Behav. Neurosci. 3, 27–38.
Delgado, M. R., Miller, M. M., Inati, S., and Phelps, E. A. (2005). An fMRI study of reward-related probability learning. Neuroimage 24, 862–873.
DeLong, M. R. (1990). Primate models of movement disorders of basal ganglia origin. Trends Neurosci. 13, 281–285.
Eliasmith, C., and Anderson, C. H. (2003). Neural Engineering: Computation, Representation, and Dynamics in Neurobiological Systems. Cambridge, MA: MIT Press.
Fellows, L. K., and Farah, M. J. (2005). Different underlying impairments in decision-making following ventromedial and dorsolateral frontal lobe damage in humans. Cereb. Cortex 15, 58–63.
Frank, M. J. (2005). Dynamic dopamine modulation in the basal ganglia: a neurocomputational account of cognitive deficits in medicated and nonmedicated Parkinsonism. J. Cogn. Neurosci. 17, 51–72.
Frank, M. J., and Claus, E. D. (2006). Anatomy of a decision: striato-orbitofrontal interactions in reinforcement learning, decision making, and reversal. Psychol. Rev. 113, 300–326.
Frank, M. J., Loughry, B., and O’Reilly, R. C. (2001). Interactions between frontal cortex and basal ganglia in working memory: a computational model. Cogn. Affect. Behav. Neurosci. 1, 137–160.
Frank, M. J., Samanta, J., Moustafa, A. A., and Sherman, S. J. (2007). Hold your horses: impulsivity, deep brain stimulation, and medication in Parkinsonism. Science 318, 1309–1312.
Frank, M. J., Seeberger, L. C., and O’Reilly, R. C. (2004). By carrot or by stick: cognitive reinforcement learning in Parkinsonism. Science 306, 1940–1943.
Fum, D., and Stocco, A. (2004). “Memory, emotion, and rationality: an ACT-R interpretation for Gambling Task results,” in Proceedings of the 6th International Conference on Cognitive Modeling, eds C. D. Schunn, M. C. Lovett, C. Lebiere, and P. Munro (Mahwah, NJ: Lawrence Erlbaum Associates), 106–111.
Gardner, T. J., Naef, F., and Nottebohm, F. (2005). Freedom and rules: the acquisition and reprogramming of a bird’s learned song. Science 308, 1046–1049.
Gläscher, J., Daw, N., Dayan, P., and O’Doherty, J. P. (2010). States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron 66, 585–595.
Gonzalez, C., Lerch, J. F., and Lebiere, C. (2003). Instance-based learning in dynamic decision making. Cogn. Sci. 27, 591–635.
Gurney, K., Prescott, T. J., and Redgrave, P. (2001). A computational model of action selection in the basal ganglia. I. A new functional anatomy. Biol. Cybern. 84, 401–410.
Hernandez-Lopez, S., Tkatch, T., Perez-Garci, E., Galarraga, E., Bargas, J., Hamm, H., and Surmeier, D. J. (2000). D2 dopamine receptors in striatal medium spiny neurons reduce L-type Ca2+ currents and excitability via a novel PLCβ1-IP3-calcineurin-signaling cascade. J. Neurosci. 20, 8987–8995.
Humphries, M. D., Wood, R., and Gurney, K. (2009). Dopamine-modulated dynamic cell assemblies generated by the GABAergic striatal microcircuit. Neural Netw. 22, 1174–1188.
Humphries, M. D., Wood, R., and Gurney, K. (2010). Reconstructing the three-dimensional GABAergic microcircuit of the striatum. PLoS Comput. Biol. 6, e1001011. doi: 10.1371/journal.pcbi.1001011
Ibáñez-Sandoval, O., Tecuapetla, F., Unal, B., Shah, F., Koós, T., and Tepper, J. M. (2010). Electrophysiological and morphological characteristics and synaptic connectivity of tyrosine hydroxylase-expressing neurons in adult mouse striatum. J. Neurosci. 30, 6999–7016.
Jaeger, D., Kita, H., and Wilson, C. J. (1994). Surround inhibition among projection neurons is weak or nonexistent in the rat neostriatum. J. Neurophysiol. 72, 2555–2558.
Jankovic, J. (2008). Parkinson’s disease: clinical features and diagnosis. J. Neurol. Neurosurg. Psychiatry 79, 368–376.
Jankovic, J., and Aguilar, L. G. (2008). Current approaches to the treatment of Parkinson’s disease. Neuropsychiatr. Dis. Treat. 4, 743–757.
Joel, D., Niv, Y., and Ruppin, E. (2002). Actor–critic models of the basal ganglia: new anatomical and computational perspectives. Neural Netw. 15, 535–547.
Knowlton, B. J., Mangels, J. A., and Squire, L. R. (1996). A neostriatal habit learning system in humans. Science 273, 1399–1402.
Koós, T., and Tepper, J. M. (2002). Dual cholinergic control of fast-spiking interneurons in the neostriatum. J. Neurosci. 22, 529–535.
Kubota, Y., Inagaki, S., Shimada, S., Kito, S., Eckenstein, F., and Tohyama, M. (1987). Neostriatal cholinergic neurons receive direct synaptic inputs from dopaminergic axons. Brain Res. 413, 179–184.
Lapper, S. R., and Bolam, J. P. (1992). Input from the frontal cortex and the parafascicular nucleus to cholinergic interneurons in the dorsal striatum of the rat. Neuroscience 51, 533–545.
Lavoie, B., Smith, Y., and Parent, A. (1989). Dopaminergic innervation of the basal ganglia in the squirrel monkey as revealed by tyrosine hydroxylase immunohistochemistry. J. Comp. Neurol. 289, 36–52.
McNab, F., and Klingberg, T. (2008). Prefrontal cortex and basal ganglia control access to working memory. Nat. Neurosci. 11, 103–107.
Morris, G., Arkadir, D., Nevet, A., Vaadia, E., and Bergman, H. (2004). Coincident but distinct messages of midbrain dopamine and striatal tonically active neurons. Neuron 43, 133–143.
Nambu, A., Tokuno, H., and Takada, M. (2002). Functional significance of the cortico-subthalamo-pallidal ‘hyperdirect’ pathway. Neurosci. Res. 43, 111–117.
Nicola, S. M., Surmeier, J., and Malenka, R. C. (2000). Dopaminergic modulation of neuronal excitability in the striatum and nucleus accumbens. Annu. Rev. Neurosci. 23, 185–215.
Nottebohm, F. (2005). The neural basis of birdsong. PLoS Biol. 3, e164. doi: 10.1371/journal.pbio.0030164
O’Doherty, J. P. (2004). Reward representations and reward-related learning in the human brain: insights from neuroimaging. Curr. Opin. Neurobiol. 14, 769–776.
Olveczky, B. P., Andalman, A. S., and Fee, M. S. (2005). Vocal experimentation in the juvenile songbird requires a basal ganglia circuit. PLoS Biol. 3, e153. doi: 10.1371/journal.pbio.0030153
O’Reilly, R., Frank, M., Hazy, T., and Watz, B. (2007). PVLV: the primary value and learned value Pavlovian learning algorithm. Behav. Neurosci. 121, 31–49.
O’Reilly, R. C., and Frank, M. J. (2006). Making working memory work: a computational model of learning in the prefrontal cortex and basal ganglia. Neural Comput 18, 283–328.
O’Reilly, R., and Munakata, Y. (2000). Computational Explorations in Cognitive Neuroscience, Cambridge, MA: MIT Press.
Packard, M. G., and Knowlton, B. J. (2002). Learning and memory functions of the basal ganglia. Annu. Rev. Neurosci. 25, 563–593.
Pakhotin, P., and Bracci, E. (2007). Cholinergic interneurons control the excitatory input to the striatum. J. Neurosci. 27, 391–400.
Pasupathy, A., and Miller, E. K. (2005). Different time courses of learning-related activity in the prefrontal cortex and striatum. Nature 433, 873–876.
Penner, M. R., and Mizumori, S. J. (2012). Neural systems analysis of decision making during goal-directed navigation. Prog. Neurobiol. 96, 96–135.
Pisani, A., Bonsi, P., Centonze, D., Calabresi, P., and Bernardi, G. (2000). Activation of D2-like dopamine receptors reduces synaptic inputs to striatal cholinergic interneurons. J. Neurosci. 20, RC69.
Prat, C. S., and Just, M. A. (2011). Exploring the neural dynamics underpinning individual differences in sentence comprehension. Cereb. Cortex 21, 1747–1760.
Redgrave, P., Prescott, T. J., and Gurney, K. (1999). The basal ganglia: a vertebrate solution to the selection problem? Neuroscience 89, 1009–1023.
Reynolds, J. N., Hyland, B. I., and Wickens, J. R. (2004). Modulation of an afterhyperpolarization by the substantia nigra induces pauses in the tonic firing of striatal cholinergic interneurons. J. Neurosci. 24, 9870–9877.
Reynolds, J. N., and Wickens, J. R. (2004). The corticostriatal input to giant aspiny interneurons in the rat: a candidate pathway for synchronising the response to reward-related cues. Brain Res. 1011, 115–128.
Schönberg, T., Daw, N. D., Joel, D., and O’Doherty, J. P. (2007). Reinforcement learning signals in the human striatum distinguish learners from nonlearners during reward-based decision making. J. Neurosci. 27, 12860–12867.
Schultz, W., Apicella, P., and Ljungberg, T. (1993). Responses of monkey dopamine neurons to reward and conditioned stimuli during successive steps of learning a delayed response task. J. Neurosci. 13, 900–913.
Seger, C. A., and Cincotta, C. M. (2005). The roles of the caudate nucleus in human classification learning. J. Neurosci. 25, 2941–2951.
Sidibé, M., Paré, J. F., and Smith, Y. (2002). Nigral and pallidal inputs to functionally segregated thalamostriatal neurons in the centromedian/parafascicular intralaminar nuclear complex in monkey. J. Comp. Neurol. 447, 286–299.
Smith, Y., Raju, D. V., Pare, J. F., and Sidibe, M. (2004). The thalamostriatal system: a highly specific network of the basal ganglia circuitry. Trends Neurosci. 27, 520–527.
Stocco, A., and Anderson, J. R. (2008). Endogenous control and task representation: an fMRI study in algebraic problem-solving. J. Cogn. Neurosci. 20, 1300–1314.
Stocco, A., Fum, D., and Napoli, A. (2009). Dissociable processes underlying decisions in the Iowa Gambling Task: a new integrative framework. Behav. Brain Funct. 5, 1.
Stocco, A., Lebiere, C., and Anderson, J. (2010). Conditional routing of information to the cortex: a model of the basal ganglia’s role in cognitive coordination. Psychol. Rev. 117, 541–574.
Sullivan, M. A., Chen, H., and Morikawa, H. (2008). Recurrent inhibitory network among striatal cholinergic interneurons. J. Neurosci. 28, 8682–8690.
Suri, R. E., and Schultz, W. (1998). Learning of sequential movements by neural network model with dopamine-like reinforcement signal. Exp. Brain Res. 121, 350–354.
Suri, R. E., and Schultz, W. (1999). A neural network model with dopamine-like reinforcement signal that learns a spatial delayed response task. Neuroscience 91, 871–890.
Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Mach. Learn. 3, 9–44.
Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning: An Introduction, Cambridge, MA: MIT Press.
Tan, C. O., and Bullock, D. (2008). A dopamine-acetylcholine cascade: simulating learned and lesion-induced behavior of striatal cholinergic interneurons. J. Neurophysiol. 100, 2409–2421.
Tepper, J. M., and Bolam, J. P. (2004). Functional diversity and specificity of neostriatal interneurons. Curr. Opin. Neurobiol. 14, 685–692.
Tepper, J. M., and Plenz, D. (2006). “Microcircuits in the striatum: striatal cell types and their interaction,” in Microcircuits: The Interface Between Neurons and Global Brain Function (Dahlem Workshop Reports), eds S. Grillner, and A. M. Graybiel (Cambridge, MA: MIT Press), 127–135.
Tepper, J. M., Tecuapetla, F., Koós, T., and Ibáñez-Sandoval, O. (2010). Heterogeneity and diversity of striatal GABAergic interneurons. Front. Neuroanat. 4:150. doi: 10.3389/fnana.2010.00150
Tom, S., Fox, C., Trepel, C., and Poldrack, R. (2007). The neural basis of loss aversion in decision-making under risk. Science 315, 515–518.
Tricomi, E., Delgado, M., and Fiez, J. (2004). Modulation of caudate activity by action contingency. Neuron 41, 281–292.
Wickens, J. R., Alexander, M. E., and Miller, R. (1991). Two dynamic modes of striatal function under dopaminergic-cholinergic control: simulation and analysis of a model. Synapse 8, 1–12.
Wickens, J. R., Begg, A. J., and Arbuthnott, G. W. (1996). Dopamine reverses the depression of rat corticostriatal synapses which normally follows high-frequency stimulation of cortex in vitro. Neuroscience 70, 1–5.
Yin, H. H., and Knowlton, B. J. (2006). The role of the basal ganglia in habit formation. Nat. Rev. Neurosci. 7, 464–476.
Appendix
This Appendix describes the details of the implementation of the BABE model and the learning algorithm it uses.
Model Neurons
In the model, neurons were implemented as simple computational units that apply an activation function f over an input value η to yield an activation value, denoted by x. The input value η is simply the sum of all the activations coming from the projecting neurons, weighted by the corresponding synaptic strengths:
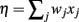
where wj is the value (or “synaptic weight”) of the synapse from neuron j, xj is the activation of neuron j. This is perhaps the simplest and most common representation for artificial neurons, and is widely adopted in many biological models (see O’Reilly and Munakata, 2000).
The activation value x is obtained from the net input η by applying the activation function f:
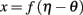
where θ is the neuron’s threshold, which can be thought of an initial resistance of every neuron to be excited. A negative threshold (so that the quantity η − θ is positive in absence of direct stimulation) can be used to model neurons with elevated tonic activities, or to compensate the effects of convergent inhibitory projections. The activation value x is supposed to be the computational counterpart of a neuron’s firing rate. Note that a neuron’s dynamic is completely characterized by its activation function and threshold.
Activation functions
With the exception of dopamine neurons (which are discussed in the next section), all the neurons in the model use only two types of activation functions. Neurons in the PVi, LVe, and LVi nuclei use a sigmoid activation function as:
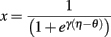
where γ is the gain parameter that determines the curves’ steepness. Value of the sigmoid activation function are always in the range [0, 1], and thus provide a convenient way to represent neuronal firing rates between a natural lower bound (x = 0, corresponding to no action potential) and a normalized maximum (x = 1).
The activation of neurons in the SN, SP, TAN, and SNr/Thalamus nuclei, on the other hand, is modeled as a hyperbolic tangent:
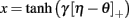
where γ is the gain parameter the […]+ notation indicates that negative values inside square brackets are treated as zeroes. This ensures that the output of the function is in the range [0, 1]. Together with the sigmoid function, the hyperbolic tangent is among the simplest formulae that fit the change of spiking rates following changes in membrane potential in biological neurons; the curve also closely mimics the variation of spike rates to a change in the membrane potentials in biological neurons (O’Reilly and Munakata, 2000).
In the reduced version of the BABE model, the activation function of SN and SP cells was changed from a hyperbolic tangent to a sigmoid. This choice was made because sigmoid functions were found to yield better performance in the reduced version of the model (but not in the normal version).
Application of kWTA
The competition between the direct and the indirect pathways in the model produces different activation values for the different possible actions represented in the SNr/Thalamus nucleus. However, eventually the model has to select only one stimulus, even if values are provided for more than one. Different mechanisms are possible for solving this competition, including some at the cortical level. However, to keep the matters as simple a possible, both the BABE model and its reduced version include a kWTA mechanism. The kWTA is a common solution to implement complex inhibitory dynamics within a population of neurons (O’Reilly and Munakata, 2000). The procedure simply consists of identifying k units whose activation is going to be maintained, and forcing to zero the activation value of the remaining ones. The probability p(i) of selecting a i as part of the k ones that will be maintained is a Boltzmann function of its activation A(i):
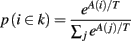
where T is the temperature. In the case of Thalamus, k = 1 and T = 0.01, which means that the procedure selects almost deterministically the most active unit.
Model dynamics
The model progresses through three phases for each trial, a decision (+) phase, a feedback (−) phase, and a learning (++) phase. The progression through each of these phases can be summarized as follows:
1. During the decision (+) phase,
1.1. The cortical “Context” units are clamped to the value corresponding to the given pair of stimuli;
1.2. The cortical “Time” units are clamped to the values corresponding to the first phase of the task;
1.3. The value of PVe is set of the neutral value of 0.5.
1.4. All the non-clamped nuclei of the model are then iteratively updated until they converge to a fixed stable state.
1.5. The value of the Thalamus cells is then read out.
1.5.1. If one Thalamus neuron is active (i.e, its activation is greater than zero), then the corresponding stimulus is taken to be the model’s decision.
1.5.2. If no Thalamus is active, then one of the six stimuli is selected at random, and the corresponding Thalamus unit activation is set to 1.0.
2. During the feedback (–) phase,
2.1. The values of cortical Context units and Thalamus output units are clamped to the their current values;
2.2. The values of the “Time” units are moved “back” (see Figure 4), to represent the moment after a decision is made.
2.3. The value of the PVe unit is set to match the outcome of the previous decision:
2.3.1. If the decision resulted in a “Correct” feedback, then the value of PVe is set to 0.8;
2.3.2. Otherwise, if the decision resulted in an “Incorrect” feedback, then the value of PVe is set to 0.2;
2.3.3. Otherwise, if the previous decision corresponded to a stimulus not currently presented in the stimulus pair (e.g., the response was “C” to the pair “AB”), then the value of PVe is set to 0.0.
2.4. All the non-clamped nuclei of the model are then iteratively updated until they converge to a fixed stable state.
3. During the learning phase (++), the synaptic values of the following projections are updated (see below for specific details pertaining each projection).
3.1. The projection from the cortical “state” units to:
3.1.1. The striatal TAN cells.
3.1.2. The striatal SN units and SP cells
3.1.3. The PVi, LVe, and LVi cells.
3.2. The projections from the cortical Time units to:
3.2.1. The PVi, LVe, and LVi cells.
Learning in the PVLV system
This section will summarize briefly the PVLV system learning rules. A complete description of the system and the rationale behind each equation is provided in O’Reilly et al. (2007). In our model, the PVe nucleus never actually learns: it simply reflects the value of primary rewards (when they are delivered). The PVi nucleus, on the other hand, learns to predict the circumstances where a primary reward will be delivered, and this cancels out the PVe excitatory effect in as much as the rewards is associated at a given state and time. Thus, in the case of PVi the strength of each synapse wi from a “time” unit i to PVi is then incremented by an amount Δwi that is calculated as follows:
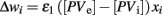
Where the notation “[…]” indicates the value encoded by the cells of the nucleus within square brackets, and xi is the activation of the projecting cell i. During the simulations, the value of ε was set to 0.25.
While PVi learns continuously, learning in LVe and LVi is contingent on the actual or expected primary rewards being noticeable, i.e., either raising above an upper threshold Tmax or falling below a predefined lower threshold Tmin. The Boolean variable PVfilter records whether PVe or PVi lay beyond the thresholds, and is calculated as follows:
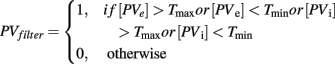
The synaptic values wi of a LVe unit receiving inputs from a “state” or “time” unit i is then updated by the following quantity:
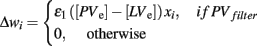
Synapses to the LVi nucleus are updated according to the same rule, but use a slower learning rate ε2 < ε1. In our simulations, ε2 = 0.025.
Dopamine activation
In PVLV the activation of dopamine neurons is partly a linear activation the difference in of activation in the PV or in the LV nuclei, depending on the presence of primary rewards. In particular, the activation of dopamine neurons was calculated as follows:
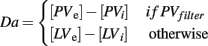
This ensures that dopamine reflects the difference in expectations in primary rewards, if there are any, or in rewards predictions if primary rewards are not present.
Modulatory effects of dopamine on striatal SN and SP neurons
In addition to a direct input to striatal units, dopamine seems to have the modulatory of sharpening and enhancing their response (Hernandez-Lopez et al., 2000; Nicola et al., 2000; Frank, 2005). To account for this effect, the model adopted the solution proposed by O’Reilly and Frank (2006) to make the contribution from dopamine projections partly a function of the difference in striatal activity between the feedback (−) and the decision (+) phases. For example, the net input di from dopamine neurons to an SN cell i was calculated as:
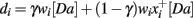
Where  is the activation of i in the decision phase,
is the activation of i in the decision phase,  is the activation during the learning phase, and [Da] is the activation value of the dopamine unit. The parameter γ balances between the net and the modulatory effects, and, as in O’Reilly and Frank (2006), was set to a fixed value for 0.5 for both models during all simulations.
is the activation during the learning phase, and [Da] is the activation value of the dopamine unit. The parameter γ balances between the net and the modulatory effects, and, as in O’Reilly and Frank (2006), was set to a fixed value for 0.5 for both models during all simulations.
Learning in the striatum
Learning in the striatum occurs at the level of synapses between the cortical “state” units and the SN, SP, and TAN cells. In all cases, learning is a function of the difference in activation between the learning (+) and the feedback (−) phases. In the case of SN and SP cells, each synapse was updated by an amount corresponding to:
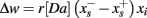
where xs is the activation of the striatal cell s, xi is the activation value of the cortical “state” or “time” unit, and [Da] is the absolute activation value of dopamine neurons. The parameter r is the learning rate, and was fixed to 1.5 for SN cells and −1.0 for SP cells. The difference is sign between the two learning rates reflects the need for learning to proceed in the opposite directions for SN and SP cells. The difference in magnitude between the two values reflects an initial bias that was given to the model for learning to perform decisions, even if possibly wrong, rather than learning to withhold a correct one. As in the case of other parameters, the value of r was kept constant across models and simulations.
Learning for TAN units follows a similar rule, with two minor variations, except that the learning was modulated by a different rate parameter t, which was fixed to 0.5.
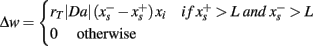
where rT is the TAN-specific learning rate, which was set to 0.5, and L is a lower limit on the activation values of striatal interneurons, which was set to 0.03. The limit is needed to avoid incurring in situations where, due to repeated negative feedback, the synaptic weights decrease to a point where only unrealistically high cortical inputs can excite the interneurons.
Keywords: basal ganglia, decision-making, exploration, actor–critic architecture, acetylcholine, dopamine
Citation: Stocco A (2012) Acetylcholine-based entropy in response selection: a model of how striatal interneurons modulate exploration, exploitation, and response variability in decision-making. Front. Neurosci. 6:18. doi: 10.3389/fnins.2012.00018
Received: 16 October 2011; Accepted: 20 January 2012;
Published online: 06 February 2012.
Edited by:
Rafal Bogacz, University of Bristol, UKReviewed by:
Ming Hsu, University of California Berkeley, USAKevin Gurney, University of Sheffield, UK
Copyright: © 2012 Stocco. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Andrea Stocco, Institute for Learning and Brain Sciences, University of Washington, 1715 Columbia Road, Room 203B, Campus Box 357988, Seattle, WA 98195-7988, USA e-mail:c3RvY2NvQHV3LmVkdQ==
