Iowa Gambling Task: There is more to consider than long-term outcome. Using a linear equation model to disentangle the impact of outcome and frequency of gains and losses.

The Iowa Gambling Task (IGT) has been widely used to assess differences in decision-making under uncertainty. Recently, several studies have shown that healthy subjects do not meet the basic predictions of the task (i.e., prefer options with positive long-term outcome), hence questioning its basic assumptions. Since choice options are characterized by gain and net loss frequency in addition to long-term outcome, we hypothesized that a combination of features rather than a single feature would influence participants’ choices. Offering an alternative way of modeling IGT data, we propose to use a system of linear equations to estimate weights that quantify the influence of each individual feature on decision-making in the IGT. With our proposed model it is possible to disentangle and quantify the impact of each of these features. Results from 119 healthy young subjects suggest that choice behavior is predominantly influenced by gain and loss frequency. Subjects preferred choices associated with high-frequency gains to those with low-frequency gains, regardless of long-term outcome. However, among options with low-frequency gains, subjects learned to distinguish between choices that led to advantageous and disadvantageous long-term consequences. This is reflected in the relationship between the weights for gain frequency (highest), loss frequency (intermediate), and long-term outcome (lowest). Further, cluster analysis of estimated feature weights revealed sub-groups of participants with distinct weight patterns and associated advantageous decision behavior. However, subjects in general do not learn to solely base their preference for particular decks on expected long-term outcome. Consequently, long-term outcome alone is not able to drive choice behavior on the IGT. In sum, our model facilitates a more focused conclusion about the factors guiding decision-making in the IGT. In addition, differences between clinical groups can be assessed for each factor individually.

Introduction

The Iowa Gambling Task (IGT, Bechara et al., 1994) has been widely used to assess decision-making under uncertainty. It has become most popular for studying differences between clinical groups (e.g., Grant et al., 2000; Bechara et al., 2001; Cavedini et al., 2004; Bark et al., 2005; Bolla et al., 2005; Shurman et al., 2005; Toplak et al., 2005; Boeka and Lokken, 2006; Garon et al., 2006; Tchanturia et al., 2007; Hermann et al., 2009; Liao et al., 2009; Brogan et al., 2010, 2011; Davis et al., 2010; Fridberg et al., 2010). This task requires participants to repeatedly draw cards from four possible card decks. The expected values of the decks differ so that two decks are associated with high immediate rewards but long-term overall loss (disadvantageous decks A and B), and two decks yield lower immediate rewards but long-term overall gains (advantageous decks C and D). The initial assumption made by Bechara et al. (1994) was that normal, healthy decision makers would learn over time to choose cards from the two advantageous decks only, assuming that they would focus on the long-term outcome and not be misled by the high immediate rewards. Since then, it has been widely agreed upon that successful task performance hinges on the evaluation of long-term outcome. Consequently, task performance on the IGT is typically assessed by computing a simple difference score between the number of cards drawn from the two advantageous decks (decks C and D) minus the number of cards drawn from the disadvantageous decks (decks A and B).

Substantial critique has been raised regarding the general assumptions on IGT performance (Dunn et al., 2006; Fernie and Tunney, 2006; Chiu and Lin, 2007; Lin et al., 2007). Several studies have shown that normal decision makers do not learn to prefer the two advantageous decks, but rather prefer one of the advantageous (deck D) and one of the disadvantageous (deck B) decks (e.g., Wilder et al., 1998; O’Carroll and Papps, 2003; Rodríguez-Sánchez et al., 2005; Toplak et al., 2005; Fernie and Tunney, 2006; Martino et al., 2007; Caroselli et al., 2010; Fridberg et al., 2010). Attention to long-term outcome alone cannot explain such choice behavior. Consequently, the validity of the simple difference score, taking into account long-term outcome only, has recently been questioned, as it may hide effects pertaining to differences between decks with identical expected long-term outcome (Chiu and Lin, 2007; Lin et al., 2007).

Possible reasons for the observed discrepancy between predicted and actual decisions on the IGT may be found in the particular payoff scheme of the task: in the original IGT, the four card decks are associated with the gain/loss structure presented in Table 1.

TABLE 1

Table 1. Payoff scheme of the Iowa Gambling Task.

The four decks differ not only in long-term outcome, but also in two additional features: the relative number of gains vs. losses (subsequently termed “gain frequency”; high for decks B and D, low for decks A and C), and the relative number of net losses (subsequently termed “loss frequency”; high for deck A, low for decks B and D, and zero for deck C). Most importantly, the exact combination of features is unique for each deck. In addition, magnitude of immediate reward and long-term outcome are dependent to the effect that it is not possible to disentangle the influence of immediate gain and long-term outcome on decision-making.

We hypothesized that participants’ choices in the IGT can only be explained by a combined influence of long-term outcome, and gain/loss frequency. In order to test this hypothesis, we propose to model IGT performance by a set of linear equations. Model parameters yield estimates for subjects’ individual weighting of (1) expected long-term outcome (i.e., the overall profitability of each deck; negative for decks A and B, positive for decks C and D), (2) gain frequency (i.e., how often is a card associated with a gain only; high for decks B and D, low for decks A and C), and (3) net loss frequency (i.e., how often is the sum of gains and losses on a card below zero; zero for deck C, intermediate for decks B and D, and high for deck A). The model offers an alternative way to quantitatively analyze IGT performance and determine the behavioral relevance of each of the tasks’ individual features on subjects’ decision-making.

Iowa Gambling Task performance has previously been analyzed by way of different computational models such as the expectancy valence (EV) model (Busemeyer and Stout, 2002; Yechiam and Busemeyer, 2005; Cheng et al., 2009; Wetzels et al., 2010) and mixture model clustering (Huizenga et al., 2007; Van Duijvenvoorde et al., 2010). While the former decomposes IGT decision-making into different interacting latent psychological processes, the latter relates task performance to possible underlying decision rules. Our proposed model differs from these approaches in that it neither mimics underlying cognitive processes nor assumes particular decision rules or strategies. Rather, our model relates the statistical properties of choice options in the IGT to the decision-making behavior of individual participants. This way, the model allows us to investigate on an individual level, whether decisions are in fact guided primarily by the long-term outcome as originally proposed by Bechara et al. (1994) and, if not, how additional properties of choice options, in particular gain and loss frequency, might influence decision-making.

We applied our model to data from 119 healthy young subjects who performed 100 trials of the IGT, and assessed sensitivity of subjects’ choice behavior to expected long-term outcome, gain frequency and loss frequency. In order to examine the development of subjects’ model parameters over the course of learning, we applied the model independently to each of the five consecutive blocks á 20 trials. For a more detailed analysis, obtained model parameters were further subjected to clustering in order to investigate the homogeneity of subjects’ feature weightings and related response patterns.

Materials and Methods

The Iowa Gambling Task

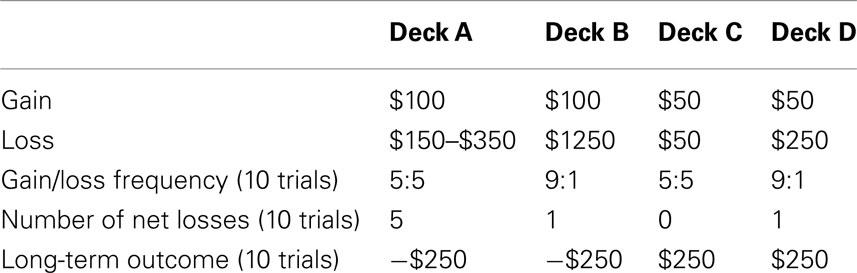
The IGT requires participants to make a series of selections from four alternative card decks. The four decks (A, B, C, D) are associated with different financial rewards. For each selection from decks A and B participants win $100. For each selection from decks C and D participants win $50. In addition, each card deck is associated with occasional losses of different amounts and frequencies. For deck A and C, 5 in 10 choices are associated with an additional loss of $250 on average and $50, respectively. Note that deck C never conveys net losses while for deck A loss trials always lead to a net loss. For decks B and D, 1 in 10 choices is accompanied by a loss of $1250 and $250, respectively. Comparable to deck A, every loss trial for decks B and D leads to a net loss. This payoff scheme (see Table 1) results in an overall long-term loss of $250 every 10 trials for decks A and B (disadvantageous decks) and an overall long-term gain of $250 every 10 trials for decks C and D (advantageous decks). Note that decks A and C have a relatively low gain frequency, whereas decks B and D are associated with a high gain frequency. Importantly, there is no advantage for participants in choosing cards from the infrequent loss decks (B and D) compared to the more frequent loss decks (A and C) with respect to overall task performance (Dunn et al., 2006).

Subjects

One hundred nineteen healthy, non-smoking, right-handed subjects [66 female (mean age 25.2 years, SD 4.9 years) and 53 male (mean age 24.7 years, SD 3.1 years)] with comparable educational background (university-entrance diploma, German Abitur, or higher) performed a computerized version of the IGT comprising 100 trials. Deck position was fully randomized between participants and information that the task will last for 100 trials was provided in the instruction. Deck position was kept stable during the task for each participant to minimize non-task-related working memory load (see Pecchinenda et al., 2006). Previous research has demonstrated a substantial influence of the amount of task-related information conveyed to the subjects prior to performing the task (Fernie and Tunney, 2006). We used the instruction proposed by Bechara et al. (1999, 2000) and described in Fernie and Tunney (2006) as “Hint” condition. The task was self-paced, as time constraints during the decision phase have been shown to impact performance substantially (Cella et al., 2007). Subjects were paid for their participation in the study and received an additional bonus related to task performance (maximum + 3€). Experiments were performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki.

Linear equation system

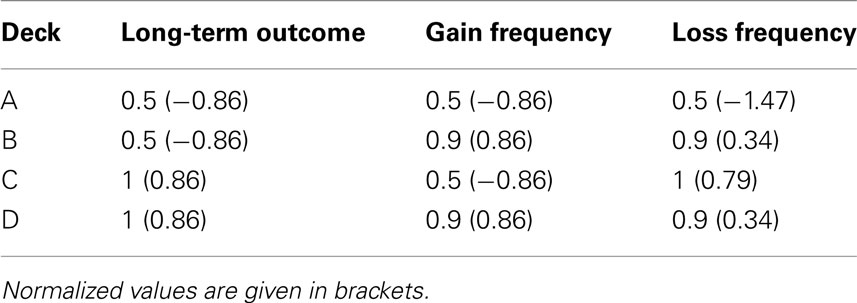
Task performance in the IGT can be modeled by a set of linear equations Ax = b. The matrix A is defined by the payoff scheme of the task with a_ij representing feature j (j = 1…3, corresponding to long-term outcome, gain frequency, loss frequency) for card deck i (i = 1…4, corresponding to decks A, B, C, D). The vector b describes the choices made by a subject with b_i representing the proportion of cards chosen from deck i in a particular number of trials (in our case in a block of 20 trials). Parameter vector x contains the weights x₁, x₂, x₃ representing the relative weight of the three features long-term outcome, gain frequency, loss frequency in the decision process. Each of the four equations describes the subject’s choice of the associated card deck as weighted sum of the three features, i.e., b_ij = Σ_j x_j a_ij for i = 1…4, j = 1…3. Thus, feature values a_ij (ranging between 0.5 and 1) were chosen such that high values reflect desirable options in the case of independence of all other features. Specifically, positive long-term outcome should be preferred over negative long-term outcome. Therefore, feature values were chosen to be 1 for advantageous decks C and D and 0.5 for disadvantageous decks A and B. Further, high gain frequency should be preferred over lower gain frequency. Consequently, feature values of 0.9 and 0.5 (reflecting a 9:1 or 5:5 gain frequency) were chosen for decks B and D, and decks A and C, respectively. Finally low net loss frequency should be preferred over high net loss frequency, reflected in feature values of 0.5 for deck A, 0.9 for decks B and D, and 1 for deck C. Feature values of all four decks are summarized in Table 2. This particular choice of feature values ensures that after parameter estimation, the relationship between the obtained weights reflects the actual importance of each factor for subjects’ decisions, with small absolute weight values representing low and high absolute values representing high importance.

TABLE 2

Table 2. Structure of the matrix A containing the feature values for the four different card decks.

We did not incorporate a feature for immediate reward in our model. As already suggested by Dunn et al. (2006) the IGT can be performed adequately even if the dimension of constant reward is neglected. Note, however, that the immediate reward is implicitly captured in the model as, according to the payoff scheme, it is inversely related to the long-term outcome parameter. In addition, we opted to examine the effect of net loss rather than the original loss frequency (5:5 or 9:1). Regarding the net profit of each deck, it becomes obvious that deck C never yields a net loss. Consequently, it is more similar to decks B and D than to deck A. Deck A has frequent losses (5:5) while decks B, C, and D have very few or no losses. As we aimed to capture this discrepancy in our model, we chose the loss frequency parameter to reflect the frequency of net losses. However, the frequency of losses per se is implicitly captured in the model by the gain frequency parameter describing the number of gains relative to the number of losses.

Initial feature values were scaled to the effect that their sum across decks was equal for each feature. In addition, values were normalized by subtraction of the mean within each feature and division by the SD, resulting in unit variance. This ensures comparability of weights across features and decks. Hence, for each subject a linear relationship of three parameter values to four observations of choice behavior is described by Ax = b, an over-determined system of four simultaneous linear equations. A solution x for this system can be obtained by least-squares estimation, minimizing the norm ||A × x − b||, if no unique solution exists.

Two-step clustering procedure

In order to investigate the homogeneity of subjects’ feature weighting at the beginning and end of the task, we applied hierarchical Two-Step clustering (Zhang et al., 1996; Chiu et al., 2001) to the estimated weights of blocks one and five. In this clustering technique, cluster distances are determined based on a log-likelihood distance measure, and Schwarz’s Bayesian information criterion (BIC) with noise handling is used to determine the optimal number of clusters for the particular data set. In our application, the maximum number of clusters was restricted to 15. After identifying clusters, we assessed the average silhouette measure of cohesion and separation for cluster validation as well as the predictor importance for all three features representing their influence on cluster separation.

Results

Performance

According to Bechara et al. (1994) healthy subjects should gradually learn to choose an approximately equal number of cards from decks C and D and avoid cards from decks A and B, assuming that they focus on the long-term outcome of the decks and ignore all other features. This behavior would result in a difference score between advantageous and disadvantageous decks that develops from around zero at the beginning of the experiment toward a clear positive value at later stages. In contrast to this prediction, in a large sample of healthy young adults we observed only a moderately positive difference score between decks C/D (advantageous) and decks A/B (disadvantageous) at the end of the task (see Figure 1). Although average difference scores increased from negative to positive values over the course of the experiment (significant effect of block; F_4.469, = 3.02, p = 0.018), and differed significantly from zero on all but the second block, subjects on average chose only 2.8 more cards from the advantageous than from disadvantageous decks in the last block of the experiment.

FIGURE 1

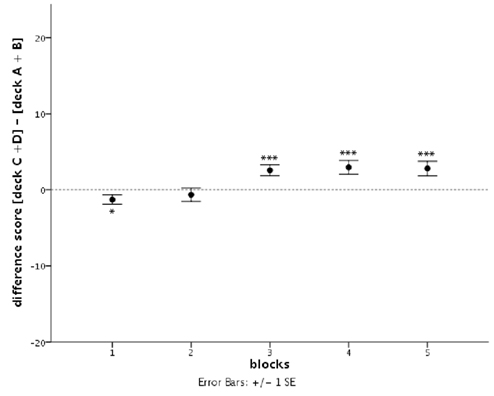
Figure 1. Development of the difference score between the sum of cards drawn from advantageous decks C and D and disadvantageous decks A and B over five consecutive blocks of 20 cards of the Iowa Gambling Task. Bars represent SE of the mean (SE), asterisks indicate the level of significance: *p < 0.05, ***p < 0.005 (Student’s t-test against zero).

A separate analysis of subjects’ choice behavior for all four decks revealed a clear preference for decks with frequent gains (decks B and D) over decks with infrequent gains (decks A and C) throughout the task (see Table 3; Figure 2, Friedman test, all p < 0.05). Furthermore, we observed that healthy subjects learned to differentiate between disadvantageous deck A and advantageous deck C from the third block on (Friedman test, all p < 0.05) but not between disadvantageous deck B and advantageous deck D (see Figure 2).

FIGURE 2

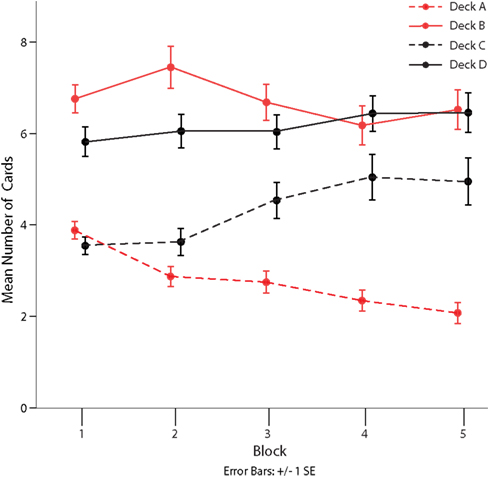
Figure 2. Mean number of cards drawn from each deck of the Iowa Gambling Task over five consecutive blocks of 20 choices. Red lines indicate decks identified as disadvantageous in the original publication of the task. Solid lines identify decks with high gain frequency, broken lines those with low gain frequency. Bars represent SE of the mean (SE).

TABLE 3

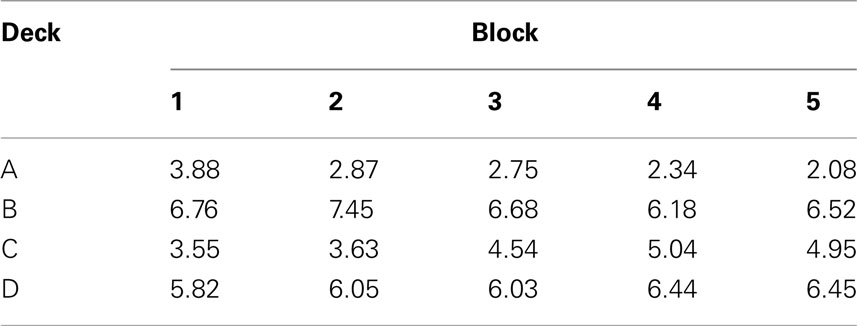
Table 3. Mean number of cards drawn from each deck for the five consecutive blocks (each containing 20 choices) of the Iowa Gambling Task.

Modeling

To analyze which combination of the task’s features elicited this particular choice pattern, we applied the linear equation model to the number of cards drawn from each deck for each subject individually in blocks of 20 choices. The least-squares solution yields subjects’ individual weights for each feature (i.e., long-term outcome, gain frequency, and net loss frequency) of the IGT’s payoff scheme. Table 4 shows an example solution for the last block of 20 choices of one subject.

TABLE 4

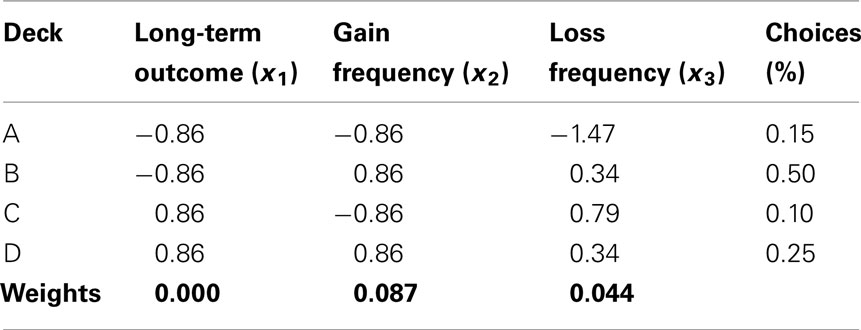
Table 4. Example (one subject’s) least-squares solution of the linear equation model for mean choices in block 5.

Table 5 shows the estimated weights of the three features (median and range of values) for each consecutive block of the IGT averaged across all subjects. Note that the distribution of weight estimates across subjects deviated from normal. We thus statistically analyzed significant differences of the medians for each feature and block using non-parametric significance tests.

TABLE 5

Table 5. Median weights calculated for the five consecutive blocks (á 20 choices) of the Iowa Gambling Task.

Development of feature weights across blocks

For gain frequency median weights are significantly above zero in all blocks (Wilcoxon signed rank, all p < 0.001). The median of loss frequency does not differ significantly from zero in the first but in all consecutive blocks (Wilcoxon signed rank, all p < 0.01). In contrast, medians of outcome weight do not significantly differ from zero in all but the first block (Wilcoxon signed rank, p < 0.05).

Relationship between feature weights

In relation to each other, weight for gain frequency has clearly the highest values at the beginning of the task and does not change significantly thereafter (see Figure 3). Median weight for loss frequency, after an initial value of zero in the first block, increases to a positive but smaller value than gain frequency on all consecutive blocks. Weights for long-term outcome stay well below those for gain frequency and loss frequency during the whole task [significantly different on block 1 with p < 0.001 (pairwise comparisons: outcome < gain frequency, p < 0.001; outcome < loss frequency, p = 0.004), on block 3 with p < 0.001 (pairwise comparisons: outcome < gain frequency, p = 0.001; outcome < loss frequency, p < 0.001), and on block 5 with p = 0.002 (pairwise comparison: outcome < gain frequency, p = 0.002), Friedman test]. On block 2 we observed a trend for different feature weights, but the comparison failed to reach significance (p = 0.055). On average, subjects give the smallest weight to long-term outcome.

FIGURE 3

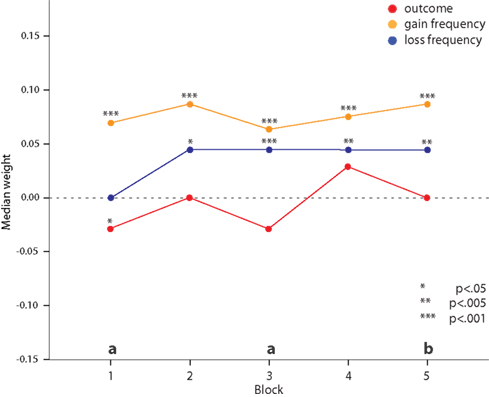
Figure 3. Estimated median weights for the features long-term outcome (red), gain frequency (orange), and loss frequency (blue) over the five consecutive blocks of 20 choices based on all participants. Asterisks indicate the level of significance of Wilcoxon signed rank test against zero, a (p < 0.001), and b (p < 0.005) indicate the level of significance of Friedman tests comparing the weights within each block.

Taken together, this confirms our hypothesis that subjects do neither primarily nor exclusively focus on long-term outcome. Instead, subjects predominantly consider a combination of gain and loss frequency features. Note that we did not find an influence of participants’ gender or age on any of the dependent measures.

As evident from Table 5 estimated weight parameters vary considerably between subjects for all three features. We thus subjected the obtained weights to multi-dimensional clustering in search for sub-groups of participants with comparable weight estimates.

Cluster analysis

The clustering procedure identified two clusters at the beginning (block one) and three clusters at the end (block five) of the experiment. The average silhouette measure of cohesion and separation was 0.6 for both.

In the first block of the task, the predictor importance was 1 for outcome, 0.93 for loss frequency, and 0.61 for gain frequency. About 78.2% of subjects belonged to cluster 1 (median weight for outcome −0.09, loss frequency 0.04, and gain frequency 0.04) and the remaining 21.8% belonged to cluster 2 (median weight for outcome 0.20, loss frequency −0.18, and gain frequency 0.20). The distribution of weights for both clusters and each feature can be seen in Figure 4A.

FIGURE 4

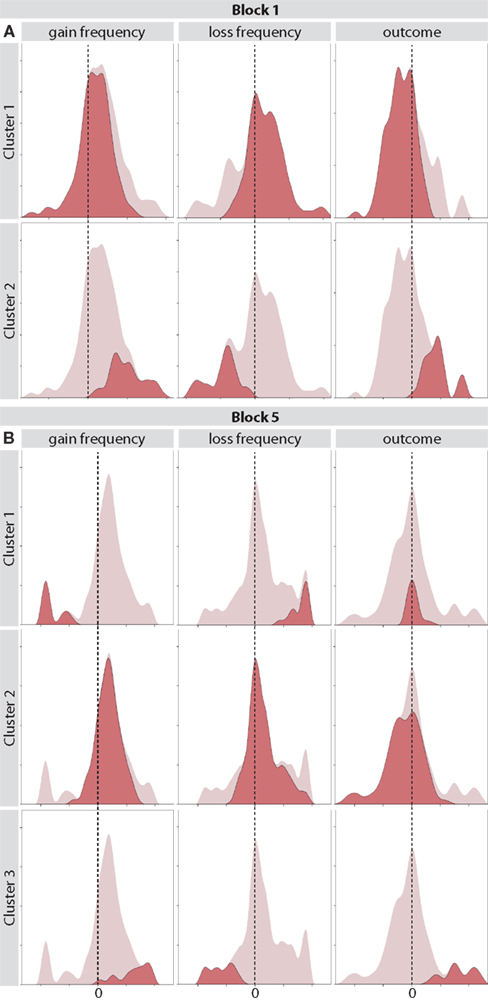
Figure 4. (A) Distribution of weight values for clusters obtained with a two-step clustering algorithm on block one of the IGT. Columns correspond to the three task features and rows correspond to different clusters. (B) Distribution of weight values for clusters obtained with a two-step clustering algorithm on the last block of the IGT.

In the last block of the task, the predictor importance for cluster separation was 1 for gain frequency, 0.75 for loss frequency, and 0.53 for outcome. About 11.8% of subjects belonged to cluster 1 (median weight for outcome 0, loss frequency 0.44, and gain frequency −0.46), 75.6% of subjects belonged to cluster 2 (median weight for outcome 0.09, loss frequency 0.04, and gain frequency −0.06), and the remaining 12.6% to cluster 3 (median weight for outcome 0.38, loss frequency −0.31, and gain frequency 0.36). The distribution of weights for all clusters and each feature can be seen in Figure 4B.

Finally, we related cluster membership in the final block back to subjects’ choice behavior and the initially proposed difference score to measure task performance. In Figure 5, cluster membership is plotted against difference score on the last block of trials. While performance of subjects in the largest cluster resulted in a difference score close to zero, subjects in cluster 1 (high weight for loss frequency, low weight for gain frequency, and a weight close to zero for outcome), and subjects in cluster 3 (low weight for loss frequency, high weight for gain frequency, and high weight for outcome) both had a high positive difference score. However, this high difference score was driven either by a clear preference for deck C (cluster 1) or deck D (cluster 3), as shown in Figure 6. Subjects in cluster 2 exhibited a more distributed choice behavior with small preferences for decks B and D.

FIGURE 5

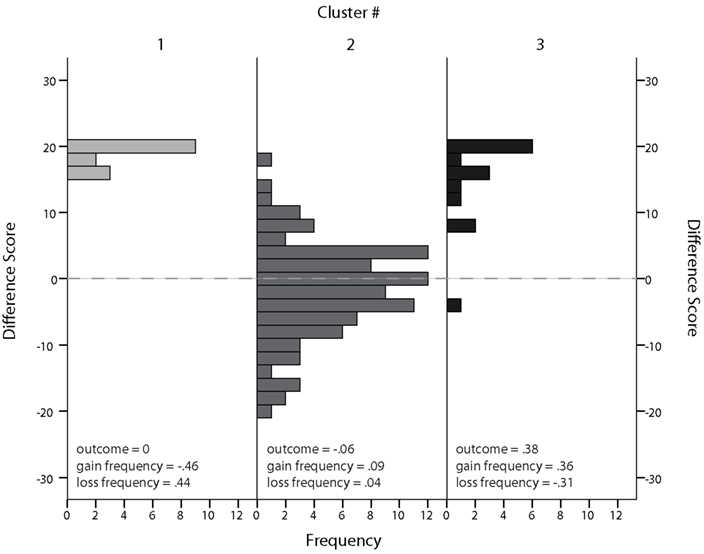
Figure 5. Histogram of difference scores for each cluster identified in block 5 (trials 81–100). Median weights for each cluster are given in the lower part of the chart.

FIGURE 6

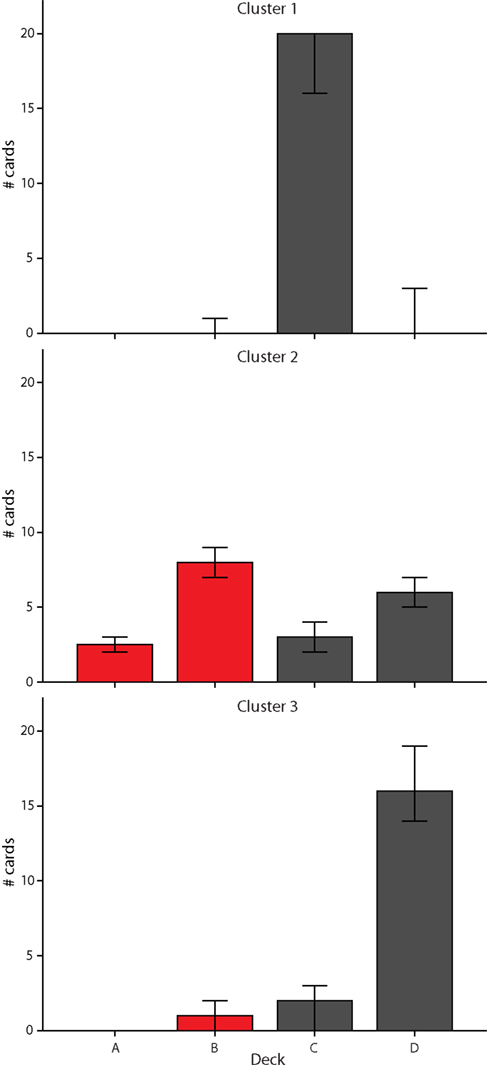
Figure 6. Pattern of card selection for each cluster identified in block 5 (trials 81–100). Bars represent the median number of cards selected from each deck (with 95% confidence intervals).

Discussion

Summary

In the current study, healthy young adults were subjected to a learning task that requires the integration of frequency and magnitude information on both gains and losses, and the assessment of the long-term consequences of decisions (IGT). Offering an alternative way of modeling IGT data, we used a system of linear equations to estimate weights that quantify the influence of the following three features on decision-making in the IGT: (1) expected long-term outcome (i.e., the overall profitability of each deck; negative for decks A and B, positive for decks C and D), (2) gain frequency (i.e., how often is a card associated with a gain only; high for decks B and D, low for decks A and C), and (3) net loss frequency (i.e., how often is the sum of gains and losses on a card below zero; zero for deck C, intermediate for decks B and D and high for deck A). We did not incorporate a feature for the constant immediate gain in our model. As already suggested by Dunn et al. (2006) the IGT can be performed adequately even if the dimension of constant reward is neglected. Note, however, that the immediate gain is implicitly captured in the model as, according to the payoff scheme, it is inversely related to the long-term outcome parameter.

Our results suggest that for normal subjects gain and loss frequency are the primary factors driving their decisions. We observed that subjects weighted both factors higher than long-term outcome. This clearly contrasts with the initial assumptions made by Bechara et al. (1994). Looking at individual preferences for each deck, we observed that subjects in general preferred choices associated with high-frequency gains (9:1, decks B and D) to those with low-frequency gains (5:5, decks A and C), regardless of their magnitude and long-term outcome (see Figure 2). This is in line with previous observations (e.g., Wilder et al., 1998; MacPherson et al., 2002; Yechiam and Busemeyer, 2005; Dunn et al., 2006; Huizenga et al., 2007; Lin et al., 2007; Carlson et al., 2009; Caroselli et al., 2010). However, among the options with low-frequency gains (decks A and C), subjects learned to distinguish between choices that led to advantageous (deck C) and disadvantageous (deck A) long-term consequences. Such distinction was not present for the decks with high-frequency gains (B and D). This can be explained by the weight given to loss frequency, the only feature where A and C but not B and D differ. As this weight increases after the first block of trials, the preference of deck C over deck A becomes observable, while cards from decks B and D are still chosen equally often. Thus, our model makes it possible to relate decisions on all four decks to the relative importance given by the subjects to one or more of the three features characterizing the options in the IGT.

Discussion with Regard to Assumptions of the Iowa Group

The general preference for decks with low loss- and high gain frequency rather than for positive overall outcome is in disagreement with the task performance that was intended and observed by Bechara et al. (1994) when designing the task. However, a growing body of literature reports comparable task performance. A number of studies observed a clear preference for decks B and D over decks A and C both in normal and clinical samples as well as in adolescents and older subjects (Wilder et al., 1998; MacPherson et al., 2002; O’Carroll and Papps, 2003; Shurman et al., 2005; Fernie and Tunney, 2006; Caroselli et al., 2010; Fridberg et al., 2010). This behavioral pattern suggests that subjects’ choices are not so much driven by the long-term outcome associated with each deck, but by the frequency with which subjects experience gains and losses for each particular deck. Large but infrequent losses seem to have less impact on the card selection strategy than smaller but frequent losses. In addition and more prominent, high gain frequency seems to be the most salient feature guiding decision-making in normal subjects. This is in line with animal research on reinforcement learning showing that animals are influenced more strongly by the frequency than by the magnitude of a reward (Schneider, 1973; Todorov, 1973). Early studies of gambling and risk taking behavior in humans also observed that the ratio of number of wins to number of losses rather than the magnitude of previously experienced wins and losses had significant effects on gamblers’ decisions (Greenberg and Weiner, 1966).

Discussion in the Light of Existing Literature

Within the decks with high-frequency gains, we observed after an initial exploration phase a comparable choice pattern for decks B and D, but within the low-frequency gain decks a clear preference for deck C over deck A. This corroborates findings by Lin et al. (2007), who observed the same pattern in a modified version of the IGT that directly contrasts deck A with C and deck B with D. The authors suggest that the clear preference for deck C over deck A in the original version of the task might be due to the fact that despite the seemingly identical gain/loss frequency, deck C in fact contains fewer trials with net losses than deck A. In our study, participants experience for 10 selections from deck A five net gains ($100 gains − $0 loss) and five net losses ($100 gains − $150…$350 losses). In contrast, for 10 selections from deck C participants experience five net gains ($50 gain − $0 loss) and five standoffs ($50 gain − $50 loss). Thus, while for both card decks participants are shown on the screen 5 losses in 10 trials, the frequency of net losses differs between these two decks. Such a distinction does not exist for decks B and D, as for both decks, comparable to deck A, every trial associated with a loss also results in a net loss. Chiu and Lin (2007) modified the task in such a way that the frequency of net losses was identical between decks A and C. After this modification, they no longer observed differences between preferences for deck A and C. Hence, it is likely that the observed effects in the current study hinge on the difference in frequency of net losses between decks A and C. But, importantly, note that deck A and C do not differ regarding their gain frequency.

The potential influence of features other than long-term outcome on task performance might remain undetected, if only difference scores between advantageous and disadvantageous decks are considered in the analysis of choice behavior. In the current study, we observed a slightly positive difference score when considering the entire group of subjects. MacPherson et al. (2002) and Fridberg et al. (2010) observed a positive difference between the number of advantageous and disadvantageous decks after 100 trials of the IGT. In contrast, Caroselli et al. (2010) reported a negative difference, and Fernie and Tunney (2006) found no difference at all. Yet, all of these studies, including ours, clearly observed participants’ preference for high gain frequencies rather than a preference for positive long-term outcome, when the four decks were analyzed separately. The use of difference scores in the analysis of task performance is based on the assumption that choices within the groups of advantageous and disadvantageous decks are directly comparable such that the number of card selections within each group can be collapsed. However, decks A and B as well as decks C and D are only comparable directly with respect to the immediate reward associated with each trial and the overall outcome, but they differ in gain and loss frequency. In fact, every card deck differs from all others in at least one feature (loss frequency, gain frequency, overall outcome) that might influence choice behavior. The independent analysis of choice behavior for all four decks is thus crucial for understanding the particular mechanisms that drive decision-making under uncertainty.

Discussion with Regard to Subjects’ Variability

Multi-dimensional clustering of parameter estimates from the linear equation model revealed sub-groups of participants with substantially different parameter patterns. Clustering revealed two groups at the beginning and three groups at the end of the experiment. In both cases the majority of subjects belonged to a cluster with no particular preference for one of the three features long-term outcome, gain frequency, or loss frequency. Only a minority of subjects developed relatively large weights for one or more of the features. However, contrary to Bechara’s initial assumptions, no group of subjects developed a high weight for long-term outcome exclusively.

Most interestingly, the profoundly different weight patterns in two groups of subjects were both associated with a high positive difference score: for subjects belonging to cluster 1 (high weight for loss frequency, low weight for gain frequency and a weight close to zero for outcome) and for subjects in cluster 3 (low weight for loss frequency, high weight for gain frequency and high weight for outcome). This is additional evidence for a more complex learning pattern involved in successful performance on the IGT than initially assumed. Interestingly, subjects in clusters with a high difference score did not learn to pick an equal amount of cards from deck C and D but preferred either deck C (cluster 1) or deck D (cluster 3). This indicates that gain and loss frequency, which determine the difference between decks C and D, are more salient features than long-term outcome. In addition, the majority of participants (members of cluster 3) seem not to pick up successful weighting of the three task features, i.e., a set of weights supporting a choice behavior that avoids disadvantageous decks A and B. One explanation for this behavior may be that for most subjects, the three features of the task are combined in a way that prohibits the evolution of a clear preference for one of them, i.e., if subjects start to prefer options associated with one feature they would have to decide actively against options associated with another feature they prefer. Another explanation would be that for most subjects, behavior is guided by something different than the extracted task features.

In sum, our results show that only a minority of subjects learned to restrict their choices to the advantageous decks C and D, whereby they generally developed a preference for only one of the two decks.

Note that Huizenga et al. (2007), in a similar vain, used clustering to examine the development of strategy across different groups of subjects. Specifically, they applied Gaussian mixture modeling to the choice patterns of subjects in different age groups. Clustering revealed four sub-groups of participants that applied strategies of different complexity derived from proportional reasoning theory. The authors conclude that the large variation in performance in their adolescent sample is due to the fact that subjects use different rules to solve the gambling task. Similarly, multivariate clustering of individual weights obtained in our linear equation model revealed the attendance to different features by sub-groups of our participants as source of the high variation in the obtained parameter estimates. Van Duijvenvoorde et al. (2010) also examined choice strategies in an adolescent sample. Their clustering revealed three sub-groups with participants in the largest sub-group applying a choice strategy that focused on the options with low-frequency loss. In the terminology of our study, those options are associated with high-frequency gains and hence are very similar to the results presented here. Both terms describe the same feature from different perspectives. We decided to use the term “gain frequency” instead of loss frequency to better distinguish this feature from the “net loss frequency.”

Discussion with Respect to the Expectancy Valence Model

Out of previously applied computational models, the EV model (Busemeyer and Stout, 2002) has become a hallmark in the analysis of IGT data. The model assumes that choice behavior in the IGT reflects the interaction of three latent psychological processes: the integration and weighting of gains vs. losses, learning, and probabilistic choosing, i.e., the ability to explore and exploit choice options.

The model assumes that subjects, after choosing a particular card, integrate the experienced gain or loss of that card into the so-called valence, modulated by a parameter reflecting the subject’s attention to gains and losses. Further, subjects learn expectancies about the valences by continuously sampling from the various decks and updating their expectancy according to the observed outcome with their individual learning rate. Finally, learned expectancies determine the subject’s choices, which are again modified by a parameter reflecting the subject’s response consistency or amount of exploration.

Although the EV model was shown to successfully map decision deficits in clinical populations to alterations in one or more of the assumed underlying psychological processes (Yechiam et al., 2005), application of the EV model has not gone uncriticized. For example, Wetzels et al. (2010) observed considerable variability in parameter recovery both from real and simulated data. They further report poor model fit for a substantial number of healthy participants performing 100 trials of the original IGT and thus argue that for single participants it is generally not possible to estimate the EV parameters precisely. This was corroborated by our own investigations. Applying the EV model to our data set resulted in at least one parameter to be located on the boundary of the parameter space for 54 out of 119 participants. Such extreme values typically signal problems with the estimation procedure, the data, or the interaction between the data and the model (Wetzels et al., 2010). Multi-level modeling approaches were proposed to alleviate this problem for the investigation of group differences (Cheng et al., 2009; Wetzels et al., 2010). However, one should remain cautious in the interpretation of EV model parameters on the individual subject level.

Christakou et al. (2009) used a probabilistic approach to calculate the expected value of a subjects’ decision based on his or her previous experience. In contrast to the EV model, the expected value is calculated from the observed wins and losses for a particular deck, weighted not by an attention parameter but by the previous probabilities of winning and losing. This model, although not a fully predictive model of decision-making behavior (Christakou et al., 2009) captures the influence of gain and loss frequency on the formation of expectations.

Integration with Current Research and Future Directions

With our proposed model we provide a new tool to quantitatively analyze IGT performance. Unlike the EV and related models, we do not attempt to model specific cognitive processes underlying decision-making in the IGT. Rather with our model we are able to determine the behavioral relevance of different factors of the IGT payoff scheme influencing subjects’ decision-making. The model can be used and adapted to re-evaluate previously obtained behavioral data on the IGT. Thus, it might help to relate behavioral differences between clinical groups to differences in sensitivity to one or more of the features of the IGT.

Conclusion

The results of our study support the observation that, in contrast to the basic assumptions for the IGT, subjects in general do not learn to solely base their preference for particular card decks on the decks’ expected long-term outcome. Rather, choice options in the IGT are predominantly characterized by gain and loss frequency, and subjects’ choice behavior is influenced by a combination of these factors. If subjects regard long-term outcome as an important task feature, they additionally take into account gain and loss frequency. Consequently, long-term outcome alone is not able to drive choice behavior on the IGT. With our proposed linear equation model it is possible to disentangle and quantify the impact of each feature. Our modeling results point at gain and loss frequency as the primary factors guiding choice behavior in healthy young subjects. From our model, more focused conclusions about the factors guiding decision-making under uncertainty can be drawn. In addition, differences between clinical groups can be assessed for each factor individually.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Andreas Below, Karolin Gohlke, Jonas Klinkenberg, Katja Macher, and Ramona Menger for their invaluable help during data acquisition. We thank Christian Kalberlah and Stefan Kiebel for fruitful discussions on our model. We are also grateful to E.-J. Wagenmakers and Helen Steingröver for valuable discussions on the IGT and EV model. This work was supported by BMBF [Neurocircuits in obesity to Annette Horstmann, Arno Villringer; IFB Adiposity Diseases (FKZ: 01EO1001) to Annette Horstmann, Jane Neumann, Arno Villringer], the DFG (Mind and Brain), and the Einstein-Stiftung (Mind and Brain Institute).

References

Bark, R., Dieckmann, S., Bogerts, B., and Northoff, G. (2005). Deficit in decision making in catatonic schizophrenia: an exploratory study. Psychiatry Res. 134, 131–141.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bechara, A., Damasio, A. R., Damasio, H., and Anderson, S. W. (1994). Insensitivity to future consequences following damage to human prefrontal cortex. Cognition 50, 7–15.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bechara, A., Damasio, H., Damasio, A. R., and Lee, G. P. (1999). Different contributions of the human amygdala and ventromedial prefrontal cortex to decision-making. J. Neurosci. 19, 5473–5481.

Pubmed Abstract | Pubmed Full Text

Bechara, A., Dolan, S., Denburg, N., Hindes, A., Anderson, S. W., and Nathan, P. E. (2001). Decision-making deficits, linked to a dysfunctional ventromedial prefrontal cortex, revealed in alcohol and stimulant abusers. Neuropsychologia 39, 376–389.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bechara, A., Tranel, D., and Damasio, H. (2000). Characterization of the decision-making deficit of patients with ventromedial prefrontal cortex lesions. Brain 123, 2189–2202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Boeka, A. G., and Lokken, K. L. (2006). The Iowa Gambling Task as a measure of decision making in women with bulimia nervosa. J. Int. Neuropsychol. Soc. 12, 741–745.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bolla, K. I., Eldreth, D. A., Matochik, J. A., and Cadet, J. L. (2005). Neural substrates of faulty decision-making in abstinent marijuana users. Neuroimage 26, 480–492.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brogan, A., Hevey, D., O’Callaghan, G., Yoder, R., and O’Shea, D. (2011). Impaired decision making among morbidly obese adults. J. Psychosom. Res. 70, 189–196.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brogan, A., Hevey, D., and Pignatti, R. (2010). Anorexia, bulimia, and obesity: shared decision making deficits on the Iowa Gambling Task (IGT). J. Int. Neuropsychol. Soc. 16, 711–715.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Busemeyer, J. R., and Stout, J. C. (2002). A contribution of cognitive decision models to clinical assessment: decomposing performance on the Bechara gambling task. Psychol. Assess. 14, 253–262.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Carlson, S. M., Zayas, V., and Guthormsen, A. (2009). Neural correlates of decision making on a gambling task. Child Dev. 80, 1076–1096.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Caroselli, J. S., Hiscock, M., Scheibel, R. S., and Ingram, F. (2010). The simulated gambling paradigm applied to young adults: an examination of university students’ performance. Appl. Neuropsychol. 13, 203–212.

CrossRef Full Text

Cavedini, P., Bassi, T., Ubbiali, A., Casolari, A., Giordani, S., Zorzi, C., and Bellodi, L. (2004). Neuropsychological investigation of decision-making in anorexia nervosa. Psychiatry Res. 127, 259–266.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cella, M., Dymond, S., Cooper, A., and Turnbull, O. (2007). Effects of decision-phase time constraints on emotion-based learning in the Iowa Gambling Task. Brain Cogn. 64, 164–169.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cheng, C.-P., Sheu, C.-F., and Yen, N.-S. (2009). A mixed-effects expectancy-valence model for the Iowa Gambling Task. Behav. Res. Methods 41, 657–663.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chiu, T., Fang, D., Chen, J., Wang, Y., and Jeris, C. (2001). “A robust and scalable clustering algorithm for mixed type attributes in large database environment,” in Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery Data Mining (San Francisco, CA: ACM).

Chiu, Y.-C., and Lin, C.-H. (2007). Is deck C an advantageous deck in the Iowa Gambling Task? Behav. Brain Funct. 3, 37.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Christakou, A., Brammer, M., Giampietro, V., and Rubia, K. (2009). Right ventromedial and dorsolateral prefrontal cortices mediate adaptive decisions under ambiguity by integrating choice utility and outcome evaluation. J. Neurosci. 29, 11020–11028.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Davis, C., Patte, K., Curtis, C., and Reid, C. (2010). Immediate pleasures and future consequences. A neuropsychological study of binge eating and obesity. Appetite 54, 208–213.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dunn, B. D., Dalgleish, T., and Lawrence, A. D. (2006). The somatic marker hypothesis: a critical evaluation. Neurosci. Biobehav. Rev. 30, 239–271.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fernie, G., and Tunney, R. J. (2006). Some decks are better than others: the effect of reinforcer type and task instructions on learning in the Iowa Gambling Task. Brain Cogn. 60, 94–102.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fridberg, D. J., Queller, S., Ahn, W.-Y., Kim, W., Bishara, A. J., Busemeyer, J. R., Porrino, L., and Stout, J. C. (2010). Cognitive mechanisms underlying risky decision-making in chronic cannabis users. J. Math. Psychol. 54, 28–38.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Garon, N., Moore, C., and Waschbusch, D. A. (2006). Decision making in children with ADHD only, ADHD-anxious/depressed, and control children using a child version of the Iowa Gambling Task. J. Atten. Disord. 9, 607–619.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grant, S., Contoreggi, C., and London, E. D. (2000). Drug abusers show impaired performance in a laboratory test of decision making. Neuropsychologia 38, 1180–1187.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Greenberg, M. G., and Weiner, B. (1966). Effects of reinforcement history upon risk-taking behavior. J. Exp. Psychol. 71, 587–592.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hermann, D., Leménager, T., Gelbke, J., Welzel, H., Skopp, G., and Mann, K. (2009). Decision making of heavy cannabis users on the Iowa Gambling Task: stronger association with THC of hair analysis than with personality traits of the Tridimensional Personality Questionnaire. Eur. Addict. Res. 15, 94–98.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huizenga, H. M., Crone, E. A., and Jansen, B. J. (2007). Decision-making in healthy children, adolescents and adults explained by the use of increasingly complex proportional reasoning rules. Dev. Sci. 10, 814–825.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Liao, P.-C., Uher, R., Lawrence, N., Treasure, J., Schmidt, U., Campbell, I. C., Collier, D. A., and Tchanturia, K. (2009). An examination of decision making in bulimia nervosa. J. Clin. Exp. Neuropsychol. 31, 455–461.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lin, C.-H., Chiu, Y.-C., Lee, P.-L., and Hsieh, J.-C. (2007). Is deck B a disadvantageous deck in the Iowa Gambling Task? Behav. Brain Funct. 3, 16.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

MacPherson, S. E., Phillips, L. H., and Della Sala, S. (2002). Age, executive function and social decision making: a dorsolateral prefrontal theory of cognitive aging. Psychol. Aging 17, 598–609.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Martino, D. J., Bucay, D., Butman, J. T., and Allegri, R. F. (2007). Neuropsychological frontal impairments and negative symptoms in schizophrenia. Psychiatry Res. 152, 121–128.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O’Carroll, R. E., and Papps, B. P. (2003). Decision making in humans: the effect of manipulating the central noradrenergic system. J. Neurol. Neurosurg. Psychiatr. 74, 376–378.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pecchinenda, A., Dretsch, M., and Chapman, P. (2006). Working memory involvement in emotion-based processes underlying choosing advantageously. Exp. Psychol. 53, 191–197.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rodríguez-Sánchez, J. M., Crespo-Facorro, B., Perez-Iglesias, R., Perez Iglesias, R., González-Blanch, C., Bosch, C. G.-B., Alvarez-Jimenez, M., Alvarez, M., Llorca, J., and Vázquez-Barquero, J. L. (2005). Prefrontal cognitive functions in stabilized first-episode patients with schizophrenia spectrum disorders: a dissociation between dorsolateral and orbitofrontal functioning. Schizophr. Res. 77, 279–288.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schneider, W. (1973). Reinforcer effectiveness as a function of reinforcer rate and magnitude: a comparison of concurrent performances. J. Exp. Anal. Behav. 20, 461–471.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shurman, B., Horan, W. P., and Nuechterlein, K. H. (2005). Schizophrenia patients demonstrate a distinctive pattern of decision-making impairment on the Iowa Gambling Task. Schizophr. Res. 72, 215–224.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tchanturia, K., Liao, P.-C., Uher, R., Lawrence, N., Treasure, J., and Campbell, I. C. (2007). An investigation of decision making in anorexia nervosa using the Iowa Gambling Task and skin conductance measurements. J. Int. Neuropsychol. Soc. 13, 635–641.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Todorov, J. C. (1973). Interaction of frequency and magnitude of reinforcement on concurrent performance. J. Exp. Anal. Behav. 19, 451–458.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Toplak, M. E., Jain, U., and Tannock, R. (2005). Executive and motivational processes in adolescents with attention-deficit-hyperactivity disorder (ADHD). Behav. Brain Funct. 1, 8.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Van Duijvenvoorde, A. C. K., Jansen, B. R. J., Visser, I., and Huizenga, H. M. (2010). Affective and cognitive decision-making in adolescents. Dev. Neuropsychol. 35, 539–554.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wetzels, R., Vandekerckhove, J., Tuerlinckx, F., and Wagenmakers, E.-J. (2010). Bayesian parameter estimation in the expectancy valence model of the Iowa Gambling Task. J. Math. Psychol. 54, 14–27.

CrossRef Full Text

Wilder, K. E., Weinberger, D. R., and Goldberg, T. E. (1998). Operant conditioning and the orbitofrontal cortex in schizophrenic patients: unexpected evidence for intact functioning. Schizophr. Res. 30, 169–174.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yechiam, E., and Busemeyer, J. R. (2005). Comparison of basic assumptions embedded in learning models for experience-based decision making. Psychon. Bull. Rev. 12, 387–402.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yechiam, E., Busemeyer, J. R., Stout, J. C., and Bechara, A. (2005). Using cognitive models to map relations between neuropsychological disorders and human decision-making deficits. Psychol. Sci. 16, 973–978.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zhang, T., Ramakrishnon, R., and Livny, M. (1996). “BIRCH: an efficient data clustering method for very large databases,” in Proceedings of the ACM SIGMOD Conference on Management of Data (Montreal: ACM).