- 1 Département d’Etudes Cognitives, Group for Neural Theory, Ecole Normale Supérieure, Paris, France
- 2 Groupe de Neuroscience Théorique, Collège de France, Paris, France
To make fast and accurate behavioral choices, we need to integrate noisy sensory input, take prior knowledge into account, and adjust our decision criteria. It was shown previously that in two-alternative-forced-choice tasks, optimal decision making can be formalized in the framework of a sequential probability ratio test and is then equivalent to a diffusion model. However, this analogy hides a “chicken and egg” problem: to know how quickly we should integrate the sensory input and set the optimal decision threshold, the reliability of the sensory observations must be known in advance. Most of the time, we cannot know this reliability without first observing the decision outcome. We consider here a Bayesian decision model that simultaneously infers the probability of two different choices and at the same time estimates the reliability of the sensory information on which this choice is based. We show that this can be achieved within a single trial, based on the noisy responses of sensory spiking neurons. The resulting model is a non-linear diffusion to bound where the weight of the sensory inputs and the decision threshold are both dynamically changing over time. In difficult decision trials, early sensory inputs have a stronger impact on the decision, and the threshold collapses such that choices are made faster but with low accuracy. The reverse is true in easy trials: the sensory weight and the threshold increase over time, leading to slower decisions but at much higher accuracy. In contrast to standard diffusion models, adaptive sensory weights construct an accurate representation for the probability of each choice. This information can then be combined appropriately with other unreliable cues, such as priors. We show that this model can account for recent findings in a motion discrimination task, and can be implemented in a neural architecture using fast Hebbian learning.
Introduction
Survival requires fast and accurate decisions in an uncertain and continuously changing world. Unfortunately, our sensory input is noisy, ambiguous, and unfolding across time. The outcome of actions, such as reward or punishment, is also uncertain. As a result, perceptual and motor decisions cannot be pre-defined and instantaneous. Instead, sensory evidence needs to be accumulated over time and integrated with prior knowledge and reward predictions. Decision making investigations address solutions adopted by living organisms to solve two distinct but related problems: faced with different choices, which one would yield the most desirable outcome (“what to decide”)? In addition, since delaying decisions allows more time for collecting information and increasing choice accuracy, when should this decision be made (“when to decide”)? Optimal decision strategies solve this time/accuracy trade-off in order to maximize the rewards collected per unit of time, i.e., the reward rate.
One of the most fundamental questions in the study of decision making is whether or not the strategies used by humans and animals are optimal. Indeed, recent experimental and theoretical results suggest that humans use Bayes optimal strategies in a wide variety of tasks (Doya, 2002; Knill and Pouget, 2004; Sugrue et al., 2004; Daw et al., 2006; Wolpert, 2007). In simple experimental regimes, such as a two-alternative-forced-choice (2AFC) task, the optimal decision strategy can be described quantitatively as an integration to threshold (Gold and Shadlen, 2002; Ratcliff and McKoon, 2008). In this framework, decision making is divided into two successive stages: First, the inference stage accumulates sensory evidence over time by computing the probabilities that each choice is correct given past sensory observations (“what to decide?”). Subsequently, a decision is made to commit to one of the choices, when these probabilities have satisfied a given criteria (“when to decide?”). This response criterion is critical because it shapes the time/accuracy trade-off and controls the total reward collected by the subject.
In certain contexts, Bayesian decision making is equivalent to relatively simple decision mechanisms such as the diffusion model. However, in general, Bayesian methods lead to non-linear, non-stationary models of integration and decision making (Behrens et al., 2007; Deneve, 2008a,b; Mongillo and Deneve, 2008). In order to solve a decision problem, a Bayesian integrator must constantly adapt its decision making strategy to the statistical structure of the task and the reward. Though simple to formulate, these probabilistic decision problems can have solutions that are quite difficult to analyze mathematically, and are computationally intractable. Simplifying assumptions are required.
On the other hand, a major advantage of the Bayesian approach is its adaptability and generalizability to situations where simpler decision models would be suboptimal or not work (Doya, 2002; Yu and Dayan, 2005; Behrens et al., 2007; Walton et al., 2007; Whiteley and Sahani, 2008). Here we start from an extremely simple task (a 2AFC) where Bayesian decision making may be equivalent to the diffusion model, but only if the probability distributions of sensory inputs (i.e., the sensory likelihoods) are known in advance. We then show than when these distributions are not known a priori (which is likely to be the case in realistic decision tasks) enough information can be extracted from the sensory input (in the form of sensory neuron spike trains) to estimate the precision of the sensory input on-line and adapt the decision strategy accordingly.
This has strong consequences for the decision mechanisms. In particular, it predicts that in hard decision tasks, the sensory input is weighted more strongly during early stimulus presentation. The influence of sensory input decays later, implying that a choice is made based on prior knowledge and the earliest sensory observations, not on the latest sensory inputs preceding the decision, as one might initially think. On the contrary, in easy trials, sensory weights increase, and the latest sensory inputs are most predictive of the subject’s decision. This framework also predicts that the decision threshold (i.e., the amount of integrated sensory evidence deemed necessary to commit to a choice) is not fixed but evolves as a function of time and the sensory input: for hard tasks, this threshold collapses, forcing a decision within a limited time frame; for easy tasks, this threshold increases, i.e., decisions are made with higher accuracy at the cost of slightly longer reaction times.
We present simulations of a decision task implementation that has been very influential in the study of decision making in human and non-human primates. We compare the Bayesian decision maker with a diffusion model, and show that while both models predict similar trends for the mean reaction time and accuracy, the Bayesian model also predicts some strong deviations from the diffusion model predictions consistent with observations of behaving monkeys trained at this task (Shadlen et al., 1996; Gold and Shadlen, 2003; Mazurek et al., 2003; Palmer et al., 2005).
Materials and Methods
Sequential Probability Test
Consider a 2AFC between two possible responses, “A” or “B.” This decision needs to be made based on an on-going, noisy stream of sensory data. We can express all the sensory information received up to time t as an unfolding sequence of sensory inputs, So → t = {s0, sdt, …, st − dt } where st is the sensory input received between time t and t + dt. Let us suppose that correct choices are rewarded, while incorrect choices are not. How could subjects adjust their decision strategies in order to maximize their total expected reward? This problem can be separated into an inference stage and decision stage.
Inference
The inference stage corresponds to a temporal integration of sensory evidence in order to compute the probability that each of the choices is correct. Using the sequential probability ratio test (Ratcliff and McKoon, 2008), the log odds for choices A and B is computed recurrently as:
By taking the limit for small temporal steps dt, we get
where l(st) = log(P(st | A)/P(st | B)) is the log likelihood ratio for the sensory input received at time t, and the starting point of integration corresponds to the prior probability of choices Lo = log(P(A)/P(B)) – for example, Lo = log(2) when A is a priori twice more likely than B (Gold et al., 2008).
Of course, this requires that the likelihoods P(st | A) and P(st | B) are known. These likelihoods capture the selectivity and variability of sensory responses. Their relative values describe the reliability of the sensory input at time t. Therefore, if the sensory input likelihood is much larger for choice A than for choice B, then this input will strongly support choice A opposed to choice B.
To illustrate this, let us consider a decision based on the noisy spike train of a single motion-sensitive, direction-selective neuron. In this simple decision task, the two alternative choices are between the stimulus moving in the preferred direction of this neuron (choice A) and the opposite, anti-preferred direction (choice B). The sensory input st corresponds to the spike train of the neuron, i.e., a temporal binary stream of 1 or 0 (depending on whether a spike is emitted or not at time t). We suppose that the baseline firing rate q is increased to q + dq in the preferred direction, and decreased to q − dq in the anti-preferred direction. Therefore, q + dq and q − dq describe the likelihood of a sensory spike given choice A and choice B, respectively.
The initial log odd ratio at the start of the trial is set to Lo = 0, indicating that the two stimulus directions occur with the same prior probability. The likelihood ratio is given by
In the limit of small dt, and if the change in firing rate induced by the stimulus is small compared to the baseline firing rate, i.e., if dq ≈ q, the inference equation can be simplified to
where st − q corresponds to the sensory evidence at time t and the sensory weight is set by the input signal-over-noise ratio (SNR) w = 2dq/q. The log odds Lt represent the current confidence in choice A relative to choice B. It increases on average if the input firing rate is above baseline, and decreases on average if the input firing rate is below baseline. However, this accumulation is noisy due to the Poisson variability of the sensory spike train. Three example trials are plotted in Figure 1A.
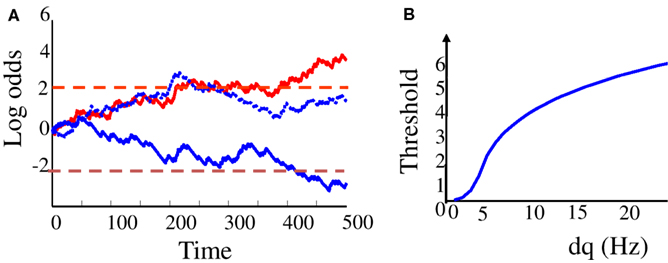
Figure 1. “Bayesian” diffusion model. (A) Log odd ratios Lt as a function of time in the trial (t = 0: start of sensory stimulation) on three different trials. Dashed lines correspond to the decision thresholds. Red plain line: a correct trial where “choice A” was made (i.e., the upward threshold was reached first), and choice “A” was indeed the correct choice. Blue plain line: another correct trial where choice B was made (the lower decision threshold was reached first) and B was indeed the correct choice. Dotted blue line: an error trial where choice “A” was made while choice “B” would have been the correct choice. (B) Optimal decision thresholds as a function of the strength of the modulation of input firing rate by motion direction (dq).
Decision criteria
We can distinguish between two variants of the 2AFC task leading to two different decision strategies (Mazurek et al., 2003). In “reaction time” tasks, subjects observe the sensory input and are required to respond as soon as they feel ready to do so. In “fixed delay” tasks, subjects observe the sensory input presented for a fixed duration. They indicate their choice only after a “go” signal, and thus cannot control the decision time.
In “fixed delay” tasks, the optimal decision strategy simply consists of measuring the sign of the log odds at the end of stimulus presentation. If the log odds is positive, choice A is more probable than choice B, and vice versa. Going for the most probable choice will maximize the probability of getting rewarded on each trial.
For “reaction time” tasks, the optimal strategy is a little more complicated. The log odds ratio indicates the on-line probability of making a correct choice if one chooses A ahead of B. If we decide on option A when the log odds ratio crosses a positive threshold D and decide on option B when it crosses a negative threshold −D (see Figure 1A), then the probability of making the correct choice will be given by PD = exp(D)/1 + exp(D).
However, the decision threshold also controls the duration of the trial, since it takes longer to reach a higher threshold. The time/accuracy trade-off can be optimized by setting D to a value that maximizes the total amount of reward collected per unit of time – the reward rate. The optimal decision threshold depends on the details of the experimental protocol. If, for example, a reward is provided only for correct choices, and each trial is followed by a fixed inter-trial interval, the total reward rate is given by
where RTD is the mean reaction time, that is, the time it takes on average for Lt to reach either D or −D (Ratcliff and McKoon, 2008). To estimate RTD, we approximate the Poisson noise in the cumulated spike counts by white Gaussian noise with variance equal to the mean. The mean first passage time (i.e., reaction time) is then RTD ≈ D/(l tanh(D)), where l = 2wdq is the average log likelihood ratio of the sensory input, or, equivalently, the average slope of Lt. In analogy with diffusion models, l corresponds to the “drift rate.”
The optimal threshold is a function of the sensory likelihoods and a solution to dRR/dD = 0.
The optimal threshold increases with the sensory reliability, as defined by the SNR w = 2dq/q. If the input is very reliable, accurate decisions can be made very quickly. Thus, the optimal threshold is high. If, on the other hand, reliabilities and sensory weights are low, reaching high choice accuracy would be very costly in terms of reaction time. In this case, the optimal threshold is low. Below a certain drift rate, waiting to make a decision is not worth the additional gain in accuracy, and the optimal threshold is zero: decisions should be made immediately, without waiting for the sensory input, resulting in a random choice with accuracy PD = 0.5 and reaction time RTD = 0. The optimal boundary as a function of the sensory “contrast” dq is plotted on Figure 1B.
This Bayesian approach is different from descriptive models of decision making such as the race model or the diffusion model (Laming, 1968; Link, 1992; Ratcliff and McKoon, 2008). These models were not initially derived from principles of optimality, but from the requirement of capturing human behavior with the simplest possible models. Interestingly, however, these decision mechanisms are equivalent to Bayesian decision making in specific contexts. For example, the parameters of a diffusion model can be adjusted to be equivalent to Bayesian optimal decision in 2AFC tasks when the sensory likelihoods are Gaussians (Ratcliff and McKoon, 2008). The diffusion model first integrates a noisy signal (analogous to the “inference stage” in the Bayesian framework), and takes a decision when the integrator reaches one of two possible bounds (analogous to the optimal criteria D). Variants of diffusion models have been shown to successfully reproduce human and animal behavior in 2AFC tasks (Ferguson, 1967; Newsome et al., 1989; Yuille and Bülthoff, 1996; Mazurek et al., 2003; Ratcliff et al., 2003; Palmer et al., 2005; Ratcliff and McKoon, 2008).
While they share similar mechanisms with diffusion models, Bayesian decision models have the advantage of being more constrained by the experimental protocol and the sensory noise. In a diffusion model, the drift rate, the threshold, and the starting point of the integration are all free parameters that can be adjusted to fit experimental data. In a Bayesian model, these are constrained respectively by the prior probabilities of the choice, the likelihoods of the sensory input, and the reward schedule. These parameters are either fixed by the experimental protocol (such as the prior) or can be estimated separately (such as the sensory reliabilities).
Unfortunately, an important disadvantage of the Bayesian framework is that the likelihood ratio of the sensory input l(st) needs to be known at the start of the trial. In other words, subjects need to know exactly what sensory signals and noise to expect for each of the choices. Without this knowledge, the optimal boundary, the sensory weight and consequently, the drift rate cannot be set. Most past models of decision making did not consider the possibility that the sensory likelihoods could be adjusted on-line as a function of the sensory input. Instead, the threshold and drift rate were assumed to be independent of sensory observations. Thus, the parallel between diffusion models and Bayesian decision making remained essentially qualitative. However, we show below that sensory reliabilities can in fact be estimated within the timescale of the decision itself. Therefore, the parameters of the decision process can be adjusted on-line to better approximate Bayesian decision making within the duration of a single trial.
Estimating Sensory Likelihoods On-Line
Sensory likelihoods are determined not only by the sensory noise, but also by the nature of the decision task. For example, categorization tasks result in very different likelihoods compared to discrimination tasks. Most of the decisions we make everyday occur in a unique context that will never be repeated. As a result, sensory likelihoods generally cannot be derived purely from past experience. For example, consider the choice between investing in one of two different stock options. If stock option “A” suddenly rises and stock option “B” falls, this could be due to a higher yield of option “A,” or just random fluctuations in the stock market. We will never know what to make of this observation without accumulating enough experience on the reliability of stock prices. However, in order to maximize the outcome, we should evaluate the reliability of market fluctuations at the same time that we accumulate evidence, thus making our investment as early as possible. Is this realistic?
There is an equivalent problem in 2AFC tasks. Usually, these protocols inter-mix trials with various levels of difficulties in order to measure psychophysical curves. For example, subjects could be asked to decide between two directions of motion, while varying the level of noise in the motion display (Shadlen and Newsome, 1998), or to do a categorization task, while varying the distance between the test stimulus and the category boundary (Ratcliff et al., 2003). In these protocols the “quality” of the sensory input (i.e., the sensory likelihood ratio) is not known at the start of a trial. In our toy model, varying task difficulties would correspond to changes in the sensory “contrast” dq, which affects the sensory weights and optimal boundary for decision making (Figure 1B).
For example, let us suppose that the task difficulty in our toy example is varied by controlling the amount of noise in the visual motion stimulus. This can be done by using motion displays composed of moving dots while varying the proportion of dots moving coherently in a single direction, with the rest of the dots moving in random directions (Britten et al., 1992). The proportion of dots moving coherently corresponds to the “motion coherence.” These kind of stimuli have been used intensively to investigate the neural basis of decision making in humans and non-human primates. They induce responses in direction-selective sensory neurons (e.g., in the medio-temporal area MT) that can roughly be described by an increase or decrease of the background firing rate by an amount proportional to motion coherence (Newsome et al., 1989; Britten et al., 1992). Schematically, the firing rate of the sensory neuron is q + cdq for choice A, and q − cdq for choice B, where c is a function of motion coherence (see Figure 2A). The sensory weights and the bounds should be updated accordingly. But how can this happen when trials with high and low coherences are randomly intermixed?
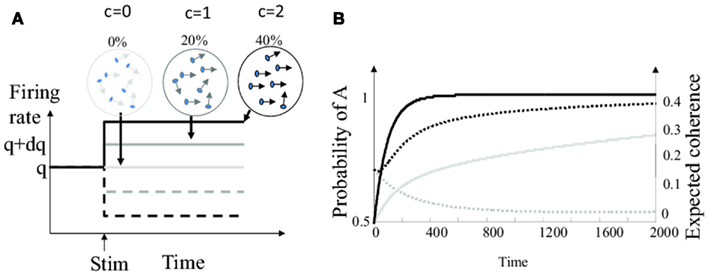
Figure 2. Bayesian decision making with varying levels of motion coherence. (A) Firing rate of the model sensory neuron in response to motion stimuli (start of stimulation marked by upward pointing arrow) for different levels of coherence. Plain lines: stimulus is in the preferred direction. Dashed lines: stimulus is in the anti-preferred direction. The gray scale indicates the strength of motion coherence. (B) Outcome of the “full” Bayesian integrator computing the joint probabilities of all pairs of choices and coherences. Time 0 correspond to the start of the trial. Plain black line: probability of choice A for coherence c = 0.2 (averaged over 20000 trials were A was the correct choice). Plain gray line: probability of choice A for coherence c = 0.05. Dotted black line: expected value for motion coherence ĉ for true coherence c = 0.2. Dotted gray line: expected value for motion coherence ĉ for true coherence c = 0.05.
There are two possible approaches to addressing this issue: one is to set a “compromise” between the different levels of coherence by using a fixed sensory weight and a fixed threshold. Alternatively, one could attempt to estimate the coherence on-line, adjusting the sensory weight, and the bound on-line during trial.
Motion coherence influences the firing rate of sensory neurons, and therefore, can be estimated from the sensory input at the same time as the direction of motion. Using the Bayes theorem, we can compute the joint probability of both contrast and choice, P(A, c | so → t ) and P(B, c | so → t ), based on augmented sensory likelihoods; let us call x the unknown direction of motion, with x = 1 for direction A and x = 0 for direction B. To compute the joint probability of all choices and coherence Pt(x, c) = P(x, c | so → t ), we use the sensory likelihood
resulting in the following recurrent equation:
where Z is a normalization term. An estimate of contrast can be obtained by computing its expected value while the probability for choice A is given by marginalizing over all possible coherence values P(A | so → t ) = ΣcP(A, c | so → t ).
The temporal evolution of the estimated coherence and the choice probability are plotted for two motion coherence values in Figure 2B. Observe that the coherence estimate evolves on a similar time scale than the choice probability. Consequently, sensory weights and decision thresholds based on motion coherence could, in theory, be adjusted during the time scale of a single decision trial.
However, implementing the full Bayesian integration algorithm requires the accumulation of evidence for all possible combinations of coherence and choice. This is considerably more computationally intensive than a diffusion model, and it is unclear how this could be implemented in a neural architecture. Instead, we considerably simplify the computation using approximate Bayesian optimal decision making, by separately estimating the reliability of the sensory input and the choice probability. By integrating the sensory input, we extract an on-line estimate of coherence ĉ(t). This estimate is used to adjust both the sensory weights and the boundary on-line during the decision trial. This method is suboptimal, but still reaches higher levels of performance than fixed boundaries and fixed sensory weights while requiring only one additional sensory integrator.
To do this approximate inference, we use an on-line version of the “Expectation Maximization” algorithm (Mongillo and Deneve, 2008). At each time step, we update the log odds Lt using the current estimate of coherence:
These log odds provide us with an on-line estimate of motion direction (or choice probability) We then estimate the coherence by performing a stochastic gradient descent on the log likelihood (see mathematical derivations):
where l = 2(dq2/q) is the “default” drift rate for coherence c = 1.
The learning time constant η is a free parameter that controls the amount of past observation used to estimate the coherence. A short time constant provides rapidly adapted but highly variable coherence estimates, while a long time constant provides less variable, slower estimates. In practice, we adjusted η in order to best approximate the mean dynamics of the coherence estimate during exact inference (Figure 2B). An even better approximation can be obtained by using a learning rate that decays as an inverse of time (i.e., by implementing a running average). However, we found that this has only a very minor impact on the reward rate or dynamics of the weights and threshold. Therefore, we used a simpler and more biologically plausible stochastic gradient descent rule to update the coherence estimate on-line.
In order to estimate the optimal threshold, we define the function Dopt (c) as the maximal value between zero and the numerical solution of
with the reward rate defined as
Here we used the fact that the mean drift rate for coherence c is c2l. The time-varying optimal threshold is set on-line to Dopt (ĉ).
Extension to a Population of Input Neurons
To test the predictions of the model in a biologically relevant setting, we focused on a noisy motion integration task that has been extensively used for studying the neural basis of decision making. The task is the same as that in our toy example, except that the decision is based on the activities of population of neurons rather than a single spike train.
Subjects in these experiments were required to watch a stimulus consisting of randomly moving dots and chose between two opposite direction of motion (direction A or direction B). The level of noise in the motion stimulus is controlled by the “coherence,” that is, the proportion of dots moving coherently in direction A or direction B. Motion coherence varied randomly from trial to trial, so the subject did not know the coherence at the start of the trial. The subjects indicated their choice by an eye movement in the direction of perceived motion, and were rewarded for correct choices. In a “reaction time” version of this task, the subject responded as soon as ready. In “fixed delay” version of this task, the stimulus is presented for a fixed duration and the subjects respond when prompted by a “go signal.”
A series of experimental studies with macaque monkeys trained at this task showed that at least two brain areas are involved. In particular, the role of the “sensory input” is played (at least in part) by the medio-temporal area MT. Neural responses from area MT are integrated in the lateral intraparietal area LIP, a sensorimotor brain area involved in the generation of eye movements. Thus LIP is a potential candidate for a Bayesian integrator. However, we focus here on the behavioral prediction of a Bayesian decision model based on the sensory input from area MT.
The firing rates of MT cells are modulated by the direction of motion and by motion coherence. MT neurons have a background response to purely noisy visual displays (with zero coherence) and a “preferred” direction of motion, i.e., their firing rate will be higher in response to motion in this direction and lower in the opposite direction. To a first approximation, if qi is the baseline firing of a MT cell, its firing rate is qi + cdqi in the preferred direction, and qi − cdqi in the anti-preferred direction, where c parameterize motion coherence. To simplify notation, we suppose that the MT population is balanced between the two directions of motions, i.e., Σidqi = 0.
As before, the log odds are computed as a weighted sum of the spikes from the population of MT cells, gain modulated by an on-line coherence estimate:
The initial value for the log odds correspond to the prior odds: Lo = log(P(A)/P(B)).
The on-line coherence estimate is obtained by a weighted average of motion coherence extracted from each spike train (see mathematical derivations). This gives a single leaky integration equation:
where is the drift rate for coherence 1. Without loss of generality, we can assume that the “default” coherence is 1, i.e., integration starts at ĉ(0) = 1.
Finally, the optimal threshold is set as before at Dopt (ĉ).
We compare the predictions from the Bayesian decision model with a diffusion model with fixed sensory weights and a fixed threshold. This diffusion model is similar to a model previously used to account for behavioral and neurophysiological data (Mazurek et al., 2003). The “integrated input” in the diffusion model is:
The boundary is set at a fixed level and the starting point of integration (for each setting of the prior) is set at a fixed value For easier comparison with the Bayesian decision model, was adjusted in order to achieve the same mean reaction time. For each prior, was adjusted in order to reproduce the mean response biases in the Bayesian model.
Simulation Parameters
For the single neuron model, we used q = 200 Hz and dq = 20 Hz. For the population model, we employed a population of 100 MT neurons, with baseline firing rate q = 10 Hz and modulation by motion stimulus dq = 1 Hz (50 neurons) or dq = −1 Hz (50 neurons). The time constant for coherence estimation was set to 1/η = 112 ms. Motion coherence was varied between 0 and 4. The inter-trial interval Titi was set to 1 s.
Mathematical Derivation of the Coherence Estimate
We describe here the stochastic gradient descent method for estimating the coherence c(t) on-line. We do so in the case of a single spike train. The generalization to a population of input neurons is straightforward.
Standard “batch” expectation maximization would consist in choosing a fixed temporal window T, and then repeating the following procedure until convergence: First, compute the expected motion direction given the current coherence estimate, then update the coherence estimate by the value of c that optimizes the log likelihoods (summed for all input s0 → T in the temporal window) given the current direction estimate. This is an off-line method and thus biologically implausible. Instead, we perform on-line expectation maximization using stochastic gradient descent. At each time step we update the coherence estimate using only the current training example (input st) instead of the whole sequence s0 → T. Using regularization parameter η, coherence is updated iteratively by the value of contrast that maximizes the sensory likelihood. In discrete time, this corresponds to:
where 〈s〉 is the frequency of observation st [qdt if st = 1 (1 − qdt) if st = 0] and is the value of coherence that maximizes the current likelihood:
Taking the limit dt → 0 and neglecting terms of higher order in dt leads to the following differential equation:
From which it is straightforward to derive eq. 5.
Free Parameters in the Diffusion and Bayesian Models
Here, our goal is to show that the Bayesian model reproduces qualitative trends in the data that are not captured by a diffusion model. However, it is crucial to identify the free parameters (and thus, the complexity) of both models if they are to be fitted quantitatively to behavioral data. Since the true sensory likelihoods q, dq, and the modulation of firing rate by each level of coherence c are not observables in behavioral tasks, they would have to be fitted to the data for each model. In addition, our version of the diffusion model has the following additional free parameters: the starting point of integration for each priors and the decision threshold The simplified Bayesian model has the following free parameters: the initial coherence estimate ĉ(0) and the coherence estimate update rate η. Other parameters (dynamics of thresholds and sensory weight, starting point of sensory integration) are imposed by parameters of the task (e.g., Titi, priors for choices P(A), P(B)) and approximate Bayesian inference equations. Our simplistic diffusion model have thus at least as many free parameters as the simplified Bayesian model.
More complex diffusion models can provide better fits to experimental data and capture some of these qualitative trends, but it comes at the cost of additional free parameters, i.e., variability in starting point of integration and drift rates (Ratcliff and McKoon, 2008), urgency signals (Hanks et al., 2011), or time-varying costs for sensory integration (Drugowitsch et al., 2012).
Results
Dynamics of Sensory Weights and Decision Threshold
The sensory weight (i.e., the weight given to each new spike for updating the log odds) is proportional to the coherence estimate. Thus the sensory weight is a dynamic function of time and the integrated sensory signal (see Figure 3A). At the start of the trial, the coherence estimate is equal to the initial estimate c = 1. As time increases, the coherence estimate converges to its true value. When the true motion coherence is higher than 1, the sensory weight increases over the duration of the trial. As a result, sensory inputs have a larger impact on the log odds at the end of the trial than at the beginning of trial. If, on the other hand, the true coherence is lower than 1, the sensory weight decreases over the duration of the trial. Thus, an input spike has a larger impact on the log odds at the beginning of the trial than at the end.
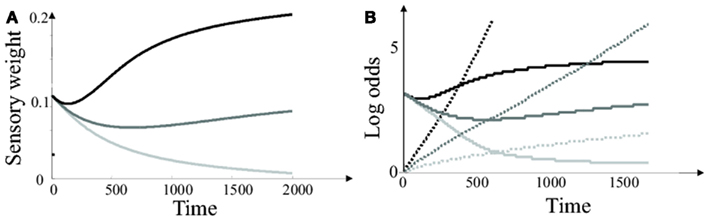
Figure 3. Simplified Bayesian model. (A) Sensory weights in the simplified Bayesian model (average of 20000 trials) as a function of time after stimulus presentation. Black line: c = 2. Light gray line: c = 0 (i.e., sensory input is pure noise). Dark gray line: c = 1. (B) Average log odds Lt (plain lines) and decision threshold (dashed lines) in the simplified Bayesian model. These temporal profiles were obtained by averaging over 20000 trials. The decision variables and threshold on individual trials (as well as the sensory weights) are varying randomly due to sensory noise (e.g., see Figure 1A). Black lines: c = 2 Dark gray lines: c = 1. Light gray lines: c = 0.2.
The decision threshold also needs to be updated on-line, since it depends on motion coherence. Figure 3B represents the average temporal evolution of the log odds and optimal threshold, for two levels of (true) motion coherence. Notice that the threshold follows the same trend than the sensory weight: it collapses for hard tasks, but stays constant or increases moderately for easy tasks. The effect of the collapsing bound at low contrast is to force a decision within a limited time frame if the trial is too difficult. In this case, the cost of waiting longer to make a decision outweighs the benefit of improved accuracy. Collapsing bounds have indeed been proposed as an upgrade for diffusion-based decision models with varying levels of sensory input strength. In particular, approximate Bayesian decision making predicts that a decision is not made at a fixed level of accuracy. Rather, the decision is made with a more permissive threshold (i.e., at a lower confidence level) when the trial is more difficult.
Behavioral Predictions
Simulated behavioral results are presented separately for “Reaction time” and “Fixed delay” tasks. To investigate the effect of priors, we either presented the two directions of motion with equal probability (Lo = 0) or direction A was presented more often than direction B (Lo = 0.6) or vice-versa ().
Reaction time task
Psychophysical curves and reaction times as a function of motion coherence and priors are plotted in Figure 4. While the psychophysical curves are qualitatively similar for the diffusion model and the Bayesian model (Figures 4A,B), the mean reaction times (Figures 4C,D) and reaction time distribution (Figures 4E,F) are notably different. In particular, RTs are shorter at low coherence and larger at high coherence than expected from a diffusion model (Figures 3C,D). This is mainly because for low coherence trials, the on-line estimate of coherence tends to decrease the decision threshold, thus shortening the reaction time. The reverse is true at high coherence. As a consequence, the animal spends less time on difficult trials (they are not worth the wait), and more time on easy trials (little extra-time result in a large increase in accuracy) than would be predicted by a diffusion model.
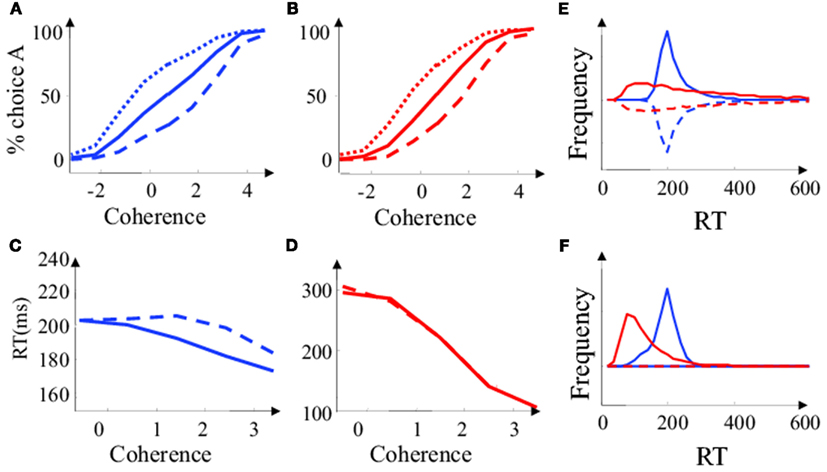
Figure 4. Simplified Bayesian and “diffusion” decision model in the “reaction time” task. (A) Proportion of choice A as a function of motion coherence for the simplified Bayesian model. Positive coherence corresponds to stimuli moving in direction (A), negative coherence to stimuli moving in the opposite direction. Plain Lines: the two choices are a priori equiprobable (Lo = 0). Dashed line: (B) is a priori more probable than A (Lo = −0.6). Dotted line: (A) is a priori more probable than B (Lo = 0.6). (B) Same as is (A), for the diffusion model. (C) Mean reaction time as a function of motion coherence for the simplified Bayesian model. Plain line: correct trial. Dashed line: error trials. (D) Same as in (C) for the diffusion model. (E) Reaction time distribution for low coherence trials (c = 0.05). The frequency was estimated by counting the number of RT observed over 20000 decision trials. Blue: Bayesian model. Red: diffusion model. Plain: correct trials. Dashed: error trials. Error trials are presented upside down for clarity. (F) Same as in (E) for high coherence trials (c = 0.3).
While the reaction time distributions for a diffusion model are very asymmetrical, with a fast rise and a long tail, the reaction time distributions predicted by the Bayesian model are quasi-symmetrical. The decision threshold is initially high, resulting in an absence of very short reaction time. The collapsing bound also prevents very long reaction times, which explains why the reaction time distributions of the Bayesian model do not have long tails. This occurs at all motion coherence levels even if, on average, the threshold does not collapse at high coherence: Long trials correspond to “bad trials” were the quality of the sensory input was low (since the decision threshold was not crossed early). In these trials, the estimated motion coherence is also low (even if true motion coherence is high). The bound collapses, resulting in a shortening of the duration of these “bad trials,” which would have formed the tail of the RT distribution in a diffusion model.
For the same reason, the Bayesian model predicts longer reaction times for error trials than for correct trials (Figure 4C). In contrast, a diffusion model would predict the same reaction time for correct and error trials (Figure 4D). This is another consequence of the correlation between the length of the trial and the estimated coherence. In trials where the quality of the sensory input is low (due to sensory noise) the threshold collapses and is crossed at a lower value of accuracy. These “bad trials” have both longer reaction times and lower accuracy.
The benefit of using a Bayesian decision model is particularly strong when it comes to incorporating prior knowledge with the sensory evidence. By estimating motion coherence, the Bayesian integrator can appropriately adjust the contribution of the sensory evidence compared to its prior (see results from the fixed delay tasks). The diffusion model, on the other hand, over-estimates the quality of the sensory input at low coherence and under-estimates it at high coherence. Consequently, the overall effect of the prior (as implemented by a bias in the starting point of integration) is too weak at low coherence and too high at high coherence.
By adjusting the sensory weights and decision thresholds on-line as a function of the coherence estimate, the Bayesian decision model constantly re-evaluates the influence of the prior during the entire duration of the trial. The effect of the prior is thus much more than setting the starting point for sensory integration. In particular, this can paradoxically make the prior appears as an additional “sensory evidence,” as illustrated in Figure 5. While the diffusion model (Figures 5A,B) starts integration at a level set by the prior, but later behaves as a simple integrator, the influence of the prior in the Bayesian model (Figures 5C,D) is amplified during the trial. This strongly resembles a change in the drift rate, as if the priors were in fact an additional “pseudo” motion signal.
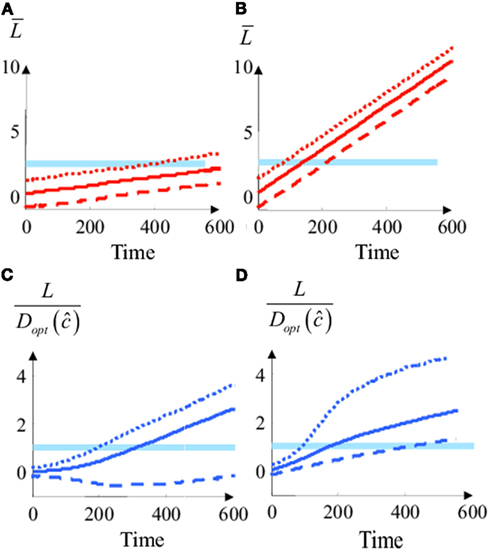
Figure 5. Simplified Bayesian model and “diffusion” model with changing priors. (A) Average integrated input divided by the threshold as a function of time in the diffusion model at low coherence (c = 0.2). Plain Lines: the two choices are a priori equiprobable (Lo = 0). Dashed line: B is a priori more probable than A (Lo = −0.6). Dotted line: A is a priori more probable than B (Lo = 0.6). In the diffusion model, the prior is implemented by a constant offset of the decision variable, i.e., a different starting point for integration. (B) The same as in (A) for medium motion coherence (c = 1). (C) Log odds divided by the decision threshold [i.e., L/Dopt (ĉ)] for the simplified Bayesian decision model at low coherence (c = 0.2). Dashed, dotted and plain lines correspond to different priors [same as in (A)] (D). Same as (C) but for a high value of motion coherence (c = 2).
Fixed delay tasks
During fixed delay tasks, subjects see the stimulus for a fixed duration and are required to respond only after presentation of a “go” signal. Thus, in this case, there is no time/accuracy trade-off and no need for a dynamic decision threshold. Instead, the decision is determined by the sign of the log odds ratio at the end of stimulus presentation.
In a diffusion model, all sensory inputs are taken equally into account, regardless of whether they occur at the beginning or at the end of stimulus presentation. By contrast, the Bayesian decision model re-weights the sensory evidence as a function of the estimated motion coherence, and thus, sensory inputs do not all contributes equally to the final decision. This is illustrated in Figure 6A where we plotted the average sensory input at different times during stimulus presentation, conditioned on the fact that the final choice was A. Here we consider only trials with zero coherence, i.e., c = 0. In this case the decision is purely driven by random fluctuations in the sensory input. The curves are a result of averaging over 20000 trials. The stimulus was presented for 2000 ms and the decision was made at t = 2000 ms. Only trials resulting in choice A (L2000 > 0) were selected for averaging. For a diffusion model (red), the curve is flat and slightly above zero. This is because positive inputs tend to increase the probability that the final log odds will be positive, and the final choice will be “A.” In a diffusion model, the order of arrival of these inputs does not matter, resulting in a flat curve. In contrast, the Bayesian decision model (blue line) gives more confidence to inputs presented early in the trial. This is because the initial coherence estimate [ĉ(0) = 1] is actually larger that the real motion coherence (c = 0 in this case). This results in the first inputs being taken into account more so than later inputs. As a consequence, the decision-triggered average of the input decays over time.
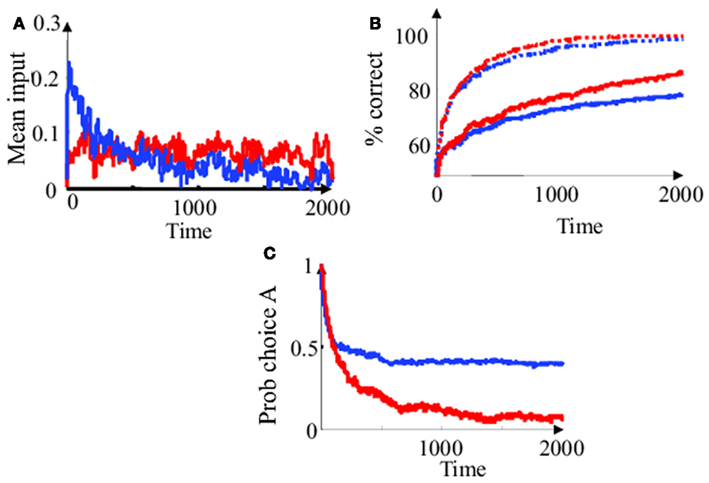
Figure 6. Simplified Bayesian and “diffusion” decision model in the “fixed delay” task. (A) Choice-averaged inputs as a function of time in a zero coherence trial (c = 0). The noisy sensory input (i.e., the input spike train st) was averaged in 10 ms sliding time windows over 20000 trials. Only trials were choice A was made after a 2 s stimulus presentation (i.e., L2000 > 0) were used for this choice-triggered average. Blue line: simplified Bayesian model. Red line: diffusion model. The diffusion model weights all sensory inputs equally while the Bayesian model relies on inputs only early in the trial. (B) Percent of correct choices as a function of the duration of stimulus presentation. Plain blue line: Bayesian model at low coherence (c = 0.1). Dotted blue line: Bayesian model at higher coherence (c = 0.5). Plain red line: diffusion model at low coherence (c = 0.1). Dotted red line: Bayesian model at higher coherence (c = 0.5). In contrast to the diffusion model, the Bayesian model stops integrating early in the trial (i.e., the probability of correct choice saturates whereas it keeps increasing for the diffusion model). (C) Probability of choosing A in zero coherence trial (c = 0), with a prior favoring choice A (Lo = 0.6), as a function of the duration of stimulus presentation. Since the input is pure noise, optimal strategy (if coherence was known) would be to always respond “A” (i.e., probability of choice A should be 1). The Bayesian model saturates to a suboptimal but still high probability of choice A. In the diffusion model, the influence of the prior decays over time.
A non-intuitive consequence of estimating motion coherence on-line is to decrease the apparent temporal window of integration for the Bayesian decision model. For low coherence trials, the initial input will influence the final decision much more than it should. Later in the trial, the influence of the input decays, but can never completely overcome the initial bias produced by early sensory noise. Consequently, integration is initially fast and later slows down considerably, to a point where the decision accuracy does not appear to benefit much from longer stimulus presentation (Figure 6B). This does not happen in a diffusion model, where each sensory input is equally weighted at all time. For long presentations of low coherence stimuli, the diffusion model performs paradoxically better than a Bayesian model. This is a consequence of approximate inference: coherence is estimated separately from motion direction, thus ignoring correlations between the two estimates.
Finally, the diffusion model and the Bayesian model behave very differently in the presence of priors. This is illustrated on Figure 6C. At zero coherence trial, the influence of the prior is very strong for short stimulus presentation, but decays for longer stimulus presentation, even when the stimulus is pure noise. This decay is not a desirable feature: the sensory input is completely uninformative so the influence of prior information about the choice should stay strong regardless of the length of stimulus presentation (the ideal strategy would be to always respond according to the sign of the prior and completely ignore sensory information). Unfortunately, this decay cannot be completely prevented if one does not know initially that the coherence is zero. By dynamically reweighing sensory evidence, the Bayesian decision model can prevent this “washing away” of prior information by noise. Once enough sensory information has been collected to bring the coherence estimate to zero, it stops integrating the sensory noise and relies only on the prior. The diffusion model, on the other hand, keeps accumulating noise and quickly forgets the prior information.
Discussion
Experimental Predictions
The Bayesian model predicts significant deviation from the prediction of a diffusion model when the precision of the sensory input (or the task difficulty) is varied randomly from trial to trial. Some of these predictions qualitatively fit previous results.
Thus, we predict that the reaction times are slower for error trials than correct trials, as shown in Figure 4C. This was indeed reported experimentally (Mazurek et al., 2003).
The model also predicts quasi-symmetrical reaction time distribution, as shown in Figures 4E,F. Such quasi-symmetrical RT distributions were observed in macaque monkeys performing this motion discrimination task (Ditterich, 2006). This is one of the most striking deviations of this behavior from the predictions of a diffusion model. An “urgency signal” increasing the probability of a choice with time during the trial has been proposed to account for these data (Ditterich, 2006). The effect of the urgency signal is similar to the effect of a collapsing bound.
The modulation by the prior resembles a pseudo “motion” signal, as shown in Figures 4C,D. Indeed, this was also reported experimentally (Palmer et al., 2005; Hanks et al., 2011). Once again, this data was attributed to a collapsing bound or an urgency signal forcing faster decisions in low coherence trials (Palmer et al., 2005; Hanks et al., 2011).
Finally, we predict that the influence of the sensory signal is stronger early in the trial than later in the trial, as shown in Figure 6A. Indeed, this effect is also observed in monkeys performing the motion discrimination task in zero coherence trials (Kiani et al., 2008). The decrease in sensory weights in low coherence trials limits the effective integration time window, causing saturation of performance with longer stimulus presentation, as shown in Figure 6B. Indeed, this was reported as well in the fixed duration task (Kiani et al., 2008). The authors accounted for these data by assuming that the animal reaches an internal decision bound after which it stops integration until the “go signal” is provided. We predict on the contrary that there is no “internal bound.” The monkey stops integrating in low coherence trials as soon as it realizes that the sensory input in entirely unreliable. This should not occur in high coherence trial.
Finally, a strong prediction of the adaptive Bayesian model is that the effect of the prior will not “wash away” for longer presentation times when the motion coherence is zero (Figure 6C), in contrast to the decay in prior influence normally observed when coherence is higher. To our knowledge, this prediction has not been tested experimentally.
Comparison with Other Behavioral Models
Our model is not the first variant of a diffusion model that accounts for the observed animal behavior in the motion discrimination task. Other models of decision making have focused on proposing a biologically plausible neural basis for decision mechanisms (Gold and Shadlen, 2002; Kiani et al., 2008; Wang, 2008; Churchland et al., 2011). They did not consider that the drift rate of a diffusion process or the bound could be adjusted on-line as a function of the sensory input. However, they share similar mechanisms with Bayesian decision models, such as a decision thresholds that collapses over time or, equivalently, an urgency signal that increases over time (Ditterich, 2006). The “integration to bound” model (Kiani et al., 2008) assumes that sensory integration takes place as in a diffusion model, but only until the integrated evidence reaches an internal bound. No further integration is performed after that. This could indeed account for the stronger weight of sensory evidence at the beginning of the trial and the saturation of performance for longer stimulus duration.
One of the strongest motivations in building a Bayesian model is to have the capability to not only extract a single estimate from the sensory input (e.g., direction of motion) but also to extract the uncertainty associated with this estimate. This is extremely useful since this information can then be combined optimally with other noisy sensory cues (Ernst and Banks, 2002) or used to compute probabilistically optimal policies (Dayan and Daw, 2008). Unfortunately, this is also costly. Uncertainties are harder to estimate since they generally require much more data than a simple estimate. Fortunately, biological spike trains are Poisson distributed to a first approximation. In a Poisson process, uncertainty is directly reflected in the gain of the neural responses (Zemel et al., 1998). Uncertainty can then be relatively easy to extract, which is what we exploited here.
Note that an even easier solution is available when both the modulation of firing rate (dq) as well as the baseline firing rate (q) are both equally gain modulated by certainty. For our toy model, this could correspond to an effect of coherence corresponding to multiplying both the dq and q by c. In this case, the sensory weights are constant (independent of c) and the diffusion model is exactly equivalent to a Bayesian decision model. This solution has been proposed previously in the context of population coding, in a variant of the motion discrimination task involving a continuous direction estimate (Beck et al., 2008). Unfortunately, the firing rate modulation reported in MT during motion discrimination tasks does not support this assumption. The baseline firing rate appears to be largely independent of motion coherence (Britten et al., 1992).
Other solutions have also been proposed involving the use of elapsed time rather than an explicit representation of the choice probability (Kiani and Shadlen, 2009; Hanks et al., 2011). Indeed, each level of integrated evidence and time during the trial can be mapped to a particular level of accuracy for the sensory signal. The predictions for the effect of priors are similar to ours and have been shown to fit experimental data (Hanks et al., 2011). Note, however, that a policy based on elapse time is only useful if coherence is constant during the whole duration of the trial and if the “beginning” of sensory stimulation is clearly marked. This strategy also assumes that “elapsed time” is directly available to the decision maker. While this use of elapsed time could represent a strategy learnt by highly trained subjects, it is not clear whether it could be applied to “single shot” decision making or in the presence of on-going sensory data whose reliability may vary, as in our stock market example. Moreover these models cannot deal with sensory signals starting and ending unpredictably. For example, a coherent motion signal could suddenly appear in an initially random motion display. Our framework constantly adapts the sensory integration and decision strategy to the on-going sensory signal. It can thus detect and properly respond to such events. Models based on elapsed time could not do so, since the start of sensory integration (time 0) cannot be inferred before the motion stimulus is actually detected.
The trials for which the Bayesian model makes predictions that are most notably different from previous models are the easy trials, where coherence is high. In this case, our model predicts an increase in sensory weights and a constant or slightly increasing (not collapsing) decision threshold. This means in particular that “motion pulses” would have more impact if given at the end of the trial. This contrasts with zero coherence trials, where they have more impact at the beginning of the trial than at the end (Kiani et al., 2008). This suggests a simple ways of testing our theory experimentally.
A recent approach used dynamic programming to model optimal decision strategies under varying motion coherence (Drugowitsch et al., 2012). This model maximized the reward rate by estimating (for each time in the trial) the value of three possible actions: collecting more evidence, making choice A or making choice B. This method is similar to the full Bayesian integration algorithm, except that it replaces the joint probability distribution over motion direction and coherence with a probability distribution over cumulated sensory evidence and time in the trial. It can indeed reproduce the behavioral results with high accuracy, in particular the RT distributions. However, in order to do so one must assume an explicit cost to cumulating more sensory evidence (rather than taking the decision immediately). This cost varies with the time in the trial (i.e., a full temporal profile for the cost of cumulating evidence as a function of time is fitted to the data). This additional degree of freedom can capture many deviations from what would be Bayesian optimal. Note that the measured cost was initially stable at the beginning of the trial then increased rapidly in both monkeys and humans (Drugowitsch et al., 2012). Rather than assuming a time-varying cost, we propose instead that these deviations are a result of approximate inference. Instead of computing the probability distribution over all sensory likelihoods, which would in general be intractable, the brain uses two coupled integrators separately estimating the sensory precision and motion direction on-line. Whether our model fits behavior quantitatively (and not only qualitatively) will need to be further investigated.
Possible Neural Implementation
An example of biologically plausible mechanisms for decision making involves recurrent network models with two competing populations of neurons receiving evidence for each direction of motion (Wang, 2002, 2008; Wong and Wang, 2006). Parameters can be adjusted to ensure a slow time constant of integration during the sensory integration phase (line attractor), similar to a diffusion process. The network eventually reaches a basin of attraction, converging to one of two possible stable states, which implement the threshold crossing and decision (Wong et al., 2007). This is however not an instantaneous process. As the network reaches the basin of attraction, it gradually loses its sensitivity to the input, resulting in a decaying sensory input influence on the final decision, and, if in addition, both populations receive an on-going background signal, an urgency signal or “collapsing bound” could also be implemented.
Recurrent dynamics could indeed implement the decreasing sensory weights and collapsing bound required in low coherence trials. However, they cannot implement the increasing sensory weights predicted in easy trials. We notice however, that the on-line coherence estimate (and thus, the synaptic gain) can be understood as fast Hebbian plasticity with a strong regularization term (the decay η). More precisely, it is equivalent to the “BCM” rule (Bienenstock et al., 1982) measuring covariance between pre and post-synaptic activity. Here, we interpret the pre-synaptic input as st (with mean q) and the post-synaptic activity as the probability of choice (with mean is 0.5). For example, fast Hebbian plasticity between MT cells and LIP cells could implement such mechanism in the motion integration task Therefore, local synaptic plasticity rules could provide an on-line estimate of sensory precision, thereby gain-modulating the incoming sensory information by its reliability at each level of the cortical processing hierarchy, while recurrent network dynamics could implement the collapsing bound. Note that if the decay η was replaced by a much smaller learning rate and gain modulated by reward prediction error, this rule would correspond to a reinforcement learning rule previously proposed to account for the improved performance of monkeys learning coarse versus fine motion discrimination tasks (Law and Gold, 2009). This suggests that on-line changes in sensory weights during a single decision trial could rely on neural mechanism similar to those implementing perceptual learning at a much slower time scale.
Limitations of the Approach
In order to avoid accumulating information for all combinations of coherence and motion directions while proposing a biologically plausible implementation, we separated the estimate of coherence and the estimate of motion direction, thus implementing approximate (not exact) inference. The cost of this approximation is the introduction of biases, e.g., a differential weighting of sensory information at different moment of the trials. In the reaction time task, the improvement acquired using an approximate Bayesian framework is also moderate compare to an optimized diffusion model (corresponding to an increase of about 5% in the reward rate).
We also chose to concentrate on the inference stage (i.e., extracting and using sensory likelihoods to infer the probability of sensory interpretations) rather than the decision stage (i.e., the threshold). Our greedy method for setting the threshold to the value that would be optimal if motion coherence was always (i.e., in all trials) equal to its current estimate is naive and probably strongly suboptimal. We suspect, however, that any efficient policy based on an on-line estimation of sensory likelihoods will result in qualitatively similar predictions, i.e., dynamic sensory weights and thresholds.
Finally, RT distributions in humans performing the same motion discrimination task are more non-symmetrical than monkey RT distributions, and are better fitted by a diffusion model. Moreover, the effect of priors in humans is well fitted by a change in the starting point of integration (Ratcliff and McKoon, 2008). Note that in contrast to monkeys, there were no 0 coherence trials in these human experiments, which may have decreased the interest of using a collapsing bound (the collapsing bound essentially prevents “guess” trials based on pure noise from taking too long). In a more recent experiment including zero coherence trials, evidence for an urgency signal was also found in human subjects (Drugowitsch et al., 2012) albeit its exact influence on RT distributions is not shown. Moreover, it is unclear whether humans used the same criteria for reward rate than monkeys performing for juice reward.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Beck, J. M., Ma, W. J., Kiani, R., Hanks, T., Churchland, A. K., Roitman, J., Shadlen, M. N., Latham, P. E., and Pouget, A. (2008). Probabilistic population codes for Bayesian decision making. Neuron 60, 1142–1152.
Behrens, T. E., Woolrich, M. W., Walton, M. E., and Rushworth, M. F. (2007). Learning the value of information in an uncertain world. Nat. Neurosci. 10, 1214–1221.
Bienenstock, E. L., Cooper, L. N., and Munro, P. W. (1982). Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48.
Britten, K. H., Shadlen, M. N., Newsome, W. T., and Movshon, J. A. (1992). The analysis of visual motion: a comparison of neuronal and psychophysical performance. J. Neurosci. 12, 4745–4765.
Churchland, A. K., Kiani, R., Chaudhuri, R., Wang, X. J., Pouget, A., and Shadlen, M. N. (2011). Variance as a signature of neural computations during decision making. Neuron 69, 818–831.
Daw, N. D., O’Doherty, J. P., Dayan, P., Seymour, B., and Dolan, R. J. (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–879.
Dayan, P., and Daw, N. D. (2008). Decision theory, reinforcement learning, and the brain. Cogn. Affect. Behav. Neurosci. 8, 429–453.
Ditterich, J. (2006). Computational approaches to visual decision making. Novartis Found. Symp. 270, 114–126. [Discussion].
Drugowitsch, J., Moreno-Bote, R., Churchland, A. K., Shadlen, M. N., and Pouget, A. (2012). The cost of accumulating evidence in perceptual decision making. J. Neurosci. 32, 3612–3628.
Ernst, M. O., and Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433.
Ferguson, T. (1967). Mathematical Statistics: A Decision Theoretic Approach. New York: Academic Press.
Gold, J. I., Law, C. T., Connolly, P., and Bennur, S. (2008). The relative influences of priors and sensory evidence on an oculomotor decision variable during perceptual learning. J. Neurophysiol. 5, 2653–2668.
Gold, J. I., and Shadlen, M. N. (2002). Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron 36, 299–308.
Gold, J. I., and Shadlen, M. N. (2003). The influence of behavioral context on the representation of a perceptual decision in developing oculomotor commands. J. Neurosci. 23, 632–651.
Hanks, T. D., Mazurek, M. E., Kiani, R., Hopp, E., and Shadlen, M. N. (2011). Elapsed decision time affects the weighting of prior probability in a perceptual decision task. J. Neurosci. 31, 6339–6352.
Kiani, R., Hanks, T. D., and Shadlen, M. N. (2008). Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J. Neurosci. 28, 3017–3029.
Kiani, R., and Shadlen, M. N. (2009). Representation of confidence associated with a decision by neurons in the parietal cortex. Science 324, 759–764.
Knill, D. C., and Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719.
Law, C. T., and Gold, J. I. (2009). Reinforcement learning can account for associative and perceptual learning on a visual-decision task. Nat. Neurosci. 12, 655–663.
Link, S. W. (1992). The Wave Theory of Difference and Similarity. Hillsdale, NJ: Lawrence Erlbaum Associates
Mazurek, M. E., Roitman, J. D., Roitman, J. D., Ditterich, J., and Shadlen, M. N. (2003). A role for neural integrators in perceptual decision making. Cereb. Cortex 13, 1257–1269.
Mongillo, G., and Deneve, S. (2008). Online learning with hidden markov models. Neural Comput. 20, 1706–1716.
Newsome, W. T., Britten, K. H., and Movshon, J. A. (1989). Neural correlates of a perceptual decision. Nature 341, 52–54.
Palmer, J., McKinley, M. K., Mazurek, M., and Shadlen, M. N. (2005). Effect of prior probability on choice and response time in a motion discrimination task. J. Vis. 5, 235–235.
Ratcliff, R., Cherian, A., and Segraves, M. (2003). A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of two-choice decisions. J. Neurophysiol. 90, 1392–1407.
Ratcliff, R., and McKoon, G. (2008). The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 20, 873–922.
Shadlen, M. N., Britten, K. H., Newsome, W. T., and Movshon, J. A. (1996). A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J. Neurosci. 16, 1486–1510.
Shadlen, M. N., and Newsome, W. T. (1998). The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci. 18, 3870–3896.
Sugrue, L. P., Corrado, G. S., and Newsome, W. T. (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787.
Walton, M. E., Croxson, P. L., Behrens, T. E., Kennerley, S. W., and Rushworth, M. F. (2007). Adaptive decision making and value in the anterior cingulate cortex. Neuroimage 36(Suppl. 2), T142–T154.
Wang, X. J. (2002). Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36, 955–968.
Whiteley, L., and Sahani, M. (2008). Implicit knowledge of visual uncertainty guides decisions with asymmetric outcomes. J. Vis. 8, 2 1–15.
Wolpert, D. M. (2007). Probabilistic models in human sensorimotor control. Hum. Mov. Sci. 26, 511–524.
Wong, K. F., Huk, A. C., Shadlen, M. N., and Wang, X. J. (2007). Neural circuit dynamics underlying accumulation of time-varying evidence during perceptual decision making. Front. Comput. Neurosci. 1:6. doi:10.3389/neuro.10.006.2007
Wong, K. F., and Wang, X. J. (2006). A recurrent network mechanism of time integration in perceptual decisions. J. Neurosci. 26, 1314–1328.
Yuille, A. L., and Bülthoff, H. H. (1996). “Bayesian decision theory and psychophysics,” in Perception as Bayesian Inference, eds D. C. Knill and W. Richards (New York: Cambridge University Press), 123–162.
Keywords: Bayesian, decision making, uncertainty, adaptation, expectation-maximization, prior, evidence, decision threshold
Citation: Deneve S (2012) Making decisions with unknown sensory reliability. Front. Neurosci. 6:75. doi: 10.3389/fnins.2012.00075
Received: 25 January 2012; Accepted: 04 May 2012;
Published online: 05 June 2012.
Edited by:
Gabriel José Corrêa Mograbi, Federal University of Mato Grosso, BrazilReviewed by:
Floris P. De Lange, Radboud University Nijmegen, NetherlandsPhilippe N. Tobler, University of Zurich, Switzerland
Copyright: © 2012 Deneve. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Sophie Deneve, Département d’Etudes Cognitives, Group for Neural Theory, Ecole Normale Supérieure, 29, rue d’Ulm, 75005 Paris, France. e-mail:c29waGllLmRlbmV2ZUBlbnMuZnI=
