- 1Department of Mathematics, Illinois State University, Normal, IL, USA
- 2Department of Mathematics, Benedictine University, Lisle, IL, USA
- 3Department of Mathematics and Computer Sciences, Chicago State University, Chicago, IL, USA
Song and Xiang (2006) developed an impulsive differential equations model for a two-prey one-predator model with stage structure for the predator. They demonstrate the conditions on the impulsive period for which a globally asymptotically stable pest-eradication periodic solution exists, as well as conditions on the impulsive period for which the prey species is permanently maintained under an economically acceptable threshold. We extend their model by including stage structure for both predator and prey as well as by adding stochastic elements in the birth rate of the prey. As in Song and Xiang (2006), we find the conditions under which a globally asymptotically stable pest eradication periodic solution exists. In addition, we numerically show the relationship between the stochastically varying birth rate of the prey and the necessary efficacy of the pesticide for which the probability of eradication of the prey species is above 90%. This is significant because the model recognizes varying environmental and climatic conditions which affect the resources needed for pest eradication.
1. Introduction
It is well-known that a variety of pest species pose a serious health risk to humans and pets, as well as causing great damage to property and crops. For virtually all pest species, biological eradication is biologically impossible or economically infeasible (Zhang et al., 2007). However, it has been shown that with an integrated pest management (IPM) approach, utilizing combinations of pesticides, predator species, and prey disease, prey species can be controlled at economically and environmentally feasible levels. The IPM approach has been proven superior to either purely biological control or chemical control (Song and Xiang, 2006).
A number of recent articles have mathematically modeled a variety of IPM approaches using impulsive differential equations, taking into account, for example, stage structure in the predator species and periodically varying environmental conditions (Song and Xiang, 2006). In the current literature, similar models also have been considered (Tang et al., 2005; Zhang et al., 2007). These deterministic models assume fixed birth rates for the prey species. As is more realistic in most ecosystems, we consider a random birth rate following a prior distribution with a mean that replaces the fixed birth rate of the previous models considered in Zhang et al. (2003, 2005, 2007); Tang et al. (2005); Song and Xiang (2006). This approach generalizes the model to accommodate random fluctuations, not just periodic fluctuations, in the birth rate due to environmental and climatic factors. In ecosystems, it is common for the reproductive behavior and fecundity of insect species to be altered by varying environmental and climatic factors such as temperature, light levels, and day length (Paulson et al., 2009). The stochastic birth rate component in the proposed model accommodates factors such as shortened day length and lower temperatures, which may induce varying levels of egg production (Paulson et al., 2009). Also, it recognizes that a fixed birth rate really represents an “average” birth rate, which may produce misleading results as to the resources necessary to ensure a high probability of pest eradication. This is most important in cases in which the population of the prey species is especially sensitive to changes in the potency of the pesticide. This semi-deterministic method is a novel approach. It can be applied to cases in which a priori information is available for birth rate distributions, even if it is not informative. The results we obtain will provide information on the values of other parameters that will ensure a high probability of eradication of the prey species under varying birth rates of the prey species.
The present paper is organized as follows: In Section 2, we discuss our impulsive differential equations model, introducing the essential variables and parameters. In Section 3, we use Floquet theory and results from Song and Xiang (2006) to establish conditions on the impulsive period for which our pest eradication solution is (i) locally asymptotically stable and (ii) globally asymptotically stable. In Section 4, we introduce a right-skewed distribution for the birth rate parameter b for the prey species. We present numerical results showing the relationship between the birth rate parameter b and value of E, the pesticide potency or application effectiveness.
2. The Deterministic Model
Our deterministic model consists of a prey species with a juvenile class x1 and a mature class x2, and a predator species with a juvenile class y1 and a mature class y2. The prey species is born periodically at time intervals of length T via a Ricker-type birth pulse b exp(−(x1(nT) + x2(nT))x2(nT), where b is the growth parameter, as considered in the model in Tang and Chen (2002). Immediately after the births, pesticide is sprayed, which kills a fraction E of both the juvenile and mature prey classes, whereas the two predator classes y1 and y2 are augmented by p1 and p2, respectively. The prey population is also decreased due to predation by the mature predators only, with parameter r > 0. The handling time of both x1 and x2 by the predator is h, and the conversion rate of killed prey in excess of what is needed for maintenance into births of new predators is λ. For instance, if λ = 0, then there is no effect of kills on predator births. Similarly, for very small positive values of λ, the efficiency of conversion is minimal. This conversion rate expression was also used in the models in Tang et al. (2005); Song and Xiang (2006). The maturity rates for the prey and predator species are mx and my, respectively. That is, 1/mi is the mean length of the juvenile period. The death rate of the predator is μ. The model equations are given by
This is a system of impulsive differential equations, which we consider only in the biologically meaningful domain D = {(x1, x2, y1, y2) | x1 ≥ 0, x2 ≥ 0, y1 ≥ 0, y2 ≥ 0}. For details on the theory of impulsive differential equations, we refer to the reader to the monograph (Lakshmikantham et al., 1989). For periodic solutions of such impulsive differential equations, see Bainov and Simenov (1993). Furthermore, Lemmas 3.1 and 3.2 provide simple examples of such periodic solutions.
3. Stability
We will need the following lemmas for the arguments in this section.
Lemma 3.1 (Song and Xiang, 2006). The system
has a unique positive, periodic, globally asymptotic solution ũ with period T, given by
and
For any other solution u(t) of the system, we have |u(t) − ũ(t)| → 0 as t → ∞.
Lemma 3.2 (Song and Xiang, 2006). Consider the subsystem
The subsystem (3) has the positive, periodic, globally asymptotic solution
with initial values
Theorem 3.1. The pest eradication periodic solution (0, 0, ỹ1(t), ỹ2(t)) of system (1) is locally asymptotically stable if
or equivalently, if
and globally asymptotically stable if
where
Proof. We first prove that the solution is locally asymptotically stable using Floquet Theory for impulsive differential equations (see Bainov and Simenov, 1993). We begin by taking a small amplitude perturbation (u1(t), u2(t), ỹ1(t) + v1(t), ỹ2(t) + v2(t)) of the pest eradication solution (0, 0, ỹ1(t), ỹ2(t)). Linearizing, we obtain the system
where Φ(t) is the fundamental solution matrix of the system with Φ(0) = I, the identity matrix. The linearization of the pulse behavior is given by
Hence, the monodromy matrix of the system is
where
and
By Floquet Theory, the solution is locally asymptotically stable if the absolute values of the eigenvalues of M are less than one. This is always the case for the two eigenvalues exp(−(my + μ)T) and exp(−μ T). The other two eigenvalues are the eigenvalues of the submatrix
The two eigenvalues of the matrix are less than one in absolute value if (see Li and Yang, 2011)
Clearly, inequality (7) is always satisfied, and inequality (8) is satisfied by the hypothesis. Hence, the solution is locally asymptotically stable.
We next prove the global attractivity of our solution following the technique in Song and Xiang (2006). Choose ϵ1 > 0 and ϵ2 > 0 sufficiently small so that
We observe that
and consider the following comparison impulsive differential equation:
By Lemma 3.1, system (9) has a globally asymptotically stable, positive, periodic solution
By the Comparison Lemma for impulsive differential equations (see Lakshmikantham et al., 1989), we have
From this inequality, we obtain
We next consider the comparison system
By direct calculation, we observe that for nT < t ≤ (n + 1)T,
is a positive, periodic, globally asymptotically stable solution of system (11). Again by the Comparison Lemma, we have
for sufficiently large t.
Now let w(t) = x1(t) + x2(t). From the first two equations of system (1), we obtain
for nT < t ≤ (n + 1)T, and
for t = nT. For w(t), we consider the comparison system
By integrating from t = nT+ to t = (n + 1)T, we obtain
where
We now obtain the stroboscopic map
Hence, z3(nT+) = δnz3(0+), and z3(nT+) → 0 as n → ∞. Equation (18) has the unique equilibrium z*3 = 0, which is globally asymptotically stable. Thus, system (16) has the globally asymptotically stable solution . We can conclude that limt → ∞ w(t) = 0, and hence limt → ∞ x1(t) = 0 and limt → ∞x2(t) = 0, since x1(t) ≥ 0 and x2(t) ≥ 0.
We next show that limt → ∞ y1(t) = 0 and limt → ∞ y2(t) = 0. For sufficiently small ϵ3 > 0, there exists T1 > 0 such that
0 < x1(t) < ϵ3 and 0 < x2(t) < ϵ3 for all t > T1. The function
is monotonically increasing for w(t) ≥ 0. Let
We now have
Consider the comparison system
By Lemma 3.1, this comparison system has the positive, periodic, globally asymptotically stable solution
Hence, for sufficiently small ϵ4 > 0 and large enough t, we have
From the inequalities (10) and (20), we obtain
for sufficiently large t. Letting ϵ1 → 0, ϵ3 → 0, and ϵ4 → 0, we obtain and as t → ∞. Hence, limt → ∞ y1(t) = ỹ1(t).
Using the fourth equation from system (1) and the inequality (20), we obtain the inequality
For this inequality, we consider the comparison system
This system has a periodic, globally asymptotically stable solution
for nT < t ≤ (n + 1)T. By the Comparison Lemma, we have
for sufficiently large t. The inequalities (12) and (22) imply that
for sufficiently large t. Letting ϵ2 → 0, ϵ3 → 0, and ϵ5 → 0, we obtain and as t → ∞. Hence, limt → ∞ y2(t) = ỹ2(t). □
4. Discussion
4.1. Stochastic Birth Rate Model
In this paper, we consider an integrated pest management (IPM) model with two stages for both predator and prey, where prey births occur according to a birth pulse. We found conditions for global stability of the pest eradication periodic solution. In particular, we express this relationship in terms of an upper bound on b, the parameter in the birth pulse expression.
We now turn to the stochastic model. Specifically, we consider the birth rate parameter b of the prey species given in system (1) to be random. As special case, we consider b to follow a right-skewed distribution reflecting the ecosystem where small birth rates are prevalent, while due to climatic changes, infrequent but large spikes in the birth rate are probable. However, the approach employed here can be easily implemented if a priori information indicates a different birth rate behavior. In fact, even if no information regarding the nature of the birth rate of the prey species is available, one can still implement the model given herein by simply using a uniform distribution for the birth rate, where all possible values of the birth rate are equally likely.
The model in Song and Xiang (2006) considers only periodically varying environments, where the environmental and climatic conditions follow a predictable pattern. Our model includes the behavior of this model as a particular instance. In other words, we extend the model given in Song and Xiang (2006) such that environmental and climatic conditions of a more random nature can be modeled.
5. Conclusions and Remarks
Here we seek a value of E, the pesticide potency or application effectiveness, under randomly varying birth rates in an attempt to maximize the eradication probability. Our approach with stochastic birth rate parameter forms a class of models, which accommodate a wide spectrum of cases where the eradication probability depends not only on the pesticide use but also on the abundance of the prey species.
In a model with deterministic birth rate, whether the eradication occurs depends on the model parameters. Using our model, with the introduction of a stochastic parameter, we capture the process of varying birth rates that result in a realization for b, while holding all other values fixed and then compute the probability of eradication. To be more specific, we simulate a population of exponentially distributed birth rate parameters with mean b. Next we check the proportion of runs for which the total pest population is below a predetermined tolerance after a given length of time, which we define as eradication. Figure 1 depicts the probability of eradication for given values of E and mean of b values. In this particular case when the magnitude of the prey birth rate follows a right-skewed random behavior with varying averages, the pesticide amount or potency may be determined based on the eradication probability. As expected, large pesticide values while the birth rates vary around a small mean result in high eradication probability.
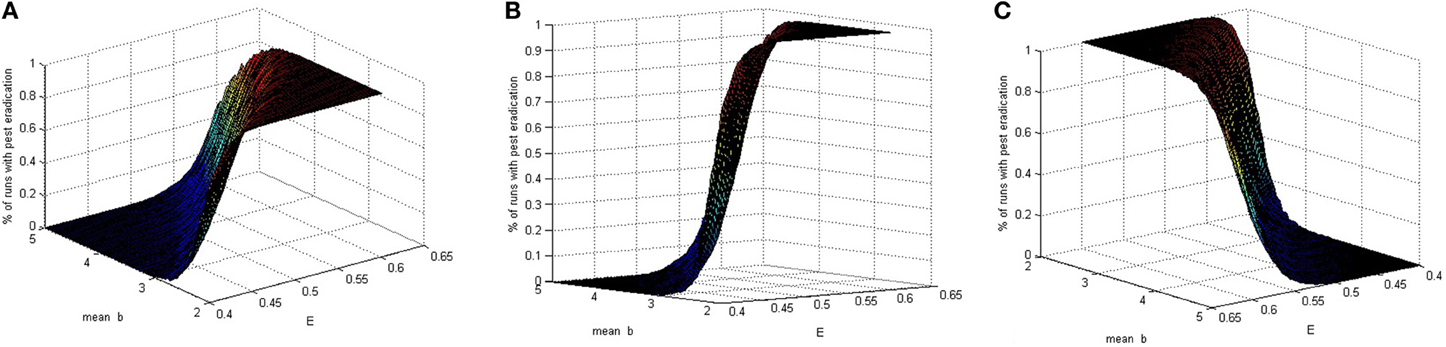
Figure 1. Three views of the percentage of runs with eradication for ordered pairs (E, b), where b is stochastic and E is deterministic.
The graph in Figure 1 is obtained using arbitrarily chosen fixed parameter values mx = 0.8, my = 0.7, r = 0.1, μ = 0.2, h = 0.5, λ = 0.1, p1 = 0.4, p2 = 0.3, and T = 1. With these values and E = 0.5, local asymptotic stability of the pest eradication solution occurs when b < 2.5985428. This is consistent with the results shown in Figure 1.
We began this study by considering an integrated pest management IPM model in which prey births occur according to a deterministic birth pulse. We established conditions for global stability of the pest eradication solution in terms of the birth rate parameter b of the prey species. We modified the model by considering b to be random. The stochastic version of our model extends the model in Song and Xiang (2006) by allowing for random environmental and climatic conditions. The stochastic model more clearly explains the relationship between the birth rate parameter b and the efficacy of the pesticide E needed for pest eradication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like the thank the referees for their helpful comments, which greatly improved the exposition of the manuscript.
References
Bainov, D. D., and Simenov, P. S. (1993). Impulsive Differential Equations: Periodic Solutions and Applications. New York, NY: Wiley.
Lakshmikantham, V., Bainov, D. D., and Simeonov, P. S. (1989). Theory of Impulsive Differential Equations. Singapore: World Scientific. doi: 10.1142/0906
Li, J., and Yang, Y. (2011). SIR-SVS epidemic models with continuous and impulsive vaccination strategies. J. Theor. Biol. 280, 108–116. doi: 10.1016/j.jtbi.2011.03.013
Paulson, M. D., Houston, A. I., McNamara, J. M., and Payne, R. J. H. (2009). Seasonal dispersal of pests: one surge or two? J. Evol. Biol. 2, 1193–1202. doi: 10.1111/j.1420-9101.2009.01730.x
Song, X., and Xiang, Z. (2006). The prey-dependent consumption two-prey one-predator models with stage structure for the predator and impulsive effects. J. Theor. Biol. 242, 683–698. doi: 10.1016/j.jtbi.2006.05.002
Tang, S., and Chen, L. (2002). Density-dependent birth rate, birth pulse and their population dynamic consequences. J. Math. Biol. 44, 185–199. doi: 10.1007/s002850100121
Tang, S., Xiao, Y., Chen, L., and Checke, R. A. (2005). Integrated pest management models and their dynamical behavior. Bull. Math. Biol. 67, 115–135. doi: 10.1016/j.bulm.2004.06.005
Zhang, H., Georgescu, P., and Chen, L. (2007). An impulsive predator-prey model of integrated pest management. CEU, Department of Mathematics.
Zhang, Y., Liu, B., and Chen, L. (2003). Extinction and permanence of a two-prey one-predator system with impulsive effect. Math. Med. Biol. 20, 309–325. doi: 10.1093/imammb/20.4.309
Keywords: predator-prey interactions, eradication, permanent suppression, stability, environment
Citation: Akman O, Comar TD and Hrozencik D (2013) Integrated pest management with stochastic birth rate for prey species. Front. Neurosci. 7:141. doi: 10.3389/fnins.2013.00141
Received: 18 April 2013; Paper pending published: 14 June 2013;
Accepted: 19 July 2013; Published online: 08 August 2013.
Edited by:
Xiaogang Wu, Indiana University-Purdue University Indianapolis, USAReviewed by:
Young R. Kim, Hankuk University of Foreign Studies, South KoreaHannah Callender, University of Portland, USA
Tianxiao Huan, Framingham Heart Study, USA
Jian Han, Pennsylvania State University, USA
Copyright © 2013 Akman, Comar and Hrozencik. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Olcay Akman, Department of Mathematics, Illinois State University, 100 N University St., Normal, IL 61761, USA e-mail:b2FrbWFuQGlsc3R1LmVkdQ==

