- 1Material Systems for Nanoelectronics, Faculty of Electrical and Information Engineering, Chemnitz University of Technology, Chemnitz, Germany
- 2Neuromorphic Cognitive Systems Group, Institute of Neuroinformatics, University of Zurich and ETH Zurich, Zurich, Switzerland
- 3Semiconductor Materials, Institute of Ion Beam Physics and Materials Research, HZDR Innovation GmbH, Dresden, Germany
- 4Institute for Integrative Nanosciences, IFW Dresden, Dresden, Germany
Memristive devices are popular among neuromorphic engineers for their ability to emulate forms of spike-driven synaptic plasticity by applying specific voltage and current waveforms at their two terminals. In this paper, we investigate spike-timing dependent plasticity (STDP) with a single pairing of one presynaptic voltage spike and one post-synaptic voltage spike in a BiFeO3 memristive device. In most memristive materials the learning window is primarily a function of the material characteristics and not of the applied waveform. In contrast, we show that the analog resistive switching of the developed artificial synapses allows to adjust the learning time constant of the STDP function from 25 ms to 125 μs via the duration of applied voltage spikes. Also, as the induced weight change may degrade, we investigate the remanence of the resistance change for several hours after analog resistive switching, thus emulating the processes expected in biological synapses. As the power consumption is a major constraint in neuromorphic circuits, we show methods to reduce the consumed energy per setting pulse to only 4.5 pJ in the developed artificial synapses.
Introduction
Since the discovery of spike-timing dependent plasticity (STDP) in biological synapses (Bi and Poo, 1998; Snider, 2008; Di Lorenzo and Victor, 2013), scientists have been captivated by the idea of changing the synaptic weight, i.e., the strength between the pre- and post-neuron, in bioinspired electronic systems in a fashion similar to biology (Indiveri et al., 2006). However, the circuit-oriented approach is complicated because the “synaptic weight” variable has to be stored typically either as charge in a capacitor (Koickal et al., 2006) or even digitally in neuromorphic IC (Schemmel et al., 2012; Mayr et al., 2013). This adds circuit complexity and increases energy consumption (Indiveri et al., 2006; Adee, 2009; Ananthanarayanan et al., 2009). Therefore, nonvolatile analog resistive switches, namely resistive random-access memory (RRAM) or memristors (Chua, 1971; Du et al., 2013), responding to well-defined input signals by suitably changing their internal state (“weight”) are currently developed. For example, the emulation of STDP with 60–80 pairings of pre- and post-synaptic spikes has been shown for artificial synapses based on memristive TiOx (Seo et al., 2011; Thomas and Kaltschmidt, 2014), WOx (Chang et al., 2011), HfOx (Yu et al., 2011), GST (Kuzum et al., 2012), and on the memristive BiFeO3 (Mayr et al., 2012; Cederström et al., 2013).
Figure 1A shows a memristor between the electrical Integrate & Fire (I&F) neurons. The synaptic weight of the memristor can be controlled by the time delay Δt between pre- and post-spike from the 1st layer I&F neuron (Figure 1A) (Zamarreño-Ramos et al., 2011). The 2nd layer I&F neuron sums up the signals from all incoming neurons and generates voltage spikes transmitted to other neurons (not shown) through memristor-based artificial synapses. The memristive BiFeO3(BFO) can serve as an analog resistive switch (Shuai et al., 2011) with multiple distinguishable low resistance states (LRSs) (Shuai et al., 2013; Jin et al., 2014) and with a single detectable high resistance state (HRS). Due to the thermal diffusion of Ti atoms and their substitutional incorporation into the lower part of the BiFeO3 (BFO) layer during BFO thin film growth on a Pt/Ti bottom electrode, the barrier at the Pt/Ti bottom electrode is flexible.
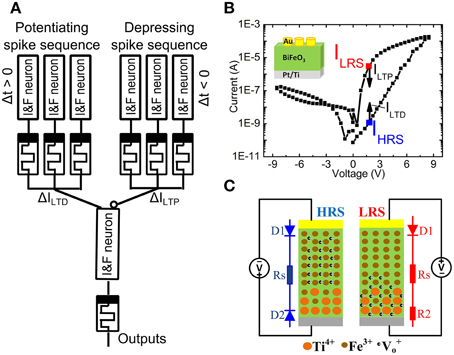
Figure 1. (A) Schematic illustration of the memristor-based synaptic electronics. The artificial synapses are placed between Integrate & Fire neurons (I&F neuron). With a well-defined time delay Δt between the pre- and post-spikes the internal state (“weight”) of the memristor is suitably changed. (B) Hysteretic current-voltage (IV) characteristics of a Au/BiFeO3/Pt memristor in LRS and HRS with a top electrode area of 4.5E4 μm2 under source voltages with maximum sweeping pulse amplitude of 8.5 V and a pulse width of 100 ms. The current in high resistance state IHRS and in low resistance state ILRS is read out at +2.0 V, after having switched the memristor into HRS and LRS, respectively. The long term potentiation current ILTP and the long term depression current ILTD lie below the reading current in LRS (ILRS) and HRS (IHRS). Inset shows the structure of a BFO memristor. (C) Schematic demonstration of the distribution of fixed Ti4+, fixed Fe3+ and mobile V+o.
Earlier we have shown that STDP and triplet plasticity with learning windows on the millisecond time scale can be faithfully emulated on BFO-based artificial synapses by applying 60–80 pairings of pre- and post-synaptic spikes (Mayr et al., 2012; Cederström et al., 2013). In this work we investigate a significantly wider range of timescale configurability, ranging from 25 ms to 125 μs. To the best of our knowledge, this kind of timescale configurability has not been shown in memristive synapses before. We also examine the evolution of the induced memristive weight change over time and provide several power consumption figures. By increasing the programming voltage (HRS/LRS writing pulse amplitude), it is possible to decrease the switching pulse width as well as the power consumption during a single STDP writing process on BFO-based artificial synapses. Furthermore, the increased programming voltage also shortens the total pairing spike time, and enables to move from the standard biology-like 60–80 spike pairing STDP experiment to a single pairing STDP experiment that results in the same weight/memristance change.
Our work is structured as follows: In Section Materials and Methods, we describe the non-volatile resistive switching of BFO–based artificial synapses and introduce the single pairing STDP pulse sequence. In Section Results, we present the measured learning window, memory consolidation, and energy consumption of the single pairing STDP in BFO-based artificial synapses and discuss configurability, energy consumption, and retention of weight change in Section Discussion. The paper is summarized and an outlook is given in Section Summary and Outlook.
Materials and Methods
Nonvolatile, Analog Resistive Switching in BiFeO3
Polycrystalline, 600 nm thick BiFeO3 (BFO) thin films with a flexible bottom barrier have been grown by pulsed laser deposition on Pt/Ti/SiO2/Si substrates. Circular Au top contacts have been magnetron sputtered on the BFO thin films using a shadow mask (Shuai et al., 2011, 2013; Jin et al., 2014). The Pt/Ti bottom electrode and the Au top contacts posses a flexible and a fixed barrier height, respectively. As illustrated in Figure 1B, by applying the sweeping source voltage from 0 V → −8.5 V → +8.5 V → 0 V between the Au top electrode and the bottom electrode, the current-voltage characteristics, which were recorded using a Keithley source meter 2400, reveal reproducible nonvolatile hysteretic bipolar resistive switching in BFO memristors with mobile donors (oxygen vacancies) and fixed donors (Ti donors). As illustrated in Figure 1C which has been adapted from Ref. (You et al., 2014), the physical mechanism underlying resistive switching in BFO memristors is related with the nonvolatile change of flexible barriers in Ti-containing BFO memristors. Due to voltage application of a LRS writing pulse, fixed Ti donors close to the bottom electrode can effectively trap mobile oxygen vacancies in BFO. The bottom electrode becomes non-rectifying and the BFO memristor is in LRS. On the other hand, when applying the HRS switching pulse, the mobile donors in BFO memristors are redistributed between the top and the bottom electrode. The bottom electrode becomes rectifying and the BFO memristor is in HRS. Note that for both writing pulses the Au top electrode remains rectifying.
A single writing pulse with an amplitude Vw = +8.0 V and −8.0 V can be used to switch the BFO memristor into LRS and HRS, respectively. The maximum possible amplitude increases with the thickness of the BFO memristor and decreases with the length of the writing pulse. For a BFO layer thickness of 600 nm and a writing pulse length of 100 ms, the barrier height of the bottom electrode typically starts to change at a writing pulse of amplitude Vw = +3.0 V. Applying a dc voltage below +2.0 V to the BFO memristor does not change the barrier height of the bottom electrode, and the state of the BFO memristor does not change. Therefore, the +2.0 V dc voltage is defined as the reading bias for the 600 nm thick BFO memristor. The ratio between the resistance RHRS in HRS and the resistance RLRS in LRS amounts to RHRS/RLRS = 2770 (Figure 1B). For changing the synaptic weight the absolute value of the amplitude Vp of the pre-synaptic and post-synaptic spike has to be larger than the reading bias amplitude +2.0 V (Smerieri et al., 2008; Borghetti et al., 2009; Lai et al., 2009). In our previous work, we used a 500 nm thick BFO layer and an amplitude of 2.3 and 2.0 V for STDP with 60–80 pairings of pre- and post-synaptic spikes. In this work, we use a 600 nm thick BFO layer and an amplitude Vp of 3.0 V for STDP with single pairing of pre- and post-synaptic spikes. For the potentiating (depressing) spike sequence, the long term potentiation current ILTP (long-term depression current ILTD) decreases exponentially with decreased pulse amplitude in positive (negative) voltage range: ILRS > ILTP (IHRS < ILTD).
The nonvolatile resistive switching of BFO was examined by a retention test (Figure 2A). A single writing pulse of Vw = +8.0 V and − 8.0 V and a pulse width of tp = 100 ms was used to switch the BFO memristor into LRS and HRS, respectively. The reading currents have been read out with a reading bias of Vr = +2.0 V and are defined as the current of HRS (IHRS) and LRS (ILRS). As shown in Figure 2A the BFO memristor exhibits degradation of the LRS within the testing time of 2 h. No significant change has been observed for HRS during the retention time of 5 h. This non-ideal retention motivated us to investigate memory consolidation (Clopath et al., 2008) in BFO with the shortened pulse sequence of single pairing STDP.
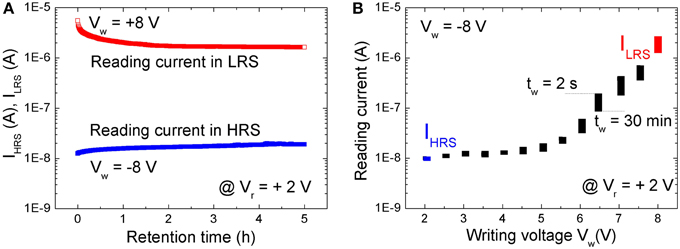
Figure 2. (A) Retention test with a reading bias of Vr = +2.0 V after setting the BFO memristor to LRS (red symbols) and to HRS (blue symbols). The reading current has been recorded every 30 s. (B) Retention of multilevel resistive switching in a BFO memristor, which has been initially set to HRS by a writing voltage of Vw = −8.0 V. The reading current has been measured at a small reading bias of Vr = +2.0 V directly after switching BFO into one of the multiple LRSs with a positive writing bias of Vw ranging from +2.0 to +8.0 V (top edge of the rectangles, tw = 2 s) and 30 min later (bottom edge of the rectangles, tw = 30 min). Note that the reading current starts to increase for a writing voltage of ca. +3.0 V, i.e., the state of the BFO starts to change. All states in (B) are read with a pulsed reading bias amplitude of Vr = +2.0 V and length 100 ms. Because the reading current changes from Ir = 1.1E-2 μA in HRS with R = 1.8E8 Ω to Ir = 2 μA in LRS with R = 1E6 Ω, the power (P = R · I2) will change from 2.2E-8 W in HRS to 4.0E-6 W in LRS. The resolution of a pulsed power meter amounts to 0.01 dB. So theoretically more than 2000 power levels would be achievable, and we expect that at least 32/64 levels are possible in a power efficient manner.
A BFO memristor with multilevel resistive switching can be considered as an analog resistive switch and used as an artificial synapses. The retention of multilevel resistive switching is illustrated in Figure 2B. Positive writing pulses ranging from 2.0 to 8.0 V are applied to the BFO-based artificial synapse. As expected from the current-voltage characteristics (Figure 1B), the reading current at 2.0 V increases with increasing amplitude of the writing bias. After applying the positive writing pulses Vw (as switched, tw = 2 s), the reading current was largest and slightly decreased (30 mins, tw = 30 min) with increasing waiting time tw (Figure 2B). However, due to the degradation (Figure 2B) different LRSs will become indistinguishable. E.g., the reading current for a writing bias of Vw = 5.5 V and a waiting time of tw = 2 s is the same as the reading current for Vw = 6.0 V and tw = 30 min. We have already shown that the retention of BFO memristors can be significantly improved by an additional BFO surface modification using low energy Ar+ ion irradiation before depositing the Au top electrode (Shuai et al., 2011). Optimized parameters for the Ar+ irradiation process are discussed in Ref. (Ou et al., 2013). The Ar+ irradiation helps to homogenize the average crystallite size in the polycrystalline BFO memristors.
Pulse Sequence for Single Pairing Spike-timing Dependent Plasticity
In our previous work, we have used a bias amplitude of Vp = 2.3 V for STDP with 60–80 pairings of pre- and post-synaptic spikes (Mayr et al., 2012; Cederström et al., 2013). Especially, Mayr et al. illustrates how the pre- and post-synaptic waveforms of a specific biology-derived synaptic plasticity rule (Mayr and Partzsch, 2010) can be adjusted to operate the BFO memristors. The resulting waveforms are comparable to the waveforms proposed by Zamarreño-Ramos et al. (2011). In order to shorten the total pairing spike time, in this work we slightly increased the bias amplitude to Vp = 3.0 V and applied a single pre- and post-synaptic spike. In comparison to what is discussed in Mayr et al. (2012), the single spike pairing instead of multiple (60–80) pairings allows us to shorten the total spike time and to adjust the learning time constant of the STDP function from 25 ms to 125 μs. The detailed signal scheme of Memristor initialization, single pairing STDP, and memory consolidation for long-term potentiation (LTP) and long-term depression (LTD) are shown in Figure 3. In order to facilitate reproducing this signal scheme, the parameters used in every step in the pulse sequence are listed in Table 1. As illustrated in Figure 6A the signal scheme for resistive switching from HRS into a single LRS (Figure 6B) can be simplified and reduced to Memristor initialization for LTP and to Memory consolidation for LTD (Figure 6A). The step labeled Memristor initialization refers to the application of a writing pulse to set the BFO memristor in HRS and LRS. In the HRS the BFO memristor has both rectifying top and bottom electrodes whereas in the LRS the BFO memristor has a rectifying top electrode and a non-rectifying bottom electrode (You et al., 2014). For the pulse order leading to potentiation (Figure 3A), a single negative pulse, i.e., the HRS writing pulse, is applied to switch the memristive device into HRS. After the waiting time tw a single pre- and a single post-spike is applied to the top electrode of device. The pre- and post-spikes superimpose at the BFO memristor as potentiating spike, and the spike timing difference Δt determines the waveform of the potentiating spike (Δt = tp > 0 for the potentiating inputs). Each pre- and post-spike consists of one rectangular pulse with pulse amplitude Vp and one exponentially decaying pulse Vexp
with the decay time τ = τpre = τpost, where τpre and τpost are the exponential decay times of pre- and post-spikes, respectively. In order to reduce the influence of the exponential decay on the single pairing STDP function, we choose τ = 2.5 · tp. For the potentiating (depressing) spike order, the spike timing difference Δt between the pre- and post-spike is positive (negative) and lies in the range: tp = |Δt | = 10 · tp. In both pre- and post-spikes, the rectangular pulse is short compared to the decay time of the exponential waveform, and the amplitude of the overlapped spike pulses depends on the spike time difference Δt between both waveforms. After the measurement waiting time tw the synaptic weight of BFO-based artificial synapses has been checked by applying a reading bias of Vr = +2.0 V with a pulse width of tr = 100 ms. The reading current is defined as the potentiation current ILTP anddepression current ILTD after sourcing potentiating spike and depressing spike, respectively.
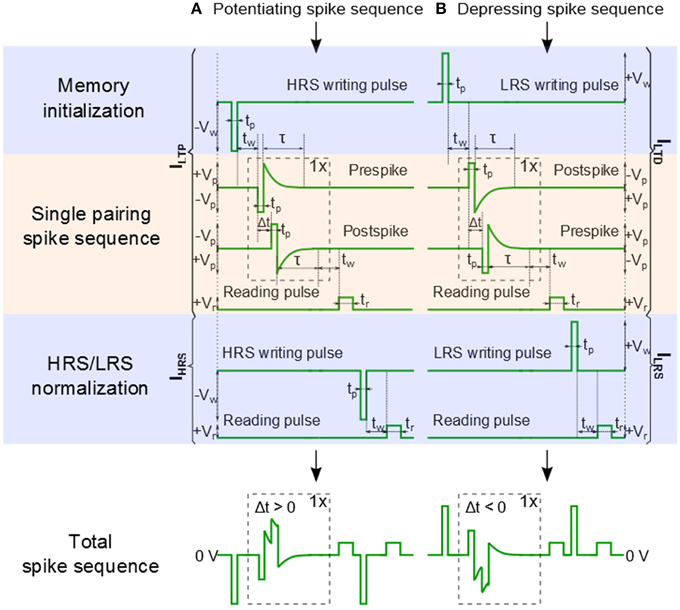
Figure 3. Signal scheme of Memristor initialization, Single pairing STDP, and Memory consolidation. (A) A pre-post spike order is used for long term potentiation (LTP). (B) A post-pre spike order is used for long term depression (LTD). The potentiation current ILTP (depression current ILTD)and the initial HRS current IHRS (and the initial LRS current ILRS) are used to normalize the long term potentiation current ΔILTP (the long term depression current ΔILTD) as defined in Equations (2) and (3). tp is the pulse width and tw is the measurement waiting time before applying the reading pulse Vr.

Table 1. Parameters for the potentiating spike sequence (Δt > 0) and for the depressing spike sequence (Δt < 0) during Memristor initialization, Memory consolidation, and Single pairing STDP.
Finally, the reading current IHRS (ILRS) of BFO in HRS (LRS) is measured at a reading bias of Vr = +2.0 V after recording ILTP (ILTD). For biological reasons it is desirable to keep STDP bounded. Therefore, we have normalized the LTP and LTD current values. After a potentiating spike sequence the synaptic weight scales with the normalized potentiation current ΔILTP
and after a depressing spike sequence the synaptic weight scales with the normalized depression current ΔILTD
After normalization using Equations (2) and (3) LTP lies in the range from 0 to +100% and LTD lies in the range from 0 to −100%, respectively. As we have shown in Mayr et al. (2012), the specific STDP characteristics can be configured through the waveform. Specifically, τpre directly translates to the STDP pre-post time window, while τpost translates to the post-pre time window. The Vp of the pre- and post-pulses translate to the respective scaling of the STDP amplitudes.
Results
In the following single pairing STDP in BFO-based artificial synapses (Section Nonvolatile, Analog Resistive Switching in BiFeO3) is demonstrated by using different pulse widths tp and measurement waiting times tw. The potentiating and depressing input signals (Section Pulse Sequence for Single Pairing Spike-timing Dependent Plasticity) have been generated with an Agilent pulse function arbitrary generator 81150A. The reading current has been measured with a Keithley 2400 source meter.
Learning Window
According to the input signal scheme (Figure 3) the BFO memristor is set in the HRS and in the LRS with a writing pulse amplitude of Vw = −8.0 and +8.0 V, respectively. For the single pairing STDP measurements on a BFO-based artificial synapse pre- and post-spikes of different pulse widths tp = 10 ms, 1 ms, 500 μs, and 50 μs, and with a pulse amplitude of |± Vp | = 3.0 V, and a waiting time tw 10 s have been chosen (Figure 4). The exponential decay time constant (τ = 2.5 · tp) amounts to τ = 25 ms (Figure 4A), 2.5 ms (Figure 4B), 1.25 ms (Figure 4C), and 125 μs (Figure 4D). After recording ILTP (ILTD) the reading current IHRS (ILRS) of BFO in HRS (LRS) has been measured at a reading bias of Vr = +2.0 V and the normalized potentiation current ΔILTP Equation (2) and the normalized depression current ΔILTD Equation (3) are calculated. The synaptic weight of the BFO memristor scales with the normalized potentiation current ΔILTP and the normalized depression current ΔILTD. If the prespike precedes the post-spike (Δt > 0) biological synapses (Bi and Poo, 1998) undergo long term potentiation LTP, i.e., the connection between two neurons becomes stronger. On the other hand, if the post-spike precedes the prespike (Δt < 0), biological synapses undergo long term depression LTD, i.e., the connection between two neurons becomes weaker. We have measured the LTD current ILTD and the LTP current ILTP in a BFO-based artificial synapse and can show that the BFO memristor emulates the STDP function of biological synapses. The normalized current ΔI decreases with increasing delay time |Δt|. The normalized current curve for positive and negative Δt is the LTP and LTD curve (Figure 4), respectively. As an example, in the following we discuss the LTP curve in Figure 4 for Δt = tp > 0. Initially the BFO-based artificial synapse is set into HRS. The maximum amplitude of the potentiating spike amounts to 2Vp = +6.0 V. For this potentiating spike the BFO-based artificial synapse is fully switched to LRS. The normalized potentiation current ΔILTP at Δt = tp amounts to ca. 100%. In the time delay range 0 < tp < Δt ≤ 10 · tp, the maximum amplitude of potentiating spikes is reduced from 6.0 to 3.2 V. Therefore, the exponential-like decay of the normalized current dominates STDP with increasing Δt and the synapse cannot be fully switched to LRS by applying these potentiating spikes. For both positive and negative time delays | Δt | = 10 · tp, ΔI decreases with decreasing pulse width tp. At tp = 500 μs and 50 μs, ΔILTP amounts to 0% at |Δt | = 10 · tp. It is also noticed that ΔILTP decreases more strongly than ΔILTD in the larger time delay range. That is because the threshold voltage for LRS is higher than the threshold voltage for HRS. For example in Ref. (Mayr et al., 2012) a voltage of 2.3 V and of 2.0 V has been used as the threshold voltage to switch a BFO-based artificial synapse to LRS and HRS, respectively. The shaded regions in Figure 4 show the ranges of the delay time Δt where the normalized current is larger than 50% for four different pulse widths tp. This range is also called learning window and decreases from 25 ms to 125 μs with decreasing pulse width tp from 10 ms to 50 μs.
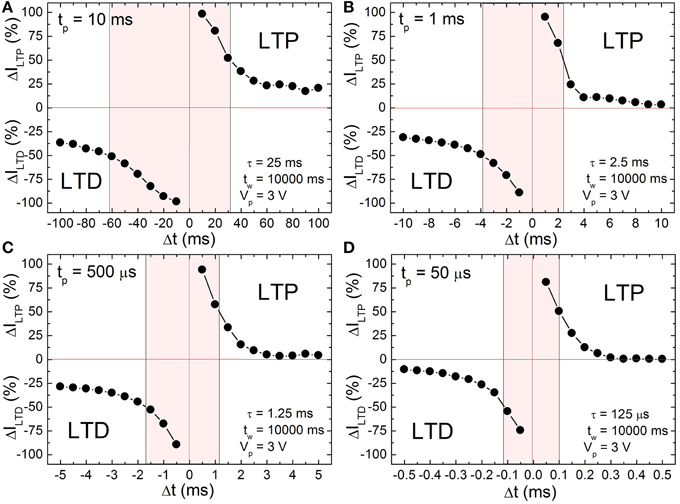
Figure 4. Long term depression current ΔILTD (negative range of y-axis) and long term potentiation current ΔILTP (positive range of y-axis) of a ca. 600 nm thick BFO memristor with a contact area of 4.5E4 μm2 for single pairing STDP with pulse width (A) tp = 10 ms, (B) tp = 1 ms, (C) tp = 500 μs and (D) tp = 50 μs, measurement waiting time tw = 10000 ms, pulse amplitude Vp = 3.0 V, reading pulse amplitude Vr = +2.0 V and reading pulse width tr = 100 ms. ΔILTD and ΔILTP have been normalized using Equations (2) and (3), respectively. The memristor was preset in HRS and LRS (Memristor initialization in Table 1) with a writing pulse amplitude of Vw = −8.0 V and Vw = +8.0 V, respectively.
As can be seen from Figure 4, the STDP time windows can be finely controlled. Specifically, making Δt longer results in a monotonous decrease in both potentiation and depression with increasing Δt, i.e., the memristance change directly and fine grainedly follows the applied waveform resulting from the overlay of pre- and post-pulse. This is in contrast to most other reported memristive synapses, where the time difference between pre- and post-pulse only translates to a stochastic, average change of memristance (Jo et al., 2010; Alibart et al., 2012).
Memory Consolidation
Memory consolidation has been investigated in models of biology in order to improve the understanding of the translation of an initially induced weight change to long term weight stabilization (Anokhin, 2005; Clopath et al., 2008). This motivated us to investigate the memristance weight, i.e., memory consolidation, in BFO-based artificial synapses in more details by performing single pairing STDP measurements with different waiting times tw (2 s = tw = 5 h). In biological systems, the waiting time corresponds to the time which elapses before something learned is retrieved. On the other hand, for the memory consolidation measurements, we have again used the ca. 600 nm thick BFO-based artificial synapses and applied a writing voltage of Vw = +6.0 V. In Figure 5A the corresponding STDP data are plotted for tw = 2, 60, and 300 s. We have chosen single pre- and post-synaptic spikes with the same absolute value of the pulse amplitude Vp = 3.0 V, pulse width tp = 10 ms and exponential decay time τ = 25 ms. As shown in Figure 5A, the LTP and LTD curves shift toward low normalized current values with increasing waiting time in both positive and negative spike timing ranges. Therefore, the dependence of LTP and LTD on the writing pulse amplitude can be used to trace differences in the LTP and LTD curves of single pairing STDP. For BFO-based artificial synapses with a smaller writing voltage Vw, the optimized STDP curve with more significant exponential-like function (as shown in Figure 4) is reproducible by choosing a smaller pulse amplitude Vp, e.g., Vp = 2.5 V.
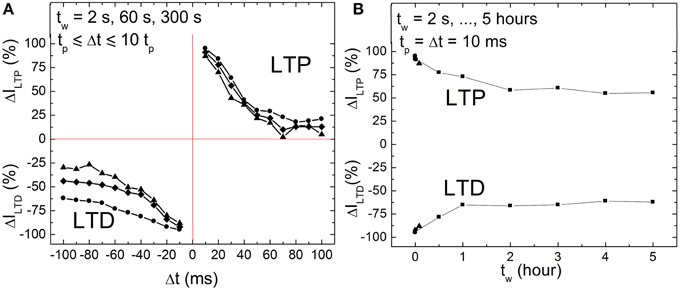
Figure 5. (A) STDP of a BFO-based artificial synapses with different waiting times tw = 2 s (circles), 1 min (quadrangles), and 5 min (triangles) for tp = Δt = 10 tp. Pulse amplitude Vp = 3.0 V, pulse width tp = 10 ms, and exponential decay time τ = 25 ms. (B) Memristance weight consolidation for a fixed Δt = tp = 10 ms and for a waiting time of tw = 2 s (circles), 60 s (quadrangles), and 300 s (triangles) from (A) and tw = 0.5, 1, 2, 3, 4, 5 h (squares). The pulse amplitude Vp amounts to 3.0 V. The exponential decay amounts to τ = 25 ms. The writing voltage for Memristor initialization amounts to |± VW | = 6.0 V.
Furthermore, memory consolidation measurements (Figure 5B) reveal that for a waiting time tw shorter than 1 h there is a visible change of reading current (degradation) both in positive and negative spike timing ranges after applying a single pre-synaptic and post-synaptic pulse sequence, whereas for a waiting time tw longer than 2 h the current is stabilized. This is in agreement with the results from retention measurements (Figure 2A).
Energy Consumption
Low energy efficiency, large chip size, and complex STDP synapse circuits are major bottlenecks of today's bio-inspired systems, e.g., neural networks where synapses typically outnumber neurons by more than 500:1. In order to reliably observe STDP functionality the corresponding current changes should lie in the nA current range and above. In addition to the stabilization of multilevel resistive switching, we can also increase the current level in a controlled manner by low-energy Ar+ ion irradiation (Ou et al., 2013). This will allow for integrating BFO-based artificial synapses with smaller contact area A (Table 2), e.g., in neural networks, without adding another device for amplifying current changes. The estimated energy consumption of each synapse in human brain amounts to only 1–10 fJ (Table 2). In order to approach the high energy efficiency of biological synapses, we applied single pairing (not 60–80 pairing) STDP pulses to BFO-based artificial synapses. For single pairing STDP most of the energy is consumed during SET operation, e.g., Memristor initialization into LRS (Table 1, Figure 3). For example, in TiN/Ge2Sb2Te5/TiN/W artificial synapses the energy for SET operation is 50 pJ while the energy for RESET operation is 0.675 pJ Ref. (Kuzum et al., 2012).
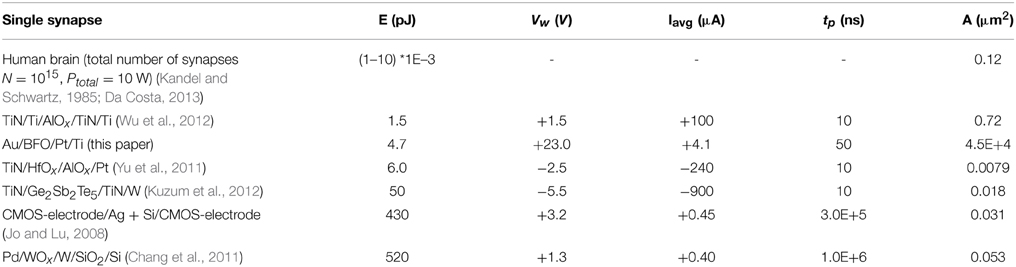
Table 2. Energy consumption E, setting potential amplitude Vw, average setting current Iavg, pulse width tp and top electrode area size A of resistive switching during SET operation of different memristor-based artificial synapses (Kandel and Schwartz, 1985; Jo et al., 2010; Chang et al., 2011; Yu et al., 2011; Kuzum et al., 2012; Wu et al., 2012).
The energy consumed during SET operation is
with Iavg = Ipeak/2. The writing voltage amplitude Vw, the setting current Ipeak, and writing pulse width tp are the crucial parameters for evaluating the energy consumption. Note that for the polycrystalline BFO memristors with different sizes of BFO crystallites, larger BFO crystallites below the top electrode are possibly not switchable. Therefore, the effective area of the top electrode might be smaller than the nominal area of the top electrode. Using BFO-based artificial synapses we can downscale the size of the top electrodes (Jin et al., 2014), increase the pulse amplitude V′w and also reduce the pulse width t′p Equation (4) to further decrease the energy consumption per setting process (Figure 6).
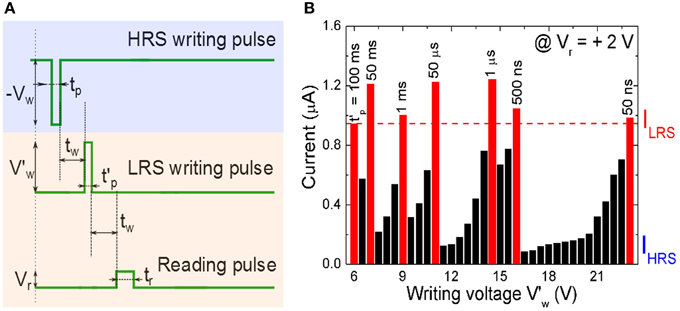
Figure 6. (A) Signal scheme for resistive switching a BFO memristor in HRS into LRS. The memristor is initialized into the HRS by applying a writing voltage Vw = −6.0 V with a pulse width tp = 100 ms, and is then switched back to different LRSs with different pulse amplitudes V′w and pulse widths t′p. (B) Reading current of the BFO memristor with a contact area of 4.5E4 μm2 in LRS in dependence on the writing voltage V′w in the range from 6.0 to 23.0 V and with different constant pulse widths of t′p = 50 ms, 1 ms, 50 μs, 1 μs, 500 ns, and 50 ns. The reading voltage amounts to +2.0 V. For a given pulse width at least one writing voltage (red bar) is large enough to set the BFO memristor in the LRS. In that case the reading currents is even larger than the current ILRS read out after applying a writing voltage of Vw = +6.0 V with a pulse width of t′p = 100 ms (first red bar).
In order to optimize the energy efficiency of BFO-based artificial synapses, we have applied a large writing pulse amplitude of 23.0 V to compensate the short pulse width of 50 ns. The corresponding energy consumption amounts to 4.7 pJ. The LRS reading current and HRS reading current at 2.0 V amount to 980 and 64 nA, respectively. The theoretical maximum normalized current ranges from 93.5 to 0% and from 0 to 93.5% in both curves Equation (2) and (3).
In Table 2 (Kandel and Schwartz, 1985; Jo et al., 2010; Chang et al., 2011; Yu et al., 2011; Kuzum et al., 2012; Wu et al., 2012) different memristor-based artificial synapses are listed and compared with respect to their energy consumption per (re)setting process. The TiN/Ti/AlOx/TiN/Ti memristor (Wu et al., 2012) shows the smallest energy consumption of 1.5 pJ per SET pulse. It is expected that to a certain extent the energy consumption can be further reduced by further reducing the electrode area size A. However, one has to consider that BFO is a polycrystalline thin film and that only 1–0.1% of the crystallites below the top electrode of the polycrystalline BFO are switched in single pairing STDP.
Discussion
Configurability
In this work single pairing STDP in BFO-based artificial synapses has been demonstrated for emulating the functionality and the plasticity of biological synapses. The waveform-defined plasticity of BFO memristors in addition to their multilevel memristive programming capability enables easy control of the STDP time windows, as evidenced by the three orders of magnitude timescale configurability shown in this paper. While there has been a lot of simulation work on this topic, the number of devices where STDP or variations have actually been implemented and measured is still fairly small (Jo et al., 2010; Alibart et al., 2012). Among those, our highly-configurable, finely grained learning curves are unique, other implementations exhibit statistical variations (Jo et al., 2010), can only assume a few discrete levels (Alibart et al., 2012) or the learning windows are device-inherent, i.e., cannot be adjusted (Ohno et al., 2011). We expect that for BFO-based artificial synapses at least 32/64 levels are possible in a power efficient manner. In addition, the wide range of timescales possible in BFO-based synapses enables e.g., a timebase-tunable system that could learn a classification offline in an accelerated manner, while still able to interact with real-time sensors before or after this learning.
As mentioned in the introduction, BFO-based artificial synapses can be used for conventional STDP experiments, where only multiple spike pairings exhibit significant weight change, as well as in the mode used in this paper, where a single pairing already induces a significant weight change. By changing the voltage of the pre- and post-synaptic pulses, any point in between these two extremes can also be chosen, again showing the excellent configurability of BFO-based artificial synapses. However, the versatility of BFO memristors comes at the price that in contrast to e.g., phase-change materials, BFO is not easily integrated on top of CMOS (Shuai et al., 2013).
Energy Consumption
In Table 2, we have shown an energy consumption of E = 4.7 pJ in a BFO-based artificial synapse with electrode size of 4.52E4 μm2. While this is still three orders of magnitude above the energy consumption of biological synapses, it is one of the lowest reported so far for other artificial synapses. Compared to neuromorphic approaches, all memristive approaches are several orders of magnitude better (Azghadi et al., 2014). In terms of absolute area, the BFO memristor is comparable to some neuromorphic implementations (Hasler and Marr, 2013; Noack et al., 2015), but not competitive with memristor crossbar devices, as we are employing a single device test structure that has a large contact size for reasons of convenience. However, BFO device scaling is well established, thus we can aggressively scale the size of the top electrode to 10 μm2 and the thickness of the BFO to 100 nm (Jin et al., 2014). For BFO with larger electrode area size, the current scales linearly with area size. For smaller electrode area size we would expect that the current scales with the number of BFO crystallites below the electrode. And in the limit case of nanoscale electrodes, the smallest possible current should be the current through single BFO crystallites.
Retention of Weight Change
We have investigated the retention of memristance weight change across time. As Figure 5A shows, the basic shape of the STDP curves is preserved across time. Figure 5B illustrates that even after memory consolidation, we retain a graded weight, i.e., a unimodal weight distribution. Our synapse does not collapse in either a potentiated or depressed (bimodal) distribution as predicted in some synaptic models (Fusi et al., 2000; Clopath et al., 2008). In memristive literature, there is usually no investigation of these phenomena, the weight change is taken at some unspecified time after induction and then assumed to be non-volatile. Only very few articles have investigated the actual non-volatility/weight retention across time and shown that the assumption of a non-volatile change is not necessarily valid (Chang et al., 2011). Thus, compared to other reports, this article gives a neuromorphic designer a clear guide on how to utilize the memristive synapses for long-term storage.
Interestingly, this investigation of memory consolidation is also somewhat missing in the original biological measurements. Usually, data on the weight evolution ca. 30–60 min after induction is provided, but only on single example pairing experiments. These data points show various behaviors, from unchanged weights after initial weight induction (Froemke and Dan, 2002) to increases of weight change across time (Bi and Poo, 1998), decreases across time (Markram et al., 1997) or slow oscillations around the initial potentiated/depressed weight value (Sjöström et al., 2001). However, it is unclear how the overall STDP window consolidates over time. Thus, measuring the evolution of an STDP curve across time after induction at biological synapses similar to our investigation on memristive synapses may actually be a quite interesting scientific question.
Summary and Outlook
In this work we have investigated a wide range of timescale configurability, ranging from 25 ms to 125 μs. Also, we have investigated power consumption figures and have shown that it is possible to decrease the switching pulse width and to reduce the power consumption during a single STDP writing process on BFO-based artificial synapses to only 4.5 pJ. Furthermore, the increased programming voltage also shortens the total pairing spike time, and enables to move from the standard biology-like 60–80 spike pairing STDP experiment to a single pairing STDP experiment with the same weight/memristance change.
One important advantage of single STDP in comparison to 60–80 spike STDP is that both pre- and post-synaptic waveform are causal, i.e., they start only at the pre- respectively post-synaptic pulse. This is in contrast to most currently proposed waveforms for memristive learning, where the waveforms have to start well in advance of the actual pulse (Zamarreño-Ramos et al., 2011), which requires pre-knowledge of a pulse occurrence. Especially, in an unsupervised learning context with self-driven neuron spiking, this pre-knowledge is simply not existent.
In a wider neuroscience context, waveform defined plasticity as shown here could be seen as a general computational principle, i.e., synapses are not likely to measure time differences as in native forms of STDP rules, they are more likely to react to local static (Ngezahayo et al., 2000) and dynamic (Dudek and Bear, 1992) state variables. In the future some interesting predictions could be derived from that, e.g., STDP time constants that are linked to synaptic conductance changes or to the membrane time constant (Pfister et al., 2006; Mayr and Partzsch, 2010). These predictions could be easily verified experimentally.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
ND acknowledges funding by BMWi-ZIM (VP2999601ZG2). CM acknowledges funding by the European Union Seventh Framework Programme (FP7/2007- 2013) under grant agreement no. 269459 (CORONET) and no. 612058 (RAMP). HS and DB are grateful for financial support from the Deutsche Forschungsgemeinschaft (SCHM 1663/4-1,2, BU 2956/1-1) and the Networking Fund of the Helmholtz Association (VH-VI-422).
References
Adee, D. (2009). IBM Unveils a New Brain Simulator. IEEE Spectr. Available online at: http://spectrum.ieee.org/computing/hardware/ibm-unveils-a-new-brain-simulator
Alibart, F., Pleutin, S., Bichler, O., Gamrat, C., Serrano-Gotarredona, T., Linares-Barranco, B., et al. (2012). A memristive nanoparticle/organic hybrid synapstor for neuroinspired computing. Adv. Funct. Mater. 22, 609–616. doi: 10.1002/adfm.201101935
Ananthanarayanan, R., Esser, S. K., Simon, H. D., and Modha, D. S. (2009). “The cat is out of the bag: cortical simulations with 109 neurons and 1013 synapses,” in Proceedings IEEE/ACM Conference High Performance Networking Computing (Portland, OR: IEEE), 1–12. doi: 10.1145/1654059.1654124
Anokhin, K. V. (2005). “Memory consolidation: narrowing the gap between systems and molecular genetics neurosciences,” in Complex Brain Functions: Conceptual Advances in Russian Neuroscience, eds R. Miller, A. M. Ivanitsky, and P. M. Balaban (Amsterdam, FL: CRC Press), 51–71.
Azghadi, M. R., Iannella, N., Al-Sarawi, S., Indiveri, G., and Abbott, D. (2014), Spike-based synaptic plasticity in silicon: design, implementation, application, and challenges. Proc. IEEE, 102, 717–737. doi: 10.1109/JPROC.2014.2314454
Bi, G. Q., and Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.
Borghetti, J., Li, Z., Straznicky, J., Li, X., Ohlberg, D. A. A., Wu, W., et al. (2009). A hybrid nanomemristor/transistor logic circuit capable of self-programming. Proc. Nat. Acad. Sci. U.S.A. 106, 1699–1703. doi: 10.1073/pnas.0806642106
Cederström, L., Starke, P., Mayr, C., Shuai, Y., Schmidt, H., and Schüffny, R. (2013). “A model based comparison of BiFeO3 device applicability in neuromorphic hardware,” in 2013 IEEE International Symposium on Circuits and Systems (ISCAS) (Beijing: IEEE), 2323–2326. doi: 10.1109/ISCAS.2013.6572343
Chang, T., Jo, S. H., and Lu, W. (2011). Short-term memory to long-term memory transition in a nanoscale memristor. ACS Nano 5, 7669–7676. doi: 10.1021/nn202983n
Chua, L. O. (1971). Memristor – The missing circuit element. IEEE Transact. Circuit Theory 18, 507–519.
Clopath, C., Ziegler, L., Vasilaki, E., Büsing, L., and Gerstner, W. (2008). Tag-trigger-consolidation: a model of early and late long-term-potentiation and depression. PLoS Comput. Biol. 4:e1000248. doi: 10.1371/journal.pcbi.1000248
Da Costa, N. M. (2013). Diversity of thalamorecipient spine morphology in cat visual cortex and its implication for synaptic plasticity. J. Comp. Neurol. 521, 2058–2066. doi: 10.1002/cne.23272
Di Lorenzo, P. M., and Victor, J. D. (2013). Spike Timing: Mechanisms and Functions, Front. Neurosci. Boca Raton, FL: CRC Press.
Du, N., Shuai, Y., Luo, W. B., Mayr, C., Schüffny, R., Schmidt, O. G., et al. (2013). Practical guide for validated memristance measurements. Rev. Sci. Instrum. 84:023903. doi: 10.1063/1.4775718
Dudek, S., and Bear, M. (1992). Homosynaptic long-term depression in area CAl of hippocampus and effects of N-methyl-D-aspartate receptor blockade. Proc. Natl. Acad. Sci. U.S.A. 89, 4363–4367. doi: 10.1073/pnas.89.10.4363
Froemke, R. C., and Dan, Y. (2002). Spike-timing-dependent synaptic modification induced by natural spike trains. Nature 416, 433–438. doi: 10.1038/416433a
Fusi, S., Annunziato, M., Badoni, D., Salamon, A., and Amit, D. J. (2000). Spike-driven synaptic plasticity: theory, simulation, VLSI implementation. Neural Comput. 12, 2227–2258. doi: 10.1162/089976600300014917
Hasler, J., and Marr, B. (2013). Finding a roadmap to achieve large neuromorphic 593 hardware systems, Front. Neurosci. 7:118. doi: 10.3389/fnins.2013.00118
Indiveri, G., Chicca, E., and Douglas, R. (2006). A VLSI array of low power spiking neurons and bistable synapses with spike-timing dependent plasticity. IEEE Trans. Neural. Netw. 17, 211–221. doi: 10.1109/TNN.2005.860850
Jin, L., Shuai, Y., Ou, X., Siles, P. F., Zeng, H. Z., You, T., et al. (2014). Resistive switching in unstructured, polycrystalline BiFeO3 thin films with downscaled electrodes. Phys. Status Solidi. A 211, 2563–2568. doi: 10.1002/pssa.201431298
Jo, S. H., Chang, T., Ebong, I., Bhadviya, B. B., Mazumder, P., and Lu, W. (2010). Nanoscale memristor device as synapse in neuromorphic systems. Nano. Lett. 10, 1297–1301. doi: 10.1021/nl904092h
Jo, S. H., and Lu, W. (2008). CMOS compatible nanoscale nonvolatile resistance switching memory. Nano Lett. 8, 392–397. doi: 10.1021/nl073225h
Kandel, E. R., and Schwartz, J. H. (1985). Principles of Neural Science, 2nd Edn. New York; Amsterdam; Oxford: Elsevier.
Kuzum, D., Jeyasingh, R. G. D., Lee, B., and Wong, H.-S. P. (2012). Nanoelectronic programmable synapses based on phase change materials for brain-inspired computing. Nano Lett. 12, 2179–2186. doi: 10.1021/nl201040y
Koickal, T. J., Hamilton, A., Pearce, T. C., Tan, S. L., Covington, J. A., and Gardner, J. W. (2006). “Analog VLSI design of an adaptive neuromorphic chip for olfactory systems,” in Proceedings: IEEE International Symposium on: Circuits and Systems 2006. ISCAS 2006 (New York, NY: IEEE). doi: 10.1109/TCSI.2006.888677
Lai, Q., Zhang, L., Li, Z., Stickle, W. F., Williams, R. S., and Chen, Y. (2009). Analog memory capacitor based on field-configurable ion-doped polymers. Appl. Phys. Lett. 95, 213503. doi: 10.1063/1.3268433
Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215. doi: 10.1126/science.275.5297.213
Mayr, C., Stärke, P., Partzsch, J., Cederstroem, L., Schüffny, R., Shuai, Y., et al. (2012). Waveform driven plasticity in BiFeO3 memristive devices: model and implementation. Adv. Neural Inf. Process. Syst. 25, 1700–1708. Available online at: http://papers.nips.cc/paper/4595-waveform-driven-plasticity-in-bifeo3-memristive-devices-model-and-implementation.pdf
Mayr, C. G., and Partzsch, J. (2010). Rate and pulse based plasticity governed by local synaptic state variables. Front. Synaptic. Neurosci. 2:33. doi: 10.3389/fnsyn.2010.00033
Mayr, C., Partzsch, J., Noack, M., and Schüffny, R. (2013), “Live demonstration: multiple-timescale plasticity in a neuromorphic system,” in IEEE International Symposium on Circuits and Systems ISCAS 2013 (Beijing: IEEE), 666–670. doi: 10.1109/ISCAS.2013.6571933
Ngezahayo, A., Schachner, M., and Artola, A. (2000). Synaptic activity modulates the induction of bidirectional synaptic changes in adult mouse hippocampus. J. Neurosci. 20, 2451–2458. Available online at: http://www.jneurosci.org/content/20/7/2451.abstract
Noack, M., Partzsch, J., Mayr, C., Hänzsche, S., Scholze, S., Höppner, S., et al. (2015). Switched-capacitor realization of presynaptic short-term plasticity and stop-learning synapses in 28 nm CMOS. Front. Neurosci. 9:10. doi: 10.3389/fnins.2015.00010
Ohno, T., Hasegawa, T., Tsuruoka, T., Terabe, K., Gimzewski, J., and Aono, M. (2011), Short-term plasticity and long-term potentiation mimicked in single inorganic synapses. Nat. Mater. 10, 591–595. doi: 10.1038/nmat3054
Ou, X., Shuai, Y., Luo, W., Siles, P. S., Kögler, R., Fiedler, J., et al. (2013). Forming-free resistive switching in multiferroic BiFeO3 thin films with enhanced nanoscale shunts. ACS Appl. Mater. Interfaces 5, 12764–12771. doi: 10.1021/am404144c
Pfister, J.-P., Toyoizumi, T., Barber, D., and Gerstner, W. (2006). Optimal spike-timing dependent plasticity for precise action potential firing in supervised learning. Neural Comput. 18, 1309–1339. doi: 10.1162/neco.2006.18.6.1318
Schemmel, J., Grübl, A., Hartmann, S., Kononov, A., Mayr, C., Meier, K., et al. (2012). “Live demonstration: a scaled-down version of the BrainScaleS wafer-scale neuromorphic system,” in IEEE International Symposium on Circuits and Systems ISCAS 2012 (Seoul: IEEE), 702. doi: 10.1109/ISCAS.2012.6272131
Seo, K., Kim, I., Jung, S., Jo, M., Park, S., Park, J., et al. (2011). Analog memory and spike-timing-dependent plasticity characteristics of a nanoscale titanium oxide bilayer resistive switching device. Nanotechnology 22:254023. doi: 10.1088/0957-4484/22/25/254023
Shuai, Y., Ou, X., Luo, W. B., Du, N., Wu, C., Zhang, W., et al. (2013). Nonvolatile multilevel resistive switching in Ar+ irradiated BiFeO3 thin films. IEEE Electron Device Lett. 34, 54–56. doi: 10.1109/LED.2012.2227666
Shuai, Y., Zhou, S. Q., Bürger, D., Helm, M., and Schmidt, H. (2011). Nonvolatile bipolar resistive switching in Au/BiFeO3/Pt. J. Appl. Phys. 109, 124117. doi: 10.1063/1.3601113
Sjöström, P. J., Turrigiano, G. G., and Nelson, S. B. (2001). Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164. doi: 10.1016/S0896-6273(01)00542-6
Smerieri, A., Berzina, T., Erokhin, V., and Fontana, M. P. (2008). Polymeric electrochemical element for adaptive networks: pulse mode. J. Appl. Phys. 104, 114513. doi: 10.1063/1.3033399
Snider, G. S. (2008). “Spike-timing-dependent learning in memristive nanodevices,” in Proceedings IEEE International Symposium Nanoscale Architechtures (Anaheim, CA: IEEE), 85–92. doi: 10.1109/NANOARCH.2008.4585796
Thomas, A., and Kaltschmidt, C. (2014). Elektronische Nervenzellen. Phys. Unserer. Zeit. 45, 21–25. doi: 10.1002/piuz.201301344
Wu, Y., Yu, S., Wong, H.-S. P., Chen, Y. S., Lee, H.-Y., Wang, S.-M., et al. (2012). “AlOx-based resistive switching device with gradual resistance modulation for neuromorphic device application,” in Memory Workshop (IMW), 2012 4th IEEE International (Milan: IEEE), 1–4. doi: 10.1109/IMW.2012.6213663
You, T., Du, N., Slesazeck, S., Mikolajick, T., Li, G., Bürger, D., et al. (2014). Bipolar electric-field enhanced trapping and detrapping of mobile donors in BiFeO3 memristors. ACS Appl. Mater. Interfaces 6, 19758–19765. doi: 10.1021/am504871g
Yu, S., Wu, Y., Jeyasingh, R., Kuzum, D., and Wong, H.-S. P. (2011). An electronic synapse device based on metal oxide resistive switching memory for neuromorphic computation. IEEE Trans. Electron Devices 58, 2729–2737. doi: 10.1109/TED.2011.2147791
Keywords: BiFeO3 memristor, artificial synapse, single pairing STDP, memory consolidation, learning window, low-power device
Citation: Du N, Kiani M, Mayr CG, You T, Bürger D, Skorupa I, Schmidt OG and Schmidt H (2015) Single pairing spike-timing dependent plasticity in BiFeO3 memristors with a time window of 25 ms to 125 μs Front. Neurosci. 9:227. doi: 10.3389/fnins.2015.00227
Received: 19 February 2015; Accepted: 11 June 2015;
Published: 30 June 2015.
Edited by:
Themis Prodromakis, University of Southampton, UKReviewed by:
Siddharth Joshi, University of California, San Diego, USAJoaquin Sitte, Queensland University of Technology, Australia
Copyright © 2015 Du, Kiani, Mayr, You, Bürger, Skorupa, Schmidt and Schmidt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nan Du, Material Systems for Nanoelectronics, Faculty of Electrical and Information Engineering, Chemnitz University of Technology, Reichenhainer Str. 39/41, 09126 Chemnitz, Germany,bmFuLmR1QHMyMDEyLnR1LWNoZW1uaXR6LmRl;
Christian G. Mayr, Neuromorphic Cognitive Systems Group, Institute of Neuroinformatics, University of Zurich and ETH Zurich, Winterthurerstr. 190, CH-8057 Zurich, Switzerland,Y2hyaXN0aWFuLm1heXJAdHUtZHJlc2Rlbi5kZQ==;
Heidemarie Schmidt, Material Systems for Nanoelectronics, Faculty of Electrical and Information Engineering, Chemnitz University of Technology, Reichenhainer Str. 39/41, 09126 Chemnitz, Germany,aGVpZGVtYXJpZS5zY2htaWR0QGV0aXQudHUtY2hlbW5pdHouZGU=
 Nan Du
Nan Du Mahdi Kiani
Mahdi Kiani Christian G. Mayr
Christian G. Mayr Tiangui You
Tiangui You Danilo Bürger1
Danilo Bürger1 Heidemarie Schmidt
Heidemarie Schmidt